Что такое t1 и t2 в физике?
Что такое t1 и t2 в физике?
Начальную температуру тела обозначим t1, конечную температуру t2. Опыт показывает, что количество теплоты, полученное телом, прямо пропорционально массе тела m и разности конечной и начальной температур: Q = cm(t2 – t1). Коэффициент пропорциональности c называется удельной теплоёмкостью вещества тела.
Как называется формула Q CM t2 t1?
Q=cm( ) – формула для расчета количества теплоты, выделенной при изменении температуры тела с t1 на t2. Здесь C – удельная теплоемкость тела – данные о удельной теплоемкости тела можно найти в таблице удельных теплоемкостей, а m – масса тела.
Как найти затраченное количество теплоты?
Количество теплоты, затраченной на обогрев тела или выделившейся при его охлаждении равно произведению удельной теплоёмкости вещества, массы тела и разницы конечной и начальной температур.
Как рассчитать количество теплоты в проводнике?
1) количество теплоты (Дж), выделенное проводником при прохождении по нему электрического тока, пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока и вычисляется по закону Джоуля -Ленца : Q = I² Rt , где I -сила тока, А , R- сопротивления проводника, Ом, t -время, с. /span>
/span>
Чему эквивалентно количество выделяемой теплоты при прохождении электрического тока по проводнику?
Мощность тока равна отношению работы тока ко времени прохождения тока. Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока.
Как найти силу тока через количество теплоты?
Если обозначить количество теплоты, создаваемое током, буквой Q (Дж), ток, протекающий по проводнику – I, сопротивление проводника – R и время, в течение которого ток протекал по проводнику – t, то закону Ленца – Джоуля можно придать следующее выражение: Q = I2Rt. Так как I = U/R и R = U/I, то Q = (U2/R) t = UIt.
Как рассчитать мощность электрического тока?
Р = I*U=U2/R (3) Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды.
Как рассчитать мощность если известно напряжение и сила тока?
Таким образом: Мощность электрического тока равна произведению напряжения на силу тока: P = U ⋅ I . Из этой формулы можно определить и другие физические величины.
Из этой формулы можно определить и другие физические величины.
Как узнать мощность по напряжению и силе тока?
Формула расчета мощности электрического тока Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U./span>
Как посчитать мощность в трехфазной сети?
Мощность трехфазного тока равна тройной мощности одной фазы. При соединении в звезду PY=3·Uф·Iф·cosфи =3·Uф·I·cosфи. При соединении в треугольник P=3·Uф·Iф·cosфи=3·U·Iф·cosфи.
Какая сила тока в сети 220?
Чаще всего, современные домашние розетки 220В рассчитаны на максимальный ток 10 или 16 Ампер. Некоторые производители заявляют, что их розетки выдерживают и 25 Ампер, но таких моделей крайне мало. Старые, советские розетки, которые еще встречаются в наших квартирах, вообще рассчитаны всего на 6 Ампер.
Как узнать потребляемую силу тока?
Определите мощность источника питания.
- Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. …
- Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт. …
- Вот почему внесистемной единицей измерения мощности является вольт-ампер.
Как определить мощность ламп?
Расчет мощности производится по простой формуле P = U x I. Напряжение питания умножаем на силу тока в амперах./span>
Как рассчитать мощность усилителя?
Первый способ: Замеряем максимальное напряжение на выходе усиителя к примеру оно 23вольта. Дальше делим его на сопротивление нагрузки например 4.
Как рассчитать сколько ватт?
Итак, чтобы получить ватты, нужно указанные амперы умножить на вольты: P = I*U – ток умножить на напряжение (в розетке у нас примерно 220-230 вольт). Это главная формула для нахождения мощности в однофазных электрических цепях. Или случай, когда мощность в ваттах нужно перевести в амперы.
Или случай, когда мощность в ваттах нужно перевести в амперы.
Сколько ватт в ампер?
А значит, если имеем дело с автомобильной сетью на 12 вольт, то 1 ампер — это 12 Ватт, а в бытовой электросети 220 V такая сила тока будет в электроприборе мощностью 220 Вт (0,22 кВт). В промышленном оборудовании, питающемся от 380 Вольт, целых 657 Ватт.
Какое сечение провода для 2 квт?
По таблице получается, что нужен провод сечением 1,0 мм2, с учетом вышеизложенного 1,0 / 1,75 = 0,5 мм2. Следовательно, для подключения электродвигателя мощностью 2,0 кВт к трехфазной сети 380 В понадобится медный трехжильный кабель с сечением каждой жилы 0,5 мм2.
как найти модуль, от чего зависит, формула расчета, в чем измеряется
Содержание:
- Сила натяжения нити — основные понятия, обозначение, единица измерения
-
Как определить для разных условий, формулы для расчета
- Определение силы натяжения на одной нити
- Нахождение силы натяжения на нескольких нитях
- Примеры решения задач
Содержание
- Сила натяжения нити — основные понятия, обозначение, единица измерения
-
Как определить для разных условий, формулы для расчета
- Определение силы натяжения на одной нити
- Нахождение силы натяжения на нескольких нитях
- Примеры решения задач
Сила натяжения нити — основные понятия, обозначение, единица измерения
Сила натяжения — сила, которую прикладывают к концам объекта, она создает внутри объекта упругую деформацию.
Длина тела, к которому прилагают силу, обычно во много раз больше, чем толщина этого тела. Такими телами могут быть обыденные вещи — канат, веревка, трос, проволока, леска и т. д.
Приведем примеры силы натяжения нити в быту:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- применение отвеса для строительства;
- установка растяжек для того, чтобы зафиксировать радиоантенны;
- характер арматуры внутри напряженного бетона;
- устройство такелажа корабля.
Фото такелажа:
Источник: rusgvozdi.ru
Сила натяжения нити является суммой сил, которые действуют на нить, а также противоположна по своему направлению.
F=-F
Здесь F — сила натяжения. Также встречаются обозначения силы натяжения нити с помощью букв «T» и «N». За единицу измерения у силы натяжения нити принимают Ньютон (сокращенно — H).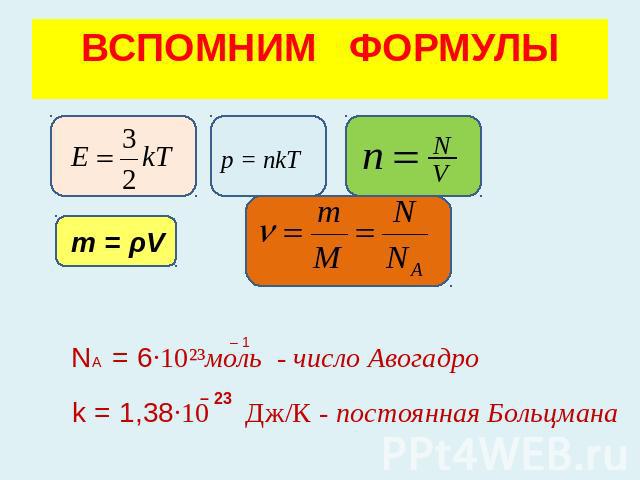
Как определить для разных условий, формулы для расчета
Существует множество разных вариантов определения силы напряжения нити. Рассмотрим некоторые из них.
Определение силы натяжения на одной нити
Определение силы натяжения на одной нити происходит в несколько этапов.
Первый этап — нужно определить силы на обоих концах нити. Сила натяжения этой нити или веревки считается результатом сил, которые натягивают веревку с каждого из концов.
Напомним, что сила будет равна произведению массы m на ускорение a.
Предположим, что веревка туго натянута. Каждое изменение массы или ускорения объекта, который подвешен на веревке, приведет к тому, что силы на самой веревке изменятся. Не стоит забывать также о постоянном ускорении силы тяжести. Учитывать его нужно даже тогда, когда система остается в покое, а составляющие системы являются объектами воздействия силы тяжести.
Формула 1
Можно сделать предположение, что сила натяжение этой веревки будет рассчитываться по следующей формуле: \(T=(m\times{g})+(m\times{a})\). В данной формуле \(g\) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.
В данной формуле \(g\) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.
Примечание 1
Для решения большей части физических задач предполагается, что веревка идеальна. То есть, она идеально тонкая, у нее нет массы, она не способна рваться и растягиваться.
Пример 1
Рассмотрим пример, в котором груз подвешивается к деревянной балке при помощи одной веревки. Ни веревка, и груз не передвигаются — система в абсолютном покое. Чтобы груз находился в полном равновесии, сила натяжения обязана равняться силе тяжести: \(F_{т}=F_{g}=m\times{g}\). Если у груза масса 10 кг, то сила натяжения будет равна \(98 Н (10\times9,8)\).
Второй этап — нужно учитывать ускорение. Сила тяжести является не единственной силой, которая может повлиять на силу натяжения нити. Ровно такое же действие совершает каждая сила, которую прикладывают к объекту на нити с ускорением.
В этой формуле m является массой, v — скоростью, r — радиусом окружности, по которой происходит движение груза.
Так как значение и направление центробежной силы изменяются в зависимости от того, как тело передвигается и изменяет собственную скорость, полное натяжение нити становится параллельным нити в центральной точке.
Важно запомнить, что сила притяжения всегда воздействует на тело, тянет его вниз. Если объект совершает амплитудное действие вертикально, полное натяжение сильнее всего будет в нижней точке дуги (точка равновесия для маятника) — когда тело достигает самой большой скорости, а слабее всего — в верхней точке дуги, когда тело начинает замедляться.
Пример 3
Приведем пример: объект не ускоряется вверх, а раскачивается как маятник. Допустим, что нить будет иметь длину 1,5 м, а груз передвигается со скоростью 2 м/с (в случае прохождения через нижнюю точку размаха). {2}}{1,5}\)
{2}}{1,5}\)
\(F=10\times2,67=26,7 Н.\)
Так полное натяжение нити будет \(98+26,7=124,7 Н.\)
Еще одна формула — сила натяжения способна изменяться по мере того, как проходит груз по дуге. Величина и направление центробежной силы изменяются по мере того, как тело качается. Даже если сила тяжести постоянная, результирующая сила натяжения изменяется. В тот момент, когда качающееся тело располагается не в нижней точке дуги, сила тяжести тащит тело вниз, однако сила натяжения тянет тело вверх под углом. По данной причине сила натяжения обязана находиться в противодействии лишь части силы тяжести, а не всей.
Деление силы гравитации на два вектора может помочь визуально показать данное состояние. В каждой точке дуги объекта, который раскачивается вертикально, нить создает угол \(\ominus\) с линией, проходящей через точку равновесия, центр вращения. После того как маятник раскачивается, сила гравитации разделяется на два вектора:
- \(mg\sin\ominus\), воздействует по касательной к дуге по направлению к точке равновесия;
- \(mg\cos\ominus\), воздействует параллельно силе натяжения, однако в ином направлении.
 {2}}{1,5}=10\times1,5=15\).
{2}}{1,5}=10\times1,5=15\). - Полное натяжение будет следующим: \(T + F = 94,08 + 15 = 109,08 Н\).
- Груз, который подвешивают, намного тяжелее, трение не создается, потому что мы знаем, что груз ускоряется вниз. Натяжение в веревке тащит вверх, поэтому объект ускоряется по отношению к силе (равнодействующей) \(F=m1\times{g}-T=98-Т.
 {2}(g)\sin60=T-5(9,8)(0,87)=T-42,14\).
{2}(g)\sin60=T-5(9,8)(0,87)=T-42,14\). - Если сравнять оба уравнения, то получится следующее: \(98-T=T-42,12\). Вычисляем T, получается, что \(2T=140,14. Так T=70,07 \)Н.
- По законам тригонометрии, соотношение между T=m(g) и Т1, Т2 будет равно косинусу угла между нитями и потолком. Для натяжения T1 будет \(\cos30=0,87\). Для натяжения T2 будет \(\cos60=0,5\).
- Нужно умножить натяжение в нижней нити на косинус всех углов, чтобы найти общее натяжение. \(T1=0,87\times{mg}=0,87\times10(9,8)=85,26\) Ньютонов. \(T2=0,5\times{mg}=0,5\times10(9,8)=49\) Ньютонов.
Еще одна формула — с учетом расчета трения. Каждый объект, который тянут нитью по поверхности, чувствует на себе силу замедления из-за трения, и передает данное воздействие натяжению в нити.
Сила трения между двумя телами рассчитывается, как и в другой любой ситуации, в соответствии со следующим уравнением: \(F=(\mu)N\). В данной формуле \(\mu\) является коэффициентом силы трения между телами, N является силой взаимодействия двух объектов\сила, с которой они воздействуют друг на друга.
Примечание 2
Трение покоя — трение, возникающее в итоге попыток привести тело, находящееся в состоянии покоя, в движение.
Трение движения — трение, которое возникает в итоге попыток заставить движущееся тело продолжать это движение.
Приведем пример: представим, что груз в 10 кг не раскачивается, его тянут по горизонтальной плоскости при помощи нити\веревки.
Нужно сделать следующие расчеты: \(F=10\times9,8 =98 Н.\)
Сила трения будет рассчитана по формуле: \(F=0,5\times98=49 Н.\)
Сила ускорения будет рассчитана по формуле: \(F=10\times1=10 Н\).
Общее натяжение: \(F+F=49+10=59 Н.\)
Нахождение силы натяжения на нескольких нитях
Один из способов нахождения силы натяжения нити — использовать вертикальные параллельные грузы при помощи блока.
Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения веревки.
В обычном расположении блока кабель\нить\веревка начинаются от подвешенного объекта вверх к блоку, потом вниз к иному объекту. Так создаются два разных участка веревки. В таком случае натяжение на всех участках становятся одинаковыми, если оба конца натягиваются силами различных величин.
Для системы масс, подвешенных вертикально в блоке, сила натяжения будет равна \(T=\frac{2g(m1)(m2)}{m2+m1)}\). В данной формуле g будет ускорением силы тяжести, m1 — массой первого тела, m2 — массой второго тела.
Примечание 3
Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.
Приведем пример: есть два груза, которые подвешены через блок на параллельных концах нити. Один груз обладает массой в 10 кг, а второй груз обладает массой в 5 кг. В данном случае нужно произвести расчет по следующим формулам:
\(T=\frac{2g(m1)(m2)}{m2+m1)}\)
\(T=\frac{2(9,8)(10)(5)}{5+10)}=\frac{980}{15}=65,33 Н.\)
Важно понимать, что из-за того, что один груз является более тяжелым, другие элементы будут равны, данная система будет ускоряться, значит, груз в 10 кг будет передвигаться вниз, заставляя второй объект идти вверх.
Другая формула — подвешиваем грузы, берем блоки с нитями, которые не параллельны. Блоки часто используют для того, чтобы направить силу натяжения в другую сторону. Если груз подвешивается вертикально к одному концу нити, а другой конец поддерживает груз в диагональной плоскости, то система блоков — непараллельная — формирует треугольную форму с углами в точках с первым грузом, вторым, а также самим блоком. В данном случае натяжение в веревке будет зависеть от силы тяжести, силы натяжения, которая будет параллельная диагональной части нити.
Пример 5
Приведем пример: есть система с объектом в 10 кг, подвешенным вертикально, соединяющимся с грузом в 5 кг, который находится на наклонной плоскости в 60° (нет трения). Для нахождения натяжения в нити нужно составить следующие уравнения:
Последняя формула — использование нескольких нитей для того, чтобы подвесить тело. Представим, что объект подвешивается на «Y-образной» системе нитей — две нити закрепляются на потолке, встречаются в центральной точке, из которой третья нить идет с объектом. Сила натяжения третьей нити проста — обычное натяжение в итоге действия силы тяжести или же m(g).
Натяжение на других нитях отличается, они обязаны составлять в совокупности силу, которая равна силе тяжести вверх в вертикальном положении, а также равны нулю в обоих горизонтальных направлениях. Однако нужно взять во внимание, что система покоится. Натяжение в нити зависит напрямую от массы подвешенных грузов, а также от угла, на который происходит наклон каждой нити от потолка.
Пример 6
Приведем пример: в системе Y-образной нижний груз обладает массой в 10 кг, подвешивается на двух нитях, угол одной из нитей составляет 30° с потолком. Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:
Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:
Примеры решения задач
Задача
Нерастяжимая, с малым весом нить может выдержать силу натяжения в T=4400 Н. Какое максимальное ускорение может быть, чтобы поднять груз с массой в 400 кг? Груз подвешивают на данную нить. Нужно, чтобы нить при этом не разорвалась, и не произошло падение груза.
На рисунке ниже изображены все силы, которые воздействуют на груз.
Запишем второй закон Ньютона. Объект считается материальной точкой, все силы прикладываются к центру масс объекта: \(T+mg=ma\).
Далее записываем проекции уравнения на ось Y: \(T-mg=ma\).
Получаем уравнение: \(a=\frac{T-mg}{m}\).
Произведем расчеты: \(a=\frac{4400-400\times9,8}{400}=1,2 м/с²\).
Ответ: 1,2 м/с².
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
2$ или что-то третье?спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 37 тысяч раз
$\begingroup$
У меня возникли проблемы с пониманием некоторых вещей, касающихся движения на моем вводном уроке физики (никогда не думал, что скажу это. 2}$. 92 = 4$.
2}$. 92 = 4$.
$\endgroup$
1
$\begingroup$
Мы знаем 1. s=at²
2. s=vt+1/2(at²)
Приведенные выше два уравнения действительны для равномерного движения.
Уравнение два делим на t получаем.
с/т= v+1/2(ат)
s/t= Средняя скорость или средняя скорость также равна (u+v)/2. Поместите в приведенное выше уравнение.
(v+u)/2 = v + 1/2(at)
Поместите v = 0 выше, уравнение станет
у=ат. —————-[1] для нахождения скорости формула скорости представляет собой скорость изменения смещения. Математически (s2-s1)/t
Положим s2-s1=s Уравнение станет s/t
Где s2= конечная точка s1= начальная точка Введите [1]
s/t=at
s=at² следовательно доказано
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор закона Чарльза
Создано Wojciech Sas, PhD
Рассмотрено Bogna Szyk и Jack Bowater
Последнее обновление: 22 декабря 2022 г.
Содержание:- Определение закона Чарльза0024
- Примеры закона Чарльза
- Как закон Чарльза применяется в реальной жизни?
- Другие термодинамические процессы
Калькулятор закона Чарльза представляет собой простой инструмент, который описывает основные параметры идеального газа в изобарическом процессе . В тексте вы можете найти ответ на вопрос «Что такое закон Шарля?», узнать, как выглядит формула закона Шарля, и прочитать, как решать термодинамические задачи с некоторыми примерами закона Шарля.
Если вам нужно вычислить результаты для изохорного процесса, воспользуйтесь нашим калькулятором закона Гей-Люссака.
Определение закона Шарля
Закон Шарля (иногда называемый законом объемов) описывает соотношение между объемом газа и его температурой , когда давление и масса газа постоянны . В нем говорится, что объем пропорционален абсолютной температуре .
В нем говорится, что объем пропорционален абсолютной температуре .
Есть несколько других способов записать определение закона Шарля, один из которых таков: соотношение объема и температуры газа в замкнутой системе остается постоянным, пока не изменяется давление.
Закон Шарля описывает поведение идеального газа (газов, которые мы можем охарактеризовать уравнением закона идеального газа) во время изобарического процесса , что означает, что давление остается постоянным во время перехода.
Формула закона Чарльза
Основываясь на определении закона Чарльза, мы можем написать уравнение закона Чарльза следующим образом: T₁ — начальный объем и температура соответственно. Точно так же V₂ и T₂ являются конечными значениями этих параметров газа.
Как работает калькулятор закона Чарльза? Сначала вам нужно вставить три параметра, а четвертый будет рассчитан автоматически. Допустим, мы хотим найти окончательный объем, тогда формула закона Шарля дает:
Допустим, мы хотим найти окончательный объем, тогда формула закона Шарля дает:
V₂ = V₁ / T₁ × T₂ .
Если вы предпочитаете установить конечный объем и хотите оценить результирующую температуру, то уравнение закона Шарля изменится на:
Т₂ = Т₁ / V₁ × V₂ .
В расширенном режиме вы также можете определить давление и посмотреть, сколько молей атомов или молекул содержится в контейнере.
💡 Если температура постоянна во время перехода , это изотермический процесс. В таком случае вы можете быстро оценить его параметры с помощью калькулятора закона Бойля от Omni!
Примеры закона Шарля
Мы можем использовать калькулятор закона Чарльза для решения некоторых термодинамических задач. Посмотрим, как это работает:
Представьте, что у нас есть мяч, накачанный воздухом. Его начальный объем равен
2 литра, и он лежит на пляже, где температура35 °C. Затем мы перемещаем его в кондиционируемую комнату с температурой
Затем мы перемещаем его в кондиционируемую комнату с температурой 15 °C. Как изменится объем мяча?Во-первых, формула закона Шарля требует абсолютных значений температуры , поэтому мы должны преобразовать их в кельвины:
T₁ = 35 °C = 308,15 K ,
T₂ = 15 °C = 288,15 K .Тогда мы можем применить уравнение закона Шарля в форме, где оценивается конечный объем:
V₂ = V₁ / T₁ × T₂
= 2 л / 308,15 К × 288,15 К
= 1,8702 л .
Мы видим, что объем уменьшается, когда мы перемещаем мяч из более теплого места в более прохладное . Иногда вы можете испытать этот эффект, меняя свое местоположение или просто оставляя объект в покое, когда погода меняется. Мяч кажется недостаточно надутым, и кто-то может подумать, что в нем есть дырка, через которую выходит воздух. К счастью, это всего лишь физика, поэтому вам не нужно покупать еще один мяч — просто надуйте тот, который у вас есть, и наслаждайтесь!
Одно маленькое замечание: воздух является примером реального газа, так что результат будет лишь приблизительным , но до тех пор, пока мы избегаем экстремальных условий (давление, температура).
 Результат достаточно близок к реальному значению.
Результат достаточно близок к реальному значению.Во второй задаче нагреваем легко растягивающийся контейнер. Он заполнен азотом, что является хорошим приближением к идеальному газу. Мы можем найти, что его начальный объем составляет
0,03 фут³при комнатной температуре,295 K. Затем ставим близко к источнику тепла и оставляем на некоторое время. Через несколько минут его объем увеличился до0,062 ft³. Имея все эти данные, можем ли мы оценить температуру нашего обогревателя?Применим формулу закона Шарля и перепишем ее в такой форме, чтобы можно было вычислить температуру:
T₂ = T₁ / V₁ × V₂
= 295 K × 0,03 фут³ / 0,062 фут³
= 609,7 K .Мы можем записать результат в более любезной форме T₂ = 336,55 °C или T₂ = 637,79 °F .
Это отличный пример, который показывает нам, что мы можем использовать этот тип устройства в качестве термометра ! Что ж, это не очень практичный метод и, возможно, не такой точный, как обычные, но все же заставляет задуматься, а какие еще необычные приложения можно получить из других повседневных предметов?
Как закон Чарльза применяется в реальной жизни?
Существуют различные области, в которых мы можем использовать закон Чарльза. Вот список нескольких самых популярных и интригующих примеров:
Вот список нескольких самых популярных и интригующих примеров:
Полет на воздушном шаре – Вы, должно быть, хотя бы раз в жизни видели в небе воздушный шар. Вы когда-нибудь задумывались, как он может летать и почему на его борту есть огонь или другие источники тепла? Закон Чарльза – ответ! Всякий раз, когда воздух нагревается, его объем увеличивается . В результате одно и то же количество (масса) газа занимает большее пространство, а значит плотность уменьшается. Плавучесть окружающего воздуха делает остальную часть работы, поэтому воздушный шар начинает плавать.
Рулевое управление в любом заданном направлении — это, вероятно, отдельная история, но мы можем объяснить общую концепцию движения вверх и вниз с помощью закона Шарля .
Эксперименты с жидким азотом . Вы когда-нибудь видели эксперимент, в котором кто-то кладет мяч или воздушный шар в контейнер, наполненный жидким азотом, а затем перемещает его наружу? Во-первых, он сжимается независимо от того, насколько большим он был в начале.
 Затем, после освобождения, возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.
Затем, после освобождения, возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.Термометр – Как показано в предыдущем разделе, можно сконструировать устройство, измеряющее температуру на основе закона Шарля. Хотя мы должны знать о его ограничениях, которые в основном связаны с прочностью объекта на растяжение и устойчивостью к высоким температурам, мы можем изобрести оригинальное устройство, которое идеально подходит для наших нужд. Всякий раз, когда вы не уверены в результате, проверьте этот калькулятор закона Чарльза, чтобы найти ответ.
Другие термодинамические процессы
Закон Шарля, закон Бойля и закон Гей-Люссака входят в число основных законов, описывающих подавляющее большинство термодинамических процессов. Мы собрали все основные газовые переходы в нашем калькуляторе комбинированного газового закона, где вы можете оценить не только конечную температуру, давление или объем, но также изменение внутренней энергии или работу, совершаемую газом.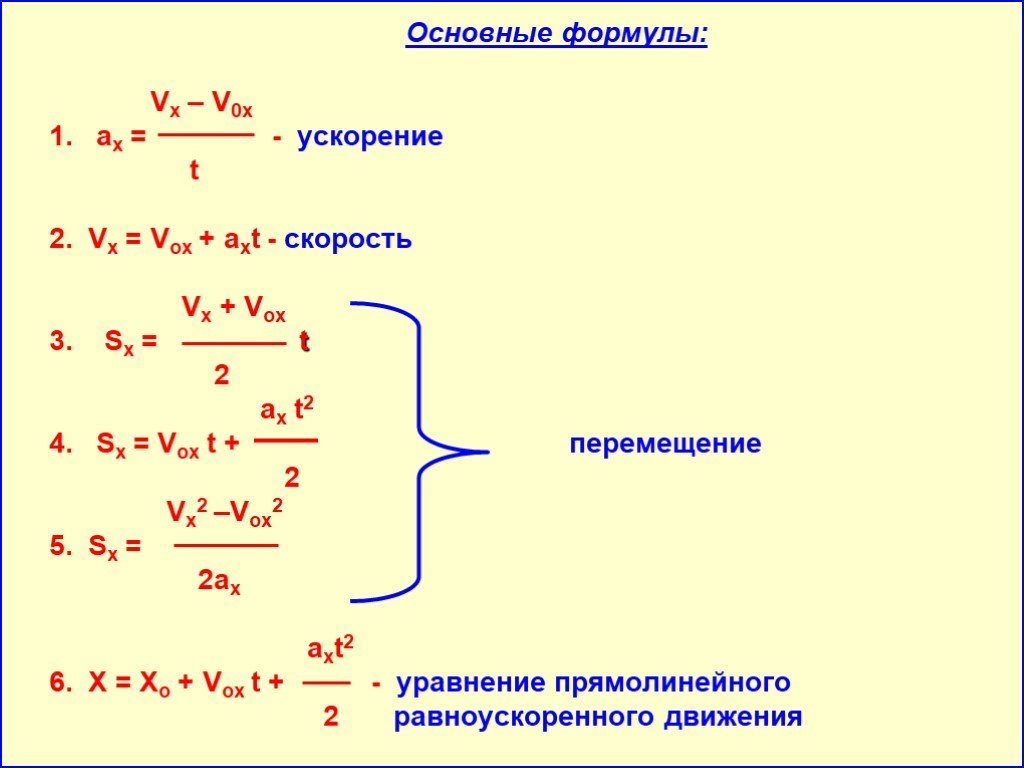

 {2}}{1,5}=10\times1,5=15\).
{2}}{1,5}=10\times1,5=15\). {2}(g)\sin60=T-5(9,8)(0,87)=T-42,14\).
{2}(g)\sin60=T-5(9,8)(0,87)=T-42,14\). Затем мы перемещаем его в кондиционируемую комнату с температурой
Затем мы перемещаем его в кондиционируемую комнату с температурой  Результат достаточно близок к реальному значению.
Результат достаточно близок к реальному значению. Затем, после освобождения, возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.
Затем, после освобождения, возвращается в исходное состояние. Опять же, всякий раз, когда изменяется температура, изменяется и объем.