Как найти мощность, зная силу тока, напряжение и сопротивление
- Статья
- Видео
В физике достаточно много внимания уделено энергии и мощности устройств, веществ или тел. В электротехнике эти понятия играют не менее важную роль чем в других разделах физики, ведь от них зависит насколько быстро установка выполнит свою работу и какую нагрузку понесут линии электропередач. Исходя из этих сведений подбираются трансформаторы для подстанций, генераторы для электростанций и сечение проводников передающих линий. В этой статье мы расскажем, как найти мощность электрического прибора или установки, зная силу тока, напряжение и сопротивление.
- Определение
- Формулы для расчётов цепи постоянного тока
- Для переменного тока
- Пример расчёта полной мощности для электродвигателя
- Расчет для параллельного и последовательного подключения
- Заключение
Определение
Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:
P=dA/dt
Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.
Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.
Электрическая мощность равна произведению тока на напряжение или:
P=UI
Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.
Формулы для расчётов цепи постоянного тока
Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:
P=UI
Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:
P=U2/R
Также можно выполнить расчет, зная ток и сопротивление:
P=I2*R
Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.
Для переменного тока
Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.
Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:
S=UI
Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.
P=UIcosФ
Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.
Q=UIsinФ
Или выразить из этого выражения:
И отсюда вычислить искомую величину.
Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:
S=3UфIф
А зная Uлинейное:
S=1,73*UлIл
1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.
Тогда по аналогии чтобы найти P активную:
P=3UфIф*cosФ=1,73*UлIл*cosФ
Определить реактивную мощность можно:
Q=3UфIф*sinФ=1,73*UлIл*sinФ
На этом теоретические сведения заканчиваются и мы перейдём к практике.
Пример расчёта полной мощности для электродвигателя
Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.
Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:
- Pна валу=160 кВт = 160000 Вт
- n=0,94
- cosФ=0,9
- U=380
Тогда найти активную электрическую мощность можно по формуле:
P=Pна валу/n=160000/0,94=170213 Вт
Теперь можно найти S:
S=P/cosφ=170213/0,9=189126 Вт
Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.
На этом расчёты окончены.
Расчет для параллельного и последовательного подключения
При расчете схемы электронного устройства часто нужно найти мощность, которая выделяется на отдельном элементе. Тогда нужно определить, какое напряжение падает на нём, если речь идёт о последовательном подключении, или какая сила тока протекает при параллельном включении, рассмотрим конкретные случаи.
Здесь Iобщий равен:
I=U/(R1+R2)=12/(10+10)=12/20=0,6
Общая мощность:
P=UI=12*0,6=7,2 Ватт
На каждом резисторе R1 и R2, так как их сопротивление одинаково, напряжение падает по:
U=IR=0,6*10=6 Вольт
И выделяется по:
Pна резисторе=UI=6*0,6=3,6 Ватта
Тогда при параллельном подключении в такой схеме:
Сначала ищем I в каждой ветви:
I1=U/R1=12/1=12 Ампер
I2=U/R2=12/2=6 Ампер
И выделяется на каждом по:
PR1=12*6=72 Ватта
PR2=12*12=144 Ватта
Выделяется всего:
P=UI=12*(6+12)=216 Ватт
Или через общее сопротивление, тогда:
Rобщее=(R1*R2)/( R1+R2)=(1*2)/(1+2)=2/3=0,66 Ом
I=12/0,66=18 Ампер
P=12*18=216 Ватт
Все расчёты совпали, значит найденные значения верны.
Заключение
Как вы могли убедиться найти мощность цепи или её участка совсем несложно, неважно речь идёт о постоянке или переменке. Важнее правильно определить общее сопротивление, ток и напряжение. Кстати этих знаний уже достаточно для правильного определения параметров схемы и подбора элементов – на сколько ватт подбирать резисторы, сечения кабелей и трансформаторов. Также будьте внимательны при расчёте S полной при вычислении подкоренного выражения. Стоит добавить лишь то, что при оплате счетов за коммунальные услуги мы оплачиваем за киловатт-часы или кВт/ч, они равняются количеству мощности, потребленной за промежуток времени. Например, если вы подключили 2 киловаттный обогреватель на пол часа, то счётчик намотает 1 кВт/ч, а за час – 2 кВт/ч и так далее по аналогии.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Также читают:
- Как определить потребляемую мощность приборов
- Как рассчитать сечения кабеля
- Маркировка резисторов по мощности и сопротивлению
detector
способы на практике узнать значение с помощью приборов и расчетных формул
Передвижение положительно заряженных частиц, движущихся в едином направлении, в физике называют силой тока. По своей сути это физическая величина, демонстрирующая заряд, происходящий в определенное время через специальный проводник. Найти силу тока можно несколькими способами. Первый — это расчет величины по выведенным готовым формулам при наличии первоначальных данных. Второй — это использование специальных измерительных приборов.
- Зачем нужна сила тока
- Расчет величины по формулам
- Вычисление значений приборными системами
- Измерение амперметром
Зачем нужна сила тока
Работа любой электротехники напрямую связана с физической величиной заряженных частиц. Знание того, как найти силу тока, позволяет понимать нюансы работы такого оборудования, отдельной цепи либо схемы. Расчет подобного значения у настоящего профессионала не вызовет особых трудностей, а вот у начинающих электриков это может вызвать некоторые проблемы. Для этого стоит знать определенные расчетные формулы или иметь под рукой специальный измерительный прибор.
Знание того, как найти силу тока, позволяет понимать нюансы работы такого оборудования, отдельной цепи либо схемы. Расчет подобного значения у настоящего профессионала не вызовет особых трудностей, а вот у начинающих электриков это может вызвать некоторые проблемы. Для этого стоит знать определенные расчетные формулы или иметь под рукой специальный измерительный прибор.
По своей сути различают несколько разновидностей тока — это постоянный (содержащийся в аккумуляторных батарейках) и переменный (находящийся в розетке). Именно второй вид отвечает за освещение в помещении, работу электроприборов. Особенность переменного тока заключается в быстрой передаче и трансформации, ярким примером тому может служить работа люминесцентных лампочек (движение токовых частиц при включении).
Расчет величины по формулам
Так как самым распространенным видом тока, использующимся в быту, является переменный, то для его расчета используется известная каждому школьнику формула расчета «Закон Ома».
- I — это переменное токовое значение;
- U — это напряжение;
- R — это сопротивление.
Из этой формулы тока можно вывести и другие, не менее полезные вычисления, позволяющие определить другие значения, имея только фактические показатели двух других величин (R = U / I и U = I * R). При расчете рекомендуется использовать основные единицы измерения — амперы, вольты и омы. Данная расчетная формула чаще всего используется для вычисления силы в цепях с активной нагрузкой, например, нагревательных приборах, электрочайниках, светодиодах и т. д.
В других же случаях используется иная вычислительная формула, содержащая в себе мощность и напряжение. Выглядит она следующим образом — I = P / U. Также сила тока рассчитывается по формуле I = q / t, где q — это заряд, идущий по проводнику, измеряющийся в кулонах, а t — это время прохождения электрического заряда, вычисляющееся в секундах.
Вычисление значений приборными системами
Помимо формул при отсутствии четких показателей необходимых значений используются специальные приборные системы. Преимущество такого метода заключается в быстроте и точности получаемых данных, минус — в необходимости покупать требуемые устройства. К основным способам, как определить силу тока, стоит отнести:
- Магнитоэлектрический метод вычисления, отличающийся высокой чувствительностью, точностью показаний, минимальным потреблением электроэнергии. Используется он зачастую для определения значения силы постоянного тока.
- Электромагнитный, основным вычислительным элементом которого становится магнитомодульный датчик, на который из магнитного поля поступает сигнал. Таким способом можно узнать силу постоянного и переменного тока.
- Косвенный, где по старинке используется вольтметр, определяющий показания напряжения на определенном сопротивлении.

Стоит отметить, что подобные методы редко применяются самими электрикам, так как они отнимают много времени. Гораздо проще использовать специальные приборы, а не приборные системы.
Измерение амперметром
Самым простым способом узнать силу тока является измерение показаний амперметром. Особенности его использования заключаются в подключении прибора к разрывам электрической цепи. Для этого выбирается подходящее место, после чего остается дождаться, когда на экране амперметра высветится значение силы тока (заряда), прошедшего через кабельное сечение через определенное время.
Помимо классического прибора используются похожие на них аналоги, предназначенные для того, чтобы быстро найти силу тока малого электричества — это миллиамперметры, микроамперметры, гальванометры. Процедура подключения установки мало чем отличается от обычных измерительных приборов, их нужно зафиксировать на том участке цепи, где требуется узнать значение заряда.
- подготовка прибора, из которого выходит провод с двумя кабелями питания;
- выставление необходимого измерительного диапазона на вычислительной установке;
- прикладывание одного щупа к проводу питания прибора;
- подключение второго щупа к любому контакту электропитания;
- подсоединение оставшегося провода ко второму щупу;
- включение измерительного прибора;
- получение величины токовой силы, показанной на измерителе.
При измерении токовой силы нельзя забывать о том, что особую роль в этом деле играет его вид (переменный либо постоянный). Особое внимание следует уделить постоянному типу тока, например, если внутри устройства установлен блок питания, снижающий сетевое напряжение до меньших значений.
В таком случае необходимо измерять токовую силу в той части цепи, где установлен выпрямляющий мост диодов.
Немаловажную роль в измерении играет напряжение, в таком случае измерительные щипы прибора прикладываются не к разрыву цепи, а к параллельным контактам электропитания. Тут также стоит уделить внимание типу напряжения, которое бывает переменным и постоянным.
8.3 Сохранение энергии | University Physics Volume 1
В этом разделе мы уточняем и расширяем результат, полученный нами в статье «Потенциальная энергия системы», где мы переписали теорему о работе-энергии в терминах изменения кинетической и потенциальной энергий частицы. Это приведет нас к обсуждению важного принципа сохранения механической энергии. Продолжая изучать другие темы физики, в следующих главах этой книги вы увидите, как этот закон сохранения обобщается, чтобы охватить другие типы энергии и передачи энергии. В последнем разделе этой главы представлен предварительный просмотр.
В последнем разделе этой главы представлен предварительный просмотр.
Термины «сохраняющаяся величина» и «закон сохранения» имеют в физике особое научное значение, которое отличается от повседневного значения, связанного с использованием этих слов. (То же замечание верно и в отношении научного и повседневного использования слова «работа».) В повседневном использовании вы можете сохранить воду, не используя ее, или используя меньше ее, или используя ее повторно. Вода состоит из молекул, состоящих из двух атомов водорода и одного атома кислорода. Соедините эти атомы вместе, чтобы сформировать молекулу, и вы создадите воду; диссоциируйте атомы в такой молекуле, и вы разрушите воду. Однако в научном использовании сохраняющаяся величина для системы остается постоянной, изменяется на определенную величину, которая передается другим системам и/или преобразуется в другие формы этой величины. Сохраняющаяся величина в научном смысле может быть преобразована, но не строго создана или уничтожена. Таким образом, физического закона сохранения воды не существует.
Таким образом, физического закона сохранения воды не существует.
Системы с одной частицей или объектом
Сначала рассмотрим систему с одной частицей или объектом. Возвращаясь к нашему развитию (рис.), вспомним, что сначала мы разделили все силы, действующие на частицу, на консервативные и неконсервативные виды, а работу, совершаемую каждым видом сил, записали в отдельный член теоремы о работе-энергии. Затем мы заменили работу консервативных сил на изменение потенциальной энергии частицы, соединив ее с изменением кинетической энергии частицы, чтобы получить (рисунок). Теперь запишем это уравнение без промежуточного шага и определим сумму кинетической и потенциальной энергий [латекс] K+U=E; [/латекс] быть механическая энергия частицы.
Сохранение энергии
Механическая энергия E частицы остается постоянной, если только внешние силы или неконсервативные силы не совершают над ней работу, и в этом случае изменение механической энергии равно работе, совершаемой неконсервативные силы:
[латекс] {W}_{\text{nc},AB}=\text{Δ}{(K+U)}_{AB}=\text{Δ}{E} _{АВ}. [/latex]
[/latex]
Это утверждение выражает концепцию энергосбережения для классической частицы, пока нет неконсервативной работы. Вспомним, что классическая частица — это просто точечная масса, она нерелятивистская и подчиняется законам движения Ньютона. В теории относительности мы увидим, что закон сохранения энергии по-прежнему применим к неклассической частице, но для того, чтобы это произошло, мы должны внести небольшую поправку в определение энергии.
Иногда бывает удобно отделить случай, когда работа неконсервативных сил равна нулю, либо потому, что такие силы не предполагаются, либо, подобно нормальной силе, они совершают нулевую работу, когда движение параллельно поверхности . Затем
[латекс] 0={W}_{\text{nc},AB}=\text{Δ}{(K+U)}_{AB}=\text{Δ}{E}_{AB} . [/latex]
В этом случае закон сохранения механической энергии можно выразить следующим образом: Механическая энергия частицы не изменяется, если все неконсервативные силы, которые могут действовать на нее, не совершают работы. Важно понимать концепцию сохранения энергии, а не конкретное уравнение, которое вы используете для ее выражения.
Важно понимать концепцию сохранения энергии, а не конкретное уравнение, которое вы используете для ее выражения.
Стратегия решения проблем: сохранение энергии
- Идентифицировать тело или тела, подлежащие изучению (систему). Часто в приложениях к закону сохранения механической энергии мы одновременно изучаем несколько тел.
- Определите все силы, действующие на тело или тела.
- Определите, является ли каждая работающая сила консервативной. Если неконсервативная сила (например, трение) совершает работу, то механическая энергия не сохраняется. Затем система должна быть проанализирована с помощью неконсервативной работы (рисунок).
- Для каждой силы, которая совершает работу, выберите точку отсчета и определите функцию потенциальной энергии силы. Контрольные точки для различных потенциальных энергий не обязательно должны находиться в одном и том же месте.
- Примените принцип сохранения механической энергии, уравняв сумму кинетической и потенциальной энергий в каждой интересующей точке.

Пример
Простой маятник
Частица массой м подвешена к потолку на безмассовой нити длиной 1,0 м, как показано на (рис.). Частица выходит из состояния покоя, когда угол между струной и вертикальным направлением вниз составляет [латекс] 30\текст{°.} [/латекс] Какова будет ее скорость, когда она достигнет нижней точки своей дуги?
Рис. 8.7 Частица, подвешенная на веревке, представляет собой простой маятник. Он отображается при выходе из состояния покоя вместе с некоторыми расстояниями, используемыми при анализе движения.
Стратегия
Используя нашу стратегию решения проблем, первым шагом будет определение того, что нас интересует система частица-Земля. Во-вторых, на частицу действует только гравитационная сила, что является консервативным (шаг 3). Сопротивлением воздуха в задаче пренебрегаем, и работа натяжения струны, перпендикулярной дуге движения, не совершается. Следовательно, механическая энергия системы сохраняется, как показано на рисунке (рис.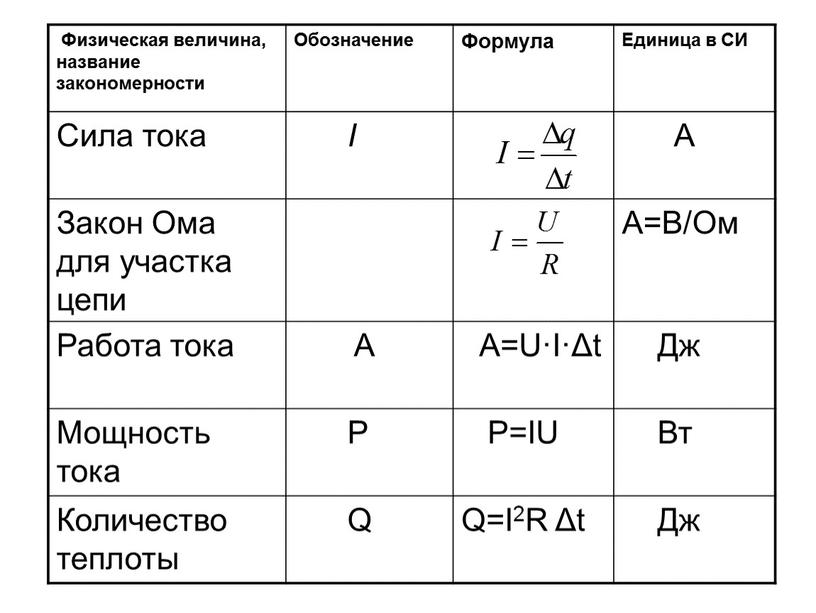 ), [латекс] 0=\text{Δ}(K+U) [/латекс]. Поскольку частица стартует из состояния покоя, увеличение кинетической энергии равно кинетической энергии в самой нижней точке. Это увеличение кинетической энергии равно уменьшению гравитационной потенциальной энергии, которую мы можем вычислить из геометрии. На шаге 4 мы выбираем точку отсчета для нулевой гравитационной потенциальной энергии, чтобы она находилась в самой нижней вертикальной точке, которую достигает частица, то есть в середине движения. Наконец, на шаге 5 мы устанавливаем сумму энергий в самой высокой точке (начальной) колебания до самой низкой точки (конечной) колебания, чтобы в конечном итоге определить конечную скорость.
), [латекс] 0=\text{Δ}(K+U) [/латекс]. Поскольку частица стартует из состояния покоя, увеличение кинетической энергии равно кинетической энергии в самой нижней точке. Это увеличение кинетической энергии равно уменьшению гравитационной потенциальной энергии, которую мы можем вычислить из геометрии. На шаге 4 мы выбираем точку отсчета для нулевой гравитационной потенциальной энергии, чтобы она находилась в самой нижней вертикальной точке, которую достигает частица, то есть в середине движения. Наконец, на шаге 5 мы устанавливаем сумму энергий в самой высокой точке (начальной) колебания до самой низкой точки (конечной) колебания, чтобы в конечном итоге определить конечную скорость.
Решение
Мы пренебрегаем неконсервативными силами, поэтому запишем формулу сохранения энергии, связывающую частицу в высшей (начальной) и низшей (конечной) точках колебания как
[латекс] {K}_ {\text{i}}+{U}_{\text{i}}={K}_{\text{f}}+{U}_{\text{f}}. [/latex]
Поскольку частица выходит из состояния покоя, начальная кинетическая энергия равна нулю. В самой нижней точке мы определяем гравитационную потенциальную энергию как нулевую. Поэтому наша формула сохранения энергии сводится к 9{2}+0\hfill \\ \hfill v& =\hfill & \sqrt{2gh}.\hfill \end{array} [/latex]
В самой нижней точке мы определяем гравитационную потенциальную энергию как нулевую. Поэтому наша формула сохранения энергии сводится к 9{2}+0\hfill \\ \hfill v& =\hfill & \sqrt{2gh}.\hfill \end{array} [/latex]
Высота частицы по вертикали непосредственно в задаче не указана. Это можно решить с помощью тригонометрии и двух данных: длины маятника и угла, на который частица поднимается вертикально вверх. На диаграмме вертикальная пунктирная линия — это длина струны маятника. Высота по вертикали обозначена как h . Другая частичная длина вертикальной струны может быть рассчитана с помощью тригонометрии. Эта часть решается на
[латекс] \text{cos}\,\theta =x\text{/}L,x=L\,\text{cos}\,\theta . [/latex]
Следовательно, взглянув на две части строки, мы можем найти высоту h ,
[latex] \begin{array}{ccc}\hfill x+h& =\hfill & L\hfill \\ \hfill L\,\text{cos}\,\theta +h& =\hfill & L\hfill \\ \hfill h& =\hfill & L-L\,\text{cos}\,\theta = L(1-\text{cos}\,\theta ). \hfill \end{array} [/latex]
\hfill \end{array} [/latex]
Подставим эту высоту в предыдущее выражение для скорости, чтобы вычислить наш результат: 9{2})(1\,\текст{м})(1-\текст{cos}\,30\текст{°})}=1,62\,\текст{м/с}. [/latex]
Значение
Мы нашли скорость непосредственно из закона сохранения механической энергии, без необходимости решать дифференциальное уравнение движения маятника (см. Колебания). Мы можем подойти к этой проблеме с точки зрения гистограмм полной энергии . Изначально частица обладает всей потенциальной энергией, находясь в высшей точке, и не имеет кинетической энергии. Когда частица пересекает самую низкую точку в нижней части качелей, энергия перемещается из столба потенциальной энергии в столбец кинетической энергии. Следовательно, мы можем представить последовательность этого переноса, когда частица перемещается между своей высшей точкой, самой низкой точкой колебания и обратно в самую высокую точку ((рисунок)). По мере того, как частица движется от самой низкой точки колебания к самой высокой точке в правой части диаграммы, энергетические столбцы перемещаются в обратном порядке от (c) к (b) и (a).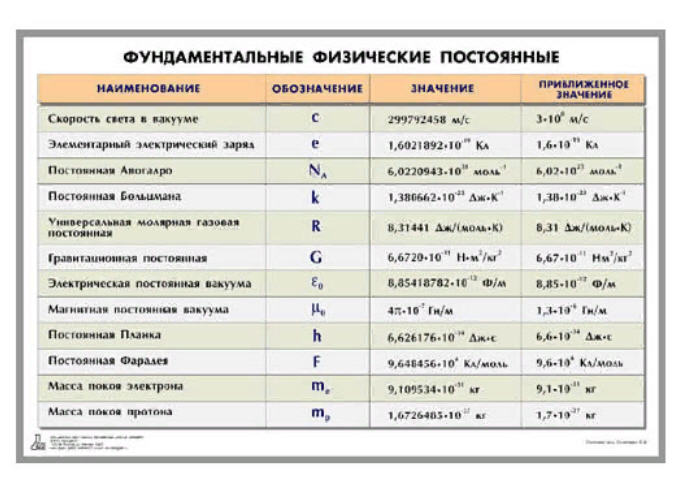
Рисунок 8.8 Гистограммы, представляющие полную энергию (E), потенциальную энергию (U) и кинетическую энергию (K) частицы в различных положениях. (а) Полная энергия системы равна потенциальной энергии, а кинетическая энергия равна нулю, которая находится в высшей точке, которой достигает частица. (b) Частица находится посередине между самой высокой и самой низкой точками, поэтому гистограммы кинетической энергии плюс потенциальная энергия равны полной энергии. (c) Частица находится в самой низкой точке качания, поэтому гистограмма кинетической энергии является самой высокой и равна полной энергии системы.
Проверьте свое понимание
Как высоко над основанием своей дуги находится частица в простом маятнике вверху, когда ее скорость [латекс] 0,81\,\текст{м}\текст{/}\текст{с}? [/latex]
Показать решение
Пример
Сопротивление воздуха падающему объекту
Вертолет зависает на высоте [латекс] 1\,\text{км} [/латекс], когда панель снизу отрывается и падает на земля ((Рисунок)). Масса панели составляет [латекс] 15\,\text{кг}, [/латекс] и она ударяется о землю со скоростью [латекс] 45\,\текст{м}\текст{/}\текст{ с} [/латекс]. Сколько механической энергии было рассеяно сопротивлением воздуха при опускании панели?
Масса панели составляет [латекс] 15\,\text{кг}, [/латекс] и она ударяется о землю со скоростью [латекс] 45\,\текст{м}\текст{/}\текст{ с} [/латекс]. Сколько механической энергии было рассеяно сопротивлением воздуха при опускании панели?
Рисунок 8.9 Вертолет теряет панель, которая падает, пока не достигнет предельной скорости 45 м/с. Какой вклад в рассеяние энергии в этой задаче вносит сопротивление воздуха?
Стратегия
Шаг 1: Здесь исследуется только одно тело.
Шаг 2: На панель действует сила тяжести, а также сопротивление воздуха, которое заявлено в задаче.
Этап 3: Сила гравитации консервативна; однако неконсервативная сила сопротивления воздуха совершает отрицательную работу над падающей панелью, поэтому мы можем использовать закон сохранения механической энергии в форме, выраженной (рисунок), чтобы найти рассеянную энергию. Эта энергия является величиной работы:
[латекс] \text{Δ}{E}_{\text{diss}}=|{W}_{\text{nc,if}}|=|\text{Δ}{(K+U) }_{\текст{если}}|. [/latex]
[/latex]
Шаг 4: Начальная кинетическая энергия при [latex] {y}_{\text{i}}=1\,\text{km}, [/latex] равна нулю. Мы устанавливаем гравитационную потенциальную энергию равной нулю на уровне земли из соображений удобства.
Шаг 5: Неконсервативная работа устанавливается равной энергии, которую нужно найти для работы, рассеиваемой сопротивлением воздуха.
Решение
Механическая энергия, рассеиваемая сопротивлением воздуха, представляет собой алгебраическую сумму прироста кинетической энергии и потери потенциальной энергии. Следовательно, расчет этой энергии равен 9{2})(1000\,\text{м})|=130\,\text{кДж}.\hfill \end{array} [/latex]
Значимость
Большая часть начальной механической энергии панели [латекс] ({U}_{\text{i}}) [/латекс], 147 кДж, был потерян из-за сопротивления воздуха. Обратите внимание, что мы смогли рассчитать рассеиваемую энергию, не зная, что такое сила сопротивления воздуха, а только то, что она была диссипативной.
Проверьте свое понимание
Вы, наверное, помните, что если пренебречь сопротивлением воздуха, если вы подбрасываете снаряд прямо вверх, время, необходимое для достижения максимальной высоты, равно времени, которое требуется для падения с максимальной высоты обратно на начальную высоту. Предположим, вы не можете пренебречь сопротивлением воздуха, как на (рис.). Время, которое требуется снаряду, чтобы взлететь (а), больше, (б) меньше или (в) равно времени, которое требуется для падения? Объяснять.
Предположим, вы не можете пренебречь сопротивлением воздуха, как на (рис.). Время, которое требуется снаряду, чтобы взлететь (а), больше, (б) меньше или (в) равно времени, которое требуется для падения? Объяснять.
Показать раствор
В этих примерах мы смогли использовать закон сохранения энергии для расчета скорости частицы только в определенных точках ее движения. Но метод анализа движения частиц, начиная с сохранения энергии, более мощный. Более продвинутые методы теории механики позволяют вычислить полную зависимость движения частицы от времени для заданной потенциальной энергии. Фактически, часто бывает так, что лучшая модель движения частицы обеспечивается формой ее кинетической и потенциальной энергии, а не уравнением для силы, действующей на нее. (Это особенно верно для квантово-механического описания таких частиц, как электроны или атомы.) 9{2}=E-U(x)\hfill \\ \hfill v& =\hfill & \frac{dx}{dt}=\sqrt{\frac{2(EU(x))}{m}}.\hfill \ end{array} [/latex]
Разделите переменные x и t и проинтегрируйте от начального времени [latex] t=0 [/latex] до произвольного времени, чтобы получить
[latex] t =\underset{0}{\overset{t}{\int }}dt=\underset{{x}_{0}}{\overset{x}{\int }}\frac{dt}{\sqrt{ 2[E-U(x)]\text{/}m}}. [/latex]
[/latex]
Если вы можете вычислить интеграл в (Рисунок), то вы можете решить для x как функция t .
Пример
Постоянное ускорение
Используйте потенциальную энергию [латекс] U(x)=\text{−}E(x\text{/}{x}_{0}), [/latex] для [латекс ] E>0, [/latex] на (Рисунок), чтобы найти положение x частицы как функцию времени t .
Стратегия
Поскольку мы знаем, как изменяется потенциальная энергия в зависимости от x , мы можем заменить [латекс] U(x) [/латекс] на (рисунок), проинтегрировать, а затем найти 9{2} [/латекс].
Значение
Положение как функция времени для этого потенциала представляет собой одномерное движение с постоянным ускорением, [латекс] a=(E\text{/}m{x}_{0}), [/ латекс] начиная с позиции [латекс] {x}_{0}. [/latex] Это не так уж удивительно, так как это потенциальная энергия для постоянной силы, [latex] F=\text{−}dU\text{/}dx=E\text{/}{x}_{ 0}, [/latex] и [latex] a=F\text{/}m.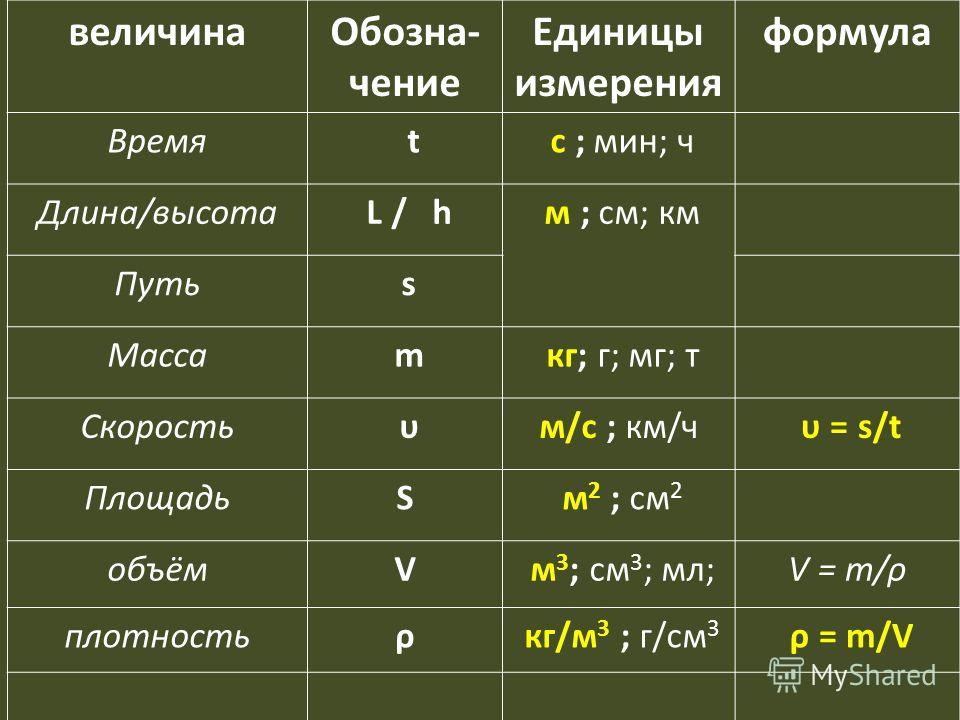 [/latex]
[/latex]
Проверьте свое понимание
Какую потенциальную энергию [латекс] U(x) [/латекс] вы можете подставить в (рисунок), которая приведет к движению с постоянной скоростью 2 м/с для частицы массы 1 кг и механической энергии 1 Дж?
Показать раствор
Мы рассмотрим еще один более физически подходящий пример использования (Рисунок) после того, как изучим некоторые дальнейшие следствия, которые можно извлечь из функциональной формы потенциальной энергии частицы.
Системы с несколькими частицами или объектами
Системы обычно состоят из более чем одной частицы или объекта. Однако сохранение механической энергии в одной из форм на (Рисунок) или (Рисунок) является фундаментальным законом физики и применимо к любой системе. Вам просто нужно включить кинетическую и потенциальную энергии всех частиц, а также работу всех неконсервативных сил, действующих на них. Пока вы не узнаете больше о динамике систем, состоящих из многих частиц, в линейном импульсе и столкновениях, вращении с фиксированной осью и угловом моменте, лучше отложить до этого обсуждение применения сохранения энергии.
Задачи
Мальчик бросает мяч массой [латекс] 0,25\,\text{кг} [/latex] прямо вверх с начальной скоростью [латекс] 20\,\text{м}\text{/} \text{s} [/latex] Когда мяч возвращается к мальчику, его скорость [latex] 17\,\text{m}\text{/}\text{s} [/latex] Сколько работы сопротивление воздуха действует на мяч во время его полета?
Показать раствор
Мышь массой 200 г падает с высоты 100 м вниз по вертикальной шахте и приземляется на дно со скоростью 8,0 м/с. Какую работу совершает мышь при падении сопротивление воздуха?
Используя энергетические соображения и пренебрегая сопротивлением воздуха, покажите, что камень, брошенный с моста на высоте 20 м над водой с начальной скоростью 15,0 м/с, ударяется о воду со скоростью 24,8 м/с независимо от направления броска. ( Подсказка: показывают, что [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} = {K} _ {\ text {f}} + {U}_ {\text{f}}) [/latex]
Показать решение
Шарик массой 1,0 кг на конце 2,0-метровой нити качается в вертикальной плоскости. В нижней точке мяч движется со скоростью 10 м/с. а) Какова его скорость в начале пути? б) Чему равно натяжение нити, когда мяч находится внизу и вверху пути?
В нижней точке мяч движется со скоростью 10 м/с. а) Какова его скорость в начале пути? б) Чему равно натяжение нити, когда мяч находится внизу и вверху пути?
Не обращая внимания на детали, связанные с трением, дополнительными усилиями мышц рук и ног и другими факторами, мы можем рассматривать прыжок с шестом как преобразование кинетической энергии бега спортсмена в гравитационную потенциальную энергию. Если спортсмен должен поднять свое тело на 4,8 м во время прыжка, какую скорость он должен иметь, когда ставит шест?
Показать раствор
Тарзан хватает лиану, свисающую вертикально с высокого дерева, когда он бежит со скоростью [латекс] 9.0\,\text{m}\text{/}\text{s}. [/latex] (а) Как высоко он может подняться вверх? б) Влияет ли длина виноградной лозы на эту высоту?
Предположим, что сила воздействия лука на стрелу аналогична силе пружины. При наведении стрелы лучник оттягивает лук на 50 см назад и удерживает его в этом положении с силой [латекс] 150\,\text{N} [/латекс]. Если масса стрелы [латекс] 50\,\text{г} [/латекс] и «пружина» не имеет массы, какова скорость стрелы сразу после того, как она покинет лук?
Если масса стрелы [латекс] 50\,\text{г} [/латекс] и «пружина» не имеет массы, какова скорость стрелы сразу после того, как она покинет лук?
Показать раствор
[латекс] 100-\text{кг} [/латекс] человек едет на лыжах по ровной поверхности со скоростью [латекс] 8,0\,\текст{м/с} [/латекс], когда он подходит к маленькому уклон на 1,8 м выше уровня земли, показанный на следующем рисунке. а) Если лыжник движется вверх по склону, какова будет его скорость, когда он достигнет верхнего плато? Считать, что трением между снегом и лыжами можно пренебречь. б) Какова будет его скорость, когда он достигнет верхнего уровня, если на лыжи действует сила трения [латекс] 80-\text{N} [/латекс]?
Сани массой 70 кг трогаются с места и скользят по [латексному] 10\text{°} [/latex] склону [латекс] 80\,\text{м} [/латекс] длиной. Затем он проходит 20 м по горизонтали, а затем снова начинает подниматься по склону [латекс] 8\text{°} [/латекс]. Он проходит 80 м по этому склону, прежде чем остановиться.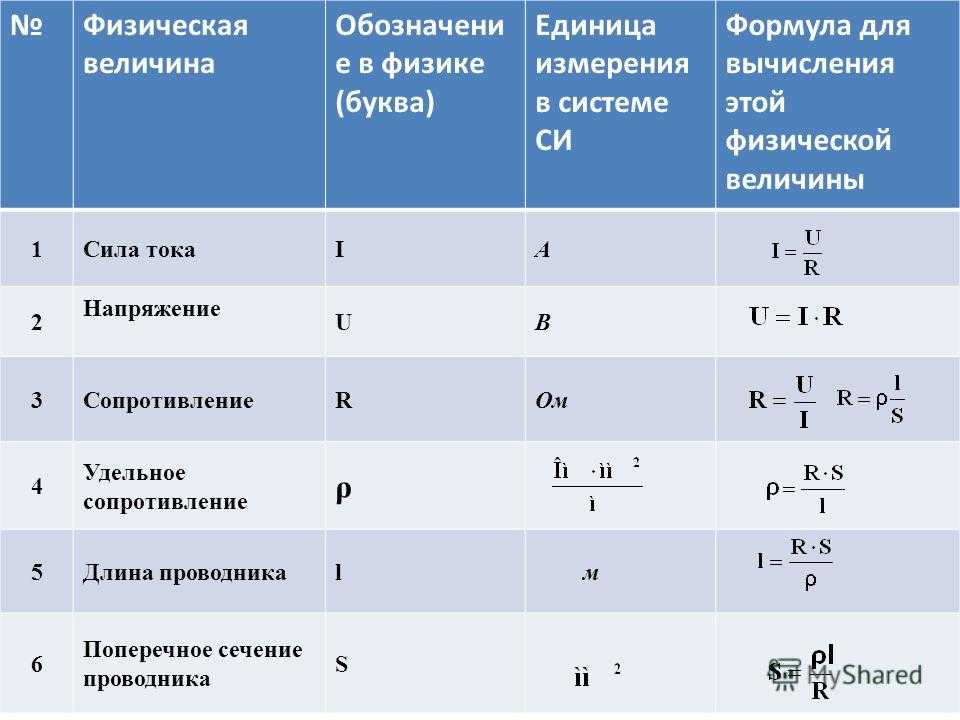 Какова чистая работа, совершаемая трением на салазках?
Какова чистая работа, совершаемая трением на салазках?
Показать раствор
Девушка на скейтборде (общая масса 40 кг) движется со скоростью 10 м/с по дну длинного пандуса. Пандус наклонен под углом [latex] 20\text{°} [/latex] к горизонтали. Если она перед остановкой пройдет 14,2 м вверх по пандусу, какова результирующая сила трения, действующая на нее?
Бейсбольный мяч массой 0,25 кг попал в исходную пластину со скоростью 40 м/с. Когда он приземляется на трибуну левого поля на горизонтальном расстоянии 120 м от стартовой площадки, он движется со скоростью 30 м/с. Если мяч приземлится на 20 м выше места удара, какую работу совершит сопротивление воздуха?
Показать раствор
Небольшой брусок массой м скользит без трения по устройству «петля за петлей», показанному ниже. (a) Если блок начинается из состояния покоя в точке A , какова его скорость на B ? (b) Какова сила, с которой гусеница действует на брусок в точке B ?
Безмассовая пружина пружинного пистолета имеет постоянную силы [латекс] k=12\,\text{Н/см}.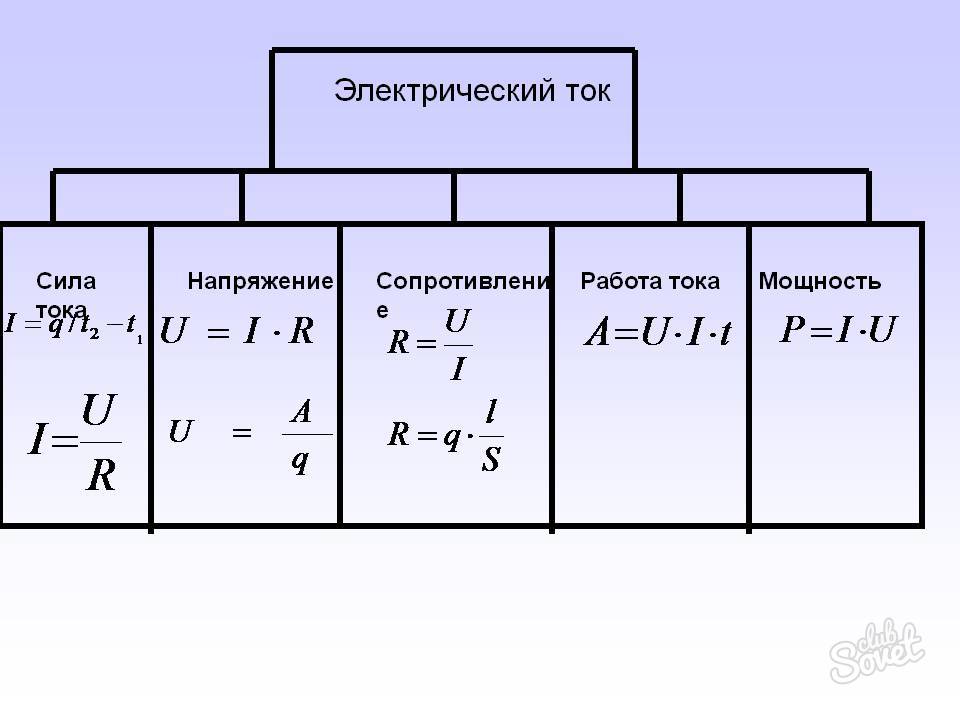 [/latex] При вертикальном наведении орудия 15-граммовый снаряд выбрасывается на высоту 5,0 м над концом расширенной пружины. (См. ниже.) Насколько изначально была сжата пружина?
[/latex] При вертикальном наведении орудия 15-граммовый снаряд выбрасывается на высоту 5,0 м над концом расширенной пружины. (См. ниже.) Насколько изначально была сжата пружина?
Показать решение
Маленький шарик привязан к нити и вращается с незначительным трением по вертикальной окружности. Докажите, что натяжение нити в нижней части круга превышает натяжение в верхней части круга в восемь раз больше, чем вес мяча. Предположим, что скорость мяча равна нулю, когда он пролетает над вершиной круга, и во время вращения к мячу не добавляется дополнительная энергия.
Что такое Mu (µ) и что оно обозначает?
К
- Рахул Авати
Строчная греческая буква µ (произносится как мю) обычно представляет множитель префикса 0,000001, то есть 10 -6 или одну миллионную. Например, 0,000001 фарад или 10 -6 F электрической емкости обычно записывается как 1 мкФ. Точно так же 0,000000001 или 10 -9 фарад записывается как 0,001 мкФ.
Например, 0,000001 фарад или 10 -6 F электрической емкости обычно записывается как 1 мкФ. Точно так же 0,000000001 или 10 -9 фарад записывается как 0,001 мкФ.
Символ μ — это строчная запись 12-й буквы греческого алфавита. Представление M в верхнем регистре совпадает с латинско-английской буквой M. Mu произошло от финикийской буквы mem, , которая в свою очередь произошла от египетского иероглифа вода .
Как и многие другие греческие буквы, μ используется для обозначения нескольких величин и явлений реального мира в различных академических и практических областях, включая следующие:
- Физика
- Биология
- Химия
- Машиностроение
- Фармакология
- Информатика
- Математика
В некоторых текстах символ µ является аббревиатурой микрометров или микронов. Он используется для представления многих реальных величин, включая магнитную проницаемость, коэффициент трения, электрическую подвижность заряженных частиц и массу на единицу длины.
В физике буква μ обычно используется для обозначения коэффициента трения и магнитной проницаемости.
Коэффициент трения представляет собой отношение силы трения (F), противодействующей движению двух поверхностей, находящихся в контакте, с нормальной силой (Н), прижимающей две поверхности друг к другу. Сила трения и движение тела направлены в противоположные стороны.
Математически коэффициент трения представляется как:
мк = Ф/№
Коэффициент трения безразмерен, поскольку и F, и N измеряются в единицах силы (например, в ньютонах или фунтах).
Значение μ отличается для статического и кинетического трения. При статическом трении объект остается в покое до тех пор, пока сила статического трения не будет устранена. Кроме того, сила трения сопротивляется силе, приложенной к объекту. Напротив, при кинетическом трении сила трения сопротивляется движению объекта.
Магнитная проницаемость относится к относительному изменению (увеличению или уменьшению) магнитного поля внутри материала по сравнению с намагничивающим полем, в котором находится материал.
Математически представляется как:
мк = В/Ч
В в данном случае – плотность магнитного потока, установившаяся внутри материала. Это зависит от концентрации силовых линий магнитного поля (потока) на единицу площади поперечного сечения.
Гн — напряженность магнитного поля намагничивающего поля. Поле создается протеканием электрического тока по проводу.
Обозначение μ 0 (произносится как mu ноль или mu zero ) относится к проницаемости свободного пространства. Он также известен как проницаемость вакуума и магнитная постоянная . В единицах СИ μ 0 ранее равнялось 4π × 10 -7 веберов на амперметр.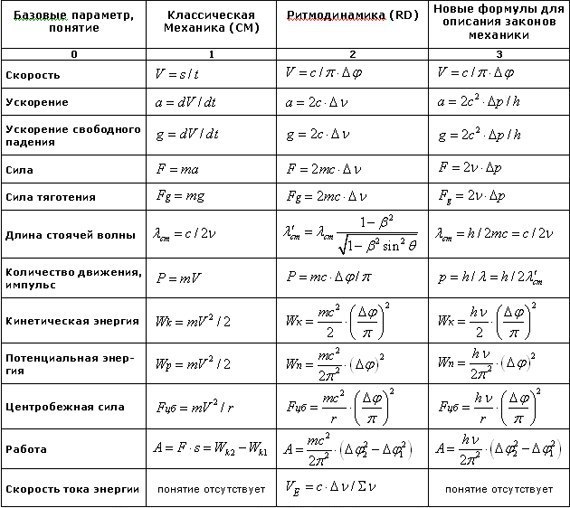 Но с переопределением ампера в 2019 г., μ 0 уже не равно этому значению, поэтому его необходимо определить экспериментально. Относительная проницаемость μ r представляет собой отношение μ/μ0. В свободном пространстве или в вакууме эта величина равна 1. Как и коэффициент трения, μ r также безразмерно.
Но с переопределением ампера в 2019 г., μ 0 уже не равно этому значению, поэтому его необходимо определить экспериментально. Относительная проницаемость μ r представляет собой отношение μ/μ0. В свободном пространстве или в вакууме эта величина равна 1. Как и коэффициент трения, μ r также безразмерно.
Линейная плотность – это степень массы на единицу длины. Это значение особенно полезно для измерения веса объектов, которые кажутся одномерными, таких как нити, струны, пряжа и провода.
Линейная плотность математически представляется как:
µ = масса/длина
Единицей линейной плотности в системе СИ является кг/м.
В дополнение к кг/м для представления массы на единицу длины также используется другая единица измерения. Это известно как текс, который представляет собой количество граммов (1 грамм = 10 -3 кг) на 1000 метров.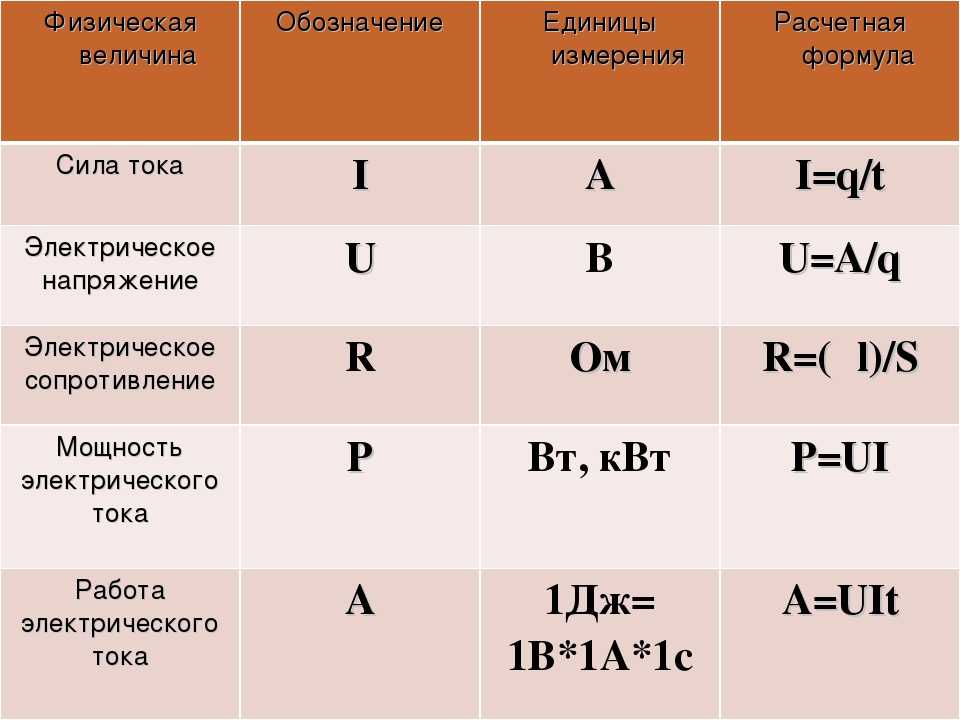 Другой единицей является денье, который представляет собой количество граммов на 9000 метров нити. В реальных приложениях денье является мерой веса нити и, следовательно, непрозрачности или тонкости материала.
Другой единицей является денье, который представляет собой количество граммов на 9000 метров нити. В реальных приложениях денье является мерой веса нити и, следовательно, непрозрачности или тонкости материала.
В химии µ относится к элементарным частицам мюону и антимюону. Мюон подобен электрону. Однако его масса примерно в 207 раз больше массы электрона. Он создается, когда электрон сталкивается со своей античастицей позитроном (e + ). Столкновение создает фотон, который впоследствии формирует мюон и его античастицу, антимюон .
Мюон представлен как μ − , а антимюон как μ + . В двухмерном представлении, где ось x представляет пространство, а ось y представляет время, позитрон (e + ) и антимюон (μ + ) показаны как движущиеся назад во времени. Другими словами, эти частицы показаны движущимися в прошлое. Такие диаграммы очень полезны для изображения различных типов взаимодействий частиц, особенно для визуализации эффектов электромагнитных взаимодействий между электронами и фотонами.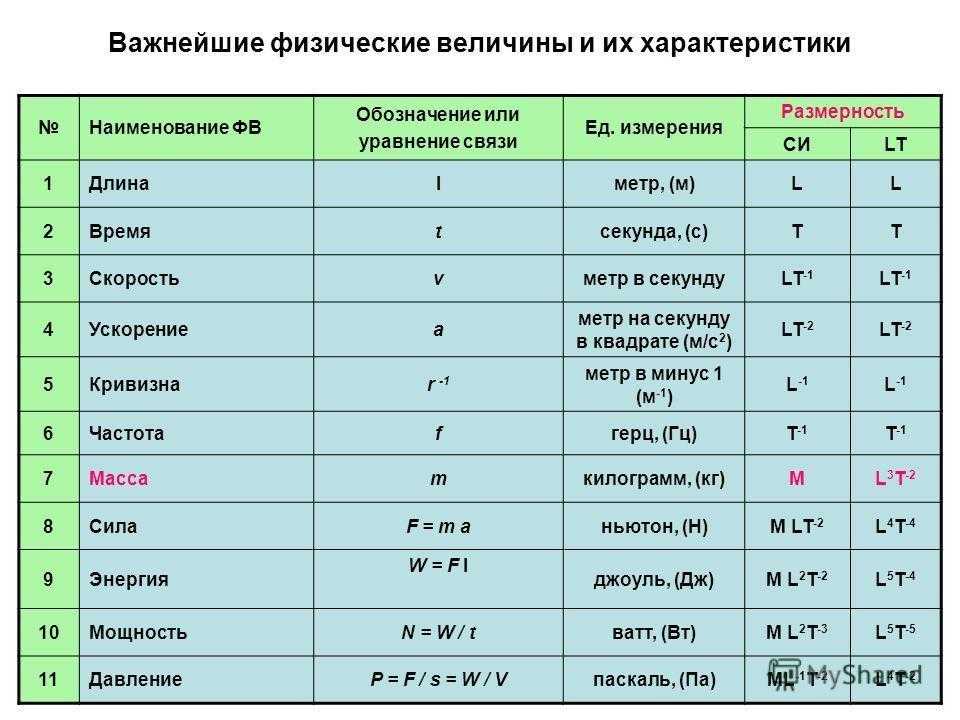
В материаловедении µ используется для обозначения магнитного момента. Эта векторная величина измеряет склонность объекта к взаимодействию с внешним магнитным полем. Он также представляет магнитную силу и ориентацию магнита.
Обычно магнитные свойства объекта визуально представляют в виде петель, исходящих из стержневого магнита с северным и южным полюсами (диполями). Вот почему магнитный момент также известен как магнитный дипольный момент. Магнитное поле магнитного диполя пропорционально его магнитному дипольному моменту.
Магнитный момент может быть представлен математически как:
µ = i . А
i = ток, проходящий по краю петли
A = площадь поперечного сечения петли
Направление магнитного дипольного момента перпендикулярно А.
Все следующие объекты имеют магнитные дипольные моменты, представленные как µ :
- Электромагниты
- Постоянные магниты
- Элементарные частицы: атомы, ядра или субатомные частицы
- Молекулы
- Много планет
- Некоторые луны
- Некоторые звезды
В гидромеханике µ обозначает вязкость. Вязкость измеряет сопротивление жидкости течению. Это сопротивление вызвано напряжением сдвига в жидкости, а также напряжением сдвига между жидкостью и ее контейнером.
Вязкость измеряет сопротивление жидкости течению. Это сопротивление вызвано напряжением сдвига в жидкости, а также напряжением сдвига между жидкостью и ее контейнером.
Математически вязкость представляется как отношение напряжения сдвига к скорости изменения скорости (градиенту скорости).
Касательное напряжение = τ (тау)
Скорость изменения скорости = dv/dy = v
dv/dy — производная скорости по расстоянию y .
Вязкость = µ = τ
dv/dy
Буква µ в электротехнике и электронной техникеВ электротехнике и электронной технике µ представляет собой электрическую подвижность заряженной элементарной частицы, такой как электрон или протон. Мобильность просто означает стремление заряженных частиц двигаться. Он пропорционален суммарному заряду частицы.
Когда на эту заряженную частицу действует однородное электрическое поле, она будет ускоряться, пока не достигнет постоянной скорости дрейфа. Это явление представлено математически как:
Это явление представлено математически как:
мк = V d / E
В d = Скорость дрейфа
E = электрическое поле
Единицей электрической подвижности в системе СИ является м 2 / В с. Это явление лежит в основе электростатического осаждения, которое используется для удаления частиц из выхлопных газов в больших масштабах.
Буква µ в термодинамикеВ термодинамике µ представляет собой химический потенциал системы или компонента системы. Он относится к химической энергии (U c ), которой обладает 1 моль вещества. Другой способ описать химический потенциал – это «энергия, добавляемая к системе, когда к ней добавляется частица».
Математически химический потенциал представляется как:
мкм = U c /N
Когда химический потенциал между двумя точками изменяется, создается градиент химического потенциала. Это вызывает миграцию соответствующих химических соединений из области с высоким химическим потенциалом в область с более низким химическим потенциалом.
Химический потенциал µ может быть связан с любым типом вещества, включая следующие:
- Группы атомов
- Молекулы
- Электроны
- Электронные дырки
- Атомные вакансии
- Фононы
- фотонов
См. также: математические символы, Таблица физических единиц
Последнее обновление: август 2022 г.
Продолжить чтение о мю- Почему физики хорошо подходят для работы в области обработки данных
- Зачем миру нужны технические стандарты для Целей ООН в области устойчивого развития
- Китай хочет больше влиять на установление глобальных технологических стандартов
враждебный ML
Состязательное машинное обучение — это метод, используемый в машинном обучении для обмана или введения в заблуждение модели с помощью злонамеренных входных данных.
Сеть
- межсоединение центра обработки данных (DCI)
Технология соединения центров обработки данных (DCI) объединяет два или более центров обработки данных для совместного использования ресурсов.

- Протокол маршрутной информации (RIP)
Протокол маршрутной информации (RIP) — это дистанционно-векторный протокол, в котором в качестве основной метрики используется количество переходов.
- доступность сети
Доступность сети — это время безотказной работы сетевой системы в течение определенного интервала времени.
Безопасность
- GPS-глушение
Подавление сигналов GPS — это использование устройства, передающего частоту, для блокирования или создания помех радиосвязи.
- контрольная сумма
Контрольная сумма — это значение, представляющее количество битов в передаваемом сообщении, которое используется ИТ-специалистами для обнаружения…
- информация о безопасности и управление событиями (SIEM)
Управление информацией о безопасности и событиями (SIEM) — это подход к управлению безопасностью, который объединяет информацию о безопасности .
 ..
..
ИТ-директор
- FMEA (анализ видов и последствий отказов)
FMEA (анализ видов и последствий отказов) представляет собой пошаговый подход к сбору сведений о возможных точках отказа в …
- доказательство концепции (POC)
Доказательство концепции (POC) — это упражнение, в котором работа сосредоточена на определении того, можно ли превратить идею в реальность.
- зеленые ИТ (зеленые информационные технологии)
Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислений.
HRSoftware
- самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой .




 ..
..