Как найти ускорение через путь: Как найти ускорение зная путь и время

Как найти ускорение на графике скорость-время: задачи и примеры

В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.

Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.

График скорости во времени для положительного ускорения

Давайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.

График зависимости скорости от времени для положительного ускорения

По оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением [латекс] м = \ гидроразрыва {\ Delta y} {\ Delta t} [/ латекс]. Здесь наклон графика скорость-время дает ускорение объекта.

[латекс] а = м = \ гидроразрыва {\ Delta V} {\ Delta T} = \ гидроразрыва {v_2-v_1} {t_2-t_1} [/ латекс]

Из приведенного выше графика ускорение будет положительным, если V₂>V₁ то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V₂<V₁, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.

Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.

1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.

Решение: Изменение скорости объекта определяется как.

V₁= 2 м / с

V₂= 4 м / с

Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. {2}[/latex]

Ускорение тела равно 0.5 м/с.².

График зависимости скорости от времени для нулевого ускорения

Приведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.

Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.

Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.

2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?

Решение: V₁=0.5 м/с; В₂=0.5 м/с, временной интервал t=5 минут=300 секунд.

[latex]a=\frac{v_2-v_1}{t_2-t_1}=\frac{0.5-0.5}{300}=0[/latex]

Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.

Подробнее о ускорение.

График зависимости скорости от времени для отрицательного ускорения

Если объект замедляется со временем, то наклон графика скорость-время будет отрицательным. Это показано на приведенном ниже графике зависимости скорости от времени.

График зависимости скорости от времени для отрицательного ускорения

Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.

3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже. 2[/latex]

Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.².

Подробнее о График постоянного отрицательного ускорения: что, как, примеры.

График отрицательной скорости для отрицательного ускорения

Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.

Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.

График отрицательной скорости во времени для положительного ускорения

Ниже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение. 2[/latex]

Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.².

Почему ускорение является векторной величиной?

Ускорение имеет величину и направление.

Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2. 5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

Вопрос Видео: Расчет ускорения для кругового движения

Стенограмма видео

Вертолет летит по кругу радиусом 375 метров, совершая один оборот за 42 секунды. Какова величина ускорение вертолета к центру его круговой траектории?

Начнем с рисования диаграмма. Вот вертолет летит в своем круговой путь с радиусом, который мы назовем 𝑟, 375 метров. Теперь, потому что вертолет просто летя по кругу, мы можем описать его движение, используя угловую скорость, представленную 𝜔. Напомним, что угловая скорость определяется как изменение углового смещения, или Δ𝜃, деленное на изменение во времени, или Δ𝑡. Теперь, формулировка вопроса сказала нам временной интервал в 42 секунды, столько времени требуется вертолету для завершения один полный оборот по круговой траектории. Мы будем использовать это как наш Δ𝑡 ценность.

За это время изменение углового смещения вертолета Δ𝜃 составляет один оборот или один полный оборот по кругу. Но помните, что когда мы вычисления, мы должны описать угловое смещение, используя радианы.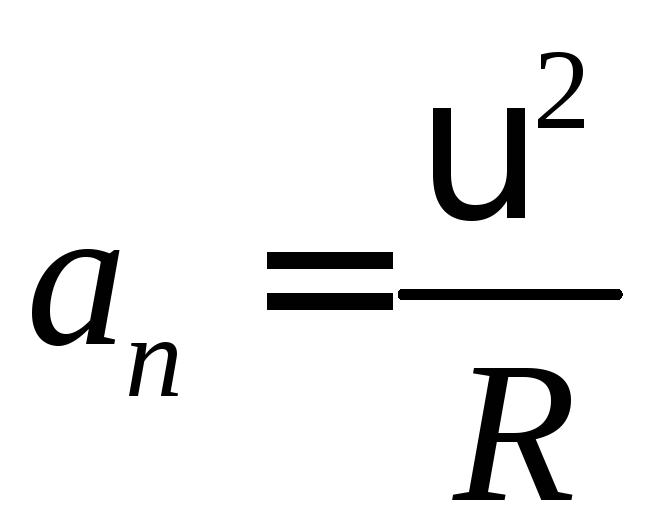 А один полный оборот равен два 𝜋 радиана. Теперь замените оба этих значений в формулу для угловой скорости, мы имеем 𝜔 равно двум 𝜋 радианам разделить на 42 секунды. А так как 42 равно дважды 21, мы можем сократить множитель два из числителя и знаменателя, таким образом упрощая дробь до 𝜋 радиан, деленное на 21 секунду или 𝜋 более 21 радиана в секунду.

Теперь этот вопрос требует от нас найти величину ускорения, которое испытывает вертолет при направление центра его круговой траектории. Чтобы лучше понять это, вспомним что любой объект, совершающий равномерное круговое движение, как здесь вертолет, должен быть постоянно ускоряясь к центру своей круговой траектории. Это ускорение называется центростремительное ускорение, представленное нижним индексом 𝑎 c. Далее, напомним, что при заданном угловую скорость объекта 𝜔 и радиус 𝑟 его круговой траектории, мы можем рассчитайте его центростремительное ускорение по формуле 𝜔 в квадрате, умноженной на 𝑟.

Теперь у нас уже есть значения для оба 𝜔 и 𝑟 выражены в основных единицах СИ. Итак, давайте скопируем формулу и подставьте их. Это дает нам 𝜋 более 21 радиана на секунду в квадрате умножить на 375 метров. Прежде чем мы начнем вычисления, давайте на минутку подумаем о единицах измерения. Мы должны помнить, что пока угловые единицы, такие как радианы, градусы и обороты, помогают нам отслеживать угловое смещение, технически они безразмерны. У них нет физического элемента связанные с ними, в отличие от других единиц, с которыми мы могли бы быть более знакомы, таких как метров или секунд.

Но это не значит, что все угловые единицы эквивалентны. Еще очень важно, какой тот, который мы используем. Уравнения физики были на самом деле разработан с учетом радианов. И, таким образом, для вычислений, таких как здесь, нам нужно выразить угловую скорость, используя радианы в секунду.

Вот только когда дело доходит до физические размеры угловой скорости, нас интересует только скорость в секунду часть.

Хорошо, теперь вернемся к единицам измерения центростремительное ускорение. Квадрат угловой скорости даст нас на секунду в квадрате, и, конечно, радиус вносит свой вклад в метры. Вместе у нас будут единицы метров в секунду в квадрате, которые являются правильными единицами СИ для ускорения. Теперь введите это в калькулятор, 𝜔 умножить на квадрат 𝑟 получается 8,393 и так далее метров в секунду в квадрате. И, наконец, округляя это значение до один десятичный знак, мы нашли, что величина ускорения вертолета к центру его кругового пути составляет 8,4 метра в секунду в квадрате.

Исчерпывающие подходы и факты — Lambda Geeks

Как найти ускорение с помощью угла и коэффициента кинетического трения — часто задаваемые вопросы. В ускоряющей системе одним из основных факторов является коэффициент трения.

Ускорение в движущейся системе может принимать разные формы. Например, в наклонной плоскости мы должны учитывать угол, под которым движется тело. Таким образом, учитывая все эти атрибуты, мы будем иметь дело с факторами, главным образом ответственными за ускорение тела.

Если наклон имеет тело или любой объект, который находится в постоянном движении, он будет рассчитан в соответствии с поставленной задачей. Здесь мы обсудим, как найти ускорение с углом и коэффициентом кинетического трения.

Мы должны знать, как мы ускоряемся с точки зрения движущегося автомобиля. Когда автомобиль движется с определенной скоростью, мы, как правило, возвращаемся на сиденье, когда скорость увеличивается. Когда машина притормаживает, мы склонны двигаться вперед, а на поворотах склонны двигаться боком. Это способы ускорения.

Несколько различных факторов обеспечивают ускорение. В одном из них нам нужно сосредоточиться на заданных деталях. Здесь мы будем иметь дело с коэффициентом трения и углом, под которым оно будет ускоряться.

«Старый гоночный автомобиль» от oatsy40 лицензируется в соответствии с CC BY 2.0

Подробная информация о коэффициенте трения и его влиянии на ускорение

под движение. В его основе лежат силы, действующие на тело, находящееся в постоянном движении.

Во-первых, это сила гравитации, единственная причина, по которой тело находится на земле без какой-либо левитации. Далее будет нормальная сила, действующая на тело. Эта нормальная сила является силой из окружения. Далее следует сила трения, которая в основном отвечает за то, чтобы тело действительно могло совершать любые движения.

Сила нормали и сила трения являются одними из основных факторов, влияющих на ускорение. Когда тело движется с определенной скоростью, а затем внезапно набирает скорость и движется с другой скоростью, говорят, что оно ускорено.

 На самом деле мы должны были узнать, как это трение влияет на ускорение и как работает коэффициент трения при ускорении. Когда тело находится под ускорением, в игру вступают несколько аспектов.

На движущееся тело действует множество сил. В этой системе ускоряющего мы должны найти вид сил, присутствующих и действующих на это тело . Затем нам нужно рассчитать ускорение соответственно.

Фокусировка на силе трения является фактором, определяющим движение тела по земле. Например, автомобиль движется, потому что между шиной автомобиля и дорогой есть трение, или это может быть любая поверхность, рассматриваемая в данном случае.

«Dayia 2CV Citroen Tin Friction Car» от Loopdeeloop под лицензией CC BY-NC 2.0

Как найти ускорение с помощью угла и коэффициента кинетического трения

Здесь нам нужно рассмотреть столько же примеров, как найти ускорение с помощью угол и коэффициент кинетического трения. Сначала идет угол, затем коэффициент трения. Угол имеет большое значение в том, как тело движется по наклонной плоскости.

Теперь рассмотрим случай, когда объект помещается поверх поверхности, ниже которой он фактически наклонен. Теперь по каким-то причинам объект теряет равновесие и скатывается по наклонной поверхности. Следовательно, необходимо оценить ускорение тела, движущегося в наклонной плоскости.

В этом случае сила трения является кинетической и действует противоположно силе тяжести. Чистая сила также должна быть рассчитана. Нам нужно определить результирующую силу, чтобы найти ускорение тела с углом и коэффициентом трения.

F = Fg + Fk; F = mg (sine θ) + μ mg (cos θ)

Мы знаем, что ускорение равно [силе, деленной на массу, следовательно, a = F/m. Следовательно, из формулы чистой силы мы получаем ускорение как а = г (синус θ) + мкг (cosθ) .

Используя эту формулу, мы можем найти ускорение с коэффициентом трения и углом, под которым он движется.

Задача на нахождение ускорения по углу и коэффициенту кинетического трения

Задача 1:

Допустим, автомобиль массой 1200 кг движется по неровной дороге. Значение коэффициента трения дается как 0,8. Fnet = 7000 Н будет считаться результирующей силой, действующей на это движущееся тело. Теперь первое, что нужно оценить, это ускорение этой конкретной системы.

Решение 1:

Поскольку результирующая сила известна, мы можем найти нормальную силу, используя значение массы и силы тяжести, поскольку сила тяжести и нормальная сила равны друг другу, но действуют в разных направлениях. Сила трения находится по значению коэффициента трения и значению нормальной силы.

м = 1200; Fнет = 7000 Н; μ= 0,8 

Сила нормали = сила тяжести x масса тела

Fn = 9,8 x 1200; Фн = 11270

Сила трения = μ x нормальная сила; FF = 0,8x 11270 = 9016 N

A = F / M

A = 9016/1200

A = 7,51 мс ^-2

Проблема 2:

Как найти с учетом сведения о том коэффициент трения и угол, под которым он наклонен.

Итак, в задаче, где заданы коэффициент трения и угол, под которым оно движется. Тело массой 100 кг движется вниз по наклонной плоскости под углом θ=45⁰. Коэффициент трения μ=0,9.

С каким ускорением тело совершает движение вниз?

Решение 2:

Фактор силы, направленной вдоль плоскости, равен mgSinθ, а фактор, перпендикулярный плоскости, равен mgCosθ. И мы знаем, что f=ma, значит, a= f/m. исходя из этого, мы можем использовать значение коэффициента трения или нет.

Таким образом, мы получаем следующую формулу:

Часто задаваемые вопросы

Как найти ускорение с учетом трения и под углом?

Трение является единственной причиной движения тела в любом направлении, и когда движение происходит под наклоном, будет учитываться угол.

Формула для нахождения ускорения с учетом трения, а также угла: a= μgCosθ. Нам нужно знать, что действующие силы будут двух типов: одна будет направлена ​​вдоль склона, а другая будет перпендикулярна наклону.