Как найти ускорение физика: 404 - Страница не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Ускорение свободного падения — формулы, примеры и определение

Сила тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F = G * (Mm/R²)

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6,67 × 10^-11

м³·кг^-1·с^-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние

R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей. 🤓

@keepalmagain
Приливы и отливы #физика #огэ #егэ #математика #школа #онлайншкола
♬ оригинальный звук – 43 43

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести

F = mg

F — сила тяжести [Н]

m — масса тела [кг]

g — ускорение свободного падения [м/с²]

На планете Земля g = 9,8 м/с², но подробнее об этом чуть позже. 😉

На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

F = mg

F = G * (Mm/R²)

Приравниваем правые части:

mg = G * (Mm/R²)

Делим на массу левую и правую части:

g = G * (M/R²)

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Формула ускорения свободного падения

g = G * (M/R²)

g — ускорение свободного падения [м/с²]

— масса планеты [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6,67 × 10^-11м³·кг^-1·с^-2

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Ускорение свободного падения на разных планетах

Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.

Для этого нам понадобятся следующие величины:

Гравитационная постоянная
G = 6,67 × 10^-11м³·кг^-1·с^-2
Масса Земли
M = 5,97 × 10²⁴ кг
Радиус Земли
R = 6371 км

Подставим значения в формулу:

Есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с

2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с².

И кому же верить?

Все просто: для кого решается задача, тот и главный.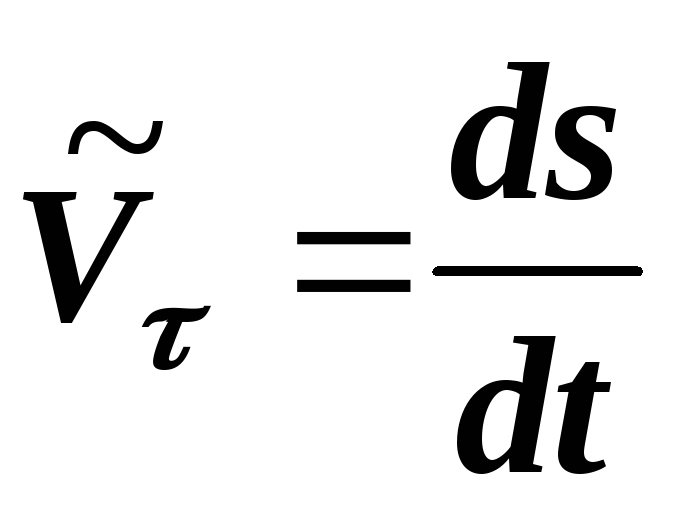 В экзаменах берем g = 10 м/с², в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с².

Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.

Равноускоренное движение – материалы для подготовки к ЕГЭ по Физике

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение – это движение с постоянным вектором ускорения . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения.

Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

. (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор ? Разумеется, функцию . Но не только: к ней можно добавить ещё произвольный постоянный вектор (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы ? В начальный момент времени скорость равна своему начальному значению: . Поэтому, полагая в формуле (2), получим:

Итак, константа – это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

. (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

, (4)

. (5)

Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

Подставляем сюда выражение для скорости, даваемое формулой (3):

(6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить , надо продифференцировать функцию . Чтобы получить , нужно продифференцировать . Не забудем добавить и произвольную константу :

Ясно, что – это начальное значение радиус-вектора в момент времени . В результате получаем искомый закон равноускоренного движения:

. (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

. (8)

. (9)

. (10)

Формулы (8) – (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что – перемещение тела. Тогда
получаем зависимость перемещения от времени:

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

где – проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

и подставим в формулу для перемещения:

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение.

Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения , направленным вертикально вниз. Почти во всех задачах при расчётах полагают м/с.

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

Имеем: – искомая скорость приземления, . Получаем: , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Здесь , так что . Вычисляем: м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

Имеем: так что , или . Решая квадратное уравнение, получим c.

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат так, как показано на рис. 1.

Рис.

1. Горизонтальный бросок

Используем формулы:

В нашем случае . Получаем:

. (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

Дальность полёта – это значение координаты в момент времени :

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью , направленной под углом к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

В нашем случае . Получаем:

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

Код и классификация направлений подготовки	Код группы образовательной программы	Наименование групп образовательных программ	Количество мест
8D01 Педагогические науки
8D011 Педагогика и психология	D001	Педагогика и психология	45
8D012 Педагогика дошкольного воспитания и обучения	D002	Дошкольное обучение и воспитание	5
8D013 Подготовка педагогов без предметной специализации	D003	Подготовка педагогов без предметной специализации	22
8D014 Подготовка педагогов с предметной специализацией общего развития	D005	Подготовка педагогов физической культуры	7
8D015 Подготовка педагогов по естественнонаучным предметам	D010	Подготовка педагогов математики	30
	D011	Подготовка педагогов физики (казахский, русский, английский языки)	23
	D012	Подготовка педагогов информатики (казахский, русский, английский языки)	35
	D013	Подготовка педагогов химии (казахский, русский, английский языки)	22
	D014	Подготовка педагогов биологии (казахский, русский, английский языки)	18
	D015	Подготовка педагогов географии	18
8D016 Подготовка педагогов по гуманитарным предметам	D016	Подготовка педагогов истории	17
8D017 Подготовка педагогов по языкам и литературе	D017	Подготовка педагогов казахского языка и литературы	37
	D018	Подготовка педагогов русского языка и литературы	24
	D019	Подготовка педагогов иностранного языка	37
8D018 Подготовка специалистов по социальной педагогике и самопознанию	D020	Подготовка кадров по социальной педагогике и самопознанию	10
8D019 Cпециальная педагогика	D021	Cпециальная педагогика	20
		Всего	370
8D02 Искусство и гуманитарные науки
8D022 Гуманитарные науки	D050	Философия и этика	20
	D051	Религия и теология	11
	D052	Исламоведение	6
	D053	История и археология	33
	D054	Тюркология	7
	D055	Востоковедение	10
8D023 Языки и литература	D056	Переводческое дело, синхронный перевод	16
	D057	Лингвистика	15
	D058	Литература	26
	D059	Иностранная филология	19
	D060	Филология	42
		Всего	205
8D03 Социальные науки, журналистика и информация
8D031 Социальные науки	D061	Социология	20
	D062	Культурология	12
	D063	Политология и конфликтология	25
	D064	Международные отношения	13
	D065	Регионоведение	16
	D066	Психология	17
8D032 Журналистика и информация	D067	Журналистика и репортерское дело	12
8D032 Журналистика и информация	D069	Библиотечное дело, обработка информации и архивное дело	3
		Всего	118
8D04 Бизнес, управление и право
8D041 Бизнес и управление	D070	Экономика	39
	D071	Государственное и местное управление	28
	D072	Менеджмент и управление	12
	D073	Аудит и налогообложение	8
	D074	Финансы, банковское и страховое дело	21
	D075	Маркетинг и реклама	7
8D042 Право	D078	Право	30
		Всего	145
8D05 Естественные науки, математика и статистика
8D051 Биологические и смежные науки	D080	Биология	40
	D081	Генетика	4
	D082	Биотехнология	19
	D083	Геоботаника	10
8D052 Окружающая среда	D084	География	10
	D085	Гидрология	8
	D086	Метеорология	5
	D087	Технология охраны окружающей среды	15
	D088	Гидрогеология и инженерная геология	7
8D053 Физические и химические науки	D089	Химия	50
8D053 Физические и химические науки	D090	Физика	70
8D054 Математика и статистика	D092	Математика и статистика	50
8D054 Математика и статистика	D093	Механика	4
		Всего	292
8D06 Информационно-коммуникационные технологии
8D061 Информационно-коммуникационные технологии	D094	Информационные технологии	80
8D062 Телекоммуникации	D096	Коммуникации и коммуникационные технологии	14
8D063 Информационная безопасность	D095	Информационная безопасность	26
		Всего	120
8D07 Инженерные, обрабатывающие и строительные отрасли
8D071 Инженерия и инженерное дело	D097	Химическая инженерия и процессы	46
	D098	Теплоэнергетика	22
	D099	Энергетика и электротехника	28
	D100	Автоматизация и управление	32
	D101	Материаловедение и технология новых материалов	10
	D102	Робототехника и мехатроника	13
	D103	Механика и металлообработка	35
	D104	Транспорт, транспортная техника и технологии	18
	D105	Авиационная техника и технологии	3
	D107	Космическая инженерия	6
	D108	Наноматериалы и нанотехнологии	21
	D109	Нефтяная и рудная геофизика	6
8D072 Производственные и обрабатывающие отрасли	D111	Производство продуктов питания	20
	D114	Текстиль: одежда, обувь и кожаные изделия	9
	D115	Нефтяная инженерия	15
	D116	Горная инженерия	19
	D117	Металлургическая инженерия	20
	D119	Технология фармацевтического производства	13
	D121	Геология	24
8D073 Архитектура и строительство	D122	Архитектура	15
	D123	Геодезия	16
	D124	Строительство	12
	D125	Производство строительных материалов, изделий и конструкций	13
	D128	Землеустройство	14
8D074 Водное хозяйство	D129	Гидротехническое строительство	5
8D075 Стандартизация, сертификация и метрология (по отраслям)	D130	Стандартизация, сертификация и метрология (по отраслям)	11
		Всего	446
8D08 Сельское хозяйство и биоресурсы
8D081 Агрономия	D131	Растениеводство	22
8D082 Животноводство	D132	Животноводство	12
8D083 Лесное хозяйство	D133	Лесное хозяйство	6
8D084 Рыбное хозяйство	D134	Рыбное хозяйство	4
8D087 Агроинженерия	D135	Энергообеспечение сельского хозяйства	5
8D087 Агроинженерия	D136	Автотранспортные средства	3
8D086 Водные ресурсы и водопользование	D137	Водные ресурсы и водопользования	11
		Всего	63
8D09 Ветеринария
8D091 Ветеринария	D138	Ветеринария	21
		Всего	21
8D11 Услуги
8D111 Сфера обслуживания	D143	Туризм	11
8D112 Гигиена и охрана труда на производстве	D146	Санитарно-профилактические мероприятия	5
8D113 Транспортные услуги	D147	Транспортные услуги	5
8D113 Транспортные услуги	D148	Логистика (по отраслям)	4
8D114 Социальное обеспечение	D142	Социальная работа	10
		Всего	35
		Итого	1815
		АОО “Назарбаев Университет”	65
		Стипендиальная программа на обучение иностранных граждан, в том числе лиц казахской национальности, не являющихся гражданами Республики Казахстан	10
		Всего	1890

Скорость, ускорение, равномерное и равноускоренное прямолинейное движение

Основные понятия и законы кинематики

Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.

Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.

По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.

Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x₀ + V_xt, где x₀ — начальная координата тела, V_x — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с², не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:

Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости ω:

Угловая скорость связана с линейной скоростью соотношением

где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν

Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.

Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).

Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде

где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле

где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения

Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.

Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.

Сила тяжести — это сила, с которой все тела притягиваются к Земле:

При неподвижной опоре вес тела равен по модулю силе тяжести:

Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес

Видно, что вес тела больше веса покоящегося тела.

При движении тела с ускорением, направленным вниз, его вес

В этом случае вес тела меньше веса покоящегося тела.

Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.

где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна

1.3. Основные понятия и законы статики и гидростатики Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).

Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.

Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.

Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:

Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей

где ρ — плотность жидкости, h — глубина проникновения в жидкость.

Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае

Высоты столбов жидкости обратно пропорциональны плотностям:

Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то

Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:

где ρ_жидк — плотность жидкости, в которую погружено тело; V_погр — объём погружённой части тела.

Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.

1.4. Законы сохранения Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:

Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:

Мощность — это работа, совершённая в единицу времени:

Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле

Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле

где h — высота подъёма

Энергия сжатой пружины:

где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.

Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.

1.5. Механические колебания и волны Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.

Величина A, равная наибольшему абсолютному значению колеблющейся физической величины x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:

Частота измеряется в с^-1. Эта единица называется герц (Гц).

Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.

Период колебаний математического маятника определяется по формуле

где l — длина маятника.

Период колебаний груза на пружине определяется по формуле

где k — жёсткость пружины, m — масса груза.

Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:

где v — скорость распространения волны.

Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.

Ускорение. Равноускоренное движение | LAMPA

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

“Движение” — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

“Ускоренное” — значит “убыстренное”, с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее… То есть скорость все время увеличивается.

Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, – это тоже “ускоренное” движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением.

Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 555 км/ч, потом 101010 км/ч, потом 151515 км/ч, 202020 км/ч, 252525 км/ч, 303030 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 101010 км/ч, потом 555 км/ч, а потом 000 км/ч. То есть скорость все время уменьшается на 555 км/ч.

Следуя этой логике, через мгновение после скорости в 000 км/ч скорость должна вновь уменьшиться на 555 км/ч, и тогда скорость будет равна −5-5−5 км/ч, а потом еще уменьшиться на 555 км/ч и стать уже −10-10−10 км/ч, а потом и −15-15−15 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о “стрелочке”), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы “Два вида физических величин: скалярные величины и векторные величины” и “Проектирование векторов на оси”. В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме “Равноускоренное движение”, а второй случай — с поворотом — в теме “Движение по окружности”, когда тело поворачивает, а значит — изменяет направление скорости.

1.6 Ускорение. Единица ускорения – Физика по учебнику 10 класса

При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.

Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.

Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости. Эту величину называют ускорением.

Ускорение- это величина, которая характеризует быстроту изменения скорости.

Среднее ускорение

Среднее ускорение – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

где – вектор ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости Δ = – ₀ (здесь ₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость ₀. В момент времени t2 тело имеет скорость. Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = – ₀. Тогда определить ускорение можно так:

Рис. 1.8. Среднее ускорение.

В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Взаимодействие тел, инертность, масса — ЗФТШ, МФТИ

Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.

Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.

Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.

Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!)

Мерой инертности является инертная масса.

Масса (инертная) – мера инертности тела.

Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: a∼1m\boxed{a\sim\frac 1m}.

Данная зависимость записана единственно правильным способом, т. к. форма m∼1am \sim \frac 1a не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела.

Данная зависимость подтверждается многочисленными опытными результатами.

Рис. 2 Измерение массы методом взаимодействия тел.

Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс:

\[\frac{a_1}{a_2} = \frac{m_2}{m_1};\]

если взять первую массу за эталонную (m1=mэтm_1 = m_\mathrm{эт}), то m2=mэтaэтa2m_2 = m_\mathrm{эт}\frac{a_\mathrm{эт}}{a_2}.

Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной.

Измерение массы методом взвешивания тел.

Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2).

Рис. 2

Рис. 3

Масса, измеренная путём взвешивания, называется гравитационной.

В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой 39 мм39\ \mathrm{мм} и диаметром 39 мм39\ \mathrm{мм}, изготовленного из сплава 10 % иридия и 90 % платины (рис.{-12} % эти массы равны.

Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности.

Принцип эквивалентности утверждает, что

1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта.

2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле.

Пример 1.

Два тела массами 400 г400\ \mathrm{г} и 600 г600\ \mathrm{г} двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с3\ \mathrm{м}/\mathrm{с}?

Решение.

Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1\frac{a_1}{a_2} = \frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:

\[\frac{m_2}{m_1} = \frac{a_1}{a_2} = \frac{\frac{\Delta v_1}{\Delta t}}{\frac{\Delta v_2}{\Delta t}} = \frac{v_\mathrm{к1}-v_{01}}{v_\mathrm{к2}-v_{02}} = \frac{v_{01}}{v_{02}},\]

откуда получим искомую скорость: v02=m1m2·v01.v_{02} = \frac{m_1}{m_2}\cdot v_{01}.

Количественно ответ будет таким: v02=0,4 кг0,6 кг·3 мс=2 мсv_{02} = \frac{0,4\ \mathrm{кг}}{0,6\ \mathrm{кг}}\cdot 3\ \frac{\mathrm{м}}{\mathrm{с}} = 2\ \frac{\mathrm{м}}{\mathrm{с}}.

Acceleration – The Physics Hypertextbook

Обсуждение

определение

Когда скорость объекта изменяется, говорят, что он ускоряется. Ускорение – это скорость изменения скорости во времени.

В повседневном английском слово «ускорение» часто используется для описания состояния увеличения скорости. Для многих американцев единственный опыт разгона – это реклама автомобилей. Когда рекламный ролик кричит «от нуля до шестидесяти за шесть целых семь десятых секунды», они говорят, что этот конкретный автомобиль занимает 6 секунд.7 с для достижения скорости 60 миль в час после полной остановки. Этот пример иллюстрирует ускорение в общепринятом понимании, но ускорение в физике – это гораздо больше, чем просто увеличение скорости.

Любое изменение скорости объекта приводит к ускорению: увеличение скорости (что люди обычно имеют в виду, когда говорят об ускорении), уменьшение скорости (также называемое замедлением или замедление ) или изменение направления (называемое центростремительным ускорением ). ).Да, верно, изменение направления движения приводит к ускорению, даже если движущийся объект не ускоряется и не замедляется. Это потому, что ускорение зависит от изменения скорости, а скорость является векторной величиной, имеющей как величину, так и направление. Таким образом, падающее яблоко ускоряется, машина, остановившаяся на светофоре, ускоряется, а Луна на орбите вокруг Земли ускоряется. Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление.

Как и скорость, есть два вида ускорения: среднее и мгновенное. Среднее ускорение определяется за «длинный» интервал времени. Слово «длинный» в этом контексте означает конечное – нечто, имеющее начало и конец. Скорость в начале этого интервала называется начальной скоростью , представленной символом v ₀ (vee ноль), а скорость в конце называется конечной скоростью , представленной символом . v (vee).Среднее ускорение – это величина, рассчитанная на основе двух измерений скорости.

а =	∆ v	=	в – в ₀
	∆ т		∆ т

Напротив, мгновенное ускорение измеряется в течение «короткого» временного интервала. Слово «короткий» в этом контексте означает бесконечно малое или бесконечно малое – не имеющее вообще никакой продолжительности или протяженности.Это математический идеал, который может быть реализован только как предел. Предел ставки, когда знаменатель приближается к нулю, называется производной . Таким образом, мгновенное ускорение является пределом среднего ускорения, когда временной интервал приближается к нулю, или, альтернативно, ускорение является производной скорости.

а =		∆ v	=	d v
		∆ т		дт

Ускорение – это производная скорости от времени, но скорость сама по себе является производной положения от времени.Производная – это математическая операция, которую можно многократно применять к паре изменяющихся величин. Выполнив это один раз, вы получите первую производную . Выполнение этого дважды (производная от производной) дает вам , вторую производную . Это делает ускорение первой производной скорости по времени и второй производной позиции по времени.

а =	d v	=	г		г с	=	г ² с
	дт		дт		дт		дт ²

Несколько слов об обозначениях.В формальном математическом письме векторы выделяются жирным шрифтом и . Скаляры и величины векторов написаны курсивом . Числа, размеры и единицы измерения пишутся римским шрифтом (не курсивом, не жирным шрифтом, не наклонным шрифтом – обычный текст). Например…

a = 9,8 м / с ², θ = −90 °

или

a = 9,8 м / с ² при −90 °

(Примечание по дизайну: я считаю, что греческие буквы плохо смотрятся на экране, когда они выделены курсивом, поэтому я решил игнорировать это правило для греческих букв, пока красивые греческие шрифты не станут нормой в Интернете.)

шт.

международных единиц

Вычисление ускорения включает деление скорости на время – или в единицах СИ, деление метра в секунду [м / с] на секунду [с]. Разделить расстояние на время дважды – это то же самое, что разделить расстояние на квадрат времени. Таким образом, единица ускорения в системе СИ – это метров в секунду в квадрате .

⎡ ⎢ ⎣	м	=	м / с	=	м		1	⎤ ⎥ ⎦
	с ²		с		с		с

натуральные единицы

Еще одна часто используемая единица – стандартное ускорение свободного падения – g.Поскольку все мы знакомы с влиянием силы тяжести на себя и окружающие нас объекты, это удобный стандарт для сравнения ускорений. Все ощущается нормально при 1 г, вдвое тяжелее при 2 г и невесомым при 0 г. Эта единица имеет точно определенное значение 9,80665 м / с ², но для повседневного использования достаточно 9,8 м / с ², а 10 м / с ² удобно для быстрой оценки.

Единица, называемая стандартным ускорением свободного падения (обозначается латинскими буквами g), отличается от естественного явления, называемого ускорением свободного падения (обозначается курсивом g ).Первый имеет определенное значение, тогда как второй необходимо измерить. (Подробнее об этом позже.)

Хотя термин «перегрузочная сила» часто используется, g является мерой ускорения, а не силы. (Подробнее о силах позже.) Особую озабоченность у людей вызывают физиологические эффекты ускорения. Для сравнения, все значения указаны в g.

В дизайне американских горок скорость имеет решающее значение. Либо это? Если бы скорость была всем, что нужно для создания захватывающей поездки, то автострада была бы довольно захватывающей.Большинство американских горок редко превышают 30 м / с (60 миль в час). Вопреки распространенному мнению, именно ускорение делает поездку интересной. Хорошо спроектированные американские горки подвергают гонщика кратковременным максимальным ускорениям от 3 до 4 g. Это то, что придает поездке ощущение опасности.
Несмотря на огромную мощность двигателей, ускорение космического челнока было ниже 3 g. Что-то большее создаст ненужную нагрузку на космонавтов, полезную нагрузку и сам корабль.Оказавшись на орбите, вся система входит в длительный период свободного падения, что дает ощущение невесомости. Такую среду с нулевым ускорением можно также смоделировать внутри специально пилотируемого самолета или башни для свободного падения. (Подробнее об этом позже.)
Пилоты-истребители могут на короткое время испытывать ускорение до 8 g во время тактических маневров. Если выдерживать более нескольких секунд, достаточно от 4 до 6 г, чтобы вызвать затемнение. Чтобы предотвратить «потерю сознания из-за перегрузки» (G-LOC), летчики-истребители носят специальные скафандры, которые сжимают ноги и живот, заставляя кровь оставаться в голове.
Пилоты и космонавты могут также тренироваться на человеческих центрифугах, способных развивать до 15 g. Воздействие таких сильных ускорений кратковременно из соображений безопасности. Люди редко подвергаются воздействию чего-либо выше 8 g дольше нескольких секунд.
Ускорение связано с травмой. Вот почему наиболее распространенным датчиком манекена для краш-тестов является акселерометр. Сильное ускорение может привести к смерти. Ускорение во время аварии, в результате которой погибла Диана, принцесса Уэльская, в 1997 году, по оценкам, составило порядка 70-100 г, что было достаточно интенсивным, чтобы оторвать легочную артерию от ее сердца – травму, пережить которую практически невозможно. .Если бы она была пристегнута ремнем безопасности, ускорение было бы примерно 30 или 35 g – достаточно, чтобы сломать одно или два ребра, но не настолько, чтобы убить большинство людей.

гауссовых единиц

Точное измерение силы тяжести над поверхностью Земли или других небесных объектов называется гравиметрией . По историческим причинам предпочтительной единицей в этой области является сантиметр на секунду в квадрате, также известный как галлонов . В символической форме…

[ галлонов = см / с ²]

Да, верно.Название единицы пишется строчными буквами (gal), а символ – заглавной (Gal). Галла была названа в честь итальянского ученого Галилео Галилея (1564–1642), который был первым ученым, изучавшим ускорение силы тяжести, и, возможно, первым ученым любого рода. Поскольку ускорение силы тяжести на поверхности большинства небесных объектов изменяется на незначительную величину, отклонения силы от идеализированных моделей (называемые гравитационными аномалиями ) измеряются в тысячных долях галлона или миллигал (мГал).

[1000 мГал = 1 галлон]

Гал и миллигал являются частью предшественника Международной системы единиц, называемой системой единиц сантиметр-грамм-секунда или гауссовой системой единиц. Возможно, однажды я действительно напишу что-нибудь важное в этом разделе этой книги.

Вот несколько примеров ускорений в конце этого раздела.

Лифт Шаттл Пуля

Ускорение выбранных событий (от наименьшего к наибольшему)
a (м / с ²)	событие
0	неподвижен или движется с постоянной скоростью
5 × 10 ⁻¹⁴	наименьшее ускорение в научном эксперименте
2.32 × 10 ⁻¹⁰	галактическое ускорение на Солнце
9 × 10 ⁻¹⁰	аномальное ускорение космического корабля “Пионер”
0,5	лифт гидравлический
0,63	Ускорение свободного падения на Плутоне
1	, трос
1,6	Ускорение свободного падения на Луне
8,8	Международная космическая станция на орбите
3.7	Ускорение свободного падения на Марсе
9,8	Ускорение свободного падения на Земле
10–40	пилотируемая ракета при старте
20	, пик
24,8	Ускорение свободного падения на Юпитере
20–50	американские горки
80	предел устойчивой толерантности человека
0–150	центрифуга для обучения человека
100–200	катапультное сиденье
270	Ускорение свободного падения на Солнце
600	подушки безопасности автоматически срабатывают
10 ⁴ –10 ⁶	медицинская центрифуга
10 ⁶	в стволе пистолета
10 ⁶	Ускорение свободного падения на звезде белого карлика
10 ¹²	Ускорение свободного падения нейтронной звезды

Автомобильные ускорения (g)
событие	типичный автомобиль	спортивный автомобиль	Гоночный автомобиль Ф-1	большой грузовик
начиная с	0.3–0,5	0,5–0,9	1,7	<0,2
торможение	0,8–1,0	1,0–1,3	2	~ 0,6
поворот	0,7–0,9	0,9–1,0	3

Авария

Ускорение и человеческое тело
a (г)	событие
02.9	чихать
03,5	кашель
03,6	толпа толпа
04,1	шлепок по спине
08,1	подножка
10,1	плюхнуться на стул
60	Ускорение грудной клетки при ДТП со скоростью 48 км / ч с подушкой безопасности
70–100	, в которой погибла Диана, принцесса Уэльская, 1997 г.
150–200	Предел ускорения головы при велосипедной аварии со шлемом

Ускорение в калькуляторе электрического поля

Есть два основных типа полей, которые действуют на заряженные частицы: электрическое и магнитное.В нашем калькуляторе ускорения в электрическом поле мы сосредоточились на первом. Если вы хотите узнать больше о последнем, ознакомьтесь с нашим калькулятором силы Лоренца. В тексте ниже мы объясняем, какова сила, действующая на заряженную частицу в электрическом поле, и как можно вычислить ускорение этой частицы.

Заряженная частица в электромагнитном поле

Одна из фундаментальных сил природы, электромагнитная сила, состоит из электрического и магнитного полей.С одной стороны, электрическое поле всегда действует на заряженную частицу, а с другой стороны, магнитное поле действует только тогда, когда эта частица движется.

Величина силы F , которая действует на заряженную частицу в электрическом поле E , может быть описана законом Кулона. В нем указано, что F = q * E , где q – заряд частицы. Вы можете видеть, что частицы с более высоким зарядом всегда будут сильнее притягиваться (или отталкиваться).

Ускорение в электрическом поле

Если мы также учтем массу частицы, мы сможем вычислить ее ускорение. Для этого воспользуемся следующей формулой:

a = q * E / м

где

a – ускорение частицы,
q – заряд частицы,
м – масса частицы,
E – электрическое поле.(-19) C одного электрона. Вышеприведенное уравнение легко вывести из второго закона Ньютона: F = m * a . Нам просто нужно совместить это с электростатической силой F = q * E , описанной в предыдущем разделе.
Ускорение электронов
Какова величина ускорения электрона в типичном электрическом поле? Похоже ли это на гравитационную силу нашей Земли? Давайте проверим это с помощью нашего калькулятора, предположив, что у нас есть электрон с массой me и зарядом e в относительно слабом электрическом поле E = 1 N / C .Результат потрясающий! Электрон ускоряется почти в 20 миллиардов раз быстрее, чем среднее ускорение свободного падения на Земле.
В поисках ускорения
Как было сказано ранее в Уроке 3 (а также в Уроке 2), результирующая сила – это векторная сумма всех индивидуальных сил. В Уроке 2 мы узнали, как определить чистую силу, если известны величины всех отдельных сил. В этом уроке мы узнаем, как определить ускорение объекта, если известны величины всех индивидуальных сил.Три основных уравнения, которые будут полезны: уравнение для чистой силы (F _net = m • a), уравнение для гравитационной силы (F _grav = m • g) и уравнение для силы трения (F _frict = μ • F _норма).
Процесс определения ускорения объекта требует, чтобы известны масса и чистая сила. Если масса (м) и полезная сила (F _net) известны, то ускорение определяется с помощью уравнения.
a = F _нетто / м
Ваша очередь практиковаться
Таким образом, задача включает использование приведенных выше уравнений, данной информации и вашего понимания законов Ньютона для определения ускорения. Чтобы понять, как применяется этот метод, попробуйте выполнить следующие практические задачи. Решив проблемы, нажмите кнопку, чтобы проверить свои ответы.
Практика №1
Приложенная сила 50 Н используется для ускорения объекта вправо по фрикционной поверхности.Объект встречает трение 10 Н. Используйте диаграмму, чтобы определить нормальную силу, чистую силу, массу и ускорение объекта. (Пренебрегая сопротивлением воздуха.)

Практика №2
Приложенная сила 20 Н используется для ускорения объекта вправо по фрикционной поверхности.Объект встречает трение 10 Н. Используйте диаграмму, чтобы определить нормальную силу, чистую силу, коэффициент трения (μ) между объектом и поверхностью, массу и ускорение объекта. (Пренебрегая сопротивлением воздуха.)

Практика №3
Объект весом 5 кг скользит вправо и сталкивается с силой трения, которая его замедляет.Коэффициент трения (μ) между объектом и поверхностью составляет 0,1. Определите силу тяжести, нормальную силу, силу трения, чистую силу и ускорение. (Пренебрегая сопротивлением воздуха.)
Ниже представлены еще пара практических задач. Вы должны постараться решить как можно больше проблем без помощи заметок, решений, учителей и других учеников.Примите решение индивидуально решать проблемы. А пока стоит упомянуть важное предостережение:
Избегайте превращения проблемы в форму ранее решенной проблемы. Проблемы в физике редко выглядят одинаково. Вместо того чтобы решать проблемы наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свое понимание веса и массы, чтобы найти m или Fgrav в проблеме.Используйте свое концептуальное понимание чистой силы (векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы. Не отделяйте решение физических задач от вашего понимания концепций физики. Если вы не можете решать физические задачи, подобные приведенным выше, это не обязательно означает, что у вас есть математические трудности. Вполне вероятно, что у вас проблемы с физическими концепциями.
Мы хотели бы предложить… Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений прилагаемой силы, чистой силы, массы и трения на ускорение объекта.
Проверьте свое понимание
1. Эдвардо применяет направленную вправо силу 4,25 Н к книге весом 0,765 кг, чтобы ускорить ее по столешнице. Коэффициент трения между книгой и столешницей 0,410. Определите ускорение книги.

2. В физической лаборатории Кейт и Роб используют подвесную массу и систему шкивов, чтобы приложить 2.Сила 45 Н, направленная вправо на тележку массой 0,500 кг, чтобы разогнать ее по гусенице с низким коэффициентом трения. Если общая сила сопротивления движению тележки составляет 0,72 Н, то каково ускорение тележки?
Как рассчитать ускорение | Sciencing
Обновлено 14 декабря 2020 г.
Крис Дезил
Скорость и ускорение – два фундаментальных понятия в механике или физике движения, и они взаимосвязаны.Если вы измеряете скорость объекта во время записи времени, а затем снова измеряете ее немного позже, также во время записи времени вы можете найти ускорение, которое представляет собой разницу этих скоростей, деленную на временной интервал. Это основная идея, хотя в некоторых задачах вам может потребоваться получить скорость из других данных.
Есть еще один способ рассчитать ускорение на основе законов Ньютона. Согласно первому закону, тело остается в состоянии равномерного движения, если на него не действует сила, а второй закон выражает математическую зависимость между величиной силы ( F ) и ускорением ( a ) тело массой м испытывает из-за этой силы.Соотношение: F = ma . Если вы знаете величину силы, действующей на тело, и знаете массу тела, вы можете сразу же вычислить ускорение, которое оно испытывает.
Уравнение среднего ускорения
Представьте себе машину на шоссе. Если вы хотите узнать, насколько быстро он идет, а спидометр не работает, вы выбираете две точки на его пути: x ₁ и x _2, и смотрите на свои часы. как машина проезжает каждую точку.Средняя скорость автомобиля – это расстояние между двумя точками, деленное на время, которое требуется автомобилю, чтобы проехать их обе. Если время на часах x ₁ равно t _1,, а время x ₂ равно t ₂, скорость автомобиля ( s ):
s = \ frac {\ Delta x} {\ Delta t} = \ frac {x_2-x_1} {t_2-t_1}
Теперь предположим, что спидометр автомобиля работает, и он записывает две разные скорости в точках x ₁ и x ₂.Поскольку скорости разные, машина должна была разгоняться. Ускорение определяется как изменение скорости за определенный промежуток времени. Это может быть отрицательное число, что означает, что автомобиль замедлился. Если мгновенная скорость, записанная спидометром в момент времени t ₁, составляет с ₁, а скорость в момент времени t ₂ составляет с ₂, ускорение ( a ) между точками x ₁ и x ₂ составляет:
a = \ frac {\ Delta s} {\ Delta t} = \ frac {s_2-s_1} {t_2-t_1}
Это уравнение среднего ускорения говорит вам, что если вы измеряете скорость в определенное время и снова измеряете ее в другое время, ускорение – это изменение скорости, деленное на временной интервал.Единицами скорости в системе СИ являются метры в секунду (м / с), а единицами ускорения – метры в секунду в секунду (м / с / с), что обычно обозначается как м / с ². В британской системе единиц измерения ускорения предпочтительными являются футы в секунду в секунду или фут в секунду ².
Пример : самолет летит со скоростью 100 миль в час сразу после взлета и достигает крейсерской высоты через 30 минут, когда он летит со скоростью 500 миль в час. Каково было его среднее ускорение при подъеме на крейсерскую высоту?
Мы можем использовать полученную выше формулу ускорения.2
Второй закон Ньютона предоставляет калькулятор ускорения
Уравнение, которое выражает второй закон Ньютона, F = ма , является одним из наиболее полезных в физике и служит формулой ускорения. Единицей силы в системе СИ является Ньютон (Н), названный в честь самого сэра Исаака. Один Ньютон – это сила, необходимая для того, чтобы придать массе в 1 килограмм ускорение в 1 м / с ². В имперской системе единицей измерения силы является фунт.Вес также измеряется в фунтах, поэтому, чтобы отличить массу от силы, единицы силы называются фунтами-силой (фунт-сила).
Вы можете изменить уравнение Ньютона, чтобы найти ускорение, разделив обе части на м . Вы получите:
a = \ frac {F} {m}
Используйте это выражение в качестве калькулятора ускорения, когда вы знаете массу и величину приложенной силы.
Пример: Объект массой 8 кг. испытывает силу 20 Ньютонов.2
3.3 Среднее и мгновенное ускорение
Цели обучения
К концу этого раздела вы сможете:
Рассчитайте среднее ускорение между двумя точками времени.
Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
Объясните векторную природу мгновенного ускорения и скорости.
Объясните разницу между средним ускорением и мгновенным ускорением.
Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космического пространства и крошечный мир субатомной физики. В бытовом разговоре ускорить означает ускориться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени.Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение – это скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t} _ {\ text {f}} – {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] – среднее ускорение, v – скорость, а t – время.(Полоса над и означает среднее ускорение .)
Поскольку ускорение – это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с ², то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду скорость меняется каждую секунду. Напомним, что скорость – это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение направления.Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях. Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение – это вектор в том же направлении, что и , изменение скорости на , [latex] \ text {Δ} v [/ latex].Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением , (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10 Поезд метро в Сан-Паулу, Бразилия, замедляется при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки)
Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы его не используем. Ускорение – это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат.В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление на противоположное. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это проиллюстрировано на (Рисунок).
Рисунок 3.11 Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление. Через достаточно долгое время он проходит исходную точку в обратном направлении.
Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, ускоряется из состояния покоя до скорости 15,0 м / с на запад за 1,80 с. Какое у него среднее ускорение?
Рисунок 3.12 Скаковые лошади ускоряются из-за ворот. (кредит: Джон Салливан)
Стратегия
Сначала мы рисуем эскиз и назначаем систему координат задаче (рисунок). Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.
Мы можем решить эту проблему, определив [latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t} _ {\ text {f}} – {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = – 15.0 \, \ text {m / s} [/ latex] (отрицательный знак указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ text {Δ} v = {v} _ {\ text {f}} – {v} _ {0} = {v} _ {\ text {f}} = – 15.0 \, \ text { РС}. [/ латекс]
Наконец, подставьте известные значения ([latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex]) и решите для неизвестного [latex] \ overset {\ text {-}} {a} [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {-15.{2}. [/ латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с ² на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с ². Это действительно среднее ускорение, потому что езда не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ латекс]
Мгновенное ускорение
Мгновенное ускорение Ускорение или в определенный момент времени получается с использованием того же процесса, который описан для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя точками времени, разделенными [латексом] \ text {Δ} t [/ latex], и позволяем [latex] \ text {Δ} t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая составляет мгновенное ускорение и математически выражается как
.
[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На (Рисунок) мгновенное ускорение в момент времени t ₀ – это наклон касательной к графику зависимости скорости от времени в момент времени t ₀. Мы видим, что среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} [/ latex] приближается к мгновенному ускорению, как [латекс] \ text {Δ} t [/ latex] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14 На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ { \ text {f}} – {v} _ {i}} {{t} _ {\ text {f}} – {t} _ {i}} [/ latex] между временами [латекс] \ text {Δ} t = {t} _ {6} – {t} _ {1}, \ text {Δ} t = {t} _ {5} – {t} _ {2} [/ латекс] и [латекс] \ текст {Δ} t = {t} _ {4} – {t} _ {3} [/ latex]. Когда [latex] \ text {Δ} t \ to 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости.В этой точке мгновенное ускорение – это наклон касательной, равный нулю. В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием (Рисунок) (b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок) (а), который представляет собой прямую линию.Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на (Рисунок) (b). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15 (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).
Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя (рисунок).{2} \, \ text {m / s} [/ латекс].
Найдите функциональную форму ускорения.
Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную от функции скорости.{2} [/ латекс]
При t = 1 с, скорость [latex] v (1 \, \ text {s)} = 15 \, \ text {m / s} [/ latex] положительна, а ускорение положительно, поэтому и скорость, и ускорение в том же направлении. Частица движется быстрее.

При t = 2 с, скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.

При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.

При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = – 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.

Мы можем увидеть эти результаты графически на (Рисунок).

Рис. 3.16 (a) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклон касательных – это ускорение. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица поменяла направление на обратное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.

Значение

Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться.Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.

Проверьте свое понимание

Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.

Показать решение
Если принять восток за положительное значение, тогда самолет имеет отрицательное ускорение, потому что он ускоряется на запад.Он также замедляется; его ускорение противоположно направлению его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта. (Рисунок) представлено ускорение различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
Типичные значения ускорения (кредит: Википедия: порядки величин (ускорение))
Разгон Значение (м / с ²)
Скоростной поезд 0,25
Лифт 2
Гепард 5
Объект в свободном падении без сопротивления воздуха у поверхности Земли 9,8
Максимум космического челнока во время запуска 29
Пик парашютиста при нормальном раскрытии парашюта 59
Самолет F16 выходит из пикирования 79
Взрывное выброс сиденья с самолета 147
Ракета Sprint 982
Максимальное максимальное ускорение ракетных салазок 1540
Прыгающая блоха 3200
Бейсбольный мяч, пораженный битой 30 000
Закрытие губки ловушки-ловушки 1 000 000
Протон в большом адронном коллайдере [латекс] 1.{9} [/ латекс]
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массивностью. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.(Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.
Рис. 3.17 Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (б) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Сводка
Ускорение – это скорость изменения скорости. Ускорение – это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ – метр на секунду в квадрате.
Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение – это наклон графика зависимости скорости от времени.
Отрицательное ускорение (иногда называемое замедлением) – это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость оставалась постоянной, когда ускорение не равно нулю?
Показать решение
Нет, в одном измерении для постоянной скорости требуется нулевое ускорение.
Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение – нет.
Показать решение
Мяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным g (9,80 м / с ²), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Покажи ответ
Пассажир выезжает на машине из гаража с ускорением 1,40 м / с ². а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены).Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с ²)?
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
среднее ускорение
скорость изменения скорости; изменение скорости с течением времени
мгновенное ускорение
ускорение в определенный момент времени
3.3 Среднее и мгновенное ускорение – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
Рассчитайте среднее ускорение между двумя точками времени.
Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
Объясните векторную природу мгновенного ускорения и скорости.
Объясните разницу между средним ускорением и мгновенным ускорением.
Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космического пространства и крошечный мир субатомной физики. В бытовом разговоре ускорить означает ускориться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени.Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение – это скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ { 0}} {{t} _ {\ text {f}} – {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] – среднее ускорение, v – скорость, а t – время.(Полоса над и означает среднее ускорение .)
Поскольку ускорение – это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с ², то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду скорость меняется каждую секунду. Напомним, что скорость – это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение направления.Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях. Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение – это вектор в том же направлении, что и , изменение скорости на , [latex] \ Delta v [/ latex].Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением Рисунок , мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10 Поезд метро в Сан-Паулу, Бразилия, замедляется, когда он заходит на станцию. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки)
Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы его не используем. Ускорение – это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат.В случае поезда на рисунке ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление на противоположное. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на рисунке.
Рисунок 3.11 Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление. Через достаточно долгое время он проходит исходную точку в обратном направлении.
Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, ускоряется из состояния покоя до скорости 15,0 м / с на запад за 1,80 с. Какое у него среднее ускорение?
Рисунок 3.12 Скаковые лошади ускоряются из-за ворот. (кредит: Джон Салливан)
Стратегия
Сначала мы рисуем эскиз и назначаем систему координат проблемному рисунку. Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.
Мы можем решить эту проблему, определив [latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнения [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ {0}} {{t } _ {\ text {f}} – {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = – 15.0 \, \ text {m / s} [/ latex] (отрицательный знак указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ Delta v = {v} _ {\ text {f}} – {v} _ {0} = {v} _ {\ text {f}} = – 15,0 \, \ text {м / с }. [/ latex]
Наконец, подставьте известные значения ([latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex]) и найдите неизвестное [latex] \ overset {\ text {-}} {a } [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {-15.{2}. [/ Латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с ² на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с ². Это действительно среднее ускорение, потому что езда не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ Латекс]
Мгновенное ускорение
Мгновенное ускорение Ускорение или в определенный момент времени получается с использованием того же процесса, который описан для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя точками времени, разделенными [латексом] \ Delta t [/ latex], и позволяем [latex] \ Delta t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая составляет мгновенное ускорение и математически выражается как
.
[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На рисунке мгновенное ускорение в момент времени t ₀ – это наклон касательной к графику зависимости скорости от времени в момент времени t ₀. Мы видим, что среднее ускорение [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} [/ latex] приближается к мгновенному ускорению, как [latex] \ Delta t [/ latex ] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14 На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} – {v} _ {i}} {{t} _ {\ text {f}} – {t} _ {i}} [/ latex] между временами [латекс] \ Delta t = {t} _ {6} – {t} _ {1}, \ Delta t = {t} _ {5} – {t} _ {2} [/ latex] и [latex] \ Delta t = {t} _ {4} – { t} _ {3} [/ latex]. Когда [latex] \ Delta t \ равняется 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение – это наклон касательной, равный нулю.В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием рисунка (b), графика зависимости скорости от времени на рисунке, чтобы найти ускорение графически. Этот график изображен на рисунке (а), который представляет собой прямую линию. Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на рисунке (b).В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15 (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).
Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя рисунок.{2} \, \ text {m / s} [/ латекс].
Найдите функциональную форму ускорения.
Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную от функции скорости.{2} [/ латекс]
При t = 1 с, скорость [latex] v (1 \, \ text {s)} = 15 \, \ text {m / s} [/ latex] положительна, а ускорение положительно, поэтому и скорость, и ускорение в том же направлении. Частица движется быстрее.
При t = 2 с скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.
При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = – 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем видеть эти результаты графически на рисунке.
Рис. 3.16 (a) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклон касательных – это ускорение. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица поменяла направление на обратное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.
Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться.Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
Показать решение
Если мы возьмем восток за положительное значение, тогда самолет будет иметь отрицательное ускорение, потому что он ускоряется на запад.Он также замедляется; его ускорение противоположно направлению его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта. На рисунке представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
Типичные значения ускорения (кредит: Википедия: порядки величин (ускорение))
Разгон Значение (м / с ²)
Скоростной поезд 0,25
Лифт 2
Гепард 5
Объект в свободном падении без сопротивления воздуха у поверхности Земли 9,8
Максимум космического челнока во время запуска 29
Пик парашютиста при нормальном раскрытии парашюта 59
Самолет F16 выходит из пикирования 79
Взрывное выброс сиденья с самолета 147
Ракета Sprint 982
Максимальное максимальное ускорение ракетных салазок 1540
Прыгающая блоха 3200
Бейсбольный мяч, пораженный битой 30 000
Закрытие губки ловушки-ловушки 1 000 000
Протон в большом адронном коллайдере [латекс] 1.{9} [/ латекс]
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массивностью. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.На рисунке показано графическое сравнение среднего ускорения с мгновенным ускорением для двух очень разных движений.
Рис. 3.17 Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (б) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Сводка
Ускорение – это скорость изменения скорости. Ускорение – это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ – метр на секунду в квадрате.
Ускорение может быть вызвано изменением величины или направления скорости, или и тем, и другим.
Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение – это наклон графика зависимости скорости от времени.
Отрицательное ускорение (иногда называемое замедлением) – это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость оставалась постоянной, когда ускорение не равно нулю?
Показать решение
Нет, в одном измерении постоянная скорость требует нулевого ускорения.
Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение – нет.
Показать решение
Мяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным g (9,80 м / с ²), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Показать ответ
Пассажир выезжает на машине из гаража с ускорением 1,40 м / с ². а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, межконтинентальная баллистическая ракета выходит из состояния покоя на суборбитальную скорость 6,50 км / с за 60 секунд.0 с (фактическая скорость и время классифицируются). Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с ²)?
Показать решение
[латекс] a = 11,1 г [/ латекс]
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
среднее ускорение
скорость изменения скорости; изменение скорости с течением времени
мгновенное ускорение
ускорение в определенный момент времени
Расчет ускорения свободного падения: формула и концепция – стенограмма видео и урока
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что объект ускоряется всякий раз, когда на него действует чистая внешняя сила, и чистая сила равна массе объекта, умноженной на его ускорение.Математически это задается формулой F = m * a , где F – чистая сила, действующая на объект, m – масса объекта, а a – ускорение.
Как видно из формулы, масса является мерой сопротивления объекта ускорению. Масса также является мерой количества вещества в объекте. Массу часто путают с весом. Вес – сила тяжести, действующая на объект. Вес объекта зависит от его местоположения во Вселенной.
Например, если бы вы стояли на поверхности Луны, ваш вес был бы примерно 1/6 вашего веса на поверхности Земли. Это связано с тем, что среднее ускорение свободного падения на поверхности Луны составляет примерно 1/6 среднего ускорения свободного падения на поверхности Земли. Если вы хотите быстро похудеть, отправляйтесь на Луну!
К сожалению, поскольку масса – это количество вещества, содержащегося в вашем теле, ваша масса постоянна во всей Вселенной.Если вы хотите похудеть, правильнее будет сказать, что вы пытаетесь сбросить массу. Это потому, что на самом деле вы пытаетесь уменьшить размер своего тела, а не просто уменьшить количество чешуек.
Когда ускорение происходит под действием силы тяжести, мы заменяем a на g во втором законе движения Ньютона, где g представляет ускорение свободного падения. Как мы заявляли ранее, сила тяжести, действующая на вещество, определяется как вес, поэтому мы заменяем F на W .Тогда формула принимает вид Вт = мг.
Мы могли бы решить для г , чтобы получить формулу г = Вт / м , но эта форма уравнения не обеспечивает практического применения для определения ускорения свободного падения. Второй закон Ньютона в форме W = mg наиболее полезен для связи веса и массы, когда ускорение свободного падения уже известно.
Закон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона гласит, что каждый объект оказывает гравитационную силу на любой другой объект.2.
Довольно часто, когда мы используем эту формулу, масса одного объекта намного больше массы другого объекта. Например, когда мы рассматриваем силу тяжести, действующую на наши тела, два вовлеченных объекта – это наши тела и Земля. Другой пример – сила тяжести, действующая на мяч, когда он свободно падает на землю после того, как его бросили прямо вверх.
И масса наших тел, и масса шара ничтожны по сравнению с массой Земли.В этом случае мы можем заменить m1 и m2 в формуле на m для представления гораздо меньшего объекта и M для представления гораздо большего объекта. Как показывает формула, d – это расстояние между центрами двух объектов. Расстояние от центра Земли до центра наших тел или до центра шара по существу такое же, как расстояние от центра Земли до поверхности Земли. Следовательно, мы также можем заменить d на R , что является средним радиусом Земли.2 , который определяет ускорение свободного падения, когда у нас есть массивный объект, оказывающий гравитационную силу на другой объект с относительно незначительной массой. Примером такой ситуации является сила притяжения Земли на наши тела.
Выделенный словарь
Гравитация и Ньютон
Второй закон движения Ньютона : объект ускоряется всякий раз, когда на него действует чистая внешняя сила, и чистая сила равна массе объекта, умноженной на его ускорение
Масса : мера сопротивления объекта ускорению; мера количества материи в объекте
Вес : сила тяжести, действующая на объект
Закон всемирного тяготения Ньютона : каждый объект оказывает гравитационную силу на любой другой объект; он пропорционален массе обоих объектов и обратно пропорционален квадрату расстояния между их центрами
Результаты обучения
Этот урок направлен на то, чтобы пролить свет на гравитационное ускорение, чтобы помочь вам:
Обсудить основы формулы, связанные с ускорением свободного падения
Различия между массой и массой
Государственные законы Ньютона
Рассчитайте ускорение по формулам Ньютона
.

Разгон	Значение (м / с ²)
Скоростной поезд	0,25
Лифт	2
Гепард	5
Объект в свободном падении без сопротивления воздуха у поверхности Земли	9,8
Максимум космического челнока во время запуска	29
Пик парашютиста при нормальном раскрытии парашюта	59
Самолет F16 выходит из пикирования	79
Взрывное выброс сиденья с самолета	147
Ракета Sprint	982
Максимальное максимальное ускорение ракетных салазок	1540
Прыгающая блоха	3200
Бейсбольный мяч, пораженный битой	30 000
Закрытие губки ловушки-ловушки	1 000 000
Протон в большом адронном коллайдере	[латекс] 1.{9} [/ латекс]

Ускорение свободного падения — формулы, примеры и определение

Сила тяготения

Ускорение свободного падения

Ускорение свободного падения на разных планетах

И кому же верить?

Равноускоренное движение – материалы для подготовки к ЕГЭ по Физике

Зависимость скорости от времени.

Закон движения.

Прямолинейное равноускоренное движение.

Свободное падение.

Горизонтальный бросок.

Бросок под углом к горизонту.

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

Скорость, ускорение, равномерное и равноускоренное прямолинейное движение

Основные понятия и законы кинематики

Основные понятия и законы динамики

Ускорение. Равноускоренное движение | LAMPA

Что такое ускоренное движение

1.6 Ускорение. Единица ускорения – Физика по учебнику 10 класса

Среднее ускорение

Взаимодействие тел, инертность, масса — ЗФТШ, МФТИ

Acceleration – The Physics Hypertextbook

Обсуждение

определение

шт.

международных единиц

натуральные единицы

гауссовых единиц

Ускорение в калькуляторе электрического поля

Заряженная частица в электромагнитном поле

Ускорение в электрическом поле

Ускорение электронов

В поисках ускорения

Как рассчитать ускорение | Sciencing

Уравнение среднего ускорения

Второй закон Ньютона предоставляет калькулятор ускорения

3.3 Среднее и мгновенное ускорение

Цели обучения

Среднее ускорение

Среднее ускорение

Ускорение как вектор

Пример

Расчет среднего ускорения: скакун покидает ворота

Стратегия

Решение

Значение

Мгновенное ускорение

Стратегия

Значение

Проверьте свое понимание

Ощущение ускорения

Сводка

Концептуальные вопросы

Глоссарий

3.3 Среднее и мгновенное ускорение – Университетская физика, том 1

Цели обучения

Среднее ускорение

Среднее ускорение

Ускорение как вектор

Пример

Расчет среднего ускорения: скакун покидает ворота

Стратегия

Решение

Значение

Мгновенное ускорение

Стратегия

Значение

Проверьте свое понимание

Ощущение ускорения

Сводка

Концептуальные вопросы

Глоссарий

Расчет ускорения свободного падения: формула и концепция – стенограмма видео и урока

Второй закон движения Ньютона

Закон всемирного тяготения Ньютона

Выделенный словарь

Результаты обучения

Оставить комментарий Отменить ответ