Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4.  § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23.  УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48.  § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7.  Элементы статики§ 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 36.  КИНЕТИЧЕСКАЯ ЭНЕРГИЯ§ 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
Как найти ускорение от равнодействующей силы? – Обзоры Вики
Второй закон Ньютона можно выразить как «результирующая сила = масса × ускорение»Или« Ускорение объекта прямо пропорционально результирующей (или чистой) силе, в том же направлении, что и сила, и обратно пропорционально массе объекта ».
Точно так же, как вы находите ускорение с силой трения и массой? Сила трения зависит от массы объекта плюс коэффициент трения скольжения между объектом и поверхностью, по которой он скользит. Вычесть эту силу из приложенной силы найти ускорение тела.
Во-вторых, как найти ускорение без учета коэффициента трения? если на тело массой m действует горизонтальная сила F, когда оно покоится на горизонтальной поверхности, где коэффициент трения равен u, как найти ускорение? Без трения мы бы просто использовали F = m*a, поэтому а = Ф / м.
Как вы рисуете векторы ускорения?
Определение ускорения по диаграмме движения
выберите два последовательных вектора скорости, нарисуйте их, начиная с одной точки, постройте вектор (стрелку), соединяющий вершину первого вектора скорости с вершиной второго вектора скорости.
Построенный вами вектор представляет собой ускорение.
тогда как найти ускорение частицы? Ускорение (a) представляет собой изменение скорости (Δv) за изменение времени (Δt), представленное уравнением а = Δv / Δt.
Как найти ускорение, имея только массу?
Например, если объект ускоряется в течение 5 секунд: 30 ÷ 5 = 6 м/с². Разделите силу, действующую на тело, на это ускорение. Если, например, на него действует сила в 12,000 12,000 ньютонов: 6 2,000 ÷ XNUMX = XNUMX XNUMX. Это масса объекта, измеряемая в килограммах.
Как найти ускорение шкива с трением?
com/embed/y1kqH63-828″ frameborder=”0″ allowfullscreen=”allowfullscreen” data-original-w=”720″ data-original-h=”520″> Как показать ускорение на диаграмме движения?
Как найти ускорение на графике движения?
Ускорение может быть рассчитывается путем деления изменения скорости (измеряемой в метрах в секунду) на время, затраченное на изменение (в секундах). Единицы ускорения – м / с / с или м / с. 2.
Чему равно ускорение за 2 секунды? Ускорение 2 м/с/с означает, что скорость автомобиля изменяется на 2 м/с каждую секунду. Если скорость автомобиля начинается с 0 м/с и изменяется на 2 м/с в первую секунду, то через 2 секунду он будет двигаться со скоростью 1 м/с.
Как найти ускорение частицы на графике?
Как найти ускорение через массу и время? Физика для детей
- Ускорение = (изменение скорости)/(изменение во времени) или. а = Δv ÷ Δt.
- Сила = масса * ускорение. золото. Ф = мой.
- ускорение = сила/масса. золото. а = Ф/м.
Как найти ускорение системы с несколькими шкивами?
Как найти ускорение двух тел на шкиве? Два груза массами 80 и 140 кг висят на веревке, натянутой на шкив. Вы можете считать, что веревка невесома и нерастяжима, а шкив не имеет трения. Найти ускорение меньшей массы вверх и силу натяжения веревки.
…
Мы хотим знать.
| = | М−м | g |
|---|---|---|
| М+м |
Как найти ускорение тела с помощью шкива?
Рассчитайте силу тяжести, воздействующую на базовую систему шкивов, используя следующее уравнение: G = M xn (ускорение свободного падения). Гравитационное ускорение является постоянной величиной, равной 9.8 м/с². Масса M = 9 г, поэтому G = 9 г x 9.8 м/с² = 88.2 г/с² или 88.2 ньютона.
Как найти ускорение в бегущей ленте?
2.
4 Ускорение – физика колледжа 2eЦели обучения
К концу этого раздела вы сможете:
- Определение и различие между мгновенным ускорением, средним ускорением и замедлением.
- Вычислить ускорение, зная начальное время, начальную скорость, конечное время и конечную скорость.
Рисунок 2.12 Самолет снижает скорость или замедляется перед посадкой на Сен-Мартене. Его ускорение противоположно направлению его скорости. (кредит: Стив Конри, Flickr)
В повседневном разговоре ускорить означает ускорить. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше ускорение, тем больше изменение скорости за данное время. Формальное определение ускорения соответствует этим понятиям, но более широкое.
Среднее ускорение
Среднее ускорение — это скорость изменения скорости ,
0005
, где a-a- — среднее ускорение, vv — скорость, tt — время.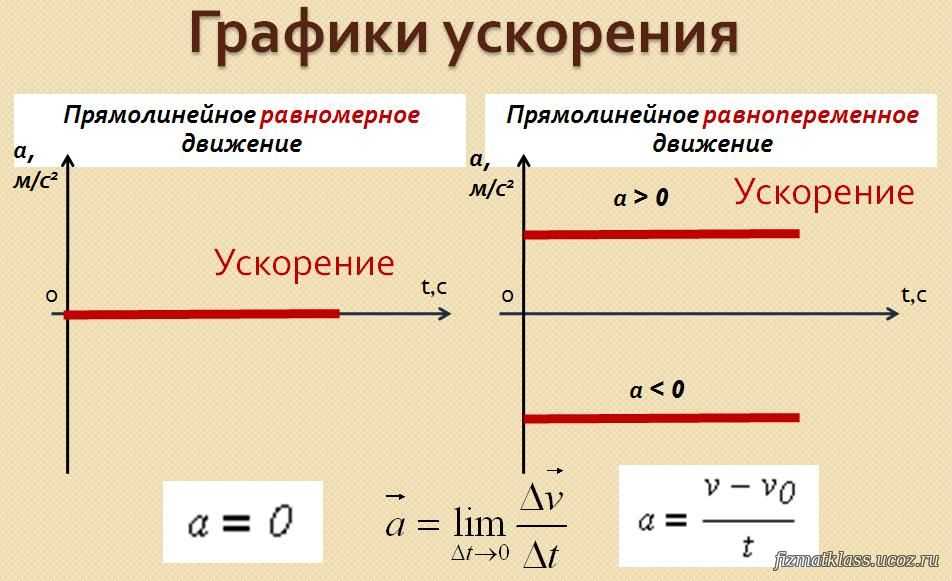
Поскольку ускорение представляет собой скорость в м/с, деленную на время в с, единицами СИ для ускорения являются м/с2 м/с2, метры в секунду в квадрате или метры в секунду на секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.
Напомним, что скорость — это вектор, у нее есть и величина, и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направление . Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
Ускорение как вектор
Ускорение — это вектор в том же направлении, что и изменение скорости, ΔvΔv.
Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление.
Рисунок 2.13 Поезд метро в Сан-Паулу, Бразилия, замедляет скорость, приближаясь к станции. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки, Flickr)
Предупреждение о неправильном представлении: замедление против отрицательного ускорения
Под замедлением всегда подразумевается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Отрицательное ускорение, однако, является ускорением 
Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим рисунок 2.14.
Рисунок
2.14
а) Этот автомобиль ускоряется, двигаясь вправо. Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется ( , а не замедление).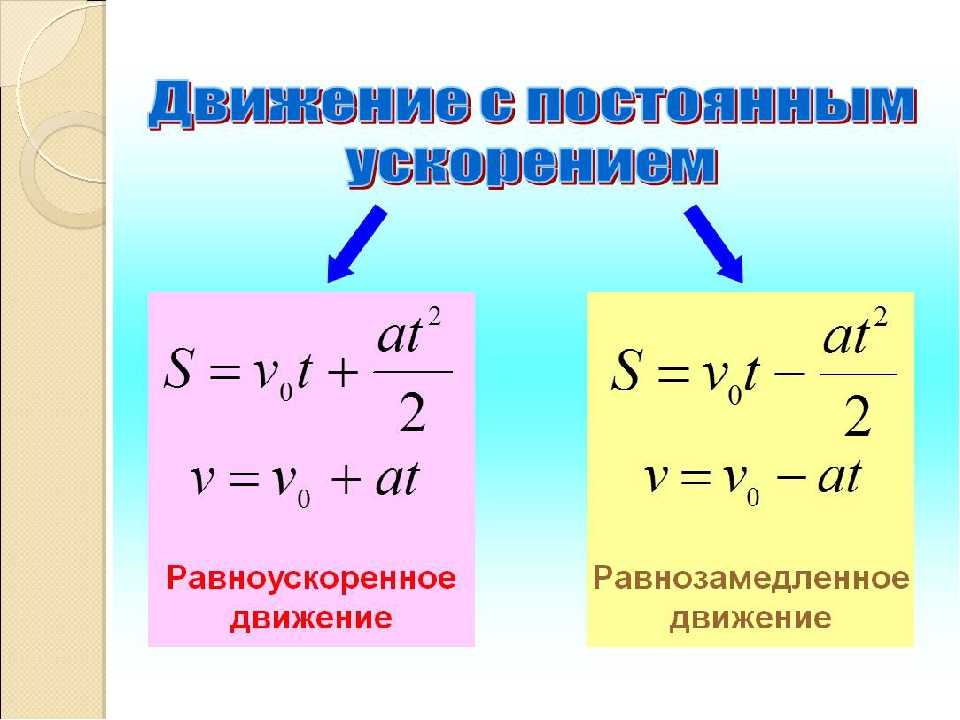
Пример 2.1
Расчет ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?
Рисунок 2,15 (Фото: Jon Sullivan, PD Photo.org)
Стратегия
Сначала мы рисуем эскиз и назначаем проблеме систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 2.16
Мы можем решить эту проблему, определив ΔvΔv и ΔtΔt из данной информации, а затем рассчитав среднее ускорение непосредственно из уравнения a-=ΔvΔt=vf−v0tf−t0a-=ΔvΔt=vf−v0tf−t0.
Решение
1. Определите известные. v0=0v0=0, vf=-15,0 м/svf=-15,0 м/с (знак минус указывает направление на запад), Δt=1,80 с, Δt=1,80 с.
2. Найти изменение скорости. Поскольку лошадь движется от нуля до -15,0 м/с-15,0 м/с, изменение ее скорости равно ее конечной скорости: Δv=vf=-15,0 м/с Δv=vf=-15,0 м/с.
3. Подставьте известные значения (ΔvΔv и ΔtΔt) и найдите неизвестное a-a-.
a-=ΔvΔt=-15,0 м/с 1,80 с=-8,33 м/с2.a-=ΔvΔt=-15,0 м/с 1,80 с=-8,33 м/с2.
2.11
Обсуждение
Отрицательный знак ускорения означает, что ускорение направлено на запад. Ускорение 8,33 м/с28,33 м/с2 строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду, то есть на 8,33 метра в секунду в секунду, что мы запишем как 8,33 м/с28. 33 м/с2. Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.
Мгновенное ускорение
Мгновенное ускорение аа или ускорение в конкретный момент времени получается тем же процессом, который обсуждался для мгновенной скорости во времени, скорости и скорости, то есть путем рассмотрения бесконечно малого интервала времени.
Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рис. 2.17 показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рис. 2.17(а) ускорение незначительно меняется, а среднее значение по всему интервалу почти совпадает с мгновенным ускорением в любой момент времени. В этом случае мы должны рассматривать это движение так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1,8 м/с21,8 м/с2). На рис. 2.17(b) ускорение резко меняется со временем. В таких ситуациях лучше рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с можно рассматривать как отдельные движения с ускорениями +3,0 м/с2+3,0 м/с2 и –2,0 м/с2–2,0 м/с2, соответственно.
Рисунок
2.17
Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений.
а) Здесь ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
В следующих нескольких примерах рассматривается движение поезда метро, показанное на рис. 2.18. В (а) челнок движется вправо, а в (б) он движется влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.
Рисунок
2.18
Одномерное движение поезда метро, рассмотренное в примере 2.2, примере 2.3, примере 2.4, примере 2.5, примере 2.6 и примере 2.7. Здесь мы выбрали ось xx таким образом, что + означает вправо, а −− означает влево для перемещений, скоростей и ускорений.
(a) Поезд метро движется вправо от x0x0 до
xfxf. Его водоизмещение
ΔxΔx составляет +2,0 км. б) Поезд движется влево от
от x′0x′0 до
х’fx’f. Его смещение Δx′Δx′ составляет −1,5 км−1,5 км. (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различить перемещение в двух разных ситуациях. Для того, чтобы все отображалось на диаграмме, расстояния и размеры автомобилей представлены в разных масштабах.)
Пример 2.2
Расчет перемещения: поезд метро
Каковы величина и знак перемещений поезда метро, показанного в частях (а) и (б) рис. 2.18?
Стратегия
Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает. Обратите особое внимание на систему координат. Чтобы найти перемещение, мы используем уравнение Δx=xf−x0Δx=xf−x0. Это просто, поскольку заданы начальная и конечная позиции.
Решение
1. Определите известные. На рисунке мы видим, что xf=6,70 кмxf=6,70 км и x0=4,70 кмx0=4,70 км для участка (a), x′f=3,75 кмx′f=3,75 км и x′0=5,25 кмx′0=5,25 км для участка (b).
2. Найдите смещение в части (a).
Δx=xf−x0=6,70 км−4,70 км=+2,00 кмΔx=xf−x0=6,70 км−4,70 км=+2,00 км
2,12
3. Решить перемещение в части (b).
Δx′=x′f−x′0=3,75 км−5,25 км=−1,50 кмΔx′=x′f−x′0=3,75 км−5,25 км=−1,50 км
2.13
Обсуждение
Направление движения в (а) вправо и, следовательно, его перемещение имеет положительный знак, тогда как движение в (б) происходит влево и, следовательно, имеет отрицательный знак.
Пример 2.3
Сравнение пройденного расстояния с перемещением: поезд метро
Какие расстояния пройдены при движениях, показанных в частях (a) и (b) поезда метро на рис.
2.18?
Стратегия
Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, найденная в примере 2.2. Пройденное расстояние — это общая длина пути, пройденного между двумя точками. (См. Перемещение.) В случае поезда метро, показанного на рис. 2.18, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.
Решение
1. Перемещение для части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.
2. Перемещение по части (b) составило −1,5 км −1,5 км. Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.
Обсуждение
Расстояние является скаляром.
У него есть величина, но нет знака, указывающего направление.
Пример 2,4
Расчет ускорения: ускорение поезда метро
Предположим, что поезд на рис. 2.18(a) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с движения. Каково его среднее ускорение за этот промежуток времени?
Стратегия
На этом этапе стоит сделать простой набросок:
Рисунок 2.19
Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.
Решение
1. Определите известные. v0=0v0=0 (поезда стартуют из состояния покоя), vf=30,0 км/hvf=30,0 км/ч, Δt=20,0 с, Δt=20,0 с.
2. Рассчитайте ΔvΔv. Поскольку поезд трогается с места, изменение его скорости составляет Δv=+30,0 км/ч, Δv=+30,0 км/ч, где плюс означает скорость вправо.
3.
Подставьте известные значения и найдите неизвестное, а-а-.
a-=ΔvΔt=+30,0 км/ч30,0 sa-=ΔvΔt=+30,0 км/ч30,0 с
2,14
4. Поскольку единицы измерения смешанные (у нас есть и часы, и секунды для времени), нам нужно перевести все в единицы СИ метры и секунды. (Дополнительные указания см. в разделе «Физические величины и единицы измерения».)
a-=+30 км/ч30,0 с103 м1 км1 ч4600 с=0,417 м/с2а-=+30 км/ч30,0 с103 м1 км1 ч4600 с=0,417 м/с2
2,15
Обсуждение
- 9 Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости , как это всегда и бывает.
- Скорость объекта увеличивается с 30 м/с до 40 м/с равномерно при преодоление дистанции 10 м. Найдите ускорение
- Мяч брошен вертикально вверх с начальной скоростью 25 м/с. Какой высоты достигает мяч. Возьмем g=10 м/с2
- Заряженная частица в однородном электрическом поле ускоряется по прямой из состояния покоя до 1000 км/с на расстоянии 1 м.
Пример 2,5
Расчет ускорения: поезд метро замедляется
Теперь предположим, что в конце пути поезд на рис.
2.18(а) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?
Стратегия
Рисунок 2.20
В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.
Решение
1. Определите известные. v0=30,0 км/hv0=30,0 км/ч, vf=0 км/hvf=0 км/ч (поезд стоит, поэтому его скорость равна 0), Δt=8,00 с, Δt=8,00 с.
2. Найдите изменение скорости ΔvΔv.
Δv=vf−v0=0−30,0 км/ч=−30,0 км/чΔv=vf−v0=0−30,0 км/ч=−30,0 км/ч
2,16
3. Подставим известные значения, ΔvΔv и ΔtΔt, и решить для a-a-.
a-=ΔvΔt=-30,0 км/ч8,00 с-=ΔvΔt=-30,0 км/ч8,00 с
2,17
4. Преобразовать единицы измерения в метры и секунды.
a-=ΔvΔt=-30,0 км/ч8,00 с103 м1 км1 ч4600 с=-1,04 м/с2.
a-=ΔvΔt=-30,0 км/ч8,00 с103 м1 км1 ч4600 с=-1,04 м/с2.
2,18
Обсуждение
Знак минус указывает на то, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь отрицательная. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.
Графики зависимости положения, скорости и ускорения от времени для поездов из примеров 2.4 и 2.5 показаны на рис. 2.21. (Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется.)
Рисунок
2.21
а) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути.
В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.
Пример 2,6
Вычисление средней скорости: поезд метро
Какова средняя скорость поезда в части b примера 2.2, показанном еще раз ниже, если путь до места занимает 5,00 мин?
Рисунок 2.22
Стратегия
Средняя скорость равна смещению, деленному на время. Здесь оно будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.
Решение
1. Определите известные. x′f=3,75 кмx′f=3,75 км, x′0=5,25 кмx′0=5,25 км, Δt=5,00 мин, Δt=5,00 мин.
2. Определить водоизмещение Δx′Δx′. В примере 2.2 мы нашли, что Δx′Δx′ равно −1,5 км−1,5 км.
3. Найдите среднюю скорость.
v-=Δx′Δt=−1,50 км5,00 minv-=Δx′Δt=−1,50 км5,00 min
2,19
4. Перевести единицы.
v-=Δx′Δt=−1,50 км5,00 мин60 мин1 ч=−18,0 км/hv-=Δx′Δt=−1,50 км5,00 мин60 мин1 ч=−18,0 км/ч
2,20
Обсуждение
Отрицательная скорость указывает на движение влево.
Пример 2,7
Расчет замедления: поезд метро
Наконец, предположим, что поезд на рис. 2.22 замедляется до полной остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?
Стратегия
Еще раз нарисуем эскиз:
Рисунок
2.
23
Как и раньше, мы должны найти изменение скорости и изменение времени, чтобы вычислить среднее ускорение.
Решение
1. Определите известные. v0=-20 км/hv0=-20 км/ч, vf=0 км/hvf=0 км/ч, Δt=10,0 сΔt=10,0 с.
2. Рассчитайте ΔvΔv. Изменение скорости здесь действительно положительное, так как
Δv=vf−v0=0−−20 км/ч=+20 км/ч. Δv=vf−v0=0−−20 км/ч=+20 км/ч. час
2.21
3. Найдите а-а-.
a-=ΔvΔt=+20,0 км/ч20,0 са-=ΔvΔt=+20,0 км/ч20,0 с
2,22
4. Перевести единицы.
а-=+20,0 км/ч20,0 с103м1 км1 ч4600 с=+0,556 м/с2а-=+20,0 км/ч20,0 с103м1 км1 ч4600 с=+0,556 м/с2
2,23
- Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо).
Опять же, ускорение в том же направлении, что и изменяет скорость , которая здесь положительна. Как и в примере 2.5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.Знак и направление
Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере 2.7, где положительное ускорение замедляло отрицательную скорость. Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рис.
2.22, ускоряется за счет ускорения влево. В этом случае и vv, и aa отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, направляясь на восток. Опишите его ускорение.
Решение
Если мы возьмем восток за положительное значение, то ускорение самолета будет отрицательным, так как он движется на запад. Он также замедляется: его ускорение противоположно направлению его скорости.
Исследования ФЕТ
Моделирование движущегося человека
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
Нажмите, чтобы просмотреть содержимое.
Как найти ускорение по скорости и расстоянию
Оставить комментарий / От физикакатализатор / 19 января 2019 г. 4 ноября 2022 г.
В этой статье вы узнаете, как найти ускорение через скорость и расстояние. Мы рассмотрим случаи движения с равномерным и неравномерным ускорением в одном измерении.
Мы знаем, что ускорение определяется как изменение скорости в единицу времени. Итак, зная скорость и время, мы можем вычислить ускорение. Сейчас мы проверим, как найти ускорение, зная скорость и расстояние 9.2 +11x + 5$
При \(x=0\)
a= 5 м/с 2
Практические задачи
