Как найти ускорение зная путь время и скорость: Как найти ускорение зная путь и время - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Движение | Физика

Равномерное движение

Величина скорости показывает, какое расстояние s может преодолеть тело за определенное время t. Если машина ехала со скоростью 100 километров в час, это значит, что расстояние в 100 километров машина проехала за один час. Если эта скорость является постоянной, то мы имеем дело с равномерным движением тела.

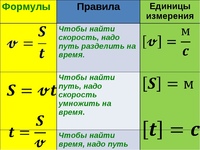
Таким образом, скорость тела определяет отношение между расстоянием s и временем t. Зная эти величины, можно легко вычислить скорость тела V. Скорость равна расстоянию, деленному на время: v = s/t.

Средняя и мгновенная скорость

Так как любая машина вряд ли будет ехать весь путь с одинаковой скоростью, то часто речь идет о средней скорости движения. Скорость машины может меняться каждую секунду, но это не помешает машине преодолеть 100 километров за 1 час.

Движение с ускорением

При равноускоренном движении, то есть при постоянном ускорении, машина за равные отрезки времени будет проходить все большее расстояние.

Если мы рассмотрим такое движение, то моментальная скорость V_м в конце пути будет в два раза больше, чем средняя скорость V_ср. В любом случае среднюю скорость тела можно вычислить таким образом: скорость тела в начале пути, обозначенная как V₀, плюс моментальная скорость в конце пути V_м, деленная на 2.

Машина, которая только начинает движение и набирает желаемую скорость 100 км/ч или 27,8 м/с за 10 секунд, имеет постоянное ускорение 2,78 м/с². Ускорение тела показывает, как быстро машина набирает определенную скорость, и обозначается a.

Если машина в течение 5 секунд после начала пути развила скорость от 0 до 100 км/ч, то ее ускорение было в два раза больше, чем в предыдущем примере.

Если машина в начале пути находилась в состоянии покоя, то, зная ускорение, можно вычислить путь, который она пройдет за определенное время. Обратимся к известным нам формулам: S = V_ср * t, где V_ср = Vм/2, а моментальная скорость измеряется следующим образом: V_м = a * t. Отсюда мы можем вывести формулу для пройденного пути: s = (a * t²) / 2.

При торможении движение машины замедляется, что означает движение с отрицательным ускорением.

Сила и ускорение

Если мы хотим, чтобы машина массой 1 тонна за 10 секунд развила скорость от нуля до 100 км/ч, то необходимо приложить силу F.

Если машина массой 2 тонны будет набирать скорость 100 км/ч за 20 секунд, то понадобится сила 1F.

Если машина массой 1 тонна разгонится от 0 до 100 км/ч, но уже за 5 секунд, то есть в два раза быстрее, то для этого понадобится приложить силу, равную 2F. При постоянной массе m сила F будет пропорциональна ускорению a: m = F/a.

Если необходимо сохранить прежнее ускорение машины, а масса составляет уже 2 тонны, то в этом случае к машине нужно приложить силу в 2F. Отсюда следует, что при постоянном ускорении сила пропорциональна массе тела: a = F/m (чем больше масса, тем больше силы надо приложить).

Отсюда следует вывод, который лег в основу закона Ньютона: F = m * a. Таким образом, сила F – это произведение массы тела m на его ускорение a.

Свободное падение

К большому удивлению своих современников Галилео Галилей утверждал, что тяжелые и легкие тела падают на Землю с одинаковой скоростью. Когда тело находится в состоянии свободного падения, то в качестве тормозящей силы будет выступать сопротивление воздуха, поэтому тела различной формы и веса будут падать с разной скоростью. Доказательством этого, может служить пример, когда мы поместим тело в вакуум, где сила сопротивления воздуха будет “выключена”. Ты можешь убедиться в этом сам!

При свободном падении речь идет о равномерно ускоренном движении, которое возникает посредством действия силы гравитации Земли. Сила гравитации влияет на то, что в безвоздушном пространстве все тела за одинаковое время достигают одинаковой скорости. Ускорение при свободном падении можно вывести из формулы равномерного ускоренного движения. Исходя из того, что

Движение по окружности

Линейную скорость тела, которое двигается по окружности, в принципе можно вычислить таким же образом, как и скорость прямолинейно двигающегося тела.

Линейная скорость вращения — это отношение расстояния S, в данном случае длины окружности, и времени, затраченного на прохождение этого пути. Таким образом, мы получаем, что

Время, затраченное двумя машинками карусели, для того чтобы сделать полный круг, будет одинаково. А вот проделанный путь у крайней машинки будет значительно больше, так как она находится на большем расстоянии от центра окружности.

Чем больше расстояние от центра окружности, тем больше должна быть линейная скорость вращения крайней машинки.

Так как внутренняя и внешняя машинка совершают полный оборот за одинаковое время, то их угловая скорость будет одинаковой. Угловой скоростью называется отношение угла поворота к интервалу времени, за который этот поворот произошел.

Сила, которая удерживает машины на треке, называется центробежной силой.

Расстояние, скорость, время

В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Расстояние

Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).

Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.

Скорость

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд.

Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 м : 25 с = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час

(км/ч).

У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)

100м : 25с = 4 (м/с)

Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 м : 50 c = 2 (м/с)

Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).

Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.

Время

Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.

Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?

Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?

Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров.

Тогда мы получим время, за которое доедем до спортивной секции:

1000 : 500 = 2 (мин)

Время движения обозначается маленькой латинской буквой t.

Взаимосвязь скорости, времени, расстояния

Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

s = v × t

Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:

v = 50 (м/мин)

t = 10 минут

s = v × t = 50 × 10 = 500 (метров до магазина)

Если известно время и расстояние, то можно найти скорость:

v = s : t

Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?

Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:

s = 900 метров

t = 10 минут

v = s : t = 900 : 10 = 90 (м/мин)

Если известна скорость и расстояние, то можно найти время:

t = s : v

Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:

s = 500 метров

v = 100 (м/мин)

t = s : v = 500 : 100 = 5 (минут до спортивной секции)

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Новосибирский государственный архитектурно-строительный университет – Сибстрин

Ректор Юрий Сколубович принял участие в обсуждении перспектив строительства новых городов в России и Сибири

24 сентября 2021 года ректор НГАСУ (Сибстрин) Юрий Сколубович принял участие в заседании Клуба межнаучных контактов СО РАН. Широко признанная дискуссионная площадка Академгородка собрала ученых, представителей власти и бизнеса из Новосибирска и других городов, в том числе из Красноярска и Крыма.

С приветствиями к участникам обратились председатель СО РАН Валентин Пармон, сенатор Александр Карелин, министр науки Новосибирской области Алексей Васильев, депутат Законодательного собрания Новосибирской области Александр Аксененко. Темой заседания стала «Могущество России – новые города». На встрече обсуждали новые технополисы …

Студенты НГАСУ (Сибстрин) поучаствовали в строительстве новой ледовой арены МЧМ – 2023 в Новосибирске

В 2023 году Новосибирск примет молодежный чемпионат мира по хоккею. Матчи будут проводиться на новой многофункциональной ледовой арене, которая сейчас строится вблизи улицы Немировича-Данченко, в 500 метрах от берега реки Обь. Ввести в эксплуатацию новый спортивный комплекс планируют уже летом 2022 года. Студенты Новосибирского государственного архитектурно-строительного университета (Сибстрин) поучаствовали в стройке главного объекта МЧМ – 2023 в рамках производственной практики этим летом.

Инициатива привлечь к строительству знаковых объектов области – ЛДС и станции метро «Спортивная» – студентов профильных вузов и бойцов студотрядов принадлежит Губернатору Андрею Травникову. «Сегодняшние новосибирские студенты смогут…

Приглашаем на мероприятия для первокурсников «Время первых 2021»!

Дорогие первокурсники НГАСУ (Сибстрин)! ЦВВР приглашает к участию в традиционных мероприятиях для новобранцев университета «Время первых 2021». Для вас организованы конкурсы среди групп первого курса: Интеллектуальный турнир – 4-5 октября «Эмблема моей группы» – 6 октября Конкурс на самую творческую группу – 6 октября Спартакиада на «Приз первокурсника» – 28-30 сентября Заявки на участие в конкурсах принимаются в свободной форме в учебном корпусе №4, ком. 4203, 4211 или на электронную почту [email protected] Пришло время первых – прояви свои таланты! Подробности – в Положениях о конкурсах.

Интеллектуальный турнир Положение Спартакиада 1 курс 2021 Самая творческая группа Эмблема моей группы

Измерение ускорения свободного падения на различных высотах при помощи математического маятника

Участник: Мингалеев Артур Эдуардович
Руководитель: Баскова Мария Аркадьевна

1. Введение

Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.

Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:

Ознакомиться с историей открытия свободного падения тел;
Изучить методы измерения ускорения свободного падения на поверхности Земли;
Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
Провести измерения на различных высотах.

Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с² и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.

Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.

Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с² и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.

В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.

2. Основная часть

2.1. Исторические сведения об открытии свободного падения и методах его измерения

Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.

Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с “постоянным ускорением”; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.

Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:

S₁ : S₂ : S₃ : … = 1 : 2 : 3 : … (при V₀ = 0)

Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:

S₁ : S₂ : S₃ = t₁² : t₂² : t₃² (2)

Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.

2.2. Практическая значимость нахождения значения ускорения свободного падения

Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.

2.3. Методы измерения ускорения свободного падения

На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.

1) Измерение ускорения свободного падения с помощью наклонной плоскости

Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:

Записывая второй закон Ньютона в проекциях на оси координат:

О_х: – F_тр+ mgsinα = ma

O_y: N – mgcosα = 0

и учитывая, что N = mgcosα; F_тр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:

g =	a
	sinα – μcosα

При этом ускорение a можно вычислить из формулы

так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:

Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.

Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:

Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.

При равномерном движении бруска эти силы будут попарно равны: F_тр = F_упр, F_тяж = N, т. е. F_упр = μF_тяж, тогда коэффициент трения равен

Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.

2) Определение

g благодаря давлению жидкости

Как известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.

Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м³.

При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.

3) Измерение ускорения свободного падения с помощью математического маятника

Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период

и ускорения свободного падения может быть вычислено по формуле

Подготовка к проведению работы

В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника

Тогда период

и ускорения свободного падения может быть вычислено по формуле

Результаты измерений и вычислений представлены в разделе 2.5

2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах

Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:

где G — гравитационная постоянная (G = 6,6743 · 10^–11 (H ·м²)/кг²).

При вычислениях я применял такие значения:

R = 6370 · 10³ м – радиус Земли на широте Казани;

M = 5,9722 · 10²⁴ кг – масса Земли.

Таким образом теоретическое значение g_т = 9,823386 м/с².

Согласно формуле

естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.

Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.

Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:

В классе

На станции метро Кремлевская

На 36-м этаже небоскреба

R = 6370 км,

h = 0

R = 6370 км,

h = –16 м

R = 6370 км,

h = +120 м

9,8234

9,8231

9,8227

2.5. Экспериментальное определение ускорения свободного падения с помощью математического маятника

Как уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

и ускорения свободного падения может быть вычислено по формуле

Ход работы

Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.

Я установил на краю стола штатив. У его верхнего конца укрепил с помощью муфты кольцо и подвесил к нему шарик на нити. Шарик должен висеть и свободно совершать колебания.
Нить я взял метровой длины для удобства вычислений.
Отклонив шарик на небольшое расстояние (5-8 см), я возбудил колебания маятника.
Измерил в пяти экспериментах время t 20 колебаний маятника и вычислил t_ср:

t_ср =	t₁ + t₂ + t₃ + t₄ + t₅
	5

Затем вычислил среднюю абсолютную погрешность измерения времени:

∆t_ср =	│t₁ – t_ср│ + │t₂ – t_ср│+ │t₃– t_ср│ + │t₄– t_ср│ + │t₅– t_ср│
	5

Вычислил ускорение свободного падения по формуле:

Таблица результатов измерений в классе

n	N	t, c	t_ср, с	Δt_ср, с	g, м/с²
1	20	40,26	39,94	0,36	9,88924
2	20	39,20
3	20	40,30
4	20	40,18
5	20	39,78

Я определил относительную погрешность измерения времени εt.

ε =	∆t	=	∆t_и + ∆t_{отсчета}	=	1 с + 1 с	=	2 c	=	2 с	= 0,05 = 5%
	t		t		t		t_средн		39,94 с

Определил относительную погрешность измерения длины маятника:

εl =	∆l	=	∆l_и + ∆l_{отсчета}	=	половина цены деления + цена деления	=
	l		l		длина маятника

=	0,0005 м + 0,001 м	=	0,0015 м	=	0,0015 м	= 0,0015 = 0,15%
	l		l		1 м

Вычислил относительную погрешность измерения g:
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3%
Определил абсолютную погрешность вычисления ускорения свободного падения:
∆g = ε_gg_{средняя} = 0,053 · 9,73971 м/с² = 0,5162 м/с² ≈ 0,520

Итог моих измерений и вычислений:

9,37 ≤ g ≤ 10,41

Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».

Таблица результатов измерений на станции метро Кремлевская

n	N	t, c	t_ср, с	Δt_ср, с	g, м/с²
1	20	31,80	31,71	0,042	9,96232
2	20	31,72
3	20	31,62
4	20	31,69
5	20	31,71

При измерениях в метро пришлось использовать длину нити 63,5 см.

Относительная погрешность измерения времени ε_t = 0,063 = 6,3%.

Относительная погрешность измерения длины маятника: ε_l = 0,24%

Относительная погрешность измерения g: ε_g = 6,78%

Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с².

Итог моих измерений и вычислений:

9,33 ≤ g ≤ 10,59

Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»

n	N	t, c	t_ср, с	Δt_ср, с	g, м/с²
1	20	28,59	28,57	0,10	9,85664
2	20	28,56
3	20	28,81
4	20	28,52
5	20	28,39

Здесь при измерениях пришлось длину нити еще сократить до 51 см.

Относительная погрешность измерения времени εt = 7%.

Относительная погрешность измерения длины маятника: ε_l = 0,29%

Относительная погрешность измерения g: ε_g = 7,58%

Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с².

Итог моих измерений и вычислений:

9,11 ≤ g ≤ 10,61

Таблица сравнения теоретически полученных значений g (м/с²) и полученных экспериментально

	В классе	На станции метро Кремлевская	На 36-м этаже небоскреба
	R = 6370 км, h = 0	R = 6370 км, h = –16 м	R = 6370 км, h = +120 м
Теория	9,8234	9,8231	9,8227
Эксперимент	9,8892	9,9623	9,8566

3. Заключение

При подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.

Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.

Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.

Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается. Экспериментально полученные значения хорошо это показывают.

Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.

В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.

Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.

Разгон

Как упоминалось ранее в Уроке 1, объект, движущийся равномерно по кругу, движется по кругу с постоянной или постоянной скоростью. Вектор скорости постоянен по величине, но меняется по направлению. Поскольку скорость такого движения постоянна, многие студенты ошибочно полагают, что ускорения нет. «В конце концов, – могут сказать они, – если бы я вел машину по кругу с постоянной скоростью 20 миль / ч, тогда скорость не уменьшалась и не увеличивалась, поэтому не должно быть ускорения.”В основе этого распространенного заблуждения студентов лежит неправильное представление о том, что ускорение связано со скоростью, а не со скоростью. Но факт в том, что ускоряющийся объект – это объект, который меняет свою скорость. А поскольку скорость – это вектор, который имеет как по величине, так и по направлению, изменение величины или направления представляет собой изменение скорости. По этой причине можно с уверенностью заключить, что объект, движущийся по кругу с постоянной скоростью, действительно ускоряется. Он ускоряется, потому что направление вектора скорости меняется.

Геометрический

Доказательство внутреннего ускорения

Чтобы понять это на более глубоком уровне, нам придется объединить определение ускорения с обзором некоторых основных векторных принципов. Напомним, из раздела 1 Физического класса, что ускорение как величина определялось как скорость, с которой изменяется скорость объекта. Таким образом, он рассчитывается с использованием следующего уравнения:

, где v _i представляет начальную скорость, а v _f представляет конечную скорость через некоторое время t .Числитель уравнения находится путем вычитания одного вектора ( v _i ) из второго вектора ( v _f ). Но сложение и вычитание векторов друг из друга выполняется иначе, чем сложение и вычитание скалярных величин. Рассмотрим случай, когда объект движется по окружности вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v _i на v _f .Процесс вычитания v _i из v _f показан на векторной диаграмме; этот процесс приводит к изменению скорости.

Направление вектора ускорения

Обратите внимание на диаграмму выше, что есть изменение скорости для объекта, движущегося по кругу с постоянной скоростью. Тщательный осмотр вектора изменения скорости на приведенной выше диаграмме показывает, что он указывает вниз и влево.В средней точке дуги, соединяющей точки A и B, изменение скорости направлено в сторону точки C – центра окружности. Ускорение объекта зависит от этого изменения скорости и находится в том же направлении, что и это изменение скорости. Ускорение объекта совпадает с направлением вектора изменения скорости; ускорение также направлено к точке C – центру окружности. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются к центру круга.

Ускорение объекта часто измеряется с помощью устройства, известного как акселерометр. Простой акселерометр состоит из объекта, погруженного в жидкость, например воду. Рассмотрим герметичную банку, наполненную водой. Пробка, прикрепленная к крышке шнурком, может служить акселерометром. Чтобы проверить направление ускорения объекта, движущегося по кругу, банку можно перевернуть и прикрепить к концу короткой секции деревянного 2х4. Второй акселерометр, сконструированный таким же образом, может быть прикреплен к противоположному концу 2×4.Если 2×4 и акселерометры закреплены на вращающейся платформе и вращаются по кругу, направление ускорения можно четко определить по направлению наклона пробок. Когда смесь пробки и воды вращается по кругу, пробка наклоняется к центру круга. Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае пробки и воды пробка менее массивна (в расчете на мл) и, следовательно, испытывает большее ускорение. Имея меньшую инерцию (из-за меньшей массы на 1 мл), пробка меньше всего сопротивляется ускорению, и, таким образом, наклоняется на внутрь банки к центру круга.Это очевидное свидетельство того, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение, направленное к центру круга.

Другой простой самодельный акселерометр – это зажженная свеча, расположенная вертикально по центру открытого стакана. Если стакан держать ровно и неподвижно (так, чтобы не было ускорения), то пламя свечи распространяется вверх. Однако, если вы держите систему стекло-свеча вытянутой рукой и вращаете по кругу с постоянной скоростью (так, чтобы пламя испытывало ускорение), то пламя свечи больше не будет распространяться вертикально вверх.Вместо этого пламя отклоняется от вертикального положения. Это означает, что есть ускорение, когда пламя движется по круговой траектории с постоянной скоростью. Отклонение пламени будет в сторону ускорения. Это можно объяснить, утверждая, что горячие газы пламени менее массивны (в расчете на миллилитр) и, следовательно, имеют меньшую инерцию, чем более холодные газы, которые его окружают. Впоследствии более горячие и легкие газы пламени испытывают большее ускорение и наклоняются в направлении ускорения.Тщательное изучение пламени показывает, что пламя направлено к центру круга, указывая, таким образом, на то, что есть не только ускорение; но есть внутреннее ускорение. Это еще одно наблюдаемое свидетельство того, что объекты, движущиеся по кругу с постоянной скоростью, испытывают ускорение, направленное к центру круга.

До сих пор мы видели геометрическое доказательство и две реальных демонстрации этого внутреннего ускорения.На этом этапе ученик принимает решение верить или не верить. Разве разумно, что объект, движущийся по кругу, испытывает ускорение, направленное к центру круга? Можете ли вы придумать логическую причину, чтобы верить в отсутствие ускорения или даже внешнего ускорения, испытываемого объектом, движущимся в равномерном круговом движении? В следующей части Урока 1 будут представлены дополнительные логические доказательства, подтверждающие представление о внутренней силе для объекта, движущегося по кругу.

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства однородного кругового движения. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.

Проверьте свое понимание

1. Начальная и конечная скорости мяча в два разных момента времени показаны ниже. Направление мяча указано стрелкой. Для каждого случая укажите, есть ли ускорение. Объясните, почему да или почему нет. Укажите направление ускорения.

а.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком оно направлении?

б.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком оно направлении?

c.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком оно направлении?

d.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком оно направлении?

е.
Ускорение: да или нет? Объяснять.	Если есть ускорение, то в каком оно направлении?

2.Объясните связь между вашими ответами на вышеуказанные вопросы и аргументацией, использованной для объяснения того, почему можно сказать, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение.

3. Диззи Смит и Гектор Вектор все еще обсуждают № 1e. Диззи говорит, что мяч не ускоряется, потому что его скорость не меняется. Гектор говорит, что, поскольку мяч изменил свое направление, происходит ускорение.С кем ты согласен? Обсудите свою позицию, объяснив несоответствие в аргументе другого ученика.

4. Найдите три элемента управления автомобилем, которые позволяют автомобилю ускоряться.

Для вопросов № 5- № 8: Объект движется в направлении по часовой стрелке и по кругу с постоянной скоростью.Используйте свое понимание концепций скорости и ускорения, чтобы ответить на следующие четыре вопроса. Используйте диаграмму, показанную справа.

5. Какой вектор ниже представляет направление вектора скорости, когда объект находится в точке B на окружности?

6. Какой вектор ниже представляет направление вектора ускорения, когда объект находится в точке C на окружности?

7.Какой вектор ниже представляет направление вектора скорости, когда объект находится в точке C на окружности?

8. Какой вектор ниже представляет направление вектора ускорения, когда объект находится в точке A на окружности?

Speedy Science: как ускорение влияет на расстояние?

Bring Science Home

Веселый физический проект от Science Buddies

Ключевые концепции
Физика
Скорость
Разгон
Гравитация

Введение
Вы когда-нибудь что-то роняли и задавались вопросом, с какой скоростью это движется при падении? (Если бы это было что-то хрупкое, вы, возможно, не думали об этом в то время – вы, вероятно, были слишком заняты, пытаясь схватить объект!) Все мы знаем, что гравитация заставляет объект падать.Но как это повлияет на то, как быстро что-то падает и каково его влияние? Например, объект двигался быстрее сразу после того, как покинул вашу руку, или непосредственно перед тем, как упасть на землю? В этом научном упражнении вы исследуете связь между временем и пройденным расстоянием, когда движущийся объект находится под постоянным ускорением силы тяжести.

Фон
По опыту вы знаете, что когда вы едете на велосипеде под гору, легко тронуться с места. Гравитация дает вам дополнительный толчок, поэтому вам не нужно делать всю работу с педалями.Вы также знаете по опыту, что чем длиннее холм, тем быстрее вы идете. Чем дольше вы чувствуете этот толчок гравитации, тем быстрее он заставляет вас двигаться. Наконец, вы знаете, что чем круче холм, тем быстрее вы едете. Самый крутой «холм», который вы можете себе представить, совсем не похож на холм, а скорее представляет собой отвесный перепад – где предметы падают в свободное падение и где сила тяжести дает самый большой толчок из всех. Вы бы не захотели попробовать это на своем велосипеде!

В свободном падении гравитация постоянно ускоряет объект (увеличивает его скорость), пока он не достигнет предельной скорости.В частности, гравитация увеличивает скорость падающего объекта на 9,8 метра в секунду (м / с) с каждой секундой. (В то время как скорость измеряется в м / с, ускорение измеряется в метрах в секунду в квадрате, или м / с ².) Как это постоянное ускорение влияет на расстояние, которое объект проходит с течением времени? В этом эксперименте вы скатываете шарик по пандусу, чтобы узнать.

Материалы

Длинная картонная трубка, например пустой рулон оберточной бумаги, для пандуса.Он должен быть не менее двух с половиной футов в длину.
Тонкая книга или небольшой деревянный брусок для поднятия одного конца пандуса. Его толщина должна составлять от полутора до одного дюйма.
Ножницы для резки картонной трубки
Перманентный маркер
Мрамор
Таймер. Убедитесь, что он может точно считать отдельные секунды. Многие сотовые телефоны имеют такой точный таймер.
Линейка (по желанию)
Помощник (по желанию)

Препарат

Возьмите длинную картонную трубку и разрежьте ее вдоль одной из (длинных) сторон.Затем отрежьте его с другой стороны так, чтобы в итоге получилось два длинных полукруга. Вы будете использовать одну из этих частей как рампу для мрамора.
Возьмите один из полукруглых кусков, которые вы только что отрезали, и слегка приподнимите один конец, поместив его на тонкую книгу или небольшой блок (не толще одного дюйма – вам нужен низкий наклон, чтобы шарик не катился слишком быстро, чтобы его можно было измерить).
Используйте перманентный маркер, чтобы отметить стартовую линию на верхнем конце пандуса, примерно в половине дюйма от конца.Пандус готов к катанию по мрамору!

Процедура

Установите таймер на одну секунду, а затем удерживайте шарик на стартовой линии.
Точно в то же время, как вы запускаете таймер, отпустите шарик (будьте осторожны, чтобы не толкнуть его, когда вы отпускаете его). В то же время будьте готовы с помощью маркера отметить положение шарика после того, как второй будет поднят. Если у вас есть помощник, попросите его присмотреть за мрамором.Используйте перманентный маркер, чтобы отметить, где находился шарик через одну секунду после того, как его выпустили. Как далеко продвинулся мрамор?
Повторите этот процесс еще как минимум девять раз. Это означает, что у вас должно получиться по крайней мере десять разных отметок на рампе, показывающих, где был шарик через одну секунду после того, как каждый раз его отпускали. Путешествовал ли мрамор каждый раз на одинаковые расстояния?
Повторите этот процесс, но на этот раз отметьте, где находится шарик через две секунды после его освобождения.Сделайте это как минимум 10 раз, чтобы вы сделали еще как минимум 10 отметок на рампе. Как расстояние, пройденное шариком за одну секунду, по сравнению с расстоянием, которое он прошел за две секунды? В частности, как расстояние между стартовой линией и односекундными отметками соотносится с расстоянием между односекундными и двухсекундными отметками?
Если у вас есть линейка, вы можете измерить расстояние, на которое шарик катится каждый раз от стартовой линии.
В целом, как изменилось расстояние, пройденное шариком, когда он катился по рампе в течение более длительного периода времени? Что это говорит вам о влиянии силы тяжести на скорость и ускорение шарика, когда он катится?
Дополнительно: Используйте линейку, чтобы измерить отметки, сделанные вами на пандусе, и вычислить среднее расстояние, которое шарик преодолел за одну секунду и две секунды (усредняя время отдельно).Затем нанесите на график свои результаты, поместив среднее пройденное расстояние на одну ось, а время – на другую. На основании вашего графика, как изменилось расстояние, пройденное шариком, когда он катился в течение более длительного периода времени?
Дополнительно: Попробуйте повторить это упражнение, используя более длинный пандус, например плоскую доску длиной не менее шести футов (с пазом посередине или другой прямой кусок дерева, приклеенный по длине первой доски, чтобы действовать. в качестве руководства).Катите шарик по более длинному пандусу в течение увеличивающегося количества времени (одна секунда, две секунды, три секунды и т. Д.), Пока шарик не пройдет мимо конца пандуса. Каждый раз отмечайте пройденное расстояние на рампе. При использовании более длинного пандуса, как сила тяжести влияет на скорость и ускорение шарика, катящегося под гору?
Дополнительно: Попробуйте повторить это упражнение с разными мячами, например, с резиновым мячом, большим металлическим шарикоподшипником, мячом для пинг-понга и т. Д. Как тип мяча влияет на его спуск по рампе?

Наблюдения и результаты
Мрамор двигался быстрее по мере того, как спускался вниз по склону?

Когда объект находится в свободном падении, сила тяжести увеличивает его скорость на 9,8 м / с с каждой секундой. Таким образом, через одну секунду объект будет падать со скоростью 9,8 м / с. Через две секунды объект будет падать со скоростью 19,6 м / с. Через три секунды объект будет падать со скоростью 29.4 м / с и так далее.

Хотя это упражнение не выполнялось в свободном падении (наличие пандуса обеспечивает сопротивление, замедляющее падение мрамора), здесь применима та же идея. Гравитация должна была постоянно ускорять мрамор, когда он скатывался с рампы в этой деятельности. Это можно увидеть, сравнив (среднее) расстояние между стартовой линией и односекундными отметками с расстоянием между односекундными и двухсекундными отметками. В частности, расстояние между односекундными и двухсекундными отметками должно быть больше, чем расстояние между стартовой линией и односекундными отметками, показывая, что шарик двигался тем быстрее, чем дольше он катился.В зависимости от точных условий настройки рампы расстояние между односекундными и двухсекундными отметками может быть примерно в 1,5–2,5 раза больше расстояния между линией старта и односекундными отметками.

Больше для изучения
Наклонные самолеты, из класса физики
Ускорение, из Калифорнийского университета, Беркли
Расстояние и постоянное ускорение, от друзей науки
Научная деятельность для всех возрастов !, от друзей науки

Это мероприятие предоставлено вам в сотрудничестве с Science Buddies

ОБ АВТОРЕ (-АХ)

Последние статьи от Science Buddies

Информационный бюллетень

Станьте умнее.Подпишитесь на нашу новостную е-мэйл рассылку.

Поддержите научную журналистику

Откройте для себя науку, меняющую мир. Изучите наш цифровой архив 1845 года, в котором есть статьи более 150 лауреатов Нобелевской премии.

Подпишитесь сейчас!

Расчет ускорения ракеты – Science Learning Hub

Как можно сравнить ускорение модели ракеты с ускорением космического корабля “Шаттл”? Используя результирующую силу и массу, можно рассчитать ускорение.

Силы, действующие

Две силы, действующие на ракеты в момент пуска, – это тяга вверх и вес вниз.Вес – это сила тяжести, которая рассчитывается (на поверхности Земли) путем умножения массы (в килограммах) на 9,8.

Результирующая сила, действующая на каждую ракету, рассчитывается с использованием уравнения результирующая сила = тяга – вес.

Расчет ускорения модели ракеты

Ускорение – это мера того, насколько скорость увеличивается каждую секунду. Его можно рассчитать, используя уравнение:
ускорение = результирующая сила (ньютоны, Н), разделенная на массу (килограммы, кг).

Одна модель ракеты имеет массу 50 грамм и ракетный двигатель, который развивает тягу 5 Н в течение 1 секунды.

Чтобы найти вес, необходимо преобразовать 50 г в килограммы путем деления на 1000. Это дает массу 0,050 кг. Вес – это масса (в кг) x 9,8, что дает 0,050 x 9,8 = 0,49 Н.

Результирующая сила – тяга – вес = 5 – 0,49 = 4,51 Н (без окружности).

Ускорение = равнодействующая сила, деленная на массу = 4,51 ÷ 0,050 = 90 метров в секунду в квадрате (90 м / с ²).Это означает, что каждую секунду скорость ракеты увеличивается на 90 м / с.

Это в девять раз больше обычного ускорения свободного падения.

Тот же метод можно использовать для полноразмерной ракеты, такой как Space Shuttle.

Расчет ускорения космического челнока

Миссия космического челнока, запущенная 24 февраля 2011 года, получила название STS-133. Он имел взлетную массу 2 миллиона килограммов (2000 тонн). Это означает, что общий вес при отталкивании составляет 2 миллиона х 9.8, что составляет примерно 20 миллионов ньютонов (20 мега-ньютонов).

Тяга каждого из больших белых твердотопливных ракетных ускорителей по бокам составляла 12,5 миллионов ньютонов, а три главных двигателя в хвостовой части долота, которая выглядит как самолет (орбитальный аппарат Space Shuttle), имели общую тягу 5,5. миллион ньютонов. Это дает огромную общую тягу в 30,5 миллионов ньютонов!

Результирующая сила = тяга – вес = 30,5 миллионов – 20 миллионов = 10,5 миллионов ньютонов.

Ускорение = результирующая сила ÷ масса = 10.5 миллионов ÷ 2 миллиона = 5,25 м / с ².

Сравнение ускорений

Ускорение модели ракеты со скоростью 90 м / с ² намного больше, чем у Space Shuttle со скоростью 5,25 м / с ², но есть существенная разница в движении после запуска.

Во-первых, у модели ракеты хватило топлива только на 1 секунду тяги. Через 1 секунду она достигает максимальной скорости 90 м / с (без учета сопротивления и изменения массы), но после этой 1 секунды тяги модельная ракета начинает терять скорость из-за веса и сил сопротивления, действующих в противоположном направлении. к его движению.

Для космического корабля “Шаттл” твердотопливные ракетные ускорители (ТРД) имеют достаточно топлива, чтобы обеспечить тягу в течение 124 с. Это означает, что космический шаттл разгоняется более чем на 2 минуты, прежде чем твердотопливные ракетные ускорители отделятся. (Поскольку шаттл использует свое топливо, он также становится намного легче, что увеличивает ускорение.)

Через 124 секунды шаттл уже достиг высоты 45 км и движется со скоростью 1380 м / с (4973 км / ч). В это время (когда все топливо израсходовано) SRB отделяются от внешнего бака (большая оранжевая часть).Топливо продолжает перекачиваться к трем основным двигателям еще в течение 6 минут. Ускорение продолжается до тех пор, пока орбитальный аппарат “Спейс Шаттл” в конечном итоге не достигнет скорости 28 000 км / ч и высоты более 300 км. Это позволяет ему вращаться вокруг Земли.

Сопутствующие материалы

Изучите некоторые идеи, которые являются основополагающими для понимания ракет:

Идеи действий

Изучите интерактивное использование задачи запуска ракеты в упражнении задачи запуска ракеты.

Выполните это упражнение с исследованием движения ракеты. Учащиеся исследуют движение ракеты, используя электронную таблицу с графиками движения. Они регулируют переменные и исследуют, как это влияет на высоту и скорость.

Полезная ссылка

Просмотр запуска космического корабля. Отметьте время, скорость и высоту на каждом этапе своего путешествия. (Чтобы изменить скорость с миль / ч на км / ч, умножьте на 1,6.)

Равномерное круговое движение

Объект, движущийся по окружности радиуса r с постоянной скоростью v ускоряется.В направление его вектора скорости все время меняется, но величина вектор скорости остается постоянным. Вектор ускорения не может иметь составляющей в направлении вектора скорости, так как такая составляющая будет вызвать изменение скорости. Следовательно, вектор ускорения должен быть перпендикулярно вектору скорости в любой точке окружности. Этот ускорение называется радиальное ускорение или центростремительное ускорение , и это указывает к центру круга.Величина центростремительного вектор ускорения: _c = v ² / r. (Мы пропускаем вывод этого выражения.)

Ссылка: Равномерное круговое движение

Задача:

Орбита Луны вокруг Земля приблизительно круглая со средним радиусом 3,85 * 10 ⁸ м. Луна совершает один оборот вокруг Луны за 27,3 дня. Земля. Найти
(а) средняя орбитальная скорость Луны и
(б) его центростремительное ускорение.

Решение:

Рассуждение:
Расстояние, которое луна проходит за один орбитальный период T, равно d = 2πr.
Его скорость v = расстояние / время = d / T.
Центростремительное ускорение Луны v ² / r.
Детали расчета:
(а) Расстояние, которое луна проходит за 27,3 дня, равно d = 2πr = 2,41 * 10 ⁹ г.
Его скорость равна v = d / (27,3 суток) = (d / (2,36 * 10 ⁶ с)) = 1023 м / с.
(b) Центростремительное ускорение Луны v ² / r = 2,725 * 10 ^-3 м / с ².

Объект, движущийся по кругу с постоянной или неравномерной скоростью, считается ускоряется. Поскольку он ускоряется, на него должна действовать сила. Такой сила называется центростремительной силой .

В каких обстоятельствах сила?

Пусть мы решаем некоторые проблемы, исследуя этот вопрос.

Задача:

Масса 3 кг, прикрепленная к легкой струне, вращается по горизонтали. стол без трения. Радиус круга составляет 0,8 м, а струна может выдержать массу 25 кг до разрыва. В каком диапазоне скоростей может масса есть до того, как струна порвется?

Решение:

Рассуждение:
Масса, прикрепленная к струне, вращается по горизонтали, стол без трения.
Мы предполагаем, что масса вращается с постоянной скоростью.это ускоряется. Направление ускорения – в сторону центр круга, а его величина равна v ² / r. Струна натянута. Веревка натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = mv ² / r.
Перед разрывом струна может выдержать массу 25 кг, т. Е. Мы может подвешивать груз массой до 25 кг на веревке рядом с поверхность земли.Максимальное натяжение струны следовательно, F _max = mg = (25 кг) (9,8 м / с ²) ^{= 245 N.
Учитывая F _max = 245 Н и F = mv ² / r, мы можем найти v _max.}
Детали расчета:
v _max ² = F _max об / м = (250 Н) (0,8 м) / (3 кг). v _макс = 8,1 м / с.

Проблема:

Монета, помещенная в 30 см от центра вращающегося горизонтального поворотный стол проскальзывает при его скорости 50 см / с.
(а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижен относительно поворотного стола?
(б) Каков коэффициент статического трения между монетой и Проигрыватель?

Решение:

Рассуждение:
Когда монета покоится относительно вращающегося подноса, сила статическое трение между монетой и поворотным столом обеспечивает центростремительную ускорение.
Сила статического трения имеет максимальное значение f _с = μ _с Н = μ _с мг.
Настройка μ _с mg = mmv ² / r, мы можем решить для μ _s.
Детали расчета:
(a) Сила статического трения между монетой и поворотным столом обеспечивает центростремительное ускорение.
(б) Величина максимального сила статического трения f _с = μ _с Н. Это максимальная сила трения покоя равна mv ² / r при v = 0,5 м / с. Имеем μ _с N = μ _с mg = mv ² / r,
или μ _с = v ² / (rg) = (0.5 м / с) ² /(0,3 м 9,8 м / с ²) = 0,085.

Модуль 3: Вопрос 1

Чувствуете ли вы, что вас бросает в любую сторону, когда вы проезжаете поворот, который идеально подходит для скорости вашего автомобиля? В каком направлении действует сила на вас у автокресла?

Обсудите это со своими однокурсниками на дискуссионном форуме!

Для получения дополнительной информации о равномерном круговом движении, изучите этот материал из “Физического класса”.

Link: Характеристики движения для кругового движения

Скорость и скорость
Разгон
Требование центростремительной силы
Запретное слово на слово
Математика кругового движения

Ссылка: приложения кругового движения

Второй закон Ньютона – новый взгляд
Парк развлечений с физикой
Легкая атлетика

60+ решенных задач скорости, скорости и ускорения для старшей школы

Проблемы скорости, скорости и ускорения на прямолинейном пути:

Для старшеклассников представлено более 60 простых задач на скорость, скорость и ускорение с описательными ответами.В каждом решении вы можете найти краткое руководство.

Скорость и проблемы скорости:

Задача (1): Какова скорость ракеты, которая движется по $ 8000 \, {\ rm m} $ за $ 13 \, {\ rm s} $?

Решение : Скорость определяется в физике как общее расстояние, деленное на прошедшее время, поэтому скорость ракеты составляет $ \ frac {8000} {13} = 615.38 \, {\ rm m / s} $.

Задача (2): Сколько времени потребуется, если вы проедете $ 400 \, {\ rm km} $ со средней скоростью $ 100 \, {\ rm m / s} $?

Решение : Средняя скорость – это отношение общего расстояния к общему времени.{3} \, {\ rm m}} {100 \, {\ rm m / s}} \\ \\ & = 4000 \, {\ rm s} \ end {align *} Чтобы преобразовать его в часы, необходимо делится на $ 3600 \, {\ rm s} $, что дает $ t = 1.11 \, {\ rm h} $.

Задача (3): Человек проходит $ 100 \, {\ rm m} $ за $ 5 $ минут, затем $ 200 \, {\ rm m} $ за $ 7 $ минут и, наконец, $ 50 \, {\ rm m} $ за 4 доллара за минуты. Найти его среднюю скорость?

Решение : Сначала найдите общее пройденное расстояние $ D $, суммируя все расстояния в каждом разделе, что дает $ D = 100 + 200 + 50 = 350 \, {\ rm m} $.Теперь, по определению средней скорости, разделите ее на общее время, прошедшее $ T = 5 + 7 + 4 = 11 $ минут. Но имейте в виду, что, поскольку расстояние указывается в единицах СИ, пройденное время также должно быть в единицах СИ, что составляет $ м / с $. Следовательно, у нас есть \ begin {align *} \ text {средняя скорость} & = \ frac {\ text {общее расстояние}} {\ text {total time}} \\ \\ & = \ frac {350 \, {\ rm m}} {11 \ times 60 \, {\ rm s}} \\ \\ & = 0,53 \, {\ rm m / s} \ end {align *}

Прочтите статьи по теме:

Уравнения кинематики: проблемы и решения

Позиция vs.Временные графики

График зависимости скорости от времени

Задача (4): Человек идет 750 \, {\ rm m} $ на север, затем 250 \, {\ rm m} $ на восток. Если на всю прогулку уходит $ 12 минут, найдите среднюю скорость человека?

Решение : Средняя скорость – это смещение, деленное на прошедшее время. Смещение также является вектором, который подчиняется правилам вектора сложения. Таким образом, в этой задаче добавьте каждое смещение, чтобы получить общее смещение.

В первой части смещение составляет $ \ Delta x_1 = 750 \, \ hat {j} $, а для второй части $ \ Delta x_2 = 250 \, \ hat {i} $.{2}} \\ \\ & = 790.5 \, {\ rm m} \ end {align *} Следовательно, величина средней скорости равна $ v = \ frac {790.5} {12 \ times 60} = 1.09 \ , {\ rm m / s} $

Задача (5): объект движется по прямой линии. Сначала он движется со скоростью $ 12 \, {\ rm m / s} $ для $ 5 \, {\ rm s} $, а затем продолжает в том же направлении $ 20 \, {\ rm m / s} $ для $ 3 \ , {\ rm s} $. Какая у него средняя скорость?

Решение: Средняя скорость – это смещение, деленное на затраченное время i.е. $ \ bar {v} \ Equiv \ frac {\ Delta x_ {tot}} {\ Delta t_ {tot}} $. В этой задаче объект проходит две стадии с двумя разными смещениями, поэтому сложите их, чтобы найти полное смещение. Таким образом, \ [\ bar {v} = \ frac {x_1 + x_2} {t_1 + t_2} \] Смещения получаются как $ x_1 = v_1 \, t_1 = 12 \ times 5 = 60 \, {\ rm m} $ и $ x_2 = v_2 \, t_2 = 20 \ times 3 = 60 \, {\ rm m} $. Следовательно, у нас есть \ begin {align *} \ bar {v} & = \ frac {x_1 + x_2} {t_1 + t_2} \\ \\ & = \ frac {60 + 60} {5 + 3} \\ \ \ & = 15 \, {\ rm м / с} \ end {align *}

Задача (6): самолет пролетает расстояние между двумя городами за $ 1 $ час и $ 30 $ минут со скоростью $ 900 \, {\ rm км / ч} $.Другой самолет преодолевает это расстояние с $ 600 \, {\ rm км / ч} $. Сколько летит второй самолет?

Решение: сначала найдите расстояние между двумя городами, как показано ниже \ begin {align *} x & = vt \\ & = 900 \ times 1.5 \\ & = 1350 \, {\ rm km} \ end {align *}. снова используйте то же кинематическое уравнение, указанное выше, чтобы найти время, необходимое для другой плоскости \ begin {align *} t & = \ frac xv \\ \\ & = \ frac {1350} {600} \\ \\ & = 2.25 \, { \ rm h} \ end {align *} Таким образом, время на второй самолет составляет $ 2 $ часов и $ 0.25 долларов в час, которые преобразуются в минуты как 2 доллара в часы и (0,25 доллара \ умноженное на 60 = 15) минут.

Задача (7): частица движется по прямолинейному пути. Иногда $ t_1 = 2 \, {\ rm s} $ и $ t_2 = 4 \, {\ rm s} $ его позиция от начала координат равна $ x_1 = 2 \, {\ rm m} $ и $ x_2 = – 8 \, {\ rm m} $. Найдите среднюю скорость и среднюю скорость частицы.

Решение: Средняя скорость определяется как отношение длины пути (расстояния) к общему затраченному времени, \ [\ text {Средняя скорость} = \ frac {\ text {длина пути}} {\ text {прошедшее время} } \] С другой стороны, средняя скорость – это смещение $ \ Delta x = x_2-x_1 $, деленное на прошедшее время $ \ Delta t $.

Расстояние между этими двумя точками равно $ D = 12 \, {\ rm m} $, но его смещение равно $ \ Delta x = x_2-x_1 = -8-4 = -12 \, {\ rm m} $. Расстояние – это скалярная величина, и ее значение всегда положительно, но смещение – это вектор. В приведенном выше примере знак минус смещения указывает его направление к оси $ -x $.

Таким образом, средняя скорость составляет $ = \ frac {12} {4-2} = 6 \, {\ rm m / s} $, а средняя скорость составляет $ \ bar {v} = \ frac {-12} {4- 2} = – 6 \, {\ rm m / s} $. Знак минус показывает направление скорости, совпадающее с направлением смещения.

Задача (8): объект движется по оси $ x $. В момент $ t = 1 \, {\ rm s} $ он находится в позиции $ x = + 4 \, {\ rm m} $ и имеет скорость $ 4 \, {\ rm m / s} $. . При $ t = 5 \, {\ rm s} $ объект находится в точке $ x = + 9 \, {\ rm m} $ и его скорость $ -12 \, {\ rm m / s} $ . Каково его среднее ускорение за интервал времени $ 1 \ leq t \ leq 5 $?

Решение: Среднее ускорение определяется как разница скоростей, деленная на временной интервал, в котором произошло изменение.2} \ end {align *} отрицательное значение указывает, что вектор среднего ускорения направлен к оси $ -x $.

Задача (9): Автомобиль движется по оси $ x $ за $ 4 \, {\ rm s} $ со средней скоростью $ 10 \, {\ rm m / s} $ и $ 2 \, {\ rm s} $ со средней скоростью $ 30 \, {\ rm m / s} $ и, наконец, $ 4 \, {\ rm s} $ со средней скоростью $ 25 \, {\ rm m / s} $. Какова его средняя скорость на всем пути?

Решение: Есть три разные части с разными средними скоростями.Смещения в соответствующих частях получаются как \ begin {align *} \ Delta x_1 & = v_1 \, \ Delta t_1 \\ & = 10 \ times 4 = 40 \, {\ rm m} \\ \\ \ Delta x_2 & = v_2 \, \ Delta t_2 \\ & = 30 \ times 2 = 60 \, {\ rm m} \\ \\ \ Delta x_3 & = v_3 \, \ Delta t_3 \\ & = 25 \ times 4 = 100 \, {\ rm m} \ end {align *} Теперь используйте определение средней скорости $ \ bar {v} = \ frac {\ Delta x_ {tot}} {\ Delta t_ {tot}} $, чтобы найти ее по всему пути \ begin {align *} \ bar {v} & = \ frac {\ Delta x_ {tot}} {\ Delta t_ {tot}} \\ \\ & = \ frac {\ Delta x_1 + \ Delta x_2 + \ Delta x_3} { \ Delta t_1 + \ Delta t_2 + \ Delta t_3} \\ \\ & = \ frac {40 + 60 + 100} {4 + 2 + 4} \\ \\ & = 20 \, {\ rm m / s} \ end {align *}

Проблема (10): объект движется по прямой линии.Он движется со средней скоростью $ 2 \, {\ rm m / s} $ за $ 20 \, {\ rm s} $ и $ 12 \, {\ rm m / s} $ за $ t $ секунд. Если общая средняя скорость на всем пути $ 10 \, {\ rm m / s} $, то найти неизвестное время $ t $?

Решение: В этой задаче весь путь $ \ Delta x $ разделен на две части $ \ Delta x_1 + \ Delta x_2 $ с разными средними скоростями и прошедшим временем, поэтому общая средняя скорость на всем пути получается как \ begin {align *} \ bar {v} & = \ frac {\ Delta x} {\ Delta t} \\ & = \ frac {\ Delta x_1 + \ Delta x_2} {\ Delta t_1 + \ Delta t_2} \\ & = \ frac {\ bar {v} _1 \, t_1 + \ bar {v} _2 \, t_2} {t_1 + t_2} \\ 10 & = \ frac {2 \ times 20 + 12 \ times t} {20 + t} \\\ Стрелка вправо t & = 80 \, {\ rm s} \ end {align *}

Примечание: всякий раз, когда движущийся объект преодолевает расстояния $ x_1, x_2, x_3, \ cdots $ в $ t_1, t_2, t_3, \ cdots $ с постоянной или средней скоростью $ v_1, v_2, v_3, \ cdots $ по прямой – линии без изменения ее направления, то ее общая средняя скорость на всем пути определяется по одной из следующих формул

Расстояние и время известны: \ [\ bar {v} = \ frac {x_1 + x_2 + x_3 + \ cdots} {t_1 + t_2 + t_3 + \ cdots} \]
Известны скорости и время: \ [\ bar {v} = \ frac {v_1 \, t_1 + v_2 \, t_2 + v_3 \, t_3 + \ cdots} {t_1 + t_2 + t_3 + \ cdots} \]
Известны расстояния и скорости: \ [\ bar {v} = \ frac {x_1 + x_2 + x_3 + \ cdots} {\ frac {x_1} {v_1} + \ frac {x_2} {v_2} + \ frac {x_3} {v_3} + \ cdots} \]

Задача (11): Автомобиль проезжает одну четверть своего пути с постоянной скоростью $ 10 \, {\ rm m / s} $, а оставшуюся часть – с постоянной скоростью $ v_2 $.Если общая средняя скорость на всем пути составляет $ 16 \, {\ rm m / s} $, то найти $ v_2 $?

Решение: Это третий случай предыдущей заметки. Пусть длина пути равна $ L $, поэтому \ begin {align *} \ bar {v} & = \ frac {x_1 + x_2} {\ frac {x_1} {v_1} + \ frac {x_2} {v_2}} \\ 16 & = \ frac {\ frac 14 \, L + \ frac 34 \, L} {\ frac {\ frac 14 \, L} {10} + \ frac {\ frac 34 \, L} {v_2}} \ \\ Стрелка вправо v_2 & = 20 \, {\ rm м / с} \ end {align *}

Проблема (12): объект движется по прямой линии.Он движется за $ t_1 $ секунд со средней скоростью $ 50 \, {\ rm m / s} $ и $ t_2 $ секунд с постоянной скоростью $ 25 \, {\ rm m / s} $. Если общая средняя скорость на всем пути составляет $ 30 \, {\ rm m / s} $, то найти отношение $ \ frac {t_2} {t_1} $?

Решение: скорости и время известны, поэтому мы имеем \ begin {align *} \ bar {v} & = \ frac {v_1 \, t_1 + v_2 \, t_2} {t_1 + t_2} \\ 30 & = \ frac {50 \, t_1 + 25 \, t_2} {t_1 + t_2} \\\ Rightarrow \ frac {t_2} {t_1} & = 4 \ end {align *}

Проблемы с ускорением:

Задача (13): Автомобиль, движущийся со скоростью $ 15 \, {\ rm m / s} $, равномерно замедляет свою скорость.2} \ end {align *} Знак минус указывает направление вектора ускорения в направлении $ -x $.

Задача (14): объект движется с постоянным ускорением по прямой. Если его скорость в момент $ t_1 = 3 \, {\ rm s} $ равна $ 10 \, {\ rm m / s} $, а в момент $ t_2 = 8 \, {\ rm s} $ равна $ 20 \ , {\ rm m / s} $, тогда какова его начальная скорость?

Решение: Пусть начальная скорость в момент времени $ t = 0 $ равна $ v_0 $. Теперь примените определение среднего ускорения во временных интервалах $ [t_0, t_1] $ и $ [t_0, t_2] $ и приравняйте их.\ begin {align *} \ text {среднее ускорение} \ \ bar {a} & = \ frac {\ Delta v} {\ Delta t} \\\ frac {v_1 – v_0} {t_1-t_0} & = \ frac {v_2-v_0} {t_2-t_0} \\ \ frac {10-v_0} {3-0} & = \ frac {20-v_0} {8-0} \\\ Rightarrow v_0 & = 4 \, {\ rm m / s} \ end {align *} Выше $ v_1 $ и $ v_2 $ – скорости в моменты $ t_1 $ и $ t_2 $ соответственно.

Задача (15): Для $ 10 \, {\ rm s} $ скорость автомобиля, движущегося с постоянным ускорением, изменяется с $ 10 \, {\ rm m / s} $ на $ 30 \, {\ пм м / с} $. Как далеко едет машина?

Решение: Известно: $ \ Delta t = 10 \, {\ rm s} $, $ v_1 = 10 \, {\ rm m / s} $ и $ v_2 = 30 \, {\ rm m / s} $.

Метод (I) Без вычисления ускорения: вспомните, что в случае постоянного ускорения у нас есть следующие кинематические уравнения для средней скорости и смещения: \ begin {align *} \ text {средняя скорость}: \, \ bar {v} & = \ frac {v_1 + v_2} {2} \\\ text {displacement}: \, \ Delta x & = \ frac {v_1 + v_2} {2} \ times \ Delta t \\\ end {align *} где $ v_1 $ и $ v_2 $ – скорости в заданном временном интервале. Теперь у нас есть \ begin {align *} \ Delta x & = \ frac {v_1 + v_2} {2} \\ & = \ frac {10 + 30} {2} \ times 10 \\ & = 200 \, {\ rm m} \ end {align *}

Метод (II) с ускорением вычислений: Используя определение среднего ускорения, сначала определите его, как показано ниже \ begin {align *} \ bar {a} & = \ frac {\ Delta v} {\ Delta t} \\ & = \ frac {30-10} {10} \\ & = 2 \, {\ rm m / s ^ 2} \ end {align *} Поскольку скорости в начальной и конечной точках задачи даны, используйте приведенное ниже кинематическое уравнение, не зависящее от времени, чтобы найти необходимое смещение \ begin {align *} v_2 ^ {2} -v_1 ^ {2} & = 2 \, a \ Delta x \\ (30) ^ {2} – (10 ) ^ {2} & = 2 (2) \, \ Delta x \\\ Rightarrow \ Delta x & = 200 \, {\ rm m} \ end {align *}

Задача (16): Автомобиль движется из состояния покоя со скоростью $ 72 \, {\ rm км / ч} $ за $ 4 \, {\ rm s} $.2} \ end {align *}
Выше мы преобразовали $ km / h $ в единицу скорости в системе СИ ($ m / s $) как \ [1 \, \ frac {km} {h} = \ frac {1000 \, m} {3600 \, s} = \ frac {10} {36} \, m / s \], поэтому получаем
$ 72 \, км / ч = 72 \ times \ frac {10} {36} = 20 \, м / с $.

Задача (17): Гоночный автомобиль разгоняется от начальной скорости $ v_i = 10 \, {\ rm m / s} $ до конечной скорости $ v_f = 30 \, {\ rm m / s} $ в временной интервал $ 2 \, {\ rm s} $. Определить его среднее ускорение?

Решение:
Известно: $ v_i = 10 \, {\ rm m / s} $, $ v_f = 30 \, {\ rm m / s} $, $ \ Delta t = 2 \, {\ rm s } $.2} \ end {align *}

Задача (18): Мотоцикл начинает движение по прямой со скоростью $ 10 \, {\ rm m / s} $ и заканчивается $ 20 \, {\ rm m / s} $ в противоположном направлении. во временном интервале $ 2 \, {\ rm s} $. Какое среднее ускорение у машины?

Решение:
Известно: $ v_i = 10 \, {\ rm m / s} $, $ v_f = 20 \, {\ rm m / s} $, $ \ Delta t = 2 \, {\ rm s } $, $ \ bar {a} =? $. 2} \ end {align *} Напомним, что в приведенном выше определении скорости являются векторными величинами.Конечная скорость находится в направлении, противоположном начальной скорости, поэтому необходимо учитывать отрицательное значение.

Задача (19): Автомобиль движется по прямой с равномерным ускорением. Если его скорость в момент $ t_1 = 2 \, {\ rm s} $ равна $ 36 \, {\ rm км / с} $, а в момент $ t_2 = 6 \, {\ rm s} $ равна $ 72 \ , {\ rm км / ч} $, а затем найти его начальную скорость (при $ t_0 = 0 $)?

Решение: Используйте равенство определения среднего ускорения $ a = \ frac {v_f-v_i} {t_f-t_i} $ во временных интервалах $ [t_0, t_1] $ и $ [t_0, t_2] $, чтобы найти начальная скорость, как показано ниже \ begin {align *} \ frac {v_2-v_0} {t_2-t_0} & = \ frac {v_1-v_0} {t_1-t_0} \\ \ frac {20-v_0} {6-0 } & = \ frac {10-v_0} {2-0} \\\ Rightarrow v_0 & = 5 \, {\ rm m / s} \ end {align *}

Одномерные задачи движения с постоянным ускорением
Задача (20): объект перемещается на расстояние $ 45 \, {\ rm m} $ за интервал времени $ 5 \, {\ rm s} $ с начальной скоростью и ускорением $ v_0 $ и $ 2 \, { \ rm m / s ^ 2} $ соответственно. 2} $.Какова средняя скорость автомобиля в первые $ 5 \, {\ rm s} $ движения?
Решение: Вспомните, что если у вас есть начальная и конечная скорости движущегося объекта во время движения с постоянным ускорением, вы можете использовать $ \ bar {v} = \ frac {v_i + v_f} 2 $, чтобы найти среднее ускорение. В этой задаче $ v_i = 0 $ и конечная скорость получается как \ begin {align *} v_f & = v_0 + a \, t \\ & = 0+ (4) (5) = 20 \, {\ rm m / s} \ end {align *} Теперь используйте приведенную выше формулу, чтобы найти среднюю скорость как \ begin {align *} \ bar {v} & = \ frac {0 + 20} {2} \\ & = 10 \, { \ rm м / с} \ end {align *}
Задача (23): частица выходит из состояния покоя с равномерным ускорением и движется по $ 40 \, {\ rm m} $ в $ 4 \, {\ rm s} $.{2} +0 \\ & = 250 \, {\ rm m} \ end {align *}
Проблема (24): объект начинает движение из состояния покоя с постоянным ускорением. В момент $ t = 2 \, {\ rm s} $ находится на расстоянии $ 1 $ метра от начала координат, а в $ t = 4 \ {\ rm s} $ находится на расстоянии $ 13 \, {\ rm m} $. {2}} $ и $ x_0 = -3 \, {\ rm m} $.
Задача (25): Автомобиль движется со скоростью $ 72 \, {\ rm км / ч} $ по прямой. Водитель внезапно тормозит, и машина полностью останавливается после $ 5 \, {\ rm s} $. Предположим, что в течение периода замедления ускорение автомобиля остается постоянным. Как далеко автомобиль проехал между нажатием на педаль тормоза и остановкой?
Решение: Во всех кинематических задачах вы должны сначала определить две точки с известными кинематическими переменными (например, $ x, v, a $), а затем применить уравнения между этими точками.{2} & = 2 (-4) \ Delta x \\\ Rightarrow \ Delta x & = 50 \, {\ rm m} \ end {align *}
Альтернатива Решение : Между вышеуказанными точками мы можем применить известное кинематическое уравнение ниже, чтобы найти полное смещение \ begin {align *} \ Delta x & = \ frac {v_i + v_f} {2} \, t \\ & = \ frac {0 + 20} {2} \ times 5 \\ & = 50 \, {\ rm m} \ end {align *}
Задача (26): Мотоцикл начинает движение по прямой из позиции $ x_0 = 5 \, {\ rm m} $ со скоростью $ 8 \, {\ rm m / s} $ с постоянной скоростью. .{2} + 8t + 5 \ end {align *}
Задача (27): Две машины начинают гонку, чтобы достичь одного и того же пункта назначения со скоростью $ 54 \, {\ rm км / ч} $ и $ 108 \, {\ rm км / ч} $. Если более быстрый автомобиль прибывает на два часа раньше, какое расстояние между отправлением и местом назначения?
Решение: Пусть машина будет медленнее $ v_B = 54 \, {\ rm км / ч} $ с общим временем $ t $ для прохождения полного пути $ D $. Двумя часами раньше для более быстрой машины, скажем, $ v_A = 108 \, {\ rm км / ч} $ означает $ t-2 $. Расстояние, пройденное $ A $ и $ B $, одинаково i.{2} + (8) (2) \\ & = 8 \, {\ rm m} \ end {align *} Следовательно, полное смещение равно $ D = \ Delta x_1 + \ Delta x_2 = 16 \, {\ rm м} $.
Задача (29): объект движется с замедляющимся ускорением по прямой. После $ 10 \, {\ rm s} $ и расстояния $ 60 \, {\ rm m} $ его скорость достигает $ 4 \, {\ rm m / s} $. Какова его начальная скорость?
Решение: Примените независимое от ускорения кинематическое уравнение $ \ Delta x = \ frac {v_i + v_f} 2 \, \ Delta t $ между этими точками с расстоянием $ 60 \, {\ rm m} $. {2} + v_f \, t $.{2} +3 \ times 2 \\ & = 14 \, {\ rm m} \\\ Rightarrow \ Delta x & = 27-14 = 13 \, {\ rm m} \ end {align *}
Задача (39): пуля вылетает из винтовки и попадает в деревянный брус глубиной $ 10 \, {\ rm cm} $ со скоростью $ 400 \, {\ rm m / s} $ и появляется с $ 100 \, {\ rm m / s} $ с другой стороны блока. Предположим, что путь пули через блок – прямая линия.
(a) Найдите ускорение пули в блоке.
(b) Сколько времени требуется пуле, чтобы пройти через блок?
Решение:
(a) Рассмотрим скорости входа и выхода как начальную и конечную скорости соответственно.2} $ проходит некоторое расстояние до полной остановки. Определите время и расстояние между точками торможения и остановки.
Решение: в момент торможения прежняя постоянная скорость служит начальной скоростью (которая должна быть преобразована в единицы СИ $ м / с $). Напишите кинематическое уравнение скорости $ v = v_i + a \, t $ и подставьте в него известные значения выше, чтобы найти необходимое время как \ begin {align *} v & = v_i + a \, t \\ 0 & = 20 + ( -4) \, t \\\ Rightarrow a & = 5 \, {\ rm m / s ^ 2} \ end {align *}, где в приведенном выше примере мы преобразовали $ km / h $ в $ m / s $, умножив его автор: $ \ frac {10} {36} $. {2} +0 \\ & = 1800 \, {\ rm m} \ end {align *}
Задача (42): объект движется с постоянной скоростью по прямолинейному пути.Если объект в $ t_1 = 5 \, {\ rm s} $ находится в позиции $ x_1 = + 6 \, {\ rm m} $ и в $ t_2 = 20 \, {\ rm s} $ находится в $ x_2 = 36 \, {\ rm m} $, затем найдите его уравнение положения как функцию времени.
Решение: Кинематическое уравнение положения с постоянной скоростью имеет вид $ x = x_0 + vt $, где $ x_0 $ – начальное положение в момент времени $ t = 0 $, когда движущаяся частица начинает свое движение. Подставляя в него время $ t = 5 \, {\ rm s} $ и позицию $ x = + 6 \, {\ rm m} $, получаем $ 6 = x_0 + 5v $, в момент времени и позиции $ t = 20 \, {\ rm s} $ и $ x = + 36 \, {\ rm m} $ получаем $ 36 = x_0 + 20v $.Приравнивание этих уравнений приводит к системе двух уравнений с двумя неизвестными, как показано ниже \ [\ left \ {\ begin {array} {rcl} 6 & = & 5v + x_0 \\ 36 & = & 20v + x_0 \ end {array} \ right . \] Решая для неизвестных, получаем $ v = 2 \, {\ rm m / s} $ и $ x_0 = -4 \, {\ rm m} $. Следовательно, позиция стиха time равна $ x = 2t-4 $.
Задача (43): объект движется по оси $ x $. При $ t_0 = 0 $ он проходит позицию $ x = + 4 \, {\ rm m} $ со скоростью $ + 3 \, {\ rm m / s} $. Если объект в точке $ t = 4 \, {\ rm s} $ находится на наибольшем расстоянии от начала координат, то в момент $ t = 8 \, {\ rm s} $ он находится на каком расстоянии от начала координат?
Решение: Наибольшее расстояние от начала координат без изменения направления означает, что объект в этот момент останавливается и меняет свое направление.{2} +3 (8) +4 \\ & = 4 \, {\ rm m} \ end {align *}
Проблемы скорости, скорости и ускорения для свободного падения:
Задача (44): Камень брошен вертикально вверх из здания высотой $ 15 \, {\ rm m} $ с начальной скоростью $ 10 \, {\ rm m / s} $. Какова скорость камня перед ударом о землю?
Решение: В задачах свободного падения важным примечанием является выбор источника. Обычно точка броска (сброса или сброса) является лучшим выбором.{2} & = 2 \, (- 10) (- 15) \\\ Rightarrow v_f & = \ pm 20 \, {\ rm m / s} \ end {align *} Поскольку скорость является векторной величиной и непосредственно перед ударом к земле его направление – вертикально вниз, поэтому необходимо выбрать отрицательное значение, т.е. $ v_f = -20 \, {\ rm m / s} $.
Практическая задача (45): пуля выпускается без начальной скорости с высоты $ h $ и в последнюю секунду падения падает на расстояние $ 35 \, {\ rm m} $. Определить высоту $ h $?
Решение: это оставлено для вас в качестве практической задачи.{2} + 7t-34 \ end {align *} Так как начальная скорость является вектором и изначально направлена вниз, перед ней добавлен отрицательный элемент. Вышеупомянутое квадратное уравнение имеет два решения: $ t_1 = 2 \, {\ rm s} $ и $ t_2 = -3.4 \, {\ rm s} $. Отрицательное значение отклоняется, так как начальное время $ t_0 = 0 $.
Вторая часть представляет собой равномерное движение, поскольку скорость звука постоянна, поэтому мы можем рассчитать время его нарастания как \ begin {align *} t & = \ frac {\ Delta y} {v} \\ & = \ frac {34} {340} = 0,1 \, {\ rm s} \ end {align *} Таким образом, общее время получается как $ t_T = 2 + 0.{2} -0 & = – 2g (- \ frac h3) \\\ Стрелка вправо v_2 & = \ sqrt {gh} \ end {align *}
Практическая задача (49): Маленькая пуля выпускается без начальной скорости из башни и проходит последние $ 80 \, {\ rm m} $ своего движения за $ 2 \, {\ rm s} $. Какая высота башни?
Решение: это оставлено для вас в качестве практической задачи.
Задача (50): пуля выстреливается вертикально вверх с высоты $ 90 \, {\ rm m} $ от поверхности земли и после того, как $ 10 \, {\ rm s} $ достигает земли.{2} + (40) (2) +0 \\\ Стрелка вправо y & = 60,4 \, {\ rm m} \ end {align *}
Задача (51): мяч бросается вертикально вверх с начальной скоростью $ 18 \, {\ rm m / s} $. Через сколько секунд после броска мяч движется вниз со скоростью $ 9 \, {\ rm m / s} $?
Решение: Во всех кинематических уравнениях $ x, y, v, v_0 $ и $ a $ являются векторами, поэтому их знаки имеют значение. Скорость вниз $ 9 \, {\ rm m / s} $ означает скорость $ -9 \, {\ rm m / s} $. Вниз или вверх указывают направление скорости.Теперь используйте уравнение $ v_f = v_i-g \, t $, чтобы найти скорость в любое более позднее время. \ Begin {align *} v_f & = v_i-g \, t \\ – 9 & = + 18- (10) \, t \\\ Стрелка вправо t & = 2.7 \, {\ rm s} \ end {align *}
Практическая задача (52): мяч выпущен с высоты. В первую секунду он преодолевает расстояние $ \ Delta x_1 $, а во второй – расстояние $ \ Delta x_2 $. Найдите соотношение $ \ frac {\ Delta x_2} {\ Delta x_1} $.
Решение: это оставлено для вас в качестве практической задачи.{2} + v_0 \, t \\\ Rightarrow v_0 & = – 5 \, {\ rm m / s} \ end {align *} знак минус указывает, что начальная скорость направлена вниз с величиной (скоростью) $ 5 \, { \ rm m / s} $.
Задача (54): С высоты $ 15 \, {\ rm m} $ мяч подбрасывается вертикально в воздух с начальной скоростью $ v_0 $. Он достигает наивысшей точки своего пути с высотой $ 20 \, {\ rm m} $ от поверхности. Найти начальную скорость $ v_0 $?
Решение: Наивысшая точка находится на $ 5 \, {\ rm m} $ выше точки удара.{2} & = – 2 (10) (5) \\\ Rightarrow v_i & = \ pm 10 \, {\ rm m / s} \ end {align *} Поскольку мяч ударил вверх, мы должны выбрать знак плюса, т.е. $ v_i = + 10 \, {\ rm m / s} $. Выше мы использовали тот факт, что в задаче свободного падения в наивысшей точке (вершине) скорость равна нулю ($ v_f = 0 $).
Напомним, что снаряды представляют собой особый вид свободного падения с углом пуска $ \ theta = 90 $ по собственным формулам.
Задача (55): Со дна колодца $ 25 \, {\ rm m} $ вертикально вверх бросается камень с начальной скоростью $ 30 \, {\ rm m / s} $.{2} +30 \, (t) \ end {align *} Решая относительно $ t $ (используя формулу корней квадратного уравнения), мы получаем $ t_1 = 1 \, {\ rm s} $ и $ t_2 = 5 \, {\ rm s} $ один для восходящего пути, а второй для нисходящего.
Практическая задача (59): камень бросается вертикально вверх с высоты $ 60 \, {\ rm m} $ с начальной скоростью $ 20 \, {\ rm m / s} $. Найти отношение смещения за третью секунду к смещению за последнюю секунду движения?
Решение: это оставлено для вас в качестве практической задачи.{2}} & = \ frac {-2 \, g \, h_A} {- 2 \, g \, h_B} \\ & = \ frac {h} {h / 4} \\ & = 4 \\\ Стрелка вправо \ frac {v_A} {v_B} & = 2 \ end {align *}
Практическая задача (61): со скалы $ 45 – {\ rm m} $ два шара направляются вниз, один выпущен, а другой сброшен с начальной скоростью $ 12,5 \, {\ rm м / с} $. Какая разница между расстояниями, пройденными за последнюю секунду их движения?
Решение: это оставлено для вас в качестве практической задачи. Вы можете найти решение позже.
Задача (62): камень запускается прямо вверх от уровня поверхности с начальной скоростью $ 20 \, {\ rm m / s} $. Через сколько секунд после запуска камень падает со скоростью $ 5 \, {\ rm m / s} $?
Решение:
Пусть начало координат будет уровнем поверхности и положительным направлением вверх. Следовательно, мы имеем начальную скорость $ v_0 = + 20 \, {\ rm m / s} $ и конечную скорость $ v = -5 \, {\ rm m / s} $. Используйте кинематическое уравнение скорости $ v = v_0-g \, t $, чтобы найти необходимое время как \ begin {align *} v & = v_0-g \, t \\ – 5 & = + 20-10 \ times t \\\ Стрелка вправо t & = 2.5 \, {\ rm s} \ end {align *}
Задача (63): камень падает с башни высотой $ 60 \, {\ rm m} $. В момент, когда камень достигает $ 15 \, {\ rm m} $ над уровнем земли, его скорость составляет какую долю от его скорости в момент удара о землю?
Решение: Пусть точка сброса будет исходной точкой и положительным направлением вверх. Скорость $ v_1 $ на высоте $ h = 60-15 = 45 \, {\ rm m} $ ниже полученной точки начала координат (должна быть включена с минусом в кинематическое уравнение) как \ begin {align *} v_1 ^ { 2} -v_0 ^ {2} & = – 2 \, g \ Delta y \\ v ^ {2} -0 & = – 2 (10) (- 45) \\\ Стрелка вправо v & = – 30 \, {\ rm м / с} \ end {align *} Выше мы выбрали знак минус, так как камень направлен вниз. {2} -4 (1) (- 5)}} {2 (1)} \ \ & = – 1 \ \ text {and} \ 5 \ end {align *} Следовательно, время, необходимое для того, чтобы мяч ударился о землю, составляет $ 5 \, {\ rm s} $.{2} & = 1600 \\\ Rightarrow v & = 40 \, {\ rm m / s} \ end {align *} Следовательно, скорость камня при ударе о землю равна $ v = -40 \, {\ rm m / s} $.
Все эти кинематические задачи о скорости, скорости и ускорении легко решаются путем выбора подходящего кинематического уравнения. Имейте в виду, что эти задачи движения в одном измерении относятся к типу равномерного или постоянного ускорения. Снаряды – это еще один тип движения в двух измерениях с постоянным ускорением.
Автор: PhysicsExams
Издатель: PhysExams.com
Дата публикации: 06.09.2020
Путь брошенного мяча
Урок NTTI: Изменение: Путь брошенного мяча

ИЗМЕНЕНИЕ: ПУТЬ БРОСАЮЩЕГО МЯЧА

8–12 классы
Когда объект бросают, стреляют или иным образом отбрасывают в в воздухе, он будет следовать по воздушной траектории, известной как траектория. Если на объект не действуют никакие силы, кроме силы тяжести, его путь может быть легко и точно определено. На этом уроке физики или физических наук учащиеся в 9-12 классах научатся применять законы Ньютона и кинематические уравнения чтобы предсказать путь снаряда.Если математические уравнения опущены, урок можно адаптировать для 8 класса. На видео объекты, движущиеся под наглядно показаны условия постоянной скорости и постоянного ускорения. Практическая деятельность дает студентам возможность построить физическая модель для проверки их прогнозов. Расследование можно завершить за два-три академических часа.
Этот урок может служить предпосылкой к дополнительному уроку под названием Кривые шары, в которых учащиеся будут использовать качественное понимание Ньютона. законы, чтобы объяснить, как реальные переменные, такие как сопротивление воздуха и вращение, будут изменить прогнозируемую траекторию полета снаряда.
3-2-1 Контактное лицо в классе №20: Играть в мяч!

Студенты смогут:
понимать законы Ньютона применительно к движению снаряда. в идеальных (т.е. без сопротивления воздуха) условиях.
нарисовать силовые диаграммы снаряда под
идеальные условия.
применить основные кинематические уравнения к движению
снаряд.
описать, нарисовать и рассчитать приблизительный путь снаряда в идеальных условиях.
Техасская оценка академических навыков (TAAS), 8 класс
Научные цели:
№ 3: Сообщать научные данные и / или информацию.
# 4: Интерпретация научных данных и / или информации.
# 5: Делайте выводы, формулируйте обобщенные утверждения и / или делайте прогнозы.
# 7: Сделайте выводы о процессе (ах) и / или результате (ах) научного изучение.
№ 8: Свяжите и примените научную и техническую информацию в повседневной жизни.
Math Objectives:
# 11: Определить стратегии решения и проанализировать или решить проблемы.
# 12: Выражайте или решайте проблемы, используя математическое представление.
# 13: Оцените разумность решения проблемной ситуации.
Стандарты NCTM для классов 9–12
Стандарт 13: Концептуальные основы исчисления
Стандарт 14: Математическая структура
В группе из 3-4 человек:
4 пятидюймовых кольца и стойки для колец (кольца должны регулироваться по вертикали и может вращаться)
2-х метровые палки
таймеры для гранатометов, круглых снарядов и фотозатворов, или
Металлический шар диаметром 1 дюйм, желобчатая рампа и секундомер
лист заданий (прилагается к этому уроку)
Рабочий лист Shooting Hoops (прилагается к этому уроку)

снаряд-объект, движущийся под действием инерции и силы тяжести.
траектория – траектория, по которой снаряд движется.
вектор – физическая величина, обладающая величиной и направлением.
компонентных векторов – два или более вектора, которые могут быть объединены математически для создания результирующего вектора.
дальность полета снаряда в горизонтальном направлении.
кинематика – исследование движущихся объектов.
независимость движения – явления, при которых горизонтальное движение снаряда, кажется, действует независимо от вертикального движения (т.е. объект движется по горизонтали с постоянной скоростью и движется по вертикали с постоянное ускорение). Эта кажущаяся независимость позволяет движениям быть разделенными и рассчитанными независимо друг от друга.

В качестве задания накануне урока учащиеся должны просмотрите первый и второй законы Ньютона, соответствующие силовые диаграммы, и кинематические уравнения для расчета скоростей и расстояний. Студенты должен уметь рассчитывать скорости и расстояния объектов, движущихся под условия постоянной скорости и постоянного ускорения (в первую очередь, ускорение силы тяжести).Студенты должны уметь правильно рисовать диаграммы сил для каждой ситуации и соответствующим образом применяют законы Ньютона. Студенты также должны уметь сочетать горизонтальную и вертикальную скорость. компоненты с помощью теоремы Пифагора. Эти концепции будут рассмотрены ненадолго перед просмотром видео.
Попросите одного из студентов сформулировать первый закон Ньютона. После того, как это было правильно сказано, положите его на доску или накладку. Попросите другого ученика нарисовать силу диаграмма, соответствующая первому закону. Спросите, может ли кто-нибудь нарисовать другой диаграмма сил, которая все еще показывает движение с постоянной скоростью.Диаграммы должны указывают на отсутствие сил или уравновешенных сил. Попросите учащегося представить уравнение для расчета расстояния, пройденного объектом в условиях первого закона. (d = v * t)
Попросите одного из студентов сформулировать второй закон Ньютона. После того, как это было правильно сказано, положите его на доску или накладку. Попросите другого ученика нарисовать силу диаграмма, соответствующая второму закону. Спросите, может ли кто-нибудь нарисовать другой силовая диаграмма, указывающая на постоянно ускоренное движение. Диаграммы должны указывают на неуравновешенные силы.Попросите учащегося предоставить уравнения для скорости и расстояние, пройденное объектом, путешествующим в условиях второго закона. (v = v0 + a * t; d = v0 * t + 1/2 * a * t2)
Изобразите объект, движущийся с постоянной горизонтальной скоростью 10 м / с, и постоянная вертикальная скорость 5 м / с. Попросите одного ученика указать направление результирующей скорости, второй студент вычисляет результирующую скорость, а третий – для расчета расстояния, которое он пройдет за три секунды. Указывать что путь, по которому следует объект, называется его «траекторией».Если объекту придается начальная скорость, а затем ему разрешается двигаться по его Собственно, это называется «снаряд». Спросите студентов, все ли предметы движение в двух измерениях всегда движется с постоянной скоростью.

Чтобы дать учащимся определенные обязанности во время просмотра, попросите учащихся просмотреть видео и быть готовыми:
a) рисовать диаграммы сил и описывать движение конкретных объектов на видео; и
b) качественно прогнозировать двумерный путь конкретных объектов в видео и поддержка прогнозов, основанных на законах Ньютона и кинематических уравнениях.

BEGIN the 3-2-1 Classroom Контактное видео без звука когда ведущий наблюдает за неподвижным мячом. ПАУЗА лента. Иметь студенты рисуют диаграмму силы мяча, описывают движение и указывают какой из законов Ньютона соответствует ситуации. После соответствующего время, попросите учащихся ответить индивидуально или в группе.
FAST FORWARD видео до точки, где у хозяина мяч висит из строки. РЕЗЮМЕ видео, показывающее неподвижно висящий мяч на веревочке. ПАУЗА видео. Попросите учащихся нарисовать диаграмму сил шара, опишите движение и укажите, какой из законов Ньютона соответствует к ситуации. Спустя подходящее время попросите учащихся ответить индивидуально. или как группа.
РЕЗЮМЕ видео. ПАУЗА видео, когда молодой человек пинает шар. Попросите учащихся нарисовать диаграмму силы мяча, описать движение, и указать, какой из законов Ньютона соответствует ситуации. После в подходящее время попросите учащихся ответить индивидуально или в группе.
Мягко пните футбольный или баскетбольный мяч по полу. Попросите студентов опишите движение мяча после того, как он покинет вашу ногу. Студенты должны поймите, что, покинув вашу ногу, мяч летит примерно на постоянная скорость с некоторыми потерями из-за трения. Студенты должны четко обратите внимание, что мяч не ускоряется после того, как покидает вашу ногу. Обеспечить разумное расстояние и время. Попросите учащихся рассчитать среднюю скорость мяча.
РЕЗЮМЕ видео. PAUSE видео так же, как хост производит ножницы. Попросите учащихся предсказать, как она планирует заставить мяч двигаться. ВОЗОБНОВИТЬ видео, чтобы проверить правильность прогноза. ПАУЗА видео так же, как она перерезает веревку. Попросите учащихся нарисовать диаграмму сил шара, спрогнозируйте движение и укажите, какой из законов Ньютона соответствует к ситуации. Спустя подходящее время попросите учащихся ответить индивидуально. или как группа.
Спросите, чем эта ситуация отличается от удара по мячу.Студенты должны указывают, что это ситуация постоянного ускорения из-за постоянного сила и гравитация, и мяч продолжает ускоряться, пока падает. Обеспечьте разумную высоту. Попросите учащихся рассчитать время, которое возьмите мяч, чтобы достичь земли. Пройдите расчет на доске.
РЕЗЮМЕ видео. ПАУЗА незадолго до того, как машина подачи бросает шар. Предложите учащимся объединиться в группы по 3-4 человека. Попросите учеников нарисовать силу диаграмму мяча, предсказать траекторию брошенного мяча и объяснить рассуждения, основанные на законах Ньютона и уравнениях кинематики.После трех до четыре минуты, попросите группу объяснить свой прогноз и проложить свой путь по доска. Спросите другие группы, поддерживают ли они предсказание, и попросите их Объясните, почему да или почему нет. [Примечание: проецирование миллиметровой бумаги на переходное отверстие проектор может помочь учащимся более точно нарисовать путь.] Учащимся следует в конечном итоге сделать вывод, что мяч должен двигаться с постоянной скоростью по горизонтали, с постоянным ускорением по вертикали и с параболической траекторией. Путь начинается почти горизонтально, но изгибается вниз под все более крутым углом на протяжении всего полета.
РЕЗЮМЕ видео. ПАУЗА видео между каждым полетом мяч и спросите учащихся, соответствует ли реальный путь предсказанию. Спросите студентов, почему важно (с точки зрения демонстрации) машина подачи, чтобы придать мячу постоянную начальную скорость и высоту. Студенты должны понимать это как экспериментальный контроль, который позволяет легко сравнение траекторий. Попросите учащихся предсказать, как изменится полет если качающая машина (а) применяет большую начальную скорость, (б) применяет меньшая начальная скорость, (c) увеличивается еще на 12 дюймов.У студентов нарисуйте в своих блокнотах различные диаграммы сил и прогнозируемые траектории. Попросите группы нарисовать и объяснить на доске различные ситуации.
РЕЗЮМЕ видео. Просмотрите отрывок видео, показывающий, как мяч выстрелил через обручи. СТОП видео после того, как мяч прошел обручи один раз. Попросите учащихся определить, как можно расположить обручи. быть предсказанным без использования метода проб и ошибок.

После просмотра видео, рисования диаграмм и ответа вопросы, студенты должны иметь хорошее качественное представление о траектория полета снаряда под действием силы тяжести.Они должны сейчас уметь применять кинематические уравнения для расчета высоты проектируемого мяч на разном расстоянии от точки проекции. Предоставляя несколько Рабочие примеры и домашние задания помогут подкрепить эти расчеты. В следующем упражнении учащиеся экспериментально проверит свое понимание движения снаряда.
На оставшуюся часть периода группы из трех или четырех студентов должны обсудить, как они могут предсказать расположение четырех обручей так, чтобы они располагались по горизонтали. проецируемый мяч будет проходить беспрепятственно.Остановите группы с пятью осталось минут на то, чтобы повторить, что они узнали о движении снаряда. Подчеркнуть следующее: (а) горизонтальное движение происходит с постоянной скоростью на всем протяжении путь; (б) вертикальное движение происходит с постоянным ускорением; (c) начальная вертикальная скорость горизонтально брошенного объекта равна нулю; и (г) кинематика уже известные им уравнения справедливы для снарядов.
Задание: Студенты должны выполнить следующее домашнее задание:
1) Определите, какие переменные вам необходимо знать, чтобы определить рост. мяча на любом заданном расстоянии от точки выброса и метод для экспериментального определения этих переменных.
2) На листе заданий (прилагается к этому уроку) вычислите диапазон, высота, горизонтальная и вертикальная скорости горизонтально проецируемых объектов используя уравнения кинематики.
На следующий день кратко рассмотрите концепции / решения домашнего задания. проблемы. Студенты должны четко понимать, что во время полета мяч движется с постоянной горизонтальной скоростью и постоянным вертикальным ускорением. Студенты должны уметь рассчитывать время полета и вертикальное положение. снаряда, учитывая начальную горизонтальную скорость мяча.Студенты также должен уметь вычислять среднюю скорость с учетом расстояния и время путешествия.
В следующем задании учащиеся предскажут путь горизонтального спроецированный мяч путем расчета высоты мяча на нескольких горизонтальных позиции. Они проверит предсказанный путь, поместив кольца в соответствующие места. высоты, позволяющей мячу проходить через кольца. Студенты должны ни угадывать положение колец, ни ставить кольца пробным путем и ошибка. Вместо этого учащиеся должны использовать свои знания о предмете движения и кинематических уравнений для определения соответствующих высот.
Упражнение: Обручи для стрельбы
Необходимо разработать метод проецирования мяча горизонтально с постоянным и измеримая скорость. Возможно, стоит позволить учащимся определить метод. Один из способов – использовать гранатомет с фотозатвором. приобретены у компании, производящей лабораторное оборудование, или взяты взаймы в местном университете. Если это невозможно, стальной шар может разгоняться от указанного высота вниз по наклонной плоскости, катится по плоскому гладкому столу и проецируется с конца.Скорость мяча можно рассчитать, рассчитав время полета мяча. при перемещении между двумя отмеченными точками на плоском участке. Усредняя несколько прогонов помогут уменьшить ошибку. Важно остановить мяч до того, как он покинет стол, чтобы исключить возможность наблюдать за траектории мяча перед ее расчетом. Изготовление желобчатого пандуса и дорожки с частями 2х4 может значительно уменьшить проблемы с прицеливанием.
Раздайте лист задания Shooting Hoops (прилагается к этому уроку) каждой группе.Предоставьте группам достаточно времени и места для проведения деятельность. После завершения задания дайте студентам время обсудить что они узнали, и чтобы прояснить концепции, необходимые для эксперимента отчет. Можно включить следующие вопросы: Насколько точны были прогнозы? Каковы возможные источники ошибок в эксперименте? (трение, плохое время мяча на первом шаге, прицеливаться и т. д.) Была ли траектория мяча согласованной что вы узнали о движении снаряда? Если путь был последовательным, что, если что-либо говорит об истинности законов Ньютона и кинематические уравнения?
Попросите пары учеников найти здание некоторой высоты, над которым мяч можно смело бросать.По очереди бросая мяч, студенты следите за движением мяча до земли. Они рисуют его путь, вычисляют его дальность и время полета и сравните с реальными значениями. Пусть они узнают как рассчитать дальность попадания мячей вверх под углом. Рассчитать начальные скорости, необходимые для выполнения хоум-ранов, ударов по воротам, игры в гольф мяч с ти на грин и т. д.
Если бейсбольная команда имеет две машины для подачи, попросите тренера установить машины с разными начальными скоростями. Сравните и сопоставьте пути шаров.Обратите особое внимание на то, какой мяч первым ударяется о землю, какой мяч проходит дальше всех и у какого шара самый плоский путь.

История : Студенты могут исследовать эволюцию качки в бейсболе, а также в эволюции бейсбола в американском обществе. Сериал Кена Бернса «Бейсбол» – отличный ресурс. Особенно интересный фрагмент программы №7 бейсбола показывает знаменитый захват плеча и бросок в тарелку, который многие считают лучшим на поле играть в историю игры.
История : Студенты могут изучать развитие артиллерии, например катапульты, пушки и авиационные бомбы, которые в значительной степени зависят от способности для расчета траекторий. Особенно интересный пример – германский разработка Большой Берты, артиллерийского орудия дальнего действия, которая потерпела неудачу из-за проблем с правильным расчетом пути снаряда.
Language Arts : Студенты могут читать различные книги о бейсболе и его роль в американской жизни. Одна особенно хорошая книга – W.П. Кинселлы Босоногий Джо, исследование мистического воздействия бейсбола на американца. пище. Это книга, по которой снят фильм «Поле грез». основывался.
Математика : Расчет траектории мяча в упражнении с обручем обеспечивает отличное применение навыков построения графиков и работы с квадратичными уравнения.
1995–1996 Национальный институт подготовки учителей / Остин
Главный учитель: Брендан Макси

База данных планов уроков
NTTI
Thirteen Ed Online
wNetStation
Быстрое обучение скорости, скорости и ускорению – Часть 2
В февральском выпуске мы рассмотрели скорость и скорость обучения.Теперь мы готовы заняться ускорением.
Ускорение
Это главное – возможно, одна из самых сложных концепций в вашем курсе. Вы можете поспешить с понятиями скорости и скорости, потому что они интуитивно понятны. Но так быстро разгоняться нельзя, потому что не интуитивно понятно.
Попросите три элемента управления в автомобиле, которые позволяют изменять свое состояние движения – производить ускорение .Это акселератор , педаль тормоза и рулевое колесо . Ускорение можно почувствовать в автомобиле или мотоцикле по мере увеличения скорости, замедления и изменения направления (рис. 1). Ускорение – это скорость изменения скорости во времени, которая включает изменения скорости, направления или и того, и другого.
РИСУНОК 1
В то время как скорость – это скорость пройденного расстояния, ускорение – это скорость прохождения расстояния или даже скорость поворота.Это может быть вдвое сложнее для учащегося и, как уже говорилось, не интуитивно понятно. Понимание ускорения будет иметь решающее значение для понимания второго закона Ньютона – закона, который привел людей на Луну в 1969 году.
Численные примеры ускорения
Попросите свой класс рассчитать ускорение автомобиля, который разгоняется до 100 км / ч за 10 секунд, при условии равномерного ускорения.Попросите их проверить свою работу со своими соседями, пока вы планируете время доставки. Только после того, как они разберутся, вводите в примерах метры в секунду в секунду, чтобы лучше понять единицу измерения: м / с ². Будьте готовы к постоянному вопросу: «Почему секунды в квадрате м / с ²?» Для любознательных студентов, у которых возникают проблемы с м / с ² после первоначального объяснения, я советую им «отпустить». Продолжайте пока что, и, скорее всего, это будет понятно позже.Мудрость – это знание, когда можно не заметить отсутствие начального понимания.
Наклонные самолеты
Galileo представил концепцию ускорения при экспериментах с наклонными плоскостями. Он отметил, что мяч, катящийся по наклонной плоскости, набирает скорость с постоянной скоростью (постоянная скорость в раз, не на расстоянии). Чем круче наклон, тем больше коэффициент усиления и тем больше ускорение мяча (рис. 2, где значения ускорения и обозначены символами разных размеров).Когда наклон повышен до 90 °, происходит максимальное ускорение – ускорение свободного падения.
ФИГУРА 2
Свободное падение
Свободное падение означает падение только под действием силы тяжести – без сопротивления воздуха или когда сопротивление воздуха настолько незначительно, что его можно не учитывать. Приведите примеры свободного падения, например, монета и перо, упавшие в вакууме, или валун, упавший с небольшого расстояния.Падение при наличии сопротивления воздуха составляет , а не свободного падения. Позже в вашем курсе будет изучена физика парашютов и прыжков с парашютом. Пока ваш урок ограничен свободным падением. Перво-наперво.
Падающий валун со спидометром
Представьте себе валун, упавший с обрыва. Почему от отдыха? Потому что физика проще, чем в противном случае. (Лучше, чтобы студенты понимали простую физику, чем запутались в непростой физике, по крайней мере, в начале вашего курса !) Далее представьте, что валун оснащен спидометром, который может регистрировать скорость его падения (рис. ).
РИСУНОК 3
В момент падения спидометр показывает нулевую начальную скорость.
Как быстро?
Картина свободного падения должна быть очевидна – скорость увеличивается на ту же величину каждую секунду, 10 м / с. (Чтобы учащимся легче понять последовательность падения, мы можем округлить 9,8 м / с ² до 10 м / с ².В лаборатории вы можете использовать более точный 9,8 м / с ².) Это ускорение свободного падения обусловлено силой тяжести, 10 м / с ² или просто g .
Итак, как быстро валун падает в каждую последующую секунду? В сокращенной записи v = gt , что можно отнести к показаниям спидометра. После вопросов, обсуждения и примеров заявите, что вы собираетесь задать другой вопрос – спрашивать не о том, насколько быстро или , а о том, насколько далеко.
Как далеко?
Как быстро что-то падает, связано с тем, как далеко что-то падает. Осторожно выведите d = 1/2 gt ². От ваших учеников не ожидают вывода, а вместо этого демонстрируют аргументированное утверждение, которое не появляется ниоткуда. Затем спросите, как далеко пролетает свободно падающий объект за 1 секунду. Через 2 секунды? Вернитесь к падающим спидометрам и запишите показания одометра (на рисунке 3 не показаны).Отображение расстояний: 5 м, 20 м, 45 м, 80 м, 125 м.
Первая секунда свободного падения
Как мы только что видели, свободно падающий объект падает на вертикальное расстояние 5 м за первую секунду. Почему не 10 м? Начните обсуждение, задав вопрос: «Если вы будете поддерживать постоянную скорость 10 км / ч в течение 1 часа, как далеко вы поедете?» [10 км] Затем: «Если вы поддерживаете постоянную скорость 10 м / с в течение 1 секунды, как далеко вы проедете?» [10 м] В этих вопросах единицы км / ч и м / с переходят в расстояния км и м. Важный момент : Вы значительно улучшите свои инструкции, если дадите достаточно «времени ожидания» после того, как зададите вопрос. Невыполнение этого требования – безумие, с которым сталкиваются слишком многие учителя.
Затем продолжите: «Почему объект, изначально находящийся в состоянии покоя, не падает с 10 метров в первую секунду падения?» После подходящего «времени ожидания» выявите, что он не падает с постоянной скоростью , а затем перейдите к соотношению между средней скоростью и пройденным расстоянием.
Средняя скорость и пройденное расстояние
Средняя скорость равномерно ускоряющегося объекта или объекта в свободном падении равна
.
Для объектов, которые начинают падать из положения покоя, средняя скорость равна половине конечной скорости. В то время как объект набирает скорость 10 м / с в первую секунду падения из состояния покоя, его средняя скорость составляет 5 м / с. Важное отличие состоит в том, что в то время как мгновенная скорость падающего объекта, когда она достигает одной секунды, составляет 10 м / с, средняя скорость падения в течение этого односекундного интервала составляет 5 м / с.А расстояние свободного падения от покоя за одну секунду – 5 м.
Время зависания
Увлекательная тема времени зависания может дополнить ваши уроки кинематики. Бросьте вызов своим ученикам, пообещав, что вы дадите пятерку любому ученику, который может совершить 1-секундный прыжок с места (без оборудования)! У вас будут берущие; но за этот подвиг ты не награждаешь.
Время зависания – это время, когда парашютист отрывается от земли в прыжке с места.Время зависания для лучших баскетболистов составляет менее секунды. Уравнение d = 1/2 gt ² предсказывает высоту перемычки по вертикали. Считайте, что время зависания составляет целую секунду. Это означает 0,5 с вверх и 0,5 с вниз. Расстояние в одну сторону составляет d = 1/2 gt ² = 5 (0,5) ² = 1,25 м (что составляет около 4 футов!). Так что великие спортсмены и артисты балета прыгают по вертикали не более чем на 4 фута! Конечно, можно очистить более высокий забор или решетку; но центр тяжести не может быть поднят более чем на 4 фута в прыжке с места.Фактически, очень немногие люди могут прыгнуть на 2 фута в высоту!
Сообщите своим ученикам, что они могут измерить свою высоту прыжка и рассчитать свое личное время зависания следующим образом: «Встаньте прямо перед стеной. Сделайте отметку маркером в вытянутой руке. Затем подпрыгните вверх и в верхней части прыжка сделайте еще одну отметку на стене. Расстояние между двумя отметками – это ваша высота прыжка »(рис. 4). Если ученик прыгает более чем на 1,25 м (4 фута), в вашем классе есть спортсмен мирового класса.
РИСУНОК 4
В верхней части траектории прыгуна расстояние до пола определяется нашим теперь уже знакомым d = 1/2 gt ², что также является высотой прыжка. Решение этого уравнения для t дает t = √2 d / g . Обратите внимание, что это время для , половина скачка . Двойная т на время зависания перемычки!
В перспективе
Одно из замечательных качеств учителя физики – это актуальность изучения законов природы.

Движение | Физика

Равномерное движение

Средняя и мгновенная скорость

Движение с ускорением

Сила и ускорение

Свободное падение

Движение по окружности

Расстояние, скорость, время

Расстояние

Скорость

Время

Навигация по записям

Новосибирский государственный архитектурно-строительный университет – Сибстрин

Измерение ускорения свободного падения на различных высотах при помощи математического маятника

1. Введение

2. Основная часть

2.1. Исторические сведения об открытии свободного падения и методах его измерения

2.2. Практическая значимость нахождения значения ускорения свободного падения

2.3. Методы измерения ускорения свободного падения

1) Измерение ускорения свободного падения с помощью наклонной плоскости

2) Определение

Подготовка к проведению работы

2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах

2.5. Экспериментальное определение ускорения свободного падения с помощью математического маятника

Ход работы

Таблица результатов измерений в классе

Таблица результатов измерений на станции метро Кремлевская

Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»

3. Заключение

Разгон

Геометрический

Speedy Science: как ускорение влияет на расстояние?

ОБ АВТОРЕ (-АХ)

Последние статьи от Science Buddies

Информационный бюллетень

Станьте умнее.Подпишитесь на нашу новостную е-мэйл рассылку.

Поддержите научную журналистику

Расчет ускорения ракеты – Science Learning Hub

Силы, действующие

Расчет ускорения модели ракеты

Расчет ускорения космического челнока

Сравнение ускорений

Сопутствующие материалы

Идеи действий

Полезная ссылка

Равномерное круговое движение

Равномерное круговое движение

Задача:

В каких обстоятельствах сила?

Задача:

Проблема:

Модуль 3: Вопрос 1

60+ решенных задач скорости, скорости и ускорения для старшей школы

Проблемы скорости, скорости и ускорения на прямолинейном пути:

Проблемы скорости, скорости и ускорения для свободного падения:

Путь брошенного мяча

ИЗМЕНЕНИЕ: ПУТЬ БРОСАЮЩЕГО МЯЧА

Главный учитель: Брендан Макси

Быстрое обучение скорости, скорости и ускорению – Часть 2

Ускорение

Численные примеры ускорения

Наклонные самолеты

Свободное падение

Падающий валун со спидометром

Как быстро?

Как далеко?

Первая секунда свободного падения

Средняя скорость и пройденное расстояние

Время зависания

В перспективе

Оставить комментарий Отменить ответ