Как найти ускорение зная время и путь: Как найти ускорение зная путь и время

Калькулятор остановочного пути автомобиля • Механика • Онлайн-конвертеры единиц измерения

Функциональность этого сайта будет ограничена, так как в Вашем браузере отключена поддержка JavaScript!

Random converter

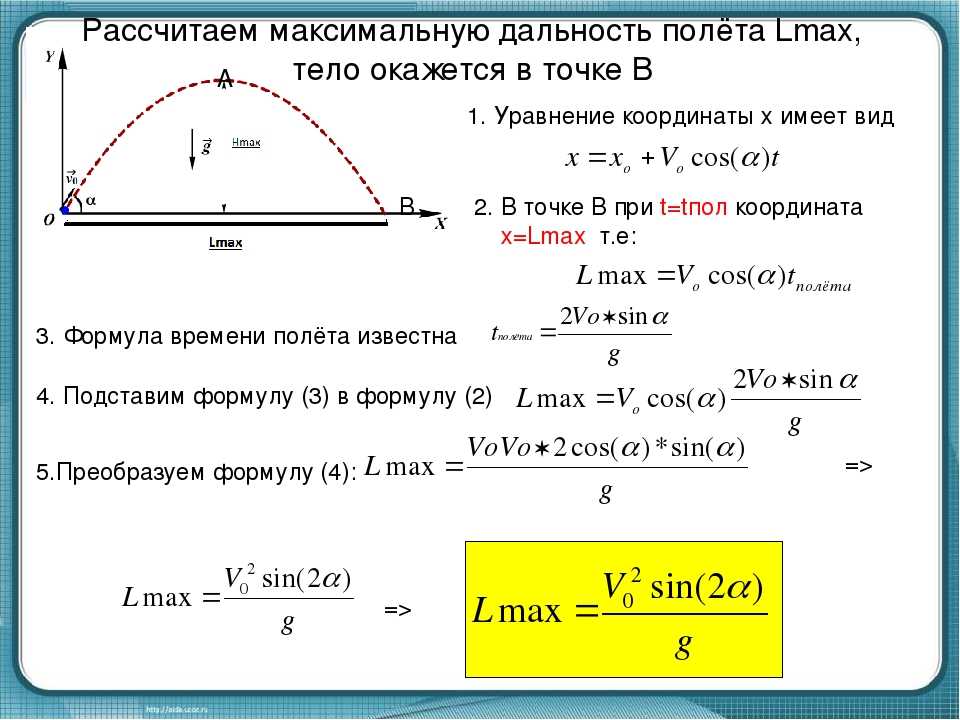
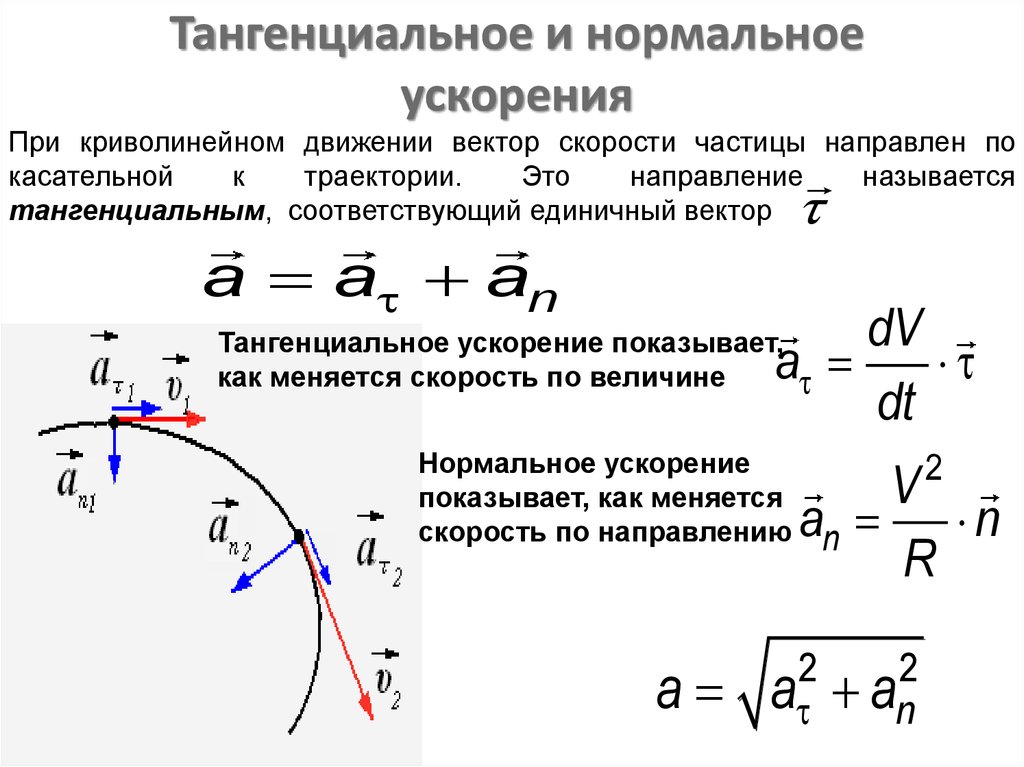
Калькуляторы Механика Калькулятор остановочного пути автомобиля Калькулятор определяет остановочный путь автомобиля с момента обнаружения водителем опасности до момента полной остановки автомобиля, а также другие параметры, связанные с этим событием, в частности, время восприятия водителем сигнала о необходимости торможения, время реакции водителя, а также расстояние, которое прошел автомобиль во время этих событий. Калькулятор также определяет начальную скорость (скорость до начала торможения) по известной длине торможения (длины тормозного пути) с учетом дорожных условий. Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности. Пример 1: Рассчитать расстояние, необходимое для остановки автомобиля, движущегося со скоростью 90 км/ч по мокрой горизонтальной дороге с асфальтобетонным покрытием (коэффициент трения μ = 0,4) если время восприятия водителя 0,5 с и время реакции водителя 0,7 с. Пример 2: Рассчитать начальную скорость автомобиля, движущегося по дороге с мокрым асфальтобетонным покрытием (μ = 0.4), если длина тормозного пути равна 100 м. Автомобиль движется на спуске с уклоном 10%. Калькулятор остановочного пути Входные данные Начальная скорость v0м/скм/чфут/смиля/ч Время восприятия опасности водителем thp с Время реакции водителя thr с Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Тип привода тормозов —ПневматическийГидравлический или Время срабатывания тормозной системы tbrl с Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Угол крутизны уклона θ= ° Замедление a= м/с² Время торможения tbr= с Расстояние, которое проедет автомобиль во время восприятия водителем опасности Shp= м Расстояние, которое проедет автомобиль во время реакции водителя на опасность Shr= м Расстояние, которое проедет автомобиль за время задержки срабатывания тормоза Sbrl= м Тормозной путь Sbr= м Остановочный путь Sstop= м Критический угол наклона для заданного коэффициента трения θcrit= ° Критический уклон для заданного коэффициента трения σcrit= % Калькулятор определения скорости по тормозному пути Входные данные Длина тормозного следа Sbrметр (м)футярд Уклон σградус% Движение вверх Движение вниз Состояние дороги —Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальт или Коэффициент трения μ Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Скорость перед началом торможения v0  м/с   км/ч Определения и формулы Остановочный путь Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации Расстояние, которое пройдет автомобиль во время реакции водителя Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы Замедление Тормозной путь автомобиля Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона Вывод зависимости тормозного пути от скорости и трения с помощью энергетического метода Время торможения Движение вверх и вниз по уклону Уклон Критический угол Определения и формулы Остановочный путь Остановочный путь — это расстояние, которое проходит автомобиль с момента, когда водитель видит опасность, оценивает ее, принимает решение остановиться и нажимает на педаль тормоза и до момента полной остановки автомобиля. Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки. где shr — расстояние, которое проедет автомобиль во время восприятия и оценки водителем ситуации, shr — расстояние, которое проедет автомобиль во время во время реакции водителя на ситуацию, sbrl — расстояние, которое проедет автомобиль во время задержки срабатывания тормозов, и sbr — тормозной путь. Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации Расстояние человеческого восприятия ситуации — это расстояние, которое пройдет автомобиль в то время, пока водитель оценивает опасность и принимает решение уменьшить скорость и остановиться. Оно определяется по формуле где shp расстояние человеческого восприятия в метрах, v скорость автомобиля в км/ч, thp — время человеческого восприятия в секундах и 1000/3600 — коэффициент преобразования километров в час в метры в секунду (1 километр равен 1000 метров и 1 час равен 3600 секундам). Расстояние, которое пройдет автомобиль во время реакции водителя Расстояние реакции водителя — это расстояние, которое пройдет автомобиль пока водитель выполняет решение остановить автомобиль после оценки опасности и принятия решения об остановке. Оно определяется по формуле где shp — расстояние реакции водителя с метрах, v — скорость автомобиля в км/ч и thr — время реакции водителя в секундах. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, зависит от типа тормозной системы, установленной на автомобиле. Почти на всех легковых автомобилях и малотоннажных грузовых автомобилях используются гидравлическая тормозная система. На большинстве большегрузных автомобилей используются тормоза с пневматическим приводом. Задержка срабатывания пневматических тормозов приблизительно равна 0,4 с, а гидравлических (жидкость несжимаема!) 0,1–0,2 с. Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический. Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, определяется по формуле где sbrl — расстояние в метрах, которое пройдет автомобиль во время срабатывания тормозной системы, v — скорость движения автомобиля в км/ч, tbrl — время срабатывания тормозной системы в секундах. Замедление Для упрощения расчетов предположим, что автомобиль движется с постоянным ускорением или замедлением, которое определяется по известной из курса элементарной физики формуле равноускоренного или равнозамедленного движения где a — ускорение, v — начальная скорость, v0 — конечная скорость и t — время. Тормозной путь автомобиля Тормозной путь автомобиля — это расстояние, которое проходит автомобиль с момента полного нажатия на педаль тормоза до момента полной остановки. Это расстояние зависит от скорости автомобиля перед началом торможения и от коэффициента трения между шинами и дорожным покрытием. В этом калькуляторе мы не учитываем другие факторы, влияющие на тормозной путь, например, сопротивление качению шин или лобовое сопротивление воздуха В результатах исследования1, в котором коэффициент трения определялся путем измерения замедления, определено, что антиблокировочная тормозная система (АБС) влияла на коэффициент трения таким образом: он увеличивается с увеличением скорости при использовании АБС и уменьшается, если АБС не используется. В этом исследовании также подтверждается, что на коэффициент трения между шинами и дорожным покрытием влияет температура и интенсивность дождя. Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона Коэффициент трения определяется как отношения силы трения к силе нормального давления, прижимающей тело к опоре: или где Ffr — сила трения, μ коэффициент трения и Fnorm — сила реакции опоры. Действующая на тело нормальная сила реакции опоры определяется как составляющая силы реакции, перпендикулярная к поверхности опоры тела. В простейшем случае, когда тело находится на плоской горизонтальной поверхности, нормальная сила равна весу этого тела: где m — масса тела и g — ускорение свободного падения. Эта формула выведена из второго закона Ньютона: В более сложном случае, если тело расположено на наклонной плоскости, нормальная сила рассчитывается как где θ — угол наклона между плоскостью поверхности и горизонтальной плоскостью. В этом случае нормальная сила меньше веса тела. Случай наклонной поверхности мы рассмотрим чуть позже. В случае же горизонтальной поверхности, если коэффициент трения между телом и поверхностью равен μ, то сила трения равна В соответствии со вторым законом Ньютона, эта сила трения, приложенная к движущемуся телу (автомобилю) приводит к возникновению пропорционального ей замедления: или Теперь, в соответствии с уравнением ускоренного (замедленного) движения имеем Из курса элементарной физики известно, что при равнозамедленном движении с постоянным замедлением, если конечная скорость равна нулю, то тормозной путь определяется уравнением Это уравнение можно переписать в более удобной форме с использованием преобразования скорости в км/час в м/с: Подставляя в это уравнение a = μg, получаем формулу тормозного пути: где скорость v задается в км/час, а ускорение силы тяжести g в м/с². Решая это уравнение относительно v, получаем: Аналогичную формулу для определения тормозного пути можно получить с помощью энергетического метода. Вывод зависимости тормозного пути от скорости и трения с помощью энергетического метода Теоретическое значение тормозного пути можно найти, если определить работу по рассеиванию кинетической энергии автомобиля. Если автомобиль, движущийся со скоростью v, замедляет движение до полной остановки, работа тормозной системы Wb, требуемая для полного рассеяния кинетической энергии автомобиля Ek, равна этой энергии: Кинетическая энергия движущегося автомобиля Ek определяется формулой где m — масса автомобиля и v — скорость движения автомобиля перед началом торможения. Работа Wb, выполненная тормозной системой, определяется как где m — масса автомобиля, μ — коэффициент трения между шинами и дорожным покрытием, g — ускорение силы тяжести и sbr — тормозной путь, то есть расстояние, которое прошел автомобиль от начала торможения до полной остановки. Теперь, с учетом того, что Ek = Wb, имеем: или Скорость автомобиля до начала торможения является наиболее важным фактором, влияющим на величину остановочного пути. Другими, менее важными, факторами, влияющими на остановочный путь, являются время оценки водителем ситуации, время реакции водителя, скорость работы тормозной системы автомобиля и состояние дороги. Время торможения Из курса элементарной физики известно, что средняя скорость при равноускоренном движении равна полусумме начальной и конечной скорости: С учетом, что конечная скорость равна нулю, время торможения определяется в калькуляторе как Движение вверх и вниз по уклону Силы, действующие на автомобиль на уклоне: Fg — сила тяжести (вес автомобиля), Fgd — скатывающая вниз составляющая веса автомобиля, Ffr — сила трения, действующая параллельно поверхности дорожного полотна с уклоном, Fgn — нормальная составляющая веса автомобиля, направленная перпендикулярно поверхности дороги, и Fnr — сила реакции опоры, равная нормальной составляющей веса автомобиля. Когда водитель нажимает на педаль тормоза, замедляющий движение автомобиль может быть представлен в виде тела на поверхности с углом наклона θ (см. рисунок выше). Для простоты мы будем рассматривать только две силы, действующие на автомобиль, находящийся на уклоне. Это вес автомобиля и сила трения. Автомобиль, движущийся с начальной скоростью, замедляет движение, если сила трения, действующая параллельно дорожному полотну, больше, чем скатывающая сила, являющаяся составляющей силы тяжести, которая также параллельна дорожному полотну. Если начальная скорость автомобиля равна нулю, он в этой ситуации остается на месте при условии, что угол уклона меньше критического (об этом — ниже). В то время, как сила тяжести Fg стремится скатывать автомобиль вниз, сила трения Ffr сопротивляется этому движению. Чтобы автомобиль мог в этой ситуации остановиться, сила трения должна превышать скатывающую составляющую силы тяжести Fgd. В то же время, если сила трения превышает скатывающую составляющую силы тяжести, автомобиль будет двигаться вниз с постоянным ускорением и его тормозная система будет неспособна его остановить. Это может произойти, если угол наклона (уклон) дорожного полотна слишком велик или коэффициент трения слишком мал (вспомним как ведет себя автомобиль с обычными шинами на уклоне, если он покрыт коркой льда!). По определению коэффициента трения, можно записать уравнение для силы трения: или Скатывающая составляющая силы тяжести: Результирующая сила Ftotal, действующая на автомобиль на уклоне: или Как мы уже отмечали, сила Ftotal должна быть направлена вверх, иначе автомобиль при движении вниз остановить невозможно. В соответствии со вторым законом Ньютона, ускорение (точнее, замедление) автомобиля, движущегося под действием силы Ftotal, определяется как Подставляя ускорение в выведенную выше формулу тормозного пути, получаем: Решая это уравнение для vpre-braking, получим: Отметим еще раз, что в этих формулах g задается в м/с, v в км/ч и s в метрах. В нашем калькуляторе используются две последние формулы. Припаркованные и движущиеся по ул. Дивисадеро в Сан-Франциско (Калифорния) автомобили. Уклон дорожного полотна в этом месте равен 31% или 17°. Уклон Величина уклона дороги (показателя крутизны склона) равна тангенсу угла плоскости дорожного покрытия к горизонтали. Он рассчитывается как отношение перпендикуляра, опущенного из точки на поверхность (превышения местности) к длине горизонтальной поверхности от начала склона до перпендикуляра (горизонтальному расстоянию). По определению уклона считается, что при движении вверх уклон является положительным, а при движении вниз уклон является отрицательным, когда превышение в действительности является понижением дороги. Уклон дороги σ выражают как угол наклона к горизонтали в градусах или как отношение в процентах. Например, подъёму 15 метров на 100 метров перемещения по горизонтали соответствует уклон, равный 0,15 или 15%. В этом калькуляторе мы используем уклон в процентах, определяемый по формуле где Δh — превышение местности и d — проекция уклона на горизонталь (см. рисунок выше). Если известен уклон, то угол наклона можно определить по формуле Критический угол При увеличении угла наклона дорожного полотна выше определенного значения, называемого критическим углом, движущийся вниз автомобиль затормозить невозможно, так как действующая на него сила трения становится меньше скатывающей силы. Этот критический угол находится из условия или или Из этой формулы можно найти критический угол для данного коэффициента трения, при котором автомобиль не сможет затормозить: Уклон, выраженный в процентах, определяется по известному углу наклона таким образом: Пример В этом примере мы покажем, как использовать формулу для определения тормозного пути. Пусть автомобиль движется с начальной скоростью vpre-braking = 90 км/ч вниз по уклону σ = 5% по мокрому асфальту (коэффициент трения μ = 0,4). Нужно определить тормозной путь. Для расчетов используем выведенные выше формулы. Особые случаи Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах: Критический угол. Действующая на автомобиль скатывающая сила равна силе трения. В этой ситуации удерживать автомобиль тормозом практически невозможно. Движущийся вверх автомобиль остановится и может самопроизвольно начать движение вниз. Уклон больше критического. Скатывающая сила больше, чем сила трения. Тормозная система не способна удерживать автомобиль. Движущийся вверх автомобиль остановится и начнет движение вниз с постоянным ускорением. Критический угол. Действующая на автомобиль скатывающая сила равна силе трения. В этой ситуации удерживать автомобиль тормозом практически невозможно. Движущийся вниз автомобиль остановится после очень большого тормозного пути и может самопроизвольно начать движение вниз. Уклон больше критического. Скатывающая сила больше, чем сила трения. Тормозная система не способна удерживать автомобиль. Движущийся вниз автомобиль не может быть остановлен и будет двигаться вниз с постоянным ускорением. Литература Hartman, J 2014, Effects of velocity, temperature And rainfall on the friction coefficient of pneumatic tyres And bitumen roads, Doctor of Philosophy (PhD), Aerospace, Mechanical And Manufacturing Engineering, RMIT University PDF 48 MB Wikibooks. Fundamentals of Transportation Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Механика»: Калькулятор скорости, времени и расстояния при свободном падении Калькулятор выигрыша в силе Калькуляторы рычага Калькулятор выигрыша в силе, даваемого воротом Калькулятор выигрыша в силе, даваемого полиспастом Калькулятор выигрыша в силе наклонной плоскости Калькулятор выигрыша в силе винта Калькулятор выигрыша в силе, даваемого клином Калькулятор давления Калькулятор импульса (количества движения) и импульса силы Калькулятор закона сохранения импульса: столкновения и взрывы при условии, что два тела находятся на прямой линии Калькуляторы Механика

За время 4 с тело прошло 40 м.

Какой путь пройдет тело за 8 с от начала отсчета времени, если начальная скорость равна 5 м/с? Движение равноускоренное. (120 м)

1. Скорость автомобиля за 20 с уменьшилась с 20 м/с до 10 м/с. С каким ускорением двигался автомобиль? (0,5 м/с²)

2. Участок пути длиной 1 км мотоциклист, двигаясь из состояния покоя, проходит с постоянным ускорением 0,2 м/с². За какое время пройден этот путь? (100 с)

3. Двигаясь в одном направлении с ускорением 2 м/с², тело на пути 50 м увеличило свою скорость в 3 раза. Найти начальную скорость. (5 м/с)

4. За время 4 с тело прошло 40 м. Какой путь пройдет тело за 8 с от начала отсчета времени, если начальная скорость равна 5 м/с? Движение равноускоренное. (120 м)

5. Тело начинает двигаться вдоль прямой с постоянным ускорением. Спустя 4 с ускорение тела, оставаясь таким же по величине, меняет направление на противоположное. Через какое время после начала движения тело остановится? (8 с)

6. Пуля, летящая со скоростью 200 м/с, ударяет в земляной вал и проникает в него на глубину 36 см. Сколько времени она двигалась внутри вала, если движение пули считать равнопеременным. (0,0036 с)

7. Тормозной путь автомобиля, двигавшегося со скоростью 40 км/ч, равен 8 м. Чему будет равен тормозной путь, если скорость автомобиля увеличится до 80 км/ч? (32 м)

8. Тело, свободно падающее из состояния покоя, в конце первой половины пути достигло скорости 20 м/с. С какой высоты оно упало? (40 м)

9. Тело падает вертикально с высоты 125 м без начальной скорости. За какое время тело проходит последние 45 м пути? (1 с)

10. Тело падало с некоторой высоты и последние 200 м пролетело за 4 с. Сколько времени падало тело? (7 с)

11. С вертолета сбросили без начальной скорости два груза, причем второй на 1 с позже первого.

    Определить расстояние между грузами через 2 с после начала движения первого груза. (15 м)

12. Движение точки задано уравнением S = 12 + 2t². Определить среднюю скорость движения точки в интервале от 2 с до 4 с. (12 м/с)

13. Небольшая монетка после толчка начала скользить вверх по наклонной плоскости с начальной скоростью 5 м/с. Через какое время она вернется в исходную точку, если ускорение монетки остается постоянным и равным по величине 2 м/с²? (5 с)

14. Мяч, брошенный вертикально вверх, упал на землю через 3 с. С какой скоростью был брошен мяч и на какую высоту он поднялся? (15 мс; 11,25 м)

15. Тело бросили вертикально вверх со скоростью 8 м/с. Одновременно с предельной высоты, которой оно может достичь, бросают вертикально вниз другое тело с той же начальной скоростью. Определить время, по истечении которого тела встретятся. (0,2 с)

16. Струя воды вытекает из садового шланга вертикально вверх с высоты 0,8 м. Затем садовод отклоняет шланг в сторону, чтобы полить далекий куст, но в течение времени 1,6 с слышит шум падающей воды рядом с собой. С какой скоростью вода вытекает из шланга? (7,5 м/с)

17. Какова начальная скорость пули при вертикальном выстреле, если звук выстрела и пуля одновременно достигли высоты 680 м? Скорость звука 340 м/с. (350 м/с)

18. С крыши падают одна за другой две капли. Через 2 с после начала падения второй капли расстояние между каплями стало равно 25 м. На сколько раньше второй начала падать первая капля? (1 с)

19. Велосипедист, двигаясь равноускоренно, увеличил свою скорость за 4 с от нуля до 8 м/с, а затем за следующие 8 с, двигаясь равнозамедленно, уменьшил свою скорость до нуля. Определит путь, пройденный за все время движения. (48 м)

20. Тело брошено вертикально вверх с высоты 3,75 м с начальной скоростью 5 м/с. За какое время оно пройдет последние 0,95 м перед падением на землю? (0,1 с)

21. С некоторой высоты сбросили без начальной скорости тело. Спустя 1 с было сброшено второе тело. Определить расстояние между телами через 2 с от начала падения первого тела. (15 м)

22. Тело падает с высоты 5 м без начальной скорости. Определить среднюю скорость падения. (5 м/с)

23. Водитель автомобиля, движущегося со скоростью 54 км/ч, замечает красный сигнал светофора. Вычислить расстояние, пройденное автомобилем с этого момента до остановки, если водитель нажал на тормоз через 0,7 с, после чего автомобиль движется равнозамедленно с ускорением 6 м/с

    2. (29,25 м)

24. Мотоциклист, трогаясь с места с постоянным ускорением, достигает скорости 30 км/ч за 6 с. Какое расстояние от начала движения пройдет мотоциклист к тому моменту, когда его скорость станет равна 60 км/ч? (100 м)

25. С крыши здания счищают лед.

    Человек, стоящий на крыше, слышит удар куска льда о мостовую через 3 с. Скорость звука 330 м/с. Определить высоту здания. (41,3 м)

26. Зная уравнение движения тела , найти скорость тела в момент времени 6 с. Все величины в уравнении движения выражены в системе СИ. (3,4 м/с)

27. Точка совершает движение в плоскости x,y. Закон изменения ее координат от времени задан уравнениями: . Определить начальные координаты, начальную скорость, ускорение. Вывести уравнение траектории. (0, 4, 0,5, 2, )

28. На рис. 2.1 дан график зависимости координаты от времени. Отрезки кривых являются параболами. Постройте соответствующие графики зависимости пути, скорости и ускорения от времени.

29. На рис. 2.2 дан график изменения скорости движения некоторого тела от времени. Постройте соответствующие графики перемещения, пути и ускорения от времени. Определите перемещение, путь и среднюю скорость за 4 с движения. (0, 10 м, 2,5 м/с)

30. По данному графику зависимости ускорения автомобиля от времени (рис. 2.3) определить путь, пройденный за 3 с после начала движения. Начальная скорость равна нулю. (10,5 м)

31. Найти среднюю скорость автомобиля за 8 с движения по графику зависимости скорости от времени (рис 2.4). (7,5 м/с)

32. З ависимость пути, пройденного телом от времени дается параболой, изображенной на рис. 2.5. Какова средняя скорость тела за первые 2,25 секунды движения? Начальная скорость равна нулю. (1,8 м/с)

33. По графику зависимости скорости тела от времени (рис. 2.6) определить среднюю скорость за 4 с движения. (4,5 м/с)

34. Тело движется из состояния покоя с ускорением 3 м/с² в течение 4 с. Какую скорость приобрело тело за это время? (12 м/с)

35. Точка начинает двигаться равноускоренно и первый метр пути проходит за 2 с. За какое время точка пройдет 64 м? (16 с)

36. Велосипедист, движущийся со скоростью 2 м/с, начинает спускаться с горы с ускорением 0,4 м/с². Определить среднюю скорость велосипедиста за 8 с после начала спуска. (3,6 м/с)

38. Тело, двигаясь равноускоренно с некоторой начальной скоростью, проходит последовательно два одинаковых отрезка по 16 м каждый. Найти начальную скорость и ускорение, если первый отрезок пройден за 8 с, а второй – за 2 с. (2,8 м/с, 1,2 м/с

    2)

39. Тело движется равноускоренно. За первые 2 с оно проходит 12 м, а за следующие 2 с – 24 м. Определить начальную скорость и ускорение тела. (3 м/с, 3 м/с²)

40. Скорость тела на пути 106,25 м увеличилась на 5 м/с. Определить ускорение тела, если начальная скорость равна 6 м/с. (0,4 м/с²)

41. Начальная скорость поезда 7 м/с. На пути 245 м скорость равномерно увеличилась в 3 раза. С каким ускорением двигался поезд? (0,8 м/с

    2)

42. Начальная скорость самолета при посадке равна 60 м/с, а длина пробега самолета до остановки равна 720 м. Определить величину среднего ускорения самолета при посадке. (2,5 м/с²)

43. Начальная скорость самолета при посадке равна 100 м/с, а длина пробега до остановки равна 1000 м. Определить время пробега при посадке. (20 с)

44. На пути 60 м скорость поезда уменьшилась в 3 раза за время 20 с. Определить скорость поезда в конце этого участка. (1,5 м/с)

45. Мальчик, двигаясь равноускоренно из состояния покоя, съехал на санках с горы длиной 50 м за 10 с, а затем проехал по горизонтальному участку еще 25 м до остановки. Найти ускорение мальчика на втором участке движения. (-2 мс²)

46. Тело двигалось в течение времени 20 с равномерно, затем такой же промежуток времени равноускоренно. Определить скорость равномерного движения, если путь за все время движения составил 275 м, а скорость на втором участке увеличилась в 2 раза. (5,5 м/с)

47. Поезд в течение 10 с равномерно увеличил свою скорость с 7 м/с до 13 м/с, а следующие 5 с двигался равномерно. Определить пройденное расстояние и среднюю скорость за это время. (165 м, 11 м/с)

48. По одному направлению из одной точки одновременно начали движение два тела. Одно движется равномерно со скоростью 40 м/с, а второе равноускоренно без начальной скорости и с ускорением 5 м/с². Через какое время второе тело догонит первое? (16 с)

49. Найти конечную скорость материальной точки при свободном падении с высоты 45 м. (30 м/с)

50. Тело свободно падало без начальной скорости в течение времени 5 с. Определить путь, пройденный телом за последнюю секунду движения. (45 м)

51. Тело свободно падает без начальной скорости с высоты 1210 м. Найти среднюю скорость тела на нижней половине пути. (132,8 м/с)

52. Определить начальную скорость тела, которое было брошено вертикально вниз с высоты 135 м и достигло земли через 5 с. (2 м/с)

53. Определить начальную скорость тела, которое брошено с высоты 129,6 м вертикально вверх и достигло земли через 8 с. (23 м/с)

54. Шарик брошен вертикально вверх из точки, находящейся над землей на высоте h = 125 м. Определить начальную скорость шарика, если за время движения до падения на землю он пролетел путь 3h. (50 м/с)

55. На какой высоте скорость тела уменьшится в 8 раз, если оно брошено вертикально вверх со скоростью 40 м/с. (78,75 м)

56. Тело брошено вертикально вверх с поверхности земли и через 12 с упало обратно на землю. Определить наибольшую высоту подъема тела. (180 м)

57. Пуля, летящая со скоростью 300 м/с, попадает в препятствие и останавливается в нем на глубине 0,9 м. Какую скорость будет иметь пуля на глубине 0,5 м, считая ускорение постоянным? (200 м/с)

58. Пуля, летящая со скоростью 400 м/с, попадает в земляной вал и проникает в него на глубину 36 см. На какой глубине скорость пули уменьшилась в три раза? На какую глубину углубится пуля, летящая со скоростью 200 м/с? (32 см; 9 см)

59. Д ва велосипедиста проехали одинаковый путь за одно и то же время. Один велосипедист проехал весь путь равноускоренно с ускорением 0,03 м/с², а другой первую половину пути двигался со скоростью 3 м/с, а вторую половину пути – со скоростью 7 м/с. Чему равен путь, пройденный велосипедистами, если начальная скорость первого равнялась нулю? (1176 м)

60. По графику зависимости скорости от времени определить тормозной путь автомобиля. (112,5 м)

61. Два тела свободно падают с разных высот и достигают земли одновременно. Первое тело падало 5 с, второе 3 с. На какой высоте находилось первое тело, когда второе начало падать? g = 9,8 м/с². (102,9)

62. Тело бросили вертикально вверх. За вторую секунду оно поднялось на 10,3 м. С какой начальной скоростью бросили тело? (25 м/с)

63. Тело свободно падает с высоты 313,6 м. Какой путь оно пройдет за последнюю секунду движения? (73,5 м)

64. Неподвижное тело начало двигаться равноускоренно с ускорением 2 м/с² и достигло скорости 10 м/с. Затем, двигаясь еще 10 с равнозамедленно, остановилось. Определить путь, пройденный телом. (75 м)

65. Определить высоту, с которой свободно падало тела, если его средняя скорость равна 19,6 м/с. (78,4 м)

66. Начальная скорость автомобиля 4 м/с. На пути 400 м она возросла в 4 раза. С каким ускорением двигался автомобиль на этом участке? (0,3 м/с²)

67. Свободно падающее тело за последнюю секунду прошло путь 24,5 м. 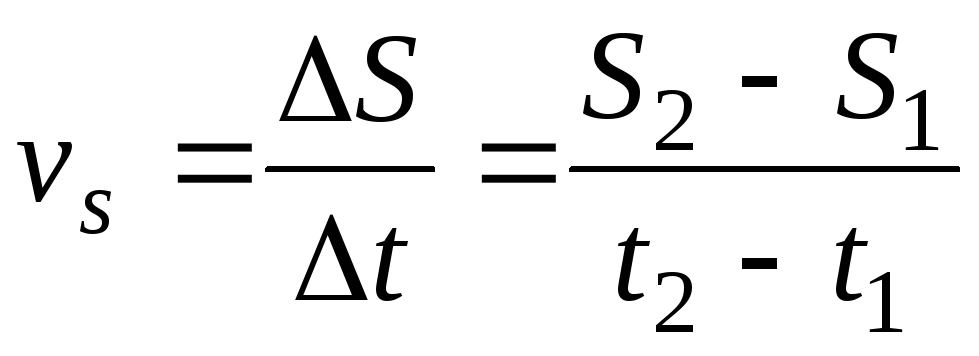С какой высоты оно падало? (44,1 м)

68. Два тела брошены вертикально вверх из одной точки, одно вслед за другим с интервалом 2 с, с одинаковыми начальными скоростями 50 м/с. Через сколько времени и на какой высоте они встретятся? (6 с; 120 м)

69. Автомобиль на участке длиной 25 м равноускоренно увеличил свою скорость с 10 м/с до 20 м/с. Следующие 55 м он двигался равномерно. Определить среднюю скорость. (18,1 м/с)

70. Автомобиль первую половину расстояния проехал с постоянной скоростью 60 км/ч, а вторую половину расстояния – равноускоренно и увеличил свою скорость вдвое. Найти среднюю скорость на всем пути. (72 км/ч)

71. Автомобиль движется равноускоренно с некоторой начальной скоростью и проходит за первые 4 с путь 80 м, а за первые 8 с – 150 м. Какая будет скорость автомобиля через 12 с от начала отсчета времени? (13,75 м/с)

72. Автомобиль начинает движение из состояния покоя и проходит путь 120 м. Первые 80 м он движется равноускоренно, а оставшиеся 40 м – равномерно и проходит их за 2 с. Какова средняя скорость автомобиля на всем пути? (12 м/с)

73. Автомобиль, двигаясь из состояния покоя, за 6 с проехал путь 180 м. Причем первую половину времени он двигался равноускоренно, а затем равномерно. Какой путь проехал автомобиль за вторую секунду движения? (20 м)

74. С крыши здания высотой 16 м через одинаковые промежутки времени падают капли. Причем первая ударяется о землю в момент, когда пятая отрывается от крыши. Определить расстояние между третьей и четвертой каплями в момент падения первой. (3 м)

75. Тело без начальной скорости падает с высоты 540 м. Разделите эту высоту на три части, на прохождение которых тело затрачивает одинаковое время. (60 м; 180 м; 300 м)

76. Тело падало с некоторой высоты без начальной скорости и последние 196 м прошло за 4 с. Сколько времени и с какой высоты падало тело? (7 с; 240 м)

77. Тело, движущееся равнозамедленно, проходит за 8 с расстояние 180 м и после этого имеет скорость 5 м/с. Определить начальную скорость и ускорение тела. (40 м/с;  4,37 м/с²)

79. Тело свободно падало (v₀ = 0) с некоторой высоты в течение 2 с. С какой скоростью его надо подбросить вверх, чтобы оно поднялось на высоту вдвое большую? ( 28,2 м/с)

80. В последнюю секунду свободного падения тело прошло четвертую часть пути. Сколько времени оно падало? (7,46 с)

81. Из точки А выезжает первое тело с начальной скоростью 3 м/с и ускорением 2 м/с². Спустя секунду из точки В ему навстречу с постоянной скоростью 5 м/с выезжает второе тело. Сколько времени первое тело будет двигаться до встречи со вторым, если АВ = 100 м? (7 с)

82. Сколько времени падало тело, если за последние 2 с падения оно пролетело 60 м? Начальная скорость равна нулю. (4 с)

83. Одно тело свободно падает с высоты 10 м. Одновременно второе тело брошено вниз с высоты 20 м. Оба тела упали на землю одновременно. С какой скоростью бросили второе тело? (7 м/с)

84. Два шарика брошены из одной точки с одинаковыми начальными скоростями 5 м/с вертикально вверх с интервалом 0,5 с один после другого. Через какое время после вылета первого шарика они встретятся в полете? (0,75 с)

85. Из одной точки, находящейся на высоте 3 м, одновременно брошены с одинаковыми скоростями два шарика: один вертикально вверх, второй вниз. Первый шарик достиг высшей точки своей траектории в момент падения второго шарика на землю. На какую максимальную высоту поднялся первый шарик? (4 м)

86. Шарик бросили с высоты 25 м вертикально вниз с начальной скоростью 5 м/с. Одновременно с высоты 10 м вертикально вверх бросили второй шарик. С какой скоростью его бросили, если шарики встретились на высоте 15 м? (10 м/с)

87. С высоты 3,2 м от поверхности земли начинает падать без начальной скорости маленький шарик. Одновременно другой шарик брошен вертикально вверх с поверхности земли с начальной скоростью в 1,5 раза меньше, чем имел бы первый шарик при падении на землю. На какой высоте шарики встретятся? (1,4 м)

88. Шарик брошен вертикально вверх с начальной скоростью 4 м/с. Когда он достиг верхней точки траектории из той же точки, из которой он был брошен, с той же начальной скоростью вертикально вверх был брошен второй шарик. На каком расстоянии от точки бросания шарики встретились? (0,6 м)

89. Из одной точки, находящейся на высоте 3 м, одновременно брошены с одинаковыми скоростями два шарика: один вертикально вверх, второй вниз. Первый шарик достиг высшей точки своей траектории в момент падения второго шарика на землю. На какую максимальную высоту поднялся первый шарик? (4 м)

90. С аэростата, спускающегося с постоянной скоростью 3,2 м/с, бросают вверх тело со скоростью 6,6 м/с относительно земли. Через какое время тело вернется обратно? (2 с)

91. Тело, движущееся равнозамедленно, проходит за 8 с расстояние 180 м и после этого имеет скорость 5 м/с. Определить начальную скорость и ускорение тела. (40 м/с;  4,37 м/с²)

92. Два тела начали свободно падать с одной и той же высоты, одно вслед за другим через 5 с. Определить время, считая от начала движения первого тела, через которое расстояние между телами будет равно 200 м. (6,5 с)

93. Двигаясь от стоянки равноускоренно и прямолинейно, автомобиль за 10 с достигает скорости 20 м/с. Следующие 5 с он движется равномерно, а затем равнозамедленно останавливается в течение 5 с. Какое расстояние проехал автомобиль? (250 м)

94. Поезд въезжает на участок пути длиной 0,5 км с начальной скоростью 15 м/с и проходит его за 25 с, двигаясь равноускоренно. Какова скорость локомотива в конце этого участка? (25 м/с)

95. Одно тело свободно падает с высоты 10 м. Одновременно второе тело брошено вниз с высоты 20 м. Оба тела упали на землю одновременно. С какой скоростью бросили второе тело? ( 7 м/с)

96. Спортсмен пробежал расстояние 100 м за 10 c, из которых он 2 c потратил на разгон, а остальное время двигался равномерно. Чему равна скорость равномерного движения? (≈ 11,1 м/с)

97. Камень брошен с высоты 10 м вертикально вверх со скоростью 10 м/с и падает на землю. Определить среднюю скорость движения камня. ( 7,33 м/с)

Как рассчитать ускорение — советы по линейному движению

15 июня 2017 г. By Danielle Collins Оставить комментарий

Как только вы узнаете, какой профиль движения используется, вам нужно знать, как рассчитать ускорение на основе общего расстояния перемещения и общего времени перемещения. При определении размера линейной системы большое внимание уделяется скорости, но влияние ускорения на систему и ее компоненты часто бывает более значительным, чем влияние скорости.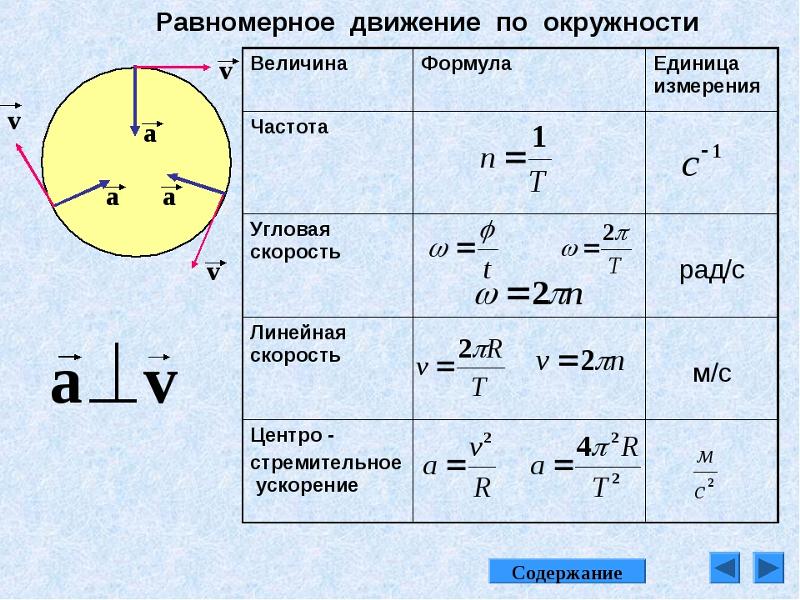

Ускорение больше всего связано с профилем движения и с тем, как наилучшим образом достичь требуемого перемещения за указанное время, но оно также вызывает дополнительные силы на систему и компоненты (вспомним второй закон Ньютона, F=ma), которые необходимо учитывать в размерах и выборе. Он также играет важную роль в определении того, какой крутящий момент требуется от двигателя для привода нагрузки.

---

Ускорение — это скорость изменения скорости: изменение скорости, деленное на изменение во времени. С точки зрения вычислений ускорение является производной скорости (dv/dt) и может быть определено путем вычисления наклона кривой профиля движения (скорости в зависимости от времени).

---

Первым шагом в расчете необходимого ускорения для перемещения является определение того, какой тип профиля движения будет использовать приложение — треугольный или трапециевидный.

Треугольный профиль движения имеет фазы ускорения и фазы замедления, которые обычно равны. Трапециевидный профиль движения имеет фазы ускорения, постоянной скорости и замедления. Время для каждой из трех фаз может быть одинаковым, но фаза постоянной скорости часто короче или длиннее, чем фазы ускорения и замедления.
Изображения предоставлены: Womack Machine Supply Co.

Как рассчитать ускорение для треугольного профиля перемещения

Для треугольного профиля перемещения ускорение достигается за половину общего времени перемещения и половину общего расстояния перемещения. (Точно так же торможение занимает оставшуюся половину времени движения и половину расстояния перемещения.) Таким образом, время ускорения (t _a ) равно 1/2 общего времени движения:

И расстояние ускорения (d _a ) составляет 1/2 от общего расстояния перемещения.

Напомним, что ускорение — это скорость изменения скорости или скорость, деленная на время. Чтобы определить ускорение, нужно знать максимальную скорость. Для простоты начнем с определения средней скорости.

Средняя скорость — это просто общее расстояние перемещения, деленное на общее время перемещения:

Для треугольного профиля движения максимальная скорость в 2 раза превышает среднюю скорость, что может быть выражено как:

Ускорение – это максимальная скорость, деленная на время разгона:

Подставляя вместо v _max и используя уравнение для t _a сверху:

Как рассчитать ускорение для трапецеидального профиля движения

Чисто трапециевидный профиль движения использует 1/3 общего времени движения для ускорения, 1/3 для постоянной скорости и 1/3 для замедления: 1/3 при постоянной скорости и 1/3 при замедлении:

Как и для треугольного профиля движения, средняя скорость для треугольного профиля движения представляет собой просто общее расстояние перемещения, деленное на общее время движения:

Но максимальная скорость для трапециевидного профиля движения немного ниже, чем будет для того же движения, выполненного с треугольным профилем движения. ta(u)du. $$ 92.$$ $\квадрат$

Напомним, что интеграл функции скорости дает чистых расстояний пройдено, то есть водоизмещение. Если вы хотите узнать всего пройденное расстояние, вы должны найти, где функция скорости пересекает ось $t$, интегрируем отдельно по интервалам времени, когда $v(t)$ положительна, а когда $v(t)$ отрицательна, складываем абсолютную значения различных интегралов. Например, если предмет брошен прямо вверх на 19{3/2} {1\over \pi}\left({1\over2}+\sin(\pi t)\right)\,dt\Bigr|\cr &={1\over \pi}\left( {7\over 12}+{1\over \pi}\cos(7\pi/6)+{1\over \пи}\справа)+ {1\более \pi}\Bigl|{3\более 4}-{7\более 12} +{1\over\pi}\cos(7\pi/6)\Bigr|\cr &={1\over \pi}\left( {7\over 12}+{1\over \pi}{\sqrt3\over2}+{1\over \пи}\справа)+ {1\более \pi}\Bigl|{3\более 4}-{7\более 12} +{1\over \pi}{\sqrt3\over2}.\Bigr| \приблизительно 0,409 \hbox{метров}\cr }$$ $\квадрат$

Для каждой функции скорости найти как чистое расстояние, так и полное расстояние, пройденное за указанный интервал времени (график $v(t)$ до определить, когда он положительный, а когда отрицательный):

Пример 8. 2.1 $v=\cos(\pi t)$, $0\le t\le 2.5$ (отвечать)

Пример 8.2.2 $v=-9.8t+49$, $0\le t\le 10$ (отвечать)

Пример 8.2.3 $v=3(t-3)(t-1)$, $0\le t\le 5$ (отвечать)

Пример 8.2.4 $v=\sin(\pi t/3)-t$, $0\le t\le 1$ (отвечать)

Пример 8.2.5 Объект выстреливается вверх с уровня земли с начальным скорость 2 метра в секунду; подчиняется только силе сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на что он падает на землю. (отвечать)

Пример 8.2.6 Объект выстреливается вверх с уровня земли с начальным скорость 3 метра в секунду; подчиняется только силе сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на что он падает на землю. (отвечать)

Пример 8.2.7 Объект выстреливается вверх с уровня земли с начальным скорость 100 метров в секунду; подчиняется только силе сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на что он падает на землю.