Задание 4 ЕГЭ по физике 2023: теория и практика
Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27 Задание 28 Задание 29 Задание 30
За это задание ты можешь получить 2 балла. 2}/{2}$.
2}/{2}$.
Ответ: 34
Показать решение
Бесплатный интенсив
Задача 2
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
- Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
- В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
- Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение
1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см.
Ответ: 35
Показать решение
Бесплатный интенсив
Задача 3
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.
- Период колебаний тела равен 1 с.
- Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
- Тело совершает колебания с периодом 0,1 с.
- Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
- Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).

Решение
1) Из графика видно, что период колебаний тела равен 1с.
4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см – амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.
Ответ: 14
Показать решение
Бесплатный интенсив
Задача 4
Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, м | 0 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 |
- Коэффициент упругости пружины равен 2,5 Н/м.
- При увеличении массы груза растяжение пружины уменьшается.
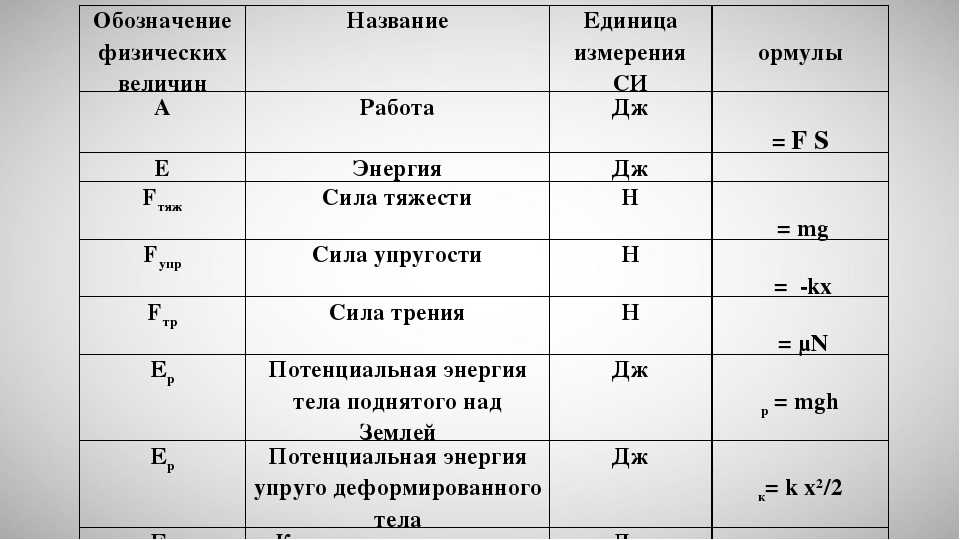
 2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.Ответ: 45
Показать решение
Бесплатный интенсив
Задача 5
Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
t, c 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 x, см 6 3 0 3 6 3 0 3 - Максимальная скорость грузика равна 0,15 м/с.
- Период колебаний шарика равен 0,4 с.
- В момент времени 0,1 с кинетическая энергия шарика максимальна.
- Полная механическая энергия шарика остаётся неизменной.
- Амплитуда колебаний шарика равна 6 мм.

Решение
Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 – верно).
Период колебании – время за которое происходит одно полное колебание – 0,4 с (2 – верно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 – верно)
Амплитуда колебания – это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 – неверно)Ответ: 234
Показать решение
Бесплатный интенсив
Задача 6
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта.
 2$, $F_p=ma_4=15·1.5=22.5H$
2$, $F_p=ma_4=15·1.5=22.5H$Ответ: 25
Показать решение
Бесплатный интенсив
Задача 7
На рисунке представлен график зависимости скорости V от времени t для тела, движущегося прямолинейно. Используя данные графика, выберите из приведённого ниже списка все верные утверждения и укажите их номера.
- Первые две секунды тело двигалось равноускоренно.
- Со 2-й по 6-ю секунду тело переместилось на 40 м.
- Со 2-й по 6-ю секунду тело переместилось на меньшее расстояние, чем за первые две секунды.
- Средняя скорость тела во время движения со 2-й по 10-ю секунду равна 12,5 м/с.
- С 6-й по 10-ю секунду тело двигалось равноускоренно.
Решение
1) Неверно, так как равноускоренному движению соответствует линейный график: $v(t)=v_0+at$.
2)Верно. Из данного рисунка видно, что с 2 по 6 сек, тело прошло 40 м (площадь под графиком)
3) Неверно.
 Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.
Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.4)Чтобы найти среднюю скорость, нужно разделить весь путь со 2-й по 10-ю секунду на всё соответствующее время, т.е. на 8 с. При этом путь определяем как площадь под графиком, так как у нас есть график в координатах v(t):
$S=S_1+S_2=8·10+{4·7,5}/2=110$ м.
Тогда $v_{ср}={110}/8=13,75$. Утверждение 4 – неверно.5) Верно. С 6 по 10 сек, тело двигалось равноускоренно, т.к. за равные промежутки времени скорость увеличивается на одну ту же величину (линейная зависимость v(t)).
Ответ: 25
Показать решение
Бесплатный интенсив
Задача 8
Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.

- За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
- При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
- В точке О кинетическая энергия маятника максимальна.
- Расстояние АБ соответствует амплитуде колебаний координаты.
- В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
- За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ – “туда и обратно”. 1 – неверно.
- При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 – неверно
- В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью – верно
- Амплитуда колебаний координаты – это половина расстояния АБ – отклонение от положения равновесия.

- В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 – верно.
В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.
Ответ: 35
Показать решение
Бесплатный интенсив
Задача 9
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Период колебаний тела равен 1 с.
- Амплитуда колебаний равна 8 см.
- Частота колебаний равна 1,25 Гц.
- Амплитуда колебаний равна 4 см.
- Период колебаний тела равен 0,4 с.
Решение
Из данного графика очевидно, что $A=4$см (2 – неверно, 4 – верно), период колебаний T=0.8 c (1, 5 – неверно), а частота $v={1}/{T}={1}/{0.

Ответ: 34
Показать решение
Бесплатный интенсив
Задача 10
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.
- Коэффициент упругости пружины примерно равен 20 Н/м.
- Коэффициент упругости пружины примерно равен 30 Н/м.
- Коэффициент упругости пружины примерно равен 50 Н/м.
- Коэффициент упругости пружины примерно равен 10 Н/м.
- Для данного эксперимента выполняется закон Гука.
Решение
$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/мОтвет: 15
Показать решение
Бесплатный интенсив
Задача 11
Бусинка скользит по неподвижной горизонтальной спице.
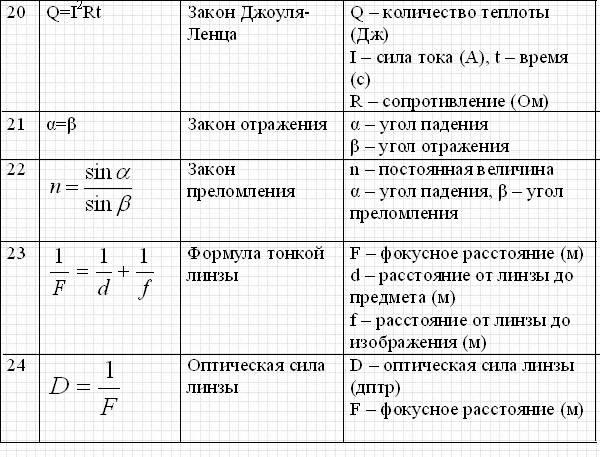
 На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.- На участке 1 проекция ускорения ax бусинки отрицательна.
- На участке 1 модуль скорости остаётся неизменным, а на участке 2 — уменьшается.
- На участке 1 модуль скорости увеличивается, а на участке 2 — уменьшается.
- На участке 1 модуль скорости уменьшается, а на участке 2 — остаётся неизменным.
- В процессе движения вектор скорости бусинки менял направление на противоположное.
Решение
Скорость – это производная координаты по времени. Графически это $tgα$ наклонной графика зависимости координаты от времени. Заметим, что координата все время растет, но на участке 1 – скорость уменьшается, следовательно, проекция ускорения отрицательна. На участке 2, скорость неизменна, а координата растет, тело не меняет направление движения.

Ответ: 14
Показать решение
Бесплатный интенсив
Задача 12
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.
- В конце наблюдения кинетическая энергия тела равна нулю.
- Кинетическая энергия тела в течение всего времени наблюдения увеличивается.
- Кинетическая энергия тела в начальный момент времени максимальна.
- Тело брошено вертикально вверх с балкона и упало на Землю.
- В конце наблюдения скорость тела не равна нулю.
Решение
1) В конце наблюдения $E_к=0$, неверно, т.к. при $t=t_к⇒E_к≠0$, если $E_к=0$, то график должен проходить через ось ординат.
2) $E_к$, в течении всего времени увеличивается, неверно, т.к. при $t={t_к}/{2}$ $E_к=min$, в середине пути кинетическая энергия минимальна.

3) Исходя из графика $E_к$ максимальная в момент (верно) $t=0$.
4) Неверно, т.к. график вертикально брошенного тела, выглядит иначе.
5) При $t_к=t; E_к≠0$ (верно), т.к. $υ≠0⇔E_к≠0$.
Ответ: 35
Показать решение
Бесплатный интенсив
Задача 13
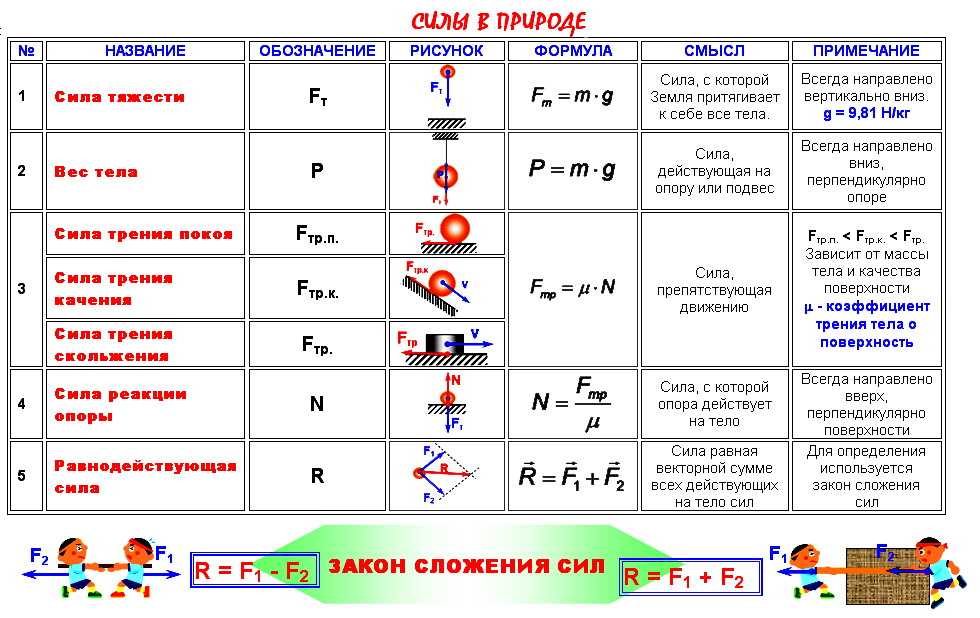
На рисунке приведены графики зависимости координаты от времени для двух тел A и B, движущихся по прямой, вдоль которой и направлена ось Ox. Из приведённого ниже списка выберите два верных утверждения о характере движения тел и укажите их номера.
- Тело A движется равномерно.
- Тело A движется с постоянным ускорением, равным 5 м/с2.
- Первый раз тела A и B встретились в момент времени, равный 3 с.
- Вторично тела A и B встретились в момент времени, равный 7 с.
- В момент времени t = 5 с тело B достигло максимальной скорости движения.
Решение
1) Тело А движется равномерно, т.
 к. равномерное движение – это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).
к. равномерное движение – это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).2) Ускорение тела А равно нулю, т.к. оно движется с постоянной скоростью $υ={20-10}/{7-3}=2.5м/с$ (не подходит).
3) Графики зависимости координаты от времени для двух тел А и В пересекаются в момент времени $t=3c$, значит, первый раз тела А и В встретились в момент времени, равный 3с (подходит).
Ответ: 13
Показать решение
Бесплатный интенсив
Задача 14
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.
- Длина пружины в недеформированном состоянии равна 6 см.

- Длина пружины в недеформированном состоянии равна 3 см.
- При действии силы 2 Н деформация пружины равна 2 см.
- При действии силы 4 Н деформация пружины равна 2 см.
- Коэффициент жёсткости пружины равен 50 Н/м.
Решение
1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).
2) Длина пружины в не деформированном состоянии равна 3 см (подходит).
3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).
4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).
Ответ: 24
Показать решение
Бесплатный интенсив
Задача 15
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения
- Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.

- Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
- Максимальная скорость движения на всём пути равна 2,4 м/с.
- За всё время движения тело прошло путь 120 м.
- За всё время движения тело прошло путь 240 м.
Решение
1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6м/с$. Знак “минус” говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2м/с$(подходит).
2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).
3) Максимальная скорость на всем пути равна 6м/с (не подходит).
4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).
5) За все время движения тело прошло путь 240м (подходит).
Ответ: 15
Показать решение
Бесплатный интенсив
Задача 16
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом.
 2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).Ответ: 24
Показать решение
Бесплатный интенсив
Задача 17
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.
- Шарик движется с переменным ускорением.
- Скорость шарика уменьшается.
- Шарик движется под действием постоянной силы.
- Если промежуток времени между двумя последовательными положениями шарика равен 2 с и он начинал движение из состояния покоя, то его скорость в точке с координатой 9 см равна 3 см/с.
- Импульс шарика в процессе движения уменьшается.
Решение
1) Шарик движется с постоянным ускорением (не подходит).
 2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).
2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).Ответ: 34
Показать решение
Бесплатный интенсив
Задача 18
На рисунке приведён график зависимости кинетической энергии тела от времени t. Выберите все верные утверждения на основании анализа представленного графика.
- Тело движется под действием постоянной силы.
- Потенциальная энергия тела в точке Б равна 1,5 Дж.
- Период колебаний тела равен 4 с.
- Максимальное значение потенциальной энергии равно значению потенциальной энергии в точке А.
- Полная механическая энергия тела равна 4 Дж.
Решение
1. Из графика видно, что время одного полного колебания равно 4с, т.к. в течение одного полного колебания тело проходит три максимальных значения (или три минимальных значения) кинетической энергии, т.
 е. период колебаний тела равен 4с (верно).
е. период колебаний тела равен 4с (верно).2. Поскольку полная механическая энергия тела равна: $E=E_{к,max}=E_{к,max}=E_к+Е_п$(1), а максимальная кинетическая энергия тела равна 4 Дж, то полная механическая энергия тела равна 4 Дж (верно).
Ответ: 35
Показать решение
Бесплатный интенсив
Задача 19
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.
- Тело совершает гармонические колебания.
- Потенциальная энергия тела в точке A равна 1 Дж.
- Период колебаний тела равен 2 с.
- Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
- Частота колебаний тела равна 4 Гц.
Решение
1. Тело совершает гармонические колебания, т.к. гармонические колебания – это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 – верно).

2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ – кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ – потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 – верно)
3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 – неверно)
4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 – неверно)
5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 – неверно)
Ответ: 12
Показать решение
Бесплатный интенсив
Задача 20
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленных графиков и укажите их номера.

- Наибольшей начальной скоростью обладало второе тело.
- Первое тело покоится.
- Наименьший путь за первые три секунды прошло второе тело.
- Третье тело движется равноускоренно.
- Пятое тело совершает равнопеременное движение.
Решение
Из графика видно, что в момент времени t=0с наибольшей начальной скоростью обладает тело 2.
Третье тело движется равноускоренно, т.к. график скорости напрвлен вверх.
Ответ: 14
Показать решение
Бесплатный интенсив
Показать еще
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Включить уведомления
Бесплатный интенсив по физике
3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 4 сентября. Бесплатный интенсивПочему в школе оказался в яме предмет “физика”, без которого не будет инженера
Свежий номер
РГ-Неделя
Родина
Тематические приложения
Союз
Свежий номер
Общество
13.02.2023 19:02
Поделиться
Мария Агранович
Впервые за последние несколько лет физика “сползла” на 4-е место по популярности среди предметов ЕГЭ по выбору, уступив свое место в тройке лидеров информатике. Вузы отмечают: снижается и средний балл ЕГЭ у абитуриентов.
Артем Барат: Когда в классе и физики, и лирики, приходится серьезно думать над подходами к каждой группе. / Александр Корольков/ РГ
Минобрнауки и минпросвещения решили: предмет нужно срочно вытягивать из “ямы” и даже создали для этого специальную рабочую группу.
Как спасать науку Эйнштейна и Бора? Зачем школьникам парадоксы? Можно ли на уроках физики выучить русский? Об этом мы беседуем с учителем физики московской “Цифровой школы”, призером конкурса “Учитель года России-2021” Артемом Баратом.

Артем Александрович, ваш предмет сдает позиции. Тревожно?
Артем Барат: Знаю, что, согласно статистике, любовь к физике – удел немногих. Чтобы это исправить, нужно интереснее преподавать, конечно. Возможно, меняя содержание. Дети должны узнавать о физике XXI века, а мы, педагоги, – повышать собственную квалификацию, следить за тем, что происходит в науке.
А еще нужно понимать, как потом об этом ребенка спрашивать, какие составлять вопросы, если, например, включать современные открытия в задания ЕГЭ.
Министр просвещения предложил дополнить урок физики и других естественно-научных предметов новыми разделами о современных открытиях. Чем бы с учениками поделились вы?
Артем Барат: Моя родная тема – квантовая физика, квантовые парадоксы. Или парадоксы специальной теории относительности. Честно говоря, обсуждение физических парадоксов на уроках полезно, даже если они берут начало не в XXI веке. Например, парадокс Ольберса, который начинается с банального вопроса: “Почему ночью темно, ведь вокруг столько звезд?”.
 Мы отвернулись от одной звезды, но почему другие нам не светят? Отталкиваясь от парадокса Ольберса, можно прийти к теории Большого взрыва и вообще к доказательству того, что Большой взрыв существовал. Замечательная тема. Я бы еще выделил квантовую теорию гравитации и гравитационные волны как одно из последних достижений науки. Оно уже в достаточной степени популяризировано, можно найти простые и понятные объяснения. Хотя, признаюсь, я против излишних упрощений. Так мы иногда выхолащиваем смысл.
Мы отвернулись от одной звезды, но почему другие нам не светят? Отталкиваясь от парадокса Ольберса, можно прийти к теории Большого взрыва и вообще к доказательству того, что Большой взрыв существовал. Замечательная тема. Я бы еще выделил квантовую теорию гравитации и гравитационные волны как одно из последних достижений науки. Оно уже в достаточной степени популяризировано, можно найти простые и понятные объяснения. Хотя, признаюсь, я против излишних упрощений. Так мы иногда выхолащиваем смысл.Физика – это факты, но не только. Какие опыты на уроках вы проводите?
Артем Барат: Моя любимая технология работы с физическим экспериментом была описана в старом журнале “Квант” в 1979 году. Тогда Е.Н. Юносов придумал “турнир юных физиков” – исследования, которые можно ввести в течение года, которые требуют и экспериментов, и уравнений, и совпадения разных результатов… Например, если посветить естественным светом на компакт-диск, можно наблюдать красивые дифракционные картины.
 Изучаем это явление. Есть еще задачка “рисовые гири” – про физику сыпучих материалов. Оказывается, если в емкость, плотно наполненную рисом, буквально “вбить” ложку, то потом за эту ложку можно поднять всю емкость с крупой. Дети очень эффективно учатся на подобных задачках и узнают гораздо больше.
Изучаем это явление. Есть еще задачка “рисовые гири” – про физику сыпучих материалов. Оказывается, если в емкость, плотно наполненную рисом, буквально “вбить” ложку, то потом за эту ложку можно поднять всю емкость с крупой. Дети очень эффективно учатся на подобных задачках и узнают гораздо больше.Вообще, эксперимент для современных детей необычайно важен. И ценность представляет не только натурный эксперимент, но и имитационное моделирование. Поэтому я рекомендую своим ученикам использовать виртуальные лаборатории МЭШ. Это интерактивные онлайн-симуляторы опытов и экспериментов. Они помогают воспроизвести опыт или исследования бесконечное число раз, изменяя условия и изучая, что при этом происходит. Например, недавно появилась лаборатория по физике “Архимед” для учеников 7 класса, которая позволяет наблюдать и изучать взаимодействия тел, давление жидкостей, плавание тел и воздухоплавание, механическую работу и энергию, и даже способы измерения различных величин: размеров, массы, силы, давления.

Современному человеку сложнее воображать, особенно что-то трёхмерное, потому что вокруг нас слишком много всего происходит “на плоскости”. А воображать и представлять надо, это очень хороший способ познания.
В самом начале надо решить главную задачу: объяснить ребятам, что физика – это интересно. Фото: РИА Новости
Интересные уроки и подготовка к ЕГЭ – вещи совместимые?
Артем Барат: Честно скажу, я большой поклонник Единого государственного экзамена. Почему? Еще до повсеместного введения ЕГЭ я работал в вузе, проводил вступительные экзамены, и могу точно сказать: права детей со всей страны уравнялись. Где бы ребенок ни родился, у него есть равный с москвичом шанс поступить в московский вуз, и вообще в любой вуз страны. Это большое достижение. Кроме того, в этом году в школах Москвы стартовал новый формат обучения одиннадцатиклассников с акцентом на подготовку к ЕГЭ. До 1 февраля московские школьники прошли всю учебную программу по ряду непрофильных предметов и перешли к работе по гибким учебным планам.
 В зависимости от профиля класса или нахождения в предпрофессиональном классе, у ребят сейчас продолжается углубленное изучение профильных предметов. Но вместо пройденных предметов у ребят появились практикумы по выбранным ими предметам для подготовки к ЕГЭ. Они позволят ребятам подготовиться к самой процедуре проведения экзамена, проработать сложные вопросы и задания, а также систематизировать изученный материал.На мой взгляд, такой подход помогает ученикам эффективно готовиться к ЕГЭ прямо на занятиях в школе, а родителям позволяет сэкономить деньги на репетиторов. Для учителей важно еще и то, что ученики собраны в группы по нужным им предметам, схожему уровню подготовки и нацеленности на результат. Так заинтересованность в изучении предмета гораздо выше, поэтому подготовка идет более результативно.Считаю, что благодаря этому нововведению образовательный процесс в школе для будущих выпускников организован более рационально и эффективно.
В зависимости от профиля класса или нахождения в предпрофессиональном классе, у ребят сейчас продолжается углубленное изучение профильных предметов. Но вместо пройденных предметов у ребят появились практикумы по выбранным ими предметам для подготовки к ЕГЭ. Они позволят ребятам подготовиться к самой процедуре проведения экзамена, проработать сложные вопросы и задания, а также систематизировать изученный материал.На мой взгляд, такой подход помогает ученикам эффективно готовиться к ЕГЭ прямо на занятиях в школе, а родителям позволяет сэкономить деньги на репетиторов. Для учителей важно еще и то, что ученики собраны в группы по нужным им предметам, схожему уровню подготовки и нацеленности на результат. Так заинтересованность в изучении предмета гораздо выше, поэтому подготовка идет более результативно.Считаю, что благодаря этому нововведению образовательный процесс в школе для будущих выпускников организован более рационально и эффективно.Физика – действительно сложный предмет. Парадокс в том, что она вокруг нас, на каждом шагу.
 Задача учителя – сделать так, чтобы дети это увидели
Задача учителя – сделать так, чтобы дети это увиделиВ 90-е годы прошлого века в подмосковных школах был эксперимент: предлагали на выбор отказаться от химии, биологии, физики или иностранного языка в старших классах. Я, не сомневаясь, вычеркнула физику. Сейчас жалею. Кого в этом винить?
Артем Барат: А я понимаю ваш выбор. Физика – действительно сложный предмет. Парадокс в том, что она на каждом шагу: рассчитываем время поездки до дачи, делаем проводку, кабельный ввод в дом, копаем колодец… Задача преподавателя – сделать так, чтобы дети видели связь физики с жизнью, и одновременно, понимали, что есть что-то большее, потому что, например, субатомных частиц мы в повседневной жизни не наблюдаем, а это очень интересно. В идеале учитель должен удовлетворить запросам государства, семьи и ребёнка.
Расскажите, какие запросы у государства, семьи и ребенка, на ваш взгляд?
Артем Барат: В наши задачи перед государством входит подготовить человека, который готов обучаться дальше и приносить пользу стране: будущих инженеров, учёных, готовых развивать технологическую мощь страны.
 Семья, помимо этого, хочет успешного будущего для ребенка и в связи с этим хороших баллов на ЕГЭ. Ребёнок хочет, чтобы ему было интересно, он хочет человеческого отношения.
Семья, помимо этого, хочет успешного будущего для ребенка и в связи с этим хороших баллов на ЕГЭ. Ребёнок хочет, чтобы ему было интересно, он хочет человеческого отношения.Физика начинается в 7-м классе. Как сразу “зацепить” детей?
Артем Барат: Мне как-то коллега из моей первой школы сказал, что физика в первый год изучения должна быть гуманитарным предметом. Я тогда возмутился, а сейчас думаю, так ли он был не прав? В 7 классе надо решить главную задачу: объяснить детям, что физика – это интересно. Поэтому в 7 классе я сейчас рассказываю, что такое физическое мышление, что разные явления можно объяснять, что есть разница между описанием и объяснением явления. В 8 классе мы пытаемся идти дальше и наращивать интерес. Далее – девятый, для кого-то выпускной класс. Тут два направления: подготовка к ОГЭ и задел для 10 класса, где будет более глубокая физика. 10 класс для меня и моих учеников – это чистое творчество. И выпускной 11 – ищем баланс между творчеством и подготовкой к ЕГЭ и олимпиадам
А что такое творчество в физике?
Артем Барат: Это умение разглядеть интересную задачу, чётко её поставить.
 Затем перевести её на язык математики или информатики, провести какие-то свои эксперименты, до которых могу додуматься только я. Создать свои собственные математические модели, и не постесняться всем этим поделиться с сообществом.
Затем перевести её на язык математики или информатики, провести какие-то свои эксперименты, до которых могу додуматься только я. Создать свои собственные математические модели, и не постесняться всем этим поделиться с сообществом.На своем мастер-классе на конкурсе “Учитель года” вы сказали, отвечая на вопрос жюри: “Важно решать здесь и сейчас те задачи, к которым ты готов, а не ждать, что научишься впрок”. А разве учиться впрок, на будущее – это не главное?
Артем Барат: Это частая проблема начинающих студентов. Открою секрет: знаний всегда не хватает. Особенно сейчас, когда все так стремительно меняется. Большая иллюзия, думать: “не буду делать что-то интересное сейчас, подожду, подучусь, и вот потом…”. Нет никакого потом. Только здесь и сейчас. Научная состоятельность должна быть заложена достаточно рано, и те студенты, которые начинают заниматься наукой или что-то интересное делать только на стадии подготовки диплома, существенно отстают от тех, кто начал этим заниматься в школе.
 Самое важное – не пытаться прыгнуть выше головы. Понять, что на своём уровне мы уже можем много чего сделать.
Самое важное – не пытаться прыгнуть выше головы. Понять, что на своём уровне мы уже можем много чего сделать.Вопрос ребром
На волне повышенного внимания к физике предложено снизить требования по русскому языку для абитуриентов-технарей. Как вам такая инициатива?
Артем Барат: Слышал опасения, мол, инженеры станут безграмотными и их не разделяю. Знаете, я сдавал ЕГЭ по русскому. И большего страха не испытывал. Потому что, ну как можно родной язык сдать плохо? И потом уверен: изучением русского языка можно заниматься в том числе и на физике. У меня ребята делают проекты, пишут тезисы докладов, описывают результаты экспериментов. И в них, конечно, бывают грамматические и орфографические ошибки. И когда я проверяю работы, начинаю именно с этого – с исправления ошибок по русскому языку. И только потом начинаю вникать в суть по физике. И знаете, заметил: дети не так трагично воспринимают эти ошибки, если они замечены не на уроке русского языка, а на физике и, может быть, даже более эффективно делают работу над ошибками.

Вы окончили Московский энергетический институт, а как попали в школу?
Артем Барат: Абсолютно случайно. Мой начальник в 2007 году рассказал, что одной школе очень нужен физик, “иди попробуй, у тебя получится”. Я пошел и не жалею. Мне показали, куда можно и нужно расти.
Как работать учителю, когда в одном классе сидят и физики, и “лирики”? Как заинтересовать всех и надо ли?
Артем Барат: Есть разные моменты урока, адресованные разным группам детей. У меня есть “лирические отступления”, какие-то философские моменты – тут включаются гуманитарии, а физики в это время могут изучать формулы. Да, приходится серьезно планировать урок, думать над подходами к каждой группе. Дети разные, но самое важное, что они все дети – это их объединяет.
Российская газета – Федеральный выпуск: №32(8977)
Поделиться
ОбразованиеМосква
Как найти конечную скорость любого объекта
Обновлено 29 марта 2023 г.

Автор S. Hussain Ather
Многие формулы и уравнения в физических задачах включают расчет начальной и конечной скорости. Разница между начальной и конечной скоростью в уравнениях сохранения импульса или уравнениях движения говорит вам о скорости объекта до и после того, как что-то произойдет. Это может быть сила, приложенная к объекту, столкновение или что-то еще, что может изменить его траекторию и движение.
Конечная скорость объекта — это мгновенная скорость в определенный момент времени t в конце интервала. Он измеряет конечную скорость (с направленной составляющей) через заданное время.
Для расчета конечной скорости объекта при равномерном ускорении можно использовать соответствующее уравнение движения. Эти уравнения используют комбинации расстояния, начальной скорости, конечной скорости, ускорения и времени, чтобы связать их друг с другом.
Финальная скорость Формулы
Определение изменений скорости зависит от ускорения объекта.
 Ускорение – это изменение скорости во времени. Например, формула конечной скорости (v f ), которая использует начальную скорость ( v i ), ускорение ( a ) и время ( t ):
Ускорение – это изменение скорости во времени. Например, формула конечной скорости (v f ), которая использует начальную скорость ( v i ), ускорение ( a ) и время ( t ):v_f = v_i + a\Delta t
Для данной начальной скорости объекта вы можете умножить ускорение из-за силы на время приложения силы и добавить его к начальной скорости, чтобы получить конечную скорость. «Дельта» Δ перед t означает, что это изменение во времени, которое можно записать как t f − t i .
Эта формула работает только с постоянным ускорением (или, в случае переменного ускорения, со средним ускорением за интервал времени).
Идеально подходит для мяча, падающего на землю под действием силы тяжести. В этом примере ускорение под действием силы тяжести будет постоянной ускорения свободного падения г = 9,8 м/с 2 .
 Эта постоянная ускорения говорит вам, насколько быстро ускоряется любой объект, когда вы бросаете его на Землю, независимо от массы объекта.
Эта постоянная ускорения говорит вам, насколько быстро ускоряется любой объект, когда вы бросаете его на Землю, независимо от массы объекта.Если вы бросите мяч с заданной высоты и подсчитаете, сколько времени потребуется мячу, чтобы достичь земли, то вы можете определить скорость непосредственно перед тем, как он упадет на землю, как конечную скорость. Начальная скорость была бы равна 0, если бы вы уронили мяч без какой-либо внешней силы. Используя приведенное выше уравнение, вы можете определить конечную скорость объекта v f .
Альтернативные уравнения расчета конечной скорости
Вы всегда можете использовать другие кинематические уравнения для любой ситуации, с которой вы работаете, поскольку они всегда логически и математически эквивалентны друг другу. Если бы вы знали расстояние, пройденное объектом (Δ x ), а также начальную скорость и время, необходимое для прохождения этого расстояния, вы могли бы рассчитать конечную скорость, используя уравнение для конечного положения по прошедшему времени на основе среднего скорость:
\Delta x = \bar{v} t = \frac{1}{2}(v_f+v_i)t \\ \newline{} \\ \text{Затем это можно изменить, чтобы найти } v_f: \ \ \newline{} \\ v_f = \frac{2\Delta x}{t} – v_i
Убедитесь, что в этих расчетах используются правильные единицы измерения.

A Цилиндр качения
Для цилиндра, катящегося по наклонной плоскости или холму, конечную скорость можно рассчитать по формуле сохранения энергии. Эта формула диктует, что, если цилиндр начинает движение из состояния покоя, энергия, которую он имеет в своем начальном положении, должна равняться его энергии после скатывания на определенное расстояние.
В исходном положении цилиндр не имеет кинетической энергии, поскольку не движется. Вместо этого вся его энергия является потенциальной энергией, что означает, что его энергия может быть записана как:
E = mgh
с массой m , гравитационной постоянной г = 9,8 м/с 2 и высота х . После того как цилиндр скатился на расстояние ч = 0, его энергия представляет собой только сумму кинетической энергии поступательного движения и кинетической энергии вращения. Это дает вам: 92
для скорости v , инерции вращения I и угловой скорости «омега» ω .
 2 \\ \newline{} \\ \text{находя $v$, получаем:} \\ \ новая строка {} \\ v = \ sqrt {\ frac {4} {3} gh}
2 \\ \newline{} \\ \text{находя $v$, получаем:} \\ \ новая строка {} \\ v = \ sqrt {\ frac {4} {3} gh}Эта формула для конечной скорости не зависит от веса или массы цилиндра. Если бы вы знали вес формулы цилиндра в кг (технически, массу) для различных цилиндрических объектов, вы могли бы сравнить разные массы и найти, что их конечные скорости одинаковы, потому что масса сокращается из приведенного выше выражения.
Другие воздействия на скорость
Все, что влияет на ускорение движущегося объекта, влияет на состояние скорости (или постоянного ускорения). Если сила приложена в направлении, противоположном скорости, то ускорение отрицательно по отношению к скорости, поэтому конечная скорость будет меньше начальной скорости.
Более сложный сценарий может быть найден с объектом в свободном падении. Если объект падает под действием силы тяжести, он также будет испытывать силу сопротивления воздуха в противоположном направлении.
 В конце концов, в сложном соотношении скоростей и сил объект действительно достигнет постоянной скорости, известной как конечная скорость для падающего объекта.
В конце концов, в сложном соотношении скоростей и сил объект действительно достигнет постоянной скорости, известной как конечная скорость для падающего объекта.2.3 Время, скорость и скорость – Колледж физики главы 1-17
2 Кинематика
Резюме
Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, перемещением и временем.
Вычислить скорость и скорость, зная начальное положение, начальное положение, конечное положение и конечное время.
Построить график зависимости скорости от времени по графику зависимости положения от времени.
Интерпретация графика зависимости скорости от времени. Рисунок 1. Движение этих мчащихся улиток можно описать их скоростями и скоростями. (кредит: tobitasflickr, Flickr).Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий.
 В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.Как обсуждалось в Главе 1.2 Физические величины и единицы измерения, наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени связано с измерением изменения некоторой физической величины. Это может быть цифра на цифровых часах, сердцебиение или положение Солнца на небе. В физике определение времени простое — время равно изменению или интервалу, в течение которого происходит изменение. Невозможно узнать, что время прошло, если что-то не изменится.
Количество времени или изменения калибруется путем сравнения со стандартом. Единицей времени в СИ является секунда, сокращенно с. Мы могли бы, например, заметить, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно же, подключив маятник к часовому механизму, который регистрирует время на циферблате.
 Это позволяет нам не только измерять количество времени, но и определять последовательность событий.
Это позволяет нам не только измерять количество времени, но и определять последовательность событий.Как время связано с движением? Обычно нас интересует время, затраченное на определенное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета. Чтобы найти прошедшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00. и закончить в 11:50, так что прошедшее время будет 50 мин. Прошедшее время [латекс]\жирныйсимвол{\Delta{t}}[/латекс] — разница между временем окончания и временем начала,
[латекс]\boldsymbol{\Delta{t}=t_f-t_0}[/латекс],
, где[latex]\boldsymbol{\Delta{t}}[/latex] — изменение времени или прошедшее время, [latex]\boldsymbol{t_f}[/latex] — время в конце движения, а [latex]\boldsymbol{t_0}[/latex] — время начала движения. (Как обычно, дельта-символ [латекс]\жирныйсимвол{\Дельта}[/латекс] означает изменение величины, следующей за ним.
 )
)Жизнь проще, если время начала[latex]\boldsymbol{t_0}[/latex]принято равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если[латекс]\boldsymbol{t_0=0}[/латекс], то[латекс]\жирныйсимвол{\Delta{t}=t_f\equiv{t}}[/латекс].
В этом тексте для простоты
- движение начинается в момент времени, равный нулю[latex]\boldsymbol{(t_0=0)}[/latex]
- символ t используется для обозначения прошедшего времени, если не указано иное[latex]\boldsymbol{(\Delta{x}=t_f\equiv{t})}[/latex]
Ваше представление о скорости, вероятно, совпадает с ее научным определением. Вы знаете, что если у вас есть большое перемещение за небольшой промежуток времени, у вас будет большая скорость, и эта скорость имеет единицы измерения расстояния, деленные на время, такие как мили в час или километры в час.
СРЕДНЯЯ СКОРОСТЬ
Средняя скорость равна смещению (изменению положения), деленному на время движения ,
[латекс]\boldsymbol{\bar{v}=}[/latex][латекс]\boldsymbol{\frac {\Delta{x}}{\Delta{t}}}[/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{x_f-x_0}{t_f-t_0}} [/latex],
, где[latex]\boldsymbol{\bar{v}}[/latex]является средней скоростью (обозначенной чертой над v),[latex]\boldsymbol{\Delta{x }}[/latex]это изменение положения (или смещения), а[latex]\boldsymbol{x_f}[/latex]и[latex]\boldsymbol{x_0}[/latex]являются конечной и начальной позициями в моменты времени [латекс]\boldsymbol{t_f}[/латекс] и [латекс]\жирныйсимвол{t_0}[/латекс] соответственно.
 Если начальное время[latex]\boldsymbol{t_0}[/latex] принимается равным нулю, то средняя скорость равна просто
Если начальное время[latex]\boldsymbol{t_0}[/latex] принимается равным нулю, то средняя скорость равна просто[латекс]\boldsymbol{\bar{v}=}[/латекс][латекс]\boldsymbol{\frac{\Delta{x}}{t}}[/латекс].
Обратите внимание, что это определение указывает, что скорость является вектором, потому что перемещение является вектором . Она имеет как величину, так и направление. Единицей скорости в СИ является метр в секунду или м/с, но широко используются многие другие единицы, такие как км/ч, мили/ч (также пишется как миль/ч) и см/с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на -4 м (знак минус указывает, что перемещение происходит в направлении задней части самолета). Его средняя скорость была бы
[латекс]\boldsymbol{\bar{v}=}[/latex][латекс]\boldsymbol{\frac{\Delta{x}}{t}}[/latex][латекс]\boldsymbol{=} [/латекс][латекс]\boldsymbol{\frac{-4\textbf{м}}{5\textbf{s}}}[/латекс][латекс]\boldsymbol{=-0,8\:м/с}[ /latex]
Знак минус указывает, что средняя скорость также направлена к задней части самолета.

Однако средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками. Например, по средней скорости мы не можем сказать, остановился ли пассажир самолета на мгновение или дал задний ход перед тем, как подойти к задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие отрезки пути за меньшие промежутки времени.
Рисунок 2. Более подробная запись пассажира самолета, направляющегося к задней части самолета, показывающая небольшие сегменты его поездки.Чем меньше временных интервалов, учитываемых в движении, тем детальнее информация. Когда мы доводим этот процесс до его логического завершения, остается бесконечно малый интервал. За такой интервал средняя скорость становится мгновенной скоростью или скоростью в конкретный момент времени . Автомобильный спидометр, например, показывает величину (но не направление) мгновенной скорости автомобиля. (Полиция выдает штрафы на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время дорожного путешествия, вам необходимо использовать среднюю скорость.
 ) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).
) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).Математически, нахождение мгновенной скорости,[latex]\boldsymbol{v}[/latex], в конкретный момент времени[latex]\boldsymbol{t}[/latex]может потребовать принятия предела, вычислительной операции, выходящей за рамки этот текст. Однако во многих случаях мы можем найти точные значения мгновенной скорости без вычислений.
В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. Однако в физике они не имеют одинакового значения и представляют собой разные понятия. Одним из основных отличий является то, что скорость не имеет направления. Таким образом, скорость является скаляром . Точно так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.
Мгновенная скорость — величина мгновенной скорости.
 Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.
Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.Мы заметили, что пройденное расстояние может быть больше, чем перемещение. Таким образом, средняя скорость может быть больше, чем средняя скорость, которая равна смещению, деленному на время. Например, если вы едете в магазин и через полчаса возвращаетесь домой, а одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю.
Рисунок 3. За 30-минутный путь до магазина туда и обратно общее пройденное расстояние составляет 6 км. Средняя скорость 12 км/ч. Перемещение для кругового рейса равно нулю, так как нет чистого изменения положения. Таким образом, средняя скорость равна нулю. (Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости.
(Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости.Другой способ визуализации движения объекта — использование графика. График зависимости положения или скорости от времени может быть очень полезен. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рис. 4. (Обратите внимание, что эти графики изображают очень упрощенную модель поездки. Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся у магазина. Но для простоты мы будем моделировать его без остановок или изменения скорости.
Рисунок 4. Положение в зависимости от времени, скорость в зависимости от времени и скорость в зависимости от времени в пути. Обратите внимание, что скорость обратного пути отрицательна. Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.)
Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.)УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ ДЛЯ ДОМА — ПОЛУЧЕНИЕ ЧУВСТВА СКОРОСТИ
Если вы провели много времени за рулем, вы, вероятно, хорошо чувствуете скорость от 10 до 70 миль в час. Но что это в метрах в секунду? Что мы имеем в виду, когда говорим, что что-то движется со скоростью 10 м/с? Чтобы лучше понять, что на самом деле означают эти значения, сделайте несколько наблюдений и расчетов самостоятельно:
- рассчитайте типичную скорость автомобиля в метрах в секунду
- оценить скорость бега трусцой и ходьбы, засекая время самостоятельно; конвертировать измерения как в м/с, так и в мили/ч
- определить скорость муравья, улитки или падающего листа
- Время измеряется в единицах изменения, и его единицей СИ является секунда (с).
 Прошедшее время для события
Прошедшее время для события[латекс]\boldsymbol{\Delta{t}=t_f -t_0}[/латекс]
, где[latex]\boldsymbol{t_f}[/latex] — конечное время, а [latex]\boldsymbol{t_0}[/latex] — начальное время. Начальное время часто принимается равным нулю, как если бы оно измерялось секундомером; прошедшее время равно просто[латекс]\жирныйсимвол{т}[/латекс].
- Средняя скорость[латекс]\boldsymbol{\bar{v}}[/латекс]определяется как смещение, деленное на время в пути. В символах средняя скорость
[латекс]\boldsymbol{\bar{v} =}[/латекс][латекс]\boldsymbol{\frac{\Delta{x}}{\Delta{t}}}[/latex][латекс]\boldsymbol {=}[/латекс][латекс]\boldsymbol{\frac{x_f -x_0}{t_f – t_0}}[/латекс].
- Единицей скорости в системе СИ является м/с.
- Скорость является вектором и поэтому имеет направление.
- Мгновенная скорость[latex]\boldsymbol{v}[/latex]– это скорость в конкретный момент времени или средняя скорость за бесконечно малый интервал.
- Мгновенная скорость — величина мгновенной скорости.



 2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.
 2$, $F_p=ma_4=15·1.5=22.5H$
2$, $F_p=ma_4=15·1.5=22.5H$ Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.
Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.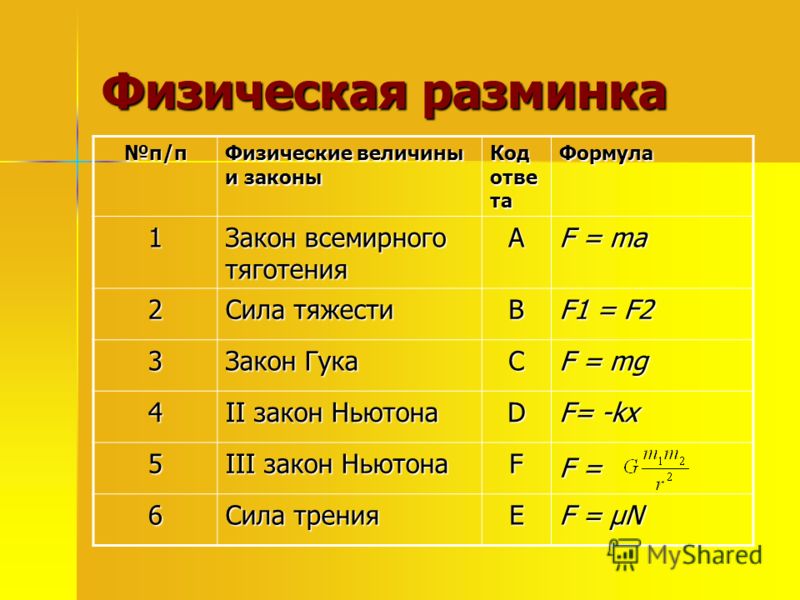
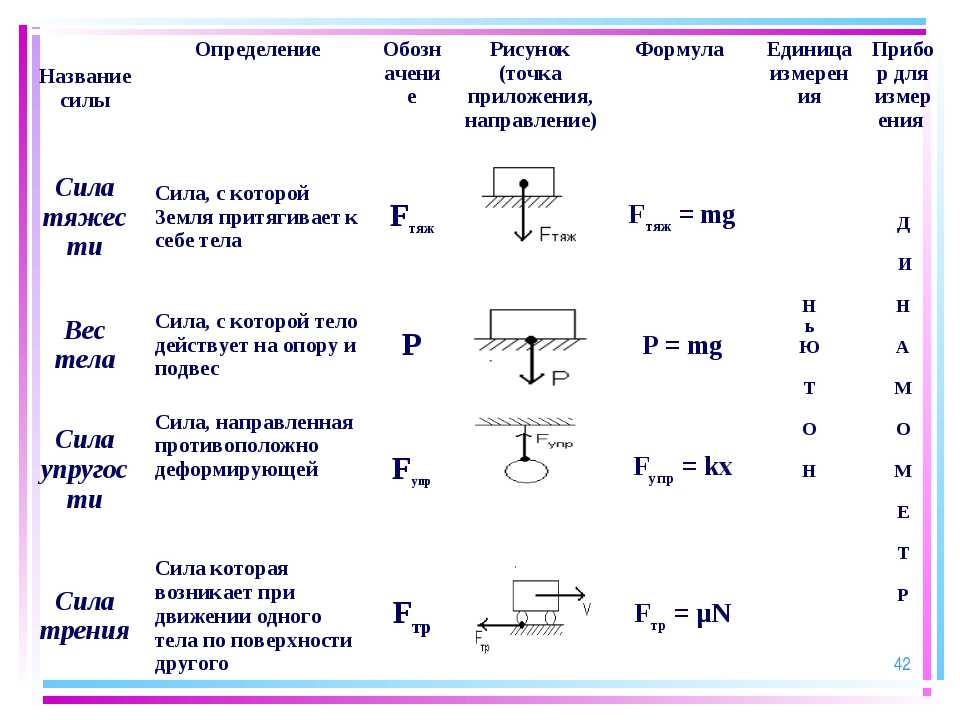
 На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.
 к. равномерное движение – это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).
к. равномерное движение – это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).

 2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).
2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит). 2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).
2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит). е. период колебаний тела равен 4с (верно).
е. период колебаний тела равен 4с (верно).



 Мы отвернулись от одной звезды, но почему другие нам не светят? Отталкиваясь от парадокса Ольберса, можно прийти к теории Большого взрыва и вообще к доказательству того, что Большой взрыв существовал. Замечательная тема. Я бы еще выделил квантовую теорию гравитации и гравитационные волны как одно из последних достижений науки. Оно уже в достаточной степени популяризировано, можно найти простые и понятные объяснения. Хотя, признаюсь, я против излишних упрощений. Так мы иногда выхолащиваем смысл.
Мы отвернулись от одной звезды, но почему другие нам не светят? Отталкиваясь от парадокса Ольберса, можно прийти к теории Большого взрыва и вообще к доказательству того, что Большой взрыв существовал. Замечательная тема. Я бы еще выделил квантовую теорию гравитации и гравитационные волны как одно из последних достижений науки. Оно уже в достаточной степени популяризировано, можно найти простые и понятные объяснения. Хотя, признаюсь, я против излишних упрощений. Так мы иногда выхолащиваем смысл. Изучаем это явление. Есть еще задачка “рисовые гири” – про физику сыпучих материалов. Оказывается, если в емкость, плотно наполненную рисом, буквально “вбить” ложку, то потом за эту ложку можно поднять всю емкость с крупой. Дети очень эффективно учатся на подобных задачках и узнают гораздо больше.
Изучаем это явление. Есть еще задачка “рисовые гири” – про физику сыпучих материалов. Оказывается, если в емкость, плотно наполненную рисом, буквально “вбить” ложку, то потом за эту ложку можно поднять всю емкость с крупой. Дети очень эффективно учатся на подобных задачках и узнают гораздо больше.
 В зависимости от профиля класса или нахождения в предпрофессиональном классе, у ребят сейчас продолжается углубленное изучение профильных предметов. Но вместо пройденных предметов у ребят появились практикумы по выбранным ими предметам для подготовки к ЕГЭ. Они позволят ребятам подготовиться к самой процедуре проведения экзамена, проработать сложные вопросы и задания, а также систематизировать изученный материал.На мой взгляд, такой подход помогает ученикам эффективно готовиться к ЕГЭ прямо на занятиях в школе, а родителям позволяет сэкономить деньги на репетиторов. Для учителей важно еще и то, что ученики собраны в группы по нужным им предметам, схожему уровню подготовки и нацеленности на результат. Так заинтересованность в изучении предмета гораздо выше, поэтому подготовка идет более результативно.Считаю, что благодаря этому нововведению образовательный процесс в школе для будущих выпускников организован более рационально и эффективно.
В зависимости от профиля класса или нахождения в предпрофессиональном классе, у ребят сейчас продолжается углубленное изучение профильных предметов. Но вместо пройденных предметов у ребят появились практикумы по выбранным ими предметам для подготовки к ЕГЭ. Они позволят ребятам подготовиться к самой процедуре проведения экзамена, проработать сложные вопросы и задания, а также систематизировать изученный материал.На мой взгляд, такой подход помогает ученикам эффективно готовиться к ЕГЭ прямо на занятиях в школе, а родителям позволяет сэкономить деньги на репетиторов. Для учителей важно еще и то, что ученики собраны в группы по нужным им предметам, схожему уровню подготовки и нацеленности на результат. Так заинтересованность в изучении предмета гораздо выше, поэтому подготовка идет более результативно.Считаю, что благодаря этому нововведению образовательный процесс в школе для будущих выпускников организован более рационально и эффективно. Задача учителя – сделать так, чтобы дети это увидели
Задача учителя – сделать так, чтобы дети это увидели Семья, помимо этого, хочет успешного будущего для ребенка и в связи с этим хороших баллов на ЕГЭ. Ребёнок хочет, чтобы ему было интересно, он хочет человеческого отношения.
Семья, помимо этого, хочет успешного будущего для ребенка и в связи с этим хороших баллов на ЕГЭ. Ребёнок хочет, чтобы ему было интересно, он хочет человеческого отношения. Затем перевести её на язык математики или информатики, провести какие-то свои эксперименты, до которых могу додуматься только я. Создать свои собственные математические модели, и не постесняться всем этим поделиться с сообществом.
Затем перевести её на язык математики или информатики, провести какие-то свои эксперименты, до которых могу додуматься только я. Создать свои собственные математические модели, и не постесняться всем этим поделиться с сообществом. Самое важное – не пытаться прыгнуть выше головы. Понять, что на своём уровне мы уже можем много чего сделать.
Самое важное – не пытаться прыгнуть выше головы. Понять, что на своём уровне мы уже можем много чего сделать.

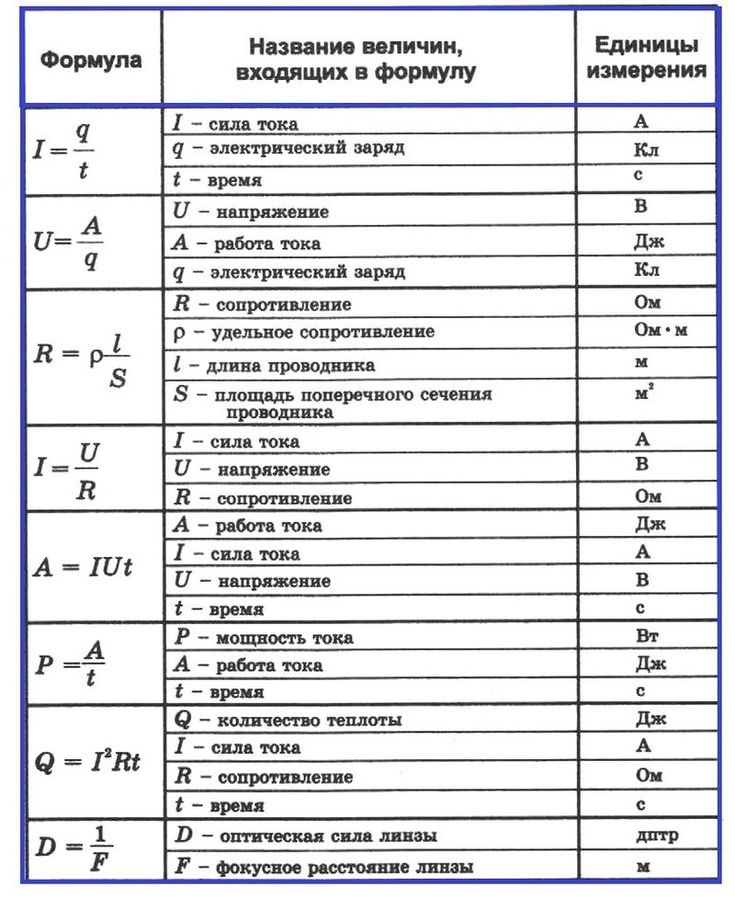 Ускорение – это изменение скорости во времени. Например, формула конечной скорости (v f ), которая использует начальную скорость ( v i ), ускорение ( a ) и время ( t ):
Ускорение – это изменение скорости во времени. Например, формула конечной скорости (v f ), которая использует начальную скорость ( v i ), ускорение ( a ) и время ( t ): Эта постоянная ускорения говорит вам, насколько быстро ускоряется любой объект, когда вы бросаете его на Землю, независимо от массы объекта.
Эта постоянная ускорения говорит вам, насколько быстро ускоряется любой объект, когда вы бросаете его на Землю, независимо от массы объекта.
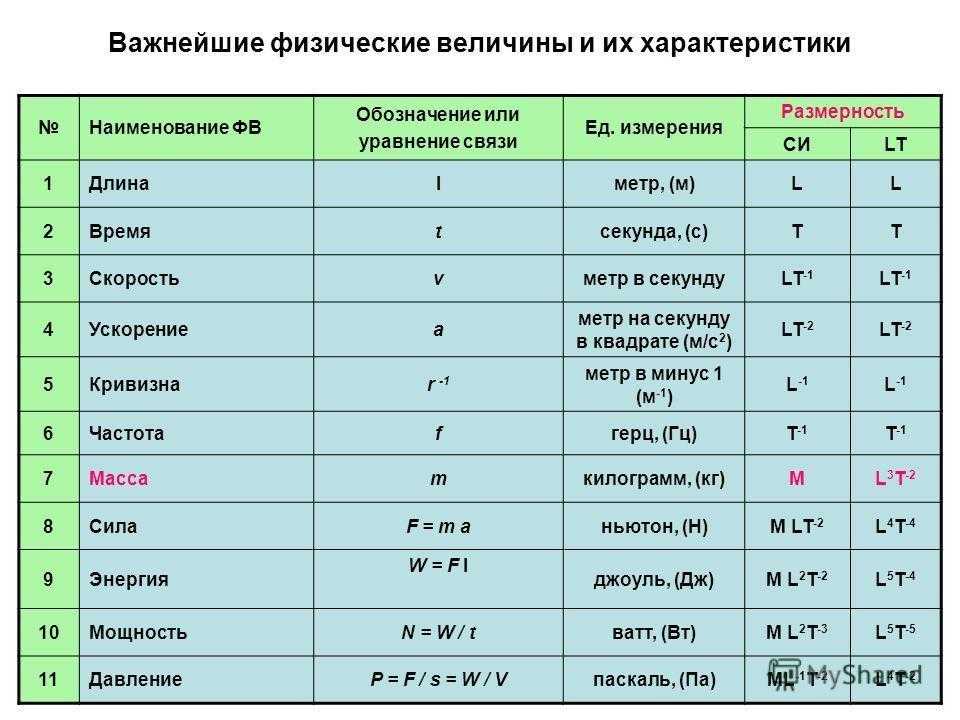 2 \\ \newline{} \\ \text{находя $v$, получаем:} \\ \ новая строка {} \\ v = \ sqrt {\ frac {4} {3} gh}
2 \\ \newline{} \\ \text{находя $v$, получаем:} \\ \ новая строка {} \\ v = \ sqrt {\ frac {4} {3} gh} В конце концов, в сложном соотношении скоростей и сил объект действительно достигнет постоянной скорости, известной как конечная скорость для падающего объекта.
В конце концов, в сложном соотношении скоростей и сил объект действительно достигнет постоянной скорости, известной как конечная скорость для падающего объекта. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения. Это позволяет нам не только измерять количество времени, но и определять последовательность событий.
Это позволяет нам не только измерять количество времени, но и определять последовательность событий. )
) Если начальное время[latex]\boldsymbol{t_0}[/latex] принимается равным нулю, то средняя скорость равна просто
Если начальное время[latex]\boldsymbol{t_0}[/latex] принимается равным нулю, то средняя скорость равна просто
 ) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени).
) Мгновенная скорость [latex]\boldsymbol{v}[ /latex] — средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени). Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.
Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время. (Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости.
(Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости. Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.)
Мы также предполагаем, что маршрут между магазином и домом — совершенно прямая линия.) Прошедшее время для события
Прошедшее время для события