Как найти время в кинематике: Ошибка: 404 Материал не найден - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Кинематика — что это такое? Что изучает?

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Время — в международной системе единиц СИ измеряется в секундах [с].
Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]

S — путь [м]

t — время [с]

В чем разница между перемещением и путем?

Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости

V ср.путевая = S/t

Подставим значения:

V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) = x₀ + v_x

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

Уравнение движения при движении против оси

x(t) = x₀ − v_xt

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц.

«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

То есть равноускоренное прямолинейное движение — это движение с ускорением по прямой линии, движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени

У равноускоренного движения в уравнении появляется ускорение.

x(t) = x₀ + v_0xt + a_xt²/2

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с²]

Для данного процесса также важно уметь находить конечную скорость. Это часто упрощает решение задач. Она находится по формуле

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с²]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч²
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt²/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с², а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с². В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с².

И кому же верить?

Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с².

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя.

Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки. Очень важно разделить движение по окружности и вращение тела.

При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.

При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.

Центростремительное ускорение

При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.

Центростремительное ускорение

a_ц = v²/R

aц — центростремительное ускорение [м/с²]

v — скорость [м/с]

R — радиус окружности [м]

Задачка

Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?

Решение:

Возьмем формулу центростремительного ускорения тела

a_ц = v²/R

В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.

36 км/с = 10 м/с

Теперь можно подставить значения в формулу:

a_ц = 10²/120 = 100/120 = 10/12 ≃ 0,83 м/с²

Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с²

Эту и другие темы мы разбираем на курсе физики за 9 класс.

Кинематика точки и твердого тела. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей

Модели тел и движений

Грузовик едет со средней скоростью 70 км/час. Сколько времени он потратит на дорогу из одного города в другой, если расстояние между городами 350 км?

Вы решите эту задачу в одно действие, получится 5 часов. Но для водителя может быть важнее ответ на другой вопрос: сколько времени займёт обгон другого такого же грузовика, который движется со скоростью 60 км/ч, а длина каждого грузовика – 7 м? Попробуйте решить задачу самостоятельно, ответ получится около 5 с.

Задачи простые, но вот что интересно: в первой нам было вообще всё равно, совершал ли обгоны грузовик, важно было только общее время движения. Мы рассмотрели его как материальную точку, которая движется с постоянной скоростью. А вторую задачу мы бы не решили, не зная длин грузовиков, здесь модель материальной точки уже неприменима.

У нас есть в запасе различные модели – это инструменты. Которые мы можем с той или иной степенью точности использовать для решения различных практических задач. Если эта точность нас не устраивает, то мы используем другую модель или разрабатываем новую, например, уточняя текущую.

Так, для описания движения в кузове пустого баллона или вибрации двигателя грузовика описанные выше модели не подойдут, понадобятся новые.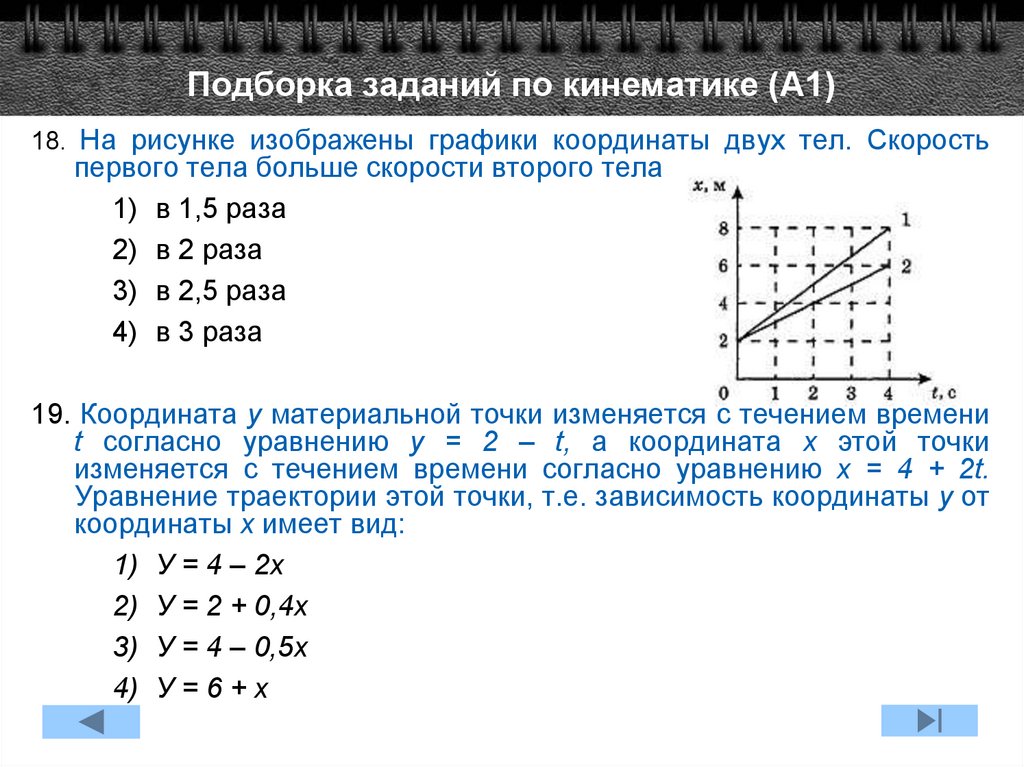 При этом рассмотренные модели не имеют отношения к грузовику – они могут применяться к автобусу, поезду, бильярдному шару или любому другому объекту. Задачи могут быть самыми разными, но то немногое, что для нас в них является самым важным, может быть описано одной и той же моделью.

Обратите внимание, что в рассмотренных задачах про грузовик нас интересовали только время, скорость и расстояние, которое он проехал. Нам было не важно, как работал двигатель, сколько бензина понадобилось, почему вообще грузовик двигался и тяжелый ли вёз груз.

Решением таких задач занимается кинематика – раздел физики, посвященный моделям движения, которые не учитывают причины движения, а только описывают его. О задачах кинематики и моделях, которые используются для их решения, мы сегодня и будем говорить.

Рассмотрим такую задачу: с горки известной высоты и известного наклона соскальзывает шайба и скатывается шар. На одинаковом ли расстоянии от горки они остановятся?

Рис. 1. Задача на скатывание тел с наклонной поверхности

Может оказаться, что не на одинаковом, даже при одинаковом трении с поверхностью. Если использовать модель материальной точки и для шайбы, и для шара, то этот результат необъясним.

Рис. 2. В модели материальной точки тела неразличимы

Действительно, потенциальная энергия перешла в кинетическую – можем вычислить скорость тела внизу горки, а по ней рассчитать расстояние, на котором они оба остановятся. Чтобы объяснить разные расстояния, нам придётся учесть вращение шара – тогда потенциальная энергия будет расходоваться не только на увеличение кинетической энергии, но и на увеличение энергии вращения шара. В данном случае для шара мы можем применить модель твёрдого тела, в которой различаются поступательное и вращательное движения.

Поступательное и вращательное движение

Поступательное движение – это такое движение, при котором все точки тела движутся одинаково: с одинаковой скоростью, совершая одинаковое перемещение.

Рис. 3. Поступательное движение

А как еще может быть? Взмахните рукой и проследите: понятно, что ладонь и плечо двигались по-разному. Посмотрите на колесо обозрения: точки вблизи оси почти не движутся, а кабинки движутся с другой скоростью и по другим траекториям.

Рис. 4. Вращательное движение

Посмотрите на прямолинейно движущийся автомобиль: если не учитывать вращение колес и движение частей мотора, все точки автомобиля движутся одинаково, движение автомобиля считаем поступательным. Тогда нет смысла описывать движение каждой точки, можно описать движение одной. Автомобиль считаем материальной точкой. Обратите внимание, что при поступательном движении линия, соединяющая любые две точки тела при движении, остается параллельной сама себе.

Второй вид движения по этой классификации – вращательное движение. При вращательном движении все точки тела движутся по окружности вокруг какой-то одной оси. Эта ось может пересекать тело, как в случае с колесом обозрения, а может не пересекать, как в случае с автомобилем на повороте (рисунок).

Но не любое движение можно отнести к какому-то одному из двух видов. Как описать движение педалей велосипеда относительно земли – это какой-то третий тип? Наша модель удобна тем, что можно рассматривать движение как комбинацию поступательного и вращательного движений: относительно своей оси педали вращаются, а ось вместе со всем велосипедом движется поступательно относительно Земли.

Возьмем другой пример: фигуристка вращается на месте, и, когда она прижимает руки к груди, она начинает вращаться значительно быстрее.

Рис. 5. Вращение фигуристки

Момент инерции

Как узнать, варёное перед нами яйцо или сырое? Можно это определить по вращению. Раскрутить яйцо на столе: варёное будет долго вращаться, а сырое остановится быстрее. Как это объяснить? Для описания вращательного движения ввели понятие момента инерции. Можно провести аналогию с массой.

Масса – это мера инертности при поступательном движении: чтобы разогнать или остановить более тяжелое тело, потребуется бóльшая сила, чем для более легкого тела. Для момента инерции справедливо то же, только описывается вращательное движение и угловая скорость. Кинетическая энергия вращательного движения определяется моментом инерции и угловой скоростью.

Возвращаемся к вращению яйца. У сырого яйца во вращении участвует по сути только скорлупа, её момент инерции меньше, чем момент инерции вареного яйца – сплошного твердого тела. Поэтому и энергия вращения, а значит и время вращения меньше. Мы не учли, что жидкость внутри сырого яйца вязкая и тоже как-то движется, но мы и не делаем точных расчетов, а для сравнения такого предположения достаточно.

Рассмотрим в рамках нашей модели вращение фигуристки. Момент инерции зависит от распределения массы – чем она ближе к оси вращения, тем меньше момент инерции. Прижимая руки к груди, фигуристка меняет распределение массы, и момент инерции уменьшается. И из закона сохранения энергии понятно: если уменьшился момент инерции, увеличилась скорость.

Мы иногда и не замечаем, как используются модели: фигуристка умеет управлять моментом инерции, даже не зная о нём.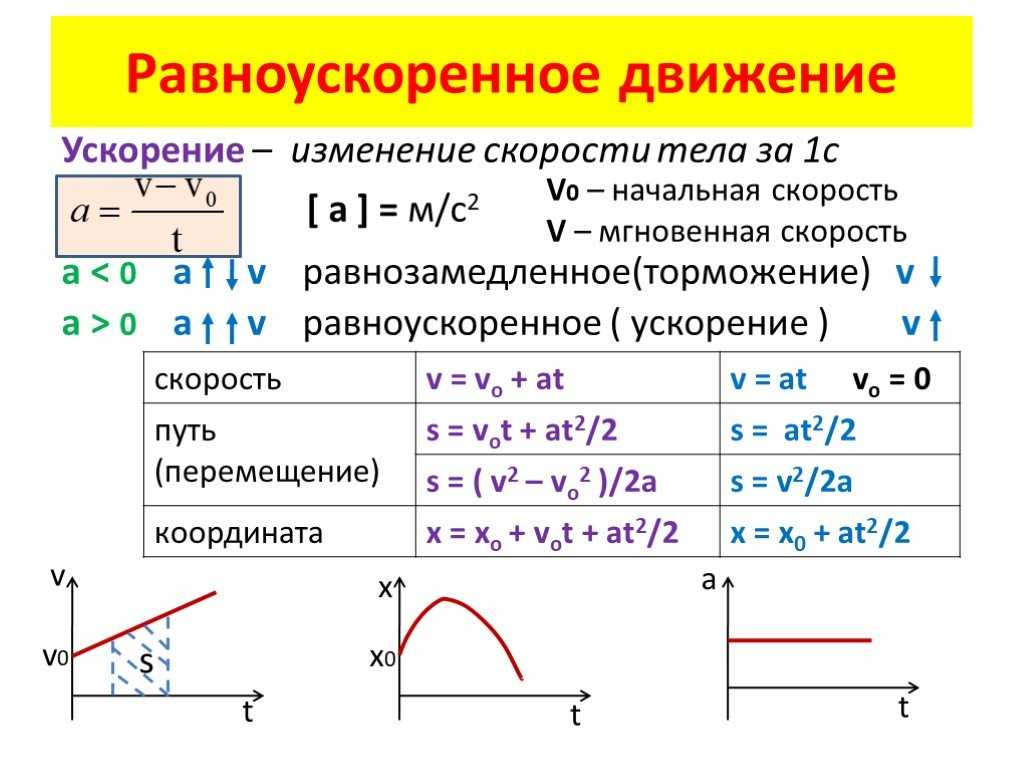 Задача физики – создать модель, чтобы можно было управлять осознанно. Тогда можно посчитать, как управлять, поставить задачу компьютеру, чтобы он всё рассчитал.

В целом ясно, что энергия одного вида движения превращается в энергию другого, и это нельзя описать, считая фигуристку материальной точкой. Как материальная точка она вообще неподвижна.

Как это вращение описать? Удобно использовать то, что уже хорошо разобрали. Обычно, чтобы описать движение тела, достаточно описать движение нескольких его точек, а для описания движения у нас есть готовые инструменты. Например, для катящегося с горки шара можно рассматривать движение одной из точек поверхности относительно центра шара, и движение центра шара относительно горки.

Инструменты кинематики

Итак, несколько моделей в нашем наборе инструментов уже есть: это равномерное и равноускоренное прямолинейное движение материальной точки и равномерное движение по окружности. И некоторые задачи мы уже умеем решать.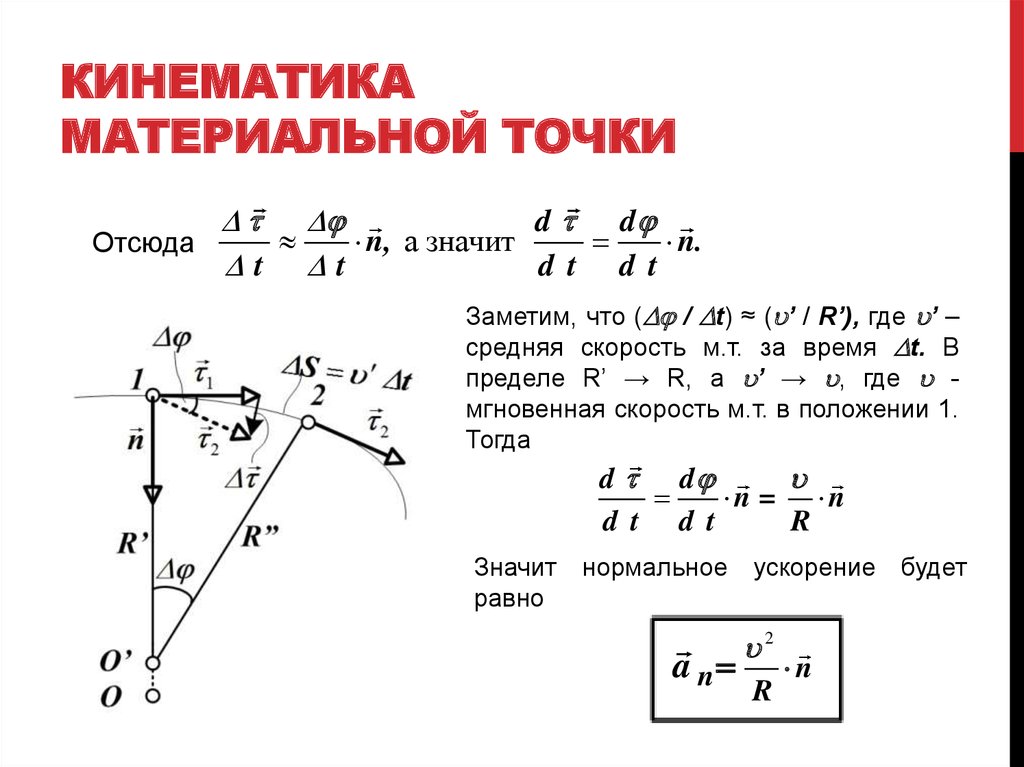

На уроках математики мы успели овладеть новыми математическими инструментами, такими, как вектор и система координат, с помощью которых мы можем создать более удобные физические модели и решать с их помощью больше задач. Давайте упорядочим информацию о тех инструментах кинематики, которые у нас уже есть, и заодно научимся пользоваться новыми.

Рис. 6. Определение материальной точки

Здесь мы под точкой понимаем то же, что и в геометрии: дать определение точке нельзя, это базовое понятие, но мы можем сформулировать, что мы с её помощью будем описывать – объект, на размеры которого мы при решении данной задачи можем не обращать внимания, но на положение которого мы можем указать. Только в отличие от точки в геометрии, в физике мы ей приписываем еще и массу.

Обратите внимание, что само по себе выражение «материальная точка» – оксюморон (как, например, «живой труп»). Действительно, сама по себе точка не может быть материальной, у неё нет длины, ширины, мы, в принципе, не можем на неё указать. Но в этом и заключается смысл модели – не существовать в реальности, а приближать с достаточной точностью множество реальных ситуаций и помогать их описывать.

Мы говорим о движении, то есть об изменении положения точки со временем. Но изменение положения может быть только относительно других объектов. В жизни, чтобы обозначить положение чего-либо, мы говорим: возле окна, в десяти километрах от города. Можем указать адрес: улица Пушкина, и номер дома и квартиры. Можем указать место в театре: ряд 7, место 15. В зависимости от задачи, которую мы решаем, мы выбираем точку отсчёта и систему координат.

Воспользуемся уже готовым математическим инструментом – декартовой (прямоугольной) системой координат. Но система координат позволяет задать положение точки относительно какого-то объекта, то есть нужно еще задать этот объект – тело отсчета.

Добавим к системе координат и телу отсчета часы, чтобы рассматривать процессы с течением времени, и получим систему отсчета. Раздел физики, механика, занимается решением следующей задачи, которая так и называется:

Основная задача механики – точно определять положение тела в пространстве в любой момент времени.

В этой стандартной формулировке все слова следует пояснить.

Абсолютно точно мы в реальном мире ничего не определяем. Точность всегда конечна: иногда нас устраивает определить положение чего-то с точностью до метра, иногда – до миллиметра, а ведь можно и до десятой, и до тысячной доли миллиметра – на чём-то всё равно остановимся. И, как мы уже много раз говорили, точность определяется конкретной задачей, которую мы сейчас решаем.
Для тела можно использовать разные модели, мы договорились изучать модель материальной точки.
Нас не интересует любой момент времени, нас интересует конкретный период в рамках решаемой задачи. Если автомобиль едет с постоянной скоростью 70 км/ч, то через 5 часов он будет в 350 километрах от начала пути. В решение мы действительно можем подставить любое время и получить ответ: за 10 часов проедет 700 км, а за месяц обогнёт земной шар. Только эти результаты лишены смысла, автомобиль не будет ехать дальше пункта назначения, и уж тем более плыть во время кругосветного путешествия по океану.

На математическом языке основная задача механики звучит так: определить положение точки в пространстве в данной системе отсчёта, описав изменение её координат x, y, z от времени: то есть, найдя функции x(t), y(t), z(t). Зададим положение точки в пространстве с помощью вектора.

Рассмотрим для простоты точку на плоскости с координатам (x, y) – в пространстве будет то же самое, только на одну координату больше, (x, y, z).

Рис. 7. Трехмерная система координат

Проведем вектор из начала координат (0, 0) в эту точку, и мы получим радиус-вектор, обозначим его , с координатами (x, y). Положение точки в любой момент времени определяется зависимостью радиус-вектора от времени .

Рис. 8. Радиус-вектор

Зависимость положения материальной точки от времени называют её законом движения.

Рис. 9. – закон движения

Можно задать положение точки в виде координат, и эти координаты зависят от времени: x(t), y(t) (и, если в пространстве, то еще z(t)).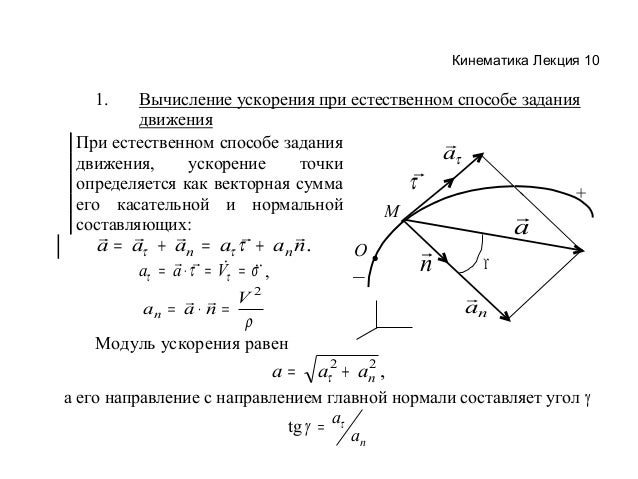 Это будет закон движения в координатной форме. Можно записать закон движения в векторной форме, . Причем проекции вектора на оси координат и и будут координатами точки , , и для них мы записали, как они изменяются со временем, x(t), y(t)! Так мы с лёгкостью переходим от одной формы к другой.

Точка движется, меняет положение. Вы помните, что если последовательно соединить все положения материальной точки в процессе её движения, то получим кривую, которую назвали траекторией. Длина участка траектории называется путь, а если соединить отрезком начальную и конечную точки движения, то получим перемещение.

Рис. 10. Путь и перемещение

У нас тогда не было удобной модели, чтобы описать перемещение. Мы говорили о нём как об отрезке, который имеет направление, и это направление мы обозначали знаком плюс или минус – мы рассматривали движение вдоль одной прямой, и этого было достаточно, так как при движении вдоль прямой возможны всего два направления.

Сейчас мы можем строго определить перемещение как вектор, проведённый из начального положения материальной точки в конечное. А в другом обозначении – проведённый из конца радиус-вектора в конец радиуса-вектора .

Рис. 11. Перемещение как разность радиусов-векторов

Такой вектор – это вектор разности, запишем:

Используя свойства векторов, несложно получить из определения:

Если записать проекции радиус-векторов и перемещения на оси координат, то получим то, что мы записывали для движения вдоль одной оси. Проекции вектора перемещения равны разностям проекций радиусов-векторов:

Проекция перемещения – это скаляр, равный разности координат точки. А знак скаляра соответствует направлению составляющей вектора перемещения: параллельной оси х или у.

Рис. 12. Проекции перемещения

Модуль перемещения можно найти, как и модуль любого вектора, по его координатам:

Если вектор перемещения параллелен одной из осей, например, х, то составляющая , и:

Равномерное и равноускоренное движение

Мы заново ввели понятие перемещения, используя удобные универсальные инструменты, сделав его тоже более удобным и универсальным. Теперь посмотрим, как в нашу модель вписываются понятия скорости и ускорения, которые мы ввели раньше. Мы различали путевую скорость и скорость по перемещению. Это соответственно путь, пройденный точкой за единицу времени, и перемещение, совершенное точкой за единицу времени.

Чаще всего, говоря о скорости, мы подразумеваем скорость по перемещению: это отношение перемещения точки к промежутку времени, за который это перемещение произошло.

Это вектор перемещения, умноженный на скаляр , поэтому по направлению скорость и перемещение совпадают.

Такое определение скорости по сути означает среднюю скорость, с которой тело двигалось на протяжении времени .

Рис. 13. Средняя скорость по перемещению

Мы точно не знаем, как изменялась скорость и каким было перемещение на разных частях этого промежутка. Но разделив всё перемещение на этом промежутке на всё время , мы получаем, что в среднем точка перемещалась каждую секунду на определенное расстояние в определенном направлении. Если в нашей модели скорость меняется, то нужно взять настолько короткий промежуток , чтобы можно было считать, что скорость не успевает измениться.

Рис. 14. Мгновенная скорость

В математике ввели модель: стремится к нулю, . Среднюю скорость на таком малом промежутке назвали мгновенной (очень короткий промежуток времени часто называют мгновением). Математическая запись всего, что мы указали, выглядит так:

Мы рассматриваем две простейших модели: когда скорость постоянна и когда скорость меняется равномерно. Если скорость постоянна (а скорость – вектор), это значит, что она не меняется ни по направлению, ни по модулю. Значит, в формулу для скорости можно подставлять любой промежуток времени. Будем считать начало наблюдения моментом , а время, прошедшее с этого момента, обозначим просто . За это время перемещение равно:

Тело переместилось из начального положения, соответствующего радиусу-вектору , в некоторое положение, которое нас интересует в момент времени t. Запишем:

Получили закон движения в случае равномерного прямолинейного движения.

Следующая модель – скорость равномерно меняется, то есть, запишем в векторной форме, за равные промежутки времени изменение скорости одинаково и равно .

Рис. 15. Равноускоренное движение

Чтобы описывать скорость изменения скорости, мы ввели величину ускорение, это для нас не ново. В общем случае скорость может меняться не одинаково в разные промежутки времени, и есть смысл ввести понятие мгновенного ускорения, взять изменение скорости за короткий промежуток времени:

Но если говорить о равноускоренном движении, то ускорение одинаково на любом промежутке времени, и среднее ускорение за любое время одинаково. Если считать, что – это изменение скорости от некоторого нулевого значения в момент времени до интересующего нас значения в момент времени , то можем записать закон изменения скорости:

Уравнение равноускоренного движения мы уже вычисляли для движения вдоль одной оси, и мы получили известную вам формулу:

Главное, что это уравнение справедливо в проекции на каждую ось координат, и в векторной форме оно будет выглядеть похоже:

Уже известный нам закон сложения скоростей тоже можно записать в векторной форме.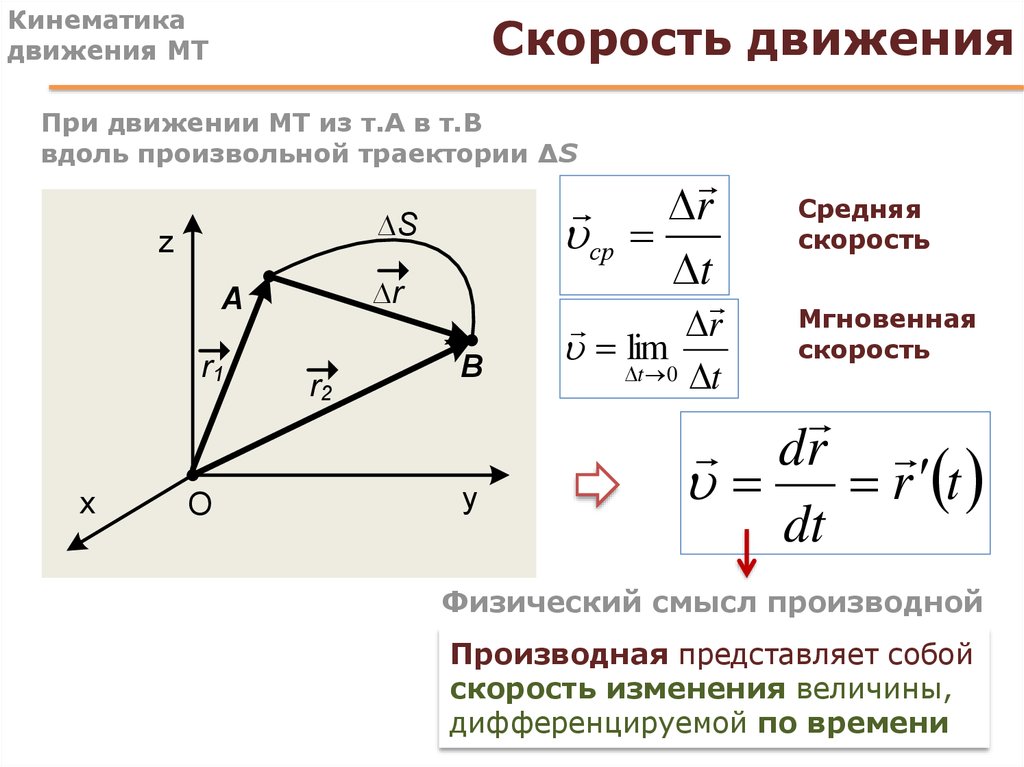 Напомню, он используется при переходе из одной системы отсчета к другой. Например, у нас есть тело, которое движется в системе отсчета, которая сама движется относительно Земли. Скорость такого тела относительно Земли равна:

Что нам это даёт? Мы теперь не привязаны к одной координатной оси. Если дана точка, которая движется из другой точки с начальной скоростью, а ускорение направлено в произвольном направлении к скорости (рис. 16), то такую задачу мы тоже можем решить.

Рис. 16. Криволинейное ускоренное движение

Применяем к точке наши уравнения в векторном виде, записываем их в проекциях на координатные оси, а в проекциях уравнения такие же, как для прямолинейного движения.

Если точка движется прямолинейно, модель тоже работает. Мы можем выбрать систему координат так, чтобы одна из осей координат была параллельна направлению движения. Тогда записанное изначально в векторном виде уравнение в проекции на одну ось даст простой одномерный случай, а в проекции на остальные оси получится уравнение 0=0, на которое можно не обращать внимания.

Решение задач. Закон сложения скоростей

Задача 1. Два автомобиля находятся на расстоянии 625 км и движутся навстречу друг другу. Первый автомобиль движется равномерно со скоростью , а второй начал двигаться со скоростью и каждый час увеличивал скорость на 10 км/ч. Через какое время и на каком расстоянии от начального положения первого автомобиля они встретятся?

Рис. 17. Условие задачи 1

Анализ условия.

В задаче описано равномерное движение одного автомобиля и равноускоренное движение второго. Это как раз те модели, которые охватывает наше уравнение:

Выберем систему координат и будем описывать эти движения математически.

Физическая часть решения задачи.

Выберем систему отсчета: рассмотрим движение автомобилей относительно земли. Так как автомобили движутся друг другу навстречу вдоль одной прямой, удобно направить одну из осей вдоль этой прямой. Начало координат для удобства поместим в начальное положение первого автомобиля, оттуда отсчитывается расстояние до места встречи, как показано на рисунке (рисунок).

Запишем закон движения для каждого автомобиля

В проекции на ось х:

В выбранной системе координат у первого автомобиля начальная координата равна нулю, проекция ускорения равна нулю, их можем убрать из уравнения, а проекция начальной скорости равна . Начальная координата второго автомобиля в этой системе координат равна 625 км, его начальная скорость равна . Минусом обозначаем, что скорость направлена против оси координат. А ускорение равно . По условию задачи понятно, что скорость по модулю возрастала, значит ускорение сонаправлено со скоростью, то есть направлено тоже против оси х, поэтому знак проекции ускорения – минус.

В момент встречи автомобили находятся в одной точке, их координаты равны, запишем это:

Получили систему уравнений, в которую осталось подставить значения и решить. С математической частью решения вы можете ознакомиться в ответвлении.

Математическая часть решения задачи 1

Запишем систему уравнений сразу с числами:

Значения у нас указаны в одной системе, расстояния в километрах, время в часах, скорость в километрах за час и т. д., поэтому мы позволили себе не переводить их в СИ. Просто получим ответ в той системе, в которой работаем.

Итак, подставим координаты автомобилей в момент встречи в третье уравнение:

Получили квадратное уравнение, решим его:

Разделим обе части уравнения на 5:

Получим два корня уравнения:

Что означает момент времени ? Это момент времени за 25 ч до начала наблюдения, но в момент движение только началось, поэтому нас этот момент не интересует. Оставляем одно решение: .

Осталось найти расстояние от начального положения первого автомобиля до места встречи, то есть координату места встречи. В момент оба автомобиля находятся в этой точке, поэтому можно найти координату любого из них. Возьмем уравнение движения первого автомобиля:

Задача решена.

Задача 2. Камень бросили вертикально вверх с начальной скоростью 12 м/с. Определите максимальную высоту, на которую поднимется камень. Ускорение свободного падения считайте равным .

Рис. 18. Условие задачи 2

Анализ условия.

В задаче описано движение камня, когда на него не действует ничего, кроме силы тяжести (о трении воздуха ничего не сказано, им пренебрегаем). В таких условиях тело движется с постоянным ускорением – ускорением свободного падения, направленным вниз. Будем применять уравнение равноускоренного движения:

Уравнение для скорости тоже может пригодиться, запишем:

Физическая часть решения задачи.

Выберем систему координат. Давайте направим ось вертикально вверх, в направлении движения камня, а начало координат поместим в точку броска. Оси x и z будут расположены в горизонтальной плоскости, проекции на них будут равны нулю, поэтому о них можно даже не упоминать. Тогда в проекции на ось уравнения примут вид:

Начальная координата тела равна нулю, мы ее сразу не записали. Начальная скорость по условию задачи равна 12 м/с и направлена вдоль оси координат. Ускорение свободного падения направлено против оси координат, поэтому его проекция в данной системе координат равна .

Максимальная высота , на которую поднимется камень – это его координата в точке, в которой он остановится и начнет падать обратно. Мы не знаем момент времени t, в который камень там окажется, чтобы обойтись первым уравнением, поэтому будем использовать второе. В точке камень остановится, то есть его скорость станет равна нулю. Перепишем уравнения и решим систему:

Решение системы вы можете проследить в ответвлении.

Математическая часть решения задачи 2

Найдем из второго уравнения время t, за которое камень долетит до верхней точки траектории:

Подставим время в первое уравнение:

Получили ответ, осталось подставить численные значения:

Задача решена.

Границы применимости моделей

Мы сегодня рассмотрели две модели движения: с постоянной скоростью и постоянным ускорением. И это всё, других моделей быть не может? Нет, это не всё, но это самые простые модели, которые мы можем использовать для приближённого описания реального движения и решения конкретных задач.

Мы сегодня говорим о кинематике и не упоминаем причины движения, но вам знаком второй закон Ньютона: ускорение пропорционально силе, действующей на тело (или в нашем случае на материальную точку). Так вот, часто мы можем считать, что силы уравновешены, тогда движение равномерно, или что силу можно считать постоянной, тогда движение равноускорено.

А что если сила равномерно изменяется? Например, когда мы едем на автомобиле и равномерно усиливаем нажатие на педаль газа. Тогда можно дополнить модель: ускорение равномерно увеличивается, можно ввести скорость изменения ускорения и вывести новые формулы. Получим еще одну модель – всего одну из множества, которые еще можно придумать. Профессиональные гонщики, которым на соревнованиях важны доли секунды, сталкиваются с описанной нами задачей, и конструкторы их автомобилей научились рассчитывать описанную модель разгона. Но мы этого делать не стали, потому что с такими задачами сталкиваемся редко.

Чаще возникают задачи, процессы в которых можно описать как равномерное движение по окружности. Это простая модель: скорость в ней не меняется по модулю, а меняется только по направлению. А окружность можно описать одним параметром: радиусом. Поэтому такое движение достаточно легко описать, вывести для него формулы, решать с их помощью множество задач.

Мы ранее уже подробно разобрали движение материальной точки по окружности, научились вычислять ускорение, которое при равномерном движении по окружности всегда направлено к центру этой окружности и не меняется по модулю.

Рис. 19. Движение тела по окружности

Иногда и этого недостаточно: возникают задачи, в которых ускорение всё время меняется и по модулю, и по направлению. Мы пытаемся найти в них закономерности, один из таких примеров – колебательное движение. В случае с гармоническими колебаниями модуль ускорения пропорционален отклонению тела от положения равновесия.

Рис. 20. Колебательное движение

Список моделей может пополняться, по мере возникновения перед человеком тех или иных задач, решение которых в рамках уже разработанных моделей окажется недостаточно точным и будет слишком сильно отличаться от реальности. У любой модели есть границы применимости. Модель – это упрощение, которое справедливо только для описания ограниченного круга задач. К примеру, основная задача механики – описание движения материальной точки в пространстве с течением времени.

А ведь само пространство, для которого справедливы законы геометрии – это идеализированная модель. И время, как мы его в этой модели представили, – тоже идеализация. Оказалось, что при скоростях, близких к скорости света, нельзя считать, что в разных системах отсчета время течет одинаково и пространственные меры не меняются. Эти эффекты стала изучать релятивистская механика, они выходят за границы применимости нашей первой модели, которую назвали классической механикой.

Модель классической механики также неприменима к объектам, размеры которых меньше одного нанометра – это больше размеров атомов, самый большой атом, атом цезия, имеет размер примерно 0,2 нм. В таких масштабах к объектам неприменимы понятия координаты, точного положения и другие. Такие малые объекты изучает квантовая механика. С ней мы познакомимся позже.

Список литературы

Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
Касьянов В.А. Физика 10. – М.: Дрофа, 2000.
М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Физика: Механика 10. – М.: Дрофа, 2004.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал Класс!ная физика
Интернет-портал Класс!ная физика
Интернет-портал Класс!ная физика
Интернет-портал Класс!ная физика

Домашнее задание

За 2 с прямолинейного равноускоренного движения тело прошло путь 20 м, увеличив свою скорость в 3 раза. Определите конечную скорость тела.
Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. За час автомобилист проезжает на 55 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 6 минут позже автомобилиста. Ответ дайте в км/ч.

Что такое путь в физике и как его обозначают? Формулы и пример задачи

Что такое путь в физике

Кинематика является одним из важных разделов механики, который рассматривает законы перемещения тел в пространстве (причины возникновения движения изучает динамика). В данной статье рассмотрим одну из основных величин кинематики, ответим на вопрос: «Что такое путь в физике?»

Понятие о пути

Что такое путь в физике? Это величина, равная длине отрезка в пространстве, который преодолело в ходе своего движения изучаемое тело. Чтобы вычислить путь, необходимо знать не только начальное и конечное положения тела, но и траекторию его перемещения. На вопрос о том, что такое путь в физике, можно ответить иначе. Под этой величиной понимают длину траектории, то есть воображаемой линии, по которой тело перемещалось.

Для обозначения пути используют разные символы.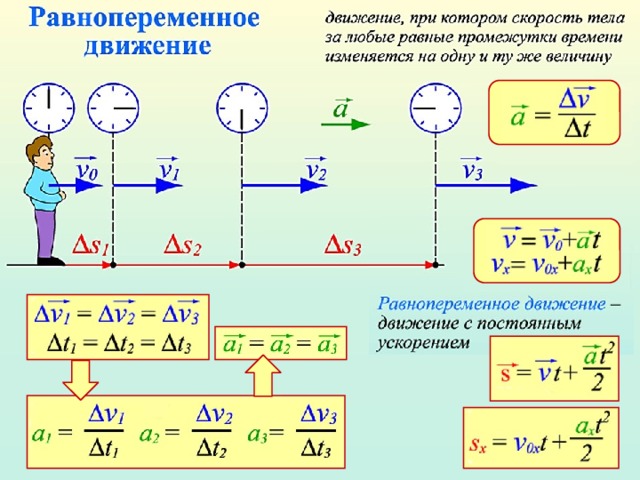 Так, если речь идет об одномерном перемещении, то могут использовать символ Δx, где Δ означает изменение координаты x. Кроме этого символа, часто для обозначения рассматриваемой величины пользуются буквами s, l и h, причем две последние означают длину и высоту соответственно. Таким образом, в кинематике чаще всего для обозначения пути можно встретить букву s.

Если известно, что тело перемещается по прямой в трехмерном пространстве, а также известны координаты его положения начального (x0; y0; z0) и конечного (x1; y1; z1), тогда путь можно определить по формуле:

Формулы кинематики

Рассмотрев, как обозначается путь в физике и что собой эта величина представляет, приведем пару формул кинематики, которые применяются для вычисления изучаемой характеристики движения. Это следующие формулы:

Здесь первое выражение соответствует ситуации, когда тело равномерно прямолинейно перемещается со скоростью v в течение времени t. Второе выражение справедливо для равноускоренного перемещения, где символами v0 и a обозначены начальная скорость и ускорение соответственно. Знак «плюс» следует использовать, если тело ускоряется, а знак «минус» — если оно замедляет свою скорость.

Пример задачи

Разобрав, что такое путь в физике, решим следующую задачу. Катер со скоростью 13 км/ч движется против течения реки в течение 1,5 часов из одного пункта в другой. Какой путь проходит катер, если скорость течения реки составляет 3 км/ч?

Это классическая задача на применение формулы для равномерного движения тела. Сложность задачи состоит только в том, чтобы определить реальную скорость перемещения катера. Поскольку его движение происходит против течения, то она будет равна разности: 13 — 3 = 10 км/ч. Теперь остается подставить известные величины в формулу для s и получить ответ:

В задачах на вычисление пути необходимо следить за размерностями используемых значений скорости, времени и ускорения, чтобы не допустить ошибки.

Что такое путь в физике.

Fb. ru

29.10.2017 9:13:11

2017-10-29 09:13:11

Источники:

Https://fb. ru/article/465286/chto-takoe-put-v-fizike-i-kak-ego-oboznachayut-formulyi-i-primer-zadachi

Что такое пройденный путь в физике? Бесконечные ответы на вопросы » /> » /> .keyword { color: red; }

Что такое путь в физике

Пройденный путь — это скалярная величина, которая обозначает расстояние, пройденное телом, в процессе перемещения. … Перемещение же представляет собой направленный отрезок, соединяющий начальную и конечную точки. А если тело в процессе движения вернулось в исходную точку, то его перемещение будет равно нулю.

Как определить пройденный путь в физике?

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t.

Как отмечается пройденный путь?

Путь Первой характеристикой движения, введенной нами ранее, был пройденный путь. Напомним, что обозначается он буквой S (иногда встречается обозначение L) и измеряется в СИ в метрах. Пройденный путь – это скалярная величина, т.

Как называется пройденный путь?

Траектория линия, вдоль которой движется материальная точка. Перемещение вектор, проведенный из начальной в конечную точку движения.

Что такое путь в физике?

Путь (или траектория) материальной точки или тела — физическая абстракция; линия перемещения в пространстве. в топологическое пространство.

Что такое пройденный путь или путь?

Как определить путь пройденный телом при равномерном движении?

Таким образом, путь, пройденный телом при неравномерном движении, равен произведению средней скорости на время движения, т. е. s = vсрt. Время, необходимое для прохождения какого-нибудь пути при неравномерном движении, равно частному от деления этого пути на среднюю скорость.

Какой буквой обычно обозначают пройденный путь?

Для обозначения пути обычно используется строчная (маленькая) буква [эль], т. е. l, реже — заглавная (большая) буква [эль], т. е.

Как найти путь пройденный материальной точкой?

Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t). где ˉr – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.

Какой буквой означает путь?

Буквой s (лат. spatium) иногда обозначают расстояние (путь), положение или смещение. Буквой S обозначают энтропию. Буквой S обозначают действие.

Что такое путь пройденный телом?

Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.

Что делает одометр?

Ὁδός «дорога» + μέτρον «мера»), в просторечии счётчик — прибор для измерения количества оборотов колеса. При помощи него может быть измерен пройденный транспортным средством путь. Первый одометр был изобретён Героном Александрийским.

В чем измеряется путь?

Путь — это длина линии, по которой двигалось тело, то есть это число. Единица измерения расстояний в системе Си — [метр] = [м].

Как найти путь в физике с ускорением?

Формула выглядит следующим образом:

s = v 0 t + a t 2 2 , где а — это ускорение. … Зависимость ускорения от времени. … Зависимость скорости от времени. … Правило определения пути по графику v(t): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости. Зависимость пути от времени.

Что такое путь обозначение единицы измерения?

Он является энергетической физической величиной и связан обычно с выполняемой работой или с предстоящими затратами энергии. … Обозначение пути – s. Единицей измерения пути является метр пути; обозначение – мп.

Что делает одометр.

Infinity-discounts. ru

06.08.2018 20:10:24

2018-08-06 20:10:24

Источники:

Https://infinity-discounts. ru/chto-takoe-proydennyy-put-v-fizike/

Что такое путь в физике 7 класс? Бесконечные ответы на вопросы » /> » /> .keyword { color: red; }

Что такое путь в физике

Путь – это физическая величина, равная длине траектории, по которой двигалось тело, в течение данного промежутка времени.

Что такое путь 7 класс физика?

Траектория линия, вдоль которой движется материальная точка. В СИ единица измерения модуля вектора перемещения метр: м. … Путь длина траектории.

Что такое траектория 7 класс?

Предмет, относительно которого оценивается движение других тел, называется телом отсчёта. Перемещение одного тела относительно других тел называют движением. … Линию, которую описывает тело при своём движении, называют траекторией движения этого тела.

Как найти пройденный путь в физике?

Как найти путь в физике с ускорением?

Формула выглядит следующим образом:

Что такое путь в физике?

Что такое механическое движение 7 класс?

Механическим движением тела называют положения тела в пространстве относительно других тел с течением. … Линия, которую описывает тело в следствии своего движения – это. – длина траектории, по которой двигалось тело в заданный промежуток времени. Соотнесите типы траектории с видами движения.

Как называется скорость?

Vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени. …

Что такое система отсчета 7 класс?

Систе́ма отсчёта — это совокупность неподвижных относительно друг друга тел (тело отсчёта), по отношению к которым рассматривается движение (в связанной с ними системе координат), и отсчитывающих время часов (системы отсчёта времени), по отношению к которой рассматривается движение каких-либо тел.

Какие есть виды движения в физике?

Поступательное движение Плоскопараллельное движение (Параллельный перенос) Сферическое движение (Вращательное движение Круговое движение Прецессия Нутация)

Что такое S в физике 7 класс?

Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.

Как найти среднее время в физике?

Для оценки численной величины средней скорости на практике используют следующее определение ⟨v⟩: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение: ⟨v⟩=st(7).

Как решать задачи на расстояние скорость и время?

Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
…
В таких задачах важно понимать:

если мы умножаем скорость на время, то получаем расстояние; если расстояние делим на время, то получаем скорость; если расстояние делим на скорость, то получаем время ;

Как найти путь по графику скорости?

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости. Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени.

Если расстояние делим на скорость, то получаем время ;.

Infinity-discounts. ru

13.10.2020 16:39:04

2020-10-13 16:39:04

Источники:

Https://infinity-discounts. ru/chto-takoe-put-v-fizike-7-klass/

Решение задач по кинематике | Студенческая жизнь

In естественные наукиТэги задачи, кинематика, примеры, решение, теория, физика, формулы25/06/2015Просмотров: 12.5K

В области раздела физики, который изучает движение материальных точек по криволинейной траектории, в основном изучаются процессы, называемые равноускоренными. Решение задач по кинематике включает в себя, прежде всего, методику преобразования формул в единую конечную. Если это невозможно сделать, действия производятся поэтапно, до тех пор, когда формулу в пределах одной области расчета невозможно упростить. Рассмотрим на примерах.

Пример задачи, связанной с изменением параметров физического тела

Дано: есть маховик, который вращается, частота составляет 10 оборотов в секунду. Прилагают усилия для замедления скорости вращения. В результате такого действия маховик стал вращаться с частотой 6 оборотов в секунду. Требуется найти время, в течение которого прилагалось усилие, если известно, что маховик во время торможения сделал 50 оборотов.

Решение

Задача состоит в том, чтобы определить величину углового ускорения, которое образовалось во время торможения. Таким образом, решение на первом этапе сводится к пониманию и упрощению основных формул. Сначала запишем данные, которые известны, приведя их в систему СИ.

начальная частота вращения n0 = 10 1/c;
конечная частота n = 6 1/c;
число оборотов N = 50.

Как видим, все параметры уже стандартизированы и не требуют преобразования.

Угловое ускорение связано с начальной и конечной угловой скоростью. 2)/N

Здесь решение задач по кинематике сводится к анализу двух процессов. Один — снижение скорости вращения, грубо говоря, равноускоренный процесс. Второй — нахождение времени — можно рассматривать с позиции прохождения вращения с постоянной скоростью. То есть, анализировать средние показатели величин, как это делалось бы при прямолинейном движении с постоянной скоростью.

Искомое время удобно определить с помощью простой формулы, определяющей угол поворота:

µ=w/t

средняя угловая скорость вращения в пределах диапазона измерения, деленная на вычисляемое время. Так как торможение, согласно условиям задачи, производилось равномерно, можно вычислить среднюю угловую скорость простым расчетом:

w=(w+w0)/2

Тогда угол поворота можно записать следующим образом:

µ=(w+w0)*t/2

Подставив в выражение базовые формулы, приведенные выше, получим готовое выражение, основанное на известных значениях:

µ=(w+w0)*t/2 = П*(n0+n)/t

t= µ/ (П*(n0+n)) = 2*N/( n0+n)=6. 2, причем коэффициент А равен 10 м, В — 10 метров в секунду, ускорение С составляет -0,5 метров на секунду в квадрате. Требуется найти скорость в момент времени, равный 5 с с момента начала отсчета. А также все ускорения — полное, тангенциальное и нормальное.

Решение задачи

Все рассмотрение процесса движения рассматривается, исходя из простых базовых понятий и правил. Решение задач по кинематике такого типа сводится к элементарным преобразованиям формул и вычислениям.

По известному уравнению движения, которое приводится в условии задачи, можно найти скорость. Она будет определяться как первая производная от координаты по времени. Это простое базовое правило, применимое не только к подобным задачам. Запишем формулу, полученную простым математическим преобразованием:

v=de/dt = B+2*C

Все единицы измерения параметров находятся в системе СИ, поэтому можно просто подставить известные значения в формулу и получить готовый ответ:

v=de/dt = B+2*C = 10+2*(-0. 2

Оценка правильности ответа может быть произведена методом соответствия величин. Все найденные значения скорости, а также ускорения — лежат в области начальных данных, соответствуют порядку величин, следовательно — достоверны.

Краткое резюме

Как видно из приведенных примеров, решение задач по кинематике всегда использует метод аналитического преобразования формул. Для упрощения, было произведено поэтапное вычисление. Так процесс выглядит нагляднее и проще для понимания. Но нужно понимать, что все формулы для нахождения нужных величин могут быть записаны в полностью самостоятельном символьном виде и применяться для подстановки в другие выражения.

Решение задач по кинематике

Решение задач по кинематике равнопеременного движения традиционно вызывает у учащихся затруднения, что связано в основном с тем, что здесь впервые встает проблема формализации физической задачи, т.е. перевода ее с языка “текстовой задачи” по физике на язык математики. До этого учащимся приходилось в основном решать задачи, если можно так выразиться, “по формулам”, а теперь необходимо осмыслить задачу не только с точки зрения физики, но и суметь записать ее в терминах уравнений кинематики и затем из этих уравнений, опираясь на условие задачи, получить нужные “формулы”. В настоящей работе представлен ход обзорного урока по этой теме.

Чтобы научиться решать задачи по кинематике нужно прежде всего уметь правильно выбрать систему отсчета (СО), которая включает в себя:

Точку отсчета (выбираем произвольно из соображений удобства)

Систему координат, связанную с точкой отсчета

Начало отсчета времени (счетчик времени, выбираем из соображений удобства).

Вообще важно, чтобы учащиеся отдавали себе отчет, что для решения задач по кинематике необходимо:

Выбрать СО подходящим образом, чтобы в этой СО уравнения кинематики принимали наиболее простой вид. Обязательно обратить внимание на выбор начала отсчета времени.

Сделать чертеж, иллюстрирующий описанное в условии задачи явление: начертить систему координат, траекторию движения, вектора скоростей и ускорений.

Записать основные уравнения кинематики равнопеременного движения в выбранной СО для произвольного момента времени:

где x_0,y₀ – начальное положение тела, v_0x,v_0y – проекции начальной скорости тела, a_x,a_y – проекции ускорений.

4. Записать уравнения (1)-(4) для характерных моментов времени, из которых находить требуемые в условии задачи величины, т.е. получить рабочие формулы.

Важно, чтобы учащиеся понимали, что можно получить решение любой задачи кинематики равнопеременного движения, если записаны основные уравнения (1)-(4). Важно также, чтобы они осознавали, что вид этих уравнений меняется в зависимости от выбора СО. В связи с этим, решим несколько задач, иллюстрирующих сказанное.

Задача 1. Теннисист при подаче запускает мяч с высоты h над землей. На каком расстоянии от подающего мяч ударится о землю, если начальная скорость равна v₀ и направлена вверх под углом к горизонту?

Решение: а). Точку отсчета (начало координат) поместим в точку на поверхности земли, где стоял теннисист в момент удара. Время начнем отсчитывать от момента удара по мячу. На рис.1 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.

Рис. 1

В выбранной СО начальные условия имеют вид: x₀= 0, y₀ = h, a_x = 0, a_x= – g,

и кинематические уравнения (1)-(4) запишутся в виде:

Требуемое в условии задачи расстояние D (дальность полета) найдем из условия: D = x(t_n), где время полета t_n определяется из соотношения y(t_n) = 0, т. е.можем записать уравнение:

При решении этого квадратного уравнения удобнее записывать его в приведенном виде x² + 2qx + + q = 0 и находить корни по формуле

Опыт показывает, что учащиеся зачастую не знают этого и находят корни такого уравнения по общей формуле, что осложняет выкладки. Перепишем уравнение в виде

тогда его решение

Т.к. t >= 0, то физический смысл имеет корень

Теперь из условия D =x(t_n) получим рабочую формулу

б). Решим эту задачу, выбрав за точку отсчета (начало координат) точку, где находился мяч в момент удара. Время по-прежнему отсчитываем от момента удара по мячу. На рис.2 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.

Рис. 2

В выбранной СО начальные условия имеют вид: x₀= 0, y₀ = 0, a_x = 0, a_x= – g,

Кинематические уравнения (1)-(4) теперь запишутся так

и время полета t_n мяча до земли найдется из условия: y(t_n) = – h. Дальше решение задачи повторяет способ а).

В рассмотренной задаче было безразлично, где поместить начало координат, однако в задачах, где высота, на которой происходит событие, не задана, начало координат лучше всего помещать именно в эту точку на неизвестной высоте. Направление осей выбирается из соображений удобства.

Задача 2. Тело, свободно падающее с некоторой высоты, последние h м пути прошло за время с. Какое время и с какой высоты падало тело?

Решение: Начало координат поместим в точку на неизвестной высоте H, ось Y направим вертикально вниз. Время начнем отсчитывать с момента начала падения тела. На рис.3 изображена система координат и ускорение свободного падения тела.

Рис. 3

В выбранной СО v_0y= 0, y₀ = 0, a_y = g и уравнения кинематики (1)-(4) сведутся к двум

Т.к. в условии задачи речь идет о свободном падении тела, то в любой момент времени его координата будет равна пройденному пути. Выразим из уравнения для координаты отрезки пути H и h. Из рис.3 очевидно, что

где t_n – время падения тела на землю. Получили два уравнения с двумя неизвестными H и t_n. Уравнение (6) после преобразований принимает вид

Откуда

Подставляя найденное t_n в (5), получим искомое выражение для высоты

Таким образом, требуемые в задаче величины определены.

Следует отметить, что если на размещение начала отсчета и направление осей системы координат учащиеся еще обращают внимание, то выбор начала отсчета времени обычно ускользает из их поля зрения. Это особенно заметно при решении задач, где в движении участвует несколько тел.

Если тела начинают свое движение одновременно, то отсчет времени начинается с момента начала движения тел, а кинематические уравнения пишутся для каждого из тел.

Задача 3. Два тела, расстояние между которыми l, начинают одновременно двигаться навстречу друг другу: первое – равномерно со скоростью v, а второе – из состояния покоя равноускоренно с ускорением a. Через какое время тела встретятся?

Решение: Поместим начало координат в точку, где находилось первое тело в начальный момент, ось OX направим по движению первого тела. Отсчет времени начнем с момента начала движения тел. На рис.4 изображена ось ОХ, вектора скоростей и ускорений обоих тел.

Рис. 4

В этой СО x₁₀ = 0, x₂₀ = l. Уравнение движения для первого тела

Уравнение движения для второго тела

В момент встречи x₁(t) = x₂(t), t – время в пути до встречи, т.е.

откуда

Задача 4. Лифт поднимается с ускорением a. В тот момент, когда его скорость стала равна v, с потолка кабины лифта начал падать болт. Высота кабины лифта h. Вычислить время падения болта.

Решение: Свяжем начало неподвижной системы координат с точкой, в которой находится пол лифта в момент, когда болт начинает падать. Время начнем отсчитывать от момента начала падения болта. На рис.5 изображена система координат (ось ОY), вектора скоростей и ускорений.

Рис. 5

Пусть y_kv_k– координата и проекция скорости кабины лифта, y_б v_б- координата и проекция скорости болта. Для кабины лифта основные уравнения (1) – (4) запишутся в виде

а для болта примут вид

Когда болт упадет на пол, будет выполняться: y_k(t) = y_б(t), где t – время падения болта:

Наибольшие затруднения вызывает у учащихся выбор начала отсчета времени, и особенно запись уравнений кинематики в случае, когда тела, участвующие в движении, начинают двигаться неодновременно.

Задача 5. Тело с начальной скоростью v₀и ускорением a₁начинает двигаться из некоторой точки по прямолинейной траектории. Через время из той же точки вслед за первым телом начинает двигаться другое тело без начальной скорости с ускорением a₂. Через какое время после выхода первого тела второе тело его догонит?

Решение: Начало координат свяжем с точкой, из которой начинают двигаться тела. Ось ОХ направим по движению тел. Время начнем отсчитывать от начала движения первого тела. На рис.6 изображена система координат, вектора скоростей и ускорение.

Рис.6

В этой СО уравнения кинематики для первого тела имеют вид

а для второго тела, с учетом того, что оно начало свое движение на секунд позже первого, запишутся в виде

На запись этих уравнений нужно особенно обратить внимание учащихся. В момент, когда второе тело догонит первое, будет выполняться x₁(t) = x₂(t), т.е.

Получаем квадратное уравнение для определения времени t

С учетом того, что t >= 0 находим

Задача 6. Два тела брошены вертикально вверх с поверхности Земли из одной точки вслед друг за другом с интервалом времени , с одинаковыми начальными скоростями v₀. Определить, через какое время тела встретятся.

Решение: Начало отсчета поместим в точку бросания. Ось OY направим вертикально вверх. Отсчет времени начнем с момента бросания первого тела. На рис.7 изображена ось OY и вектора начальной скорости и ускорения свободного падения.

Рис. 7

В выбранной СО y₁₀= y₂₀= 0, v_01y = v_02y= v₀, a_1y = a_2y= -g. Уравнения кинематики для первого тела имеют вид

Основные уравнения кинематики для второго тела с учетом того, что оно начала свое движение на секунд позже первого, запишутся в виде

Тела “встретятся”, когда y₁ (t)_{= y₂(t)}, т.е. получаем уравнение для нахождения искомого времени “встречи”

откуда

Что это – путь в физике и как его обозначают? Формулы и пример задачи – Справочник

Путь это физике

Понятие о пути

Формулы кинематики

Пример задачи

Что это — путь в физике и как его обозначают.

Autogear. ru

24.03.2019 10:26:11

2019-03-24 10:26:11

Источники:

Https://autogear. ru/article/465/286/chto-takoe-put-v-fizike-i-kak-ego-oboznachayut-formulyi-i-primer-zadachi/

Формула пути » /> » /> .keyword { color: red; }

Путь это физике

Путь тела, движущегося равноускорено, прямо пропорционален ускорению тела, скорости тела и времени движения.

Здесь – пройденный путь, – ускорение тела, – начальная скорость тела, — время ускоренного движения.

Единица измерения пути – М (метр).

Путь – скалярная величина. Путь – это мера того, какое расстояние преодолело тело в ходе движения. – это скорость, с которой тело двигалось к моменту начала ускорения. У этой формулы есть 2 частных случая:

1) Движение равномерное (без ускорения)

Это самый распространённый в задачах, простейший случай. Когда про ускорение ничего не сказано, то под формулой пути имеется в виду именно эта формула.

2) Движение, начатое с неподвижного состояния (без начальной скорости)

Путь не нужно путать с перемещением – мерой расстояния между конечной и начальной точкой движения.

Примеры решения задач по теме «Путь тела»

Задание	Найти путь, который прошло тело, движущееся с ускорением 1 м/с в течение 16 с. Начальная скорость была 30 м/с.
Решение	Все исходные данные нам известны. Подставим их в формулу:

(м)

Задание

В первый промежуток времени тело двигалось равномерно со скоростью vв течение времени.

Затем на него подействовало ускорение, действующее в направлении, обратном направлению движения. Найти скорость тела к моменту повторного прохождения точки начала движения.

Решение

Пусть – скорость, которую нужно найти. Положим точку начала движения началом координат. Рассмотрим характер движения. В первый период времени ( ) тело двигалось равномерно, преодолев за это время расстояние :

Затем тело замедлялось, пока его скорость не обнулилась ( – время замедления):

Пусть – расстояние, пройденное в ходе замедления:

Затем тело прошло расстояние в обратную сторону без начальной скорости с ускорением, за время :

(м)

Найти скорость тела к моменту повторного прохождения точки начала движения.

Ru. solverbook. com

30.12.2019 21:23:24

2019-12-30 21:23:24

Источники:

Http://ru. solverbook. com/spravochnik/formuly-po-fizike/formula-puti/

Что такое пройденный путь в физике? Бесконечные ответы на вопросы » /> » /> . keyword { color: red; }

Путь это физике

Как определить пройденный путь в физике?

Как отмечается пройденный путь?

Как называется пройденный путь?

Что такое путь в физике?

Что такое пройденный путь или путь?

Как определить путь пройденный телом при равномерном движении?

Какой буквой обычно обозначают пройденный путь?

Как найти путь пройденный материальной точкой?

Какой буквой означает путь?

Что такое путь пройденный телом?

Что делает одометр?

В чем измеряется путь?

Как найти путь в физике с ускорением?

Формула выглядит следующим образом:

Что такое путь обозначение единицы измерения?

Что такое пройденный путь или путь.

Infinity-discounts. ru

27.03.2018 17:52:04

2018-03-27 17:52:04

Источники:

Https://infinity-discounts. ru/chto-takoe-proydennyy-put-v-fizike/

3.4 Движение с постоянным ускорением

Цели обучения

К концу этого раздела вы сможете:

Определить, какие уравнения движения следует использовать для решения неизвестных.
Используйте соответствующие уравнения движения для решения задачи преследования двух тел.

Можно догадаться, что чем больше ускорение, скажем, автомобиля, удаляющегося от знака остановки, тем больше перемещение автомобиля за заданное время. Но мы не разработали конкретное уравнение, связывающее ускорение и перемещение. В этом разделе мы рассмотрим некоторые удобные уравнения для кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем один объект в движении, называемое движением одного тела. Затем мы исследуем движение двух объектов, называемых задачи преследования двух тел .

Обозначение

Сначала давайте сделаем некоторые упрощения в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно [латекс] \text{Δ}t={t}_{\text{f}}-{t}_{0} [/latex], принимая [латекс] {t}_{0}= 0 [/latex] означает, что [latex] \text{Δ}t={t}_{\text{f}} [/latex], последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем нижний индекс 0 для обозначения начальных значений положения и скорости. То есть [латекс] {x}_{0} [/латекс] — это начальная позиция , а [latex] {v}_{0} [/latex] — начальная скорость . Мы не помещаем нижние индексы в окончательные значения. То есть t — конечное время , x — конечное положение , а v — конечная скорость . Это дает более простое выражение для прошедшего времени: [латекс] \текст{Δ}t=t[/латекс]. Это также упрощает выражение для смещения x , которое теперь равно [латекс] \текст{Δ}х=х-{х}_{0} [/латекс]. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно [латекс] \текст{Δ}v=v-{v}_{0} [/латекс]. Подводя итог, используя упрощенную запись, с начальным временем, принятым равным нулю,

[латекс] \begin{array}{c}\text{Δ}t=t\hfill \\ \text{Δ}x=x-{x}_{0}\hfill \\ \text{Δ} v=v-{v}_{0},\hfill \end{array} [/latex]

, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса обозначает конечное значение в любом рассматриваемом движении.

Теперь мы делаем важное предположение, что ускорение является постоянным . Это предположение позволяет нам избежать использования исчисления для нахождения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, т. е.

[латекс] \overset{\text{–}}{a}=a=\text{константа}\текст{. } [/latex]

Таким образом, мы можем использовать символ a для ускорения вообще раз. Предположение, что ускорение является постоянным, серьезно не ограничивает ситуации, которые мы можем изучать, и не снижает точность нашего лечения. Во-первых, ускорение является постоянным в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, при котором ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет свое постоянное ускорение.

Смещение и положение по скорости

Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:

[латекс] \overset{\text{–}}{v}=\frac{\text{Δ }x}{\text{Δ}t}. [/latex]

Подстановка упрощенных обозначений для [латекс] \text{Δ}x [/latex] и [латекс] \text{Δ}t [/latex] дает

[латекс] \overset{\text{ –}}{v}=\frac{x-{x}_{0}}{t}. [/latex]

Решение для x дает нам

[latex] x={x}_{0}+\overset{\text{–}}{v}t, [/latex]

, где средняя скорость равна

[латекс] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2}. [/latex]

Уравнение [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] отражает тот факт, что при ускорении постоянна, v — это просто среднее арифметическое начальной и конечной скоростей. (Рисунок) иллюстрирует эту концепцию графически. В части (а) рисунка ускорение постоянно, а скорость увеличивается с постоянной скоростью. Средняя скорость на часовом интервале от 40 км/ч до 80 км/ч составляет 60 км/ч:

[латекс] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2}=\frac{40\,\text{км/ч}+80 \,\text{км/ч}}{2}=60\,\text{км/ч}\text{.} [/latex]

В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км/ч, чем к 40 км/ч. Таким образом, средняя скорость больше, чем в части (а).

Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости [латекс] {v}_{0}\,\text{and}\,v [/latex]. Средняя скорость равна [латекс] \frac{1}{2}({v}_{0}+v)=60\,\text{км}\text{/}\text{ч} [/latex]. (b) График зависимости скорости от времени с ускорением, изменяющимся со временем. Средняя скорость не определяется как [latex] \frac{1}{2}({v}_{0}+v) [/latex], но превышает 60 км/ч.

Нахождение конечной скорости по ускорению и времени

Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:

[латекс] a=\frac{\text{Δ}v}{\text{Δ}t} . [/latex]

Замена [латекс] \text{Δ}v [/latex] и [латекс] \text{Δ}t [/latex] упрощенными обозначениями дает нам

[латекс] a=\frac{ v-{v}_{0}}{t}\enspace(\text{константа}\,a). [/latex]

Решение для v дает

[latex] v={v}_{0}+at\enspace(\text{constant}\,a). [/латекс] 9{2},t=40\,\text{s} [/latex].

Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость [латекс] {v}_{\text{f}} [/латекс].

Наконец, мы определяем, какое уравнение использовать. Для этого выясняем, какое кинематическое уравнение дает неизвестное через известные. Мы рассчитываем конечную скорость, используя (Рисунок), [латекс] v={v}_{0}+at [/латекс].

Решение

Показать ответ

Рисунок 3.19 Самолет приземляется с начальной скоростью 70,0 м/с и замедляется до конечной скорости 10,0 м/с, прежде чем взять курс на аэродром. Обратите внимание, что ускорение отрицательно, потому что его направление противоположно его скорости, которая положительна.

Значимость

Конечная скорость намного меньше начальной скорости, как и требуется при замедлении, но все еще положительна (см. рисунок). С реактивными двигателями реверсивная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение его назад, на что указывает отрицательная конечная скорость, но здесь это не так.

Уравнение [латекс] v={v}_{0}+at [/латекс] не только полезно при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что

Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀ ), как и ожидалось (другими словами, скорость постоянна)
Если a отрицательно, то конечная скорость меньше начальной скорости

Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.

Решение конечного положения с постоянным ускорением

Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволит нам вычислить конечное положение объекта, испытывающего постоянное ускорение. Начнем с

[латекс] v={v}_{0}+at. [/latex]

Добавление [latex] {v}_{0} [/latex] к каждой стороне этого уравнения и деление на 2 дает

[latex] \frac{{v}_{0}+v} {2}={v}_{0}+\frac{1}{2}at. [/latex]

Так как [latex] \frac{{v}_{0}+v}{2}=\overset{\text{–}}{v} [/latex] для постоянного ускорения, мы имеем 9{2}\enspace(\text{константа}\,а). [/latex]

Пример

Расчет смещения ускоряющегося объекта

Драгстеры могут развивать среднее ускорение 26,0 м/с ² . Предположим, драгстер разгоняется с такой скоростью за 5,56 с (рисунок). Какое расстояние он проходит за это время?

Рисунок 3.20 Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемым выгоранием. (Источник: подполковник Уильям Турмонд. Фото предоставлено армией США.) 9{2} [/latex], когда мы идентифицируем [латекс] {v}_{0} [/латекс], [латекс] а [/латекс] и t из условия задачи.

Рисунок 3.21 Эскиз разгоняющегося драгстера.

Решение

Показать ответ

Значение

Если мы преобразуем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартной дистанции для дрэг-рейсинга. Итак, наш ответ разумен. Это впечатляющее смещение, которое можно преодолеть всего за 5,56 с, но первоклассные драгстеры могут проехать четверть мили за еще меньшее время. Если бы драгстеру была задана начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении используются те же ускорение и время, то пройденное расстояние будет намного больше. 9{2}\,\text{становится}\,x={x}_{0}+{v}_{0}t. [/латекс]

Решение конечной скорости по расстоянию и ускорению

Четвертое полезное уравнение можно получить из другой алгебраической обработки предыдущих уравнений. Если мы решим [латекс] v={v}_{0}+at [/латекс] для t , мы получим

[латекс] t=\frac{v-{v}_{0}}{a }. [/latex]

Подставив это и [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] в [latex] x ={x}_{0}+\overset{\text{–}}{v}t [/latex], получаем 9{2}+2a(x-{x}_{0}) [/latex] идеально подходит для этой задачи, поскольку связывает скорость, ускорение и перемещение, а информация о времени не требуется.

Решение

Показать ответ

Значение

Скорость 145 м/с составляет около 522 км/ч, или около 324 миль/ч, но даже эта головокружительная скорость не соответствует рекорду на четверть мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение. 9{2}+2a(x-{x}_{0}) [/latex] может дать дополнительные сведения об общих соотношениях между физическими величинами:

Конечная скорость зависит от того, насколько велико ускорение и расстояние, на котором это действует.
При фиксированном ускорении автомобиль, который едет в два раза быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо больше. (Вот почему мы установили зоны пониженной скорости возле школ.)

Составление уравнений

В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих более сложных алгебраических операций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию. 9{2}+2a(x-{x}_{0}) [/latex]

Прежде чем перейти к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя (рисунок), мы имеем

[латекс] a=\frac{v-{v}_{0}}{t}. [/latex]

Отсюда мы видим, что за конечное время, если разница между начальной и конечной скоростями мала, ускорение мало, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Наоборот, в пределе [латекс] t\to 0 [/латекс] при конечной разности между начальной и конечной скоростями ускорение становится бесконечным. 9{2}}{2(х-{х}_{0})}. [/latex]

Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе перемещение приближается к нулю. Ускорение стремится к нулю в пределе, когда разность начальной и конечной скоростей стремится к нулю при конечном перемещении.

Пример

Как далеко едет машина?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м/с ² , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м/с ² . Найдите расстояние, необходимое для остановки автомобиля, движущегося со скоростью 30,0 м/с (около 110 км/ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите перемещение от точки, в которой водитель видит красный сигнал светофора, учитывая время его реакции 0,500 с, чтобы нажать на педаль тормоза.

Стратегия

Сначала нам нужно нарисовать эскиз (Рисунок). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.

Рисунок 3.22 Пример эскиза для визуализации замедления и тормозного пути автомобиля.

Решение

Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м/с, v = 0 и a = −7,00 м/с ² ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Мы принимаем x ₀ за ноль. Ищем смещение [латекс] \текст{Δ}х[/латекс], или 9{2}+2а(х-{х}_{0}). [/латекс]
Это уравнение лучше, потому что оно включает только одно неизвестное, x . Мы знаем значения всех остальных переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которого мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
В-третьих, мы перестраиваем уравнение для решения x :
. {2}}{2a} [/latex] 9{2})}. [/латекс]
Таким образом,
[латекс] x=64,3\,\text{м на сухом бетоне}\text{.} [/латекс]
Эту часть можно решить точно так же, как (а). Единственное отличие состоит в том, что ускорение равно −5,00 м/с ² . Результат
[латекс] {x}_{\text{мокрый}}=90,0\,\text{м на мокром бетоне.} [/латекс]
Показать ответ

Рисунок 3.23 Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны тормозные пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося изначально со скоростью 30,0 м/с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит красный свет, при условии времени реакции 0,500 с.

Значение

Перемещения, найденные в этом примере, кажутся подходящими для остановки быстро движущегося автомобиля. На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.

Пример

Расчет времени

Предположим, что автомобиль въезжает в полосу движения на съезде длиной 200 м. Если его начальная скорость равна 10,0 м/с, а ускорение составляет 2,00 м/с ² , за какое время автомобиль проедет 200 м вверх по пандусу? (Эта информация может пригодиться инженеру-дорожнику.)

Стратегия

Сначала рисуем эскиз (рисунок). Нас просят решить для времени t . Как и раньше, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t .)

Рисунок 3.24 Эскиз автомобиля, разгоняющегося на съезде автострады.

Решение

Показать ответ

Значение

Всякий раз, когда уравнение содержит неизвестное в квадрате, есть два решения. В некоторых задачах оба решения имеют смысл; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичного съезда с автострады.

Проверьте свои знания

Пилотируемая ракета разгоняется со скоростью 20 м/с ² во время запуска. За какое время ракета достигнет скорости 400 м/с?

Показать решение

Пример

Разгон космического корабля

Космический корабль покинул орбиту Земли и направляется к Луне. Он разгоняется со скоростью 20 м/с ² за 2 мин и преодолевает расстояние 1000 км. Каковы начальная и конечная скорости космического корабля?

Стратегия

Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не даст ответа. Мы должны использовать одно кинематическое уравнение, чтобы найти одну из скоростей, и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.

Решение

Показать ответ

Значимость

Существует шесть переменных перемещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальными условиями данной задачи может быть множество комбинаций этих переменных. Из-за этого разнообразия решения могут быть не такими простыми, как простые подстановки в одно из уравнений. Этот пример показывает, что для решения кинематики может потребоваться решение двух одновременных кинематических уравнений.

Познакомившись с основами кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также заметили общий подход к решению задач, который дает как правильные ответы, так и понимание физических взаимосвязей. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .

Задачи преследования двух тел

До этого момента мы рассматривали примеры движения одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задача преследования двух тел , движения объектов связаны — это означает, что искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти задачи, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на (рис.).

Рисунок 3. 25 Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.

Время и расстояние, необходимые для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния между автомобилем 1 и автомобилем 2, а также от скоростей обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны решить, чтобы найти эти неизвестные.

Рассмотрим следующий пример.

Пример

Гепард ловит газель

Гепард ждет, прячась за кустом. Гепард замечает газель, пробегающую мимо со скоростью 10 м/с. В момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м/с ² поймать газель. а) Сколько времени потребуется гепарду, чтобы поймать газель? б) Каково водоизмещение газели и гепарда?

Стратегия

Для решения этой задачи мы используем систему уравнений для постоянного ускорения. Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, то станет ясно, что общим параметром для каждого животного является их позиция 9.0019 x позже t . Поскольку они оба начинаются с [latex] {x}_{0}=0 [/latex], их смещения одинаковы в более позднее время t , когда гепард догоняет газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время.

Раствор

Показать ответ
Показать ответ

Значение

Важно проанализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания движения каждого отдельного объекта. Также важно иметь хорошее визуальное представление о задаче преследования двух тел, чтобы увидеть общий параметр, связывающий движение обоих объектов.

Проверьте свои знания

Велосипед движется с постоянной скоростью 10 м/с. Человек стартует с места и бежит, чтобы догнать велосипед за 30 с. Каково ускорение человека?

Показать решение

Резюме

При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных. Для решения неизвестных необходимо одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
Задачи преследования двух тел всегда требуют одновременного решения двух уравнений для неизвестных.

Концептуальные вопросы

При анализе движения отдельного объекта, какое количество известных физических переменных требуется для решения неизвестных величин с помощью кинематических уравнений?

Приведите два сценария кинематики одиночного объекта, в которых три известных величины требуют решения двух кинематических уравнений для неизвестных.

Показать решение

Задачи

Частица движется прямолинейно с постоянной скоростью 30 м/с. Каково его перемещение между t = 0 и t = 5,0 с?

Показать решение

Частица движется прямолинейно с начальной скоростью 30 м/с и постоянным ускорением 30 м/с ² . Если в [латекс] t=0,x=0 [/латекс] и [латекс] v=0 [/латекс], каково положение частицы в момент t = 5 с?

Частица движется прямолинейно с начальной скоростью 30 м/с и постоянным ускорением 30 м/с ² . а) Чему равно его водоизмещение при т = 5 с? б) Какова его скорость в это же время?

Показать решение

(a) Нарисуйте график зависимости скорости от времени, соответствующий графику зависимости смещения от времени, представленному на следующем рисунке. б) Определите время или моменты времени ( t _a, t _b, t _c и т. д.), в которые мгновенная скорость имеет наибольшее положительное значение. в) В какие моменты времени он равен нулю? г) В какие моменты он отрицательный?

Показать ответ

(a) Нарисуйте график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на следующем рисунке. (b) Определите время или времена ( t _a , t _b , t _c и т. д.), при которых ускорение имеет наибольшее положительное значение. в) В какие моменты времени он равен нулю? г) В какие моменты он отрицательный?

Показать ответ

Частица имеет постоянное ускорение 6,0 м/с ² . а) Если его начальная скорость равна 2,0 м/с, то в какой момент времени его перемещение составит 5,0 м? б) Какова его скорость в этот момент?

При t = 10 с частица движется слева направо со скоростью 5,0 м/с. В 9{\ text {−} 4} \, \ text {s} [/ латекс]. Какова его начальная скорость (то есть конечная скорость)?

Показать решение

(a) Легкий пригородный поезд движется со скоростью 1,35 м/с ² . Сколько времени требуется, чтобы достичь максимальной скорости 80,0 км/ч, начиная с состояния покоя? (b) Тот же поезд обычно замедляется со скоростью 1,65 м/с ² . Сколько времени требуется, чтобы остановиться на максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь со скорости 80,0 км/ч за 8,30 с. Каково его аварийное ускорение в метрах в секунду в квадрате?

При выезде на автостраду автомобиль разгоняется из состояния покоя со скоростью 2,04 м/с ² за 12,0 с. а) Нарисуйте схему ситуации. б) Перечислите известные в этой задаче. в) Какой путь проедет автомобиль за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем укажите, как вы выбрали подходящее уравнение для его решения. После выбора уравнения покажите, как вы решаете неизвестное, проверьте свои единицы измерения и обсудите, разумен ли ответ. г) Чему равна конечная скорость автомобиля? Решите для этого неизвестного так же, как в (c), явно показывая все шаги.

Показать решение

Необоснованные результаты В конце забега бегун замедляется со скорости 9,00 м/с до скорости 2,00 м/с ² . а) Какое расстояние она пройдет за следующие 5,00 с? б) Какова его конечная скорость? в) Оцените результат. Имеет ли это смысл?

Кровь ускоряется из покоя до 30,0 см/с на расстоянии 1,80 см левым желудочком сердца. а) Составьте схему ситуации. б) Перечислите известные в этой задаче. в) Сколько времени занимает ускорение? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали подходящее уравнение для его решения. Выбрав уравнение, покажите свои шаги в решении неизвестного, проверив свои единицы измерения. (d) Является ли ответ разумным по сравнению со временем сердцебиения? 9{2} [/latex], сколько времени потребуется, чтобы остановиться с такой скоростью? в) Какое расстояние он пройдет в каждом случае?

Снаряд фейерверка разгоняется из состояния покоя до скорости 65,0 м/с на расстоянии 0,250 м. {2} [/латекс ], какое расстояние он пролетит, прежде чем поднимется в воздух? б) Сколько времени это занимает?

Мозг дятла специально защищен от больших ускорений сухожилиями внутри черепа. Клевая дерево, голова дятла останавливается с начальной скоростью 0,600 м/с на расстоянии всего 2,00 мм. а) Найдите ускорение в метрах в секунду в квадрате и в единицах, кратных г , где г = 9,80 м/с ² . б) Рассчитайте время остановки. (c) Сухожилия, удерживающие мозг, растягиваются, делая его тормозной путь равным 4,50 мм (больше, чем у головы, и, следовательно, меньшее ускорение мозга). Чему равно ускорение мозга, выраженное в кратном г ?

Показать решение

Неосторожный футболист сталкивается со стойкой ворот с обивкой во время бега со скоростью 7,50 м/с и полностью останавливается после сжатия обивки и своего тела на 0,350 м. а) Чему равно его ускорение? б) Как долго длится столкновение?

Посылка выпадает из грузового самолета и приземляется в лесу. Если мы предположим, что скорость пакета помощи при ударе составляет 54 м/с (123 мили в час), то каково его ускорение? Предположим, что деревья и снег останавливают его на расстоянии 3,0 м. 9{2} [/latex] по мере прохождения. Длина станции 210,0 м. а) С какой скоростью он движется, когда нос покидает станцию? б) Какова длина носа поезда на станции? в) Если поезд имеет длину 130 м, какова скорость конца поезда при выходе из него? г) Когда поезд отходит от станции?

Необоснованные результаты Драгстеры могут достичь максимальной скорости 145,0 м/с всего за 4,45 с. а) Рассчитайте среднее ускорение такого драгстера. (b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, указанной в (а), на протяжении 402,0 м (четверть мили) без использования какой-либо информации о времени. в) Почему конечная скорость больше той, которая использовалась для нахождения среднего ускорения? ( Подсказка : Подумайте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.)

Показать решение

Глоссарий

задача преследования двух тел: задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов

Калькулятор кинематических уравнений для постоянного ускорения

Как вы знаете, существуют два основных кинематических уравнения движения для равномерного или постоянного ускорения.

Таким образом, мы имеем пять параметров движения: начальную скорость V₀ , конечную скорость V , ускорение a , время t и перемещение, или расстояние, S , и два уравнения. Следовательно, чтобы использовать эти уравнения, нам нужны три известных параметра и два неизвестных параметра. Кроме того, как говорит нам Комбинаторика — комбинации, расположения и перестановки, количество комбинаций 3 из 5 равно 10, так что всего существует десять типов задач кинематических уравнений; каждый имеет различный набор известных параметров.

Этот калькулятор позволяет ввести любые три известных параметра и очистить параметры, которые необходимо найти, и он их любезно находит. Кинематические уравнения для каждого набора параметров приведены под калькулятором. Кстати, по умолчанию ускорение имеет значение постоянной силы тяжести g , что создает проблему свободного падения.

Калькулятор кинематических уравнений

Начальная скорость, Vo

м/с 

Конечная скорость, V

м/с 

Ускорение,

м/с² 

, T

SEC 

DISPLACET, S

M  9064

DISPLACETION, S

M  9064

DISTRICELMIST, S

M  9064

. 2

Initial velocity, Vo

m/s 

Final velocity, V

m/s 

Acceleration, a

m/s² 

Time, T

Sec 

Смещение, S

M 

Кинематические уравнения

Ниже приведены десять видов проблем с формами решения.

Случай 1. Найдите неизвестные, зная начальную скорость, ускорение и время

Пример задачи: Самолет движется по взлетно-посадочной полосе с ускорением n м/с² в течение м секунд, пока наконец не оторвется от земли. Определить конечную скорость и расстояние, пройденное до взлета.
Решение: Хотя в задаче указаны только ускорение и время, третий параметр известен неявно. В задаче предполагается, что самолет стартует с места, следовательно, его начальная скорость равна нулю. Таким образом, мы можем использовать наши кинематические уравнения следующим образом:

Случай 2.

Найдите неизвестные, зная начальную скорость, конечную скорость и время
Пример задачи. Земля со скоростью м м/с. Определить ускорение и расстояние, пройденное до взлета.
Решение: Мы снова знаем, что начальная скорость равна нулю. Чтобы решить эту задачу, нам нужно изменить наши кинематические уравнения следующим образом:
Случай 3. Найдите неизвестные, зная начальную скорость, конечную скорость и ускорение
Пример задачи: Самолет ускоряется вниз по взлетно-посадочной полосе на высоте n м. /с², пока наконец не оторвется от земли со скоростью м м/с. Определить время и расстояние, пройденное до взлета.
Решение: Тот же случай с нулевой начальной скоростью. Итак, наши кинематические уравнения будут такими:
Случай 4. Найдите неизвестные, зная начальную скорость, конечную скорость и расстояние
Пример задачи: Самолет летит по взлетно-посадочной полосе с ускорением до тех пор, пока, наконец, не оторвется от земли со скоростью n м/с после прохождения расстояния м метров. Определить время и ускорение.
Решение: Как обычно, мы знаем, что начальная скорость равна нулю. И мы используем кинематические уравнения так:
Здесь проще сначала найти время, а затем подставить время во второе уравнение.
Случай 5. Найдите неизвестные, зная начальную скорость, время и расстояние
Пример задачи: Самолет ускоряется вниз по взлетно-посадочной полосе в течение n секунд, пока, наконец, не оторвется от земли, преодолев расстояние м метров. Определить скорость отрыва и ускорение.
Решение: В этой задаче начальная скорость также равна нулю. Кинематические уравнения для этого случая:
Обратите внимание, что здесь проще сначала найти конечную скорость, а затем подставить ее во второе уравнение.
Случай 6. Найдите неизвестные, зная начальную скорость, ускорение и расстояние
Пример задачи: Самолет движется вниз по взлетно-посадочной полосе со скоростью n м/с², пока, наконец, не оторвется от земли, преодолев расстояние м метров . Определить скорость отрыва и время.
Решение: снова начальная скорость равна нулю. Однако этот случай достаточно сложен, поскольку единственный способ найти время — это решить квадратное уравнение:
Конечно, чтобы найти время нужно подобрать положительный корень. После этого вы можете подставить время в следующее уравнение, чтобы найти конечную скорость:
Случай 7. Найдите неизвестные, зная конечную скорость, время и расстояние
Пример задачи: Автомобиль замедляется в течение n секунд до тех пор, пока наконец, он останавливается, преодолев расстояние м метров. Определить начальную скорость и замедление.
Решение: Теперь начальная скорость неизвестна, а конечная скорость равна нулю. Кроме того, мы получим отрицательное значение ускорения, что означает, что автомобиль замедляется. Для решения задачи необходимо использовать следующий вид кинематических уравнений:
Здесь проще сначала найти начальную скорость, а потом подставить ее во второе уравнение.
Случай 8. Найдите неизвестные, зная конечную скорость, время и ускорение
Пример задачи: автомобиль ускоряется на скорости n м/с² за t секунд, пока не достигнет м м/с. Определить начальную скорость и пройденный путь.
Решение: Мы снова не знаем начальную скорость. Нам нужно использовать кинематические уравнения следующим образом:
Случай 9. Найдите неизвестные, зная конечную скорость, ускорение и расстояние
Пример задачи: Автомобиль движется с ускорением n м/с² на протяжении м метров, пока не достигнет м м/с. Определить начальную скорость и время.
Решение: Это тоже сложный случай, здесь нам снова нужно решить квадратное уравнение, чтобы найти время. Наше уравнение будет:
Тогда время находится, найти начальную скорость:
Случай 10. Найдите неизвестные, зная время, ускорение и расстояние
Пример задачи: Автомобиль ускоряется со скоростью n м/с² за м секунд и проехал с метров. Определить начальную скорость и конечную скорость.
Решение: используйте следующие кинематические уравнения:
 ускорение постоянная уравнения кинематики кинематика движение физика равномерная скорость
физика:кинематика
Кинематика
Концепции
Положение, скорость и ускорение
Формулы
Свободное падение
Примеры
Обсуждение
Кинематика (от греческого слова кинема для движение ) изучает траектории движущихся объектов. Уравнения кинематики можно использовать для расчета того, как долго мяч, брошенный вверх, будет оставаться в воздухе, или для расчета ускорения, необходимого для разгона от 0 до 100 км/ч за 5 секунд. Для выполнения этих расчетов нам нужно знать, какие уравнение движения для использования и начальные условия (начальное положение $x_i$ и начальная скорость $v_{i}$). 2$].
$x_i=x(0), v_i=v(0)$: начальное (при $t=0$) положение и скорость объекта (начальные условия).
Положение, скорость и ускорение
Движение объекта характеризуется тремя функциями: функция положения $x(t)$, функция скорости $v(t)$ и функция ускорения $a(t)$. Функции $x(t)$, $v(t)$ и $a(t)$ связаны — они все описывают разные аспекты одного и того же движения.
Вы уже знакомы с этими понятиями из своего опыта вождения автомобиля. Уравнение движения $x(t)$ описывает положение автомобиля как функцию времени. Скорость описывает изменение положения автомобиля, или математически \[ v(t) \equiv \text{скорость изменения } x(t). \] Если мы измеряем $x$ в метрах [м] и время $t$ в секундах [с], тогда единицами измерения $v(t)$ будут метры в секунду [м/с]. Например, объект движется с постоянной скоростью $30$[м/с]. будет менять свою позицию на $30$[m] каждую секунду. 92$]. Постоянное положительное ускорение означает скорость движения неуклонно увеличивается, как при нажатии на педаль газа. Постоянное отрицательное ускорение означает, что скорость неуклонно уменьшается, как при нажатии на педаль тормоза.
На иллюстрации справа показан одновременный график положение, скорость и ускорение автомобиля за некоторый промежуток времени. Через пару абзацев мы обсудим точные математические уравнения, которые описать $x(t)$, $v(t)$ и $a(t)$. Но прежде чем мы перейдем к математике, давайте визуально проанализируйте движение, показанное справа.
Автомобиль стартует с начальной позиции $x_i$ и просто сидит некоторое время. Водитель затем этажей педаль для получения максимального ускорения в течение некоторого времени, набирает скорость, а потом отпускает акселератор, но держит его достаточно нажатым, чтобы поддерживать постоянную скорость. Внезапно водитель видит вдалеке полицейскую машину и врезается на тормозах (отрицательное ускорение) и вскоре после этого останавливает машину. Водитель ждет несколько секунд, чтобы убедиться, что копы проехали. Затем автомобиль немного ускоряется назад (задняя передача) и затем поддерживает постоянную скорость назад в течение длительного периода времени. Обратите внимание, как «движение назад» соответствует отрицательной скорости. В конце водитель снова нажимает на тормоз, чтобы остановить машину. до остановки. Конечная позиция $x_f$.
В приведенном выше примере мы можем наблюдать два различных типа движения. Движение с постоянной скоростью (равномерно-скоростное движение, УВМ) и движение с постоянным ускорением (равномерно-ускоренное движение, УАМ). Конечно, может быть много других типов движения, но для Цель этого раздела вы несете ответственность только за эти два.
UVM: Когда нет ускорения,
автомобиль сохраняет постоянную скорость, т.

$v(t)$ будет постоянной функцией. Постоянная скорость означает, что функция положения будет линией с постоянным наклоном, потому что по определению $v(t)= \text{наклон } x(t)$. * UAM: Во время, когда автомобиль испытывает постоянное ускорение $a(t)=a$, скорость функции будет изменяться с постоянной скоростью. Скорость изменения скорости постоянна $a=\text{наклон } v(t)$, поэтому функция скорости должна выглядеть как линия с наклоном $a$. 2 + v_i t + x_i, \nl v(t) &= at + v_i, \nl а(т) &= а, \конец{выравнивание*} \] где $v_i$ — начальная скорость объекта, а $x_i$ — его начальное положение. 92 + 2а\Дельта х, \] где $v_f$ обозначает конечную скорость, а $\Delta x$ обозначает изменение в координате $x$.
Вот и все. Запомните эти уравнения, подставьте правильные числа, и вы можете решить любую задачу кинематики, какую только может вообразить человек. Глава сделана.
Равномерное скоростное движение (UVM)
Частный случай, когда ускорение равно нулю ($a=0$), называется равноскоростным движением или УВМ. Скорость остается постоянной (постоянной), потому что ускорение отсутствует. Следующие три уравнения описывают движение объекта. при равномерной скорости: \[ \начать{выравнивать} х(т) &= v_it + x_i, \nl v(t) &= v_i, \nl а(т) &= 0. \end{выравнивание} \] Как видите, это действительно те же уравнения, что и в случае UAM. выше, но поскольку $a=0$, некоторые термины отсутствуют. 92$]. Отрицательный знак здесь, потому что ускорение свободного падения направлено вниз, и мы предполагаем, что ось $y$ направлена вверх. Движение объекта при свободном падении описывается уравнениями УАМ.
Примеры
Теперь мы проиллюстрируем, как используются уравнения кинематики. для решения задач по физике.
Марокканский образец
Предположим, ваш друг хочет отправить вам мяч, завернутый в алюминий. фольгу со своего балкона, расположенного на высоте $x_i=44,145$[м]. Через какое время мяч упадет на землю? 92+0(t_{падение}) + 44,145, \] решение которого $t_{fall} = \sqrt{\frac{44,145\times 2}{9,81}}= 3$[s].
от 0 до 100 за 5 секунд
Предположим, вы хотите иметь возможность разогнаться с $0$ до $100$[км/ч] за $5$ секунд на своем автомобиле. Какое ускорение должен развивать ваш двигатель, при условии, что он производит постоянное ускорение.
Мы можем рассчитать необходимое значение $a$, подставив требуемые значения в уравнение скорости для UAM: \[ v(t) = at + v_i. 2$] или больше.
Марокканский пример II
Некоторое время спустя ваш друг хочет отправить вам еще один алюминий. мяч из своей квартиры, расположенной на 14 этаже (высота $44,145$[м]). Чтобы уменьшить время полета, он кидает мячей прямо вниз с начальной скоростью $10$[м/с]. Через какое время мяч упадет на землю?
Представьте себе здание с осью $y$, измеряющей расстояние вверх. начиная с первого этажа. Мы знаем, что балкон находится на высоте $y_i=44,145$[м], и что при $t=0$[s] мяч стартует с $v_i=-10$[м/с]. Начальная скорость отрицательна, так как направлена в сторону, противоположную оси $y$. Мы знаем, что ускорение свободного падения равно $a_y=-g=-9.2 - 4ac }}{2a} = \frac{-10 \pm \sqrt{ 25 + 866,12}}{9,81} = 2,53 \text{ [s]}. \] Мы проигнорировали решение с отрицательным временем, потому что оно соответствует времени в прошлом. Сравнивая с первым марокканским примером, мы видим, что ответ имеет смысл — бросить мяч вниз заставит его упасть на землю быстрее, чем просто уронив его.
Обсуждение
Большинство задач кинематики, которые вам будет предложено решить, следуют той же схеме, что и приведенные выше примеры. Вам дадут некоторые начальные значения и попросят решить некоторую неизвестную величину. Важно помнить о означает чисел, которые вы подставляете в уравнения. Вы должны всегда рисовать систему координат и четко указывать (для себя) Ось $x$, измеряющая смещение. Если величина скорости или ускорения указывает в том же направлении, что и ось $x$, то это положительное число, в то время как величины, указывающие в противоположном направлении, являются отрицательными числами.
Все эти разговоры о том, что $v(t)$ является «скоростью изменения $x(t)$», начинают действовать мне на нервы. Выражение «скорость изменения» является эвфемизмом термина исчисления производная . Теперь мы совершим короткую экскурсию в страну исчисления, чтобы определить некоторые основные понятия (производные и интегралы), чтобы мы могли использовать это более точно терминология в оставшейся части книги.
Объяснение урока: Кинематические уравнения | Nagwa
В этом толкователе мы узнаем, как применять законы равномерное ускоренное движение частицы по прямой линии.
Начнем с того, что вспомним, как меняется со временем смещение равномерно движущейся частицы. Возможно, мы уже знакомы с формула скоростьперемещениевремя=.
Это также может быть выражено через переменные. Предположим, что мы начинаем измерять положение частицы в момент времени 𝑡 и закончите измерение во время 𝑡. Тогда вектор скорости ⃑𝑣, равно времени, в течение которого он движется, Δ𝑡=𝑡−𝑡, деленному на вектор смещения, ⃑𝑠. Это можно выразить как ⃑𝑣=⃑𝑠Δ𝑡.
Кроме того, смещение можно записать в терминах векторов положения (т. е. векторов, указывающих от начала координат к положение частицы). Предполагая, что вектор начального положения частицы равен ⃑𝑟 и конечный вектор положения равен ⃑𝑟, мы имеем ⃑𝑟=⃑𝑟+⃑𝑠.
То есть, добавляя вектор смещения к начальному вектору положения, мы получаем конечный вектор положения. Это может быть переставить, чтобы быть с точки зрения смещения: ⃑𝑠=⃑𝑟−⃑𝑟.
Комбинируя это уравнение с уравнением для скорости, получаем следующие формулы.
Формула: скорость частицы при равномерном движении
Скорость ⃑𝑣 частицы при равномерном движении определяется выражением ⃑𝑣=⃑𝑠Δ𝑡=⃑𝑟−⃑𝑟𝑡−𝑡, где ⃑𝑠 — смещение, Δ𝑡=𝑡−𝑡 — интервал времени, а ⃑𝑟 и ⃑𝑟 — векторы начального и конечного положения частицы соответственно.
В качестве альтернативы может быть так, что частица не совершает равномерного движения, но имеет равномерное ускорение (т. е. постоянное ускорение). Это очень типичная ситуация в реальном мире, поскольку гравитация заставляет все объекты иметь равномерное ускорение вниз. Напомним, что ускорение определяется как изменение скорости во времени, определяемое выражением ускорение, изменение скорости, время =.
Как и прежде, это можно выразить через переменные.
Формула: Равномерное ускорение частицы
Ускорение ⃑𝑎 частицы, если она однородна, определяется выражением ⃑𝑎=Δ⃑𝑣Δ𝑡=⃑𝑣−⃑𝑢𝑡−𝑡, где 𝑢 — начальная скорость (которую также можно обозначить как ⃑𝑣), ⃑𝑣 — конечная скорость, Δ⃑𝑣=⃑𝑣−⃑𝑢 — изменение скорости, а Δ𝑡=𝑡−𝑡 — интервал времени.
Эту формулу также можно преобразовать в термины конечной скорости ⃑𝑣. Начиная с ⃑𝑎=⃑𝑣−⃑𝑢𝑡−𝑡, мы можем умножить обе части на 𝑡−𝑡, чтобы получить ⃑𝑎(𝑡−𝑡)=⃑𝑣−⃑𝑢, или, переставленный в терминах ⃑𝑣, ⃑𝑣=⃑𝑢+⃑𝑎(𝑡−𝑡).
Это уравнение можно упростить еще некоторыми способами. Как правило, мы принимаем время начала 𝑡 равным 0, означает, что 𝑡−𝑡 — это просто 𝑡. Затем мы можем просто написать это без нижнего индекса как 𝑡. Это дает нам ⃑𝑣=⃑𝑢+⃑𝑎𝑡.
Другое упрощение, которое мы можем сделать, заключается в том, что, поскольку ускорение равномерное, все движения будут в одном направлении (или в прямо противоположном направлении). Таким образом, мы можем написать это уравнение без использования векторов, используя знак минус, если движение указывает в противоположном направлении. На самом деле это предположение, которое мы можем сделать на протяжении всего этого объяснения. Если мы сделаем это предположение, тогда мы получим первую из трех кинематических формул, которые мы рассмотрим в этом объяснении.
Формула: первое кинематическое уравнение
Для частицы, движущейся с постоянным ускорением, ее скорость 𝑣 через период времени 𝑡 равна данный 𝑣=𝑢+𝑎𝑡, где 𝑢 — начальная скорость, а 𝑎 — ускорение.
Стоит отметить, что если ускорение равно 0, то 𝑣=𝑢, что показывает нам, что начальная скорость будет быть равным конечной скорости, как и следовало ожидать. Также в случае, если начальная скорость 𝑢=0, то 𝑣=𝑎𝑡, что означает, что скорость прямо пропорциональна ускорению и периоду времени.
В любом случае приведенное выше уравнение можно использовать для решения любой задачи, в которой известны три из четырех переменных, и мы Требуется найти четвертый.
Теперь рассмотрим пример, в котором скорость равномерно ускоряющегося определяется частица.
Пример 1. Определение конечной скорости равномерно ускоряющейся частицы
Если частица начала двигаться прямолинейно с начальной скоростью 25,1 см/с и униформа ускорение 2,4 см/с ² , определите его скорость через 9 секунд.
Ответ
Скорость частицы после ее ускорения можно определить по формуле 𝑣=𝑢+𝑎𝑡.
Мы можем заменить значения, указанные для 𝑢, 𝑎, и 𝑡 в формулу.
Затем мы находим, что 𝑣=25,1+2,4(9)=46,7/.см
Смещение частицы есть произведение ее скорости на время, в течение которого она движется. Скорость частицы зависит от ее ускорения и времени, за которое она ускоряется, поэтому смещение частицы, изначально покоящейся, может быть выражается через его ускорение и время, за которое оно ускоряется.
Для частицы с постоянной скоростью ее перемещение можно выразить как 𝑠=𝑠+𝑣𝑡.fi
Если предположить, что 𝑠i равно нулю, и обозначить 𝑠f как 𝑠, это становится 𝑠=𝑣𝑡.
Для равномерно ускоряющейся частицы, которая первоначально находится в состоянии покоя и имеет конечную скорость 𝑣, среднее значение начальной и конечной скоростей определяется выражением 𝑣=𝑣2.mean
Тогда смещение частицы за интервал времени 𝑡 определяется выражением 𝑠=𝑣2𝑡.
Для частицы, изначально находящейся в состоянии покоя, 𝑣=𝑎𝑡.
Подставляя это выражение для 𝑣 в выражение для 𝑠, получаем 𝑠=𝑎𝑡2𝑡,𝑠=12𝑎𝑡.
Для равномерно ускоряющейся частицы, которая первоначально имеет скорость 𝑢 и имеет конечная скорость 𝑣, среднее значение начальной и конечной скоростей определяется выражением 𝑣=𝑣+𝑢2.mean
Смещение частицы за интервал времени 𝑡 определяется выражением 𝑠=𝑣+𝑢2𝑡.
Это выражение также можно изобразить с помощью графика, как показано на следующем рисунке.
На графике видно, что площадь под синей линией состоит из суммы площадей прямоугольник, 𝑠, который задается 𝑠=𝑢𝑡 и площадь прямоугольного треугольника, 𝑠, которая определяется выражением 𝑠=(𝑣−𝑢)2𝑡.
Мы можем обозначить скорость в 𝑡2 как 𝑣. На следующем рисунке показано, что площадь заштрихованный синим прямоугольный треугольник с длиной стороны 𝑣−𝑢2 равна площади заштрихованного белым прямоугольного треугольника с длиной стороны 𝑣−𝑢2.
Таким образом, площадь под синей линией равна площади прямоугольника, показанного на следующий рисунок.
Эта площадь равна смещению частицы в момент 𝑡, предоставлено 𝑠=𝑣+𝑢2𝑡.
Для частицы с начальной скоростью 𝑢 это так, что 𝑣=𝑢+𝑎𝑡.
Подставляя это выражение для 𝑣 в выражение для 𝑠, получаем 𝑠=𝑢+𝑎𝑡+𝑢2𝑡,𝑠=2𝑢+𝑎𝑡2𝑡,𝑠=𝑢𝑡+12𝑎𝑡.
Это наше второе кинематическое уравнение, и оно полезно для любой задачи, в которой нам нужно определить смещение частица с равномерным ускорением.
Формула: второе кинематическое уравнение
Для частицы, движущейся с постоянным ускорением, ее перемещение 𝑠 через период времени 𝑡 дан кем-то 𝑠=𝑢𝑡+12𝑎𝑡, где 𝑢 — начальная скорость, а 𝑎 — ускорение.
Заметим, что, как и в предыдущей формуле, здесь есть несколько полезных частных случаев, которые мы можем рассмотреть. Если частица начинает свое движение в состоянии покоя, а это означает, что начальная скорость 𝑢=0, тогда мы просто имеем 𝑠=12𝑎𝑡. Кроме того, если ускорения нет, то есть 𝑎=0, то имеем 𝑠=𝑢𝑡, что описывает частица в равномерном движении, как мы видели в начале объяснения.
Теперь рассмотрим пример, в котором перемещение ускоряющегося тела определен.
Пример 2. Определение расстояния, пройденного равномерно ускоряющейся частицей
Небольшой шарик начал двигаться горизонтально со скоростью 16,3 м/с. Он двигался по прямой линия с равномерным замедлением 3 м/с ² . Определить расстояние до мяча покрывается в первые 2 секунды.
Ответ
Мяч движется прямолинейно с равноускоренным ускорением. Смещение равномерно ускоренное тело, движущееся прямолинейно, определяется формулой 𝑠=𝑢𝑡+12𝑎𝑡, где 𝑢 — начальная скорость тела и 𝑎 — ускорение тела.
Утверждается, что мяч в вопросе замедляется равномерно. Тормозящее тело ускоряется в направлении, противоположном направлению его движения. скорость, когда он начинает ускоряться. Поэтому знак ускорения имеет противоположный знаку начальной скорости.
Подставляя значения, указанные в вопросе, мы имеем 𝑠=16,3(2)+12(−3)2𝑠=32,6+12(−3)(4)=32,6−6=26,6,m
Рассмотрим еще один такой пример.
Пример 3. Расчет начальной и конечной скорости равномерно ускоряющейся частицы
Частица, двигаясь по прямой линии, ускорялась со скоростью 22 см/с ² в том же направлении, что и его начальная скорость. Если величина его смещение через 10 секунд после него начало движения было 29 м, рассчитать величину его начального скорость 𝑣 и его скорость 𝑣 в конце этого периода.
Ответ
Перемещение равномерно ускоряющегося тела находится по формуле 𝑠=𝑢𝑡+12𝑎𝑡, где 𝑢 — начальная скорость тела и 𝑎 — ускорение тела. В этом вопросе 𝑢 обозначается от 𝑣.
Нам известны перемещение тела, его ускорение и время, которое он ускоряется для. Подставляя эти значения в формулу, имеем 29=10𝑣+120,2210.
Перемещение указано в метрах, поэтому ускорение преобразуется из 22 см/с ² к 0,22 м/с ² .
Это выражение можно переставить так, чтобы 𝑣 стало подлежащим: 𝑣=29−0,221010=1,8/.мс
Конечная скорость 𝑣 тела определяется выражением 𝑣=𝑣+𝑎𝑡.
Подставляя известные значения, находим, что 𝑣=1,8+0,22(10)=4/.мс
Если неизвестно время движения тела, но известно перемещение и начальное известна скорость тела, то можно определить конечную скорость. Эквивалентно, если известно перемещение и конечная скорость тела, то начальная можно определить скорость.
Соотношение между начальной и конечной скоростью, когда время неизвестно использует кинематические формулы 𝑣=𝑢+𝑎𝑡 а также 𝑠=𝑢𝑡+12𝑎𝑡.
Формула 𝑣=𝑢+𝑎𝑡 можно преобразовать, чтобы выразить 𝑡 через скорость и ускорение: 𝑡=𝑣−𝑢𝑎.
Это выражение для 𝑡 можно заменить на 𝑠=𝑢𝑡+12𝑎𝑡.
Это дает нам 𝑠=𝑢𝑣−𝑢𝑎+12𝑎𝑣−𝑢𝑎.
Это выражение можно преобразовать следующим образом: Fult 𝑣+𝑢 - 2𝑢𝑣2𝑎𝑠 = 2𝑢𝑣 - 2𝑢2𝑎+𝑣+𝑢 - 2𝑢𝑣2𝑎𝑠 = 2𝑢𝑣 - 2𝑢+𝑣+𝑢 -2𝑢𝑣2𝑎, 2𝑎𝑠 = 2𝑢𝑣 - 2𝑢+𝑣+𝑢 2𝑢𝑣2𝑎𝑠 = 𝑣 - 𝑢𝑣 = 𝑢 +2𝑎𝑠.
Это окончательное кинематическое уравнение, и оно идеально подходит в тех случаях, когда нам дано перемещение, но не период времени.
Формула: Третье кинематическое уравнение
Для частицы, движущейся с постоянным ускорением, ее скорость 𝑣 следует за смещением 𝑠 дан кем-то 𝑣=𝑢+2𝑎𝑠, где 𝑢 — начальная скорость, а 𝑎 — ускорение.
Давайте теперь рассмотрим пример того, как моделировать движение частицы, которое происходит в неизвестный интервал времени.
Пример 4. Определение конечной скорости равномерно ускоряющейся частицы
Частица двигалась прямолинейно с постоянным ускорением 2 см/с ² . Учитывая, что его начальная скорость была 60 см/с, найдите скорость тела в момент 15 м от начальной точки.
Ответ
Поскольку время движения частицы неизвестно, скорость частицы определяется по формуле 𝑣=𝑢+2𝑎𝑠, где 𝑣 — конечная скорость, 𝑢 — начальная скорость, 𝑎 — ускорение, а 𝑠 это смещение.
Скорость и ускорение указаны в сантиметрах в секунду и сантиметров на секунду в квадрате соответственно, поэтому смещение преобразуется из 15 метров до 1‎ ‎500 сантиметров. Подставив известные значения в формулу, получим 𝑣=60+2(2)(1500)𝑣=√9600.
С точностью до сантиметра в секунду 𝑣 равно 98 см/с.
Давайте теперь рассмотрим пример движения частицы, который требует анализируя его движение в двух отдельных временных интервалах.
Пример 5. Использование кинематических уравнений для решения многошаговой задачи
Тело равномерно ускорялось по прямой так, что оно 72 м в первом 3 секунды и 52 м в следующем 4 секунды. Найдите его ускорение 𝑎 и начальную скорость 𝑣.
Ответ
Расстояние, пройденное частицей за первый 3 секунды больше, чем в последующие 4 секунды; следовательно, частица замедляется с неизвестной начальной скоростью.
Средняя скорость равномерно ускоряющейся частицы за интервал времени равна данный 𝑣=𝑣+𝑢2, среднее где 𝑢 — начальная скорость, а 𝑣 есть конечная скорость. Средняя скорость также определяется выражением 𝑣=𝑠𝑡, среднее где 𝑠 — смещение, а 𝑡 — длина временного интервала. Имеем, таким образом, что 𝑠𝑡=𝑣+𝑢2.
Это выражение можно преобразовать, чтобы получить 𝑣+𝑢=2𝑠𝑡.
В первые 3 секунды движения частицы мы видим, что 𝑣+𝑢=2(72)3=48.
В следующие 4 секунды что частица движется, мы видим, что 𝑣+𝑢=2(52)4=26.
Начальная скорость 𝑢 равна конечной скорости 𝑣; следовательно, мы видим, что 𝑣+𝑢=𝑣+𝑣, а также 𝑣+𝑣=𝑣+48−𝑢. 
Таким образом, имеем, что 𝑣+48−𝑢=26𝑣−𝑢=−22.
Конечная скорость после 7 секунд ускорения, это 22 м/с меньше начальной скорости. Ускорение частицы в направлении поэтому его начальная скорость определяется выражением 𝑎=-227/.мс
Теперь можно определить начальную скорость 𝑢 по формуле 𝑠=𝑢𝑡+12𝑎𝑡.
Подставляя известные значения, получаем 72+52=7𝑢+12−2277124=7𝑢−2214(49)124=7𝑢−77𝑢=124+777=2017/.ms
Другой способ решения этого вопроса заключается в использовании одновременных уравнений.
Мы можем использовать формулу 𝑠=𝑢𝑡+12𝑎𝑡 во-первых 3 секунды движения, получение 72=3𝑢+𝑎2372=3𝑢+92𝑎.
Мы можем использовать ту же формулу для последующего 4 секунды движения, получение 124=7𝑢+𝑎27124=7𝑢+492𝑎.
Оба этих уравнения содержат два неизвестных. Чтобы исключить одно из неизвестных, мы можем умножить одно из уравнений на коэффициент, чтобы получить коэффициент для этого неизвестный равен коэффициенту перед неизвестным в другом уравнении.
Умножаем 72=3𝑢+92𝑎 к 73, получив 168=7𝑢+212𝑎.
Теперь мы можем вычесть уравнение 124=7𝑢+492𝑎 из уравнения 168=7𝑢+212𝑎.
Это дает нам 44=212−492𝑎𝑎=44−𝑎=44−14𝑎=−227/.мс
Это позволяет найти 𝑢 путем подстановки, так же, как и в первом способе решения вопроса.
Давайте теперь обобщим то, что мы узнали из этих примеров.
Ключевые моменты
Скорость частицы (ускоряющейся с постоянной скоростью) может быть выражена через ускорение и время по формуле 𝑣=𝑢+𝑎𝑡, где 𝑣 — конечная скорость, 𝑢 — начальная скорость, 𝑎 — ускорение, а 𝑡 — время, за которое частица ускоряется.
Смещение частицы можно выразить через ускорение и время по формуле 𝑠=𝑢𝑡+12𝑎𝑡, где 𝑠 — смещение частицы, 𝑎 — ускорение частицы, 𝑢 — начальная скорость частицы, а 𝑡 — время, за которое частица ускоряется.
Скорость частицы до и после ускорения можно выразить через ускорения и перемещения по формуле 𝑣=𝑢+2𝑎𝑠, где 𝑢 — начальная скорость частицы, 𝑣 — конечная скорость частицы, 𝑎 — ускорение частица, а 𝑠 — смещение частицы.
Если ускорение тела направлено в сторону, противоположную направлению его начальная скорость, то ускорение и начальная скорость имеют противоположные знаки.
Кинематические уравнения: объяснение, обзор и примеры
Теперь, когда вы узнали о смещении, скорости и ускорении, вы уже на пути к тому, чтобы описать с помощью физики практически любое движение, которое вы можете наблюдать вокруг себя. Осталось только узнать, как эти ценности на самом деле влияют друг на друга. Мы знаем несколько способов перемещения между ними, но все они довольно ограничены. Что произойдет, если вам нужно найти перемещение, но вы знаете только ускорение и время? У нас пока нет способа объединить все эти ценности. Введите четыре кинематических уравнения. 9{2}+2a\Delta x
Пусть вас не пугают все эти цифры и символы. Мы поговорим о каждом из них — что они означают и когда мы их используем. К концу этого поста вы станете мастером понимания и реализации каждого из этих физических уравнений. Давайте начнем с определения того, что означают все эти символы.
Первое кинематическое уравнение
v=v_{0}+at
Это уравнение физики следует читать как «конечная скорость равна начальной скорости плюс ускорение, умноженное на время». Все это означает, что если у вас есть постоянное ускорение в течение некоторого времени, вы можете найти конечную скорость. Вы будете использовать его всякий раз, когда будете смотреть на изменение скорости с постоянным ускорением. 9{2}
Этот может выглядеть немного страшнее, поскольку он длиннее других, но он читается как «перемещение равно начальной скорости, умноженной на время, плюс половина ускорения, умноженного на время в квадрате». {2}. Хотя это может показаться еще более пугающим, на самом деле это то же самое. Единственная разница здесь в том, что мы разделили \Delta x на x-x_{0}, а затем решили получить x самостоятельно. Эта версия может быть особенно полезна, если вы ищете именно конечную или начальную позицию, а не просто общее смещение. 9{2}+2a\Delta x
Наше последнее кинематическое уравнение читается как «квадрат конечной скорости равен квадрату начальной скорости плюс удвоенное ускорение, умноженное на смещение». Стоит отметить, что это единственное кинематическое уравнение без учета времени. Многие начинающие физики были поставлены в тупик, придя к проблеме без оценки времени. Глядя на лист уравнений, изобилующий буквами и цифрами, может быть ошеломляюще, но помнить, что это единственное уравнение без времени, будет возникать снова и снова на протяжении всей вашей карьеры физика.
Возможно, стоит отметить, что все это кинематические уравнения для постоянного ускорения. Хотя это может показаться ограничением, ранее мы узнали, что курсы физики в старших классах обычно используют постоянное ускорение, поэтому нам пока не нужно беспокоиться об его изменении. Если вы окажетесь на более продвинутом курсе, новые физические уравнения будут введены в соответствующее время.
Заинтересованы в лицензии школы Альберта?
Как подойти к задаче кинематики
Итак, теперь, когда у нас есть все эти различные кинематические уравнения, как нам узнать, когда их использовать? Как мы можем посмотреть на задачу по физике и узнать, какое из этих уравнений применить? Вы должны использовать шаги решения проблемы. Следуйте этим нескольким шагам при попытке решить какие-либо сложные проблемы, и у вас не будет проблем.
Шаг 1: определите, что вы знаете
Возможно, этот шаг кажется очевидным, но его пропуск может иметь катастрофические последствия для любого решения проблемы. В задачах по физике это просто означает вытягивание значений и направлений. Если вы можете добавить символ к значению (например, написав t=5\text{s} вместо просто 5\text{s}), это даже лучше. Это сэкономит время и сделает дальнейшие шаги еще проще.
Шаг 2. Определите цель
В физике это означает выяснить, какой вопрос вам на самом деле задают. Вопрос хочет, чтобы вы нашли смещение? Ускорение? Сколько времени заняло движение? Выясните, что вас просят сделать, а затем запишите символ значения, которое вы ищете, со знаком вопроса рядом с ним (например, t=\text{?}). Опять же, это кажется очевидным, но это также жизненно важный шаг.
Шаг 3: Соберите свои инструменты
Как правило, это калькулятор и уравнение. Вы захотите просмотреть все символы, которые вы записали, и выбрать уравнение физики для всех них, включая неизвестное значение. Записав все заранее, вам будет проще составить соответствующее уравнение, чем вспоминать, какие значения вам нужны при поиске правильного уравнения. Вы можете использовать последний метод, но вы, скорее всего, совершите ошибку и почувствуете разочарование.
Шаг 4. Соберите все вместе
Подставьте свои значения в уравнение и найдите неизвестное значение. Обычно это будет ваш последний шаг, хотя вам может потребоваться повторить его несколько раз для исключительно сложных задач. Хотя, вероятно, это еще долго не произойдет. После того, как вы нашли ответ, рекомендуется обвести его кружком, чтобы он был очевиден. Таким образом, кто бы ни оценивал, вы можете легко найти его, и вы можете легко отслеживать, какие задачи вы уже выполнили, пролистывая свою работу.
Практика решения кинематических уравнений на Альберте
Кинематическое уравнение 1: обзор и примеры
Чтобы научиться решать задачи с помощью этих новых, более длинных уравнений, мы начнем с v=v_{0}+at. Это кинематическое уравнение показывает взаимосвязь между конечной скоростью, начальной скоростью, постоянным ускорением и временем. Мы исследуем это уравнение применительно к задачам со словами по физике. Это уравнение настроено для решения скорости, но его можно изменить для решения любого из содержащихся в нем значений. Для этого физического уравнения и следующих за ним мы рассмотрим один пример поиска переменной, которая уже была изолирована, и один пример, в котором необходимо выделить новую переменную, используя шаги, которые мы только что описали. Итак, давайте перейдем к применению этого кинематического уравнения к реальной задаче. 92 для 7\текст{с}. Какова конечная скорость автомобиля?
Шаг 1: определите, что вы знаете
У нас есть четко определенные ускорение и время, но здесь нет четко определенной начальной скорости. Вместо этого мы должны взять это из контекста. Мы знаем, что автомобиль «сидит в покое», прежде чем начать движение. Это означает, что наша начальная скорость в этой ситуации равна нулю. Другие контекстные подсказки для объекта, находящегося в состоянии покоя, — это если он «уронился» или «падает». Другие наши известные значения будет еще проще получить, поскольку нам фактически были даны числовые значения. Теперь пришло время поместить все в список. 92
t=7\text{ s}
Шаг 2: Определение цели
Наша цель здесь была четко сформулирована: найти конечную скорость. Мы по-прежнему хотим перечислить это, чтобы мы могли точно видеть, с какими символами нам нужно работать в этой задаче.
v=\text{?}
Шаг 3: Соберите свои инструменты лист уравнений для правильного. В любом случае, мы тоже захотим записать это. 92\cdot 7\текст{ы}
v=28\text{ м/с}
Пример 2
Теперь давайте немного усложним задачу, которая потребует от нас изменения нашего кинематического уравнения.
Мяч катится к холму со скоростью 3\text{ м/с}. Он скатывается с холма за 5\text{ с} и имеет конечную скорость 18\text{ м/с}. Каково было ускорение мяча, когда он катился с горки?
Шаг 1: Определите, что вы знаете
Как и раньше, мы составим список наших известных значений:
v_{0}=3\text{ м/с}
t=5\text{ с}
v=18\text{ м/с}
Шаг 2. Определение цели
Опять же, наша цель была четко сформулирована, поэтому давайте добавим ее в наш список:
a=\text{?}
Шаг 3: Соберите свои инструменты
Мы уже знаем, какое уравнение мы используем, но давайте притворимся, что мы этого не сделали. Мы знаем, что нам нужно решить для ускорения, но если вы посмотрите на наш первоначальный список кинематических уравнений, нет ни одного, которое настроено для решения для ускорения: 9{2}+2a\Delta x
Теперь нам нужно взглянуть на первый список, который мы составили из того, что мы знаем. Мы знаем начальную скорость, время и конечную скорость. Есть только одно уравнение, которое имеет все значения, которые мы ищем, и все значения, которые мы знаем, и ни одно из которых нам не известно. Это первое кинематическое уравнение:
v=v_{0}+at
В этом случае мы знали, какое кинематическое уравнение вводится, поэтому этот процесс исключения не был необходим, но в будущем это будет происходить нечасто. Скорее всего, вам придется находить правильное уравнение гораздо чаще, чем оно будет вам передано. Лучше всего попрактиковаться в его поиске сейчас, пока у нас есть только несколько уравнений для работы.
Шаг 4. Соберите все вместе
Как и раньше, мы перепишем всю необходимую информацию ниже, но вам не нужно это делать, если вы работаете на бумаге.
v_{0}=3\text{ м/с}
t=5\text{ s}
v=18\text{ м/с}
a=\text{?}
v=v_{0}+в
Хотя вы можете подставлять значения перед изменением уравнения, в физике вы обычно видите, что уравнение перестраивается до добавления значений. В основном это делается для того, чтобы единицы оставались там, где они должны быть, и чтобы избежать ошибок, которые могут возникнуть из-за перемещения чисел и единиц, а не просто переменной. Здесь мы будем использовать последний подход. Следуйте стандартным правилам PEMDAS для преобразования уравнения, а затем запишите его с переменной, которую мы выделили слева. Хотя в этой последней части нет необходимости, это полезная организационная практика: 92
Изучение кинематического уравнения Практика на Альберте
Кинематическое уравнение 2: обзор и примеры
Следующим в наших четырех уравнениях кинематики является \Delta x=\dfrac{v+v_{0}}{2} t. Этот связывает смещение объекта с его средней скоростью и временем. В правой части показана конечная скорость плюс начальная скорость, деленная на два – сумма некоторых значений, деленная на количество значений, или среднее значение. Хотя это уравнение напрямую не показывает постоянное ускорение, оно все же предполагает его. Применение этого уравнения, когда ускорение непостоянно, может привести к некоторой ошибке, поэтому лучше не применять его, если упоминается изменяющееся ускорение.
Пример 1
Автомобиль начал движение со скоростью 10\text{ м/с} и разогнался до скорости 24\text{ м/с}. Какое перемещение совершает автомобиль при этом изменении скорости, если оно происходит за 10\text{ с}?
Шаг 1: определите, что вы знаете
Шаг 2. Определите цель
\Delta x=\text{?}
Шаг 3. Соберите инструменты
\Delta x=\dfrac{v+v_{0}}{2} t
Шаг 4. Соберите все вместе
На этот раз мы не будем повторять все здесь. Вместо этого мы сразу перейдем к подключению наших значений и решению нашей проблемы:
\Delta x=\dfrac{v+v_{0}}{2} t
\Delta x=\dfrac{24\text{ м/с}+10\text{ м/с}}{2} \cdot 10\text{ с}
\Delta x=\dfrac{34\text{ м/с}}{2} \cdot 10\text{ с}
\Delta x=17\text{ м/с} \cdot 10\text{ с}
\Дельта х=170\текст{ м}
Пример 2
Мяч замедляется с 15\text{ м/с} до 3\text{ м/с} на расстоянии 36\text{ м}. Сколько времени это заняло?
Шаг 1: определите, что вы знаете }
Шаг 2: Определите цель
t=\text{?}
Шаг 3: Соберите инструменты
перед этим мы можем изменить некоторые уравнения, чтобы решить их для разных переменных. Итак, мы возьмем уравнение со всеми нужными нам значениями и выделим нужную нам переменную позже:0005
\Delta x=\dfrac{v+v_{0}}{2} t
Шаг 4. Соберите все вместе
Опять же, мы не будем ничего переписывать, но начнем с переставляя наше уравнение для решения для времени:
\Delta x=\dfrac{v+v_{0}}{2} t
2\Дельта х=(v+v_{0})t
t=\dfrac{2\Delta x}{v+v_{0}}
Теперь мы можем подставить известные значения и вычислить время.
t=\dfrac{2\cdot 36\text{м}}{3\текст{м/с}+15\текст{м/с}}
t=\dfrac{72\text{м}}{18\текст{м/с}} 9{2}. На этот раз мы связываем наше перемещение с нашей начальной скоростью, временем и ускорением. Единственная странность, которую вы можете заметить, это то, что она не включает нашу конечную скорость, а только начальную. Это уравнение пригодится, когда у вас нет конечной скорости, которая была бы указана либо непосредственно в виде числа, либо с помощью фразы, указывающей, что объект остановился. Как и раньше, мы сначала воспользуемся этим уравнением, чтобы найти смещение, а затем изменим его, чтобы найти другое значение.
Пример 1 92)
\Delta x=250\text{ м}+\frac{1}{2}(250\text{ м})
\Дельта х=250\текст{м}+125\текст{м}
\Дельта х=375\текст{ м}
На данный момент кажется, что эти проблемы кажутся довольно длинными и требуют нескольких шагов. Хотя это во многом неотъемлемая часть физики, со временем она начнет казаться проще. Эта задача представляет собой идеальный пример. Хотя математически объединить строки 4 и 5, возможно, было легко, здесь они показаны отдельно, чтобы сделать процесс максимально понятным. Хотя вы всегда должны показывать все основные этапы процесса решения задач, вы можете обнаружить, что можете комбинировать некоторые из более мелких шагов после некоторого времени работы с этими кинематическими уравнениями.
Пример 2
Позже в своем полете ракета движется со скоростью 20\text{ м/с}, когда ей снова приходится запускать двигатели. На этот раз он преодолевает расстояние 500\text{ м} за 10\text{ с}. Каково было ускорение ракеты во время работы этого двигателя?
Шаг 1: определите, что вы знаете
Шаг 2. Определение цели
9{2}+2a\Дельта х. Это, как правило, самое сложное на вид, но оно также невероятно важно, поскольку это наше единственное кинематическое уравнение, которое не включает время. Он связывает конечную скорость, начальную скорость, ускорение и перемещение, не требуя времени, в течение которого произошло данное движение. 2. Какова скорость автомобиля в конце съезда? 92
Обратите внимание, что ускорение здесь имеет отрицательное значение. Это потому, что наша постановка задачи дала нам замедление вместо ускорения. Всякий раз, когда у вас есть замедление, вы делаете значение отрицательным, чтобы использовать его как ускорение при решении проблем. Это также говорит нам о том, что наша конечная скорость должна быть меньше нашей начальной скорости, поэтому мы можем добавить это в список того, что мы знаем.
Конечная скорость будет меньше начальной.
9{2}+2a\Delta x
Шаг 4. Соедините все вместе
Хотя обычно мы стараемся не выполнять никаких операций для изолированной переменной, иногда так проще. Когда ваша изолированная переменная возведена в степень, обычно время решить перед упрощением. Это может показаться произвольным правилом, и в некотором смысле так оно и есть, но по мере вашего путешествия по физике вы придумаете свои собственные методы, облегчающие решение задач.
9{2}
Теперь, когда мы упростили обе части, мы возьмем квадратный корень, чтобы исключить показатель степени в левой части:
v=5\text{ м/с}
Если мы помним, в самом начале мы сказали, что наша конечная скорость должна быть меньше нашей начальной скорости, потому что в постановке задачи говорилось, что мы замедляемся. Наша начальная скорость была 25\text{ м/с}, что на самом деле больше, чем 5\text{ м/с}, так что наш ответ подтверждается.
Пример 2
Призрак водит гаечным ключом по столу, чтобы напугать смертного зрителя. Ключ стартует со скоростью 2\text{ м/с} и разгоняется до скорости 5\text{ м/с} на расстоянии 7\text{ м}. С каким ускорением призрак двигал гаечный ключ?
Шаг 1. Определите, что вы знаете }
Здесь также можно сделать вывод о нашем ускорении – оно будет положительным. Не каждая задача четко скажет вам направление ускорения, но если ваша конечная скорость больше начальной скорости, вы можете быть уверены, что ваше ускорение будет положительным.
Положительное ускорение 92
Опять же, мы можем вернуться к началу, когда мы сказали, что наше ускорение будет положительным числом, и подтвердить, что это так.
Заинтересованы в лицензии школы Альберта?
Стратегии решения проблем
К этому моменту вы, вероятно, поняли, что физика будет решать множество сложных задач. Если да, то ваши чувства верны. Во многих отношениях физика — это наука об объяснении природы с помощью математических уравнений. На разработку и применение этих уравнений уходит много времени, но на данном этапе вашей карьеры физика вы обнаружите, что большую часть своего времени, вероятно, будете тратить на применение уравнений к текстовым задачам. Если вы чувствуете, что ваши навыки решения проблем все еще нуждаются в оттачивании, ознакомьтесь с дополнительными примерами и стратегиями из этого поста в Physics Classroom или из этого видеоурока от Khan Academy.
<noscript><img loading='lazy' src='' /></noscript> youtube.com/embed/P3jCdsWJa38?feature=oembed" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen="">
Практика решения кинематических уравнений на Альберте
Заключение
Было много уравнений и примеров, которые нужно было принять. когда у вас нет значения для времени, вы будете точно знать, какое из четырех кинематических уравнений применить и как. Просто помните шаги решения задач, которые мы здесь использовали, и вы сможете пройти курс физики без неразрешимых задач.
Как решать кинематические уравнения
Если вы изучаете физику, вскоре вы начнете слышать о кинематических уравнениях. Это набор уравнений, описывающих движение объекта либо с постоянной скоростью (ускорение 0 м/с/с), либо с постоянным ускорением.
Чтобы помочь вам научиться решать кинематические уравнения с легкостью, мы рассмотрим некоторые основные концепции, лежащие в их основе.
Понятия, лежащие в основе кинематических уравнений
Уравнения и единицы
Кинематика — это физический принцип, изучающий движение. В частности, одномерная кинематика рассчитывает движение объектов, движущихся в одном направлении: вверх, вниз или по горизонтали. Мы используем три основных уравнения, чтобы найти различные аспекты движущихся объектов.
В физике большинство чисел являются векторами, что означает, что они должны иметь либо положительный, либо отрицательный знак. Мы обычно следуем системе координат, чтобы ставить знаки на числах. Например, все, что движется вправо или вверх, имеет положительный знак. Все, что движется влево или вниз, имеет отрицательный знак.
Краткие советы
Перемещение — это расстояние между двумя точками, а не общее пройденное расстояние.
Скорость на максимальной высоте равна 0 м/с2
Скорость падения равна отрицательной начальной скорости в том же положении.
Ускорение обычно равно a = -9,80 м/с2
Торможение представляет собой ускорение с отрицательным знаком
Время достижения максимальной высоты = время падения
Практика
Стратегия решения проблем
Шаг 1: Нарисуй! Это поможет вам визуализировать проблему и поможет вам проверить свой ответ в конце.
Шаг 2: Перечислите свои подарки! Запишите все свои известные и неизвестные из задачи на диаграмме из шага 1.
Шаг 3: Проверьте, какое уравнение вы должны использовать. Правое уравнение будет содержать все переменные из шага 2.
Шаг 4: Подключи и пыхни! Чтобы облегчить себе жизнь, сначала найдите неизвестное, а затем добавьте числа.
Шаг 5: Проверьте правильность ответа, сравнив его с диаграммой.
Давайте потренируемся!
Пример 1
Бобби пинает футбольный мяч вертикально вверх со скоростью 10,0 м/с с края обрыва высотой 86,0 м. а) Через какое время мяч упадет на дно скалы? б) Какова скорость мяча в момент удара о землю? и в) какое расстояние пролетел футбольный мяч по вертикали?
Ответ:
A) 5,33 S
B) -42,2 м/с
C) 96,2 M

КЛЮЧ 1:

. это из!
Шаг 2: Список известных и неизвестных.
Шаги 3, 4, 5: Решить
Для детали a) нужно найти t . Лучшее уравнение для использования было бы:
Обратите внимание, что теперь мы используем y, вместо x, , так как мяч движется вверх и вниз по оси y . Чтобы найти t , используйте полиномиальный решатель в своем калькуляторе или решите вручную, используя квадратичную формулу.
Мы выбираем положительный ответ, потому что он более логичен! Таким образом, требуется 5,33 с , чтобы мяч коснулся земли.

Для часть b) лучшее уравнение для нахождения v :
Скорость отрицательна, потому что он падает! Таким образом, мяч движется -42,2 м/с прямо перед тем, как врезаться в землю.
Для , часть c) , мы должны разбить пройденное расстояние на 3 части: расстояние для подъема, расстояние для спуска до начальной точки и высоту обрыва. Расстояние, на которое мяч может подняться, равно расстоянию, на которое он может вернуться вниз, и мы находим его, используя:
Итак, общее пройденное расстояние равно сумме расстояния до вершины, расстояния до начальной точки и расстояния между начальной точкой и подножием скалы.
5,10 м + 5,10 м + 86 м = 96,2 м
Основные выводы:
Ускорение не всегда будет дано вам в задаче, поэтому вы должны запомнить, что это ускорение свободного падения. Обязательно используйте диаграмму, чтобы увидеть, что вам нужно решить. Так как следующая задача может зависеть от ответа, который вы получили для предыдущей задачи, мы должны убедиться, что последнее вычисление было правильным, иначе мы получим два неправильных ответа.
Вот более простой последний пример! 🤩
Пример 2
Во время тренировки астронавт Шари подпрыгивает на высоте 3,6 м в своей космической капсуле, где ускорение свободного падения составляет 9,76 м/с2. Сколько времени потребуется ей, чтобы вернуться в исходную точку?
Ответ: 1,71 с
Ключ решения 2
Эта задача требует двух шагов.