Как найти значение производной функции в точке: Ваш браузер не поддерживается

6.3.3.Численное вычисление производной функции одного переменного

Известно, что численными приближенными методами производная функции в заданной точке может быть вычислена с использованием формулы конечных разностей. Выражение для вычисления производной функции одного переменной в точке x_k, записанное в конечных разностях, имеет вид:

,

где Δx – очень малая конечная величина.

При достаточно малых значениях Δх, можно с приемлемой точностью получить величину производной функции в точке. Для вычисления производной в MS Excel будем использовать приведенную зависимость. Рассмотрим технологию вычисления производной на примере.

Найти производную функции Y= 2x³ + x²в точкеx=3. Заметим, что производная приведенной функции в точкеx=3 . Напомним, что производная приведенной функции, вычисленная аналитическим методом, равна 60 – это значение нам понадобится для проверки результата, полученного путем вычисления численным методом в электронной таблице.

2))/B2.

После нажатия клавиши Enter получим результат вычисления 60,0000.

Как видим, результат получен такой же, как и при первом способе. Приведенный второй способ является более предпочтительным в случаях, когда нужно построить таблицу значений производной функции для заданных значений аргумента.

Используя приведенную технологию численного вычисления производной функции в заданной точке, проверим, является ли найденная точка x= -0,5 точкой экстремума функцииY= X²+X +2 . Решение приведено на рис. 6.11

Рис. 6.11

Как видно, производная в найденной точке равна нулю, следовательно, найденное в примере значение функции является ее экстремальным значением.

Известно, что чем ниже цена (p), тем больше спрос (D) при постоянной покупательной способности населения. Обычно зависимость спроса от цены в графическом представлении имеет вид ниспадающей линии, чаще всего приближающейся к прямой. В свою очередь, предложение растет с увеличением цены на товар и в графическом представлении имеет восходящей линии.

В экономике представляет интерес условие равновесия спроса и предложения.

Если зависимость спроса от цены определяется функцией D=f(p), а зависимость предложения от цены – S=φ(p), то условие равновесия определяется уравнением:

f(p)= φ(p)

и соответствует точке пересечения кривых D и S. Цена Р₀, при которой выполняется это условие, называется равновесной.

Рассмотрим технологию решения задачи определения точки равновесия на примере.

Зависимость спроса yна некоторый товар от цены

x выражается уравнением f₁(x) =2/x-y + 2, а зависимость предложения от цены – уравнениемf₂(x) = x² – y + 1. Требуется, решив систему уравнений, найти точку равновесия в диапазонес точностью 0,001.

Решение

Приведем исходные уравнения к системе следующего вида:

Создадим последовательность значений xс шагом 0,2.

Рассчитаем значения функций спроса f(x) и предложения φ(x) для сформированной последовательности значенийx(рис. 33).

Построим графики функций по данным таблицы.

Подведем указатель мыши к точке пересечения кривых – отобразятся приближенные координаты точки равновесия. В данном случае цена хв точке равновесия равна 1,6, предложение и спрос характеризуются величиной 3,6 (рис. 6.12).

Рис. 6.12

Применяя приведенную выше технологию, уточним решение. Результат уточнения приведен на рис. 6.13.

Рис. 6.13

Таким образом, равновесное значение цены составляет 1,521, а спрос и предложение находятся в равновесии и выражаются величиной 3,315.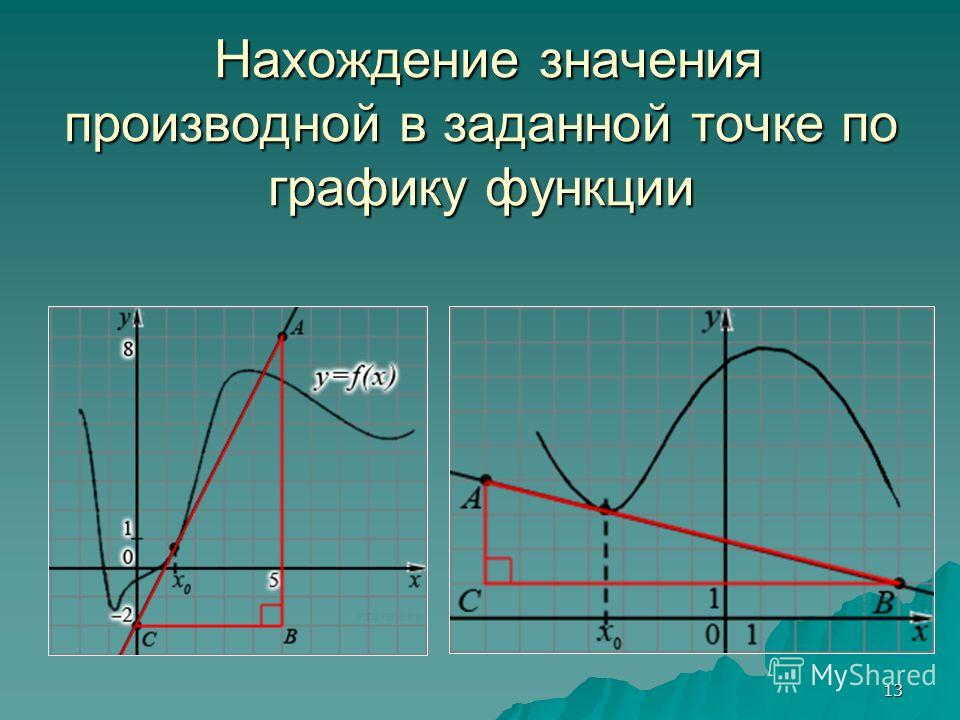

В экономических задачах одни экономические показатели являются функциями Y=f(x) каких – либо других показателей или величин. Иначе говоря, существует зависимость одних показателей от других –Y=f(x).

Так, например, себестоимость продукции зависит от производимого объема C=f(Q), издержки производства – зависят от количества выпускаемой продукции и т.п.

Предельные экономические показатели характеризуют величину прироста величины функции ΔY от прироста ее аргумента Δx:

Так, например, предельная себестоимость характеризует себестоимость ΔС прироста продукции ΔQ:

Если зависимость ΔY от Δx непрерывна, то приведенное разностное уравнение можно заменить производной .

Пусть зависимость издержек производства от объема выпускаемой продукции в денежных единицах выражается формулой C=20Q – 0,05Q³

Требуется определить предельные издержки производства при объеме выпускаемой продукции 10 ден.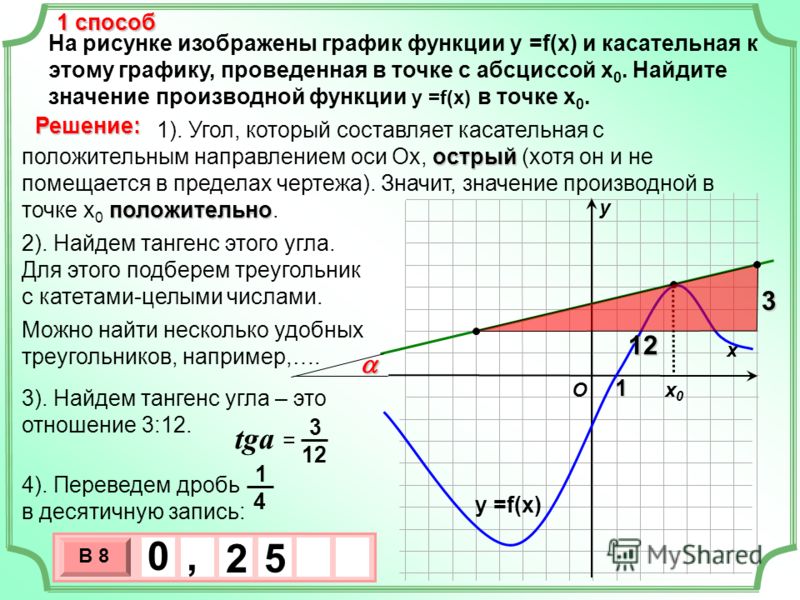 3.

Скопируем введенную формулу в ячейку В3 (рис.6.14).

В ячейку С3 введем формулу вычисления производной: =(B3-B2)/(A3-A2). В ячейки А2 и А3 введем значения Qдля левой и правой окрестности, соответственно (рис. 6.14).

Рис. 6.14

После выполнения приведенных выше операций в ячейке С2 будет получен результат (рис. 6.15).

Рис. 6.15

Таким образом, предельные издержки производства при объеме выпускаемой продукции 10 ден.ед. составляют примерно 4,99999 ден. ед. Зависимость затрат от объема производства задана приведенной ниже таблицей. Требуется найти предельные издержки производства при объеме выпуска х=1,9.

Указания: в данной задаче функция зависимости затрат от объема производства задана не аналитически, а таблично. Поэтому, нужно прежде всего получить аналитическую зависимость в виде интерполяционной функции и используя ее решить задачу в соответствии с приведенной в примере технологией.

Объем производства	Затраты
1	2,7
1,2	3,2
1,4	3,7
1,6	4,1
1,8	4,7
2	5,1
2,2	5,6
2,4	5,8

№ 28.

21 ГДЗ Алгебра 10-11 класс Мордкович. Найдите значение производной функции – Рамблер/класс № 28.21 ГДЗ Алгебра 10-11 класс Мордкович. Найдите значение производной функции – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?

Помогите решить!
Найдите значение производной функции в точке х₀:
а) у = х² + 2х – 1, х₀ = 0;
б) у = х³ – Зх + 2, х₀ = -1;
в) у = х² + Зх – 4, х₀ = 1;
г) у = х³ – 9х² + 7, х₀ = 2.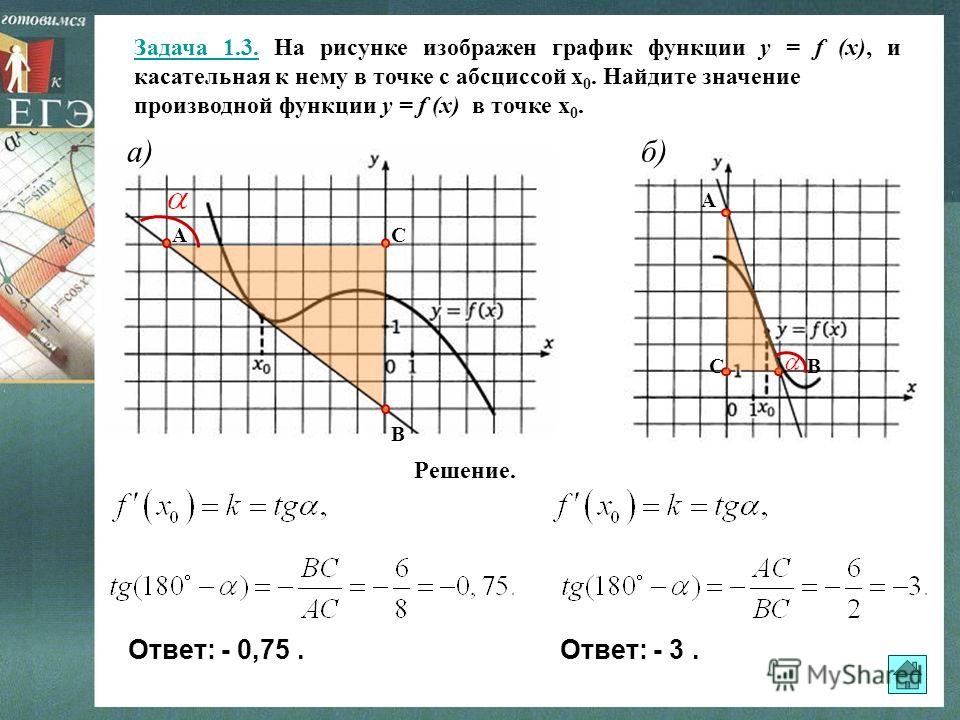
 

ответы

Помогу тебе

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х – 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)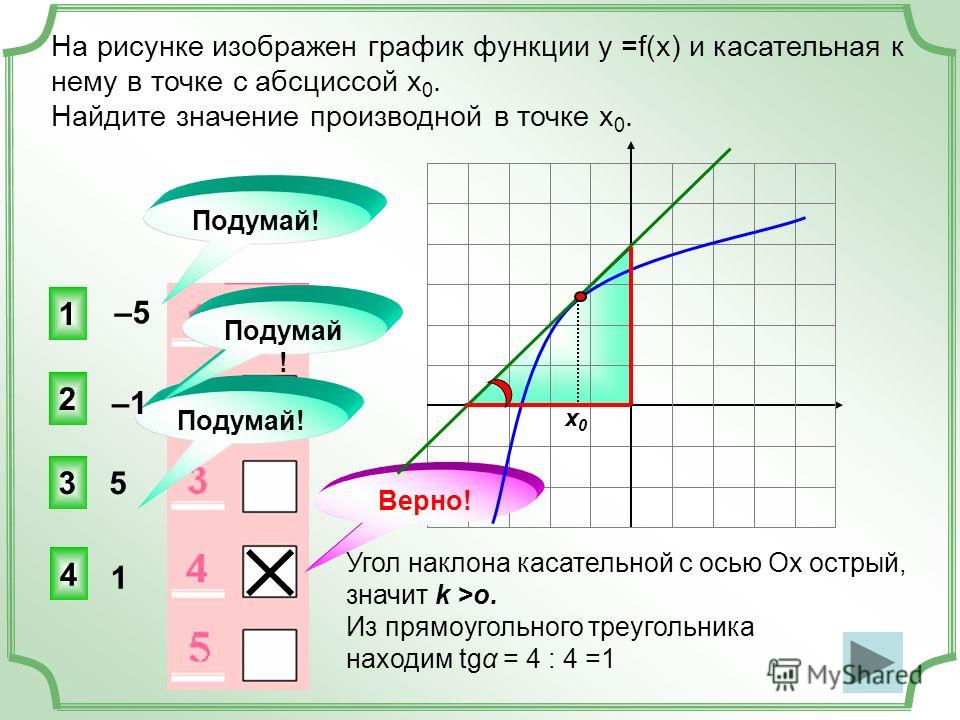

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

Калькулятор производных

– Google

AlleBilderVideosBücherMapsNewsShopping

suchoptionen

Калькулятор производных • С шагами!

www.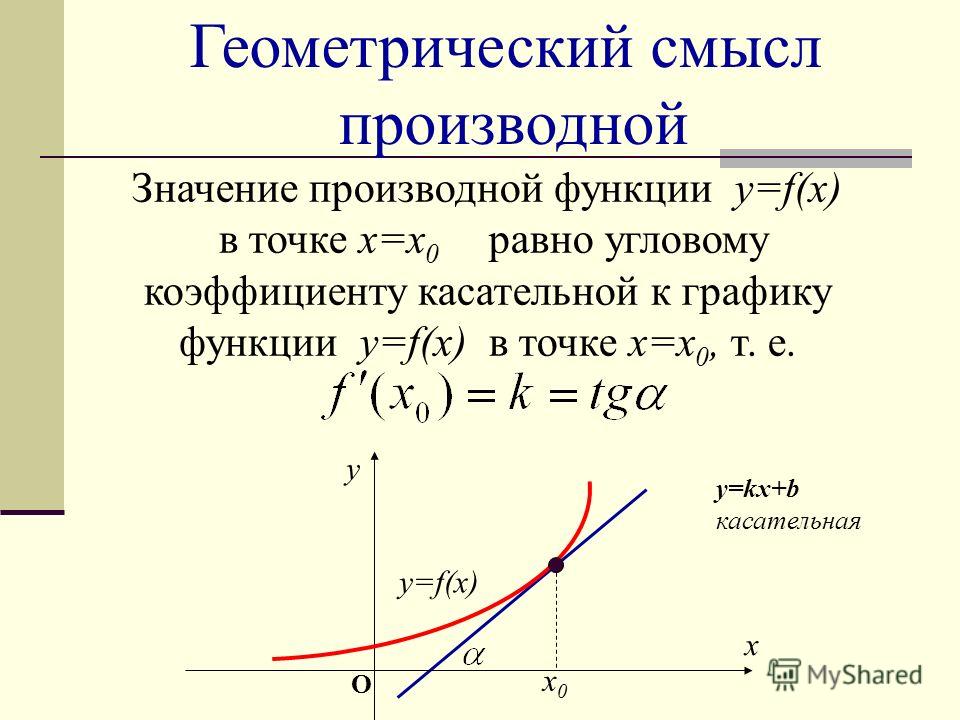 derivative-calculator.net

Решите производные с помощью этого бесплатного онлайн-калькулятора. Пошаговое решение и графики прилагаются!

Сколько раз дифференцировать?: 1 2 3 4 5
Зависимая переменная: (будет рассматриваться как функция): ax_____abcdfghjklmnopqrstuvwxyz

Калькулятор производных – – Symbolab

www.symbolab.com › Step-by-Step › Исчисление

Бесплатный калькулятор производных – дифференцируйте функции со всеми шагами. Введите любую производную функции, чтобы получить решение, шаги и график.

Калькулятор производной первой производной · Калькулятор производной в точке

Калькулятор производной – Wolfram|Alpha

www.wolframalpha.com › калькуляторы › производная-c… производные порядка и более высокого порядка, предоставляя информацию, необходимую для понимания производных …

Калькулятор производных – Mathway

www.mathway.com › Калькулятор › производный-калькулятор

Калькулятор производных поддерживает вычисление первой, второй.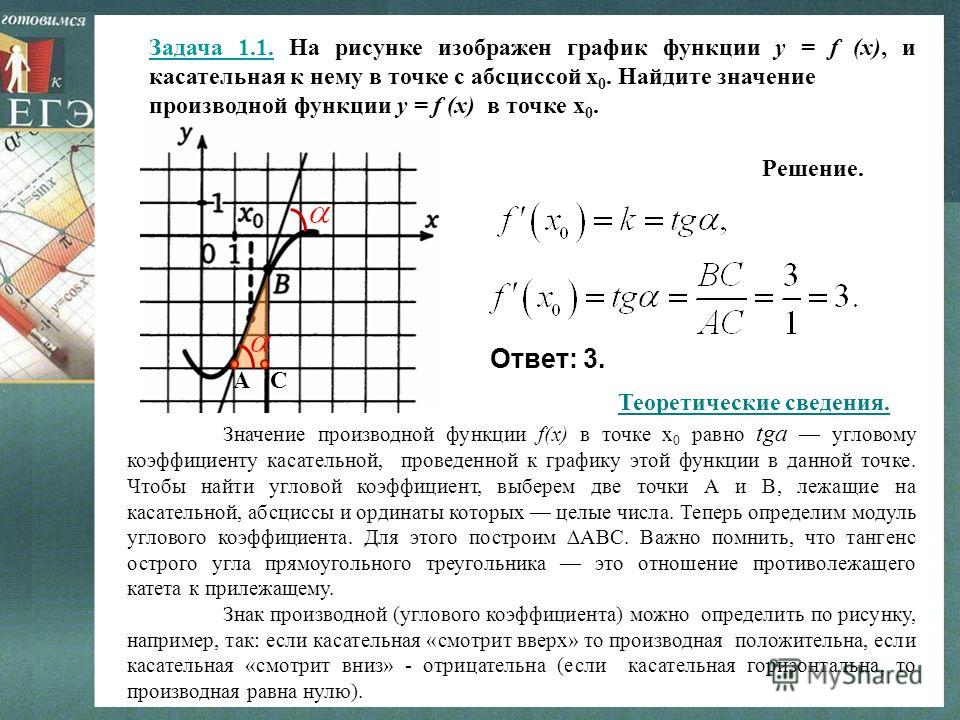 …, четвертой производной, а также неявное дифференцирование и нахождение нулей/корней .

Калькулятор производных с шагами | Калькулятор дифференциации

calculate-derivative.com

Калькулятор производных поможет вам оценить производные онлайн. Калькулятор дифференцирования с шагами показывает промежуточные шаги, графики, корни, домен и т. д.

Калькулятор производных – MathPapa

www.mathpapa.com › Калькулятор производных

Калькулятор производных дает пошаговую помощь в нахождении производных. Этот калькулятор находится в стадии бета-тестирования. Мы ценим ваши отзывы, чтобы помочь нам улучшить его.

Ähnliche Fragen

Как рассчитать производные?

Какой калькулятор для деривативов лучше?

Какая производная от 3×2?

Калькулятор производных с шагами – Open Omnia

openomnia.com › калькулятор производной

Вычисление производной функции. Получите пошаговые решения. Попробуйте Open Omnia сегодня.

Калькулятор деривативов – Börse Frankfurt

www.boerse-frankfurt.de › производные › деривативы-…

Калькулятор деривативов. С помощью калькулятора деривативов вы можете проанализировать, как цена вашего дериватива будет вести себя в будущем, если цена базового …

Калькулятор и решатель производных – SnapXam

www.snapxam.com › калькуляторы › расчет производных…

Калькулятор производных онлайн с решением и шагами. Подробные пошаговые решения ваших задач на производные онлайн с помощью нашего математического решателя и калькулятора …

Калькулятор производных – eMathHelp

www.emathhelp.net › калькуляторы › исчисление-1 › вычисление…

Онлайн-калькулятор будет вычислять производную любой функции, используя общие правила дифференцирования (правило произведения, частное правило, цепное правило и т. д.)

ähnliche suceanfragen

Интегральный калькулятор

Калькулятор неявного дифференцирования

Рассчитайте производственный питон

Правила производного

DERVATIATE DERVATIATE

9000SH. Дифференциация

Следующие шаги были бы полезны, чтобы найти максимальное и минимальное значение функции, используя первую и вторую производные.

Шаг 1: 

Пусть f(x) f(x) — функция. Найдите первую производную от f(x), которая равна f'(x).

Шаг 2 : 

Приравняйте первую производную f'(x) к нулю и найдите x, которые называются критическими числами.

Шаг 3: 

Найдите вторую производную f(x), которая равна f”(x). 

Шаг 4: 

Подставьте критические числа, найденные на шаге 2, во вторую производную f”(x).

Шаг 5:

Если f”(x) < 0 для некоторого значения x, скажем, x = a, то функция f(x) максимальна при x = a. 

Если f”(x) > 0 для некоторого значения x, скажем, x = b, то функция f(x) минимальна при x = b. 

Шаг 6: 

Чтобы получить максимальное и минимальное значения замена функции x = a и x = b в f(x). 

Максимальное значение = f(a)

Минимальное значение = f(b)

Шаг 7: 

Максимальная точка: (a, f(a) )

Минимальная точка: (b, f(b))

Найдите максимальную и минимальную точки следующих функций:

Пример 1:

2x ³ – 3x ² – 12x + 5

Решение:

let F (x) = 2x ³ – 3x ² – 12x + 5.

49.

4.

3

40003

400044.

4.

4.

.

4.

4.

4.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

. – 3x ² – 12x 5.

. ‘(x) = 2(3x ² ) – 3(2x) – 12(1) + 0

f'(x) = 6x ² – 6x – 12

Приравнивание f'(x) к нулю ,

f'(x) = 0

 6x ² – 6x – 12 = 0

Разделите обе части на 6. (х + 1) = 0

x – 2 = 0 или x + 1 = 0

x = 2 или x = -1

Найдите вторую производную “(x) = 6(2x) – 6(1) – 0

f”(x) = 12 x – 6

Подставим x = 2 в f”(x).

f”(2) = 12(2) – 6

= 24 – 6

f”(2)  =  18 > 0 Минимум

Чтобы найти минимальное значение, подставьте x = 2 в f(x).

f(x ) = 2x ³  – 3 x ² – 12 х + 5

f (2) = 2(2) ³ – 3(2) ² – 12(2) + 5

  = 2(8) – 3(4) – 24 + 5

= 16 – 12 – 24 + 5

= 21 – 36

= -15

Замена x = -1 в f”(x).
‘-

3) = 12(-1) -6

  =  -12 – 6

f”(-1) = -18 > 0 Максимум

Чтобы найти максимальное значение, подставьте x = -1 в f(x).

f(x) = 2x ³  – 3x ²  – 12 х + 5

f(-1) = 2(-1) ³  – 3(-1) ²  – 12(-1) + 5

= 2(-1) – 3(1) + 12 + 5

= -2 – 3 + 12 + 5

= -5 + 17

= 12

Следовательно,

, максимальная точка = 1 ((1)

точка минимума = (2, 15)

Пример 2:

Найдите максимальное и минимальное значение функции0003

Решение:

Пусть f(x) = x ³ – 3x ² – 9 x + 12.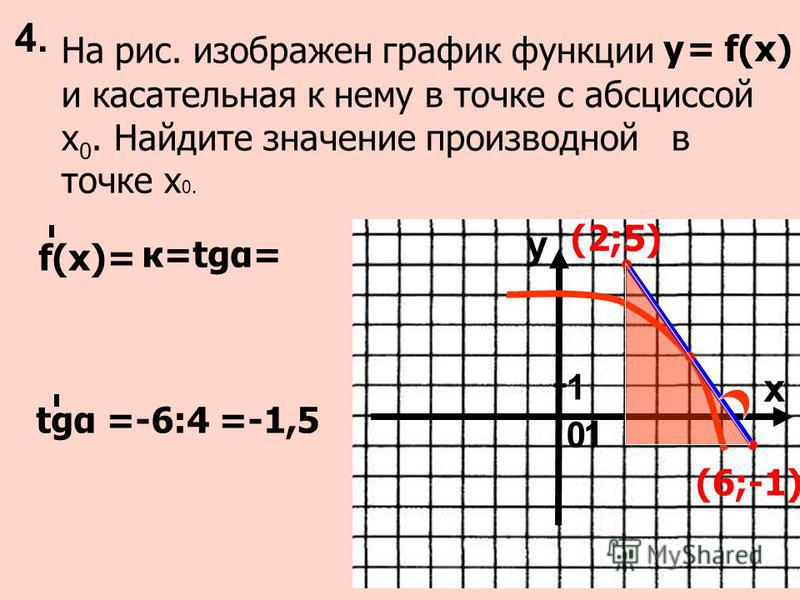

f'(x) = 3x ² – 3(2x) – 9(1) + 0

f'(x) = 3x ² – 6x – 9

f'(x) = 0

3x ² – 6x – 9 = 0

Разделить обе части на ² – 2x – 3 = 0

(x + 1)(x – 3) = 0

x + 1 = 0 или x – 3 = 0

x = -1 или x = 3

Найдите вторая производная:

f'(x) = 3х ² – 6х – 9

f”(х) = 3(2х) – 6(1) – 0 x = -1 в f”(x).

f”(-1) = 6(-1) – 6

= -6 – 6

f”(-1) = -12 < 0 - ---> f(x) является максимальным

Чтобы найти максимальное значение, подставьте x = -1 в f(x).

f(-1) = (-1) ³ – 3(-1) ²  – 9(-1) + 12

= -1 – 3(1) + 9 + 12

= -1 – 3 + 9 + 12

= -4 + 21

= 17

Замена x = 3 в f”(x)

f”(3) = 6(3) – 6

  = 18 – 6

 f”(3) = 12 > 0 —-> f(x) минимально

Чтобы найти минимальное значение, замените x = 3 в f(x).