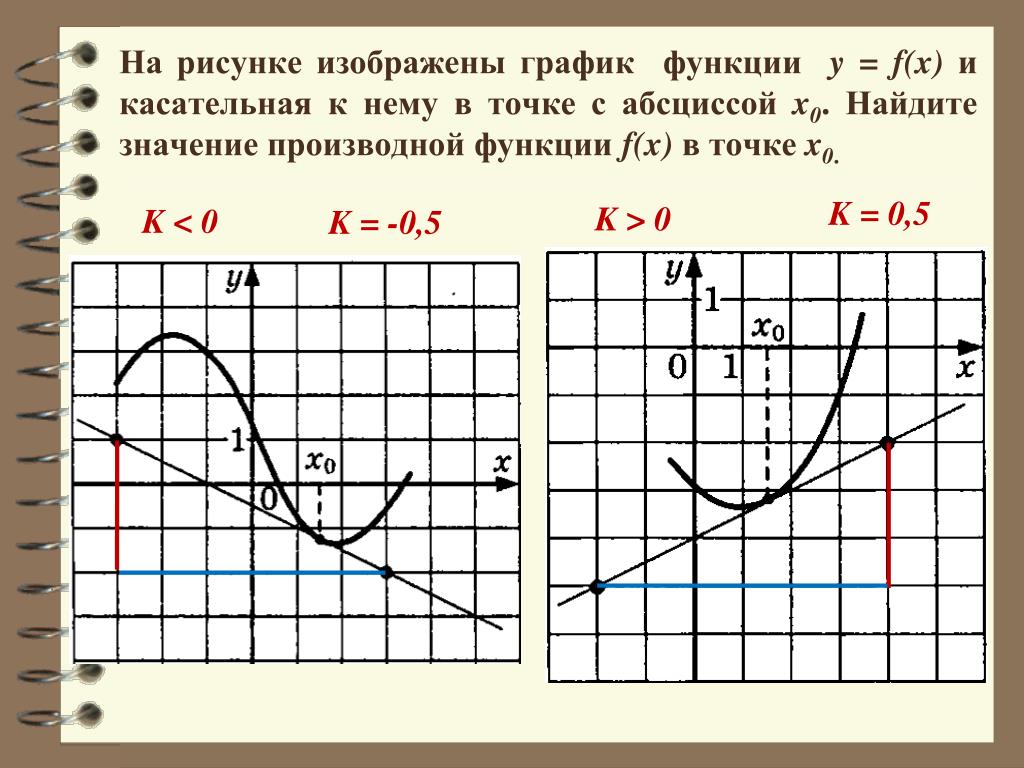
Как определить значение производной по графику. Производная функции. Геометрический смысл производной. Вычисление точек максимума и минимума
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями.
 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. - Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2).
 Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.

- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Производная функции – одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна . Мы не будем сейчас стремиться к математической строгости изложения. Самое главное – понять смысл.
Запомним определение:
Производная – это скорость изменения функции.
На рисунке – графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден – третья. У нее самая большая скорость изменения, то есть самая большая производная.
У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная , – разная. Что касается Матвея – у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами – насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной – то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
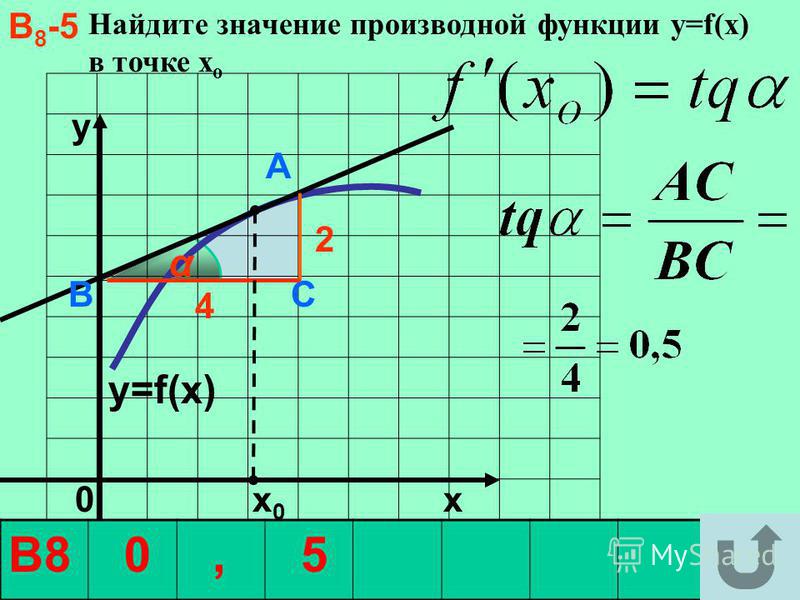
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого – тангенс угла наклона касательной .
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание – в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других – убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси .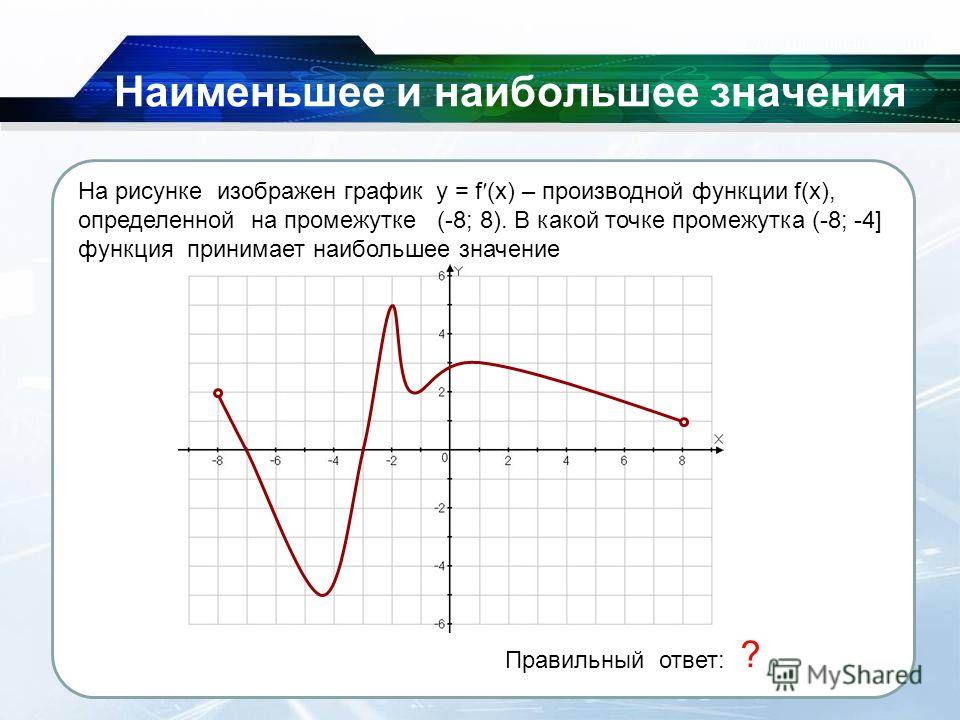 Значит, в точке производная положительна.
Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка – точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке – точке минимума – производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | – | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое – на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала – и после точки продолжает возрастать. Знак производной не меняется – она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев 26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции – все они возрастают на отрезке
Рассмотрите, например, функции – все они возрастают на отрезке
Владлен Писарев 02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) – входят.
Учитывая, что первая часть ЕГЭ для “средней группы детского сада”, то наверное такие нюансы- перебор.
Отдельно, большое спасибо за “Решу ЕГЭ” всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова 20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z 28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x = −3 меньше, чем её значение в правом конце x = −2.
Ответ: φ 2 (−3) φ 2 (−2)
2) Пользуясь графиком первообразной Φ 2 (x ) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ 2 (−1) или φ 2 (4)?
По графику первообразной видно, что точка x = −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно.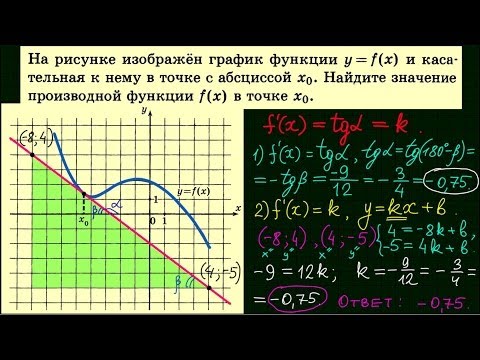 Точка x = 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод – значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Точка x = 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод – значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ 2 (−1) > φ 2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: “−10″,”−9”, “−8″,”0”, “1”,”2″, “3”,”4″, “5”,”6″, “7”,”8″, “16”,”17″, “18”. Всего 15 точек.
Перечислим целые точки внутри этих интервалов: “−10″,”−9”, “−8″,”0”, “1”,”2″, “3”,”4″, “5”,”6″, “7”,”8″, “16”,”17″, “18”. Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать “точки”, как правило, имеют в виду только значения аргумента x , которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек – значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а “разворачивается”. Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f ” (x ) отрицательна.
Определите количество целых точек, в которых производная функции f ” (x ) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: “−7″,”−6”, “−5″,”−4”, “−3″,”−2”, “9”,”10″, “11”,”12″, “13”,”14″, “15”. Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием – точки экстремума .
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума ).
Однако необходимое условие – это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума является смена знака производной: если производная в точке меняет знак с “+” на “−”, то это точка максимума функции; если производная в точке меняет знак с “−” на “+” , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции.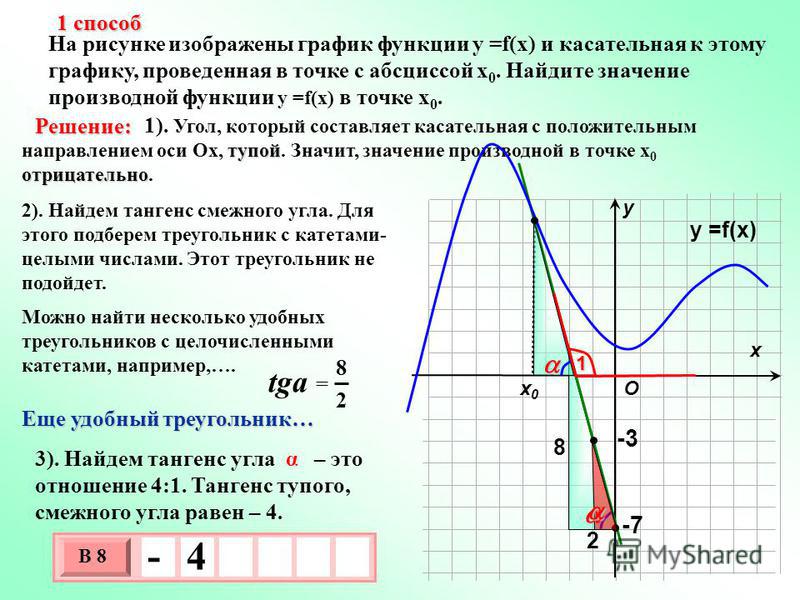 Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y = kx + b , где k – коэффициент наклона этой прямой к оси Ox . В нашем случае k = 0, т.е. прямая y = 6 не наклонена, а параллельна оси Ox . Значит искомые касательные также должны быть параллельны оси Ox и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 – две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y = f (x ), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x 1 = 4, минимум в точке x 2 = 8.
x 1 + x 2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f ” (x ) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−11;23).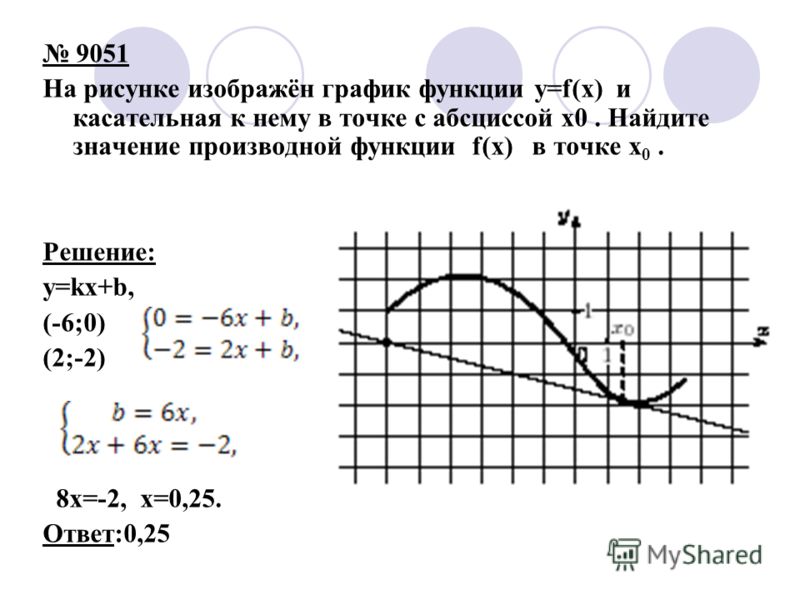 В какой точке отрезка [−6;2] функция f (x ) принимает наибольшее значение.
В какой точке отрезка [−6;2] функция f (x ) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x = −6.
Ответ: −6
Замечание: По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x = −6, x = −2, x = 2. Но в точке x = −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x = 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек максимума функции f (x ), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть в точках, где её производная равна нулю. На заданном отрезке это точки: x = −2, x = 2, x = 6, x = 10. Но согласно достаточному условию он точно будет только в тех из них, где знак производной меняется с “+” на “−”. На графике производной мы видим, что из перечисленных точек такой является только точка x = 6.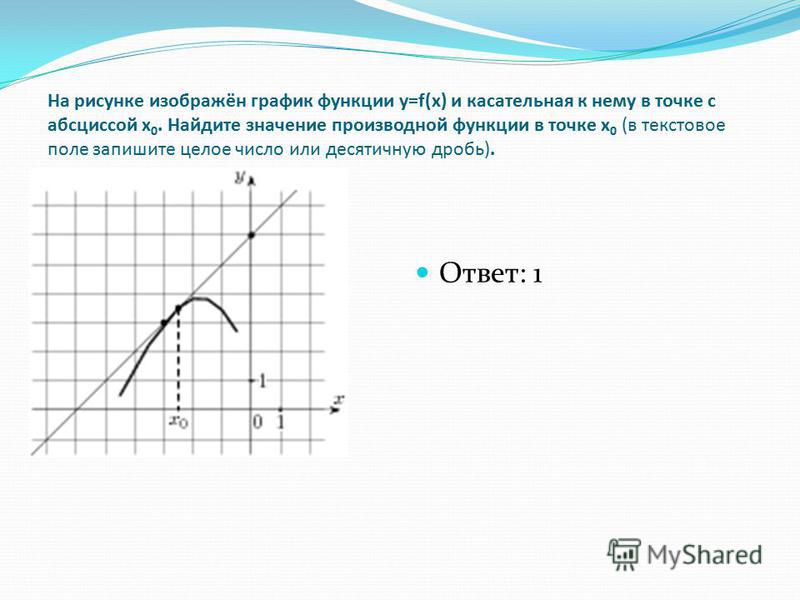
Ответ: 1
Задача 9
На рисунке 2 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек экстремума функции f (x ), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x = 2, x = 6, x = 10, x = 14, x = 18. Но в точке x = 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f (x ). В ответе укажите длину наибольшего из них.
В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три – (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l = 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f ” (x ) – производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f (x ) параллельна прямой y = −2x − 11 или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной – угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy .
На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy .
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания – на геометрический смысл первообразной – будут рассмотрены в другом разделе.
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
на какой высоте над поверхностью Земли ускорение свободного падения в 4 раза меньше, чем на поверхности Земли? Радиус Земли примите 6400 км.
Решено
1. Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10 см. 2
2
Как найти наибольшее и наименьшее значения функции на отрезке.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции , то функция возрастает на этом промежутке.
Если на промежутке I производная функции , то функция убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с “+” на “-“.
В точке минимума функции производная меняет знак с “-” на “+”.
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию . График этой функции выглядит так:
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее – в левом: .
2. Рассмотрим функцию на отрезке
Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее – в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.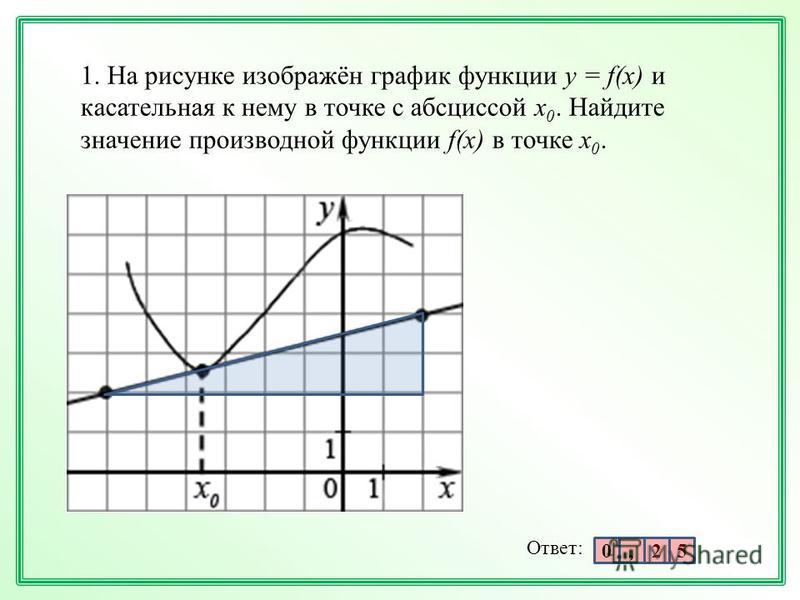
3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть и .
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть и .
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции – множество действительных чисел.
2.
3. , если или
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции на отрезке .
1. Функция определена при всех действительных значениях х
2.
3.
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции на отрезке [].
1. ОДЗ функции
2.
Производная равна нулю при , однако, в этих точках она не меняет знак:
, следовательно, , значит, , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при .
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции на отрезке [].
1. ОДЗ функции :
2.
3.
,
Расположим корни этого уравнения на тригонометрической окружности.
Промежутку принадлежат два числа: и
Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки и производная меняет знак.
Изобразим смену знаков производной функции на координатной прямой:
Очевидно, что точка является точкой минимума ( в ней производная меняет знак с “-” на “+”), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции
Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.
Наибольшее и наименьшее значение функции | ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= – sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ – это точка минимума.
 3-5=6-90-5= -89$
3-5=6-90-5= -89$Наибольшее значение равно $967$
Ответ: $967$
Практика: решай 12 задание и тренировочные варианты ЕГЭ по математике (профильной)
В какой точке значение производной набольшее
Дорогие друзья! В группу заданий связанных с производной входят задачи — в условии дан график функции, несколько точек на этом графике и стоит вопрос:
В какой точке значение производной наибольшее (наименьшее)?
Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.
Кратко повторим:
Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.
Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.

*Имеется ввиду угол между касательной и осью абсцисс.
Далее:
1. На интервалах возрастания функции производная имеет положительное значение.
2. На интервалах её убывания производная имеет отрицательное значение.
Рассмотрим следующий эскиз:
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.
В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.
Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.
При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки 3, 5 и 6 образуют с осью оХ углы лежащие в пределах от 0 до 90о, а прямые проходящие через точки 1, 2 и 4 образуют с осью оХ углы в пределах от 90о до 180о.

*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.
Теперь важный вопрос!
А как изменяется значение производной? Ведь касательная в разных точках графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.
*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:
Прямые образуют с осью оХ углы в пределах от 0 до 90о
Прямые образуют с осью оХ углы в пределах от 90о до 180о
Поэтому, если будут стоять вопросы:
— в какой из данных точек графика значение производной имеет наименьше значение?
— в какой из данных точек графика значение производной имеет наибольшее значение?
то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180о.

*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.
Значение тангенса изменяется следующим образом:
При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;
При изменении угла наклона прямой от 90о до 180о значение тангенса, а значит и производной, изменяется соответственно –∞ до 0.
Наглядно это видно по графику функции тангенса:
Говоря простым языком:
При угле наклона касательной от 0о до 90о
Чем он ближе к 0о, тем больше значение производной будет близко к нулю (с положительной стороны).
Чем угол ближе к 90о, тем больше значение производной будет увеличиваться к +∞.
При угле наклона касательной от 90о до 180о
Чем он ближе к 90о, тем больше значение производной будет уменьшаться к –∞.

Чем угол будет ближе к 180о, тем больше значение производной будет близко к нулю (с отрицательной стороны).
317543. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки –1 и 1) и две интервалам на которых функция возрастает (это точки –2 и 2).
Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим.

Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.
Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:
Видим, что тупой угол между прямой b и осью оХ находится «ближе» к 180о, поэтому его тангенс будет больше тангенса угла, образованного прямой а и осью оХ.
Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.
317544. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки –1 и 4) и две интервалам, на которых функция возрастает (это точки –2 и 1).
Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках –2 и 1 она имеет положительное значение.
 Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке х = 4 будет наименьшим.
Ответ: 4
Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180о.
Общие рекомендации:
1. Сначала определите знаки производной в данных точках (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).
2. Постройте касательные в этих точках.
3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.
4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.

*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без графика.
На этом всё. Успехов Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
{\prime}\left(a\right)\left(x-a\right)$, но это дает неверный ответ. Я также пытался приблизиться к созданию сериала о Тейлоре; но это ужасно провалилось.Я знаю, что значение должно быть меньше $f\left(6\right)$, потому что тангенс отрицателен и вторая производная тоже отрицательна.
скопировал вопрос именно из pdf.
- исчисление
$\endgroup$
8
$\begingroup$
Поскольку это вопрос с несколькими вариантами ответов, в котором спрашивается только, какое значение $f(7)$ может иметь , вы должны работать над устранением возможных вариантов. Функция имеет значение $f(6) = 3$, а первая производная равна $f(6) = -\frac{1}{2}$, так что если бы не было изменения наклона на интервале ($f ”(x) = 0$), функция будет иметь $f(7) = 2,5$.
 Однако наклон составляет , уменьшающийся на при $x = 6$ ($f”(6) < 0$), поэтому наклон, вероятно, будет более отрицательным, чем $-\frac{1}{2}$ на интервале , оставив только 9{\prime\prime}(6) = -2$, мы знаем, что $|M| \geq 2$, что создает нижнюю границу для $|M|$.
Итак, любое значение $y \in \mathbb{R}$, удовлетворяющее этому уравнению, является возможным ответом,
$$
\frac{3}{2} = \frac{5}{2} - 1 \leq y \leq \frac{5}{2} + 1 = \frac{7}{2}
$$
Таким образом, наилучший возможный ответ действительно $2$, однако $2,5$ также находится в допустимых пределах.
Однако наклон составляет , уменьшающийся на при $x = 6$ ($f”(6) < 0$), поэтому наклон, вероятно, будет более отрицательным, чем $-\frac{1}{2}$ на интервале , оставив только 9{\prime\prime}(6) = -2$, мы знаем, что $|M| \geq 2$, что создает нижнюю границу для $|M|$.
Итак, любое значение $y \in \mathbb{R}$, удовлетворяющее этому уравнению, является возможным ответом,
$$
\frac{3}{2} = \frac{5}{2} - 1 \leq y \leq \frac{5}{2} + 1 = \frac{7}{2}
$$
Таким образом, наилучший возможный ответ действительно $2$, однако $2,5$ также находится в допустимых пределах.edit: добавлено больше информации об определении границы ошибки Лагранжа поэтому $\frac{3}{2} \leq y \leq \frac{5}{2}$, поскольку производная не может быть больше, чем $\frac{-1}{2}$.
$\endgroup$
3
$\begingroup$
В упражнении указано, что точек перегиба нет, т.е. $f”$ всегда меньше $0$.
 Это означает, что $f(6+a) \leq f(6) + f'(6)*(a-6)$. В наших случаях это дает нам $f(7)=f(6+1) \leq 3+ (-0,5)*1 = 2,5$ . Это означает, что $2,5$ и $2$ являются единственными возможными ответами. Но поскольку $f”$ меньше, чем $0$, производная становится еще меньше, поэтому правильным ответом является $2$.
Это означает, что $f(6+a) \leq f(6) + f'(6)*(a-6)$. В наших случаях это дает нам $f(7)=f(6+1) \leq 3+ (-0,5)*1 = 2,5$ . Это означает, что $2,5$ и $2$ являются единственными возможными ответами. Но поскольку $f”$ меньше, чем $0$, производная становится еще меньше, поэтому правильным ответом является $2$.$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Нахождение максимума и минимума с помощью производных
Где находится функция в верхней или нижней точке? Расчет может помочь!
Максимум — это верхняя точка, а минимум — нижняя точка:
В плавно изменяющейся функции максимум или минимум всегда находится там, где функция сглаживает (за исключением седловой точки ).
Где он выравнивается? Где наклон равен нулю .
Где нулевой наклон? Производная говорит нам!
Перейдем сразу к примеру:
Пример: Мяч подброшен в воздух. Его высота в любой момент времени t определяется как:
h = 3 + 14t − 5t 2
Какова его максимальная высота?
Используя производные, мы можем найти наклон этой функции:
d dt h = 0 + 14 − 5(2t)
= 14 − 10t(см.
 ниже этот пример, как мы нашли, что производная.)
ниже этот пример, как мы нашли, что производная.)Теперь найдите, когда наклон составляет ноль :
14 – 10t = 0
10t = 14
t = 14 /10 = 1,4
. Склон равен нуле. секунд
А высота в это время равна:
h = 3 + 14×1,4 − 5×1,4 2
h = 3 + 19,6 − 9,8 = 12,8
900 А 2 максимум высота 12,8 м (при t = 1,4 с)Краткий обзор производных
Производная в основном находит наклон функции.
В предыдущем примере мы взяли это:
h = 3 + 14t − 5t 2
и получили следующую производную:
d dt 5 h = 0 + 20 14 = 14 − 10t
Что говорит нам о наклоне функции в любой момент времени t
Мы использовали следующие производные правила:
- Наклон постоянного значения (например, 3) равен 0
- Наклон линии например, 2x равно 2, поэтому 14t имеет наклон 14
- Функция квадрата , такая как t 2 , имеет наклон 2t, поэтому 5t 2 имеет наклон 5(2t)
- А затем мы сложили их: 0 + 14 − 5(2t)
Откуда мы знаем, что это максимум (или минимум)?
Мы видели это на графике! Но в остальном.
 .. на помощь снова приходят производные.
.. на помощь снова приходят производные.Возьмите производную от наклона (вторая производная исходной функции):
Производная от 14 − 10t равна −10
Это означает, что наклон постоянно уменьшается (-10): при перемещении слева направо наклон начинается с положительного значения (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :
Наклон, который становится меньше (и проходит через 0), означает максимум.Это называется тестом второй производной
На графике выше я показал наклон до и после, но на практике мы делаем тест в точке, где наклон равен нулю :
Проверка второй производной
Когда наклон функции равен нулю при x , а вторая производная при x :
- меньше 0, это локальный максимум
- больше 0, это локальный минимум
- равно 0, то тест не пройден (хотя могут быть и другие способы узнать)
«Вторая производная: меньше 0 — максимум, больше 0 — минимум»
Example: Find the maxima and minima for:
y = 5x 3 + 2x 2 − 3x
The derivative (slope) is:
d dx y = 15x 2 + 4x − 3
Квадратичный с нулями в:
- x = −3/5
- х = +1/3
Могут ли они быть максимальными или минимальными? (Пока не смотрите на график!)
Вторая производная y” = 30x + 4
При x = −3/5:
y” = 30(−3/5) + 4 = −14
меньше чем 0, поэтому −3/5 является локальным максимумом
При x = +1/3:
y” = 30(+1/3) + 4 = +14
больше 0, поэтому + 1/3 — локальный минимум
(Теперь можно посмотреть на график.
 )
)Слов
Высшая точка называется максимум (множественное число максимум ).
Нижняя точка называется минимумом (множественное число минимум ).
Общее слово для обозначения максимума или минимума экстремум (множественное число экстремум ).
Мы говорим местный максимум (или минимум), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.
Еще один пример
Пример: Найдите максимум и минимум для:
y = x 3 − 6x 2 + 12x − 5
Производная:
d dx y = 3x 2 − 12x + 12
Какое квадратичное число с одним нулем в x = 2
является минимумом или максимумом?
Вторая производная равна y” = 6x − 12
При x = 2:
y” = 6(2) − 12 = 0 И вот почему:
Это точка перегиба («седловая точка»)… наклон действительно становится нулевым, но это не максимум и не минимум.

Должен быть дифференцируемым
И есть важный технический момент:
Функция должна быть дифференцируемой (производная должна существовать в каждой точке своей области определения).
Пример: Как насчет функции f(x) = |x| (абсолютная величина) ?
|х| выглядит так: При x=0 очень резкое изменение!
На самом деле он там не дифференцируем (как показано на дифференцируемой странице).
Таким образом, мы не можем использовать метод производной для функции абсолютного значения.
Функция также должна быть непрерывной, но любая дифференцируемая функция также непрерывна, так что мы защищены.
Производные / Дифференциальное исчисление: определения, правила
Производная — это другое название наклона касательной в точке. Здесь производные в точках А и В равны нулю.
Содержание :
Основы
- Что такое производная?
- Формула: предельное определение производной
- Формула: предельное определение производной
- Примеры TI-89
- Обозначение дифференциации
- Таблицы производных (Краткое справочное руководство по общим производным
- Правило постоянного коэффициента
- Правило продукта
- Цепное правило
- Функции с показателями степени (степенное правило ).

- Частное правило
- Правило взаимности: определение, примеры
- Правило суммы
Специальные функции
- Как найти производную простых функций:
- Постоянные функции (например, y = 5, y = 99)
- лн (натуральное бревно)
- Грех 3x
- Тан х
- Производные обратной функции.
- Производная тригонометрической функции.
Дополнительные определения и примеры
- Автоматическое дифференцирование
- Непрерывная производная
- Конвективная производная
- Критические числа
- Производная не существует в точке: 7 примеров
- Левая производная и правая производная
- Отличие по частям
- Направленные производные
- Эпидериваты
- Явное дифференцирование
- Внешняя производная
- Формула Фаа ди Бруно: определение, пример, шаги
- Четвертые производные
- Дробное исчисление
- Пятая производная (треск)
- Тест первой производной
- Дифференциал Гато
- Общее правило Лейбница
- Обобщенная производная: обзор, примеры
- Производные высшего порядка
- Производная Хукухара: определение
- Неявное дифференцирование
- Lanczos Производная
- Производная Ли
- Линейность дифференцировки
- Местная производная
- Логарифмическая производная
- Смешанная производная (частичная, повторяющаяся)
- N-ая производная
- Численное дифференцирование
- Односторонняя производная
- Параметрическая производная
- Частная производная
- Полярная производная
- Тест второй производной
- Симметричная производная
- Третьи производные
- Общий дифференциал/производная: формула, пример
- Когда функция не дифференцируема?
- Слабые производные
Проще говоря, это мгновенная скорость изменения.
 Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени.
Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени.Следующая формула дает более точное (т.е. более математическое) определение.
Есть коротких пути, , но когда вы впервые начнете изучать исчисление, вы будете использовать формулу.
Нередко дойдя до конца семестра, вы все еще не знаете точно, что это такое! Это потому, что определение не сразу интуитивно понятно; вы действительно поймете, что это такое, после того, как вы практиковались — и практиковались. Это как знать, что такое амбушюр при игре на кларнете; вам могут сказать, что это размещение языка, но требуется много недель (иногда месяцев) практики, прежде чем вы действительно хорошо поймете, как сделать идеальный анбушер и почему это важно.
Производные можно найти несколькими способами. Нахождение производных с использованием предельного определения производной — это один из способов, но он требует некоторых сильных навыков алгебры.
 Посмотрите видео с парой быстрых пошаговых примеров:
Посмотрите видео с парой быстрых пошаговых примеров: Предельное определение производных примеров
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Пример задачи №1: Найдите производную f(x) = √(4x + 1)Шаг 1: Вставить функцию в формулу. Функция равна √(4x + 1), поэтому:
f'(x) = lim Δx → 0 √( 4( x + Δx ) + 1 – √(4x + 1)) / Δx.
Если это выглядит запутанно, все, что мы сделали, это заменили «x» в формуле на x + Δx в первой части формулы.Шаг 2: Используйте алгебру для работы с формулой. Здесь вам пригодятся сильные навыки алгебры, потому что все формулы разные.
- Умножить верх и низ на √( 4( x + ∆x) + 1 + √(4x + 1):
f'(x) = lim ∆x → 0 √( 4( x + ∆x) + 1 – √(4x + 1 ) ) * √( 4( x + ∆x) + 1 + √(4x + 1) / ∆x* √( 4( x + ∆x) + 1 + √(4x + 1)
, что сводится к:
= lim ∆x → 0 4(x + Δx) + 1 – (4x + 1) / Δx(√ (4x + Δx) + 1) + √ 4x + 1 - Распределить 4:
= lim Δx → 0 (4x + 4Δx + 1 – 4x – 1) / (Δx(√ (4x + Δx) + 1) + √ (4x + 1) - Удалить термины.
 В этом случае можно удалить 4x, Δx и 1.
В этом случае можно удалить 4x, Δx и 1.
= lim Δx → 0 4 / ((√ (4x + Δx) + 1) + √ 4x + 1))
Шаг 3: Возьмите предел. Δx выпадет (потому что это незначительное приращение). Опять же, здесь помогут сильные навыки алгебры:
= 4 / ((√ (4x + 1) + √ 4x + 1)
= 4 / 2 √(4x + 1)
= 2 / √(4x + 1)Вот так
Вернуться к началу
Почему важна производная
По сути, они важны, потому что позволяют извлекать информацию, о которой вы не знали 9.0045 Например, если вы знаете, где находится объект (т. е. у вас есть функция положения), вы можете использовать производную, чтобы найти скорость, ускорение или рывок (скорость изменения ускорения). Как? Производная от…
- …положения – это скорость.
- …скорость — это ускорение.
- …ускорение резкое.
Вы можете продолжать брать производные (например, четвертую, пятую), извлекая все больше и больше информации из этой простой функции положения.
 И это работает не только с позицией; Исчисление может работать с любой функцией.
И это работает не только с позицией; Исчисление может работать с любой функцией.Поиск производных на TI 89 или TI 89 Titanium включает те же шаги. Это потому, что два калькулятора по сути одинаковы, за исключением нескольких наворотов на Титаниуме, таких как дополнительная память. Эти обновления не влияют на то, как вы находите деривативы.
- Производная TI 89/титановые ступени
- Оценка производной по определенному значению,
- Нахождение высших производных (2-я, 3-я…),
Пример задачи: Найдите производную f(x) = 3x.
Шаг 1: Нажмите F3.
Шаг 2: Выберите «1: d(дифференцировать». Используйте клавишу со стрелкой вниз или , введите «1», чтобы выбрать его.
Шаг 3: Нажмите ENTER.
Шаг 4: Введите
Шаг 5: Введите X
Шаг 6: Введите закрывающую скобку
Шаг 7: Нажмите ENTER.
 Решение (3 в этом примере) находится в правой части экрана.
Решение (3 в этом примере) находится в правой части экрана.
2. Оценка производной по определенному значению
Шаг 1: Выполните шаги с 1 по 4 выше.
- Нажмите кнопку F3
- Выберите «1: d(дифференцировать»
- Нажмите ВВОД
- Введите имя функции с запятой.
- Тип Х
Шаг 2: Закройте круглые скобки «)», затем введите вертикальную черту (называемую символом «с»). На TI-89 вы найдете « | ” с левой стороны. Пока не нажимайте ввод .
Шаг 3: Введите значение, которое вы пытаетесь найти. Например, введите x=3, если вы пытаетесь найти значение производной при x = 3. Нажмите ENTER .
3. Нахождение старших производных (2-я, 3-я…)
Пример задачи: Найдите вторую производную f(x) = 3x 2 на TI 89.
Шаг 1: Выполните шаги с 1 по 4 в первом разделе выше:
- Нажмите кнопку F3 92,x)|x=2
Шаг 3: Нажмите ENTER.

Вот и все! Готово!
Расчетные таблицы: Содержание
- Производные:
- Общие правила
- Степени и многочлены
- Тригонометрические функции
- Экспоненциальные и логарифмические функции
- Обратные тригонометрические функции
- Гиперболические и обратные гиперболические функции
См.: Что такое гиперболическая функция?
Ссылки
Викиучебник Таблицы производных
Посмотрите это 10-минутное введение или прочитайте ниже:
Дробное исчисление за 10 минут.
Посмотрите это видео на YouTube.
Дробное исчисление — это когда вы расширяете определение производной n-го порядка (например, первая производная, вторая производная,…), допуская n , чтобы иметь дробное значение.

Еще в 1695 году Лейбниц (основатель современного исчисления) получил письмо от математика Лопиталя, в котором он спрашивал, что произойдет, если «n» в D n x/Dx n будет равно 1/2. Ответ Лейбница: «Это приведет к парадоксу, из которого будут извлечены однодневные полезные следствия».
Не существует очевидного графического понимания дробного исчисления, и не все основные правила, которые мы вывели для классического исчисления, применимы или становятся очень сложными. Простые идеи, такие как основа цепного правила или правила произведения, больше не являются простыми идеями, когда дело доходит до этого нового вида исчисления, и иногда они просто не работают.
Простой пример исчисления дробей: производная степенной функции
Вычисление производной степенной функции — одна из самых простых задач в исчислении, поэтому, возможно, это хорошее место для начала изучения того, как может вести себя функция половинной производной.
Давайте определим нашу интересующую функцию f(x) как:
Наши знания в области исчисления говорят нам, что первая производная будет
И мы можем повторить это a раз, чтобы получить обобщенный результат
Теперь мы знаем, что факториал эквивалентен гамма-функции,.
 производной, мы должны заменить k = 1 и a = ½.
производной, мы должны заменить k = 1 и a = ½. На приведенном ниже графике эта половинная производная показана фиолетовым цветом, наряду с исходной функцией (синим цветом) и первой производной (красным цветом).
Производная по направлению показывает мгновенную скорость изменения функции в определенном направлении.
Вы можете записать этот тип производной как:
Это обозначение указывает, что вы смотрите на скорость изменения функции f(x,y,z) в определенной точке (x 0 , y 0 , г 0 ). Символ ∇ называется «набла» или «дель».
Эта идея на самом деле является обобщением идеи частной производной. Для частной производной вы берете скорость изменения вдоль одной из кривых координат, сохраняя все остальные координаты постоянными. Для производной по направлению вы должны учитывать все части вашего вектора направления.
Производная по направлению скалярной функции
Производная по направлению скалярной функции (т.
 е. одномерной функции) относительно легко определить. Вдоль вектора v это определяется как:
е. одномерной функции) относительно легко определить. Вдоль вектора v это определяется как:Это представляет собой скорость изменения функции f в направлении вектора v по отношению ко времени, прямо в точке x.
Свойства производной по направлению
У производной по направлению есть одно особенно хорошее свойство; многие свойства обычных производных справедливы и для него.
Например, если наши функции f и g дифференцируемы в точке p:
- Правило сумм выполняется:
- Для любой константы c выполняется правило постоянного множителя:
- Правило произведения (также известное как правило Либница) выполняется:
- И, если g дифференцируема в p и h дифференцируема в g(p), цепное правило также выполняется:
Автоматическое дифференцирование ( autodiff ) использует компьютер для расчета производных по некоторому заданному значению, используя механическое применение цепного правила.

Это не формула, а значение производной в интересующей точке.
Приложения для автоматического дифференцирования
Autodiff используется в:
- Усвоение данных,
- Оптимизация конструкции,
- Обратные задачи,
- Численные методы,
- Анализ чувствительности.
Может работать с очень сложными функциями; Одним из крупнейших приложений был код из 1,6 миллиона строк (написанный на Fortran 77) для исследований в области гидродинамики.
Преимущества
Преимущества:
- Эффективность и стабильность,
- Ответы достаточно точны,
- Обычно это хороший выбор, если вам нужно вычислить производную в точке.
- Обычно считается, что это лучший выбор, чем другие компьютерные методы дифференциации, такие как конечное дифференцирование, символическое дифференцирование или ручное кодирование (Gebremedhin, 2014).
Типы автоматической дифференциации
Существует два основных типа автодифференциации:
- Автодифф в прямом режиме,
- Автодиф.
 в обратном режиме.
в обратном режиме.
Прямой режим (также известный как линейный режим тангенса директора ), обычно используется для вычисления производных по направлению. Он включает в себя нахождение производных промежуточных переменных по независимым переменным. Переход от одного оператора к другому осуществляется с помощью цепного правила.
Обратный режим (также известный как обратный , смежный или котангенсный линейный режим ) вычисляет производные зависимых переменных относительно промежуточных значений. Опять же, распространение от одного оператора к другому выполняется в соответствии с цепным правилом.
Эти два режима математически эквивалентны и основаны на одних и тех же принципах, но могут требовать разного количества времени и компьютерной памяти.
Автоматическая дифференциация: ссылки
Бишоф, Бакер, Раш, Слусански и Ланг. Автоматическое дифференцирование универсального пакета вычислительной гидродинамики.
 Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Bücker, Schiller, Hovland et al. Автодиф. Получено с http://www.autodiff.org/?module=Introduction 31 марта 2019 г.
Гроссе, Роджер. CSC32 Лекция 10: Автоматическое дифференцирование. Университет Торонто CS. Получено с https://www.cs.toronto.edu/~rgrosse/courses/csc321_2018/slides/lec10.pdf 30 марта 2019 г..
Курунис, Д. и др. (2017). Символьное дифференцирование во время компиляции с использованием шаблонов выражений C++. Получено 1 июня 2019 г. с: http://arxiv-export-lb.library.cornell.edu/pdf/1705.01729
Wang, Chi-Feng. Автоматическое дифференцирование, объяснение. Как компьютеры рассчитывают производные? Получено с https://towardsdatascience. com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.
com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.Метод объединяет дельта- и набла-подходы к исчислению вариаций во временных масштабах (Гирейко и др., 2010).
Эпидериватив Определение
Эпидериваты обычно делятся на категории:
- Контингентные эпидеривативы (введены Jahn & Rauh в 1997 г.) или
- Генерализованные контингентные эпидериваты .
Многозначная зависимая производная многозначной функции H в определенной точке представляет собой карту с графом, равным условному конусу Булигана графа H в выбранной точке (Bigi & Castellani, 2002). Более формально его можно описать с помощью обозначений:
A контингентная эпидеривация из F at ( x , y ) определяется как (Rodriguez-Marin et al., 1997):
2 «… Однозначное отображение DF (x, y): X → Y, надграфик которого совпадает с контингентным конусом надграфа F в точке (x, y), т.
 е. epi (DF (x, y) = T (epi(F), (х, у)».
е. epi (DF (x, y) = T (epi(F), (х, у)».The generalized contingent epiderivative of F at ( x , y ) is defined as the following set-valued map:
D g F ( x , y ): X → 2 Y if
D g F ( x , y ) (x) = Min ({y ∈ Y: (x, y) ∈ T (epi(F), ( х , у )))}).
Производные высшего порядка – это любые производные, кроме первого (второго, третьего, четвертого, …). Производная функции также является функцией, поэтому вы можете продолжать брать производные до тех пор, пока ваша функция не станет f(x) = 0 (в этот момент уже нельзя брать производную).
Повторение производной снова и снова может показаться педантичным упражнением, но производные более высокого порядка имеют множество применений , особенно в физике и технике.
Пример нахождения производных более высокого порядка
Производная — это наклон касательной в точке.
 Здесь производные в точках А и В равны нулю.
Здесь производные в точках А и В равны нулю.Первая производная функции f(x) = x 4 – 5x 2 + 12x – 13 равна:
f′(x) = 4x 3 – 10x + 12 (найдено по степенному правилу) .Но вы можете снова различать эту функцию. Поскольку вы дифференцируете два раза, это называется второй производной. Снова используя правило степени, вы получаете: f′′(x) = 12x 2 – 10
Вы можете пять раз брать производную этой конкретной функции, когда пятая производная равна нулю. Вы не можете взять производную от нуля, поэтому остановитесь на этом.
Высшие производные функции положения
Высшие производные имеют много теоретических применений, , но у них есть и несколько практических. Какой именно тип информации вы извлекаете, зависит от того, с какой функции вы начинаете. Например, допустим, вы начинаете с функции положения.
Первая производная функции положения дает вам функцию скорости, которая дает вам скорость объекта.

Вторая производная (функции положения) дает вам ускорение объекта.
Третья производная дает вам рывок — скорость изменения ускорения. Это называется «рывком», потому что именно так ощущается быстрое изменение ускорения. Представьте, что вы едете на спускающемся лифте, который внезапно замедляется: ощущение рывков, которое вы чувствуете, связано с ускорением изменений.
Четвертая производная функции положения дает скорость изменения «рывка». На этом этапе производные более высокого порядка становятся более теоретическими, но у них есть несколько важных применений, особенно для обеспечения безопасности высокоскоростных объектов (таких как американские горки!).
Третья производная является производной второй производной. Другими словами, это скорость изменения или наклон кривой второй производной.
Рывки и рывки
Третья производная функции положения называется рывком , который представляет собой скорость изменения ускорения.
 Предположим, что s(t) — функция положения объекта:
Предположим, что s(t) — функция положения объекта:- Первая производная s′(t) — функция скорости объекта,
- Вторая производная, s′′(t), представляет собой его ускорение,
- s′′′(t) – рывок объекта.
Это называется рывком (или, реже, толчком, креном или всплеском), потому что изменения в ускорении имеют тенденцию ощущаться «рывками», особенно большие. Плавная поездка на лифте кажется именно такой — гладкой. Но прокатившись на Башне Ужаса, башне ускоренного падения в голливудских студиях Disney World, ваш желудок подскажет вам, почему изменения в ускорении также называют «кренами».
Обозначение
Для любой функции f(x), f ”’ (x) может быть определен несколькими различными обозначениями, все из которых означают одно и то же (из Stewart, 2009):
Пример
Общие шаги:
- Взять производную функции (используя установленные правила производных) . Это называется первой производной.

- Возьмите производную новой функции (т.е. первую производную). Эта новая функция называется второй производной.
- Возьмем производную в третий раз.
Пример : Чему равна третья производная f (x) = x n ?
Решение , многократно используя правило степени:- f′(x) = nx n − 1
- f′′′(x) = n(x n − 1 )′ = n(n − 1) x n − 2
- f′′′(x) = n(n − 1)(x n − 2 )′ = n(n − 1)(n − 2) x n − 3
Четвертые и более высокие производные
Четвертые и более высокие производные менее распространены. Чтобы найти четвертая производная , взять производную еще раз (т.е. взять производную от 3-й производной). По сути, вы можете продолжать и продолжать до бесконечности, беря производные — можно найти сотую, тысячную или миллионную производную. Однако на самом деле (и с типами уравнений, с которыми вы, вероятно, столкнетесь) вы, скорее всего, сможете брать производные только до пятой производной.
 После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.
После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.Шестая производная (также называемая pop или pounce ) является результатом шестикратного взятия производной функции (обычно функции положения). Другими словами, это производная от пятой производной.
Производные более высокого порядка, такие как эта, редко встречаются за пределами физики. А когда они случаются, они обычно не имеют большого значения. В физике вы обычно находите приближение, используя ряд Тейлора, а не занимаетесь трудоемким процессом поиска шестых производных. Для простых функций, таких как приведенная ниже, найти шестую производную относительно легко. Но большинство задач реального мира будут включать в себя функции большей сложности, а это значит, что вы все равно захотите аппроксимировать ответ с помощью ряда Тейлора.
Шестая производная: пример задачи
Пример вопроса: Чему равна шестая производная f(x) = x 6 – 3x 4 + 9 x – 11?
Решение : Воспользуйтесь правилом степени и правилом констант, чтобы взять производные шесть раз:
- f′(x) = 6x 5 – 12x 3 + 9 (первая производная)
- f′′(x) = 30x 4 – 36x 2 (Вторая производная)
- f′′′(x) = 120x 3 – 72x (Третья производная)
- f (4) = 360x 2 – 72 (Четвертая производная)
- f (5) = 720x (Пятая производная)
- f (6) = 720 (Шестая производная)
Snap, Crackle, and Pop
Шестая производная называется pop после Snap, Crackle, and Pop of Rice Krispies.
 Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.
Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.Связанные статьи
- Пятая производная (треск)
Ссылки
Абрамовиц, М. и Стегун, И. А. (ред.). Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, с. 11, 1972.
Антон, Х. Исчисление: новый горизонт, 6-е изд. Нью-Йорк: Wiley, 1999
Beyer, WH «Производные». Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 229-232, 1987.
Биги, Г. и Кастеллани, М. (2002). K-эпипроизводные для многозначных функций и оптимизация. Математические методы исследования операций. 401-412.
Гирейко и др., Условная эпипроизводная и исчисление вариаций во временных масштабах. в области оптимизации – журнал математического программирования и исследования операций. 2010.
Гриванк, А. Принципы и методы алгоритмического дифференцирования. Филадельфия, Пенсильвания: SIAM, 2000.
Филадельфия, Пенсильвания: SIAM, 2000.
Ян, Дж. Раух, Р. Условные эпидеривативы и многозначная оптимизация
Math. Методы Опер. Res., 46 (1997), pp. 193-211
Khan, A. et al. (2015). Многозначная оптимизация: введение в приложения (векторная оптимизация). Спрингер.
Кимеу, Джозеф М., «Дробное исчисление: определения и приложения» (2009). Магистерские диссертации и специализированные проекты. Документ 115. digitalcommons.wku.edu/theses/115 Получено с https://digitalcommons.wku.edu/cgi/viewcontent.cgi?article=1115&context=theses 12 апреля 2018 г.
Kisak, P. (Ed.) ( 2017). Обзор физики рывков: «Значение третьей производной».
ScienceDirect Дробные производные и исчисление. Получено с https://www.sciencedirect.com/topics/physics-and-astronomy/fractional-calculus 8 апреля 2019 г.
Родригес-Марин, Л. и Сама, М. О контингентных эпидеривативах. Дж. Матем. Анальный. заявл. 327 (2007). 745-762.
Скотт, Дж. Некоторые простые хаотические рывковые функции в Am. J. Phys., Vol. 65, № 6, июнь.
J. Phys., Vol. 65, № 6, июнь.
Стюарт, Дж. (2009). Исчисление: концепции и контексты. Cengage Learning.
Стюарт, Джеймс. Исчисление: ранние трансцендентальные. Частные производные: производные по направлениям и вектор градиента. Получено с https://math.libretexts.org/Bookshelves/Calculus/Map%3A_Calculus_-_Early_Transcendentals_(Stewart)/14%3A_Partial_Derivatives/14.6%3A_Directional_Derivatives_and_the_Gradient_Vector 27 июля 2019 г.. по эксплуатации
TI89.
Трольцш, Ф. Оптимальное управление и дифференциальные уравнения. Maik Nauka/Interperiodica Publishing, 1995.
Viljoen, C & Van der Merwe, L. (1999). Элементарная статистика: расчеты и проценты для бизнеса и экономики. Пирсон Южная Африка.УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Производные / Дифференциальное исчисление: определения, правила» Из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/derivatives/————————————————– ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
 Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!ИсчислениеHowTo.com
Максимальные и минимальные значения. Подход к исчислению
Подход
к
К А Л К У Л И С
Содержание | Дом
10
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) больше , чем любое предшествующее или предшествующее значение.Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на непосредственно предшествует или последует за любым значением, непосредственно предшествующим или следующим за ним.Опять же, другие значения функции на самом деле могут быть меньше.
 При таком понимании мы отбросим термин «относительный».
При таком понимании мы отбросим термин «относительный».Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Это мы видим в точках A и B . Наклон каждой касательной линии — производной при оценке как a или b — равен 0,
.f ‘ ( x ) = 0,
Более того, в точках сразу на слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x ) > 0. В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на – .
Как минимум, f ‘ ( x ) меняет знак с − на + . Мы видим, что в точках E и F .

Также можно заметить, что в максимуме при A график вогнут вниз. (Тема 14 предварительного исчисления.) Хотя, как минимум, на B он вогнут вверх.
Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если они есть — будут решений от до f ‘ ( x ) = 0,
Пример 1. Пусть f ( x ) = x 2 – 6 x + 5.
Есть ли критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Раствор . f ‘ ( x ) = 2 x − 6 = 0 означает x = 3.
 (Урок 9 алгебры.)
(Урок 9 алгебры.)x = 3 — единственное критическое значение. Это x координат точки поворота. Чтобы определить y -координат, оцените f при этом критическом значении — оцените f (3):
f ( x ) = х 2 − 6 х + 5 f (3) = 3 2 − 6 · 3 + 5 = −4. Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — это парабола, и мы видим, что точка поворота является минимумом.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).

Но не всегда мы сможем посмотреть на график. Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с − на + . Мы видим это в точках E , B , F выше. Значение наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (урок 9) — скорость изменения наклона — равна положительной .
Опять же, вот f ( x ):
f ( x ) = х 2 − 6 х + 5. f ‘ ( x ) = 2 х − 6, f ” ( x ) = 2. f ” оценивается при критическом значении 3 — f” (3) = 2 — положительный.
 Это говорит нам алгебраически, что критическое значение 3 определяет минимум.
Это говорит нам алгебраически, что критическое значение 3 определяет минимум.Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение при x = a , если f ‘ ( a ) = 0
и f ” ( a ) = положительное число.Функция имеет максимальное значение при x = a if f ‘ ( a ) = 0
и f ” ( a ) = отрицательное число.В случае максимума наклон касательной равен уменьшению — он идет от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 − 9 x 2 + 12 х – 3,
Есть ли экстремальные значения? Во-первых, существуют ли какие-либо критические значения — решения f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
Решение .  f’ ( х ) = 6 х 2 – 18 х + 12
f’ ( х ) = 6 х 2 – 18 х + 12= 6( х 2 − 3 х + 2) = 6( х – 1)( х – 2) = 0 подразумевает:
х = 1 или x = 2.
(Урок 37 Алгебры.)
Это критические значения. Каждое из них определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении.
е ( х ) = 6 x 2 − 18 x + 12. f ” ( x ) = 12 х − 18. 
ж” (1) = 12 – 18 = -6. Вторая производная отрицательна. Таким образом, функция имеет максимум при разрешении 90 115 x 90 116 = 1,
.Чтобы найти y -координата — экстремальное значение — в этом максимуме мы оцениваем f (1):
f ( x ) = 2 x 3 − 9 x 2 + 12 x − 3 f (1) = 2 − 9 + 12 − 3 = 2. Максимум приходится на точку (1, 2).
Далее, определяет ли x = 2 максимум или минимум?
ж ” ( х ) = 12 х − 18. 
ф” (2) = 24 – 18 = 6. Вторая производная положительна. Таким образом, функция имеет минимум при 90 115 x 90 116 = 2,
.Чтобы найти y -координату — экстремальное значение — в этом минимуме, мы оцениваем f (2):
f ( x ) = 2 х 3 − 9 х 2 + 12 х − 3. f (2) = 16 – 36 + 24 – 3 = 1. Минимум приходится на точку (2, 1).
Вот, собственно, график f ( x ):
Решения f ” ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум.
 Пример: y = x 3 . y” = 6 x = 0 означает x = 0. Но x = 0 является точкой перегиба на графике y = x 7, а не минимумом 7 .
Пример: y = x 3 . y” = 6 x = 0 означает x = 0. Но x = 0 является точкой перегиба на графике y = x 7, а не минимумом 7 .Другой пример: y = sin x . Решения y ” = 0 – это произведения π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы
у = х 2 – 8 х + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите “Обновить” (“Reload”).
Сначала решай задачу сам!у’ = 2 х – 8 = 0,
Отсюда следует, что x = 4. Это x -координата вершины. Чтобы найти координату y , оцените y как x = 4:
.y = 4 2 − 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).

Проблема 2. Исследуйте каждую функцию на наличие максимумов и минимумов.
а) y = x 3 − 3 x 2 + 2,
y’ = 3 x 2 – 6 x = 3 x ( x – 2) = 0 подразумевает
x = 0 или x = 2.
у” ( х ) = 6 х – 6,
г” (0) = -6.
Вторая производная отрицательна. Это означает, что максимальное значение составляет 90 115 x 90 116 = 0. Это максимальное значение равно
.г (0) = 2.
Далее,
г” (2) = 12 – 6 = 6.
Вторая производная положительна. Это означает, что есть минимум в x = 2. Это минимальное значение равно
.y (2) = 2 3 − 3 · 2 2 + 2 = 8 − 12 + 2 = −2.
б) y = −2 х 3 − 3 х 2 + 12 х + 10,
При х = 1 максимум у = 17.

При x = −2 минимум г = -10.
c) y = 2 x 3 + 3 x 2 + 12 x − 4,
Поскольку f ‘ ( x ) = 0 не имеет действительных решений, экстремальных значений нет.
г) y = 3 х 4 − 4 х 3 − 12 х 2 + 2,
В х = 0 есть максимум у = 2.
При x = -1 есть минимум y = -3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Критические точки и тест первой производной — Криста Кинг Математика
Что такое критические точки и как их найти?
Процесс оптимизации заключается в поиске наименьшего и наибольшего значений функции.
 Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.
Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Например, для функции, показанной ниже, мы можем увидеть, просто взглянув на график, что функция достигает своего наименьшего значения в точке ???A???. Эта нижняя возможная точка является глобальным минимумом функции .
Есть причина, по которой важно найти этот глобальный минимум. Давайте на мгновение представим, что функция, показанная на графике, на самом деле моделирует вероятность того, что продукты испортятся в морозильной камере ресторана при различных температурах.
Если я владелец этого ресторана и хочу свести к минимуму вероятность того, что моя еда испортится, то мне очень интересно найти этот глобальный минимум.
 Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.
Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.И это действительно ценно! Правильное соблюдение этого правила может сэкономить мне время и деньги, а также поможет обеспечить бесперебойную работу моего ресторана и добиться успеха в долгосрочной перспективе.
Вот что такое оптимизация. Это позволяет нам рассчитать точку, в которой функция максимизируется или минимизируется, и у этого есть все виды реальных приложений, о которых мы подробно поговорим позже в курсе.
В этом разделе мы поговорим о процессе оптимизации, начиная с того, как найти наименьшее и наибольшее значения функции. Мы закончим раздел, переведя эти шаги оптимизации в изучение того, как рисовать график функции.
Локальные и глобальные экстремумы
В общем случае наименьшее и наибольшее значения функции являются ее экстремумами .
 Думайте об экстремумах как о «экстремальных точках» функции.
Думайте об экстремумах как о «экстремальных точках» функции.Экстремумы функции состоят из ее наименьших точек, которые мы называем минимумами , и ее наибольших точек, которые мы называем максимумами .
Внутри минимумов функции различают локальные (относительные) минимумы и глобальные (абсолютные) минимумы. А внутри максимумов функции мы различаем локальные (относительные) максимумы и глобальные (относительные) максимумы.
В качестве примера давайте снова посмотрим на тот же график, что и раньше.
Мы уже сказали, что абсолютный/глобальный минимум функции находится в точке ???A???, и это потому, что ???A??? это точка, в которой функция имеет наименьшее значение во всей области определения. Но функция также имеет локальный минимум при ???C???, потому что ???C??? является низшей точкой функции в области вблизи ???C???.
Функция также имеет локальный максимум в точке ???B???, потому что ???B??? является наивысшей точкой функции в районе ???B???.

Мы не стали бы определять абсолютный максимум для функции, потому что он стремится вверх к ???\infty??? оба слева от ???A??? и справа от ???C???, так что мы не можем назвать конечную точку, которая описывала бы наибольшее значение, которое когда-либо достигает функция.
Таким образом, в общем случае
локальный/относительный максимум существует везде, где функция меняет направление с возрастания на убывание. Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.
Локальный/относительный минимум существует везде, где функция меняет направление с убывающего на возрастающее. Если локальный минимум также оказывается самой низкой точкой функции в любом месте ее области определения, то это также глобальный/абсолютный минимум .
 У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.
У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.Другой пример: строка ???y=x??? это линия, которая проходит через начало координат с наклоном ???m=1???, и у нее вообще нет экстремумов (нет локальных максимумов или минимумов, а также нет глобальных максимумов или минимумов), потому что она никогда не меняет направление.
Таким образом, какие экстремумы вы сможете классифицировать, всегда будет зависеть от конкретной функции, с которой вы работаете.
Критические точки
Первым шагом в любом процессе оптимизации всегда является поиск критических точек функции.

Критические точки существуют, где производная равна ???0??? (или, возможно, где производная не определена), и они представляют собой точки, в которых график функции изменит направление либо с убывания на возрастание, либо с возрастания на убывание.
Поскольку функция меняет направление в критических точках, функция всегда будет иметь по крайней мере локальный максимум или минимум в критической точке, если не глобальный максимум или минимум там.
Чтобы найти критические точки, мы просто берем производную, устанавливаем ее равной ???0???, а затем находим переменную.
Как использовать критические точки для поиска локальных и глобальных экстремумов
Пройти курс
Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого. 🙂
Учить больше
Пошаговый пример поиска критических точек и применения теста первой производной 92=4???
???x=\pm2???
Это критические точки ???f(x)???.

Критические точки существуют там, где производная равна 0, и представляют собой точки, в которых график функции меняет направление с убывающего на возрастающее и наоборот.
Увеличение и уменьшение
Поскольку критические точки — это точки, в которых функция меняет направление с возрастания на убывание или с убывания на возрастание, следующим шагом является исследование поведения между критическими точками.
Если производная положительна, функция возрастает. Функция — это , увеличивающая , когда она движется вверх, когда мы движемся слева направо.
Если производная отрицательна, функция убывает. Функция на уменьшается на , когда она движется вниз по мере нашего движения слева направо.
Чтобы проверить знак производной, мы просто выберем значение между каждой парой критических точек и подставим это тестовое значение в производную, чтобы посмотреть, получим ли мы положительный или отрицательный результат.
 Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.Если мы найдем одну критическую точку для функции, то нам просто нужно посмотреть на знак производной слева и справа от этой одной критической точки.
Но если мы находим несколько критических точек, то нам нужно найти знак производной слева от самой левой критической точки, справа от самой правой критической точки и между каждой критической точкой.
Продолжим один из предыдущих примеров, взглянув на знак производной между каждой критической точкой.
Пример
Критические точки функции: ???x=\pm2???. Где функция возрастает, а где убывает?
???f(x)=x+\frac{4}{x}???
Ранее мы использовали производную, чтобы найти, что функция имеет критические точки в ???x=\pm2???. Когда у нас есть критические точки, полезно нанести их на числовую линию от наименьшего к наибольшему, слева направо.

Из этой диаграммы видно, что нам нужно протестировать три интервала. 92}???
???f'(3)=1-\frac{4}{9}???
???f'(3)=\frac{9}{9}-\frac{4}{9}???
???f'(3)=\frac{5}{9}>0???
Производная была положительной на первом интервале, отрицательной на втором интервале и положительной на третьем интервале. Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.
Помните, что исходная функция ???f(x)??? увеличивается там, где мы нашли положительный результат, и уменьшается там, где мы нашли отрицательный результат. Так что можно сказать
???f(x)??? увеличивается на ???-\infty
???f(x)??? убывает на ???-2
???f(x)??? увеличивается на ???2
Первая проверка производной
После того, как мы нашли интервалы, на которых функция возрастает и убывает, мы фактически уже завершили первую проверку производной, за исключением явных формулировок выводов о максимальном и минимальном значениях функции.
 .
.Потому что тест первой производной — это просто тест для нахождения максимума и минимума функции.
Другими словами, когда у нас есть диаграмма критических точек, заполненная знаками производной,
критерий первой производной позволяет сделать следующие выводы:
Если слева от критической точки производная отрицательна, а справа от нее положительна, то график имеет в этой точке локальный минимум (возможно, это местный минимум может быть глобальным минимумом).
Если производная положительна слева от критической точки и отрицательна справа от нее, график имеет локальный максимум в этой точке (и, возможно, этот локальный максимум может быть глобальным максимумом).
Итак, для предыдущего примера проверка первой производной позволяет сделать вывод, что функция имеет локальный максимум в точке ???x=-2??? и локальный минимум при ???x=2???.

Получите доступ к полному курсу исчисления 1
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, приложения производных, приложения дифференцирования, производные приложения, рисование графиков, рисование кривых, зарисовка кривых, зарисовка графиков, критические точки, поиск критических точек, тест первой производной, локальный максимум, локальные максимумы, локальные экстремумы, локальный экстремум, локальный минимум, локальные минимумы, глобальные экстремумы, глобальные максимумы, глобальный максимум, глобальные минимумы, глобальный минимум, относительный экстремум, относительный экстремум, относительный максимум, относительный максимум, относительный минимум, относительный минимум, абсолютный экстремум, абсолютный экстремум, абсолютный максимум, абсолютный максимум, абсолютный минимум, абсолютный минимум, оптимизация
0 лайковМатематическая сцена – Производные – Урок 2
Математическая сцена – Производные – Урок 2 – Дифференцирующие многочлены2009 Расмус Эф и Джанн Сак
Урок 2
Дифференцирующие многочлены
Наклон касательной меняется в зависимости от формула функции, обычно называемая f(x), и точка, в которой касательная касается кривой.

Три разных касательных в трех разных цвета были нарисованы на приведенной выше диаграмме. Красный тангенс, для например, касается график f(x) только в одной точке (0,1). Градиент касательной равен можно найти, вычислив среднюю скорость изменения или градиент на бесконечном небольшой интервал вокруг точки (0, 1).
Теперь мы собираемся найти общий метод или формула для нахождения градиента в любой точке функции. Эта формула или новой функции, называется производной исходной функции. Когда мы найдем это мы говорим, что мы дифференцируем функцию. Производная f (x) равна пишется с использованием апострофа после f. Обозначается f(x) или y. также часто используется обозначение dy/dx.
Первый взгляд на константу функция, или f(x) = k, где k — постоянное значение, для пример f(x) = 2 или y = 2 График показан здесь.
В этом случае трудно говорить о касательной, так как сам график представляет собой горизонтальную линию.
 Градиент линии
очевидно, 0, поэтому мы можем сказать, что если f(x) = 2
тогда f(x) = 0. Это верно для всех постоянных функций, их графики
горизонтальные линии и градиент 0,
Градиент линии
очевидно, 0, поэтому мы можем сказать, что если f(x) = 2
тогда f(x) = 0. Это верно для всех постоянных функций, их графики
горизонтальные линии и градиент 0,Правило таково: если f(x) = k тогда f(x) = 0,
На второй диаграмме показано три прямые линии с разными градиентами. Производная функции градиент и поэтому мы получаем следующие результаты:
y = 2x + 1 имеет градиент 2, поэтому y = 2
год = x + 1 имеет градиент 1, поэтому у = 1
г. = х + 1 имеет градиент следовательно у =
Все функции первой степени имеют прямую линию графиков и поэтому заключаем, что если дифференцировать функции вида f(x) = ax + b мы получаем f(x) = a.
Далее мы рассмотрим квадратичная функция е (х) = х 2 .
Мы можем найти производная путем нахождения средней скорости изменения на бесконечно малом интервале как мы делали в урок 1.
Определение производной:
Рассчитываем это используя функцию f(x) = x 2 .

Кому найти f(x+h) мы подставить (x+h) в формулу функции вместо x.
Пример 1
Дифференцировать функцию f(x) = 2x 2 + 4x.
Обратите внимание, что если мы продифференцируем 2x 2 мы получаем 22x (выше мы обнаружили, что производная от x 2 равна 2x). Линия y = 4x имеет градиент 4, поэтому производная 4x равна 4.
Добавление этих двух результатов вместе дает нам результат, что производная от 2x 2 + 4х это 4х + 4, тот же результат, что и раньше,
Следующее правило, которое легко доказать, относится к добавлению функций:
f(x) = ах 2 + bx + c имеет производную f(x) = 2ax + b.
Пример 2
Дифференцировать функцию .
Вместо деления на 2 можно подумать об этом например, как умножение каждого члена на, и поэтому мы можем применить приведенное выше правила.
 Обратите внимание, что они применяются только при делении на постоянное число.
Заметьте также, что константа имеет производную 0, такую же, как и любая другая
постоянный.
Обратите внимание, что они применяются только при делении на постоянное число.
Заметьте также, что константа имеет производную 0, такую же, как и любая другая
постоянный.Отмена для упрощения получить
Пример 3
Дифференцировать f(x) = х 3 . У нас нет правил, поэтому далеко для функций третьей степени, поэтому мы должны использовать определение:
Пример 4
Дифференцировать f(x) = х 4 .
Приведенные выше примеры дают нам следующие результаты:
f(х) = х 0 имеет производную f(x) = 0
f(x) = x 1 имеет производную f(x) = 1x 0
f(x) = x 2 имеет производную f(x) = 2x 1
f(x) = x 3 имеет производную f(x) = 3x 2
f(x) = x 4 имеет производную f(x) = 4x 3
В любом случае результат может получить путем умножения на исходный показатель или степень и уменьшения мощность на одного.

Можно показать, что этот результат применим в целом, и мы можем написать следующее правило:
е (х) = х номер имеет производную f(x) = nx №1
Пример 5
Используйте правила, которые мы нашли различать е (х) = х 5 2x 4 + 3x 3 4x 2 + 5x 6.
f(x) = 5x 4 24x 3 + 33x 2 42x + 5 0
= 5x 4 8x 3 + 9x 2 8x + 5
Пример 6
Найдите уравнение касательной к кривой f(x) = x 5 5x 3 + 4x в точке , где x = 1,
Начнем с поиска y значение при x = 1.
f(1) = 1 5 + 4 = 0
Касательная находится в точке (1, 0).
Далее находим формулу для градиент путем дифференцирования функции.
f(x) = 5x 4 53x 2 + 4
= 5x 4 15x 2 + 4
Мы можем найти градиент когда x = 1, путем вычисления f(1).

- Производные:


 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.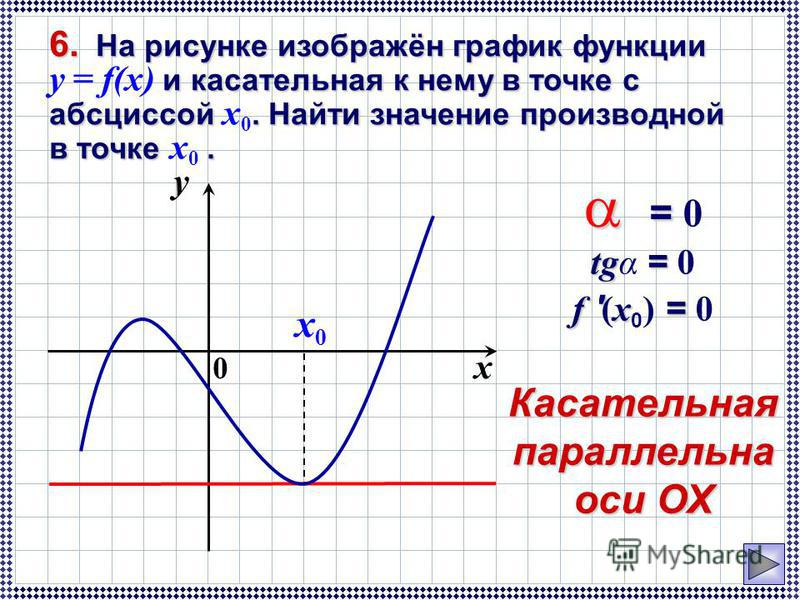
 11.17
11.17

 2}$
2}$ 3-5=6-90-5= -89$
3-5=6-90-5= -89$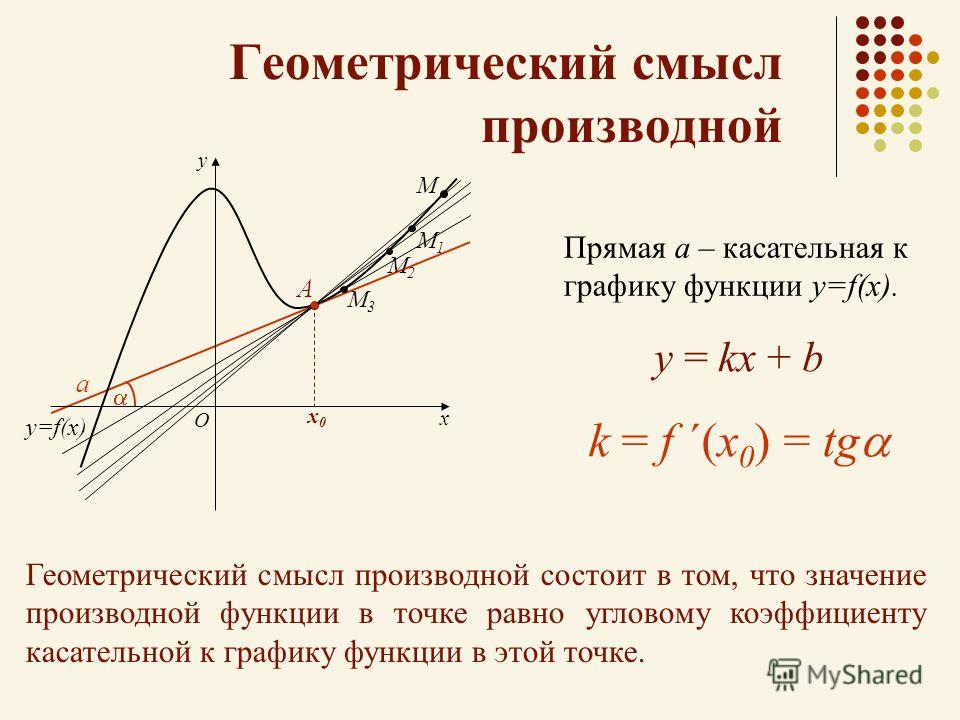

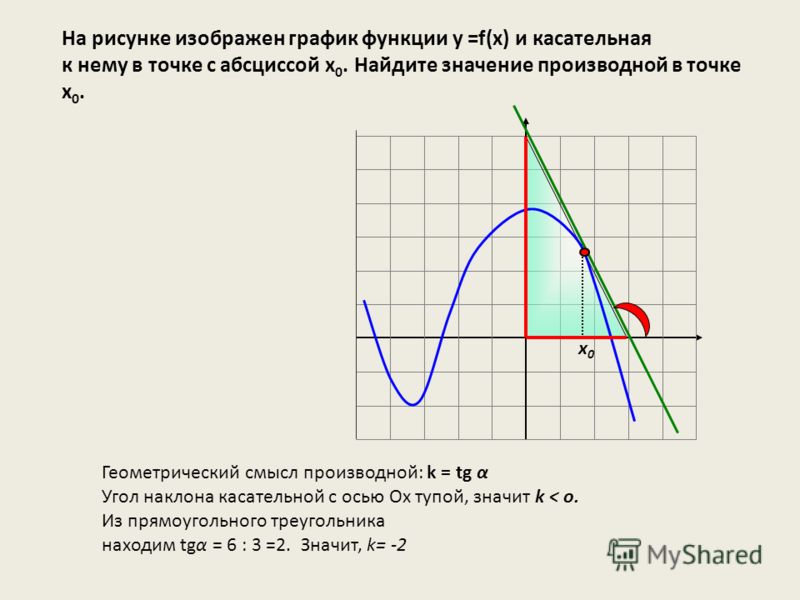


 Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
 Однако наклон составляет , уменьшающийся на при $x = 6$ ($f”(6) < 0$), поэтому наклон, вероятно, будет более отрицательным, чем $-\frac{1}{2}$ на интервале , оставив только 9{\prime\prime}(6) = -2$, мы знаем, что $|M| \geq 2$, что создает нижнюю границу для $|M|$.
Итак, любое значение $y \in \mathbb{R}$, удовлетворяющее этому уравнению, является возможным ответом,
$$
\frac{3}{2} = \frac{5}{2} - 1 \leq y \leq \frac{5}{2} + 1 = \frac{7}{2}
$$
Таким образом, наилучший возможный ответ действительно $2$, однако $2,5$ также находится в допустимых пределах.
Однако наклон составляет , уменьшающийся на при $x = 6$ ($f”(6) < 0$), поэтому наклон, вероятно, будет более отрицательным, чем $-\frac{1}{2}$ на интервале , оставив только 9{\prime\prime}(6) = -2$, мы знаем, что $|M| \geq 2$, что создает нижнюю границу для $|M|$.
Итак, любое значение $y \in \mathbb{R}$, удовлетворяющее этому уравнению, является возможным ответом,
$$
\frac{3}{2} = \frac{5}{2} - 1 \leq y \leq \frac{5}{2} + 1 = \frac{7}{2}
$$
Таким образом, наилучший возможный ответ действительно $2$, однако $2,5$ также находится в допустимых пределах. Это означает, что $f(6+a) \leq f(6) + f'(6)*(a-6)$. В наших случаях это дает нам $f(7)=f(6+1) \leq 3+ (-0,5)*1 = 2,5$ . Это означает, что $2,5$ и $2$ являются единственными возможными ответами. Но поскольку $f”$ меньше, чем $0$, производная становится еще меньше, поэтому правильным ответом является $2$.
Это означает, что $f(6+a) \leq f(6) + f'(6)*(a-6)$. В наших случаях это дает нам $f(7)=f(6+1) \leq 3+ (-0,5)*1 = 2,5$ . Это означает, что $2,5$ и $2$ являются единственными возможными ответами. Но поскольку $f”$ меньше, чем $0$, производная становится еще меньше, поэтому правильным ответом является $2$.
 ниже этот пример, как мы нашли, что производная.)
ниже этот пример, как мы нашли, что производная.) .. на помощь снова приходят производные.
.. на помощь снова приходят производные. )
)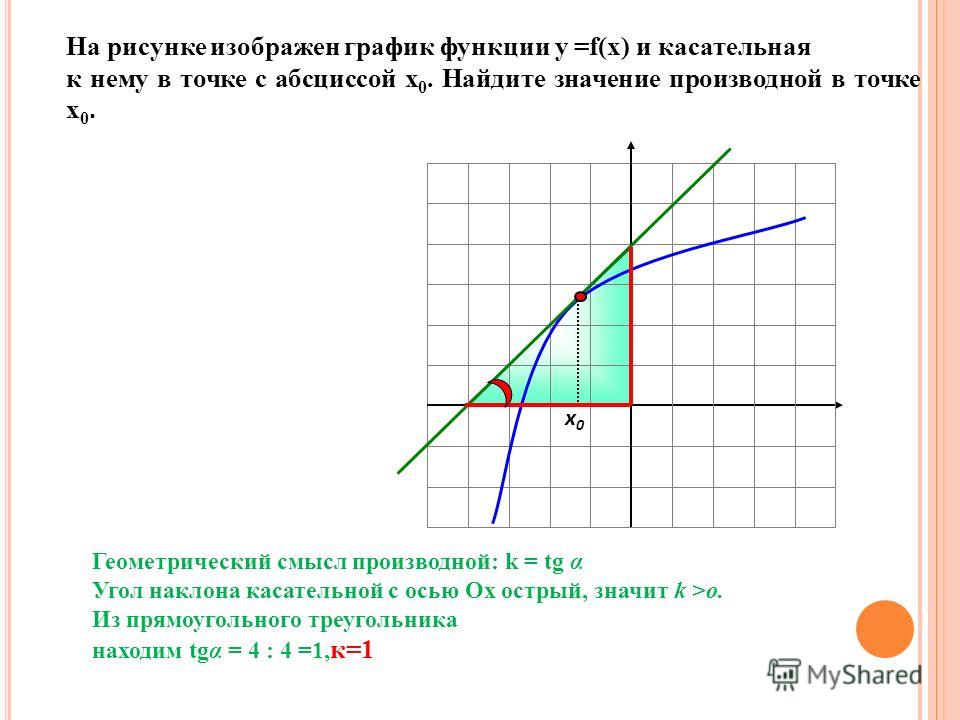

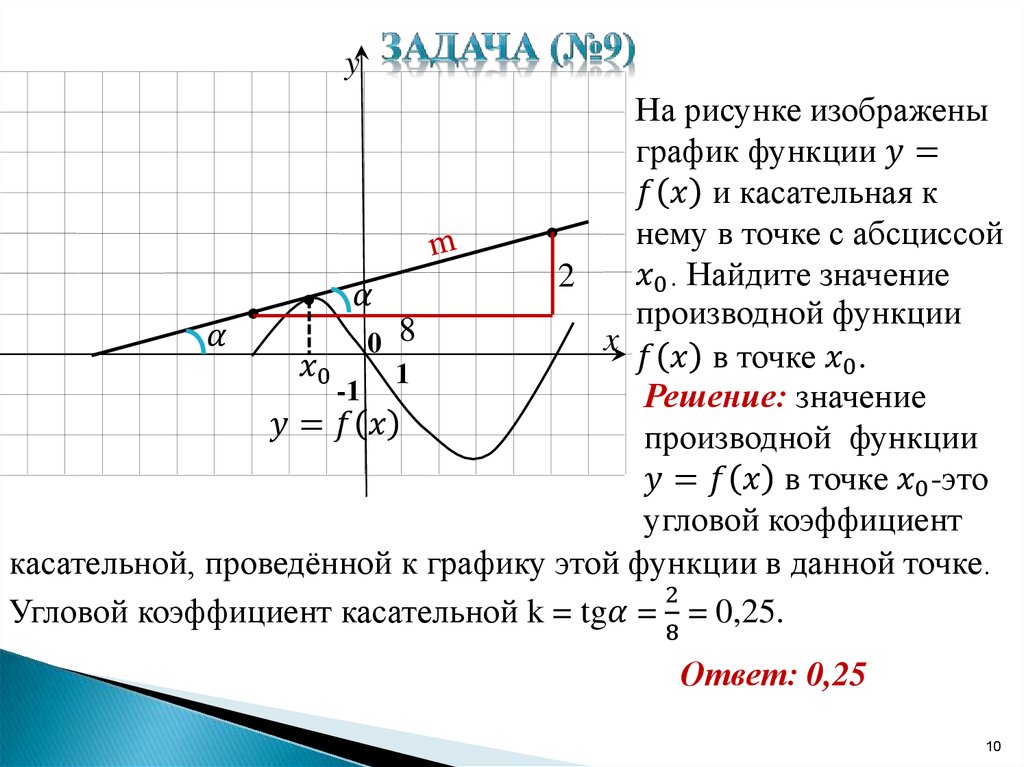 Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени.
Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени. Посмотрите видео с парой быстрых пошаговых примеров:
Посмотрите видео с парой быстрых пошаговых примеров:  В этом случае можно удалить 4x, Δx и 1.
В этом случае можно удалить 4x, Δx и 1.  И это работает не только с позицией; Исчисление может работать с любой функцией.
И это работает не только с позицией; Исчисление может работать с любой функцией. Решение (3 в этом примере) находится в правой части экрана.
Решение (3 в этом примере) находится в правой части экрана.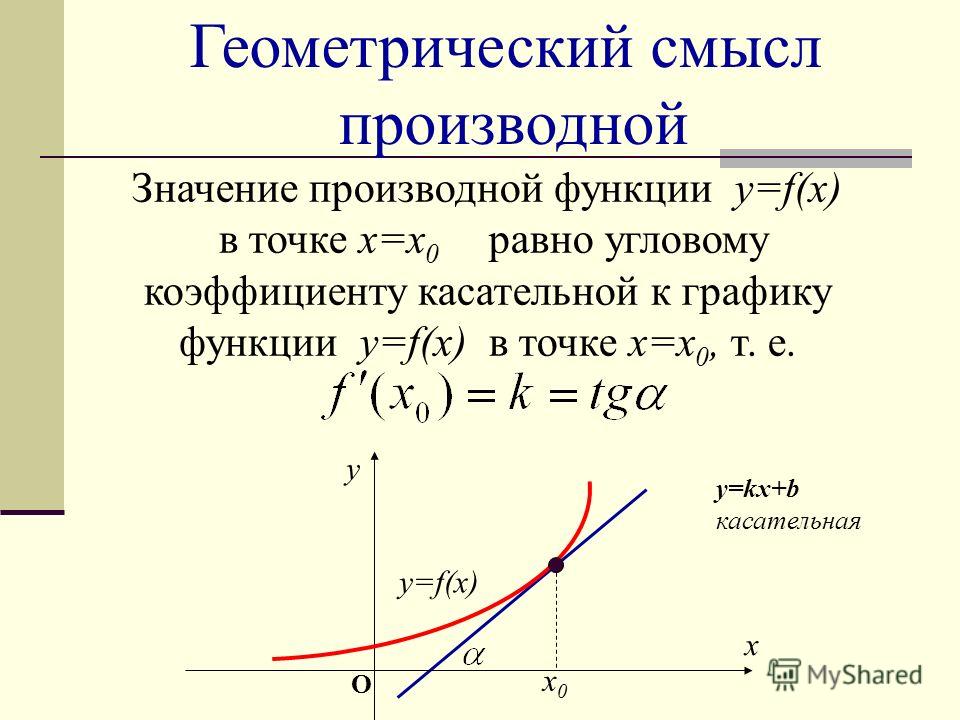

 производной, мы должны заменить k = 1 и a = ½.
производной, мы должны заменить k = 1 и a = ½.  е. одномерной функции) относительно легко определить. Вдоль вектора v это определяется как:
е. одномерной функции) относительно легко определить. Вдоль вектора v это определяется как: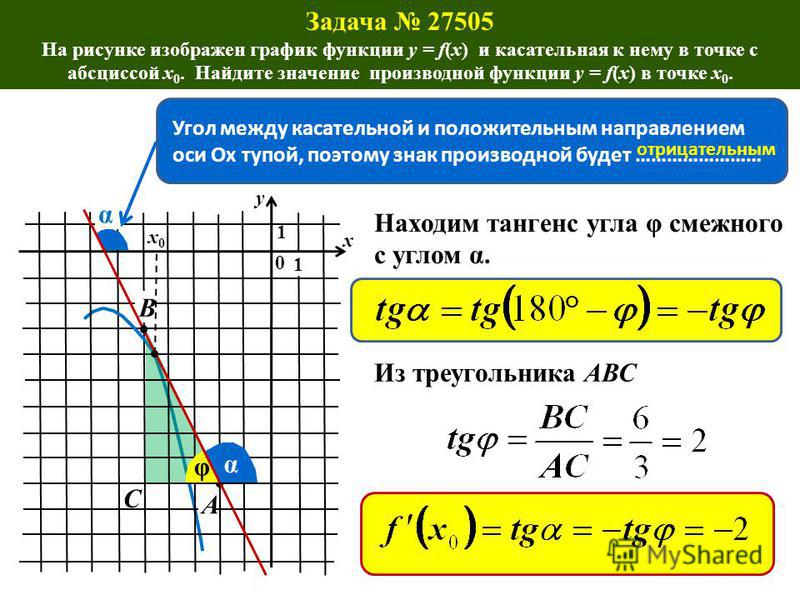
 в обратном режиме.
в обратном режиме. Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html 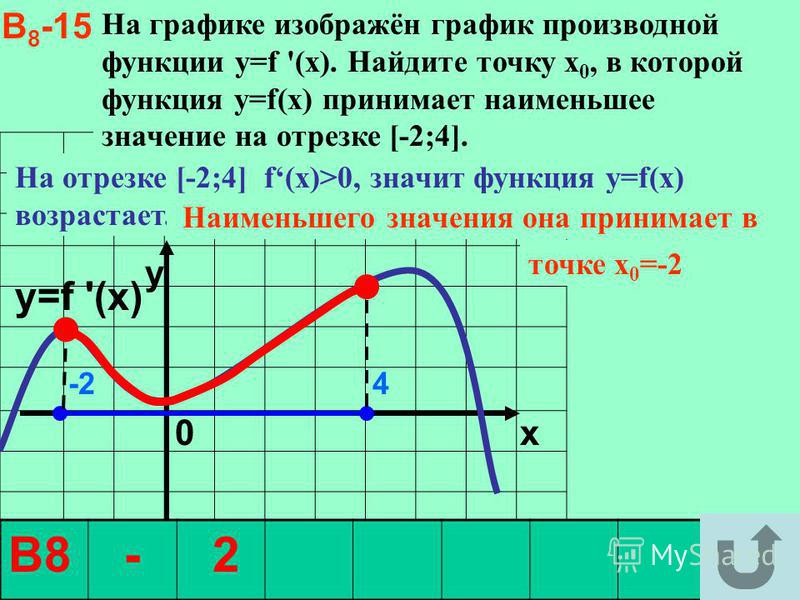 com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.
com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией. е. epi (DF (x, y) = T (epi(F), (х, у)».
е. epi (DF (x, y) = T (epi(F), (х, у)». Здесь производные в точках А и В равны нулю.
Здесь производные в точках А и В равны нулю.
 Предположим, что s(t) — функция положения объекта:
Предположим, что s(t) — функция положения объекта:
 После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.
После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.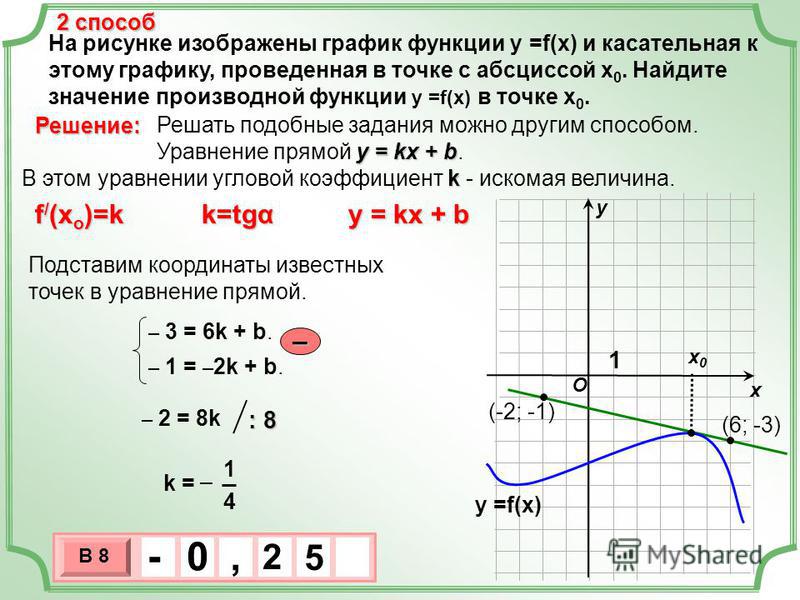 Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.
Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics. Филадельфия, Пенсильвания: SIAM, 2000.
Филадельфия, Пенсильвания: SIAM, 2000.  J. Phys., Vol. 65, № 6, июнь.
J. Phys., Vol. 65, № 6, июнь.  Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!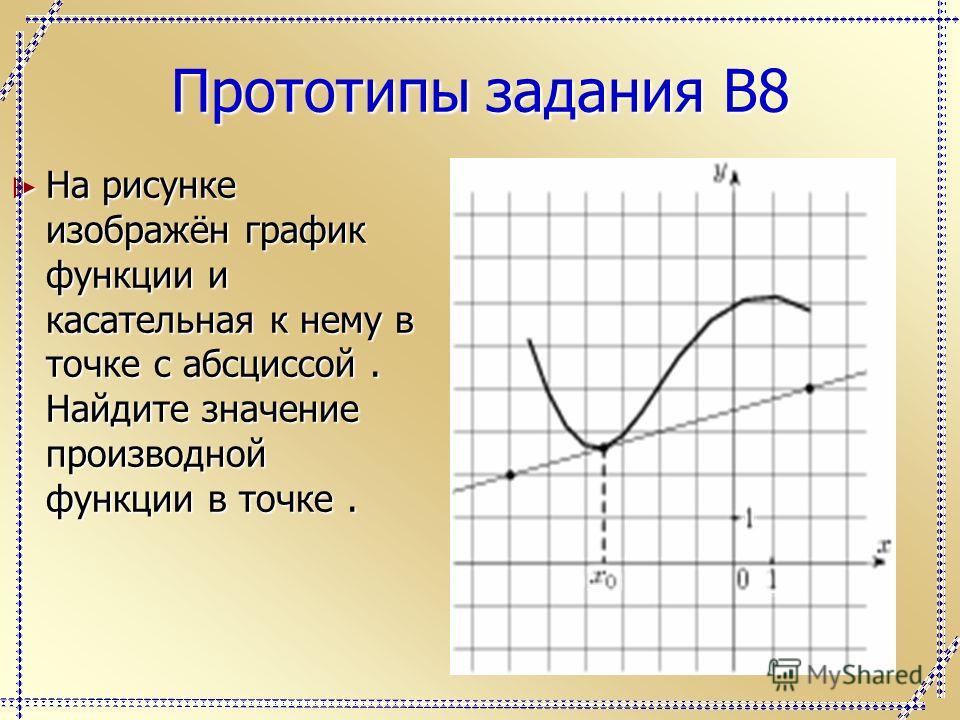 При таком понимании мы отбросим термин «относительный».
При таком понимании мы отбросим термин «относительный».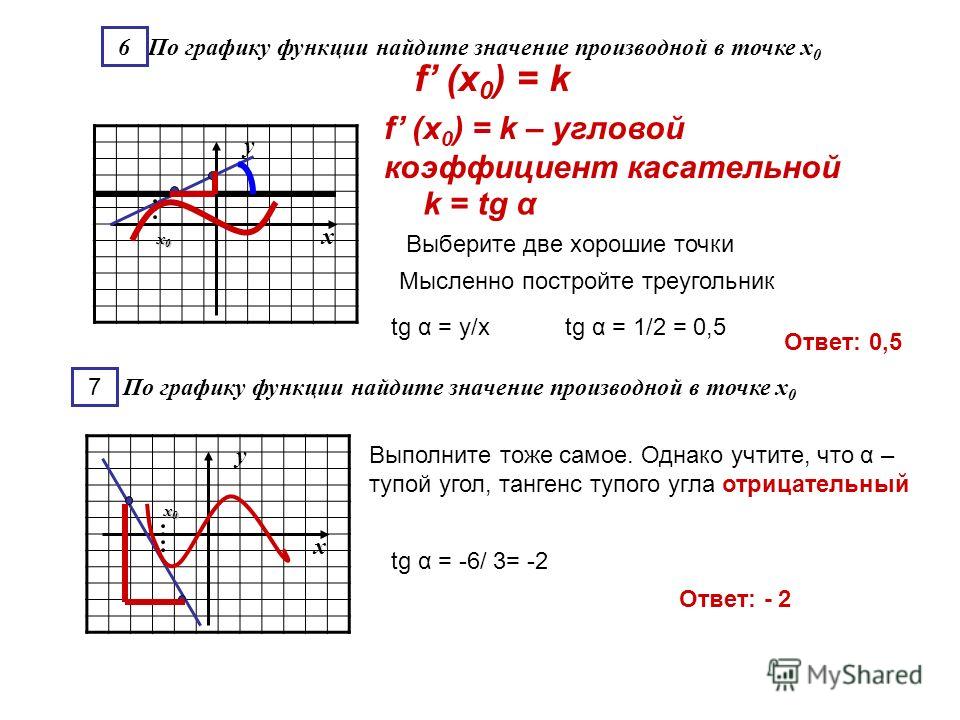
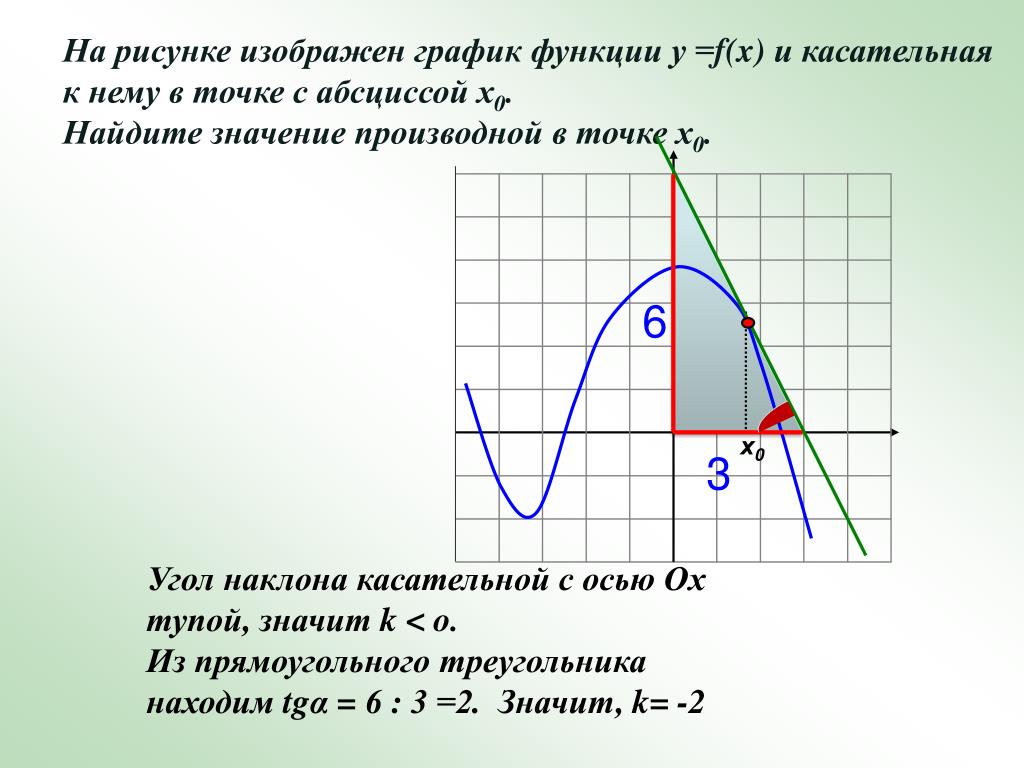 (Урок 9 алгебры.)
(Урок 9 алгебры.)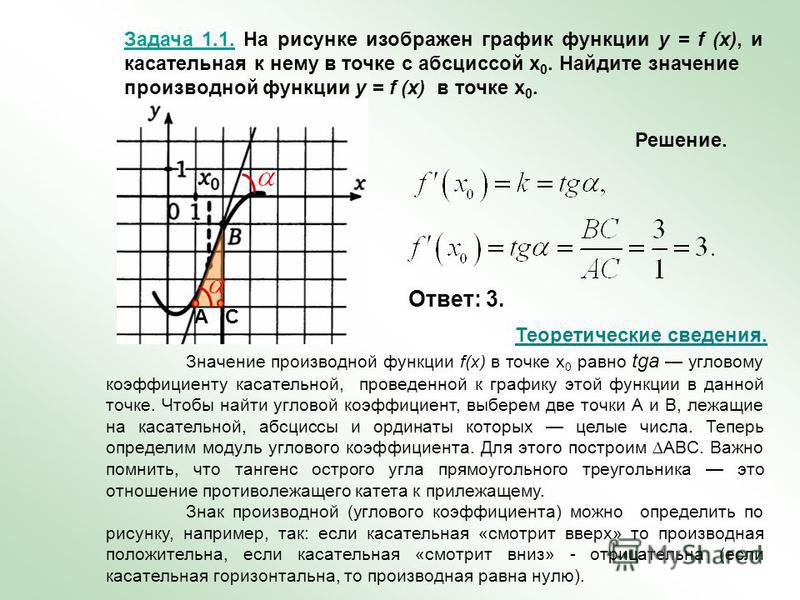
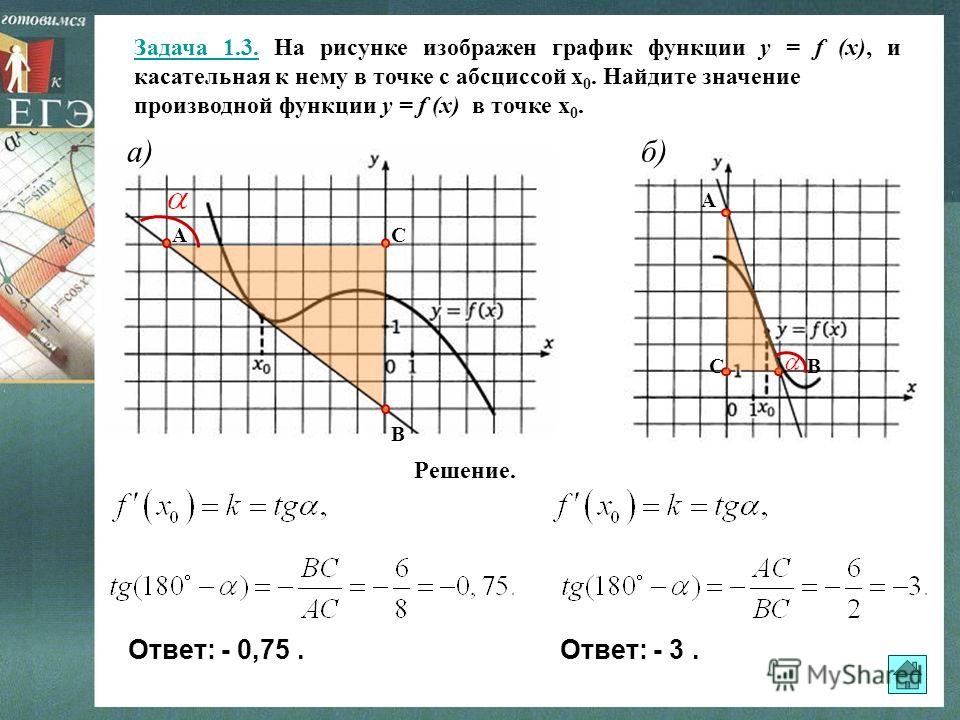 Это говорит нам алгебраически, что критическое значение 3 определяет минимум.
Это говорит нам алгебраически, что критическое значение 3 определяет минимум. f’ ( х ) = 6 х 2 – 18 х + 12
f’ ( х ) = 6 х 2 – 18 х + 12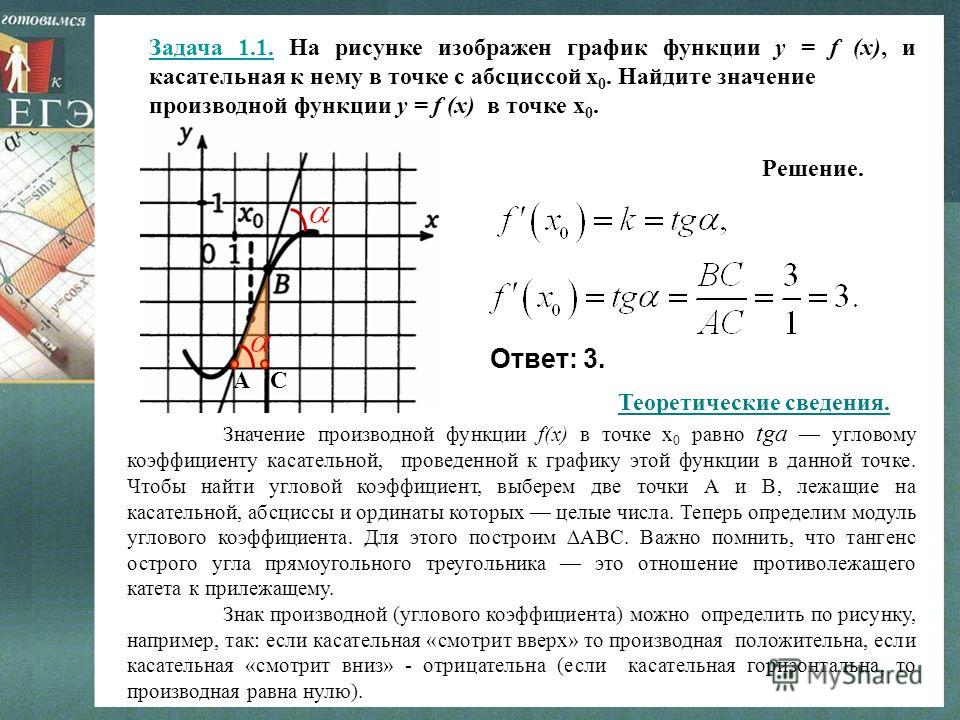

 Пример: y = x 3 . y” = 6 x = 0 означает x = 0. Но x = 0 является точкой перегиба на графике y = x 7, а не минимумом 7 .
Пример: y = x 3 . y” = 6 x = 0 означает x = 0. Но x = 0 является точкой перегиба на графике y = x 7, а не минимумом 7 .

 Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.
Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения. Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.
Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится. Думайте об экстремумах как о «экстремальных точках» функции.
Думайте об экстремумах как о «экстремальных точках» функции.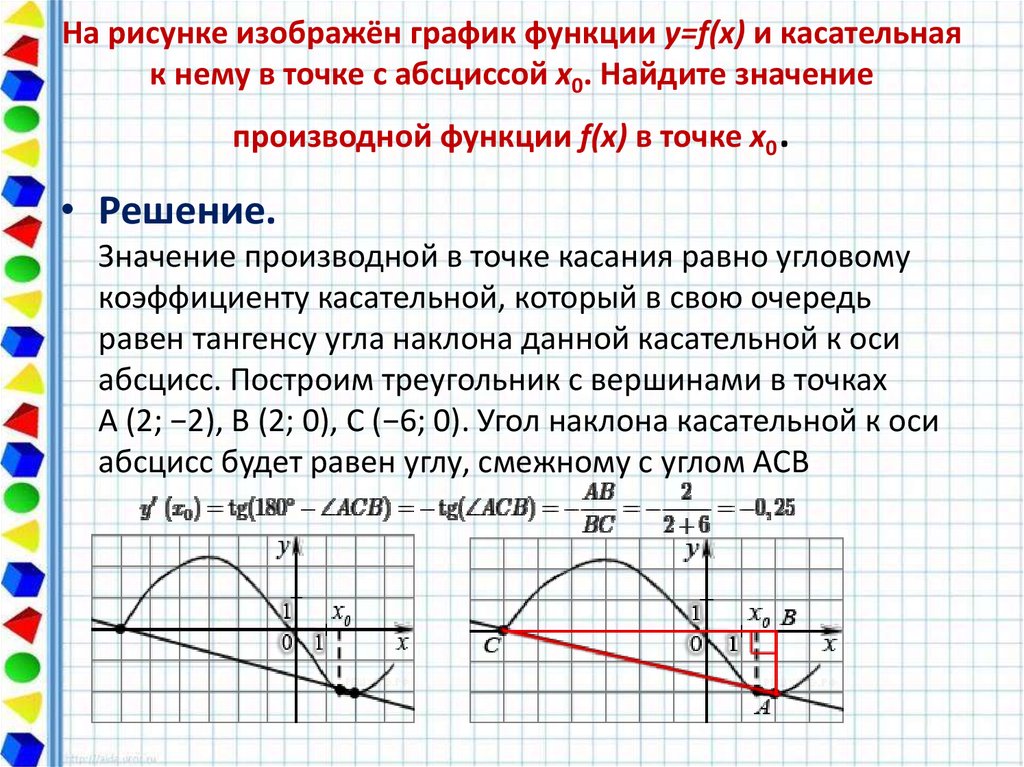
 У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.
У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.
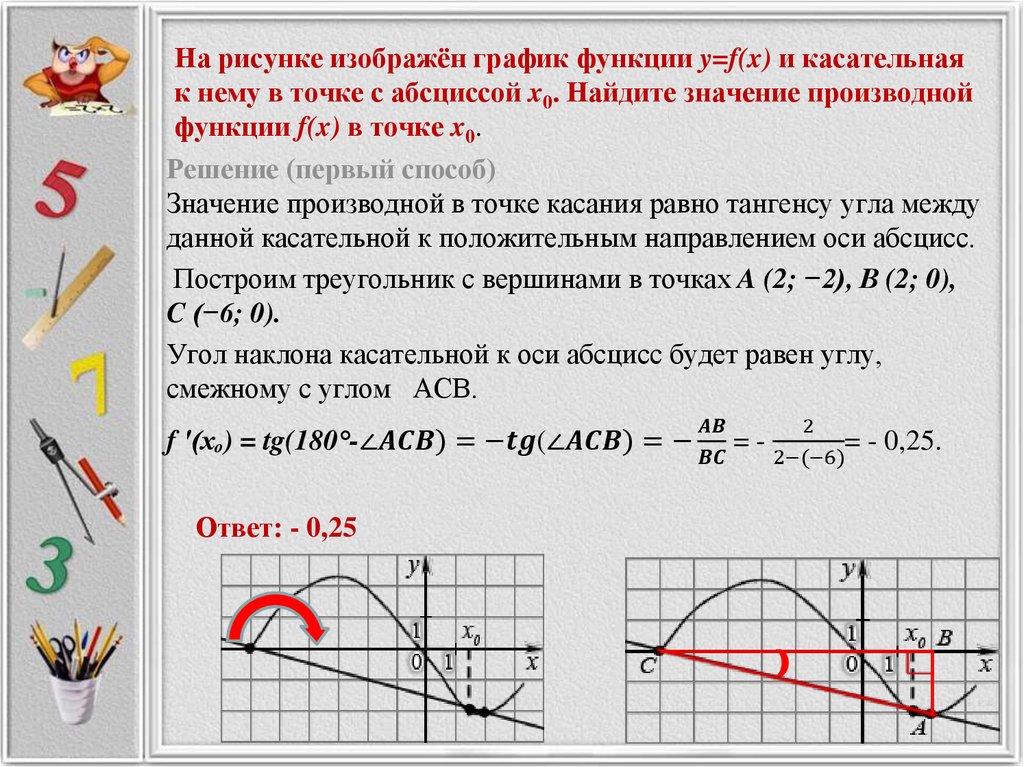
 Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
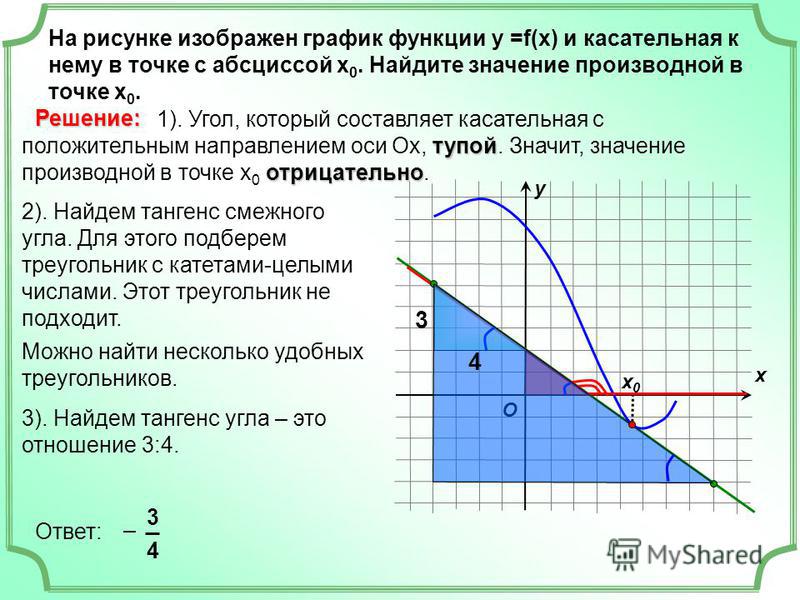 .
.
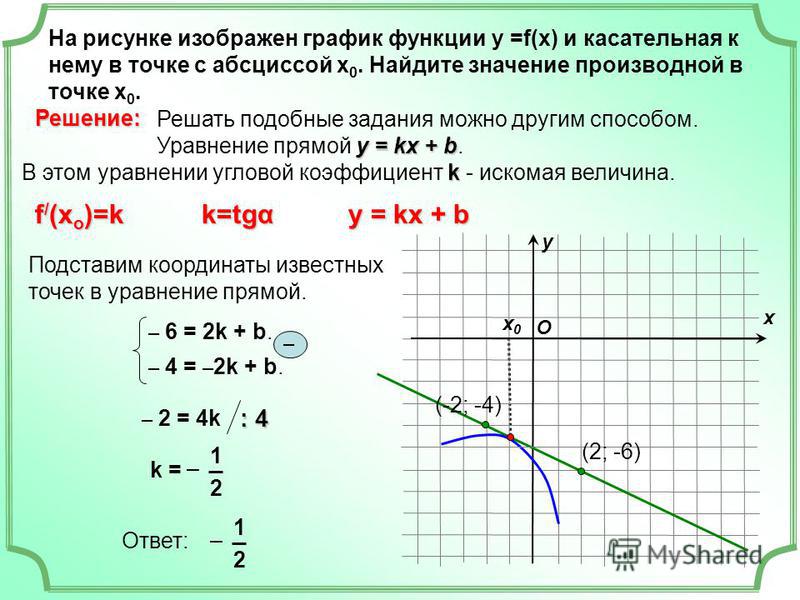
 Градиент линии
очевидно, 0, поэтому мы можем сказать, что если f(x) = 2
тогда f(x) = 0. Это верно для всех постоянных функций, их графики
горизонтальные линии и градиент 0,
Градиент линии
очевидно, 0, поэтому мы можем сказать, что если f(x) = 2
тогда f(x) = 0. Это верно для всех постоянных функций, их графики
горизонтальные линии и градиент 0,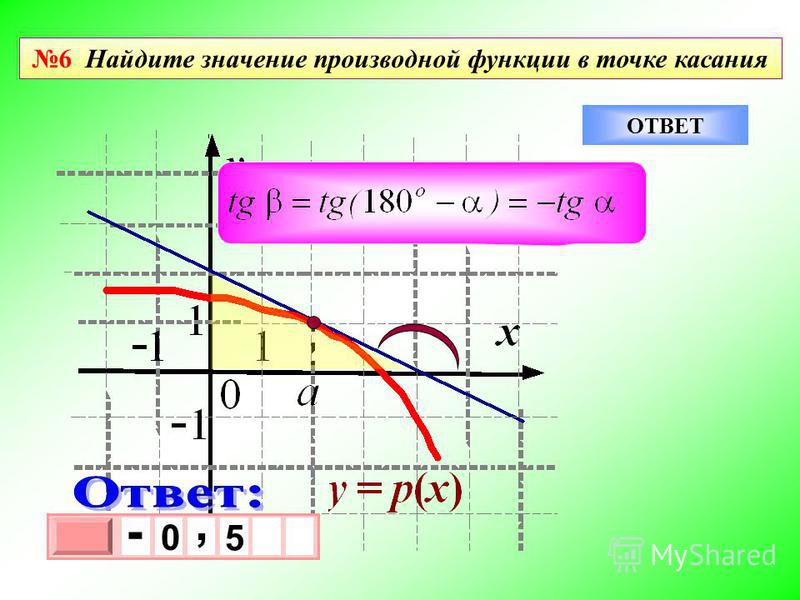
 Обратите внимание, что они применяются только при делении на постоянное число.
Заметьте также, что константа имеет производную 0, такую же, как и любая другая
постоянный.
Обратите внимание, что они применяются только при делении на постоянное число.
Заметьте также, что константа имеет производную 0, такую же, как и любая другая
постоянный.