Как по графику определить знак производной. Производная функции. Геометрический смысл производной. Вычисление точек максимума и минимума
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
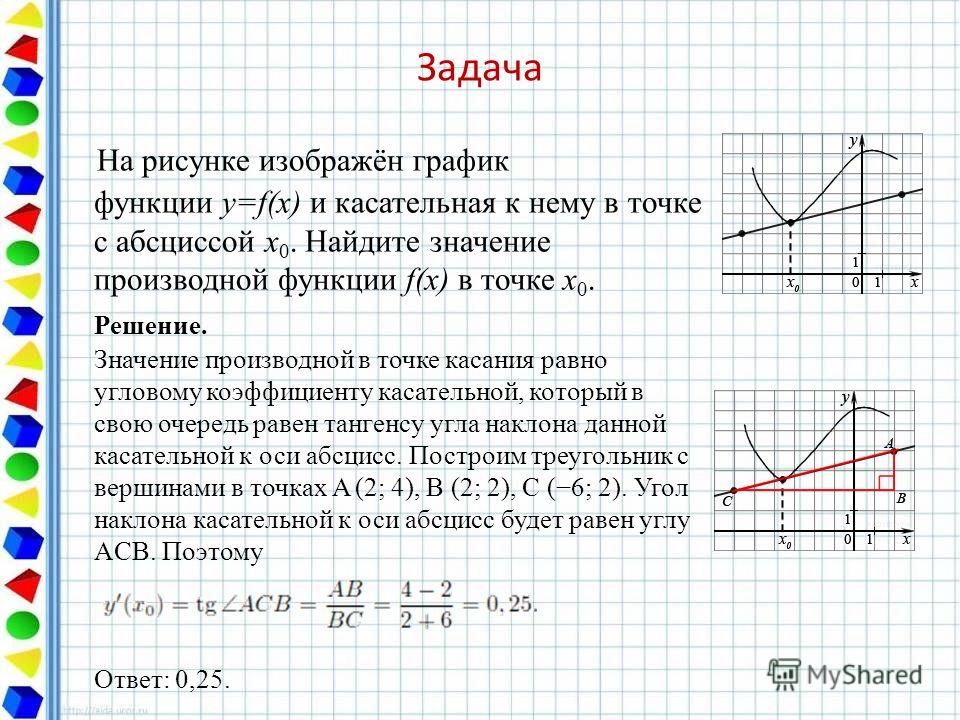
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями.
 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0. - Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2).
 Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.

- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Производная функции – одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна . Мы не будем сейчас стремиться к математической строгости изложения. Самое главное – понять смысл.
Запомним определение:
Производная – это скорость изменения функции.
На рисунке – графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден – третья. У нее самая большая скорость изменения, то есть самая большая производная.
У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная , – разная. Что касается Матвея – у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами – насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной – то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого – тангенс угла наклона касательной .
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание – в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .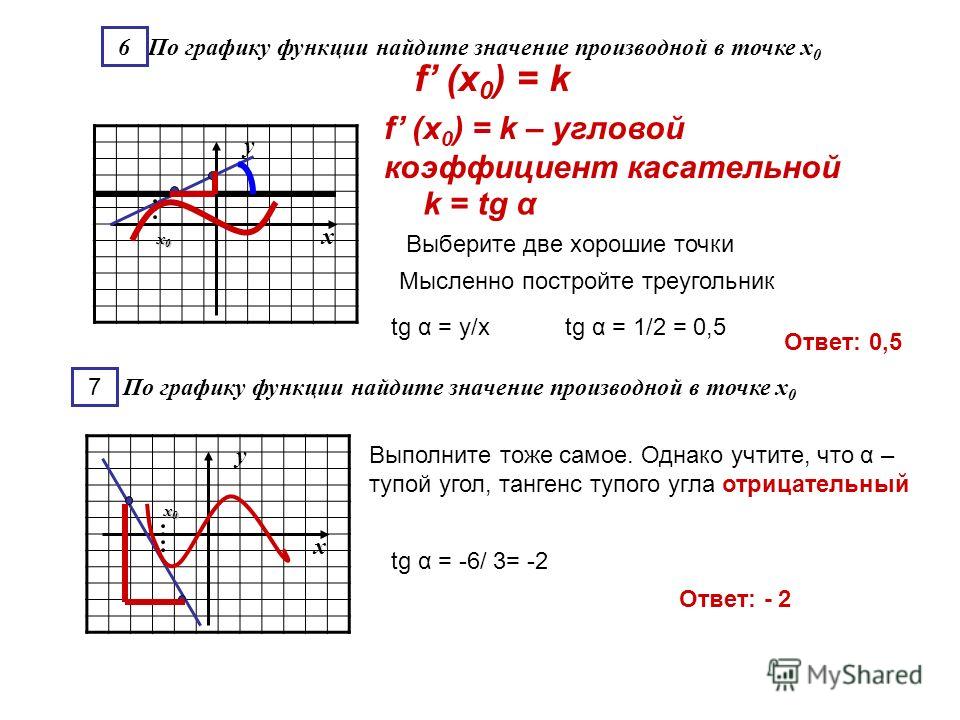
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других – убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка – точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке – точке минимума – производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | – | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое – на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала – и после точки продолжает возрастать. Знак производной не меняется – она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев 26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции – все они возрастают на отрезке
Рассмотрите, например, функции – все они возрастают на отрезке
Владлен Писарев 02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) – входят.
Учитывая, что первая часть ЕГЭ для “средней группы детского сада”, то наверное такие нюансы- перебор.
Отдельно, большое спасибо за “Решу ЕГЭ” всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова 20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z 28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке }
Производная функции в точке. Геометрическая и механическая интерпретация
Производная функции в точке
Пусть
функция f(x) определена на промежутке
(a; b), и – точки этого промежутка. Производной
функции f(x) в точке называется предел
отношения приращения функции к приращению
аргумента при . Обозначается .
Обозначается .
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.
Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.
Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x) на интервале (a; b).
Операция нахождения производной называется дифференцированием.
Проведем
разграничения в природе понятий
производной функции в точке и на
промежутке: производная функции в точке
– это есть число, а производная функции
на промежутке – это есть функция.
Геометрическая и механическая интерпретация
1)Механический смысл производной
Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.
Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.
Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).
Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость vматериальной точки в момент времени t0.
Для этого рассмотрим какой-нибудь другой момент времени t0+Δt. Ему соответствует пройденный путь s=s(t0+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t0+Δt)–s(t).
Рассмотрим
отношение .
Оно называется средней скоростью в
промежутке времени Δt. Средняя скорость
не может точно охарактеризовать быстроту
перемещения точки в момент t0 (т. к. движение
неравномерно). Для того, чтобы точнее
выразить эту истинную скорость с помощью
средней скорости, нужно взять меньший
промежуток времени Δt.
к. движение
неравномерно). Для того, чтобы точнее
выразить эту истинную скорость с помощью
средней скорости, нужно взять меньший
промежуток времени Δt.
Итак, скоростью движения в данный момент времени t0 (мгновенной скоростью) называется предел средней скорости в промежутке от t0 до t0+Δt, когда Δt→0: ,т.е. скорость неравномерного движения это производная от пройденного пути по времени.
2)Геометрический смысл производной
Введем сначала определение касательной к кривой в данной точке.
Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0.
Т.о.,
касательной к кривой в данной точке М0
называется предельное положение секущей
М0М, когда точка М стремится вдоль кривой
к точке М0.
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х0 функция принимает значение y0=f(x0). Этим значениям x0 и y0 на кривой соответствует точка М0(x0; y0). Дадим аргументу x0 приращение Δх. Новому значению аргумента соответствует наращенное значение функции y0+Δ y=f(x0–Δx). Получаем точку М(x0+Δx; y0+Δy). Проведем секущую М0М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .
Если
теперь Δx→0, то в силу непрерывности
функции Δу→0, и поэтому точка М, перемещаясь
по кривой, неограниченно приближается
к точке М0. Тогда секущая М0М будет
стремиться занять положение касательной
к кривой в точке М0, а угол φ→α при Δx→0,
где через α обозначили угол между
касательной и положительным направлением
оси Ox. Поскольку функция tg φ непрерывно
зависит от φ при φ≠π/2 то при φ→α tg φ →
tg α и, следовательно, угловой коэффициент
касательной будет: т.е.
f ‘(x) = tg α .
Т.о., геометрически у ‘(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox.
Пример. Найти угловой коэффициент касательной к кривой у = х2 в точке М(-1; 1).
Ранее мы уже видели, что (x2)’ = 2х. Но угловой коэффициент касательной к кривой есть tg α = y’|x=-1 = – 2.
Дифференцируемые функции. Необходимое и достаточное условие дифференцируемости. Дифференциал. Непрерывность дифференцируемой функции.
Дифференцируемые функции
Функция y = f(x), определенная в окрестности точки x0, называется дифференциируемой в точке x0, если ее приращение Δy представимо в виде Δy = f(x0+Δx)-f(x0) = AΔx+α(Δx)Δx, где А – число, не зависящее от Δx, а α(Δx) – бесконечно малая функция при Δx→0.
Отметим, MP = Δy, NP = dy, MN = α(Δx)Δx
Необходимое
и достаточное условие дифференцируемости.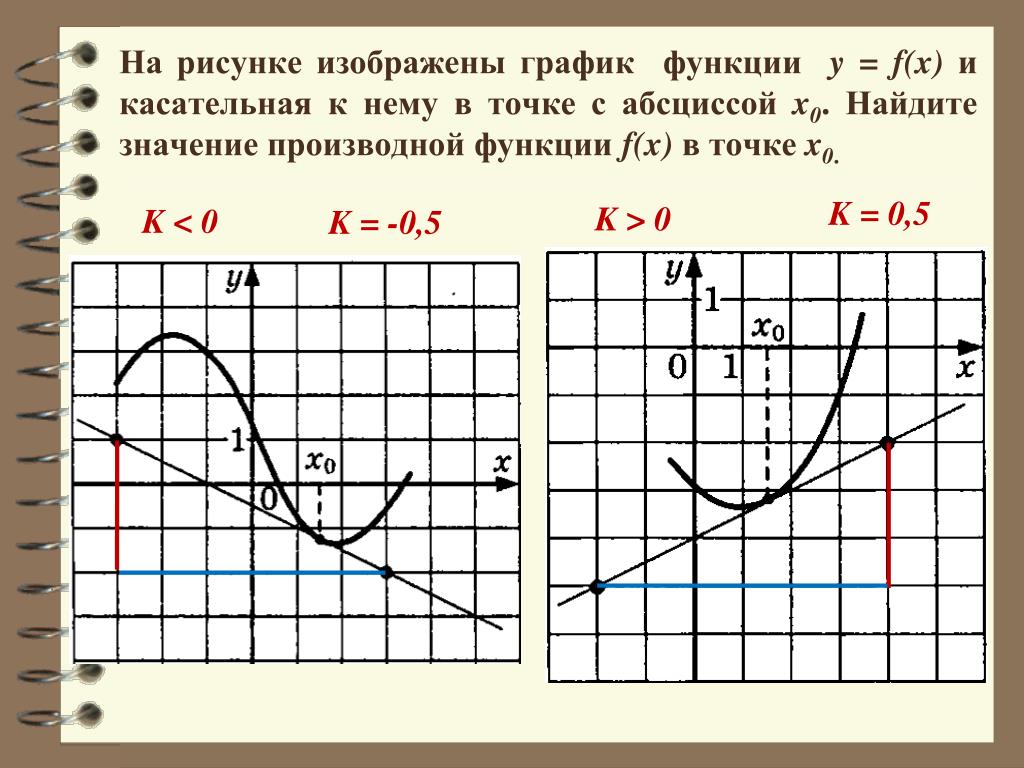
Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.
При этом Δy = f(x0+Δx)-f(x0) = f ‘(x0)Δx+α(Δx)Δx, где α(Δx) – бесконечно малая функция, при Δx→0.
Дифференциал.
Пусть функция y = f(x) дифференцируема в точке x0,то есть ее приращение представимо в виде: Δy = f(x0+Δx)-f(x0) = AΔx+α(Δx)Δx, где А – число, не зависящее от Δx, а α(Δx) – бесконечно малая функция при Δx→0.
Тогда выражение AΔx называется дифференциалом функции f(x) в точке х0 и обозначается символом dy = AΔx.
Непрерывность дифференцируемой функции.
Если
функция y = f (x) имеет производную в точке
х = х0, то говорят, что при данном значении
аргумента х = х0 функция дифференцируема.Если
функция дифференцируема в каждой точке
интервала (a, b), то говорят, что она
дифференцируема на этом интервале. Если
функция дифференцируема в некоторой
точке х = х0, то она в этой точке непрерывна. Доказательство. Пусть в точке х = х0
существует производная .
Так как разность между функцией и её
пределом есть бесконечно малая величина,
то и определения производной следует
соотношение ,
где γ (Δx) — является бесконечно малой
величиной своего аргумента. Тогда Δy =
f ‘(x0)·Δx + γ (Δx)·Δx и откуда следует, что
Δy → 0 при Δx → 0, а это означает непрерывность
функции у = f (x) в точке х0. Таким образом,
в точках разрыва функция не может иметь
производной. Однако и непрерывность
функции не гарантирует существование
производной в некоторой точке. Примером
может служить функция ,
график которой представлен на рисунке
ниже. Для
этой функции левая и правая производные
не совпадают, хотя функция обладает
свойством непрерывности. Если функция
y = f (x) имеет конечную производную в
каждой точке х Х, то производную f ‘(x)
можно рассматривать как функцию от х,
также определенную на Х.
Доказательство. Пусть в точке х = х0
существует производная .
Так как разность между функцией и её
пределом есть бесконечно малая величина,
то и определения производной следует
соотношение ,
где γ (Δx) — является бесконечно малой
величиной своего аргумента. Тогда Δy =
f ‘(x0)·Δx + γ (Δx)·Δx и откуда следует, что
Δy → 0 при Δx → 0, а это означает непрерывность
функции у = f (x) в точке х0. Таким образом,
в точках разрыва функция не может иметь
производной. Однако и непрерывность
функции не гарантирует существование
производной в некоторой точке. Примером
может служить функция ,
график которой представлен на рисунке
ниже. Для
этой функции левая и правая производные
не совпадают, хотя функция обладает
свойством непрерывности. Если функция
y = f (x) имеет конечную производную в
каждой точке х Х, то производную f ‘(x)
можно рассматривать как функцию от х,
также определенную на Х.
Производная функция в точке. Правила дифференцирования суммы, произведения, частного.

Производная функция в точке.
Пусть функция f(x) определена на промежутке (a; b), и – точки этого промежутка. Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при . Обозначается .
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.
Функцию f(x) называют дифференцируемой в точке , когда она имеет в ней конечную производную.
Если
функция f(x) дифференцируема в каждой
точке некоторого промежутка (a; b), то
функцию называют дифференцируемой на
этом промежутке. Таким образом, любой
точке x из промежутка (a; b) можно поставить
в соответствие значение производной
функции в этой точке
, то есть, мы имеем возможность определить
новую функцию
, которую называют производной функции
f(x) на интервале (a; b).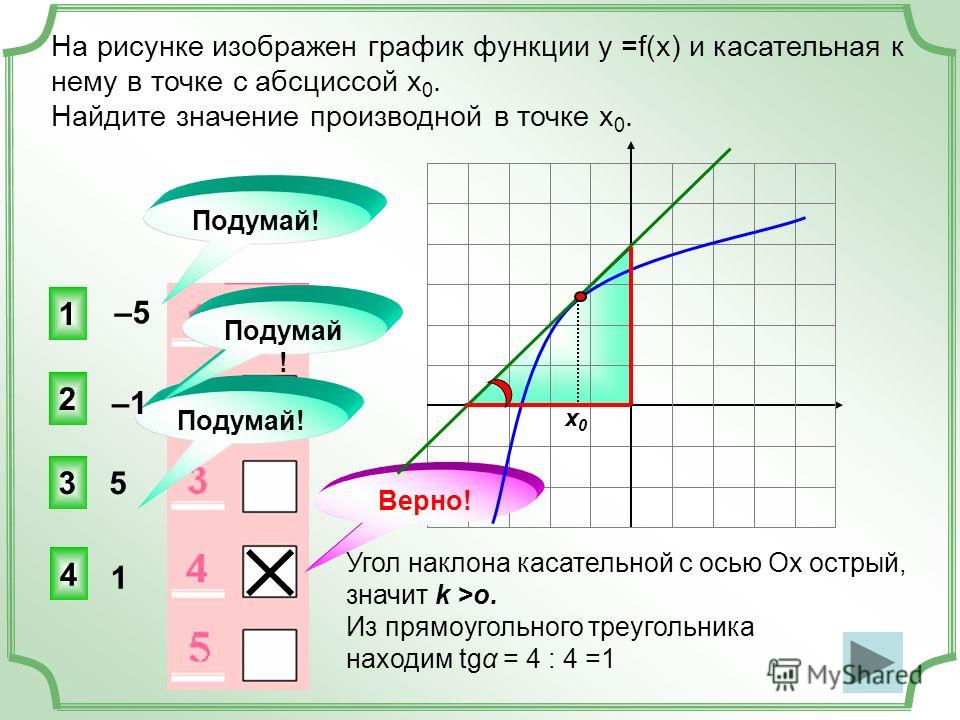
Операция нахождения производной называется дифференцированием.
Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.
Правила дифференцирования суммы, произведения, частного.
Правило дифференцирования суммы
Если функции u = u(x) и v = v(x) дифференцируемы в точке х, то ( u ± v ) ‘ = u ‘ ± v ‘.
Доказательство. Из определения производной получим: что и требовалось доказать.
Правило дифференцирования произведения
Если функции u = u(x) и v = v(x) дифференцируемы в точке х, то ( u · v ) ‘ = u ‘·v + v ‘ · u.
Доказательство. По определению производной имеем
Здесь учтена связь между дифференцируемостью и непрерывностью: .
Правило дифференцирования частного.
Если
функции u = u(x) и v = v(x) дифференцируемы в
точке х, то . Для вывода этого правила дифференцирования
частного воспользуемся правилом
дифференцирования произведения. Введём
обозначение
Введём
обозначение
.
Из этого соотношения получим u (x) = φ(x)·v(x). Продифференцируем левую и правую части этого равенства u ‘ = φ’·v + φ·v’, откуда окончательно получим искомое правило .
Производная постоянной функции
Производная константы равна нулю (C)’ = 0.
Доказательство. Для любых х и Δx имеем f (x) = C, f (x + Δx) = C, вследствие чего имеем
Δ y = f ( x + Δ x ) − f( x ) = 0.
Отсюда при любом Δx ≠ 0 и, следовательно,
Счет, математика и статистика – Набор академических навыков
Стационарные точки
ContentsToggle Главное меню 1 Определение 2 Классификация стационарных точек 2.1 Тест второй производной 2.2 Тест первой производной 2.3 Тест первой производной или тест второй производной? 3 Видеопримеры 4 Учебники 5 Проверьте себя 6 Внешние ресурсы
Определение
стационарная точка функции $f(x)$ — это точка, в которой производная от $f(x)$ равна 0. Эти точки называются «стационарными», поскольку в этих точках функция не возрастает и не убывает.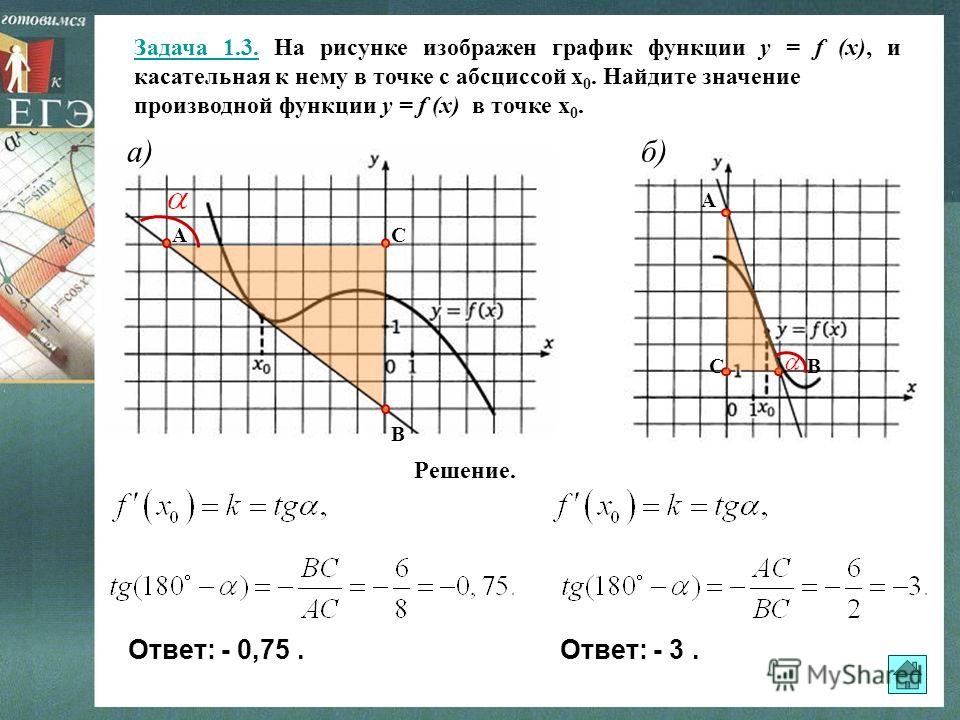 Графически это соответствует точкам на графике $f(x)$, где касательной к кривой является горизонтальная линия.
Графически это соответствует точкам на графике $f(x)$, где касательной к кривой является горизонтальная линия.
Стационарные точки функции $y=f(x)$ являются решениями
\[\cfrac{\mathrm{d}y}{\mathrm{d}x}=0.\]
Это повторяет в математической записи определение, данное выше: «точки, где градиент функции равен нулю».
Классификация стационарных точек
Стационарная точка называется поворотной точкой , если в этой точке производная меняет знак (с положительного на отрицательный или наоборот). Есть два типа точки поворота:
- A локальный максимум , наибольшее значение функции в локальном регионе.
- Локальный минимум , наименьшее значение функции в локальной области.
Примечание: все точки поворота являются стационарными, но не все стационарные точки являются точками поворота.
Точка, в которой производная функции равна нулю, но производная не меняет знака, называется точкой перегиба , или седловая точка . Их иногда называют восходящих или падающих точек перегиба, в зависимости от того, является ли производная функции положительной или отрицательной по обе стороны от стационарной точки.
Их иногда называют восходящих или падающих точек перегиба, в зависимости от того, является ли производная функции положительной или отрицательной по обе стороны от стационарной точки.
Тест второй производной
Тест второй производной используется для определения того, является ли стационарная точка локальным максимумом или минимумом . Стационарная точка $x$ классифицируется в зависимости от того, является ли вторая производная положительной, отрицательной или равной нулю.
$\gt 0$ | Местный минимум |
$\lt 0$ | Локальный максимум |
$= 0$ | Тест не дает результатов |
Если тест не дает результатов, мы должны использовать какой-либо другой метод для определения характера стационарной точки (например, тест первой производной).
Тест первой производной
Тест первой производной определяет характер стационарной точки $x$ путем оценки знака первой производной в точках $x+\epsilon$ и $x-\epsilon$, где $\epsilon\ll1 \in\mathbb{R}$. Это определяет, является ли функция возрастающей или убывающей в этих точках, что указывает на форму графика.
Примечание :
- Если $\dfrac{\mathrm{d}y}{\mathrm{d}x}>0$ в точке $x$, то функция возрастает в $x$.
- Если $\dfrac{\mathrm{d}y}{\mathrm{d}x}<0$ в точке $x$, то функция убывает в $x$.
В следующей таблице показана классификация стационарной точки на основе теста первой производной.
$>0$ | $0$ | $<0$ | Локальный максимум | |
Форма графика | $\narrow$ | $\стрелка вправо$ | $\searrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $<0$ | $0$ | $>0$ | Местный минимум |
Форма графика | $\searrow$ | $\стрелка вправо$ | $\narrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $>0$ | $0$ | $>0$ | Восходящий перегиб |
Форма графика | $\narrow$ | $\стрелка вправо$ | $\narrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $<0$ | $0$ | $<0$ | Нисходящий перегиб |
Форма графика | $\searrow$ | $\стрелка вправо$ | $\searrow$ |
Первая производная проверка или вторая производная проверка?
Если вычислить вторую производную несложно, то может быть проще и быстрее выполнить проверку второй производной, чем проверку первой производной. 2.\] 92+24\cdot0 \\ &= 0. \end{align}
2.\] 92+24\cdot0 \\ &= 0. \end{align}
Здесь проверка второй производной не удалась. Критерий первой производной должен использоваться для определения характера стационарной точки при $x=0.$
Напомним, что критерий первой производной определяет характер стационарной точки путем изучения формы функции в близлежащей области.
Рассмотрим точку $x=-\epsilon$, где $\epsilon$ положительна и сколь угодно мала. Первая производная, оцененная в этот момент, равна:
92 \\ \end{align}Это положительное значение, поэтому функция $f(x)$ также на увеличивается на справа от $x=0$.
Функция $f(x)$ возрастает в точках немного левее и немного правее точки $x=0.$ Отсюда следует, что стационарная точка $x=0$ является восходящей точкой перегиба.
- Стационарная точка, найденная при $x=-3$, является локальным минимумом.
- Стационарная точка, найденная при $x=0$, является восходящей точкой перегиба. 93-56x)\sqrt{x}$. vimeo.com/video/66239018″ frameborder=”0″ webkitallowfullscreen=”” mozallowfullscreen=”” allowfullscreen=””>
- Стационарные точки
- Максимум и минимум
- Применение дифференцирования — рабочая тетрадь максимумов и минимумов в математике center
Найдите первую производную числа f , используя степенное правило.
Установите производную равной нулю и найдите x.
x = 0, –2 или 2.
Эти три значения x- являются критическими числами f. Дополнительные критические числа могли бы существовать, если бы первая производная была неопределенной при некоторых значениях x , но поскольку производная
определено для всех входных значений, приведенный выше набор решений, 0, –2 и 2, представляет собой полный список критических чисел.
 Поскольку производная (и наклон) f равно нулю при этих трех критических числах, кривая имеет горизонтальные касательные при этих числах.
Поскольку производная (и наклон) f равно нулю при этих трех критических числах, кривая имеет горизонтальные касательные при этих числах.Возьмите числовую прямую и запишите найденные критические числа: 0, –2 и 2.
Вы делите эту числовую прямую на четыре области: слева от –2, от –2 до 0, от 0 до 2 и справа от 2.
Выберите значение из каждой области, подставьте его в первую производную и отметьте, будет ли ваш результат положительным или отрицательным.
В этом примере вы можете использовать числа –3, –1, 1 и 3 для проверки областей.
Эти четыре результата соответственно положительные, отрицательные, отрицательные и положительные.
Возьмите свою числовую прямую, отметьте каждую область соответствующим положительным или отрицательным знаком и укажите, где функция увеличивается и уменьшается.

Увеличивается, когда производная положительна, и уменьшается, когда производная отрицательна. В результате получается так называемый знаковый график функции.
Эта цифра просто говорит вам то, что вы уже знаете, если смотрели на график f — что функция идет вверх до –2, вниз от –2 до 0, далее вниз от 0 до 2 и снова вверх от 2 на.
А вот и ракетостроение. Функция переключается с возрастания на убывание при –2; другими словами, вы поднимаетесь до -2, а затем падаете. Итак, при –2 у вас есть холм или локальный максимум. И наоборот, поскольку функция переключается с убывания на возрастание в 2, у вас есть впадина или локальный минимум. И поскольку знак первой производной не меняется при нуле, в этом 9 нет ни минимума, ни максимума.0447 x -значение.
Получите значения функции (другими словами, высоты) этих двух локальных экстремумов, подставив x- значений в исходную функцию.
Таким образом, локальный максимум находится в точке (–2, 64), а локальный минимум – в точке (2, –64).

Рабочие тетради
Эти рабочие тетради, созданные HELM, являются хорошими вспомогательными средствами, содержащими ключевые моменты для повторения и множество рабочих примеров.
Проверь себя
Проверь себя: тест Numbas по нахождению максимумов и минимумов
Внешние ресурсы
Как найти локальные экстремумы с помощью теста первой производной Исчисление для чайников
Исследуйте книгу Купить на Amazon
Все локальные максимумы и минимумы на графике функции, называемые локальными экстремумами, возникают в критических точках функции (где производная равна нулю или не определена). Не забывайте, однако, что не все критические точки обязательно являются локальными экстремумами.
Первым шагом в поиске локальных экстремумов функции является нахождение ее критических чисел ( x -значений критических точек). Затем вы используете тест первой производной. Этот тест основан на идеях уровня Нобелевской премии, согласно которым, когда вы преодолеваете вершину холма, вы сначала поднимаетесь, а затем спускаетесь, и что когда вы въезжаете в долину и выезжаете из нее, вы спускаетесь, а затем вверх. Этот математический материал довольно удивителен, а?
На рисунке показан график
Чтобы найти критические числа этой функции, выполните следующие действия:


 Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.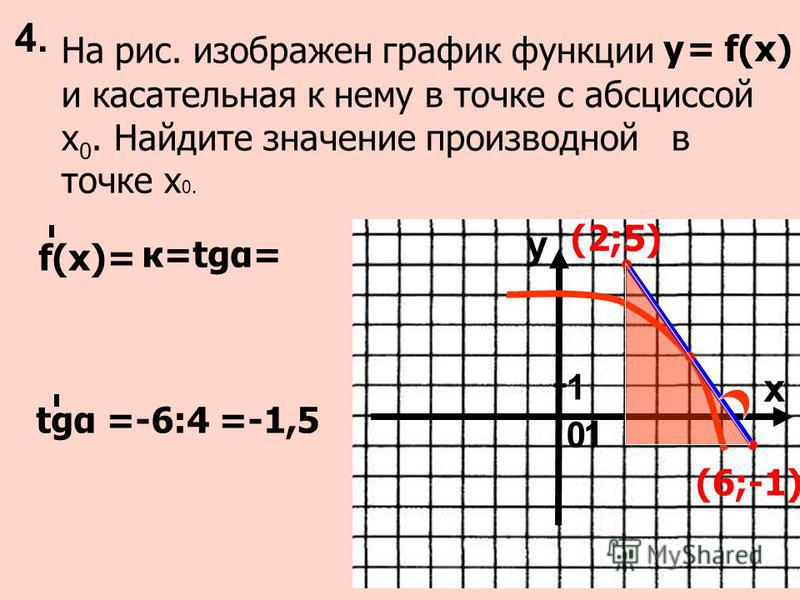 Т.е. большему значению аргумента соответствует меньшее значение функции.
Т.е. большему значению аргумента соответствует меньшее значение функции.

 Поскольку производная (и наклон) f равно нулю при этих трех критических числах, кривая имеет горизонтальные касательные при этих числах.
Поскольку производная (и наклон) f равно нулю при этих трех критических числах, кривая имеет горизонтальные касательные при этих числах.
