Движение тела, брошенного под углом к горизонту
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0.

Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории.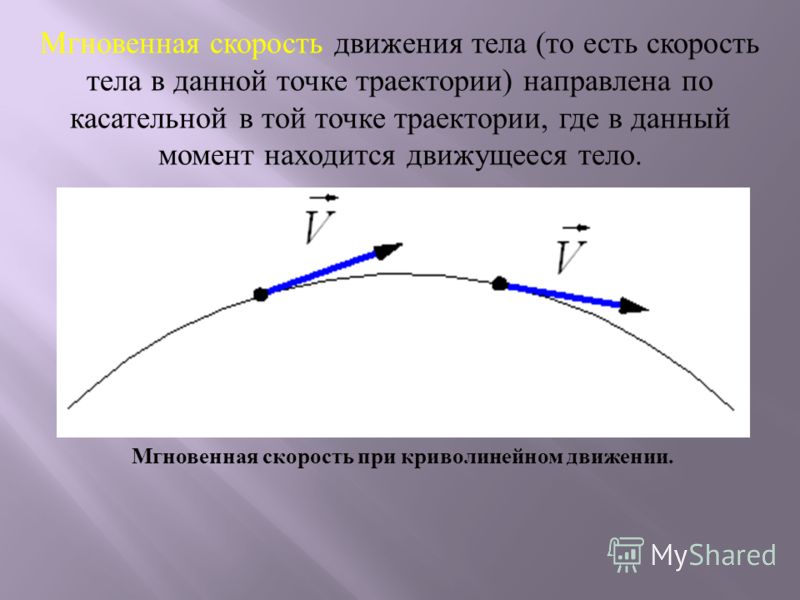 Наибольшая высота подъема обозначается h и вычисляется по формуле:
Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562 С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22..
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22..
Отсюда высота H равна:
H=mgl1mg..+mv22mg..=l1+v22g..
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2.β2g..=v2sin2.(90−2α)o2g..
Отсюда:
l1=h−v2sin2.(90−2α)o2g..
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g..=h−(gt)2sin2.(90−2α)o2g..+(gt)22g..
H=h−gt2sin2.(90−2α)2..+gt22..=h−gt22..(sin2.(90−2α)o−1)
H=1,4−10·0,422..(sin2.(90−60)o−1)
H=1,4−5·0,16(sin2. 30o−1)
30o−1)
H=1,4−0,8((12..)2−1)=1,4−0,8(14..−1)
H=1,4+0,6=2 (м)
.
.
.
.
Ответ: 20pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17980Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.

- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18741Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 37.3k
Движение тела, брошенного горизонтально | СПАДИЛО
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Важные факты!Графически движение горизонтально брошенного тела описывается следующим образом:
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.

- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления.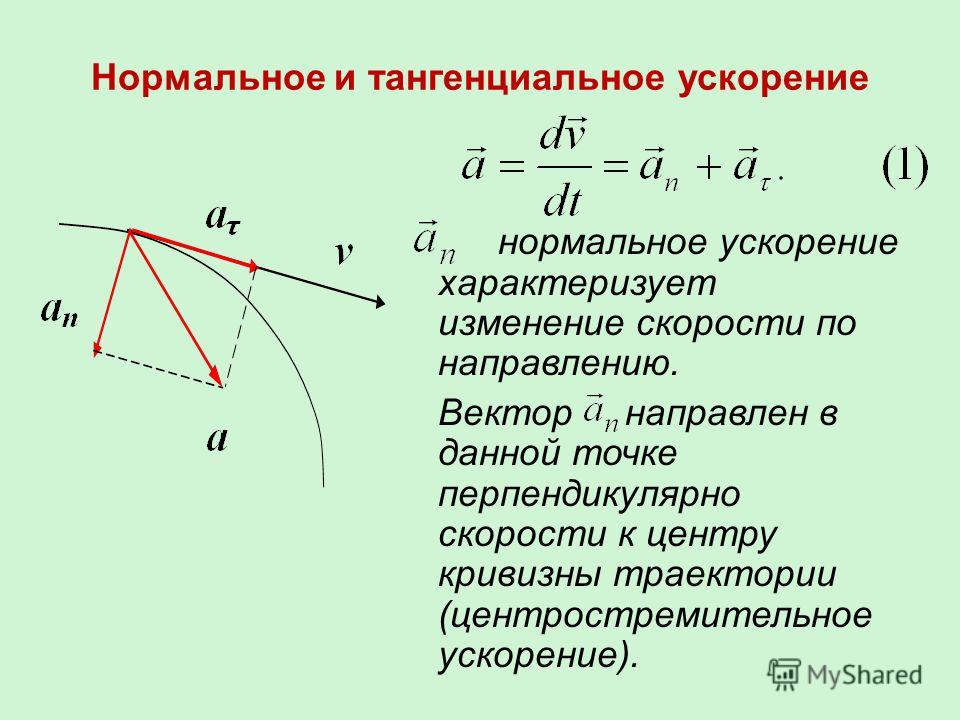 Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0tпад
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
x = v0t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Она вычисляется по формуле координаты y:
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
Выразим начальную скорость и вычислим ее:
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
График горизонтального броска тела с горыα — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
l = s • cosα
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
h0 = s sinα
Пример №2. На горе с углом наклона 30о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
Дальность полета выражается по формуле:
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
Выразим с учетом формулы начальной высоты:
Преобразуем:
Поделим обе части выражения на общий множитель s:
Подставим известные значения:
Задание EF18083Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
рисунок).
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2υ0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
Ответ: 313pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18048Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
Ответ: 323pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 15.2k
4.S: Движение в двух и трех измерениях (краткое содержание)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5689
- OpenStax
- OpenStax
Основные термины
| вектор ускорения | мгновенное ускорение, найденное путем взятия производной функции скорости по времени в виде единичного вектора |
| угловая частота | \(\omega\), скорость изменения угла, с которым объект движется по круговой траектории |
| центростремительное ускорение | составляющая ускорения объекта, движущегося по окружности, направленная радиально внутрь к центру окружности |
| вектор смещения | вектор из начального положения в конечное положение на траектории частицы |
| вектор положения | вектор от начала выбранной системы координат до положения частицы в двух- или трехмерном пространстве |
| движение снаряда | движение объекта, подверженное только ускорению свободного падения |
| диапазон | максимальное горизонтальное расстояние, которое проходит снаряд |
| система отсчета | система координат, в которой измеряются положение, скорость и ускорение неподвижного или движущегося объекта |
| относительная скорость | скорость объекта, наблюдаемая из конкретной системы отсчета, или скорость одной системы отсчета относительно другой системы отсчета |
| тангенциальное ускорение | величина которого есть скорость изменения скорости во времени. Его направление касается окружности. Его направление касается окружности. |
| время полета | время нахождения снаряда в воздухе |
| общее ускорение | векторная сумма центростремительного и тангенциального ускорений |
| траектория | путь снаряда по воздуху |
| вектор скорости | вектор, задающий мгновенную скорость и направление движения частицы; касательной к траектории |
Ключевые уравнения
| Вектор положения | $$\vec{r} (t) = x (t) \hat{i} + y(t) \hat{j} + z(t) \hat{k}$$ |
| Вектор смещения | $$\Delta \vec{r} = \vec{r} (t_{2}) – \vec{r} (t_{1})$$ |
| Вектор скорости | $$\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) – \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt}$$ |
| Скорость в пересчете на компоненты | $$\vec{v} (t) = v_{x}(t) \hat{i} + v_{y}(t) \hat{j} + v_{z}(t) \hat{k} $$ |
| Компоненты скорости | $$v_{x} (t) = \frac{dx(t)}{dt} v_{y}(t) = \frac{dy(t)}{dt} v_{z}(t) = \ frac{d z(t)}{dt}$$ |
| Средняя скорость | $$\vec{v}_{avg} = \frac{\vec{r} (t_{2}) – \vec{r} (t_{1})}{t_{2} – t_{1} }$$ |
| Мгновенное ускорение | $$\vec{a} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{v} (t + \Delta t) – \vec{v} (t)}{\Delta t} = \frac{d \vec{v}}{dt}$$ |
| Мгновенное ускорение, форма компонента | $$\vec{a} (t) = \frac{dv_{x}(t)}{dt} \hat{i} + \frac{dv_{y}(t)}{dt} \hat{j } + \frac{dv_{z}(t)}{dt} \hat{k}$$ |
| Мгновенное ускорение как вторые производные положения 9{2}}{r}$$ | |
| Вектор положения, равномерное круговое движение | $$\vec{r} (t) = A \cos \omega t \hat{i} + A \sin \omega t \hat{j}$$ |
| Вектор скорости, равномерное круговое движение | $$\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \ омега т\шляпа{j}$$ |
| Вектор ускорения, равномерное круговое движение | $$\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} – A \ omega^{2} \sin \omega t \hat{j}$$ |
| Тангенциальное ускорение | $$a_{T} = \frac{d|\vec{v}|}{dt}$$ |
| Общее ускорение | $$\vec{a} = \vec{a}_{C} + \vec{a}_{T}$$ |
| Вектор положения в кадре S — это вектор положения в кадре S′ плюс вектор от начала координат S до начала координат S’ | $$\vec{r}_{PS} = \vec{r}_{PS’} + \vec{r}_{S’S}$$ |
| Уравнение относительной скорости, соединяющее две системы отсчета | $$\vec{v}_{PS} = \vec{v}_{PS’} + \vec{v}_{S’S}$$ |
| Уравнение относительной скорости, связывающее более двух систем отсчета | $$\vec{v}_{PC} = \vec{v}_{PA} + \vec{v}_{AB} + \vec{v}_{BC}$$ |
| Уравнение относительного ускорения | $$\vec{a}_{PS} = \vec{a}_{PS’} + \vec{a}_{S’S}$$ |
Резюме
4.
 1 Векторы смещения и скорости
1 Векторы смещения и скорости- Функция положения \(\vec{r}\)(t) дает положение как функцию времени частицы, движущейся в двух или трех измерениях. Графически это вектор от начала выбранной системы координат до точки, в которой находится частица в определенное время.
- Вектор смещения \(\Delta \vec{r}\) дает кратчайшее расстояние между любыми двумя точками на траектории частицы в двух или трех измерениях.
- Мгновенная скорость дает скорость и направление движения частицы в определенный момент времени на ее траектории в двух или трех измерениях и представляет собой вектор в двух и трех измерениях.
- Вектор скорости касается траектории частицы.
- Перемещение \(\vec{r}\)(t) можно представить в виде векторной суммы одномерных перемещений \(\vec{x}\)(t), \(\vec{y}\)( t), \(\vec{z}\)(t) вдоль направлений x, y и z.
- Скорость \(\vec{v}\)(t) может быть записана как векторная сумма одномерных скоростей v x (t), v y (t), v z (t) по осям x, y и z.

- Движение в любом заданном направлении не зависит от движения в перпендикулярном направлении.
4.2 Вектор ускорения
- В двух- и трехмерном пространстве вектор ускорения может иметь произвольное направление и не обязательно указывает на заданную составляющую скорости.
- Мгновенное ускорение создается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение представляет собой вектор в двух или трех измерениях. Его находят, взяв производную функции скорости по времени.
- В трех измерениях ускорение \(\vec{a}\)(t) может быть записано как векторная сумма одномерных ускорений a x (t), a y (t) и a z (t) по осям x, y и z.
- Кинематические уравнения для постоянного ускорения можно записать в виде векторной суммы уравнений для постоянного ускорения в направлениях x, y и z.
4.3 Снарядное движение
- Снарядное движение — это движение объекта, подверженное только ускорению свободного падения, где ускорение постоянно, как вблизи поверхности Земли.

- Для решения задач о движении снаряда мы анализируем движение снаряда в горизонтальном и вертикальном направлениях, используя одномерные кинематические уравнения для x и y.
- Время полета снаряда, запущенного с начальной вертикальной скоростью v 0y по ровной поверхности, определяется выражением $$T_{tof} = \frac{2(v_{0} \sin \theta)}{g}$ $Это уравнение справедливо только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью полета. Опять же, уравнение для дальности справедливо только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен. 9{2}}{г}\).
- Неравномерное круговое движение возникает, когда существует тангенциальное ускорение объекта, совершающего круговое движение, так что скорость объекта изменяется. Это ускорение называется тангенциальным ускорением \(\vec{a}_{T}\). Величина тангенциального ускорения есть скорость изменения величины скорости во времени.
 Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений. - Объект, совершающий равномерное круговое движение, может быть описан уравнениями движения. Вектор положения объекта равен \(\vec{r}\)(t) = A cos \(\omega\)t \(\hat{i}\) + A sin \(\omega\)t \( \hat{j}\), где A — величина |\(\vec{r}\)(t)|, которая также является радиусом окружности, а \(\omega\) — угловая частота.
4.5 Относительное движение в одном и двух измерениях
- При анализе движения объекта необходимо указать систему отсчета с точки зрения положения, скорости и ускорения.
- Относительная скорость — это скорость объекта, наблюдаемая из определенной системы отсчета, и она зависит от выбора системы отсчета.
- Если S и S′ – две системы отсчета, движущиеся относительно друг друга с постоянной скоростью, то скорость объекта относительно S равна его скорости относительно S′ плюс скорость S′ относительно S.

- Если две системы отсчета движутся относительно друг друга с постоянной скоростью, то ускорения объекта, наблюдаемые в обеих системах отсчета, равны.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 4.S: Движение в двух и трех измерениях (краткое описание) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- source@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1
- source@https://openstax.
кинематика – Почему мгновенная скорость касается траектории?
$\begingroup$
Траектория — это путь объекта в пространстве как функция времени. Однако на многих графиках траектории, когда движение плоское, вместо этого используются горизонтальная ось положения и вертикальная ось положения. Тем не менее, на этих же графиках мгновенный вектор скорости нарисован по касательной к кривой, но скорость является производной вектора положения по времени, поэтому, согласно моей логике, она касается только кривой, где ось x — это время. и ось y – это положение, а не там, где ось x – горизонтальное положение, а ось y – вертикальное положение.
Является ли построение вектора мгновенной скорости касательной к кривой траектории с правильным положением осей по горизонтали и вертикали, или это просто небрежность, так как два графика являются лишь частью друг друга? И если это правильно, то почему?
- кинематика
- скорость
- дифференцирование
$\endgroup$
$\begingroup$
Ответ в определении мгновенной скорости. Во время движения вдоль пути небольшое изменение положения ${\rm d}\vec{r}$ за небольшой промежуток времени ${\rm d}t$ мгновенная скорость определяется как $$\vec{v} = \ frac{{\rm d}\vec{r}}{{\rm d}t}$$
Во время движения вдоль пути небольшое изменение положения ${\rm d}\vec{r}$ за небольшой промежуток времени ${\rm d}t$ мгновенная скорость определяется как $$\vec{v} = \ frac{{\rm d}\vec{r}}{{\rm d}t}$$
Напротив, изменение положения равно
$${\rm d}\vec{r } = \vec{v}\, {\rm d}t$$
, что означает, что, поскольку время является скаляром, то и ${\rm d}\vec{r}$, и $\vec{v}$ должны указывать в одном направлении.
Все сводится к слову наряду с при описании движения частицы. Поскольку движение ограничено/определено точно по пути, это означает, что каждое небольшое изменение ${\rm d}\vec{r}$ должно касаться пути.
$\endgroup$
$\begingroup$
В траектории, где $x = x(t)$ и $y = y(t)$, верно, что $v_x = x'(t)$ и $v_y = y'(t)$ касаются соответственно к кривым $x\times t$ и $y\times t$.
В малой окрестности точки $x_0 = x(t_0), y_0 = y(t_0)$, $$\frac{v_y}{v_x} = lim_{\delta t \to 0}\frac{\frac {y(t_0+\delta t) – y(t_0)}{\delta t}}{\frac{x(t_0+\delta t) – x(t_0)}{\delta t}} = lim _{\delta t \ в 0} \frac{y(t_0+\delta t) – y_0}{x(t_0+\delta t) – x_0}$$ Это эквивалентно касательной к траектории: $$lim_{\delta x \to 0} \frac{y(x_0 + \delta x) – y(x_0)}{\delta x}$$
Итак, вектор скорости касается траектории.






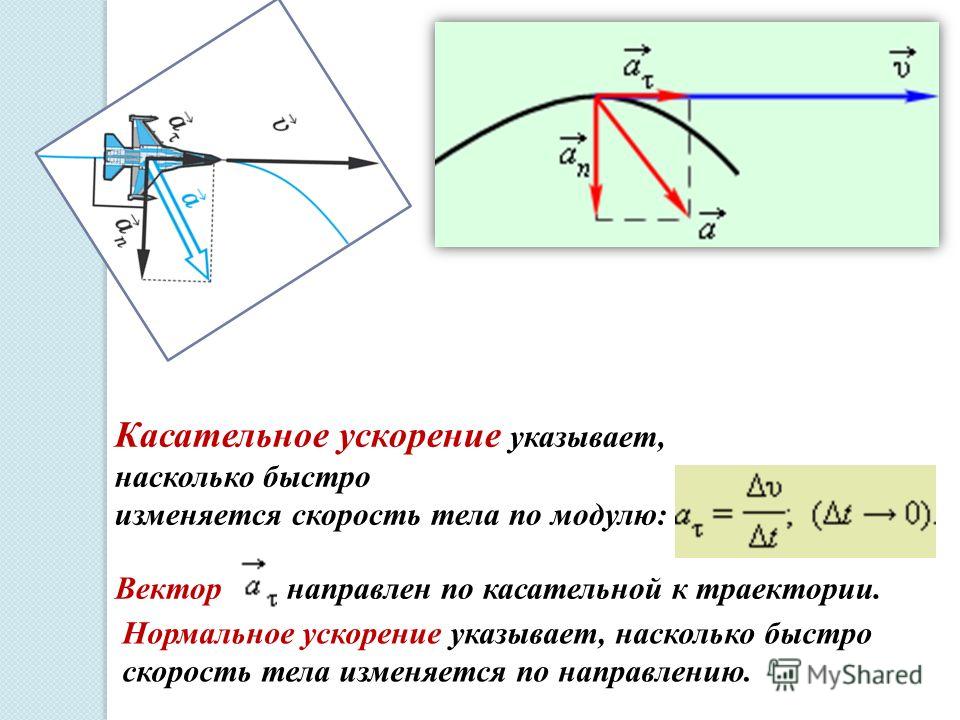 Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1