Как направлена мгновенная скорость в данной точке траектории: Как направлена мгновенная скорость в данной точке траектории? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Мгновенная и средняя скорости – Класс!ная физика

Мгновенная и средняя скорости

Подробности: Просмотров: 632

«Физика – 10 класс»

Какую скорость показывает спидометр?
Может ли городской транспорт двигаться равномерно и прямолинейно?

Реальные тела (человек, автомобиль, ракета, теплоход и т. д.), как правило, не движутся с постоянной скоростью. Они начинают двигаться из состояния покоя, и их скорость увеличивается постепенно, при остановке скорость уменьшается также постепенно, таким образом, реальные тела движутся неравномерно.

Неравномерное движение может быть как прямолинейным, так и криволинейным.

Чтобы полностью описать неравномерное движение точки, надо знать её положение и скорость в каждый момент времени.

Скорость точки в данный момент времени называется мгновенной скоростью.

Что же понимают под мгновенной скоростью?

Пусть точка, двигаясь неравномерно и по кривой линии, в некоторый момент времени t занимает положение М (рис.

1.24). По прошествии времени Δt₁ от этого момента точка займёт положение М₁, совершив перемещение Δ₁. Поделив вектор Δ₁ на промежуток времени Δt₁ найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время Δt попасть из положения М в положение М₁. Эту скорость называют средней скоростью перемещения точки за время Δt₁.

Обозначив её через _ср1, запишем: Средняя скорость направлена вдоль секущей ММ

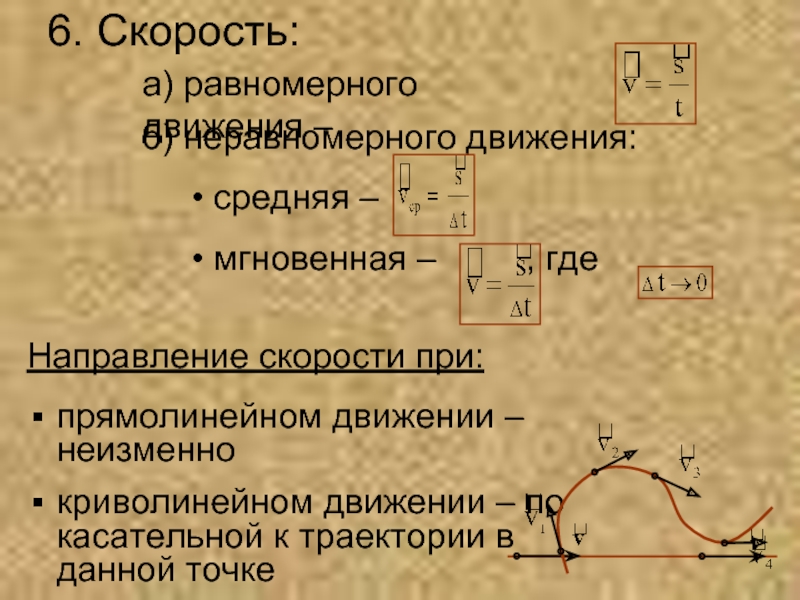
1. По той же формуле мы находим скорость точки при равномерном прямолинейном движении.

Скорость, с которой должна равномерно и прямолинейно двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени, называется средней скоростью перемещения.

Для того чтобы определить скорость в данный момент времени, когда точка занимает положение М, найдём средние скорости за всё меньшие и меньшие промежутки времени:

Интересно, верно ли следующее определение мгновенной скорости: «Скорость тела в данной точке траектории называется мгновенной скоростью»?

При уменьшении промежутка времени Δt перемещения точки уменьшаются по модулю и меняются по направлению.

Соответственно этому средние скорости также меняются как по модулю, так и по направлению. Но по мере приближения промежутка времени Δt к нулю средние скорости всё меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени Δt к нулю отношение стремится к определённому вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени или просто мгновенной скоростью и обозначают

Мгновенная скорость точки есть величина, равная пределу отношения перемещения Δ к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении промежутка Δt к нулю.

Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени Δt к нулю, направлена средняя скорость перемещения. Эта средняя скорость в течение промежутка времени Δt направлена так, как направлен вектор перемещения Δ Из рисунка 1. 24 видно, что при уменьшении промежутка времени Δt вектор Δ уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор Δ, тем ближе он к касательной, проведённой к траектории в данной точке М, т. е. секущая переходит в касательную. Следовательно,

мгновенная скорость направлена по касательной к траектории (см. рис. 1.24).

В частности, скорость точки, движущейся по окружности, направлена по касательной к этой окружности. В этом нетрудно убедиться. Если маленькие частички отделяются от вращающегося диска, то они летят по касательной, так как имеют в момент отрыва скорость, равную скорости точек на окружности диска. Вот почему грязь из-под колёс буксующей автомашины летит по касательной к окружности колёс (рис. 1.25).

Понятие мгновенной скорости — одно из основных понятий кинематики. Это понятие относится к точке. Поэтому в дальнейшем, говоря о скорости движения тела, которое нельзя считать точкой, мы можем говорить о скорости какой-нибудь его точки.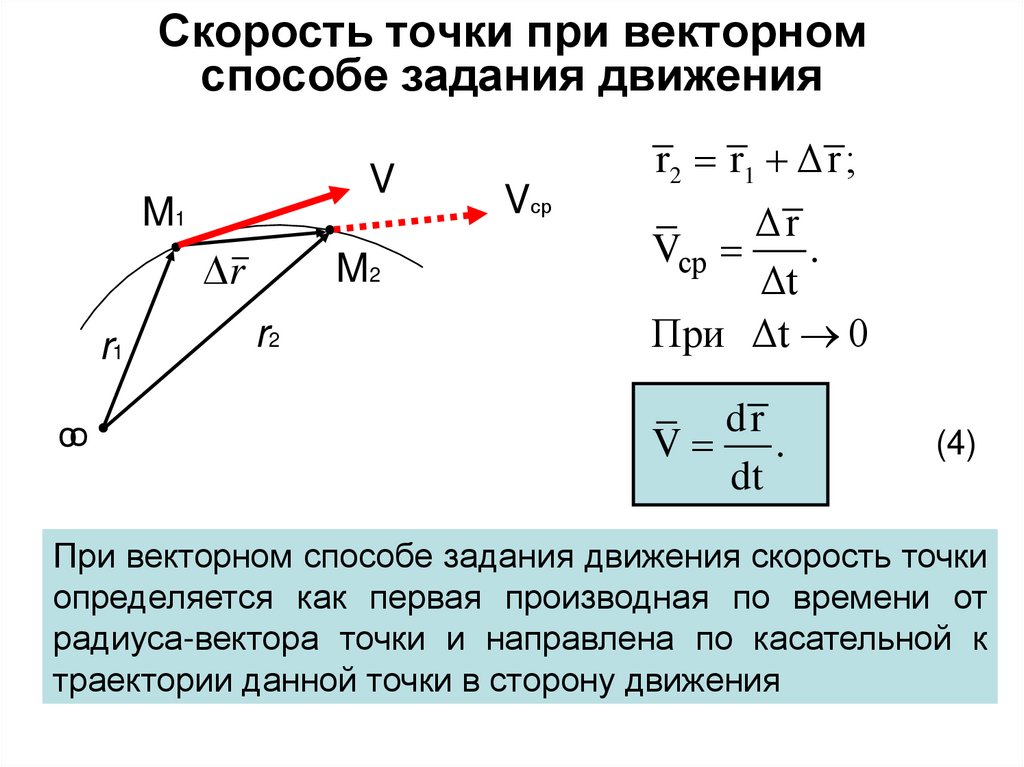

Помимо средней скорости перемещения, для описания движения чаще пользуются средней путевой скоростью _cps.

Средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден:

Когда мы говорим, что путь от Москвы до Санкт-Петербурга поезд прошёл со скоростью 80 км/ч, мы имеем в виду именно среднюю путевую скорость движения поезда между этими городами. Модуль средней скорости перемещения при этом будет меньше средней путевой скорости, так как s > |Δ|.

Для неравномерного движения также справедлив закон сложения скоростей. В этом случае складываются мгновенные скорости.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика – Физика, учебник для 10 класса – Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

Криволинейное движение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении

изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.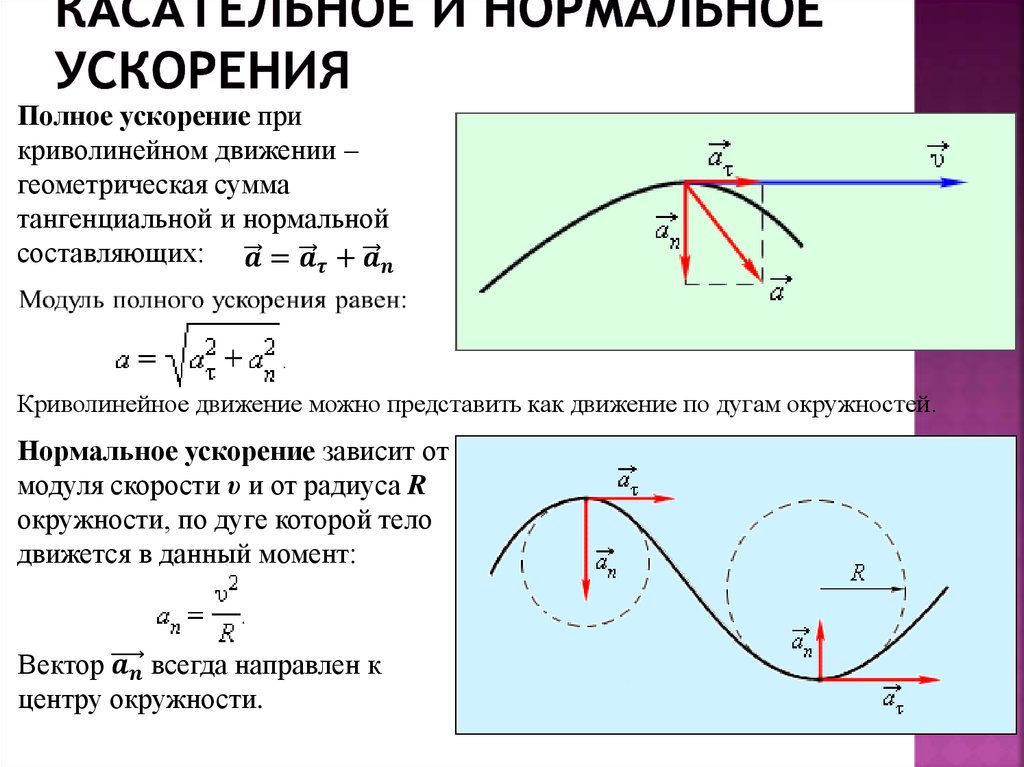

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

или

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение – это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.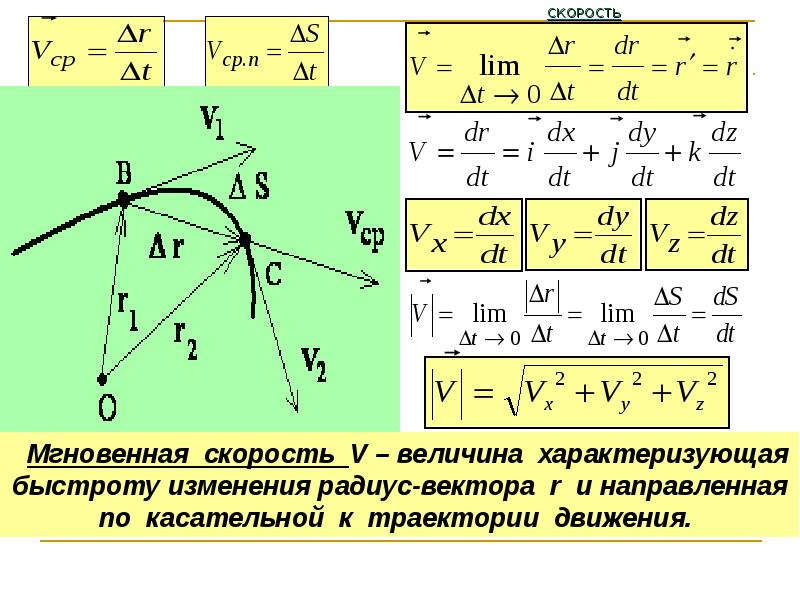

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Рис. 1.21. Движение тела при криволинейном движении.

Мгновенная скорость при криволинейном движении. Конспект урока “Прямолинейное и криволинейное движение

Мы знаем, что при прямолинейном движении направление вектора скорости всегда совпадает с направлением перемещения. Что можно сказать о направлении скорости и перемещения при криволинейном движении? Чтобы ответить на этот вопрос, мы воспользуемся тем же приемом, которым пользовались в предыдущей главе при изучении мгновенной скорости прямолинейного движения.

На рисунке 56 представлена некоторая криволинейная траектория. Допустим, что тело движется по ней из точки А в точку В.

При этом пройденный телом путь – это дуга А В, а его перемещение это вектор Конечно, нельзя считать, что скорость тела во время движения направлена вдоль вектора перемещения.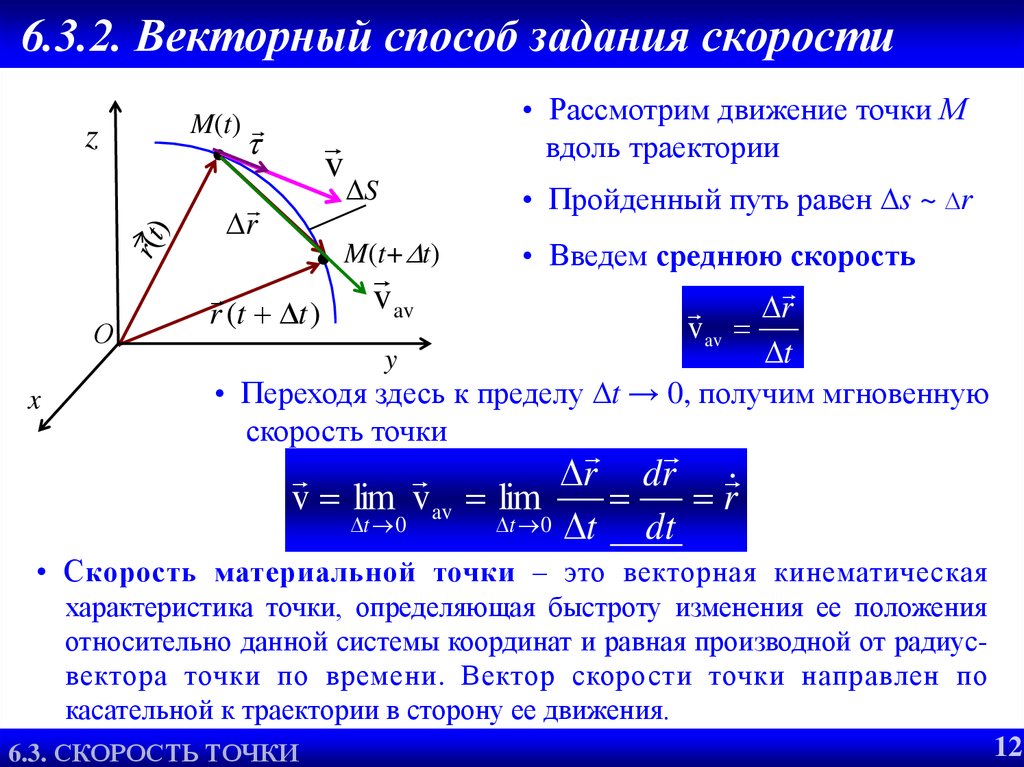 Проведем между точками А и В ряд хорд (рис. 57) и представим себе, что движение тела происходит именно по этим хордам. На каждой из них тело движется прямолинейно и вектор скорости направлен вдоль хорды.

Сделаем теперь наши прямолинейные участки (хорды) более короткими (рис. 58). По-прежнему на каждом из них вектор скорости направлен вдоль хорды. Но видно, что ломаная линия на рисунке 58 уже более похожа на плавную кривую.

Ясно поэтому, что, продолжая уменьшать длину прямолинейных участков, мы их как бы стянем в точки и ломаная линия превратится в плавную кривую. Скорость же в каждой точке этой кривой будет направлена но касательной к кривой в этой точке (рис. 59).

Скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

В том, что скорость точки при криволинейном движении действительно направлена по касательной, убеждает нас, например, наблюдение за работой гочнла (рис. 60). Если прижать к вращающемуся точильному камню концы стального прутка, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр.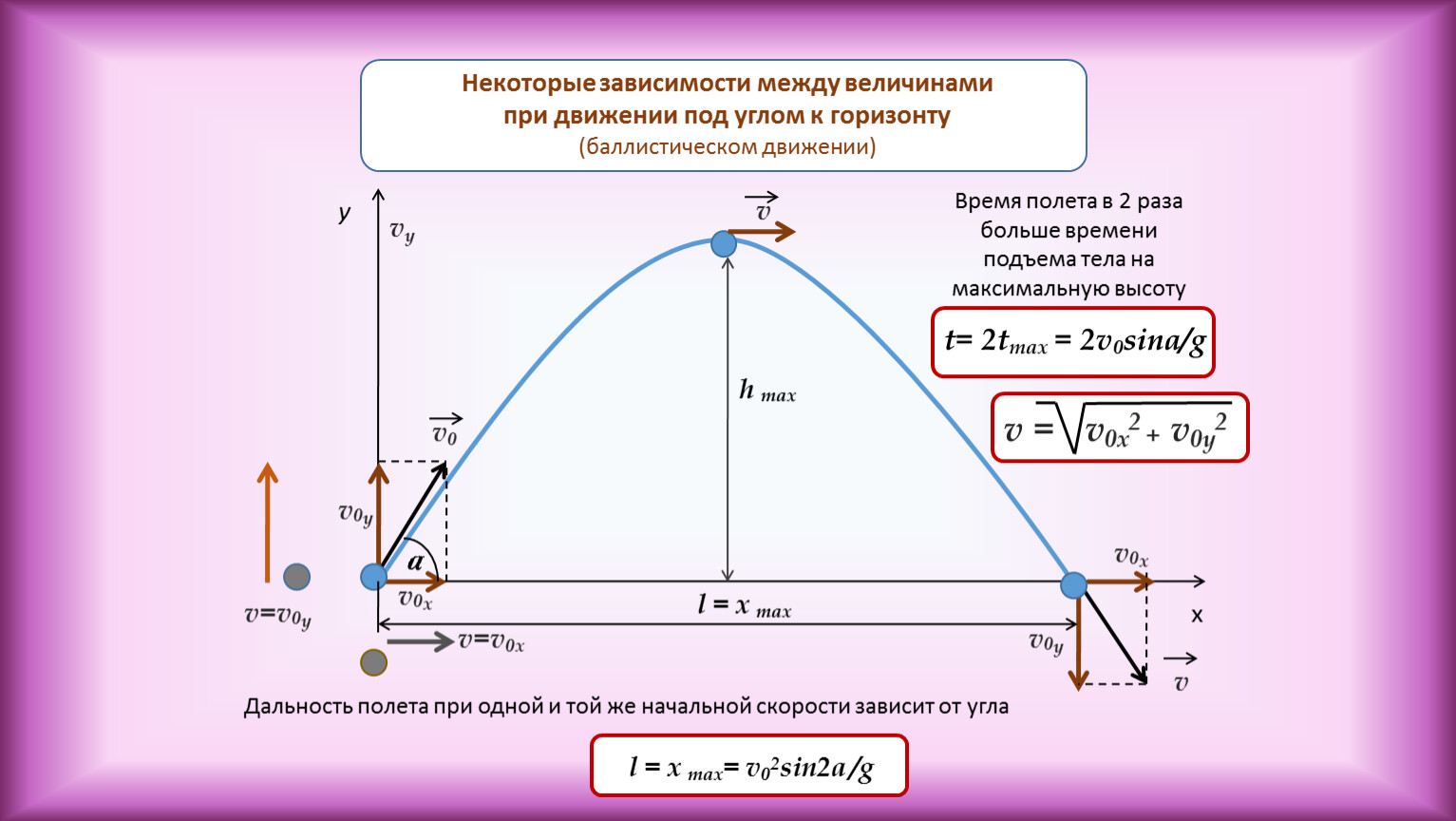 Эти частицы летят с той скоростью, которой

они обладали в момент отрыва от камня. Хорошо видно, что направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся и брызги от колес буксующего автомобиля (рис. 61).

Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различные направления, как это показано на рисунке 62. Модуль же скорости может быть во всех точках траектории одинаковым (см. рис. 62) или изменяться от точки к точке, от одного момента времени к другому (рис. 63).

При криволинейном движении у вектора скорости изменяется направление. При этом может меняться и его модуль, т. е. длина. В этом случае вектор ускорения раскладывается на две составляющие: касательную к траектории и перпендикулярную к траектории (рис. 10). Составляющая называется тангенциальным (касательным) ускорением, составляющая –нормальным (центростремительным) ускорением.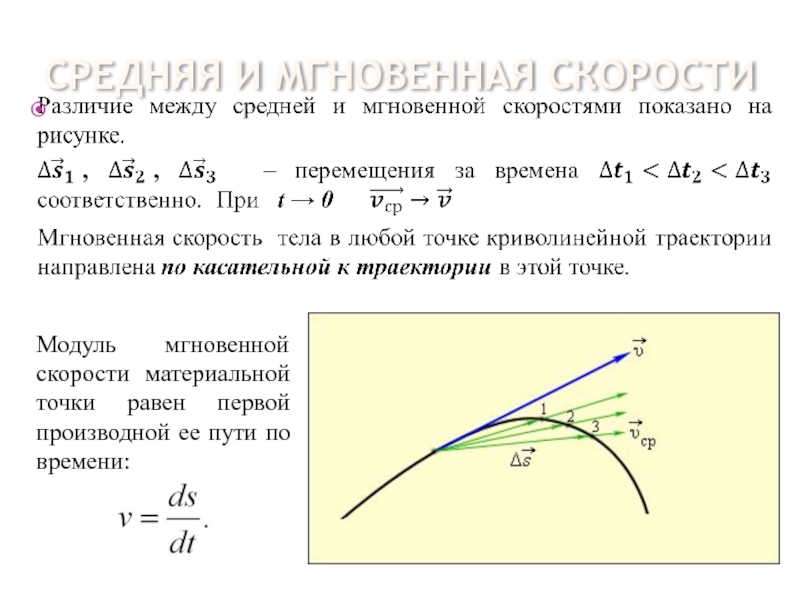

Ускорение при криволинейном движении

Тангенциальное ускорение характеризует быстроту изменения линейной скорости, а нормальное ускорение характеризует быстроту изменения направления движения.

Полное ускорение равно векторной сумме тангенциального и нормального ускорений:

(15)

Модуль полного ускорения равен:

Рассмотрим равномерное движение точки по окружности. При этом и . Пусть в рассматриваемый момент времени t точка находится в положении 1 (рис. 11). Спустя время Δt точка окажется в положении 2, пройдя путь Δs , равный дуге 1-2. При этом скорость точки v получает приращение Δv , в результате чего вектор скорости, оставаясь неизменным по величине, повернется на угол Δφ , совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs :

(16)

где R-радиус окружности, по которой движется точка. Найдем приращение вектора скорости Для этого перенесем вектор так, чтобы его начало совпадало с началом вектора . Тогда вектор изобразится отрезком, проведенным из конца вектора в конец вектора . Этот отрезок служит основанием равнобедренного треугольника со сторонами и и углом Δφ при вершине. Если угол Δφ невелик (что выполняется для малых Δt), для сторон этого треугольника можно приближенно написать:

Подставляя сюда Δφ из (16), получаем выражение для модуля вектора :

Разделив обе части уравнения на Δt и сделав предельный переход, получим величину центростремительного ускорения:

Здесь величины v и R постоянные, поэтому их можно вынести за знак предела. Предел отношения – это модуль скорости Его также называют линейной скоростью.

Радиус кривизны

Радиус окружности R называется радиусом кривизны траектории. Величина, обратная R, называется кривизной траектории:

где R – радиус рассматриваемой окружности. Если α есть центральный угол, соответствующий дуге окружности s, то, как известно, между R, α и s имеет место соотношение:

s = Rα . (18)

Понятие радиуса кривизны применимо не только к окружности, но и любой кривой линии. Радиус кривизны (или обратная ему величина – кривизна) характеризует степень изогнутости линии. Чем меньше радиус кривизны (соответственно, чем больше кривизна), тем сильнее изогнута линия. Рассмотрим это понятие подробнее.

Кругом кривизны плоской линии в некоторой точке A называется предельное положение окружности, проходящей через точку А и две другие точки В 1 и В 2 при их бесконечном приближении к точке А (на рис. 12 кривая проведена сплошной линией, а круг кривизны – пунктирной). Радиус круга кривизны дает радиус кривизны рассматриваемой кривой в точке A, а центр этого круга – центр кривизны кривой для той же точки А.

Проведем в точках B 1 и В 2 касательные B 1 D и В 2 Е к окружности, проходящей через точки В 1 , А и B 2 . Нормали к этим касательным B 1 С и В 2 С представят собой радиусы R окружности и пересекутся в ее центре С. Введем угол Δα между нормалями В1С и В 2 С; очевидно, он равен углу между касательными В 1 D и В 2 E. Обозначим участок кривой между точками B 1 и В 2 как Δs. Тогда по формуле (18):

Круг кривизны плоской кривой линии

Определение кривизны плоской кривой в разных точках

На рис. 13 изображены круги кривизны плоской линии в разных точках. В точке A 1 , где кривая является более пологой, радиус кривизны больше, чем в точке A 2 , соответственно, кривизна линии в точке A 1 будет меньше, чем в точке A 2 . В точке A 3 кривая является еще более пологой, чем в точках A 1 и A 2 , поэтому радиус кривизны в этой точке будет больше, а кривизна меньше. Кроме того, круг кривизны в точке A 3 лежит по другую сторону кривой. Поэтому величине кривизны в этой точке приписывают знак, противоположный знаку кривизны в точках A 1 и A 2: если кривизну в точках A 1 и A 2 будем считать положительной, то кривизна в точке A 3 будет отрицательной.

Понятия скорости и ускорения естественным образом обобщаются на случай движения материальной точки по криволинейной траектории .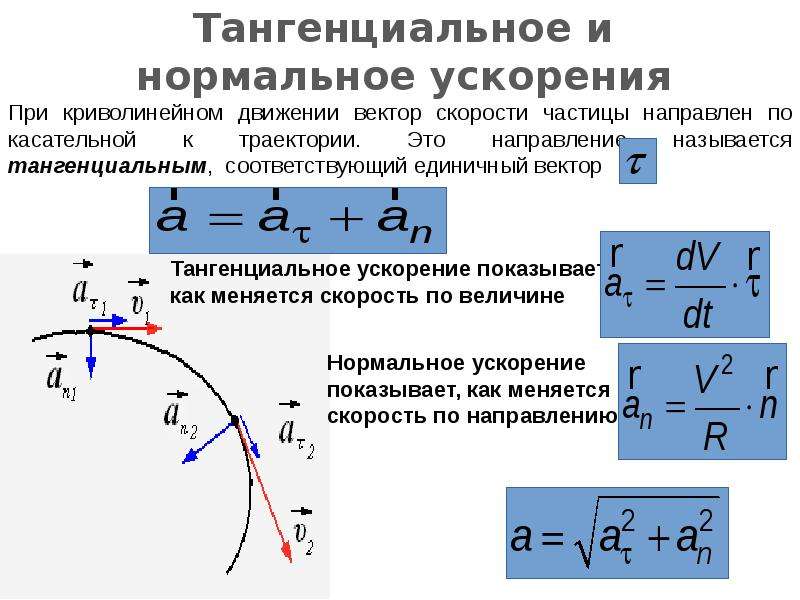 Положение движущейся точки на траектории задается радиус-вектором r , проведенным в эту точку из какой-либо неподвижной точки О , например, начала координат (рис. 1.2). Пусть в момент времени t материальная точка находится в положении М с радиус-вектором r = r (t ). Спустя короткое время Dt , она переместится в положение М 1 с радиусом – вектором r 1 = r (t + Dt ). Радиус – вектор материальной точки получит приращение, определяемое геометрической разностью Dr = r 1 – r . Средней скоростью движения за время Dt называется величина

Направление средней скорости V ср совпадает с направлением вектора Dr .

Предел средней скорости при Dt ® 0, т. е. производная радиуса – вектора r по времени

(1.9)

называется истинной или мгновенной скоростью материальной точки. Вектор V направлен по касательной к траектории движущейся точки.

Ускорением а называется вектор, равный первой производной вектора скорости V или второй производной радиуса – вектора r по времени:

(1.10)

(1.11)

Отметим следующую формальную аналогию между скоростью и ускорением. Из произвольной неподвижной точки О 1 будем откладывать вектор скорости V движущейся точки во всевозможные моменты времени (рис. 1.3).

Конец вектора V называется скоростной точкой . Геометрическое место скоростных точек есть кривая, называемая годографом скорости. Когда материальная точка описывает траекторию, соответствующая ей скоростная точка движется по годографу.

Рис. 1.2 отличается от рис. 1.3 только обозначениями. Радиус – вектор r заменен на вектор скорости V , материальная точка – на скоростную точку, траектория – на годограф. Математические операции над вектором r при нахождении скорости и над вектором V при нахождении ускорения совершенно тождественны.

Скорость V направлена по касательной траектории. Поэтому ускорение a будет направлено по касательной к годографу скорости. Можно сказать, что ускорение есть скорость движения скоростной точки по годографу . Следовательно,

Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное . С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.

Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.

Для начала определимся, какие принципиальные отличия есть у криволинейного движения (рис. 1) относительно прямолинейного и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения

Поговорим о том, как удобно описывать движение тела при криволинейном движении.

Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 2).

Рис. 2. Разбиение криволинейного движения на участки прямолинейного движения

Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (рис. 3). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. К тому же примеры движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:

Для того чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.

Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей

Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории (рис. 4). Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рассмотрим движение тела по дуге окружности (рис. 5).

Рис. 5. Скорость тела при движении по окружности

Обратите внимание, что в данном случае модуль скорости тела в точке равен модулю скорости тела в точке :

Однако вектор не равен вектору . Итак, у нас появляется вектор разности скоростей (рис. 6):

Рис. 6. Вектор разности скоростей

Причем изменение скорости произошло через некоторое время .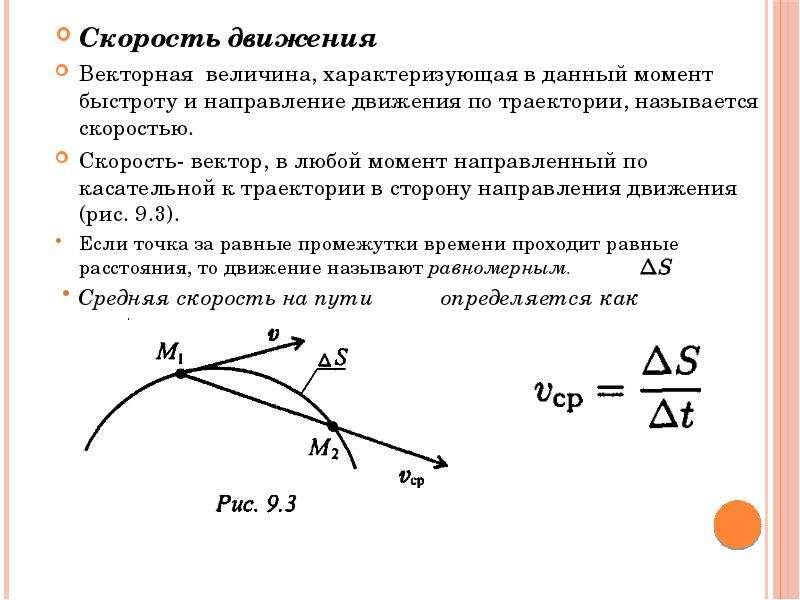 Таким образом, мы получаем знакомую комбинацию:

Это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:

Движение по криволинейной траектории является ускоренным. Природа этого ускорения – непрерывное изменение направление вектора скорости.

Еще раз отметим, что, даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется. Однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.

В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (рис. 7). Центростремительное ускорение всегда направлено к центру окружности, по которой движется тело.

Рис. 7. Центростремительное ускорение

Модуль центростремительного ускорения может быть рассчитан по формуле:

Переходим к описанию равномерного движения тела по окружности. Договоримся, что скорость , которой вы пользовались по время описания поступательного движения, теперь будет называться линейной скоростью.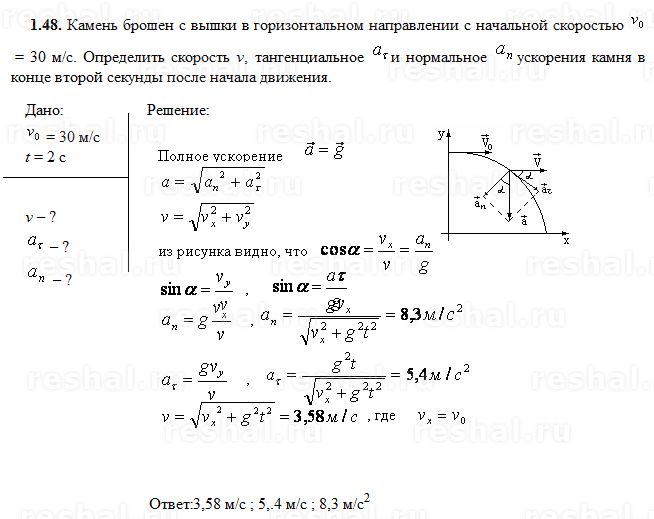 И под линейной скоростью мы будем понимать мгновенную скорость в точке траектории вращающегося тела.

Рис. 8. Движение точек диска

Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки и (рис. 8). Рассмотрим их движение. За некоторое время эти точки переместятся по дугам окружности и станут точками и . Очевидно, что точка совершила большее перемещение, чем точка . Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется

Однако если внимательно посмотреть на точки и , можно сказать, что неизменным остался угол , на который они повернулись относительно оси вращения . Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.

Начнем рассмотрение движения по окружности с самого простого случая – равномерного движения по окружности. Напомним, что равномерным поступательным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. По аналогии можно дать определение равномерного движения по окружности.

Равномерным движением по окружности называется движение, при котором за любые равные промежутки времени тело поворачивается на одинаковые углы.

Аналогично понятию линейной скорости вводится понятие угловой скорости.

Угловой скоростью равномерного движения ( называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.

В физике чаще всего используется радианная мера угла. Например, угол в равен радиан. Измеряется угловая скорость в радианах в секунду:

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью

Точка проходит при вращении дугу длиной , поворачиваясь при этом на угол . Из определения радианной меры угла можно записать:

Разделим левую и правую части равенства на промежуток времени , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:

Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.

Такая зависимость линейной и угловой скоростей используется в геостационарных спутниках (спутники, которые всегда находятся над одной и той же точкой земной поверхности). Благодаря таким спутникам мы имеем возможность получать телевизионные сигналы.

Вспомним, что ранее мы вводили понятия периода и частоты вращения.

Период вращения – время одного полного оборота. Период вращения обозначается буквой и измеряется в секундах в СИ:

Частота вращения – физическая величина, равная количеству оборотов, которое тело совершает за единицу времени.

Частота обозначается буквой и измеряется в обратных секундах:

Они связаны соотношением:

Существует связь между угловой скоростью и частотой вращения тела. Если вспомнить, что полный оборот равен , легко увидеть, что угловая скорость:

Подставляя эти выражения в зависимость между угловой и линейной скоростью, можно получить зависимость линейной скорости от периода или частоты:

Запишем также связь между центростремительным ускорением и этими величинами:

Таким образом, мы знаем связь между всеми характеристиками равномерного движения по окружности.

Подытожим. На этом уроке мы начали описывать криволинейное движение. Мы поняли, каким образом можно связать криволинейное движение с движением по окружности. Движение по окружности всегда является ускоренным, а наличие ускорения обуславливает тот факт, что скорость всегда меняет свое направление. Такое ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики движения по окружности (линейную скорость, угловую скорость, период и частоту вращения) и нашли соотношения между ними.

Список литературы

Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Аyp.ru ().
Википедия ().

Домашнее задание

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

Задачи 92, 94, 98, 106, 110 – сб. задач А.П. Рымкевич, изд. 10
Вычислите угловую скорость движения минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.

Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.

Основные кинематические величины:

– Перемещение() – вектор, соединяющий начальную и конечную точки.

r – радиус-вектор, определяет положение МТ в пространстве.

– Скорость – отношение пути ко времени.

– Путь – множество точек через которое прошло тело.

– Ускорение – скорость изменения скорости, то есть первая производная от скорости.

2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.

Криволинейное движение – это движение, траектория которого представляет собой кривую линию. Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.

Изменение величины скорости за единицу времени – это тангенциальное ускорение :

Где 𝛖 τ , 𝛖 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно.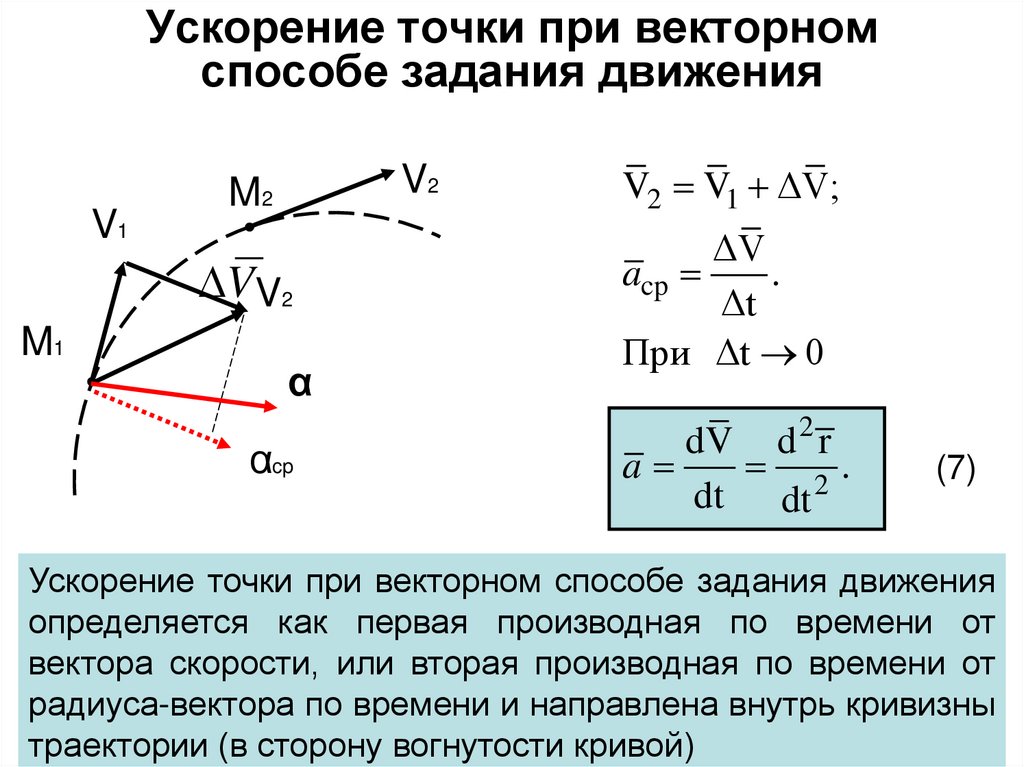 Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение – это изменение скорости по направлению за единицу времени:

Полное ускорение при равнопеременном криволинейном движении тела равно:

–угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ – рад/с.

Плоское вращение – это вращение всех векторов скоростей точек тела в одной плоскости.

3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Нормальное (центростремительное) ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой.

Материальная точка движется ускоренно по криволинейной траектории. Скорость и ускорение при криволинейном движении

6. Криволинейное движение. Угловое перемещение, угловые скорость и ускорение тела. Путь и перемещение при криволинейном движении тела.

Криволинейное движение материальной точки считается равномерным движением, если модульскорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), аl – длина траектории . Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

или

Где v τ , v 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение – это изменение скорости по направлению за единицу времени:

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Рис. 1.21. Движение тела при криволинейном движении.

Криволинейное движение

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v x и v y ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времениt определяется по формулам

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:

Нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.

Тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

Полное ускорение, с которым движется материальная точка, равно:

Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.

Период обращения – это время, за которое тело совершается один оборот.

Обозначается период буквой Т (с) и определяется по формуле:

где t – время обращения, п – число оборотов, совершенных за это время.

Частота обращения – это величина, численно равная числу оборотов, совершенных за единицу времени.

Обозначается частота греческой буквой (ню) и находится по формуле:

Измеряется частота в 1/с.

Период и частота – величины взаимно обратные:

Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив скорость v на время одного оборота:

l = vT. С другой стороны, этот путь равен длине окружности 2πr . Поэтому

vT = 2πr,

где w (с -1) – угловая скорость.

При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.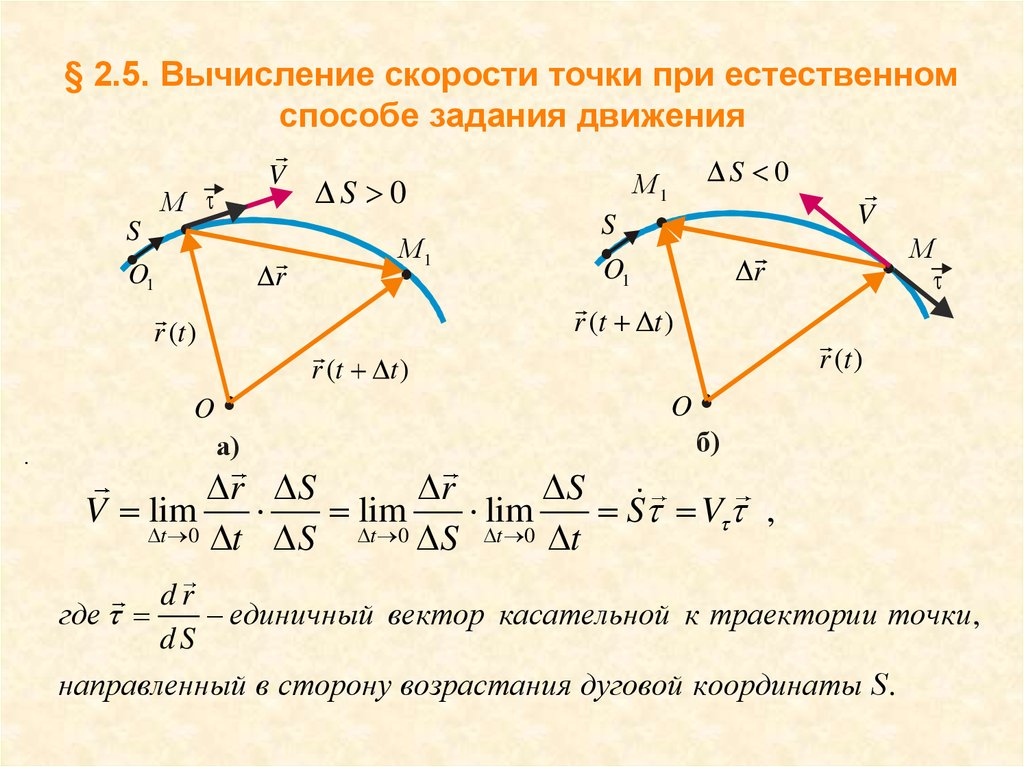

Угловая скорость (w ) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:

Связь между линейной и угловой скоростями:

Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.

С прямолинейным движением мы более или менее научились работать на предыдущих уроках, а именно, решать главную задачу механики для такого вида движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.

Для начала определимся, какие принципиальные отличия есть у криволинейного движения (Рис. 1) относительно прямолинейного, и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения

Поговорим о том, как удобно описывать движение тела при криволинейном движении.

Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (Рис. 2).

Рис. 2. Разбиение криволинейного движения на поступательные движения

Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (см. Рис. 3.). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. Кроме того, примеров движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:

Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей

Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории. Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рассмотрим движение тела по окружности (Рис. 4).

Рис. 4. Скорость тела при движении по окружности

Обратите внимание, что в данном случае модуль скорости тела в точке А равен модулю скорости тела в точке B.

Однако, вектор не равен вектору . Итак, у нас появляется вектор разности скоростей (см. Рис. 5).

Рис. 5. Разность скоростей в точках A и B.

Причем изменение скорости произошло через некоторое время . Таким образом, мы получаем знакомую комбинацию:

это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:

Еще раз отметим, что даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется, однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.

В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (см. Рис. 6). Центростремительное ускорение всегда направлено к центру окружности, по которой движется тело.

Рис. 6.Центростремительное ускорение

Модуль центростремительного ускорения может быть рассчитан по формуле

Рис. 7. Движение точек диска

Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки A и B. И рассмотрим их движение. За некоторое время эти точки переместятся по дугам окружности и станут точками A’ и B’. Очевидно, что точка А совершила большее перемещение, чем точка B. Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется.

Однако, если внимательно посмотреть на точки А и В, можно сказать, что неизменным остался угол , на который они повернулись относительно оси вращения О. Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности, можно использовать угловые характеристики. Прежде всего, напомним понятие о радианной мере углов.

Угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности.

Таким образом, легко заметить, что например угол в равен радиан. И, соответственно, можно перевести любой угол, заданный в градусах, в радианы, умножив его на и поделив на . Угол поворота при вращательном движении аналогичен перемещению при поступательном движении. Заметим, что радиан – это безразмерная величина:

поэтому обозначение «рад» часто опускают.

Аналогично понятию линейной скорости вводится понятие угловой скорости.

Угловой скоростью называется физическая величина, равная отношению угла, на который повернулось тело ко времени, за которое произошел этот поворот.

Измеряется угловая скорость в радианах в секунду, или просто в обратных секундах.

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью

Точка А проходит при вращении дугу длиной S, поворачиваясь при этом на угол φ. Из определения радианной меры угла можно записать, что

Разделим левую и правую части равенства на промежуток времени , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей

Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее угловая и линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.

Вспомним, что ранее мы вводили понятия периода и частоты вращения.

Период вращения – время одного полного оборота. Период вращения обозначается буквой и измеряется в секундах в системе СИ:

Частота вращения – число оборотов в единицу времени. Частота обозначается буквой и измеряется в обратных секундах:

Они связаны соотношением:

Кроме того, если вспомнить, каким образом мы определили понятие радиана, станет ясно, как связать линейную скорость тела с угловой:

Запишем также связь между центростремительным ускорением и этими величинами:

Таким образом, мы знаем связь между всеми характеристиками равномерного движения по окружности.

Подытожим. На этом уроке мы начали описывать криволинейное движение. Мы поняли, каким образом можно связать криволинейное движение с движением по окружности. Движение по окружности всегда является ускоренным, а наличие ускорения обуславливает тот факт, что скорость всегда меняет свое направление. Такое ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики движения по окружности (линейную скорость, угловую скорость, период и частоту вращения), и нашли соотношения между ними.

Список литературы:

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10. – М.: Просвещение, 2008.
А. П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
О. Я. Савченко. Задачи по физике. – М.: Наука, 1988.
А. В. Пёрышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Энциклопедия ().
Аyp.ru ().
Википедия ().

Домашнее задание:

Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.

Задачи 92, 94, 98, 106, 110 сб. задач А. П. Рымкевич изд. 10 ()
Вычислите угловую скорость движения минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.
Рассмотрите следующие вопросы и ответы на них:

Вопрос: Есть ли на поверхности Земли точки, в которых угловая скорость, связанная с суточным вращением Земли, равна нулю?

Ответ: Есть. Такими точками являются географические полюсы Земли. Скорость в этих точках равна нулю, потому что в этих точках вы будете находиться на оси вращения.

Ускорение при криволинейном движении

Полное ускорение равно векторной сумме тангенциального и нормального ускорений:

(15)

Модуль полного ускорения равен:

(16)

Подставляя сюда Δφ из (16), получаем выражение для модуля вектора :

Радиус кривизны

s = Rα . (18)

Круг кривизны плоской кривой линии

Определение кривизны плоской кривой в разных точках

Нам известно, что всякое криволинейное движение происходит под действием силы, направленной под углом к скорости. В случае равномерного движения по окружности этот угол будет прямым. В самом деле, если, например, вращать шарик, привязанный к верёвке, то направление скорости шарика в любой момент времени перпендикулярно верёвке.

Сила же натяжения верёвки, удерживающая шарик на окружности, направлена вдоль верёвки к центру вращения.

По второму закону Ньютона эта сила будет вызывать ускорение тела в том же направлении. Ускорение, направленное по радиусу к центру вращения, называется центростремительным ускорением .

Выведем формулу для определения величины центростремительного ускорения.

Прежде всего, заметим, что движение по окружности – сложное движение. Под действием центростремительной силы тело движется к центру вращения и одновременно по инерции удаляется от этого центра по касательной к окружности.

Пусть за время t тело, двигаясь равномерно со скоростью v, переместилось из D в Е. Допустим, что в тот момент, когда тело находилось в точке D, на него перестала бы действовать центростремительная сила. Тогда за время t оно переместилось бы в точку К, лежащую на касательной DL. Если же в начальный момент тело оказалось бы под действием только одной центростремительной силы (не двигалось по инерции), то оно за время t, двигаясь равноускоренно, переместилось бы в точку F, лежащую на прямой DC. В результате сложения этих двух движений за время t получается результирующее движение по дуге DE.

Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой .

Чтобы получить формулу для расчёта величины центростремительной силы, надо воспользоваться вторым законом Ньютона, который применим и к любому криволинейному движению.

Подставляя в формулу F = ma значение центростремительного ускорения a = v 2 / R , получим формулу центростремительной силы:

F = mv 2 / R

Величина центростремительной силы равна произведению массы тела на квадрат линейной скорости , делённому на радиус .

Если дана угловая скорость тела, то центростремительную силу удобнее рассчитывать по формуле: F = m? 2 R, где? 2 R – центростремительное ускорение.

Из первой формулы видно, что при одной и той же скорости чем меньше радиус окружности, тем больше центростремительная сила. Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.

Центростремительная сила зависит от линейной скорости: с увеличением скорости она увеличивается. Это хорошо известно всем конькобежцам, лыжникам и велосипедистам: чем с большей скоростью движешься, тем труднее сделать поворот. Шофёры очень хорошо знают, как опасно круто поворачивать автомобиль на большой скорости.

Бросим какое-нибудь тело л од углом к горизонту. Следя за его движением, мы заметим, что тело сначала поднимается, двигаясь по кривой, потом также по кривой падает вниз.

Если направлять струю воды под разными углами к горизонту, то можно видеть, что сначала с увеличением угла струя бьёт всё дальше и дальше. При угле в 45° к горизонту (если не учитывать сопротивления воздуха) дальность наибольшая. При дальнейшем увеличении угла дальность уменьшается.

Для построения траектории движения тела, брошенного под углом к горизонту, проведём горизонтальную прямую OA и к ней под заданным углом – прямую ОС.

На линии ОС в выбранном масштабе откладываем отрезки, численно равные путям, пройденным в направлении бросания (0–1, 1–2, 2–3, 3–4). Из точек 1, 2, 3 и т. д. опускаем перпендикуляры на ОА и на них откладываем отрезки, численно равные путям, проходимым свободно падающим телом в течение 1 сек (1–I), 2 сек (2–II), 3 сек (3–III) и т. д. Точки 0, I, II, III, IV и т. д. соединяем плавной кривой.

Траектория тела симметрична относительно вертикальной прямой, проходящей через точку IV.

Сопротивление воздуха уменьшает как дальность полёта, так и наибольшую высоту полёта, и траектория становится несимметричной. Таковы, например, траектории снарядов и пуль. На рисунке сплошная кривая показывает схематически траекторию снаряда в воздухе, а пунктирная – в безвоздушном пространстве.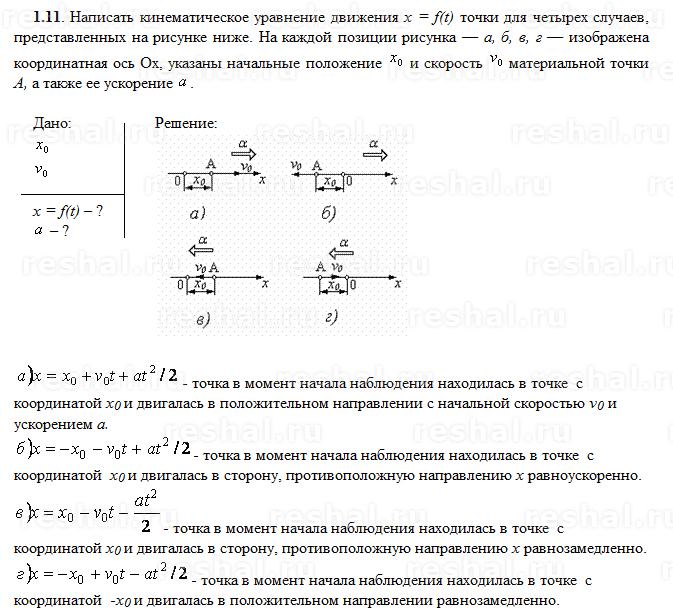 Насколько сопротивление воздуха изменяет дальность полёта, видно из следующего примера. При отсутствии сопротивления воздуха снаряд 76-миллиметрового орудия, выпущенный под углом 20° к горизонту, пролетел бы 24 км. В воздухе же этот снаряд пролетает около 7 км.

Независимость движений

Всякое криволинейное движение является сложным движением, состоящим из движения по инерции и движения под действием силы, направленной под углом к скорости тела. Это можно показать на следующем примере.

Допустим, что шарик движется по столу равномерно и прямолинейно. Когда шарик скатывается со стола, вес его больше уже не уравновешивается силой давления стола и он, по инерции сохраняя равномерное и прямолинейное движение, одновременно начинает падать. В результате сложения движений – равномерного прямолинейного по инерции и равноускоренного под действием силы тяжести – шарик перемещается по кривой линии.

Можно на опыте показать, что эти движения независимы одно от другого.

На рисунке изображена пружина, которая, выгибаясь под ударом молотка, может привести один из шариков в движение в горизонтальном направлении и одновременно освободить другой шарик, так что оба они начнут движение в один и тот же момент: первый – по кривой, второй – по вертикали вниз. Оба шарика ударятся о пол одновременно; следовательно, время падения обоих шариков одинаково. Отсюда можно заключить, что движение шарика под действием силы тяжести не зависит от того, покоился ли шарик в начальный момент или двигался в горизонтальном направлении.

Этот опыт иллюстрирует очень важное положение механики, называемое принципом независимости движений .

Одним из простейших и весьма распространённых видов криволинейного движения является равномерное движение тела по окружности. По окружности, например, движутся части маховиков, точки земной поверхности при суточном вращении Земли и т. д.

Введём величины, характеризующие это движение. Обратимся к рисунку. Пусть при вращении тела одна из его точек за время t перешла из A в В. Радиус, соединяющий точку А с центром окружности, повернулся при этом на угол? (греч. «фи»). Быстроту вращения точки можно характеризовать величиной отношения угла? ко времени t, т. е. ? / t .

Угловая скорость

Отношение угла поворота радиуса, соединяющего движущуюся точку с центром вращения, к промежутку времени, за который происходит этот поворот, называется угловой скоростью .

Обозначая угловую скорость греческой буквой? («омега»), можно написать:

? = ? / t

Угловая скорость численно равна углу поворота в единицу времени.

При равномерном движении по окружности угловая скорость есть величина постоянная.

При вычислении угловой скорости угол поворота принято измерять в радианах. Радиан есть центральный угол, длина дуги которого равна радиусу этой дуги.

При рассмотрении прямолинейного движения стало известно, что если на тело действует сила в направлении движения, то движение тела будет оставаться прямолинейным. Изменяться будет только величина скорости. При этом если направление силы совпадает с направлением скорости, движение будет прямолинейным и ускоренным. В случае же противоположного направления силы движение окажется прямолинейным и замедленным. Таковы, например, движение тела, брошенного вертикально вниз, и движение тела, брошенного вертикально вверх.

Рассмотрим теперь, как будет двигаться тело под действием силы, направленной под углом к направлению скорости.

Обратимся сначала к опыту. Создадим траекторию движения стального шарика около магнита. Сразу замечаем, что вдали от магнита шарик двигался прямолинейно, при приближении же к магниту траектория шарика искривлялась и шарик двигался по кривой. Направление скорости его при этом непрерывно менялось. Причиной этого было действие магнита на шарик.

Мы можем заставить двигаться по кривой прямолинейно перемещающееся тело, если будем толкать его, тянуть за привязанную к нему нить и так далее, лишь бы сила была направлена под углом к скорости перемещения тела.

Итак, криволинейное движение тела происходит под действием силы, направленной под углом к направлению скорости тела .

В зависимости от направления и величины силы, действующей на тело, криволинейные движения могут быть самыми разнообразными. Наиболее простыми видами криволинейных движений являются движения по окружности, параболе и эллипсу.

В некоторых случаях центростремительная сила является равнодействующей двух сил, действующих на движущееся по окружности тело.

Рассмотрим несколько таких примеров.

1. По вогнутому мосту движется автомобиль со скоростью v, масса автомобиля т, радиус кривизны моста R. Чему равна сила давления, производимого автомобилем на мост, в низшей его точке?

Установим прежде всего, какие силы действуют на автомобиль. Таких сил две: вес автомобиля и сила давления моста на автомобиль. (Силу трения в этом и во всех последующих призерах мы исключаем из рассмотрения).

Когда автомобиль неподвижен, то эти силы, будучи равными по величине и направленными в противоположные стороны» уравновешивают друг друга.

Когда же автомобиль движется по мосту, то на него, как и на всякое тело, движущееся по окружности, действует центростремительная сила. Что является источником этой силы? Источником этой силы может быть только действие моста на автомобиль. Сила Q, с которой мост давит на движущийся автомобиль, должна не только уравновешивать вес автомобиля Р, но и вынуждать его двигаться по окружности, создавая необходимую для этого центростремительную силу F. Сила F может быть только равнодействующей сил Р и Q, так как она является результатом взаимодействия движущегося автомобиля и моста.

Сообщение про прямолинейное и криволинейное движение.

Сегодня мы продолжим изучать движение. Нами были рассмотрены случаи, когда тела двигались только прямолинейно, то есть по прямой линии. Но так ли уж часто такое движение мы встречаем в жизни? Конечно же, нет. Тела обычно движутся по криволинейным траекториям. Движение планет, поездов, животных – все это будет примером криволинейного движения. Описать такое движение сложнее. Изменение координат будет происходить, как минимум, по двум осям, например OX и OY. Сравним, как направлены вектора скорости и перемещения при прямолинейном и криволинейном движении. Когда тело движется по прямой, то направление вектора скорости и вектора перемещения всегда совпадают. Для того, чтобы ответить на этот же вопрос в случае криволинейного движения, рассмотрим рисунок. Предположим, что тело движется из точки М1 в точку М2 по дуге. Путь – это длина дуги, перемещение – вектор М1М2. В геометрии, такой отрезок называют хордой. Мы видим, что направление скорости и перемещения не совпадают. При криволинейном движении мы будем говорить о мгновенной скорости. Мгновенная скорость тела в каждой точки криволинейной траектории направлена по касательной к траектории в этой точке. Убедиться в этом можно, наблюдая за брызгами из-под колес автомобиля, они так же вылетают по касательной к окружности колеса. Обратите внимание, что скорость имеет в каждой точке криволинейной траектории различное направление, поэтому даже при условии, что модуль скорости остался прежним, если изменилось направление движения, то рассматривать нужно новый вектор. Из того, что скорость непрерывно меняется, следует, что и ускорение так же будет меняться. Следовательно, криволинейное движение – это движение с ускорением. Предположим, тело движется по некоторой криволинейной траектории. Таких траекторий может быть бесчисленное множество, неужели, для каждого из них придется описывать свои законы движения? Оказывается, отдельные части траектории можно, приблизительно, представить, как дуги окружностей. И само криволинейное движение, в большинстве случаев, можно представить как совокупность движений по дугам окружностей различного радиуса. Изучив движение по окружности, мы сможем описывать более сложные случаи движения. Запомним, если скорость тела и действующая на него сила направлены вдоль одной прямой, то тело движется прямолинейно, а если они направлены вдоль пересекающихся прямых, то тело движется криволинейно. Определите, по какой траектории полетит камень, вращающийся на нити, если нить внезапно оборвется? Мгновенная скорость камня направлена по касательной к криволинейной линии, следовательно, в момент обрыва, согласно закону инерции, тело будет двигаться, сохраняя прежнюю скорость, то есть по этой же касательной. Грузовик движется по криволинейной траектории. Скорость движения по модулю величина постоянная. Можно ли утверждать, что ускорение грузовика равно нулю? Утверждать, что ускорение грузовика равно нулю нельзя, так как скорость имеет в каждой точке криволинейной траектории различное направление, поэтому даже при условии, что модуль скорости остался прежним, то рассматривать нужно новый вектор. Из того, что скорость непрерывно меняется, следует, что и ускорение так же будет изменяться. Мы уже знаем, что причиной ускорения является сила. Укажите, на каких участках криволинейного движения сила действовала?
Ответ обоснуйте. На траектории сделаны отметки положения тела через равные промежутки времени. Сила действовала на участке 0-3. Тело двигалось прямолинейно, но скорость тела менялась (тело двигалось ускоренно), то есть под действием силы. Сила действовала на участке 7-8. Величина скорости не изменилась, но направление поменялось (тело двигалось ускоренно), то есть под действием силы.

Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью
Законы взаимодействия и движения тел

При помощи данного урока вы сможете самостоятельно изучить тему «Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью». Вначале мы охарактеризуем прямолинейное и криволинейное движение, рассмотрев, как при этих видах движения связаны вектор скорости и приложенная к телу сила. Далее рассмотрим частный случай, когда происходит движение тела по окружности с постоянной по модулю скоростью.

На предыдущем уроке мы рассмотрели вопросы, связанные с законом всемирного тяготения. Тема сегодняшнего урока тесно связана с этим законом, мы обратимся к равномерному движению тела по окружности.

Ранее мы говорили, что движение – это изменение положения тела в пространстве относительно других тел с течением времени. Движение и направление движения характеризуются в том числе и скоростью. Изменение скорости и сам вид движения связаны с действием силы. Если на тело действует сила, то тело изменяет свою скорость.

Если сила направлена параллельно движению тела, то такое движение будет прямолинейным (рис. 1).

Рис. 1. Прямолинейное движение

Криволинейным будет такое движение, когда скорость тела и сила, приложенная к этому телу, направлены друг относительно друга под некоторым углом (рис. 2). В этом случае скорость будет изменять свое направление.

Рис. 2. Криволинейное движение

Итак, при прямолинейном движении вектор скорости направлен в ту же сторону, что и сила, приложенная к телу. А криволинейным движением является такое движение, когда вектор скорости и сила, приложенная к телу, расположены под некоторым углом друг к другу.

Рассмотрим частный случай криволинейного движения, когда тело движется по окружности с постоянной по модулю скоростью. Когда тело движется по окружности с постоянной скоростью, то меняется только направление скорости. По модулю она остается постоянной, а направление скорости изменяется. Такое изменение скорости приводит к наличию у тела ускорения, которое называется центростремительным .

Рис. 6. Движение по криволинейной траектории

Если траектория движения тела является кривой, то ее можно представить как совокупность движений по дугам окружностей, как это изображено на рис. 6.

На рис. 7 показано, как изменяется направление вектора скорости. Скорость при таком движении направлена по касательной к окружности, по дуге которой движется тело. Таким образом, ее направление непрерывно меняется. Даже если скорость по модулю остается величиной постоянной, изменение скорости приводит к появлению ускорения:

В данном случае ускорение будет направлено к центру окружности. Поэтому оно называется центростремительным.

Почему центростремительное ускорение направлено к центру?

Вспомним, что если тело движется по криволинейной траектории, то его скорость направлена по касательной. Скорость является векторной величиной. У вектора есть численное значение и направление. Скорость по мере движения тела непрерывно меняет свое направление. То есть разность скоростей в различные моменты времени не будет равна нулю (), в отличие от прямолинейного равномерного движения.

Итак, у нас есть изменение скорости за какой-то промежуток времени . Отношение к – это ускорение. Мы приходим к выводу, что, даже если скорость не меняется по модулю, у тела, совершающего равномерное движение по окружности, есть ускорение.

Куда же направлено данное ускорение? Рассмотрим рис. 3. Некоторое тело движется криволинейно (по дуге). Скорость тела в точках 1 и 2 направлена по касательной. Тело движется равномерно, то есть модули скоростей равны: , но направления скоростей не совпадают.

Рис. 3. Движение тела по окружности

Вычтем из скорость и получим вектор . Для этого необходимо соединить начала обоих векторов. Параллельно перенесем вектор в начало вектора . Достраиваем до треугольника. Третья сторона треугольника будет вектором разности скоростей (рис. 4).

Рис. 4. Вектор разности скоростей

Вектор направлен в сторону окружности.

Рассмотрим треугольник, образованный векторами скоростей и вектором разности (рис. 5).

Рис. 5. Треугольник, образованный векторами скоростей

Данный треугольник является равнобедренным (модули скоростей равны). Значит, углы при основании равны. Запишем равенство для суммы углов треугольника:

Выясним, куда направлено ускорение в данной точке траектории. Для этого начнем приближать точку 2 к точке 1. При таком неограниченном прилежании угол будет стремиться к 0, а угол – к . Угол между вектором изменения скорости и вектором самой скорости составляет . Скорость направлена по касательной, а вектор изменения скорости направлен к центру окружности. Значит, ускорение тоже направлено к центру окружности . Именно поэтому данное ускорение носит название центростремительное .

Как найти центростремительное ускорение?

Рассмотрим траекторию, по которой движется тело. В данном случае это дуга окружности (рис. 8).

Рис. 8. Движение тела по окружности

На рисунке представлены два треугольника: треугольник, образованный скоростями, и треугольник, образованный радиусами и вектором перемещения. Если точки 1 и 2 очень близки, то вектор перемещения будет совпадать с вектором пути. Оба треугольника являются равнобедренными с одинаковыми углами при вершине. Таким образом, треугольники подобны. Это значит, что соответствующие стороны треугольников относятся одинаково:

Перемещение равно произведению скорости на время: . Подставив данную формулу, можно получить следующее выражение для центростремительного ускорения:

Угловая скорость обозначается греческой буквой омега (ω), она говорит о том, на какой угол поворачивается тело за единицу времени (рис. 9). Это величина дуги в градусной мере, пройденной телом за некоторое время.

Рис. 9. Угловая скорость

Обратим внимание, что если твердое тело вращается, то угловая скорость для любых точек на этом теле будет величиной постоянной. Ближе точка располагается к центру вращения или дальше – это не важно, т. е. от радиуса не зависит.

Единицей измерения в этом случае будет либо градус в секунду (), либо радиан в секунду (). Часто слово «радиан» не пишут, а пишут просто . Для примера найдем, чему равна угловая скорость Земли. Земля делает полный поворот на за ч, и в этом случае можно говорить о том, что угловая скорость равна:

Также обратите внимание на взаимосвязь угловой и линейной скоростей:

Линейная скорость прямо пропорциональна радиусу. Чем больше радиус, тем больше линейная скорость. Тем самым, удаляясь от центра вращения, мы увеличиваем свою линейную скорость.

Необходимо отметить, что движение по окружности с постоянной скоростью – это частный случай движения. Однако движение по окружности может быть и неравномерным. Скорость может изменяться не только по направлению и оставаться одинаковой по модулю, но и меняться по своему значению, т. е., кроме изменения направления, существует еще изменение модуля скорости. В этом случае мы говорим о так называемом ускоренном движении по окружности.

Что такое радиан?

Существует две единицы измерения углов: градусы и радианы. В физике, как правило, радианная мера угла является основной.

Построим центральный угол , который опирается на дугу длиной .

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока: дать школьникам представление о криволинейном движении, частоте, угловом перемещении, угловой скорости, периоде. Познакомить с формулами для нахождения этих величин и единицами измерения. (Слайды 1 и 2 )

Ззадачи:

Образовательные : дать учащимся представление о криволинейном движении его траектории, величинах его характеризующих, единицах измерения этих величин и формулах для вычисления.
Развивающие :продолжать формирование умений применять теоретические знания для решения практических задач, развивать интерес к предмету и логическое мышление.
Воспитательные : продолжать развивать кругозор учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.

Оборудование: наклонный жёлоб, шарик, шарик на нити, игрушечный автомобиль, юла, модель часов со стрелками, мультимедийный проектор, презентация.

ХОД УРОКА

1. Актуализация знаний

Учитель.

– Какие виды движения вы знаете?
– Чем отличаются прямолинейные и криволинейные движения?
– В какой системе отсчёта можно говорить об этих видах движения?
– Сравните траекторию и путь для прямолинейного и криволинейного движений. (Слайды 3, 4).

2. Объяснение нового материала

Учитель. Демонстрирую: падение шарика по вертикали, его скатывание по желобу, вращение шарика на нити, перемещение игрушечного автомобиля по столу, падение теннисного мячика брошенного под углом к горизонту.

Учитель. Чем отличаются траектории движения предложенных тел? (Ответы учащихся)
Попробуйте сами дать определения криволинейного и прямолинейного движений. (Запись в тетрадях):
– прямолинейное движение – движение по прямой траектории, причём направление векторов силы и скорости совпадают; (слайд 7)
– криволинейное движение – движение по непрямой траектории.

Рассмотреть два примера криволинейного движения: по ломаной линии и по кривой (Зарисовать, слайды 5, 6 ).

Учитель. Чем отличаются эти траектории?

Ученик. В первом случае траекторию можно разбить на прямолинейные участки и рассмотреть каждый участок отдельно. Во втором случае можно разбить кривую на дуги окружностей и прямолинейные участки Т.о. это движение можно рассматривать как последовательность движений, происходящих по дугам окружностей различного радиуса (Слайд 8)

Учитель. Приведите примеры прямолинейного и криволинейного движения, с которыми вы встречались в жизни.

3. Сообщение ученика. В природе и технике очень часто встречаются движения, траектории которых представляют собой не прямые, а кривые линии. Это криволинейное движение. По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли, а на Земле всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т.д.
Если прижать к вращающемуся точильному камню конец стального прутика, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной движутся брызги от колес буксующего автомобиля. (Слайд 9)

Учитель. Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различное направление, причём, обратите внимание: вектора скорости и силы, действующей на тело, направлены по пересекающимся прямым. (Слайды 10 и 11).
По модулю же скорость может быть всюду одинакова или изменяться от точки к точке.
Но даже если модуль скорости не изменяется, ее нельзя считать постоянной. Скорость – векторная величина. Для векторной величины модуль и направление одинаково важны. А раз меняется скорость , значит есть ускорение. Поэтому криволинейное движение – это всегда движение с ускорением , даже если по модулю скорость постоянная. (Слайд 12).
Ускорение тела, равномерно движущегося по окружности, в любой точке центростремительное , т.е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. (Нарисовать)
Модуль центростремительного ускорения: а ц = V 2 /R (написать формулу), где V – линейная скорость тела, а R – радиус окружности. (Слайды 12, 13)

Учитель. Движение по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот. Эта величина называется периодом обращения и обозначается буквой Т. (Записать определение периода). Найдем связь между периодом обращения Т и модулем скорости при равномерном движении по окружности радиуса R. Т.к. V = S/t = 2R/Т. (Записать формулу в тетради) (Слайд 14)

Сообщение ученика. Период – это величина, которая достаточно часто встречается в природе и технике . Так, мы знаем. Что Земля вращается вокруг своей оси и средний период вращения равен 24 часам. Полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток. Рабочие колеса гидротурбин делают один полный оборот за время, равное 1 секунде. А винт вертолета имеет период обращения от 0,15 до 0,3 секунды. Период кровообращения у человека равен примерно 21-22 секундам.

Учитель. Движение тела по окружности можно охарактеризовать еще одной величиной – числом оборотов в единицу времени. Ее называют частотой обращения: ν = 1/Т. Единицей измерения частоты: с –1 = Гц. (Записать определение, единицу и формулу ) (слайд 14)

Сообщение ученика. Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля, вылетающая из автомата Калашникова, вращается с частотой 3000 об/с.
Для измерения частоты существуют приборы, так называемые круги для измерения частоты, основанные на оптических иллюзиях. На таком круге нанесены черные полоски и стоят частоты. При вращении такого круга черные полоски образуют круг при соответствующей этому кругу частоте. Также для измерения частоты используются тахометры. (Слайд 15)

(Дополнительные характеристики слайды 16, 17)

4. Закрепления материала (слайд18)

Учитель. На этом уроке мы познакомились с описанием криволинейного движения, с новыми понятиями и величинами. Ответьте мне на следующие вопросы:
– Как можно описать криволинейное движение?
– Что называется угловым перемещением? В каких единицах измеряется?
– Что называется периодом и частотой? Как связаны между собой эти величины? В каких единицах измеряются? Как их можно определить?
– Что называется угловой скоростью? В каких единицах она измеряется? Как можно её рассчитать?

(Если остаётся время, можно выполнить экспериментальное задание по определению периода и частоты вращения тела, подвешенного на нити.)

5. Экспериментальная работа: измерение периода, частоты тела, подвешенного на нити и вращающегося в горизонтальной плоскости. Для этого на каждую парту приготовить набор принадлежностей: нить, тело (бусинка или пуговица), секундомер; инструкцию по выполнению работы: тело вращать равномерно, (для удобства работу можно выполнять вдвоём) и измерить время 10 (вспомнить определение полного оборота). (После выполнения работы обсудить полученные результаты). (Cлайд 19)

6. Контроль и самопроверка

Учитель. Следующее задание на проверку, как вы усвоили новый материал. У каждого из вас на столах лежат тесты и две таблицы, в которые вы должны внести букву ответа. Одну из них вы подпишите и сдадите на проверку. (Тест 1 выполняет 1 вариант, тест 2 – второй вариант)

Тест 1 (слайд 20)

1. Примером криволинейного движения являются…

а) падение камня;
б) поворот машины на право;
в) бег спринтера на 100 – метровке.

2. Минутная стрелка часов делает один полный оборот. Чему равен период обращения?

а) 60 с; б) 1/3600 с; в) 3600 с.

3. Колесо велосипеда делает один оборот за 4 с. Определите частоту вращения.

а) 0,25 1/с; б) 4 1/с; в) 2 1/с.

4. Винт моторной лодки делает 25 оборотов за 1 с. Чем, равна угловая скорость винта?

а) 25 рад/с; б) /25 рад/с; в) 50 рад/с.

5. Определите частоту вращения сверла электрической дрели, если его угловая скорость равна 400 .

а)800 1/с; б) 400 1/с; в) 200 1/с.

Тест 2 (слайд 20)

1. Примером криволинейного движения является…

а) движение лифта;
б) прыжок лыжника с трамплина;
в) падение шишки с нижней ветки ели в безветренную погоду.

2. Секундная стрелка часов делает один полный оборот. Чему равна её частота обращения?

а) 1/60 с; б) 60 с; в) 1 с.

3. Колесо машины делает 20 оборотов за10 с. Определите период обращения колеса?

а) 5 с; б) 10 с; в) 0,5 с.

4. Ротор мощной паровой турбины делает 50 оборотов за 1 с. Вычислите угловую скорость.

а) 50 рад/с; б) /50 рад/с; в) 10 рад/с.

5. Определите период обращения звёздочки велосипеда, если угловая скорость равна.

а) 1 с; б) 2 с; в) 0,5 с.

Ответы на тест 1: б; в; а; в; в
Ответы на тест 2: б; а; в; в; б(слайд 21)

7. Подведение итогов

8. Домашнее задание: § 18, 19, вопросы к §§, упр.17, (устно) (слайд 21)

МБОУ «Чубаевская ООШ» Урмарского района ЧР

УРОК ФИЗИКИ в 9 КЛАССЕ

«Прямолинейное и криволинейное движение.

Движение тела по окружности.»

Учитель: Степанова Е.А.

Чубаево – 2013

Тема: Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью.

Цели урока: дать школьникам представление прямолинейном и о криволинейном движении, частоте, периоде. Познакомить с формулами для нахождения этих величин и единицами измерения.
Образовательные задачи: сформировать понятие о прямолинейном и криволинейном движении, величинах его характеризующих, единицах измерения этих величин и формулах для вычисления.
Развивающие задачи: продолжать формирование умений применять теоретические знания для решения практических задач, развивать интерес к предмету и логическое мышление.
Воспитательные задачи: продолжать развивать кругозор учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.

Оборудование: Презентация.Компьютер. Мультимедийный проектор Мяч, шарик на нити, наклонный желоб, шарик, игрушечный автомобиль, юла, модель часов со стрелками, секундомеры

Ход урока

I. Организационный момент. Вводное слово учителя.Здравствуйте, мои юные друзья!Позвольте начать наш сегодняшний урок с таких строк «Загадки страшные природы повсюду в воздухе висят» (Н.Заболоцкий, поэма «Безумный волк») (слайд 1)

2. Актуализация знаний

– Какие виды движения вы знаете? – Чем отличаются прямолинейные и криволинейные движения? – Сравните траекторию и путь для прямолинейного и криволинейного движений. Уч:.Мы знаем, что все тела притягиваются друг к другу. В частности, Луна, например, притягивается к Земле. Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю? (сл-)

Для того чтобы ответить на этот вопрос, необходимо рассмотреть виды движения тел. Мы уже знаем, что движение может быть равномерным и неравномерным, но существуют и другие характеристики движения (слайд)

3.Проблемная ситуация: Чем отличаются следующие движения?

Демонстрации : падение шарика по прямой, скатывание шарика по прямому желобу. И по круговой дорожке, вращение шарика на нити, перемещение игрушечного автомобиля по столу, движение шарика, брошенного под углом к горизонту…(по виду траектории )

Уч: По виду траектории эти движения можно разделить на движения по прямой линии и по кривой линии.(слайд)

Попробуем дать определения криволинейного и прямолинейного движений. (Запись в тетради ) прямолинейное движение – движение по прямой траектории. Криволинейное движение – движение по непрямой (кривой) траектории.

4. Итак, Тема урока

Прямолинейное и криволинейное движение. Движение по окружности (слайд)

Уч: Рассмотрим два примера криволинейного движения: по ломаной линии и по кривой (зарисовать ). Чем отличаются эти траектории?

Ученики: В первом случае траекторию можно разбить на прямолинейные участки и рассмотреть каждый участок отдельно. Во втором случае можно разбить кривую на дуги окружностей и прямолинейные участки. Т.об. это движение можно рассматривать как последовательность движений, происходящих по дугам окружностей различного радиуса. Поэтому чтобы изучить криволинейное движение, нужно изучить движение по окружности. (слайд 15)

Сообщение 1 Движение тела по окружности

В природе и технике очень часто встречаются движения, траектории которых представляют собой не прямые, а кривые линии. Это криволинейное движение. По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли, а на Земле всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т.д.

Если прижать к вращающемуся точильному камню конец стального прутика, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной движутся брызги от колес буксующего автомобиля. (Зарисовать .)

Направление и модуль скорости

Уч: Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различное направление. По модулю же скорость может быть всюду одинакова или изменяться от точки к точке.(слайд)

Но даже если модуль скорости не изменяется, ее нельзя считать постоянной. Скорость – векторная величина. Для векторной величины модуль и направление одинаково важны. А раз меняется скорость , значит есть ускорение. Поэтому криволинейное движение – это всегда движение с ускорением , даже если по модулю скорость постоянная.(слайд)(видиоролик1)

Ускорение тела, равномерно движущегося по окружности, в любой точке центростремительное , т.е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. (Нарисовать )

Модуль центростремительного ускорения: а ц =V 2 /R (написать формулу ), где V – линейная скорость тела, а R – радиус окружности.(слайд)

Центростремительная сила – сила, действующая на тело при криволинейном движении в любой момент времени, всегда направлена вдоль радиуса окружности к центру (как и центростремительное ускорение). А сила, действующая на тело пропорционально ускорению. F=ma, то

Характеристики движения тела по окружности

Движение по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот. Эта величина называется периодом обращения и обозначается буквой Т. (Записать определение периода ). При движении по окружности тело за определенный промежуток времени вернется в первоначальную точку. Поэтому движение по окружности – периодическое.

Период – время одного полного оборота.

Если тело за время t совершает N оборотов, то как найти период? (формула)

Найдем связь между периодом обращения Т и модулем скорости при равномерном движении по окружности радиуса R. Т.к. V=S/t = 2πR/Т. (Записать формулу в тетради )

Сообщение2 Период – это величина, которая достаточно часто встречается в природе и технике . Так, мы знаем. Что Земля вращается вокруг своей оси и средний период вращения равен 24 часам. Полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток. Рабочие колеса гидротурбин делают один полный оборот за время, равное 1 секунде. А винт вертолета имеет период обращения от 0,15 до 0,3 секунды. Период кровообращения у человека равен примерно 21-22 секундам.

Уч: Движение тела по окружности можно охарактеризовать еще одной величиной – числом оборотов в единицу времени. Ее называют частотой обращения:ν= 1/Т. Единицей измерения частоты: с -1 =Гц. (Записать определение, единицу и формулу )(слайд)

Как найти частоту если тело за время t совершает N оборотов (формула)

Уч: Какой вывод можно сделать о соотношении между этими величинами? (период и частота – это взаимообратные величины)

Сообщение3 Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля. Вылетающая из автомата Калашникова, вращается с частотой 3000 об/с. Для измерения частоты существуют приборы, так называемые круги для измерения частоты, основанные на оптических иллюзиях. На таком круге нанесены черные полоски и стоят частоты. При вращении такого круга черные полоски образуют круг при соответствующей этому кругу частоте. Также для измерения частоты используют тахометры. (слайд)

Связь Скорости вращения и периода вращения

ℓ – длина окружности

ℓ=2πr V=2πr/T

Дополнительные характеристики движения по окружности. (слайд)

Уч: Вспомним, какими величинами характеризуется прямолинейное движение?

Перемещение, скорость,ускорение.

Уч: по аналогии движение по окружности – теми же величинами – угловое перемещение, угловая скорость и угловое ускорение.

Угловое перемещение: (слайд) Это угол между двумя радиусами. Обозначается – Измеряется в рад.или град.

Уч: Вспомним из курса алгебры как радиан связан с градусом?

2пи рад.=360 град. Пи=3,14, то 1 рад.=360/6.28=57 град.

Угловая скорость w=

Единица измерения угловой скорости – рад/с

Уч:. Подумайте, чему будет равна угловая скорость, если тело совершило один полный оборот?

Ученик. Так как тело совершило полный оборот, то время его движения равно периоду, а угловое перемещение 360° или 2 . Следовательно, угловая скорость равна .

Учитель: Итак о чем мы сегодня говорили? (о криволинейном движении)

5. Вопросы для закрепления.

Какое движение называется криволинейным?

Какое движение является частным случаем криволинейного движения?

Как направлена мгновенная скорость при криволинейном движении?

Почему ускорение называется центростремительным?

Что называют периодом и частотой? В каких единицах измеряют?

Как эти величины взаимосвязаны?

Как же можно описать криволинейное движение?

Как направлено ускорение тела, движущегося по окружности с постоянной по модулю скоростью?

6.Экспериментальная работа

Измерить период и частоту тела, подвешенного на нити и вращающегося в горизонтальной плоскости.

(на партах у вас тела, подвешенные на.нити, секундомер. Тело вращайте в горизонтальной плоскости равномерно и измерьте время 10 полных вращений.Вычислите период и частоту)

7. Закрепление. Решение задач. (слайд)

А.С.Пушкин. «Руслан и Людмила»

У лукоморья дуб зеленый,

Златая цепь на дубе том,

И днем и ночью кот ученый

Все ходит по цепи кругом.

В: Как называется такое движение кота? Определить частоту и период и угловую скорость если за 2 мин. Он делает 12 кругов. (ответ: 0,1 1/с, Т=10с, w=0,628рад/с)

П.П.Ершов «Конек-Горбунок»

Ну-с, так едет наш Иван

За кольцом на окиян

Горбунок летит как ветер,

И почин на первый вечер

Верст сто тысяч отмахал

И нигде не отдыхал.

В: Сколько раз за первый вечер Конек-Горбунок обогнул Землю? Земля имеет форму шара, а одна верста равна примерно 1066 м. (ответ:2,5 раза)

8.Тест Проверка усвоения нового материала (тесты на бумаге)

Тест 1.

1. Примером криволинейного движения являются…

а) падение камня;
б) поворот машины на право;
в) бег спринтера на 100 – метровке.

2. Минутная стрелка часов делает один полный оборот. Чему равен период обращения?

а) 60 с; б) 1/3600 с; в) 3600 с.

3. Колесо велосипеда делает один оборот за 4 с. Определите частоту вращения.

а) 0,25 1/с; б) 4 1/с; в) 2 1/с.

4. Винт моторной лодки делает 25 оборотов за 1 с. Чем, равна угловая скорость винта?

а) 25 рад/с; б) /25 рад/с; в) 50 рад/с.

5. Определите частоту вращения сверла электрической дрели, если его угловая скорость равна 400 .

а)800 1/с; б) 400 1/с; в) 200 1/с.

Ответы: б; в; а; в; в.

Тест 2.

1. Примером криволинейного движения является…

а) движение лифта;
б) прыжок лыжника с трамплина;
в) падение шишки с нижней ветки ели в безветренную погоду.

Секундная стрелка часов делает один полный оборот. Чему равна её частота обращения?

а) 1/60 с; б) 60 с; в) 1 с.

3. Колесо машины делает 20 оборотов за10 с. Определите период обращения колеса?

а) 5 с; б) 10 с; в) 0,5 с.

4. Ротор мощной паровой турбины делает 50 оборотов за 1 с. Вычислите угловую скорость.

а) 50 рад/с; б) /50 рад/с; в) 10 рад/с.

5. Определите период обращения звёздочки велосипеда, если угловая скорость равна.

а) 1 с; б) 2 с; в)0,5 с.

Ответы: б; а; в; в; б.

Самопроверка

9. Рефлексия.

Давайте вместе с вами заполним Механизм ЗУХ (знаю, узнал, хочу узнать)

10.Подведение итогов, оценки за урок

11. Домашнее задание параграфы 18,19,

домашнее исследование: вычислить по возможности все характеристики любого вращающегося тела (колеса велосипеда, минутной стрелки часов)

Я. И. Перельман. Занимательная физика. Кн. 1 и 2 – М.: Наука, 1979.

С. А. Тихомирова. Дидактический материал по физике. Физика в художественной литературе. 7 – 11 классы. – М.: Просвещение. 1996.

Скорость и скорость

Любой движущийся объект можно описать с помощью кинематических концепций, обсуждаемых в Блоке 1 Физического Класса. Движение движущегося объекта может быть объяснено либо с помощью законов Ньютона (блок 2 в классе физики) и векторных принципов (блок 3 в классе физики), либо с помощью теоремы работы-энергии (блок 5 в классе физики). Те же концепции и принципы, которые используются для описания и объяснения движения объекта, могут быть использованы для описания и объяснения параболического движения снаряда.В этом модуле мы увидим, что те же самые концепции и принципы могут также использоваться для описания и объяснения движения объектов, которые либо движутся по кругу, либо могут быть аппроксимированы движущимися по кругу. Кинематические концепции и принципы движения будут применены к движению объектов по кругу, а затем будут расширены для анализа движения таких объектов, как американские горки, футболист, совершающий круговой поворот , и планета, вращающаяся вокруг Солнца. Мы увидим, что красота и сила физики заключаются в том, что несколько простых концепций и принципов могут быть использованы для объяснения механики всей вселенной.Урок 1 этого исследования начнется с разработки кинематических и динамических идей, которые можно использовать для описания и объяснения движения объектов по кругу.

Предположим, вы ведете машину с повернутым рулевым колесом таким образом, что ваша машина движется по идеальному кругу с постоянным радиусом. Предположим, что во время движения ваш спидометр постоянно показывает 10 миль в час. В такой ситуации движение вашего автомобиля можно описать как равномерное круговое движение. Равномерное круговое движение – это движение объекта по кругу с постоянной или постоянной скоростью.

Расчет средней скорости

Равномерное круговое движение – круговое движение с постоянной скоростью – это одна из многих форм кругового движения. Объект, движущийся равномерно по кругу, преодолеет такое же линейное расстояние за каждую секунду. При движении по кругу объект проходит расстояние по периметру круга.Таким образом, если ваша машина будет двигаться по кругу с постоянной скоростью 5 м / с, то она будет проходить 5 метров по периметру круга за каждую секунду. Расстояние одного полного цикла по периметру круга известно как окружности . С постоянной скоростью 5 м / с автомобиль мог совершить полный цикл по кругу с окружностью 5 метров. При этой равномерной скорости 5 м / с каждый цикл по окружности 5 м потребует 1 секунду. На скорости 5 м / с круг с окружностью 20 метров можно было сделать за 4 секунды; и при этой равномерной скорости каждый цикл по 20-метровой окружности будет занимать один и тот же период времени в 4 секунды.Эта взаимосвязь между длиной окружности круга, временем завершения одного цикла по кругу и скоростью объекта является просто расширением уравнения средней скорости, изложенного в Блоке 1 Физического Класса.

Окружность любого круга может быть вычислена с использованием радиуса в соответствии с уравнением

Окружность = 2 * Пи * Радиус

Объединение этих двух приведенных выше уравнений приведет к новому уравнению, связывающему скорость объекта, движущегося в равномерном круговом движении, с радиусом круга и временем, чтобы сделать один цикл по кругу ( период ).

, где R представляет радиус окружности, а T представляет период. Это уравнение, как и все уравнения, можно использовать как алгебраический рецепт для решения проблемы. Его также можно использовать, чтобы направлять наши размышления о том, как переменные в уравнении связаны друг с другом. Например, уравнение предполагает, что для объектов, движущихся по кругам разного радиуса за один и тот же период, объект, пересекающий круг большего радиуса, должен двигаться с наибольшей скоростью.Фактически, средняя скорость и радиус круга прямо пропорциональны. Двукратное увеличение радиуса соответствует двукратному увеличению скорости; трехкратное увеличение радиуса соответствует трехкратному увеличению скорости; и так далее. Чтобы проиллюстрировать это, рассмотрим цепочку из четырех светодиодных ламп, расположенных в разных местах вдоль жилы. Прядь держится за один конец и быстро закручивается по кругу. Каждый светодиодный светильник проходит по кругу разного радиуса. Тем не менее, поскольку они подключены к одному проводу, период их вращения одинаков.Впоследствии светодиоды, которые находятся дальше от центра круга, перемещаются быстрее, чтобы охватить окружность большего круга за то же время. Если освещение в комнате выключено, светодиоды создают дугу, которая может казаться более длинной для тех светодиодов, которые перемещаются быстрее – светодиодов с наибольшим радиусом. Это показано на диаграмме справа.

Направление вектора скорости

Объекты, движущиеся равномерно по кругу, будут иметь постоянную скорость.Но означает ли это, что они будут иметь постоянную скорость? Вспомните из блока 1 Физического класса, что скорость и скорость относятся к двум совершенно разным величинам. Скорость – это скалярная величина, а скорость – это векторная величина. Скорость, будучи вектором, имеет как величину, так и направление. Величина вектора скорости – это мгновенная скорость объекта. Направление вектора скорости направлено в том же направлении, что и объект. Поскольку объект движется по кругу, его направление постоянно меняется.В какой-то момент объект движется на север так, что вектор скорости направлен на север. Четверть цикла спустя объект будет двигаться на восток, так что вектор скорости будет направлен на восток. Поскольку объект огибает круг, направление вектора скорости отличается от того, что было в предыдущий момент. Таким образом, хотя величина вектора скорости может быть постоянной, направление вектора скорости меняется. Лучшее слово, которое можно использовать для описания направления вектора скорости, – это слово тангенциальный .Направление вектора скорости в любой момент находится в направлении касательной линии, проведенной к окружности в месте расположения объекта. (Касательная линия – это линия, которая касается окружности в одной точке, но не пересекает ее.) На диаграмме справа показано направление вектора скорости в четырех разных точках для объекта, движущегося по часовой стрелке по окружности. В то время как фактическое направление объекта (и, следовательно, вектора скорости) изменяется, его направление всегда касается окружности.

Подводя итог, объект, движущийся равномерно по кругу, движется по периметру круга с постоянной скоростью. Пока скорость объекта постоянна, его скорость меняется. Скорость, будучи вектором, имеет постоянную величину, но меняющееся направление. Направление всегда направлено касательно окружности, и когда объект поворачивает круг, касательная линия всегда указывает в новом направлении.

Хотим предложить… Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства однородного кругового движения. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.

Проверьте свое понимание

1. На стол кладут трубку, придающую ей форму круга в три четверти. Мяч для гольфа с большой скоростью проталкивается в трубку одним концом. Мяч катится по трубке и выходит на противоположном конце. Опишите путь мяча для гольфа, когда он выходит из трубы.

3.2 Мгновенная скорость и скорость – Университетская физика, том 1

Задачи обучения

К концу этого раздела вы сможете:

Объясните разницу между средней и мгновенной скоростью.
Опишите разницу между скоростью и скоростью.
Рассчитайте мгновенную скорость по математическому уравнению для скорости.
Рассчитайте скорость по мгновенной скорости.

Теперь мы увидели, как рассчитать среднюю скорость между двумя положениями.Однако, поскольку объекты в реальном мире непрерывно движутся в пространстве и времени, мы хотели бы найти скорость объекта в любой отдельной точке. Мы можем определить скорость объекта в любом месте на его пути, используя некоторые фундаментальные принципы исчисления. Этот раздел дает нам лучшее представление о физике движения и будет полезен в следующих главах.

Мгновенная скорость

Величина, которая сообщает нам, насколько быстро объект движется в любом месте на своем пути, является мгновенной скоростью, обычно называемой просто скоростью .Это средняя скорость между двумя точками на пути в пределе, когда время (и, следовательно, смещение) между двумя точками приближается к нулю. Чтобы проиллюстрировать эту идею математически, нам нужно выразить положение x как непрерывную функцию от t , обозначенную как x ( t ). Выражение для средней скорости между двумя точками с использованием этого обозначения: v– = x (t2) −x (t1) t2 − t1v– = x (t2) −x (t1) t2 − t1. Чтобы найти мгновенную скорость в любом положении, положим t1 = tt1 = t и t2 = t + Δtt2 = t + Δt.Подставив эти выражения в уравнение для средней скорости и взяв предел Δt → 0Δt → 0, находим выражение для мгновенной скорости:

v (t) = lim∆t → 0x (t + ∆t) −x (t) ∆t = dx (t) dt.v (t) = lim∆t → 0x (t + ∆t) −x (t) ∆t = dx (t) dt.

Мгновенная скорость

Мгновенная скорость объекта – это предел средней скорости, когда истекшее время приближается к нулю, или производная x по отношению к t :

v (t) = ddtx (t). v (t) = ddtx (t).

3,4

Как и средняя скорость, мгновенная скорость представляет собой вектор с размерностью длины за время. Мгновенная скорость в определенный момент времени t0t0 – это скорость изменения функции положения, которая представляет собой наклон функции положения x (t) x (t) в момент t0t0. На рисунке 3.6 показано, как средняя скорость v– = ΔxΔtv– = ΔxΔt между двумя временами приближается к мгновенной скорости в t0.t0. Мгновенная скорость отображается в момент времени t0t0, который является максимумом функции положения.В этой точке наклон графика положения равен нулю, и, следовательно, мгновенная скорость равна нулю. В других случаях, t1, t2t1, t2 и так далее, мгновенная скорость не равна нулю, потому что наклон графика положения будет положительным или отрицательным. Если бы функция положения имела минимум, наклон графика положения также был бы равен нулю, что также давало бы нулевую мгновенную скорость. Таким образом, нули функции скорости дают минимум и максимум функции положения.

Фигура 3.6 На графике зависимости положения от времени мгновенная скорость представляет собой наклон касательной в данной точке. Средние скорости v– = ΔxΔt = xf − xitf − tiv– = ΔxΔt = xf − xitf − ti между моментами времени Δt = t6 − t1, Δt = t5 − t2 и Δt = t4 − t3Δt = t6 − t1, Δt = t5− t2 и Δt = t4 − t3 показаны. Когда Δt → 0Δt → 0, средняя скорость приближается к мгновенной скорости при t = t0t = t0.

Пример 3,2

Определение скорости на основе графика зависимости положения от времени

Учитывая график зависимости положения от времени на рисунке 3.7 найдите график зависимости скорости от времени. Фигура 3,7 Объект начинает движение в положительном направлении, останавливается на короткое время, а затем меняет направление, возвращаясь к исходной точке. Обратите внимание, что объект мгновенно останавливается, что потребует бесконечной силы. Таким образом, график является приближением движения в реальном мире. (Концепция силы обсуждается в Законах Ньютона.)

Стратегия

График состоит из трех прямых линий на трех временных интервалах.Мы находим скорость в течение каждого временного интервала, беря наклон линии с помощью сетки.

Решение

Интервал времени от 0 до 0,5 с: v– = ΔxΔt = 0,5 м – 0,0 м0,5 с – 0,0 с = 1,0 м / сv– = ΔxΔt = 0,5 м – 0,0 м0,5 с – 0,0 с = 1,0 м / с

Интервал времени от 0,5 с до 1,0 с: v– = ΔxΔt = 0,5 м − 0,5 м1,0 с − 0,5 с = 0,0 м / сv– = ΔxΔt = 0,5 м − 0,5 м1,0 с − 0,5 с = 0,0 м / с

Временной интервал от 1,0 до 2,0 с: v– = ΔxΔt = 0,0 м – 0,5 м 2,0 с – 1,0 с = –0,5 м / сv– = ΔxΔt = 0,0 м – 0,5 м2,0 с – 1,0 с = –0,5 м / с

График этих значений скорости в зависимости от времени показан на рисунке 3.8.

Фигура 3.8 Скорость положительна для первой части пути, равна нулю, когда объект остановлен, и отрицательна, когда объект меняет направление.

Значение

В течение интервала времени от 0 до 0,5 с положение объекта смещается от начала координат, а кривая зависимости положения от времени имеет положительный наклон. В любой точке кривой в течение этого временного интервала мы можем найти мгновенную скорость, взяв ее наклон, равный +1 м / с, как показано на рисунке 3.8. В последующий интервал времени между 0,5 и 1,0 с положение не меняется, и мы видим, что наклон равен нулю. От 1,0 до 2,0 с объект движется назад к исходной точке, и наклон составляет -0,5 м / с. Объект изменил направление и имеет отрицательную скорость.

Скорость

На обиходе большинство людей используют термины скорость и скорость как синонимы. В физике, однако, они не имеют одинакового значения и представляют собой разные понятия. Одно из основных различий состоит в том, что скорость не имеет направления; то есть скорость – это скаляр.

Мы можем вычислить среднюю скорость, найдя общее пройденное расстояние, разделенное на затраченное время:

Средняя скорость = s– = Общее пройденное время. Средняя скорость = s– = Общее пройденное время.

3.5

Средняя скорость не обязательно совпадает с величиной средней скорости, которая определяется делением величины общего смещения на затраченное время. Например, если поездка начинается и заканчивается в одном и том же месте, общее смещение равно нулю, и, следовательно, средняя скорость равна нулю.Однако средняя скорость не равна нулю, потому что общее пройденное расстояние больше нуля. Если мы отправляемся в путешествие на 300 км и должны быть в пункте назначения в определенное время, то нас будет интересовать наша средняя скорость.

Однако мы можем вычислить мгновенную скорость по величине мгновенной скорости:

Мгновенная скорость = | v (t) |. Мгновенная скорость = | v (t) |.

3,6

Если частица движется по оси x в +7.0 м / с, а другая частица движется по той же оси со скоростью -7,0 м / с, они имеют разные скорости, но обе имеют одинаковую скорость 7,0 м / с. Некоторые типичные скорости показаны в следующей таблице.

Скорость	м / с	миль / ч
Континентальный дрифт	10-710-7	2 × 10-72 × 10-7
Бодрая прогулка	1,7	3,9
Велосипедист	4.4	10
Спринтерский бегун	12,2	27
Ограничение скорости в сельской местности	24,6	56
Официальный рекорд наземной скорости	341,1	763
Скорость звука на уровне моря	343	768
Космический челнок при входе в атмосферу	7800	17 500
Скорость убегания Земли *	11 200	25 000
Орбитальная скорость Земли вокруг Солнца	29,783	66 623
Скорость света в вакууме	299 792 458	670 616 629

Стол 3.1 Скорости различных объектов * Скорость убегания – это скорость, с которой объект должен быть запущен, чтобы он преодолевал земное притяжение и не тянулся обратно к Земле.

Расчет мгновенной скорости

При вычислении мгновенной скорости нам необходимо указать явный вид функции положения x (t) x (t). Если каждый член в уравнении x (t) x (t) имеет форму AtnAtn, где AA – константа, а nn – целое число, это можно дифференцировать, используя правило мощности:

d (Atn) dt = Antn− 1.d (Atn) dt = Antn − 1.

3,7

Обратите внимание, что если есть дополнительные члены, сложенные вместе, это степенное правило дифференцирования может быть выполнено несколько раз, и решение представляет собой сумму этих членов. Следующий пример иллюстрирует использование уравнения 3.7.

Пример 3.3

Мгновенная скорость в сравнении со средней скоростью

Положение частицы определяется выражением x (t) = 3,0t + 0,5t3mx (t) = 3,0t + 0,5t3m.

Используя уравнения 3.4 и 3.7, найдите мгновенную скорость при t = 2.0t = 2,0 с.
Рассчитайте среднюю скорость от 1,0 до 3,0 с.

Стратегия

Уравнение 3.4 дает мгновенную скорость частицы как производную функции положения. Глядя на форму данной функции положения, мы видим, что это многочлен от t . Следовательно, мы можем использовать уравнение 3.7, правило мощности из исчисления, чтобы найти решение. Мы используем уравнение 3.6 для вычисления средней скорости частицы.

Решение

v (t) = dx (t) dt = 3.0 + 1.5t2m / sv (t) = dx (t) dt = 3.0 + 1.5t2m / s.
Подставляя t = 2,0 с в это уравнение, получаем v (2,0 с) = [3,0 + 1,5 (2,0) 2] м / с = 9,0 м / с (2,0 с) = [3,0 + 1,5 (2,0) 2] м / s = 9,0 м / с.
Чтобы определить среднюю скорость частицы между 1,0 и 3,0 с, мы вычисляем значения x (1,0 с) и x (3,0 с): x (1,0 с) = [(3,0) (1,0) +0,5 (1,0) 3] м = 3,5 м x (1,0 с) = [(3,0) (1,0) +0,5 (1,0) 3] м = 3,5 м x (3,0 с) = [(3,0) (3,0) +0,5 (3,0) 3] м = 22,5 м. x (3,0 с) = [(3,0) (3,0) +0,5 (3,0) 3] м = 22,5 м. Тогда средняя скорость равна v– = x (3.0s) −x (1.0s) t (3.0s) −t (1.0s) = 22.5−3.5m3.0−1.0s = 9.5m / sv– = x (3.0s) −x (1.0s) t (3.0 с) −t (1,0 с) = 22,5−3,5 м3,0−1,0 с = 9,5 м / с.

Значение

В пределе, когда временной интервал, используемый для вычисления v − v−, стремится к нулю, значение, полученное для v − v−, сходится к значению v.

Пример 3,4

Мгновенная скорость в зависимости от скорости

Рассмотрим движение частицы, положение которой равно x (t) = 3.0t − 3t2mx (t) = 3.0t − 3t2m.

Какова мгновенная скорость при t = 0.25 с, т = 0,50 с и т = 1,0 с?
Какова скорость частицы в это время?

Стратегия

Мгновенная скорость – это производная функции положения, а скорость – это величина мгновенной скорости. Мы используем уравнение 3.4 и уравнение 3.7 для определения мгновенной скорости.

Решение

v (t) = dx (t) dt = 3,0−6,0tm / sv (t) = dx (t) dt = 3,0−6,0tm / sv (0,25s) = 1,50 м / с, v (0,5s) = 0 м / с, v (1,0 с) = – 3,0 м / с (0.25 с) = 1,50 м / с, v (0,5 с) = 0 м / с, v (1,0 с) = – 3,0 м / с
Скорость = | v (t) | = 1,50 м / с, 0,0 м / с и 3,0 м / с Скорость = | v (t) | = 1,50 м / с, 0,0 м / с и 3,0 м / с

Значение

Скорость частицы дает нам информацию о направлении, указывая на то, что частица движется влево (запад) или вправо (восток). Скорость дает величину скорости. Построив график положения, скорости и скорости как функции времени, мы можем визуально понять эти концепции. Рис. 3.9. На графике (а) показана частица, движущаяся в положительном направлении до тех пор, пока t = 0.5 с, когда он меняет направление. Изменение направления также можно увидеть на (b) через 0,5 с, когда скорость равна нулю, а затем становится отрицательной. Через 1,0 с он возвращается в исходную точку, откуда начался. Скорость частицы при 1,0 с в (b) отрицательна, потому что она движется в отрицательном направлении. Но в (c), однако, его скорость положительна и остается положительной на протяжении всего времени прохождения. Мы также можем интерпретировать скорость как наклон графика зависимости положения от времени. Наклон x ( t ) уменьшается до нуля, становясь нулевым в 0.5 с, а после этого становится все более отрицательным. Этот анализ сравнения графиков положения, скорости и скорости помогает выявить ошибки в расчетах. Графики должны согласовываться друг с другом и помогать интерпретировать расчеты. Фигура 3.9 (a) Положение: x ( t ) в зависимости от времени. (b) Скорость: v ( t ) в зависимости от времени. Наклон графика положения – это скорость. Грубое сравнение наклонов касательных на (а) при 0,25 с, 0.5 с и 1,0 с со значениями скорости в соответствующие моменты времени указывают на то, что они являются одинаковыми значениями. (c) Скорость: | v (t) || v (t) | против времени. Скорость всегда положительное число.

Проверьте свое понимание 3,2

Положение объекта как функция времени: x (t) = – 3t2mx (t) = – 3t2m. а) Какова скорость объекта как функция времени? (б) Скорость когда-либо положительна? (c) Каковы скорость и скорость при t = 1,0 с?

3.4: Среднее и мгновенное ускорение

Цели обучения

Рассчитайте среднее ускорение между двумя точками времени.
Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
Объясните векторную природу мгновенного ускорения и скорости.
Объясните разницу между средним ускорением и мгновенным ускорением.
Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.

Важность понимания ускорения распространяется на наш повседневный опыт, а также на огромные просторы космического пространства и крошечный мир субатомной физики.В повседневном разговоре до разогнаться, означает ускориться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени. Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной.В космосе космические лучи – это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.

Среднее ускорение

Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.

Среднее ускорение

Среднее ускорение – это скорость изменения скорости:

\ [\ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {v_ {f} – v_ {0}} {t_ {f} – t_ {0}}, \ label { 3.8} \]

, где \ (\ bar {a} \) – среднее ускорение , v – скорость, а t – время. (Полоса над значком означает среднее ускорение .)

Поскольку ускорение – это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с ², то есть метры в секунду в квадрате или метры в секунду в секунду.Это буквально означает, на сколько метров в секунду скорость меняется каждую секунду. Напомним, что скорость – это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение направления. Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях.Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.

Ускорение как вектор

Ускорение – это вектор в том же направлении, что и , изменение скорости на , \ (\ Delta \) v. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение – это изменение скорости или направления, или и того, и другого.

Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения.Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением Рисунок \ (\ PageIndex {1} \), мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.

Рис. \ (\ PageIndex {1} \): Поезд метро в Сан-Паулу, Бразилия, замедляется при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки)

Термин замедление может вызвать путаницу в нашем анализе, потому что он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы не используем его.Ускорение – это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на рисунке \ (\ PageIndex {1} \) ускорение имеет отрицательное направление в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.

Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление.Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на рисунке \ (\ PageIndex {2} \).

Рисунок \ (\ PageIndex {2} \): объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление. Через достаточно долгое время он проходит исходную точку в обратном направлении.

Пример 3.5: Расчет среднего ускорения: скакун покидает ворота

Скаковая лошадь, выходящая из ворот, набирает скорость от состояния покоя до 15.0 м / с на запад за 1.80 с. Какое у него среднее ускорение?

Рисунок \ (\ PageIndex {3} \): Скачки, вылетая из ворот. (кредит: Джон Салливан)

Стратегия

Сначала мы рисуем эскиз и назначаем систему координат задаче Figure \ (\ PageIndex {4} \). Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.

Рисунок \ (\ PageIndex {4} \): Определите систему координат, данную информацию и то, что вы хотите определить.

Мы можем решить эту проблему, определив \ (\ Delta \) v и \ (\ Delta \) t из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнения \ (\ bar {a} = \ frac {\ Дельта v} {\ Delta t} = \ frac {v_ {f} – v_ {0}} {t_ {f} – t_ {0}} \).

Решение

Сначала определите известные: v ₀ = 0, v _f = -15,0 м / с (отрицательный знак указывает направление на запад), \ (\ Delta \) t = 1,80 с. Во-вторых, найдите изменение скорости.{2} \ ldotp \]

Значение

Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с ² на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с ². Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.

Упражнение 3.3

Протоны в линейном ускорителе ускоряются из состояния покоя до 2,0 × 10 ⁷ м / с за 10 ^–4 с. Какое среднее ускорение протонов?

Мгновенное ускорение

Мгновенное ускорение a, или ускорение в определенный момент времени , получается с использованием того же процесса, который обсуждался для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными \ (\ Delta \) t, и позволяем \ (\ Delta \) t приближаться к нулю.Результатом является производная функции скорости v (t), которая составляет мгновенного ускорения и математически выражается как

\ [a (t) = \ frac {d} {dt} v (t) \ ldotp \ label {3.9} \]

Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На рисунке \ (\ PageIndex {5} \) мгновенное ускорение в момент времени t ₀ – это наклон касательной к графику зависимости скорости от времени в момент времени t ₀.Мы видим, что среднее ускорение \ (\ bar {a} = \ frac {\ Delta v} {\ Delta t} \) приближается к мгновенному ускорению, когда Δt приближается к нулю. Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость

Рисунок \ (\ PageIndex {5} \): На графике зависимости скорости от времени мгновенное ускорение – это наклон касательной.(a) Показано среднее ускорение \ (\ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {v_ {f} – v_ {0}} {t_ {f} – t_ {0 }} \) между моментами времени \ (\ Delta \) t = t ₆ – t ₁, \ (\ Delta \) t = t ₅ – t ₂ и \ (\ Delta \) t = t ₄ – t ₃. Когда \ (\ Delta \) t → 0, среднее ускорение приближается к мгновенному ускорению в момент времени t ₀. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение – это наклон касательной, равный нулю.В любое другое время наклон касательной – и, следовательно, мгновенное ускорение – не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.

Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием рисунка 3.3.4 (b), графика зависимости скорости от времени из примера 3.3, для графического определения ускорения. Этот график изображен на рисунке \ (\ PageIndex {6} \) (a), который представляет собой прямую линию. Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на рисунке \ (\ PageIndex {6} \) (b).В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.

Рисунок \ (\ PageIndex {6} \): (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).

Если мы знаем функциональную форму скорости v (t), мы можем вычислить мгновенное ускорение a (t) в любой момент времени в движении, используя уравнение \ ref {3.9}.

Пример 3.6: Расчет мгновенного ускорения

Частица движется и ускоряется. Функциональный вид скорости v (t) = 20t – 5t ² м / с.

Найдите функциональную форму ускорения.
Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.

Стратегия

Функциональную форму ускорения находим, взяв производную от функции скорости. Затем мы вычисляем значения мгновенной скорости и ускорения по заданным функциям для каждой. Для части (d) нам нужно каждый раз сравнивать направления скорости и ускорения.

Решение

a (t) = \ (\ frac {dv (t)} {dt} \) dv (t) dt = 20 – 10t м / с ₂
v (1 с) = 15 м / с, v (2 с) = 20 м / с, v (3 с) = 15 м / с, v (5 с) = −25 м / с
a (1 с) = 10 м / с ², a (2 с) = 0 м / с ², a (3 с) = −10 м / с ², a (5 с) = −30 м / с ²
При t = 1 с скорость v (1 с) = 15 м / с положительна, а ускорение положительно, поэтому и скорость, и ускорение идут в одном направлении.Частица движется быстрее.

При t = 2 с скорость увеличилась до v (2 с) = 20 м / с, где она максимальна, что соответствует моменту времени, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.

При t = 3 с скорость равна v (3 с) = 15 м / с, а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.

При t = 5 с скорость v (5 с) = -25 м / с, а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом меняя направление на противоположное. Теперь частица снова ускоряется, но в противоположном направлении.

Мы можем видеть эти результаты графически на Рисунке \ (\ PageIndex {7} \).

Рисунок \ (\ PageIndex {7} \): (a) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с.Наклоны касательных – это ускорения. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.

Значение

Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении.Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления.Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимальной, после чего он начинает замедляться, останавливается, а затем меняет направление движения.

Упражнение 3.4

Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.

Ощущение ускорения

Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта.В таблице 3.2 представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.

Таблица 3.2 – Типичные значения ускорения

(источник: Википедия: порядки величин (ускорение))

Разгон	Значение (м / с ²)
Скоростной поезд	0,25
Лифт	2
Гепард	5
Объект в свободном падении без сопротивления воздуха у поверхности Земли	9.8
Максимум космического челнока во время запуска	29
Пик парашютиста при нормальном раскрытии парашюта	59
Самолет F16 выходит из пикирования	79
Взрывной выброс сиденья с самолета	147
Ракета Sprint	982
Максимальное максимальное ускорение ракетных салазок	1540
Прыгающая блоха	3200
Бейсбольный удар битой	30 000
Захваты муравья-ловушки	1 000 000
Протон в большом адронном коллайдере	1.9 х 10 ⁹

В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют ничего общего с размером объекта или его массивностью. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.На рисунке \ (\ PageIndex {8} \) графически среднее ускорение сравнивается с мгновенным ускорением для двух очень разных движений.

Рисунок \ (\ PageIndex {8} \): графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.

Моделирование

Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка туда-сюда мышкой и намечайте его движения. Задайте положение, скорость или ускорение и позвольте симуляции перемещать человека за вас. Посетите эту ссылку, чтобы использовать симуляцию движущегося человека.

Авторы и авторство

Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

конспектов лекций

Самолет общего назначения Движение

Обычное плоское движение – это просто суперпозиция поступательного перемещения и вращения фиксированной оси.

Абсолют Движение
Родственник Движение

Родственник Скорость
мгновенно Центр нулевой скорости
Родственник Разгон

Взяв производные по времени от уравнения относительного положения, получаем

, что справедливо для любых двух частиц A и Б.

Однако, если частицы A и B являются двумя точек в том же твердом теле, то расстояние между они постоянны, и точка B, кажется, движется по круговой путь вокруг точки A (если смотреть по отношению к точке A) .

Следовательно, относительное ускорение можно записать как

, где принцип суперпозиции говорит что ускорение точки B твердого тела равно на переводное ускорение, a _A, оф все твердое тело с точкой A плюс неподвижная ось вращение твердого тела вокруг оси через A.

Тангенциальная составляющая перпендикулярно вектору относительного положения r _{A / B} и указывает в направлении вращения тела.

Нормальная составляющая направлена вдоль вектор относительного положения и указывает на A, точка, относительно которой происходит относительное движение.

Обратите внимание, что когда два твердых тела приколол (пригнано) вместе, точка соединяющие тела будут иметь одинаковую скорость и ускорение на обоих телах. Следовательно, скорости и ускорения двух тел могут быть связаны соотношением глядя на эту общую точку.

Мгновенный центр нуля скорость твердого тела в общее движение плоскости не фиксировано, поэтому ускорение эта точка обычно не равна нулю.Следовательно, эта точка не должны использоваться для расчета ускорений.

Мгновенный центр нуля ускорение можно найти для твердое тело так же, как и для скоростей, но обычно не пригодится при решении простых задач.

Мгновенная скорость. Связанные ставки – Подход к исчислению

Прямолинейное движение

Определение мгновенной скорости

Вторая производная

Похожие оценки

ОДНО из наиболее важных приложений математического анализа является движение по прямой линии, которое называется прямолинейным движением.

Рассмотрим частицу, движущуюся по прямой от фиксированной точки O до данной точки P , и пусть t будет прошедшим временем. Тогда каждому значению t будет соответствовать расстояние s , которое будет функцией t :

с = с ( т ).

Когда мы знаем s ( t ), мы имеем то, что называется уравнением движения.

Итак, если частица движется с постоянной скоростью – что называется равномерным движением – тогда нам не нужны вычисления. Другими словами, если уравнение движения равно

с = 22 т ,

, то в каждый момент времени скорость v ( t ) равна 22 м / сек. Наклон этой линии – 22 – это скорость изменения с по отношению к t , которая по определению является скоростью.

За каждую секунду времени частица перемещается на расстояние 22 метра.

Δ с
Δ т

22 метра в секунду.

Это, конечно, нереалистичная картина, потому что в 0 секунд скорость определенно не 22 метра в секунду. Должно было быть ускорение

до этой постоянной скорости. Во время этого ускорения скорость не была постоянной. График не был прямой линией.

Определение мгновенной скорости

Для любого уравнения движения с ( t ), по мгновенной скорости в момент времени t – v ( t ) – мы подразумеваем предел из средней скорости , между t и t + Δ t , поскольку Δ t приближается к 0.

Мгновенная скорость – это значение наклона касательной при t .

Пример 1. Пусть уравнение движения выглядит следующим образом:

с ( т ) = 6 т ² + т + 8.

Пусть t измеряется в минутах, а с – в метрах. И пусть 10:05 соответствует t = 0.

а) Какова мгновенная скорость в 10:05?

Ответ.	ds dt	=	12 т + 1

		=	12 · 0 + 1

		=	1 м / мин.

б) Какова мгновенная скорость в 10:15?

Ответ. В 10:15, t = 10.

DS dt	=	12 · 10 + 1

	=	121 м / мин.

Мгновенная скорость – это не обычная скорость.Это предел последовательности скоростей, поскольку Δ t приближается к 0; это чисто логично; его никогда нельзя наблюдать или измерять. Чтобы измерить скорость, необходимо знать как расстояние Δ с , так и время Δ t , пусть даже небольшое.

Движущееся тело находится в движении в течение каждого промежутка времени, в течение которого оно движется. Если мы скажем каждые мгновений времени – и предположим, что время состоит из мгновений – тогда мы предложим парадокс стрел Зенона.Он утверждал, что в любой момент времени нет интервала времени, следовательно, нет смены позиции; что означает: нет движения.

Определение мгновенной скорости не подразумевает, что время состоит из мгновений. Он определяет, как оценить эту скорость в любой конкретный момент времени t , который мы называем. Это все, что нам нужно, и все, что мы когда-либо делаем.

См. Приложение, действительно ли линия состоит из точек.

Проблема 1.Экспериментально установлено, что тело, падающее из состояния покоя под действием силы тяжести, приблизительно следует этому уравнению движения:

с ( t ) = 4 . 9 т ².

s – расстояние падения, измеренное в метрах; t – это время в секундах.

a) Как далеко упало тело по истечении 3 секунд?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

с (3) = 4 . 9 × 3 ² = 4 . 9 × 9 = 44 . 1 мес.

б) Какова его мгновенная скорость по истечении 3 секунд?

DS dt	=	9 . 8 т

	=	9 . 8 × 3

	=	29 . 4 м / сек.

Вторая производная

Производная от y = f ( x ) – y ‘ ( x ) – сама будет функцией x .Эта новая функция может быть дифференцируемой. В этом случае мы называем производную первой производной от y второй производной. Обозначение

для второй производной

или y ‘.

Рассмотрим это уравнение движения,

с ( т ) = 3 т ².

Тогда первая производная – это скорость v :

Вторая производная – это скорость изменения скорости во времени.Это называется ускорением a :

Если t измеряется в секундах и s в метрах, то единицами измерения скорости являются метров в секунду , что мы сокращаем как м / сек. Тогда единицы ускорения равны метров в секунду в секунду , что мы сокращаем как м / сек ².

Задача 2. Тело движется по прямой в соответствии с этим уравнением движения:

с ( т ) = 10 т ²-4 т + 8,

, где t измеряется в секундах, а s – в метрах.

а) Каково его положение по истечении 5 секунд?

с (5) = 10 · 5 ² – 4 · 5 + 8 = 238 м.

б) Каково уравнение для его скорости v в любой момент времени t ?

v ( t ) =

ds
dt

= 20 т – 4.

c) Какова его скорость v по истечении 5 секунд?

v (5) = 20 · 5 – 4 = 96 м / сек.

d) Каково уравнение его ускорения a в любой момент времени t ?

( т ) =

d ² s
dt ²

дв
dt

= 20.

д) Каково его ускорение по истечении 5 секунд?

a (5) = 20 м / сек ².

Ускорение постоянное.

Задача 3. Под действием силы тяжести тело движется по этому уравнению движения:

s ( t ) = ½ gt ² + s ₀

а) Каков физический смысл постоянной s ₀?

Это исходное положение тела, с (0).

б) Как быстро движется тело через 5 секунд?

v ( t ) =

ds
dt

= GT . При t = 5, v (5) = 5 g .

c) Каков физический смысл постоянной g ?

г =

d ² s
dt ²

. g – ускорение свободного падения, которое равно

примерно 9,8 м / сек ².

Похожие оценки

Пример 2.

a) Если радиус круга увеличивается, запишите уравнение, которое показывает
a) насколько быстро увеличивается площадь круга. ( A = π r ².)

Решение. Рассчитаем

dA
dt

. У нас

А	=	π r ².

При неявном дифференцировании относительно t :

dA dt	=		=

b) Если радиус расширяется со скоростью 2 см / мин, насколько быстро расширяется область
a) при радиусе 15 см?

Решение. Нам дано, что

др
дт

= 2 см / мин. Следовательно,

при r = 15 см:

dA dt	=	2π · 15 · 2
		188.4 см ² / мин.

Пример 3. Мальчик идет со скоростью 5 миль в час к основанию флагштока высотой 60 футов. С какой скоростью изменяется его расстояние от вершины столба, когда он находится в 80 футах от его основания?

Решение . Нарисуйте картинку Во всех задачах этого типа нарисуйте картинку.

Пусть мальчик будет в точке A , которая находится на расстоянии x от основания флагштока.Пусть s будет его расстоянием от вершины шеста.

Рассчитаем

ds
dt

Фигура представляет собой прямоугольный треугольник. Следовательно,

Неявно дифференцировать т. .

Следовательно,

Теперь нам дается x = 80 футов и

dx
dt

= −5 миль / час.Ср

напишите знак минус, потому что x уменьшается по мере приближения к флагштоку.

Согласно строке 1),

Следовательно,

Задача 4. Сторона квадрата составляет х см в длину и увеличивается со скоростью b см в час. Как быстро увеличивается площадь?

2 ab см ² / час.

Задача 5. Сторона равностороннего треугольника составляет х см в длину и увеличивается со скоростью b см в час. Как быстро увеличивается площадь?

½ ab см ² / час.

Проблема 6.

a) Площадь поверхности S сферы определяется формулой S = 4π r ².

Если r изменяется со временем, как изменится S ?

б) Объем V сферы определяется формулой V = π r ³.

Если r изменяется со временем, как изменяется V ?

c) Доказательство:

dV
dt

½ r

DS
dt

dV
dt

4π r ²

др
дт

= ½ · 8π r ²

др
дт

= ½ r · 8π r

др
дт

= ½ r

DS
dt

Задача 7. Основание и высота прямоугольника равны b и h , и они изменяются со скоростью p , q соответственно. Докажите, что площадь А изменяется со скоростью бк + л.с. .

A = bh .

Согласно правилу продукта:

dA
dt

dh
dt

дб
дт

бк + лс .

Задача 8.

а) К стене прислонена лестница длиной 50 футов. Если основание лестницы
a) отодвигается от стены с определенной скоростью, выведите формулу
a) для определения скорости опускания вершины лестницы.
a) (Пусть x будет расстоянием от основания лестницы до стены,
a) и пусть h будет расстоянием от верха до земли. Нарисуйте
а) картинку)

dh
dt

= –

x
h

dx
dt

b) Если ступня отрывается со скоростью 3 фута / мин:

1) как быстро опускается вершина, если ступня находится на расстоянии 14 футов от стены
1)?

7/8 футов / мин.

2) когда вершина опускается со скоростью 4 фута / мин?

Когда дно находится в 40 футах от стены.

c) Когда верх и низ будут двигаться с одинаковой скоростью?

Когда дно находится в 25 футах от стены.

Следующий урок: Максимальные и минимальные значения

Содержание | Дом

Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.

Вопросы или комментарии?

Эл. Почта: [email protected]

Мгновенная скорость – обзор

3.3 Свободно падающие тела

Движение некоторых объектов можно определить с помощью решения уравнения первого порядка. Мы начинаем с объяснения некоторых теорий, необходимых для построения дифференциального уравнения, моделирующего ситуацию.

Второй закон движения Ньютона Скорость, с которой импульс тела изменяется во времени, равна результирующей силе, действующей на тело.

Хотя Ньютон сформировал ранние версии своих трех законов движения к 1666 году, они появляются в его главном достижении, Principia , которое он опубликовал в 1687 году. . »

Импульс тела определяется как произведение его массы и скорости, поэтому это утверждение моделируется как

ddt (mv) = F,

, где м и v представляют массу и скорость тела, соответственно, а F – это сумма сил, действующих на тело.Масса м тела постоянна, поэтому дифференцирование приводит к дифференциальному уравнению

mdvdt = F.

Если на тело действует сила тяжести, то его скорость определяется путем решения дифференциального уравнения

mdvdt = mgordvdt = g,

, где g≈32 ft / s2 (английская система) или g≈9,8 м. / s2 (международная система). См. Сводку единиц в таблице 3.4.

Таблица 3.4. Единицы, используемые для решения задач, связанных со вторым законом движения Ньютона

	Английский	Международный
Масса	Снаряд (фунт-с2 фут)	килограмм (кг) 0 кг фунт (фунт)	Ньютон (м-кгс2)
Расстояние	фут (фут)	метр (м)
Время	секунда (с)	секунда (с)

Это дифференциальное уравнение применимо только тогда, когда не учитывается сила сопротивления среды (например, сопротивление воздуха).Если принять во внимание это компенсирующее сопротивление, мы должны обсудить все силы, действующие на объект. Математически мы запишем уравнение как

mdvdt = ∑ (силы, действующие на объект),

, где направление движения принимается положительным.

Мы используем силовую диаграмму на рис. 3.6, чтобы составить дифференциальное уравнение, моделирующее ситуацию. Сопротивление воздуха действует на объект при его падении, и g действует в том же направлении, что и движение.Сформулируем дифференциальное уравнение в виде:

Рисунок 3.6. Диаграмма силы.

mdvdt = mg + (- FR) или mdvdt = mg-FR,

, где FR представляет эту силу сопротивления. Обратите внимание, что вниз считается положительным направлением. Сила сопротивления обычно пропорциональна скорости тела ( v ) или степени его скорости. Следовательно, дифференциальное уравнение является линейным или нелинейным в зависимости от принимаемого во внимание сопротивления среды.

Пример 3.10

(a) Определите скорость и расстояние, пройденное объектом с массой m = 1 пуля, брошенная вниз с начальной скоростью 2 фута / с с высоты 1000 футов. Предположим, что объект подвергается воздействию сопротивление воздуха, эквивалентное мгновенной скорости объекта. (b) Определите время, в которое объект ударяется о землю, и его скорость, когда он ударяется о землю.

Решение: (a) Сначала мы устанавливаем задачу начального значения для определения скорости объекта.Сопротивление воздуха эквивалентно мгновенной скорости, поэтому FR = v. Формула mdv / dt = mg − FR тогда дает нам dv / dt = 32 − v, а наложение начальной скорости v (0) = 2 дает начальную задачу dv / dt = 32 − v, v (0) = 2, которую можно решить несколькими способами. Мы решаем его как линейное уравнение первого порядка и используем интегрирующий коэффициент. (Это также можно решить путем разделения переменных.) С интегрирующим фактором et мы имеем ddt (etv) = 32et. Интегрирование обеих сторон дает etv = 32et + C1, поэтому v = 32 + C1e − t, а применение начальной скорости дает нам v (0) = 32 + C1e0 = 32 + C1 = 2, поэтому C1 = −30.Следовательно, скорость объекта v = 32−30e − t.

Обратите внимание, что скорость объекта не может превышать 32 фут / с, что называется предельной скоростью , которая определяется путем вычисления limt → ∞⁡v (t).

Чтобы определить расстояние, пройденное за время t , s (t), мы решаем уравнение первого порядка ds / dt = v = 32−30e − t с начальным условием s (0) = 0. Это дифференциальное уравнение решается путем интегрирования обеих частей уравнения, чтобы получить s (t) = 32t + 30e − t + C2. Применение s (0) = 0 тогда дает нам s (0) = 32⋅0 + 30e0 + C2 = 30 + C2 = 0, поэтому C2 = −30, а расстояние, пройденное объектом, определяется как s (t) = 32t + 30e − t − 30.

(b) Объект ударяется о землю, когда s (t) = 1000. Следовательно, мы должны решить уравнение s (t) = 32t + 30e − t − 30 = 1000 для t . Решения этого уравнения могут быть аппроксимированы численными методами, такими как метод Ньютона. Из графика этой функции, представленного на рис. 3.7, видно, что s (t) = 1000 вблизи t = 35. Численные методы показывают, что s (t) = 32t + 30e − t − 30 = 1000 при t≈32,1875 с.

Рисунок 3.7. График с ( t ) = 32 t +30 e ^{– t} −30.

Скорость в точке удара составляет 32,0 фут / с путем оценки производной в момент удара объекта о землю, заданной как s ′ (32,1875). □

Пример 3.11

Предположим, что объект в Примере 3.10 с пулей массой 1 бросается вниз с начальной скоростью 2 фута / с, и этот объект прикреплен к парашюту, увеличивая это сопротивление так, чтобы пользователя v2. Найти скорость в любой момент времени t и определить предельную скорость объекта.

Решение: Эта ситуация моделируется задачей начального значения

dvdt = 32 − v2, v (0) = 2.

Мы решаем дифференциальное уравнение, разделяя переменные и используя частные дроби:

132 − v2dv = dt1 (42 + v) (42 − v) dv = dt182 (1v + 42−1v − 42) dv = dtln⁡ | v + 42 | −ln⁡ | v − 42 | = 82t + C1ln⁡ | v + 42v − 42 | = 82t + C1 | v + 42v − 42 | = C2e82t (C2 = eC1) v + 42v − 42 = C3e82t ( C3 = ± C2 или 0).

Решая для v , находим, что

v + 42 = C3e82t (v − 42) или (1 − C3e82t) v = −42 (C3e82t + 1),

, поэтому v = −42C3e82t + 11 − C3e82t .Применение начального условия дает C3 = (1 + 22) / (1-22). Предельная скорость объекта определяется с помощью правила Л’Опиталя: limt → ∞⁡v (t) = – 42C3 / (- C3) = 42 ft / s.

В примере 3.10 предельная скорость составляет 32 фута / с, поэтому парашют снижает скорость объекта (см. Рис. 3.8). Это показывает, что объект не должен выдерживать такие сильные удары, как без парашюта. □

Рисунок 3.8. Скоростные функции из примера 3.10 (пунктир) и примера 3.11. Обратите внимание, как различные силы, возникающие из-за сопротивления воздуха, влияют на скорость объекта.

Пример 3.12

Определите решение (для скорости и высоты) дифференциального уравнения, которое моделирует движение объекта массой м , когда он направлен вверх с начальной скоростью v0 из начального положения s0, при условии, что сопротивление воздуха равно cv , где c – положительная константа.

Решение: Объект движется вверх, поэтому g и FR действуют против восходящего движения объекта, как показано на рис.3.9.

Рисунок 3.9. Изобразив силовую диаграмму, мы видим, что g и F _R находятся в отрицательном направлении.

Следовательно, дифференциальное уравнение, которое необходимо решить в этом случае, – это линейное уравнение dv / dt = −g− (c / m) v. Мы решаем задачу начального значения

(3.12) dvdt = −g − cmv.v (0) = v0

, сначала переписывая уравнение dv / dt = −g− (c / m) v как dv / dt + (c / m) v = −g, а затем вычислить интегрирующий коэффициент e∫ (c / m) dt = ect / m.Умножение каждой части уравнения на ect / m дает нам ect / mdv / dt + (c / m) ect / mv = −gect / m, так что ddt (ect / mv) = – gect / m. Интегрируя, получаем ect / mv = −gm / cect / m + C и, следовательно, общее решение:

v (t) = – gmc + Ce − ct / m.

Применение начального условия v (0) = v0 и решение для C дает C = (cv0 + gm) / c, так что решение задачи начального значения равно

(3.13) v (t) = – gmc + cv0 + gmce − ct / m.

Например, функция скорости для случая с m = 1/128 снарядов, c = 1/160, g = 32 фут / с ² и v0 = 48 фут / с: v (t) = 88e − 4t / 5-40.Эта функция изображена на рис. 3.10A. Обратите внимание, где v (t) = 0. Это значение t представляет время, в которое объект достигает максимальной высоты и начинает падать на землю.

Рисунок 3.10. (A) График v ( t ) = 88 e ^{−4 t /5} −40. (B) График v ( t ) вместе с s ( t ) = 110−40 t −110 e ^{−4 t /5} (штриховая линия).

Точно так же эту функцию (3.13) можно использовать для исследования множества ситуаций без решения дифференциального уравнения (3.12) при каждом изменении значений параметров.

Функция высоты s (t), которая представляет расстояние над землей в момент времени t , определяется путем интегрирования функции скорости:

s (t) = ∫v (t) dt = ∫ (−gmc + cv0 + gmce − ct / m) dt = −gmct + cmv0 + gm2c2e − ct / m + C.

Если начальная высота задается как s (0) = s0, решение для C дает C = (gm2 + c2s0 + cmv0) / c2, так что

(3.14) s (t) = – gmct + cmv0 + gm2c2e − ct / m + gm2 + c2s0 + cmv0c2.

Функции высоты и скорости показаны на рис. 3.10B с использованием параметров m = 1/128 снарядов, c = 1/160, g = 32 фут / с ² и v0 = 48 фут / с, а также s0 = 0.

Время, в которое объект достигает своей максимальной высоты, наступает, когда производная функции высоты равна нулю. Из рис. 3.10B мы видим, что s ′ (t) = v (t) = 0, когда t≈1. Решение s ′ (t) = 0 для t дает лучшее приближение t≈0,985572. □

Вес и масса Обратите внимание, что в английской системе фунта описывают силы .Следовательно, когда дан вес W объекта, мы должны вычислить его массу с соотношением W = мг или m = Вт / г. И наоборот, в международной системе обычно указывается масса объекта (в килограммах).

Теперь мы объединяем несколько тем, обсуждаемых в этом разделе, чтобы решить следующую проблему.

Пример 3.13

Объект весом 32 фунта упал с высоты 50 футов над поверхностью небольшого пруда. Пока объект находится в воздухе, сила сопротивления воздуха составляет v .Однако, когда объект находится в пруду, на него действует сила плавучести, эквивалентная 6 v . Определите, сколько времени требуется, чтобы объект достиг глубины 25 футов в пруду.

Решение: Масса этого объекта находится с помощью соотношения W = mg, где W – это вес объекта. Таким образом, мы находим, что 32 фунта = м (32 фут / с2), поэтому m = 1 (фунт-с2) / фут (снаряд).

Эта проблема должна быть разбита на две части: проблема начальной стоимости для объекта над прудом и проблема начальной стоимости для объекта ниже поверхности пруда.Используя методы, описанные в предыдущих примерах, было найдено, что проблема начального значения над поверхностью пруда составляет

dv / dt = 32 − v, v (0) = 0.

Однако для определения задачи начального значения, которая дает скорость объекта под поверхностью пруда, необходимо знать скорость объекта, когда он достигает поверхности. Следовательно, сначала необходимо определить скорость объекта над поверхностью.

Уравнение dv / dt = 32 − v разделимо, и его переписывание дает 1 / (32 − v) dv = dt.Интегрирование и применение начального условия приводит к v (t) = 32−32e − t. Чтобы найти скорость, когда объект ударяется о поверхность пруда, мы должны знать время, когда объект упал на 50 футов. Таким образом, мы находим расстояние, пройденное объектом, решая ds / dt = v (t), s (0 ) = s0, получаем s (t) = 32e − t + 32t − 32. Из графика s (t), показанного на рис. 3.11A, мы видим, что значение t , при котором объект прошел 50 футов, составляет около 2,5 с.

Рисунок 3.11. (A) График с ( t ) = 32 e ^{– t} +32 t −32.(B) График s (t) = 3.99722−3.9972e − 6t + 163t.

Более точное значение времени падения объекта на поверхность t≈2,47864. Затем скорость в это время определяется путем подстановки в функцию скорости, что дает v (2.47864) ≈29.3166. Обратите внимание, что это значение является начальной скоростью объекта, когда он ударяется о поверхность пруда.

Таким образом, задача начального значения, определяющая скорость объекта под поверхностью пруда, задается как dv / dt = 32−6v, v (0) = 29.3166. Решением этой задачи начального значения является v (t) = 16/3 + 23.9833e − 6t, и, решая ds / dt = 16/3 + 23.9833e − 6t, s (0) = 0, мы получаем

s (t) = 3.99722−3.99722e − 6t + 163t,

, что дает глубину объекта в момент времени t . Из графика этой функции, показанного на рис. 3.11B, мы видим, что объект находится на глубине 25 футов ниже поверхности пруда примерно через 4 секунды.

Более точное приближение времени, когда объект находится на 25 футов ниже поверхности пруда, составляет t≈3.93802.

Наконец, время, необходимое объекту для достижения поверхности пруда, добавляется ко времени, необходимому ему для прохождения 25 футов под поверхностью, чтобы увидеть, что примерно 6,41667 с требуется для того, чтобы объект переместился с высоты 50. футов над водоемом на глубину 25 футов ниже поверхности. ² □

Примечание Модель, представленная в этом разделе, в которой сила, вызванная сопротивлением воздуха, пропорциональна скорости mdv / dt = mg − cv, является упрощенной моделью, используемой для иллюстрации того, как дифференциальные уравнения используются для моделирования физических ситуации.В большинстве случаев уравнение, в котором сила, обусловленная сопротивлением воздуха, считается пропорциональной квадрату скорости, mdv / dt = mg-cv2, гораздо лучше справляется с предсказанием скорости падающего объекта. Фактически, первая модель обычно работает только тогда, когда объект падает в высоковязкую среду или когда объект имеет незначительную массу.

Движение объекта из-за боковой силы

Сэр Исаак Ньютон впервые представил свои три законы движения в “Principia Mathematica Philosophiae Naturalis” в 1686 г.Его первый закон гласит, что каждый объект будет оставаться в покое. или в равномерном движении по прямой, если не требуется изменить его состояние под действием внешней силы. Когда приложена внешняя сила F , объект ускоренный в направлении силы с величиной прямо пропорциональной силе и обратно пропорциональной пропорциональна массе м объекта. Это повторное утверждение Ньютона. второй закон движения:

а = Ф / м

На этой странице мы показываем два примера движения объекта, который подвергается единственной внешней боковой силе.В обоих случаях мы наблюдаем движение сверху. Объект, представленный черным кружком входит в домен снизу при движении при постоянной начальной скорости V . Маленькие черные круги представлять положение объекта по прошествии времени; красный line – это путь или траектория движения объекта. Изначально на объект не действует никакая внешняя сила, поэтому в соответствии с первый закон, объект движется вверх с постоянной скоростью. Затем объект подвергается боковому усилию F .

Траектория A – Мгновенная сила

В левой части рисунка сила F направлен вправо от тропы и мгновенно применяется к объекту. Этот тип приложения силы возникает, если объект испытывает столкновение с другим объектом, движущимся вправо. В ответ на второй закон Ньютона объект получает мгновенное ускорение вправо; скорость вправо изменяется с нуля на какое-то новое значение.Помните, что силы, ускорения и скорости векторные величины имеющий как величину, так и направление, и что ускорение объект в ответ на внешнюю силу находится в направлении силы. Поскольку сила моментально снимается, объект продолжает движение по прямой в соответствии с первым законом. В объект теперь имеет дополнительный составная часть скорости (вправо), которая остается до тех пор, пока на объект не воздействует какая-то будущая внешняя сила.

Траектория B – Непрерывная сила

В правой части рисунка сила F направлена вправо от траектории. и непрерывно применяется к объекту.Этот тип приложения силы возникает, если объект подвергается действию аэродинамический боковая сила, перпендикулярная направлению полета, например, крен самолета, или брошенный, вращающийся шар. Если сила остается постоянной и применяется перпендикулярно движению, полученный путь представляет собой дугу окружности. Радиус круга называется радиус кривизны – R и зависит от относительной величины скорости V и ускорения a , создаваемого боковой силой.2 / а

Когда сила снимается (кренованный самолет доведен до уровня крыльев) объект продолжает движение по прямой в соответствии с первым законом. Непрерывная сила, приложенная перпендикулярно движению, называется централизованная сила , так как она производит круговое движение вокруг некоторого центральная точка.

Мгновенная и средняя скорости – Класс!ная физика

Мгновенная и средняя скорости

Криволинейное движение

Мгновенная скорость при криволинейном движении. Конспект урока “Прямолинейное и криволинейное движение

2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.

3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.

Материальная точка движется ускоренно по криволинейной траектории. Скорость и ускорение при криволинейном движении

Независимость движений

Угловая скорость

Сообщение про прямолинейное и криволинейное движение.

Скорость и скорость

3.2 Мгновенная скорость и скорость – Университетская физика, том 1

Задачи обучения

Мгновенная скорость

Мгновенная скорость

Пример 3,2

Определение скорости на основе графика зависимости положения от времени

Стратегия

Решение

Значение

Скорость

Расчет мгновенной скорости

Пример 3.3

Мгновенная скорость в сравнении со средней скоростью

Стратегия

Решение

Значение

Пример 3,4

Мгновенная скорость в зависимости от скорости

Стратегия

Решение

Значение

Проверьте свое понимание 3,2

3.4: Среднее и мгновенное ускорение

Среднее ускорение

Мгновенное ускорение

Ощущение ускорения

Таблица 3.2 – Типичные значения ускорения

Авторы и авторство

конспектов лекций

Мгновенная скорость. Связанные ставки – Подход к исчислению

Мгновенная скорость – обзор

3.3 Свободно падающие тела

Движение объекта из-за боковой силы

Оставить комментарий Отменить ответ