Как направлены векторы скорости и ускорения при равномерном движении: Как направлены векторы скорости и центростремительного ускорения при равномерном движении по окружности? 1) Параллельно друг другу, направлены в противоположные стороны 2) Перпендикулярно друг к другу 3) Параллельно друг другу, направлены в одну сторону 4) Под острым углом друг к другу

Равномерное движение по окружности, теория и онлайн калькуляторы

Равномерное движение по окружности, теория и онлайн калькуляторы

Пусть материальная точка движется по окружности равномерно. Если движение называют равномерным, значит, модуль скорости при перемещении точки является постоянным ($v=const$). Но нельзя сказать, что ускорение точки при этом равно нулю, так как скорость – величина векторная и кроме модуля у нее есть еще направление, а при криволинейном движении, каким является движение по окружности, направление скорости постоянно изменяется. (Мы знаем, что вектор скорости является касательным к траектории, по которой перемещается наша точка, то есть является касательной к окружности в рассматриваемой точке).

Скорость и ускорение при равномерном движении по окружности

Пусть A и B – точки, принадлежащие траектории движения нашей частицы. При перемещении из точки А в точку В вектор изменения скорости ($\Delta \overline{v}$) равен:

\[\Delta \overline{v}={\overline{v}}_B-{\overline{v}}_A\left(1\right). 2R\ \left(7\right),\]

где $\omega $ – угловая скорость движения материальной точки ($v=\omega \cdot R$).

Местоположение точки на окружности можно задавать не только с помощью расстояния от некоторой начальной точки, а так же с помощью угла $\varphi $, поворота радиус-вектора, который определяет положение частицы на траектории (рис.2).

Совместно с углом поворота движение точки по окружности характеризуют при помощи угловой скорости движения ($\omega $), которую определяют как

\[\omega =\frac{d\varphi }{dt}\left(8\right).\]

где $\omega $ характеризует быстроту изменения угла $\varphi $.

При равномерном движении по окружности угловая скорость постоянная величина.

Линейная и угловая скорости движения по окружности связывает формула:

\[v=R\omega \left(9\right).\]

Период и частота при равномерном движении по окружности

Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. 2}=\frac{d}{dt}\left(2At+B\right)=2А\left(1.3\right).\]

Мы получили, что:

\[a_{\tau }=2A\ne 0=const.\]

Ответ: Движение материальной точки в заданном случае не равномерное.

   

Пример 2

Задание: Найдите отношение ускорений двух материальных точек ($\frac{a_1}{a_2}$), которые равномерно движутся по окружностям, имеющим радиусы: $R_1\ и\ R_2\ (R_1\ >R_2)$ с одинаковыми скоростями.

Решение: Так как точки движутся по окружностям с равномерно, то они будут иметь только центростремительные ускорения:

\[{\overline{a}}_1={\overline{a}}_{n1};;{\overline{a}}_2={\overline{a}}_{n2}\ \left(2.1\right),\]

которые направлены перпендикулярно вектору скорости в рассматриваемой точке и направлены к центру окружности. Модуль центростремительного ускорения при этом равен, для первой частицы:

\[a_{n1}=\frac{{v_1}^2}{R_1}\left(2. 2}{R_2}=\frac{R_2}{R_1}.\]

Ответ: $\frac{a_1}{a_2}=\frac{R_2}{R_1}$

   

Читать дальше: сила упругости. Закон Гука.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Богданов К.Ю. – учебник по физике для 10 класса

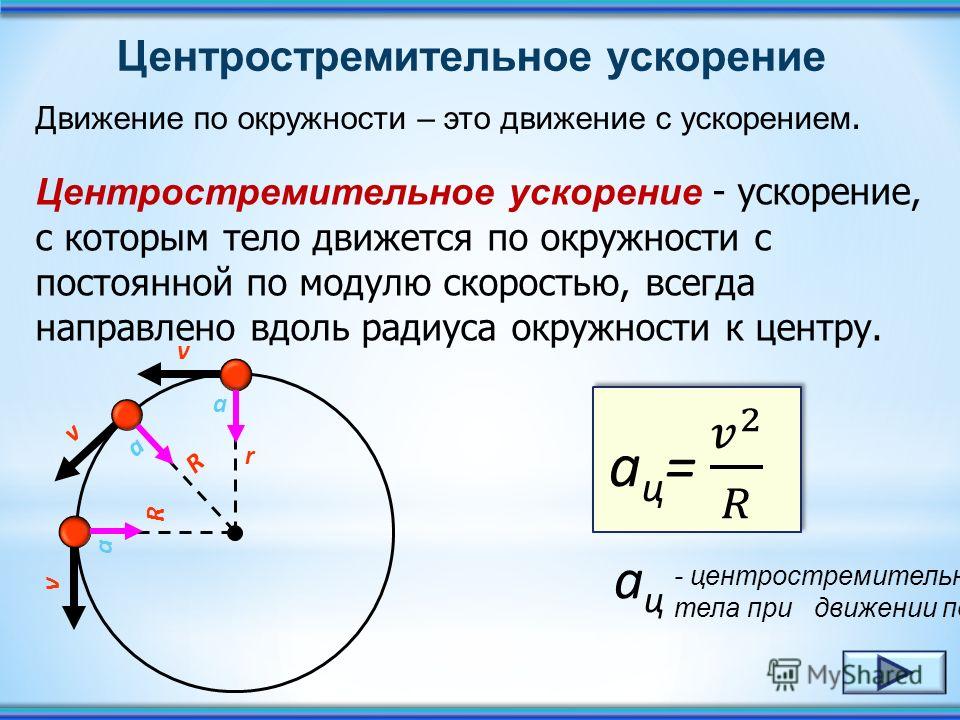
§ 6. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ: ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ.

Вектор скорости тела, движущегося по окружности, непрерывно изменяет своё направление, и поэтому такое движение является ускоренным.                                             

Любое движение по криволинейной траектории происходит с ускорением, так как вектор скорости, направленный по касательной к траектории, меняет своё направление со временем. Примерами криволинейного движения могут служить движение планет вокруг Солнца и электронов вокруг атомного ядра. По криволинейной траектории движется автомобиль, поворачивающий на перекрёстке, и самолёт, заходящий на посадку.

Простейшим криволинейным движением является равномерное движение по окружности, при котором модуль скорости остаётся постоянным, а его направление меняется. Чтобы найти величину и направление вектора ускорения при равномерном движении по окружности с центром в точке О, отметим на ней две близко расположенные точки A и B (см. верх рис. 6, слева). Пусть, в точке А тело было в момент времени t, а в точке В – в момент времени t+Dt. На том же рисунке выходящими из точек А и В нарисованы векторы v_A и v_B, соответствующие скоростям тела в данных точках.

Ускорение a, как известно (см. § 4), равно отношению изменения вектора скорости Dv, произошедшего за интервал времени Dt, к величине этого интервала, откуда следует, что Dv =a^. Dt. В нашем случае Dv = v_A – v_B. Справа вверху на рис.6 показано, как, используя правило треугольника, найти Dv по известным v_A и v_B. При сближении точек Б и А направление  приближается к направлению, перпендикулярному к , а значит  становится направленным к центру окружности, по которой движется тело. Такое движение называют движением с центростремительным ускорением.

Так как v_A и v_B перпендикулярны ОА и ОВ, соответственно, а модули v_A и v_B равны между собой, то треугольники ОАВ и О’A’B’ подобны, как равнобедренные треугольники с равными углами (см. верх рис.6). Поэтому справедливо следующее отношение между длинами сторон этих треугольников:

Для близко расположенных точек А и В длину отрезка АВ можно считать равной длине соответствующей дуги АВ окружности, а длина этой дуги окружности равна произведению модуля скорости, v на Dt

. Подставляя в (6.1) A’B’ = a^.Dt , АВ = v^.Dt,    О’A’ = v, ОА = R (радиус окружности), получаем после несложных преобразований следующее выражение для величины центростремительного ускорения:

Любое криволинейное движение на коротких участках траектории всегда можно рассматривать как движение по малой дуге окружности с радиусом, более всего подходящим для данного участка траектории (см.

R₁, R₂ и R₃ в нижней части рис.6). Этот радиус называют радиусом кривизны траектории в данной её точке. Если тело движется равномерно (модуль скорости, v не изменяется) по криволинейной траектории, то по формуле 6. 2 и известным радиусам кривизны можно вычислить центростремительное ускорение, направленное к центру кривизны траектории в любой её точке.  

Так как вектор центростремительного ускорения всегда направлен перпендикулярно касательной к траектории, то направление вектора ускорения при криволинейном движении никогда не совпадает с направлением касательной к траектории. Поэтому вектор ускорения в этих случаях представляют в виде суммы двух взаимно перпендикулярных составляющих: тангенциальной, a_т (направленной по касательной к траектории) и нормальной, a_н (направленной перпендикулярно к касательной). При этом a_т соответствует изменению модуля скорости движения, а a_н – изменению направления его вектора.

Вопросы для повторения:

·        Куда направлено центростремительное ускорение, и как оно зависит от скорости и радиуса окружности?

·        Чему равны модули тангенциального и нормального ускорения при равномерном движении по окружности?

Рис. 6. Верх – к выводу формулы для центростремительного ускорения; низ – криволинейная траектория, несколько участков которой можно заменить дугами окружностей обозначенных радиусов.

ньютоновской механики – Как при равномерном круговом движении ускорение тела может быть направлено к центру вращения, если скорость касается орбиты?

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 261 раз

$\begingroup$

Вот картинка, иллюстрирующая мой вопрос:

https://upload.wikimedia.org/wikipedia/commons/7/71/Uniform_circular_motion.svg

Я не должен понимать, что такое ускорение, потому что не понимаю, как ускорение вращающегося тела может быть направлено к центру вращения, когда скорость – нет.

Мы просто говорим, что ускорение направлено к центру вращения, потому что это направление центростремительной силы? Когда на самом деле нет ускорения к центру вращения?

• ньютоновская механика
• кинематика
• системы отсчета
• орбитальное движение
• центростремительная сила

$\endgroup$

1

$\begingroup$

Как вы предполагаете в своем комментарии к ответу левитофера, вы запутались, потому что связываете ускорение с изменением скорости. Вместо этого вы должны рассматривать это как причину изменения скорости, которая может быть изменением направления движения с постоянной скоростью. Круговое движение возникает при приложении силы, всегда перпендикулярной скорости движущегося тела.

$\endgroup$

$\begingroup$

Определение (среднего) ускорения:

$$\vec{a}=\frac{\Delta \vec{v}}{dt}$$

Где $\Delta \vec{v}=\vec {v}_f-\vec{v}_i$ (конечный минус начальный).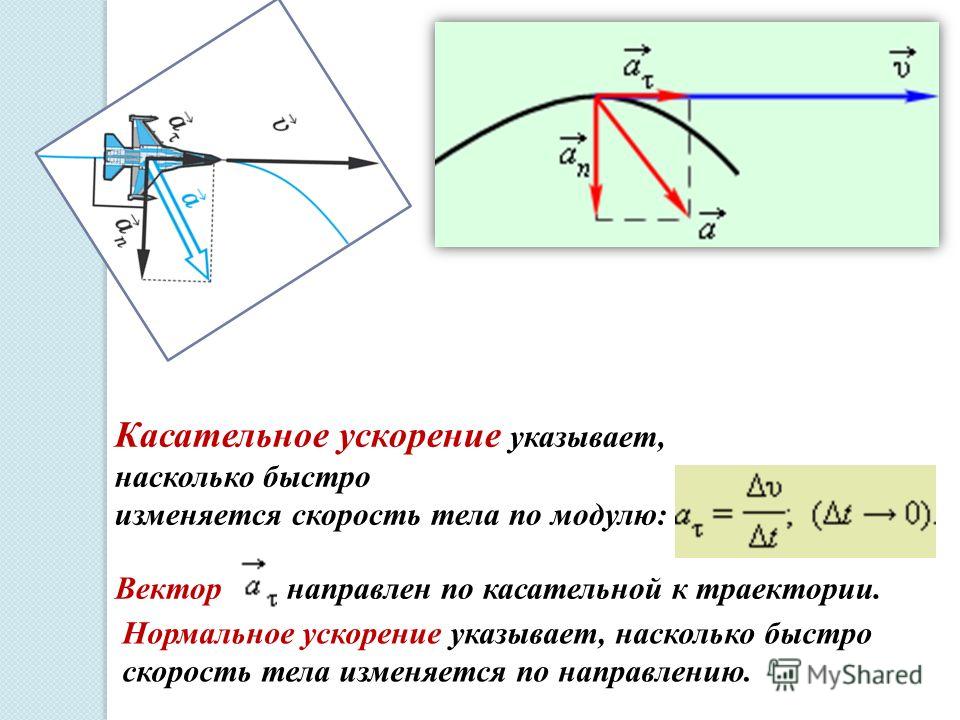 Важная вещь, которую вы упускаете, это то, что $\vec{v}$ имеет знак вектора над ним – направление имеет значение, и если направление меняется, то ускорение не равно нулю. Давайте попробуем этот расчет на вашем конкретном изображении.

Я добавил систему координат к вашему рисунку и рассчитываю ускорение между скоростью в положениях 3 и 12 часов (поэтому я поместил вектор ускорения примерно на 1:30). Компоненты вектора ускорения равны

$$a_x=-v_f/\Delta t, \qquad a_y=-v_i/\Delta t$$

(разумеется, как величины $|v_f|=|v_i|$, поэтому ускорение происходит под углом 45 градусов, вплоть до третьего квадранта.)

$\endgroup$

3

$\begingroup$

Подумайте о том, как меняется положение, несмотря на то, что расстояние остается постоянным, потому что положение зависит от направления на исходную точку, а не только от расстояния до исходной точки.

Точно так же скорость может изменяться, даже если скорость постоянна, поскольку скорость зависит от направления движения, а не только от того, насколько быстро что-то движется.

Уравнение единичного круга:

$$x=\cos т$$ $$y=\sin t$$

Скорость – это производная по времени от положения, а ускорение – это производная по времени от скорости, а производная от $\cos t$ равна $-\sin t$, а производная от $\sin t $ равно $\cos t$

$\endgroup$

3

$\begingroup$

Скорость является вектором, т.е. имеет как величину (скорость), так и направление. Изменение величины (скорости) является результатом составляющей ускорения в направлении скорости, а изменение направления скорости – результатом составляющей ускорения, перпендикулярной скорости. При равномерном круговом движении скорость постоянна, значит составляющая ускорения в направлении скорости (по касательной к окружности) равна нулю, но направление скорости меняется, поэтому ускорение перпендикулярно окружности ( = радиальный).

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

[Решено] Объект совершает равномерное круговое движение.

1. Вектор ускорения направлен к центру окружности
2. Вектор скорости касается окружности
3. Вектор ускорения касается окружности
4. Векторы скорости и ускорения перпендикулярны друг другу

Вариант 3: вектор ускорения касается окружности

Бесплатно

Электрические заряды и закон Кулона (базовый)

87,9 тыс. пользователей

10 вопросов

10 баллов

10 минут

Правильный ответ — вариант 3), т. е. Вектор ускорения касается окружности.

• ​Под окружностью понимается многоугольник с бесконечным числом сторон, каждая из которых приближается к точке.
• Итак, объект, движущийся по круговой траектории, меняет направление в каждой точке.
• Поскольку направление меняется, а скорость остается постоянной, скорость меняется.

Центростремительное ускорение: Ускорение, связанное с изменением скорости при круговом движении, называется центростремительным ускорением. Он направлен к центру кругового пути.

ОБЪЯСНЕНИЕ :

• Окружность считается многоугольником с бесконечным числом сторон, каждая из которых приближается к точке. Таким образом, объект, движущийся по круговой траектории, претерпевает изменение направления в каждой точке, то есть скорость изменяется в каждой точке.
  • Следовательно, в любой точке кругового движения вектор скорости будет направлен по касательной, чтобы представить направление стороны многоугольника.
• Центростремительное ускорение удерживает объект в круговом движении и, следовательно, направлено к центру .
• Таким образом, вектор скорости и вектор ускорения будут перпендикулярны друг другу.