Как научиться быстро делить: Как делить в уме 🚩 как быстро делить числа 🚩 Математика

Деление в столбик 3 класс. Примеры для тренировки и объяснения. Блог Кувырком

Таблица умножения – это не самое трудное, с чем сталкивается младший школьник. Гораздо сложнее освоить деление в столбик. Многие дети без помощи родителей не могут понять этот процесс. Давайте разберёмся, как легко и без лишней нервотрёпки обучить ребёнка делить в столбик.

Что нужно знать, чтобы научиться делить в столбик?

Деление столбиком школьники обычно начинают изучать на уроках математики в третьем классе. Чтобы понять процесс деления и начать использовать его на практике, школьник должен уметь следующее:

•   без труда решать примеры на сложение и вычитание;
•   знать наизусть таблицу умножения;
•   знать разряды чисел;
•   уметь быстро считать в уме.

Если в этих знаниях у ребёнка есть пробел, ему трудно будет научиться делить столбиком. Поэтому перед началом обучения нужно обязательно повторить пройденный ранее материал, особенно таблицу умножения.

Учимся считать и считать вместе с КУВЫРКОМ

С чего начать учить ребёнка делению?

Прежде всего, объясните школьнику суть этого математического действия. Он должен понять, что деление – это процедура обратная умножению. Когда школьник усвоит, что эти два действия взаимосвязаны друг с другом, научиться делить будет несложно.

Учить проще всего на практических, понятных детям примерах. Выдайте сыну или дочери конфеты и предложите разделить их между членами семьи. Вместо конфет можно использовать разрезанный на куски пирог. Главное, чтобы школьник уяснил суть действия: раздать угощение так, чтобы все получили поровну и без остатка.

Проявите фантазию, придумывая разные примеры, а затем запишите ваши действия в тетради, чтобы ребёнок увидел, как выглядит математическая запись деления (пока что не столбиком, а в строку). 

Теперь возьмите таблицу умножения и выберите оттуда любой пример. Покажите сыну или дочери, что, если произведение разделить на один из множителей, результат такого действия будет равен второму множителю. Поэкспериментируйте с разными примерами из таблицы, чтобы школьник наглядно увидел эту закономерность.

Играем вместе с КУВЫРКОМ

Алгоритм деления в столбик

Для решения любых примеров на деление используется следующий алгоритм

:

1. Найдите в примере делимое (число, находящееся слева от знака деления, то есть число, которое нужно разделить) и делитель (число, находящиеся справа от знака, то есть число, на которое нужно разделить).
2. Запишите первое число – делимое – слева, а второе – делитель – справа, а между ними нарисуйте «уголок».
3. Определите неполное делимое, то есть часть первого числа, которую можно взять для первичного деления. Сначала возьмите первую цифру. Если она не подходит для деления, добавьте к ней следующую и т. д.
4. Посчитайте, сколько раз второе число (делитель) помещается в неполном делимом.
5. Для проверки правильности действия умножьте делитель на полученное число и запишите результат умножения под выбранную часть делимого. Это будет неполное частное.
6. Вычислите разницу – это будет остаток.
7. Повторяйте эти действия до тех пор, пока в остатке не получится 0.

Некоторые числа нельзя разделить так, чтобы в остатке получился 0. Примеры, в которых остаток больше нуля, называются делением с остатком.  

Играем вместе с КУВЫРКОМ

Деление в столбик без остатка

Теперь применим этот алгоритм к конкретному примеру. Возьмём простой пример 35:5=?

Запишите делимое и делитель и нарисуйте между ними «уголок».

Попросите школьника найти неполное делимое – часть делимого, на которую можно разделить число 5 (делитель). Первая цифра в делимом – 3. Спросите у него, сколько пятёрок поместится в число 3? Ребёнок скажет, что ни одной. Значит, добавляем к тройке следующую цифру из делимого – пятёрку и получаем 35 (наше полное делимое).  

Спросите у ребёнка, сколько троек поместится в число 35? Школьник, знающий таблицу умножения, без труда посчитает, что в 35 помещается 7 пятёрок. Число 7 записываем под «уголок». Это и будет ответ.

Это очень простой пример деления двузначного числа на однозначное без остатка. Результат можно проверить с помощью таблицы умножения. Потренируйтесь на подобных примерах, чтобы ребёнок хорошо усвоил алгоритм действий.

Теперь попробуйте решить пример с трёхзначным делимым. Возьмём пример 372:6=?

Запишите пример в столбик.

Попросите ребёнка определить неполный делитель. Первое число в делимом – 3. Сколько шестёрок (шестёрка – делитель) помещается в тройку? Ни одной. Значит добавляем к тройке следующее число из делимого – семерку. Получаем 37. Теперь смотрим, сколько шестёрок поместится в 37. Ребёнок, вспомнив таблицу умножения, без труда вычислит, что в 37 поместится шесть шестёрок и единица останется в остатке.

Запишите неполное частное (6) под делитель, а число 36 под делимое. Вычтите из 37 число 36. Получится 1 (это остаток). Запишите. 

Теперь посмотрите, сколько шестёрок поместится в остаток (1)? Ни одной. Теперь добавьте к единице число, оставшееся в делимом – 2. Получилось 12. Сколько шестёрок поместится в 12? Две шестёрки. Добавьте двойку к уже имеющемуся у нас неполному частному 6. Получится 62. Из 12 вычтите 12. Получится 0. Запишите.

Предложите ребёнку попробовать решить примеры с четырёх-, пяти-, шестизначными делимыми, а также с двузначными делителями. Независимо от величины чисел принцип действий будет одинаковым.

Деление в столбик с остатком

Расскажите ребёнку, что некоторые числа нельзя разделить без остатка. Для лучшего понимания продемонстрируйте это действие на наглядном примере. Дайте сыну или дочери пять конфет и попросите разделить их между ним и вами. Ребёнок даст вам и себе по две конфеты и останется ещё одна.

Объясните ему, что так произошло потому, что число 5 не делится на 2 поровну. Остаётся одна конфета, которая и является в данном случае остатком. Дайте ребёнку больше конфет и снова попросите его разделить на троих, четверых, пятерых. Снова обратите внимание на то, что далеко не всегда конфеты можно разделить поровну.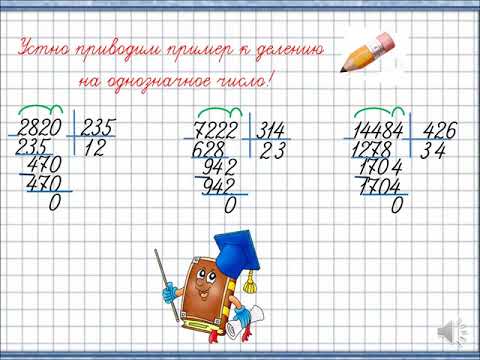

После того как ребёнок поймёт суть такого деления, переходите к решению примеров в столбик. Решаются они по тому же принципу, только вместо нуля в остатке получается какое-либо другое число.

Почему ребёнку сложно освоить деление в столбик?

Деление – это наиболее сложное арифметическое действие из четырёх основных. Многие дети прекрасно справляются со сложением, вычитанием, умножением, но буксуют, когда дело доходит до деления. Проблема здесь заключается в том, что ребёнок не понимает сам принцип деления. Постарайтесь объяснить ему алгоритм этого математического действия как можно доходчивее. Если не получается, обратитесь за помощью к учителю.

Если же ребёнок не умеет быстро считать в уме и плохо знает таблицу умножения, то с делением у него обязательно возникнут проблемы. В этом случает важно до автоматизма отточить навык сложения и вычитания и хорошо выучить таблицу умножения. На первых порах обучения делению столбиком можно держать таблицу при себе и изредка подсматривать в неё.

Не ругайте ребёнка, если у него не получается быстро освоить деление столбиком. Вспомните себя в его возрасте – наверняка у вас тоже были подобные проблемы. Наберитесь терпения и объясняйте правила столько раз, сколько требуется. Не ставьте цель научить сына или дочь делить столбиком за один вечер. Избыток информации утомит ребёнка и снизит его обучаемость. Занимайтесь в комфортном для него темпе и вскоре он научится решать примеры самостоятельно, без вашей помощи. Не забывайте хвалить и вознаграждать школьника за старание – это повысит его мотивацию.

Как объяснить ребенку деление в столбик, или уголком: простой принцип с примерами

Содержание статьи

• Как правильно делить в столбик?
• Что нужно знать ребенку для понимания деления столбиком?
• Методика обучения детей делению столбиком
• Работа с многозначными числами
• Как объяснить деление с остатком?

Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.

Как правильно делить в столбик?

Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).

Как найти частное двух чисел – 35 и 5?

1. Пишем числа, участвующие в делении, так:
   
   Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное.
2. Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
3. Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
   
4. Проверяем правильность действий путем умножения: 7 X 5=35. Все верно, решение выполнено точно.

Что нужно знать ребенку для понимания деления столбиком?

Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:

• отличное знание таблицы умножения;
• умение быстро считать в уме.

В конце 3 класса ученики усваивают, как разделить простые двузначные числа.

При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.

Методика обучения детей делению столбиком

Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.

Проверьте знание таблицы умножения. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.

Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).

Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.

Работа с многозначными числами

Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:

1. Определяем делимое (372) и делитель (6), оформляем запись в уголок:
   
2. Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
3. Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
4. Вычитаем из 37-36=1. Пишем единичку слева внизу под чертой:
   
5. В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
   

Пример решен, можно проверить правильность путем умножения: 62X6=372.

Как объяснить деление с остатком?

Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:

В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.

Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).

Обучение школьника должно проходить поэтапно, от простых примеров к более сложным.  Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.

Объяснение короткого деления и длинного деления

Мы работали с экспертами по начальной математике, чтобы создать руководство для родителей и новых учителей по короткому делению (включая метод автобусной остановки) и страшному длинному делению.

В этой статье мы объяснили все, что вам нужно знать, чтобы помочь вашему ребенку разобраться с этими сложными темами!

Неважно, короткое это деление или длинное, для многих детей и их родителей одно только упоминание слова «Д» может вызвать мурашки по спине у многих юных математиков, но это не так. должно быть дело!

Здесь, в Third Space Learning, мы стремимся сделать математику доступной для всех, включая деление на короткое и длинное деление… представляют собой математическую задачу), поэтому неудивительно, что многие из нас до сих пор находят ее сложной.

В настоящее время, когда дети проводят много времени в школе, понимая как работает деление , а не просто запоминая метод, страх перед делением KS2 тает, но подведение итогов и поиск будут иметь большое значение, особенно если родители могут поддержка из дома.

Но прежде чем вы узнаете все, что вам нужно знать о дивизионах для детей, мы подготовили для вас краткий обзор дивизионов!

Эта статья является частью нашей серии статей, предназначенных для учителей, чтобы информировать их о своих знаниях по математическим предметам, и для родителей, чтобы помочь детям в домашнем обучении. Также доступны дополнительные бесплатные ресурсы для домашнего обучения.

Рабочие листы на деление в длинное число для 3-6 классов

Этот БЕСПЛАТНЫЙ ресурс содержит 3 готовых к использованию рабочих листа для вашего класса, которые помогут им со всеми аспектами деления в длинное число, от однозначных чисел до вычисления кратных!

---

Как учить делению:

Вкратце о методах деления

Мы знаем, насколько чертовски сложным может быть деление, поэтому давайте начнем с некоторых определений и резюме того, что вы, возможно, забыли со школы.

Что такое деление в математике?

Деление — это операция, обратная умножению и заключающаяся в разделении на равные части или группы.

В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Их:

• Разделение на части
• Укороченное деление (также известное как метод автобусной остановки)
• Длинное деление

Подробнее: Что такое деление?

Что такое фрагментация?

Разбиение на части — это метод, используемый для деления больших чисел, которые невозможно разделить в уме.

При использовании метода фрагментации дети будут многократно вычитать делитель из делимого, пока не будет получен ответ. Например, 12 ÷ 3 можно решить, выполнив 12 – 3, чтобы получить 9., 9 – 3, чтобы получить 6, 6 – 3, чтобы получить 3, а затем 3 – 3, чтобы получить 0.

Когда все 3 вычитаются из 12, подсчитываются (4), становится ясно, что ответ 4.

Что такое короткое деление?

Короткое деление — это быстрый и эффективный метод деления больших чисел.

После того, как ваш ребенок освоится с делением на фрагменты, он перейдет к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым, выполнив ряд простых шагов.

Например:

В этом примере у нас есть 9 десятков, которые нужно разделить на четыре. 9 десятков ÷ 4 = 2 десятка, и у нас остался один десяток.

Этот остаток затем передается следующему числу (шесть), чтобы получилось 16 единиц. 16 единиц ÷ 4 равно 4, поэтому при суммировании ответ становится 24.

Какой метод автобусной остановки?

Метод деления на автобусной остановке — это просто еще одно название сокращенного деления. Он получил свое название от идеи, что делимое (число, которое вы хотите разделить) находится внутри автобусной остановки, а делитель ждет снаружи.

Учителя расходятся во мнениях относительно того, действительно ли это изображение полезно при изучении деления, поэтому в большинстве случаев мы просто будем называть его коротким делением.

Что такое длинное деление?

Длинное деление — это метод, который используется при делении большого числа (обычно трех или более цифр) на двузначное (или большее) число. Он изложен аналогично методу автобусной остановки, который используется для короткого деления.

Взгляните на наш пример ниже, чтобы увидеть, как деление в длину объясняется наглядным примером.

Лучше всего это объяснить на примере – см. ниже.

У нас есть очень подробная статья, написанная для учителей на эту тему, которая может вам понравиться, если вы хотите более подробно изучить метод деления в KS2.

Терминология, которую необходимо знать при обучении разделу

В наших блогах мы стараемся избегать слишком большого количества профессионального жаргона, но следующие три термина действительно важны для всех, кто изучает раздел.

• Дивиденд — это число, которое вы делите (число внутри «автобусной остановки»).
• Делитель — это число, на которое вы делите.
• Частное – это сумма, которую получает каждый делитель, т.е. ответ в большинстве случаев.

Хороший способ запомнить это делимое   ÷ делитель = частное .

Части задачи на деление, помеченные для детей и родителей

Изучив правильный словарный запас всех частей задачи на деление, ваш ребенок найдет многие элементы задачи на деление намного проще.

Что мой ребенок должен знать о коротком и длинном делении в KS1 и KS2?

В связи с тем, что дети меняются из года в год на протяжении всей начальной школы, в кратком и длинном делении в блоге есть что рассказать, но чтобы помочь вам, мы разбили его по годам.

Как обучать разделу

1-й год

В 1-м классе раздел обычно называется , разделяя , и это делается с использованием конкретных предметов, таких как прилавки, кубики или даже продукты питания, такие как макароны.

Это помогает детям понять разделение как разделение между группами.

Простой пример этого можно найти ниже.

Несколько простых задач на деление для 1-го класса

Возьмите математические манипуляторы или кубики, чтобы помочь юным ученикам решить эти задачки на деление.

Убедитесь, что вы не забыли использовать такие слова, как разделить и разделить повсюду, чтобы ваш ребенок познакомился с понятиями, где делитель — это количество групп, между которыми должен быть разделен дивиденд.

Начните с 4 блоков. Разделите их на 2 равные группы.

Начните с 10 блоков. Разделите их на 2 равные группы.

Начните с 6 блоков. Разделите их на 3 равные группы.

Как преподавать деление Год 2

Во втором классе дети начинают более глубоко изучать принцип деления, а это значит, что вашему ребенку предстоит научиться еще кое-чему.

Ключевая концепция, которую нужно понять и освоить в этом возрасте, — 9 лет.0003 коммутативность .

Если вы изо всех сил пытаетесь вспомнить, что именно означает коммутативность, определение простое.

В математике свойство коммутативности утверждает, что порядок не имеет значения.

Умножение коммутативное ; вы можете поменять местами числа, и это не имеет значения.

2 x 3 = 6

3 x 2 = 6

Деление не коммутативное . Если вы поменяете порядок чисел, это изменит ответ.

4 ÷ 2 = 2

2 ÷ 4 = 0,5

Деление и коммутативность во 2-м классе

В этом возрасте полезно практиковаться в изучении таблиц умножения на 2, 5 и 10 с соответствующими фактами деления. Например:

Факт умножения:

2 x 5 = 10

Соответствующие факты деления:

10 ÷ 5 = 2

10 ÷ 2 = 5

обратное умножению, и они являются отличным примером того, почему коммутативность важна.

Если вашего ребенка устраивает разница между 10 ÷ 5 и 10 ÷ 2, даже после того, как он увидит, что 5 x 2 равно 2 x 5, он будет лучше подготовлен для комфортного перехода к короткому дивизиону KS2 и длинному KS2. разделение.

Как научить делению Год 3

В 3-м классе ваш ребенок сосредоточится на записи вычислений деления и решении основных задач на деление, связанных с пропущенными числами.

Здесь очень пригодятся знания об умножении и делении, поэтому, как и в случае со 2-м классом, очень важно практиковать их со своим ребенком.

Эта проблема пропущенных чисел поможет вам понять, почему знание таблицы умножения значительно упрощает деление:

5 x 4 = 20

__ ÷ 5 = 4

20 ÷ __ = 5

Также есть два письменных метода деления, которые вводятся в этом возрасте, и они разбиты ниже.

Письменные методы деления для детей

Объяснение метода деления на фрагменты

Хотя этот метод немного медленнее, чем деление на автобусной остановке, он отлично подходит для развития умственных навыков, необходимых детям для более сложного деления в дальнейшем.

Как сделать разбиение на части метод деления

Разбиение на части — это когда вы определяете, сколько раз одно число входит в другое число.

Вы вычисляете это путем многократного вычитания делителя (или кратных делителю) до тех пор, пока не получите ноль, чтобы увидеть, сколько раз делитель может войти в число, которое вы делите (делимое).

Разделение на фрагменты — это хороший способ познакомить вашего ребенка с некоторыми из основных понятий деления, и как только они с этим смирятся, они смогут перейти к методу деления на короткие фрагменты.

Объяснение метода короткого деления или метода деления на автобусной остановке

Часто называется методом деления на автобусной остановке из-за того, что расчет на листе бумаги имеет некоторое визуальное сходство с автобусной остановкой, этот метод короткого деления KS2 является одним из самых популярных методов, которым обучают в школах.

Этот метод быстрее, чем фрагментация, но важно, чтобы дети понимали, что они делают (а не просто следовали методу).

Это значительно облегчит деление на части в будущем, но рекомендуется убедиться, что ваш ребенок научился разделять на фрагменты, прежде чем переходить к делению на короткие.

Как выполнить краткое деление

В этом возрасте краткое деление будет включать однозначные делители и 3- или 4-значные дивиденды.

Слайд из третьего урока Space Learning 1-to-1, на котором ученики шаг за шагом проходят короткие деления.

Сядьте вместе с ребенком и посмотрите на схему ниже, чтобы узнать названия и места для каждой части задачи на деление.

Они могут выглядеть очень незнакомыми, когда вы привыкли выписывать свои суммы в строку, поэтому поработайте с ребенком, чтобы убедиться, что он знает свой делитель по делимому!

Как помочь ребенку разделить трех- или четырехзначное число на однозначное число

Так как эти типы вопросов на деление составляют большинство вопросов на деление в 3-м классе, вот рисунок, в котором подробно показано, как разделить трех- или четырехзначное число число однозначным числом.

Как учить деление Год 4

В 4 классе ваш ребенок будет использовать краткое деление (метод деления на автобусной остановке, описанный выше), чтобы делить числа до четырех цифр на двузначные числа.

Метод точно такой же, как и с однозначными цифрами, за исключением того, что первый шаг всегда включает группировку.

На этом этапе процесс деления становится гораздо более трудным, если ваш ребенок не выучил наизусть свою таблицу умножения, поэтому лучшее, что вы можете сделать для него, — это помочь ему выучить ее.

Им также нужно будет выбрать, какой остаток использовать в зависимости от вопроса, а некоторые распространенные вопросы будут связаны с реальными ситуациями, например, с разделением групп между автомобилями или предметами между ящиками.

Вопросы на деление с остатком

Деление с остатком может быть сложной концепцией для понимания, когда дети впервые знакомятся как с коротким, так и с длинным делением, но важно, чтобы дети хорошо их понимали, поскольку они могут резко измениться в зависимости от вопроса, который спрашивают.

Практикуйтесь в использовании пар множителей в 4-м классе, чтобы облегчить письменное деление

Пары множителей — это два множителя (числа), которые при умножении вместе дают определенный продукт (результат).

Упражнения с парами факторов могут помочь вашему ребенку ускорить процесс деления, так как знание того, что 4 x 5 = 20, поможет ему в вычислении 20 ÷  4 = _ .

Попросите вашего ребенка найти как можно больше пар множителей для приведенного ниже числа, и почему бы не превратить это в игру?

Сядьте вместе со своим ребенком, возьмите ручку и лист бумаги и посмотрите, кто сможет вычислить наибольшее количество пар множителей для следующих чисел за минуту. Результаты могут быть ближе, чем вы думаете!

• 20
• 68
• 12
• 30
• 100

Подробнее: Что такое наибольший общий множитель

Как научить деление Год 5

К 5-му году ребенок должен уметь быстро мысленно делить числа вдвое или вчетверо.

Если им трудно, внедрение математики в реальный мир может стать отличным способом помочь им справиться с половинками и четвертинками. Например, когда вы находитесь вне дома, спросите их, сколько будет стоить предмет, если он будет стоить половину, или сколько граммов будет в половине 1-килограммового мешка сахара.

Умение быстро делить на 2 (деление пополам) и 4 (четвертование) станет важной частью деления по мере того, как ваш ребенок будет учиться в школе, поэтому будет очень полезно, если он сможет научиться этому прямо сейчас.

Сокращенное деление с десятичными знаками

Сокращенное деление будет использоваться для чисел, содержащих десятичные дроби, впервые в 5-м классе.

Это означает, что самое время пересмотреть разрядность, чтобы ваш ребенок понял, как работают десятичные дроби.

Десятичные числа являются частями целого (аналогично дробям), но при делении десятичных дробей важно помнить, что столбцы разрядных значений уменьшаются в значении каждый раз, когда вы перемещаетесь вправо.

Пример десятичного деления

Как научить деление Год 6

В 6-м классе ваш ребенок впервые познакомится со страшным делением на две части!

Однако хорошая новость заключается в том, что как только вы освоите деление на фрагменты и короткое деление, длинное деление совсем не так уж плохо!

Ключевым моментом, когда дело доходит до деления в длину для детей, является не торопиться и поощрять их аккуратно представлять свою работу, чтобы они могли легко замечать ошибки и работать над их исправлением.

Даже зная об этом, деление в длинное число все еще может быть пугающей перспективой для детей (и родителей!), поэтому взгляните на наш пример ниже, чтобы понять, как решить задачу деления в длинное число.

Вы учитель, который ищет поддержку в обучении делению в столбик? Ознакомьтесь с нашими идеями и советами по обучению делению в столбик, написанными опытными математиками-практиками.

Объяснение деления в длинное деление для детей

В приведенном ниже примере показан самый популярный метод деления в длинное деление для детей, а также тот, с которым вы, возможно, знакомы еще со времен начальной школы.

Все, что вам нужно для завершения вычисления 528 ÷ 24, это ручка, немного бумаги и ребенок, который хочет освоить этот метод!

После того, как вы попробуете ответить на несколько вопросов на деление на длинное деление (с вашей помощью для начала), ваш ребенок вскоре увидит, что этот метод может помочь ему понять, как решать задачи на деление на длинное деление, независимо от задействованных чисел, и окажется неоценимым. когда дело доходит до SAT.

Как выполнить деление в длинное число: Простой пошаговый метод деления в длинное число для использования в KS2

Не беспокойтесь, если для полного внедрения процесса потребуется некоторое время. Это длинная цепочка вещей, которые нужно запомнить, поэтому потребуется регулярная практика, чтобы запомнить этот метод. Ознакомьтесь с нашими вопросами о длинном делении и примерами длинного деления для получения дополнительной поддержки.

Просто запомните процесс: делить, умножать, вычитать, сводить; и повторить.

Тяжелая работа окупится в долгосрочной перспективе, поэтому стоит уделить время вашему ребенку сейчас, чтобы убедиться, что деление в столбик хорошо объяснено на раннем этапе, чтобы уменьшить количество раз, когда вы услышите неизбежное:

« Муммммм…….Как вы делаете деление в длинное…?»

Откуда мы знаем, когда делить и какой метод использовать?

Различные вопросы на деление требуют разных методов деления для их решения, но вот краткое и простое руководство, которое покажет, какой метод и когда должен использовать ваш ребенок:

• Разбиение лучше всего подходит для небольших чисел и арифметики.
• Короткое деление отлично подходит для деления больших чисел на однозначные числа.
• Длинное деление удобно для деления больших чисел на числа, состоящие из 2 и более цифр.

Конечно, могут быть случаи, когда каждый из вышеперечисленных методов можно использовать в немного разных сценариях, но, как правило, этого должно быть достаточно, чтобы помочь вашему ребенку принять правильное решение.

Вопросы по разделу SAT для 6-го класса

Когда придет время сдавать экзаменационные работы по математике, более чем вероятно, что вашему ребенку придется отвечать на некоторые вопросы по разделу.

Решение задач и рассуждения (бумаги 2 и 3) в 6-м классе могут быть сложными, когда речь идет о задачах на деление. Часто задачи требуют решения более чем одной операции, что может добавить элемент сложности в и без того напряженную обстановку, поэтому поощряйте ребенка обращать внимание на такие слова, как , делиться или , группировать , чтобы помочь им идентифицировать что нужно сделать для решения проблемы.

Задачи на деление в задании 1 (арифметика) будут представлены в виде числовых предложений, и ваш ребенок должен будет продемонстрировать свое решение, если вопрос оценивается более чем в 1 балл.

Эти вопросы легко определить, потому что они будут использовать символы деления:

÷

или

, или они могут включать дроби.

Как правило, поощряйте ребенка к мысленному разделению, когда это возможно.

Хотя письменные методы отлично подходят для больших чисел, возможность мысленного деления даст им преимущество. Это означает, что когда они выполнят письменный метод, они смогут увидеть, является ли их ответ примерно правильным, путем оценки.

Помимо бесплатных печатных рабочих листов и вопросов на деление, вы также можете загрузить набор бесплатных вопросов SAT по делению и умножению, чтобы расширить свою практику.

Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч учащихся начальной школы. С 2013 года мы помогли более 130 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.

Обучение в начальной школе ориентировано на потребности каждого ребенка и строго соответствует национальной учебной программе.

Длинная дивизия – Шаги | Метод

Длинное деление — это метод деления больших чисел, который разбивает задачу деления на несколько последовательных шагов. Как и в обычных задачах на деление, делимое делится на делитель, который дает результат, известный как частное, а иногда и остаток. Давайте узнаем больше о метод длинного деления

вместе с его шагами и примерами в этой статье.

1.	Что такое метод длинного деления?
2.	Части длинной дивизии
3.	Как сделать длинное деление?
4.	Часто задаваемые вопросы о Long Division

Что такое метод длинного деления?

В математике длинное деление — это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов.

Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующее длинное деление, чтобы увидеть делитель, делимое, частное и остаток.

Части длинной дивизии

При выполнении деления в длинное число нам необходимо знать важные части деления в длинное число. Основные части длинного деления можно перечислить следующим образом:

• Дивиденд
• Делитель
• Частное
• Остаток

В следующей таблице описаны части длинного деления со ссылкой на приведенный выше пример.

Дивиденд	Число, которое нужно разделить.	75
Делитель	Число, на которое делится делимое.	4
Частное	Результат деления.	18
Остаток	Оставшаяся часть или число, оставшееся после деления, которое нельзя разделить дальше.	3

Как сделать длинное деление?

Деление — одна из четырех основных математических операций, остальные три — сложение, вычитание и умножение. В арифметике длинное деление — это стандартный алгоритм деления больших чисел, разбивающий задачу деления на ряд более простых шагов. Давайте узнаем о шагах, которые выполняются в длинном делении.

Длинные шаги деления

Чтобы выполнить деление, нам нужно понять несколько шагов. Делимое отделяется от делимого правой скобкой 〈)〉 или вертикальной чертой 〈|〉, а делимое отделяется от частного винкулумом (чертой чертой). Теперь давайте выполним шаги длинного деления, приведенные ниже, чтобы понять процесс.

• Шаг 1: Возьмите первую слева цифру делимого. Проверьте, больше ли эта цифра делителя или равна ему.
• Шаг 2: Затем разделите на делитель и запишите ответ сверху как частное.
• Шаг 3: Вычтите результат из цифры и запишите разницу ниже.
• Шаг 4: Запишите следующую цифру делимого (если она есть).
• Шаг 5: Повторите тот же процесс.

Давайте взглянем на приведенные ниже примеры для лучшего понимания концепции. При делении в длинное мы можем столкнуться с проблемами, когда остатка нет, а в некоторых вопросах есть остаток. Итак, сначала научимся делению, при котором мы получаем остаток.

Деление с остатком

Случай 1: Когда первая цифра делимого больше или равна делителю.

Пример: Разделить 435 ÷ 4

Решение: Шаги этого длинного деления приведены ниже:

• Шаг 1: Здесь первая цифра делимого равна 4, и оно равно 4. делитель. Итак, 4 ÷ 4 = 1. Итак, 1 записывается сверху как первая цифра частного.
• Шаг 2: Вычтите 4 – 4 = 0. Уменьшите вторую цифру делимого и поместите ее рядом с 0.
• Шаг 3: Теперь 3 < 4. Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и ставим ее рядом с 3.
• Шаг 4: Итак, у нас есть 35 в качестве нового делимого. 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это.
• Шаг 5: Запишите 8 в частном. Вычесть: 35 – 32 = 3.
• Шаг 6: Теперь 3 < 4. Таким образом, 3 — остаток, а 108 — частное.

Случай 2: Когда первая цифра делимого меньше делителя.

Пример: Разделить 735 ÷ 9

Решение: Разделим это, используя следующие шаги.

• Шаг 1: Так как первая цифра делимого меньше делителя, в частном поставьте ноль и запишите следующую цифру делимого. Теперь рассмотрим первые 2 цифры, чтобы продолжить деление.
• Шаг 2: 73 не делится на 9, но мы знаем, что 9 × 8 = 72, так что действуем.
• Шаг 3: Напишите 8 в частном и вычтите 73 – 72 = 1.
• Шаг 4: Сбросьте 5. Число, которое будет рассматриваться сейчас, равно 15.
• Шаг 5: Поскольку 15 не делится на 9, но мы знаем, что 9 × 1 = 9, берем 9.
• Шаг 6: Вычесть: 15 – 9 = 6. Запишите 1 в частном.
• Шаг 7: Теперь 6 < 9. Таким образом, остаток = 6 и частное = 81.

Случай 3: Это случай деления в большую сторону без остатка.

Деление без остатка

Пример: Разделить 900 ÷ 5

Решение: Разделим это, используя следующие шаги.

• Шаг 1: Будем считать первую цифру делимого и она на 5. Здесь будет 9÷ 5.
• Шаг 2: Теперь 9 не делится на 5, но 5 × 1 = 5, поэтому запишите 1 как первую цифру в частном.
• Шаг 3: Запишите 5 под 9 и вычтите 9 – 5 = 4.
• Шаг 4: Поскольку 4 < 5, мы уменьшим 0 из делимого до 40.
• Шаг 5: 40 делится на 5, а мы знаем, что 5 × 8 = 40, поэтому запишите 8 в частном.
• Шаг 6: Запишите 40 под 40 и вычтите 40 – 40 = 0,
• Шаг 7: Снизьте следующий 0 из делимого. Поскольку 5 × 0 = 0, мы пишем 0 как оставшееся частное.
• Шаг 9: Следовательно, частное = 180 и после деления не остается остатка, то есть остаток = 0.

Задачи на деление в длинное число также включают задачи, связанные с многочленами в длинное деление и делением в длинное с десятичными дробями.

Длинное деление многочленов

Если нет общих множителей между числителем и знаменателем или если вы не можете найти множители, вы можете использовать процесс длинного деления, чтобы упростить выражение. Для получения дополнительной информации о полиномах деления в длину посетите страницу Полиномы деления.

Деление в длинное с десятичными дробями

Деление в длинное с десятичными дробями можно легко выполнить так же, как и обычное деление. Для получения дополнительной информации о делении в длинное с десятичными дробями посетите страницу Деление десятичных дробей.

Советы и рекомендации по делению в длину:

Ниже приведены несколько важных советов и рекомендаций, которые помогут вам при работе с делением в длину:

• Остаток всегда меньше делителя.
• При делении делитель не может быть равен 0,
• Деление — это повторное вычитание, поэтому мы можем проверить наше частное и повторными вычитаниями.
• Мы можем проверить частное и остаток от деления, используя формулу деления: Делимое = (Делитель × Частное) + Остаток.
• Если остаток равен 0, то мы можем проверить наше частное, умножив его на делитель. Если произведение равно делимому, то частное верно.

☛ Статьи по теме

• Формула длинного дивизиона
• Длинное деление многочленов
• Полное деление с остатками Рабочие листы
• Полное деление без остатка Рабочие листы
• Длинное деление с двузначными делителями Рабочие листы
• Калькулятор длинного деления

Часто задаваемые вопросы о Long Division

Что такое длинное деление в математике?

Длинное деление — это процесс деления больших чисел удобным способом.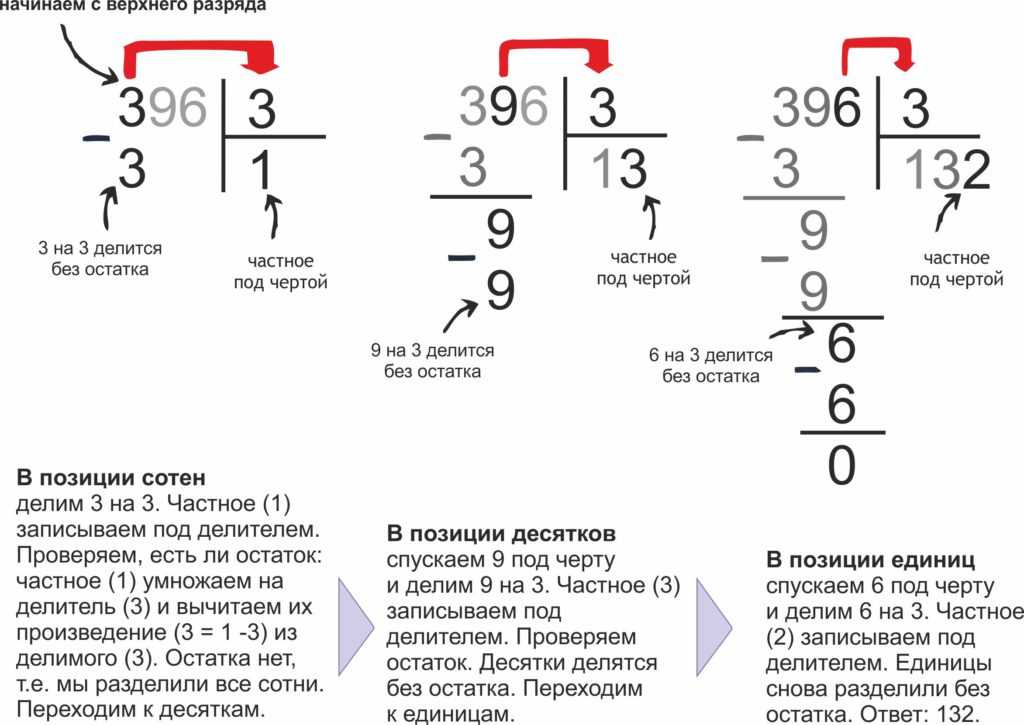 Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком.

Как сделать длинное деление?

Следующие шаги объясняют процесс деления в большую сторону:

• Запишите делимое и делитель на соответствующие позиции.
• Возьмите первую слева цифру делимого.
• Если эта цифра больше или равна делителю, то разделите ее на делитель и сверху запишите ответ как частное.
• Запишите произведение под делимым и вычтите результат из делимого, чтобы получить разницу. Если эта разность меньше делителя, а в делимом не осталось чисел, то это считается остатком и производится деление. Однако, если в делимом больше цифр, которые нужно перенести вниз, мы продолжаем тот же процесс, пока в делимом не останется больше цифр.

Каковы этапы длинного деления?

Ниже приведены 5 основных шагов деления в большую сторону. Например, давайте посмотрим, как мы делим 52 на 2.

• Шаг 1: Рассмотрим первую цифру делимого, которая в этом примере равна 5. Здесь 5 > 2. Мы знаем, что 5 не делится на 2.
• Шаг 2: Мы знаем, что 2 × 2 = 4, поэтому запишем 2 как частное.
• Шаг 3: 5 – 4 = 1 и 1 < 2 (Записав произведение 4 под делимым, мы их вычтем).
• Шаг 4: 1 < 2, поэтому мы уменьшаем 2 из делимого и теперь получаем 12 в качестве нового делимого.
• Шаг 5: Повторяйте процесс до тех пор, пока не получите остаток меньше делителя. 12 делится на 2, так как 2 × 6 = 12, поэтому мы пишем 6 в частном, а 12 – 12 = 0 (остаток).

Следовательно, частное равно 26, а остаток равен 0.

Как выполнить длинное деление с двумя цифрами?

При длинном делении на 2 цифры считаем обе цифры делителя и проверяем на делимость первых двух цифр делимого. Если первые 2 цифры делимого меньше делителя, то учитывают первые три цифры делимого. Продолжайте деление так же, как мы делим обычные числа.

Что такое длинное деление многочленов?

В алгебре длинное деление многочленов — это алгоритм деления многочлена на другой многочлен той же или меньшей степени. Например, (4x ² – 5x – 21) является многочленом, который можно разделить на (x – 3) по определенным правилам, что даст в результате 4x + 7 в качестве частного.

Как выполнить длинное деление с десятичными дробями?

Длинное деление с десятичными знаками выполняется так же, как и обычное деление. Это следует шагам, указанным ниже:

• Запишите деление в стандартной форме.
• Начните с деления целой части числа на делитель.
• Поместите десятичную точку в частном над десятичной точкой делимого.
• Опустите цифры на десятых разрядах, т. е. цифру после запятой.
• Разделите и запишите другую цифру по порядку.
• Деление до тех пор, пока не закончатся все цифры делимого и в остатке не получится число меньше делителя или 0.