Как научиться делить быстро: Как делить в уме 🚩 как быстро делить числа 🚩 Математика - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Деление в столбик ➗ примеры и правила, как научиться

Деление с остатком

Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:

Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.

Деление трехзначного числа на однозначное

Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:

322 — делимое или то, что необходимо поделить;
7 — делитель или то, на что нужно поделить:
частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.

Для этого рассмотрим первую цифру делимого. Она меньше делимого: 3 < 7 — не подходит. Рассмотрим теперь две первые цифры делимого: 32 ﹥7. Подходит!

Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.

Важно

Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.

Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Деление трехзначного числа на двузначное с примерами

Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.

Пример №1.

Разделим трехзначное число 324 на двузначное 81.

Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.

Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!

Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.

Ответ: 324:81=4.

Пример №2.

Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.

Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.

Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.

Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.

Ответ: 368:92=4.

Как делить однозначные и многозначные числа в столбик с остатком

Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.

Пример №1

Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.

Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.

Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.

Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.

Ответ: 19:5=3

Пример №2.

Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.

Шаг 1.

Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.

Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.

Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.

Ответ: 29:9=4(5)

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Примеры на деление в столбик для 3 класса

Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье.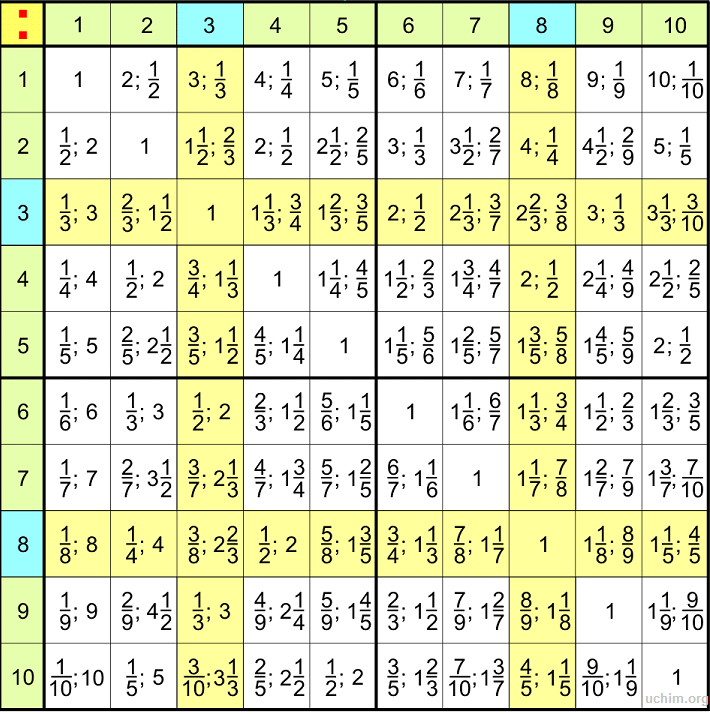 Это задание со звездочкой.

Легкий уровень

Средний уровень

Сложный уровень

27:3=

48:4=

56:8=

72:9=

95:5=

270:15=

504:14=

315:5=

728:8=

855:9=

1749:11=

1080:45=

3888:72=

5248:64=

4818:66=

Ответы:

легкий уровень: 9; 12; 7; 8; 19;
средний уровень: 18; 36; 63; 91; 95;
сложный уровень: 159; 24; 54; 82; 73.

Если вам интересно, как еще можно научить ребенка делить двузначные и трехзначные числа, приглашаем на вводный урок в Skysmart! На на онлайн-курсах по математике для детей можно закрепить тему «Деление в столбик» и разобраться в других разделах из школьной программы.

Деление

Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.

Что такое деление?

Деление это действие, позволяющее что-либо разделить.

Деление состоит из трёх параметров: делимого, делителя и частного.

Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.

Пусть у нас имеются 4 яблока:

Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:

Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:

В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.

Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4

В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».

Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2

Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷

На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.

Деление с остатком

Остаток — это то что осталось от действия деления неразделённым.

Например, пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Можно проверить это умножением:

(2 × 2) + 1 = 5

Допустим, имеются пять яблок:

Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не полýчится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:

Деление уголком

Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.

Прежде чем делить уголком, человек должен знать:

обычное деление маленьких чисел;
деление с остатком;
умножение в столбик;
вычитание в столбик.

Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:

Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:

Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:

Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:

Пример 2. Найти значение выражения 8 : 3

Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.

Сначала запишем данное выражение уголком:

Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:

В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:

Далее из 8 вычитаем 6. Полученное число и будет остатком:

8 : 3 = 2 (2 в остатке)

Проверка:

(2 × 3) + 2 = 6 + 2 = 8

Деление многозначного числа на однозначное

Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.

В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.

Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.

Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то её надо разделить на делитель, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то надо разделить их на делитель, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.

Сложно? Ни чуть, если мы разберём несколько примеров.

Пример 1. Найти значение выражения 25 : 3

25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:

Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:

Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.

Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:

Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:

25 : 3 = 8 (1 в остатке)

Проверка:

(8 × 3) + 1 = 24 + 1 = 25

Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.

В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше чем три, поэтому деление завершено. Последний остаток мéньший делителя говорит о том, что он не содержит чисел равных делителю.

В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек.

Пример 2. Разделить 326 на 4.

Смóтрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да. Значит можно выполнять деление.

Записываем уголком данное выражение:

Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:

Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:

Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:

Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:

Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:

Записываем единицу в правом уголке нашего ответа:

Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:

Затем из 6 вычитаем 4, получаем число 2, которое является остатком:

Получили 326 : 4 = 81 (2 в остатке)

Проверка: (81 × 4) + 2 = 324 + 2 = 326

Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.

Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.

А в примере 25 : 3 первое неполное делимое было 25.

Пример 3. Найти значение выражения 384 : 5

Записываем данное выражение в уголком:

Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:

Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:

Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.

Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:

Умножаем 7 на 5, получаем 35 и записываем его под 38:

Теперь из 38 вычитаем 35, получим 3:

Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:

Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:

Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:

Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:

Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5

384 : 5 = 76 (и 4 в остатке)

Проверка:

(76 × 5) + 4 = 380 + 4 = 384

Пример 4. Найти значение выражения 8642 : 4

Этот пример немного посложнее. Записываем уголком данное выражение:

Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2

Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:

Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.

Далее сносим цифру 6 и делим её на делитель, получаем 1

Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:

Получили остаток 2. Это остаток, который остался от деления 6 на 4.

Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6

Умножаем 6 на 4, получаем 24. Записываем это число под 24

Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2

Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.

Поэтому два разделить на четыре это ноль:

Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:

Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:

8642 : 4 = 2160 (2 в остатке)

Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642

Деление чисел, у которых на конце 0

Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.

Например, разделим 120 : 3

Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:

Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.

120 : 3 = 40

Проверка 40 × 3 = 120.

Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:

12 : 3 = 4 (делимое без нулей на конце)

120 : 3 = 40 (здесь у делимого один ноль)

1200 : 3 = 400 (здесь у делимого два нуля)

12000 : 3 = 4000 (здесь у делимого три нуля)

В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.

Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5

Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:

Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.

Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.

Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:

1000 + 400 = 1400

Можно по-отдельности разделить 1000 на 5 и 400 на 5:

1000 : 5 = 200

400 : 5 = 80

и сложить полученные результаты:

200 + 80 = 280

Итого: 1400 : 5 = 280

Решим этот же пример уголком:

Деление многозначного числа на многозначное

Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так-то просто.

Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.

Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 500, 600, 1000, 13000

Любое число можно превратить в круглое. Для этого первую цифру, образующую самый старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.

Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10

Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.

Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.

Превратим число 13735 в круглое число. Первая цифра 1 образуют старший разряд (разряд десятков тысяч) — эту цифру оставляем без изменений, а остальные цифры заменяем нулями. В итоге получаем 10000.

Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут рассмотрены более подробно.

Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.

Пример 1. Найти значение выражения 88 : 12

Записываем данное выражение уголком:

Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.

Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».

Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число которое меньше делимого, но очень близко к нему или равно ему.

Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12

Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.

Пробуем следующее число. Допустим частное равно 5

Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.

Попробуем сразу взять по 8

На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7

Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.

88 : 12 = 7 (4 в остатке)

Проверка: (12 × 7) + 4 = 84 + 4 = 88

Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.

Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.

Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.

Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.

В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.

Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:

800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)

800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)

900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)

400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)

320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)

Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.

Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.

Для начала превращаем делимое и делитель в круглые числа.

Круглым числом для 88 будет число 80.

А круглым числом для 12 будет число 10.

Теперь делим полученные круглые числа:

80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:

Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.

Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.

Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:

Как видно, этим способом мы решили этот пример намного быстрее.

Пример 2. Найти значение выражения 1296 : 144

Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:

Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.

Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.

Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144

Десятка не подходит, поскольку при умножении получается число, которое больше делимого.

Попробуем взять по 9, уменьшив десятку на единицу.

Проверяем девятку. Для этого умножаем её на делитель:

Красота! Полученное число оказалось не только ближе к делимому, но и равным ему.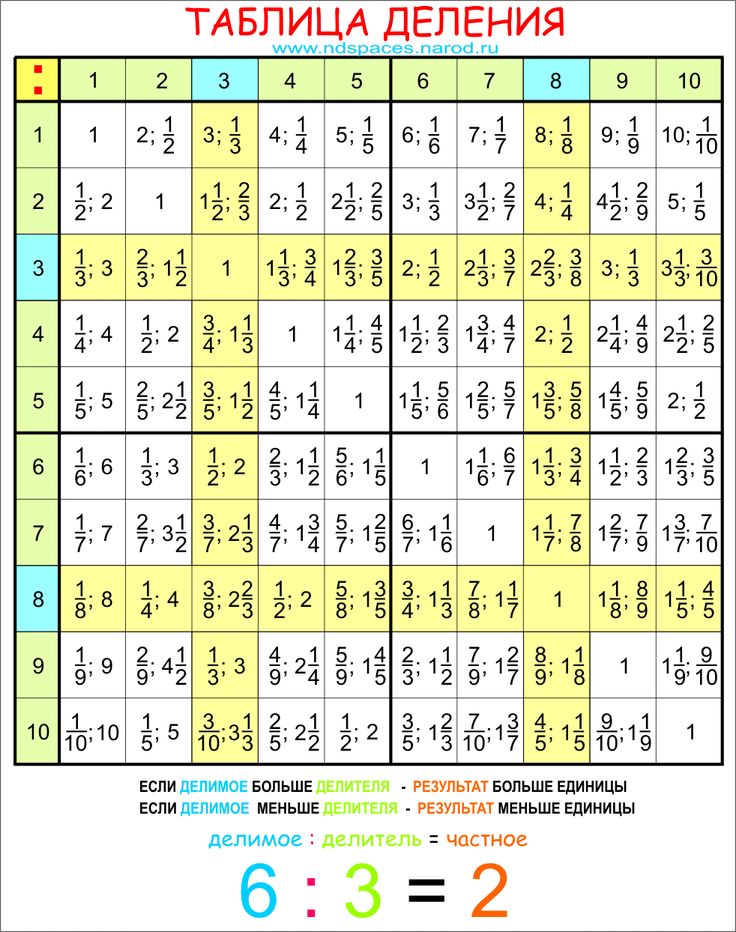 Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296

1296 : 144 = 9

Проверка: 144 × 9 = 1296

Пример 3. Попробуем решить большой и сложный пример 227 492 : 331

Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.

Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300

Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:

Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:

Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.

Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:

288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:

Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:

Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:

Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.

Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241

241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:

Теперь делим 2412 на 331. Возьмём по 7

Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:

227 492 : 331 = 687 (95 в остатке)

Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492

На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.

Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Показать решение

Задание 2. Выполните деление:

Решение:

Показать решение

Задание 3. Выполните деление:

Решение:

Показать решение

Задание 4. Выполните деление:

Решение:

Показать решение

Задание 5. Выполните деление:

Решение:

Показать решение

Задание 6. Выполните деление:

Решение:

Показать решение

Задание 7. Выполните деление:

Решение:

Показать решение

Задание 8. Выполните деление:

Решение:

Показать решение

Задание 9. Выполните деление:

Решение:

Показать решение

Задание 10. Выполните деление:

Решение:

Показать решение

Задание 11. Выполните деление:

Решение:

Показать решение

Задание 12. Выполните деление:

Решение:

Показать решение

Задание 13. Выполните деление:

Решение:

Показать решение

Задание 14. Выполните деление:

Решение:

Показать решение

Задание 15. Выполните деление:

Решение:

Показать решение

Задание 16. Выполните деление:

Решение:

Показать решение

Задание 17. Выполните деление:

Решение:

Показать решение

Задание 18. Выполните деление:

Решение:

Показать решение

Задание 19. Выполните деление:

Решение:

Показать решение

Задание 20. Выполните деление:

Решение:

Показать решение

Задание 21. Выполните деление:

Решение:

Показать решение

Задание 22. Выполните деление:

Решение:

Показать решение

Задание 23. Выполните деление:

Решение:

Показать решение

Задание 24. Выполните деление:

Решение:

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

10 простых трюков с дивизионами | Быстрые советы для больших и малых чисел

Автор: Вирджиния | 10 ноября 2021 г. , 10:17

После освоения этих трюков с делением базовая математика станет проще простого! Если вашему ученику нужна помощь в быстрых вычислениях или он запоминает математические факты, полезно иметь наготове один или два «математических лайфхака»!

Навыки деления являются одним из основных элементов элементарной математики по уважительной причине: чувство числа и логические навыки, которые учащиеся приобретают, обучаясь делению, являются ключевыми для развития их математических навыков. Как и практически любой предмет STEM, математические понятия строятся друг на друге, как ступеньки лестницы.

Чтобы перейти на следующий уровень, необходимо изучить концепции, которые помогут им понять, что их ждет впереди! Деление, как и умножение и построение квадратных уравнений, является основным навыком в наборе инструментов любого начинающего математика.

Тем не менее, делить не всегда легко! Особенно при работе со все более и более сложными числами обучение делению может быть разочаровывающим и требует столько же ластика, сколько и карандаша.

Итак, давайте немного избавимся от стресса, применив несколько полезных трюков с делением, которые удобно носить с собой в школе и в любой ситуации, требующей элементарной математики!

Полезные приемы деления

Мы познакомимся с сокращениями деления чисел от 1 до 10, которыми будет здорово поделиться с детьми. Это, возможно, не только повысит их уверенность (и, надеюсь, результаты викторины), но и подготовит их к быстрому умственному расчету для следующего соревнования по математике.

И нельзя отрицать, что сейчас самое подходящее время для многих учеников получить дополнительную поддержку по математике и репетиторство!

Согласно недавнему исследованию McKinsey, учащиеся отстают в математике примерно на пять месяцев из-за воздействия COVID-19.. Итак, немного творчества и несколько советов и хитростей не помешают, верно?

Наряду с повседневными способами сделать математику увлекательной, поощрение детей попробовать несколько математических игр и занятий может иметь большое значение для того, чтобы наверстать упущенное и даже получить удовольствие от занятий по математике!

Имея это в виду, вот несколько сокращений деления, которые могут помочь учащимся узнать, как работают числа, и освоить математические строительные блоки.

Деление на 1

Важно помнить (извините за каламбур): любое число, деленное на 1, является само числом! Например, 300 разделить на 1 равно 300.

Деление на 2

Каждое четное число делится на 2; это любое число, заканчивающееся на 0, 2, 4, 6 или 8. Например, 566 можно разделить на 2 без остатка: 283.

Деление на 3

Вот менее известный забавный факт: если сумма (общая числа, сложенного вместе) в данном числе можно разделить на три, так что число может!

Вот пример: число 21. 2+1 = 3. 21 разделить на 3 = 7.

Сомневаетесь? Давайте посмотрим на большее число: 423. 4+2+3 = 9.. 423 разделить на 3 = 141.

Деление на 4

При делении на 4 смотрите на две последние цифры числа. Эти две цифры делятся на 4? Это означает, что все число также!

Например, давайте посмотрим на безумно длинное число, такое как 5601120. 20 делится на 4, как и 5601120! 5601120, деленное на 4, равно 1400280.

Делим на 5

Еще одно важное правило: любое число, оканчивающееся на 0 или 5, всегда делится на 5. Как 10 делится на 5, так и 82984780 (частное 16 596 956).

Деление на 6

Этот трюк с делением состоит из двух шагов, но стоит потренироваться. Если приведенные выше правила для 2 и 3 верны, то вы можете разделить число и на 6.

Например, если сумма цифр числа делится на 3 и заканчивается четным числом, оно будет делиться на 2, 3 и 6. 960 разделить на 3 равно 320.

Деление на 7

Это один немного сложнее и работает с числами, состоящими из трех и более цифр, так что потерпите! Чтобы проверить, делится ли число на 7, начните с последней цифры числа. Удвойте это число, затем вычтите удвоенное число из оставшихся двух цифр числа.

Вот пример: допустим, число 161. Сначала удвойте 1, чтобы получить 2. Если вы вычтете 2 из 16, вы получите 14, которое делится на 7. Следовательно, мы можем сказать, что 161 делится на 7. И когда мы проверяем работу, конечно же, 161 разделить на 7 равно 23!

Деление на 8

Это еще один прием деления, который работает с большими числами. Если последние три цифры образуют число, которое делится на 8, все число также будет делиться на 8. Например, 9180, последние три цифры – как их собственное число – могут делиться на 8, как и 9.128. 9128 разделить на 8 равно 1141!

Деление на 9

Если сумма всех цифр числа делится на девять, то само число делится на девять. Например, сумма числа 72 равна 9, а при делении на девять получается 8!

Деление на 10

Аналогично трюку с делением на пять, если число оканчивается нулем, то оно делится на 10. В качестве бонуса ответ, который ищут делители, будет существовать в числе уже в сотнях, разряд десятков и единиц. Например, 250 разделить на 10 равно 25.

Продвигайтесь вперед в уравнении обучения

После трудностей последнего учебного года мы знаем, что на родителей оказывается большое давление, чтобы вернуть детей в нужное русло.

Не бойся, мы здесь, чтобы помочь!

Наряду с экспертными онлайн-уроками по математике для детей и подростков по темам – от начальной алгебры до исчисления и тригонометрии, у нас есть множество ресурсов для детей и родителей!

От учебных пособий по математике до учебных пособий и многого другого — ознакомьтесь с этим тщательно подобранным контентом, предназначенным для поддержки вашего начинающего математика:

Как решить для x учебник
Лучшие способы делать заметки
Как преобразовать дроби в десятичные

Вирджиния

Вирджиния начала работать с iD Tech в Денверском университете в 2015 году и с тех пор наслаждается каждой минутой! Бывший учитель по профессии, она имеет степень магистра в области образования и любит работать, чтобы вдохновлять следующее поколение с помощью STEM. Вне офиса вы обычно можете найти ее читающей хорошую книгу, борющейся на коврике для йоги или исследующей Скалистые горы.

Как делать деление в длинное: простое пошаговое руководство с иллюстрациями

Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость:

Как сделать деление в большую сторону.

Исследование 2012 года, опубликованное в журнале Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают ли они на уроках математики более высокого уровня — даже после учета различных социально-экономических факторы. Никакого давления, верно? Если при мысли об обучении делению на длинные лады у вас холодный пот и липкие ладони, не беспокойтесь — мы сделали всю работу за вас.

Как выполнить деление в длинное за шесть шагов

1.

Повторить

Первый шаг, который вы должны сделать, это шаг назад.

Для ученика 4-го класса деление в большую сторону представляет собой сложную смесь различных операций. Чтобы успешно научиться выполнять деление в большую сторону, им необходимо повторить эти фундаментальные понятия.

Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов, определяющих будущие успехи учащегося в математике. Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».

Убедитесь, что ваши ученики понимают, что умножение — это результат многократного сложения, а деление — это просто противоположное — многократное вычитание.

Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство числа. Запланируйте занятия, в которых учащимся будет предложено создать «семейство фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.

Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в учебе и развить уверенность в математике, прежде чем продолжить.

2. Начните с простого

Давайте начнем с урока словарного запаса. Уравнение деления на деление состоит из множества частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать.

Дивиденд — это число в правой части уравнения под чертой. Он представляет собой сумму, которую нужно разделить.

Делитель — это число слева — оно выполняет деление.

Частное — номер сверху. Он представляет собой ответ или количество единиц в каждом разряде после завершения уравнения.

Остаток — это число вверху справа. Он представляет оставшиеся единицы, которые не могут быть равномерно разделены на частное. Во-первых, введите уравнение, которое не имеет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что выучили:

Спросите учащихся, сколько раз 2 умещается в 4. Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?

Как только они придут к правильному ответу, поставьте 2 выше 4. Затем повторите шаг со второй цифрой в делимом.

Используйте эти простые уравнения, чтобы усилить позиционное значение. Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.

Вместо того, чтобы сразу перейти к уравнению с остатками, начните с другого предметного урока . Разделите учащихся на группы по три, четыре или шесть человек и дайте каждой группе по 50 ватных шариков (или мармеладок, или помпонов, или зефира — любой маленький предмет, доступный в вашем классе).

Попросите учеников разделить предметы так, чтобы у каждого члена группы было одинаковое количество предметов, а затем наблюдайте и ждите.

В конце концов, они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то предметы. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в большую сторону с помощью 9.0103 остатки .

Сначала покажите учащимся задачу с остатком в единицах:

Теперь начните со столбца десятков и проработайте задачу: 5 входит в 5 ровно один раз, так что там ничего не осталось. Но сколько раз 5 входит в 7, и что вы делаете с остатками?

Покажите учащимся новые шаги:

Разделить столбец единиц делимое на делитель
Умножить делитель на частное в нужном месте столбец
Вычтите произведение из столбца единиц

Оставшееся число — это остаток. Обязательно смоделируйте несколько задач всем классом, чтобы учащиеся могли начать понимать этапы и то, как правильно записывать свои ответы.

Это хорошее время на уроке, чтобы научить учащихся проверять свои ответы. Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.

4. Остаток в десятках

Теперь пришло время учащимся решить задачи, в которых делитель не вписывается в столбец десятков или единиц. Шаги более или менее такие же, за исключением одного нового дополнения:

Разделить делимое в столбце десятков на делитель
Умножить делитель на частное в столбце десятков
Вычесть произведение из делителя
Сократите делимое в столбце единиц и повторить .

Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому найдите время, чтобы смоделировать задачи на доске. Обсудите, почему эти шаги работают, и помогите им понять, какую важную роль в этом процессе играет значение места.

5. Постепенно вводите большие числа

Вот и все. Или это?

Дайте учащимся освоиться с формулой и поработать над более мелкими задачами. Когда они обретут уверенность и начнут понимать, как выполнять деление в большую сторону, начните предлагать им задачи с трехзначным делимым, а затем задачи с двузначным делителем.

Напомните учащимся, что шаги остаются одинаковыми, независимо от того, насколько велика задача , и предложите им использовать лист бумаги, чтобы «угадать и проверить» свое умножение по ходу дела. Это хороший момент, чтобы убедиться, что у них нет проблем и что они полностью понимают взаимосвязь деления с разрядным значением и умножением.

Посмотрите это видео от Khan Academy:

0104
Если вы рассмотрели весь свой контент на первых пяти шагах, поздравляем! Предложите учащимся продолжать практиковаться в делении больших и малых чисел в длинную и укреплять связь между делением и другими математическими понятиями, которые они изучают. Но процесс еще не завершен — учащиеся должны понять, как делать длинную деление с десятичной дробью. Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед.
Предложите учащимся решить задачу, как обычно. Когда они дойдут до шага, на котором они обычно останавливаются с остатком, попросите их поставить десятичную точку в конце частного и делимого и написать несколько нулей после делимого.
Предложите им продолжить обычные шаги деления на один или два разряда, опуская нули.
Соедините десятичную дробь с дробью. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.
Как выполнить деление в длинное число (без деления в длинное число)
Поздравляем! Ваш модуль подходит к концу, и вы успешно научили своих учеников выполнять деление в большую сторону.
Но знаете ли вы, что существует несколько способов деления больших чисел? Обучение учащихся другим способам проверки своей работы является важной частью математических стандартов Common Core и может улучшить понимание учащимися того, что на самом деле означает деление в столбцах в данном контексте.
Плоскостные модели
Плоскостные модели — отличный способ для визуалов понять и осмыслить деление, а также улучшить чувство числа.
Этот метод использует сетку, чтобы представить процесс деления как задачу площади: например, 148÷4 будет разделен на сетку высотой 4 единицы, площадью 148 квадратных единиц и неизвестным количеством единиц ширины.
Учащиеся разбивают сетку на более удобные области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100÷4 равно 25, 40÷4 равно 10, а 8÷4 равно 2. Эти числа идут вверху модели области и могут быть сложены, чтобы получить ответ.
Частичное частное
Подобно модели области, частичное частное побуждает учащихся разбивать вопросы на деление на «более понятные» части. Это помогает учащимся понять, что деление — это нахождение того, сколько раз одно число может перейти в другое число.
Поставьте задачу (в данном случае 450÷23) как уравнение деления на деление. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира.
Спросите, сколько раз 23 входит в число 400, но не ищите точное ближайшее число: сделайте его простым для работы, например, 230 (десять раз). Вычтите 230 из 450 и поставьте 10 справа, чтобы отслеживать результат.
Возьмите разницу и вычтите ее из делимого. Ответ должен быть 220.
Спросите, сколько раз 23 входит в 220. 5 x 23 равно 115, так что вычтите это из 220 и запишите 5.
Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное.
Частичные частные обладают гибкостью, которой нет в длинном делении. Длинное деление нужно делать точно, но с частичными частными можно просто несколько раз вычесть делитель из делимого и все равно прийти к правильному ответу.
Используйте этот метод, чтобы закрепить позиционное значение и концепцию деления как многократного вычитания.
Упражнения на деление в длинное число
Лучший способ научиться делению в длинное число – практиковаться, практиковаться и еще раз практиковаться.
Вот список из восьми заданий, которые заинтересуют ваш класс делением в длинную и помогут развить прочные математические навыки.
1. Prodigy
Prodigy — это забавный и увлекательный ресурс для занятий в классе или дома на длинные дистанции. Учащиеся исследуют мир, полный приключений, где успех зависит от правильных ответов на математические вопросы.
С помощью панели управления учителя вы можете предоставлять контент, ориентированный на урок, в зависимости от оценки, навыков или ученика. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании .
Поощряйте своих учеников практиковать все математические навыки, которые они изучили в классе, включая деление в столбик. Вот как вы можете использовать Prodigy для:
усиления уроков в классе
разнообразия материалов по математике
Проведение формирующего оценивания
Учащиеся играют в увлекательную игровую платформу, где они могут собирать питомцев, выполнять квесты и сражаться с друзьями. И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!
Зарегистрируйтесь сейчас
2. Деление в натуральную величину
Оживите математику с помощью практической головоломки с делением в натуральную величину. Вырежьте квадраты из цветной бумаги со всеми числами, которые нужны учащимся для решения задачи на деление в длину от начала до конца. Используйте клейкую ленту, чтобы разделить линии на полу, и раздайте учащимся пронумерованные карточки.
Начав с заданного уравнения, попросите учащихся разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и подумать о своих шагах, и это особенно полезно для класса, который все еще хочет освоить шаги умножения.
3. Бинго с длинными дивизионами
Бинго не просто так является классикой. Каждая из цифр в листе учащегося должна соответствовать вопросу, который вы задали перед классом. Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!
Бросьте вызов своим учащимся, но убедитесь, что вы уделяете этому упражнению достаточно времени — некоторые учащиеся могут испытывать трудности с быстрым решением задач и могут расстраиваться или совершать ошибки, если не смогут справиться с заданием.
4. Книги по математике
Повысьте уровень грамотности и обучения математике с помощью забавных книг, посвященных сложным математическим понятиям. Используйте их, чтобы объяснить учащимся деление и остатки в веселой и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут учиться выполнять деление в столбик.
Некоторые книги по математике, которые охватывают подразделение:
Остальная часть одного от Elinor J. Pinczes
Thirteen от Matthew McElligott
The Doirbell Rang By Hutchint
The Doorbell Rang By Hutchint
.
В длинном делении много шагов, и их нужно выполнять в правильном порядке, чтобы получить правильный ответ. Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости.
Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в большую сторону — разделить , умножить , вычесть и записать — чтобы стимулировать творчество в вашем классе.
Предложите им создать постер, песню, мнемоническое устройство или даже небольшую сценку, которую они могут представить своим одноклассникам. Если они заинтересованы в том, чтобы найти способ запомнить шаги, они, скорее всего, быстро научатся.
6. Реле длинного деления
Превратите практику длинных дивизий в веселую классную игру с эстафетами длинных дивизий. Разделите свой класс на команды и сделайте карточки с задачами на деление в длину.
Объедините учеников в группы. Каждая группа получает карточку для начала, и первые учащиеся выполняют первый набор шагов для своей проблемы.
Когда они закончат, второй учащийся ищет ошибки и продолжает решать задачу. Если они решат задачу, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой задачей.
Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!
7. Сундук с сокровищами
Это задание — веселый способ для вашего класса отпраздновать завершение отряда в дивизионе. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решить в группах, чтобы «открыть» коробку.
В качестве дополнительной задачи сделайте это кодом: пусть каждое частное соответствует букве алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку.
8. Генератор рабочих листов
Рабочие листы — это проверенный материал на уроках математики. К счастью для вас, существует множество веб-сайтов, которые сделают всю работу за вас и сгенерируют пользовательский рабочий лист, который даст вашим ученикам возможность практиковаться в делении в большую сторону. Вот некоторые из наших любимых:
Помощь в математике
Математические пособия
Гениальный рабочий лист
Заключительные мысли об обучении учащихся делению в длинную
Самое важное, что следует помнить при обучении студентов делению в столбик, это не торопиться с изучением материала.