Как научиться делить столбиком?
Одним из наиболее важных этапов обучения вашего ребенка математическим операциям является обучение действиям деления простых чисел. Для обучения делению ребенка, нужно, чтобы к моменту обучения он уже освоил и хорошо понимал такие математические действия, как вычитание, сложение.
Кроме того, важно иметь четкое представление о самой сущности таких действий, как деление и умножение. Таким образом, он должен понимать, что в действии с делением заключается метод разделения чего-либо на равные доли. В заключение необходимо также обучиться операциям по умножению и хорошо знать таблицу умножения.
Обучаемся операции по делению на части
На данном этапе лучше сформировать понимание того, что главное в процессе деления, это разделение чего-то на равные части. Самым простым способом научиться этому для ребенка, это будет предложить ему поделить несколько предметов между ним и членами семьи или друзьями.
Важным моментом здесь считается проводить операции по делению четных количеств предметов. Такое действие окажется полезным на дальнейшем этапе, когда ребенку будет необходимо понимание того, что разделение, это действие, обратное умножению.
Делим и умножаем, при помощи таблицы умножения
Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.

Например: 2 умножить на 4 будет восемь. Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения.
Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.
Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное». Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!
Разделяем столбиком – легко и быстро
Перед тем, как начинать обучение следует вспомнить с ребенком, какое название имеет каждое число в процессе операции разделения. Главное, научиться быстро и безошибочно научиться определять данные категории.
Наглядный пример:
Попробуем разделить 938 на 7. В этом приведенном примере число 938 будет являться делимым, а число 7 будет делителем. В результате действия, ответ будет называться частное.
- Необходимо записать числа, разделив их «уголком».
- Предложите ученику из наименьшего числа делимого выбрать то, что больше делителя. Из цифр 9, 3, 8, наибольшим будет цифра 9. Предложите проанализировать, сколько семерок может содержать в цифре 9. Одним правильным ответом здесь будет только один. Первым результатом записываем 1.
- Оформляем деление в столбик.
Умножим делитель 7 на 1, ответ будет 7. Полученный результат вписываем под первое число нашего делимого, затем вычитаем в столбик. Таким образом, из 9 отнимаем 7 и в ответе получаем 2. Это тоже записываем.

- Видим число, получившееся меньше делителя, поэтому увеличиваем его. Чтобы это сделать, объединим его вместе с неиспользованным числом делимого, то есть с цифрой 3. Дописываем 3 к полученной 2.
- Затем анализируем сколько раз делитель 7 будет содержаться в числе 23. Ответ 3 раза и фиксируем его в частном. Результат произведения 7 на 3 (21) вписываем снизу в столбик под число 23.
- Остается только найти последнее число частного. Применяя тот же алгоритм, продолжает вычисления в столбике. Вычитает в столбике 23-21 получает разницу, равной числу 2. Из всего делимого, у нас остается только неиспользованное число 8. Его объединяем с полученным результатом 2, получаем в ответе 28.
- В заключение анализируем, какое количество, раз делитель 7 содержится в полученном нами числе. Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Самым наиболее главным при обучении ребенка методу деления, будет усвоение и четкое понимание алгоритма действий, ведь на самом деле он предельно прост.

Если ваш ребенок отлично умеет оперировать таблицей умножения, то с «обратным» делением у него не должны возникнуть трудности. Поэтому очень важно все время тренировать полученные навыки. Не стоит останавливаться на достигнутом.
Для легкого обучения юного ученика методу деления следует:
- в возрасте трех лет правильно усвоить термины «целое» и «часть». Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта.
- правильно понимать и разбираться в методах деления и умножения.
Чтобы занятия доставили ребенку удовольствие, следует возбуждать интерес к математике в ситуациях в быту, а не только в процессе учебы.
Поэтому тренируйте наблюдательность у ребенка, придумывайте аналогии математических действий во время игр, в процессе конструирования либо же в простых наблюдениях за природой.
vremya-sovetov.ru
Как делить в уме 🚩 как быстро делить числа 🚩 Математика
Инструкция
Несколько десятилетий назад в обычных образовательных школах существовал предмет «Устный счет». Дети обучались производить в уме основные математические операции: сложение, вычитание, умножение и деление, которое можно считать самым сложным из них. Деление предполагает быстрый поиск максимального делителя. Метод устного деления требует знания приемов сокращенного деления и школьной таблицы умножения. Кроме того, нужно тренировать память, чтобы научиться держать в уме все промежуточные вычисления, особенно если цифры большие.Разложение частного на составляющиеНапример, вам нужно разделить число 3647 на 7. Представьте частное как сумму чисел 3500 и 147. В этом примере 3500 – самое большое очевидное число, меньшего исходного, которое делится на 7 без остатка:3647/7 = 3500/7 + 147/7 = 500 + 147/7 = 500 + 21 = 521.
Деление «столбиком» в уме, как в детствеМысленно представьте лист бумаги и воображаемым карандашом произведите вычисления. Этот метод требует хорошей зрительной памяти, которую, впрочем, можно натренировать регулярными упражнениями в счете. Этот метод предпочитают многие, т.к. он хорошо знаком со школьных времен, хоть и не такой быстрый, как предыдущий.Деление на 10, 100, 1000 и т.д.Этот способ предполагает отделение соответствующего числа запятых, начиная с правой стороны числа. Например, разделите число 567890 на 10000:567890/10000 = 56,7890 – отделение четырех нулей.
Деление на 0,1, 0,01 и т.д.Этот вариант предполагают умножение на 1 с соответствующим числом последующих нулей, т.е. десятичную дробь переворачивают. Например, разделите число 78,765 на 0,0001:78,765/0,0001 = 78,765*10000 = 787650.
Деление на десятичную дробьЗамените ее мысленно на обычную, например, 0,5 на 1/2. Умножьте исходное число на знаменатель и разделите на числитель. Например, разделите число 2250 на 0,75:2250/0,75 = 2250/(3/4) = 2250*4/3 = 9000/3 = 3000.
Деление на 5, 50, 500 и т.д.Замените делитель на соответствующую дробь: 5 = 10/2; 50 = 100/2 и т.д. Теперь достаточно отделить у частного два знака после запятой и умножить на 2. Например, разделите 1750 на 50:1750/50 = 1750*2/100 = 3500/100 = 35.
По схожему принципу происходит деление на 2,5, 25 и пр.: делитель заменяется на соответствующую дробь с 4 в знаменателе. 1,25, 12,5 и пр. – на дробь с 8 в знаменателе:285/2,5 = 285*4/10 = 1140/10 = 114;600/12,5 = 600*8/100 = 4800/100 = 48.
www.kakprosto.ru
деление в уме. Магия чисел [Моментальные вычисления в уме и другие математические фокусы]
Глава 4
Разделяй и властвуй: деление в уме
Деление в уме — чрезвычайно полезный навык как для бизнеса, так и для повседневной жизни. Сколько раз в неделю вы сталкиваетесь с ситуациями, которые требуют от вас что-то равномерно распределить, например счет в ресторане? Точно такой же навык оказывается кстати, когда вы хотите выяснить стоимость одной упаковки корма для собак, или поделить выигрыш во время игры в покер, или узнать, сколько литров бензина можно купить на 20 долларов. Способность делить в уме избавит вас от необходимости постоянно обращаться к калькулятору, когда вам нужно что-либо посчитать.
При выполнении устного деления метод вычисления слева направо вступает в свои права. Именно ему нас учили в школе, так что вы будете заниматься естественным для себя делом. Помню, что, будучи ребенком, думал, будто метод деления слева направо олицетворяет то, какой арифметика должна быть в принципе. Я часто размышлял о том, что если бы в школе нашли способ преподавать и деление справа налево, они, вероятно, так бы и сделали!
ДЕЛЕНИЕ НА ОДНОЗНАЧНОЕ ЧИСЛО
Первый шаг при делении в уме — предположить, из скольких цифр будет состоять итоговый ответ. Чтобы понять, что я имею в виду, попробуйте решить вот такую задачу: 179 ? 7
Чтобы разделить 179 на 7, нужно найти такое число Q, которое 7 раз по Q составит 179. Очевидно, что поскольку 179 находится между 7 х 10 = 70 и 7 х 100 = 700,
Попробуем решить похожую задачу, используя аналогичные расчеты.
675 ? 8
Как и раньше, если 675 находится между 8 х 10 = 80 и 8 х 100 = 800, то ответ должен быть меньше 100 и выражаться двузначным числом. Чтобы произвести деление, учтем, что 8 х 80 = 640 и 8 х 90 = 720. То есть ответ должен быть в диапазоне 80 «с хвостиком». Но с каким хвостиком? Чтобы это узнать, вычтите 640 из 675 для получения остатка 35. После произнесения вами «80» наша задача сведется к 35 ? 8. Так как 8 х 4 = 32, итоговый ответ будет 84 с остатком 3, или 84 и 3/8.
Схематически данный пример представим так:
Как и большинство устных вычислений, процесс деления можно рассматривать как процесс упрощения. Чем больше числа в первом действии, тем проще становится задача. То, что начиналось как 675 ? 8, было сведено к меньшей задаче 35 ? 8.
Теперь рассмотрим пример, при решении которого получается трехзначное число.
947 ? 4
На этот раз ответ будет содержать три цифры, потому что 947 находится между 4 х 100 = 400 и 4 х 1000 = 4000. Нам следует отыскать наибольшее кратное 100, наиболее близкое к 947.
Поскольку 4 х 200 = 800, то есть «200 плюс», так что вперед, произнесите это! Вычитание 800 из 947 преподносит новую задачу на деление 147 ? 4. Так как 4 х 30 = 120, теперь мы уже можем сказать: «30». После вычитания 120 из 147 вычисляем 27 ? 4 для получения остальной части ответа: 6 с остатком 3.
В совокупности имеем 236 с остатком 3, или 236 и 3/4.

Процесс деления четырехзначного числа на одну цифру столь же прост, как и следующий пример.
2196 ? 5
Здесь ответ будет исчисляться сотнями, потому что 2196 находится между 5 х 100 = 500 и 5 х 1000 = 5000. После вычитания 5 х 400 = 2000 из 2196 мы можем произнести «400», и наша задача сведется к деления 196 на 5, что вычисляется так же, как и в предыдущих примерах.

На самом деле существует более простой способ решения последней задачи. Ее можно упростить путем удвоения обоих чисел. Так как 2196 х 2 = 4392, то имеем 2196 ? 5 = 4392 ? 10 = 439,2, или 439 и 2/10. Мы рассмотрим другие способы упрощения при делении в следующем разделе.
УПРАЖНЕНИЕ: ДЕЛЕНИЕ НА ОДНУ ЦИФРУ
1. 318 ? 19
2. 726 ? 5
3. 428 ? 7
4. 289 ? 8
5. 1328 ? 3
6. 2782 ? 4
ПРАВИЛО БОЛЬШОГО ПАЛЬЦА
При делении в уме запоминание частей ответа может вызвать сложности в процессе вычислений. Одним из вариантов выхода из ситуации является, как мы практиковали ранее, проговаривание ответа вслух по ходу решения. Но для создания большего эффекта вы можете предпочесть (как и я) держать ответ в памяти с помощью пальцев и произносить его целиком в самом конце. Однако при этом вы рискуете столкнуться с проблемой при запоминании чисел, которые больше пяти, ведь у нас лишь пять пальцев на каждой руке. В этом вам поможет специальная техника, в основе которой лежит язык жестов. Я называю ее «Правило большого пальца». Она особенно эффективна для запоминания чисел, состоящих из трех и более цифр, и полезна не только в данной главе, но пригодится и в последующих, где придется иметь дело с задачами посложнее и числами подлиннее.
Вы уже догадались, что для запоминания чисел от 0 до 5 вам достаточно согнуть нужное количество пальцев на руке. Когда в процесс вовлечен большой палец, будет легко запомнить числа от 6 до 9. Вот список правил большого пальца.
• Чтобы задать 6, поместите большой палец на верхней части мизинца.
• Чтобы задать 7, поместите большой палец на верхней части безымянного пальца.
• Чтобы задать 8, поместите большой палец на верхней части среднего пальца.
• Чтобы задать 9, поместите большой палец на верхней части указательного пальца.
При работе с трехзначным числом задайте цифры для сотен на левой руке и для десятков на правой. Когда дело дойдет до одной цифры, вы достигнете конечной точки решения (за исключением возможного остатка). Теперь произнесите число на левой руке, число на правой руке, последнюю цифру, которую только что посчитали, и остаток (что у вас в голове).
И вот! Вы произнесли ответ!
Чтобы попрактиковаться, попробуйте решить следующую задачу на деление четырехзначного числа.

Пользуясь приемом большого пальца для запоминания ответа, вы зададите 7 на левой руке, соединив большой палец с безымянным, и 6 на правой, соединив большой палец с мизинцем. Как только вычислите последнюю цифру (она равна 3) и остаток (равный 1), можете «зачитать» итоговый ответ с ваших рук слева направо: «семь…шесть…три с остатком один».
Некоторые задачи на деление четырехзначных чисел дают четырехзначный ответ. В таком случае, поскольку у вас только две руки, вам придется вслух произнести цифру для тысячи и использовать правило большого пальца для запоминания остального ответа. Например:
Для решения этой задачи вы делите 8 на 3, чтобы получить цифру 2 для тысяч; произносите «две тысячи» вслух, затем делите 2352 на 3 привычным способом.
ДЕЛЕНИЕ НА ДВУЗНАЧНЫЕ ЧИСЛА
В этом разделе мы исходим из предположения, что вы уже освоили искусство деления на однозначные числа. Естественно, задачи на деление с увеличением делителя более сложные.
К счастью, в моем рукаве есть немного магии, чтобы облегчить вам жизнь.
Начнем с относительно простой задачи.
597 ? 14
Так как 597 находится между 14 х 10 и 14 х 100, ответ (так называемое частное) лежит между 10 и 100. Чтобы его найти, нужно в первую очередь задать вопрос: «Сколько раз по 14 даст в сумме 590?» Умножив 14 х 40 = 560, вы узнаете, что ответ будет в диапазоне «40 плюс»; так что можно смело произнести вслух «сорок».
Далее вычитаем 560 из 597 и получаем 37, что сводит задачу к делению 37 на 14. Так как 14 х 2 = 28, здесь ответ — 42. Вычитая 28 из 37, мы получаем остаток 9. Процесс решения задачи показан следующим образом.
Следующая задачка немного сложнее, потому что делитель в ней больше.
682 ? 23
В данном примере ответ будет двузначным числом, так как 682 находится между 23 х 10 = 230 и 23 х 100 = 2300. Чтобы найти цифру для десятка двузначного числа, нужно подумать: «Сколько раз по 23 даст в сумме 680?» Если вы попробуете 30, то увидите, что здесь незначительный перебор, так как 23 х 30 = 690. Но теперь вы знаете, что ответ лежит в диапазоне «20 плюс» и можете произнести это вслух. Затем вычтите 23 х 20 = 460 из 682, чтобы получить 222. Так как 23 х 9 = 207, ответ — 29 и остаток 222–207 = 15.
Теперь вычислим:
491 / 62
Так как 491 меньше, чем 62 х 10 = 620, ответ будет представлен одной цифрой с остатком. Можно попробовать 8, но 62 х 8 = 496, а это несколько больше делимого. Поскольку 62 х 7 = 434, ответ — 7 и остаток 491–434 = 57, или 7 и 57/62.
Один отличный трюк может облегчить решение таких задач. Помните, как сначала мы пытались перемножить 62 х 8 = 496, но обнаружили, что это число больше, чем нужно? Но это действие оказалось не напрасным. Помимо информации о том, что ответ — 7, оно также позволяет сразу определить остаток.
Поскольку 496 на 5 единиц больше 491, остаток будет на 5 единиц меньше делителя 62. Поскольку 62 — 5 = 57, то ответ — 7 и 57/62. Этот прием работает потому, что 491 = (62 х 8) — 5 = 62 х (7 + 1) — 5 = (62 х 7 + 62) — 5 = (62 х 7) + (62 — 5) = 62 х 7 + 57.
Теперь попробуйте решить пример 380 ? 39, используя вышеописанную уловку. Итак, 39 х 10 = 390, что больше делимого на 10. Стало быть, ответ будет 9 с остатком 39–10 = 29.
Следующий вызов для вас — деление четырехзначного числа на двузначное.
3657 / 54
Так как 54 х 100 = 5400, то ответ будет двузначным числом. Для получения первой цифры ответа необходимо выяснить, сколько раз по 54 даст в сумме 3657. Исходя из того что 54 х 70 = 3789 (что немного больше делимого), ответ будет где-то в диапазоне «60 плюс».
Далее умножаем 54 х 60 = 3240 и вычитаем 3657–3240 = 417. Как только вы произнесете «60», ваша задача упростится до 417 ? 54. Поскольку 54 х 8 = 432 (что тоже немного больше 417), последняя цифра будет 7 с остатком 54–15 = 39.
Теперь попробуйте свои силы в решении задачи с трехзначным частным:

Упрощение задач на деление
Если к этому моменту ваш мозг уже устал от перенапряжения, расслабьтесь. Как и было обещано, я поделюсь с вами несколькими приемами упрощения задач на деление в уме. Они основаны на принципе деления обеих частей задачи на общий множитель. Если оба числа в примере четные, вы можете вдвойне упростить проблему путем деления каждого числа на 2 перед началом вычислений. Например, задача 858 ? 16 содержит два четных числа, и их деление на 2 ведет к значительно более простому действию 429 ? 8.
Как видите, остатки 10 и 5 различны; но если записать их в виде дроби, получится 10/16, что равно 5/8. Поэтому в данном методе ответ всегда должен быть представлен в виде дроби.
Мы проделали оба типа вычислений для того, чтобы вы убедились, насколько второй способ легче. Теперь ваша очередь практиковаться:
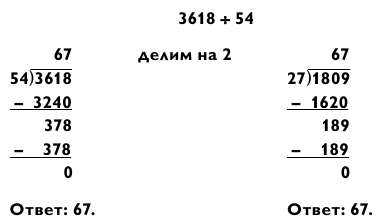
Пример справа гораздо легче решить в уме. Если вы все еще в этом не уверены, можете разделить обе части исходной задачи на 18 для получения еще более простой задачи: 201 ? 3 = 67.
Высматривайте задачи, которые можно подвергнуть делению на 2 дважды, такие как 1652 ? 36.
Мне кажется, что проще дважды разделить числа на 2, чем делить каждое из чисел на 4. Теперь рассмотрим случай, когда оба числа оканчиваются на 0. В этой ситуации можно каждое число разделить на 10.
Если оба числа заканчиваются на 5, удвойте их, а затем разделите на 10 для упрощения задачи. Например:
Наконец, если делитель оканчивается на 5, а делимое на 0, умножьте оба на 2, а затем разделите на 10 и далее действуйте так, как мы делали выше.
УПРАЖНЕНИЕ: ДЕЛЕНИЕ НА ДВУЗНАЧНЫЕ ЧИСЛА
Здесь вы найдете разнообразные задачи по делению на двузначные числа, которые проверят ваше ментальное мастерство и умение пользоваться простыми техниками упрощения, которые были объяснены в этой главе. Загляните в конец книги для получения объяснений и сверки ответов.
1. 738 ? 17
2. 591 ? 24
3. 321 ? 79
4. 4268 ? 28
5. 7214 ? 11
6. 3074 ? 18
РАЗВИВАЕМ СВОИ СПОСОБНОСТИ: ИЗУЧЕНИЕ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Как вы уже, наверное, догадались, мне нравится заниматься магией, превращая обычные дроби в десятичные. В случае с дробями, в знаменателе которых есть только одна цифра, лучший способ превратить их в десятичные — это почерпнуть их значения из памяти. Это не так сложно, как кажется. Далее вы увидите, что большинство дробей, числители и знаменатели которых представлены однозначными числами (а также 10 или 11), обладают особыми свойствами, поэтому их сложно забыть. Каждый раз, когда вы можете сократить дробь до уже известного вам значения, это ускорит процесс вычислений.
Уверен, вы уже знаете десятичные эквиваленты для следующих дробей:
1/2 = 0,50;
1/3 = 0,333…;
2/3 = 0,666…
Подобно этому
1/4 = 0,25;
2/4 = 1/2 = 0,50;
3/3 = 0,75.
Дроби с пятерками в знаменателе запомнить легче всего.
1/5 = 0,20;
2/5 = 0,40;
3/5 = 0,60;
4/5 = 0,80.
Дроби с шестерками в знаменателе требуют запоминания только двух новых значений.
1/6 = 0,1666…;
2/6 =1/3 = 0,333…;
3/6 = 1/2 = 0,50;
4/6 = 2/3 = 0,666…;
5/6 = 0,8333…
Через мгновение я вернусь к дробям с семерками в знаменателе. А сейчас дроби с восьмерками в знаменателе, преобразовать которые просто элементарно.
1/8 = 0,125;
2/8 = 1/4 = 0,25;
4/8 = 1/2 = 0,50;
6/8 = 3/4 = 0,75;
Дроби с девятками в знаменателе таят в себе особое волшебство.
где черта над цифрой обозначает бесконечное повторение этой цифры (говорят, что это дробь в периоде). Например, 4/9 = 0,444…
Дроби с десятками в знаменателе нам уже известны.
1/10 = 0,1; 2/10 = 0,2; 3/10 = 0,3;
4/10 = 0,4; 5/10 = 0,5; 6/10 = 0,6;
7/10 = 0,7; 8/10 = 0,8; 9/10 = 0,9.
Дроби со знаменателем 11 легко вычисляются, если вы запомните, что 1/11 = 0,0909.
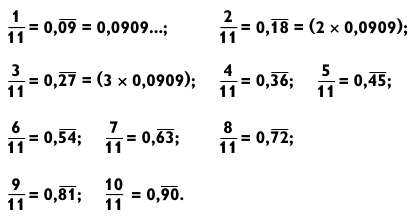
Дроби со знаменателем 7 действительно выдающиеся. Как только вы запомните, что
то сможете без труда получить значения других дробей с 7 в знаменателе.Обратите внимание, что последовательность цифр в периоде циклически повторяется в каждой дроби, при этом изменяется лишь начальная цифра последовательности. Ее можно определить путем умножения 0,14 на числитель дроби.
Например, для дроби 2/7 имеем 2 х 0,14 = 0,28. Поэтому последовательность должна начинаться с 2. Для дроби 3/7 это 3 х 0,14 = 0,42, значит, последовательность начинается с 4.
Другие дроби подчиняются тому же правилу.
Конечно, в процессе решения разнообразных задач вы обязательно столкнетесь с дробями, превышающими 10/11. Поэтому постоянно обдумывайте способы упрощения таких задач. Например, можно упростить дробь 18/34 путем деления числителя и знаменателя на 2, чтобы сократить задачу до 9/17 (ее будет легче решить).
Если знаменатель дроби — четное число, можно упростить дробь, уменьшив ее вдвое, даже если числитель нечетный.
Например,
9/14 = 4,5/7
Деление числителя и знаменателя на 2 сведет проблему к дроби с семеркой в знаменателе. Хотя ранее показанная последовательность дробей не предоставляет десятичного варианта для дроби 4,5/7, как только вы начнете считать, заученное число неожиданно всплывет в памяти.
Как видите, вам не пришлось решать задачу целиком.
Стоит вам разделить 3 на 7, и вы точно произведете огромное впечатление на публику, отбарабанив этот длинный набор цифр почти мгновенно![4]
Когда делитель заканчивается на 5, то почти всегда умножение на 2, а потом деление на 10 оправдывает себя. Например:
Числа, которые заканчиваются на 25 или 75, надо сначала умножить на 4 и затем разделить на 100.
Этот трюк можно применять даже в середине расчетов.
Если вам нужно вычислить дробь 3/16, произойдет вот что:
Как только задача сведется к вычислению 14/16, можно привести ее к виду 7/8, что, как известно, равняется 0,875.
Отсюда 3/16 = 0,1875[5].
УПРАЖНЕНИЕ: ПРИВЕДЕНИЕ ДРОБЕЙ К ДЕСЯТИЧНОЙ ФОРМЕ
Чтобы решить следующие задачи, не забудьте использовать полученные знания о десятичном виде различных «одноцифровых» дробей. Везде, где это целесообразно, упрощайте дроби, прежде чем преобразовать их в десятичные.
1. 2/5 2. 4/7 3. 3/8 4. 9/12 5. 5/12 6. 6/11
7. 14/24 8. 13/27 9. 18/48 10. 10/14 11. 6/32 12. 19/45
ПРИЗНАКИ ДЕЛИМОСТИ
В последнем разделе мы узнали, как упростить задачи на деление, если числитель и знаменатель поделить на общий множитель. В завершение этой главы обсудим, как определить, является ли одно число делителем другого. Это поможет упростить задачу на деление и ускорить процесс решения многих задач на умножение, а также пригодится, когда мы доберемся до продвинутого умножения, где часто придется искать способы разложить на множители двух-, трех- или даже пятизначные числа. Умение делать это окажется весьма полезным.
Проверить, делится ли число на 2, довольно просто. Вам нужно только определить, является ли последняя цифра четной. Если это 2, 4, 6, 8 или 0, то число целиком делится на 2.
Чтобы протестировать число на делимость на 4, проверьте, делятся ли на 4 две его последние цифры. Число 57 852 кратно 4, потому что 52 = 13 х 4. Число 69 346 не кратно 4, поскольку 46 не делится на 4 без остатка. Это правило работает потому, что 4 делит 100 и, следовательно, любое число, кратное 100.
Таким образом, поскольку 57 800 и 52 делятся на 4, то 4 поделит и их сумму, то есть 57 852.
Аналогично, так как 1000 делится на 8, для проверки кратности 8 достаточно выяснить, делятся ли на 8 последние три цифры числа. Например, для 14 918 надо проверить число 918 на делимость на 8. Однако при делении 918 на 8 имеем остаток (918 ? 8 = 114 6/8), из чего делаем вывод, что число 14 918 на 8 не делится. Можно также заметить, что 18 (две последние цифры числа 14 918) не делится на 4, а так как 14 918 не делится на 4, оно не может делиться и на 8.
Когда дело доходит до делимости на 3, предлагаю запомнить одно простое правило: число делится на 3 тогда и только тогда, когда сумма составляющих его цифр делится на 3 (независимо от того, сколько цифр в числе). Чтобы выяснить, делится ли 57 852 на 3, просто сложите 5 + 7 + 8 + 5 + 2 = 27. Так как 27 кратно 3, то и 57 852 будет кратно 3. Столь же удивительное правило справедливо и для делимости на 9. Число делится на 9 тогда и только тогда, когда сумма составляющих его цифр кратна 9. Поэтому 57 852 кратно 9, тогда как число 31 416, сумма цифр которого равна 15, на 9 не делится. Объясняется это правило тем, что числа 1, 10, 100, 1000, 10000 и т. д. всегда на единицу больше кратного 9.
Число делится на 6 только в том случае, если оно четное и делится на 3. Так что кратность 6 легко проверить.
Установить, делится ли число на 5, еще проще. Любое число, независимо от величины, кратно 5 тогда и только тогда, когда оно заканчивается на 5 или 0.
Выяснить делимость на 11 почти так же просто, как на 3 или на 9. Число делится на 11 тогда и только тогда, когда в результате попеременного вычитания и сложения составляющих его цифр вы получите либо 0, либо кратное 11.
Например, 73 958 не делится на 11, потому что 7–3 + 9–5 + 8 = 16. Однако числа 8 492 и 73 194 кратны 11, так как 8–4 + 9–2 = 11 и 7–3 + 1–9 + 4 = 0. Это правило работает потому, что числа 1, 100, 10 000, 1 000 000 на единицу больше кратного 11, в то время как числа 10, 1000, 100 000 и т. д. на единицу меньше величины, кратной 11.
Проверка делимости на 7 несколько сложнее. Если вы прибавите (или вычтите) число, кратное 7, к проверяемому (или из проверяемого) и полученный результат будет делиться на 7, ответ положительный. Я всегда выбираю такое прибавляемое или вычитаемое кратное 7, чтобы в итоге сумма или разность заканчивалась на 0. Например, для проверки числа 5292 я вычитаю 42 (кратное 7), чтобы получить 5250.
Далее избавляюсь от 0 на конце (так как деление на десять не влияет на проверку делимости на семь), получая в итоге 525. Затем повторяю процесс, прибавляя 35 (кратное 7), что дает мне 560. Когда я удалю 0, то останусь с числом 56, которое, как мне известно, кратно 7. Таким образом, исходное число 5292 делится на 7.
Этот метод работает не только для 7, но и для любого нечетного числа, кроме оканчивающегося на 5. Например, чтобы проверить, делится ли 8792 на 13, вычитаем 4 х 13 = 52 из 8792 и получаем 8740. Опуская 0, имеем 874. Затем прибавляем 2 х 13 = 26, выходит 900. Удаление двух нулей оставляет нас с числом 9, которое, очевидно, не кратно 13. Таким образом, 8792 не делится на 13.
УПРАЖНЕНИЕ: ПРОВЕРКА НА ДЕЛИМОСТЬ
В этом упражнении будьте особенно внимательны при проверке делимости на 7 и 17. Остальное не должно представлять для вас трудностей.
Делимость на 2
1. 53 428 2. 293 3. 7241 4. 9846
Делимость на 4
5. 3932 6. 67 348 7. 358 8. 57 929
Делимость на 8
9. 59 366 10. 73 488 11. 248 12. 6111
Делимость на 3
13. 83 671 14. 94 737 15. 7359 16. 3 267 486
Делимость на 6
17. 5334 18. 67 386 19. 248 20. 5991
Делимость на 9
21. 1234 22. 8469 23. 4 425 575 24. 314 159 265
Делимость на 5
25. 47 830 26. 43 762 27. 56 785 28. 37 210
Делимость на 11
29. 53 867 30. 4969 31. 3828 32. 941 369
Делимость на 7
33. 5784 34. 7336 35. 875 36. 1183
Делимость на 17
37. 694 38. 629 39. 8273 40. 13 855
ОБЫКНОВЕННЫЕ ДРОБИ
Если вы в состоянии управиться с целыми числами, то арифметические действия с дробями покажутся вам почти такими же легкими. В этом разделе мы сделаем обзор основных методов сложения, вычитания, умножения, деления и сокращения обыкновенных дробей. Те, кто знаком с дробями, могут спокойно его пропустить.
Умножение обыкновенных дробей
Чтобы перемножить две обыкновенные дроби, нужно просто перемножить их числители (верхние числа), а затем знаменатели (нижние числа). Например:
2/3 х 4/5 = 8/15
1/2 х 5/9 = 5/18
Что может быть проще! Попробуйте следующие упражнения, прежде чем двигаться дальше.
УПРАЖНЕНИЕ: УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
1. 3/5 х 2/7
2. 4/9 х 11/7
3. 6/7 х 3/4
4. 9/10 х 7/8
Деление обыкновенных дробей
Деление дробей столь же легкое, как и умножение. Однако оно требует одного дополнительного действия. Сначала переверните вторую дробь с ног на голову (это называется обратная дробь), а затем умножайте. Например, обратная дробь для 4/5 будет 5/4. Следовательно,
2/3 ? 4/5 = 2/3 х 5/4 = 10/12
1/2 ? 5/9 = 1/2 х 9/5 = 9/10
УПРАЖНЕНИЕ: ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Теперь ваша очередь. Поделите эти дроби.
1. 2/5 ? 1/2
2. 1/3 ? 6/5
3. 2/5 ? 3/5
Сокращение обыкновенных дробей
Дроби можно рассматривать как маленькие задачки на деление. Например, 6/3 то же самое, что и 6 ? 3 = 2. Дробь 1/4 то же самое, что и 1 ? 4 (или 0,25 в десятичной форме). Известно, что если умножить любое число на 1, то это число не изменится.
Например, 3/5 = 3/5 х 1. Но если заменить 1 дробью 2/2, то получим 3/5 = 3/5 х 1 = 3/5 х 2/2 = 6/10. Следовательно, 3/5 = 6/10.
По такому же принципу, заменив 1 дробью 3/3, получим 3/5 = 3/5 х 3/3 = 9/15. Другими словами, если мы умножаем числитель и знаменатель на одно и то же число, то получаем дробь, равную исходной.
Вот еще пример:
2/3 = 2/3 х 5/5 = 10/15
Верно и то, что, деля числитель и знаменатель на одинаковое число, мы получаем дробь, равную исходной.
Например:
4/6 = 4/6 ? 2/2 = 2/3
25/35 = 25/35 ? 5/5 = 5/7
Это сокращение дроби.
УПРАЖНЕНИЕ: СОКРАЩЕНИЕ ДРОБЕЙ
Найдите дробь со знаменателем 12, равную дробям, представленным ниже.
1. 1/3 2. 5/6 3. 3/4 4. 5/2
Сокращение дробей.
5. 8/10 6. 6/15 7. 24/36 8. 20/36
Сложение дробей
Это действие можно считать простым, когда знаменатели равны. В этом случае складываются числители и сохраняется прежний знаменатель.
Например:
3/5 + 1/5 = 4/5; 4/7 + 2/7 = 6/7
Иногда можно упростить ответ. Например:
1/8 + 5/8 = 6/8 = 3/4
УПРАЖНЕНИЕ: СЛОЖЕНИЕ ДРОБЕЙ (С РАВНЫМИ ЗНАМЕНАТЕЛЯМИ)
1. 2/9 + 5/9
2. 5/12 + 4/12
3. 5/18 + 6/18
4. 3/10 + 3/10
Более коварный случай — различные знаменатели. Когда знаменатели не равны, нужно заменить исходные дроби дробями с равными знаменателями.
Например, сложите
1/3 + 2/15
Заметим, что
1/3 = 5/15
Поэтому
1/3 + 2/15 = 5/15 + 2/15 = 7/15
При сложении
1/2 + 7/8
Замечаем, что
1/2 = 4/8
Тогда
1/2 + 7/8 = 4/8 + 7/8 =11/8
При сложении
1/3 + 2/5
Видим, что
1/3 = 5/15 и 2/5 = 6/15
В итоге
1/3 + 2/5 = 5/15 + 6/15 = 11/15
УПРАЖНЕНИЕ: СЛОЖЕНИЕ ДРОБЕЙ (С НЕРАВНЫМИ ЗНАМЕНАТЕЛЯМИ)
1. 1/5 + 1/10 2. 1/6 + 5/18 3. 1/3 + 1/5
4. 2/7 + 5/21 5. 2/3 + 3/4 6. 3/7 + 3/5 7. 2/11 + 5/9
Вычитание дробей
Вычитание дробей похоже на их сложение. Мы покажем это действие на примерах и обеспечим вас тренировочными упражнениями.
2/5 — 2/5 = 1/5; 4/7 — 2/7 = 2/7; 5/8 — 1/8 = 4/8 = 1/2
1/3 /2/15 = 5/15 — 2/15 = 3/15 = 1/5
7/8 — 1/2 = 7/8 — 4/8 = 3/8
1/2 — 7/8 = 4/8 — 7/8 = -3/8; 2/7 — 1/4 = 8/28 — 7/28 = 1/28
2/3 — 5/8 = 16/24 — 15/24 = 1/24
УПРАЖНЕНИЕ: ВЫЧИТАНИЕ ДРОБЕЙ
1. 8/11 — 3/11 2. 12/7 — 8/7 3. 13/18 — 5/18
4. 4/5 — 1/15 5. 9/10 — 3/5 6. 3/4 — 2/3
7. 7/8 — 1/16 8. 4/7 — 2/5 9. 8/9 — 1/2
Поделитесь на страничкеСледующая глава >
math.wikireading.ru
Как объяснить деление в столбик 🚩 делить в столбик онлайн 🚩 Образование 🚩 Другое
Вам понадобится
- – ручка или карандаш,
- – лист бумаги в клетку.
Инструкция
Деление без остатка. Разделим 1265 на 55.Проведите вниз короткую вертикальную линию, высотой в несколько клеток. От этой линии проведите перпендикуляр вправо. Получилась буква «Т», заваленная на левый бок. Над горизонтальной частью заваленной буквы «Т» пишется делитель (55), а слева от него в этой же строчке, за вертикальной частью буквы «Т» – делимое (1265). Обычно, сначала записывается делимое, потом ставится знак деления в столбик (заваленная набок буква «Т»), а после делитель.
Определите, какая часть делимого (отсчет идет слева направо по старшинству разрядов) делится на делитель. То есть: 1 на 55 – нет, 12 на 55 – нет, 126 на 55 – да. Число 126 называется неполным делимым.
Прикиньте в уме, на какое число N нужно умножить делитель, чтобы получилось число равное или максимально приближенное (но не большее) к величине неполного делимого. То есть: 1*55 – маловато, 3*55=165 – многовато. Итак, наш выбор – число 2. Записываем его под делителем (ниже горизонтальной части заваленной буквы «Т»).Умножьте 2 на 55 и запишите полученное число 110 строго под цифрами неполного делимого – слева направо: 1 под 1, 1 под 2 и 0 под 6. Сверху 126, снизу 110. Проведите под 110 короткую горизонтальную черту.
Вычтите из 126 число 110. Получится 16. Цифры записывайте четко одна под другой под проведенной чертой. То есть, слева направо: под цифрой 1 числа 110 – пусто, под цифрой 1 – 1 и под цифрой 0 – 6. Число 16 – это остаток, который должен быть меньше делителя. Если он оказался больше делителя, число N было выбрано неправильно – нужно его увеличить и повторить предыдущие действия.
Снесите следующую цифру делимого (цифра 5) и запишите ее справа от числа 16. Получилось 165.
Повторите действия третьего шага для отношения 165 к 55, то есть найдите число Q, при умножении делителя на которое, получается число максимально приближенное к 165 (но не большее его). Это число 3 – 165 делится на 55 без остатка. Запишите цифру 3 справа от цифры 2 под чертой, проведенной под делителем. Это и есть ответ: частное отношения 1265 к 55 равно 23.
Деление с остатком. Разделим 1276 на 55.Повторите все те же действия, что и при делении без остатка. Число N по-прежнему равно 2, но разница между 127 и 110 равна 17. Сносим 6 и определяем число Q. Оно также по-прежнему равно 3, но теперь появляется остаток: 176 – 165 = 11. Остаток 11 меньше 55, вроде бы все нормально. Но сносить-то больше нечего…
Допишите справа от делимого ноль и поставьте запятую, после цифры 3 в частном (то число, которое получается в ходе деления, и записывается под чертой, проведенной под делителем).
Снесите дописанный в делимом ноль (запишите его справа от 11) и проверьте, есть ли возможность разделить получившееся число на делитель. Ответ – да: 2 (обозначим его, как число G) умножить на 55 равно 110. Ответ – 23,2.Если бы снесенного в предыдущем шаге нуля не хватило бы для того, чтобы остаток с дописанным нулем оказался больше делителя, нужно было бы дописать еще один ноль в делимом и поставить 0 в частном после запятой (получилось бы 23,0…).
Деление в столбик десятичных дробей.Перенесите запятую на одинаковое количество знаков вправо в делимом и делителе так, чтобы и там, и там были целые числа. Дальше – алгоритм деления тот же.
Видео по теме
Обратите внимание
Записывайте все числа строго друг под другом согласно изложенным рекомендациям – это не даст возможности допустить ошибку в ходе выполнения расчетов.
Источники:
- Сложение, вычитание, умножение и деление десятичных дробей.
www.kakprosto.ru
Как объяснить ребенку деление столбиком
В процессе обучения в школе очень часто возникает проблема, когда ребенок не смог понять на уроке операцию деления простых чисел. Взрослые думают, что это совсем не сложно. Но школьник сталкивается с этим впервые и не всегда самостоятельно может во всем разобраться.
В такой ситуации родители, набравшись терпения, должны предельно просто и ясно объяснить ему все непонятные моменты. Как правильно и доступно объяснить ребенку деление столбиком, читайте в материалах этой статьи.
Что нужно знать, что бы научиться делить
Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.
Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел. 
Без этих основ вряд ли получится проводить арифметические операции с числами. Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен.
Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.
Принцип деления для детей
Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.
Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.
Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.
Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.
После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.
Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.
Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку». Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик.
Алгоритм деления в столбик
Для решения примеров делением в столбик рекомендуется пользоваться простым алгоритмом.
- Определить в примере, где находится делимое, а где делитель.
- Записать делимое и делитель под «уголок».
- Определить, какая часть делимого может использоваться для первичного деления.
- Определить сколько раз делитель умещается в выбранной части делимого.
- Произвести умножение делителя на полученное число под уголком, результат вписать под выбранную часть делимого.
- Найти разницу (остаток).
- Повторить действия, пока в остатке не окажется 0.
Более подробно этот алгоритм разберем на конкретном примере.
Методика обучения делению в столбик
Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.
Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.
Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.
Деление в столбик на конкретном примере
Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.
Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.
Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».
Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.
Вот и столбик скоро получится.
Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.
Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.
Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.
Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.
Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.
Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.
Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей. Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык.
Вместо заключения
Если у ребенка возникают проблемы с учебой, родители должны помочь ему преодолеть любые трудности.
Деление в столбик – программа 2-3 класса, конечно. Для родителей это давно забытые знания, но при необходимости и желании все можно восстановить в памяти и помочь своему школьнику.
childage.ru
Как научить ребенка делить столбиком быстро и легко
 Математические премудрости порой заставляют детей всячески избегать контакта с учебниками и зубрежкой, а родителей – тратить свои нервы на настоятельные рекомендации малыша все же освоить столь необходимые азы. Как научить ребенка делить столбиком, если он не хочет? Почему этот процесс может не получаться? И как достичь оптимального результата, не прибегая к помощи репетиторов? Что ж, посмотрим.
Математические премудрости порой заставляют детей всячески избегать контакта с учебниками и зубрежкой, а родителей – тратить свои нервы на настоятельные рекомендации малыша все же освоить столь необходимые азы. Как научить ребенка делить столбиком, если он не хочет? Почему этот процесс может не получаться? И как достичь оптимального результата, не прибегая к помощи репетиторов? Что ж, посмотрим.
От простого к сложному
Дети обычно проходят тему деления в столбик, когда переходят в 3 или 4 класс. На момент обучения ими в обязательном порядке должны быть усвоены простые навыки сложения и вычитания, а принципы умножения и деления должны быть известны в теории и достаточно хорошо на практике. Запомнить правила деления столбиком сложно, если до сих пор не выучена таблица умножения.
И так, что такое деление? Это разделение определенного количества на равные части. Ребенку стоит объяснить это на примере. Например, возьмите 12 яблок и предложите каждому члену семьи (маме, папе, брату/сестре и самому ученику) раздать яблоки поровну. Затем усложните задачу и предложить раздать 12 яблок трем членам семьи. Оговорите полученный в обоих случаях результат со своим малышом. Старайтесь сразу донести суть, заключающуюся в обратности умножения и деления, на разных примерах таблицы.
Скажите ребенку, что из двух чисел, участвующих в умножении (например, 4х5=20), при делении ответом будет второе из них (20/4=5 или 20/5=4).
Как научить ребенка делить столбиком: принцип наглядности
Первое, что должен запомнить ребенок в процессе деления, — это понятия делимого, делителя и частного. Объяснение делайте подробным, «разжевывайте» каждое действие. Продемонстрируем пример в таблице.
| Шаг | Описание |
|---|---|
| Предположим, что нам необходимо делимое «762» разделить на 6. Запишем эти значения, отделив перпендикулярными линиями. | |
| Рассмотрим первую цифру делимого «7». Если его разделить на делитель «6», получится «1». Записываем это значение как первую цифру частного. Кроме того, возможность поделить первое значение делимого на делитель означает в данном случае, что частное будет состоять из 3-х цифр. | |
| Прописываем под первой цифрой делимого «6» (оно у нас получилось за счет умножения делителя на 1) и вычитаем столбиком «7-6» – получается «1». | |
| Теперь переносим вниз вторую цифру делимого и подставляем ее к нашей «1» – получается «16». Сколько цифр «6» (нашего делителя) умещается в цифре «16»? Правильно, две. Записываем полученный результат после «1» в частном. | |
| Далее вычисляем, сколько остается от «16», если забрать из этого значения 2 раза по «6» (то есть 12) – получается «4». Переносим это значение вниз, как и в первом случае. И к нему подставляем оставшееся третье число в делимом – образовалась цифра «42». | |
| Осталось выяснить, сколько в «42» помещается наших делителей «6» – их там 7. Это и есть наша оставшаяся цифра с частном – оно получилось «127». | |
| Важно отметить, что «42» полностью делится на «6», не оставляя никаких остатков. |
Читайте также: Где найти репетитора по английскому языку для школьника
Несколько правил обучения
Чтобы запоминание проходило достаточно легко и быстро, соблюдайте несколько правил:
- Важно не запомнить, в какой последовательности делаются вычисления, а понять их алгоритм.
- Постоянно повторяйте таблицу умножения. Совсем не обязательно держать под рукой таблицу Пифагора для этого – ищите примеры в окружении на прогулки (считайте, умножайте и делите листья, шишки, деревья, куличики и прочее). И тогда проблема, как научить ребенка делить столбиком, будет решаться быстрее и интереснее.
- Начинать обучение стоит, используя одно- или двузначные числа, постепенно усложняя поставленную задачу.
- Никаких криков и истерик с вашей стороны. Для вас умножение и деление – простое дело, производимое в уме, а для малыша – шаг к новым знаниям. Когда-то и вы были на его месте.
Обучение детей любым математическим премудростям должно происходить максимально в игровой форме, чтобы вызвать интерес и внимание. Даже такие сложные задачи, как получение дробей, построение синусоид и прочее, станут со временем понятными и простыми. Относитесь с терпением к своим любимым деткам и не отказывайте им в помощи и поддержке.
mojdetskijsad.ru
Как объяснить ребенку деление (2 класс)?
Деление чисел с остатком или без него является самым трудным из четырех арифметических действий. С основами этого процесса ребенок знакомится еще в самом раннем детстве иногда малышу приходится поровну делить конфеты между плюшевым мишкой и куклой. Правильно разделить угощение на несколько кучек для ребенка обычно труда не составляет.
Однако позже могут возникнуть проблемы. Школьные задачи не всегда подразумевают деление нескольких предметов на количество людей. Это могут быть, например, задания на скорость – и часто они вводят ребенка в ступор.
В таком случае научить принципам деления числа обязаны родители. Математика не терпит пустоты – если ребенок что-то пропустил или просто не усвоил информацию, это может сильно затруднить изучение дальнейших тем, а также других дисциплин в более поздних классах.
Начальное обучение делению
- Чем раньше родители объяснят ребенку принципы деления с остатком или без него – тем лучше он их усвоит. А чтобы процесс прошел легко, нужно это сделать в форме игры. Например, дать шесть конфет и попросить их поделить поровну между куклой, киской и папой. А теперь – между мамой и бабушкой. Естественно, у ребенка получатся разные результаты. Важно объяснить, почему так получилось.
- Следует учесть, что для обучения лучше использовать бытовые, знакомые малышу предметы: игры со счетными палочками или бумажными квадратиками вряд ли будут ему интересны.
- Следующим шагом можно попробовать объяснить деление с остатком – принцип тот же: игра. Пусть кроха попробует пятью орехами угостить Мишу и Свету. Он отдаст каждому по 2 орешка, а оставшийся сможет съесть сам.
- Теперь ребенок сможет понять сам принцип деления: большее число делится на меньшее. Конечно, взрослые-то знают, что так происходит не всегда, но для ребенка в возрасте от 5 до 8 лет этой информации будет достаточно.
Обучение делению школьников младших классов
Если ребенок все прекрасно усвоил в игровой форме, то в школе ему придется применить свои знания и умения на практике. Именно в это время отход от привычных категорий – конфет, кукол и прочего – может вызвать серьезные затруднения.
- В этом возрасте ребенок школьник должен уже знать первые три арифметических действия и уметь оперировать ими. Он должен понимать и знать таблицу умножения. Вот она, кстати, в некоторых случаях поможет объяснить ученику, что деление – это умножение наоборот. Родителю стоит сесть рядом с ребенком и, изучая напечатанную на обложке тетради таблицу умножения, объяснить, как это работает на практике. Например, 4х7=28. А если пойти наоборот? Уточнить, на пересечении какого числа с цифрой 7 находится 28. С 4. Вот и разделили.
- Теперь ребенок должен сделать цифровую запись этого процесса: это способствует закреплению информации в памяти.
Деление столбиком
Лишь после того, как ученик освоил и хорошо запомнил предыдущие способы, можно переходить к делению столбиком, с остатком или без него.
Вначале необходимо, чтобы ребенок понял и заучил название компонентов процесса деления:
- делимое – то число, которое делят;
- делитель – то, на что делят;
- частное – конечный результат.
Далее нужно показать форму записи при делении столбиком. К примеру, нужно поделить двузначное число на однозначное:
- вначале пишется делимое – пусть это будет 98;
- справа от него рисуют уголок, как перевернутую букву «Т», в нем записывают делитель – в нашем случае 7;
- теперь определяют наименьшее число в делимом, которое делится на 7 – это 9;
- цифра 7 в числе 9 может поместиться 1 раз – значит, в частном пишем 1;
- теперь нужно умножить делитель 7 на первую цифру частного 1 – получится 7. Его надо записать под 9;
- из 9 вычесть 7 – получится 2.
Обратите внимание: полученная разность никогда не сможет быть равна или больше делителя. Если это произошло, значит, было неверно определено количество 7 в 9.
- так как 2 на 7 не делится, сносят вниз следующую цифру из двузначного делимого – 8. Получили 28. Его можно поделить на 7 – получится 4;
- эту цифру нужно записать рядом с 1 – получится 14. Это и будет частным в данном примере;
- но правильно оформить решение все-таки нужно, поэтому 7 умножают на 4 – получают результат 28, который и пишут под 28. Вычитают 28 из 28 – получают 0. Его пишут под чертой, которой подводят итог решения.
- в случае если остаток не равен нулю, то это – деление с остатком.
В первый класс идет не только малыш – родители вместе с ним начинают и заканчивают школу. Учитель не всегда имеет возможность объяснить каждому ученику ту или иную тему. И вот тогда родители должны научить свое чадо, что такое умножение, деление с остатком двузначного числа на однозначное. При переходе в третий класс задание усложнится – научить нужно будет делению с остатком и трехзначного числа на двузначное. Главное, набраться терпения и не ругать ребенка из-за малейшей оплошности. Тогда все получится, и математика, возможно, станет любимым школьным предметом.
stranadetstva.ru
