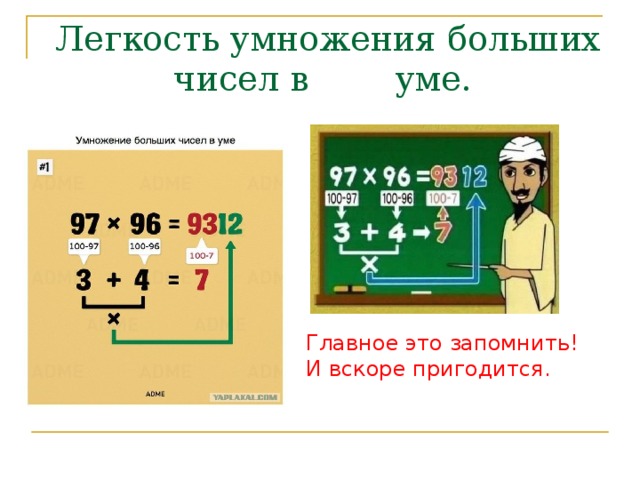
Как научиться умножать в уме: как научиться считать в уме - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Как считать в уме

Метки

Загадки Математика Примеры Смекалка Сообразительность

Как научиться считать в уме? И зачем это делать, ведь под рукой почти всегда есть калькулятор? Дело в том, что устный счет развивает мышление. Кроме того, когда ты считаешь без подручных средств, чувствуется совсем другой уровень контроля реальности.

Ты заранее знаешь, сколько сдачи тебе дадут в магазине и стоит ли набиваться всемером в лифт, если его грузоподъемность 400 кг. Использование же калькулятора, напротив, приучает нас слепо доверять технике, принципа работы которой мы даже не понимаем. Это притупляет внимание и отучает нас самостоятельно думать.

Как считать в уме

Ранее мы уже делились математическими секретами и хитростями, которые помогают умножать и делить в уме. А сегодня предлагаем твоему вниманию несколько проверочных примеров. Хорошо помнишь школьную программу? Тогда попробуй справиться с нашими заданиями за 15 секунд!

Посчитай без калькулятора
Сложи 1000 и 40. Прибавь еще 1000. Теперь 30. И снова 1000. Затем прибавь 20. И снова 1000. Еще 10. Решая эту задачку, постарайся все вычисления делать быстро и в уме. Ничего не пиши и не используй калькулятор. Уверены, что результат тебя удивит.
Сколько получится?
В школе мы щелкали такие примеры, как орешки. Но со временем много позабылось. Например, хоть кто-нибудь помнит, как делить на дробь?
Сложный пример и 15 секунд времени
Сплошные дроби, да еще и возведенные в степень… Кажется, что пример слишком сложный. Но, как говорил учитель математики, любое выражение можно упростить.
Будь внимателен
Ого, отрицательная степень! Сдаюсь. Кажется, я болел, когда мы это проходили.

Ответы

Казалось бы, всё просто. Однако комментарии убеждают в обратном. У большинства пользователей Сети почему-то получается 5000. А есть и такие, кто насчитал 5100, 4910 и даже 2060. При этом к последнему варианту ответа тяготеют юристы: мол, если перед числом нет слова «прибавь», значит считать его не обязательно.

© Pexels
На самом деле, правильным ответом будет 4100. 1000 + 40 = 1040; 1040 + 1000 = 2040; 2040 + 30 = 2070; 2070 + 1000 = 3070; 3070 + 1000 = 4090; 4090 + 10 = 4100. Но после 4090, когда люди прибавляют 10, у многих получается 5000. Видимо, в одних случаях мы психологически пытаемся подогнать ответ к более круглому числу. В других — вместо 90 запоминаем 900. Одним словом, это задача на внимательность, которой нам так часто не хватает.
Поделить число на дробь — это всё равно что умножить ее на эту же дробь, предварительно поменяв числитель и знаменатель местами. А любое число, умноженное на 0, всё равно 0. Тогда наш пример получает более понятный вид: 15 х 10 : 3 – 144 = 50 – 144 = –94.
С дробями мы уже немного разобрались. Умножение на дробь, в числителе которой единица, заменяем делением на знаменатель той же дроби. Поделить на одну вторую то же самое, что умножить на два. В результате получаем: 32 : 16 + 61 х 2 = 124
Похоже, что придется стряхнуть пыль с позабытого порядка математических действий. Мы все учили его в начальной школе: скобки, степень, умножение, деление, сложение, вычитание. Применяем правило и первым делом возводим в отрицательную степень одну пятую.
Для этого всего лишь нужно поменять местами числитель и знаменатель и возвести получившееся число в квадрат. Получается 25. Далее выполним деление, потом умножение и складываем. 25 : 25 + 12 : 2 х 3 = 1 + 6 х 3 = 1 + 18 = 19. Правильный ответ: 19.

Мы частенько возмущаемся, что в школе учат совсем не тому, что пригодится в реальной жизни. Да, наша система образования слишком устарела и продолжает устаревать каждый день. Но разносторонне образованный человек никогда не потеряется в какой-то затруднительной ситуации и обязательно сможет найти из нее выход.

10 математических секретов, которые научат легко считать в уме

Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.

1. Умножение на 11

Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:

Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2

Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.

Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Это срабатывает всегда.

2. Быстрое возведение в квадрат

Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25

2×3 = 6

625

3. Умножение на пять

Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.

Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:

2682×5 = (2682 / 2) & 5 или 0

2682 / 2 = 1341 (целое число, поэтому добавьте 0)

13410

Давайте попробуем другой пример:

5887×5

2943,5 (дробное число, пропустите запятую, добавьте 5)

29435

4. Умножение на девять

Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.

5. Умножение на четыре

Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.

6. Подсчёт чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:

15% от $25 = (10% от 25) + ((10% от 25) / 2)

$2.50 + $1.25 = $3.75

7. Сложное умножение

Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ:

32×125 всё равно что:

16×250 всё равно что:

8×500 всё равно что:

4×1000 = 4,000

8. Деление на пять

На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:

195 / 5

1. 195 * 2 = 390

2. Переносим запятую: 39,0 или просто 39.

2978 / 5

1. 2978 * 2 = 5956

2. 595,6

9. Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:

1000-648

1. От 9 отнимите 6 = 3

2. От 9 отнимите 4 = 5

3. От 10 отнимите 8 = 2

Ответ: 352

10. Систематизированные правила умножения

Умножение на 5: Умножьте на 10 и разделите на 2.

Умножение на 6: Иногда проще умножить на 3, а потом на 2.

Умножение на 9: Умножьте на 10 и отнимите исходное число.

Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.

Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.

Умножение на 14: Умножьте на 7, а затем на 2.

Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.

Умножение на 16: Если хотите, 4 раза умножьте на 2.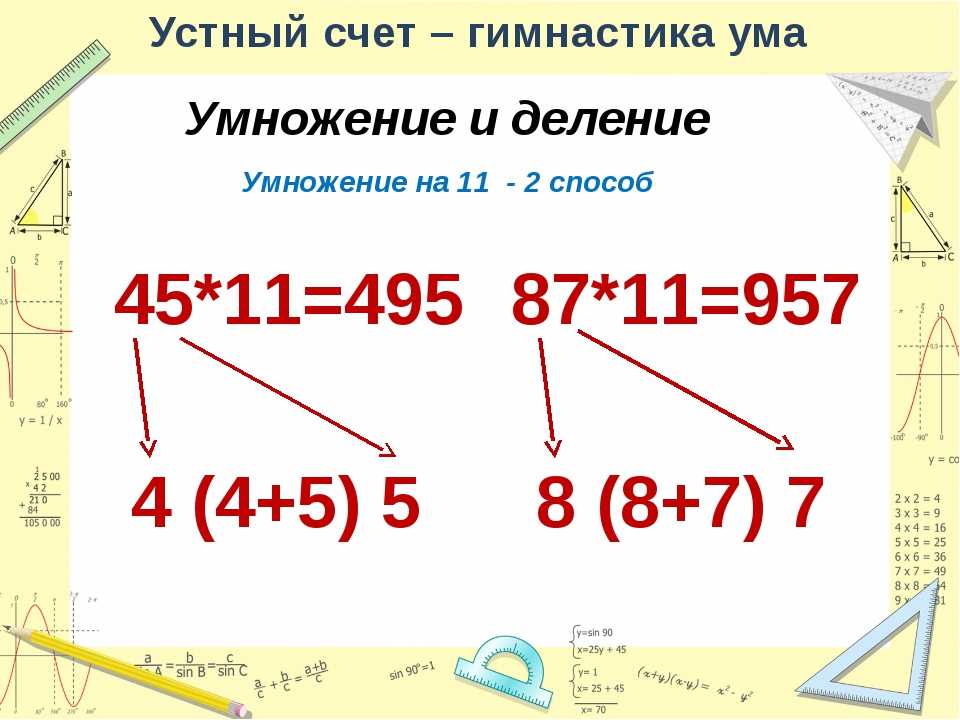 Или умножить на 8, а потом на 2.

Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.

Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.

Умножение на 19: Умножьте на 20 и отнимите исходное число.

Умножение на 24: Умножьте на 8, а потом на 3.

Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.

Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.

Умножение на 90: Умножьте на 9 и припишите 0.

Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.

Умножение на 99: Умножьте на 100 и отнимите исходное число.

БОНУС: проценты

Вычислить 7% от 300.

Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.

Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).

8% от 100 = 8.

35,73% от 100 = 35,73

Но как это может быть полезным? Вернёмся к задачке 7% от 300.

7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).

Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.

Примеры:

8%200 =? 8 + 8 = 16.

8%250 =? 8 + 8 + 4 = 20,

8%25 = 2,0 (Передвигаем запятую влево).

15%300 = 15+15+15 =45

15%350 = 15+15+15+7,5 = 52,5

Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.

Источник: Creu

Использование ментальной арифметики для умножения

Ключевые понятия

Понимание блочного умножения кратных 10

Различные примеры задач ментальной арифметики

Что вы имеете в виду под ментальной арифметикой?

Математика в уме включает в себя упрощение уравнений, чтобы узнать точный или приблизительный ответ. Как правило, задачи на умножение решаются с помощью ментальной арифметики путем уменьшения числа на 10 и 100 для решения больших чисел.

Пример 1:

В обычной коробке с карандашами 20 карандашей. Большая коробка вмещает 40 карандашей. На одной полке 4 коробки с обычными карандашами и 4 коробки с большими карандашами на другой полке. Сколько карандашей на каждой полке?

Решение:

Количество карандашей в обычной коробке = 20 карандашей

Количество коробок с обычными карандашами на одной полке = 4 коробки

Подумай о десятках

количество десятков.

4 x 20 = 4 x 2 десятка

4 x 20 = 8 десятков

4 x 20 = 80

Количество карандашей на одной полке = 80.

2. Количество карандашей в большой коробке = 40 карандашей

Количество коробок больших карандашей на другой полке = 4 коробки

Иногда основной факт умножения заставляет произведение выглядеть иначе.

4 x 40 = 4 x 4 десятка

4 x 40 = 16 десятков

4 x 40 = 160 десятков

Количество карандашей на другой полке = 160,

Пример 2:

В обычной коробке с фруктами 40 фруктов. Большая коробка вмещает 80 фруктов. На одной полке 5 коробок с обычными фруктами, а на другой полке 5 коробок с большими фруктами. Сколько фруктов на каждой полке?

Решение:

Количество фруктов в обычной коробке = 40 фруктов

Количество коробок обычных фруктов на себе = 5 коробок

Подумай об этом, умножь 5 на число десятков

5 х 40 = 5 х 4 десятки

5 x 40 = 20 десятков

5 x 40 = 200

Количество фруктов на одной полке = 200.=

товар выглядит иначе.

5 x 80 = 5 x 8 десятков

5 x 80 = 40 десятков

5 x 80 = 400

Количество фруктов на другой полке = 400.

десятки в 6 х 70.

Решение:

Дано 6 x 70

®Проверьте разрядность числа 70.

В разряде десятков «7 десятков».

Количество из десяти в 6 x 70 = 420

Существует 20 десятков в 6 x 70.

Пример 4:

Найдите продукт 9 x 80.

Решение:

. Дано 9 x 80. х 80

9 х 80 = 9 х 8 десятков

9 х 80 = 72 десятка

9 х 80 = 720

Произведение 9 х 80 = 720,

Пример 5:

Найдите недостающее число уравнения, которое делает его верным.

9 х? = 630

Решение:

Учитывая 9 x? = 630

9 x? = 63 десятки

Из таблицы умножения мы знаем, что 9 x 7 = 63.

Если умножить на 10, то вместо единицы прибавится 0, т. е. 10 x 7 = 70

Недостающее число уравнения что делает его верным = 70.

Пример 6:

Алекс и его семья идут в кинотеатр. Есть 2 взрослых и 3 детей. Сколько будут стоить билеты?

Решение:

Стоимость билета в кино для ребенка = 10$

Общая стоимость билета в кино для 3 детей = 3 x 10$ = 30$

Стоимость билета в кино для взрослого = 30$

Общая стоимость билета в кино для 2 взрослых = 2 x 30$ = 60$

Стоимость билета для взрослых и детей = 30$ + 60$ = 9$0

Оценка

Найдите произведение 2 x 30, используя блочное умножение.
Найдите пропущенное значение 8 x ___ = 640.

Какое значение делает приведенное ниже уравнение верным? (Анализ)
3 x ? = 90
Велосипед стоит 210 долларов. Сколько заплатят за 20 таких велосипедов?
В коробке 20 упаковок печенья. В каждой пачке 10 бисквитов. Сколько печенья можно упаковать в 30 пакетов?
4 папки, в каждой по 50 листов бумаги. Сколько всего листов бумаги?
Какое значение делает приведенное ниже уравнение верным?
10 х ? = 80

Что мы узнали:

Блочное умножение кратных 10

Подведем итоги

Концептуальная карта:

Стратегии умножения Прогресс | Департамент образования

Добро пожаловать в асинхронный модуль, Стратегии умножения Прогресс . В своем собственном темпе читайте материалы, смотрите короткие видеоклипы и разбирайтесь в картинках. Этот модуль длится примерно 1 час и может быть завершен за один присест или небольшими частями. Когда вы пройдете модуль, щелкните ссылку на анкету в поле справа. После успешной отправки анкеты ваш сертификат часа контакта будет автоматически отправлен по электронной почте на адрес, указанный в анкете. Если у вас есть какие-либо вопросы об этом процессе или содержании этого модуля, свяжитесь с Джен Робитайл по адресу [email protected].

Стратегии умножения
Стратегии перечислены от самых ранних стратегий до стандартного алгоритма. Многие из них используются параллельно, но важно понимать, что различные стратегии используются для более глубокого концептуального понимания и перехода к более процедурной модели, основанной на концептуальном понимании умножения. Имейте в виду, что освоение стандартного алгоритма умножения не ожидается до 5-го класса в соответствии с результатами обучения штата Мэн и общими базовыми стандартами штата, однако учащиеся начнут практиковать стандартный алгоритм наряду с другими стратегиями намного раньше 5-го класса.

Модели
Существует множество моделей умножения, каждая из которых демонстрирует различные способы отображения числа равных групп. Когда учащиеся впервые начинают работать с умножением, они могут использовать квадратные плитки для построения массивов или небольших чисел, которые они могут построить из манипуляций. Затем они переносят свои модели на чертежи равных групп, возможно, используя метки, точки, и по мере того, как они переходят к большим количествам, они могут использовать цифры для представления групп – это хорошо переходит к повторному добавлению, или они могут перейти к модели области. Контекст проблемы определяет тип модели, которая поможет учащимся разобраться в проблеме. Напоминаем, что учащимся нужны различные типы задач (отсутствующий множитель – количество групп, отсутствующий множитель – недостающее количество в группе, недостающий продукт – общее количество), чтобы практиковать свою гибкость в умножении. Эти разные типы задач должны быть представлены в разное время в процессе их обучения. Для получения дополнительной информации о различных типах задач на умножение, которые должны использовать учащиеся, ознакомьтесь с таблицей 2 глоссария из Общего основного государственного стандарта по математике.

Повторное сложение
Одной из первых стратегий умножения является многократное сложение. Когда учащиеся узнают о равных группах, они начинают добавлять одно и то же дополнение снова и снова (повторное добавление). 7 коробок по 5 карандашей могут выглядеть как 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35 карандашей. Учащиеся могут начать замечать, что повторяющееся сложение очень похоже на пропуск счета по добавляемому числу. 7 коробок по 5 карандашей могут звучать как 5, 10, 15, 20, 25, 30, 35 карандашей. Студенты должны будут отслеживать каждые 5, которые они пропускают, пока не доберутся до 7 раз или 7 коробок с карандашами. Когда учащиеся ищут более эффективные стратегии, они начинают запоминать некоторые из своих фактов и использовать их в других стратегиях.

Массивы (модели)

Умножение формы модели массива — это физическая или визуальная модель, демонстрирующая равные строки. Учащиеся могут использовать физические объекты или манипуляторы, или они могут рисовать фигуры для моделирования задачи на умножение, которую они решают. Эта стратегия прекрасно сочетается с вспомогательными фактами, удвоением и площадной моделью.

Вспомогательные факты и удвоение
Использование вспомогательных фактов позволяет учащимся опираться на известные им факты, облегчая решение более сложных задач. Учащиеся обычно сначала узнают факты о своих двойках, пятерках и десятках. С детского сада они считают 2, 5 и 10. Используя эти факты, они могут создавать более сложные проблемы. Чтобы решить 6 x 7, учащийся может думать о задаче как о 6 группах по 7, и если он знает, что 5 групп по 7 или 5 x 7 = 35, то он знает, что ему нужна дополнительная группа из 7 до 35 + 7 = 42. так что 6 х 7 = 42,
Удвоение — аналогичная стратегия с использованием вспомогательного факта или известного факта, составляющего половину исходной задачи. Например, 4 x 9 может быть сложно обдумать, но, поскольку учащиеся лучше знакомы с фактами о 2, 5 и 10, они могут знать, что 2 x 9 = 18. Думая, что 2 x 9 = 18 – это половина 4 x 9. , они могут затем удвоить 18. Учащиеся могут изобразить это как 18 x 2 или 18 + 18. На самом деле математически 4 x 9 разбивается на (2 x 9) + (2 x 9), что равно 36. Пожалуйста, посмотрите видео для другого примера, который использует удвоение и модель площади для объяснения.

Модель площади (подключается к делению)
Модель площади для умножения использует визуальное прямоугольное представление для отображения площади и может быть разбита различными способами, чтобы помочь решить большие и меньшие задачи на умножение. Учащиеся могут использовать блоки с основанием 10 для физического построения модели местности, затем переходя к графическим представлениям с некоторой детализацией по основанию 10, а затем к менее подробным представлениям. Это прекрасно ведет к модели площади для деления. Чтобы увидеть продемонстрированную модель области, посмотрите видео.

Частичные продукты
Модель площадей прекрасно ведет к стратегии частичного продукта. Подобно сложению, частичные произведения разбивают множители или умножаемые числа на их разрядные значения или развернутую форму. Чтобы начать частичные продукты, учащиеся могут использовать модель области, чтобы визуализировать, откуда берется каждый частичный продукт. По мере того, как учащиеся будут понимать частичные произведения, они смогут использовать эту стратегию без модели площадей, хотя им, возможно, придется продолжать возвращаться к модели площадей, поскольку числа, с которыми они работают, расширяются до более чем двух цифр.

Решетчатое умножение
Решетчатое умножение — это стратегия, которая при обучении с правильными разрядными значениями помогает учащимся понять, почему эта стратегия работает. При обучении после понимания частичных продуктов учащиеся могут установить связи между стратегиями. Это может показаться набором шагов или процедурным процессом, очень похожим на стандартный алгоритм, поэтому важны разговоры о стоимости.

Стандартный алгоритм США
Стандартный алгоритм — это стратегия, о которой думает большинство людей, когда их просят умножать большие числа.