Магнитное поле, характеристика магнитного поля
Для понимания того, что является характеристикой магнитного поля, следует дать определения многим явлениям. При этом заранее нужно вспомнить, как и почему оно появляется. Узнать, что является силовой характеристикой магнитного поля. При этом немаловажно то, что подобное поле может встречаться не только у магнитов. В связи с этим не помешает упомянуть характеристику магнитного поля земли.
Возникновение поля
Для начала следует описать возникновение поля. После можно описать магнитное поле и его характеристики. Оно появляется во время перемещения заряженных частиц. Может влиять на перемещающиеся электрические заряды, в особенности на токопроводящие проводники. Взаимодействие между магнитным полем и движущимися зарядами, либо проводниками, по которым течет ток, происходит благодаря силам, именуемым электромагнитными.
Интенсивность или силовая характеристика магнитного поля в определенной пространственной точке определяются с помощью магнитной индукции. Последняя обозначается символом В.
Последняя обозначается символом В.
Графическое представление поля
Магнитное поле и его характеристики могут быть представлены в графической форме с помощью линий индукции. Данным определением называют линии, касательные к которым в любой точке будут совпадать с направлением вектора у магнитной индукции.
Названные линии входят в характеристику магнитного поля и применяются для определения его направления и интенсивности. Чем выше интенсивность магнитного поля, тем больше данных линий будет проведено.
Что такое магнитные линии
Магнитные линии у прямолинейных проводников с током имеют форму концентрической окружности, центр которой располагается на оси данного проводника. Направление магнитных линий возле проводников с током определяется по правилу буравчика, которое звучит так: если буравчик будет расположен так, что он будет ввинчиваться в проводник по направлению тока, тогда направление обращения рукоятки соответствует направлению магнитных линий.
У катушки с током направление магнитного поля будет определяться также по правилу буравчика. Также требуется вращать рукоятку по направлению тока в витках соленоида. Направление линий магнитной индукции будет соответствовать направлению поступательного движения буравчика.
Также требуется вращать рукоятку по направлению тока в витках соленоида. Направление линий магнитной индукции будет соответствовать направлению поступательного движения буравчика.
Определение однородности и неоднородности является основной характеристикой магнитного поля.
Создаваемое одним током, при равных условиях, поле будет различаться по своей интенсивности в разных средах из-за различающихся магнитных свойств в этих веществах. Магнитные свойства среды характеризуются абсолютной магнитной проницаемостью. Измеряется в генри на метр (г/м).
В характеристику магнитного поля входит абсолютная магнитная проницаемость вакуума, называемая магнитной постоянной. Значение, определяющее, во сколько раз абсолютная магнитная проницаемость среды будет отличаться от постоянной, именуется относительной магнитной проницаемостью.
Магнитная проницаемость веществ
Это безразмерная величина. Вещества, имеющие значение проницаемости менее единицы, зовутся диамагнитными. В данных веществах поле будет слабее, чем в вакууме. Данные свойства присутствуют у водорода, воды, кварца, серебра и др.
Данные свойства присутствуют у водорода, воды, кварца, серебра и др.
Среды с магнитной проницаемостью, превышающей единицу, зовутся парамагнитными. В данных веществах поле будет сильнее, чем в вакууме. К данным средам и веществам относят воздух, алюминий, кислород, платину.
В случае с парамагнитными и диамагнитными веществами значение магнитной проницаемости не будет зависеть от напряжения внешнего, намагничивающего поля. Это означает, что величина является постоянной для определенного вещества.
К особой группе относятся ферромагнетики. У данных веществ магнитная проницаемость будет достигать нескольких тысяч и более. У названных веществ, имеющих свойство намагничиваться и усиливать магнитное поле, существует широкое использование в электротехнике.
Напряженность поля
Для определения характеристик магнитного поля вместе с вектором магнитной индукции может применяться значение, именуемое напряженностью магнитного поля. Данный термин является векторной величиной, определяющей интенсивность внешнего магнитного поля. Направление магнитного поля в среде с одинаковыми свойствами по всем направлениям вектор напряженности будет совпадать с вектором магнитной индукции в точке поля.
Направление магнитного поля в среде с одинаковыми свойствами по всем направлениям вектор напряженности будет совпадать с вектором магнитной индукции в точке поля.
Сильные магнитные свойства у ферромагнитов объясняются присутствием в них произвольно намагниченных малых частей, которые могут быть представлены в виде малых магнитов.
С отсутствующим магнитным полем ферромагнитное вещество может не иметь выраженных магнитных свойств, поскольку поля доменов приобретают разную ориентацию, и их общее магнитное поле равняется нулю.
По основной характеристике магнитного поля, если ферромагнит будет помещен во внешнее магнитное поле, к примеру, в катушку с током, то под влиянием наружного поля домены развернутся по направлению внешнего поля. Притом магнитное поле у катушки усилится, и магнитная индукция увеличится. Если же наружное поле достаточно слабое, то перевернётся лишь часть от всех доменов, магнитные поля которых по направлению близятся к направлению наружного поля. На протяжении увеличения силы внешнего поля число повернутых доменов будет возрастать, и при определенном значении напряжения внешнего поля почти все части будут развернуты так, что магнитные поля расположатся по направлению наружного поля.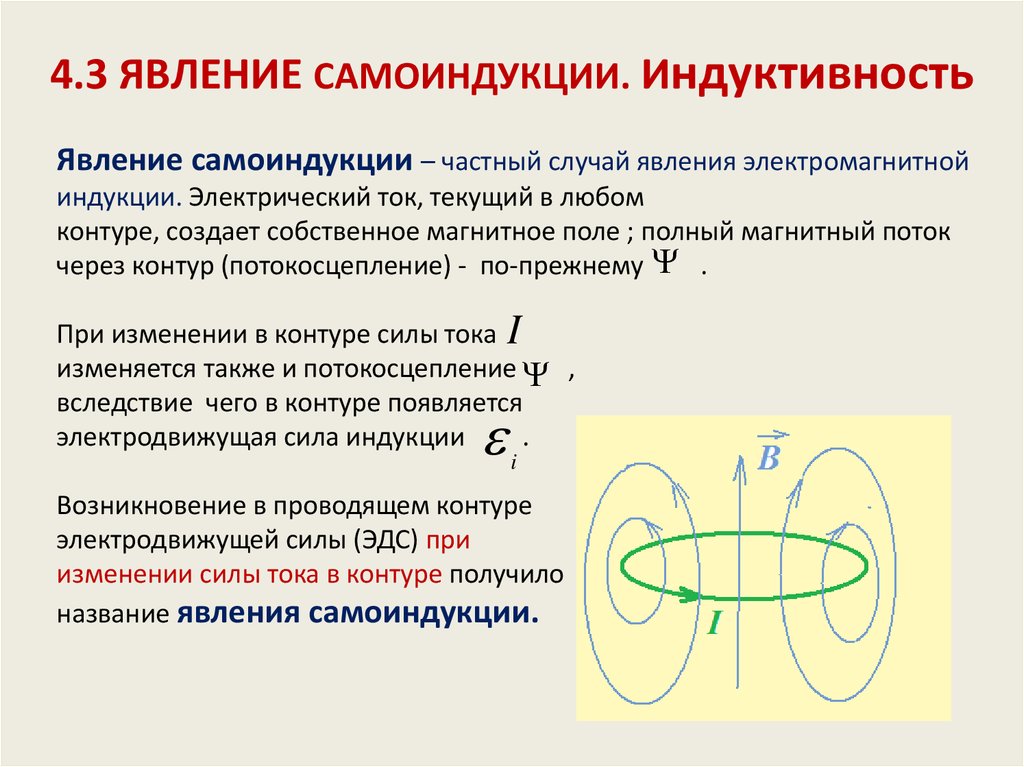 Данное состояние именуется магнитным насыщением.
Данное состояние именуется магнитным насыщением.
Связь магнитной индукции и напряженности
Взаимосвязанность магнитной индукции ферромагнитного вещества и напряженности внешнего поля может изображаться при помощи графика, называемого кривой намагничивания. В месте изгиба графика кривой скорость возрастания магнитной индукции уменьшается. После изгиба, где напряженность достигает определённого показателя, происходит насыщение, и кривая незначительно поднимается, постепенно приобретая форму прямой. На данном участке индукция все еще растет, однако достаточно медленно и лишь за счет возрастания напряженности внешнего поля.
Графическая зависимость данных показателя не является прямой, значит, их отношение не постоянно, и магнитная проницаемость материала не постоянный показатель, а находится в зависимости от наружного поля.
Изменения магнитных свойств материалов
При увеличении силы тока до полного насыщения в катушке с ферромагнитным сердечником и последующим ее уменьшением кривая намагничивания не будет совпадать с кривой размагничивания. С нулевой напряженностью магнитная индукция не будет иметь такое же значение, а приобретет некоторый показатель, именуемый остаточной магнитной индукцией. Ситуация с отставанием магнитной индукции от намагничивающей силы именуется гистерезисом.
С нулевой напряженностью магнитная индукция не будет иметь такое же значение, а приобретет некоторый показатель, именуемый остаточной магнитной индукцией. Ситуация с отставанием магнитной индукции от намагничивающей силы именуется гистерезисом.
Для полного размагничивания ферромагнитного сердечника в катушке требуется дать ток обратной направленности, который создаст необходимую напряженность. Для разных ферромагнитных веществ необходим отрезок различной длины. Чем он больше, тем больший объем энергии необходим для размагничивания. Значение, при котором происходит полное размагничивание материала, именуется коэрцитивной силой.
При дальнейшем увеличении тока в катушке индукция вновь увеличится до показателя насыщения, но с иным направлением магнитных линий. При размагничивании в обратном направлении будет получена остаточная индукция. Явление остаточного магнетизма применяется при создании постоянных магнитов из веществ с большим показателем остаточного магнетизма. Из веществ, имеющих способность к перемагничиванию, создаются сердечники для электрических машин и приборов.
Правило левой руки
Сила, влияющая на проводник с током, обладает направлением, определяемым по правилу левой руки: при расположении ладони девой руки таким образом, что магнитные линии входят в нее, и четыре пальца вытянуты по направлению тока в проводнике, отогнутый большой палец укажет направление силы. Данная сила перпендикулярна вектору индукции и току.
Перемещающийся в магнитном поле проводник с током считается прообразом электродвигателя, который изменяет электрическую энергию в механическую.
Правило правой руки
Во время движения проводника в магнитном поле внутри него индуцируется электродвижущая сила, которая имеет значение, пропорциональное магнитной индукции, задействованной длине проводника и скорости его перемещения. Данная зависимость называется электромагнитной индукцией. При определении направления индуцированной ЭДС в проводнике используют правило правой руки: при расположении правой руки так же, как в примере с левой, магнитные линии входят в ладонь, а большой палец указывает направление перемещения проводника, вытянутые пальцы укажут направление индуктированной ЭДС. Перемещающийся в магнитном потоке под влиянием внешней механической силы проводник является простейшим примером электрического генератора, в котором преобразуется механическая энергия в электрическую.
Перемещающийся в магнитном потоке под влиянием внешней механической силы проводник является простейшим примером электрического генератора, в котором преобразуется механическая энергия в электрическую.
Закон электромагнитной индукции может быть сформулирован по-другому: в замкнутом контуре происходит индуцирование ЭДС, при любой смене магнитного потока, охватываемого данным контуром, ЭДЕ в контуре численно равняется скорости смены магнитного потока, который охватывает данный контур.
Данная форма предоставляет усреднённый показатель ЭДС и указывает на зависимость ЭДС не от магнитного потока, а от скорости его изменения.
Закон Ленца
Также нужно вспомнить закон Ленца: ток, индуцируемый при изменении магнитного поля, проходящего через контур, своим магнитным полем препятствует этому изменению. Если витки у катушки пронизываются разными по величине магнитными потоками, то индуцированная по целой катушке ЭДС равняется сумме ЭДЕ в разных витках. Сумма магнитных потоков разных витков катушки именуется потокосцеплением. Единица измерения данной величины, как и магнитного потока, – вебер.
Единица измерения данной величины, как и магнитного потока, – вебер.
При изменении электрического тока в контуре происходит смена и созданного им магнитного потока. При этом, согласно закону электромагнитной индукции, внутри проводника происходит индуцирование ЭДС. Она появляется в связи со сменой тока в проводнике, потому данное явление называют самоиндукцией, и индуцированная в проводнике ЭДС именуется ЭДС самоиндукции.
Потокосцепление и магнитный поток находятся в зависимости не от одной только силы тока, но и от величины и формы данного проводника, и магнитной проницаемости окружающего вещества.
Индуктивность проводника
Коэффициент пропорциональности именуется индуктивностью проводника. Он обозначает способность проводника создавать потокосцепление при прохождении сквозь него электричества. Это является одним из основных параметров электрических цепей. Для определенных цепей индуктивность является постоянным показателем. Она будет зависеть от величины контура, его конфигурации и магнитной проницаемости среды. При этом сила тока в контуре и магнитный поток не будут иметь значения.
При этом сила тока в контуре и магнитный поток не будут иметь значения.
Вышеописанные определения и явления дают объяснение тому, что является магнитным полем. Также приводятся основные характеристики магнитного поля, с помощью которых можно дать определение данного явления.
Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
ОпределениеМагнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
ОпределениеВектор магнитной индукции — силовая характеристика магнитного поля.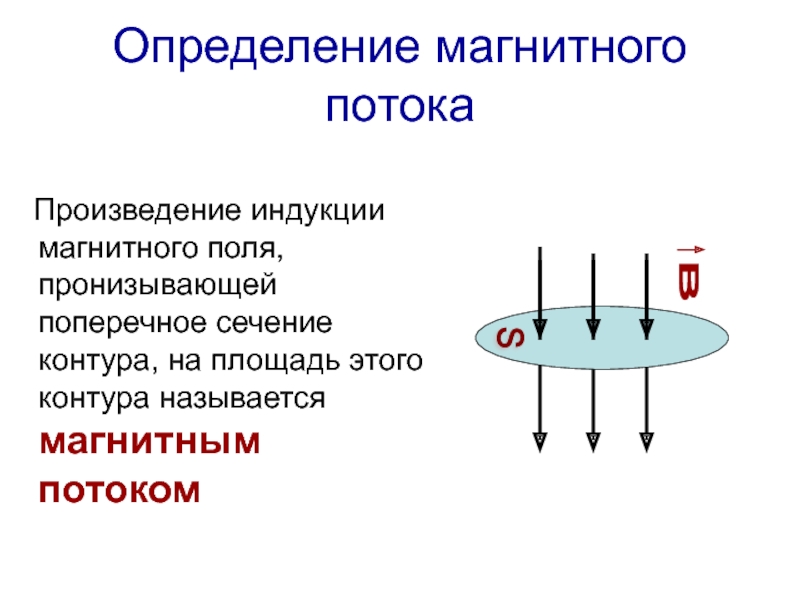 Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl..
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
ОпределениеВектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0..
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.

- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа | |
| От нас перпендикулярно плоскости чертежа |
Пример №1.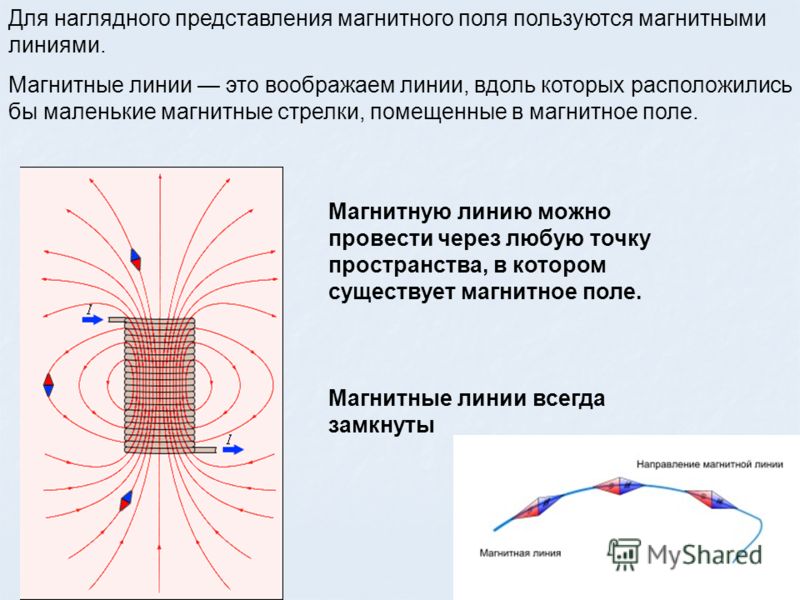 На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Вид сверху:
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr..
Модуль напряженности:
H=I2πr.
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R..
Модуль напряженности в центре витка:
H=I2R..
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
ОпределениеСоленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld..
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl..=μμ0Id..
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl..=Id..
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов.
На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: гpазбирался: Алиса Никитина | обсудить разбор | оценить
Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.

- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: гpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18266Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.
Алгоритм решения
- Определить направление тока в соленоиде.

- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 18k | Оценить:
Магнитное Поле
Если два параллельно расположенных проводника подсоединить к источнику тока так, чтобы по ним прошел электрический ток, то в зависимости от направления тока в них проводники либо отталкиваются, либо притягиваются.
Объяснение этого явления возможно с позиции возникновения вокруг проводников особого вида материи – магнитного поля.
Силы,
с которыми взаимодействуют проводники
с током, называютсямагнитными.
Магнитное поле – это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела.
История
магнетизма уходит корнями в глубокую
древность, к античным цивилизациям
Малой Азии. Именно на территории Малой
Азии, в Магнезии, находили горную породу,
образцы которой притягивались друг к
другу. По названию местности такие
образцы и стали называть “магнетиками”.
Любой магнит в форме стержня или подковы
имеет два торца, которые называются
полюсами; именно в этом месте сильнее
всего и проявляются его магнитные
свойства. Если подвесить магнит на
нитке, один полюс всегда будет указывать
на север. На этом принципе основан
компас. Обращенный на север полюс
свободно висящего магнита называется
северным полюсом магнита (N). Противоположный
полюс называется южным полюсом (S).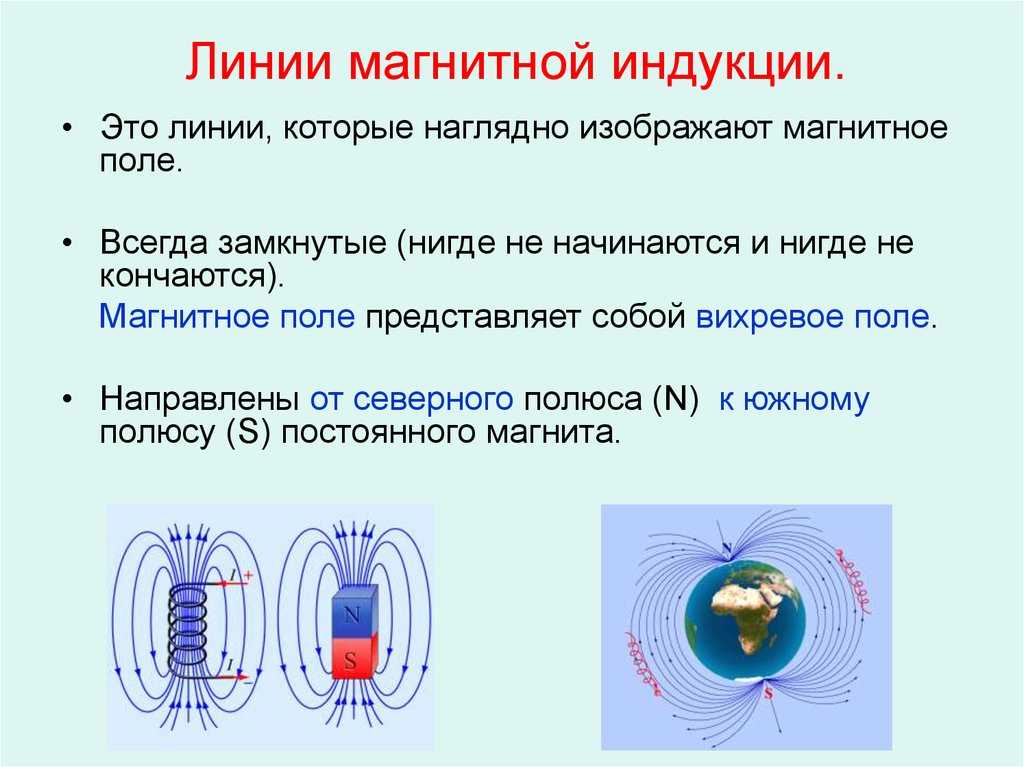
Магнитные полюсы взаимодействуют друг с другом: одноименные полюсы отталкиваются, а разноименные – притягиваются. Аналогично концепции электрического поля, окружающего электрический заряд, вводят представление о магнитном поле вокруг магнита.
В 1820 г. Эрстед (1777-1851) обнаружил, что магнитная стрелка, расположенная рядом с электрическим проводником, отклоняется, когда по проводнику течет ток, т. е. вокруг проводника с током создается магнитное поле. Если взять рамку с током, то внешнее магнитное поле взаимодействует с магнитным полем рамки и оказывает на нее ориентирующее действие, т. е. существует такое положение рамки, при котором внешнее магнитное поле оказывает на нее максимальное вращающее действие, и существует положение, когда вращающий момент сил равен нулю.
Магнитное
поле в любой точке можно охарактеризовать
вектором В, который называется вектором
магнитной индукции или магнитной
индукцией в
точке.
Магнитная индукция В – это векторная физическая величина, являющаяся силовой характеристикой магнитного поля в точке. Она равна отношению максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на ее площадь:
За направление вектора магнитной индукции В принимается направление положительной нормали к рамке, которое связано с током в рамке правилом правого винта, при механическом моменте, равном нулю.
Точно так же, как изображали линии напряженности электрического поля, изображают линии индукции магнитного поля. Линия индукции магнитного поля – воображаемая линия, касательная к которой совпадает с направлением В в точке.
Направления магнитного поля в данной точке можно определить еще как направление, которое указывает
северный
полюс стрелки компаса, помещенный в эту
точку. Считают, что линии индукции
магнитного поля направлены от северного
полюса к южному.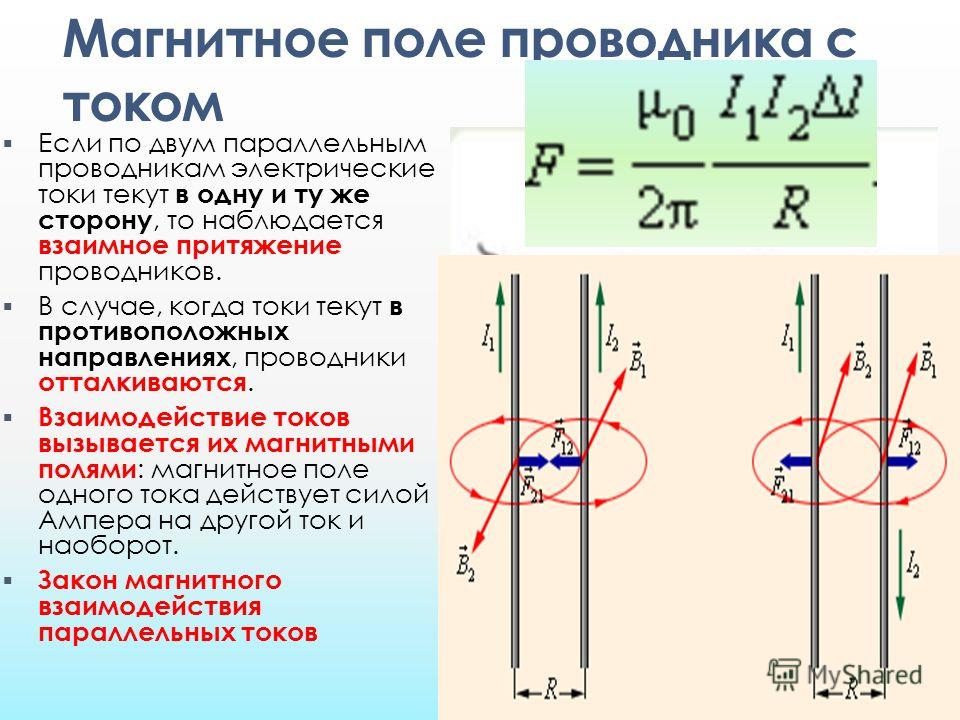
Направление линий магнитной индукции магнитного поля, созданного электрическим током, который течет по прямолинейному проводнику, определяется правилом буравчика или правого винта. За направление линий магнитной индукции принимается направление вращения головки винта, которое обеспечивало бы поступательное его движение по направлению электрического тока (рис. 59).
где n01= 4Пи• 10-7В • с/(А • м). – магнитная постоянная, R – расстояние, I – сила тока в проводнике.
В отличие от линий напряженности электростатического поля, которые начинаются на положительном заряде и оканчиваются на отрицательном, линии индукции магнитного поля всегда замкнуты. Магнитного заряда аналогично электрическому заряду не обнаружено.
За
единицу индукции принимается одна тесла
(1 Тл) – индукция такого однородного
магнитного поля, в котором на рамку
площадью 1 м2,
по которой течет ток в 1 А, действует
максимальный вращающий механический
момент сил, равный 1 Н • м.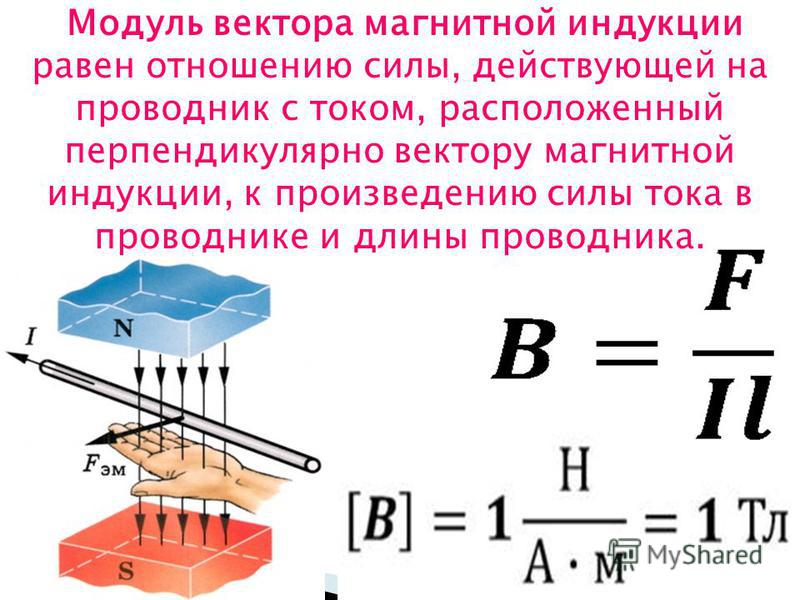
Индукцию магнитного поля можно определить и по силе, действующей на проводник с током в магнитном поле.
На проводник с током, помещенный в магнитное поле, действует сила Ампера, величина которой определяется следующим выражением:
где I – сила тока в проводнике, l –длина проводника, В – модуль вектора магнитной индукции, а – угол между вектором и направлением тока.
Направление силы Ампера можно определить по правилу левой руки: ладонь левой руки располагаем так, чтобы линии магнитной индукции входили в ладонь, четыре пальца располагаем по направлению тока в проводнике, то отогнутый большой палец показывает направление силы Ампера.
Учитывая,
что I = q0nSv,
и подставляя это выражение в (3.21), получим
F = q0nSh/B
sin a.
Число частиц (N) в заданном объеме
проводника равно N = nSl, тогда F = q0NvB
sin a.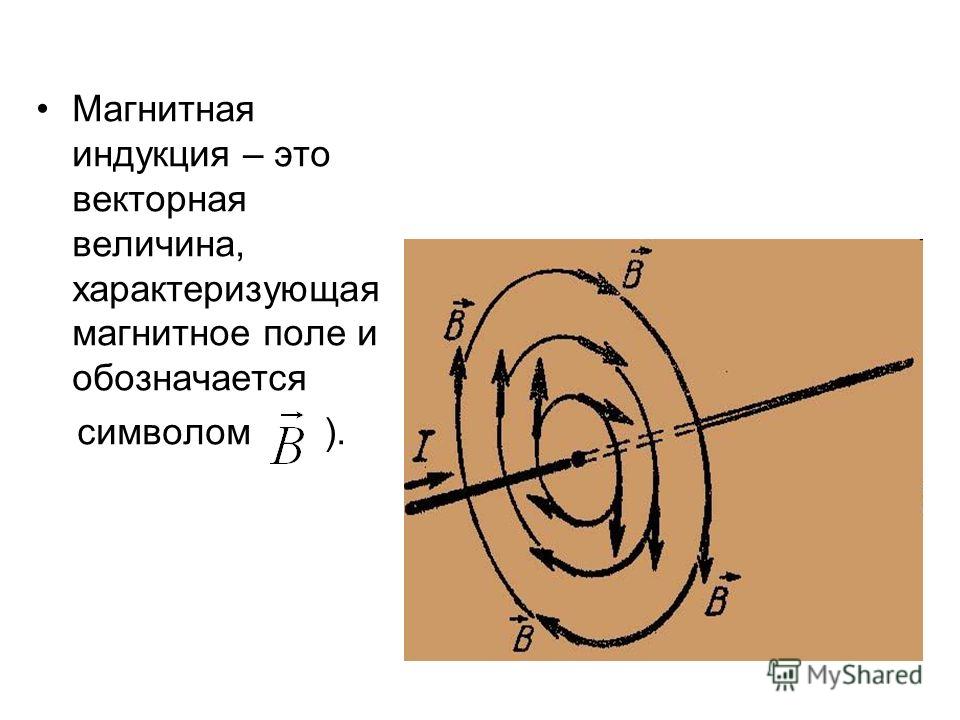
Определим силу, действующую со стороны магнитного поля на отдельную заряженную частицу, движущуюся в магнитном поле:
Эту силу называют силой Лоренца (1853-1928). Направление силы Лоренца можно определить по правилу левой руки: ладонь левой руки располагаем так, чтобы линии магнитной индукции входили в ладонь, четыре пальца показывали направление движения положительного заряда, большой отогнутый палец покажет направление силы Лоренца.
Сила взаимодействия между двумя параллельными проводниками, по которым текут токи I1 и I2 равна:
где l
–часть
проводника, находящаяся в магнитном
поле. Если токи одного направления, то
проводники притягиваются (рис. 60), если
противоположного направления –
отталкиваются. Силы, действующие на
каждый проводник, равны по модулю,
противоположны по направлению. Формула
(3.22) является основной для определения
единицы силы тока 1 ампер (1 А).
Магнитные свойства вещества характеризует скалярная физическая величина – магнитная проницаемость, показывающая во сколько раз индукция В магнитного поля в веществе, полностью заполняющем поле, отличается по модулю от индукции В0 магнитного поля в вакууме:
По своим магнитным свойствам все вещества делятся на диамагнитные, парамагнитные и ферромагнитные.
Рассмотрим природу магнитных свойств веществ.
Электроны в оболочке атомов вещества движутся по различным орбитам. Для упрощения считаем эти орбиты круговыми, и каждый электрон, обращающийся вокруг атомного ядра, можно рассматривать как круговой электрический ток. Каждый электрон, как круговой ток, создает магнитное поле, которое назовем орбитальным. Кроме того, у электрона в атоме есть собственное магнитное поле, называемое спиновым.
Если
при внесении во внешнее магнитное поле
с индукцией В0внутри
вещества создается индукция В < В0,
то такие вещества называются
диамагнитными (n
< 1).
В диамагнитных материалах при отсутствии внешнего магнитного поля магнитные поля электронов скомпенсированы, и при внесении их в магнитное поле индукция магнитного поля атома становится направленной против внешнего поля. Диамагнетик выталкивается из внешнего магнитного поля.
У парамагнитных материалов магнитная индукция электронов в атомах полностью не скомпенсирована, и атом в целом оказывается подобен маленькому постоянному магниту. Обычно в веществе все эти маленькие магниты ориентированы произвольно, и суммарная магнитная индукция всех их полей равна нулю. Если поместить парамагнетик во внешнее магнитное поле, то все маленькие магниты – атомы повернутся во внешнем магнитном поле подобно стрелкам компаса и магнитное поле в веществе усиливается (n >= 1).
Ферромагнитными называются
такие материалы, в которых n ”
1. В ферромагнитных материалах создаются
так называемые домены, макроскопические
области самопроизвольного намагничивания.
В разных доменах индукции магнитных полей имеют различные направления (рис. 61) и в большом кристалле
взаимно компенсируют друг друга. При внесении ферромагнитного образца во внешнее магнитное поле происходит смещение границ отдельных доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается.
С увеличением индукции внешнего поля В0 возрастает магнитная индукция намагниченного вещества. При некоторых значениях В0индукция прекращает резкий рост. Это явление называется магнитным насыщением.
Характерная особенность ферромагнитных материалов – явление гистерезиса, которое заключается в неоднозначной зависимости индукции в материале от индукции внешнего магнитного поля при его изменении.
Петля
магнитного гистерезиса – замкнутая
кривая (cdc`d`c), выражающая зависимость
индукции в материале от амплитуды
индукции внешнего поля при периодическом
достаточно медленном изменении последнего
(рис. 62).
62).
Петля гистерезиса характеризуется следующими величинами Bs, Br, Bc. Bs– максимальное значение индукции материала при В0s; Вr – остаточная индукция, равная значению индукции в материале при уменьшении индукции внешнего магнитного поля от B0s до нуля; -Вс и Вс – коэрцитивная сила – величина, равная индукции внешнего магнитного поля, необходимого для изменения индукции в материале от остаточной до нуля.
Для каждого ферромагнетика существует такая температура (точка Кюри (Ж. Кюри, 1859-1906), выше которой ферромагнетик утрачивает свои ферромагнитные свойства.
Существует два способа приведения намагниченного ферромагнетика в размагниченное состояние: а) нагреть выше точки Кюри и охладить; б) намагничивать материал переменным магнитным полем с медленно убывающей амплитудой.
Ферромагнетики,
обладающие малой остаточной индукцией
и коэрцитивной силой, называются
магнитомягкими.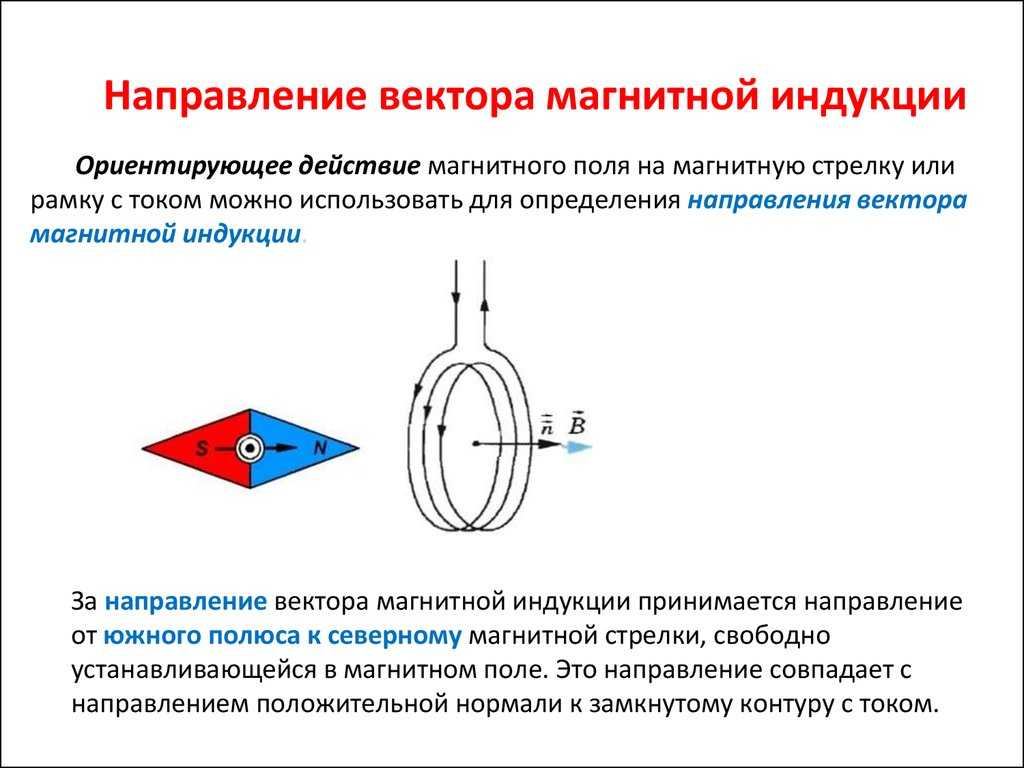 Они находят применение
в устройствах, где ферромагнетику
приходится часто перемагничиваться
(сердечники трансформаторов, генераторов
и др.).
Они находят применение
в устройствах, где ферромагнетику
приходится часто перемагничиваться
(сердечники трансформаторов, генераторов
и др.).
Магнитожесткие ферромагнетики, обладающие большой коэрцитивной силой, применяются для изготовления постоянных магнитов.
55 билет
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
F = BIlsina (a – угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.
Если проводник имеет произвольную формулу и поле неоднородно, тоЗакон Ампера принимает вид:
dF = I*B*dlsina
Закон Ампера в векторной форме:
dF = I [dl B]
Сила
Ампера направлена перпендикулярно
плоскости, в которой лежат векторы dl и
B.
Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
56 билет
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающиемагнитным моментом, независимо от состояния их движения[1], магнитная составляющаяэлектромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов ватомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Кроме этого, оно появляется при наличии изменяющегося во времениэлектрического поля.
Основной
силовой характеристикой магнитного
поля является вектор
магнитной индукции (вектор
индукции магнитного поля)[3][4]. С математической точки зрения — векторное
поле,
определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
С математической точки зрения — векторное
поле,
определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.
Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции а векторнапряжённости магнитного поля , что формально можно сделать, так как в вакууме эти два вектора совпадают[5]; однако в магнитной среде вектор не несет уже того же физического смысла[6], являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно
Магнитное
поле можно назвать особым видом
материи[7],
посредством которого осуществляется
взаимодействие между движущимися
заряженными частицами или телами,
обладающимимагнитным
моментом.
Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.
Вместе, магнитное и электрическое поля образуютэлектромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.
Электрический ток(I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника.
С точки зрения квантовой теории поля магнитное взаимодействие — как частный случайэлектромагнитного взаимодействияпереносится фундаментальным безмассовымбозоном — фотоном(частицей, которую можно представить как квантовое возбуждение электромагнитного поля), часто (например, во всех случаях статических полей) — виртуальным.
Содержание [убрать]
|
Напряженность магнитного поля [Encyclopedia Magnetica]
Содержание
Напряженность магнитного поля
Плотность магнитного потока B
Трудность с определением
Аналог электрических цепей
Электрическая цепь
Магнитная цепь
H из-за электрического тока
H из-за M и B
Уравнения Максвелла
H в электромагнитных волнах
Определение H с силой
Поколение H
Соленоид
Катушка Гельмгольца
Магнитопровод с малым зазором
Поле размагничивания
Измерение H
Энергия и плотность энергии
Петля гистерезиса и потери мощности
Модели петли B-H
Коэрцитивная сила
См.
 также
такжеКаталожные номера
Напряженность магнитного поля H – физическая величина, используемая в качестве одной из основных мер напряженности магнитного поля. Единицей напряженности магнитного поля является ампер на метр или А/м .
Электрический ток $I$ создает напряженность магнитного поля $H$, величина которого не зависит от типа однородной изотропной окружающей среды (магнитная или немагнитная)
С инженерной точки зрения напряженность магнитного поля $H$ можно рассматривать как возбуждение, а плотность магнитного потока $B$ как отклик среды. Это соглашение об именах определено в системе единиц СИ.
С точки зрения теоретической физики поле $H$ определяется как векторная разность между плотностью потока $B$ и намагниченностью $M$.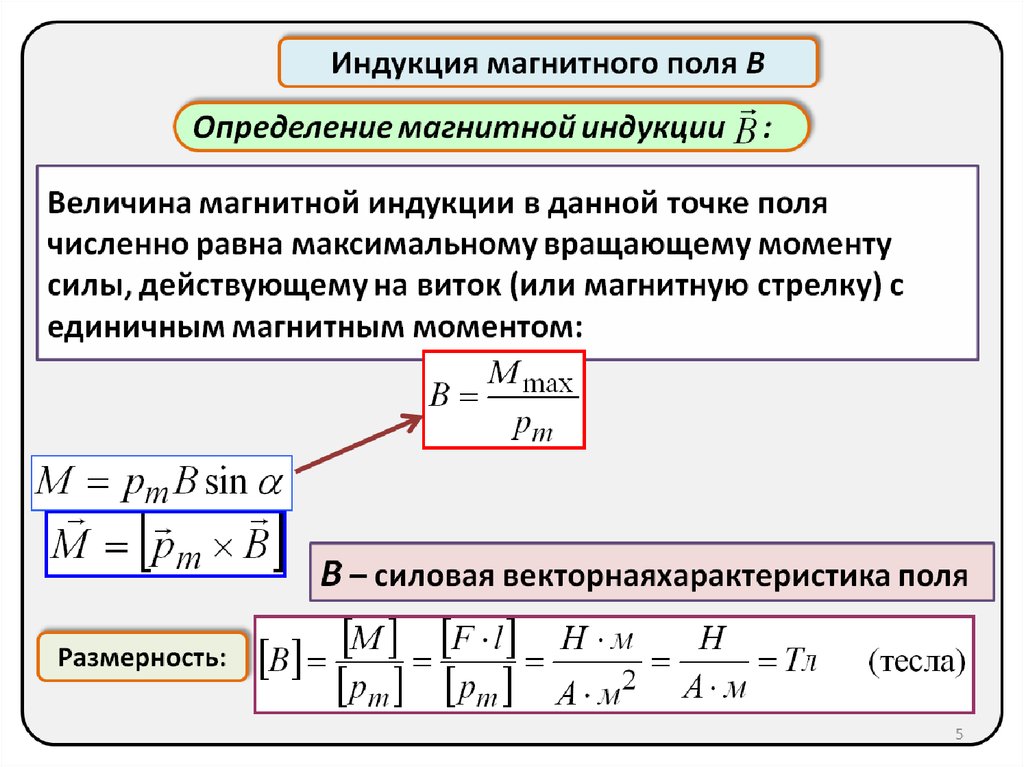 Поле H иногда называют «вспомогательным» или просто «полем H».
Поле H иногда называют «вспомогательным» или просто «полем H».
Эти два подхода идентичны в смысле рассматриваемых физических величин (с одними и теми же физическими единицами А/м), но называются разными именами, и разные акценты делаются на их значении и использовании при выводе некоторых уравнений.
Магнитное поле является векторным полем в пространстве и представляет собой разновидность энергии, полное количественное определение которой требует знания векторных полей как напряженности магнитного поля $H$, так и плотности потока $B$ (или других связанных с ними величин, таких как намагниченность M или поляризация J ). В вакууме векторы $H$ и $B$ в каждой точке ориентированы в одном направлении и прямо пропорциональны проницаемости свободного пространства, но в других средах они могут быть несовмещены (особенно в неоднородных или анизотропных материалах).
Требование двух величин аналогично, например, электричеству. Для полной количественной оценки эффектов электричества требуются как электрическое напряжение $V$, так и электрический ток $I$. количество передаваемой энергии.
Для полной количественной оценки эффектов электричества требуются как электрическое напряжение $V$, так и электрический ток $I$. количество передаваемой энергии.
Название напряженность магнитного поля и символ $H$ определены Международного бюро мер и весов (BIPM) как одна из когерентных производных физических единиц. Поэтому, строго говоря, другие имена, такие как напряженность магнитного поля или магнитное поле (или даже просто поле ), которые можно встретить в повседневном техническом жаргоне , неверны, если используются при ссылке на конкретное значение H в A/ м.
В литературе используется много других названий, обозначающих одно и то же количество:
напряженность магнитного поля H
магнитное поле H
поле H
поле H’
Напряженность H-поля
H-поле
напряженность поля намагничивания H
напряженность поля намагничивания H
сила намагничивания H
магнитная сила H
интенсивность магнитной силы H
вспомогательное поле H
и, возможно, несколько других.

| → → → Полезная страница? Поддержите нас! → → → | PayPal | ← ← ← Помогите нам с всего $0,10 в месяц? Давай… ← ← ← |
Плотность магнитного потока B
| См. отдельную статью по : Плотность магнитного потока |
| См. отдельную статью о : Путаница между B и H |
Иллюстрация напряженности магнитного поля H , плотности потока B , намагниченности M и поляризация Дж в ферромагнетике
Плотность магнитного потока B является отдельной физической величиной с разными физическими единицами в системе СИ. H и B взаимосвязаны таким образом, что:
| \vec{M}) $$ | (Т) |
| где: $µ_0$ – абсолютная проницаемость вакуума (Гн/м), $µ_r$ – относительная проницаемость материала (безразмерная), $µ = µ_0 · µ_r$ – абсолютная проницаемость материала (Гн/м), $ J$ – магнитная поляризация (Тл), $M$ – намагниченность (А/м) | |
Намагниченность M представляет собой ориентацию субатомных магнитных дипольных моментов на единицу объема, а магнитная поляризация J равна M в масштабе проницаемости вакуума.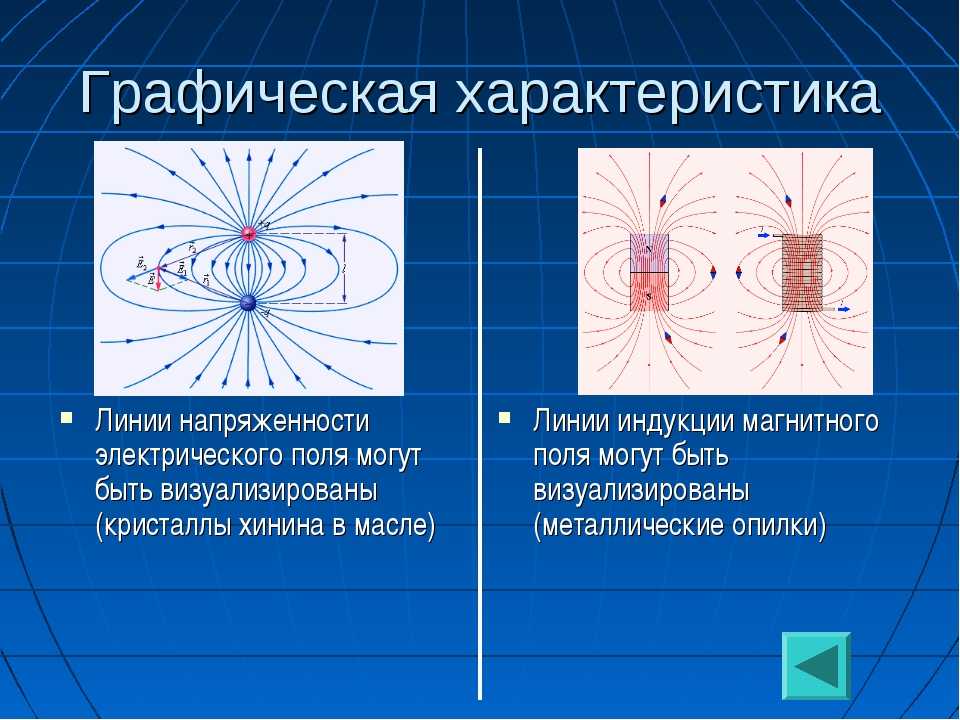
В общем случае все три вектора B , H и J (или B , H и M ) могут указывать в разных направлениях (как показано на рисунке для анизотропного материала) , но всегда так, что векторная сумма в приведенном выше уравнении выполняется.
Для одноосного намагничивания уравнение можно упростить до скалярной формы, которая широко используется в технических приложениях:
| $$B = µ_0 · µ_r · H = µ · H $$ | (T) |
Относительная магнитная проницаемость $μ_r$ является показателем качества магнитомягких материалов и имеет значения, значительно превышающие единицу.
Для магнитотвердых материалов $µ_r \приблизительно$ 1, и это гораздо менее важный параметр.
Для немагнитных материалов также $µ_r \приблизительно$ 1, но такое, что парамагнетики слабо притягиваются к любой полярности магнитного поля ($µ_r$ чуть больше единицы), а диамагнетики всегда слабо отталкиваются ($µ_r$ чуть меньше единство). В зависимости от точки зрения сверхпроводники можно отнести к идеальным диамагнетикам, для которых $µ_r$ = 0, а значит, они достаточно сильно отталкиваются от магнитного поля, достаточного для магнитной левитации.
В зависимости от точки зрения сверхпроводники можно отнести к идеальным диамагнетикам, для которых $µ_r$ = 0, а значит, они достаточно сильно отталкиваются от магнитного поля, достаточного для магнитной левитации.
Трудность с определением
Трудно дать краткое определение такой базовой величине, как магнитное поле, но разные авторы дают хотя бы описательный вариант. То же самое относится к напряженности магнитного поля , а также к другой базовой величине – плотности магнитного потока .
В таблице ниже приведены некоторые примеры определений $H$, данных в литературе (приведены точные цитаты).
| Публикация | Определение магнитного поля | Определение напряженности магнитного поля $H$ | Определение плотности магнитного потока |
|---|---|---|---|
Р. Фейнман, Р. Лейтон, М. Сэндс Лейтон, М. Сэндс Фейнмановские лекции по физике | Во-первых, мы должны несколько расширить наши представления об электрическом и магнитном векторах, E и 9 92$ в качестве нового числа 1/μ 0 | Мы можем записать силу F, действующую на заряд q, движущийся со скоростью v, как $$\mathbf{F} = q(\mathbf{E} + \mathbf {v} × \mathbf{B})$$ Мы называем E электрическим полем, а B магнитным полем в месте расположения заряда. | |
| Ричард М. Бозорт Ферромагнетизм | Магнит будет притягивать кусок железа, даже если они не соприкасаются, и считается, что это действие на расстоянии вызвано магнитным полем , или силовое поле. | Напряженность силового поля, напряженность магнитного поля или намагничивающая сила H могут быть определены с точки зрения магнитных полюсов: в одном сантиметре от единичного полюса напряженность поля равна одной эрстеде. | Фарадей показал, что некоторые свойства магнетизма можно уподобить потоку, и представил бесконечные линии индукции , которые представляют направление и, своей концентрацией, поток в любой точке. […] Общее количество линий, пересекающих данную область под прямым углом, является потоком в этой области. Поток на единицу ар – это плотность потока, или магнитная индукция и обозначается символом B. |
| Дэвид С. Джайлс Введение в магнетизм и магнитные материалы | Одной из самых фундаментальных идей в магнетизме является концепция магнитного поля. Когда поле генерируется в объеме пространства, это означает, что происходит изменение энергии этого объема и, кроме того, существует градиент энергии, так что создается сила, которую можно обнаружить по ускорению электрического заряда, движущегося в нем. поле, силой, действующей на проводник с током, крутящим моментом на магнитном диполе, таком как стержневой магнит, или даже переориентацией спинов электронов внутри определенных типов атомов. | Существует несколько способов определения напряженности магнитного поля H. В соответствии с развитыми здесь идеями мы хотим подчеркнуть связь между магнитным полем H и генерирующим электрическим током. […] Самое простое определение следующее. Ампер на метр — это напряженность поля, создаваемого бесконечно длинным соленоидом, содержащим n витков на метр катушки и пропускающим ток силой 1 /n ампер. | Когда магнитное поле H создается в среде током, в соответствии с законом Ампера реакция среды представляет собой ее магнитную индукцию B, также иногда называемую плотностью потока. |
| Магнитное поле , Encyclopaedia Britannica | Магнитное поле, область вблизи магнитного поля, электрического тока или изменяющегося электрического поля, в которой наблюдаются магнитные силы. | Магнитное поле H можно рассматривать как магнитное поле, создаваемое протеканием тока в проводах […] | […] магнитное поле B [можно рассматривать] как полное магнитное поле, включая также вклад, вносимый магнитными свойствами материалов в поле. |
| Э. М. Перселл, Д. Дж. Морин, Электричество и магнетизм | Это взаимодействие токов и других движущихся зарядов можно описать, введя магнитное поле. […] Мы предлагаем продолжать называть $\mathbf{B}$ магнитным полем. | Если теперь определить векторную функцию $\mathbf{H}(x, y, z)$ в каждой точке пространства соотношением $$ \mathbf{H} \equiv \frac{\mathbf{ B}}{µ_0} – \mathbf{M} $$ […] Что касается $\mathbf{H}$, хотя для него придуманы и другие названия, мы будем называть его полем $\mathbf{H} $, или даже магнитное поле $\mathbf{H}$. | […] на любую движущуюся заряженную частицу, оказавшуюся в этом поле, действует сила […], определяемая выражением $$ \mathbf{F} = q·\mathbf{E} + q·\mathbf{v} × \mathbf{B} $$ […] Мы возьмем уравнение в качестве определения $\mathbf{B}$. |
Аналог электрических цепей
Электрическая цепь
На фундаментальном уровне все электричество связано с наличием и движением электрических зарядов, поэтому знания их положения было бы достаточно для полной количественной оценки всех электрических эффектов, включая электрическое поле. Однако на практике гораздо проще оперировать непосредственно измеряемыми величинами, такими как ток $I$ и напряжение $V$.
Однако на практике гораздо проще оперировать непосредственно измеряемыми величинами, такими как ток $I$ и напряжение $V$.
С макроскопической точки зрения, значения $I$ и $V$ необходимы для полной количественной оценки влияния электричества в электрических цепях. В цепях постоянного тока пропорциональность между $V$ и $I$ определяется электрическим сопротивлением $R$ данной среды (согласно закону Ома), таким что $V = R·I$.
Произведение $V$ и $I$ пропорционально мощности $P$ и энергии $E$ в данной электрической цепи.
Магнитная цепь
По аналогии и напряженность магнитного поля $H$, и плотность магнитного потока $B$ (или их представление другими связанными переменными) необходимы для количественной оценки эффектов магнетизма в магнитных цепях. Соотношение между $H$ и $B$ диктуется магнитной проницаемостью $µ$ данной среды.
Все эффекты магнитного поля также связаны с движением и внутренними свойствами электрических зарядов. Зная эти свойства (например, спиновой магнитный момент) и детали движения зарядов (с учетом релятивистских эффектов), можно было бы полностью описать магнитное поле. Однако на практике гораздо проще, особенно с инженерной точки зрения, использовать непосредственно измеряемые величины, такие как $H$ и $B$, для количественного определения мощности и энергии в данной магнитной цепи.
Однако на практике гораздо проще, особенно с инженерной точки зрения, использовать непосредственно измеряемые величины, такие как $H$ и $B$, для количественного определения мощности и энергии в данной магнитной цепи.
Произведение $H$ и $B$ в стационарных условиях является мерой удельной энергии в Дж/м 3 , запасенной в магнитном поле, содержащемся в данной среде. Произведение $B·H$ (количество накопленной энергии) используется, например, для классификации постоянных магнитов.
Н за счет электрического тока
Амплитуда напряженности магнитного поля $H$ уменьшается по мере удаления от проводника с электрическим током $I$
Ориентация Прочность на магнитное поле $ H $ VECT
С макроскопической точки зрения поля можно рассматривать как усредненные по некоторому объему материала, а их величины можно связать с измеряемыми сигналами, такими как ток или напряжение. Поэтому этот подход широко используется в технике.
Поэтому этот подход широко используется в технике.
$H$ всегда генерируется вокруг электрического тока $I$, который может быть сплошным проводником с током или просто движущимся электрическим зарядом (также в свободном пространстве). Направление вектора $H$ перпендикулярно направлению порождающего его тока $I$, и предполагается, что направления векторов подчиняются правилу правой руки. Можно сказать, что H «циркулирует» вокруг текущего I .
Без других источников магнитного поля и в однородной и изотропной среде напряженность генерируемого магнитного поля $H$ зависит только от величины и направления электрического тока $I$ и задействованных физических размеров (например, длины и диаметра проводника и т. д.). .) поэтому по закону Ампера пропорциональность определяется длиной магнитного пути $l$:
| $$ \int_C \vec{H} · d \vec{l} = I $$ | (A) |
| где: C – замкнутый путь, по которому вычисляется интеграл, $dl$ – бесконечно малый фрагмент длины магнитного пути (м), $I$ – ток (А) | |
В линейной изотропной среде значения из разных источников объединяются и могут быть вычислены из суперпозиции источников. Для простых геометрических случаев значение $H$ можно вычислить аналитически, а для очень сложных систем можно выполнить расчет, например, с помощью конечно-элементного моделирования.
Для простых геометрических случаев значение $H$ можно вычислить аналитически, а для очень сложных систем можно выполнить расчет, например, с помощью конечно-элементного моделирования.
Связь между $H$ и $I$ часто показывается с помощью закона Био-Савара или закона Ампера. Часто (но не всегда ) оба они задаются с переменной плотности потока $B$, так что автоматически учитывается проницаемость среды.
Во многих примерах, приводимых в литературе, имеется неявное предположение (обычно не оговариваемое), что вывод ведется для вакуума, а не для произвольной среды с другой магнитной проницаемостью . Когда проницаемость $μ_0$ приведена в уравнениях с обеих сторон, то $H$ пропорциональна только $I$ и это верно для любой однородной изотропной среды с любой проницаемостью, даже нелинейной.
Ситуация несколько иная для анизотропной или прерывистой среды. Они могут вызывать дополнительные источники магнитного поля, так как возбужденная среда может генерировать новые магнитные полюса, которые необходимо учитывать для точного описания распределения $H$. Например, полюсные наконечники в электромагните влияют на $H$, распределение которого больше не определяется только катушками с электрическим током.
Например, полюсные наконечники в электромагните влияют на $H$, распределение которого больше не определяется только катушками с электрическим током.
H due to M and B
H , B , M , and J in a paramagnet
Микроскопическая точка зрения часто используется в теоретической физике.
Каждый атом реагирует на приложенное извне магнитное поле B некоторой намагниченностью M , которая определяется как векторная сумма магнитных моментов на данный объем. «Вспомогательное» магнитное поле H тогда определяется как как разность векторов между приложенным магнитным полем B и намагниченностью M :
| $$\vec{H} = \frac{\vec{B}} {μ_0} – \vec{M}$$ | (А/м) |
| где: $μ_0$ – абсолютная проницаемость вакуума (Гн/м) | |
Для возбуждения постоянным током в немагнитных или магнитных, но изотропных материалах векторы B и H параллельны. Для ферромагнитных (и других упорядоченных структур) анизотропия кристалла или формы может вводить значительный угол между двумя векторами.
Для ферромагнитных (и других упорядоченных структур) анизотропия кристалла или формы может вводить значительный угол между двумя векторами.
Уравнения Максвелла
Уравнения Максвелла обычно даются относительно плотности магнитного потока B , потому что в такой форме они справедливы при более общих условиях.
Однако при определенных условиях их также можно выразить по отношению к H . Этот подход широко используется в численных расчетах, таких как моделирование методом конечных элементов (МКЭ), где прямая связь между электрическим током (выражаемым плотностью тока J ) и H используется с помощью закона Ампера как для решений, так и для формулировок граничных условий.
| Пример обозначения, используемого в документации по МКЭ (после ссылки ) | |
|---|---|
| $$ \nabla · \mathbf{D} = ρ$$ | $$ \nabla · \mathbf{B} = 0$$ |
| $$ \nabla \times \mathbf{E} = – \frac {\partial \mathbf{B}}{\partial t}$$ | $$ \nabla \times \mathbf{H} = \mathbf{J} + \frac {\partial \mathbf{D}}{\partial t} $$ |
H в электромагнитных волнах
В вакууме при отсутствии зарядов и токов уравнения Максвелла упрощаются, и их можно записать либо относительно плотности магнитного потока B (как показано в таблице ниже), либо напряженности магнитного поля H . Это можно сделать из-за линейности вакуума (или другой немагнитной среды), в котором нет свободных зарядов, поэтому нет дополнительных электрических токов, которые приходится учитывать. Формат с B действителен при более общих условиях.
Это можно сделать из-за линейности вакуума (или другой немагнитной среды), в котором нет свободных зарядов, поэтому нет дополнительных электрических токов, которые приходится учитывать. Формат с B действителен при более общих условиях.
| Уравнения Максвелла в вакууме (в дифференциальной форме) | |||
|---|---|---|---|
| магнитное поле, представленное H | магнитное поле, представленное B | ||
| $$ \text{div} \mathbf{E} = 0$$ | $$ \text{div} \mathbf{H} = 0$$ | $$ \text{div} \mathbf{ Е} = 0$$ | $$ \text{div} \mathbf{B} = 0$$ |
| $$ \text{curl} \mathbf{E} = – \mu_0 · \frac {\partial \mathbf{H}}{\partial t}$$ | $$ \text{curl} \mathbf{ H} = \epsilon_0 · \frac {\partial \mathbf{E}}{\partial t} $$ | $$ \text{curl} \mathbf{E} = – \frac {\partial \mathbf{B} }{\partial t}$$ | $$ \text{curl} \mathbf{B} = \mu_0 · \epsilon_0 · \frac {\ partial \mathbf{E}}{\partial t} $$ |
В вакууме две записи с B или H точно эквивалентны, причем последний весьма популярен для анализа излучения антенн. Например, используя вектор Пойнтинга, который представляет мощность как произведение электрического поля E в В/м и магнитного поля H в А/м, результатом будет В·А/м 2 или Вт/м м 2 (удельная мощность).
Например, используя вектор Пойнтинга, который представляет мощность как произведение электрического поля E в В/м и магнитного поля H в А/м, результатом будет В·А/м 2 или Вт/м м 2 (удельная мощность).
Определение H с силой
В литературе показано, что напряженность магнитного поля в данной точке пространства можно определить как механическую силу, действующую на единичный полюс в данной точке. Однако для расчета силы требуется $B$, что зависит от свойств среды. Действительно, в первоначальном эксперименте, проведенном Био и Саваром, использовались физические силы, действующие на провода.
Силы, действующие на два намагниченных тела, будут разными, если их поместить в кислород (парамагнитный) или в воду (диамагнитный). Эта разница будет прямо пропорциональна относительной проницаемости вовлеченных сред. Однако $H$, создаваемый вокруг провода, будет одинаковым (пока среда однородна и изотропна).
Величина магнитной силы (силы Лоренца) всегда пропорциональна плотности потока $B$.
Поколение H
Известные значения H получены с использованием упомянутых выше законов Ампера или Био-Савара. Если можно пренебречь релятивистскими эффектами, то пропорциональность точно прямая такая, что мгновенным значениям напряженности магнитного поля $H$ соответствуют мгновенные значения приложенного тока $I$:
| $$ H(t) = c · I(t) $$ | (А/м) |
| где: $c$ – константа пропорциональности данного контура (1/м) | |
При определенных условиях генерируемое магнитное поле может быть рассчитано настолько точно, что его можно использовать для калибровки других датчиков или определения значений, как это рекомендовано BIPM.
Двумя типичными устройствами, которые можно использовать для получения известных значений H , являются соленоид и катушка Гельмгольца. Их можно использовать даже в комбинированной установке, в которой внешние катушки Гельмгольца компенсируют магнитное поле Земли (или другие нежелательные источники), а внутренний соленоид создает точно известное магнитное поле.
Их можно использовать даже в комбинированной установке, в которой внешние катушки Гельмгольца компенсируют магнитное поле Земли (или другие нежелательные источники), а внутренний соленоид создает точно известное магнитное поле.
Соленоид
Соленоид часто используется как источник известного значения напряженности магнитного поля H , которую можно рассчитать для его геометрического центра (черная точка)
| См. также основной артикул: Соленоид |
В бесконечно длинном однородном соленоиде величина H на его оси зависит только от величины тока в катушке и числа витков на единицу длины. 92}} \приблизительно \frac{N·I}{l} $$
Если толщина проволоки в соленоиде значительна или имеется много слоев катушки, в уравнении требуются дополнительные поправочные члены.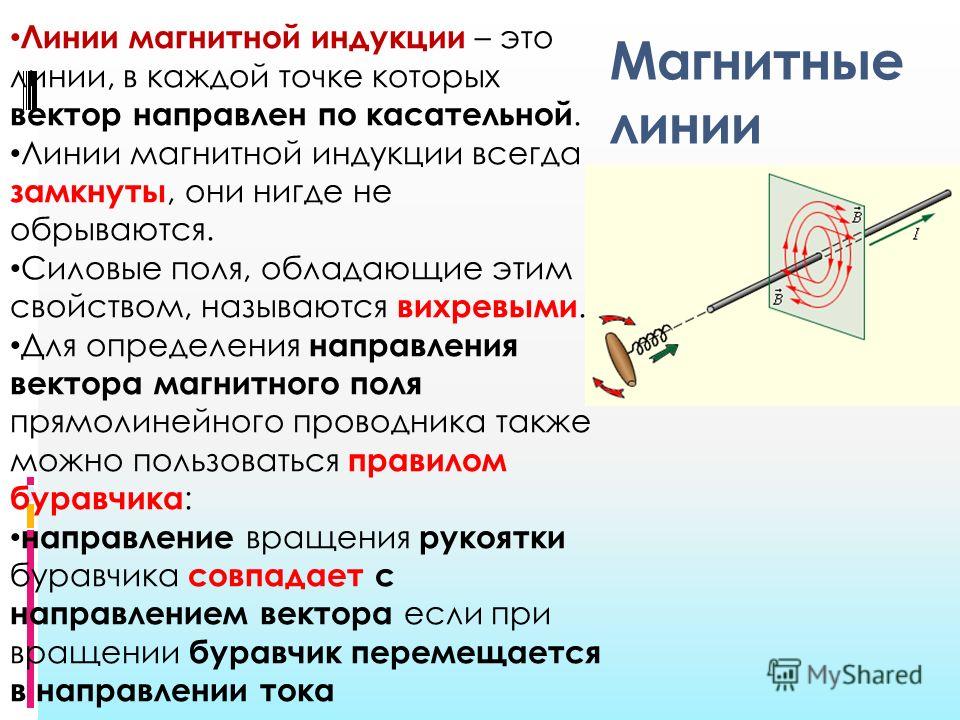
Катушка Гельмгольца
| См. также основную статью: Катушка Гельмгольца |
Другим широко используемым источником H является катушка Гельмгольца . Устройство состоит из двух одинаковых катушек, напоминающих круговые токовые петли, расположенных параллельно на одной оси и разделенных точно радиусом окружности.
Для двух катушек, каждая с радиусом r и каждая из которых содержит число витков N , каждая из которых , значение магнитного поля в геометрическом центре можно рассчитать как: 93}}{2·r} \приблизительно \frac{0,35777·N_{всего}·I}{r} $$
Также используются формы, отличные от круглых (например, квадратные), но за счет однородности полученного распределения поля.
Катушка Гельмгольца является точным источником магнитного поля в ее геометрическом центре (черная точка)
Путь движущихся электронов, изогнутых в окружность магнитным полем, создаваемым внешней катушкой Гельмгольца (красная круглая форма на заднем плане) М. Бялек, Wikimedia Commons, CC-BY-SA-3.0
Набор из трех больших ортогональных катушек Гельмгольца, используемых для компенсации магнитного поля Земли в 3D
Магнитопровод с малым зазором
Закон Ампера связывает интеграл вокруг замкнутого пути с током, протекающим по такому пути.
Это соотношение широко используется в технике с использованием понятия магнитодвижущей силы (произведение тока и витков катушки, выраженное в ампер-витках). Для простой магнитной цепи с одним воздушным зазором можно написать, что:
Для простой магнитной цепи с одним воздушным зазором можно написать, что:
| $$ N·I = H_{core}·l_{core} + H_{gap}·l_{gap} $$ | (А-витки) ≡ (A) |
| где: $N$ – число витков обмотки (безразмерное), $I$ – ток (А), $H_{core}$ – H в сердечнике (А/м), $l_{ core}$ – длина жилы (м), $H_{gap}$ – H в воздушном зазоре (А/м), $l_{gap}$ – длина воздушного зазора (м) | |
В магнитопроводе с относительно небольшим воздушным зазором значение плотности магнитного потока таково, что $B_{зазор} \ приблизительно B_{сердечник}$. Однако значение H требуется для поддержки некоторого значения B масштабируется обратной величиной относительной проницаемости. Следовательно, для магнитного материала с большой магнитной проницаемостью приводит к условию $H_{core} \ll H_{gap}$, а также к $H_{core}·l_{core} \ll H_{gap}·l_{gap }$, поэтому существенными являются только члены, относящиеся к воздушному зазору. Это позволяет упростить уравнение следующим образом:
Это позволяет упростить уравнение следующим образом:
| $$ H_{зазор} \приблизительно \frac{N·I}{l_{зазор}} $$ | (А/м) |
| где: $N$ – число витков обмотки (безразмерное), $I$ – ток (А), $l_{зазор}$ – длина воздушного зазора (м) | |
Однако для более сложных магнитных цепей необходимо учитывать такие эффекты, как окантовка потока или магнитная энергия, хранящаяся в материале, и это можно сделать с помощью численных методов, таких как моделирование методом конечных элементов.
Добавление воздушного зазора позволяет накапливать в нем энергию. Петля B-H «срезается», расширяя операцию до более высоких Н . Эти эффекты широко используются, например, в обратноходовых трансформаторах.
Magnetic circuit with magnetic path and air gap
Large electromagnet with an air gap; разработан с использованием упрощенного уравнения
Добавление случаев воздушного зазора Срезание контура B-H, линеаризация контура и расширение насыщения до более высокого уровня H
Поле размагничивания
Упрощенное изображение намагничивания в $M$$ корпусе $H_d
Магнитное поле создается не только электрическими токами, но и магнитными моментами, которые могут запасать магнитную энергию, например, путем выравнивания за счет ранее примененного процесса намагничивания. Совокупность таких собственных магнитных моментов составляет намагниченность $M$ и становится источником магнитного поля, как это имеет место в постоянных магнитах. Если создаются магнитные полюса, то линии магнитного поля ($H$) обычно предполагаются направленными от северного к южному полюсу.
Совокупность таких собственных магнитных моментов составляет намагниченность $M$ и становится источником магнитного поля, как это имеет место в постоянных магнитах. Если создаются магнитные полюса, то линии магнитного поля ($H$) обычно предполагаются направленными от северного к южному полюсу.
Силовые линии магнитного поля будут замыкаться через среду, окружающую магнит, а также через сам магнит в направлении, противоположном намагниченности $M$, уменьшая тем самым эффективную намагниченность тела, поэтому этот эффект называется поле размагничивания $H_d$.
Эффект можно количественно оценить с помощью безразмерного коэффициента размагничивания $N_d$, который пропорционален намагниченности и зависит от размеров тела, так что для очень длинных конструкций или для магнитно-замкнутых цепей $N_d=0$ и для тонкие плоские структуры бесконечных размеров, намагниченные перпендикулярно поверхности $N_d=1$.
Значение коэффициента размагничивания можно вычислить аналитически для эллипсоидов и других очень простых геометрических фигур, а также для сферы $N_d=1/3$.
| $$H_d = – N_d·M $$ | (А/м) |
| где: $N_d$ – коэффициент размагничивания (безразмерный), $M$ – намагниченность (А/м) | |
Размагничивающее поле $H_d$ в однородно намагниченном теле $M$
На рисунке показан постоянный магнит, намагниченный однородным M (или J ), окруженный вакуумом. Силовые линии магнитного поля показаны отдельно для каждого поля: M , H и B , что представляет собой векторную сумму M и H .
Размагничивающее поле H d направлено в противоположную сторону, но оно неоднородно, так как некоторый магнитный поток замыкается и снаружи тела (где M = 0 и J = 0).
В результате внутри тела B также неоднородно и по величине B < J .
Вне тела силовые линии B и H имеют одинаковую форму, потому что в вакууме две векторные величины отличаются только на скалярную константу вакуумной проницаемости μ 0 (как M , так и J равны нулю).
На этом рисунке также видно, что на границе двух сред с разными значениями проницаемости для H сохраняется тангенциальная составляющая H t , а для B сохраняется нормальная составляющая B t .
Измерение H
Значение H не может быть измерено напрямую, но получено другими способами.
В некоторых магнитных измерительных системах пропорциональность току используется явно, как, например, в таких устройствах, как рамка Эпштейна, однолистовой тестер или тороидальный образец. Измеряемая величина представляет собой ток (например, с помощью шунтирующего резистора), и H вычисляется из него.
В некоторых других случаях можно использовать принцип, согласно которому тангенциальная составляющая H не изменяется на границе раздела двух материалов. Следовательно, измеряя тангенциальную составляющую магнитного поля прямо у поверхности образца, можно узнать о поле непосредственно под поверхностью. Однако такое измерение основано на допущении, что зависимость B-H внутри датчика является линейной, поскольку работа сенсорной катушки основана на законе индукции Фарадея, в котором измеренным значением является плотность магнитного потока Б . Обычно это достигается за счет использования немагнитного материала в качестве каркаса, на который наматывается H-катушка. Сигнал в катушке индуцируется пропорционально B в H-катушке, но благодаря линейности его можно пересчитать для извлечения информации о H . Другие детекторы, такие как потенциометр Роговского-Чаттока или датчик Холла, также могут использоваться для обнаружения тангенциальной составляющей H , но они также измеряют количество B , которое затем можно пересчитать и выразить как Н .
Следовательно, измеряя тангенциальную составляющую магнитного поля прямо у поверхности образца, можно узнать о поле непосредственно под поверхностью. Однако такое измерение основано на допущении, что зависимость B-H внутри датчика является линейной, поскольку работа сенсорной катушки основана на законе индукции Фарадея, в котором измеренным значением является плотность магнитного потока Б . Обычно это достигается за счет использования немагнитного материала в качестве каркаса, на который наматывается H-катушка. Сигнал в катушке индуцируется пропорционально B в H-катушке, но благодаря линейности его можно пересчитать для извлечения информации о H . Другие детекторы, такие как потенциометр Роговского-Чаттока или датчик Холла, также могут использоваться для обнаружения тангенциальной составляющей H , но они также измеряют количество B , которое затем можно пересчитать и выразить как Н .
На границе двух материалов (с разными проницаемостями $μ_1$ и $μ_2$) тангенциальная составляющая H не меняется, поэтому: $H_{t1} = H_{t2 }$
Flat H-coil made with PCB tracks
Simple wire-wound H-coil
Энергия и плотность энергии
Плотность энергии $E_d$ запасенной в магнитном поле энергии в данном материале можно рассчитать как:
| $$E_d = \int H · дБ $$ | (Дж/м 3 ) |
который для материала с линейными характеристиками, включая высокоэнергетические постоянные магниты, можно упростить до:
| $$E_d = \frac{H·B}{2} $$ | (Дж/м 3 ) |
Следует отметить, что последнее приведенное выше уравнение охватывает как приложенное поле, так и реакцию материала на намагничивание (независимо от того, какая величина считается «основной», B или H ).
Однако в немагнитных материалах, для которых $µ_r$ ≈ 1, можно записать, что:
| $$B = μ_0 · H $$ | (Т) | и | $$\frac{B}{μ_0} = H $$ | (А/м) |
Следовательно, замена может быть сделана таким образом, чтобы исключить одну из переменных, сделав плотность энергии пропорциональной квадрату либо только B , либо только H . В зависимости от публикации используются обе формы, часто не содержит неявного предположения о том, что $μ_r$ ≈ 1. Эти две формы эквивалентны, хотя выражение с B кажется более популярным. Если предположение $µ_r$ ≈ 1 сделать невозможно, то энергия пропорциональна произведению $B·H$, или уравнение должно включать также относительную магнитную проницаемость $µ_r$. 92}{2} $$
Hysteresis loop and power loss
In ferromagnets the power or energy loss is proportional to the area of the B-H loop
Магнитомягкие материалы используются для преобразования энергии в режимах переменного или импульсного намагничивания. Энергетическая эффективность магнитной цепи зависит от мощности, теряемой в данном магнитном материале.
9T \left(\frac{dB}{dt} · H \right) dt $$
Энергетическая эффективность магнитной цепи зависит от мощности, теряемой в данном магнитном материале.
9T \left(\frac{dB}{dt} · H \right) dt $$
Удельные потери мощности являются важным показателем качества для магнитомягких материалов и, например, являются основой для классификации электротехнических сталей.
Из-за условий эксплуатации такие петли B-H измеряются в условиях синусоидального напряжения, что также обеспечивает синусоидальность Б . Форма волны H может сильно искажаться, особенно когда материал работает близко к насыщению. Этот эффект отвечает, например, за пусковой ток в трансформаторах.
Модели петли B-H
Существует несколько аналитических, статистических и численных моделей, которые используются для математического описания траекторий петли B-H с целью «предсказания» поведения материала при заранее определенных или произвольных условиях намагничивания. Общие магнитные потери можно рассчитать, потому что реальные петли BH представляют такие полные потери, а модели пытаются представить нелинейные траектории таких петель.
Общие магнитные потери можно рассчитать, потому что реальные петли BH представляют такие полные потери, а модели пытаются представить нелинейные траектории таких петель.
Такие модели, как Джайлс-Атертон или Прейзак, используют H в качестве независимой переменной, представляющей приложенное возбуждение, как это продиктовано схемным законом Ампера.
Coercivity
In high-energy magnets there are two values of coercivity: J H c and B H c
Коэрцитивная сила H c определяется как точка, в которой петля гистерезиса пересекает горизонтальную ось ( B или J или M = 0), измеренная для данного материала. Значения коэрцитивной силы используются для широкой классификации магнитных материалов на: мягкие ( H c < 1 кА/м), жесткие ( H c > 100 кА/м) и полужесткие (1 кА < H c < 100 кА/м).
Коэрцитивная сила связана с количеством энергии, необходимой для намагничивания (и размагничивания) данного магнитного материала. Магнитомягкие материалы имеют узкую петлю B-H, они легко намагничиваются и поэтому имеют низкие значения коэрцитивной силы.
В высокоэнергетических постоянных магнитах значения коэрцитивной силы очень велики (широкая петля гистерезиса), и из-за значительных различий между значениями плотности магнитного потока B и магнитной поляризации Дж можно выделить два значения коэрцитивной силы: J H c и B H c . Для таких магнитов почти прямая линия, идущая от точки коэрцитивной силы B H c до точки остаточной намагниченности B r обозначает условия работы магнита в данной магнитной цепи. Приложение магнитного поля, превышающего коэрцитивную силу, может необратимо размагнитить даже высокоэнергетический магнит. Для магнитов с более низкой энергией размагничивание может произойти даже в полях ниже коэрцитивной силы.
Для магнитов с более низкой энергией размагничивание может произойти даже в полях ниже коэрцитивной силы.
В магнитомягких материалах при нормальных рабочих условиях (значительно ниже насыщения) $B \приблизительно J$ и, следовательно, только одно значение коэрцитивной силы H c измеряется (потому что J H c ≈ B H c ).
См. также
Магнитное поле
Плотность магнитного потока B
Путаница между B и H
Каталожные номера
1) , 1) , 1) Майкл Мэнсфилд, Колм О’Салливан, Понимание физики, John Wiley & Sons, 2010, ISBN 9780470746387, с. 407
2) , 2) , 2) Encyclopaedia Britannica, Magnetism, {дата обращения: 02.05.2021}
3) , 3) , 3) , 3) , 3) , 3) , 3) , 3) , 3) Дэвид Джайлс, Введение в магнетизм и магнитные материалы, Чепмен и Холл, 1991, ISBN 9780412386404, с. 1-13
1-13
4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) С. Зурек, Характеристика магнитомягких материалов при намагничивании вращением, CRC Press, 2019, ISBN 97803678
5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) Славомир Туманьски, Справочник по магнитным измерениям, CRC Press / Taylor & Francis, Boca Raton, FL, 2011, ISBN 9780367864958
6) , 6) , 6) , 6) , 6) , 6) , 6) , 6) , 6) E.M. Purcell, D.J. Morin, Electricity and magnetism, 3rd edition, Cambridge University Press, 2013, ISBN 9781107014022
7) R Murugeshan, Electricity and Magnetism, S Chand Publishing, 2019, ISBN 9352837347
8) , 8) , 8) Ричард Фейнман, Роберт Лейтон, Мэтью Сэндс, Ферромагнетизм, Фейнмановские лекции по физике, Vol. II, Калифорнийский технологический институт, {дата обращения: 16 мая 2021 г.}
II, Калифорнийский технологический институт, {дата обращения: 16 мая 2021 г.}
9) , 9) Мэри Энн Уайт, Физические свойства материалов, второе издание, CRC Press, 2011, ISBN 9781439866511, с. 359
10) СИ Брошюра: Международная система единиц (СИ) [8-е издание, 2006; обновлено в 2014 г.], Раздел 2.2: Производные единицы СИ, {по состоянию на 15 июня 2016 г.}
11) Рональд Т. Меррилл, М. В. МакЭлхинни, Филлип Л. Макфадден (редактор), Магнитное поле Земли: палеомагнетизм, ядро и глубокая мантия, том 63 серии международных геофизических исследований, ISBN 97801245
12) D. Poljak, M. Cvetković, Human interaction with electromagnetic fields, Computational models in dosimetry, Academic Press, Elsevier, 2019, ISBN 9780128164433
13) Magnetic Field (H- Филд), Antenna-Theory.com, {дата обращения: 05 мая 2021 г.}
14) , 14) Райнер Хильцингер, Вернер Родевальд, Магнитные материалы, основы, продукты, свойства, приложения, VAC Vacuumschmelze, Publicis, 2013, ISBN 9783895783524
15) , 15) , 15) Сильванус П. Томпсон, Электромагнит, The Telegraphic Journal and Electrical Review, Vol. XXVII, 4 июля – 26 декабря 1890 г., стр. 372-377
Томпсон, Электромагнит, The Telegraphic Journal and Electrical Review, Vol. XXVII, 4 июля – 26 декабря 1890 г., стр. 372-377
16) Р Муругашан, Электричество и магнетизм, S Chand Publishing, 2019, ISBN 9352837347
17) Ричард М. Бозорт, Ферромагнетизм, IEEE Press, 2003, ISBN 0780310322, с. 1-3
18) Магнитное поле, Британская энциклопедия онлайн, {дата обращения: 07.03.2020}
19) На момент написания этой статьи не было отдельной записи под названием «напряженность магнитного поля» {проверено 7 марта 2020 г.}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г.}.
20) На момент написания этой статьи не было отдельной записи под названием «плотность магнитного потока» {дата обращения: 07.03.2020}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г.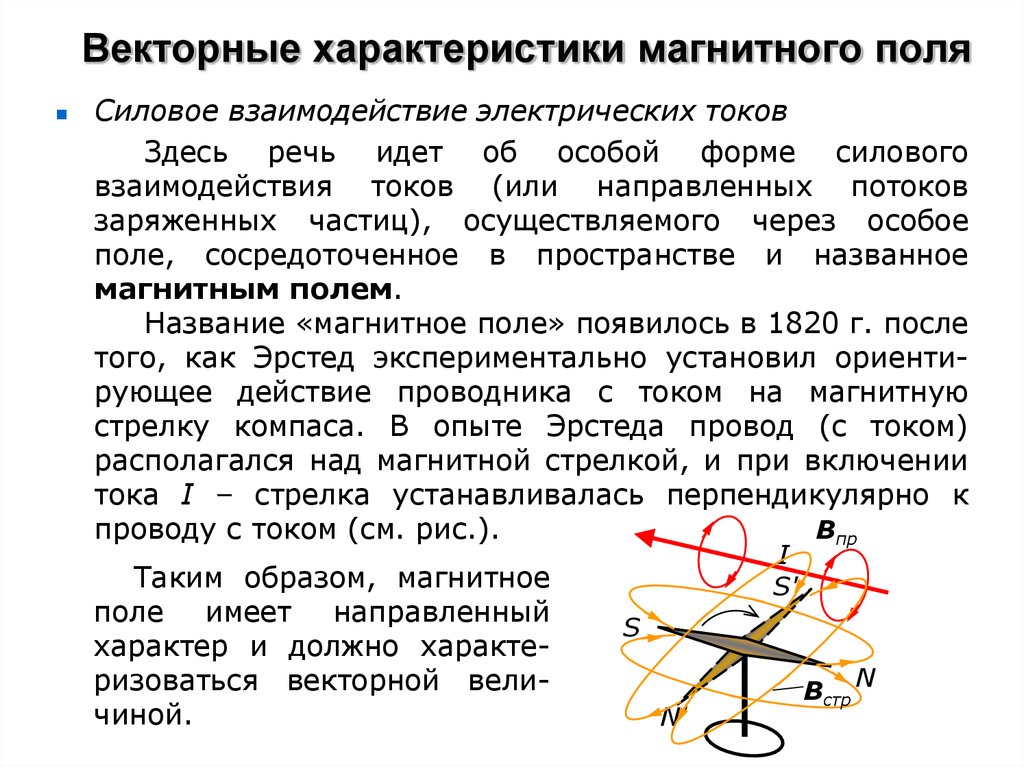 }.
}.
21) Марки неодима, NdFeB-Info.com, {дата обращения: 28.06.2016}
22) , 22) MIT OpenCourseWare, Закон Био-Савара и Закон Ампера, Глава 9
23) Уравнения Максвелла, Британская энциклопедия. Encyclopdia Britannica Online, {доступ 28 июня 2016 г.}
24) , 24) , 24) Дэвид Дж. Гриффитс, Введение в электродинамику, 4-е изд., Пирсон, Бостон, 2013, ISBN 0321856562
25) , 25) Введение в электромагнетизм поля, Мультифизическая энциклопедия, COMSOL, {дата обращения: 25 июня 2021 г.}
26) Модуль переменного/постоянного тока. Руководство пользователя, COMSOL 5.4, {дата обращения: 25.06.2021}
27) Дэвид Микер, Метод конечных элементов Magnetics: Documentation, {дата обращения: 09.06.2021}
28) Электромагнетизм, мультифизическое обучение и создание сетей, http://www. multiphysics.us, {дата обращения: 25.06.2021}
multiphysics.us, {дата обращения: 25.06.2021}
29) ANSYS Maxwell Magnetic Field Formulation, Application Brief, ANSYS , 2013, {дата обращения: 25 июня 2021}
30) , 30) Ray Kwok, Maxwell Equations, Государственный университет Сан-Хосе, Калифорния, США, www.sjsu.edu, {дата обращения: 22 июня 2021 г.}
31) Candace Suriano, et al., Antenna Основы, интерференционная технология, 3 мая 2007 г., {доступ 22 апреля 2021 г.}
32) Жан-Батист Био и Феликс Савар. Обратите внимание на магнетизм де ла пайл де Вольта. Анна. хим.физ., 15:222–223, 1820
33) , 33) Брошюра SI – 9-е издание (2019 г.) – Приложение 2, 20 мая 2019 г., {по состоянию на 27 июня 2021 г.}
34) , 34) , 34) Фаусто Фиорилло, Измерение и определение характеристик магнитных материалов, Academic Press, 2005, ISBN 9780122572517
35) , 35) , 35) А. Козловски, Р. Рыгал и С. Зурек, Большой электромагнит постоянного тока для полупромышленной термомагнитной обработки нанокристаллической ленты, IEEE Transactions on Magnetics, 50 (4), стр. 1-4, 2014 г., № ст. . 8000404, ДОИ 10.1109/Tmag.2013.2288322
Козловски, Р. Рыгал и С. Зурек, Большой электромагнит постоянного тока для полупромышленной термомагнитной обработки нанокристаллической ленты, IEEE Transactions on Magnetics, 50 (4), стр. 1-4, 2014 г., № ст. . 8000404, ДОИ 10.1109/Tmag.2013.2288322
36) E.R. Dobbs, Basic Electromagnetism, Springer Science & Business Media, 2013, ISBN: 940112125
37) 3
37), 13
37). 4431545263
38) Ji-Yeon Shim, Bong-Yong Kang, Распределение электромагнитной силы квадратной рабочей катушки для высокоскоростной магнитно-импульсной сварки с использованием FEM, Материаловедение и приложения, Vol. 4 (12), 2013, стр. 856-862. doi: 10.4236/msa.2013.412109
39) Б.Д. Каллити, К.Д. Грэм, Введение в магнитные материалы, 2-е издание, Wiley, IEEE Press, 2009, ISBN 9780471477419
40) , 40) Arnold Magnetic Technologies, TECHNotes, The Vocabulary of Magnetism, 2016, {доступ 2021-05-02}
Магнитное поле, Счетчик
Различные методы и факты – Lambda Geeks
В этом посте мы в основном сосредоточимся на том, как увеличить силу магнитного поля.
Интенсивность магнитного поля зависит от различных факторов в зависимости от источника магнитного поля. Если источником является соленоид, то сила магнитного поля зависит от трех факторов: 1) числа витков на единицу длины, 2) тока, 3) магнитного материала внутри сердечника.
Если источником является постоянный магнит, это зависит от 1) дипольного момента, 2) расстояния от источника, 3) материала, который его окружает.
Давайте сначала разберемся с «соленоидом». Что это? И как можно определить напряженность его магнитного поля?
Соленоид – одно из распространенных магнитных устройств, которое нам знакомо.
Название соленоид происходит от греческого слова «Solen», что означает трубу или канал. Это искусственный магнит, работающий по принципу электромагнетизма; когда ток проходит через проводник, он создает вокруг него круговое магнитное поле.
Как увеличить напряженность магнитного поля соленоида Когда провода свернуты в форму катушки, она создает однородные сильные магнитные поля, похожие на стержневой магнит вокруг себя. Идеальная длина соленоида очень велика по сравнению с его диаметром, чтобы избежать краевого эффекта.
Идеальная длина соленоида очень велика по сравнению с его диаметром, чтобы избежать краевого эффекта.
Соленоид имеет однородное магнитное поле внутри и незначительное магнитное поле снаружи.
«Как увеличить напряженность магнитного поля» «Файл: Электромагнитная индукция — соленоид в петлю — анимация.gif» от Ponor лицензирован под лицензией CC BY-SA 4.0Сила магнитного поля соленоида определяется по этой формуле
B=μ 0 nI
Где, μ 0 — проницаемость свободного пространства,
n — число витков на единицу длины,
I — величина тока, проходящего через него.
Из приведенного выше уравнения можно легко сделать вывод, что сила магнитного поля соленоида в основном зависит от
- Ток
- Количество витков
- Материал внутри соленоида
Три способа увеличения силы магнитного поля
ТокB∝I
Как мы видим, только ток отвечает за создание магнитного поля внутри соленоида. Увеличивая величину тока в катушке, мы можем усилить напряженность магнитного поля.
Увеличивая величину тока в катушке, мы можем усилить напряженность магнитного поля.
B∝n
Каждый виток (обмотки) соленоида рассматривается как круговая петля, по которой течет ток, и он будет генерировать вокруг себя магнитное поле. Результирующее магнитное поле соленоида является векторной суммой магнитного поля, создаваемого всеми обмотками (витками). Можно сделать вывод, что чем больше число витков на единицу длины, тем больше напряженность магнитного поля внутри соленоида.
Материал внутри соленоидаМатериалы по-разному реагируют на воздействие внешнего магнитного поля, что происходит из-за ориентации дипольного момента, который полностью отвечает за изменение магнитного поля внутри материала. Свойство материала, характеризующее его реакцию на внешнюю магнитную силу, известно как магнитная проницаемость.
Магнитная проницаемость — это свойство вещества, которое показывает способность материала пропускать через себя силовые линии магнитного поля.
Ферромагнитный материал (например, железо) обладает высокой магнитной проницаемостью, усиливая магнитное поле. Следовательно, когда такой материал содержится внутри соленоида, который сам является магнитным, он будет способствовать потоку соленоида, что в конечном итоге приводит к сильному магнитному полю внутри соленоида.
Как известно, напряженность магнитного поля (B) внутри соленоида определяется выражением воздух.
В повседневной жизни мы сталкиваемся с некоторыми постоянными магнитами, которые теряют свое магнитное поле или становятся слабее с течением времени. Есть два способа превратить слабый магнит в более сильный.
Постоянные магниты :Это наиболее распространенный источник магнитного поля.
Как мы знаем, атомы в материалах состоят из электронов и ядра, и эти электроны вращаются вокруг ядра, образуя крошечную петлю с током, создающую магнитное поле. Орбитальное движение электронов и электроны, атомы и ядерные спины также ответственны за причину магнитного поля в этих магнитных материалах.
Два способа увеличения напряженности магнитного поля постоянных магнитов :
- Путем перезарядки магнита
- Складывая вместе
. Иногда эти магниты неправильно выравнивают свои заряды или теряют часть доменов. В этой ситуации мы можем увеличить прочность магнитных материалов, постоянно растирая их сильным магнитом. Делая это, мы можем легко переносить заряды. А также это поможет перестроить магнитные домены более слабого магнита, что в конечном итоге увеличит силу магнитного поля.
Устанавливая вместеМы можем увеличить силу напряженности магнитного поля, устанавливая вместе два или более магнитов. Таким образом, сложенный магнит будет иметь большую интенсивность.
Давайте рассмотрим несколько примеров, связанных с соленоидом.
Задача 1: Соленоид имеет 350 витков на 50 см и состоит из четырех слоев. Нижний слой имеет радиус 1,4 см. если сила тока 6,0 А, Определить величину магнитной индукции а) внутри соленоида 2) снаружи соленоида.
Нижний слой имеет радиус 1,4 см. если сила тока 6,0 А, Определить величину магнитной индукции а) внутри соленоида 2) снаружи соленоида. Решение:-
Данные количества:
L = 50 см = 0,5 м
r = 1,4 см = 1,4*10 -2 м
I = 6 витков на единицу длины. n=N/L=1000/0,2=5000 витков на метр
Величина B внутри соленоида определяется выражением
Снаружи соленоида магнитное поле незначительно или равно нулю .
Задача 2 : Определить напряженность магнитного поля, создаваемого соленоидом длиной 80 см и числом витков 360. Если число витков соленоида увеличить до 400, то вычислить магнитное поле внутри катушка.Решение:-
Данные количества,
N = 360
L = 80 см = 0,8 м
n = N/L = 360/0,8 = 450 витков на метр знак равно
Величина B внутри соленоида определяется выражением;
Если число витков в соленоиде увеличить до 400,
n = N/L = 400/0,8 = 500 витков на метр;
Из этого примера видно, что по мере увеличения числа витков магнитное поле, связанное внутри соленоида, увеличивается.
Решение:-
Данные количества,
N = 360
L = 80 см = 0,8 м
n = N/L = 360/0,8 = 450 витков на метр
0 B0 0 96 I знак равно
Величина B внутри соленоида определяется выражением;
Задача 4: Соленоид имеет сердечник из материала с магнитной проницаемостью 6,3 *10-3 Гн/м. Количество витков в соленоиде 1000 на метр. Через соленоид протекает ток силой 2А. Найдите напряженность магнитного поля в ядре.Решение:-
Данные количества,
μ=6,3*10 -3 Гн/м
n = 1000 витков на метр
I = 2 A
B=?
Величина B внутри соленоида определяется выражением;
Магнитное поле резко увеличивается, когда железный сердечник находится внутри соленоида.
Часто задаваемые вопросы: Часто задаваемые вопросы Что влияет на магнитное поле соленоида? На интенсивность магнитного поля соленоида сильно влияют три фактора; ток, проходящий через него, плотность витков и материал, используемый в качестве сердечника.
Форма магнитного поля соленоида напоминает стержневой магнит, когда через него проходит электрический ток. Он имеет сильное магнитное поле внутри и почти незначительное магнитное поле снаружи.
В чем разница между соленоидом и электромагнитом?Разница между соленоидом и электромагнитом заключается в следующем:
Электромагнит — это соленоид, но соленоид не обязательно должен быть электромагнитом. Соленоид представляет собой цилиндрическую катушку; состоящий из проводов с током (в виде обмоток или петель), которые создают вокруг себя магнитное поле. Идеальный соленоид имеет больший размер длины по сравнению с его диаметром.
Электромагнит имеет магнитный сердечник, а соленоид может его не иметь. Соленоид считается разновидностью электромагнита.
В чем разница между постоянным магнитом и соленоидом? Оба создают магнитное поле вокруг себя, но оба они отличаются в какой-то сфере.
Соленоид относится к категории временных магнитов, поскольку он создает магнитное поле только при прохождении через него тока, а создаваемое им магнитное поле является более устойчивым. Большим преимуществом является то, что мы можем изменить его магнитное поле в соответствии с нашими потребностями. Как следует из названия, постоянные магниты имеют постоянное магнитное поле, в отличие от соленоидов; мы не можем включить или выключить магнитное поле. Мы не можем изменить интенсивность его магнитного поля.
Для чего используется соленоид?В качестве электромагнитов подходят соленоиды с сердечником из мягкого железа. Он имеет широкое применение, например, компьютерные принтеры, системы впрыска топлива и дверные замки.
Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле
Цели обучения
К концу этого раздела вы сможете:
- Описывать воздействие магнитных полей на движущиеся заряды.

- Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
- Рассчитайте магнитную силу, действующую на движущийся заряд.
Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Правило правой руки 1
Действие магнитного поля на движущийся заряд является одним из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы F на заряд q , движущийся со скоростью v в магнитном поле напряженностью B определяется как
F = qvB sin θ ,
, где θ — угол между направлениями v и B. Эту силу часто называют 1z 190 силой Лорента. Фактически именно так мы определяем напряженность магнитного поля B — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля B называется тесла (Тл) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F = qvB sin θ для B .
Эту силу часто называют 1z 190 силой Лорента. Фактически именно так мы определяем напряженность магнитного поля B — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля B называется тесла (Тл) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F = qvB sin θ для B .
[латекс]B=\frac{F}{qv \sin\theta}\\[/latex]
Поскольку sin θ безразмерно, тесла равен
[латекс]1\текст{ T}= \frac{1\text{ N}}{\text{ C}\cdot\text{ м/с}}=\frac{1\text{ N}}{\text{A}\cdot\text{ м} }\\[/latex]
(обратите внимание, что C/s = A). Другая меньшая единица, называемая 90 110 гаусс 90 111 (G), где 1 G = 10 −4 T, иногда используется. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5 × 10 −5 Тл, или 0,5 Гс.
Магнитное поле Земли на ее поверхности составляет всего около 5 × 10 −5 Тл, или 0,5 Гс.
, как определено правилом правой руки 1 (или RHR-1 ), которое показано на рисунке 1. RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большой палец правой руки в направлении v , пальцы в направлении B , а перпендикуляр к ладони указывает в направлении F . Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Рис. 1. Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Величина силы пропорциональна q, v, B и синусу угла между v и B.
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компасов, вы редко видите или лично испытываете на себе силы из-за слабого магнитного поля Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)
(Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)
Рис. 2. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, испытывает силу, направленную строго вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.
СтратегияНам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F = qvB sin θ , чтобы найти силу.
9{-11}\text{ N}\end{массив}\\[/latex]. Обсуждение Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
Резюме раздела
- Магнитные поля воздействуют на движущийся заряд силой q , величина которой равна
F = qvB sin θ ,
, где θ — угол между направлениями v и B .
- Единицей измерения напряженности магнитного поля в системе СИ B является тесла (Тл), которая связана с другими единицами соотношения
[латекс]1\текст{ T}=\frac{1\text{ N}}{\text{ C}\cdot\text{ м/с}}=\frac{1\text{ N}}{\ текст{A}\cdot\text{м}}\\[/латекс]
- Направление силы на движущийся заряд задается правилом правой руки 1 (RHR-1): Укажите большой палец правой руки в направлении v , пальцы в направлении B , а перпендикуляр к ладони указывает в направлении F .
- Сила перпендикулярна плоскости, образованной v и B .
 Поскольку сила равна нулю, если v параллельно B , заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.
Поскольку сила равна нулю, если v параллельно B , заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.
Концептуальные вопросы
1. Если заряженная частица движется прямолинейно через некоторую область пространства, можете ли вы сказать, что магнитное поле в этой области обязательно равно нулю?
Задачи и упражнения
1. Каково направление магнитной силы, действующей на положительный заряд, который движется, как показано в каждом из шести случаев, показанных на рисунке 3?
Рисунок 3.
2. Повторите упражнение 1 для отрицательного заряда.
3. Каково направление скорости отрицательного заряда, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 4, если предположить, что он движется перпендикулярно B ?
Рисунок 4.
4. Повторите рисунок 4 для положительного заряда.
5. Каково направление магнитного поля, которое создает магнитную силу на положительном заряде, как показано в каждом из трех случаев на рисунке ниже, при условии, что B перпендикулярно v ?
Рисунок 5.
6. Повторите упражнение 5 для отрицательного заряда.
7. Какова максимальная сила на алюминиевом стержне с зарядом 0,100 мкКл, которую вы пропускаете между полюсами постоянного магнита 1,50 Тл со скоростью 5,00 м/с? В каком направлении сила?
8. (a) Самолеты иногда приобретают небольшие статические заряды. Предположим, что сверхзвуковая струя имеет заряд 0,500 мкКл и летит строго на запад со скоростью 660 м/с над южным магнитным полюсом Земли, где 8,00 × 10 −5 -T магнитное поле указывает прямо вверх. Каковы направление и величина магнитной силы на плоскости? (b) Обсудите, подразумевает ли значение, полученное в части (а), это значительный или незначительный эффект.
9. (a) Протон космического луча, движущийся к Земле со скоростью 5,00 × 10 7 , испытывает магнитную силу 1,70 × 10 −16 Н. Какова напряженность магнитного поля, если существует угол 45º между ней и скоростью протона? (b) Соответствует ли значение, полученное в части (а), известной напряженности магнитного поля Земли на ее поверхности? Обсуждать.
Какова напряженность магнитного поля, если существует угол 45º между ней и скоростью протона? (b) Соответствует ли значение, полученное в части (а), известной напряженности магнитного поля Земли на ее поверхности? Обсуждать.
10. На электрон, движущийся со скоростью 4,00 × 10 3 м/с в магнитном поле 1,25 Тл, действует магнитная сила 1,40 × 10 −16 Н. Какой угол составляет скорость электрона с магнитной поле? Есть два ответа.
11. (a) Физик, выполняющий чувствительные измерения, хочет ограничить магнитную силу движущегося заряда в своем оборудовании величиной менее 1,00 × 10 −12 Н. Какой максимальной может быть заряд, если он движется со скоростью максимальная скорость 30,0 м/с в поле Земли? (b) Обсудите, будет ли трудно ограничить заряд меньше значения, указанного в (а), сравнив его с типичным статическим электричеством и отметив, что статическое электричество часто отсутствует.
Глоссарий
- Правило правой руки 1 (RHR-1):
- правило для определения направления магнитной силы на положительный движущийся заряд: когда большой палец правой руки указывает в направлении скорости заряда v а остальные пальцы указывают в направлении магнитного поля B , тогда сила на заряде перпендикулярна и направлена от ладони; сила на отрицательный заряд перпендикулярна и направлена на ладонь
- сила Лоренца:
- сила, действующая на заряд, движущийся в магнитном поле
- тесла:
- Тл — единица напряженности магнитного поля в системе СИ; [латекс]1\текст{Т}=\фрак{1\текст{N}}{\текст{А}\cdot\текст{м}}\\[/латекс]
- магнитная сила:
- сила, действующая на заряд при его движении через магнитное поле; сила Лоренца
- Гаусс:
- Гс — единица напряженности магнитного поля; 1 г = 10 –4 Т
Избранные решения задач и упражнения
1.


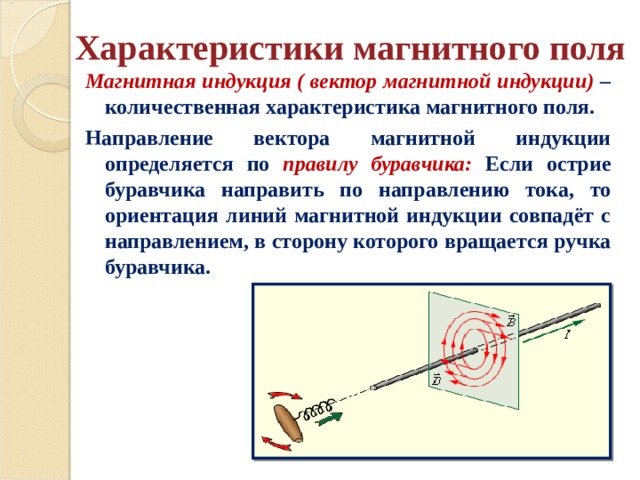

 также
также также
также

 Поскольку сила равна нулю, если v параллельно B , заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.
Поскольку сила равна нулю, если v параллельно B , заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.