Определение атмосферное давление общее значение и понятие. Что это такое атмосферное давление
Основываясь на латинском слове pressĭo, слово « давление» используется для описания результата сжатия чего-либо или сжатия вещи . Таким образом, этот термин относится к силе, которая применяется к объекту и которая может регулироваться, угнетать, сжимать или сжимать.
Атмосферный, с другой стороны, это то, что связано с атмосферой или относится к ней (как известно, слой газа, окружающий небесное тело). В общем, понятие атмосферы используется для определения слоя воздуха, который покрывает нашу планету.
Эти определения позволяют нам понять идею атмосферного давления, которое является силой, которую атмосфера создает, особенно объекты, которые находятся внутри нее .
На протяжении всей истории многие были учеными и исследователями атмосферного давления, которые, так или иначе, способствовали тому, чтобы сегодня его можно было вычислить без каких-либо проблем и можно было проанализировать с разных точек зрения.
Таким образом, среди фигур, которые внесли свой вклад в развитие этого типа давления, мы находим персонажей итальянского физика Галилео Галилея, математика Евангелиста Торричелли, французского физика Блеза Паскаля или немецкого изобретателя Отто фон Герике.
Этот последний ученый будет иметь фундаментальное значение для разработки термина, который нас интересует, потому что на основе исследований, проведенных Торричелли или Паскалем, он основал свои собственные теории и концепции. Это привело его к демонстрации в 1654 году о впечатляющей силе, которую атмосфера может оказывать на элемент. Эти эксперименты, основанные на медной сфере и вакууме, который был создан внутри, вызвали восхищение научным полем момента.
Говорят, что давление атмосферы в определенной точке эквивалентно весу статического воздуха, который простирается от этой точки до самого высокого края атмосферы. Единственный способ точно рассчитать этот вес – узнать изменение плотности воздуха, так как он становится менее плотным с ростом высоты .
В дополнение ко всему вышесказанному мы должны прояснить, что это падение вышеупомянутого атмосферного давления с высотой имеет последствия для здоровья человека. Альпинисты и альпинисты – те, кто может дать больше доказательств этого факта, потому что, когда они совершают восхождения, они страдают от таких симптомов, как головные боли, головокружение, слабость или даже проблемы с кишечником.
На уровне моря нормальное значение атмосферного давления составляет 1013 мбар или 760 мм рт . Это значение эквивалентно 1 атмосфере, единице измерения, которая не является частью Международной системы единиц, но обычно используется и сокращенно обозначается как атм .
Атмосферное давление влияет на 
Барометр-анероид — урок. Физика, 7 класс.
До середины \(XIX\) в. жидкостные барометры Торричелли были единственными приборами для измерения атмосферного давления.
Барометр-анероид (от греческого слова «анерос» — без воды) — прибор для измерения атмосферного давления, в механизме которого отсутствует жидкость (в отличие от ртутного и жидкостных барометров Торричелли).
Анероид изобретён Люсьеном Види в \(1844\) г.
Рис. \(1\). Барометр-анероид
В его конструкции использован круглый металлический корпус \(1\) с волнистыми (гофрированными) основаниями.
Из корпуса выкачан воздух либо до полного вакуума, либо до большого разрежения. Когда повышается давление снаружи корпуса, то есть атмосферное давление, то гофрированные основания корпуса прогибаются внутрь и тянут прикрепленную к ним пружину \(2\). Уменьшение атмосферного давления возвращает гофрированное основание в исходное положение, при дальнейшем уменьшении выпячивается вверх. Стрелка барометра \(4\) с помощью передаточного механизма \(3\) опускается по шкале против часовой стрелки, показывая уменьшение давления.
Стрелка барометра \(4\) с помощью передаточного механизма \(3\) опускается по шкале против часовой стрелки, показывая уменьшение давления.
Первоначальную градуировку шкалы производят по эталонному ртутному барометру. Преимуществом анероида является высокая чувствительность: стрелка реагирует на изменение высоты даже величиной \(2\)-\(3\) м. Точное значение давление необходимо для наблюдения физических процессов и эффективной работы многих приборов.
Анероиды, имеющие механическую систему, изнашиваются и подвержены коррозии. В отличие от ртутных, они безопасны, поэтому более распространены в эксплуатации.
Пропорциональная зависимость атмосферного давления от высоты над уровнем моря используется в методиках градуирования приборов для измерения высоты.
Альтиметр (от лат. altus – высокий) — прибор для измерения высоты.
Виды высотомеров (альтиметров):
- барометрические
- радиотехнические
- инерциальные
- ионизационные
Принцип действия барометрического высотометров основан на уменьшении атмосферного давления с увеличением высоты.
Рис. \(2\). Альтиметры
Ответ:
Источники:
Рис. 1. Барометр-анероид. © ЯКласс.
Как измерить давление физика. Школьная энциклопедия
Проделаем опыт. Возьмем небольшую доску, в углы которой вбиты четыре гвоздя, и поместим ее остриями вверх на песок. Сверху на нее положим гирю (рис. 81). Мы увидим, что шляпки гвоздей лишь незначительно вдавятся в песок. Если же мы перевернем доску и снова поставим ее (вместе с гирей) на песок, то теперь гвозди войдут в него значительно глубже (рис. 82). В обоих случаях вес доски был одним и тем же, однако эффект оказался разным. Почему? Вся разница в рассматриваемых случаях заключалась в том, что площадь поверхности, на которую опирались гвозди, в одном случае была больше, а в другом меньше. Ведь сначала песка касались шляпки гвоздей, а затем их острия.
Мы видим, что результат воздействия зависит не только от силы, с которой тело давит на поверхность, но и от площади этой поверхности. Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис. 83). Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.
Именно по этой причине человек, способный скользить по рыхлому снегу на лыжах, сразу же проваливается в него, как только их снимет (рис. 83). Но дело не только в площади. Важную роль играет и величина прикладываемой силы. Если, например, на ту же. доску (см. рис. 81) положить еще одну гирю, то гвозди (при той же площади опоры) погрузятся в песок еще глубже.
Силу, прикладываемую перпендикулярно поверхности, называют силой давления на эту поверхность.
Силу давления не следует путать с давлением. Давление – это физическая величина, равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности:
р – давление, F – сила давления, S – площадь.
Итак, чтобы определить давление, надо силу давления разделить на площадь поверхности, на которую оказывается давление.
При одной и той же силе давление больше в том случае, когда площадь опоры меньше, и, наоборот, чем больше площадь опоры, тем давление меньше.
В тех случаях, когда силой давления является вес находящегося на поверхности тела (F = P = mg
), давление, оказываемое телом, можно найти по формуле
Если давление р и площадь S известны, то можно определить силу давления F ; для этого надо давление умножить на площадь:
F = pS
(32. 2)
2)
Сила давления (как и любая другая сила) измеряется в ньютонах. Давление же измеряется в паскалях.
1 Па = 1 Н/м 2 .
Используются также другие единицы давления – гектопаскаль (гПа) и килопаскаль (кПа):
1 гПа = 100 Па, 1 кПа = 1000 Па.
1. Приведите примеры, показывающие, что результат действия силы зависит от площади опоры, на которую действует эта сила. 2. Почему человек, идущий на лыжах, не проваливается в снег? 3. Почему острая кнопка легче входит в дерево, чем тупая? 4. Что называют давлением? 5. Какие вы знаете единицы давления? 6. Чем отличается давление от силы давления? 7. Как можно найти силу давления, зная давление и площадь поверхности, к которой приложена сила?
Человек на лыжах, и без них.
По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.
Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует).
Этот вывод подтверждают физические опыты.
Опыт.Результат действия данной силы зависит от того, какая сила действует на единицу площади поверхности.
По углам небольшой доски надо вбить гвозди.
Опыт. Вторая иллюстрация.
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением
Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:
давление = сила / площадь .
Обозначим величины, входящие в это выражение: давление – p , сила, действующая на поверхность, – F и площадь поверхности – S .
Тогда получим формулу:
p = F/S
Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м 2 перпендикулярно этой поверхности
Единица давления – ньютон на квадратный метр (1 Н / м 2). В честь французского ученого Блеза Паскаля она называется паскалем (Па ). Таким образом,
1 Па = 1 Н / м 2 .
Используется также другие единицы давления: гектопаскаль (гПа ) и килопаскаль (кПа ).
1 кПа = 1000 Па;
1 гПа = 100 Па;
1 Па = 0,001 кПа;
1 Па = 0,01 гПа.
Запишем условие задачи и решим её.
Дано : m = 45 кг, S = 300 см 2 ; p = ?
В единицах СИ: S = 0,03 м 2
Решение:
p = F /S ,
F = P ,
P = g·m ,
P = 9,8 Н · 45 кг ≈ 450 Н,
p = 450/0,03 Н / м 2 = 15000 Па = 15 кПа
“Ответ”: p = 15000 Па = 15 кПа
Способы уменьшения и увеличения давления.

Тяжелый гусеничный трактор производит на почву давление равное 40 – 50 кПа, т. е. всего в 2 – 3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на бóльшую площадь за счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору .
В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.
Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.
С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм 2 , то давление, производимое ею, равно:
Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм 2 , то давление, производимое ею, равно:
p = 50 Н/ 0, 000 001 м 2 = 50 000 000 Па = 50 000 кПа.
Для сравнения, это давление в 1000 раз больше давления, производимого гусеничным трактором на почву. Можно найти еще много таких примеров.
Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.
Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. – все они из твердого материала, гладкие и очень острые.
Давление
Известно, что молекулы газа беспорядочно движутся.
Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.
Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см 2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, – оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа .
Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.
Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.
Как объяснить этот опыт?
Для хранения и перевозки сжатого газа используются специальные прочные стальные баллоны.
В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково . Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.
Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.
Попытаемся уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда – давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.
Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.
Итак, при уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными .
А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа , при условии, что масса газа и объем не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда .
Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.
При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.
Закон Паскаля.
Давление передается в каждую точку жидкости или газа.
Давление поршня передается в каждую точку жидкости, заполняющей шар.
Теперь газ.
В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку . Рассмотрим это явление подробнее.
Рассмотрим это явление подробнее.
На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.
Прилагая некоторую силу, заставим поршень немного переместиться внутрь и сжать газ (жидкость), находящийся непосредственно под ним. Тогда частицы (молекулы) расположатся в этом месте более плотно, чем прежде(рис, б). Благодаря подвижности частицы газа будут перемещаться по всем направлениям. Вследствие этого их расположение опять станет равномерным, но более плотным, чем раньше (рис, в). Поэтому давление газа всюду возрастет. Значит, добавочное давление передается всем частицам газа или жидкости. Так, если давление на газ (жидкость) около самого поршня увеличится на 1 Па, то во всех точках внутри газа или жидкости давление станет больше прежнего на столько же. На 1 Па увеличится давление и на стенки сосуда, и на дно, и на поршень.
Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях .
Это утверждение называется законом Паскаля .
На основе закона Паскаля легко объяснить следующие опыты.
На рисунке изображен полый шар, имеющий в различных местах небольшие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде одинаковых струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково .
Давление в жидкости и газе.
Под действием веса жидкости резиновое дно в трубке прогнется.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому, каждый слой жидкости, налитой в сосуд, своим весом создает давление, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление. В этом можно убедиться на опыте.
В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.
Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.
Силы, действующие на резиновую пленку, | одинаковы с обеих сторон. |
Иллюстрация.
Дно отходит от цилиндра вследствие давления на него силы тяжести.
Опустим трубку с резиновым дном, в которую налита вода, в другой, более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой же опыт можно провести с трубкой, в которой резиновая пленка закрывает боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на рисунке, б . Мы заметим, что пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Это означает, что силы, действующие на резиновую пленку, одинаковы со всех сторон.
Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно при этом окажется плотно прижатым к краю сосуда и не отпадет. Его прижимает сила давления воды, направленная снизу вверх.
Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.
Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.
В момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу вверх на дно передается давление такого же по высоте столба жидкости, но находящейся в банке. Оба эти давления одинаковы, дно же отходит от цилиндра вследствие действия на него собственной силы тяжести.
Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.
Итак, опыты показывают, что внутри жидкости существует давление, и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается .
Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его “весовое” давление во многих случаях можно не учитывать.
Расчет давления жидкости на дно и стенки сосуда.
Расчет давления жидкости на дно и стенки сосуда.
Рассмотрим, как можно рассчитывать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда.
Сила F , с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу P жидкости, находящейся в сосуде. Вес жидкости можно определить, зная ее массу m . Массу, как известно, можно вычислить по формуле: m = ρ·V . Объем жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h , а площадь дна сосуда S , то V = S·h .
Масса жидкости m = ρ·V , или m = ρ·S·h .
Вес этой жидкости P = g·m , или P = g·ρ·S·h .
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S , получим давление жидкости p :
p = P/S , или p = g·ρ·S·h/S,
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости .
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости .
Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы (строго говоря, наш расчет годится только для сосудов, имеющих форму прямой призмы и цилиндра. В курсах физики для института доказано, что формула верна и для сосуда произвольной формы). Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м 3), а высоту столба жидкости h – в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).
Пример . Определите давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м 3 .
Запишем условие задачи и запишем ее.
Дано :
ρ = 800 кг/м 3
Решение :
p = 9.8 Н/кг · 800 кг/м 3 · 10 м ≈ 80 000 Па ≈ 80 кПа.
Ответ : p ≈ 80 кПа.
Сообщающиеся сосуды.
Сообщающиеся сосуды.
На рисунке изображены два сосуда, соединённые между собой резиновой трубкой. Такие сосуды называются сообщающимися . Лейка, чайник, кофейник – примеры сообщающихся сосудов. Из опыта мы знаем, что вода, налитая, например, в лейку, стоит всегда на одном уровне в носике и внутри.
Сообщающиеся сосуды встречаются нам часто. Например, им может быть чайник, лейка или кофейник. | Поверхности однородной жидкости устанавливаются на одном уровне в сообщающихся сосудах любой формы. | Разные по плотности жидкости. |
С сообщающимися сосудами можно проделать следующий простой опыт. В начале опыта резиновую трубку зажимаем в середине, и в одну из трубок наливаем воду. Затем зажим открываем, и вода вмиг перетекает в другую трубку, пока поверхности воды в обеих трубках не установятся на одном уровне. Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в разные стороны. И в этом случае, как только жидкость успокоится, ее уровни в обеих трубках уравняются.
Затем зажим открываем, и вода вмиг перетекает в другую трубку, пока поверхности воды в обеих трубках не установятся на одном уровне. Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в разные стороны. И в этом случае, как только жидкость успокоится, ее уровни в обеих трубках уравняются.
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 109).
Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой. Значит, давления в обоих сосудах на любом уровне одинаковы. Жидкость в обоих сосудах одна и та же, т. е. имеет одинаковую плотность. Следовательно, должны быть одинаковы и ее высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, давление в нем увеличивается и жидкость перемещается в другой сосуд до тех пор, пока давления не уравновесятся.
Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй – другой плотности, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей будут различны.
И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей будут различны.
При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис.).
Опыт. Как определить массу воздуха.
Вес воздуха. Атмосферное давление.
Существование атмосферного давления.
Атмосферное давление больше, чем давление разреженного воздуха в сосуде.
На воздух, как и на всякое тело, находящееся на Земле, действует сила тяжести, и, значит, воздух обладает весом. Вес воздуха легко вычислить, зная его массу.
На опыте покажем, как вычислить массу воздуха. Для этого нужно взять прочный стеклянный шар с пробкой и резиновой трубкой с зажимом. Выкачаем из него насосом воздух, зажмем трубку зажимом и уравновесим на весах. Затем, открыв зажим на резиновой трубке, впустим в него воздух. Равновесие весов при этом нарушится. Для его восстановления на другую чашку весов придется положить гири, масса которых будет равна массе воздуха в объеме шара.
Равновесие весов при этом нарушится. Для его восстановления на другую чашку весов придется положить гири, масса которых будет равна массе воздуха в объеме шара.
Опытами установлено, что при температуре 0 °С и нормальном атмосферном давлении масса воздуха объемом 1 м 3 равна 1,29 кг. Вес этого воздуха легко вычислить:
P = g·m, P = 9,8 Н/кг · 1,29 кг ≈ 13 Н.
Воздушная оболочка, окружающая Землю, называется атмосфера (от греч. атмос – пар, воздух, и сфера – шар).
Атмосфера, как показали наблюдения за полетом искусственных спутников Земли, простирается на высоту нескольких тысяч километров.
Вследствие действия силы тяжести верхние слои атмосферы, подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно к Земле, сжат больше всего и, согласно закону Паскаля, передает производимое на него давление по всем направлениям.
В результате этого земная поверхность и телá, находящиеся на ней, испытывают давление всей толщи воздуха, или, как обычно говорится в таких случаях, испытывают атмосферное давление .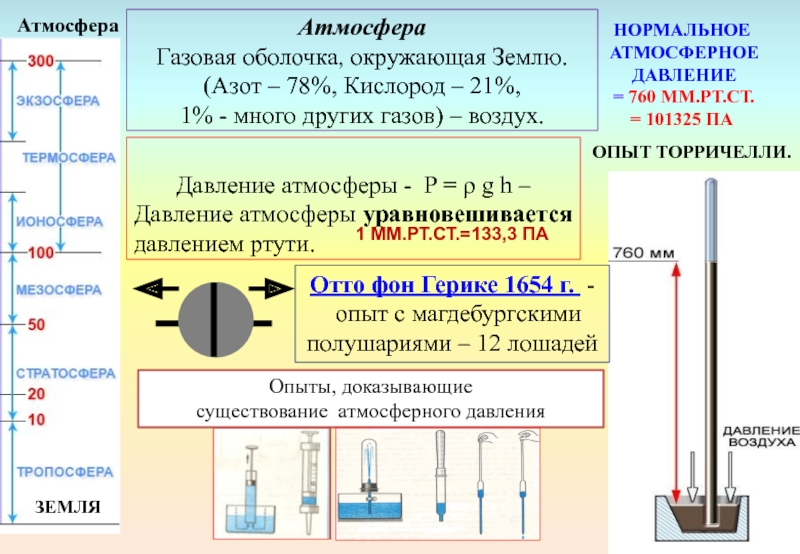
Существованием атмосферного давления могут быть объяснены многие явления, с которыми мы встречаемся в жизни. Рассмотрим некоторые из них.
На рисунке изображена стеклянная трубка, внутри которой находится поршень, плотно прилегающий к стенкам трубки. Конец трубки опущен воду. Если поднимать поршень, то за ним будет подниматься и вода.
Это явление используется в водяных насосах и некоторых других устройствах.
На рисунке показан цилиндрический сосуд. Он закрыт пробкой, в которую вставлена трубка с краном. Из сосуда насосом откачивается воздух. Затем конец трубки помещается в воду. Если теперь открыть кран, то вода фонтаном брызнет в внутрь сосуда. Вода поступает в сосуд потому, что атмосферное давление больше давления разреженного воздуха в сосуде.
Почему существует воздушная оболочка Земли.
Как и все тела, молекулы газов, входящих в состав воздушной оболочки Земли, притягиваются к Земле.
Но почему же тогда все они не упадут на поверхность Земли? Каким образом сохраняется воздушная оболочка Земли, ее атмосфера? Чтобы понять это, надо учесть, что молекулы газов находятся в непрерывном и беспорядочном движении. Но тогда возникает другой вопрос: почему эти молекулы не улетают в мировое пространство, то есть в космос.
Но тогда возникает другой вопрос: почему эти молекулы не улетают в мировое пространство, то есть в космос.
Для того, чтобы совсем покинуть Землю, молекула, как и космический корабль или ракета, должна иметь очень большую скорость (не меньше 11,2 км/с). Это так называемая вторая космическая скорость . Скорость большинства молекул воздушной оболочки Земли значительно меньше этой космической скорости. Поэтому большинство их привязано к Земле силой тяжести, лишь ничтожно малое количество молекул улетает за пределы Земли в космос.
Беспорядочное движение молекул и действие на них силы тяжести приводят в результате к тому, что молекулы газов “парят” в пространстве около Земли, образуя воздушную оболочку, или известную нам атмосферу.
Измерения показывают, что плотность воздуха быстро уменьшается с высотой. Так, на высоте 5,5 км над Землей плотность воздуха в 2 раза меньше его плотность у поверхности Земли, на высоте 11 км – в 4 раза меньше, и т. д. Чем выше, тем воздух разреженнее. И наконец, в самых верхних слоях (сотни и тысячи километров над Землей) атмосфера постепенно переходит в безвоздушное пространство. Четкой границы воздушная оболочка Земли не имеет.
И наконец, в самых верхних слоях (сотни и тысячи километров над Землей) атмосфера постепенно переходит в безвоздушное пространство. Четкой границы воздушная оболочка Земли не имеет.
Строго говоря, вследствие действия силы тяжести плотность газа в любом закрытом сосуде неодинакова по всему объему сосуда. Внизу сосуда плотность газа больше, чем в верхних его частях, поэтому и давление в сосуде неодинаково. На дне сосуда оно больше, чем вверху. Однако для газа, содержащегося в сосуде, это различие в плотности и давлении столь мало, что его можно во многих случаях совсем не учитывать, просто знать об этом. Но для атмосферы, простирающейся на несколько тысяч километров, различие это существенно.
Измерение атмосферного давления. Опыт Торричелли.
Рассчитать атмосферное давление по формуле для вычисления давления столба жидкости (§ 38) нельзя. Для такого расчета надо знать высоту атмосферы и плотность воздуха. Но определенной границы у атмосферы нет, а плотность воздуха на разной высоте различна. Однако измерить атмосферное давление можно с помощью опыта, предложенного в 17 веке итальянским ученым Эванджелиста Торричелли , учеником Галилея.
Однако измерить атмосферное давление можно с помощью опыта, предложенного в 17 веке итальянским ученым Эванджелиста Торричелли , учеником Галилея.
Опыт Торричелли состоит в следующем: стеклянную трубку длиной около 1 м, запаянную с одного конца, наполняют ртутью. Затем, плотно закрыв второй конец трубки, ее переворачивают и опускают в чашку с ртутью, где под уровнем ртути открывают этот конец трубки. Как и в любом опыте с жидкостью, часть ртути при этом выливается в чашку, а часть ее остается в трубке. Высота столба ртути, оставшейся в трубке, равна примерно 760 мм. Над ртутью внутри трубки воздуха нет, там безвоздушное пространство, поэтому никакой газ не оказывает давления сверху на столб ртути внутри этой трубки и не влияет на измерения.
Торричелли, предложивший описанный выше опыт, дал и его объяснение. Атмосфера давит на поверхность ртути в чашке. Ртуть находится в равновесии. Значит, давление в трубке на уровне аа 1 (см. рис) равно атмосферному давлению. При изменении атмосферного давления меняется и высота столба ртути в трубке. При увеличении давления столбик удлиняется. При уменьшении давления – столб ртути уменьшает свою высоту.
При изменении атмосферного давления меняется и высота столба ртути в трубке. При увеличении давления столбик удлиняется. При уменьшении давления – столб ртути уменьшает свою высоту.
Давление в трубке на уровне аа1 создается весом столба ртути в трубке, так как в верхней части трубки над ртутью воздуха нет. Отсюда следует, что атмосферное давление равно давлению столба ртути в трубке , т. е.
p атм = p ртути.
Чем больше атмосферное давление, тем выше столб ртути в опыте Торричелли. Поэтому на практике атмосферное давление можно измерить высотой ртутного столба (в миллиметрах или сантиметрах). Если, например, атмосферное давление равно 780 мм рт. ст. (говорят “миллиметров ртутного столба”), то это значит, что воздух производит такое же давление, какое производит вертикальный столб ртути высотой 780 мм.
Следовательно, в этом случае за единицу измерения атмосферного давления принимается 1 миллиметр ртутного столба (1 мм рт. ст.). Найдем соотношение между этой единицей и известной нам единицей – паскалем (Па).
Давление столба ртути ρ ртути высотой 1 мм равно:
p = g·ρ·h , p = 9,8 Н/кг · 13 600 кг/ м 3 · 0,001 м ≈ 133,3 Па.
Итак, 1 мм рт. ст. = 133,3 Па.
В настоящее время атмосферное давление принято измерять в гектопаскалях (1 гПа = 100 Па). Например, в сводках погоды может быть объявлено, что давление равно 1013 гПа, это то же самое, что 760 мм рт. ст.
Наблюдая ежедневно за высотой ртутного столба в трубке, Торричелли обнаружил, что эта высота меняется, т. е. атмосферное давление непостоянно, оно может увеличиваться и уменьшаться. Торричелли заметил также, что атмосферное давление связано с изменением погоды.
Если к трубке с ртутью, использовавшейся в опыте Торричелли, прикрепить вертикальную шкалу, то получится простейший прибор – ртутный барометр (от греч. барос – тяжесть, метрео – измеряю). Он служит для измерения атмосферного давления.
Барометр – анероид.
В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого – безжидкостный ). Так барометр называют потому, что в нем нет ртути.
Так барометр называют потому, что в нем нет ртути.
Внешний вид анероида изображен на рисунке. Главная часть его – металлическая коробочка 1 с волнистой (гофрированной) поверхностью (см. др. рис.). Из этой коробочки выкачан воздух, а чтобы атмосферное давление не раздавило коробочку, ее крышка 2 пружиной оттягивается вверх. При увеличении атмосферного давления крышка прогибается вниз и натягивает пружину. При уменьшении давления пружина выпрямляет крышку. К пружине с помощью передаточного механизма 3 прикреплена стрелка-указатель 4, которая продвигается вправо или влево при изменении давления. Под стрелкой укреплена шкала, деления которой нанесены по показаниям ртутного барометра. Так, число 750, против которого стоит стрелка анероида (см. рис.), показывает, что в данный момент в ртутном барометре высота ртутного столба 750 мм.
Следовательно, атмосферное давление равно 750 мм рт. ст. или ≈ 1000 гПа.
Значение атмосферного давления весьма важно для предвидения погоды на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр – необходимый прибор для метеорологических наблюдений.
Барометр – необходимый прибор для метеорологических наблюдений.
Атмосферное давление на различных высотах.
В жидкости давление, как мы знаем, зависит от плотности жидкости и высоты ее столба. Вследствие малой сжимаемости плотность жидкости на различных глубинах почти одинакова. Поэтому, вычисляя давление, мы считаем ее плотность постоянной и учитываем только изменение высоты.
Сложнее дело обстоит с газами. Газы сильно сжимаемы. А чем сильнее газ сжат, тем больше его плотность, и тем большее давление он производит. Ведь давление газа создается ударами его молекул о поверхность тела.
Слои воздуха у поверхности Земли сжаты всеми вышележащими слоями воздуха, находящимися над ними. Но чем выше от поверхности слой воздуха, тем слабее он сжат, тем меньше его плотность. Следовательно, тем меньшее давление он производит. Если, например, воздушный шар поднимается над поверхностью Земли, то давление воздуха на шар становиться меньше. Это происходит не только потому, что высота столба воздуха над ним уменьшается, но еще и потому, что уменьшается плотность воздуха. Вверху она меньше, чем внизу. Поэтому зависимость давления воздуха от высоты сложнее, чем жидкости.
Вверху она меньше, чем внизу. Поэтому зависимость давления воздуха от высоты сложнее, чем жидкости.
Наблюдения показывают, что атмосферное давление в местностях, лежащих на уровне моря, в среднем равно 760 мм рт. ст.
Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 °С, называется нормальным атмосферным давлением .
Нормальное атмосферное давление равно 101 300 Па = 1013 гПа.
Чем больше высота над уровнем моря, тем давление меньше.
При небольших подъемах, в среднем, на каждые 12 м подъема давление уменьшается на 1 мм рт. ст. (или на 1,33 гПа).
Зная зависимость давления от высоты, можно по изменению показаний барометра определить высоту над уровнем моря. Анероиды, имеющие шкалу, по которой непосредственно можно измерить высоту над уровнем моря, называются высотомерами . Их применяют в авиации и при подъеме на горы.
Манометры.
Мы уже знаем, что для измерения атмосферного давления применяют барометры. Для измерения давлений, бóльших или меньших атмосферного, используется манометры (от греч. манос – редкий, неплотный, метрео – измеряю). Манометры бывают жидкостные и металлические .
Для измерения давлений, бóльших или меньших атмосферного, используется манометры (от греч. манос – редкий, неплотный, метрео – измеряю). Манометры бывают жидкостные и металлические .
Рассмотрим сначала устройство и действие открытого жидкостного манометра . Он состоит из двухколенной стеклянной трубки, в которую наливается какая-нибудь жидкость. Жидкость устанавливается в обоих коленах на одном уровне, так как на ее поверхность в коленах сосуда действует только атмосферное давление.
Чтобы понять, как работает такой манометр, его можно соединить резиновой трубкой с круглой плоской коробкой, одна сторона которой затянута резиновой пленкой. Если надавить пальцем на пленку, то уровень жидкости в колене манометра, соединенном в коробкой, понизится, а в другом колене повысится. Чем это объясняется?
При надавливании на пленку увеличивается давление воздуха в коробке.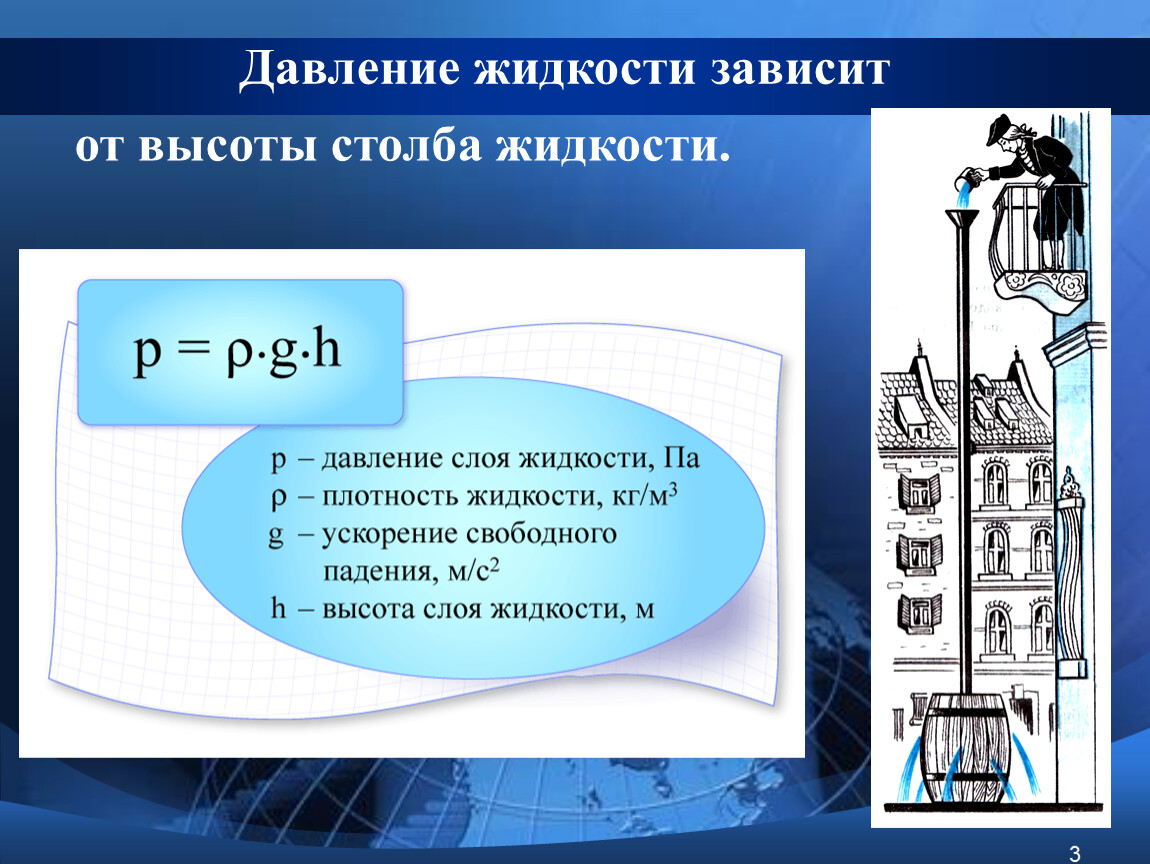 По закону Паскаля это увеличение давления передается и жидкости в том колене манометра, которое присоединено к коробке. Поэтому давление на жидкость в этом колене будет больше, чем в другом, где на жидкость действует только атмосферное давление. Под действием силы этого избыточного давления жидкость начнет перемещаться. В колене со сжатым воздухом жидкость опустится, в другом – поднимется. Жидкость придет в равновесие (остановится), когда избыточное давление сжатого воздуха уравновесится давлением, которое производит избыточный столб жидкости в другом колене манометра.
По закону Паскаля это увеличение давления передается и жидкости в том колене манометра, которое присоединено к коробке. Поэтому давление на жидкость в этом колене будет больше, чем в другом, где на жидкость действует только атмосферное давление. Под действием силы этого избыточного давления жидкость начнет перемещаться. В колене со сжатым воздухом жидкость опустится, в другом – поднимется. Жидкость придет в равновесие (остановится), когда избыточное давление сжатого воздуха уравновесится давлением, которое производит избыточный столб жидкости в другом колене манометра.
Чем сильнее давить на пленку, тем выше избыточный столб жидкости, тем больше его давление. Следовательно, об изменении давления можно судить по высоте этого избыточного столба .
На рисунке показано, как таким манометром можно измерять давление внутри жидкости. Чем глубже погружается в жидкость трубочка, тем больше становится разность высот столбов жидкости в коленах манометра , тем, следовательно, и большее давление производит жидкость .
Если установить коробочку прибора на какой-нибудь глубине внутри жидкости и поворачивать ее пленкой вверх, вбок и вниз, то показания манометра при этом не будут меняется. Так и должно быть, ведь на одном и том же уровне внутри жидкости давление одинаково по всем направлениям .
На рисунке изображен металлический манометр . Основная часть такого манометра – согнутая в трубу металлическая трубка 1 , один конец которой закрыт. Другой конец трубки с помощью крана 4 сообщается с сосудом, в котором измеряют давление. При увеличении давления трубка разгибается. Движение её закрытого конца при помощи рычага 5 и зубчатки 3 передается стрелке 2 , движущейся около шкалы прибора. При уменьшении давления трубка, благодаря своей упругости, возвращается в прежнее положение, а стрелка – к нулевому делению шкалы.
Поршневой жидкостный насос.
В опыте, рассмотренном нами ранее (§ 40), было установлено, что вода в стеклянной трубке под действием атмосферного давления поднималась вверх за поршнем. На этом основано действие поршневых насосов.
На этом основано действие поршневых насосов.
Насос схематически изображен на рисунке. Он состоит из цилиндра, внутри которого ходит вверх и вниз, плотно прилегая к стенкам сосуда, поршень 1 . В нижней части цилиндра и в самом поршне установлены клапаны 2 , открывающиеся только вверх. При движении поршня вверх вода под действием атмосферного давления входит в трубу, поднимает нижний клапан и движется за поршнем.
При движении поршня вниз вода, находящаяся под поршнем, давит на нижний клапан, и он закрывается. Одновременно под давлением воды открывается клапан внутри поршня, и вода переходит в пространство над поршнем. При следующем движении поршня вверх в месте с ним поднимается и находящаяся над ним вода, которая и выливается в отводящую трубу. Одновременно за поршнем поднимается и новая порция воды, которая при последующем опускании поршня окажется над ним, и вся эта процедура повторяется вновь и вновь, пока работает насос.
Гидравлический пресс.

Закон Паскаля позволяет объяснить действие гидравлической машины (от греч. гидравликос – водяной). Это машины, действие которых основано на законах движения и равновесия жидкостей.
Основной частью гидравлической машины служат два цилиндра разного диаметра, снабженные поршнями и соединительной трубкой. Пространство под поршнями и трубку заполняют жидкостью (обычно минеральным маслом). Высоты столбов жидкости в обоих цилиндрах одинаковы, пока на поршни не действуют силы.
Допустим теперь, что силы F 1 и F 2 – силы, действующие на поршни, S 1 и S 2 – площади поршней. Давление под первым (малым) поршнем равно p 1 = F 1 / S 1 , а под вторым (большим) p 2 = F 2 / S 2 . По закону Паскаля давление покоящейся жидкостью во все стороны передается одинаково, т. е. p 1 = p 2 или F 1 / S 1 = F 2 / S 2 , откуда:
F 2 / F 1 = S 2 / S 1 .
Следовательно, сила F 2 во столько раз больше силы F 1 , во сколько раз площадь большого поршня больше площади малого поршня . Например, если площадь большого поршня 500 см 2 , а малого 5 см 2 , и на малый поршень действует сила 100 Н, то на больший поршень будет действовать сила, в 100 раз бóльшая, то есть 10 000 Н.
Таким образом, с помощью гидравлической машины можно малой силой уравновесить бóльшую силу.
Отношение F 1 / F 2 показывает выигрыш в силе. Например, в приведенном примере выигрыш в силе равен 10 000 Н / 100 Н = 100.
Гидравлическая машина, служащая для прессования (сдавливания), называется гидравлическим прессом .
Гидравлические прессы применяются там, где требуется большая сила. Например, для выжимания масла из семян на маслобойных заводах, для прессования фанеры, картона, сена. На металлургических заводах гидравлические прессы используют для изготовления стальных валов машин, железнодорожных колес и многих других изделий. Современные гидравлические прессы могут развивать силу в десятки и сотни миллионов ньютонов.
Современные гидравлические прессы могут развивать силу в десятки и сотни миллионов ньютонов.
Устройство гидравлического пресса схематически показано на рисунке. Прессуемое тело 1 (A) кладут на платформу, соединенную с большим поршнем 2 (B). При помощи малого поршня 3 (D) создается большое давление на жидкость. Это давление передается в каждую точку жидкости, заполняющей цилиндры. Поэтому такое же давление действует и на второй, большой поршень. Но так как площадь 2-го (большого) поршня больше площади малого, то и сила, действующая на него, будет больше силы, действующей на поршень 3 (D). Под действием этой силы поршень 2 (B) будет подниматься. При подъеме поршня 2 (B) тело (A) упирается в неподвижную верхнюю платформу и сжимается. При помощи манометра 4 (M) измеряется давление жидкости. Предохранительный клапан 5 (P) автоматически открывается, когда давление жидкости превышает допустимое значение.
Из малого цилиндра в большой жидкость перекачивается повторными движениями малого поршня 3 (D).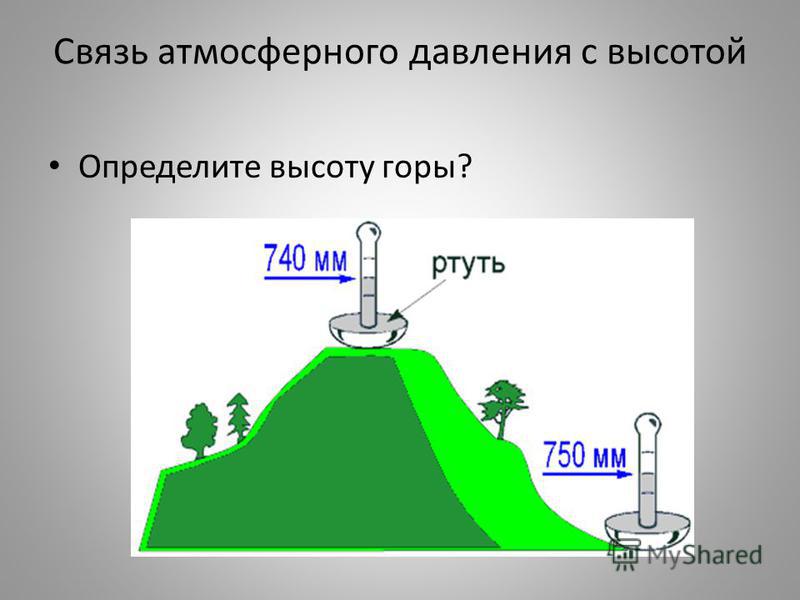 Это осуществляется следующим образом. При подъеме малого поршня (D) клапан 6 (K) открывается, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости клапан 6 (K) закрывается, а клапан 7 (K”) открывается, и жидкость переходит в большой сосуд.
Это осуществляется следующим образом. При подъеме малого поршня (D) клапан 6 (K) открывается, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления жидкости клапан 6 (K) закрывается, а клапан 7 (K”) открывается, и жидкость переходит в большой сосуд.
Действие воды и газа на погруженное в них тело.
Под водой мы легко можем поднять камень, который с трудом поднимается в воздухе. Если погрузить пробку под воду и выпустить ее из рук, то она всплывет. Как можно объяснить эти явления?
Мы знаем (§ 38), что жидкость давит на дно и стенки сосуда. И если внутрь жидкости поместить какое-нибудь твердое тело, то оно также будет подвергаться давлению, как и стенки сосуда.
Рассмотрим силы, которые действуют со стороны жидкости на погруженное в нее тело. Чтобы легче было рассуждать, выберем тело, которое имеет форму параллелепипеда с основаниями, параллельными поверхности жидкости (рис.). Силы, действующие на боковые грани тела, попарно равны и уравновешивают друг друга. Под действием этих сил тело сжимается. А вот силы, действующие на верхнюю и нижнюю грани тела, неодинаковы. На верхнюю грань давит сверху силой F 1 столб жидкости высотой h 1 . На уровне нижней грани давление производит столб жидкости высотой h 2 . Это давление, как мы знаем (§ 37), передается внутри жидкости во все стороны. Следовательно, на нижнюю грань тела снизу вверх с силой F 2 давит столб жидкости высотой h 2 . Но h 2 больше h 1 , следовательно, и модуль силы F 2 больше модуля силы F 1 . Поэтому тело выталкивается из жидкости с силой F выт, равной разности сил F 2 – F 1 , т. е.
Под действием этих сил тело сжимается. А вот силы, действующие на верхнюю и нижнюю грани тела, неодинаковы. На верхнюю грань давит сверху силой F 1 столб жидкости высотой h 1 . На уровне нижней грани давление производит столб жидкости высотой h 2 . Это давление, как мы знаем (§ 37), передается внутри жидкости во все стороны. Следовательно, на нижнюю грань тела снизу вверх с силой F 2 давит столб жидкости высотой h 2 . Но h 2 больше h 1 , следовательно, и модуль силы F 2 больше модуля силы F 1 . Поэтому тело выталкивается из жидкости с силой F выт, равной разности сил F 2 – F 1 , т. е.
Но S·h = V, где V – объем параллелепипеда, а ρ ж ·V = m ж – масса жидкости в объеме параллелепипеда. Следовательно, F выт = g·m ж = P ж, т. е. выталкивающая сила равна весу жидкости в объеме погруженного в нее тела (выталкивающая сила равна весу жидкости такого же объёма, как и объём погруженного в нее тела). Существование силы, выталкивающей тело из жидкости, легко обнаружить на опыте. На рисунке а изображено тело, подвешенное к пружине со стрелкой-указателем на конце. Стрелка отмечает на штативе растяжение пружины. При отпускании тела в воду пружина сокращается (рис., б ). Такое же сокращение пружины получится, если действовать на тело снизу вверх с некоторой силой, например, нажать рукой (приподнять). Следовательно, опыт подтверждает, что на тело, находящееся в жидкости, действует сила, выталкивающая это тело из жидкости . К газам, как мы знаем, также применим закон Паскаля. Поэтому на тела, находящиеся в газе, действует сила, выталкивающая их из газа . Под действием этой силы воздушные шары поднимаются вверх. Существование силы, выталкивающей тело из газа, можно также наблюдать на опыте. К укороченной чашке весов подвесим стеклянный шар или большую колбу, закрытую пробкой. Весы уравновешиваются. Затем под колбу (или шар) ставят широкий сосуд так, чтобы он окружал всю колбу. Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу . Поэтому пролкосмосе). Именно этим объясняется, что в воде мы иногда легко поднимаем тела, которые с трудом удерживаем в воздухе. К пружине подвешивается небольшое ведерко и тело цилиндрической формы (рис., а). Стрелка на штативе отмечает растяжение пружины. Она показывает вес тела в воздухе. Приподняв тело, под него подставляется отливной сосуд, наполненный жидкостью до уровня отливной трубки. После чего тело погружается целиком в жидкость (рис., б). При этом часть жидкости, объем которой равен объему тела, выливается из отливного сосуда в стакан. На основании этого опыта можно заключить, что сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела . Такой же вывод мы получили и в § 48. Если подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела . Сила, выталкивающая тело из жидкости или газа, называется архимедовой силой , в честь ученого Архимеда , который впервые указал на ее существование и рассчитал ее значение. Итак, опыт подтвердил, что архимедова (или выталкивающая) сила равна весу жидкости в объеме тела, т. F A = g·ρ ж ·V т Следовательно, архимедова сила зависит от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погружаемого в жидкость, так как эта величина не входит в полученную формулу. Определим теперь вес тела, погруженного в жидкость (или в газ). Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости P 1 будет меньше веса тела в вакууме P = g·m на архимедову силу F А = g·m ж (где m ж – масса жидкости или газа, вытесненной телом). Таким образом, если тело погружено в жидкость или газ, то оно теряет в своем весе столько, сколько весит вытесненная им жидкость или газ . Пример . Определить выталкивающую силу, действующую на камень объемом 1,6 м 3 в морской воде. Запишем условие задачи и решим ее. Когда всплывающее тело достигнет поверхности жидкости, то при дальнейшем его движении вверх архимедова сила будет уменьшаться. Почему? А потому, что будет уменьшаться объем части тела, погруженной в жидкость, а архимедова сила равна весу жидкости в объеме погруженной в нее части тела. Когда архимедова сила станет равной силе тяжести, тело остановится и будет плавать на поверхности жидкости, частично погрузившись в нее. Полученный вывод легко проверить на опыте. В отливной сосуд нальем воду до уровня отливной трубки. После этого погрузим в сосуд плавающее тело, предварительно взвесив его в воздухе. Опустившись в воду, тело вытесняет объем воды, равный объему погруженной в нее части тела. Взвесив эту воду, находим, что ее вес (архимедова сила) равен силе тяжести, действующей на плавающее тело, или весу этого тела в воздухе. Проделав такие же опыты с любыми другими телами, плавающими в разных жидкостях – в воде, спирте, растворе соли, можно убедиться, что если тело плавает в жидкости, то вес вытесненной им жидкости равен весу этого тела в воздухе . Легко доказать, что если плотность сплошного твердого тела больше плотности жидкости, то тело в такой жидкости тонет. Тело с меньшей плотностью всплывает в этой жидкости . Кусок железа, например, тонет в воде, но всплывает в ртути. Тело же, плотность которого равна плотности жидкости, остается в равновесии внутри жидкости. Плавает на поверхности воды лед, так как его плотность меньше плотности воды. Чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость . При равных плотностях тела и жидкости тело плавает внутри жидкости на любой глубине. Две несмешивающиеся жидкости, например вода и керосин, располагаются в сосуде в соответствии со своими плотностями: в нижней части сосуда – более плотная вода (ρ = 1000 кг/м 3), сверху – более легкий керосин (ρ = 800 кг/м 3). Средняя плотность живых организмов, населяющих водную среду, мало отличается от плотности воды, поэтому их вес почти полностью уравновешивается архимедовой силой. Благодаря этому водные животные не нуждаются в столь прочных и массивных скелетах, как наземные. По этой же причине эластичны стволы водных растений. Плавательный пузырь рыбы легко меняет свой объем. Когда рыба с помощью мышц опускается на большую глубину, и давление воды на нее увеличивается, пузырь сжимается, объем тела рыбы уменьшается, и она не выталкивается вверх, а плавает в глубине. Таким образом, рыба может в определенных пределах регулировать глубину своего погружения. Киты регулируют глубину своего погружения за счет уменьшения и увеличения объема легких. Плавание судов.Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делается из стальных листов. Все внутренние крепления, придающие судам прочность, также изготовляют из металлов. Благодаря чему суда держатся на воде, принимают на борт и перевозят большие грузы? Опыт с плавающим телом (§ 50) показал, что тело вытесняет своей подводной частью столько воды, что по весу эта вода равна весу тела в воздухе. Это также справедливо и для любого судна. Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом . Глубина, на которую судно погружается в воду, называется осадкой . Наибольшая допускаемая осадка отмечена на корпусе судна красной линией, называемой ватерлинией (от голланд. ватер – вода). Вес воды, вытесняемой судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна . В настоящее время для перевозки нефти строятся суда водоизмещением 5 000 000 кН (5 · 10 6 кН) и больше, т. Если из водоизмещения вычесть вес самого судна, то мы получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном. Судостроение существовало еще в Древнем Египте, в Финикии (считается, что Финикийцы были одними из лучших судостроителей), Древнем Китае. В России судостроение зародилось на рубеже 17-18 вв. Сооружались главным образом военные корабли, но именно в России были построены первый ледокол, суда с двигателем внутреннего сгорания, атомный ледокол “Арктика”. Воздухоплавание.Рисунок с описанием шара братьев Монгольфье 1783 года: «Вид и точные размеры „Аэростата Земной шар“, который был первым». 1786 С давних времен люди мечтали о возможности летать над облаками, плавать в воздушном океане, как они плавали по морю. Для воздухоплавания вначале использовали воздушные шары, которые наполняли или нагретым воздухом, или водородом либо гелием. Для того, чтобы воздушный шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая) F А, действующая на шар, была больше силы тяжести F тяж, т. е. F А > F тяж. По мере поднятия шара вверх архимедова сила, действующая на него, уменьшается (F А = gρV ), так как плотность верхних слоев атмосферы меньше, чем у поверхности Земли. Чтобы подняться выше, с шара сбрасывается специальный балласт (груз) и этим облегчает шар. В конце концов шар достигает своей своей предельной высоты подъема. Для спуска шара из его оболочки при помощи специального клапана выпускается часть газа. В горизонтальном направлении воздушный шар перемещается только под действием ветра, поэтому он называется аэростатом (от греч аэр – воздух, стато – стоящий). Для исследования верхних слоев атмосферы, стратосферы еще не так давно применялись огромные воздушные шары – стратостаты . До того как научились строить большие самолеты для перевозки по воздуху пассажиров и грузов, применялись управляемые аэростаты – дирижабли . Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Поэтому для того, чтобы узнать, какой груз может поднять воздушный шар, необходимо определить его подъемную силу . Пусть, например, в воздух запущен шар объемом 40 м 3 , наполненный гелием. Масса гелия, заполняющая оболочку шара, будет равна: Значит, этот шар может поднять груз весом 520 Н – 71 Н = 449 Н. Это и есть его подъемная сила. Шар такого же объема, но наполненный водородом, может поднять груз 479 Н. Значит, подъемная сила его больше, чем шара, наполненного гелием. Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части шара, располагается горелка. При помощи газовой горелки можно регулировать температуру воздуха внутри шара, а значит, его плотность и выталкивающую силу. Чтобы шар поднялся выше, достаточно сильнее нагреть воздух в нем, увеличив пламя горелки. При уменьшении пламени горелки температура воздуха в шаре уменьшается, и шар опускается вниз. Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда шар повиснет в воздухе, и с него будет легко проводить наблюдения. По мере развития науки происходили и существенные изменения в воздухоплавательной технике. Появилась возможность использования новых оболочек для аэростатов, которые стали прочными, морозоустойчивыми и легкими. Достижения в области радиотехники, электроники, автоматики позволили сконструировать беспилотные аэростаты. Всем нам мерили давление. Почти каждый знает, что нормальный показатель давления равен 120/80 мм ртутного столба. Но далеко не все могут ответить, что на самом деле обозначают эти цифры. Попытаемся разобраться, что вообще значит верхнее/нижнее давление, а также чем эти значения друг от друга отличаются. Вначале определимся с понятиями. Артериальное давление (АД) – это один из самых важных показателей, оно демонстрирует функционирование кровеносной системы. Этот показатель формируется при участии сердца, сосудов и крови, движущейся по ним. Артериальное давление — это давление крови на стенку артерии При этом он зависит от сопротивления крови, ее объема, «выбрасываемого» в результате одного сокращения (это называется систолой), и интенсивности сокращений сердца. Самый высокий показатель АД может наблюдаться, когда сердце сокращается и «выбрасывает» кровь из левого желудочка, а самый низкий – во время попадания в правое предсердие, когда главная мышца расслаблена (диастола). Под верхним давлением или, если говорить языком науки, систолическим, подразумевается давление крови при сокращении. Этот показатель демонстрирует то, как сокращается сердце. Формирование такого давления выполняется при участии крупных артерий (например, аорты), а зависит данный показатель от ряда ключевых факторов. К таковым относят:
Что же касается нижнего давления (другими словами, диастолического), то оно показывает, какое сопротивление испытывает кровь во время движения по кровеносным сосудам. Нижнее давление наблюдается, когда клапан аорты закрывается, и кровь не может вернуться в сердце. При этом само сердце наполняется другой кровью, насыщенной кислородом, и готовится к следующему сокращению. Движение крови происходит как бы самотеком, пассивно. К факторам, влияющим на диастолическое давление, относится:
Делаем вывод: в приведенном в начале статьи примере (120/80) 120 – это показатель верхнего АД, а 80 – нижнего. Артериальное давление — норма и отклонения Что характерно, формирование АД зависит преимущественно от образа жизни, питательного рациона, привычек (в том числе вредных), частоты стрессов. К примеру, при помощи употребления той или иной пищи можно специально понижать/повышать давление. Достоверно известно, что были случаи, когда люди полностью излечивались от гипертонии после изменения привычек и образа жизни. Для чего нужно знать величину АД?При каждом повышении показателя на 10 мм ртутного столба риск возникновения сердечно-сосудистых болезней увеличивается примерно на 30 процентов. Именно поэтому выяснение причины возникновения таких симптомов, как головокружение, мигрени или общая слабость, следует начинать с измерения АД. В нередких случаях давление нужно постоянно контролировать и проверять каждые несколько часов. Как проводится измерение давленияВ большинстве случаев АД измеряют при помощи специального приспособления, состоящего из следующих элементов:
Манжета накладывается на плечо. В процессе измерения необходимо придерживаться определенных требований, в противном случае результат может быть неверным (заниженным или завышенным), что, в свою очередь, может повлиять на последующую тактику лечения. Давление крови — измерение
Как оценить показатель АДЧем выше у человека АД, тем большая вероятность появления таких недугов, как инсульт, ишемия, почечная недостаточность и проч. Для самостоятельной оценки показателя давления можно использовать специальную классификацию, разработанную еще в 1999-м. Таблица №1. Оценка уровня АД. Норма * — оптимальное с точки зрения развития заболеваний сосудов и сердца, а также смертности.
Таблица №2. Оценка уровня АД. Гипертония
Физика – предмет сложный. В физике очень много разных интересных терминов и формул Полезная информация – давление измеряется в паскалях Что касается буквы, которая обозначает давление в физике – латинская буква Р P,Па больше добавить нечего, но длина сообщения должна быть 40) Давление является физической величиной. Определяется оно, как сила давления на какую-либо поверхность, к площади данной поверхности. Обозначается физическое давление маленькой английской буквой р. Буквой F обозначается сила давления, а буквой S обозначается площадь поверхности. Измеряется давление Н/м2 (Ньютон на метр квадратный). Данную величину можно перевести в Паскали (Па). Один Па будет равен одному Н/м. Ответ на этот лгкий вопрос из области физики, начальный курс, которой проходят в средней школе. С того времени отчтливо помню, что буква, обозначающая давление, p. А формула следующая p=f/s. Эту формулу можно отыскать в любом учебнике физики. Как я помню еще со школьных уроков физики, давление обозначается латинской буквой p. Думаю, что за несколько лет ничего не поменялось. Измеряется давление в паскалях (обозначается Па, или Pa латинскими буквами). Еще помню из уроков по физике, что давление измеряется в Паскалях, а обозначается данная единица в системе СИ как Па. Я думаю, что такие единицы измерения не меняются со временем, так как были еще придуманы давно и все ими пользуются. Давление представляет собой физическую величину, которая характеризует распределение силы по той площади, куда она приложена. Отношение этой силы F к площади поверхности S и показывает давление, что записывается в виде формулы. В этой формуле латинской буквой P обозначается физическая величина – давление . Пользуясь формулой можно проследить за изменением давления. Например, для того чтобы давление увеличить нужно увеличить силу (величина в числителе) или уменьшить площадь приложения (знаменатель). Как верно сказано выше, давление в физике обозначается буквой P . А единицей для измерения давления в Международной системе единиц (СИ), действительно является паскаль (Па). Своим названием, данная физическая величина обязана талантливейшему французскому учному и писателю XVII века Блезу Паскалю, который за свою короткую жизнь (39 лет), доказал не только наличие существование атмосферного давления, но и осуществил огромнейшее количество исследований и экспериментов. Особую слабость питал Паскаль к математике, в области которой иногда совершал открытия в течении одной ночи. Представьте себе, что он является одним из создателем математического анализа, проективной геометрии, теории вероятности, и помимо всего прочего – изобретателем первых счтных машин – прообраза современных компьютеров! Однако, самое главное, что слава и богатство не ожесточили сердце великого человека. Блез Паскаль, до конца своих дней заботился о простом народе, раздавая большую часть доходов на благотворительность. Счтная машина Паскаля Насколько помню, давление обозначают буквой P. Причем можно использовать и большую, и маленькую букву P. К примеру, вот формула избыточного давления газа: В формуле указаны 3 quot;pquot; – это все разные типы давления. Буквы возле quot;pquot; обозначают тип давления. В данном случае: p и – это избыточное давление. p – полное давление. p а – атмосферное давление. Единицей измерения этой физической величины (давления) в системе единиц является Па (Паскаль). Названа эта единица в честь известного фр. ученого и философа Блеза Паскаля (годы жизни 1623 – 1662). Кстати, в честь него также назван и один из языков программирования Паскаль. В физике для обозначения давления используют букву р (английская строчная). Буковка, которой показывают давление выглядит вот так: p . В системе Си давление измеряется в Паскалях (Па). Что ещ можно сказать про давление? Разве что физическое его определение, а именно что оно из себя представляет. Это отношение силы, действующей на поверхность перпендикулярно этой поверхности, к площади этой поверхности. Единица давления измеряется в СИ = 1Па (паскаль). >>Давление и сила давления Отослано читателями из интернет-сайтов Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование, физика 7 класс онлайн , книги и учебники по физике. Школьнику подготовиться к уроку. СХОЖИЕ СТАТЬИПолезное Реклама Новое |
Тест по физике на тему “Давление” для 7 класса
Тест по физике на тему “Давление” для 7 класса
1. Давление обозначается буквой, измеряется
Давление обозначается буквой, измеряется
1) р, Н
2) р, Па
3) Р, Па
2. Давление твердого тела можно найти по формуле
1) p=FS
2) p=F/S
3) p=S/F
3. Во сколько раз и как изменится давление, если сила давления уменьшится в 3 раза, а площадь поверхности увеличится в 2 раза?
1) увеличится в 6 раз;
2) уменьшится в 6 раз;
3) увеличится в 1,5 раза;
4) уменьшится в 1,5 раза.
4. Давление газа есть результат:
1) ударов частиц о стенки сосуда;
2) соударения частиц между собой;
3) ударов частиц о стенки сосуда и соударения частиц между собой.
5. При увеличении объема газа давление:
При увеличении объема газа давление:
1) увеличивается; 2) уменьшается; 3) не изменяется.
6. При повышении температуры газа давление:
1) увеличивается; 2) уменьшается; 3) не изменяется.
7. Давление жидкости на дно сосуда не зависит от:
1) плотности жидкости;
2) высоты столба жидкости;
3) формы сосуда.
8. В открытых сообщающихся сосудах поверхности однородной жидкости устанавливаются:
1) на разных уровнях в зависимости от площади сечения сосудов;
2) на разных уровнях в зависимости от формы сосудов;
3) на одном уровне.
9. При подъеме в гору атмосферное давление уменьшилось на 5 мм рт. ст.. Высота горы:
1) 12 м; 2) 60 м; 3) 120 м.
10. Каким прибором измеряют атмосферное давление?
в теории и на практике
Рассказываем, что такое давление, как оно рассчитывается и где мы сталкиваемся с ним каждый день.
Теория: что говорит нам физика
Любое вещество в условиях гравитации оказывает давление. По определению это:
Физическая величина, которая выражает воздействие силы на единицу площади поверхности.
В международной системе СИ (от франц. ‘Le Système International d’Unités’, SI) давление измеряется в Паскалях (Па) и обозначается буквой p.
Формула, вытекающая из определения, выглядит так:
Давление твердых тел, жидкости и газа проходит по-разному.
У твердого тела в условиях гравитации есть точка опоры. Все давление приходится на нее, а значит, оно неравномерно.
Жидкость и газ заполняют сосуд и оказывают давление не только на его дно, но и на стенки (а газ — и на крышку). Если надавить на любую точку заполненного сосуда (предположим, это полиэтиленовый пакет), то давление равномерно передастся во всех направлениях: вниз, вверх и вбок. Это закон Паскаля.
Если надавить на любую точку заполненного сосуда (предположим, это полиэтиленовый пакет), то давление равномерно передастся во всех направлениях: вниз, вверх и вбок. Это закон Паскаля.
Гидростатическое давление
Это давление столбика жидкости (точнее, его веса) на дно сосуда. Отсюда можно вывести новую формулу:
У поверхности жидкости ее давление на стенки сосуда будет практически равно нулю (так как чем ближе к поверхности, тем меньше вес жидкости), а ближе ко дну будет действовать формула ρgh.
Давление (любое, не только гидростатическое) может отсутствовать только в вакууме, потому что в нем нет вещества, которое могло бы его создавать. Абсолютный вакуум не достижим или достижим только в искусственных условиях, так как даже в космосе есть минимальная концентрация молекул — а значит, есть и давление, но в ничтожных количествах.
Также в науке есть понятие «физический вакуум», которое означает лишенное вещества пространство. Заполненное квантовым полем, оно все же не может быть охарактеризовано как «абсолютная пустота», так как в этих условиях постоянно рождаются и исчезают виртуальные частицы.
Заполненное квантовым полем, оно все же не может быть охарактеризовано как «абсолютная пустота», так как в этих условиях постоянно рождаются и исчезают виртуальные частицы.
Практика: давление в реальной жизни
Давление — это не всегда больно и неприятно. С некоторыми его видами мы сталкиваемся каждый день, едва ли задумываясь об этом.
Атмосферное давление
Атмосфера любой планеты состоит из газов и удерживается гравитацией. Высота атмосферы Земли — примерно 100 км.
Так как на газ действует гравитация, у воздуха тоже есть вес. Логично предположить, что у поверхности планеты он будет тяжелее, чем на вершине горы. Давление этой 100-километровой массы на поверхность планеты (а заодно и нас) называется атмосферным.
Атмосферное давление, кроме Паскалей, может измеряться в миллиметрах ртутного столба и атмосферах.
В нормальном состоянии человек не обращает внимания на атмосферное давление, потому что оно компенсируется внутренним.
Артериальное давление
Огромный вес воздуха должен был бы нас раздавить, если бы в нас не было крови, которая оказывает внутреннее давление на сосуды. В данном случае — на артерии.
Кровь движется в сосудах не равномерно, а толчками — под воздействием сокращения сердечной мышцы. Загадочные цифры «120/90» — это фиксация превышения давления крови на стенки сосудов над атмосферным давлением, где «120» — максимальное значение в момент сокращения сердца (систолическое давление), а «90» — минимальное значение (диастолическое).
Давление — основная величина в термодинамике, и понять, что это значит, не так уж и сложно. Но если учитель или преподаватель давит слишком сильно, наш студенческий сервис поможет справиться с контрольной, лабораторной, курсовой и любой другой работой. Ждем вас в FenixHelp!
Урок “Вес воздуха. Атмосферное давление” (7-й класс)
Цели урока.
Учащиеся должны усвоить, что:
- Воздух имеет вес;
- Атмосфера оказывает давление на земную поверхность и тела, находящиеся на ней.

Учащиеся должны научиться:
- Объяснять причину наличия атмосферного давления,
- Объяснять проделанные эксперименты.
Учащиеся должны убедиться, что существуют явления, вызванные действием атмосферы.
Ход урока
1. Проверка домашнего задания. Фронтальная беседа.
Вопросы:
- Какие свойства газов отличаются от свойств твердых тел и жидкостей?
- Как с точки зрения МКТ объяснить причину возникновения давления газов?
- Как можно доказать, что газ производит давление на стенки сосуда?
- Как доказать, что газ производит одинаковое давление по всем направлениям?
- От каких величин зависит давление газа? Как его можно изменить?
2. Актуализация знаний.
П. Что такое вес тела? Найдите значение веса следующих тел: гири, массой 100г, стакана с водой.
Что такое вес тела? Найдите значение веса следующих тел: гири, массой 100г, стакана с водой.
У. Вес-это сила, характеризующая действие тел на горизонтальную опору или вертикальный подвес. Вес гири приблизительно 1Н, вес стакана с водой приблизительно 2,5Н.
Это значит, что гиря и стакан с водой действуют на опору (стол и дно стакана) с силой 1Н и 2,5 Н.
3. Этап создания нового знания.
П. Мы нашли значение веса гири и веса стакана с водой. А как определить вес газа? Существует ли давление газа, аналогичное давлению жидкости?
Запишем познавательную задачу 1 (ПЗ 1). Найти вес газа.
Как найти ответ на эту задачу?
У. Нужно определить массу газа (воздуха), а затем рассчитать его вес.
П. Предложите экспериментальную установку для определения массы газа, начертите схему установки в тетради (организация обсуждения предложенных установок).
У. (Изображает схему установки у доски) Нужно взять сосуд, откачать из него воздух и найти массу сосуда, затем заполнить сосуд воздухом и найти массу сосуда с воздухом. Разность масс гирь умножить на 9,8Н/кг и получим вес воздуха.
П. Проводит эксперимент, используя для этого колбу, объемом 1 литр. Запишите значение массы одного литра воздуха. Рассчитайте его вес.
У. Воздух объемом один литр имеет массу 1,3 г. Вес воздуха приблизительно 0,01 Н.
П. А теперь рассчитайте вес 1м3 воздуха.
У.Вес 1 м3 воздуха:
П.Сформулируйте ответ на ПЗ 1. Запишите его в тетрадь (после обсуждения).
4. Мотивационный этап.
П. Воздушную оболочку, окружающую Землю, называют атмосферой. Что вы знаете об атмосфере?
У.Воздушная оболочка, которая окружает Землю. Простирается на десятки километров. Масса атмосферы 5- 1015т. Атмосфера состоит из смеси газов. Плотность уменьшается при удалении от Земли.
Масса атмосферы 5- 1015т. Атмосфера состоит из смеси газов. Плотность уменьшается при удалении от Земли.
П. В состав атмосферы входят: кислород, водород, азот, углекислый газ, водяной пар и другие газы. Оказывает ли атмосфера давление на поверхность Земли и на тела, находящиеся на Земле?
5. Этап создания нового знания.
П. Запишем ПЗ 2. Давит ли атмосфера на поверхность Земли и на тела, находящиеся на ней? Укажите, что является причиной атмосферного давления.
Как решить данную задачу?
У. Можно подобрать примеры из жизни или придумать установку, чтобы какое-то тело двигалось или деформировалось под действием атмосферы.
П. (организует обсуждение предложенных примеров: действия атмосферного давления и установок)
П. Существованием атмосферного давления объясняется целое множество явлений.
Рассмотрим опыт «фонтан в разряженном воздухе». Сначала при помощи насоса откачиваем воздух из колбы. Затем, перевернув колбу горлышком вниз, опускаем в сосуд с водой. Вода всасывается через трубку и бьет фонтаном внутри колбы.
Сначала при помощи насоса откачиваем воздух из колбы. Затем, перевернув колбу горлышком вниз, опускаем в сосуд с водой. Вода всасывается через трубку и бьет фонтаном внутри колбы.
Объясните этот опыт (проводит демонстрацию действия атмосферы: действие фонтана)
У. Вода входит в сосуд, так как атмосферное давление больше давления разряженного воздуха в колбе. Причина атмосферного давления – наличие притяжения молекул (массы) воздуха и Земли.
П. (проводит демонстрацию действия атмосферы: втягивание яйца в бутылку, автоматической поилки для птиц)
У. (отвечают на вопросы)
- Почему яйцо оказалось в бутылке?
- Почему вода не выливается из бутылки?
- Если уровень воды в корытце уменьшится, и горлышко бутылки выйдет из воды, то часть воды из бутылки выльется. Почему?
П. Сформулируйте ответ на ПЗ 2.
У. (учащиеся делают выводы и записывают ответ на ПЗ 2).Атмосфера оказывает давление на поверхность Земли и на тела при любом их расположении.
(учащиеся делают выводы и записывают ответ на ПЗ 2).Атмосфера оказывает давление на поверхность Земли и на тела при любом их расположении.
6. Закрепление изученного материала:
а) Экспериментальная задача. Объяснить действие пипетки, поршневой авторучки.
Оборудование:
- медицинская пипетка,
- стакан с водой
- Как набрать в пипетку воду?
- Как освободить пипетку от воды?
Объяснить это на основе существования атмосферного давления.
Аналогично с авторучкой. Сделайте рисунки.
б) Объясните причины вдоха и выдоха.
в) Когда трубка опускается в пакет с соком, сок устанавливается на одном уровне в пакете и трубке. А как заставить его подняться по трубке в рот?
г) Почему мы не чувствуем что на нас давит вертикальный столб воздуха?
7. Итоги урока.
Итоги урока.
- Какое физическое явление изучалось сегодня на уроке?
- Почему существует атмосферное давление?
- Опишите опыты, подтверждающие существование атмосферного давления (кратко).
8. Домашнее задание.
§40, упражнение 17, задание10 (1, 4)
Сочинение « Что произойдет с атмосферой Земли, если исчезнет
сила земного притяжения?
Придумать загадку об атмосферном давлении (по желанию).
Закон ПАскаля, Атмосферное давление_теоретический материал
Сообщающиеся сосуды. Закон Паскаля. Опыт Торричелли. Атмосферное давление
Давление – это физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности:
В СИ давление измеряется в паскалях (Па). Часто также используются внесистемные единицы давления:
1 атм = 101325 Па = 760 мм рт. |
Закон Паскаля. Внешнее давление, оказываемое на жидкость или газ, передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
Давление, обусловленное весом жидкости (гидростатическое давление), зависит от глубины:
Примером поверхностных сил, для которых выполняется закон Паскаля, является сила атмосферного давления.
Атмосферное давление – это давление, которое оказывает воздух атмосферы на все тела; оно равно силе тяжести, действующей на столб воздуха с единичной площадью основания.
Опыт Торричелли продемонстрировал наличие атмосферного давления и впервые позволил его измерить. Этот опыт был описан в 1644 году.
Рис. 5.1.3. | Рис. |
В этом опыте длинная стеклянная трубка, запаянная с одного конца, наполняется ртутью; затем открытый конец ее зажимается, после чего трубка перевертывается, опускается зажатым концом в сосуд с ртутью и зажим снимается. Ртуть в трубке при этом несколько опускается, т.е. часть ртути выливается в сосуд. Объем пространства над ртутью в трубке называется торричелевой пустотой. (Давление паров ртути в торричелевой пустоте при 0°C составляет 0,025 Па.)
Уровень ртути в трубке одинаков независимо от того, как установлена трубка: вертикально или под углом к горизонту (рис. 5.1.3). При обычных нормальных условиях вертикальная высота ртути в трубке составляет h = 760 мм. Если бы вместо ртути трубка была заполнена водой, то высота h = 10,3 м.
Приборы, применяемые для измерения атмосферного давления, называются барометрами. Простейший ртутный барометр представляет собой трубку Торричелли.
Для того, чтобы объяснить, почему трубка Торричелли
действительно позволяет измерить атмосферное давление, обратимся к рассмотрению
объемных сил и вычислению зависимости давления в жидкости от глубины h.
Давление в жидкости, создаваемое объемными силами, т.е. силой тяжести, называется гидростатическим давлением.
Атмосферное давление обусловлено весом воздушного столба. Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 ºC, называется нормальным атмосферным давлением и обозначается p0.
Чтобы рассчитать это давление в паскалях, воспользуемся формулой гидростатического давления:
p = ρgh
Подставляя в эту формулу значения ρ = 13595,1 кг/м3(плотность ртути при 0 °С), g = 9,80665 м/с2(ускорение свободного падения) и h = 760 мм = 0,76 м (высота столба ртути, соответствующая нормальному атмосферному давлению), получим следующую величину:
p = 101 325 Па.
Это и есть нормальное атмосферное давление.
Атмосферное давление,
близкое к нормальному, наблюдается обычно в местностях, находящихся на уровне
моря. С увеличением высоты над уровнем моря (например, в горах) давление
уменьшается.
С увеличением высоты над уровнем моря (например, в горах) давление
уменьшается.
Единицы давления. В СИ – Па (паскаль): 1 Па = 1 Н/м2;
Внесистемные единицы: физическая (нормальная) атмосфера (атм) равна давлению столба ртути высотой 760 мм;миллиметр ртутного столба (мм. рт. ст.).
1мм. рт. ст. = rрт.gh = (13,6×103 кг/м3)×(9,81 м/с2)×(10-3м) = 133 Па.
1 атм = 760 мм. рт. ст. = 1,01×105 Па.
Сообщающиеся сосуды — сосуды, которые имеют соединяющую их часть и заполненные покоящейся жидкостью. В открытых сообщающихся сосудах уровень поверхностей однородной жидкости устанавливается на одинаковом уровне (при условии, что давление воздуха над поверхностью жидкости одинаково) и не зависит от формы сосудов.
Слово «гидравлический» происходит от греческого «гидравликос» — водяной.
Таким образом, гидравлические
машины — это машины, работа которых основана на законе Паскаля.
Давайте рассмотрим схему простейшей гидравлической машины.
Как видно из рисунка, она состоит из двух сообщающихся сосудов с разными площадями поперечного сечения, заполненных практически несжимаемой жидкостью, обычно маслом, и закрытых подвижными поршнями. Как работает гидравлическая машина? Для этого подействуем на малый поршень небольшой силой. Эта сила будет создавать давление на жидкость, которое по закону Паскаля передается во все точки жидкости. Значит и на большой поршень подействует такое же давление. Тогда сила давления, действующая на большой поршень, будет направлена вверх и равна произведению давления и площади большого поршня. Сравним силы, действующие на малый и большой поршни.
p1 = p2
F1 = p1S1
F2 = p2S2 = p1S2
Таким
образом, можно сделать вывод о том, что гидравлическая машина дает
выигрыш в силе во столько раз, во сколько раз площадь поперечного сечения
большого поршня больше площади поперечного сечения малого поршня. Это
означает, что с помощью небольшой силы, приложенной к малому поршню
гидравлической машины, можно уравновесить существенно большую силу, приложенную
к большому поршню.
Это
означает, что с помощью небольшой силы, приложенной к малому поршню
гидравлической машины, можно уравновесить существенно большую силу, приложенную
к большому поршню.
Гидравлическую машину,
служащую для прессования, называют гидравлическим прессом. Он
широко применяется в технике для обработки металлов, прессования фанеры,
картона, древесностружечных плит. А в сельском хозяйстве гидравлический пресс
используется для прессования сена, для выжимки масла из семян подсолнуха,
кукурузы и т.д. Современные гидравлические прессы способны развивать силу
в десятки и сотни миллионов Ньютонов. Прессуемое тело кладут на платформу,
которая соединена с большим поршнем. С помощью малого поршня создается большое
давление, которое, согласно закону Паскаля, передается в каждую точку жидкости,
заполняющей цилиндры. Тогда и на большой поршень будет действовать такое же
давление. Но так как площади поршней отличаются, то сила, действующая на
большой поршень, будет больше силы, действующей на малый поршень. Под действием
этой силы большой поршень будет подниматься. При его подъеме прессуемое тело
упирается в неподвижную платформу и сжимается.
Под действием
этой силы большой поршень будет подниматься. При его подъеме прессуемое тело
упирается в неподвижную платформу и сжимается.
Из малого цилиндра в большой жидкость перекачивается с помощью поршневого жидкостного насоса.
Рассмотрим схему и принцип действия такого насоса на примере колонки.
Поршневой жидкостный насос
состоит из цилиндра, внутри которого находится плотно прилегающий к стенкам
поршень. И в поршне, и в нижней части цилиндра располагаются клапаны, которые
открываются только вверх. При движении поршня вверх жидкость под
действием атмосферного давления поднимает нижний клапан и, двигаясь вслед за
поршнем, входит в трубу. Когда поршень движется вниз, жидкость, находящаяся под
поршнем, давит на нижний клапан, и он закрывается. В это же время, под
давлением воды, открывается клапан в самом поршне, и жидкость переходит в
пространство над поршнем. При следующем движении поршня вверх вместе с ним
поднимается и находящаяся над ним жидкость, которая выливается в отводящую
трубу. При этом за поршнем поднимается новая порция жидкости, которая при
последующем опускании поршня, вновь окажется над ним.
При следующем движении поршня вверх вместе с ним
поднимается и находящаяся над ним жидкость, которая выливается в отводящую
трубу. При этом за поршнем поднимается новая порция жидкости, которая при
последующем опускании поршня, вновь окажется над ним.
Водопровод — сложная
установка. С его помощью из одного общего центра снабжаются водой город, село,
промышленные и сельскохозяйственные предприятия. Бытовой водопровод снабжает
питьевой водой население, удовлетворяет бытовые нужды людей, работающих на заводах
и фабриках. Промышленный водопровод удовлетворяет только промышленные и
технологические нужды. Принцип работы водопровода следующий: на вершине
высокой башни устанавливается большой сосуд для накопления воды. От него
протягивают трубы к домам, к потребителям. Концы труб в домах и квартирах
закрываются кранами. давление в кране равно давлению столба воды высотой,
равной разности высот крана и свободной поверхности воды в баке. Это давление
бывает значительным, поскольку водонапорная башня устанавливается на самом
высоком месте города, села и т. д. Принцип работы водонапорной башни основан на
свойствах сообщающихся сосудов.Водопровод не может подать воду на высоту,
превышающую высоту свободной поверхности воды в сосуде водонапорной башни. Вода
из водоема наливается в сосуд, установленный на башне с помощью насоса. По пути
к сосуду вода проходит через водосборник, отстойник, фильтры.
д. Принцип работы водонапорной башни основан на
свойствах сообщающихся сосудов.Водопровод не может подать воду на высоту,
превышающую высоту свободной поверхности воды в сосуде водонапорной башни. Вода
из водоема наливается в сосуд, установленный на башне с помощью насоса. По пути
к сосуду вода проходит через водосборник, отстойник, фильтры.
Первые водопроводы были
сооружены несколько тысяч лет тому назад. В древнем Египте подземная вода из
глубоких колодцев поднималась водоподъемниками и по керамическим и деревянным
трубам подавалась потребителям. В древнем Риме использовалась более сложная
система водоснабжения. Там трубы проходили через реку, дороги и т.д. В Западной
Европе (Париж) водопровод с деревянными трубами был сооружен в конце ХУII века.
В ХУIII веке начали сооружение водопровода в Англии. В Москве централизованный
коммунальный водопровод построили в 1804 году. В Алматы первый деревянный
водопровод появился в 1933 году, а с 1935 года началось плановое строительство
водопроводов, в которых использовались железобетонные и керамические трубы. Археологические раскопки свидетельствуют о том, что в Казахстане водопровод из
жженой керамики был построен в Х—ХII веках в городах Отраре и Таразе.
Археологические раскопки свидетельствуют о том, что в Казахстане водопровод из
жженой керамики был построен в Х—ХII веках в городах Отраре и Таразе.
Это интересно!
1.Магдебургские полушария имеются у каждого человека: головки бедренных костей удерживаются в таком суставе атмосферным давлением.
2. Как мы дышим? Механизм дыхания заключается в следующем: мышечным усилием мы увеличиваем объем грудной клетки, при этом давление воздуха внутри легких уменьшается, и атмосферное давление вталкивает туда порцию воздуха. При выдыхании происходит обратное явление.
3.Как мы пьем? Приставив стакан к губам, начинаем тянуть жидкость в себя. Втягивание жидкости вызывает расширение грудной клетки, воздух в легких и полости рта разрежается, и атмосферное давление «загоняет» туда очередную порцию жидкости. Так организм человека приспосабливается к атмосферному давлению и использует его.
4. Атмосферное
давление сказывается на передвижении по болотистой местности.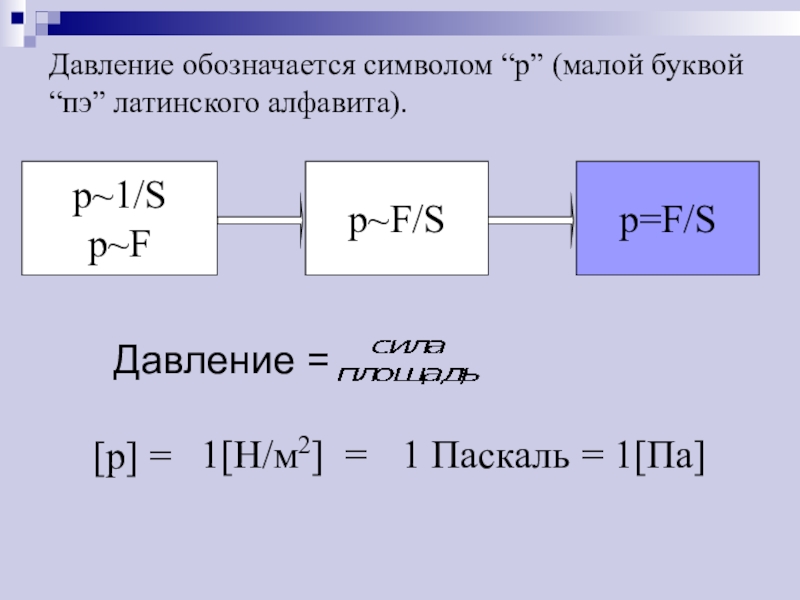 Под ногой, когда
мы ее поднимаем, образуется разреженное пространство и атмосферное давление
препятствует вытаскиванию ноги (но это только одна из причин). Если по трясине
передвигается лошадь, то твердые копыта ее действуют как поршни. Сложные же
копыта свиней и жвачных животных, состоящие из нескольких частей, при
вытаскивании ноги сжимаются (вследствие неравенства давлений снизу и сверху) и
пропускают воздух в образовавшееся углубление. В этом случае ноги животных
свободно вытягиваются из почвы.
Под ногой, когда
мы ее поднимаем, образуется разреженное пространство и атмосферное давление
препятствует вытаскиванию ноги (но это только одна из причин). Если по трясине
передвигается лошадь, то твердые копыта ее действуют как поршни. Сложные же
копыта свиней и жвачных животных, состоящие из нескольких частей, при
вытаскивании ноги сжимаются (вследствие неравенства давлений снизу и сверху) и
пропускают воздух в образовавшееся углубление. В этом случае ноги животных
свободно вытягиваются из почвы.
5. Многие живые организмы, например, глисты, спруты, черви-сосальщики, пиявки и т.д. имеют присоски, при помощи которых они могут прилипнуть к любому предмету. Пиявки пользуются присосками для передвижения по дну водоема, осьминоги для схватывания добычи
Применение полученных знаний, решение качественных и экспериментальных задач.
1) Погрузите стакан в воду, переверните его под водой вверх дном и затем медленно вытаскивайте из воды. Почему, пока края стакана находятся под водой, вода остается в стакане (не выливается)?
2) Наполните стакан водой, закройте листом бумаги и, поддерживая
лист рукой, быстро переверните стакан вверх дном. Если теперь отнять руку от
бумаги, то вода из стакана не выльется. Бумага останется как бы приклеенной к
краям стакана. Почему?
Если теперь отнять руку от
бумаги, то вода из стакана не выльется. Бумага останется как бы приклеенной к
краям стакана. Почему?
3) Почему давление атмосферы нельзя рассчитать так же, как рассчитывают давление жидкости на дно сосуда?
4) В 1648 г. Блез Паскаль продемонстраривал следующий опыт. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула. Объясните, почему?
5) В 1654 г. Герике, произвел
знаменитый опыт с «магдебургскими полушариями». На демонстрации опыта
присутствовали император Фердинанд III и члены Регенсбургского рейхстага. В их
присутствии, когда из полости между двумя сложенными вместе металлическими
полушариями выкачали воздух, их не смогли разъединить несколько пар лошадей. Объясните, почему?
Объясните, почему?
Скачано с www.znanio.ru
1.2: Закон Бойля и закон атмосфер
Мы обсуждали понятие давления в предыдущей лекции, ввели единицы измерения давления (ньютоны на квадратный метр или паскали и более знакомые фунты на квадратный дюйм) и отметили, что жидкость в сосуде оказывает давление на все стенки, как вертикальные, так и горизонтальные — если убрать часть стенки, жидкость выльется наружу.
Всем известно, что хотя вода (как и другие жидкости) в значительной степени несжимаема, воздух сжимаем — небольшой шарик можно сжать руками до заметно меньшего объема, а велосипедный насос можно до некоторой степени протолкнуть, даже если вы блокируете конец, чтобы воздух не выходил.. Бойль был первым, кто произвел количественных измерений того, как объем фиксированного количества воздуха уменьшался по мере увеличения давления.
Можно представить себе проведение эксперимента с газом в цилиндре, как показано на этой диаграмме, с использованием различных грузов и измерением объема газа. Когда поршень находится в состоянии покоя, давление газа, умноженное на площадь поршня, просто уравновешивает вес поршня плюс добавленный вес, поэтому давление легко найти.
Когда поршень находится в состоянии покоя, давление газа, умноженное на площадь поршня, просто уравновешивает вес поршня плюс добавленный вес, поэтому давление легко найти.
Но здесь есть одна хитрость: если газ сжимается довольно быстро, например, путем добавления значительного веса, так что поршень внезапно опускается, газ нагревается. Затем, по мере того как тепло постепенно уходит через стенки цилиндра, газ постепенно оседает в еще меньший объем.
Идея Бойля состояла в том, чтобы выяснить, как изменяется объем газа в зависимости от внешнего давления , если температура газа остается неизменной . Итак, если бы он провел свой эксперимент с цилиндром, изображенным выше, ему пришлось бы выждать некоторое время между измерениями объема, чтобы убедиться, что температура газа вернулась к комнатной.
Но Бойль не использовал поршень и цилиндр. Он провел эксперимент в 1662 году. Возможно, стволы, изготовленные в то время, сработали бы с замасленным поршнем (я не уверен), но он нашел очень элегантную альтернативу: он уловил воздух с помощью ртути в закрытую стеклянную трубку, и варьировал давление, как объяснено ниже (по его собственным словам).
Он нашел простой результат : если давление увеличить вдвое при постоянной температуре, газ уменьшится до половины своего прежнего объема.Если давление увеличилось втрое, оно уменьшилось до одной трети исходного объема и так далее. То есть для давления P и объема V , при постоянной температуре T , PV = константа. Это Закон Бойля .
Изучив гениальный эксперимент Бойля, мы увидим, что закон Бойля является ключом к пониманию центральной особенности земной атмосферы: как плотность и давление воздуха уменьшаются с высотой. Конечно, температура атмосферы тоже меняется в зависимости от высоты и погоды, что усложняет картину, но закон Бойля дает нам очень хороший старт для анализа ситуации.
Эксперимент Бойля
Роберт Бойль родился в 1627 году и был четырнадцатым ребенком графа Корка, ирландского землевладельца. Он написал отчет ниже в 1662 году. (Это из его книги Защита доктрины о весне и весе воздуха . Я добавил несколько примечаний в квадратных скобках, которые, я надеюсь, прояснят, что происходит. Обычные скобки , ( ), принадлежат Бойлю.)
Я добавил несколько примечаний в квадратных скобках, которые, я надеюсь, прояснят, что происходит. Обычные скобки , ( ), принадлежат Бойлю.)
«Тогда мы взяли длинную стеклянную трубку, которая ловкой рукой и с помощью лампы [ нагревая ее до размягчения ] была так искривлена внизу, что вывернутая часть была почти параллельно остальной части трубки [ они согнули ее в форму на схеме ], и отверстие этой более короткой ножки сифона (если я могу так назвать весь инструмент) было герметично закрыто, длина его была разделена на дюймы (каждый из которых был разделен на восемь частей) прямым листом бумаги, который с этими делениями был тщательно наклеен вдоль всего листа.Затем всыпать столько ртути, сколько нужно для заполнения свода или изогнутой части сифона, чтобы ртуть, стоящая на уровне, могла доходить в одной ножке до дна разделенной бумаги и точно на ту же высоту горизонтальной линии в другой; мы позаботились, часто наклоняя трубку, чтобы воздух мог свободно проходить из одной ножки в другую по краям ртути (мы позаботились, я говорю, позаботились), чтобы воздух, наконец, вошедший в более короткий цилиндр, той же расхлябанности с остальным воздухом вокруг него. [ Он означает при том же давлении, то есть при нормальном атмосферном давлении .]
[ Он означает при том же давлении, то есть при нормальном атмосферном давлении .]
Сделав это, мы начали вливать ртуть в более длинное колено сифона, которое своим весом давило на более короткое колено, постепенно выпрямляя [сжимая] находящийся внутри воздух: и продолжая это вливание ртути до тех пор, пока воздух не более короткая нога была уменьшена за счет конденсации и заняла вдвое меньше места, чем раньше; мы бросили взгляд на более длинную ножку стакана, на которую также был наклеен лист бумаги, тщательно разделенный на дюймы и части, и не без удовольствия и удовлетворения заметили, что ртути в этой более длинной части трубки было двадцать -девять дюймов выше, чем другой.
«Восторг и удовлетворение» Бойля в этом последнем предложении возникли потому, что он знал, что дополнительное давление, создаваемое добавленными двадцатью девятью дюймами ртути, равно дополнительной атмосфере, поэтому воздух, заключенный в более короткой трубке, имел вдвое меньше объема. когда давление было , удвоилось . Он повторял эксперимент много раз, с разной высотой столбика ртути в более длинной трубке и каждый день проверяя фактическое атмосферное давление во время эксперимента.
когда давление было , удвоилось . Он повторял эксперимент много раз, с разной высотой столбика ртути в более длинной трубке и каждый день проверяя фактическое атмосферное давление во время эксперимента.
Он установил закон Бойля,
\[PV = константа\]
для диапазона давлений, которые он использовал. Важно отметить, что в своих экспериментах он допускал достаточное время между измерениями объема, чтобы захваченный воздух вернулся к комнатной температуре.
Закон атмосфер: океан воды
Во-первых, краткое напоминание о том, как мы нашли изменение давления с глубиной в океане покоящейся воды. Представим изолированный цилиндр воды с вертикальной осью и построим диаграмму свободного тела:
Силы давления окружающей воды, действующие на искривленных сторон, очевидно, компенсируют друг друга.Таким образом, учитываются только силы цилиндра с водой и силы давления сверху и снизу, причем сила давления снизу больше, так как она должна уравновешивать давление сверху плюс вес, поскольку цилиндр в состоянии покоя.
Приняв, что цилиндр имеет площадь поперечного сечения A , высоту \( \Delta h \), а вода имеет плотность \( \rho \), цилиндр имеет объем \( A \Delta h \), массу \( \rho A \Delta h \), и, следовательно, вес \( \rho A \Delta h g.\)
Давление P является функцией высоты h над дном, \( P = P(h). \)
Мы измерили ч здесь на дне океана, потому что в следующем разделе мы применим тот же анализ к атмосфере, где мы делаем живем на дне «моря».
Давление на верхнюю часть цилиндра оказывает направленное вниз усилие, равное \[ давление \, \times \, площадь = P(h+ \Delta h) A \] нижняя часть ощущает направленное вверх давление \( P(h) A \),
, так как общая сила должна быть равна нулю,
\[ P(h + \Delta h) A – P(h)A + \rho \, A \Delta H g = 0 \].
Это уравнение можно преобразовать в:
\[ \dfrac { P(h + \Delta h) – P(h)}{ \Delta h} = – \rho g. \].
Напоминая, что дифференциал определяется
\[ \dfrac {df(x)}{dx} = lim \dfrac {f(x + \Delta x) – f(x)}{ \Delta x} \],
мы видим, что это уравнение давления в пределе \( \Delta h \rightarrow 0 \) принимает вид: \[ \dfrac {dP(h)}{dh} = – \rho g \].
Так как \( \rho g \) является константой, решение простое:
\[ P(h) = – \rho g(h – h_0) \]
где мы записали постоянную интегрирования в виде \( \rho gh \).
Обратите внимание, что давление в этом океане падает до нуля на высоте ч = ч 0 — очевидно, поверхность! Это означает, что наша формула описывает давление воды в океане глубиной ч 0 , и это просто другой способ записать, что давление равно \(\rhog\), умноженному на глубину под поверхностью. (Мы вычитаем атмосферное давление, действующее на поверхность океана, из воздуха над ним — мы просто учитываем дополнительное давление от веса самой воды, когда мы опускаемся.Помните, что давление воздуха такое же, как примерно тридцать футов воды, так что это небольшая поправка в реальном океане)
Океан Воздуха – Закон Атмосфер
Теперь мы проведем точно такое же рассуждение для «океана воздуха», рисуя ту же диаграмму свободного тела для маленького вертикального цилиндра и придя к тому же дифференциальному уравнению,
\[ \dfrac {dP(h)}{dh} = – \rho g \] .
Но у него нет такого же решения! Причина в том, что \(\rho\), которое мы приняли за константу для воды (отличное приближение), очевидно, является константой , а не для воздуха.Известно, что с увеличением высоты воздух разрежается.
Ключом к решению этого уравнения является закон Бойля: для данного количества газа оно имеет вид \( PV = const. \), но обратите внимание, что это означает, что если давление газа удваивается, газ сжимается в половина пространства, поэтому его плотность также удвоена .
Таким образом, альтернативным способом формулировки закона Бойля является
.\[ \ро (h) = CP(h) \]
, где C — константа (при постоянной температуре).{-C_gh} \].
Плотность воздуха уменьшается экспоненциально с высотой: это уравнение является Законом Атмосфер.
С водой такого уменьшения плотности не происходит, потому что вода практически несжимаема. Одна аналогия состоит в том, чтобы представить воду как башню из кирпичей, расположенных один поверх другого, а воздух — как башню из губок в форме кирпичей, так что губки на дне сплющены до гораздо большей плотности, но это не так. Это довольно точно, потому что в верхней части атмосферы воздух становится все тоньше и тоньше без ограничений, в отличие от губок.в\).
Это довольно точно, потому что в верхней части атмосферы воздух становится все тоньше и тоньше без ограничений, в отличие от губок.в\).
Упражнения
1. Атмосферное давление меняется изо дня в день, но 1 атм определяется как 1,01 x 10 5 Па. Подсчитайте, насколько высоко такое давление заставит столб воды подняться в «водяном барометре».
2. Плотность воздуха при комнатной температуре составляет около 1,29 кг/м 3 . Используйте это вместе с определением 1 атм выше, чтобы найти константу C в Законе Атмосфер, написанном выше. Используйте свой результат, чтобы оценить атмосферное давление на вершине Голубого хребта (скажем, 4000 футов), Снежной массы (11 000 футов) и горы Эверест (29 000 футов).
3. С практической точки зрения, как бы вы измерили плотность воздуха в помещении? На самом деле Галилей сделал это в начале 1600-х годов. Вы можете понять, как ему это удалось? (Его результат был в два раза хуже, но все равно неплохо!)
Авторы и авторство
14.
 2 Измерение давления — Университетская физика, том 1
2 Измерение давления — Университетская физика, том 1Цели обучения
К концу этого раздела вы сможете:
- Давать определение манометрическому и абсолютному давлению
- Объяснить различные методы измерения давления
- Понимание работы барометров с открытой трубкой
- Подробно опишите, как работают манометры и барометры
В предыдущем разделе мы вывели формулу для расчета изменения давления жидкости, находящейся в гидростатическом равновесии.Как оказалось, это очень полезный расчет. Измерения давления важны как в повседневной жизни, так и в науке и технике. В этом разделе мы обсудим различные способы регистрации и измерения давления.
Манометрическое давление в сравнении с абсолютным давлением
Предположим, манометр на полном баллоне с аквалангом показывает 3000 фунтов на квадратный дюйм, что составляет примерно 207 атмосфер. Когда клапан открывается, воздух начинает выходить, потому что давление внутри бака больше, чем атмосферное давление снаружи бака.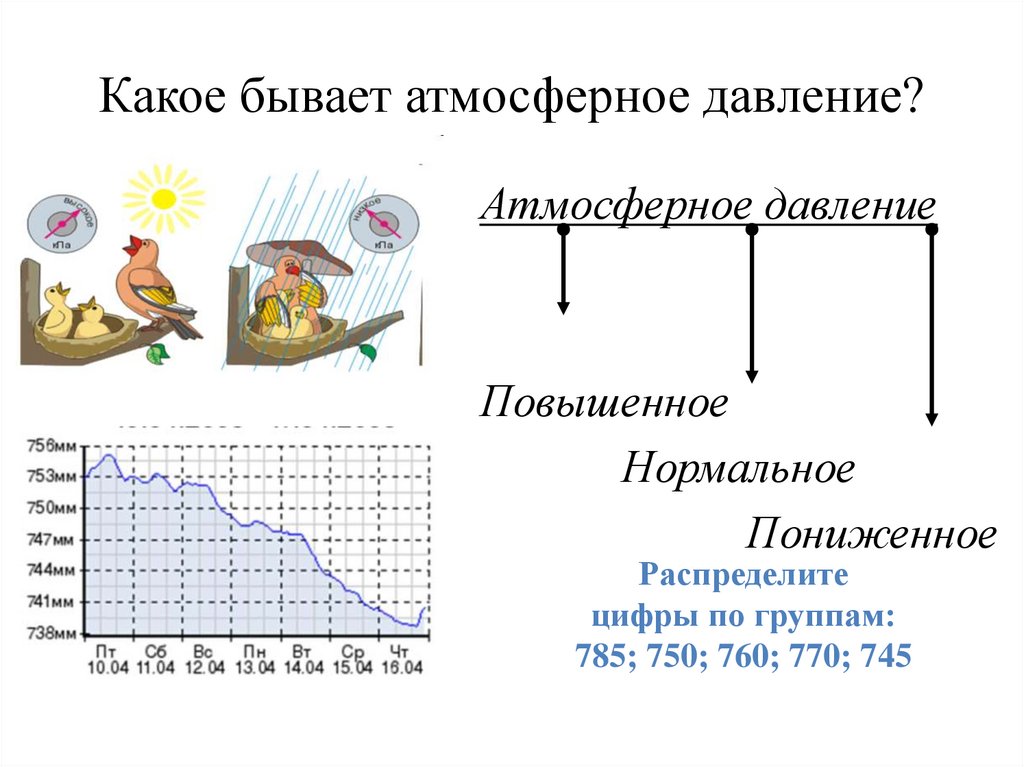 Воздух продолжает выходить из бака до тех пор, пока давление внутри бака не сравняется с давлением атмосферы снаружи бака. В этот момент манометр на баке показывает ноль, хотя давление внутри бака на самом деле составляет 1 атмосферу — такое же, как давление воздуха снаружи бака.
Воздух продолжает выходить из бака до тех пор, пока давление внутри бака не сравняется с давлением атмосферы снаружи бака. В этот момент манометр на баке показывает ноль, хотя давление внутри бака на самом деле составляет 1 атмосферу — такое же, как давление воздуха снаружи бака.
Большинство манометров, например, на акваланге, откалиброваны так, чтобы показывать ноль при атмосферном давлении. Показания таких манометров называются манометрическим давлением, то есть давлением по отношению к атмосферному давлению.Когда давление внутри резервуара превышает атмосферное давление, манометр показывает положительное значение.
Некоторые манометры предназначены для измерения отрицательного давления. Например, многие физические эксперименты должны проводиться в вакуумной камере, жесткой камере, из которой откачивается часть воздуха. Давление внутри вакуумной камеры меньше атмосферного, поэтому манометр на камере показывает отрицательное значение.
В отличие от манометрического давления, абсолютное давление учитывает атмосферное давление, которое, по сути, добавляется к давлению в любой жидкости, не заключенной в жесткий контейнер.
Абсолютное давление
Абсолютное давление или полное давление представляет собой сумму манометрического давления и атмосферного давления:
pabs=pg+patmpabs=pg+patm14.11
, где pabspabs — абсолютное давление, pgpg — манометрическое давление, а patmpatm — атмосферное давление.
Например, если шинный манометр показывает 34 фунта/кв. дюйм, то абсолютное давление равно 34 фунта/кв. дюйм плюс 14,7 фунта/кв.
В большинстве случаев абсолютное давление в жидкостях не может быть отрицательным.Жидкости толкают, а не тянут, поэтому наименьшее абсолютное давление в жидкости равно нулю (отрицательное абсолютное давление — это притяжение). Таким образом, наименьшее возможное манометрическое давление равно pg=-patmpg=-patm (что делает pabspabs равным нулю). Нет теоретического предела тому, насколько большим может быть манометрическое давление.
Измерение давления
Для измерения давления используется множество устройств, от шинных манометров до тонометров. Многие другие типы манометров обычно используются для проверки давления жидкостей, например, механические манометры.Мы рассмотрим некоторые из них в этом разделе.
Многие другие типы манометров обычно используются для проверки давления жидкостей, например, механические манометры.Мы рассмотрим некоторые из них в этом разделе.
Любое свойство, которое известным образом изменяется с давлением, может быть использовано для создания манометра. Некоторые из наиболее распространенных типов включают тензометрические датчики, в которых используется изменение формы материала под действием давления; емкостные манометры, в которых используется изменение электрической емкости из-за изменения формы под действием давления; пьезоэлектрические манометры, которые генерируют разность потенциалов на пьезоэлектрическом материале под действием разности давлений между двумя сторонами; и ионизационные датчики, которые измеряют давление путем ионизации молекул в высоковакуумных камерах.Различные манометры полезны в разных диапазонах давления и в разных физических ситуациях. Некоторые примеры показаны на рис. 14.11.
Фигура
14.11
а) Манометры используются для измерения и контроля давления в газовых баллонах. Сжатые газы используются во многих промышленных и медицинских целях. (b) Шинные манометры бывают разных моделей, но все они предназначены для одной и той же цели: измерения внутреннего давления в шине. Это позволяет водителю поддерживать давление в шинах, оптимальное для веса груза и условий движения.(c) Ионизационный датчик представляет собой высокочувствительное устройство, используемое для контроля давления газов в замкнутой системе. Молекулы нейтрального газа ионизируются за счет высвобождения электронов, и ток преобразуется в показания давления. Ионизационные датчики обычно используются в промышленных приложениях, которые полагаются на вакуумные системы.
Сжатые газы используются во многих промышленных и медицинских целях. (b) Шинные манометры бывают разных моделей, но все они предназначены для одной и той же цели: измерения внутреннего давления в шине. Это позволяет водителю поддерживать давление в шинах, оптимальное для веса груза и условий движения.(c) Ионизационный датчик представляет собой высокочувствительное устройство, используемое для контроля давления газов в замкнутой системе. Молекулы нейтрального газа ионизируются за счет высвобождения электронов, и ток преобразуется в показания давления. Ионизационные датчики обычно используются в промышленных приложениях, которые полагаются на вакуумные системы.
Манометры
Один из наиболее важных классов манометров использует то свойство, что давление, обусловленное весом жидкости постоянной плотности, определяется выражением p=hρgp=hρg.U-образная трубка, показанная на рис. 14.12, является примером манометра ; в части (а) обе стороны трубы открыты для атмосферы, что позволяет атмосферному давлению одинаково падать с каждой стороны, так что его эффекты нейтрализуются.
Манометр, только одна сторона которого открыта для атмосферы, является идеальным устройством для измерения манометрического давления. Манометрическое давление равно pg=hρgpg=hρg и определяется путем измерения ч . Например, предположим, что одна сторона U-образной трубки соединена с каким-либо источником давления pabs, pabs, таким как воздушный шар в части (b) рисунка или упакованная под вакуумом банка из-под арахиса, показанная в части (c).Давление передается на манометр в неизменном виде, и уровни жидкости уже не равны. В части (b) pabspabs больше атмосферного давления, тогда как в части (c) pabspabs меньше атмосферного давления. В обоих случаях pabspabs отличается от атмосферного давления на величину hρg,hρg, где ρρ — плотность жидкости в манометре. В части (b) pabspabs может поддерживать столб жидкости высотой h , поэтому он должен оказывать давление hρghρg больше атмосферного давления (манометрическое давление pgpg положительно). В части (c) атмосферное давление может поддерживать столб жидкости высотой h , поэтому pabspabs меньше атмосферного давления на величину hρghρg (манометрическое давление pgpg отрицательно).
В части (c) атмосферное давление может поддерживать столб жидкости высотой h , поэтому pabspabs меньше атмосферного давления на величину hρghρg (манометрическое давление pgpg отрицательно).
Барометры
Манометры обычно используют U-образную трубку жидкости (часто ртути) для измерения давления. Барометр (см. рис. 14.13) — это устройство, которое обычно использует один столбик ртути для измерения атмосферного давления. Барометр, изобретенный итальянским математиком и физиком Эванджелистой Торричелли (1608–1647) в 1643 г., представляет собой стеклянную трубку, закрытую с одного конца и наполненную ртутью.Затем трубку переворачивают и помещают в бассейн с ртутью. Это устройство измеряет атмосферное давление, а не манометрическое давление, потому что над ртутью в трубке почти чистый вакуум. Высота ртути такова, что hρg=patmhρg=patm. При изменении атмосферного давления ртутный столбик поднимается или опускается.
Барометр (см. рис. 14.13) — это устройство, которое обычно использует один столбик ртути для измерения атмосферного давления. Барометр, изобретенный итальянским математиком и физиком Эванджелистой Торричелли (1608–1647) в 1643 г., представляет собой стеклянную трубку, закрытую с одного конца и наполненную ртутью.Затем трубку переворачивают и помещают в бассейн с ртутью. Это устройство измеряет атмосферное давление, а не манометрическое давление, потому что над ртутью в трубке почти чистый вакуум. Высота ртути такова, что hρg=patmhρg=patm. При изменении атмосферного давления ртутный столбик поднимается или опускается.
Синоптики внимательно следят за изменениями атмосферного давления (часто сообщаемого как атмосферное давление), поскольку повышение ртути обычно сигнализирует об улучшении погоды, а понижение ртути указывает на ухудшение погоды.Барометр также можно использовать как высотомер, поскольку среднее атмосферное давление меняется с высотой. Ртутные барометры и манометры настолько распространены, что для измерения атмосферного давления и кровяного давления часто используются единицы мм рт.
Ртутные барометры и манометры настолько распространены, что для измерения атмосферного давления и кровяного давления часто используются единицы мм рт.
Пример 14,2
Высота жидкости в открытой U-образной трубке
U-образная трубка с открытыми обоими концами заполнена жидкостью с плотностью ρ1ρ1 до высоты h с обеих сторон (рис. 14.14). В одну сторону наливается жидкость плотностью ρ2<ρ1ρ2<ρ1, и жидкость 2 оседает поверх жидкости 1. Высота обеих сторон различна. Высота до вершины Liquid 2 от интерфейса равна h3h3, а высота до вершины Liquid 1 от уровня интерфейса равна h2h2. Вывести формулу разницы высот. Фигура
14.14
Две жидкости разной плотности показаны в U-образной трубке.
Стратегия
Давление в точках на одной высоте по обеим сторонам U-образной трубки должно быть одинаковым, пока эти две точки находятся в одной и той же жидкости. Поэтому мы рассматриваем две точки на одном уровне в двух рукавах трубки: одна точка — это граница раздела со стороны жидкости 2, а другая — точка в рукаве с жидкостью 1, которая находится на том же уровне, что и интерфейс в другой руке.Давление в каждой точке обусловлено атмосферным давлением плюс вес жидкости над ним. Давление со стороны Жидкости 1=p0+ρ1gh2Давление со стороны Жидкости 2=p0+ρ2gh3Давление со стороны Жидкости 1=p0+ρ1gh2Давление со стороны Жидкости 2=p0+ρ2gh3Решение
Поскольку две точки находятся в жидкости 1 и находятся на одной высоте, давление в этих двух точках должно быть одинаковым. Таким образом, у нас есть p0+ρ1gh2=p0+ρ2gh3.p0+ρ1gh2=p0+ρ2gh3.Следовательно,
Это означает, что разница высот с двух сторон U-образной трубы составляет
h3−h2=(1−ρ2ρ1)h3. h3−h2=(1−ρ2ρ1)h3.
h3−h2=(1−ρ2ρ1)h3.Результат имеет смысл, если мы установим ρ2=ρ1,ρ2=ρ1, что дает h3=h2.h3=h2. Если две стороны имеют одинаковую плотность, они имеют одинаковую высоту.
Проверьте свое понимание 14,2
Ртуть является опасным веществом. Как вы думаете, почему в барометрах обычно используется ртуть, а не более безопасная жидкость, такая как вода?
Единицы давления
Как указывалось ранее, единицей измерения давления в системе СИ является паскаль (Па), где
Помимо паскаля широко используются многие другие единицы измерения давления (таблица 14.3). В метеорологии атмосферное давление часто описывается в миллибарах (мбар), где
1000 мбар=1×105 Па. 1000 мбар=1×105 Па. Миллибар — удобная единица измерения для метеорологов, поскольку среднее атмосферное давление на уровне моря на Земле составляет 1,013×105 Па=1013 мбар=1 атм1,013×105Па=1013 мбар=1 атм. Используя уравнения, полученные при рассмотрении давления на глубине в жидкости, давление также можно измерить в миллиметрах или дюймах ртутного столба. Давление на дне 760-мм столбика ртути при 0°С0°С в сосуде, верхняя часть которого откачана, равно атмосферному давлению.Таким образом, вместо давления в 1 атмосферу также используется 760 мм ртутного столба. В лабораториях физики вакуума ученые часто используют другую единицу измерения, называемую торр, названную в честь Торричелли, который, как мы только что видели, изобрел ртутный манометр для измерения давления. Один торр равен давлению в 1 мм рт.
Давление на дне 760-мм столбика ртути при 0°С0°С в сосуде, верхняя часть которого откачана, равно атмосферному давлению.Таким образом, вместо давления в 1 атмосферу также используется 760 мм ртутного столба. В лабораториях физики вакуума ученые часто используют другую единицу измерения, называемую торр, названную в честь Торричелли, который, как мы только что видели, изобрел ртутный манометр для измерения давления. Один торр равен давлению в 1 мм рт.
| Блок | Определение |
|---|---|
| Единица СИ: Паскаль | 1Па=1Н/м21Па=1Н/м2 |
| Английская единица измерения: фунты на квадратный дюйм (lb/in.2 фунта/дюйм2 или фунт/кв. дюйм) | 1psi=6,895×103 Па1psi=6,895×103 Па |
| Прочие единицы измерения давления | 1 атм = 760 мм рт.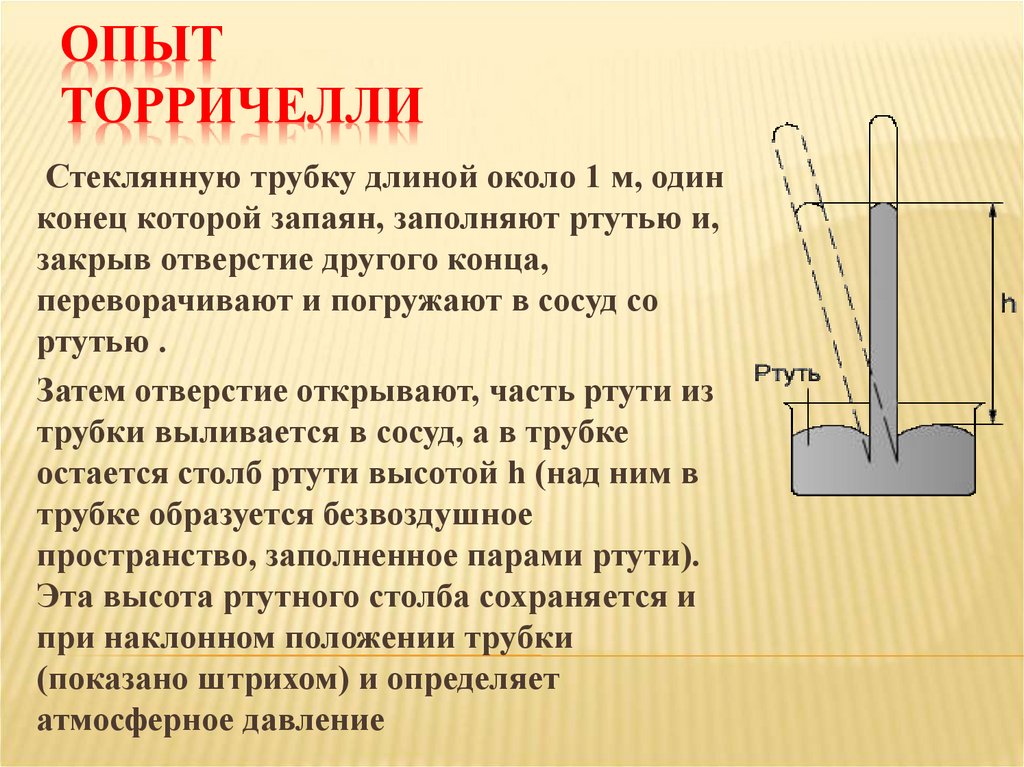 ст. = 1,013 × 105 Па = 14,7 фунта на кв. дюйм = 29,9 дюйма ртутного столба = 1013 мбар1 атм = 760 мм ртутного столба = 1,013 × 105 Па = 14,7 фунта на кв. дюйм = 29,9 дюйма ртутного столба = 1013 мбар ст. = 1,013 × 105 Па = 14,7 фунта на кв. дюйм = 29,9 дюйма ртутного столба = 1013 мбар1 атм = 760 мм ртутного столба = 1,013 × 105 Па = 14,7 фунта на кв. дюйм = 29,9 дюйма ртутного столба = 1013 мбар |
| 1бар=105Па1бар=105Па | |
| 1торр=1мм рт.ст.=133,3Па1торр=1мм рт.ст.=133,3Па |
Таблица 14.3 Краткое изложение единиц давления
Физика отрицательного давления
Поэт-романтик Джон Китс однажды определил состояние ума, при котором человек «способен пребывать в неуверенности, тайнах, сомнениях, без какого-либо раздражительного стремления к фактам и разуму.Он назвал это отрицательной способностью. Это прямо противоположно качеству, известному как отрицательное давление, научной головоломке, которая в последнее время вызывала раздражение у читателей Discover.
Проблемы начались в сентябре прошлого года, когда Discover опубликовал мои работы. в колонке «Прогресс» о том, как вода попадает на верхушки деревьев.Когда вода испаряется с листьев дерева, как я сообщал, она тянет за собой воду, оставшуюся в ксилеме, сети инертных труб, которые тянутся от корней к побегам.Молекулы воды в ксилеме, как невинно объяснил я, связаны связями, образующимися между их положительно и отрицательно заряженными полюсами. Когда вода испаряется наверху, она растягивает связи между взаимосвязанными молекулами в нижней колонне, создавая значительное напряжение. «Давление внутри ксилемных трубок самых высоких деревьев может достигать -20 атмосфер», — написал я.
в колонке «Прогресс» о том, как вода попадает на верхушки деревьев.Когда вода испаряется с листьев дерева, как я сообщал, она тянет за собой воду, оставшуюся в ксилеме, сети инертных труб, которые тянутся от корней к побегам.Молекулы воды в ксилеме, как невинно объяснил я, связаны связями, образующимися между их положительно и отрицательно заряженными полюсами. Когда вода испаряется наверху, она растягивает связи между взаимосвязанными молекулами в нижней колонне, создавая значительное напряжение. «Давление внутри ксилемных трубок самых высоких деревьев может достигать -20 атмосфер», — написал я.
И началась раздражительная хватка. «Отрицательное давление в 20 атмосфер? Это невозможно», — написал один читатель. «Вы не можете сделать пустое пространство еще более пустым!» другой протестовал.«Пожалуйста, скажите мне, что Work in Progress — это неуместная первоапрельская статья», — взмолился еще один.
Что бы это ни стоило, теория переноса воды при отрицательном давлении закреплена в учебниках по физиологии растений. Но последнее слово в физике не за физиологами растений. Поэтому я позвонил физику из Принстонского университета Полу Стейнхардту, у которого за год до этого брал интервью для статьи об ускоряющейся Вселенной. Стейнхардт приложил немало усилий, чтобы объяснить мне космологическую версию отрицательного давления.По словам Стейнхардта, уравнения Эйнштейна учитывают вездесущую внутреннюю силу притяжения во Вселенной, которая ведет себя как резиновая лента. Чем больше вы его растягиваете, тем сильнее он тянется назад. Никто точно не знает, что делает притяжение, но сжимающая сила может существовать в пустом пространстве, потому что вакуум полон энергии и других нематериальных вещей.
Но последнее слово в физике не за физиологами растений. Поэтому я позвонил физику из Принстонского университета Полу Стейнхардту, у которого за год до этого брал интервью для статьи об ускоряющейся Вселенной. Стейнхардт приложил немало усилий, чтобы объяснить мне космологическую версию отрицательного давления.По словам Стейнхардта, уравнения Эйнштейна учитывают вездесущую внутреннюю силу притяжения во Вселенной, которая ведет себя как резиновая лента. Чем больше вы его растягиваете, тем сильнее он тянется назад. Никто точно не знает, что делает притяжение, но сжимающая сила может существовать в пустом пространстве, потому что вакуум полон энергии и других нематериальных вещей.
Я спросил Стейнхардта, может ли то же отрицательное давление, которое тянет небосвод, притягивать воду к верхушкам деревьев. Ни шанса, сказал он.Жидкости не могут иметь отрицательное давление.
Я позвонил физиологу растений Мишель Холбрук из Гарвардского университета, источнику истории о деревьях, чтобы сообщить ей плохие новости. Она не покупала его. «Отрицательное давление — законный компонент гидродинамики», — сказала она мне многозначительно, если не раздраженно. Затем она дала мне список физиков, которые могли бы поручиться за это.
Она не покупала его. «Отрицательное давление — законный компонент гидродинамики», — сказала она мне многозначительно, если не раздраженно. Затем она дала мне список физиков, которые могли бы поручиться за это.
Последовала беспорядочная интерлюдия, во время которой я консультировался с несколькими знающими экспертами, включая моего брата Гарольда. Хэл, учитель физики в средней школе, часто говорит, что «вселенная не отстой, а отстой».Он имеет в виду, что жидкости текут по градиенту давления, от более высокого к более низкому давлению. Например, всасывание соломинки создает область низкого давления в верхней части соломинки, а более высокое атмосферное давление выталкивает жидкость снизу вверх.
К сожалению, закону Хэла не удается объяснить, как вода поднимается по деревьям. Эксперименты показали, что одно только атмосферное давление может поднять воду только на 33 фута вверх по вертикальной трубе, а деревья могут вырасти намного выше этой отметки. Кроме того, мне неоднократно говорили, что вода в ксилемных трубках находится под напряжением, что для меня звучало как тянущее, а не толкающее.
Наконец, благодаря контакту из списка Холбрука, я нашел Пабло Дебенедетти, эксперта по термодинамике жидкостей из Принстона, чья книга «Метастабильные жидкости» включает раздел о переносе воды в деревьях. Дебенедетти сказал мне, что на языке гидродинамики отрицательное давление — это напряжение — напряжение, возникающее в результате удлинения упругого тела. Жидкости действительно могут растягиваться. При определенных условиях, если их потянуть, они оттянутся назад. «На самом деле вы можете заставить жидкость «сосать» сосуд», — сказал Дебенедетти.«В лабораторных экспериментах можно заставить сосуды взрываться».
Все жидкости могут иметь прочность на растяжение, добавил он, порожденную мгновенным накоплением заряда от квантовых флуктуаций в атомах. Напряжение в жидкостях изучается с середины 1800-х годов. В 1950-х годах Национальный институт стандартов и технологий определил прочность на разрыв различных жидкостей, взвесив их в Z-образных стеклянных трубках с открытыми концами. Каждую пробирку помещали в центрифугу и вращали до тех пор, пока в жидкости не образовывался пузырь; прочность жидкости на растяжение рассчитывалась по центробежной силе, необходимой для образования пузыря.
Каждую пробирку помещали в центрифугу и вращали до тех пор, пока в жидкости не образовывался пузырь; прочность жидкости на растяжение рассчитывалась по центробежной силе, необходимой для образования пузыря.
Дебенедетти подтвердил, что прочность воды на растяжение частично является результатом притяжения между противоположными зарядами на полюсах молекул воды. Тем не менее, по его словам, концепция отрицательного давления в жидкостях не очевидна. В равновесии вода и другие жидкости не поддерживают напряжения. Это свойство характерно только для метастабильных жидкостей — жидкостей, которым препятствует переход в новую фазу энергетический барьер. Вода может оставаться жидкой, например, при температуре более чем на 300 градусов по Фаренгейту выше ее точки кипения, потому что для начала испарения ей требуется одноразовая инъекция энергии.Жидкость под напряжением хочет стать паром, но ей нужен толчок или снижение энергетического барьера, чтобы переходить из одной фазы в другую. Пока этого не произойдет, например, когда жидкость встряхивают или увеличивают ее натяжение, жидкость растягивается. Так обстоит дело в ксилемных трубках деревьев.
Так обстоит дело в ксилемных трубках деревьев.
Дебенедетти и Стейнхардт не работают в одном здании в Принстоне, но они знают друг друга, потому что у их дочерей один учитель игры на фортепиано. По моей просьбе они обменялись несколькими электронными письмами и пришли к выводу, что отрицательное давление каждого мужчины было чуждо другому.Я также обратился к космологу Майклу Тернеру из Чикагского университета, который посовещался со своим другом Хамфри Марисом, физиком и экспертом по гидродинамике из Университета Брауна. Поговорив с Марис, Тернер помог объединить два мира.
“Мы не говорим об одном и том же явлении”, сказал он. Однако эти два вида отрицательного давления связаны «в том смысле, что они являются примерами вещей, которые ведут себя эластично. И оба они немного нелогичны».
Если здесь и есть что-то объединяющее, сказала Тернер, то это направление — внутренняя, взрывающаяся или сжимающая сила, а не выталкивающая наружу сила, обычно определяемая как давление. Знак минус рядом с этими атмосферами не означает «меньше, чем ничего»; это произвольное означающее, обозначающее «в направлении, противоположном положительному». Твердые тела испытывают отрицательное давление, когда они втягиваются, подобно растянутым резиновым лентам или пружинам. Жидкости могут иметь отрицательное давление в метастабильных состояниях, когда они сопротивляются превращению в пар. А, по мнению астрофизиков, даже пустое пространство может иметь отрицательное давление.
Знак минус рядом с этими атмосферами не означает «меньше, чем ничего»; это произвольное означающее, обозначающее «в направлении, противоположном положительному». Твердые тела испытывают отрицательное давление, когда они втягиваются, подобно растянутым резиновым лентам или пружинам. Жидкости могут иметь отрицательное давление в метастабильных состояниях, когда они сопротивляются превращению в пар. А, по мнению астрофизиков, даже пустое пространство может иметь отрицательное давление.
Газы по-прежнему остаются темной лошадкой в метастабильных условиях. Стейнхардт слышал, что метастабильные газы могут иметь отрицательное давление, но не знает, как именно.Дебенедетти настроен скептически. «Вся суть газа в том, что силы между молекулами не имеют большого значения», — говорит он. Тернер уклончив.
Поскольку многие аспекты отрицательного давления достаточно туманны, чтобы ускользнуть от внимания профессиональных физиков, я полагаю, читателям можно простить их замешательство. Отрицательное давление, кажется, является идеальным средством для перенапряжения интеллекта.
Отрицательное давление, кажется, является идеальным средством для перенапряжения интеллекта.
14.1 Жидкости, плотность и давление – University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Назовите различные фазы вещества
- Описать характеристики фаз материи на молекулярном или атомарном уровне
- Различать сжимаемые и несжимаемые материалы
- Определение плотности и связанных с ней единиц СИ
- Сравните и сопоставьте плотности различных веществ
- Определение давления и связанных с ним единиц СИ
- Объясните взаимосвязь между давлением и силой
- Расчет силы по давлению и площади
Материя чаще всего существует в твердом, жидком или газообразном состоянии; эти состояния известны как три общие фазы материи.В этом разделе мы подробно рассмотрим каждый из этих этапов.
Характеристики твердых тел
Твердые тела твердые, имеют определенную форму и определенный объем. Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила.В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на (Рисунок). Структура этой трехмерной решетки представлена молекулами, соединенными жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в разделе «Статическое равновесие и упругость».)
Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила.В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на (Рисунок). Структура этой трехмерной решетки представлена молекулами, соединенными жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в разделе «Статическое равновесие и упругость».)
Характеристики жидкостей
Жидкости и газы считаются жидкостями , потому что они поддаются силам сдвига, тогда как твердые тела сопротивляются им. Подобно твердым телам, молекулы жидкости связаны с соседними молекулами, но таких связей гораздо меньше. Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости изменяется в зависимости от формы ее сосуда.Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, так как их молекулы движутся, чтобы заполнить сосуд, в котором они находятся ((рисунок)).
Подобно твердым телам, молекулы жидкости связаны с соседними молекулами, но таких связей гораздо меньше. Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости изменяется в зависимости от формы ее сосуда.Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, так как их молекулы движутся, чтобы заполнить сосуд, в котором они находятся ((рисунок)).
 Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.Жидкости легко деформируются при воздействии нагрузки и не возвращаются к своей первоначальной форме после прекращения действия силы. Это происходит потому, что атомы или молекулы в жидкости могут свободно скользить и менять соседей. То есть жидкости текут (поэтому они являются типом жидкости), а молекулы удерживаются вместе за счет взаимного притяжения. Когда жидкость помещается в контейнер без крышки, она остается в контейнере.Поскольку атомы плотно упакованы, жидкости, как и твердые тела, сопротивляются сжатию; для изменения объема жидкости необходима чрезвычайно большая сила.
Напротив, атомы в газах разделены большими расстояниями, и поэтому силы между атомами в газе очень слабы, за исключением случаев, когда атомы сталкиваются друг с другом. Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
В этой главе мы обычно называем газы и жидкости просто жидкостями, проводя различие между ними только тогда, когда они ведут себя по-разному. Существует еще одна фаза вещества — плазма, существующая при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень отличные свойства от трех других распространенных фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Плотность
Предположим, что брусок из латуни и брусок дерева имеют одинаковую массу. Если оба блока бросить в резервуар с водой, почему дерево всплывет, а латунь утонет ((Рисунок))? Это происходит потому, что латунь имеет большую плотность, чем вода, а древесина имеет меньшую плотность, чем вода.
Рисунок 14.3 (a) Блок из латуни и блок из дерева имеют одинаковый вес и массу, но блок из дерева имеет гораздо больший объем. (b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок всплывает.(Деревянный брусок на обеих картинках одинаков; он был перевернут на бок, чтобы соответствовать масштабу.)
(b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок всплывает.(Деревянный брусок на обеих картинках одинаков; он был перевернут на бок, чтобы соответствовать масштабу.)Плотность является важной характеристикой веществ. Это имеет решающее значение, например, при определении того, тонет ли объект в жидкости или плавает.
Плотность
Средняя плотность вещества или объекта определяется как его масса в единице объема,
где греческая буква
(ро) — символ плотности, m — масса, V — объем.
Единицей плотности в системе СИ является
.
. (Рисунок) перечислены некоторые репрезентативные значения. Единицей плотности сгс является грамм на кубический сантиметр,
.
, где
Изначально метрическая система была разработана таким образом, чтобы вода имела плотность
.
, эквивалентно
. Таким образом, основная единица массы, килограмм, была впервые разработана как масса 1000 мл воды, которая имеет объем
Таким образом, основная единица массы, килограмм, была впервые разработана как масса 1000 мл воды, которая имеет объем
.
(
)
(
)
(
101,3 кПа)
Как вы можете видеть, изучив (Рисунок), плотность объекта может помочь определить его состав. Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте. Плотность газов намного меньше, чем у жидкостей и твердых тел, потому что атомы в газах разделены большим количеством пустого пространства. Газы отображаются для стандартной температуры
Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте. Плотность газов намного меньше, чем у жидкостей и твердых тел, потому что атомы в газах разделены большим количеством пустого пространства. Газы отображаются для стандартной температуры
и стандартное давление 101.3 кПа, и наблюдается сильная зависимость плотностей от температуры и давления. Отображаемые плотности твердых и жидких тел даны для стандартной температуры
, а плотности твердых и жидких тел зависят от температуры. Плотность твердых и жидких тел обычно увеличивается с понижением температуры.
(рисунок) показывает плотность воды в различных фазах и температуре. Плотность воды увеличивается с понижением температуры, достигая максимума при
, а затем уменьшается, когда температура падает ниже
. Такое поведение плотности воды объясняет, почему на поверхности водоема образуется лед.
Такое поведение плотности воды объясняет, почему на поверхности водоема образуется лед.
| Вещество |
|
|---|---|
| Лед
|
|
| Вода
|
|
| Вода
|
|
| Вода
|
|
| Вода
|
|
| Пар
|
|
| Морская вода
|
|
Плотность вещества не обязательно постоянна по всему объему вещества. Если плотность вещества постоянна во всем веществе, говорят, что это вещество является однородным веществом . Твердый железный брусок является примером однородного вещества. Плотность постоянна на всем протяжении, а плотность любого образца вещества равна его средней плотности. Если плотность вещества непостоянна, говорят, что вещество является гетерогенным веществом . Кусок швейцарского сыра является примером гетерогенного материала, содержащего как твердый сыр, так и пустоты, заполненные газом.Плотность в определенном месте в гетерогенном материале называется локальной плотностью и определяется как функция местоположения
Если плотность вещества постоянна во всем веществе, говорят, что это вещество является однородным веществом . Твердый железный брусок является примером однородного вещества. Плотность постоянна на всем протяжении, а плотность любого образца вещества равна его средней плотности. Если плотность вещества непостоянна, говорят, что вещество является гетерогенным веществом . Кусок швейцарского сыра является примером гетерогенного материала, содержащего как твердый сыр, так и пустоты, заполненные газом.Плотность в определенном месте в гетерогенном материале называется локальной плотностью и определяется как функция местоположения
((Рисунок)).
Рисунок 14.4 Плотность может варьироваться в зависимости от гетерогенной смеси. Локальная плотность в точке получается делением массы на объем в малом объеме вокруг данной точки.Локальная плотность может быть получена с помощью процесса ограничения, основанного на средней плотности в небольшом объеме вокруг рассматриваемой точки, принимая предел, когда размер объема приближается к нулю,
где
— плотность, м — масса, V — объем.
Поскольку газы могут свободно расширяться и сжиматься, плотность газов значительно зависит от температуры, тогда как плотность жидкостей зависит от температуры незначительно. Поэтому плотности жидкостей часто считают постоянными, при этом плотность равна средней плотности.
Плотность — размерное свойство; поэтому при сравнении плотностей двух веществ необходимо учитывать единицы. По этой причине для сравнения плотностей часто используют более удобную безразмерную величину, называемую удельным весом. Удельный вес определяется как отношение плотности материала к плотности воды при
и одна атмосфера давления, что равно
:
В сравнении используется вода, поскольку плотность воды равна
.
, который первоначально использовался для определения килограмма. Удельный вес, будучи безразмерным, позволяет легко сравнивать материалы, не беспокоясь о единице плотности.Например, плотность алюминия составляет 2,7 на
.
(2700 в
), но его удельный вес равен 2,7 независимо от единицы плотности. Удельный вес — особенно полезная величина в отношении плавучести, которую мы обсудим позже в этой главе.
Давление
Вы, несомненно, слышали слово «давление», используемое по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления).Это только два из многих примеров давления в жидкостях. (Вспомните, что мы ввели понятие давления в книге «Статическое равновесие и упругость» в контексте объемного напряжения и деформации.)
Давление
Давление ( p ) определяется как нормальная сила F на единицу площади A к которой приложена сила, или
Чтобы определить давление в конкретной точке, давление определяется как сила dF , приложенная жидкостью к бесконечно малому элементу площадью dA , содержащему точку, что приводит к
.
Действие данной силы может существенно различаться в зависимости от площади, на которую она воздействует. Например, сила, приложенная к площади
имеет давление, которое в 100 раз больше, чем та же сила, приложенная к площади
.
Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, но приложение такого же усилия пальцем не прокалывает кожу ((Рисунок)).
Рис. 14.5 (a) Человек, которого тыкают пальцем, может вызвать раздражение, но сила не имеет длительного эффекта. (b) Напротив, той же силы, приложенной к участку размером с острый конец иглы, достаточно, чтобы сломать кожу.Обратите внимание, что хотя сила является вектором, давление является скаляром. Давление является скалярной величиной, поскольку по определению оно пропорционально величине силы, действующей перпендикулярно площади поверхности. Единицей давления в СИ является паскалей (Па), названная в честь французского математика и физика Блеза Паскаля (1623–1662), где
Для давления используются несколько других единиц измерения, которые мы обсудим позже в этой главе.
Изменение давления с глубиной в жидкости постоянной плотности
Давление определено для всех состояний вещества, но оно особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Рассмотрим жидкость постоянной плотности, как показано на (Рисунок). Давление на дне емкости обусловлено давлением атмосферы
плюс давление из-за веса жидкости. Давление жидкости равно весу жидкости, деленному на площадь. Вес жидкости равен произведению ее массы на ускорение свободного падения.
Рисунок 14. 6 Дно этого контейнера выдерживает весь вес жидкости в нем.Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.
6 Дно этого контейнера выдерживает весь вес жидкости в нем.Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
Таким образом, давление на дне сосуда равно атмосферному давлению, добавленному к весу жидкости, деленному на площадь:
Это уравнение годится только для давления на глубине для жидкости с постоянной плотностью.
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно атмосферному давлению плюс давление от веса жидкости, или
Где p давление на определенной глубине,
– атмосферное давление,
— плотность жидкости, г — ускорение свободного падения, ч — глубина.
Пример
Какую силу должна выдерживать плотина?
Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой ((Рисунок)). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
Среднее давление p из-за веса воды равно давлению на средней глубине ч 40,0 м, так как давление увеличивается линейно с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта,
.
раствор
- Среднее давление из-за веса жидкости равно
Введите плотность воды из (Рисунок) и примите ч за среднюю глубину 40.
 0 м, получаем
0 м, получаем - Мы уже нашли значение для p . Площадь плотины составляет
так что
Значение
Хотя эта сила кажется большой, она мала по сравнению с
.
вес воды в водохранилище. На самом деле это всего лишь 0,0800% веса.
Проверьте свое понимание
Если водохранилище на (рис.) покрывает вдвое большую площадь, но остается на той же глубине, нужно ли будет перепроектировать плотину?
[reveal-answer q=”fs-id1170958020276″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958020276″]
Давление, найденное в части (а) примера, совершенно не зависит от ширины и длины озера; он зависит только от его средней глубины у плотины.Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.
[/скрытый ответ]
Давление в статической жидкости в однородном гравитационном поле
Статическая жидкость — это жидкость, которая не находится в движении. В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.
Давление в любой точке статической жидкости зависит только от глубины в этой точке. Как обсуждалось, давление в жидкости вблизи Земли меняется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для таких жидкостей, как вода, где требуются большие силы для сжатия жидкости или изменения объема. В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху.Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью ρ на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней.Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Представьте себе тонкий элемент жидкости на глубине ч , как показано на (Рисунок). Пусть элемент имеет площадь поперечного сечения А и высоту
. Силы, действующие на элемент, обусловлены давлением p ( y ) выше и
под ним. Вес самого элемента также показан на диаграмме свободного тела.
Рисунок 14. 8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.
8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.Поскольку элемент жидкости между и и
не ускоряется, силы уравновешены. Используя декартову ось y , ориентированную вверх, мы находим следующее уравнение для y -компоненты:
Обратите внимание, что если бы элемент имел ненулевую y -компоненту ускорения, правая часть не была бы равна нулю, а вместо этого была бы массой, умноженной на y -ускорения.Массу элемента можно записать через плотность жидкости и объем элементов:
.
Составить это выражение для
на (рисунок), а затем разделив обе стороны на
, находим
Предел бесконечно тонкого элемента
, получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна плотность ρ или изменяется с глубиной; то есть функция ρ ( y ).
Решение этого уравнения зависит от того, постоянна плотность ρ или изменяется с глубиной; то есть функция ρ ( y ).
Если диапазон анализируемых глубин не слишком велик, плотность можно считать постоянной. Но если диапазон глубин достаточно велик для заметного изменения плотности, как, например, в случае с атмосферой, плотность существенно меняется с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
Давление в жидкости с постоянной плотностью
Используем (рисунок) для расчета давления на глубине ч от поверхности в резервуаре с жидкостью, такой как вода, где плотность жидкости можно считать постоянной.
Нам нужно интегрировать (рисунок) из
где давление равно атмосферному
от
до
y -координата глубины:
Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс ρgh , если плотность жидкости постоянна по высоте, как мы нашли ранее.
Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы сосуда. Таким образом, в сосуде, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне во всех частях, независимо от формы, как показано на (рис.).
Рисунок 14.9 Если жидкость может свободно течь между частями сосуда, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление на дне каждой колонны одинаково; если бы это было не то же самое, жидкость текла бы до тех пор, пока давления не сравнялись бы.Изменение атмосферного давления с высотой
Особый интерес представляет изменение атмосферного давления с высотой. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна. (Мы обсудим закон идеального газа в одной из последующих глав, но мы предполагаем, что вы знакомы с ним из средней школы и химии. ) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность
) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность
при y , температура T по шкале Кельвина (K) и масса m молекулы воздуха связаны с абсолютным давлением по закону идеального газа в виде
где
— постоянная Больцмана, которая имеет значение
.
.
Возможно, вы встречали закон идеального газа в форме
.
, где n — количество молей, а R — газовая постоянная. Здесь тот же закон записан в другой форме, с использованием плотности
.
вместо тома V . Следовательно, если давление p меняется с высотой, то и плотность
меняется.
Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
, где в скобках указано постоянное количество.Замена этих констант одним символом
уравнение выглядит гораздо проще:
Это дает решение
Таким образом, атмосферное давление падает экспоненциально с высотой, так как ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря.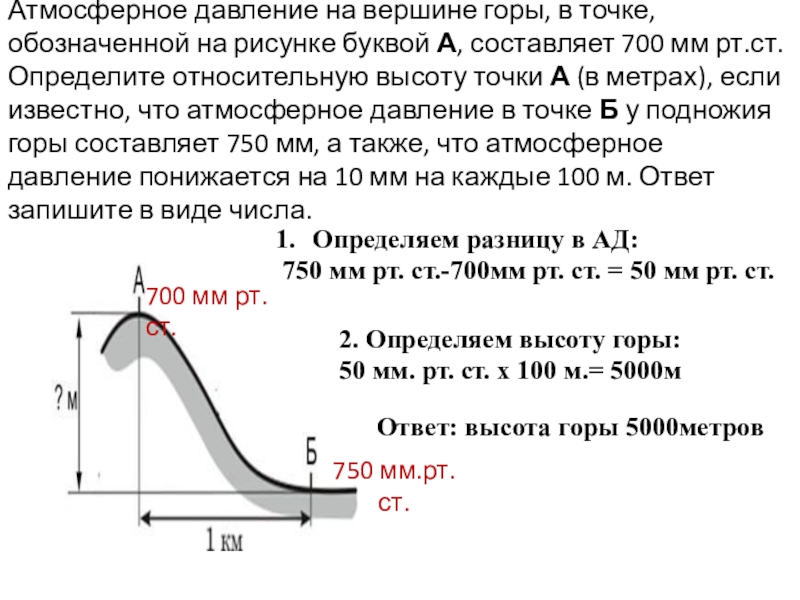 Давление падает в
Давление падает в
при высоте
, что дает нам физическую интерпретацию числа
.
: Константа
— это шкала длины, которая характеризует изменение давления в зависимости от высоты и часто упоминается как высота шкалы давления.
Мы можем получить примерное значение
, используя массу молекулы азота в качестве прокси для молекулы воздуха. При температуре
или 300 К, находим
Таким образом, на каждые 8800 метров атмосферное давление падает в 1/ e раз, или примерно на одну треть своего значения. Это дает нам лишь грубую оценку фактической ситуации, поскольку мы приняли как постоянную температуру, так и постоянную g на столь больших расстояниях от Земли, ни одно из которых в действительности не верно.
Направление давления в жидкости
Давление жидкости не имеет направления, будучи скалярной величиной, тогда как силы, вызванные давлением, имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности. Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости.(Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.
Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости.(Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.
 Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.Резюме
- Жидкость — это состояние вещества, которое поддается действию боковых или сдвигающих сил. Жидкости и газы являются жидкостями. Жидкостная статика – это физика стационарных жидкостей.
- Плотность – это масса на единицу объема вещества или объекта, определяемая как
Единицей плотности в системе СИ является
. - Давление – это сила, приходящаяся на единицу перпендикулярной площади, к которой приложена сила,
Единицей давления в системе СИ является паскаль:
.
- Давление от веса жидкости постоянной плотности определяется выражением
, где p давление, h глубина жидкости,
— плотность жидкости, г — ускорение свободного падения.
Концептуальные вопросы
Какие из следующих веществ являются жидкими при комнатной температуре и атмосферном давлении: воздух, ртуть, вода, стекло?
[reveal-answer q=”fs-id1170958994176″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958994176″]
Ртуть и вода являются жидкими при комнатной температуре и атмосферном давлении. Воздух – это газ при комнатной температуре и атмосферном давлении. Стекло представляет собой аморфный твердый (некристаллический) материал при комнатной температуре и атмосферном давлении. Одно время считалось, что стекло течет, но течет очень медленно. Эта теория возникла из наблюдения, что старые стеклянные плоскости были толще внизу. В настоящее время считается маловероятным, что эта теория точна.
Воздух – это газ при комнатной температуре и атмосферном давлении. Стекло представляет собой аморфный твердый (некристаллический) материал при комнатной температуре и атмосферном давлении. Одно время считалось, что стекло течет, но течет очень медленно. Эта теория возникла из наблюдения, что старые стеклянные плоскости были толще внизу. В настоящее время считается маловероятным, что эта теория точна.
[/скрытый ответ]
Почему газы легче сжимать, чем жидкости и твердые тела?
Объясните, как плотность воздуха меняется с высотой.
[reveal-answer q=”fs-id1170958006029″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958006029″]
Плотность воздуха уменьшается с высотой. Для столба воздуха постоянной температуры плотность экспоненциально убывает с высотой. Это справедливое приближение, но поскольку температура меняется с высотой, это всего лишь приближение.
[/скрытый ответ]
На изображении изображен стакан с ледяной водой, наполненный до краев.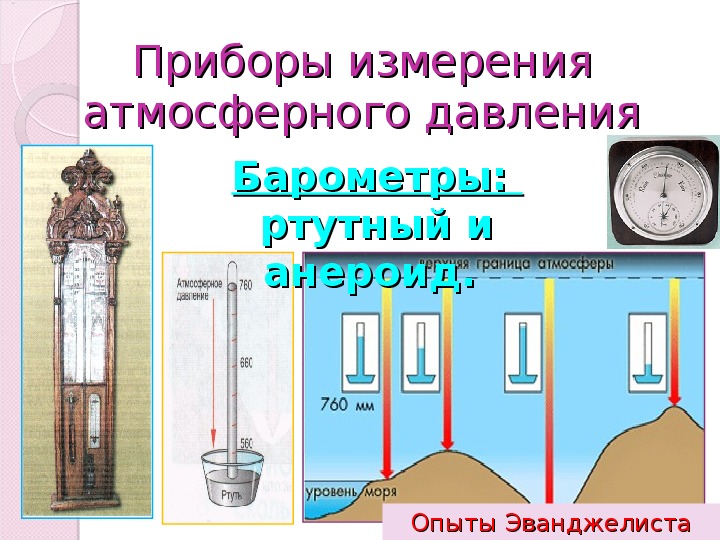 Будет ли вода переливаться через край, когда лед растает? Поясните свой ответ.
Будет ли вода переливаться через край, когда лед растает? Поясните свой ответ.
Как давление связано с остротой ножа и его режущей способностью?
[reveal-answer q=”fs-id1170958071670″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958071670″]
Давление – это сила, деленная на площадь. Если нож острый, сила, приложенная к режущей поверхности, делится на меньшую площадь, чем такая же сила, прикладываемая тупым ножом. Это означает, что давление на более острый нож будет больше, что повысит его режущую способность.
[/скрытый ответ]
Почему сила, приложенная неподвижной жидкостью к поверхности, всегда перпендикулярна поверхности?
Представьте себе, что в отдаленном месте недалеко от Северного полюса в озере плавает кусок льда. Рядом с озером на суше сидит ледник такого же объема, как и плавучий лед. Если оба куска льда должны растаять из-за повышения глобальной температуры, и весь растаявший лед попадет в озеро, какой из них вызовет наибольшее повышение уровня озера? Объяснять.
[reveal-answer q=”fs-id1170958021844″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958021844″]
Если бы два куска льда имели одинаковый объем, они произвели бы одинаковый объем воды. Однако ледник вызовет наибольшее повышение уровня воды в озере, потому что часть плавающего куска льда уже погружена в озеро и, таким образом, уже влияет на его уровень.
[/скрытый ответ]
В балете танец на пуантах (на кончиках пальцев ног) намного тяжелее для пальцев ног, чем обычный танец или ходьба.Объясните почему, с точки зрения давления.
Атмосферное давление оказывает большую силу (равную весу атмосферы над вашим телом — около 10 тонн) на верхнюю часть тела, когда вы лежите на пляже и принимаете солнечные ванны. Почему ты можешь встать?
[reveal-answer q=”fs-id1170958068067″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958068067″]
Давление действует на все ваше тело, если вы не находитесь в вакууме.
[/скрытый ответ]
Почему атмосферное давление уменьшается с высотой быстрее, чем линейно?
На изображении показано, как мешки с песком, размещенные вокруг протечки за пределами речной дамбы, могут эффективно остановить поток воды под дамбой.Объясните, как небольшое количество воды внутри столба мешков с песком может уравновесить гораздо больший объем воды за дамбой.
[reveal-answer q=»416788″]Показать решение[/reveal-answer]
[hidden-answer a=»416788″]Поскольку уровень реки очень высок, она начала протекать под дамбой. Мешки с песком помещаются вокруг места утечки, и вода, удерживаемая ими, поднимается до тех пор, пока не достигнет уровня реки, после чего вода в этом месте перестает подниматься. Мешки с песком будут поглощать воду до тех пор, пока уровень воды не достигнет уровня воды в дамбе.[/скрытый ответ]
Есть ли результирующая сила на плотине из-за атмосферного давления? Поясните свой ответ.
Влияет ли атмосферное давление на давление газа в жестком резервуаре? На игрушечном воздушном шаре? Когда вообще атмосферное давление не влияет на полное давление в жидкости?
[reveal-answer q=”fs-id1170958011807″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958011807″]
Атмосферное давление не влияет на давление газа в жестком резервуаре, но влияет на давление внутри воздушного шара. Обычно атмосферное давление влияет на давление жидкости, если только жидкость не заключена в жесткий контейнер.
Обычно атмосферное давление влияет на давление жидкости, если только жидкость не заключена в жесткий контейнер.
[/скрытый ответ]
Крепкую винную бутылку можно разбить, забив пробку кулаком, но пробка должна прижиматься непосредственно к жидкости, наполняющей бутылку — между пробкой и жидкостью не может быть воздуха. Объясните, почему бутылка разбивается только в том случае, если между пробкой и жидкостью нет воздуха.
Проблемы
Золотопродается тройскими унциями (31.103 г). Каков объем 1 тройской унции чистого золота?
[reveal-answer q=”fs-id1170958071483″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958071483″]
1,610
[/скрытый ответ]
Ртуть обычно поставляется в колбах по 34,5 кг (около 76 фунтов). Каков объем в литрах такого количества ртути?
Какова масса глубоко вдохнутого воздуха объемом 2,00 л? Обсудите влияние такого дыхания на объем и плотность вашего тела.
[reveal-answer q=”fs-id1170958073311″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958073311″]
Масса 2,58 г. Объем вашего тела увеличивается на объем вдыхаемого воздуха. Средняя плотность вашего тела уменьшается, когда вы делаете глубокий вдох, потому что плотность воздуха существенно меньше, чем средняя плотность тела.
[/скрытый ответ]
Простой метод определения плотности объекта состоит в том, чтобы измерить его массу, а затем измерить его объем, погрузив его в мерный цилиндр.Какова плотность камня массой 240 г, который вытесняет
куб.
воды? (Обратите внимание, что точность и практическое применение этого метода более ограничены, чем множество других, основанных на принципе Архимеда.)
Предположим, у вас есть кофейная кружка с круглым поперечным сечением и вертикальными сторонами (равномерный радиус). Каков его внутренний радиус, если он вмещает 375 г кофе при глубине заполнения 7,50 см? Предположим, что плотность кофе равна плотности воды.
[reveal-answer q=”fs-id1170958
9″]Показать решение[/reveal-answer][скрытый ответ a=”fs-id1170958
9″]3.99 см
[/скрытый ответ]
Полный прямоугольный бензобак вмещает 50,0 кг бензина. Какова глубина резервуара, если его ширина 0,500 м, а длина 0,900 м? (b) Обсудите, имеет ли этот бензобак достаточный объем для легкового автомобиля.
Компактор для мусора может сжимать его содержимое в 0,350 раз больше его первоначального объема. Если пренебречь массой вытесненного воздуха, во сколько раз увеличится плотность мусора?
[reveal-answer q=”fs-id1170958
5″]Показать решение[/reveal-answer][скрытый ответ a=”fs-id1170958
5″]2.в 86 раз плотнее
[/скрытый ответ]
Полная стальная канистра для бензина массой 2,50 кг вмещает 20,0 л бензина. Какова средняя плотность полного газового баллона с учетом объема, занимаемого как сталью, так и бензином?
Какова плотность 18-каратного золота, которое представляет собой смесь 18 частей золота, 5 частей серебра и 1 части меди? (Эти значения являются массовыми, а не объемными частями. ) Предположим, что это простая смесь, имеющая среднюю плотность, равную взвешенным плотностям ее компонентов.
) Предположим, что это простая смесь, имеющая среднюю плотность, равную взвешенным плотностям ее компонентов.
[reveal-answer q=”fs-id1170958073263″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958073263″]
[/скрытый ответ]
Кончик гвоздя оказывает огромное давление при ударе молотком, потому что он оказывает большую силу на небольшую площадь. Какую силу надо приложить к гвоздю с круглым кончиком диаметром 1,00 мм, чтобы создать давление
(Это высокое давление возможно потому, что молоток, ударяющий по гвоздю, останавливается на таком коротком расстоянии.)
Стеклянная трубка содержит ртуть. Какой должна быть высота столбика ртути, создающего давление, равное 1,00 атм?
[reveal-answer q=”fs-id1170958073457″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958073457″]
[/скрытый ответ]
Самые большие глубины океана на Земле находятся в Марианской впадине недалеко от Филиппин. Вычислите давление океана на дно этой впадины, если ее глубина равна 11.0 км и предположить, что плотность морской воды постоянна на всем протяжении.
Вычислите давление океана на дно этой впадины, если ее глубина равна 11.0 км и предположить, что плотность морской воды постоянна на всем протяжении.
Убедитесь, что единица СИ
это
.
[reveal-answer q=”fs-id1170958698863″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1170958698863″]
доказательство
[/скрытый ответ]
Какое давление оказывает давление на дно газового баллона шириной 0,500 м и длиной 0,900 м, вмещающего 50 г.0 кг бензина при полной загрузке?
Плотина используется для сдерживания реки. Плотина имеет высоту
и шириной
Предположим, что плотность воды равна
.
(a) Определите чистую силу, действующую на плотину. б) Почему толщина плотины увеличивается с глубиной?
[reveal-answer q=”821152″]Показать решение[/reveal-answer]
[hidden-answer a=”821152″]a. Давление на
; б. Давление увеличивается по мере увеличения глубины, поэтому плотина должна быть толще по направлению к дну, чтобы выдерживать большее давление.[/hidden-answer]
Давление увеличивается по мере увеличения глубины, поэтому плотина должна быть толще по направлению к дну, чтобы выдерживать большее давление.[/hidden-answer]
Глоссарий
- плотность
- масса на единицу объема вещества или предмета
- жидкости
- жидкости и газы; жидкость – это состояние вещества, которое поддается сдвиговым силам
- давление
- сила на единицу площади, приложенная перпендикулярно площади, на которую действует сила
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Этот месяц в истории физики
Октябрь 1644 года: Торричелли демонстрирует существование вакуума
Элегантный физический эксперимент; долговечное практическое изобретение
Евангелиста Торричелли
Изд. Примечание. Колонку этого месяца написал приглашенный автор Ричард Уильямс.
Примечание. Колонку этого месяца написал приглашенный автор Ричард Уильямс.
Евангелиста Торричелли, родившаяся в скромной семье, со временем поднялась на вершину итальянского интеллектуального сообщества. Он привел Италию, а затем и весь мир к разрешению двухтысячелетнего философского спора о вакууме и природе пространства. Он сделал это, выполнив и поняв один изящный физический эксперимент. Прибор, который он использовал, был также практическим изобретением — ртутный барометр.
Торричелли родился в Фаэнце, Италия, 15 октября 1608 года. «Оставаясь без отца в раннем возрасте», он был отправлен в Рим для получения образования. Его достижения там привлекли к нему внимание Галилея во Флоренции. Он приехал туда и жил с Галилеем. Галилей был озабочен проблемой тосканских землекопов, которые потерпели неудачу в своих попытках поднять воду более чем на десять метров с помощью подъемных насосов. Когда его попытались поднять выше, вода отделилась от плунжера насоса и дальше не пошла. Может ли это быть из-за того, что под плунжером образовался вакуум? Они спросили Галилея, почему нельзя накачать воду выше. Он серьезно рассматривал эту проблему, но умер в 1642 году, так и не решив ее.
Может ли это быть из-за того, что под плунжером образовался вакуум? Они спросили Галилея, почему нельзя накачать воду выше. Он серьезно рассматривал эту проблему, но умер в 1642 году, так и не решив ее.
Затем, в 1644 году, за проблему взялся Торричелли. После некоторого изучения более ранних экспериментов он провел один из своих собственных. Аппарат представлял собой стеклянную трубку длиной около метра, запаянную с одного конца. Он наполнил его ртутью, закрыл открытый конец и перевернул над чашкой с ртутью. Это было не так просто, как кажется сегодня.Стеклянные трубки в то время были хрупкими и труднодоступными. Они часто ломались при заполнении килограммом ртути. Но с помощью опытного помощника эксперимент был проведен. Ртуть в трубке упала и стабилизировалась на уровне примерно на 76 сантиметров выше уровня в чашке. Торричелли правильно предположил, что ртуть поднимается в трубке из-за веса атмосферы, давит на ртуть в чашке, и что пространство над ртутным столбом представляет собой вакуум. Это был первый случай, когда вакуум был создан в лаборатории и понят как таковой.
Это был первый случай, когда вакуум был создан в лаборатории и понят как таковой.
Концепция вакуума вызывала споры с древних времен. И Платон, и Аристотель считали существование вакуума невозможным вопреки природе. В средневековой Европе это выражалось выражением: «Природа не терпит пустоты». Обсуждать вакуум стало еретическим и опасным.
Слово «вакуум» впервые появилось в английском языке в 1550 году и было введено Томасом Кранмером, архиепископом Кентерберийским, который составил Книгу общей молитвы , центральный документ англиканской церкви.Фраза, которую он использовал как часть богословского аргумента, цитируется в Оксфордском словаре английского языка : «Естественный разум ненавидит пустоту, то есть должно быть любое пустое место, в котором не должно быть никакой субстанции». Это была общепринятая точка зрения, но с воцарением католической королевы Марии в 1553 году ветер ортодоксальности изменился. Кранмер был осужден за ересь в 1555 году и в следующем году сожжен на костре.
Достижение Торричелли перенесло понятие вакуума из диалектики древности в экспериментальную физику.Помня о спорах вокруг идеи вакуума, он сначала не предал гласности свой эксперимент, а раскрыл его только в письмах другу Микеланджело Риччи. В октябре 1644 года Торричелли посетил французский ученый Марин Мерсенн, который повторил для него эксперимент и передал ему копии писем к Риччи. Мерсенн отнес их Блезу Паскалю и другим во Францию, впервые публично обнародовав работу Торричелли.
Паскаль сразу понял смысл эксперимента и повторил его в 1646 году.Он считал, что атмосферное давление должно уменьшаться с высотой, и нанял родственника и нескольких друзей, чтобы они подняли барометр в гору на юге Франции. Они обнаружили ожидаемое уменьшение давления с высотой, заложив основу науки метеорологии.
Паскаль понимал, что давление равно весу атмосферы на единицу площади. Он объединил это с площадью поверхности земли и вычислил общую массу атмосферы. Его результат отличался менее чем на 30% от принятого в настоящее время значения, указанного в The Handbook of Chemistry and Physics . Что касается расчета, Паскаль отметил, что «ребенок, который знает сложение и вычитание, может это сделать», что является сильным одобрением французской школьной системы.
Что касается расчета, Паскаль отметил, что «ребенок, который знает сложение и вычитание, может это сделать», что является сильным одобрением французской школьной системы.
Аппарат Торричелли был первым ртутным барометром. Позже были внесены незначительные улучшения для повышения точности показаний, но основная конструкция осталась неизменной. На метеорологических станциях по всему миру он служил эталоном для измерения атмосферного давления более трех столетий, что, возможно, является рекордным сроком для прибора с такой же конструкцией.Наконец, в 1977 году Национальная метеорологическая служба США объявила, что ртутный барометр будет заменен в качестве эталона недавно разработанным датчиком давления на пьезоэлектрическом кристалле кварца.
Торричелли стоял на том стыке, где благодаря одному изящному эксперименту вакуум и природа пространства, определяемые в философских терминах на протяжении двух тысячелетий, уступили место современному взгляду, определяемому экспериментальной физикой. В двадцатом веке физики пошли намного дальше этого.Они нашли не «пустое место, где не должно быть никакой материи», а скорее вакуум, наполненный чудесами: электромагнитным излучением, в том числе от последнего вздоха Большого Взрыва; море виртуальных пар частица-античастица; пространство, искривленное гравитационным искривлением — все это было невообразимо для более ранних физиков.
В двадцатом веке физики пошли намного дальше этого.Они нашли не «пустое место, где не должно быть никакой материи», а скорее вакуум, наполненный чудесами: электромагнитным излучением, в том числе от последнего вздоха Большого Взрыва; море виртуальных пар частица-античастица; пространство, искривленное гравитационным искривлением — все это было невообразимо для более ранних физиков.
После работы над барометром Торричелли занялся исследованиями в области математики и физики. Его формула истечения жидкости из небольшого отверстия в сосуде до сих пор известна как теорема Торричелли.Он умер во Флоренции в 1647 году в возрасте тридцати девяти лет. Памятный памятник ему был установлен в Фаэнце в 1864 году.
Манометрическое и атмосферное давление
Атмосферное давление
Важно различать тип величины давления, используемой при измерении и расчете давления. Атмосферное давление — это величина давления в системе из-за атмосферы, например, давление, оказываемое молекулами воздуха (статическая жидкость) на поверхность земли на заданной высоте. В большинстве измерений и расчетов атмосферное давление считается постоянным на уровне 1 атм или 101 325 Па, что соответствует атмосферному давлению при стандартных условиях на уровне моря.
В большинстве измерений и расчетов атмосферное давление считается постоянным на уровне 1 атм или 101 325 Па, что соответствует атмосферному давлению при стандартных условиях на уровне моря.
Атмосферное давление обусловлено силой молекул в атмосфере и является случаем гидростатического давления. В зависимости от высоты относительно уровня моря фактическое атмосферное давление будет меньше на больших высотах и больше на более низких высотах по мере изменения веса молекул воздуха в непосредственной атмосфере, что приводит к изменению эффективного атмосферного давления.Атмосферное давление является мерой абсолютного давления, и на него могут влиять температура и состав воздуха в атмосфере, но, как правило, его можно точно приблизить к стандартному атмосферному давлению 101 325 Па. В большей части земной атмосферы давление меняется с высотой в соответствии с . В этом уравнении p 0 — давление на уровне моря (101 325 Па), g — ускорение свободного падения, M — масса одной молекулы воздуха, R — универсальная газовая постоянная, T 0 — стандартная температура на уровне моря, а h — высота относительно уровня моря.
Давление и высота
Атмосферное давление зависит от высоты или высоты.
Манометрическое давление
Для большинства применений, особенно связанных с измерением давления, более практично использовать в качестве единицы измерения манометрическое давление, а не абсолютное давление. Манометрическое давление — это измерение относительного давления, которое измеряет давление относительно атмосферного давления и определяется как абсолютное давление минус атмосферное давление.Большинство оборудования для измерения давления дает давление в системе с точки зрения манометрического давления, а не абсолютного давления. Например, давление в шинах и артериальное давление по соглашению являются манометрическими, тогда как атмосферное давление, давление глубокого вакуума и давление высотомера должны быть абсолютными.
Для большинства рабочих жидкостей, где жидкость находится в замкнутой системе, преобладает измерение манометрического давления. Приборы давления, подключенные к системе, покажут давление относительно текущего атмосферного давления.Ситуация меняется, когда измеряются экстремальные вакуумметрические давления; вместо этого обычно используются абсолютные давления.
Приборы давления, подключенные к системе, покажут давление относительно текущего атмосферного давления.Ситуация меняется, когда измеряются экстремальные вакуумметрические давления; вместо этого обычно используются абсолютные давления.
Чтобы найти абсолютное давление в системе, необходимо прибавить атмосферное давление к манометрическому давлению. Хотя манометрическое давление очень полезно при практических измерениях давления, для большинства расчетов, связанных с давлением, таких как закон идеального газа, требуются значения давления в виде абсолютных давлений и, следовательно, требуется преобразование манометрических давлений в абсолютные давления.
Типы давления: абсолютное, манометрическое, дифференциальное – WIKA Россия
Наряду с температурой давление является одной из наиболее важных переменных физического состояния.Давление определяется как сила (F N ), которая действует равномерно на определенной площади (A). Различные типы давления различаются только эталонным давлением.
Различные типы давления различаются только эталонным давлением.
Абсолютное давление
Самым четким эталонным давлением является нулевое давление, существующее в безвоздушном пространстве Вселенной. Давление, связанное с этим эталонным давлением, называется абсолютным давлением. Для необходимой дифференциации от других видов давления его обозначают индексом «abs», происходящим от латинского «absolutus», что означает обособленный, независимый.
Атмосферное давление
Вероятно, самым важным давлением для жизни на Земле является атмосферное давление, p амб (амб = окружающее = окружающее). Он создается весом атмосферы, которая окружает землю на высоте ок. 500 км. До этой высоты, на которой абсолютное давление р абс = нулю, его величина непрерывно уменьшается. Кроме того, атмосферное давление подвержено колебаниям в зависимости от погоды, о чем слишком хорошо известно из ежедневных сводок погоды.На уровне моря pamb составляет в среднем 1013,25 гектопаскаля (гПа), что соответствует 1013,25 миллибара (мбар).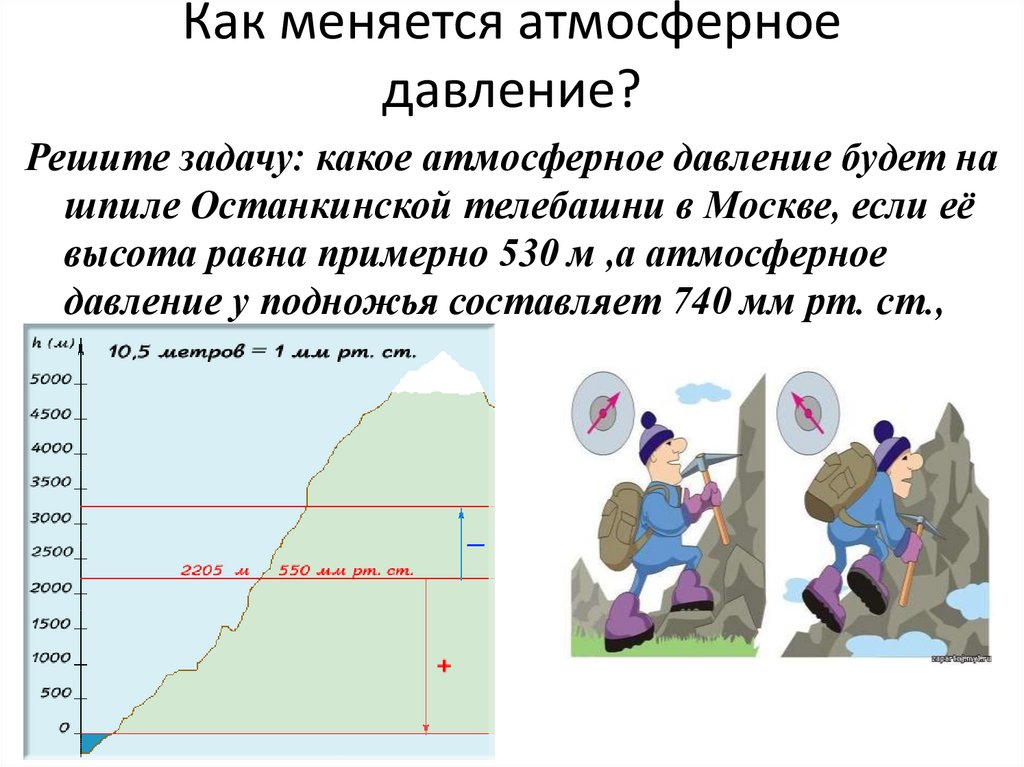 У «циклонов» и «антициклонов» это давление различается примерно на 5 %.
У «циклонов» и «антициклонов» это давление различается примерно на 5 %.
Перепад давления
Разница между двумя давлениями, p 1 и p 2 , известна как перепад давления, Δp = p 1 – p 2 . В тех случаях, когда разница между двумя давлениями сама представляет собой измеряемую переменную, один относится к перепаду давления, p 1,2 .
Избыточное давление (избыточное давление)
Наиболее часто измеряемым давлением в технологической сфере является перепад атмосферного давления, P e (e = excedens = превышение). Это разница между абсолютным давлением, pabs, и соответствующим (абсолютным) атмосферным давлением (p e = p абс – p амб ) и известна, короче говоря, как избыточное давление или манометрическое давление.
О положительном избыточном давлении говорят, когда абсолютное давление превышает атмосферное давление.В противном случае говорят об отрицательном избыточном давлении.


 Сосуд наполняется углекислым газом, плотность которого больше плотности воздуха (поэтому углекислый газ опускается вниз и заполняет сосуд, вытесняя из него воздух). При этом равновесие весов нарушается. Чашка с подвешенной колбой поднимается вверх (рис.). На колбу, погруженную в углекислый газ, действует бóльшая выталкивающая сила, по сравнению с той, которая действует на нее в воздухе.
Сосуд наполняется углекислым газом, плотность которого больше плотности воздуха (поэтому углекислый газ опускается вниз и заполняет сосуд, вытесняя из него воздух). При этом равновесие весов нарушается. Чашка с подвешенной колбой поднимается вверх (рис.). На колбу, погруженную в углекислый газ, действует бóльшая выталкивающая сила, по сравнению с той, которая действует на нее в воздухе. Пружина сокращается, и указатель пружины поднимается вверх, показывая уменьшение веса тела в жидкости. В данном случае на тело, кроме силы тяжести, действует еще одна сила, выталкивающая его из жидкости. Если в верхнее ведерко вылить жидкость из стакана (т. е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению (рис., в).
Пружина сокращается, и указатель пружины поднимается вверх, показывая уменьшение веса тела в жидкости. В данном случае на тело, кроме силы тяжести, действует еще одна сила, выталкивающая его из жидкости. Если в верхнее ведерко вылить жидкость из стакана (т. е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению (рис., в). е. F А = P ж = g·m ж. Массу жидкости m ж, вытесняемую телом, можно выразить через ее плотность ρ ж и объем тела V т, погруженного в жидкость (так как V ж – объем вытесненной телом жидкости равен V т – объему тела, погруженного в жидкость), т. е. m ж = ρ ж ·V т. Тогда получим:
е. F А = P ж = g·m ж. Массу жидкости m ж, вытесняемую телом, можно выразить через ее плотность ρ ж и объем тела V т, погруженного в жидкость (так как V ж – объем вытесненной телом жидкости равен V т – объему тела, погруженного в жидкость), т. е. m ж = ρ ж ·V т. Тогда получим:

 Для постройки судов используют различные материалы, имеющие по сравнению с водой как бóльшие, так и меньшие плотности.
Для постройки судов используют различные материалы, имеющие по сравнению с водой как бóльшие, так и меньшие плотности. е. имеющие вместе с грузом массу 500 000 т (5 · 10 5 т) и более.
е. имеющие вместе с грузом массу 500 000 т (5 · 10 5 т) и более.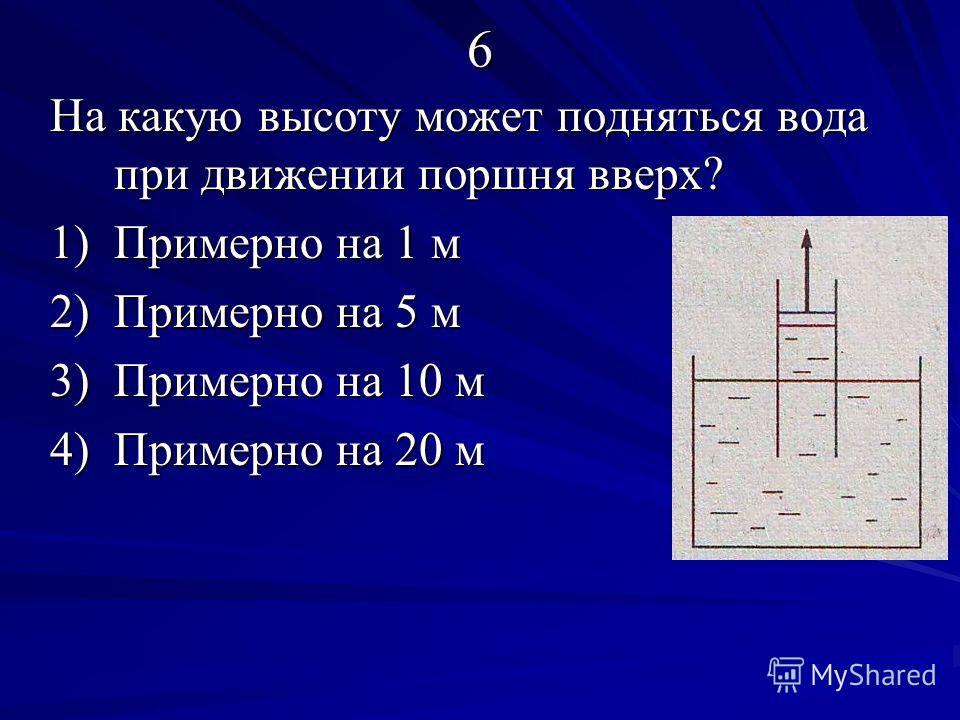
 Они имеют удлиненную форму, под корпусом подвешивается гондола с двигателем, который приводит в движение пропеллер.
Они имеют удлиненную форму, под корпусом подвешивается гондола с двигателем, который приводит в движение пропеллер. Но все же чаще используют гелий, так как он не горит и поэтому безопаснее. Водород же горючий газ.
Но все же чаще используют гелий, так как он не горит и поэтому безопаснее. Водород же горючий газ. Эти аэростаты используются для изучения воздушных течений, для географических и медико-биологических исследований в нижних слоях атмосферы.
Эти аэростаты используются для изучения воздушных течений, для географических и медико-биологических исследований в нижних слоях атмосферы. Вот мы и подошли к самому важному.
Вот мы и подошли к самому важному.
 У людей с повышенным давлением в семь раз чаще развивается инсульт, в четыре раза — ишемические заболевания сердца, в два — поражение кровеносных сосудов нижних конечностей.
У людей с повышенным давлением в семь раз чаще развивается инсульт, в четыре раза — ишемические заболевания сердца, в два — поражение кровеносных сосудов нижних конечностей.

 Дальше можно использовать одну руку – ту, на которой давление выше.
Дальше можно использовать одну руку – ту, на которой давление выше. Не каждый может понять его
Не каждый может понять его


 А представляет вот что: сила, действующая на единицу поверхности расположенная внутри тела и есть давление, а в формуле это выглядит вот так p=F/S.
А представляет вот что: сила, действующая на единицу поверхности расположенная внутри тела и есть давление, а в формуле это выглядит вот так p=F/S.
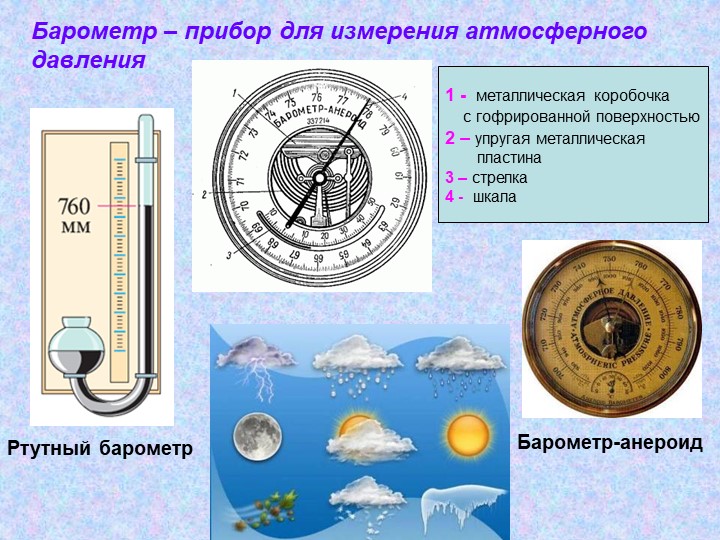 ст.
ст. 5.1.4.
5.1.4.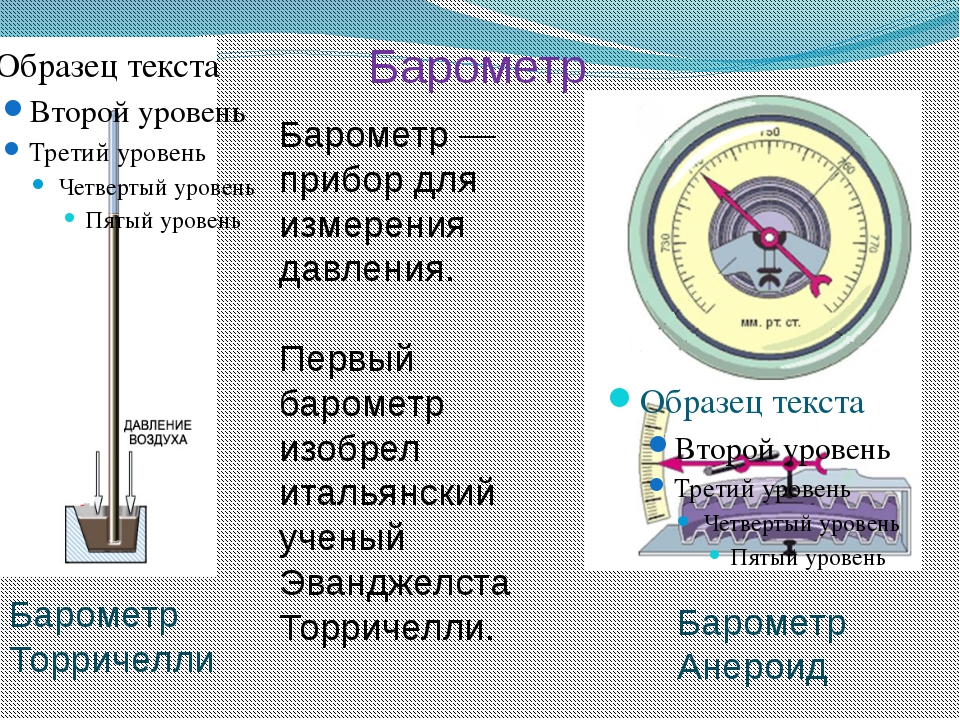 0 м, получаем
0 м, получаем