формула, от чего зависит, линии индукции
Все мы знаем, что есть магниты более сильные и менее сильные. Маленький магнитик сможет притянуть пару гвоздей и все, а гораздо более мощный электромагнит домофона удерживает дверь в подъезд так, что несколько взрослых мужчин не смогут открыть ее силой.
Величина, характеризующая величину силы магнита
То есть, мы можем говорить о некой величине, характеризующей величину силы магнитов, а точнее, магнитного поля, создаваемого ими. Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля или магнитной индукции. (см. подробнее электромагнитная индукция)
Обозначается индукция буквой B. Магнитная индукция это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле:
B=F / (I*l)
Или в виде определения:
Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.
От чего зависит магнитная индукция
Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.
Измеряется магнитная индукция в теслах (1 Тл). При этом 1 Тл=1 Н/(А*м) .
Линии индукции магнитного поля
Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и линиям магнитной индукции:
Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.
В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.
В случае неоднородного магнитного поля, например, поля вокруг проводника с током, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника. Так и будут выглядеть линии индукции магнитного поля расширяющиеся окружности вокруг проводника.
Нужна помощь в учебе?
Предыдущая тема: Обнаружение магнитного поля по его действию на электрический ток
Следующая тема:   Магнитный поток: определение, направление и количество + пример
Глава 22. Магнитные взаимодействия. Магнитная индукция.Силы Лоренца и Ампера
Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным.
В 1820 г. датский физик Х. Эрстед обнаружил, что проводник с током действует на магнитную стрелку. После этого стало ясно, что магнитное взаимодействие движущихся электрических зарядов и токов и взаимодействие постоянных магнитов имеют одну и ту же природу. На основании подробных исследований А. Ампер установил, что взаимодействие постоянных магнитов между собой и с токами можно объяснить, если предположить, что внутри магнитов есть электрические токи (в настоящее время известно, что эти токи имеют внутримолекулярную природу).
Для характеристики магнитного поля вводится векторная величина, которая называется индукцией магнитного поля и которая позволяет найти силы, действующие со стороны магнитного поля на движущиеся заряды. Как правило, эту величину обозначают буквой . Для нахождения индукции в каждой точке магнитного поля, созданного проводником с током, используется закон Био-Савара-Лапласа и принцип суперпозиции. Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать
Закон Био-Савара-Лапласа позволяет найти поле , созданное бесконечно малым элементом проводника, а принцип суперпозиции требует сложить векторы индукции, созданные всеми элементами проводников. Закон Био-Савара-Лапласа в школьный курс физики, однако, не входит. В задачи ЕГЭ входят только вопросы, связанные с направлением вектора магнитной индукции (но не с величиной). Существует несколько вариантов правила нахождения направления вектора . Наиболее удобным является правило буравчика — оно более универсально, чем правило левой руки. Правило буравчика утверждает, что если вкручивать
Магнитное поле можно изобразить графически с помощью линий магнитной индукции. Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.
Линии магнитной индукции — воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этой точке. Линии магнитной индукции проводят так, что их густота в каждой области пространства пропорциональна величине индукции в этой области. В отличие от силовых линий электрического поля линии магнитной индукции всегда являются замкнутыми.
На электрический заряд величиной , движущийся со скоростью в магнитном поле с индукцией , со стороны магнитного поля действует сила, которая называется силой Лоренца
(22.1) |
где — угол между скоростью и вектором индукции. Направление силы Лоренца определяется следующим образом (см. рисунок).
1. Сила Лоренца перпендикулярна плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля (на рисунке эта плоскость показана тонким пунктиром).
2. Выбор между двумя перпендикулярными направлениями осуществляется с помощью правила буравчика (или правила левой руки): если вращать правый буравчик так, что его ручка движется от вектора к вектору , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд (траектория ручки буравчика показана на рисунке изогнутой стрелкой).
3. Для отрицательного заряда направление силы Лоренца противоположно.
Можно также определять направление силы Лоренца по правилу левой руки: левую руку нужно расположить так, чтобы вектор входил в ладонь, направление четырех пальцев совпадало с направлением вектора скорости заряда, тогда направление отогнутого под прямым углом к четырем пальцам большого пальца покажет направление силы, действующей на положительный заряд (на отрицательный заряд действует сила противоположного направления).
Поскольку магнитное поле действует на движущиеся заряды, то магнитное поле действует и на проводник, по которому течет электрический ток. Если в магнитном поле с индукцией находится проводник длиной , по которому течет ток , то на этот проводник действует сила
(22.2) |
где — угол между током и вектором индукции. Направлен вектор силы (22.2) перпендикулярно плоскости, в которой лежат вектор и проводник, причем в таком направлении, что если поставить правый буравчик перпендикулярно указанной плоскости и вращать его так, что ручка вращается от тока к вектору , то направление его вкручивания покажет направление силы (см.
Рассмотрим теперь задачи.
Правильный ответ в задаче 22.1.1 — 4 (магнитное поле создается движущимися заряженными телами), в задаче 22.1.2 — 2 (в магнитном веществе есть незатухающие электрические токи). Что же касается того, заряжен магнит или нет, то от этого существование магнитного поля (если магнит покоится) не зависит.
В задаче 22.1.3 следует воспользоваться правилом буравчика. Если вкручивать буравчик по направлению тока в проводнике, то в точке его ручка будет двигаться за чертеж. Следовательно, за чертеж направлен в точке и вектор индукции магнитного поля (ответ 1).
Если вкручивать буравчик по току в кольце (в любой точке кольца), то ручка буравчика в центре кольца будет двигаться за чертеж.
Поскольку угол между скоростью заряда и вектором магнитной индукции равен нулю (задача 22.1.5), то согласно формуле (22.1) сила Лоренца, действующая на этот заряд, равна нулю (ответ 4).
Применим к проводнику с током из задачи 22.1.6 формулу (22.2) для силы Ампера. Имеем (ответ 2).
Как следует из формулы (22.2) сила Ампера равна нулю, если угол между током и индукцией равен нулю или 180°. Из приведенных на рисунке в задаче 22.1.7 проводников, таковым является только проводник 1. Поэтому на него магнитное поле не действует (ответ
Применяем к частице из задачи 22.1.8 (см. рисунок) правила нахождения направления силы Лоренца (пункты 1-3 после формулы (22.1)). Во-первых, сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля — т.е. либо за чертеж, либо на нас. Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ
Во-вторых, при вращении ручки буравчика, поставленного на чертеж в ту точку, где находится заряд, от вектора к вектору (в направлении меньшего угла между ними), буравчик будет «выкручиваться» из чертежа. А по-скольку частица заряжена положительно, сила Лоренца направлена «на нас» (ответ
|
Используя правила для силы Ампера (формула (22.2) и текст после нее), найдем, что сила Ампера, действующая со стороны магнитного поля на проводник с током в задаче 22.1.9, направлена «от нас» (ответ 3). |
В задаче 22.1.10 следует сначала найти направление вектора магнитной индукции поля провода в той точке, где находится заряд, а затем использовать правила для силы Лоренца (формула (22.1) и текст за ней). Согласно результатам задачи 22.1.3, вектор в той точке, где находится заряд, направлен за чертеж (см. рисунок).
Вектор силы Лоренца направлен перпендикулярно плоскости, в которой лежат векторы и , т.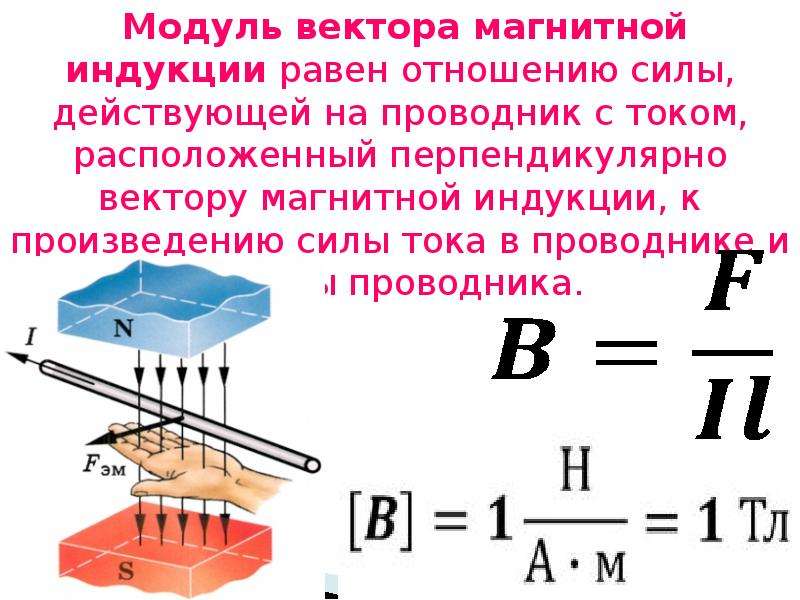 е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т.е. от провода (ответ 2).
е. либо к проводу, либо от него. Ставим буравчик перпендикулярно этой плоскости и вращаем его так, что ручка движется от вектора к вектору (см. рисунок; буравчик нужно вращать по часовой стрелке, если смотреть снизу). При таком вращении буравчик будет вкручиваться вверх. А поскольку электрон заряжен отрицательно, то действующая на него сила направлена противоположно, т.е. от провода (ответ 2).
В задаче 22.2.1 используем принцип суперпозиции. Ток в горизонтальном кольце создает поле в его центре с индукцией, направленной вверх, ток в вертикальном кольце — с индукцией, направленной вправо (см. задачу 22.1.4.). Результат сложения этих векторов — индукция суммарного магнитного поля — направлена на «северо-восток» (ответ 1).
Ток в верхнем проводе (задача 22.2.2) создает поле с индукцией, направленной «за чертеж», ток в нижнем — «на нас». Результат их сложения зависит от величин этих векторов. Поскольку поле нижнего провода в точке больше поля верхнего (меньше расстояние), то вектор суммы направлен «на нас» (ответ 1).
Сила Лоренца в любой момент времени перпендикулярна скорости частицы. Поэтому угол между бесконечно малым перемещением частицы в любой момент времени и силой Лоренца, действующей на частицу в этот момент времени, — прямой. А поскольку в формулу для работы силы на бесконечно малом участке перемещения входит косинус угла между силой и перемещением, то работа силы Лоренца равна нулю (задача 22.2.3 — ответ 3). Из этих рассуждений и теоремы об изменении кинетической энергии следует, что заряженная частица, движущаяся под действием магнитного поля, изменяет направление, но не величину своей скорости.
Если заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, то она движется по окружности, причем эта окружность лежит в плоскости, перпендикулярной линиям магнитной индукции. Радиус окружности можно найти из второго закона Ньютона для этой частицы
(22. |
где и — масса частицы и ее заряд, — ускорение, — скорость, которая не изменяется по величине (см. предыдущую задачу), — индукция магнитного поля. В формуле (22.3) использовано известное выражение для центростремительного ускорения . Из формулы (22.3) получаем для радиуса окружности
(22.4) |
Применяя формулу (22.4) к задаче 22.2.4 находим отношение радиусов окружности первой и второй частиц
(ответ 2).
Найдем сначала скорости протона и -частицы, ускоренных одним и тем же напряжением (задача 22.2.5). По теореме об изменении кинетической энергии имеем
где и — масса частицы и ее заряд, — скорость, которую частица приобретает после разгона (здесь предполагается, что начальная скорость частицы равна нулю). Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением
Из этой формулы находим отношение скоростей протона и -частицы , ускоренных одним и тем же напряжением
Поскольку заряд протона вдвое меньше заряда -частицы, а масса вчетверо меньше, то . Теперь из формулы (22.4) находим отношение радиусов окружности протона и -частицы, ускоренных одним и тем же электрическим напряжением и движущихся в одном и том же магнитном поле
(ответ 4).
Период обращения заряженной частицы в магнитном поле (задача 22.2.6) можно найти из следующих соображений. В однородном магнитном поле частица движется по окружности и за период проходит путь, равный длине этой окружности , где — ее радиус. Используя формулу (22.4) для радиуса траектории, получим для периода обращения
где — скорость частицы, — ее масса, — заряд, — индукция магнитного поля.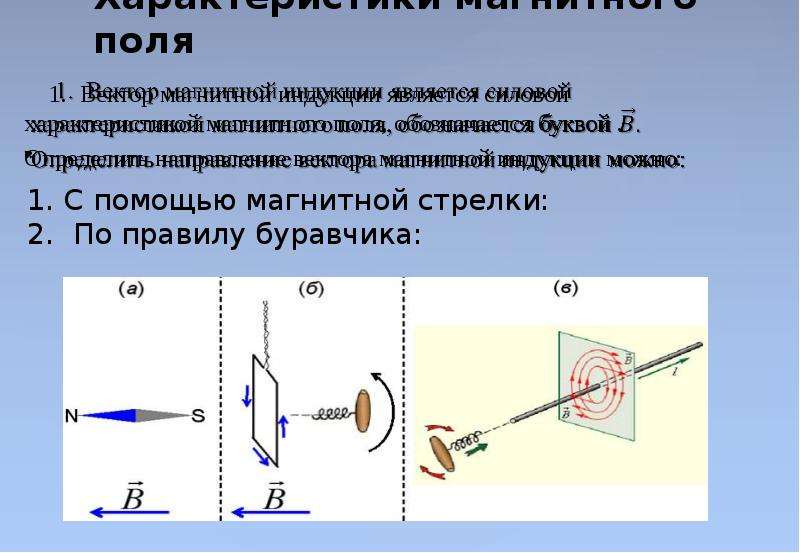 Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).
Отсюда заключаем, что период обращения заряженной частицы в магнитном поле не зависит от ее скорости (ответ 3).
Индукция магнитного поля в задаче 22.2.7 должна быть направлена так, чтобы сила Лоренца, действующая на электрон, была направлена к центру окружности, по которой он движется (см. рисунок). А поскольку сила Лоренца перпендикулярна скорости и индукции, то вектор индукции может быть направлен в этой ситуации только «за чертеж» или «на нас». Воспользуемся далее правилом буравчика (см. текст после формулы (22.1)): если вращать буравчик так, что его ручка будет вращаться от скорости заряда к индукции магнитного поля , то направление его вкручивания указывает направление силы Лоренца, действующей на положительный заряд. Для электрона ( < 0) направление силы противоположно. Непосредственной проверкой убеждаемся, что вектор индукции направлен «за чертеж» (ответ 4).
В области среднего провода (задача 22.2.8) ток в верхнем проводе создает магнитное поле с индукцией, направленной «от нас», ток в нижнем — «на нас» (см. задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.
задачу 22.1.3). Но ток в нижнем проводе вдвое меньше тока в верхнем, а индукция поля — пропорциональна току. Поэтому индукция суммарного поля верхнего и нижнего проводов в области среднего провода направлена «от нас». Согласно правилам нахождения направления силы Ампера (см. текст после формулы (22.2)) находим, что сила, действующая на средний провод со стороны магнитного поля верхнего и нижнего проводов, направлена вверх (ответ 1). Отметим, что из приведенных рассуждений также следует, что два параллельных провода, по которым текут токи одинакового направления притягиваются, противоположного — отталкиваются.
В задаче 22.2.9 магнитное поле действует на рамку следующим образом. На стороны и , которые параллельны линиям индукции, поле не действует. На стороны и действуют силы Ампера, равные по величине , где — ток в рамке, — индукция магнитного поля, — длина стороны. Сила, действующая на сторону , направлена «на нас», на сторону — «от нас». Поскольку суммарная сила, действующая на рамку, равна нулю, как целое рамка перемещаться в пространстве не будет, а будет вращаться вокруг оси, показанной на рисунке пунктиром (ответ 4).
Задача 22.2.10 по формуле (22.2) находим силы Ампера, действующие на стороны треугольника
где — ток в контуре, и — длины сторон и , — индукция магнитного поля (последняя из приведенных формул следует из того, что сторона параллельна линиям индукции). Из теоремы синусов для треугольника
заключаем, что , а из правил для направления силы Ампера — что один из векторов или направлен «за чертеж», один — «на нас» (в зависимости от направления тока в контуре). Поэтому правильный ответ в задаче — 3.
Электромагнитная индукция – материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).
2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.
3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.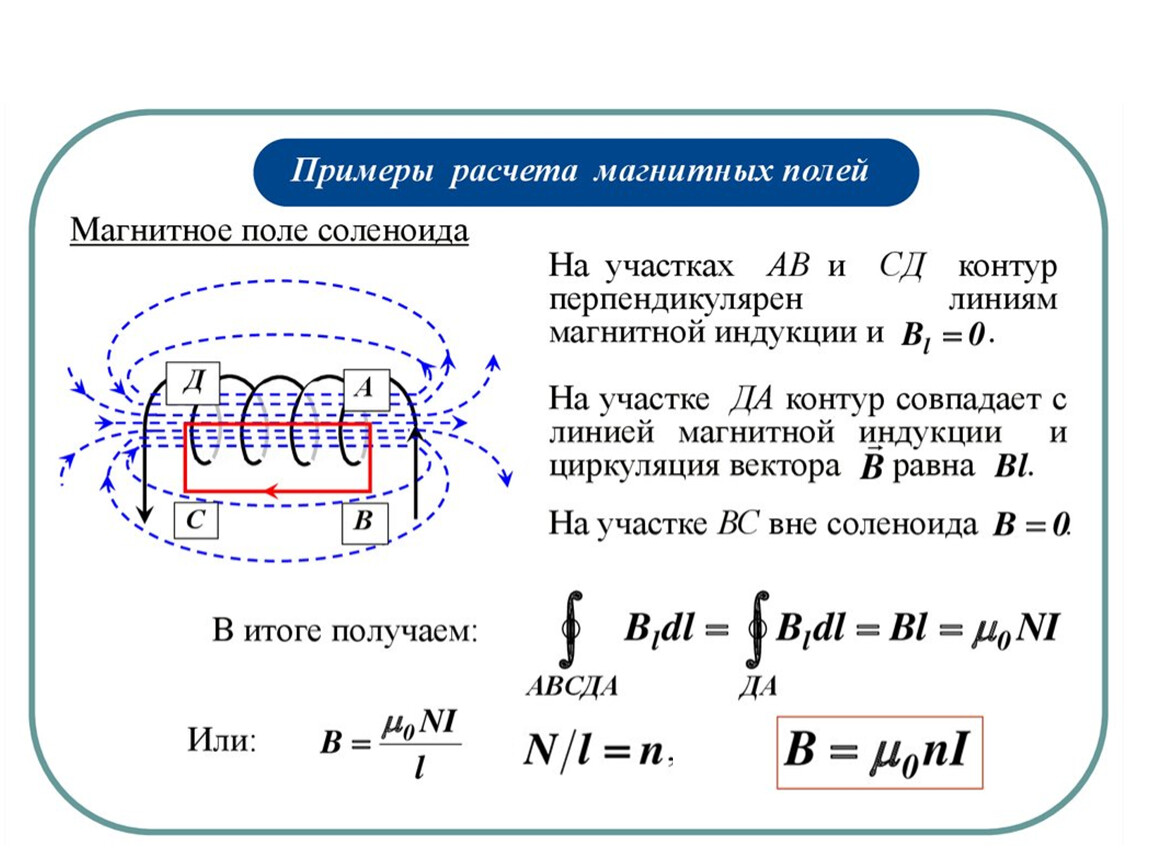
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).
Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2).
Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому
(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер (Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается .
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
(5)
Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.
Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).
Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.
Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .
ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: .
Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).
Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис. 6).
Рис. 6. Магнитный поток возрастает
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :
(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).
Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).
Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:
Следовательно, для ЭДС индукции получаем:
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле . По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9).
Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .
Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9). Площадь контура возрастает на величину площади прямоугольника :
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
Магнитное поле, силовые линии, вектор магнитной индукции, принцип суперпозиции. Курсы по физике
Тестирование онлайн
Магнитное поле. Основные понятия
Магнитное поле. Вектор магнитной индукции
Магнитное поле
Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.
Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи – электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем.
Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные – отталкиваются.
Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии – северный полюс (North), входят магнитные линии в южный полюс (South).
Магнитное поле можно сделать “видимым” с помощью железных опилок.
Магнитное поле проводника с током
А теперь о том, что обнаружили Ханс Кристиан Эрстед и Андре Мари Ампер в 1820 г. Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.
Силовые линии магнитного поля прямого тока – это окружности вокруг проводника.
Направление вектора магнитной индукции
Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенного в эту точку.
Направление линий магнитной индукции зависит от направления тока в проводнике.
Определяется направление вектора индукции по правилу буравчика или правилу правой руки.
Вектор магнитной индукции
Это векторная величина, характеризующая силовое действие поля.
Индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии r от него:
Индукция магнитного поля в центре тонкого кругового витка радиуса r:
Индукция магнитного поля соленоида (катушка, витки которой последовательно обходятся током в одном направлении):
Принцип суперпозиции
Если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция – векторная сумма индукций каждого из полей в отдельности
Земля является не только большим отрицательным зарядом и источником электрического поля, но в то же время магнитное поле нашей планеты подобно полю прямого магнита гигантских размеров.
Географический юг находится недалеко от магнитного севера, а географический север приближен к магнитному югу. Если компас разместить в магнитном поле Земли, то его северная стрелка ориентируется вдоль линий магнитной индукции в направлении южного магнитного полюса, то есть укажет нам, где располагается географический север.
Характерные элементы земного магнетизма весьма медленно изменяются с течением времени – вековые изменения. Однако время от времени происходят магнитные бури, когда в течение нескольких часов магнитное поле Земли сильно искажается, а затем постепенно возвращается к прежним значениям. Такое резкое изменение влияет на самочувствие людей.
Магнитное поле Земли является “щитом”, прикрывающего нашу планету от частиц, проникающих из космоса (“солнечного ветра”). Вблизи магнитных полюсов потоки частиц подходят гораздо ближе к поверхности Земли. При мощных солнечных вспышках магнитосфера деформируется, и эти частицы могут переходить в верхние слои атмосферы, где сталкиваются с молекулами газа, образуются полярные сияния.
Частицы диоксида железа на магнитной пленке хорошо намагничиваются в процессе записи.
Поезда на магнитной подушке скользят над поверхностью совершенно без трения. Поезд способен развивать скорость до 650 км/ч.
Работа головного мозга, пульсация сердца сопровождается электрическими импульсами. При этом в органах возникает слабое магнитное поле.
Магнитная индукция – это… Что такое Магнитная индукция?
Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)
- 1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
- (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе[4] наиболее важными являются:
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :
- Формула силы Лоренца
- Следствия из нее, такие как
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
- выражение для потенциальной энергии магнитного диполя в магнитном поле:
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- Следствия из нее, такие как
- Выражение для плотности энергии магнитного поля
- Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Примечания
- ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
- ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
- ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).
См. также
Магнитная индукция – Основы электроники
Магнитная индукция это способность влиять магнитным полем на объект.
При помещении в катушку железного стержня (сердечника) ее магнитный поток увеличивается во много раз. Объясняется это следующим. Железо имеет кристаллическое строение. Отдельные кристаллы железа, вследствие того, что внутри их происходит круговое движение электронов, т. е. существуют электрические токи, обладают свойствами маленьких магнитиков. В обычном состоянии эти молекулярные магнитики расположены в беспорядке. Магнитные поля их взаимно нейтрализуются, и поэтому кусок железа в целом не проявляет магнитных свойств. Схематически это изображено на рисунке 1. Отдельные молекулярные кристаллики изображены в виде маленьких магнитиков.
Рисунок 1. Беспорядочное расположение малекулярных кристалликов в обыном состоянии железа.
При помещении железа в магнитное поле молекулярные магнитики подобно магнитной стрелке компаса поворачиваются на некоторый угол и устанавливаются вдоль силовых линий магнитного поля. Чем сильное магнитное поле, тем большее число молекулярных магнитиков поворачивается и тем однороднее становится их расположение. Поля одинаково ориентированных магнитов не нейтрализуют уже друг друга, а наоборот, складываются, создавая дополнительные силовые линии.
Магнитный поток, создаваемый элементарными магнитиками железа, во много раз больше основного магнитного потока, создаваемого катушкой; именно поэтому магнитный поток катушки при помещении в нее железного сердечника увеличивается во много раз.
Если постепенно увеличивать ток, протекающий по виткам катушки, то магнитный поток в железном сердечнике будет увеличиваться до тех пор, пока все молекулярные магнитики не повернутся точно по направлению силовых линий магнитного поля (рисунок 2). После этого возрастание магнитного потока за счет железа прекратится. Это состояние железного сердечника называется магнитным насыщением.
Рисунок 2. В магнитном поле кристаллики направлены вдоль магнитных силовых линий.
Способностью увеличивать магнитный поток катушки обладают кроме железа и другие металлы (кобальт и никель), но у них эта способность выражена значительно слабее, чем у железа.
Очень сильными магнитными свойствами обладают также некоторые специальные сплавы. В радиотехнике эти сплавы применяются для изготовления постоянных магнитов для динамиков и магнетронов.
Число, показывающее, во сколько раз увеличивается магнитный поток соленоида при введении в него сердечника из какого-нибудь материала, называется магнитной проницаемостью данного материала и обозначается буквой µ
Магнитная проницаемость некоторых сортов железа и специальных сплавов достигает нескольких сотен тысяч. Для большинства же материалов она близка к единице.
Произведение из напряженности магнитного поля Н на проницаемость материала µ называется магнитной индукцией В.
Таким образом
B = µ *H.
Магнитная индукция определяет количество силовых линий в данном материале, проходящих через 1 см2 поперечного сечения материала.
После прекращения тока в катушке сердечник, если он сделан из мягкого железа, теряет свои магнитные свойства, потому что молекулярные магнитики снова располагаются беспорядочно. Если же сердечник стальной, то он сохраняет приобретенные магнитные свойства и после прекращения действия на него магнитного поля катушки. Объясняется это тем, что в стали молекулярные магнитики сохраняют свое упорядоченное расположение и после прекращения тока в катушке.
Катушка с железным сердечником называется электромагнитом, так как ее магнитные свойства обусловлены электрическим током.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
| Магнитное действие электрического тока | |
1820 г. X. Эрстед — датский физик, открыл магнитное действие тока. (Опыт: действие электрического тока на магнитную стрелку). 1820 г. А. Ампер — французский ученый, открыл механическое взаимодействие токов и установил закон этого взаимодействия. | |
Магнитное взаимодействие, как и электрическое, удобно рассматриватьвводя понятие магнитного поля:
| |
Для двух параллельных бесконечно длинных проводников было установлено: противоположно направленные токи отталкиваются, однонаправленные токи притягиваются, причем , где k — коэффициент пропорциональности. | |
Отсюда устанавливается единица силы тока ампер в СИ: сила тока равна 1 А, если между отрезками двух бесконечных проводников по 1 м каждый, находящимися в вакууме на расстоянии 1 м друг от друга, действует сила магнитного взаимодействия 2.10 7Н. | |
В СИ удобно ввести магнитную проницаемость вакуума . | |
| Вектор магнитной индукции. Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. | |
Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта с правой нарезкой) совпадает с направлением тока, то направление вращения ручки буравчика покажет направление линий магнитной индукции. Вектор магнитной индукции направлен по касательной к линиям. | |
На практике удобно пользоваться следующим правилом: если большой палец правой руки направить по току, то направление обхвата тока остальными пальцами совпадет с направлением линий магнитной индукции. |
|
Модуль вектора магнитной индукции Магнитная индукция В зависит от I и r, где r — расстояние от проводника с током до исследуемой точки. Если расстояние от проводника много меньше его длины (т. е. рассматривать модель бесконечно длинного проводника), то, где k — коэффициент пропорциональности. Подставляя эту формулу в уравнение для силы взаимодействия двух проводников с током, получим F=B .I.ℓ. Отсюда . Таким образом, модуль вектора магнитной индукции есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка. | |
Единица измерения в СИ – тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла. | |
| Магнитный поток | |
Магнитный поток (поток линий магнитной индукции) через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром. | |
, где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур. | |
Единица магнитного потока в СИ – вебер (Вб). В честь немецкого физика В. Вебера. | |
Опыт показывает, что линии магнитной индукции всегда замкнуты, и полный магнитный поток через замкнутую поверхность равен нулю. Этот факт является следствием отсутствия магнитных зарядов в природе. |
|
Магнитное поле токоведущего провода
Темы и файлы
E&M Тема
- Электромагнетизм, магнитное поле в катушке
Напильник Capstone
Перечень оборудования
Введение
Цель этого упражнения – измерить магнитное поле, создаваемое токоведущим проводом в форме катушки.Используйте усилитель мощности для создания и измерения тока в катушке и используйте датчик магнитного поля для измерения напряженности магнитного поля в катушке. Используйте Capstone для записи и отображения данных. Рассчитайте проницаемость свободного пространства ( μ 0 ) на основе размера и количества витков в катушке, измеренного тока и измеренного магнитного поля.Фон
Токоведущий провод испытывает магнитную силу при помещении в магнитное поле, создаваемое внешним источником, например постоянным магнитом.Токоведущий провод также создает собственное магнитное поле. Ганс Христиан Эрстед (1777–1851) впервые обнаружил этот эффект в 1820 году, когда он заметил, что провод с током влияет на ориентацию расположенной рядом стрелки компаса. Стрелка компаса выравнивается с чистым магнитным полем, создаваемым током и землей. Открытие Эрстеда, связавшее движение электрических зарядов с созданием магнитного поля, положило начало важной дисциплине, называемой электромагнетизмом.Экспериментально обнаружено, что величина B магнитного поля, создаваемого длинным прямым проводом, прямо пропорциональна току I и обратно пропорциональна радиальному расстоянию r от провода, как показано ниже. Константа пропорциональности преобразует выражение в уравнение, которое дает величину магнитного поля вокруг длинного прямого провода. Константа « μ 0 » известна как проницаемость свободного пространства, и ее значение показано ниже.(3)
мкм 0 = 4 π × 10 −7 Тлм / А
Если токопроводящий провод согнут в круговую петлю, силовые линии магнитного поля вокруг петли будут иметь рисунок, подобный тому, что и вокруг стержневого магнита. В центре петли радиусом R магнитное поле перпендикулярно плоскости петли и имеет значение, показанное в уравнении ниже, где I обозначает ток в петле. Часто петля состоит из N и витков провода, намотанных так близко друг к другу, что они образуют плоскую катушку с одной петлей.В этом случае магнитные поля отдельных витков складываются, чтобы получить результирующее поле, которое в Н, в раз больше, чем у одиночной петли. Для такой катушки магнитное поле в центре зависит от количества петель, тока и радиуса петли, как показано в уравнении ниже.Copyright © 2016 Advanced Instructional Systems, Inc. и факультет физики Университета Центральной Флориды | Кредиты
Закон Ленца – Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Используйте закон Ленца для определения направления наведенной ЭДС при изменении магнитного потока
- Используйте закон Фарадея с законом Ленца для определения наведенной ЭДС в катушке и соленоиде.
Направление, в котором индуцированная ЭДС движет ток по проволочной петле, можно определить через отрицательный знак.Однако обычно это направление легче определить с помощью закона Ленца, названного в честь его первооткрывателя Генриха Ленца (1804–1865). (Фарадей также открыл этот закон, независимо от Ленца.) Мы формулируем закон Ленца следующим образом:
Закон Ленца
Направление индуцированной ЭДС движет ток по проволочной петле, чтобы всегда противодействовать изменению магнитного потока, вызывающему ЭДС.
Закон Ленца также можно рассматривать с точки зрения сохранения энергии. Если толкание магнита в катушку вызывает ток, энергия в этом токе должна исходить откуда-то.Если индуцированный ток вызывает магнитное поле, противодействующее увеличению поля магнита, который мы втолкнули, тогда ситуация ясна. Мы приложили магнит к полю и поработали с системой, и это проявилось как ток. Если бы индуцированное поле не препятствовало изменению магнитного потока, магнит был бы втянут, создавая ток без каких-либо действий. Была бы создана электрическая потенциальная энергия, нарушив закон сохранения энергии.
Чтобы определить наведенную ЭДС, вы сначала рассчитываете магнитный поток, а затем получаете Величину, заданную по формуле. Наконец, вы можете применить закон Ленца для определения значения.Это будет развиваться на примерах, которые иллюстрируют следующую стратегию решения проблем.
Стратегия решения проблем: закон Ленца
Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:
- Сделайте набросок ситуации для использования при визуализации и записи направлений.
- Определить направление приложенного магнитного поля
- Определите, увеличивается или уменьшается его магнитный поток.
- Теперь определите направление индуцированного магнитного поля. Индуцированное магнитное поле пытается усилить магнитный поток, который уменьшается, или противодействует магнитному потоку, который увеличивается. Следовательно, индуцированное магнитное поле добавляет или вычитает приложенное магнитное поле, в зависимости от изменения магнитного потока.
- Используйте правило правой руки 2 (RHR-2; см. Магнитные силы и поля), чтобы определить направление индуцированного тока I , ответственного за индуцированное магнитное поле
- Направление (или полярность) наведенной ЭДС теперь может управлять обычным током в этом направлении.
Давайте применим закон Ленца к системе (Рисунок) (a). Мы обозначаем «перед» замкнутой проводящей петли как область, содержащую приближающийся стержневой магнит, а «заднюю часть» петли как другую область. По мере того, как северный полюс магнита движется к петле, поток через петлю из-за поля магнита увеличивается, потому что напряженность силовых линий, направленных от передней части петли к задней, увеличивается. Поэтому в контуре индуцируется ток. По закону Ленца направление индуцированного тока должно быть таким, чтобы его собственное магнитное поле было направлено так, чтобы противодействовали изменяющемуся потоку, вызванному полем приближающегося магнита.Следовательно, индуцированный ток циркулирует так, что силовые линии его магнитного поля через петлю направлены от задней части петли к передней. При использовании RHR-2 поместите большой палец напротив силовых линий магнитного поля, то есть к стержневому магниту. Ваши пальцы сгибаются против часовой стрелки, если смотреть со стороны стержневого магнита. В качестве альтернативы мы можем определить направление индуцированного тока, рассматривая токовую петлю как электромагнит, который противодействует приближению северного полюса стержневого магнита.Это происходит, когда индуцированный ток течет, как показано, поскольку тогда поверхность петли ближе к приближающемуся магниту также является северным полюсом.
Изменение магнитного потока, вызванное приближением магнита, индуцирует ток в контуре. (а) Приближающийся северный полюс индуцирует ток против часовой стрелки по отношению к стержневому магниту. (b) Приближающийся южный полюс индуцирует ток по часовой стрелке относительно стержневого магнита.
Часть (b) рисунка показывает южный полюс магнита, движущийся к проводящей петле.В этом случае поток через петлю из-за поля магнита увеличивается, потому что количество силовых линий, направленных от задней части петли к передней, увеличивается. Чтобы противодействовать этому изменению, в петле индуцируется ток, силовые линии которого через петлю направлены спереди назад. Эквивалентно, мы можем сказать, что ток течет в направлении, так что поверхность петли ближе к приближающемуся магниту является южным полюсом, который затем отталкивает приближающийся южный полюс магнита.При использовании RHR-2 ваш большой палец направлен в сторону от стержневого магнита. Ваши пальцы сгибаются по часовой стрелке, что соответствует направлению индуцированного тока.
Другой пример, иллюстрирующий использование закона Ленца, показан на (Рисунок). Когда переключатель разомкнут, уменьшение тока через соленоид вызывает уменьшение магнитного потока через его катушки, что вызывает ЭДС в соленоиде. Эта ЭДС должна противодействовать вызывающему его изменению (прекращению тока). Следовательно, наведенная ЭДС имеет указанную полярность и движется в направлении исходного тока.Это может вызвать дугу на выводах переключателя при его размыкании.
(a) Соленоид, подключенный к источнику ЭДС. (b) Размыкающий переключатель S прекращает подачу тока, что, в свою очередь, индуцирует ЭДС в соленоиде. (c) Разность потенциалов между концами заостренных стержней создается за счет индукции ЭДС в катушке. Эта разность потенциалов достаточно велика, чтобы образовалась дуга между острыми точками.
Проверьте свое понимание Найдите направление индуцированного тока в проводной петле, показанной ниже, когда магнит входит, проходит и покидает петлю.
Для показанного наблюдателя ток течет по часовой стрелке по мере приближения магнита, уменьшается до нуля, когда магнит центрируется в плоскости катушки, а затем течет против часовой стрелки, когда магнит покидает катушку.
Проверьте свое понимание Проверьте направления наведенных токов на (Рисунок).
Сводка
- Мы можем использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС.
- Направление наведенной ЭДС всегда противодействует изменению магнитного потока, вызывающему ЭДС, результат, известный как закон Ленца.
Концептуальные вопросы
Круглые токопроводящие петли, показанные на прилагаемом рисунке, параллельны, перпендикулярны плоскости страницы и соосны. (a) Когда переключатель S замкнут, каково направление тока, индуцируемого в D ? (b) Когда переключатель разомкнут, каково направление тока, индуцируемого в контуре D ?
а.CW со стороны схемы; б. Против часовой стрелки, если смотреть со стороны схемы
Северный полюс магнита перемещается к медной петле, как показано ниже. Если вы смотрите на петлю сверху магнита, скажете ли вы, что индуцированный ток циркулирует по или против часовой стрелки?
На прилагаемом рисунке показано проводящее кольцо в различных положениях, когда оно движется в магнитном поле. В чем смысл индуцированной ЭДС для каждой из этих позиций?
При входе в контур наведенная ЭДС создает ток против часовой стрелки, а при выходе из контура индуцированная ЭДС создает постоянный ток.В то время как петля полностью находится внутри магнитного поля, нет изменения потока и, следовательно, нет индуцированного тока.
Покажите это и получите те же единицы.
Укажите направление индуцированного тока для каждого случая, показанного ниже, наблюдая со стороны магнита.
а. Против часовой стрелки, если смотреть со стороны магнита; б. CW, если смотреть со стороны магнита; c. CW, если смотреть со стороны магнита; d. Против часовой стрелки, если смотреть со стороны магнита; е. CW, если смотреть со стороны магнита; f. нет тока
Проблемы
Одновитковая круговая петля из проволоки радиусом 50 мм лежит в плоскости, перпендикулярной пространственно однородному магнитному полю.За интервал времени 0,10 с величина поля равномерно увеличивается от 200 до 300 мТл. (а) Определите ЭДС, наведенную в петле. (б) Если магнитное поле направлено за пределы страницы, каково направление тока, индуцируемого в петле?
а. ; б. CCW с той же точки зрения, что и магнитное поле
При первом включении магнитного поля поток через 20-витковую петлю изменяется со временем в зависимости от того, где он находится в милливеберах, t – в секундах, и петля находится в плоскости страницы с нормальным направлением единицы измерения. наружу.(а) Какая ЭДС индуцируется в контуре как функция времени? Каково направление индуцированного тока при (б) t = 0, (в) 0,10, (г) 1,0 и (д) 2,0 с?
а. 150 А вниз через резистор; б. 46 А вверх через резистор; c. 0,019 А вниз через резистор
Используйте закон Ленца для определения направления индуцированного тока в каждом случае.
Глоссарий
- Закон Ленца
- направление наведенной ЭДС противодействует изменению магнитного потока, который ее произвел; это отрицательный знак в законе Фарадея
– обзор
4.14 Парамагнитные и ферромагнитные материалы
В парамагнитном материале атомы содержат постоянные магнитные дипольные моменты, возникающие из спина и орбитального углового момента электронов. К кристаллу прикладывается внешнее магнитное поле с индукцией B, где магнитная восприимчивость χm является константой пропорциональности между вектором намагниченности M (объемной плотностью магнитных диполей) и напряженностью магнитного поля H, так что
(4,182) M = χmH
Эта линейная зависимость от χm применима только к линейным магнитным материалам.В вакууме χm = 0, а в немагнитных материалах он обычно очень мал, в диапазоне от 10-4 до 10-5; например, χm = −0,94 × 10−5 для меди.
Магнитное поле индукции B представляет собой сумму вектора намагниченности M материала и напряженности внешнего магнитного поля H, где сумма умножается на константу проницаемости вакуума μ0, где
(4,183) B = μ0 ( H + M)
Индукционное магнитное поле B возникает из-за микроскопических (атомных) и макроскопических (проволоки) токов; тогда как напряженность магнитного поля H возникает только из-за макроскопических токов.Индукционное магнитное поле B будет стремиться к выравниванию дипольных моментов, потому что энергия меньше для параллельного выравнивания диполей. Индуцированное магнитное поле выровненных магнитных диполей M добавляет к приложенному извне магнитному полю H. Таким образом, магнитное поле составляет
(4,184) B = μ0 (1 + χm) H
Относительная проницаемость материала μr определяется как
(4,185) μr = 1 + χm
Материалы с относительной проницаемостью μr <1 являются диамагнитными. Материалы с μr> 1, но с μrÀ1 парамагнитны.Материалы с μrÀ1 являются ферромагнитными, а ферромагнитные материалы нелинейны, поэтому χm и μr меняются в зависимости от напряженности приложенного магнитного поля H.
Магнитная проницаемость μ определяется как
(4,186) μ = μ0μr
В линейных магнитных материалах, константа пропорциональности между индукционным магнитным полем B и напряженностью приложенного магнитного поля H – это магнитная проницаемость μ, где
(4,187) B = μH
В нелинейных магнитных материалах, таких как кобальт, никель и мягкое железо, проницаемость μ изменяется в зависимости от напряженности приложенного магнитного поля H, где μ может быть большим и иметь репрезентативные значения в диапазоне от 250 для кобальта, 600 для никеля и 5000 для мягкого железа.
Тепловое движение атомов, которое имеет тенденцию хаотизировать ориентацию диполей, должно преодолеваться приложенным магнитным полем или более низкими температурами. Восприимчивость при низких температурах и магнитных полях подчиняется закону Кюри, где для постоянной C характеристика материала равна
(4,188) χ = CT
Ферромагнетизм – это намагниченность, которая возникает в небольших областях материала без применения внешнего магнитного поля. поле. В ферромагнетиках естественная намагниченность, возникающая из-за неспаренных электронных спинов, достигает максимума при T = 0K и спадает до нуля при температуре Кюри TC.При температурах выше TC ферромагнитный материал становится парамагнитным, и его магнитная восприимчивость подчиняется модифицированному соотношению Кюри, в котором
(4.189) χ = CT − TC
Для температур ниже TC закон Кюри ферромагнетика больше не применим, потому что тогда материал становится ферромагнитным с постоянной намагниченностью. Ферромагнитный материал не намагничен в одном и том же направлении по всему объему, а скорее имеет множество меньших областей или доменов. Каждый домен полностью намагничен в одном направлении, но ориентация доменов случайна, так что направление намагничивания меняется от одного домена к другому.Случайная ориентация доменов происходит потому, что случайные домены создают более низкое энергетическое состояние, чем полностью выровненные домены. Приложенное магнитное поле в некоторой степени выравнивает эти домены, так что их магнитные поля более выровнены, тем самым увеличивая магнитное поле материала в целом. Увеличение приложенного магнитного поля сверх магнитного поля насыщения не приводит к дальнейшему увеличению намагниченности материала, поскольку домены достигают максимально возможного взаимного выравнивания. Когда внешнее магнитное поле удаляется, домены и их границы не возвращаются полностью к своей исходной ориентации, и, таким образом, домены проявляют гистерезис.Единственными ферромагнитными элементами являются железо, кобальт, никель, гадолиний и диспрозий.
Напомним, что идентичные атомные электроны должны быть неразличимы (следовательно, полная волновая функция должна быть симметричной), но пространственные и спиновые волновые функции компонентов могут быть симметричными или асимметричными, если произведение волновых функций спиновых и пространственных компонентов равно асимметричный. В трехмерных кристаллических полосах, где имеет место ферромагнитное действие, и в других неферромагнитных парамагнитных элементах кулоновское отталкивание между парой электронов имеет тенденцию перемещать электроны дальше друг от друга в антисимметричное пространственное состояние с минимальной энергией.Эта асимметрия полной волновой функции требует симметричного состояния спина, в котором спины неспаренных электронов ориентированы в одном направлении. Таким образом, кулоновская сила, которая раздвигает электроны для минимизации энергии, затем приводит к их параллельному выравниванию спинов в парамагнитных и ферромагнитных материалах.
Обменная сила или взаимодействие между пространственной и спиновой составляющими волновой функции для двух или более электронов отвечает за эту связь электронных спинов с параллельным выравниванием в парамагнитных и ферромагнитных материалах.В случае ферромагнетиков 3-D полоса заполнена не полностью, близкое расположение атомов железа делает неразличимыми электроны соседних атомов, а обменное взаимодействие теперь распространяется на электроны соседних атомов. Для поддержания полной асимметричной волновой функции для набора электронов, принадлежащих близко расположенным соседним атомам, которые имеют перекрывающиеся d-оболочки неспаренных электронов, есть две возможности. В ферромагнитном случае (например, для атомов железа) пространственная волновая функция может быть асимметричной, а функция спина – симметричной.В этом случае кулоновская энергия сводится к минимуму за счет разделения электронов, но разделение позволяет неспаренным электронам иметь параллельные спины. Другая возможность состоит в том, что пространственная волновая функция будет симметричной, а электроны локализованы вместе, и, следовательно, их спиновая волновая функция должна быть антисимметричной, что требует, чтобы спины электронов были антипараллельны. Возможность антиферромагнетизма не минимизирует кулоновскую энергию в железе и не возникает.Однако такие материалы, как MnO 2 , являются антиферромагнитными.
Закон электромагнитной индукции Фарадея | Электромагнетизм
10.3 Закон электромагнитной индукции Фарадея (ESBPY)
Ток, индуцированный изменяющимся магнитным полем (ESBPZ)
Хотя удивительное открытие электромагнетизма Эрстедом проложило путь для более практического применения электричества, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитная индукция .
Фарадей обнаружил, что когда он перемещал магнит рядом с проводом, на нем генерировалось напряжение. Если магнит удерживался в неподвижном состоянии, напряжение не генерировалось, оно существовало только во время движения магнита. Мы называем это напряжение индуцированной ЭДС (\ (\ mathcal {E} \)).
Контурная петля, подключенная к чувствительному амперметру, будет регистрировать ток, если он настроен, как показано на этом рисунке, и магнит перемещается вверх и вниз:
Магнитный поток
Прежде чем мы перейдем к определению закона электромагнитной индукции Фарадея и примерам, нам сначала нужно потратить некоторое время на изучение магнитного потока.Для петли площадью \ (A \) в присутствии однородного магнитного поля \ (\ vec {B} \) магнитный поток (\ (φ \)) определяется как: \ [\ phi = BA \ cos \ theta \] Где: \ begin {align *} \ theta & = \ text {угол между магнитным полем B и нормалью к петле в области A} \\ A & = \ text {область петли} \\ B & = \ text {магнитное поле} \ end {align *}
Единицей измерения магнитного потока является Вебер (Вб).
Вы можете спросить себя, почему включен угол \ (\ theta \). Поток зависит от магнитного поля, проходящего через поверхность. Мы знаем, что поле, параллельное поверхности, не может вызвать ток, потому что оно не проходит через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть компонент, который перпендикулярен, и компонент, который параллелен поверхности. Параллельная составляющая не может вносить вклад в поток, только вертикальная составляющая может.
На этой диаграмме мы показываем, что магнитное поле под углом, отличным от перпендикулярного, может быть разбито на составляющие.Компонент, перпендикулярный поверхности, имеет величину \ (B \ cos (\ theta) \), где \ (\ theta \) – угол между нормалью и магнитным полем.
- Закон электромагнитной индукции Фарадея
ЭДС \ (\ mathcal {E} \), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь A контура. Математически это можно выразить как:
\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]где \ (\ phi = B · A \), а B – напряженность магнитного поля.\ (N \) – количество контуров схемы. Магнитное поле измеряется в теслах (Тл). Знак минус указывает направление и то, что наведенная ЭДС имеет тенденцию противодействовать изменению магнитного потока. Знак минус можно не учитывать при вычислении звездных величин.
Закон Фарадея связывает наведенную ЭДС со скоростью изменения магнитного потока, который является произведением магнитного поля и площади поперечного сечения, через которое проходят силовые линии.
Это не площадь самого провода, а площадь, которую он ограничивает.Это означает, что если вы согнете проволоку в круг, площадь, которую мы будем использовать при вычислении потока, будет площадью поверхности круга, а не проволоки.
На этой иллюстрации, где магнит находится в той же плоскости, что и контур цепи, не было бы тока, даже если бы магнит был перемещен все ближе и дальше. Это связано с тем, что силовые линии магнитного поля не проходят через замкнутое пространство, а параллельны ему. Силовые линии магнитного поля должны проходить через область, ограниченную контуром цепи, чтобы возникла ЭДС.
Направление индуцированного тока (ESBQ2)
Самая важная вещь, которую следует помнить, это то, что индуцированный ток противодействует происходящему изменению.
На первом рисунке (слева) контурная петля имеет южный полюс магнита, который приближается. Величина поля от магнита становится больше. Реакция наведенной ЭДС будет заключаться в том, чтобы попытаться противодействовать усилению поля по направлению к полюсу. Поле является вектором, поэтому ток будет течь в таком направлении, что поля, возникающие из-за тока, имеют тенденцию нейтрализовать поля от магнита, сохраняя результирующее поле неизменным.
Чтобы противостоять переходу от приближающегося южного полюса сверху, ток должен приводить к силовым линиям, которые удаляются от приближающегося полюса. Следовательно, индуцированное магнитное поле должно иметь силовые линии, идущие вниз внутри петли. Направление тока, указанное стрелками на контуре цепи, будет достигнуто. Проверьте это, используя Правило правой руки. Положите большой палец правой руки в направлении одной из стрелок и обратите внимание на то, что поле закручивается вниз в область, ограниченную петлей.
На второй диаграмме южный полюс удаляется. Это означает, что поле магнита станет слабее. Отклик на индуцированный ток будет заключаться в создании магнитного поля, которое добавляется к существующему от магнитного поля, чтобы противостоять его уменьшению в силе.
Другой способ представить ту же функцию – просто использовать полюса. Чтобы противостоять приближающемуся южному полюсу, индуцируемый ток создает поле, которое выглядит как другой южный полюс со стороны приближающегося южного полюса.Подобно отталкиванию полюсов, вы можете представить себе, как течение создает южный полюс, чтобы отразить приближающийся южный полюс. На второй панели ток устанавливает северный полюс, чтобы привлечь южный полюс и остановить его движение.
Мы также можем использовать вариант правила правой руки, помещая пальцы в направлении течения, чтобы большой палец указывал в направлении силовых линий (или северного полюса).
Мы можем проверить все это на случаях, когда северный полюс приближается или удаляется от цепи.В первом случае приближения северного полюса ток будет сопротивляться изменению, создавая поле в направлении, противоположном полю, исходящему от магнита, который становится сильнее. Используйте Правило правой руки, чтобы убедиться, что стрелки создают поле с линиями поля, которые изгибаются вверх в замкнутой области, нейтрализуя те, которые изгибаются вниз от северного полюса магнита.
Подобно тому, как полюса отталкиваются, в качестве альтернативы проверьте, что если поместить пальцы правой руки в направлении течения, ваш большой палец будет указывать вверх, указывая на северный полюс.
Для второго рисунка, где северный полюс удаляется, ситуация обратная.
Направление индуцированного тока в соленоиде (ESBQ3)
Подход к изучению направления тока в соленоиде аналогичен подходу, описанному выше. Единственная разница в том, что в соленоиде есть несколько витков проволоки, поэтому величина наведенной ЭДС будет другой. Поток будет рассчитан с использованием площади поверхности соленоида, умноженной на количество петель.
Помните: направления токов и связанных с ними магнитных полей можно найти, используя только Правило правой руки. Когда пальцы правой руки направлены в направлении магнитного поля, большой палец указывает в направлении тока. Когда большой палец направлен в направлении магнитного поля, пальцы указывают в направлении тока.
Направление тока будет таким, чтобы препятствовать изменению. Мы бы использовали установку, как в этом скетче, для проведения теста:
В случае, когда северный полюс направлен к соленоиду, ток будет течь так, чтобы северный полюс установился на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте, используя Правило правой руки):
В случае, когда северный полюс движется от соленоида, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс движется от соленоида, ток будет течь так, что северный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс подводится к соленоиду, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его:
Простой способ создать магнитное поле изменяющейся интенсивности – переместить постоянный магнит рядом с проволокой или катушкой с проволокой.Магнитное поле должно увеличиваться или уменьшаться по напряженности перпендикулярно проводу (так, чтобы силовые линии магнитного поля «пересекали» проводник), иначе не будет индуцироваться напряжение.
Индуцированный ток создает магнитное поле. Индуцированное магнитное поле имеет направление, которое стремится нейтрализовать изменение магнитного поля в петле из проволоки. Итак, вы можете использовать Правило правой руки, чтобы найти направление индуцированного тока, помня, что индуцированное магнитное поле противоположно направлению изменения магнитного поля.
Индукция
Электромагнитная индукция находит практическое применение в конструкции электрических генераторов, которые используют механическую энергию для перемещения магнитного поля мимо катушек с проволокой для генерации напряжения. Однако это далеко не единственное практическое применение этого принципа.
Если мы вспомним, магнитное поле, создаваемое проводом с током, всегда перпендикулярно проводу, и что сила потока этого магнитного поля изменяется в зависимости от величины тока, который проходит через него.Таким образом, мы можем видеть, что провод может создавать напряжение на своей собственной длине , если ток изменяется. Этот эффект называется самоиндукцией . Самоиндукция – это когда изменяющееся магнитное поле создается изменением тока через провод, вызывая напряжение по длине того же провода.
Если магнитный поток усиливается путем сгибания проволоки в форме катушки и / или наматывания этой катушки на материал с высокой проницаемостью, этот эффект самоиндуцированного напряжения будет более интенсивным.Устройство, предназначенное для использования этого эффекта, называется индуктором .
Помните, что индуцированный ток создает магнитное поле, которое противодействует изменению магнитного потока. Это известно как закон Ленца.
Рабочий пример 1: Закон Фарадея
Рассмотрим плоскую квадратную катушку с 5 витками. Катушка находится в \ (\ text {0,50} \) \ (\ text {m} \) с каждой стороны и имеет магнитное поле \ (\ text {0,5} \) \ (\ text {T} \) проходящий через него. Плоскость катушки перпендикулярна магнитному полю: поле направлено за пределы страницы.Используйте закон Фарадея для вычисления наведенной ЭДС, если магнитное поле увеличивается равномерно от \ (\ text {0,5} \) \ (\ text {T} \) до \ (\ text {1} \) \ (\ текст {T} \) в \ (\ text {10} \) \ (\ text {s} \). Определите направление индуцированного тока.
Определите, что требуется
Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.
Запишите закон Фарадея
\ [\ mathcal {E} = – N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под прямым углом к поверхности и поэтому выровнено с нормалью.Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \). Начальное или начальное магнитное поле, \ (B_i \), задается как конечная величина поля, \ (B_f \). Мы хотим определить величину ЭДС, чтобы можно было игнорировать знак минус.
Площадь \ (A \) – это площадь квадратной катушки. 2 (\ text {1} – \ text {0,50})} {\ text {10}} \\ & = \ текст {0,0625} \ текст {V} \ end {выровнять *}
Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.
Рабочий пример 2: закон Фарадея
Рассмотрим соленоид из 9 витков с неизвестным радиусом \ (r \). На соленоид действует магнитное поле \ (\ text {0,12} \) \ (\ text {T} \). Ось соленоида параллельна магнитному полю. Когда поле равномерно переключается на \ (\ text {12} \) \ (\ text {T} \) в течение 2 минут, ЭДС величиной \ (- \ text {0,3} \) \ (\ text {V} \) индуцируется. Определите радиус соленоида.
Определите, что требуется
Требуется определить радиус соленоида.Мы знаем, что связь между наведенной ЭДС и полем регулируется законом Фарадея, который включает геометрию соленоида. Мы можем использовать это соотношение, чтобы найти радиус.
Запишите закон Фарадея
\ [\ mathcal {E} = – N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под прямым углом к поверхности и поэтому выровнено с нормалью. Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \).{- \ text {2}} \) \ (\ text {m} \). Соленоид подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \ (\ text {0,4} \) \ (\ text {T} \) до \ (\ text {3,4} \) \ (\ text { T} \) в интервале \ (\ text {27} \) \ (\ text {s} \). Ось соленоида составляет угол \ (\ text {35} \) \ (\ text {°} \) к магнитному полю. Найдите наведенную ЭДС.
Определите, что требуется
Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.
Запишите закон Фарадея
\ [\ mathcal {E} = – N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под углом к нормали к поверхности.{- \ text {3}} \ text {V} \ end {выровнять *}
Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.
Реальные приложения
Следующие устройства используют в своей работе закон Фарадея.
Плиты индукционные
магнитофонов
металлоискатели
трансформаторы
Реальные применения закона Фарадея
Выберите одно из следующих устройств и поищите в Интернете или библиотеке, как работает ваше устройство.В объяснении вам нужно будет сослаться на закон Фарадея.
Плиты индукционные
магнитофонов
металлоискатели
трансформаторы
Практика Сиявула дает вам доступ к неограниченному количеству вопросов с ответами, которые помогут вам в обучении. Тренируйтесь где угодно, когда угодно и на любом устройстве!
Зарегистрируйтесь, чтобы практиковаться сейчасЗакон Фарадея
Упражнение 10.2Изложите закон электромагнитной индукции Фарадея словами и запишите математическое соотношение.
ЭДС \ (\ mathcal {E} \), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь A контура. Математически это можно выразить как:
\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]где \ (\ phi = B · A \), а B – напряженность магнитного поля.\ (N \) – количество контуров схемы. Магнитное поле измеряется в теслах (Тл). Знак минус указывает направление и то, что наведенная ЭДС имеет тенденцию противодействовать изменению магнитного потока. Знак минус можно не учитывать при вычислении звездных величин.
Опишите, что происходит, когда стержневой магнит вдавливается в соленоид, подключенный к амперметру, или вытягивается из него. Нарисуйте картинки, подтверждающие ваше описание.
В случае, когда северный полюс направлен к соленоиду, ток будет течь так, чтобы северный полюс установился на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте, используя Правило правой руки):
В случае, когда северный полюс движется от соленоида, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс движется от соленоида, ток будет течь так, что северный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:
В случае, когда южный полюс подводится к соленоиду, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его:
Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.
Поток связан с магнитным полем:
\ (\ phi = BA \ cos \ theta \)Если \ (\ cos \ theta \) равно 0, то магнитный поток будет равен 0, даже если есть магнитное поле. В этом случае магнитное поле параллельно поверхности и не проходит через нее.
Используйте Правило правой руки, чтобы определить направление индуцированного тока в соленоиде ниже.
Южный полюс магнита приближается к соленоиду.Закон Ленца говорит нам, что ток будет течь, чтобы противодействовать изменению. Южный полюс на конце соленоида будет противодействовать приближающемуся южному полюсу. Ток будет циркулировать по странице в верхней части катушки, так что большой палец правой руки будет указывать влево.
Рассмотрим круговую катушку из 5 витков с радиусом \ (\ text {1,73} \) \ (\ text {m} \). Катушка подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \ (\ text {2,18} \) \ (\ text {T} \) до \ (\ text {12,7} \) \ (\ text { T} \) в интервале \ (\ text {3} \) \ (\ text {minutes} \). {2} & = \ текст {0,0479} \\ г & = \ текст {0,22} \ текст {м} \ end {выровнять *}
Найдите изменение потока, если ЭДС равна \ (\ text {12} \) \ (\ text {V} \) за период \ (\ text {12} \) \ (\ text {s} \) .
\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ 12 & = 5 \ left (\ frac {\ Delta \ phi} {12} \ right) \\ \ Delta \ phi & = \ text {28,8} \ text {Wb} \ end {выровнять *}
Если угол изменить на \ (\ text {45} \) \ (\ text {°} \), на какой временной интервал нужно изменить, чтобы наведенная ЭДС оставалась прежней?
\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ & = N \ frac {\ phi_ {f} – \ phi_ {i}} {\ Delta t} \\ & = N \ frac {B_ {f} A \ cos \ theta – B_ {i} A \ cos \ theta} {\ Delta t} \\ & = \ cos \ theta \ times N \ frac {B_ {f} A – B_ {i} A} {\ Delta t} \ end {выровнять *}Все значения остаются неизменными в двух описанных ситуациях, за исключением угла и времени.Мы можем приравнять уравнения для двух сценариев:
\ begin {align *} \ mathcal {E} _1 & = \ mathcal {E} _2 \\ \ cos \ theta_1 \ times N \ frac {B_ {f} A – B_ {i} A} {\ Delta t_1} & = \ cos \ theta_2 \ times N \ frac {B_ {f} A – B_ {i} A } {\ Delta t_2} \\ \ cos \ theta_1 \ frac {1} {\ Delta t_1} & = \ cos \ theta_2 \ frac {1} {\ Delta t_2} \\ \ Delta t_2 & = \ frac {\ Delta t_1 \ cos \ theta_2} {\ cos \ theta_1} \\ \ Delta t_2 & = \ frac {(\ text {12} \ cos (\ text {45}} {\ cos (\ text {23})} \\ \ Delta t_2 & = \ text {9,22} \ text {s} \ end {выровнять *}Правило правой руки | PASCO
Правило правой руки в физике
Правило правой руки – это мнемоника руки, используемая в физике для определения направления осей или параметров, указывающих в трех измерениях.Правило правой руки, изобретенное в XIX веке британским физиком Джоном Амброузом Флемингом для применения в электромагнетизме часто используется для определения направления третьего параметра, когда известны два других (магнитное поле, ток, магнитная сила). Есть несколько вариантов правила правой руки, которые объясняются в этом разделе.
Когда проводник, такой как медный провод, движется через магнитное поле (B), в проводнике индуцируется электрический ток (I).Это явление известно как закон индукции Фарадея. Если проводник перемещается внутри магнитного поля, то существует соотношение между направлениями движения (скорости) проводника, магнитного поля и индуцированного тока. Мы можем использовать правило правой руки Флеминга исследовать закон индукции Фарадея, который представлен уравнением:
ЭДС = индуцированная ЭДС (V или J / C)
N = количество витков катушки
Δ𝚽 B = изменение магнитного потока (Тм2)
Δ t = изменение во времени (с)
Поскольку оси x, y и z перпендикулярны друг другу и образуют прямые углы, правило правой руки можно использовать для визуализации их выравнивание в трехмерном пространстве.Чтобы использовать правило правой руки, начните с создания L-образной формы с помощью большого пальца правой руки, указателя и середины. Палец. Затем переместите средний палец внутрь к ладони так, чтобы он был перпендикулярен указательным и большим пальцам. Твоя рука должно выглядеть примерно так:
На диаграмме выше большой палец совмещен с осью z, указательный палец – с осью x, а средний палец – с осью y.
Беспроводная интеллектуальная тележка
Один из лучших способов помочь учащимся обрести уверенность в использовании правила правой руки – это провести наглядную демонстрацию, которая поможет им распознать и исправить свои неправильные представления об ортогональных отношениях и системах координат.
Многие учителя используют вращающуюся линейку, чтобы показать, что объект, который кажется вращающимся «по часовой стрелке» с точки зрения одного ученика, также кажется вращающимся «против часовой стрелки», если смотреть с другой точки зрения. Использование динамической тележки для обучения правилу правой руки позволяет преподавателям продемонстрировать как проблему с помощью терминологии «по часовой стрелке», так и «против часовой стрелки», а также решение, которое обеспечивают правило правой руки и оси вращения. С беспроводной интеллектуальной тележкой преподаватели могут использовать 3-осевой гироскоп и фиксированную систему координат для создания увлекательных демонстраций вращательного движения.Ознакомьтесь с полной демонстрацией здесь.Правило правой руки для магнетизма
Подвижные сборы
Заряженная частица – это частица с электрическим зарядом. Когда неподвижная заряженная частица существует в магнитном поле, она не испытать магнитную силу; однако, как только заряженная частица движется в магнитном поле, она испытывает наведенное магнитное поле. сила, которая смещает частицу с ее первоначального пути. Это явление, также известное как сила Лоренца, согласуется с правилом, что утверждает, что «магнитные поля не работают.”Уравнение, используемое для определения величины магнитной силы, действующей на заряженную частицу (q) перемещение магнитного поля (B) со скоростью v под углом θ составляет:
Если скорость заряженной частицы параллельна магнитному полю (или антипараллельна), то силы нет, потому что sin (θ) равен нулю. Когда это происходит, заряженная частица может сохранять прямолинейное движение даже в присутствии сильного магнитного поля.
Плоскость, образованная направлением магнитного поля и скоростью заряженной частицы, расположена под прямым углом к силе.Поскольку сила возникает под прямым углом к плоскости, образованной скоростью частицы и магнитным полем, мы можем использовать правило правой руки, чтобы определить их ориентацию.
Правило правой руки гласит: чтобы определить направление магнитной силы на положительный движущийся заряд, направьте большой палец правой руки в направление скорости (v), указательный палец в направлении магнитного поля (B) и средний палец будут указывать в направление результирующей магнитной силы (F).На отрицательные заряды будет действовать сила в противоположном направлении.
Магнитная сила, индуцированная током: ток в прямом проводе
Обычный ток состоит из движущихся зарядов, которые имеют положительный характер. Когда обычный ток проходит по проводящему проводу, на провод действует магнитное поле, которое его толкает. Мы можем использовать правило правой руки, чтобы определить направление силы, действующей на токоведущий провод. В этой модели ваши пальцы указывают в направлении магнитного поля, а большой палец – в направлении магнитного поля. обычный ток, протекающий через провод, и ваша ладонь указывает направление, в котором провод проталкивается (сила).
Магнитная сила, действующая на провод с током, определяется уравнением:
Когда длина провода и магнитное поле расположены под прямым углом друг к другу, уравнение принимает следующий вид:
F B = магнитная сила (Н)
I = ток (A)
L = длина провода (м)
B = магнитное поле (Тл)
Если рассматривать протекание тока как движение носителей положительного заряда (обычный ток) в приведенном выше image, мы замечаем, что обычный ток движется вверх по странице.Поскольку обычный ток состоит из положительных зарядов, то тот же провод с током также может быть описан как имеющий ток с отрицательным носители заряда движутся вниз по странице. Хотя эти токи движутся в противоположных направлениях, один наблюдается магнитная сила, действующая на провод. Следовательно, сила действует в том же направлении, независимо от того, рассмотрите поток положительных или отрицательных носителей заряда на изображении выше. Применение правила правой руки к направление обычного тока указывает направление магнитной силы, которое должно быть направлено вправо.Когда мы рассматриваем поток отрицательных носителей заряда на изображении выше, правило правой руки указывает на то, что направление силы, которую нужно оставить; однако отрицательный знак меняет результат на противоположный, указывая на то, что направление магнитной силы действительно указывает вправо.
Если мы рассмотрим поток зарядов в двух разных проводах, один с положительными зарядами, текущими вверх по странице, а другой с отрицательными зарядами, текущими вверх по странице, то направление магнитных сил не будет таким же, потому что мы рассматриваем две разные физические ситуации.В первом проводе поток положительных зарядов вверх по странице указывает на то, что по странице стекают отрицательные заряды. Правило правой руки говорит нам, что магнитный сила укажет в правильном направлении. По второму проводу вверх по странице текут отрицательные заряды, которые означает, что положительные заряды стекают по странице. В результате правило правой руки показывает, что магнитная сила указывает в левом направлении.
Токи, индуцированные магнитными полями
В то время как магнитное поле может быть индуцировано током, ток также может быть индуцирован магнитным полем.Мы можем использовать второе правило правой руки, иногда называемое правилом захвата правой руки, для определения направления магнитного поле, созданное током. Чтобы использовать правило захвата правой рукой, направьте большой палец правой руки в направлении течения. течь и скручивай пальцы. Направление ваших пальцев будет отражать направление искривления индуцированного магнитного поля.
Правило захвата правой рукой особенно полезно для решения проблем, связанных с токоведущим проводом или соленоидом. В обеих ситуациях правило захвата правой рукой применяется к двум приложениям закона оборота Ампера, который связывает интегрированное магнитное поле вокруг замкнутого контура к электрическому току, проходящему через плоскость замкнутого контура.
Направление вращения: соленоиды
Когда электрический ток проходит через соленоид, он создает магнитное поле. Чтобы использовать правило захвата правой рукой в проблема с соленоидом, укажите пальцами в направлении обычного тока и оберните пальцы, как будто они были вокруг соленоида. Ваш большой палец будет указывать в направлении силовых линий магнитного поля внутри соленоида. Примечание что силовые линии магнитного поля вне соленоида направлены в противоположном направлении. Они охватывают изнутри, чтобы снаружи соленоида.
Направление вращения: токоведущие провода
Когда электрический ток проходит по прямому проводу, он индуцирует магнитное поле. Чтобы применить правило захвата правой рукой, совместите большой палец с направлением обычного тока (от положительного к отрицательному), и ваши пальцы будут указывать направление магнитных линий потока.
Правило правой руки для крутящего момента
Проблемы с крутящим моментом часто являются самой сложной темой для студентов-первокурсников-физиков.К счастью, есть правило правой руки приложение для крутящего момента. Чтобы использовать правило правой руки в задачах с крутящим моментом, возьмите правую руку и наведите ее на направление вектора положения (r или d), затем поверните пальцы в направлении силы, и большой палец укажет в направлении крутящего момента.
Уравнение для расчета величины вектора крутящего момента для крутящего момента, создаваемого заданной силой:
Когда угол между вектором силы и плечом момента является прямым, синусоидальный член становится 1 и уравнение становится:
F = сила (Н)
𝜏 = крутящий момент (Нм)
r = расстояние от центра до линии действия (м)
Положительный и отрицательный крутящие моменты
Моменты, возникающие против часовой стрелки, являются положительными.В качестве альтернативы крутящие моменты, возникающие в по часовой стрелке – отрицательные моменты. Так что же произойдет, если ваша рука укажет на бумагу или из нее? Крутящие моменты, которые лицевой стороной из бумаги следует анализировать положительный крутящий момент, в то время как крутящий момент, направленный внутрь, следует анализировать. как отрицательные моменты.
Правило правой руки для перекрестного произведения
Перекрестное произведение или векторное произведение создается, когда упорядоченная операция выполняется над двумя векторами, a и b. В векторное произведение векторов a и b перпендикулярно как a, так и b и перпендикулярно плоскости, которая его содержит.С есть два возможных направления для перекрестного произведения, для определения направления следует использовать правило правой руки вектора кросс-произведения.
Например, векторное произведение векторов a и b можно представить с помощью уравнения:
(произносится как «крест б»)
Чтобы применить правило правой руки к перекрестным произведениям, выровняйте пальцы и большой палец под прямым углом. Затем укажите свой индекс пальцем в направлении вектора a и средним пальцем в направлении вектора b.Ваш большой палец правой руки укажет в направлении векторного произведения a x b (вектор c).
Правило правой руки по закону Ленца
Закон электромагнитной индукции Ленца – еще одна тема, которая часто кажется нелогичной, поскольку требует понимание того, как магнетизм и электрические поля взаимодействуют в различных ситуациях. Закон Ленца гласит, что направление тока, индуцируемого в замкнутом проводящем контуре изменяющимся магнитным полем (закон Фарадея), такова, что вторичное магнитное поле, создаваемое индуцированным током, противодействует начальному изменению магнитного поля, которое произвело Это.Так что это значит? Давайте разберемся с этим.
Когда магнитный поток через проводник с замкнутым контуром изменяется, он индуцирует ток внутри контура. Индуцированная ток создает вторичное магнитное поле, которое противодействует первоначальному изменению потока, которое инициировало индуцированный ток. Сила магнитного поля, проходящего через катушку из проволоки, определяет магнитный поток. Магнитный поток зависит от сила поля, площадь катушки и относительная ориентация между полем и катушкой, как показано в следующем уравнении.
𝚽 B = магнитный поток (Tm 2 )
B = магнитное поле (Тл)
Θ = угол между полем и нормалью (град.)
A = площадь контура (м 2 )
Чтобы понять, как закон Ленца повлияет на эту систему, нам нужно сначала определить, является ли начальное магнитное поле увеличение или уменьшение силы. Когда северный магнитный полюс приближается к петле, это вызывает существующее магнитное поле. поле для увеличения.Поскольку магнитное поле увеличивается, индуцированный ток и результирующее индуцированное магнитное поле будут противодействовать исходному магнитному полю, уменьшая его. Это означает, что первичное и вторичное магнитные поля будут возникать в противоположные направления. Когда существующее магнитное поле уменьшается, индуцированный ток и результирующее индуцированное магнитное поле поле будет противодействовать исходному, уменьшая магнитное поле, усиливая его. Таким образом, индуцированное магнитное поле будет иметь в том же направлении, что и исходное магнитное поле.
Чтобы применить правило правой руки к закону Ленца, сначала определите, увеличивается ли магнитное поле, проходящее через петлю, или уменьшается. Напомним, что магниты создают силовые линии магнитного поля, которые движутся от северного магнитного полюса в направлении магнитный южный полюс. Если магнитное поле увеличивается, то направление вектора индуцированного магнитного поля будет в обратном направлении. Если магнитное поле в контуре уменьшается, то вектор индуцированного магнитного поля будет происходят в том же направлении, чтобы заменить уменьшение исходного поля.Затем выровняйте большой палец в направлении индуцированное магнитное поле и скрученные пальцы. Ваши пальцы будут указывать в направлении индуцированного тока.
| | Эксперимент Фарадея по индукции магнитного поляКогда Майкл Фарадей сделал свое открытие электромагнитной индукции в 1831 году, он предположил, что изменяющееся магнитное поле необходимо для индукции тока в соседней цепи.Чтобы проверить свою гипотезу, он сделал катушку, обмотав бумажный цилиндр проволокой. Он подключил катушку к гальванометру, а затем перемещал магнит вперед и назад внутри цилиндра. Щелкните и перетащите магнит назад и вперед внутри катушки. Когда вы перемещаете магнит вперед и назад, обратите внимание, что стрелка гальванометра движется, указывая на то, что в катушке индуцируется ток. Также обратите внимание, что стрелка сразу же возвращается в ноль, когда магнит не движется.Фарадей подтвердил, что для возникновения электромагнитной индукции необходимо движущееся магнитное поле. НАЗАД К РУКОВОДСТВАМ ПО ЭЛЕКТРИЧЕСТВЕ И МАГНЕТИЗМУ Вопросы или комментарии? Отправить нам письмо.© 1995-2021, автор – Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей.Использование этого веб-сайта означает, что вы соглашаетесь со всеми юридическими положениями и условиями, изложенными владельцами.Этот веб-сайт обслуживается нашимКоманда разработчиков графики и веб-программирования в сотрудничестве с оптической микроскопией в Национальной лаборатории сильного магнитного поля . Последнее изменение: пятница, 31 марта 2017 г., 10:10Счетчик доступа с 6 сентября 1999 г .: 2175124 |
Закон Фарадея
Закон ФарадеяЗакон Фарадея
Закон Фарадея – одно из уравнений Максвелла.Закон Фарадея гласит, что абсолютная величина или величина обращения электрическое поле E вокруг замкнутого контура равно скорости изменения магнитный поток через область, ограниченную петлей. В приведенное ниже уравнение выражает закон Фарадея в математической форме.
ΔΦ B / Δt (через фиксированная площадь) = -Σ вокруг петли E ∙ ∆ r (при a фиксированное время)
Знак минус в этом уравнении говорит нам о направлении тираж.(См. Ниже.)
Когда магнитный поток через замкнутую область
при изменении петли Σ вокруг петли E ∙ ∆ r не равно нулю,
электрическое поле E циркулирует.
E ∙ ∆ r – работа, выполненная за
единичный заряд электрическим полем при перемещении заряда на расстояние ∆ r .
Если
петля – это настоящая проволочная петля, тогда есть фактическая работа, выполняемая индуцированным
поле на бесплатные начисления.
Σ вокруг петли E ∙ ∆ r – работа
на единицу заряда полем при однократном перемещении заряда по петле.
Это
ЭДС , наведенная ,
и измеряется в вольтах.
Индуцированная ЭДС вызывает протекание тока
без
разность потенциалов из-за разделенных зарядов.
ΔΦ B / Δt (через фиксированная площадь) = наведенная ЭДС
Индуцированное электрическое поле НЕ консервативное поле.Когда вы перемещаете заряд против индуцированного поле один раз по кругу, вам нужно работать. Но твоя работа НЕ хранится как потенциальная энергия. Вы не можете позволить электрическому полю работать, чтобы восстановиться энергия, которую вы потратили на перемещение заряда. Индуцированное электрическое поле исчезает как как только магнитный поток перестанет меняться. Работа, которую ты делаешь на заряд против индуцированного поля не локально хранится. Энергия может быть отведена в виде электромагнитная волна. Электромагнитные волны переносят энергию через свободное пространство.
Какое направление динамического (индуцированного) поля? Знак минус в уравнении, выражающем закон Фарадея, говорит нам о
направление индуцированного поля.
Есть простой способ запомнить это направление.
Циркуляция индуцированного поля равна ЭДС.
Любой текущий
течет в результате этой ЭДС создает магнитное поле, которое противодействует
изменения потока, которые его производят.
Это называется Закон Ленца.
Индуцированная ЭДС действует как противодействие изменению потока, которое произвести это.
Пример:
Магнит быстро перемещается к проволочной петле, как показано.
Поток через проволочную петлю увеличивается в направлении вниз.
Ток начинает течь
в петлю в направлении, указанном стрелкой.
Магнитное поле, создаваемое этим током
указывает вверх, противостоит потоку
изменения, которые его производят.
Магнитная сила из-за петли на магните действует, чтобы замедлить
приближающийся магнит.
Прелесть закона Ленца в том, что вам не нужно смотреть на детали. Если магнитный поток через проводник изменяется, токи будут течь встречно что бы ни вызвало изменение. Если какое-то относительное движение вызывает изменение потока, ток попытается остановить это относительное движение. Если изменение тока в цепь отвечает за изменение потока, тогда наведенная ЭДС будет пытаться предотвратить изменение тока в этой цепи.
Пожалуйста, смотрите: Электромагнитная индукция и закон Фарадея (Youtube)
Проблема:
Рассмотрим плоскую квадратную катушку с N = 5 витками.
Катушка имеет длину 20 см с каждой стороны и магнитное поле.
0,3 Тл.
Плоскость катушки перпендикулярна плоскости
магнитное поле: поле указывает за пределы страницы.
а) Если ничего не изменилось, какова наведенная ЭДС?
(б) Магнитное поле равномерно увеличивается от 0.От 3 до 0,8 Тл за 1 с.
Какова наведенная ЭДС в катушке, пока происходит изменение?
(c) При изменении магнитного поля ЭДС, индуцированная в катушке, вызывает
ток течь. Ток течет по часовой стрелке или против часовой стрелки?
вокруг катушки?
Решение:
- Рассуждение:
Если величина магнитного поля B изменяется, то поток Φ = BA изменяется, и возникает ЭДС. - Детали расчета:
(a) ЭДС индуцируется изменяющимся магнитным потоком.Если ничего изменяется, наведенная ЭДС равна нулю.
(б) Катушка имеет 5 витков. Каждый поворот имеет площадь A = (0,2 м) 2 . Начальный магнитный поток через каждый оборот катушки Φ 0 = B 0 A = 0,3 * (0,2) 2 Tm 2 = 0,012 Tm 2 .
Конечный магнитный поток через каждый виток катушки Φ ф = B f A = 0,8 * (0,2) 2 Tm 2 = 0,032 Tm 2 .
Суммарное изменение потока через катушку N (Φ ф – Φ 0 ), с N = 5. Индуцированная ЭДС
ЭДС = -N∆Φ / ∆t = -N (Φ f – Φ 0 ) / ∆t = [-5 * (0,032 -0,012) /1,0] V = -0,1 В.
(c) При изменении магнитного поля магнитный поток увеличивался. со страницы. По закону Ленца наведенная в петле ЭДС этим изменяющимся потоком образуется ток, который создает поле, противодействующее изменять.Поле, создаваемое током в катушке, указывает на страницу, противоположную направлению увеличения потока. Чтобы произвести поле на страницу, ток должен течь по кругу по часовой стрелке. согласно правилу правой руки.
Модуль 5: Вопрос 1
Стержневой магнит расположен перед горизонтальной проволочной петлей с его северный полюс, указывающий на петлю. Затем магнит отрывается от петля. Идет ли индуцированный ток в контуре по часовой стрелке или против часовой стрелки?
Обсудите это со своими однокурсниками на дискуссионном форуме!
Визуализируйте магнитное поле стержневого магнита.Как происходит поток этого
поле через проводную петлю поменять?
Самоиндукция
Если длинная катушка провода сечением A и длиной ℓ с N витками подключен или отключен от батареи, изменение магнитного потока через катушка производит наведенную ЭДС. Индуцированный ток создает магнитное поле, которое противодействует изменению магнитного потока. Величина наведенная ЭДС может быть рассчитана с помощью закона Фарадея.
- Магнитное поле внутри длинной катушки B = μ 0 (Н /) I.
- Поток через катушку равен NBA = μ 0 (N 2 /) IA.
- Изменение потока в единицу времени составляет μ 0 (N 2 /) A
∆I / ∆t = L * ∆I / ∆t, поскольку I – единственная величина
меняется со временем.
L = μ 0 (N 2 / ℓ) A называется собственная индуктивность катушки. В единицы индуктивности – Генри (Гн) .1 H = 1 Вс / А. - Индуцированная ЭДС равна ЭДС = -L * ∆I / ∆t, где знак минус является следствием закона Ленца.
Индуцированная ЭДС пропорциональна скорости изменения тока в катушка. Оно может быть в несколько раз больше напряжения источника питания. Когда выключатель в цепи, по которой проходит большой ток, размыкается, уменьшая ток до ноль за очень короткий промежуток времени, это может привести к искре. Все схемы имеют собственную индуктивность, и у нас всегда есть ЭДС = -L * ∆I / ∆t.Собственная индуктивность L зависит только от по геометрии схемы.
Проблема:
КатушкаА имеет собственную индуктивность 3 мГн, а ток через нее изменяется от 0,2 А. до 1,5 А за время 0,2 с. Найти величину средней наведенной ЭДС в катушке за это время.
Решение:
- Рассуждение:
ЭДС самоиндукции равна ЭДС = -L * ∆I / ∆t. - Детали расчета:
L = 3 мГн, ∆I / ∆t = (1.5 А – 0,2 А) / 0,2 с = 6,5 А / с.
э. Д. произвел это.
Проблема:
Круглая катушка с 25 витками проволоки диаметром 1 м. Он размещен с его ось вдоль направления магнитного поля Земли (величина 50 мкТл), а затем за 0,2 с он переворачивается на 180 на . Какая средняя ЭДС сгенерировано
Решение:
- Рассуждение:
Φ B = B ∙ A – поток B через область A. Первоначально B и A выровнены, наконец, они анти-выровнены. Точка товар меняет знак. - Детали расчета:
ЭДС = -∆Φ B / ∆t. Φ B (начальная) = NAB = 25 * π * (0,5 м) 2 50 * 10 -6 T = 9,82 * 10 -4 Tm 2 .
Φ B (окончательный) = -Φ B (начальный), так как катушка перевернута.
| ∆Φ B | = 2Φ B (начальное).
| ∆Φ B / ∆t | знак равно 2 * (9.82 * 10 -4 Tm 2 ) / (0,2 с) = 9,82 * 10 -3 В.
Проблема:
Катушка с 500 витками радиусом 0,5 м поворачивается на четверть оборота за 4,17. мс, изначально имеющая плоскость, перпендикулярную однородному магнитному полю. Найдите напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.
Решение:
- Рассуждение:
ЭДС = -∆Φ B / ∆t. Φ B = NABcosθ изменяется с NAB на 0 в 4.17 мс, так как θ изменяется от 0 до 90 o через 4,17 мс. - Детали расчета:
| ∆Φ B | = NAB = 500 * π * (0,5 м) 2 * B = (393 м 2 ) * Б.
Хотим
| emf | = | ∆Φ B / ∆t | = (393 м 2 ) / (4,17 * 10 -3 с) * B = (94174 м 2 / с) * B = 10000 В.
B = 0,1 Вс / м 2 = 0,1 Т.
Если вы пропускаете регулярные лекции, обратите внимание на эту видеолекцию.
Лекция 16: Электромагнитная индукция .
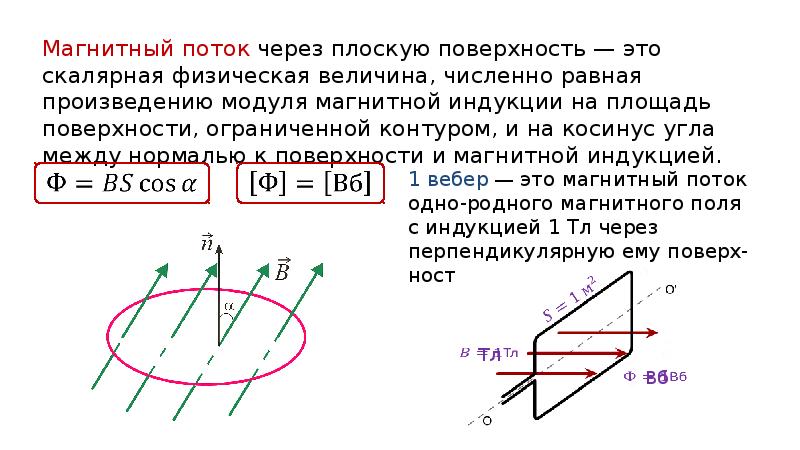 3)
3)