Как обозначается период вращения в физике: Криволинейное движение, вращение — урок. Физика, 7 класс.

HydroMuseum – Частота вращения

Частота вращения—физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — υ, f, ω или F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка «Сигналы, помехи, ошибки».

В теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается

ω). Циклическая частота связана с частотой колебаний соотношением ω=2πf. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с⁻¹, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т.  д.

Другие величины, связанные с частотой

• Ширина полосы частот — f_max − f_min
• Частотный интервал — log(f_max/ f_min)
• Девиация частоты —Δf/2
• Период — 1/f
• Длина волны — υ/f
• Угловая скорость (скорость вращения) — dφ/ dt; 2πF_BP

Метрологические аспекты

Измерения

Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра.

Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др.

Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.

Эталоны

Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ

Вторичный эталон единицы времени и частоты ВЭТ 1-10-82 — находится в СНИИМ (Новосибирск)

Период и частота обращения

Период и частота обращения

Цель урока: Ввести и изучить новые характеристики вращательного движения тела.

Ход урока

I. Повторение. Проверка домашнего задания

Урок можно начать с краткого опроса по теме предыдущего урока:

• Как меняется величина и направление скорости тела в равномерном движении по окружности?

• Что характеризует центростремительное ускорение?

• От каких величин зависит центростремительное ускорение?

• Какие точки поверхности Земли движутся с большим центростремительным ускорением: точки экватора или точки на широте 45°?

• Как меняется центростремительное ускорение, если при постоянной скорости уменьшается радиус окружности?

Во время опроса двое учеников выписывают на доске решения домашних задач. Затем решения коллективно обсуждаются, исправляются ошибки.

II. Изучение нового материала

План изложения нового материала:

1. Период вращения при движении по окружности;

2. Частота обращения при движении по окружности.

1. Переходя к изложению нового материала, нужно отметить, что он — логическое продолжение изученного на прошлом уроке.

Любое периодическое движение, а равномерное движение тела по окружности таким и является, характеризуется периодом и частотой вращения

Время, в течение которого совершается один полный оборот, называется периодом обращения.

В физике период обозначается буквой Т. Если за время t тело совершает 4 оборота, то время одного оборота будет равно: Т = t/4.

Пусть t = 10 с, тогда Т = t/4 = 2,5с.

Таким образом:

T = t

n

где t – время, n – число полных оборотов за время t.

В системе СИ период измеряется в секундах.

Т = (с)

2. Очень часто движение по окружности характеризуют частотой обращения. Она обозначается буквой ν (ν – ню).

Под частотой обращения ν понимают число оборотов за единицу времени. Пусть тело за время t = 2 с совершило n = 10 оборотов. Тогда частота обращения будет равна:

ν = n = 5

об = 5 с^-1

^{t с}

Очень легко найти связь между периодом и частотой:

Т = 1/ ν

Или:

ν = 1/Т

Формально, частота ν – величина, обратная периоду Т.

При равномерном движении тела по окружности, период или частоту можно найти и из иных соображений. Если тело движется по окружности радиуса R со скоростью ν, то период обращения можно найти из условия:

t = T = S /ν

где S – длина окружности, S = 2πR? Тогда:

T = S/ ν = 2πR/ ν

III.

Домашнее задание

1. § 6 учебника; вопросы и задания к параграфу;

2. Задачи и упражнения (учебник, стр. 126) № 32-35;

3. Сборник задач В.И. Лукашика, Е.В.Ивановой: № 170.

Вращательное движение | Блог Гэри Гарбера

 

До сих пор в этом семестре в рамках нашего изучения классической механики мы изучали поступательное движение. Теперь мы собираемся начать исследовать вращательное движение.

Каждая концепция, которую мы изучали до сих пор, имеет аналог вращения.

В начале года мы обсуждали, как объект может подвергнуться смещению x . Мы также можем повернуть объект на угол θ.

Точно так же скорость объекта или скорость изменения положения

имеет аналог вращения, скорость вращения, скорость изменения угла

ω=Δθ/Δt

Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости. Мы можем исследовать крутящий момент, который представляет собой вращательную силу. Момент инерции (или вращательная инерция) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения. Основываясь на этом, угловой момент – это вращательная инерция в состоянии вращательного движения. Мы также можем иметь кинетическую энергию вращения!

Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — изучить период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунд, часов, лет, эонов …) период показывает, сколько времени требуется для совершения одного полного оборота. Мы могли бы также описать, как часто объект вращается. Частота f объекта на самом деле является обратной величиной периода вращения.

Т=1/f

и

f =1/T

Единицей измерения частоты является Герц ( Гц ), где 1 Герц = 1 циклов/секунду . Вы, вероятно, знакомы с термином «Герц» по частотам на шкале радио, например, WBUR 90,9 МГц или WBZ 1030 кГц .

Пример

Представьте, что маленький мальчик пытается вызвать у себя головокружение, быстро вращаясь. Если он вращается с частотой 0,8 Гц, за сколько времени он сделает 1 оборот?

F = 0,8 Гц

T = 1/F = 1/0,8 Гц = 1/0,8 Циклы/второй = 1,25 секунд

Еще одна традиционная единица для частоты . или об/мин . Вы можете увидеть это на старомодном проигрывателе, который может вращаться со скоростью 33 или 45 об/мин .

 

А пока представьте двух маленьких человечков LEGO, стоящих на проигрывателе. Когда проигрыватель вращается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или скорости их вращения. Если мы установим проигрыватель на 45 оборотов в минуту, то оба человечка LEGO будут иметь одинаковую скорость вращения. Однако они имеют разные линейные или тангенциальные скорости. Мы используем слово «тангенциальный», потому что, если человечек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касательной к его круговому движению!

Мы можем рассчитать линейную скорость для каждого человека, используя уравнение

v=2πr/T

, где r — радиус окружности, а T — период вращения. Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.

Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:

Пример

f = 45 об/мин

r = 12 см

Сначала рассчитаем период. Поскольку 45 об/мин = 0,75 оборотов в секунду

Таким образом, период вращения равен 1,33 секунд .

Таким образом, скорость будет

v= 2πr/T = 2π (10 см )/ 1,33 с = 47 см/с

Для человечка, стоящего на расстоянии 4 см, он имеет гораздо меньшую линейную скорость при той же скорости вращения

v= 2πr/T = 2π (4 см )/ 1,33 с = 19 см/с

 

Существует тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.

Мы можем определить связь между линейной скоростью и угловой скоростью с помощью следующего уравнения

v = ω r

Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.

ω=Δθ/Δt

При рассмотрении приведенного выше уравнения возникает интересный вопрос о единицах измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно определить как ПОЛНЫЙ поворот на 360°.

Вероятно, вы изучали единицы измерения углов в градусах. Но когда мы говорим об угловой скорости, мы обычно не говорим о целом числе оборотов. Таким образом, нам пришлось бы использовать такие единицы, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартной единицей измерения на самом деле является радиан.

2π радиан = 360°

Если мы посмотрим на изображение единичного круга, то увидим преобразование между радианами и градусами. На самом деле это одно и то же, просто разные единицы измерения.

В каком-то смысле единственная разница между частотой и угловой скоростью составляет единицы. Угловая скорость измеряется в радиан/сек , а частота измеряется в Герц или оборотов/сек . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как

2πf = ω

Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об/мин .

ω = 2πf = 2π (0,75 об/сек ) = 4,7 радиан/сек

Пример

Вернемся к человечкам LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим

v = ω r

v = 4,7 радиан/сек x 10 см = 47 см/сек

и для человека ближе к центру

v = 4,7 радианы/секунду x 4 см = 19 см/с

Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом

Угол поворота и угловая скорость

Цели обучения

К концу этого раздела вы сможете:

• Определять длину дуги, угол поворота, радиус кривизны и угловую скорость.
• Рассчитайте угловую скорость вращения колеса автомобиля.

В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда – это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.

Угол поворота

Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 1 вращается вокруг своего центра, — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию.

Определим угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [латекс]\displaystyle\Delta\theta=\frac{\Delta{s}}{r}\\[/latex]

Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Все ямы вдоль линии от центра к краю перемещаются на один и тот же угол Δθ за время Δt .

Рис. 2. Радиус окружности повернут на угол

Δθ . Длина дуги Δs описана на окружности.

длина дуги   Δs  – это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что r  – это  радиус кривизны  круглой траектории.

Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиусом r . Длина окружности равна 2π r . Таким образом, для одного полного оборота угол поворота равен

[латекс]\displaystyle\Delta\theta=\frac{2\pi{r}}{r}=2\pi\\[/latex].

Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ до радиан  (рад), определенных таким образом, что 2π рад = 1 оборот.

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.

Таблица 1. Сравнение угловых единиц
Градусы	Измерение в радианах
30º	[латекс]\displaystyle\frac{\pi}{6}\\[/латекс]
60º	[латекс]\displaystyle\frac{\pi}{3}\\[/латекс]
90º	[латекс]\displaystyle\frac{\pi}{2}\\[/латекс]
120º	[латекс]\displaystyle\frac{2\pi}{3}\\[/латекс]
135º	[латекс]\displaystyle\frac{3\pi}{4}\\[/латекс]
180º	№

Рис. 3. Точки 1 и 2 поворачиваются на один и тот же угол (Δθ), но точка 2 перемещается по большей дуге (Δs), поскольку находится на большем расстоянии от центра вращения (r). 9{\circ}\\[/латекс].

Угловая скорость

Как быстро вращается объект? Мы определяем угловую скорость ω как скорость изменения угла. В символах это [латекс]\omega=\frac{\Delta\theta}{\Delta{t}}\\[/latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге длиной Δ с за время Δ t , поэтому она имеет линейную скорость [latex]v=\frac{\Delta{s}}{\Delta{t}}\\[/ латекс].

Из [латекс]\Delta\theta=\frac{\Delta{s}}{r}\\[/latex] мы видим, что Δ s  = r Δ θ . Подставляя это в выражение для v дает [латекс]v=\frac{r\Delta\theta}{\Delta{t}}=r\omega\\[/latex].

Мы запишем это отношение двумя разными способами и получим два разных понимания:

[latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex].

Первое соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] утверждает, что линейная скорость v пропорциональна расстоянию от центр вращения, таким образом, он является наибольшим для точки на ободе (наибольшая r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью . Второе соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости автомобиля v . См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большие против означают большие ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ( ω ), будет производить большую линейную скорость ( v ) для автомобиля.

Рис. 4. Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω.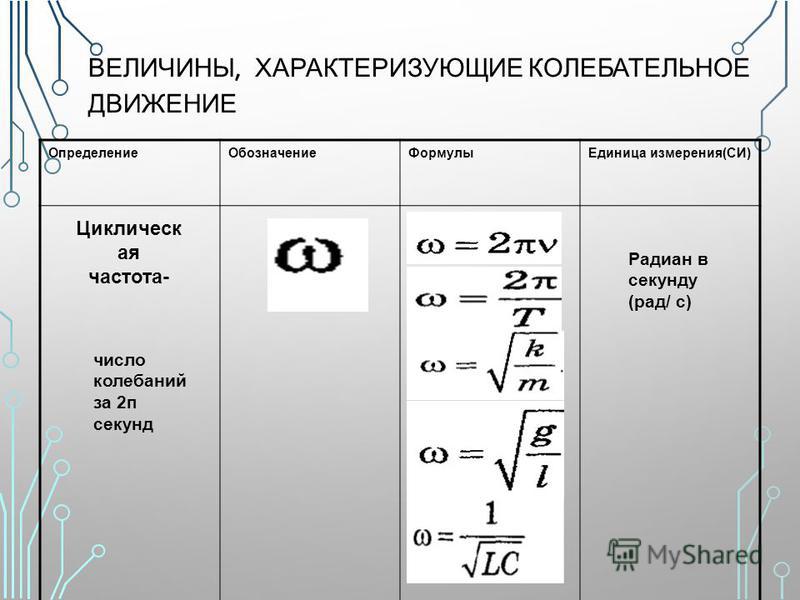 Скорость протектора шины относительно оси равна v , такая же, как если бы автомобиль были подняты. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.

Пример 1. Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). См. рис. 4.

Стратегия

Поскольку линейная скорость обода шины равна скорости автомобиля, мы имеем v = 15,0 м/с. Радиус шины равен 9.0025 r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex]v=r\omega\text{ или }\omega\frac{v}{r}\\[/latex] для вычисления угловой скорости .

Решение

Для расчета угловой скорости мы будем использовать следующую зависимость: [латекс]\омега\фрак{в}{г}\\[/латекс].

Подстановка известных,

[латекс]\omega=\frac{15,0 \text{ м/с}}{0,300\text{ м}}=50,0\text{ рад/с}\\[/latex].

Обсуждение

Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. У них будет угловая скорость [латекс]\omega=\frac{15,0\text{ м/с}}{1,20\text{ м}}=12,5\text{ рад/с}\\[/latex].

Оба ω и v имеют направления (следовательно, они являются угловой и линейной скоростями , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 5.

Самостоятельный эксперимент

Привяжите объект к концу веревки и раскачайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.

Рисунок 5. Когда объект движется по кругу, здесь муха на краю старой виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.

Исследования PhET: Революция божьей коровки

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой x ,  y положение, скорость и ускорение с использованием векторов или графиков.

Нажмите, чтобы загрузить. Запуск с использованием Java.

Резюме раздела

• Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота [латекс]\Delta\theta\\[/latex] определяется как отношение длины дуги к радиусу кривизны: [latex]\Delta\theta=\frac{\Delta{s}}{r }\\[/latex], где длина дуги Δ с — это расстояние, пройденное по круговой траектории, а 9{\circ}\\[/латекс].
• Угловая скорость ω — скорость изменения угла, [латекс]\omega=\frac{\Delta\theta}{\Delta{t}}\\[/latex], где вращение [латекс]\Delta\ theta\\[/latex] происходит во времени [latex]\Delta{t}\\[/latex]. Единицами угловой скорости являются радианы в секунду (рад/с). Линейная скорость v и угловая скорость ω связаны соотношением [latex]v=\mathrm{r\omega}\text{ или }\omega =\frac{v}{r}\text{.}[/latex]

Концептуальные вопросы

1. Существует аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости?

Задачи и упражнения

1. Полуприцепы имеют одометр на одной ступице колеса прицепа. Ступица утяжелена, чтобы не вращаться, но содержит шестерни для подсчета количества оборотов колеса — затем она рассчитывает пройденное расстояние. 6\text{ м}\\[/латекс] на экваторе, какова линейная скорость на поверхности Земли?
2. Бейсбольный питчер вытягивает руку вперед во время подачи, вращая предплечье вокруг локтя. Если скорость мяча в руке питчера 35,0 м/с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
3. В лакроссе мяч выбрасывается из сетки на конце клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча относительно локтевого сустава равна 30,0 рад/с, а мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
4. Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м/с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об/мин?
5. Интегрированные концепции. При ударе по футбольному мячу бьющий игрок вращает ногой вокруг тазобедренного сустава. (a) Если скорость носка ботинка игрока составляет 35,0 м/с, а тазобедренный сустав находится на расстоянии 1,05 м от носка ботинка, какова угловая скорость носка ботинка? (b) Башмак находится в контакте с изначально неподвижным футбольным мячом массой 0,500 кг в течение 20,0 мс.