Как обозначается вращающий момент в физике – Момент силы — Википедия

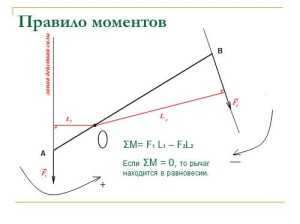
Крутящий момент – это… Что такое Крутящий момент?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

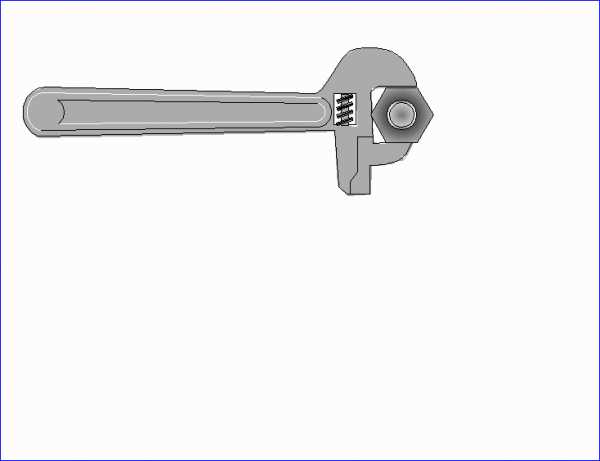
Момент силы приложенный к гаечному ключу

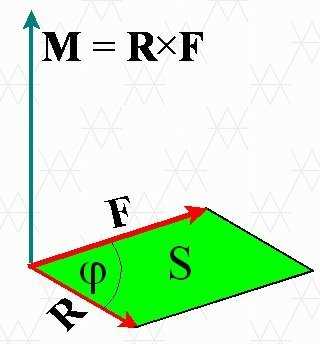
Отношение между векторами силы, момента силы и импульса во вращающейся системе

Момент силы

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки

O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

определения, единица измерения, примеры, относительно оси и точки

В статье мы расскажем про момент силы относительно точки и оси, определения, рисунки и графики, какая единица измерения момента силы, работа и сила во вращательном движении, а также примеры и задачи.

Момент силы представляет собой вектор физической величины, равный произведению векторов плеча силы (радиус-вектор частицы) и 

силы, действующей на точку. Силовой рычаг представляет собой вектор, соединяющий точку, через которую проходит ось вращения твердого тела с точкой, к которой приложена сила.

где: r — плечо силы, F — сила приложенная на тело. 

Направление вектора силы момента всегда перпендикулярно плоскости, определяемой векторами r и F.

Главный момент — любая система сил на плоскости относительно принятого полюса называется алгебраическим моментом момента всех сил этой системы относительно этого полюса.

Во вращательных движениях важны не только сами физические величины, но и то, как они расположены относительно оси вращения, то есть их моменты

. Мы уже знаем, что во вращательном движении важна не только масса, но и момент инерции. В случае силы, ее эффективность для запуска ускорения определяется способом приложения этой силы к оси вращения.

Взаимосвязь между силой и способом ее применения описывает МОМЕНТ СИЛЫ. Момент силы — это векторное произведение силового плеча R на вектор силы F:

Как в каждом векторном произведении, так и здесь

Следовательно, сила не будет влиять на вращение, когда угол между векторами силы F и рычагом R равен 0^o или 180^o. Каков эффект применения момента силы М?

Мы используем второй Закон движения Ньютона и связь между канатом и угловой скоростью v = Rω в скалярной форме, действительны, когда векторы R и ω перпендикулярны друг другу

Умножив обе части уравнения на R, получим

Поскольку mR ² = I, мы заключаем, что

Вышеуказанная зависимость справедлива и для случая материального тела. Обратите внимание, что в то время как внешняя сила дает линейное ускорение 

a, момент внешней силы дает угловое ускорение ε.

Единица измерения момента силы

Основной мерой измерения момента силы в системной координате СИ является: [M]=Н•м

В СГС: [M]=дин•см

Работа и сила во вращательном движении

Работа в линейном движении определяется общим выражением,

но во вращательном движении,

а следовательно

Исходя из свойств смешанного произведения трех векторов, можно записать

Поэтому мы получили выражение для работы во вращательном движении:

Мощность во вращательном движении:

Момент силы пример и решение задач относительно точки

Найдите момент силы, действующей на тело в ситуациях, показанных на рисунках ниже. Предположим, что r = 1m и F = 2N.

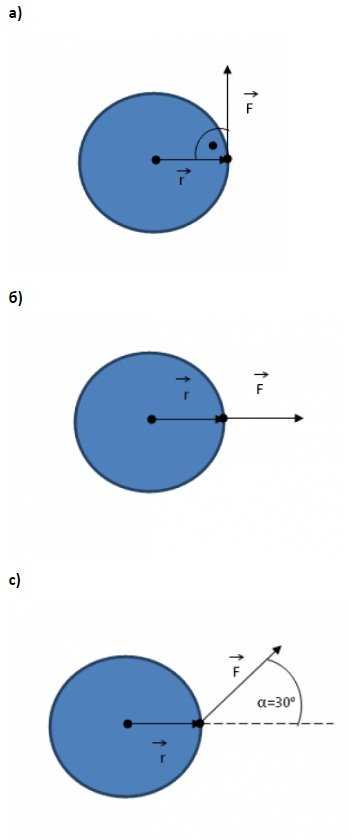
а) поскольку угол между векторами r и F равен 90°, то sin(a)=1: 

M = r • F = 1м • 2N = 2Н • м 

б) потому что угол между векторами r и F равен 0°, поэтому sin(a)=0: 

M = 0 
да направленная сила не может дать точке вращательное движение. 

c)    поскольку угол между векторами r и F равен 30°, то sin(a)=0.5: 

M = 0,5 r • F = 1Н • м. 

Таким образом, направленная сила вызовет вращение тела, однако ее эффект будет меньше, чем в случае a).

Момент силы относительно оси

Предположим, что данные являются точкой O (полюс) и мощность P. В точке O мы принимаем начало прямоугольной системы координат. Момент силы Р по отношению к полюсным O представляет собой вектор М из (Р), (рисунок ниже).

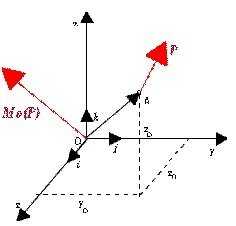
Любая точка A на линии P имеет координаты (xo , yo , zo ). 
Вектор силы P имеет координаты Px , Py, Pz. Комбинируя точку A (xo, yo, zo ) с началом системы, мы получаем вектор p. Координаты вектора силы P относительно полюса O обозначены символами Mx, My, Mz. Эти координаты могут быть вычислены как минимумы данного определителя, где ( i, j, k) — единичные векторы на осях координат (варианты): i, j, k

После решения определителя координаты момента будут равны:

Координаты вектора моментов Mo (P) называются моментами силы относительно соответствующей оси. Например, момент силы P относительно оси Oz окружает шаблон:

Mz = Pyxo — Pxyo

Этот паттерн интерпретируется геометрически так, как показано на рисунке ниже. 

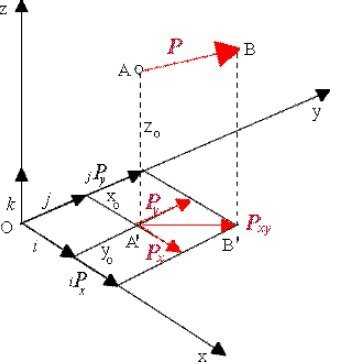
На основании этой интерпретации момент силы относительно оси Oz можно определить, как момент проекции силы P на перпендикуляр оси Oz относительно точки проникновения этой плоскости осью. Проекция силы P на перпендикуляр оси обозначена Pxy, а точка проникновения плоскости Oxy — осью Oс  символом O.
Из приведенного выше определения момента силы относительно оси следует, что момент силы относительно оси равен нулю, когда сила и ось равны, в одной плоскости (когда сила параллельна оси или когда сила пересекает ось). 
Используя формулы на Mx, My, Mz, мы можем рассчитать значение момента силы P относительно точки O и определить углы, содержащиеся между вектором M и осями системы:

Если сила лежит в плоскости Oxy, то zo = 0 и Pz = 0 (см. Рисунок ниже).

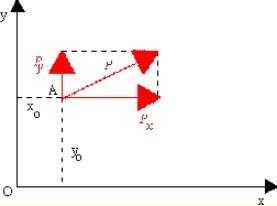
Момент силы P по отношению к точке (полюсу) O составляет: 
Mx = 0, 
My = 0, 
Mo (P) = Mz = Pyxo — Pxyo.

Метка крутящего момента: 
плюс (+) — вращение силы вокруг оси O по часовой стрелке, 
минус (-) — вращение силы вокруг оси O против часовой стрелки.

meanders.ru

Момент силы

Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта (оси, точки).

Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]

Аналогом момента силы является момент пары сил.

Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение

Момент определяется как произведение силы F на плечо h:

M(F)=F∙h

Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.

Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент M=7×0,35=2,45 кНм.

Пример момента силы

Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.

Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h3>h2).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

Рассмотрим порядок определения плеча h момента:

Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

Сила расположена перпендикулярно оси стержня

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

М_A=F×AB=F×3м

Сила расположена под углом к оси стержня

Момент силы относительно точки B:

M_B=F×cos30⁰×AB=F×cos30⁰×3м

Известно расстояние от точки до линии действия силы

Момент силы относительно точки B:

M_B=F×3м

---

См. также:

isopromat.ru

крутящий момент. объясните плиз простым русским языком, что такое крутящий момент в авто?

количество оборотов коленвала в минуту при котором выдается максимум лошадинных сил или ньютон метров

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов) В физике момент силы можно понимать как «вращающая сила» . В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение: где — сила, действующая на частицу, а — радиус-вектор частицы.

Простым русским языком объясняю-лишняя инфа в голове!

Когда тебя заносит и начинает крутить

Проще говоря это и есть тяга (тяговитость) мотора .

крутящий – в повороте закручивает кузов круголя

Это физическая величина измеряемая в ньютонах умноженных на метр, т. е. сила умноженная на плечо – длинну рычага

Крутящий момент двигает автомобиль вперёд..

момент это тяга. в салоне продают лошадей а везет момент. т. е. в первую очередь смотрите на момент.

Ты пропеллер видел у которого лопасть длинной в метр? Так вот скакой силой конец лопасти будет давить . Он может и бить, но это уже другое понятие.

блондинке ненадо, брюнэтке тоже. ложись уже не збивай себе головку…. удачи….

Это непросто. Потому, что сперва нужно понять – что такое крутящий момент вообще. Понятие довольно сложное, особенно для девушек, далеких от механики. Мысленный эксперимент. Представь себе на гладком скользком льду большую-большую шайбу. Представь, что ты тянешь за ниточку, закрепленную в разных местах шайбы. Когда нить приделана ближе к краю, шайба будет перемещаться за ниткой, и одновременно немного поворачиваться на льду. Совершать плоское движение. Когда нить проходит через центр тяжести шайбы – она поворачиваться не будет, а будет двигаться только поступательно вслед за ниткой. Внимание, вопрос: как нужно закрепить и тянуть за нитку, чтоб шайба только вращалась, не совершая никакого поступательного движения? Даже потянув за самый край мы, кроме вращения, непременно потянем шайбу за ниткой, переместив ее центр тяжести. После многих неудачных попыток приходим к важному выводу: С помощью действия одной силы невозможно заставить тело только вращаться. Поэтому в механике кроме “силы”, приходится вводить еще одну механическую сущность – “пару сил”. Две параллельные силы, равные по величине и направленные в противоположные стороны, называются парой сил. Пару сил нельзя заменить и уравновесить одной силой. Пара сил, при­ложенная к твердому телу, вызывает его “чистое вращение”, не перемещая центр тяжести. В нашем эксперименте нужно потянуть одновременно за две нитки в противоположные стороны, чтоб заставить шайбу вращаться на месте. Количественной мерой вращательного воздействия пары является ее момент. Тот самый крутящий момент. Авто – для того, чтоб он двигался, к колесу нужно приложить крутящий момент. Начинается он на коленвале двигателя. Поршень создает одну силу. Реакция подшипников – другую силу. Эта пара сил вращает коленвал своим крутящим моментом. Муфты, карданы, дифференциалы, КП – это все для того, чтоб довести крутящий момент до колеса, и управлять величиной этого момента. В конечном итоге – сила трения об асфальт заставляет крутящееся колесо двигаться, катиться и везти авто.

Простым русским и в двух словах будет примерно так, правда без математики никак. Итак, надо определить два понятия – сила/мощность и работа. По физической сути – работа (т. е. скорость движения авто и ускорение) есть произведение силы/мощности на время/расстояние. Отсюда очевидно, что чем быстрее разгон (ускорение) за фиксированное время, тем больше было приложенное усилие. Так вот физизическая суть крутящего момента в авто – то усилие, толкающее его вперед (фактически – сила уноженная на плечо) . ЗЫ: а вот мощность – это та самая сила/момент умноженная на количество оборотов коленвала.

Это сила которая ( измеряется в Ньютонах ) сможет вращать какую либо деталь то бишь колесо например или вал. Чем больше значение момента тем больше скорость. Насколько я помню 1Ньютон примерно равен 100 грамов веса. Для понятки если ВЫ приложите к колесу грузик весом 100грамм, то на него будет действовать крутящий момент равный 1Ньютону. Колесо провернется медленно ( потихоньку) , так как вес не большой 1 Ньтон. А если Вы приложите грузик весом в 1 КИЛОГРАММ то колесо провернется намного быстрее . Вот почему чем больше момент тем больше скорость детали в данном случае колеса. И машина поедит быстрее!

touch.otvet.mail.ru

что такое крутящий момент-дайте точную формулировку

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело. В физике момент силы можно понимать как «вращающая сила» . В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау) . Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние, до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние, до оси которого 6 метров.

Мощность и крутящий момент. Что это такое? Что такое мощность, знают все автомобилисты. И неплохо в этом pазбиpаются. Любой водитель скажет, что 100 л. с. вполне достаточно для компактного хэтчбека и маловато для тяжелого седана. И что 400 л. с. — это очень много для автомобиля любого типа. Но когда речь идет про кутящий момент и про «ньютон-метpы» , в которых он измеряется, возникает заминка. Например, 100 Нм — это много или мало? И почему «…очень хорошо, что мотор развивает 200 Hм всего при 1750 об/мин» ? Итак, речь пойдет о величине непонятной большинству водителей. Крутящий момент. Что это такое? Для начала вернемся к «лошадиным силам» . То есть к мощности. Этот показатель характеризует силу мотора. Однако запас силы зависит от оборотов. Наибольшую мощность современные моторы выдают в среднем при 5000–6500 об/мин. Но кто ездит в таких режимах? В обычной городской езде тахометр показывает 2000–3000 об/мин. Получается, если двигатель вашего автомобиля развивает порядка 100 л. с. почти на предельном режиме, то, двигаясь в городском потоке на средних оборотах, вы имеете в запасе около 40–50 сил. Теперь представим, что нужно обогнать грузовик. Сейчас вам потребуются все 100 л. с. мотора. Но их нельзя вот так сразу собрать в единый табун. Только постепенно: сначала двигатель раскрутится до 4000 об/мин — и поголовье под капотом увеличится примерно до 70 л. с. Затем стрелка тахометра доберется до отметки 5000 об/мин — в вашем распоряжении окажутся 90 лошадей. И только когда мотор достигнет пика, скажем в 6000 об/мин, педаль акселератора будет повелевать полноценными, обещанными по паспорту 100 лошадиными силами. В таких ситуациях и вступает в игру крутящий момент (далее КМ) . Это «пастух» , который на разгоне «сгоняет» в единую упряжку все лошадиные силы мотора. Чем больше КМ, тем быстрее двигатель набирает обороты. И тем скорее собирается в единый кулак вся мощь мотора. И соответственно, тем лучше ускоряется автомобиль. Второй важный нюанс — обороты, на которых мотор развивает максимальный КМ. Скажем максимум выдается при 4000 об/мин. До них и нужно раскрутить двигатель, чтобы рассчитывать на приличное ускорение. А разгоняться придется с тех самых 2000–3000 об/мин, которые поддерживаются при нормальной езде. Здесь-то и теряется время, столь драгоценное при том же обгоне. Другое дело, если максимальный КМ двигатель выдает, скажем, при 2000 об/мин. Тогда нет проблем. Вы просто давите на газ, и машина сразу напористо набирает ход, не теряя времени на раскрутку мотора. Теперь ясно, почему выгодно, чтобы двигатель выдавал много КМ на низких оборотах? И почему «…очень хоpошо, что мотор развивает максимальные 200 Hм всего пpи 1750 об/мин» ? В последнем контексте упор делается не столько на КМ как таковой, сколько на завидно малые обороты, при которых он развивается. Такие двигатели называют «тяговитыми» . Кстати, КМ впрямую зависит от литража. Наименее тяговиты моторы малолитражек. Например, на ВАЗ 2108 с объемом двигателя 1,5 л и ниже хороший КМ не получишь. Их водители часто переключаются на более низкие передачи, чтобы искусственно поддерживать высокие обороты. В противном случае мотор, как говорят автомобилисты, не тянет. Чтобы здесь получить «момент на низах» , необходимо увеличивать объем двигателя.

момент когда машина наварачивающая круги, несходя с места)

Не ломай голову, возьми дизель, там КМ наибольший. В городе будешь реже рычагом ворочать.

Роман Егоров наиболее доходчиво объяснил что такое крутящий момент, но тем не менее.. . Величина эта расчетная, в которую входит площадь поршня, максимальное давление в камере сгорания которое зависит от степени сжатия (и наддува в том числе) и длинна рычага на который воздействует эта сила. В характеристике указываются обороты МКМ, но на самом деле важен другой параметр – на сколько широко крутящий момент размазан по диапазону оборотов на уровне75% (у BMW M30, M50,M60 итд он от 2 до 6 тыс об, а у Toyota 2LT-E от 2300 до 3500)

Была бы пара, а момент найдётся! 🙂 (студенческая запоминалка)

touch.otvet.mail.ru

Крутящий момент двигателя – что это за характеристика и на какие параметры влияет

Контакты Menu Menu

• Главная
• Авто
  • • Audi
    • BMW
    • Cadillac
    • Chevrolet
    • Citroen
    • Ford
    • Geely
  • • Honda
    • Hyundai
    • Infiniti
    • Jaguar
    • Kia
    • Lada
    • Land Rover
  • • Lexus
    • Mazda
    • Mercedes
    • Mitsubishi

avtonam.ru

Момент силы, формулы

Определение 1

Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.

Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.

Момент силы выступает характеристикой вращательного воздействия силы на твердое тело. Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.

В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).

Понятие момента силы

Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.

Замечание 1

В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.

К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:

$\vec {M}=\vec{r}\vec{F}$, где:

• $\vec {F}$ представляет силу, воздействующая на частицу,
• $\vec {r}$ является радиусом вектора частицы.

В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н•м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:

$E = M\theta $, где:

• $E$ представляет энергию;
• $M$ считается вращающимся моментом;
• $\theta $ будет углом в радианах.

Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.

Формулы расчета момента силы

Интересным в физике является вычисление момента силы в поле, производимого по формуле:

$\vec{M} = \vec{M_1}\vec{F}$, где:

• $\vec{M_1}$ считается моментом рычага;
• $\vec{F}$ представляет величину действующей силы.

Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину. При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:

$\vec{T}=\vec{r}\vec{F}$

При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.

$P = \vec {M}\omega $

В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы— в ньютон-метрах. При этом угловая скорость определяется в радианах в секунду.

Момент нескольких сил

Замечание 2

При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия. Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).

В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.

Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.

$M={FL_1+FL-2} = F{L_1+L_2}=FL$

В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.

spravochnick.ru