Пример оформления задач по физике *
При решении задач по физике важно получить правильный ответ? Конечно. Однако нельзя забывать о требованиях, касающихся оформления. Правильный ответ при неверной записи условия, решения не гарантирует получение хорошей оценки. Чтобы добиться наиболее оптимального результата, нужно научиться оформлять задачи согласно существующим нормам. Для этого обязательно соблюдать следующий алгоритм.
СОДЕРЖАНИЕ
1. Внимательно прочитайте условие
Согласно статистике большая часть обучающихся допускает ошибки еще на этапе чтения условия задачи. Происходит это из-за невнимательности, нежелания вдуматься в текст. Такая халатность, даже при умении решать задачи по физике, нередко приводит к неверным результатам. Именно поэтому учителя-практики советуют ответственнее относиться к ознакомлению с условием задачи. Если соблюсти такое требование, то досадных ошибок можно избежать. В противном случае работа будет напрасной, результат – отрицательным.
2. Запись краткого условия
Запись условия задачи под заголовком «Дано» производится в левом столбике тетрадного листа. Это поле обозначается прямой линией. Для обозначения текстовой информации используются общепризнанные обозначения (к примеру, масса обозначается латинской буквой m, скорость – v). Рядом с буквенным обозначением указывается число, которое прозвучало в задании. Следует быть внимательным, так как нередко числа в условии нет, оно подразумевается. Например, читаем: «При кипении воды жидкость …. » (мы знаем, при какой температуре происходит), а записываем в «Дано» t + 100 °С.
Когда все данные, которые содержатся в условии, записаны, не спешите подводить черту в левой колонке. Нередко в процессе решения приходится дописывать какие-то еще дополнительные цифры и обозначения. Наличие свободного места в этой части задачи – не ошибка.
Важно! Числовые данные необходимо указывать вместе с единицами измерения. Если она должна быть представлена в виде дроби, ее именно так и нужно записывать.
Это обязательно! При несоблюдении данного правила преподаватели снижают оценку, даже если задача решена правильно.
Это обязательно! При несоблюдении данного правила преподаватели снижают оценку, даже если задача решена правильно.В «Дано» также обязательно следует указать, что именно нужно найти в итоге. Для этого используются не слова, а буквенные обозначения искомого. Если этого не сделать, ошибка неизбежна. Пренебрежение правилами приведет к снижению оценки.
3. Перевод единиц измерения в СИ
Рядом с колонкой «Дано» находится еще одна, не менее важная. Ее размер почти такой же. Называется она «СИ».
В задании могут прозвучать различные цифры и данные, которые необходимо перевести в общепринятую международную систему единиц физических величин. Даже если ничего переводить в систему СИ не нужно, колонка с этим названием должна быть записана.
4. Чертежи
Вполне возможно, что при решении задачи по физике понадобится чертеж. Это могут быть оси координат, вектора скорости, перемещения и прочее. В ряде случаев без них справиться с заданием не получится.
5. Запись решения.Запомните! Чертеж, даже если он выполняется «для себя», должен быть аккуратным, правильным.
Чтобы произвести все необходимые расчеты и найти искомые данные, можно воспользоваться двумя способами записи решения задачи:
— по действиям;
— вывести окончательную формулу и произвести окончательный расчет (учащимися 7-9 классами – по желанию, в 10-11 – обязательно).
Задача должна быть решена, поэтому выбор способа записи в этой части не столь важен.
Важно! Не можете решить задачу по физике, но понимаете примерно, что должно получиться в итоге? Попробуйте «распутать» ее с конца. Придется подумать, что нужно для того, чтобы рассчитать искомую величину.
6. Запись и проверка ответа
Одна из распространенных ошибок учеников и студентов – слишком короткая запись ответа. Формулировать ее нужно целой фразой, не забывая о правильности записи физической величины с полученным числовым значением.
Правильное оформление задачи по физике, все-таки, не самое главное.
Нужно уметь ее решать. Что делать, если правильно оформлены колонки «Дано» и «СИ», а с решением проблемы? Справиться с проблемой можно 2 способами: воспользоваться решебником, услугами учителя-физика или сторонней профессиональной помощью.
Однако в решебнике ответа к необходимой задаче можно и не найти, к тому же, гарантировать правильность записанного никто не будет. Обратиться за разъяснением к учителю физики, который сам же и задал ее решить? Это неудобно, по меньшей мере.
Поэтому наша компания предлагает свою помощь в решении и оформлении задач по физике. Услуга не ограничивается получением правильного ответа и записи условия. Специалист разъяснит ход решения, благодаря чему с однотипной задачей в следующий раз можно будет справиться самостоятельно.
Как обосновывать критерии в новой 30-ой задаче ЕГЭ по физике
Сохранить/поделиться:
Сделал файл со всеми шаблонами обоснований в новой 30ой задаче ЕГЭ по физике – лучше поздно, чем никогда
- Если задача на второй закон Ньютона, уравнение моментов, закон сохранения импульса или энергии, то нужно написать, что “рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной”.
- Если в задаче происходит движение тел и применяется второй закон Ньютона или закон сохранение импульса, или закон сохранения энергии, то пишем, что движущиеся тела мы считаем материальными точками (телами, размерами которых в данной задаче можно пренебречь). А далее, доказываем, почему именно:
а) Либо размер шарика много меньше нити, на которой он движется, либо радиуса закругленного жёлоба, по которому он скользит.
б) Либо тела движутся поступательно, поэтому к ним применима модель материальной точки независимо от их размеров. - Нужно написать: из пунктов 1 и 2 следует, что движение тел в ИСО описывается вторым законом Ньютона, если применяете данный закон.
- Если задача на уравнение моментов, то нужно написать:
а) применяем для тела модель твёрдого тела (форма и размеры тела неизменны, расстояние между любыми двумя точками тела остаётся неизменным).
б) любое движение твёрдого тела является суперпозицией поступательного и вращательного движений. Условий равновесия твёрдого тела в ИСО ровно два: одно для поступательного движения (сумма внешних сил равна нулю), другое – для вращательного (сумма моментов внешних сил равна нулю).
в) сумма приложенных к твёрдому телу внешних сил равна нулю (одно из условий равновесия тела), поэтому сумма моментов этих сил относительно любых двух параллельных осей одна и та же. Для удобства в качестве оси, относительно которой будем считать сумму моментов сил, действующих на тело, выберем ось, проходящую перпендикулярно плоскости рисунка через точку… (указать точку, от которой будете отсчитывать плечи сил).
г) напишите словами, про направление и точки приложения сил, действующих на тело, чтобы обосновать величины плеч для сил. Не забудьте про силы, плечо которых равно нулю, и они не участвуют обычно в уравнении моментов: например, сила реакции шарнира или опоры, на которой находится рычаг. Эти силы должны быть нарисованы на рисунке и словами сказано, почему их плечо равно нулю. - Если используется закон сохранения импульса, то вариантов обоснования несколько:
а) либо говорим про то, что вдоль оси, в проекции на которую записываем закон сохранения импульса, на систему не действуют внешние силы (если на самом деле не действуют). Расскажите подробно, какие силы дают проекцию ноль на выбранную ось, а какие силы в этой
системе являются внутренними. Если шарик висит на нити, а в него попадает пуля, то нужно написать, что за время их столкновения нить не успевает заметно отклониться от вертикали, поэтому проекция силы натяжения на горизонталь равна нулю.
б) либо у нас взрыв снаряда, который происходит очень быстро, а импульсы осколков меняются на конечную величину, поэтому силы расталкивающие осколки снаряда очень большие и действие силы тяжести вдоль вертикальной оси по сравнению с ними можно пренебречь.
в) либо у нас столкновение на шероховатой поверхности, которое происходит очень быстро, а импульсы брусков меняются на конечную величину, значит силы взаимодействия брусков очень большие, поэтому по сравнению с ними действием силы трения можно пренебречь.
Тогда после любого из пунктов а)-в), пишем: следовательно, систему шариков в направлении выбранной оси можно считать замкнутой и возможно применение закона сохранения импульса. Если в системе существуют объекты, масса которых много меньше, чем масса других объектов, то важно это написать и сказать, что изменением импульса этих объектов малой массы мы пренебрегаем. - Если используется закон сохранения энергии, то нужно написать:
«Изменение механической энергии системы тел в ИСО равно работе всех непотенциальных сил (например, силы трения, сопротивления воздуха, натяжения нити, силы нормальной реакции опоры), приложенных к телу.» Расскажите, какие из сил, действующих на тела, потенциальные, а какие – непотенциальные. Далее утверждение: “Работа непотенциальных сил равна нулю”.
Если есть силы натяжения нити и силы реакции опоры, то нужно доказать, почему именно работа этих сил равна нулю, а именно написать, что они в каждый момент времени перпендикулярны скорости тела. - Если в задаче есть тела, связанные нитью, то скорее всего пригодится фраза: “нить невесома, масса блока ничтожна, трения в блоке нет, поэтому модуль силы натяжения нити в любой её точке один и тот же” Обратите внимание:
а) в списке нет пункта о нерастяжимости нити, она здесь не нужна, писать её нельзя, пригодится в другом пункте для связи ускорений.
б) недостаточно просто написать, что блок и нить идеальные: без пояснений о том, что именно значит эта идеальность, балл за обоснование не поставят. - Если нужно связать ускорения двух тел, то пишем:
а) либо “нить нерастяжима, поэтому модули ускорений подвижного блока и тела m при их прямолинейном поступательном движении отличаются в 2 раза” (обычно ускорение подвижного блока в 2 раза меньше)
б) либо “нить нерастяжима, поэтому модули ускорений тел, связанных нитью, при их прямолинейном поступательном движении равны”
Обратите внимание: для связи ускорений нужна только нерастяжимость, или постоянство длины, если посередине нити находится пружина, а невесомость и отсутствие трения – это всё для пункта 7. - Если в условии есть фразы по типу “поверхность гладкая” (или другие модельные допущения), то нужно в обосновании написать, как вы используете эти допущения. Например, в случае “гладкой поверхности” нужно написать, что это значит отсутствие силы трения.
- Часто в задачах просят найти вес, а не силу нормальной реакции опоры, поэтому нужно будет написать, что эти две силы связаны 3-им законом Ньютона.
- Обратите внимание, как нужно доказывать, что угол падения равен углу отражения при абсолютно упругом ударе о поверхность:
Источник образцов оформления: рекомендации по проверке второй части ЕГЭ для экспертов 2022 года и «ЕГЭ. Физика: типовые экзаменационные варианты: 30 вариантов, под ред. М.Ю. Демидовой, издание от 2022 года, издательство «Национальное образование».
Будем считать эту систему отсчёта инерциальной”.
Эти силы должны быть нарисованы на рисунке и словами сказано, почему их плечо равно нулю.
Сохранить/поделиться:
Ближайшие вебинары
Предметы
Уровень
Будущие и прошедшие
февраль
16фев19:0020:00вебинарРазбор варианта №13/30 по сборнику Котовой-Лисковой [ЕГЭ ОБЩЕСТВОЗНАНИЕ-2023] от HistructorHISTRUCTOR19:00 – 20:00 Предметы:ИсторияУровень:ЕГЭ
17фев16:3017:30вебинарРазбор ПРОБНИКА 11.
Тестовая часть.Учим Учиться – ЕГЭ Математика и Русский язык 202216:30 – 17:30 Предметы:Русский языкУровень:ЕГЭ
17фев18:3019:30вебинарРазбор 29 варианта из сборника ЕГЭ 2023 по физике – Демидовой | Саня ЭбонитСаня Эбонит | Физика ЕГЭ | 100балльный репетитор18:30 – 19:30 Предметы:ФизикаУровень:ЕГЭ
Показать больше
Получать расписание
Каждое утро наш бот рассылает расписание бесплатных вебинаров по выбранным предметам.
Телеграм-бот
Последние посты
Если у вас есть собственный полезный текст, вы можете опубликовать его в этом блоге:
ньютоновская механика – Путаница в знаках при формулировании математических уравнений для задач физики
Сначала необходимо различать составляющую и величину вектора.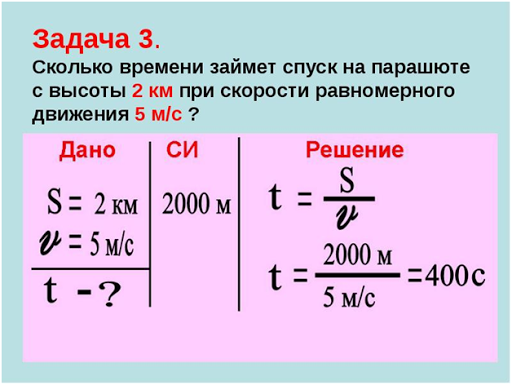
Величина всегда положительна, думайте о ней как о длине, и не имеет значения, как (слева направо или справа налево) вы измеряете длину.
Если компонент положительный, то он также равен величине.
Давайте посмотрим на ваше уравнение $m\,g-c\, v=m\, a$, но в его векторной форме, $m\,\vec g-c\, \vec v=m\, \vec a$ и предположим, что единичный вектор $\hat y$ направлен вниз.
$\bf m\vec g$
Вы знаете, что $\vec g$ указывает вниз, поэтому, если вы напишете $\vec g = g\,\hat d$, тогда $g$ будет величиной напряженности гравитационного поля.
$m \,\vec g \Rightarrow m\,g\,\hat d$, потому что численное значение $m$ положительно.
$\bf -c\, \vec v$
Почему этот термин написан именно так?
Это потому, что было решено, что сила трения всегда направлена против скорости.
Чтобы это работало, числовое значение $c$ определяется как положительное.
Если $\vec v = v\, \hat d$, где $v$ — составляющая скорости в направлении $\hat d$, то член $-c\,\vec v = -c\,v\, \hat y = c\,v\, (-\hat d)$ в противоположном направлении.
Обратите внимание, что это верно всегда, независимо от числового значения $v$.
$\bf m\,\vec a$
Как и скорость, направление ускорения может быть либо вниз, либо вверх, поэтому запишите его как $a\, \hat d$, где $a$ — составляющая ускорения в направлении $\hat d$.
Общий $m\,\vec g-c\, \vec v=m\, \vec a \Rightarrow m\, g\,\hat d – c\,v\,\hat d = m\,a\, \hat d \Rightarrow m\,g – c\, v = m\, a$.
Что делать, если положительное направление принято вверх?
Тогда единичный вектор равен $\hat u =(-\hat d) \Rightarrow \hat d = (-\hat u)$ ?
$ m\, g\,\hat d – c\,v\,\hat d = m\,a\, \hat d$ становится $m\, g\,(-\hat u) – c\, v\, (-\hat u) = m\,a\, (-\hat u) \rightarrow m\,g – c\, v = m\, a$, что является тем же уравнением, что и при вынесении за положительном направлении, за исключением того, что теперь $v$ и $a$ являются составляющими скорости и ускорения в направлении $\hat u$.
Таким образом, в конце концов, если $v$ оказывается равным $+30$ при использовании $\hat d$ как положительного, то окажется, что $-30$, если $\hat u$ было положительным направлением.
Мяч падает с крыши здания со скоростью, превышающей предельную скорость, и движется под действием сопротивления воздуха. Найти $v(t)$?
Уравнения, которые обсуждались выше, остаются в силе, и не имеет значения, больше или меньше скорость мяча, чем конечная скорость.
Если мяч брошен вниз, то составляющая силы трения будет направлена вверх, а если мяч брошена вверх, то составляющая силы трения будет направлена вниз.
Обратите внимание, что если мяч брошен вниз со скоростью, превышающей конечную скорость, сила трения вверх будет больше, чем сила гравитационного притяжения мяча к Земле.
Принимая $\hat d$ за положительное направление, это будет означать, что $mg – cv$ будет отрицательным, а значит, $a$, численное значение компонента ускорения в направлении $\hat d$, будет отрицательным.
Это, в свою очередь, означает, что ускорение направлено вверх, мяч замедлится и, в конце концов, достигнет конечной скорости.
Использование научной нотации в задачах по физике
Авторы: Стивен Хольцнер и
Обновлено: 26 марта 2016 г.
Рабочая тетрадь для чайников с онлайн-практикой Книга для изучения Купить на Amazon Физика имеет дело с очень большими и очень маленькими числами. Чтобы работать с такими числами, вы используете экспоненциальное представление . Научное представление выражается как число от 1 до 10, умноженное на степень 10. Например, предположим, что вы измеряете массу электрона в системе MKS. Вы кладете электрон на весы (на практике электроны слишком малы, чтобы их можно было измерить на весах — вам нужно увидеть, как они реагируют на притяжение магнитных или электростатических сил, чтобы измерить их массу), и вы измеряете следующее: Что это за чертовщина? Это много нулей, и это делает число очень громоздким для работы. К счастью, вы знаете все о научных обозначениях, поэтому можете преобразовать число в следующее: То есть 9,1 умножить на степень 10, 10 Например, 0,050 равно 5,0 x 10 –2 , потому что вы передвигаете десятичную точку на два знака вправо, чтобы получить 5,0. Точно так же 500 равно 5,0 х 10 2 , потому что вы переместили десятичную точку на два знака влево, чтобы получить 5.0. Что такое 0,000037 в экспоненциальном представлении? Правильный ответ: 3,7 x 10 –5 . Вы должны переместить запятую пять раз вправо, чтобы получить 3,7. Что такое 0,0043 в экспоненциальном представлении? Что такое 430 000,0 в экспоненциальном представлении? Что такое 0,00000056 в экспоненциальном представлении? Что такое 6700,0 в экспоненциальном представлении? Ниже приведены ответы на практические вопросы: 4,3 x 10–3 Вы должны переместить запятую на три позиции вправо. 0,0000000000000000000000000000000091 кг
9,1 x 10 –31 кг
Научная запись работает, извлекая степень 10 и помещая ее сбоку, где это удобно. Вы конвертируете число в экспоненциальное представление, подсчитывая количество мест, на которое нужно переместить десятичную точку, чтобы получить первую цифру перед этой десятичной точкой. Пример вопроса
Практические вопросы
