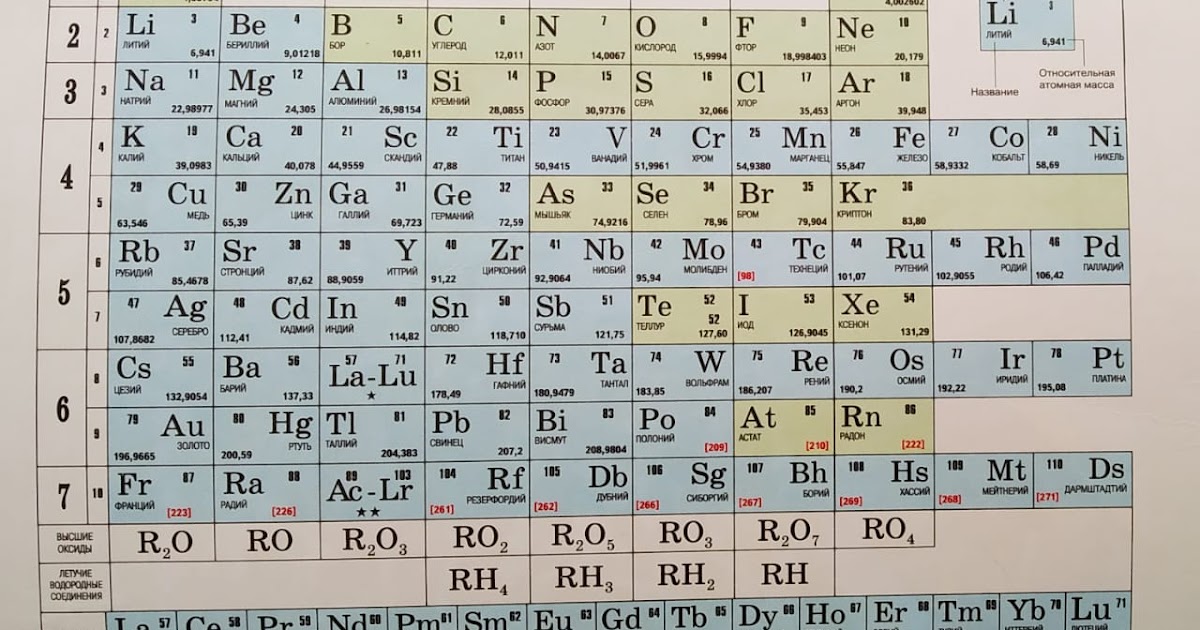
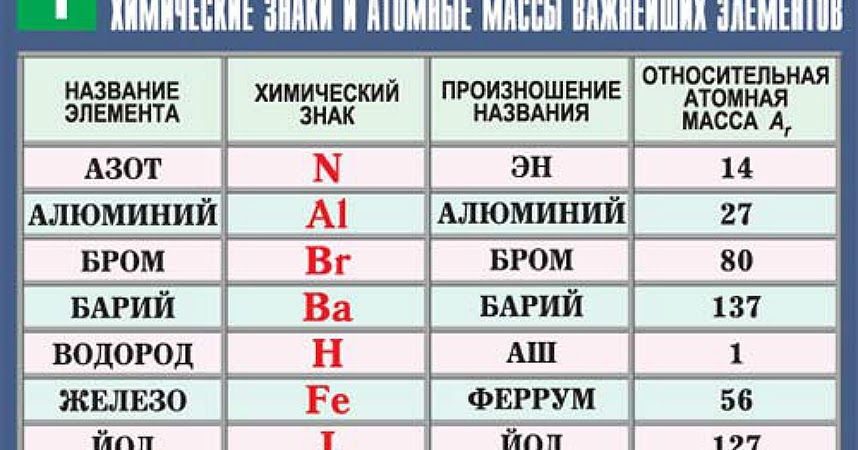
Атомные массы химических элементов
- Главная
- Справочник
- Таблицы
- Таблицы по химии
- Атомные массы химических элементов
| Элемент | Сим-вол | Атомный номер | Атомная масса | Элемент | Сим-вол | Атомный номер | Атомная масса |
|---|---|---|---|---|---|---|---|
| Азот | N | 7 | 14.0067 | Никель | 28 | 58. 7 7 | |
| Актиний | Ac | 89 | 227.0278 | Ниобий | Nb | 41 | 92.90064 |
| Алюминий | Al | 13 | 26.9815 | Нобелий | No | 102 | (259) |
| Америций | Am | 95 | (243) | Олово | Sn | 50 | 118.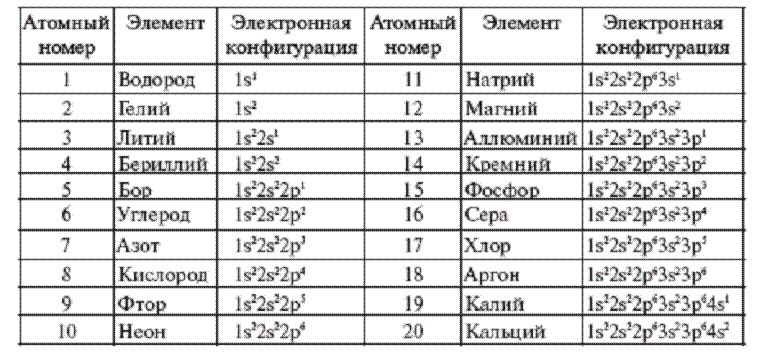 69 69 |
| Ar | 18 | 39.948 | Осмий | Os | 76 | 190.2 | |
| Астат | At | 85 | (210) | Палладий | Pd | 46 | |
| Барий | Ba | 56 | 137.33 | Платина | Pt | 78 | 195. 09 09 |
| Бериллий | Be | 4 | Плутоний | Pu | 94 | (244) | |
| Берклий | Bk | 97 | (247) | Полоний | Po | 84 | (209) |
| Бор | B | 10.81 | Празеодим | Pr | 59 | 140. 9077 9077 | |
| Бром | Br | 35 | 79.904 | Прометий | Pm | 61 | |
| Ванадий | V | 23 | 50.9115 | Протактиний | Pa | 91 | 231.0359 |
| Висмут | Bi | 83 | 208.98 | Радий | 88 | 226. 0254 0254 | |
| Водород | H | 1 | 1.0079 | Радон | Rn | 86 | (222) |
| Вольфрам | W | 74 | 183.85 | Рений | Re | 75 | 186.207 |
| Гадолиний | Gd | 64 | 157.25 | Родий | Rh | 45 |  9055 9055 |
| Галлий | Ga | 31 | 69.72 | Ртуть | Hg | 80 | 200.59 |
| Гафний | Hf | 72 | 178.49 | Rb | 37 | 85.4678 | |
| Гелий | He | 2 | 4.0026 | Рутений | Ru | 44 | 101. 07 07 |
| Германий | 32 | 72.59 | Самарий | Sm | 62 | 150.4 | |
| Гольмий | Ho | 67 | 164.93 | Свинец | Pb | 82 | 207.2 |
| Dy | 66 | 162.50 | Селен | Se | 34 | 78. 96 96 | |
| Европий | Eu | 63 | 151.96 | Сера | S | 16 | 32.06 |
| Железо | Fe | 26 | 55.847 | Серебро | Ag | 47 | 107.868 |
| Золото | Au | 79 | 196.9665 | Скандий | Sc | 21 | 44. 9559 9559 |
| Индий | In | 49 | 114.82 | Стронций | Sr | 38 | 87.62 |
| Йод | I | 53 | 126.904 | Сурьма | Sb | 51 | 121.75 |
| Иридий | Ir | 77 | 192.22 | Таллий | Tl | 81 | 204. 37 37 |
| Иттербий | Yb | 70 | 173.04 | Тантал | Ta | 73 | 180.9479 |
| Иттрий | Y | 39 | 88.9059 | Теллур | Te | 52 | 127.60 |
| Кадмий | Cd | 48 | 112.41 | Тербий | Tb | 65 | 158. 925 925 |
| Калий | K | 19 | 39.0983 | Технеций | Tc | 43 | (97) |
| Калифорний | Cf | 98 | (251) | Титан | Ti | 22 | 47.90 |
| Кальций | Ca | 20 | 40.08 | Торий | Th | 90 | 232. 0381 0381 |
| Кислород | O | 8 | 15.9994 | Тулий | Tm | 69 | 168.9342 |
| Кобальт | Co | 27 | 58.9332 | Углерод | C | 6 | 12.011 |
| Кремний | Si | 14 | 28.086 | Уран | U | 92 | 238. 029 029 |
| Криптон | Kr | 36 | 83.80 | Фермий | Fm | 100 | (257) |
| Ксенон | Xe | 54 | 131.30 | Фосфор | P | 15 | 30.97376 |
| Курчатовий | Ku | 104 | (261) | Франций | Fr | 87 | (223) |
| Кюрий | Cm | 96 | (247) | Фтор | F | 9 | 18. 9984 9984 |
| Лантан | La | 57 | 138.9055 | Хлор | Cl | 17 | 35.453 |
| Литий | Li | 3 | 6.941 | Хром | Cr | 24 | 51.996 |
| Лоуренсий | Lr | 103 | (260) | Цезий | Cs | 55 | 132. 9054 9054 |
| Лютеций | Lu | 71 | 174.967 | Церий | Ce | 58 | 140.12 |
| Магний | Mg | 12 | 24.305 | Цинк | Zn | 30 | 65.38 |
| Марганец | Mn | 25 | 54.938 | Цирконий | Zr | 40 | 91. 22 22 |
| Медь | Cu | 29 | 63.546 | Эйнштейний | Es | 99 | 254 |
| Менделевий | Md | 101 | (258) | Эрбий | Er | 68 | 167.26 |
| Молибден | Mo | 42 | 95.94 | Жолий | Jl | 105 | 262 |
| Мышьяк | As | 33 | 74. 9216 9216 | Резерфордий | Rf | 106 | 263 |
| Натрий | Na | 11 | 22.98977 | Борий | Bh | 107 | 264 |
| Неодим | Nd | 60 | 144.24 | Ганий | Hn | 108 | 265 |
| Неон | Ne | 10 | 20. 179 179 | Мейтнерий | Mt | 109 | 266 |
| Нептуний | Np | 93 | 237.0482 | (Экаплатина) | (E-Pt) | 110 |
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Таблицы по химии Таблицы Химия Справочник 5961
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Таблица названий кислот и солей
Таблицы по химии Таблицы Химия Справочник
Относительные молекулярные массы некоторых соединений
Таблицы по химии Таблицы Химия Справочник
Таблица растворимости в воде
Таблицы по химии Таблицы Химия Справочник
Физические свойства галогенов
Таблицы по химии Таблицы Химия Справочник
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a.
 Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.Вектора Формулы Геометрия Алгебра Теория Обозначения
Сколько весит ребенок?
Согласно нормам Всемирной Организацией Здравоохранения (ВОЗ)
Масса и вес Масса Теория Единицы измерения
Азбука Морзе
Справочная информация о коде Морзе
Литература 1 класс Литература Алфавит Азбука
Сколько должен весить человек?
Чтобы узнать вес человека, достаточно знать его рост в сантиметрах, из этой цифры вычесть 100, а к полученному числу либо прибавить 10, если речь идет о мужчине, либо отнять 10, если вычисляется вес женщины.
Масса и вес Масса Теория Единицы измерения
Сколько грамм в чайной ложечке, столовой ложке и стакане?
1 чайная ложка, 5 мл жидкости это приблизительно 5 грамм
Масса и вес Масса Физика Теория Единицы измерения
Что такое Ом
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.

Электротехника Формулы Физика Теория Электричество
Конвертер возраста животных и человека
Калькуляторы времени и даты Калькулятор Расчёт Конвертер Преобразовать Время
Сколько битов в байте, Кб, Мб, Гб и Тб
Разное Единицы измерения Справочник
Урок 2. Относительная атомная масса химических элементов – HIMI4KA
Архив уроков › Химия 8 класс
В уроке 2 «Относительная атомная масса химических элементов» из курса «Химия для чайников» рассмотрим разные способы выражения массы химических элементов. Напоминаю, что в прошлом уроке «Атомы и химические элементы» мы рассмотрели, кто и когда высказал идею о том, что все вокруг состоит из атомов; также выяснили, что из себя представляет химический элемент и каким образом обозначается.
Чем различаются атомы разных элементов между собой? Вы уже знаете: массой, размерами и строением. На рисунке 30 показаны шаровые модели атомов некоторых химических элементов, конечно, не в реальных размерах, а многократно увеличенные. В действительности атомы настолько малы, что их невозможно рассмотреть даже в самые лучшие оптические микроскопы.
В действительности атомы настолько малы, что их невозможно рассмотреть даже в самые лучшие оптические микроскопы.
На заметку: В конце XX в. у ученых появились более совершенные микроскопы, позволяющие достигать увеличения в несколько десятков миллионов раз. Они называются туннельными микроскопами. На рисунке 31 показана фотография поверхности кремния. На ней отчетливо видны отдельные атомы, расположенные на поверхности этого вещества.
Содержание
- Размеры и масса атомов
- Атомная единица массы
- Относительная атомная масса
Размеры и масса атомов
Современная наука обладает методами, позволяющими определять размеры и массы атомов. Так, например, самый легкий атом — атом водорода. Его масса равна 0,0000000000000000000000000016735 кг. Самым маленьким является атом гелия He. Диаметр этого атома равен приблизительно 0,00000000098 м. Записывать и читать такие числа затруднительно, поэтому обычно их представляют в более удобном виде: 1,6735·10−27 кг и 9,8·10−10 м. Атомы большинства химических элементов по своим размерам значительно больше атома гелия. Самый большой из них — атом элемента франция Fr. Его диаметр в 7 раз больше диаметра атома гелия (рис. 32).
Атомы большинства химических элементов по своим размерам значительно больше атома гелия. Самый большой из них — атом элемента франция Fr. Его диаметр в 7 раз больше диаметра атома гелия (рис. 32).
Еще больше различаются атомы разных элементов по массе. Масса атома обозначается символом ma и выражается в единицах массы СИ (кг). Так, например, масса атома углерода равна: ma(С) = 19,94·10−27 кг, а атома кислорода — ma(О) = 26,56·10−27 кг. Масса атома самого тяжелого из существующих на Земле элементов — урана U — почти в 237 раз больше массы атома водорода.
Атомная единица массы
Пользоваться такими маленькими величинами масс атомов при расчетах неудобно. К тому же, когда в XIX в. начало формироваться атомно- молекулярное учение, ученые еще не представляли реальных размеров и масс атомов. Поэтому на практике вместо истинных масс атомов стали применять их относительные значения. Они рассчитывались по массовым отношениям простых веществ в реакциях друг с другом. Химики предположили, что эти отношения пропорциональны массам соответствующих атомов. Именно так в начале XIX в. Дж. Дальтон ввел понятие относительной атомной массы, приняв за единицу сравнения массу самого легкого атома — водорода.
Они рассчитывались по массовым отношениям простых веществ в реакциях друг с другом. Химики предположили, что эти отношения пропорциональны массам соответствующих атомов. Именно так в начале XIX в. Дж. Дальтон ввел понятие относительной атомной массы, приняв за единицу сравнения массу самого легкого атома — водорода.
В настоящее время в качестве такой единицы сравнения используется 1/12 часть массы атома углерода (рис. 33). Она получила название атомной единицы массы (а. е. м.). Ее международное обозначение — u (от английского слова «unit» — единица):
Атомная единица массы — это 1/12 часть массы атома углерода, которая равна 1,66·10−27 кг.
Относительная атомная масса
Сравнивая средние массы атомов различных элементов с атомной единицей массы, получают значения относительных атомных масс химических элементов.
Относительная атомная масса элемента — это физическая величина, которая показывает, во сколько раз масса атома данного химического элемента больше 1/12 части массы атома углерода.
Относительная атомная масса обозначается символами Ar (А — первая буква английского слова «atomic» —атомный, r — первая буква английского слова «relative», что значит относительный), следовательно:
где Х — символ данного элемента.
Например, относительная атомная масса водорода:
а кислорода:
Как видите, относительная атомная масса показывает, во сколько раз масса атома данного элемента больше атомной единицы массы u.
В таблице Менделеева приведены относительные атомные массы всех элементов. В расчетах при решении задач мы будем пользоваться округленными до целых значениями этих величин (см. урок 1).
Внимание! Очень часто относительную атомную массу называют просто атомной массой. Однако следует отличать атомную массу — величину относительную (например, Ar(О) = 16) — от массы атома — величины, выражаемой в единицах массы — килограммах (ma(O) = 26,56·10−27 кг) или атомных единицах массы (ma(O) = 16·u).
Пример. Во сколько раз атом ртути тяжелее атома кальция?
Решение. Относительные атомные массы элементов равны: Ar(Hg) = 201 и Ar(Ca) = 40.
Масса атома ртути равна: ma(Hg) = Ar(Hg)·u (кг).
Масса атома кальция равна: ma(Са) = Ar(Са)·u (кг).
Другими словами, отношение масс атомов этих элементов равно отношению их относительных атомных масс. Следовательно, отношение масс атомов ртути и кальция равно:
Ответ: в 5,03 раза.
Краткие выводы урока:
- Атомная единица массы представляет собой 1/12 часть массы атома углерода.
- Относительная атомная масса химического элемента равна отношению массы его атома к 1/12 части массы атома углерода.
- Относительная атомная масса химического элемента является величиной безразмерной и показывает, во сколько раз масса атома данного элемента больше атомной единицы массы.

Надеюсь урок 2 «Относительная атомная масса химических элементов» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии.
Урок 3. Молекулы и простые вещества →
← Урок 1. Атомы и химические элементы
4.6: Значащие цифры и округление
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3555
- Стивен Лоуэр
- Университет Саймона Фрейзера
Цели обучения
- Приведите пример измерения, в котором количество значащих цифр явно слишком велико, и объясните, почему.
- Укажите цель округления и опишите информацию, которую необходимо знать, чтобы сделать это правильно.

- Округление числа до указанного количества значащих цифр.
- Объясните, как округлить число, у которого вторая по значимости цифра равна 9.
- Выполните простой расчет, включающий две или более наблюдаемых величин, и выразите результат в соответствующем количестве значащих цифр.
Числовые значения, с которыми мы имеем дело в науке (и во многих других аспектах жизни), представляют собой измерения, значения которых никогда точно не известны. Наши карманные калькуляторы или компьютеры этого не знают; они рассматривают числа, которые мы в них вводим, как «чистые» математические объекты, в результате чего арифметические операции часто дают ответы, которые физически нелепы, хотя и математически правильны. Цель этого раздела — помочь вам понять, почему это происходит, и показать, что с этим делать.
Цифры: значащие и прочие
Рассмотрим два утверждения, показанные ниже:
- «Население нашего города составляет 157 872 человека».

- “Количество зарегистрированных избирателей на 1 января составило 27 833 человека.
Какие из них вы бы немедленно уволили? Конечно, не второй, потому что он, вероятно, исходит из базы данных, которая содержит одну запись для каждого избирателя, поэтому число находится просто путем подсчета количества записей. Первое утверждение не может быть правильным. Даже если бы население города можно было точно определить (постоянные жители? теплые тела?), как мы можем объяснить ежеминутные изменения, происходящие по мере того, как люди рождаются и умирают, въезжают и уезжают?
В чем разница между двумя цифрами населения, указанными выше? Первый выражает величину, которую нельзя точно знать, т. е. несет в себе некоторую степень неопределенности. Вполне возможно, что последняя перепись дала именно 157 872 записи, и это может быть «население города» для юридических целей, но это, конечно, не «настоящее» население. Чтобы лучше отразить этот факт, можно указать население (например, в атласе) как 157 900 или даже 158 000 . Эти две величины были округлены до четырех и трех значащих цифр, соответственно, и имеют следующие значения: в пределах от примерно 1578 50 до примерно 1579 50. Другими словами, население составляет 1579 00±50. Добавление «плюс-минус 50» к этому числу означает, что мы считаем абсолютную неопределенность измерения населения равной 50 – (–50) = 100. Мы также можем сказать, что относительная неопределенность составляет 100/1579.00, что мы также можем выразить как 1 часть на 1579, или 1/1579 = 0,000633, или около 0,06 процента.
Эти две величины были округлены до четырех и трех значащих цифр, соответственно, и имеют следующие значения: в пределах от примерно 1578 50 до примерно 1579 50. Другими словами, население составляет 1579 00±50. Добавление «плюс-минус 50» к этому числу означает, что мы считаем абсолютную неопределенность измерения населения равной 50 – (–50) = 100. Мы также можем сказать, что относительная неопределенность составляет 100/1579.00, что мы также можем выразить как 1 часть на 1579, или 1/1579 = 0,000633, или около 0,06 процента.
Какое из этих двух значений мы будем указывать как «население», будет зависеть от степени нашей уверенности в исходных данных переписи; если перепись была завершена на прошлой неделе, мы могли бы округлить до четырех значащих цифр, но если это было год или около того назад, округление до трех знаков могло бы быть более разумным выбором. В таком случае нет действительно объективного способа выбора между двумя альтернативами.
В таком случае нет действительно объективного способа выбора между двумя альтернативами.
Это иллюстрирует важный момент: концепция значащих цифр имеет меньше общего с математикой, чем с нашей уверенностью в измерении. Эта уверенность часто может быть выражена численно (например, высота жидкости в измерительной трубке может быть определена с точностью до ±0,05 см), но когда это невозможно, как в примере с нашей популяцией, мы должны полагаться на наш личный опыт и суждения.
Итак, что такое значащая цифра? Согласно обычному определению, это все числительные в измеряемой величине (считая слева), значения которых считаются точно известными, плюс еще одно, значение которого может быть на единицу больше или меньше:
- В « 1579 00» (четыре значащие цифры) точно известны три крайние левые цифры, но четвертая цифра, «9», вполне может быть «8», если «истинное значение» находится в подразумеваемом диапазоне. от 1578 50 до 1579 50.

- В « 158 000» (три значащие цифры) две крайние левые цифры известны точно, а третья цифра может быть либо «7», либо «8», если истинное значение находится в подразумеваемом диапазоне 157 . от 500 до 158 500.
Хотя округление всегда приводит к потере числовой информации, то, от чего мы избавляемся, можно считать «числовым шумом», который не способствует качеству измерения. Цель округления состоит в том, чтобы избежать выражения значения с большей степенью точности, чем это согласуется с неопределенностью измерения.
Подразумеваемая погрешность
Если вы знаете, что точность весов составляет, скажем, 0,1 мг, то погрешность любого измерения массы, выполненного на этих весах, составит ±0,1 мг. Предположим, однако, что вам просто сказали, что объект имеет длину 0,42 см, без указания его точности. В этом случае все, что вам нужно сделать, это количество цифр, содержащихся в данных. Таким образом, количество «0,42 см» указано до 0,01 единицы в 0 42 или одной части в 42 . Подразумеваемая относительная неопределенность этой цифры составляет 1/42, или около 2%. Таким образом, точность любого числового ответа, рассчитанного на основе этого значения, ограничена примерно такой же величиной.
Подразумеваемая относительная неопределенность этой цифры составляет 1/42, или около 2%. Таким образом, точность любого числового ответа, рассчитанного на основе этого значения, ограничена примерно такой же величиной.
Ошибка округления
Важно понимать, что количество значащих цифр в значении дает лишь приблизительное представление о его точности, и что при округлении информация теряется. Предположим, например, что мы измеряем вес объекта как 3,28 г на весах, которые, как полагают, имеют точность в пределах ±0,05 грамма. Полученное значение 3,28 ± 0,05 грамма говорит нам о том, что истинный вес объекта может быть где-то между 3,23 г и 3,33 г. Абсолютная неопределенность здесь составляет 0,1 г (±0,05 г), а относительная неопределенность составляет 1 часть на 32,8, или около 3 процентов.
Сколько значащих цифр должно быть в сообщаемом измерении? Так как только крайняя левая «3» в «3,28» определена, вы, вероятно, предпочтете округлить значение до 3,3 г. Все идет нормально. Но что кто-то другой должен думать об этой цифре, когда увидит ее в вашем отчете? Значение «3,3 г» предполагает подразумеваемую неопределенность , равную 3,3±0,05 г, что означает, что истинное значение, вероятно, находится между 3,25 г и 3,35 г. Этот диапазон на 0,02 г ниже, чем связанный с первоначальным измерением, поэтому округление внесло погрешность в результат на эту величину. Поскольку это составляет менее половины погрешности взвешивания ±0,05 г, само по себе это не очень серьезно. Однако, если в расчете объединяются несколько значений, округленных таким образом, ошибки округления могут стать значительными.
Но что кто-то другой должен думать об этой цифре, когда увидит ее в вашем отчете? Значение «3,3 г» предполагает подразумеваемую неопределенность , равную 3,3±0,05 г, что означает, что истинное значение, вероятно, находится между 3,25 г и 3,35 г. Этот диапазон на 0,02 г ниже, чем связанный с первоначальным измерением, поэтому округление внесло погрешность в результат на эту величину. Поскольку это составляет менее половины погрешности взвешивания ±0,05 г, само по себе это не очень серьезно. Однако, если в расчете объединяются несколько значений, округленных таким образом, ошибки округления могут стать значительными.
Правила округления
Стандартные правила округления хорошо известны. Прежде чем мы их изложим, давайте договоримся, как называть различные компоненты числового значения.
- Самая значащая цифра — самая левая цифра (не считая начальных нулей, которые служат только заполнителями и никогда не являются значащими цифрами).
- Если округлить до n значащих цифр, то младшая значащая цифра — это n -я цифра от старшего разряда.
 Младшая значащая цифра может быть нулем.
Младшая значащая цифра может быть нулем. - Первая незначащая цифра — это n +1-я цифра.
Правила округления
- Если первая незначащая цифра меньше 5, то младшая значащая цифра остается неизменной.
- Если первая незначащая цифра больше 5, младшая значащая цифра увеличивается на 1.
- Если первая незначащая цифра равна 5, младшая значащая цифра может быть либо увеличена, либо оставлена без изменений ( см. ниже! )
- Все незначащие цифры удаляются.
Фантазии о пятерках
Иногда учащимся предлагается увеличить младшую значащую цифру на 1, если она нечетная, и оставить ее без изменений, если она четная. Интересно, отражает ли это какую-то идею о том, что четные числа как-то «лучше» нечетных! (Древнее суеверие как раз противоположное, что только нечетные числа являются «счастливыми».)
На самом деле, вы могли бы сделать то же самое и наоборот, увеличивая только четные числа. Если вы округляете только одно число, на самом деле не имеет значения, что вы делаете. Однако при округлении ряда чисел, которые будут использоваться в расчетах, если вы одинаково обработаете каждую первую незначащую 5, вы завысите или занизите значение округленного числа, тем самым накапливая ошибку округления. . Поскольку существует одинаковое количество четных и нечетных цифр, увеличение только одного из них предотвратит возникновение ошибки такого рода. Конечно, вы могли бы сделать то же самое, подбросив монетку!
Если вы округляете только одно число, на самом деле не имеет значения, что вы делаете. Однако при округлении ряда чисел, которые будут использоваться в расчетах, если вы одинаково обработаете каждую первую незначащую 5, вы завысите или занизите значение округленного числа, тем самым накапливая ошибку округления. . Поскольку существует одинаковое количество четных и нечетных цифр, увеличение только одного из них предотвратит возникновение ошибки такого рода. Конечно, вы могли бы сделать то же самое, подбросив монетку!
число округлить до | количество значащих цифр | результат | комментарий |
|---|---|---|---|
| 34,216 | 3 | 34,2 | Первая незначащая цифра (1) меньше 5, поэтому число просто усекается. |
| 2,252 | 2 | 2,2 или 2,3 | Первая незначащая цифра — 5, поэтому наименьший знак. цифра может либо оставаться неизменной, либо увеличиваться. |
| 39,99 | 3 | 40,0 | Пересечение «десятичной границы», поэтому все числа меняются. |
| 85 381 | 3 | 85,4 00 | Два нуля — это просто заполнители |
| 0,04597 | 3 | 0,0460 | Два начальных нуля не являются значащими цифрами. |
Округление девяток
Предположим, что вес объекта составляет 3,98 ± 0,05 г. Это поместит его истинный вес где-то в диапазоне от 3,93 г до 4,03 г. Решая, как округлить это число, вы подсчитываете количество цифр в «3,98», которые точно известны, и не находите ни одной! Поскольку «4» — это самая левая цифра, значение которой является неопределенным, это будет означать, что результат следует округлить до одной значащей цифры и указать просто как 4g. Альтернативой может быть изменение правила и округление до двух значащих цифр, что дает 4,0 г. Как вы можете решить, что делать? В таком случае вы должны посмотреть на подразумеваемые неопределенности в двух значениях и сравнить их с неопределенностью, связанной с исходным измерением.
округленное значение | подразумеваемый максимум | подразумеваемый минимум | абсолютная неопределенность | относительная неопределенность |
|---|---|---|---|---|
| 3,98 г | 3,985 г | 3,975 г | ±0,005 г или 0,01 г | 1 из 400, или 0,25% |
| 4 г | 4,5 г | 3,5 г | ±0,5 г или 1 г | 1 из 4, 25% |
| 4,0 г | 4,05 г | 3,95 г | ±0,05 г или 0,1 г | 1 из 40, 2,5% |
Ясно, что округление до двух цифр является единственным разумным вариантом в этом примере. Наблюдаемые значения следует округлить до числа цифр, наиболее точно отражающего неопределенность измерения.
Наблюдаемые значения следует округлить до числа цифр, наиболее точно отражающего неопределенность измерения.
- Обычно это означает округление до количества значащих цифр в количестве; то есть количество цифр (считая слева), которые точно известны, плюс еще одна.
- Если это неприменимо (как в приведенном выше примере, когда добавление вычитания абсолютной неопределенности связывает десятую степень), то мы округляем таким образом, чтобы относительная подразумеваемая неопределенность результата была как можно ближе к неопределенности наблюдаемое значение.
Округление результатов вычислений
При выполнении вычислений, состоящих из нескольких шагов, следует избегать округления до получения окончательного результата. Предположим, вы используете свой калькулятор для расчета площади прямоугольника:
округленное значение | относительная подразумеваемая неопределенность |
|---|---|
| 1,58 | 1 часть на 158 или 0,6% |
| 1,6 | 1 часть на 16, или 6 % |
Примечание
Ваш калькулятор, конечно, верен в чистом виде, но вы ошибетесь, записав «1,57676 см 9». 0404 2 “. Справа показаны два возможных варианта округления ответа калькулятора.
0404 2 “. Справа показаны два возможных варианта округления ответа калькулятора.
Понятно, что ни один из вариантов не является полностью удовлетворительным; правило, и округление до двух цифр в “.42” приводит к потере некоторой точности. В этом случае можно утверждать, что округление до трех цифр оправдано, поскольку подразумеваемая относительная неопределенность в ответе, 0,6%, больше в соответствии с двумя факторами.
«Правила» округления, как правило, полезны и удобны, но они не всегда приводят к желаемому результату. В случае сомнений лучше полагаться на относительную подразумеваемую неопределенность.
Сложение и вычитание
В операциях со значащими цифрами ответ сообщается таким образом, чтобы он отражал надежность наименее точной операции. Ответ не более точен, чем наименее точное число, использованное для получения ответа. При сложении или вычитании мы идем по числу десятичных знаков (т. е. количество цифр справа от десятичной точки), а не по количеству значащих цифр. Определите количество, имеющее наименьшее количество знаков после запятой, и используйте это число, чтобы задать количество знаков после запятой в ответе.
е. количество цифр справа от десятичной точки), а не по количеству значащих цифр. Определите количество, имеющее наименьшее количество знаков после запятой, и используйте это число, чтобы задать количество знаков после запятой в ответе.
Умножение и деление
Результат должен содержать такое же количество значащих цифр, как и значение с наименьшим количеством значащих цифр.
Логарифмы и антилогарифмы
Если число выражено в виде а × 10 Ь («научная запись») с дополнительным ограничением, что коэффициент а не меньше 1 и меньше 10, число находится в его нормализованная форма . Выразите логарифм по основанию 10 значения, используя то же количество значащих цифр, которое присутствует в нормализованной форме этого значения. Точно так же для антилогарифмов (числа, выраженные в степени 10) используйте то же количество значащих цифр, что и в этой степени.
Примеры \(\PageIndex{1}\)
Следующие примеры иллюстрируют наиболее распространенные проблемы, с которыми вы, вероятно, столкнетесь при округлении результатов вычислений. Они заслуживают вашего внимательного изучения!
Они заслуживают вашего внимательного изучения!
результат калькулятора | закругленный | замечания |
|---|---|---|
| 1,6 | Округление до двух значащих цифр дает подразумеваемую неопределенность 1/16 или 6 %, что в три раза больше, чем у наименее точно известного коэффициента. Это хорошая иллюстрация того, как округление может привести к потере информации. | |
| 1.9E6 | Фактор “3.1” указан как 1 часть из 31, или 3%. В ответе 1. 9 значение выражено в 1 части 19, или 5%. Эти точности сопоставимы, поэтому правило округления дало нам разумный результат. 9 значение выражено в 1 части 19, или 5%. Эти точности сопоставимы, поэтому правило округления дало нам разумный результат. | |
Некая книга имеет толщину 117 мм; найдите высоту стопки из 24 одинаковых книг: | 281 0 мм | «24» и «1» являются точными, поэтому единственным неопределенным значением является толщина каждой книги, представленная 3 значащими цифрами. Конечный ноль в ответе — это только заполнитель. |
| 10,4 | При сложении или вычитании найдите термин с наименьшим числом знаков после запятой и округлите ответ до такого же числа знаков. | |
| 23 см | см. ниже ниже |
Последний из показанных выше примеров представляет очень распространенную операцию преобразования одной единицы в другую. Здесь есть некоторая двусмысленность; если мы возьмем “9дюймов” означает расстояние в диапазоне от 8,5 до 9,5 дюймов, то подразумеваемая неопределенность составляет ±0,5 дюйма, что составляет 1 часть на 18, или примерно ± 6%. Относительная неопределенность ответа должна быть одинаковой, поскольку все значения умножаются на один и тот же коэффициент 2,54 см/дюйм. В этом случае мы вправе записывать ответ с двумя значащими цифрами, что дает погрешность около ±1 см. Если бы мы использовали ответ «20 см» (один значащий цифра), его подразумеваемая неопределенность будет ±5 см, или ±25%.
Если возникает вопрос о подходящем количестве значащих цифр, расчет относительной неопределенности может помочь вам принять решение.
Эта страница под названием 4.6: Значимые цифры и округление распространяется под лицензией CC BY 3. 0 и была создана, изменена и/или курирована Стивеном Лоуэром с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Стивеном Лоуэром с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Стивен Лоуэр
- Лицензия
- СС BY
- Версия лицензии
- 3,0
- Показать страницу TOC
- № на стр.

- Теги
- источник@http://www.chem1.com/acad/webtext/virtualtextbook.html
Атомный вес | Определение, единицы измерения и таблица
- Ключевые люди:
- Йонс Якоб Берцелиус Джон Далтон Станислао Канниццаро Амедео Авогадро Огюст Лоран
- Похожие темы:
- атом химическая шкала атомного веса физическая шкала атомного веса Гипотеза Праута
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
атомный вес , также называемый относительная атомная масса , отношение средней массы атомов химического элемента к некоторому эталону. С 1961 стандартной единицей атомной массы была одна двенадцатая массы атома изотопа углерода-12. Изотоп — это один из двух или более видов атомов одного и того же химического элемента, которые имеют разные атомные массовые числа (протоны + нейтроны). Атомный вес гелия составляет 4,002602, это среднее значение, отражающее типичное соотношение естественного содержания его изотопов. Атомный вес измеряется в атомных единицах массы (а.е.м.), также называемых дальтонами. См. ниже список химических элементов и их атомный вес.
Изотоп — это один из двух или более видов атомов одного и того же химического элемента, которые имеют разные атомные массовые числа (протоны + нейтроны). Атомный вес гелия составляет 4,002602, это среднее значение, отражающее типичное соотношение естественного содержания его изотопов. Атомный вес измеряется в атомных единицах массы (а.е.м.), также называемых дальтонами. См. ниже список химических элементов и их атомный вес.
Понятие атомного веса является фундаментальным для химии, поскольку большинство химических реакций протекают в соответствии с простыми числовыми соотношениями между атомами. Поскольку почти всегда невозможно подсчитать непосредственно вовлеченные атомы, химики измеряют реагенты и продукты путем взвешивания и делают выводы с помощью расчетов с использованием атомных весов. Стремлением определить атомный вес элементов занимали крупнейшие химики 19 и начала 20 веков. Их тщательная экспериментальная работа стала ключом к химической науке и технике.
Надежные значения атомных весов служат важной цели совсем по-другому, когда химические товары покупаются и продаются на основе содержания одного или нескольких определенных компонентов. Примерами являются руды дорогих металлов, таких как хром или тантал, и промышленная химическая кальцинированная сода. Содержание указанного компонента должно быть определено количественным анализом. Вычисленная ценность материала зависит от атомных весов, используемых в расчетах.
Примерами являются руды дорогих металлов, таких как хром или тантал, и промышленная химическая кальцинированная сода. Содержание указанного компонента должно быть определено количественным анализом. Вычисленная ценность материала зависит от атомных весов, используемых в расчетах.
Первоначальным стандартом атомной массы, установленным в 19 веке, был водород со значением 1. Примерно с 1900 по 1961 год в качестве эталона использовался кислород с присвоенным значением 16. Единицей атомной массы была таким образом определяется как 1 / 16 масса атома кислорода. В 1929 году было обнаружено, что природный кислород содержит небольшое количество двух изотопов, немного более тяжелых, чем самый распространенный, и что число 16 представляет собой средневзвешенное значение трех изотопных форм кислорода, встречающихся в природе. Эта ситуация считалась нежелательной по нескольким причинам, и, поскольку можно определить относительные массы атомов отдельных изотопов, вскоре была установлена вторая шкала с 16 как значением основного изотопа кислорода, а не значением натуральная смесь. Эта вторая шкала, предпочитаемая физиками, стала известна как физическая шкала, а более ранняя шкала продолжала использоваться в качестве химической шкалы, которую предпочитали химики, которые обычно работали с природными смесями изотопов, а не с чистыми изотопами.
Эта вторая шкала, предпочитаемая физиками, стала известна как физическая шкала, а более ранняя шкала продолжала использоваться в качестве химической шкалы, которую предпочитали химики, которые обычно работали с природными смесями изотопов, а не с чистыми изотопами.
Хотя две шкалы различались незначительно, соотношение между ними не могло быть точно установлено из-за незначительных различий в изотопном составе природного кислорода из разных источников. Было также сочтено нежелательным иметь две разные, но тесно связанные шкалы для одних и тех же величин. По обеим этим причинам химики и физики установили новую шкалу в 1961 году. Эта шкала, основанная на углероде-12, требовала лишь минимальных изменений в значениях, которые использовались для химических атомных весов.
Поскольку образцы встречающихся в природе элементов содержат смеси изотопов с разным атомным весом, Международный союз теоретической и прикладной химии (IUPAC) начал публиковать атомные веса с неопределенностями. Первым элементом, атомный вес которого получил неопределенность, была сера в 1951 году. К 2007 году 18 элементов имели связанные неопределенности, а в 2009 году ИЮПАК начал публиковать диапазоны атомного веса некоторых элементов. Например, атомный вес углерода равен [12,0096, 12.0116].
Первым элементом, атомный вес которого получил неопределенность, была сера в 1951 году. К 2007 году 18 элементов имели связанные неопределенности, а в 2009 году ИЮПАК начал публиковать диапазоны атомного веса некоторых элементов. Например, атомный вес углерода равен [12,0096, 12.0116].
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
В таблице приведен список химических элементов и их атомный вес.
| элемент | условное обозначение | атомный номер | атомный вес |
|---|---|---|---|
Элементы с атомным весом, указанным в квадратных скобках, имеют атомный вес, указанный в виде диапазона. Элементы с атомным весом в скобках указывают вес изотопа с самым длинным периодом полураспада. | |||
| Источники: Комиссия по изотопному содержанию и атомному весу, «Атомный вес элементов, 2015 г.»; и Национальный центр ядерных данных, Брукхейвенская национальная лаборатория, NuDat 2.6. | |||
| водород | ЧАС | 1 | [1.00784, 1.00811] |
| гелий | Он | 2 | 4.002602 |
| литий | Ли | 3 | [6,938, 6,997] |
| бериллий | Быть | 4 | 9.0121831 |
| бор | Б | 5 | [10,806, 10,821] |
| углерод | С | 6 | [12. 0096, 12.0116] 0096, 12.0116] |
| азот | Н | 7 | [14.00643, 14.00728] |
| кислород | О | 8 | [15.99903, 15.99977] |
| фтор | Ф | 9 | 18.998403163 |
| неон | Не | 10 | 20.1797 |
| натрий | На | 11 | 22,98976928 |
| магний | мг | 12 | [24. 304, 24.307] 304, 24.307] |
| алюминий (алюминий) | Ал | 13 | 26.9815385 |
| кремний | Си | 14 | [28.084, 28.086] |
| фосфор | п | 15 | 30.973761998 |
| сера (сера) | С | 16 | [32.059, 32.076] |
| хлор | Кл | 17 | [35,446, 35,457] |
| аргон | Ар | 18 | 39. 948 948 |
| калий | К | 19 | 39.0983 |
| кальций | Ca | 20 | 40.078 |
| скандий | наук | 21 | 44,955908 |
| титан | Ти | 22 | 47.867 |
| ванадий | В | 23 | 50,9415 |
| хром | Кр | 24 | 51,9961 |
| марганец | Мн | 25 | 54. 938044 938044 |
| железо | Fe | 26 | 55,845 |
| кобальт | Ко | 27 | 58.933194 |
| никель | ни | 28 | 58,6934 |
| медь | Cu | 29 | 63,546 |
| цинк | цинк | 30 | 65,38 |
| галлий | Га | 31 | 69,723 |
| германий | Ge | 32 | 72. 630 630 |
| мышьяк | В качестве | 33 | 74.921595 |
| селен | Се | 34 | 78,971 |
| бром | бр | 35 | [79,901, 79,907] |
| криптон | Кр | 36 | 83,798 |
| рубидий | руб. | 37 | 85,4678 |
| стронций | старший | 38 | 87,62 |
| иттрий | Д | 39 | 88. |
| цирконий | Zr | 40 | 91,224 |
| ниобий | Nb | 41 | 92. |
| молибден | Мо | 42 | 95,95 |
| технеций | Тс | 43 | (97) |
| рутений | Ру | 44 | 101.07 |
| родий | Rh | 45 | 102. |
| палладий | Pd | 46 | 106,42 |
| Серебряный | Аг | 47 | 107,8682 |
| кадмий | Компакт диск | 48 | 112.414 |
| индий | В | 49 | 114.818 |
| банка | Сн | 50 | 118.710 |
| сурьма | Сб | 51 | 121. 760 760 |
| теллур | Те | 52 | 127,60 |
| йод | я | 53 | 126. |
| ксенон | Хе | 54 | 131.293 |
| цезий (цезий) | Cs | 55 | 132. |
| барий | Ба | 56 | 137,327 |
| лантан | Ла | 57 | 138. |
| церий | Се | 58 | 140,116 |
| празеодим | Пр | 59 | 140. |
| неодим | Нд | 60 | 144,242 |
| прометий | Вечера | 61 | (145) |
| самарий | см | 62 | 150,36 |
| европий | ЕС | 63 | 151,964 |
| гадолиний | Б-г | 64 | 157,25 |
| тербий | ТБ | 65 | 158. 92535 92535 |
| диспрозий | Ди | 66 | 162.500 |
| гольмий | Хо | 67 | 164.93033 |
| эрбий | Эр | 68 | 167,259 |
| тулий | тм | 69 | 168.93422 |
| иттербий | Ыб | 70 | 173.045 |
| лютеций | Лу | 71 | 174,9668 |
| гафний | Хф | 72 | 178,49 |
| тантал | Та | 73 | 180. 94788 94788 |
| вольфрам (вольфрам) | Вт | 74 | 183,84 |
| рений | Ре | 75 | 186.207 |
| осмий | Операционные системы | 76 | 190,23 |
| иридий | Ир | 77 | 192,217 |
| платина | Пт | 78 | 195.084 |
| золото | Au | 79 | 196. 966569 966569 |
| Меркурий | ртутного столба | 80 | 200.592 |
| таллий | Тл | 81 | [204.382, 204.385] |
| Свинец | Pb | 82 | 207,2 |
| висмут | би | 83 | 208.98040 |
| полоний | По | 84 | (209) |
| астат | В | 85 | (210) |
| радон | Рн | 86 | (222) |
| франций | Пт | 87 | (223) |
| радий | Ра | 88 | (226) |
| актиний | Ас | 89 | (227) |
| торий | Чт | 90 | 232. 0377 0377 |
| протактиний | Па | 91 | 231.03588 |
| уран | U | 92 | 238.02891 |
| нептуний | Нп | 93 | (237) |
| плутоний | Пу | 94 | (244) |
| америций | Являюсь | 95 | (243) |
| курий | См | 96 | (247) |
| берклий | Бк | 97 | (247) |
| Калифорния | ср | 98 | (251) |
| эйнштейний | Эс | 99 | (252) |
| фермий | FM | 100 | (257) |
| менделевий | Мэриленд | 101 | (258) |
| нобелий | Нет | 102 | (259) |
| Лоуренсиум | Лр | 103 | (262) |
| резерфордий | РФ | 104 | (263) |
| дубний | Дб | 105 | (268) |
| сиборгиум | сержант | 106 | (271) |
| борий | ч | 107 | (270) |
| гассиум | Hs | 108 | (270) |
| мейтнерий | Мт | 109 | (278) |
| Дармштадциум | Дс | 110 | (281) |
| рентгений | Rg | 111 | (281) |
| коперниций | Сп | 112 | (285) |
| унунтриум | Уут | 113 | (286) |
| флеровий | Флорида | 114 | (289) |
| унунпентий | Ууп | 115 | (289) |
| ливерморий | Ур. | ||

 Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.

 Младшая значащая цифра может быть нулем.
Младшая значащая цифра может быть нулем.