Определение момента инерции тела и положения центра масс
+7 (495) 781 39 39
Главная/Испытательное оборудование/SPACE ELECTRONICS/Определение момента инерции и положения центра масс
Space Electronics KSR – самые точные инструменты в мире для определения момента инерции (МИ) и положения центра масс (ЦМ).
Данная линейка инструментов настоятельно рекомендуется для определения масс-инерционных характеристик ракет, спутников и баллистических объектов.
Оборудование может быть использовано для полезной нагрузки массой от 100 грамм до 10 тонн и тяжелее.
Концепция измерения
Сферический подшипник поддерживает поворотный стол и выступает в роли шарнира для измерения дисбаланса, возникающего от смещения центра масс испытуемого объекта относительно оси подшипника.
Определение момента инерции тела происходит при помощи торсиона, зажатого снизу и прикрепленного сверху к газовому подшипнику, образуя, таким образом, перевернутый крутильный маятник.
Наилучшая достигаемая точность – измерение ЦМ с точностью до 25 микрон и МИ с точностью до 0.1% Один инструмент может измерять полезную нагрузку, вес которой составляет всего 4% от максимального веса, на который рассчитан инструмент.
Полная автоматизация процесса – выберите определение момента инерции или центра масс на экране компьютера и процесс измерения запуститься автоматически.
Использование газовых подшипников значит полную совместимость с чистыми комнатами. Нет риска загрязнения, нет высокого давления, нет опасности взрыва.
Огромная устойчивость от опрокидывающих моментов. Инструмент не опрокидывается даже при высоком расположении ЦМ.
Полностью программная поддержка метрических и дюймовых единиц. Система координат определяется пользователем – значения ЦМ и МИ сообщаются непосредственно в системе координат полезной нагрузки.
Оборудование для калибровки согласно стандартам НИСТ входит в комплект поставки каждого инструмента.
- Дисбаланс от центра масс измеряется непосредственно;
- Изменение положения ЦМ можно наблюдать в живую;
- Автоматическое устранение ошибоквыравнивания.
Опциональная весоизмерительная платформа и манипулятор для определения координат позволяет напрямую собирать данные о весе и системе координат испытуемого объекта непосредственно на инструменте.
Общая спецификация линейки (для конкретной модели значения необходимо уточнять)
Измерения за один установ: 2 координаты центра масс и 1 значение момента инерции;
Диапазон масс нагрузок: От 100 грамм до 10 тонн;
Точность определения ЦМ: 0.1% от измеренного значения дисбаланса;
Точность определения МИ: 0.1% от измеренного значения;
Требования к электросети: 115 ВAC, 60 Hz или 220 ВAC, 50 Hz, одна фаза;
Требования к сетия сжатого воздуха: Источник чистого сухого воздуха или азота, 7 бар, 60 л/мин;
Требования к полу: Бетонный пол, 15 см. толщиной.
Цена
По запросу
Ф.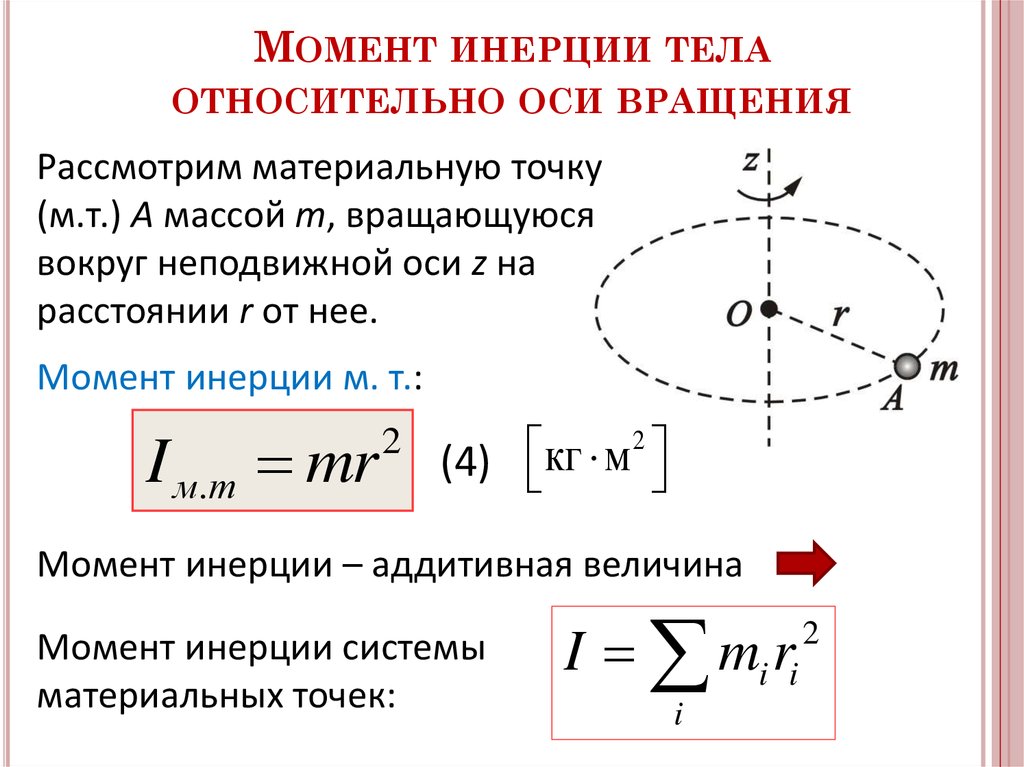 И.О.*
И.О.*
Предприятие (работаем только с юр. лицами)*
E-mail для связи*
Телефон для связи*
Загрузка файла
не более: 5
Комментарий
* Нажимая кнопку “Отправить” вы принимаете условия обработки информации
+7 (495) 781 39 39
107023, г. Москва, ул. Электрозаводская, д.24,
стр.3, оф. В303
Copyright © 2007 – 2021 ООО “БЛМ Синержи”
Мегагрупп.ру
Этот сайт использует cookie-файлы и другие технологии для улучшения его работы. Продолжая работу с сайтом, Вы разрешаете использование cookie-файлов. Вы всегда можете отключить файлы cookie в настройках Вашего браузера.
Хорошо
Определение момента инерции твердого тела методом крутильных колебаний
Лабораторная работа 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: определить момента инерции твердого тела методом крутильных колебаний.
Оборудование: лабораторная установка – крутильный маятник.
1. ОБЩИЕ СВЕДЕНИЯ
Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения
В твёрдом теле все точки жестко связаны между собой и могут вращаться вокруг неподвижной оси под действием момента внешней силы. При этом вектор момента силы М и вектор углового ускорения ε всегда направлены в одну сторону и справедлив основной закон динамики вращательного движения
M = I ε
где I – момент инерции твердого тела относительно неподвижной оси вращения, кг· м2.
Момент инерции I характеризует инертные свойства твердого тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
 Её удаление от оси вращения обозначим через ri (рис. 1). Тогда линейная скорость этой
точки равна
Её удаление от оси вращения обозначим через ri (рис. 1). Тогда линейная скорость этой
точки равнаvi = ωiri, где ωi – угловая скорость вращения, рад/с.
Момент импульса относительно оси вращения равен
Li = miVi
Величина равная Ii = miri2 называется моментом инерции материальной точки.
Для твёрдого тела моменты импульсов складываются по всем материальным точкам, образующим это тело. Тогда суммарный момент импульса равен
или
L = Iω.
Здесь
и
есть момент инерции твердого тела относительно оси вращения.
Суммирование производится по всем материальным точкам, входящих в твердое тело.
Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы труда не составляет, то есть
где ρ – плотность, кг/м3, V – объем, занимаемый телом, м3.
Интегрирование производится по всему объёму тела.
Для любого твёрдого тела можно указать три взаимно перпендикулярные оси, проходящие через его центр инерции. Эти оси называются главными осями тела. А момент инерции относительно любой оси вращения выражается через моменты инерции тела относительно этих главных осей.
Главные оси просто определить для однородных симметричных тел (шара, куба, параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями симметрии тела.
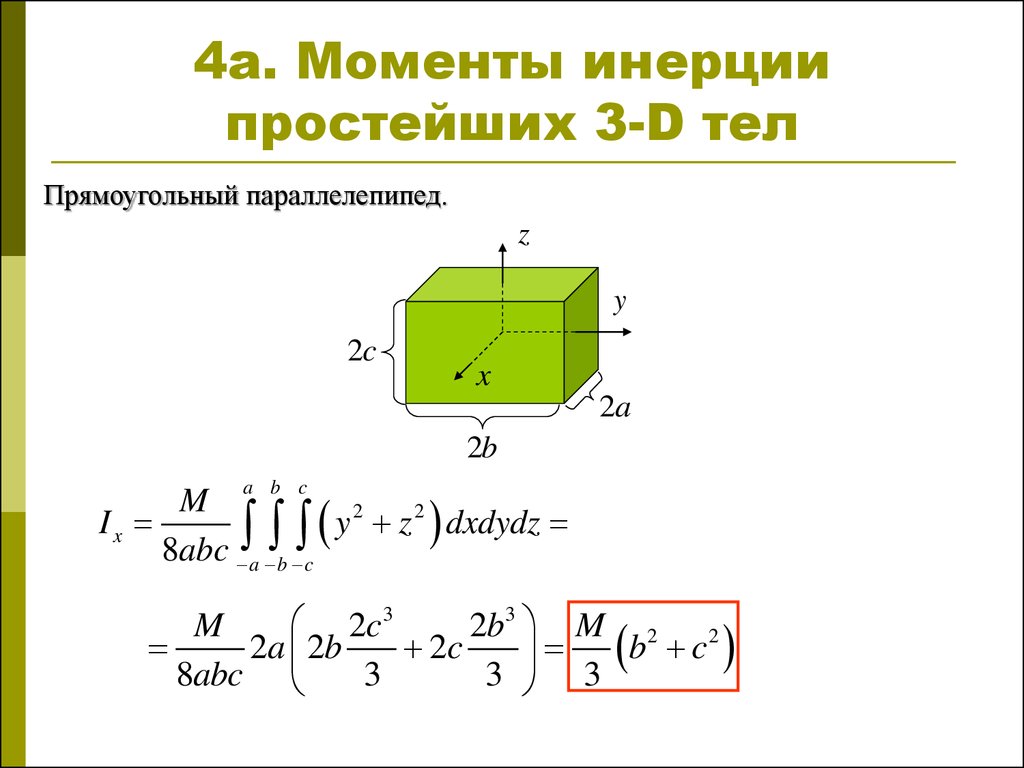
Например, главные оси однородного прямоугольного
параллелепипеда проходят через его геометрический центр перпендикулярно граням
(рис. 2).
2).
Для тел сложной формы главные оси и моменты инерции определяют экспериментально.
Если известны главные оси твердого тела, то с ними связывают прямоугольную систему координат
Возьмём произвольную ось вращения, проходящую через центр инерции, ось ОС (рис. 3).
Момент инерции тела относительно оси ОС выражается через моменты инерции главных осей, то есть
I= Ix cos2α + Iy сos2 + Iz cos2 γ (1)
где Ix, Iy, Iz – моменты инерции тела относительно осей
Моменты инерции Ix, Iy, Iz определяются экспериментально. Момент инерции тела относительно произвольной оси вращения находится простым суммированием по формуле (1).
Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции следует вычислять заново.
Если известен момент инерции тела относительно оси, проходящей через центр инерции, то момент инерции тела относительно любой оси, параллельной первой и смещенной на расстояние
где I0 – момент инерции относительно оси вращения, проходящей через центр инерции, кг · м3; m – масса тела, кг; d – расстояние между осями, м.
Используемый в лабораторной работе крутильный маятник позволяет определить момент инерции тел любой формы.
Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне. При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
Mупр = –D Θ, где Θ – угол поворота рамки, рад; D – коэффициент, характеризующий момент упругих сил, Н · м.
При достаточно тонкой и длинной струне зависимость М(Θ) выполняется и для больших углов поворота, а затухания при крутильных колебаниях можно считать малыми.
Пренебрегай затуханиями, движение рамки записывают уравнением для свободных незатухающих колебаний
или
(2)
где – угловое ускорение, рад · с2, вторая производная по времени от угла попорота; ω0 – циклическая частота колебаний, рад/с. Циклическая частота колебаний выражается как
Период таких колебаний равен
(3)
Решение дифференциального уравнения (2) имеет вид
где Θ0 – угловая амплитуда колебаний, рад; α – начальная фаза
колебаний, рад.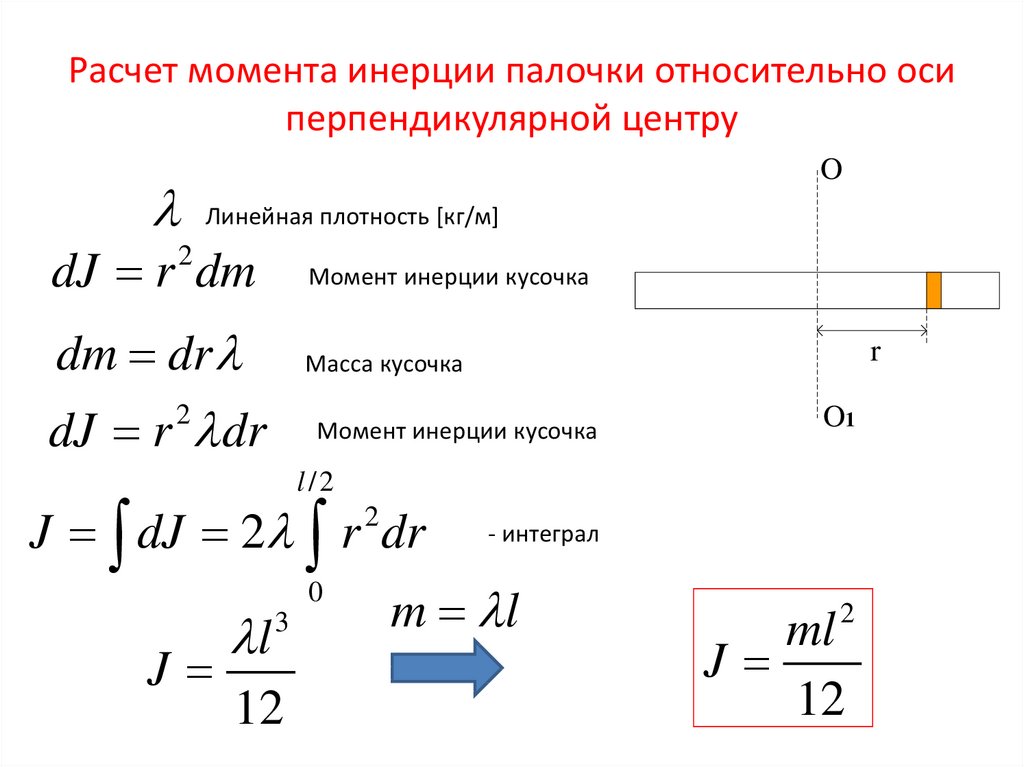
Если известен момент инерции I, то найти период колебаний рамки не составляет труда, а следовательно, и найти постоянную D. И наоборот, зная постоянную D, используя формулу (3) можно рассчитать момент инерции тела.
В данной лабораторной работе постоянная D не определяется. Для нахождения момента инерции рамки используется тело с известным моментом инерции. В качестве такого тела взят куб с достаточно идеальными поверхностями и гранями. Его момент инерции относительно оси, походящей через центр, вычисляется по формуле
(4)
где m – масса куба, кг, а – сторона куба, м.
Такой куб жестко закрепляется в рамке крутильного маятника. Если вывести нагруженную рамку из положения равновесия, то она будет совершать крутильные колебания, а её период колебаний равен
домашних заданий и упражнений – Как можно рассчитать момент инерции?
спросил
Изменено 1 месяц назад
Просмотрено 1к раз
$\begingroup$
Я хочу рассчитать угловое ускорение объекта, к которому приложена сила $F$ в точке $P$. Сцена двухмерная, а сложный объект состоит из множества прямоугольников, выровненных по осям.
Сцена двухмерная, а сложный объект состоит из множества прямоугольников, выровненных по осям.
Я вычислил центр масс $O$ с помощью средневзвешенного значения центроидов прямоугольников.
После этого вектор направления $r$ равен $P-O$, а крутящий момент можно рассчитать как: $ \tau = r \times F $, что в двумерном случае: $ r_x F_y – F_x r_y $
угловое ускорение можно рассчитать как $\alpha = \frac{\tau}{I}$, где $I$ — момент инерции.
Здесь я застрял. Мне нужно рассчитать момент инерции этого объекта. Я нашел страницу с моментами площади простых объектов. Там написано, что для прямоугольника: 92 $$
Где $C$ содержит центроиды, $w$ и $h$ размеры, а $m$ массы прямоугольников.
- домашние задания и упражнения
- ньютоновская механика
- динамика вращения
- крутящий момент
- момент инерции
$\endgroup$
7
$\begingroup$
Момент инерции массы относительно z (вне плоскости) двумерного прямоугольника, измеренный на центроиде, равен $$I = \frac{m}{12} (w^2+h^2) $$, где $w$ — ширина, а $h$ — высота.
Итак, рассмотрим общий случай приложения к телу двумерной силы с компонентами $A_x$ и $A_y$, а также момента $\tau_A$ в точке A с координатами $x_A$ и $y_A$.
Уравнения движения отслеживают движение центра масс с координатами $x_C$ и $y_C$, а также углом ориентации $\theta$.
$$\begin{выровнено} A_x & = м \ddot{x}_C \\ A_y & = m \ddot{y}_C \\ \tau_A-A_x (y_A-y_C) + A_y (x_A-x_C) & = I \ddot{\theta} \end{выровнено} $$
Теперь, чтобы ответить на более общий вопрос, как рассчитать MMOI для 2D-фигур.
- Предположим, что твердое тело имеет одинаковую толщину $t$ в плоскости, и задайте малый элемент объема $${\rm d}V = t\, {\rm d}A$$
- Таким образом, общая масса вычисляется из объема с использованием однородной плотности $\rho$ $$ m = \int \rho\, {\rm d}V $$
- Центр масс вычисляется с помощью аналогичного интеграла
$$ \pmatrix{x_C \\ y_C} = \frac{1}{m} \int \rho \pmatrix{x\\y} {\rm d}V $$ 92$.
Вам также может понадобиться знать теорему о перпендикулярной оси : для тонкой пластинки момент инерции относительно оси, проходящей через центр масс, перпендикулярной пластинке, равен сумме моментов инерции относительно двух перпендикулярные оси в плоскости.
 Итак, если ваш прямоугольник центрирован в начале координат в плоскости XY, то момент инерции относительно оси Z находится из $I_Z = I_X + I_Y$
Итак, если ваш прямоугольник центрирован в начале координат в плоскости XY, то момент инерции относительно оси Z находится из $I_Z = I_X + I_Y$Это должно позволить вам понять, как решить вашу проблему. 92) + Сумма угловых моментов инерции каждой детали в отдельности. Под dx и dy мы подразумеваем расстояние между ЦТ каждого компонента и ЦТ интегрированной конечной формы.
Ваш крутящий момент равен Fp
P – ваш моментный рычаг, но его необходимо отрегулировать по центру центра тяжести системы, а F – усилие.
И ваше угловое ускорение, омега = I* крутящий момент.
$\endgroup$
Вращательный момент инерции
Вращательный момент инерции Авторское право © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.Дата: четверг, 29 марта, 16:00.
Вы знакомы со вторым законом Ньютона для перевода:
F = м * аВ этом квартале вы узнаете об аналоге по очереди:
крутящий момент = (момент инерции) * (угловое ускорение)На этой неделе вы измерите момент инерции большого обруча.
 экспериментально, используя это уравнение.
Поскольку обруч представляет собой относительно простую геометрическую форму,
также можно рассчитать его момент инерции
теоретически.
Цель эксперимента на этой неделе — выяснить,
значения совпадают в пределах погрешностей; и, если нет,
объяснить несоответствие.
экспериментально, используя это уравнение.
Поскольку обруч представляет собой относительно простую геометрическую форму,
также можно рассчитать его момент инерции
теоретически.
Цель эксперимента на этой неделе — выяснить,
значения совпадают в пределах погрешностей; и, если нет,
объяснить несоответствие.Теоретический момент инерции
Для простых твердых тел можно рассчитать момент инерции от массы, размера и формы. Попросите одного члена каждой лабораторной группы сосредоточиться на делать это для вашего обруча.
Измерьте массу обруча M и ее неопределенность. Предположим, что обруч идеально круглый и однородный. толщина. Измерьте его внутренний и внешний диаметры. Вычислить его внутренний и внешний радиусы, R(внутренний) и Р(наружный) . Найдите уравнение момента инерции обруча. в вашем учебнике. Используйте его и ваши измерения, чтобы рассчитать момент инерция вашего обруча и неуверенность в нем.
Динамический момент инерции
Вы можете приложить постоянный крутящий момент к ступице, удерживающей обруч, подвешивая грузы на веревке, которая обмотана вокруг ступицы.
 Когда веса падают, они заставляют ступицу вращаться.
Вы можете предположить, что крутящий момент, приложенный весами, равен
Когда веса падают, они заставляют ступицу вращаться.
Вы можете предположить, что крутящий момент, приложенный весами, равенкрутящий момент = (масса веса) * г * (радиус ступицы)На самом деле крутящий момент немного меньше, чем это. Почему?Благодаря этому крутящему моменту втулка и обруч вращаются. Их угловое ускорение равно
угловое ускорение = (крутящий момент) / (момент инерции)Груз падает вниз с линейным ускорением, равным связано с угловым ускорением ступицы через:
линейное ускорение = (угловое ускорение) * (радиус ступицы)Составьте уравнение, связывающее линейное ускорение веса к его массе. Выразите его в виде:
линейное ускорение = (что-то) * (масса веса)Выполните серию экспериментов, чтобы измерить это ускорение. Поместите не менее 4 различных грузов на подвесной груз. (от 100 до 500 грамм). Для каждой гири измерьте время, за которое гиря падать до самого мягкого ящика.


 Итак, если ваш прямоугольник центрирован в начале координат в плоскости XY, то момент инерции относительно оси Z находится из $I_Z = I_X + I_Y$
Итак, если ваш прямоугольник центрирован в начале координат в плоскости XY, то момент инерции относительно оси Z находится из $I_Z = I_X + I_Y$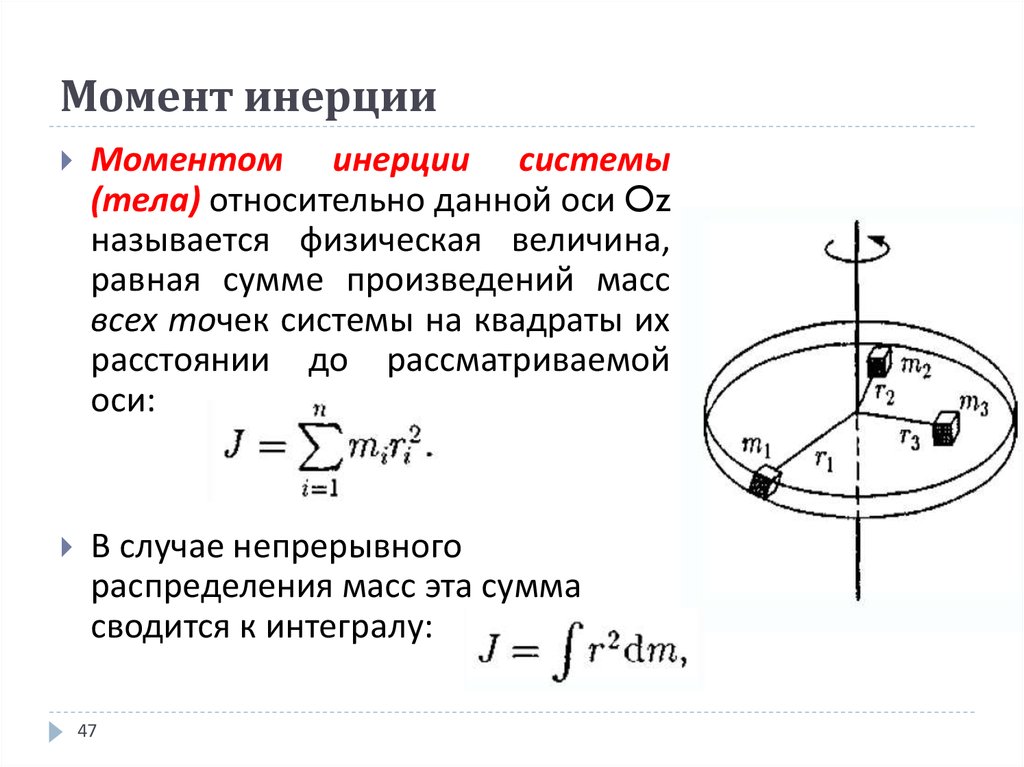 экспериментально, используя это уравнение.
Поскольку обруч представляет собой относительно простую геометрическую форму,
также можно рассчитать его момент инерции
теоретически.
Цель эксперимента на этой неделе — выяснить,
значения совпадают в пределах погрешностей; и, если нет,
объяснить несоответствие.
экспериментально, используя это уравнение.
Поскольку обруч представляет собой относительно простую геометрическую форму,
также можно рассчитать его момент инерции
теоретически.
Цель эксперимента на этой неделе — выяснить,
значения совпадают в пределах погрешностей; и, если нет,
объяснить несоответствие. Когда веса падают, они заставляют ступицу вращаться.
Вы можете предположить, что крутящий момент, приложенный весами, равен
Когда веса падают, они заставляют ступицу вращаться.
Вы можете предположить, что крутящий момент, приложенный весами, равен