Как определить по графику производную: График производной функции - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

описание, свойства, значение, отличие от графика функции

Содержание:

График производной функции — описание
Свойства графика
Знак производной на интервалах возрастания
Знак производной на интервалах убывания
Производная и угловой коэффициент касательной
В каких точках производная равна нулю
Примеры производной на графике функции

Содержание

График производной функции — описание
Свойства графика
Знак производной на интервалах возрастания
Знак производной на интервалах убывания
Производная и угловой коэффициент касательной
В каких точках производная равна нулю

Примеры производной на графике функции

График производной функции — описание

Производная функции — это скорость изменения у при изменении х. При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: $f'(x)$.

Зависимость производной функции от скорости изменения y заключается в том, что они прямо пропорциональны. Значение производной может быть как больше, так и меньше нуля. Производную функции используют для нахождения точек максимума и минимума функций, а также промежутков их возрастания и убывания.

При помощи вычисления производной и приравнивания её к нулю, возможно найти точки, разбивающие числовую ось на интервалы. Знак производной будет определяться на каждом из найденных интервалов, что позволит сделать в дальнейшем сделать вывод о возрастании или убывании функции.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Производная функции $f(x)$ в точке $x_0$ эквивалентна тангенсу угла наклона касательной к графику функции в $x_0$.

$f'(x_0)\;=\;tg\alpha$

Свойства графика

Производная будет положительной на интервалах возрастания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает положительным значением, график функции возрастает в обозначенном интервале.
Производная будет отрицательной на интервалах убывания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает отрицательным значением, график функции убывает в обозначенном интервале.

В точке х производная будет равняться угловому коэффициенту касательной к графику функции в обозначенной точке.
Производная равняется нулю в точках максимума и минимума функции, в тех же случаях параллельности касательной к графику функции и оси $ОХ$.

Знак производной на интервалах возрастания

Определим, какая функция называется возвращающей.

$y = f(x)$ будет возрастать на интервале $X$, если для любых $x_1\;\in\;X$ и $x_2\;\in\;X$, где $x_2\;>\;x_1$, справедливо неравенство $f(x_2)\;\geq\;f(x_1)$.

В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид $f(x_1) < f(x_2)$, функция $y = f(x)$ будет называться

строго возрастающей на интервале $(a, b)$.

На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.

В тех случаях, когда производная функции $y = f(x)$ положительна для любого x из интервала $X$, функция возрастает на $X$.

Знак производной на интервалах убывания

Определим, какая функция называется убывающей.

$y = f(x)$ будет убывать на интервале $X$, если для любых $x_1\;\in\;X$ и $x_2\;\in\;X$, где $x_2\;>\;x_1$ справедливо неравенство $f(x_2)\;\leq\;f(x_1).$

В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть имеет вид $f(x_1) < f(x_2)$, функция $y = f(x)$ будет называться строго убывающей на интервале $(a, b)$.

На интервалах убывания производная будет иметь отрицательный знак. То есть при подстановке значения из интервала в производную, получившееся число будет отрицательным.

В тех случаях, когда производная функции $y = f(x)$ отрицательна для любого x из интервала $X$, функция убывает на $X$.

Производная и угловой коэффициент касательной

Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.

В случае, когда при $x_1\;\rightarrow\;x_0$ имеется предельное положение секущей графика функции $y = f(x)$, оно будет носить название касательной к графику функции $y = f(x)$ в точке $A\;=\;((x_0;\;f(x_0))$. А значение производной в точке касания $x_0$ будет эквивалентно угловому коэффициенту касательной.

Угловой коэффициент касательной равен значению производной в точке касания $x_0$. И в соответствии с тем, что касательная параллельна прямой $y = -x$, ее угловой коэффициент равен -1.

Геометрический смысл производной состоит в том, что производная в точке $x_0$ равна угловому коэффициенту касательной к графику функции $y = f(x)$ в этой точке.

Формула уравнения касательной к графику функции $y = f(x)$ в точке $x_0$ выглядит следующим образом:

$y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)$

Рассмотрим рисунок графика функции $y = f(x)$. Очевидно, что для каждой из точек $A$ и $B$ графика функции справедливо следующее разностное отношение:

$\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha$

Здесь $\alpha$ — угол между прямой и осью $ОХ$, а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке $A$.

Зафиксируем точку $A$ и будем продвигать точку $B$ в направлении к ней. Тогда $\triangle x$ бесконечно уменьшается и приближается к 0, а секущая $АВ$ приближается к касательной $АС$.

Пример

Необходимо записать уравнение касательной к графику функции $y=x+e^{-2x}$, если эта функция параллельна прямой $y = -x. {-2x_0}\;=\;1\\-2x\;=\;0\\x_0\;=\;0$

Используем уравнение касательной

$y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x$

В каких точках производная равна нулю

Производная будет эквивалентна нулю в точках минимума, максимума и перегиба, при параллельной оси $ОX$ касательной. Рассмотрим следующий рисунок:

Очевидно, что в точках $C$ и $D$ касательная горизонтальна, тогда тангенс угла ее наклона будет равняться 0. Отсюда можно сделать вывод, что и производная равна 0. Точка C здесь будет являться точкой максимума. В этой точке возрастание функции изменяется на убывание, как меняется и знак производной — с плюса на минус. Точка $D$ здесь — точка минимума. В это случае также происходят изменения, но в обратном порядке.

Примечание

Важно отметить, что производная может не существовать в точке максимума. Такое происходит, если на графике изображен резкий излом, к которому невозможно провести касательную.

Рассмотрим еще одно изображение функции:

В данном случае производная будет эквивалентна нулю в точке перегиба, так как в точке $E$ касательная к функции параллельна оси $ОX$. В этом случае знак производной не будет изменяться, потому что до точки перегиба и после функция возрастает. Знак был и остается положительным.

Пример

Рассмотрим рисунок, на котором начерчен график функции $y = f(x)$. График определен на интервале (−3; 9). Необходимо определить количество точек, где производная функции $f(x)$ эквивалентна 0.

На данном рисунке очевидно, что производная функции f(x) эквивалентна нулю в точках максимума и минимума, то есть в точках −2; −1; 1; 4 и 6. Таким образом производная равна нулю в 5 точках.

Примеры производной на графике функции

Задача №1

Рассмотрим рисунок.

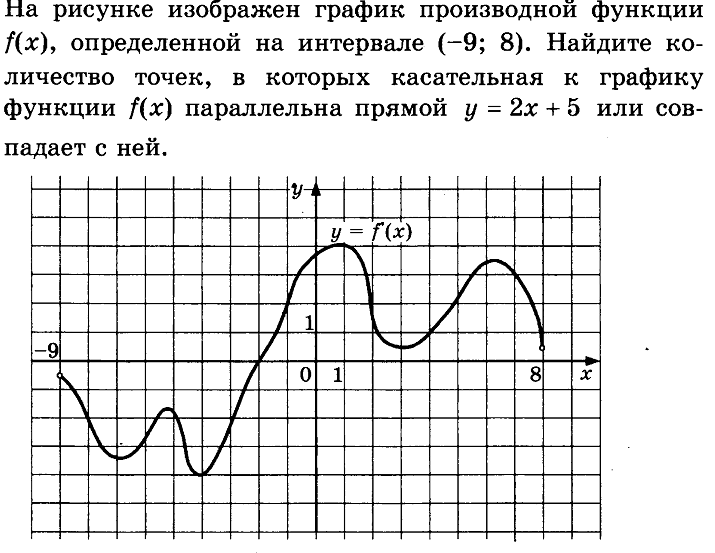
Рисунок изображает график производной функции $f(x)$. Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции $f(x)$ будет параллельна прямой $y = -2x – 11$ или совпадать с ней.

Решение

Используем правило о значении производной, которое в точке касания эквивалентно угловому коэффициенту касательной. Тогда, зная, что касательная параллельна прямой $y = -2x – 11$ или идентична с ней, можно утверждать, что угловые коэффициенты равны $-2$.

Теперь необходимо найти число точек, в которых $f'(x)\;=\;-2$. Искомое значение соответствует числу точек, где график производной пересекается с прямой $y = -2$. На заданном интервале 5 таких точек.

Ответ: 5.

Задача №2

Первый рисунок изображает график функции $y = f(x)$ и касательную к нему в точке с абсциссой $x_0$. Необходимо установить значение производной функции $f(x)$ в точке $x_0$.

Решение

Используем правило, гласящее, что угловой коэффициент касательной эквивалентен значению производной в точке касания, который в свою очередь эквивалентен тангенсу угла наклона данной касательной к оси абсцисс. На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол $ACB$, которому он будет равен:

$y'(x_0)\;=\;tg\angle ABC\;=\;\frac{AB}{BC}\;=\;\frac{2+4}{1+2}\;=\;2$

Ответ: 2.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Как определить наибольшее значение производной по графику. Производная функции

В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:

Значение производной в некоторой точке x 0 ,
Точки максимума или минимума (точки экстремума),
Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:

Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи.

Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т. е. f’(x) ≥ 0.
Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

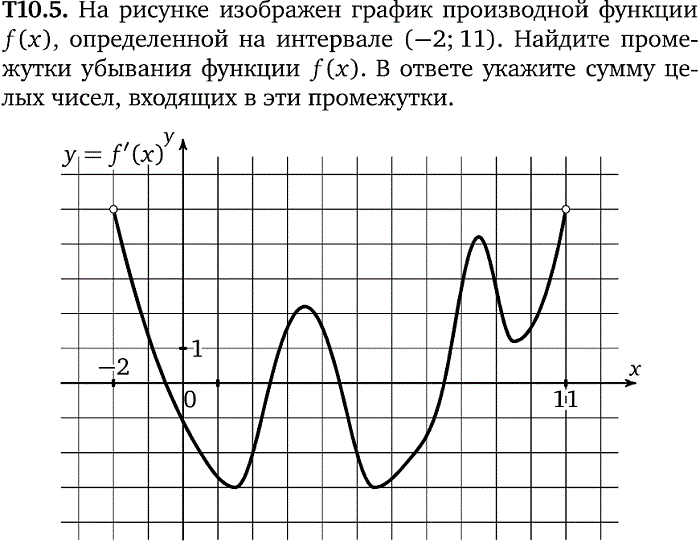
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.

Сергей Никифоров

Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.

Фарит Ямаев 26.10.2016 18:50

Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство. Спасибо.

Служба поддержки

Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции – все они возрастают на отрезке

Владлен Писарев 02. 11.2016 22:21

Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.

Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.

Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) – входят.

Учитывая, что первая часть ЕГЭ для “средней группы детского сада”, то наверное такие нюансы- перебор.

Отдельно, большое спасибо за “Решу ЕГЭ” всем сотрудникам- отличное пособие.

Сергей Никифоров

Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции. Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.

Ирина Ишмакова 20.11.2017 11:46

Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.

Александр Иванов

В заданиях 6429 и 7089 совершенно разные вопросы.

В одном про промежутки возрастания, а в другом про промежутки с положительной производной.

Противоречия нет.

Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.

A Z 28.01.2019 19:09

Коллеги, есть понятие возрастания в точке

(см. Фихтенгольц например)

и ваше понимание возрастания в точке x=2 противочет классическому определению.

Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.

В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.

Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.

Александр Иванов

Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке }

Разработка производных методов

Как и в случае с пределами, мы можем вычислять производные, используя алгебраические свойства.

Подраздел 2.3.1 Расчет производных с использованием определения

Определение вытекает из понятий. Использование его для расчета производных требует некоторого творчества.

Пример 2.3.1. Вычислите производную от $f(x)=x$.

Производная $f(x)=x$ в любой точке равна $f'(x)=1. $

Раствор.

\begin{выравнивание*} \lim_{x \to a} \frac{f(x)-f(a)}{x-a} = \amp \text{определение}\\ \lim_{x \to a} \frac{x-a}{x-a} = \amp \text{ подставляя функцию}\\ \lim_{x \to a} 1 = \amp \text{алгебра}\\ 1. \amp \text{известный предел} \end{выравнивание*} 92)}{x-a} = \amp \text{ фактор}\\ \lim_{x \to a} \frac{3(x-a)(x+a)}{x-a} = \amp \text{ фактор больше}\\ \lim_{x \to a} 3(x+a) = \amp \text{разделить}\\ 6a \amp \text{ известные пределы} \end{выравнивание*}

Подраздел 2.3.2 Производная суммы

Что мы можем сделать, если мы хотим вычислить производную суммы функций, т. е. $f(x)+g(x)\text{?}$ Мы можем попробовать использовать определение.

\начать{выровнять*} \frac{d(f(x)+g(x))}{dx} = \amp \\ \lim_{x \to a} \frac{(f(x)+g(x))-(f(a)-g(a))}{x-a} = \amp \text{определение}\\ \lim_{x \to a} \frac{(f(x)-f(a))+(g(x)-g(a))}{x-a} = \amp \text{ коммутативное свойство}\\ \lim_{x \to a} \frac{f(x)-f(a)}{x-a}+\frac{g(x)-g(a)}{x-a} = \amp \text{алгебраическое свойство} \\ \lim_{x \to a} \frac{f(x)-f(a)}{x-a}+ \lim_{x \to a} \frac{g(x)-g(a)}{x-a} = \amp \text{ ограничение свойства суммирования}\\ \frac{d f(x)}{dx}+ \frac{d g(x)}{dx} = \amp \text{определение} \end{выравнивание*}

Подраздел 2.

3.3 Производная скалярного произведения

Что мы можем сделать, если хотим вычислить производную скаляра, умноженную на функцию, т. е. $k \cdot f(x)\text{?}$ Снова воспользуемся определением.

\начать{выровнять*} \frac{d k f(x)}{dx} = \amp \\ \lim_{x \to a} \frac{k f(x)- k f(a)}{x-a} = \amp \text{определение} \конец{выравнивание*}

Завершите это доказательство. Вспомните пример выше.

Подраздел 2.3.4 Производное продукта

Существует также свойство для производного продукта, но это не просто применение предельного свойства для продукта. Укажите причину для каждой строки этого доказательства.

\начать{выровнять*} \frac{d f(x)g(x)}{dx} = \amp \text{вопрос}\\ \lim_{x \to a} \frac{f(x)g(x)-f(a)g(a)}{xa} = \amp \underline{\hspace{4.545454545454546em}}\\ \lim_{x \to a} \frac{f(x)g(x)-f(x)g(a)+f(x)g(a)-f(a)g(a)}{x-a} = \amp \text{ очень умный шаг} \\ \lim_{x \to a} \frac{f(x)[g(x)-g(a)]+[f(x)-f(a)]g(a)}{x-a} = \amp\ подчеркивание{\hspace{4. 545454545454546em}} \\ \lim_{x \to a} \frac{f(x)[g(x)-g(a)]}{x-a} + \frac{[f(x)-f(a)]g(a)} {xa} = \amp \underline{\hspace{4.545454545454546em}}\\ \lim_{x \to a} \frac{f(x)[g(x)-g(a)]}{x-a} + \lim_{x \to a} \frac{[f(x)-f( a)]g(a)}{xa} = \amp \underline{\hspace{4,545454545454546em}} \\ \lim_{x \to a} f(x)\lim_{x \to a} \frac{g(x)-g(a)}{x-a} + g(a)\lim_{x \to a} \ frac {f (x) -f (a)} {xa} = \ amp \ underline {\ hspace {4,545454545454546em}} \\ f(a)g'(a)+g(a)f'(a). \amp \underline{\hspace{4.545454545454546em}} \end{выравнивание*}

Мы можем проиллюстрировать правило произведения, используя произведение для представления площади прямоугольника, как показано на рисунке 2.3.4. Обратите внимание, что изменение площади прямоугольника представляет собой гномон (перевернутая буква L), состоящий из $f(a)g ‘(a)\text{,}$ $f'(a)g'(a)\text{,}$ и $g(a)f'(a)\text{.}$ Это соответствует правилу произведения $f(a)g'(a)+g(a)f'(a)$, за исключением маленького квадрата $f'(a)g'(a)\text{.}\ ) В пределе площадь этого квадрата стремится к нулю. Действительно, на ранних стадиях разработки производной именно так они и поступали. 9\пи.$

Подраздел 2.3.7 Производные тригонометрических функций

Мы можем доказать, что для $f(x)=\sin(x)\text{,}$ $f'(x)=\cos(x).$ Аналогичным образом мы можем показать, что для $g (x)=\cos(x)\text{,}$ $g'(x)=-\sin(x).$

КПП 2.3.6.

Используя тождества триггеров и свойства производных, найдите производные для $\tan(x)\text{,}$ $\cot(x)\text{,}$ $\sec(x)\text {,}$ и $\csc(x)\text{.}$

Как вычислить производную от (x,y) точек данных в Excel

В этом примере мы сэмплируем функцию f(x)=x⁢sin(x2)+1 затем вычислите его производную по точкам выборки данных, используя DERIVXY , и сравните результат с аналитическими производными, заданными формулой f'(x)=sin(x2)+2⁢x2⁢cos(x2)

Решение

Используя формулы, показанные в таблице 1, мы генерируем с помощью автозаполнения (x,y) значений данных и аналитические производные для значений x . Числовые значения показано в Таблице 2 ниже:

Таблица 1
	A	B	C
3	X_DATA	Y_DATA	АНАЛИТИЧЕСКИЕ ПРОИЗВОДИТЕЛЬНЫ2)
6			⇓ Перетащите вниз до строки 20

⇓

Таблица 2
	A	B	C
3	x_data	y_data	Analytic der
4	0	1	0
5	0.25	1.015615	0.1872153
6	0.5	1.123702	0.7318602
7	0.75	1.399977	1. 4849677
8	1	1.841471	1.9220756
9	1.25	2.249957	1.0258913
10	1.5	2.16711	-2.0487081
11	1.75	1.138268	-6.0268418
12	2	-0.5136	-5.9859515
13	2.25	-1.1135	2.5335616
14	2.5	0.917052	12.459939
15	2.75	3.634003	5.3043158
16	3	2.236355	-15.988226
17	3.25	-1.94996	-9.773066
18	3.5	-0.08892	22.972966
19	3. 75	4.739551	3,0952707
20	4	-0,15161	-30,933007

Используя формулы DERIVXY , показанные в таблице 3, мы генерируем с помощью автозаполнения числовые производные на x -значения и вычислить относительную ошибку относительно аналитические производные. Численные результаты показаны в Таблице 4 ниже.

Обратите внимание, что мы передали определенные имена x_data и y_data для столбцов A4:A20 и B4:B20 соответственно. Это один из способов заблокировать данные, поэтому автозаполнение игнорирует эти аргументы и увеличивает только третий аргумент. В качестве альтернативы мы могли бы использовать знак доллара, $, чтобы заблокировать первые два аргумента во время автозаполнения с помощью формула =ПРОИЗВОДНЫЙXY($A$4:$A$20, $B$4:$B$20, A4) .

Стол 3
	E	F
3	Numerical Derivatives	% Errors
4	=DERIVXY(x_data,y_data,A4)	1
5	=DERIVXY(x_data ,y_data,A5)	=ABS((E5-C5)/C5)
	⇓ Перетащите вниз до строки 20

⇓

Таблица 4
	E	F
3	Numerical Derivatives	% Errors
4	-0.006256108	100.00%
5	0.189289352	1.11%
6	0.733522457	0.23%
7	1.488966928	0. 27%
8	1.923837894	0.09%
9	1.015441218	1.02%
10	-2.07793704	1.43%
11	-6.043962293	0.28%
12	-5.914791221	1.19%
13	2.68187738	5.85%
14	12.35516509	0.84%
15	4.867529358	8.23%
16	-15.99364056	0.03%
17	-7. 4125	19.16%
18	19.69241868	14.28%
19	9.404971886	203.85%
20	-58,06465252	87,71%

Обратите внимание, что ошибки максимальны вблизи конечных точек данных, поскольку сплайн по умолчанию не ограничивает производные в конечной точке. Но в этом примере мы знаем точное производные в концевых точках от аналитической формулы. Мы можем повысить точность, поставив эти данные с помощью ключей ISLOPE и ESLOPE в дополнительном элементе управления аргумент за ДЕРИВКСИЙ . Мы называем диапазон K1:L2 end_slopes и определяем следующие пары ключ/значение для начального и конечного наклона. с использованием вычисленных значений аналитических производных в C4 и C20 из Таблицы 2 выше.

96 2

	К	Л
1	ISLOPE	0	ЭСЛОПА	-30,933

Мы регенерируем новые производные и ошибки в столбцах h5:h30 и I4:I20 из расширенных формул DERIVXY в таблице 5. Числовые значения, полученные с помощью автозаполнения, показаны в Таблице 6 ниже.

Таблица 5
	H	I
3	Nummerical Derivative with end slopes	% Errors
4	=DERIVXY(x_data,y_data,A4,1,end_slopes)	1
5	=DERIVXY(x_data,y_data,A5,1,end_slopes)	=ABS((H5-C5)/C5)
	⇓ Drag down to row 20

⇓

Таблица 6
	H	I
3	Кол. Дер. with end slopes	% Errors
4	0	0.00%
5	0. 187612966	0.21%
6	0.733971891	0.29%
7	1,488845578	0,26%
8	1.923873859	0.09%
9	1.015418708	1.02%
10	-2.077882964	1.42%
11	-6.044156087	0.29%
12	-5,91407012	1,20%
13	2,679186771	5,75%
14	12,3656520649999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999979009r9009.4	15	4.830054635	8.94%
16	-15.853783	0.84%
17	-8.422469647	13.82%
18	21. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Поиск: Рубрики Вакансии Востребованные вакансии Обучение в Европе Обучение за границей Работа Работа для всех Советы абитуриенту Студенту Студенческие будни Разное 2019 © Все права защищены. Карта сайта Меню Поиск: Советы абитуриенту Работа для всех Востребованные вакансии Студенческие будни Обучение за границей

описание, свойства, значение, отличие от графика функции

График производной функции — описание

Свойства графика

Знак производной на интервалах возрастания

Знак производной на интервалах убывания

Производная и угловой коэффициент касательной

В каких точках производная равна нулю

Примеры производной на графике функции

Поиск по содержимому

Как определить наибольшее значение производной по графику. Производная функции

Вычисление значения производной. Метод двух точек

Вычисление точек максимума и минимума

Нахождение интервалов возрастания и убывания функции

Разработка производных методов

Подраздел 2.3.1 Расчет производных с использованием определения

Пример 2.3.1. Вычислите производную от \(f(x)=x\).

Подраздел 2.3.2 Производная суммы

Подраздел 2.

Подраздел 2.3.4 Производное продукта

Подраздел 2.3.7 Производные тригонометрических функций

КПП 2.3.6.

Как вычислить производную от (x,y) точек данных в Excel

Решение

96 2

Оставить комментарий Отменить ответ