Сила Ампера. Правило левой руки | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Магнитное поле действует на проводник с током. Силу, которая возникает при этом, называют силой Ампера.
Сила Ампера действует на проводник с током в магнитном поле.
Исследуем, от чего зависит модуль и направление данной силы. С этой целью используем установку, в которой прямолинейный проводник подвешен на тонких проволочках в магнитном поле постоянного магнита (рис. 6.16). Гибкие проволочки, присоединенные к концам проводника, позволяют включать его в электрическую цепь, сила тока в которой регулируется с помощью реостата и измеряется амперметром.
Легкая, но жесткая тяга соединяет проводник с чувствительным измерителем силы.
Замкнув электрическую цепь, в которую входит исследуемый проводник, увидим, что он отклонится от положения равновесия, а измеритель покажет определенное значение силы. Увеличим силу тока в проводнике в 2 раза и увидим, что сила, действующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока в проводнике вызовут соответствующие изменения силы, которая действует на проводник. Сопоставление полученных результатов позволяет сделать вывод, что сила
Увеличим силу тока в проводнике в 2 раза и увидим, что сила, действующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока в проводнике вызовут соответствующие изменения силы, которая действует на проводник. Сопоставление полученных результатов позволяет сделать вывод, что сила
F ~ I.
Сила Ампера пропорциональна силе тока в проводнике.
| Рис. 6.16. Установка для измерения силы Ампера, действующей на прямой проводник с током в магнитном поле |
Расположим еще один магнит рядом с первым. Длина той части проводника, которая находится в магнитном поле, увеличится приблизительно в 2 раза. Значение силы, действующей на проводник, также увеличится приблизительно в два раза. Таким образом, сила F, действующая на проводник с током в магнитном поле, пропорциональна длине части проводника Δl, которая находится в магнитном поле:
Таким образом, сила F, действующая на проводник с током в магнитном поле, пропорциональна длине части проводника Δl, которая находится в магнитном поле:
F ~ Δl.
Сила Ампера пропорциональна длине активной части проводника.
Сила увеличится также тогда, когда применим другой, более «сильный» магнит с большей магнитной индукцией. Это позволяет сделать вывод о зависимости силы F от магнитной индукции поля B:
F ~ B. Материал с сайта http://worldofschool.ru
| Рис. 6.17. С помощью левой руки можно определить направление силы Ампера |
Максимальной сила будет тогда, когда между магнитной индукцией и проводником угол α = 90°. Если же этот угол равен нулю, то есть магнитная индукция будет параллельной проводнику, то сила будет равна нулю.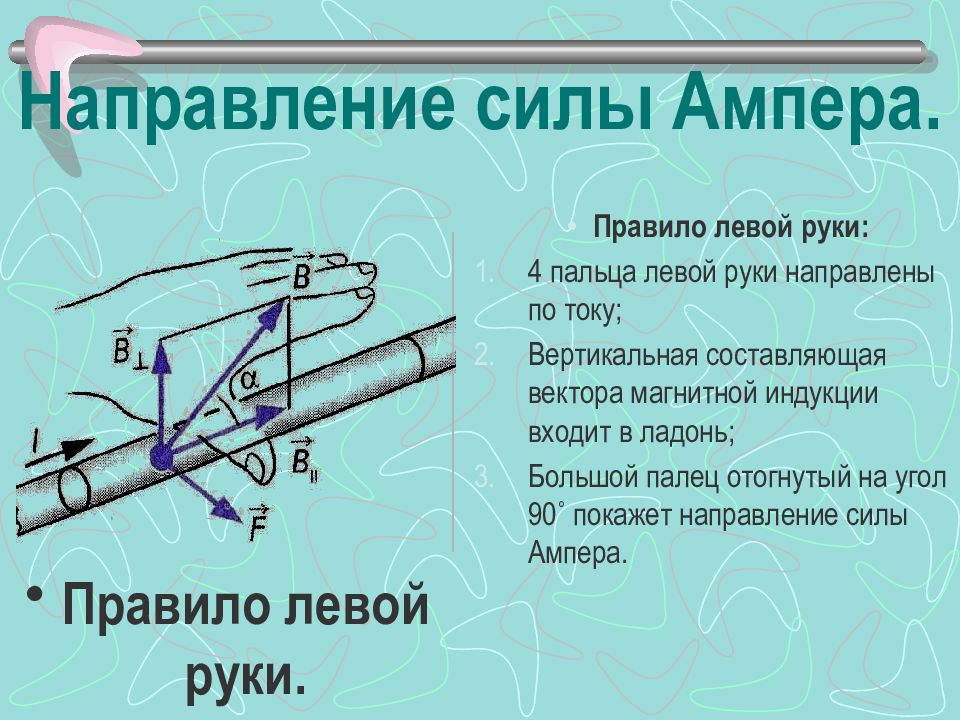
Окончательно формула для расчета силы Ампера будет иметь вид
FА = BIΔl • sin α.
Направление силы Ампера определяется по правилу левой руки (рис. 6.17).
Правило левой руки. Если левую руку разместить так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца показывали направление тока, то отставленный большой палец покажет направление силы, действующей на проводник с током в магнитном поле.
Пальцы левой руки для определения силы ампера
Доклад на тему применение закона ампера
Как действует установка для силы ампера
Реакция разложения перманганата калия уравнение
9.
 сила ампера (формула, правило левой руки
сила ампера (формула, правило левой руки
Какое явление описывает сила Ампера?
Какой может быть установка для исследования силы Ампера?
От каких величин зависит сила Ампера?
Как определяется направление силы Ампера?
Правило левой руки
Проводник с током в магнитном поле. Магнитная индукция.
Если проводник, по которому проходит электрический ток, внести в магнитное поле, то в результате взаимодействия магнитного поля и проводника с током проводник будет перемещаться в ту или иную сторону.
Допустим, что в магнитном поле магнита NS находится проводник, расположенный перпендикулярно плоскости рисунка; по проводнику протекает ток в направлении от нас за плоскость рисунка.
Ток, идущий от плоскости рисунка к наблюдателю, обозначается условно точкой, а ток, направляющийся за плоскость рисунка от наблюдателя,— крестом.
Движение проводника с током в магнитном поле
2 — результирующее магнитное поле.
Всегда всё уходящее на изображениях обозначается крестом,
а направленное на смотрящего – точкой.
Под действием тока вокруг проводника образуется свое магнитное поле рис.1.
Применяя правило буравчика, легко убедиться, что в рассматриваемом нами случае направление магнитных линий этого поля совпадает с направлением движения часовой стрелки.
При взаимодействии магнитного поля магнита и поля, созданного током, образуется результирующее магнитное поле, изображенное на рис.2.
Густота магнитных линий результирующего поля с обеих сторон проводника различна. Справа от проводника магнитные поля, имея одинаковое направление, складываются, а слева, будучи направленными встречно, частично взаимно уничтожаются.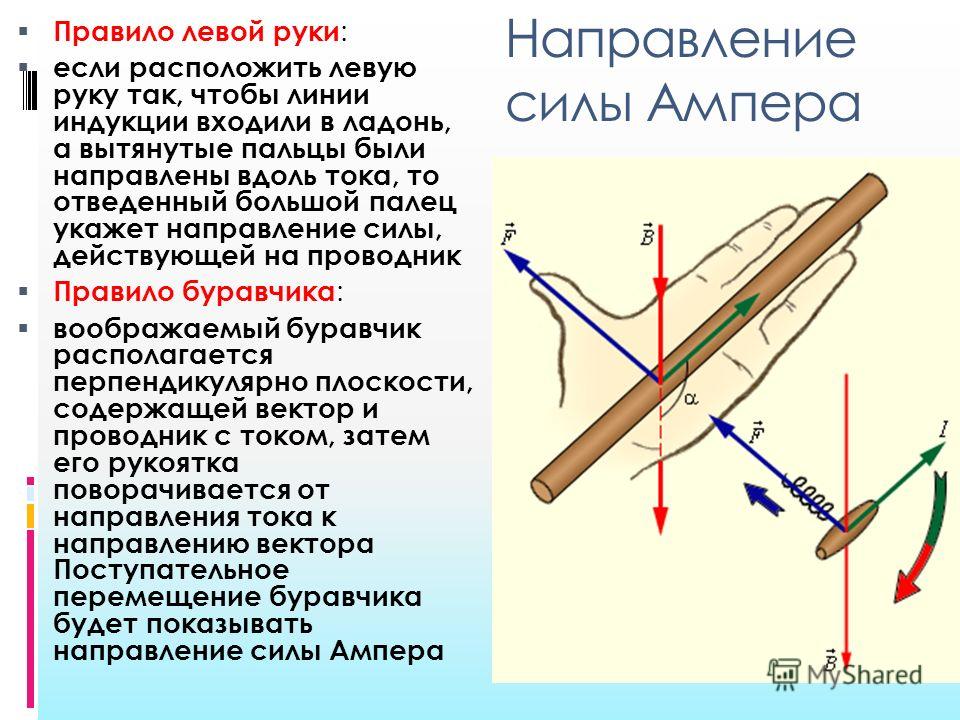
Следовательно, на проводник будет действовать сила, большая справа и меньшая слева. Под действием большей силы проводник будет перемещаться по направлению силы F.
Перемена направления тока в проводнике изменит направление магнитных линий вокруг него, вследствие чего изменится и направление перемещения проводника.
Для определения направления движения проводника в магнитном поле можно пользоваться правилом левой руки, которое формулируется следующим образом:
Если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление движения проводника.
Сила, действующая на проводник с током в магнитном поле, зависит как от тока в проводнике, так и от интенсивности магнитного поля.
Основной величиной, характеризующей интенсивность магнитного поля, является магнитная индукция В.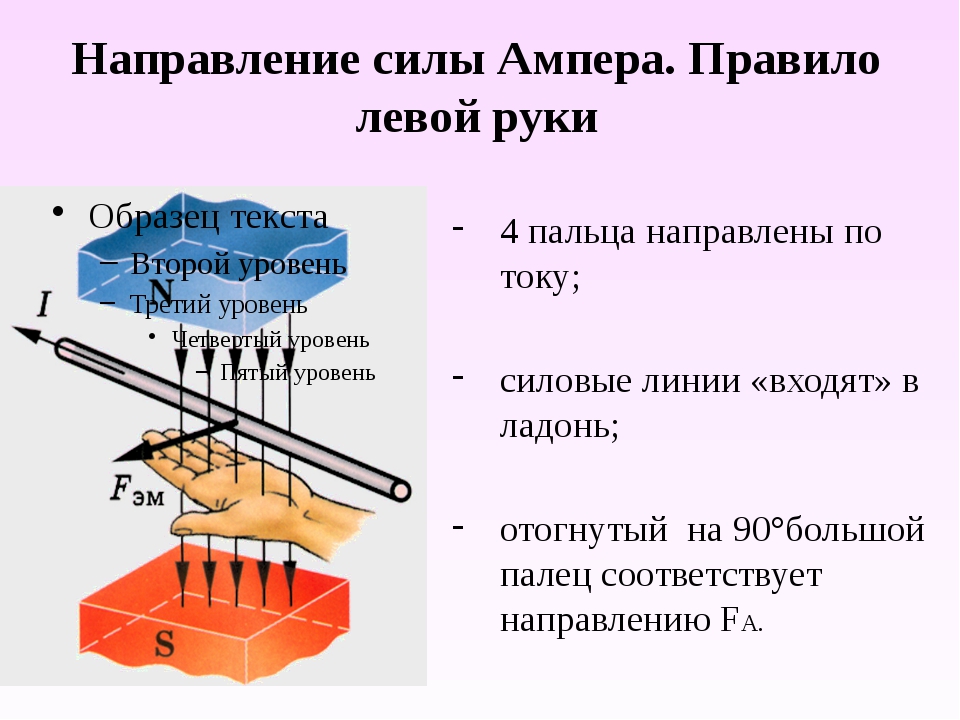 Единицей измерения магнитной индукции является тесла (
Единицей измерения магнитной индукции является тесла (
О магнитной индукции можно судить по силе действия магнитного поля на проводник с током, помещенный в это поле. Если на проводник длиной 1 м и с током 1 А, расположенный перпендикулярно магнитным линиям в равномерном магнитном поле, действует сила в 1 Н (ньютон), то магнитная индукция такого поля равна 1 Тл (тесла).
Магнитная индукция является векторной величиной, ее направление совпадает с направлением магнитных линий, причем в каждой точке поля вектор магнитной индукции направлен по касательной к магнитной линии.
Сила F, действующая на проводник с током в магнитном поле, пропорциональна магнитной индукции
F=BIl.
Эта формула верна лишь в том случае, когда проводник с током расположен перпендикулярно магнитным линиям равномерного магнитного поля.
Если проводник с током находится в магнитном поле под каким-либо углом а по отношению к магнитным линиям, то сила равна:
F=BIl sin a.
Если проводник расположить вдоль магнитных линий, то сила F станет равной нулю, так как
(Подробно и доходчиво в видеокурсе “В мир электричества – как в первый раз!”)
Формула силы Ампера в физике
Содержание:
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$\bar{F}, \bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее. Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.1).
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
большой палец укажет направление силы Ампера (рис.1).
Закон Ампера
Элементарная сила Ампера ($d\bar{F}_A$) определена законом (или формулой) Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(1)$$где I – сила тока, $d \bar{l}$ – малый элемент длины проводника – это вектор, равный по модулю длине проводника, направленный в таком же направлении как вектор плотности тока, $\bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d \bar{F}_{A}=\bar{j} \times \bar{B} d V(2)$$где $\bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I \cdot B \cdot d l \cdot \sin \alpha(3)$$где $\alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током. {7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B \operatorname{lsin} \alpha$$где $\alpha$ – искомый угол. Следовательно:
Следовательно:
Ответ. $\alpha=\arcsin \left(\frac{F}{I B l}\right)$
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга. Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d \bar{F}_{A}=I d \bar{l} \times \bar{B}(2.1)$$Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$где ток, который течет в элементе проводника dx, выразим как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B \cdot 2 \pi x=\mu_{0} I_{1} \rightarrow B=\frac{\mu_{0} I_{1}}{2 \pi x}$$где из рис.1 видно, что $a \leq x \leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 \leq l \leq 1$ . {a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
{a+b} \frac{\mu_{0} I_{1}}{2 \pi x} \cdot \frac{I_{2}}{b} d x=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=\frac{\mu_{0} I_{1}}{2 \pi} \cdot \frac{I_{2}}{b} \ln \left|\frac{a+b}{a}\right|$
Читать дальше: Формула силы выталкивания.
Формула силы Ампера
ОПРЕДЕЛЕНИЕСила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Здесь – сила Ампера, – сила тока в проводнике, – модуль вектора индукции магнитного поля, – длина участка проводника, на который воздействует магнитное поле, – угол между вектором индукции магнитного поля и направления тока.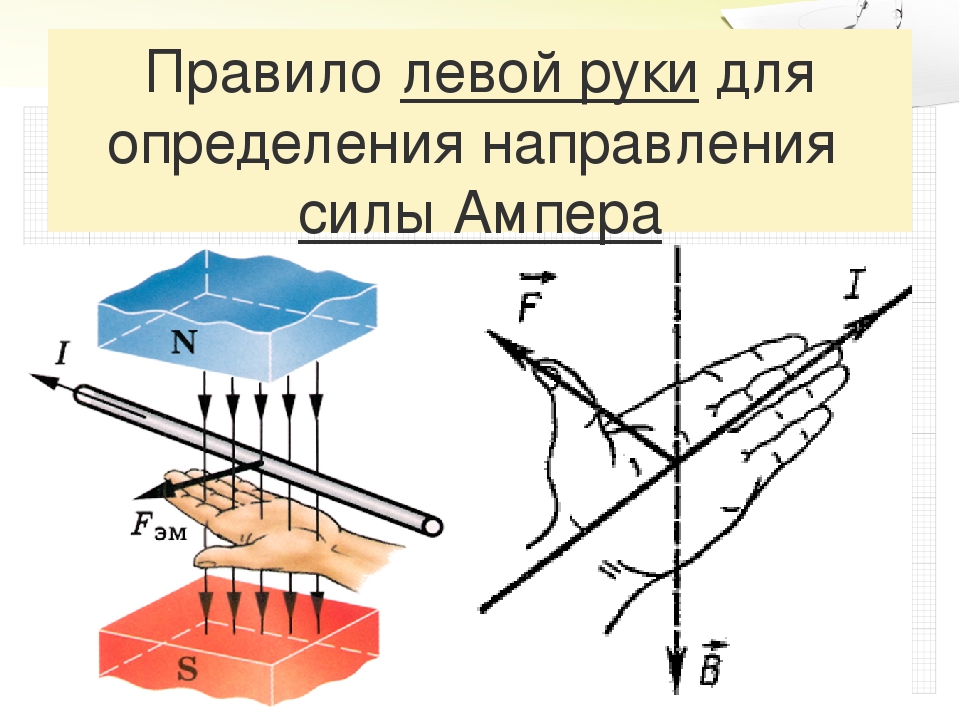
Единица измерения силы – Н (ньютон).
Сила Ампера — векторная величина. Сила Ампера принимает своё наибольшее значение когда векторы индукции и направления тока перпендикулярны ().
Направление силы ампера определяют по правилу левой руки:
Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Ампера.
Исторически электрическим током принято считать движение положительного заряда, то есть направление сила тока – от плюса к минусу.
Примеры решения задач по теме «Сила Ампера»
ПРИМЕР 1| Задание | Найти силу Ампера, действующую на прямой проводник длиной 3 м, по которому проходит ток силой 7 А. Вектор магнитной индукции составляет угол с проводником, его абсолютное значение – 2 Тл. |
| Решение | Электрический ток течёт по проводнику, значит направлен он также, как расположен проводник. Следовательно, угол между вектором магнитной индукции и проводником равен углу между ним и вектором движения тока. Остаётся только подставить значения в формулу: Следовательно, угол между вектором магнитной индукции и проводником равен углу между ним и вектором движения тока. Остаётся только подставить значения в формулу:
|
| Ответ | Сила ампера равна 21 ньютон. |
| Задание | На рисунке изображены два параллельно расположенных проводника, указаны направления сил тока и вектора магнитной индукции. В ответе указать, каким образом будет действовать на них сила Ампера (сближать проводники, отталкивать или действовать как-то иначе). Как изменится ситуация, если направить вектор магнитной индукции параллельно проводникам? |
| Решение | Определим направление силы Ампера по правилу левой руки. Очевидно, если расположить левую руку так, чтобы вектор входил в ладонь, а пальцы направить по линии движения тока в первом случае (вертикально вверх), то отогнутый большой палец будет направлен от наблюдателя. Также будет направлена и сила Ампера. Во втором проводнике ток направлен вертикально вниз, а сила Ампера – на наблюдателя. Оказалось, что под действием силы Ампера первый проводник отталкивается от наблюдателя, а второй притягивается к нему. Также будет направлена и сила Ампера. Во втором проводнике ток направлен вертикально вниз, а сила Ампера – на наблюдателя. Оказалось, что под действием силы Ампера первый проводник отталкивается от наблюдателя, а второй притягивается к нему.
Пусть вектор сонаправлен движению тока в первом проводнике, тогда и При вычислении силы Ампера нас интересуют не сами углы, а их синусы: и Сила Ампера в обоих проводниках равна нулю. |
| Ответ | Если вектор магнитной индукции направлен так, как показано на рисунке, то сила Ампера в первом проводнике будут направлена на наблюдателя, во втором – от него. Если вектор магнитной индукции направить параллельно проводникам, то сила Ампера возникать не будет. |
| Понравился сайт? Расскажи друзьям! | |||
Презентация по физике на тему ” решение задач на правило буравчика, правой и левой руки!(8 класс)
Сила Ампера: варианты расчета
Прежде чем сформулировать данную величину, необходимо разобраться, что такое понятие «сила» в физике.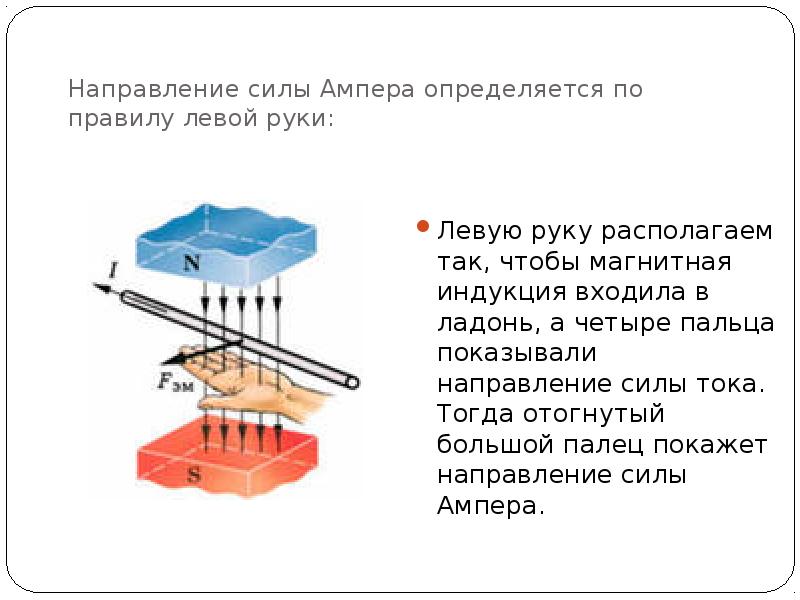 Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.
Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.
Рассчитывается элементарная сила Ампера по формуле:
где, dl – часть длины проводника, B –индукция магнитного контура, I – сила тока.
Рассчитывается также сила Ампера по формуле:
где, J – направление плотности тока, dv– элемент объема проводника.
Формулировка расчета модуля силы Ампера, согласно литературе, звучит так: данный показатель напрямую зависит от силы тока, протяженности проводника, синуса, образуемого между этим вектором и самим проводником угла, и величины значения вектора магнитного контура в модуле. Она и носит название модуля силы Ампера. Формула данного закона математически строится так:
где, B – модуль индукции магнитного контура, I – сила тока, l – длина проводника, α – образуемый угол. Максимальное значение будет при перпендикулярном их пересечении.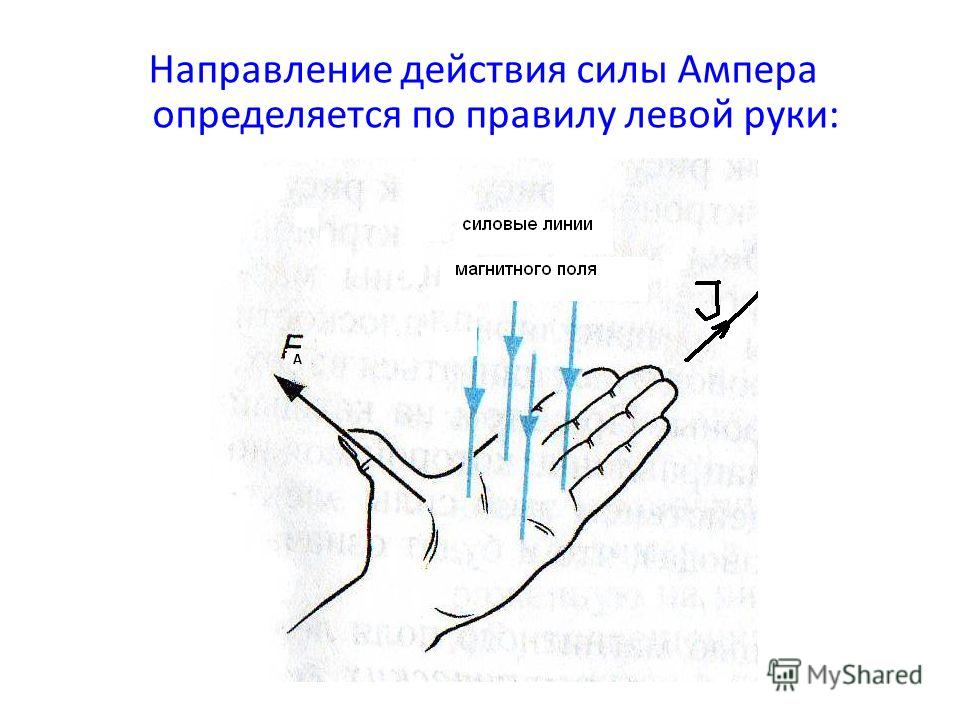
Показатель измеряется в ньютонах (условное обозначение – Н) или
. Он является векторной величиной и зависит от вектора индукции и тока.
Существуют и другие формулы для расчета силы Ампера. Но на практике они достаточно редко востребованы и тяжелы для понимания.
Какое правило применить
Слова синонимы: рука, винт, буравчик
Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.
Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.
Декартова система координат
Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.
Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.
В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:
- Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
- Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
- Тройка векторов (по порядку упоминания контекстом) правая.
Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом. Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:
- Правило буравчика применяется к произведению двух векторов.

- Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).
Простые приемы запоминания правил буравчика
Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.
Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.
И это неправильно. Поэтому приходится применять правило левой руки.
Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:
- Вектор радиуса круговой траектории направлен из центра к окружности.
- Если вектор ускорения направлен вверх, тело движется против часовой стрелки.
Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.
Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.
Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов. Можно значительно упростить вычисления.
Аналитическая геометрия в пространстве
Каждому известна задачка: стоя на одном берегу реки, определить ширину русла. Кажется уму непостижимым, решается в два счета методами простейшей геометрии, которую изучают школьники. Проделаем ряд несложных действий:
- Засечь на противоположном берегу видный ориентир, воображаемую точку: ствол дерева, устье ручейка, впадающего в поток.

- Под прямым углом линии противоположного берега сделать засечку на этой стороне русла.
- Найти место, с которого ориентир виден под углом 45 градусов к берегу.
- Ширина реки равна удалению конечной точки от засечки.
Определение ширины реки методом подобия треугольников
Используем тангенс угла. Не обязательно равен 45 градусов. Нужна большая точность – угол лучше брать острым. Просто тангенс 45 градусов равен единице, решение задачки упрощается.
Аналогичным образом удается найти ответы на животрепещущие вопросы. Даже в микромире, управляемом электронами. Можно однозначно сказать одно: непосвященному правило буравчика, векторное произведение векторов представляются скучными, занудными. Удобный инструмент, помогающий в понимании многих процессов. Большинству будет интересным принцип работы электрического двигателя (безотносительно к конструкции). Легко может быть объяснен использованием правила левой руки.
Во многих отраслях науке бок-о-бок идут два правила: левой, правой руки. Векторное произведение иногда может описываться так или эдак. Звучит расплывчато, предлагаем немедленно рассмотреть пример:
Векторное произведение иногда может описываться так или эдак. Звучит расплывчато, предлагаем немедленно рассмотреть пример:
Допустим, движется электрон. Отрицательно заряженная частица бороздит постоянное магнитное поле. Очевидно, траектория окажется изогнута благодаря силе Лоренца. скептики возразят, по утверждениям некоторых ученых электрон не частица, а скорее, суперпозиция полей. Но принцип неопределенности Гейзенберга рассмотрим в другой раз. Итак, электрон движется:
Расположив правую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление полета частицы, отогнутый на 90 градусов в сторону большой палец вытянется в направлении действия силы. Правило правой руки, являющееся иным выражением правила буравчика. Слова-синонимы. Звучит по-разному, по сути – одно.
Правило левой руки
Приведем фразу Википедии, отдающую странностью. При отражении в зеркале правая тройка векторов становится левой, тогда нужно применять правило левой руки вместо правой.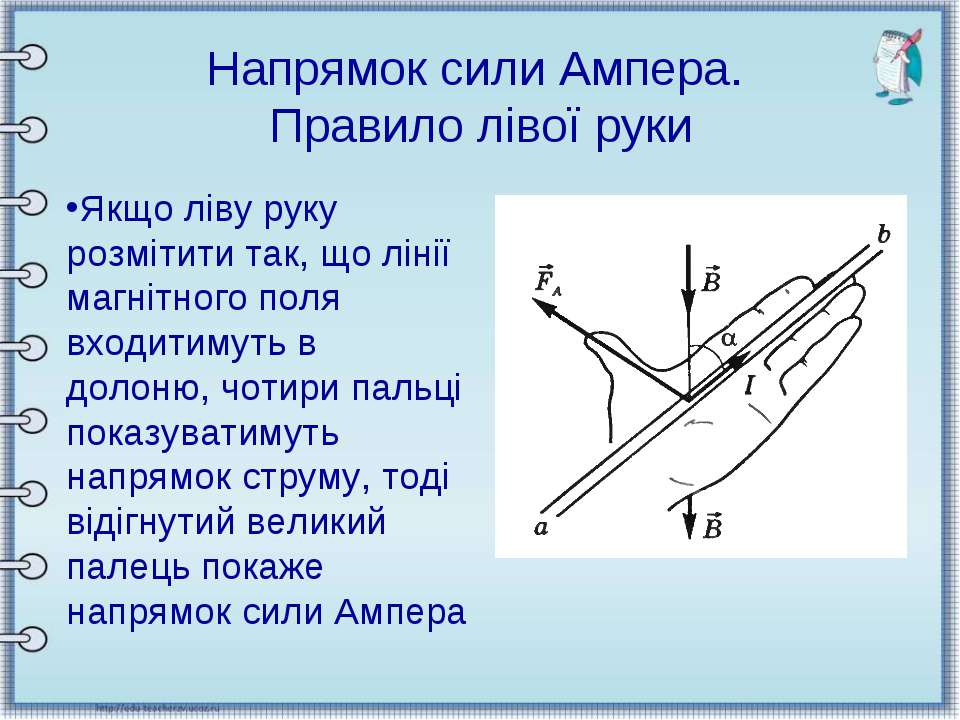 Летел электрон в одну сторону, по методикам, принятым в физике, ток движется в противоположном направлении. Словно отразился в зеркале, поэтому сила Лоренца определяется уже правилом левой руки:
Летел электрон в одну сторону, по методикам, принятым в физике, ток движется в противоположном направлении. Словно отразился в зеркале, поэтому сила Лоренца определяется уже правилом левой руки:
Если расположить левую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление течения электрического тока, отогнутый на 90 градусов в сторону большой палец вытянется, указывая вектор действия силы.
Видите, ситуации похожие, правила просты. Как запомнить, которое применять? Главный принцип неопределенности физики. Векторное произведение вычисляется во многих случаях, причем правило применяется одно.
Как связано магнитное поле с буравчиком и руками
В задачах по физике, при изучении электрических величин, часто сталкиваются с необходимостью нахождения направления тока, по вектору магнитной индукции и наоборот. Также эти навыки потребуются и при решении сложных задач и расчетов, связанных магнитным полем систем.
Прежде чем приступить к рассмотрению правил, хочу напомнить, что ток протекает от точки с большим потенциалом к точке с меньшим. Можно сказать проще — ток протекает от плюса к минусу.
Можно сказать проще — ток протекает от плюса к минусу.
Правило буравчика имеет следующий смысл: при вкручивании острия буравчика вдоль направления тока – рукоятка будет вращаться по направлению вектора B (вектор линий магнитной индукции).
Правило правой руки работает так:
Поставьте большой палец так, словно вы показываете «класс!», затем поверните руку так, чтобы направление тока и пальца совпадали. Тогда оставшиеся четыре пальца совпадут с вектором магнитного поля.
Наглядный разбор правила правой руки:
Чтобы увидеть это более наглядно проведите эксперимент – рассыпьте металлическую стружку на бумаге, сделайте в листе отверстие и проденьте провод, после подачи на него тока вы увидите, что стружка сгруппируется в концентрические окружности.
Опыт Эрстеда
Продолжительное время электрические и магнитные поля изучались раздельно. Но в 1820 году датский учёный Ханс Кристиан Эрстед во время лекции по физике обнаружил, что магнитная стрелка поворачивается возле проводника с током (см. Рис. 1). Это доказало магнитное действие тока. После проведения нескольких экспериментов Эрстед обнаружил, что поворот магнитной стрелки зависел от направления тока в проводнике.
Рис. 1. Опыт Эрстеда
Для того чтобы представить, по какому принципу происходит поворот магнитной стрелки вблизи проводника с током, рассмотрим вид с торца проводника (см. Рис. 2, ток направлен в рисунок, – из рисунка), возле которого установлены магнитные стрелки. После пропускания тока стрелки выстроятся определённым образом, противоположными полюсами друг к другу. Так как магнитные стрелки выстраиваются по касательным к магнитным линиям, то магнитные линии прямого проводника с током представляют собой окружности, а их направление зависит от направления тока в проводнике.
Рис. 2. Расположение магнитных стрелок возле прямого проводника с током
Для более наглядной демонстрации магнитных линий проводника с током можно провести следующий опыт. Если вокруг проводника с током высыпать железные опилки, то через некоторое время опилки, попав в магнитное поле проводника, намагнитятся и расположатся по окружностям, которые охватывают проводник (см. Рис. 3).
Рис. 3. Расположение железных опилок вокруг проводника с током (Источник)
Правило буравчика для магнитных полей
Речь шла о постоянных магнитах. У них все всегда понятно: где какой полюс и куда направлены линии магнитного поля — от северного полюса к южному. Но магнитное поле возникает и вокруг проводников, по которым течет ток. Просто оно слабое, так что даже если поднести два участка, по которым течет ток, особого притяжения или отталкивания мы не ощутим. Чтобы создать сильное электромагнитное поле, проводник накручивают вокруг какого-то сердечника. Это изделие называют соленоидом. Когда по нему течет ток, создается ощутимое магнитное поле. Но как направлены линии магнитного поля в электромагнитах? Где у них северный, где южный полюс? Вот это и выясняют с помощью правила буравчика.
Когда по нему течет ток, создается ощутимое магнитное поле. Но как направлены линии магнитного поля в электромагнитах? Где у них северный, где южный полюс? Вот это и выясняют с помощью правила буравчика.
Буравчик можно себе представить как обычный штопор с ручкой-перекладиной и витками, накрученными вправо. Чтобы закручивать такой штопор, ручку надо вращать вправо — по часовой стрелке. При этом острие штопора/буравчика продвигается вниз. Чтобы выкручивать его, надо рукоятку вращать влево — против часовой стрелки. Острие при этом движется вверх.
Правило буравчика для магнитного поля
С движением острия буравчика и направлением вращения рукоятки и связано определение направление магнитного поля. Вот как звучит правило буравчика (еще называют правило винта):
С ровными проводниками все просто. Представляете, вкручивать или выкручивать надо буравчик, получаете направление силовых линий. Если по условиям задачи есть только направление линий магнитного поля, при помощи правила буравчика можно установить направление тока.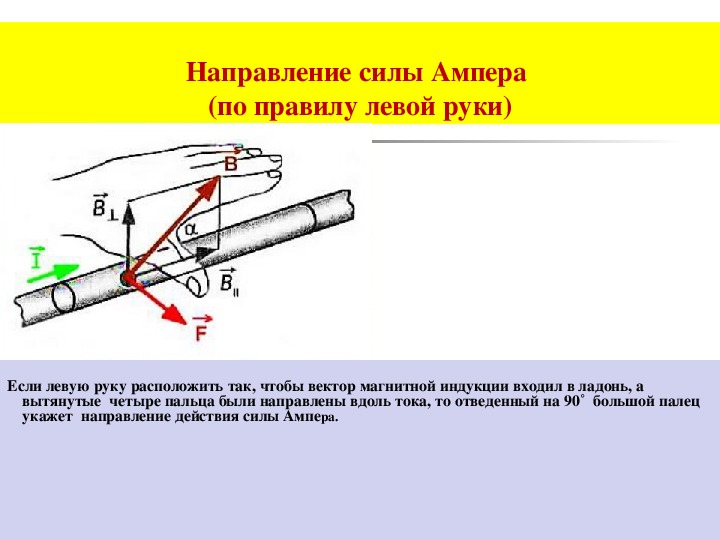 Для этого мысленно представляем, что ручка штопора крутится в указанном направлении. В зависимости от этого, определяем куда движется острие, а, значит, и куда течет ток.
Для этого мысленно представляем, что ручка штопора крутится в указанном направлении. В зависимости от этого, определяем куда движется острие, а, значит, и куда течет ток.
Применение правила буравчика
правило гласит
Чтобы определить траекторию вращения магнитного контура на представленном графическом изображении нужно знать несколько особенностей.
Часто в задачах по физике нужно, наоборот, определить траекторию движения тока. Чтобы это сделать, дается направление вращения кругов магнитного поля. Ручка буравчика начинается вращаться в сторону, указанную в условиях. Если буравчик движется в поступательном направлении, значит, ток направлен в сторону движения, если же он направлен в обратную, то и ток движется соответственно.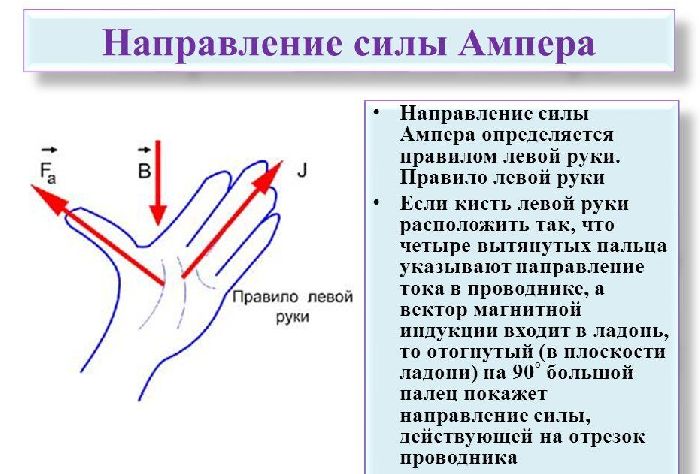
Для определения траектории движения тока в случае, представленном на втором рисунке, тоже можно воспользоваться правилом штопора. Для этого необходимо вращать ручку буравчика в сторону, указанную на изображении контура магнитного поля. Если он будет двигаться поступательно, то ток будет двигаться в сторону от наблюдателя, если же, наоборот, только к наблюдателю.
Важно! Если указана траектория движения потока, то определить траекторию вращения линии магнитного контура можно по вращению ручки буравчика.
Оно обозначается при помощи точки или крестика. Точка означает движение в сторону наблюдателя, крестик означает обратное. Легко запомнить этот случай, используя так называемое правило «стрелы», если острие «смотрит», а в лицо, то траектория движения тока в сторону наблюдателя, если же в лицо «смотрит хвост стрелы», то она двигается от наблюдателя.
Как правило буравчика, так и правило правой руки, достаточно легко применить на практике. Для этого нужно расположить кисть соответствующей руки таким образом, чтобы в лицевую сторону направлялся силовой контур магнитного поля, после чего большой палец, отведенный перпендикулярно, необходимо направить сторону движения тока, соответственно, остальные выпрямленные пальцы укажут на траекторию магнитного контура.
Различают исключительные случаи использования правила правой руки для вычисления:
- уравнения Максвелла;
- момента силы;
- угловой скорости;
- момента импульса;
- магнитной индукции;
- тока в проводе, движущегося через магнитное поле.
Что такое магнитное поле
Все, наверное, знают что такое постоянные магниты — они «липнут» к железу и некоторым другим материалам. Если приблизить два магнита, то они будут притягиваться или отталкиваться — в зависимости от того, как мы их повернем друг относительно друга. Почему и за счет чего так происходит? За счет того, что вокруг магнитов создается магнитное поле. Оно возникает при движении заряженных частиц. Например, вокруг провода, по которому протекает электрический ток, есть магнитное поле. Оно слабое, но оно есть.
Магнитное поле нельзя увидеть, но можно ощутить
Постоянные магниты
Как же тогда с магнитами? Откуда в них магнитное поле, ведь в них нет направленного движения частиц? Все просто. В них магнитное поле создается зарядами частиц. Как известно, любой материал состоит из положительно и отрицательно заряженных частиц. В некоторых материалах частицы можно расположить так, чтобы положительные были сконцентрированы с одной стороны, отрицательные — с другой. Эти «две стороны» называют полюсами магнита. Отрицательный — северный, обозначается латинской буквой N и закрашивается обычно синим цветом, положительный называют «южный» и обозначается S, закрашивается в красный цвет.
В них магнитное поле создается зарядами частиц. Как известно, любой материал состоит из положительно и отрицательно заряженных частиц. В некоторых материалах частицы можно расположить так, чтобы положительные были сконцентрированы с одной стороны, отрицательные — с другой. Эти «две стороны» называют полюсами магнита. Отрицательный — северный, обозначается латинской буквой N и закрашивается обычно синим цветом, положительный называют «южный» и обозначается S, закрашивается в красный цвет.
Постоянные магниты и их виды
Причем, стоит помнить, что однополюсных магнитов не бывает. Всегда есть два полюса. Если есть у вас большой магнит, его можно распилить пополам. И вы получите два магнита меньшего размера с двумя полюсами. Если распилите их — получите еще более мелкие двухполюсные магнитики.
Постоянные магниты можно сделать далеко не из всех материалов. Для этих целей подходят всего три вещества: железо (Fe), никель (Ni) и кобальт (Co). Если их выдержать в магнитном поле, частицы «рассортируются» по полюсам, материал станет магнитом. Но не все будут долго сохранять эти свойства. По способности удерживать магнитные свойства, материалы разделают на магнитомягкие и магнитотвердые материалы. Первые быстро намагничиваются, но и быстро теряют свои свойства. К таким относится железо (не обработанное). Магнитотвердый материал — например, сталь — в магнитном поле надо выдерживать долго. Зато после «выдержки» он становится магнитом на значительный промежуток времени. Можете поэкспериментировать со стальными скрепками.
Но не все будут долго сохранять эти свойства. По способности удерживать магнитные свойства, материалы разделают на магнитомягкие и магнитотвердые материалы. Первые быстро намагничиваются, но и быстро теряют свои свойства. К таким относится железо (не обработанное). Магнитотвердый материал — например, сталь — в магнитном поле надо выдерживать долго. Зато после «выдержки» он становится магнитом на значительный промежуток времени. Можете поэкспериментировать со стальными скрепками.
Что такое магнитное поле
Приближая магниты друг к другу, на некотором расстоянии вы начнете ощущать, как они притягиваются или отталкиваются. Чем ближе подносите, тем сильнее они взаимодействуют. Все потому, что вокруг них существует магнитное поле. И чем ближе к магниту, тем поле сильнее. Причем выглядит это поле как округлые линии, которые выходят из северного полюса и «заходят» в южный.
Магнитное поле можно представить в виде линий
Почему так решили? А потому что можно эти линии увидеть «вживую». Для этого надо провести эксперимент. На лист фанеры положить магнит, насыпать вокруг мелких металлических опилок и лист фанеры немного потрусить. Металлические опилки расположатся именно так, как показано на рисунке ниже справа
Для этого надо провести эксперимент. На лист фанеры положить магнит, насыпать вокруг мелких металлических опилок и лист фанеры немного потрусить. Металлические опилки расположатся именно так, как показано на рисунке ниже справа
Обратите внимание — чем ближе к магниту, тем опилок больше, чем дальше — тем меньше. Это потому что магнитное поле ослабевает по мере удаления
Экспериментальное подтверждение: смотрим на магнитное поле и на взаимодействие полюсов
Опилки помогут понять и правила притяжения или отталкивания полюсов. На левом рисунке мы видим что происходит, если приблизить два противоположных полюса. Они притягиваются. Причем когда процесс завершится, картинка будет один в один как та, что справа. Как видите, они даже немного похожи.
Если поднести поближе два одноименных полюса — юг-юг или север-север — они будут отталкиваться. Это демонстрирует средний рисунок. И чем ближе их подносите, тем сильнее будет ощущаться противодействие.
youtube.com/embed/P9O4oSmdOcY?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””/>
Что связано с левой рукой
Не путайте буравчика и правило левой руки, оно нужно для определения действующей на проводник силы. Выпрямленная ладонь левой руки располагается вдоль проводника. Пальцы показывают в сторону протекания тока I. Через раскрытую ладонь проходят линии поля. Большой палец совпадает с вектором силы – в этом и заключается смысл правила левой руки. Эта сила называется силой Ампера.
Можно это правило применить к отдельной заряженной частице и определить направление 2-х сил:
- Лоренца.
- Ампера.
Представьте, что положительно заряженная частица двигается в магнитном поле. Линии вектора магнитной индукции перпендикулярны направлению её движения. Нужно поставить раскрытую левую ладонь пальцами в сторону движения заряда, вектор B должен пронизывать ладонь, тогда большой палец укажет направление вектора Fа. Если частица отрицательная – пальцы смотрят против хода заряда.
Если частица отрицательная – пальцы смотрят против хода заряда.
Если какой-то момент вам был непонятен, на видео наглядно рассматривается, как пользоваться правилом левой руки:
https://youtube.com/watch?v=vyYK9otQsTw
Важно знать! Если у вас есть тело и на него действует сила, которая стремится его повернуть, вращайте винт в эту сторону, и вы определите, куда направлен момент силы. Если вести речь об угловой скорости, то здесь дело обстоит так: при вращении штопора в одном направлении с вращением тела, завинчиваться он будет в направлении угловой скорости
Примечания
Математические детали общего понятия ориентации базиса, о котором здесь идёт речь — см. в статье Ориентация.
Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.
Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.
Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.
Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).
Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведённое здесь определение, указано там.
Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса
Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.
В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более лёгким, чем запоминание всего одного общего правила.
Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.
Строго говоря, при этом сопоставлении есть ещё постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.
Не обязательное требование.
Выводы
Освоить эти способы определения направления сил и полей очень просто. Такие мнемонические правила в электричестве значительно облегчают задачи школьникам и студентам. С буравчиком разберется даже полный чайник, если он хотя бы раз открывал вино штопором. Главное не забыть, куда течет ток. Повторюсь, что использование буравчика и правой руки чаще всего с успехом применяются в электротехнике.
Напоследок рекомендуем просмотреть видео, благодаря которому вы на примере сможете понять, что такое правило буравчика и как его применять на практике:
Наверняка вы не знаете:
- Зависимость сопротивления проводника от температуры
- Как стать электриком
- Что такое фаза, ноль и земля
- Тесты по электротехнике
Закон Ампера
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: \( \overrightarrow{F} \),\( \overrightarrow{F}_{A} \). Сила (\( \overrightarrow{F} \)), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции (\( \overrightarrow{B} \)). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны.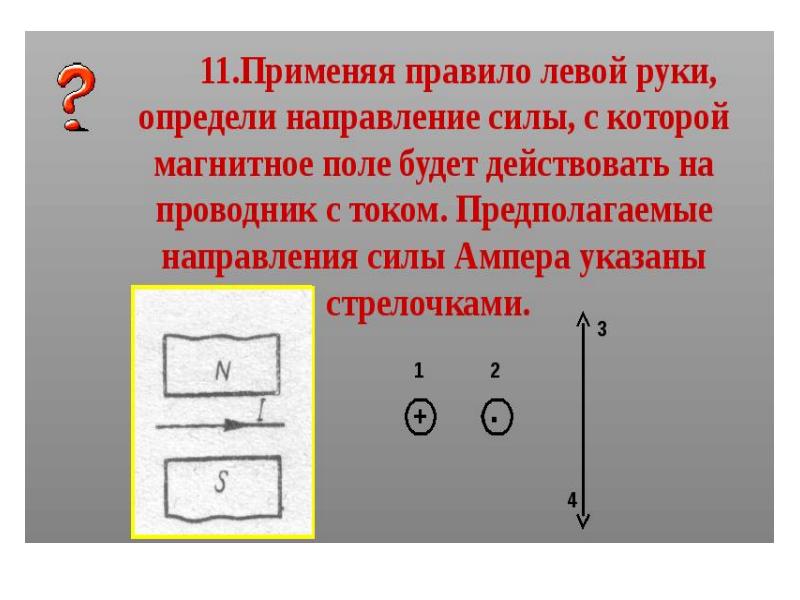 Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера имеет вид:
\[ \large{\overrightarrow{F}_{A}} = I \cdot \overrightarrow{B} \cdot \overrightarrow{l} \cdot sin(α) \]
где: \( I \) — сила тока, которая течет в проводнике, \( \overrightarrow{B} \) — вектор индукции магнитного поля, в которое проводник помещен, \( \overrightarrow{l} \) — длина проводника в поле, направление задано направлением тока, \( \alpha \) — угол между векторами \( \overrightarrow{l\ }и\ \overrightarrow{B} \).
Этой формулой можно пользоваться:
- если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
- если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
\[ \large{d\overrightarrow{F}_{A}} = I \cdot \overrightarrow{B} \cdot d\overrightarrow{l} \cdot sin(α) \]
Значение закона Ампера
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную \( 2\cdot {10}^{-7}Н \) на каждый метр длины. {-7} \) Ньютона.
{-7} \) Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxПравило левой руки для протона. Правило буравчика, правой и левой руки
В физике и электротехнике широко используются различные приемы и способы, позволяющие определить одну из характеристик магнитного поля – направленность напряженности. С этой целью используется закон буравчика, правой и левой руки. Данные способы позволяют получить довольно точные результаты.
Правило буравчика и правой руки
Закон буравчика используется для определения направленности напряженности магнитного поля. Оно работает при условии прямолинейного расположения магнитного поля, относительно проводника с током.
Оно работает при условии прямолинейного расположения магнитного поля, относительно проводника с током.
Это правило заключается в совпадении направленности магнитного поля с направленностью рукоятки буравчика, при условии вкручивания буравчика с правой нарезкой в направлении электрического тока. Данное правило применяется и для соленоидов. В этом случае, большой палец, оттопыренный на правой руке, указывает направление линий . При этом, соленоид обхватывается так, что пальцы указывают направление тока в его витках. Обязательным условием является превышение длиной катушки ее диаметра.
Правило правой руки противоположно правилу буравчика. При обхватывании исследуемого элемента, пальцы в сжатом кулаке указывают направление магнитных линий. При этом, учитывается поступательное движение по направлению магнитных линий. Большой палец, который отогнут на 90 градусов по отношению к ладони, указывает направление .
При движущемся проводнике, силовые линии перпендикулярно входят в ладонь. Большой палец руки вытянут перпендикулярно, и указывает направление движения проводника. Оставшиеся четыре оттопыренных пальца, расположены в направлении индукционного тока.
Большой палец руки вытянут перпендикулярно, и указывает направление движения проводника. Оставшиеся четыре оттопыренных пальца, расположены в направлении индукционного тока.
Правило левой руки
Среди таких способов, как правило буравчика, правой и левой руки, следует отметить правило левой руки. Для того, чтобы это правило работало, необходимо расположить левую ладонь таким образом, чтобы направление четырех пальцев было в сторону электрического тока в проводнике. Индукционные линии входят в ладонь перпендикулярно под углом 900. Большой палец отогнут, и указывает направление силы, действующей на проводник. Обычно, этот закон применяется, когда нужно определить направление отклонения проводника. В данной ситуации проводник располагается между двумя магнитами и по нему пропущен электрический ток.
Правило левой руки формулируется еще и таким образом, что четыре пальца на левой руке располагаются в направлении, куда движутся положительные или отрицательные частицы электрического тока. Индукционные линии, как и в других случаях, должны перпендикулярно располагаться относительно ладони и входить в нее. Большой оттопыренный палец указывает на направление силы Ампера или Лоренца.
Индукционные линии, как и в других случаях, должны перпендикулярно располагаться относительно ладони и входить в нее. Большой оттопыренный палец указывает на направление силы Ампера или Лоренца.
Магнитное поле действует на проводник с током. Силу, которая возникает при этом, называют силой Ампера .
Сила Ампера действует на про-водник с током в магнитном поле.
Исследуем, от чего зависит модуль и направление данной силы. С этой целью используем установку, в которой прямо-линейный проводник подвешен на тонких проволочках в магнитном поле постоянного магнита (рис. 6.16). Гибкие проволочки, присоединенные к концам проводника, по-зволяют включать его в электрическую цепь, сила тока в которой регулируется с помощью реостата и измеряется ампермет-ром.
Легкая, но жесткая тяга соединяет про-водник с чувствительным измерителем силы.
Замкнув электрическую цепь, в которую входит исследуемый проводник, увидим, что он отклонится от положения равно-весия, а измеритель покажет определенное значение силы. Увеличим силу тока в про-воднике в 2 раза и увидим, что сила, дейст-вующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока в проводнике вызовут соответствующие изме-нения силы, которая действует на провод-ник. Сопоставление полученных результатов позволяет сделать вывод, что сила F, дейст-вующая в магнитном поле на проводник с током, пропорциональна силе тока I в нем:
Увеличим силу тока в про-воднике в 2 раза и увидим, что сила, дейст-вующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока в проводнике вызовут соответствующие изме-нения силы, которая действует на провод-ник. Сопоставление полученных результатов позволяет сделать вывод, что сила F, дейст-вующая в магнитном поле на проводник с током, пропорциональна силе тока I в нем:
Сила Ампера пропорциональна силе тока в проводнике.
Расположим еще один магнит рядом с первым. Длина той части проводника, которая находится в магнитном поле, уве-личится приблизительно в 2 раза. Значение силы, действующей на проводник, также увеличится приблизительно в два раза. Та-ким образом, сила F, действующая на про-водник с током в магнитном поле, про-порциональна длине части проводника Δ l , которая находится в магнитном поле:
F ~ Δ l.
Сила Ампера пропорциональна длине активной части провод-ника.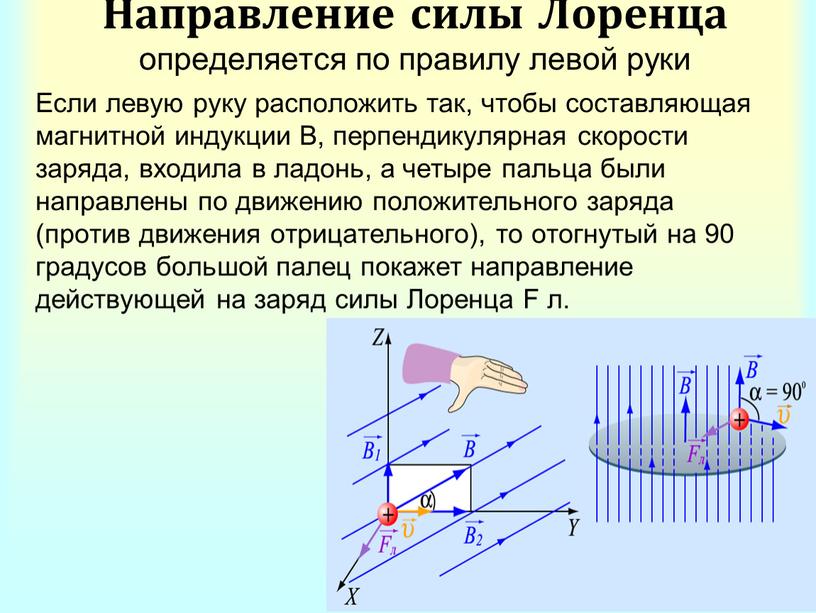
Сила увеличится также тогда, когда при-меним другой, более «сильный» магнит с большей магнитной индукцией. Это позво-ляет сделать вывод о зависимости силы F от магнитной индукции поля B:
F ~ B. Материал с сайта
Максимальной сила будет тогда, когда между магнитной индукцией и проводни-ком угол α = 90°. Если же этот угол равен нулю, то есть магнитная индукция будет па-раллельной проводнику, то сила будет равна нулю. Отсюда нетрудно сделать вывод о за-висимости силы Ампера от угла между маг-нитной индукцией и проводником.
Окончательно формула для расчета силы Ампера будет иметь вид
F А = BI Δ l . sin α .
Направление силы Ампера определяется по правилу левой руки (рис. 6.17).
Правило левой руки. Если левую руку разместить так, чтобы линии магнитной индукции входили в ладонь, а четыре пальца показывали направление тока, то отставленный большой палец пока-жет направление силы, действующей на про-водник с током в магнитном поле.
Сила Лоренца Сила Лоренца Модуль силы Лоренца. Модуль силы Лоренца. Направление силы Лоренца Направление силы Лоренца Правило левой руки Правило левой руки Плоские траектории движения заряженных частиц в однородном магнитном поле Плоские траектории движения заряженных частиц в однородном магнитном поле Вопросы по теме. Вопросы по теме. Сила Лоренца Сила Лоренца Модуль силы Лоренца. Модуль силы Лоренца. Направление силы Лоренца Направление силы Лоренца Правило левой руки Правило левой руки Плоские траектории движения заряженных частиц в однородном магнитном поле Плоские траектории движения заряженных частиц в однородном магнитном поле Вопросы по теме. Вопросы по теме.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Х.Лоренц ()–голландский физик, основатель электронной теории строения вещества.
Если кисть левой руки расположить так, что четыре вытянутых пальца указывают направление скорости положительного заряда, а вектор магнитной индукции входит в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы действующей на данный заряд.
Плоские траектории движения заряженных частиц в однородном магнитном поле Заряженная частица влетающая в однородное магнитное поле параллельно линиям магнитной индукции, движется равномерно вдоль этих линий. Вращение отрицательного заряда по окружности происходит в направлении противоположенном вращению положительного заряда (рис.в)
1. Каким образом, зная силу Ампера, можно найти силу Лоренца? 2. Дайте определение силе Лоренца. Чему равен её модуль? 3. Как определяется направление силы Лоренца с помощью правила левой руки? 4. Почему заряженная частица, влетающая в однородное магнитное поле в плоскости, перпендикулярно линиями магнитной индукции, движется по окружности? В каком случае частица движется в магнитном поле прямолинейно? 5. Докажите, что период обращения по окружности заряженной частицы в поперечном магнитном поле не зависит от её скорости.
Объяснение правил Флеминга для большого пальца левой и правой руки
Что такое правила Флеминга для левой и правой руки?
Всякий раз, когда проводник с током попадает в магнитное поле, на проводник действует сила. Направление этой силы можно найти с помощью правила левой руки Флеминга (также известного как «правило левой руки Флеминга для двигателей»).
Направление этой силы можно найти с помощью правила левой руки Флеминга (также известного как «правило левой руки Флеминга для двигателей»).
Аналогичным образом, если проводник принудительно поместить в магнитное поле, в этом проводнике возникнет индуцированный ток.Направление этой силы можно найти с помощью правила правой руки Флеминга.
В обоих правилах левой и правой руки Флеминга существует связь между магнитным полем, током и силой. Это отношение направленно определяется правилом левой руки Флеминга и правилом правой руки Флеминга соответственно.
Эти правила не определяют величину, а вместо этого показывают направление любого из трех параметров (магнитное поле, ток, сила), когда известно направление двух других параметров.
Правило левой руки Флеминга в основном применимо к электродвигателям, а правило правой руки Флеминга в основном применимо к электрическим генераторам.
Что такое правило левой руки Флеминга?
Установлено, что всякий раз, когда проводник с током помещается в магнитное поле, на проводник действует сила в направлении, перпендикулярном как направлению тока, так и магнитному полю.
На рисунке ниже часть проводника длиной «L» помещена вертикально в однородное горизонтальное магнитное поле напряженностью «H», создаваемое двумя магнитными полюсами N и S.Если по этому проводнику течет ток I, величина силы, действующей на проводник, равна:
Вытяните левую руку так, чтобы указательный, безымянный и большой пальцы находились под прямым углом друг к другу. Если указательный палец представляет направление поля, а второй палец представляет направление тока, то большой палец указывает направление силы.
Когда ток течет по проводнику, вокруг него индуцируется одно магнитное поле. Магнитное поле можно представить, рассмотрев количество замкнутых магнитных силовых линий вокруг проводника.
Направление магнитных силовых линий можно определить по правилу штопора Максвелла или правилу правой руки.
В соответствии с этими правилами направление магнитных силовых линий (или силовых линий) по часовой стрелке, если ток течет от наблюдателя, то есть если направление тока через проводник направлено внутрь от базовой плоскости, как показано на рисунке. на рисунке.
на рисунке.
Теперь, если горизонтальное магнитное поле приложено извне к проводнику, эти два магнитных поля, т.е.е. поле вокруг проводника из-за тока через него и внешнее приложенное поле будут взаимодействовать друг с другом.
На рисунке мы видим, что магнитные силовые линии внешнего магнитного поля проходят от северного к южному полюсу, то есть слева направо.
Магнитные силовые линии внешнего магнитного поля и магнитные силовые линии, обусловленные током в проводнике, находятся в одном направлении над проводником и в противоположном направлении под проводником.
Следовательно, над проводником будет больше сонаправленных магнитных силовых линий, чем под проводником.
Следовательно, будет большая концентрация магнитных силовых линий в небольшом пространстве над проводником. Поскольку магнитные силовые линии больше не являются прямыми линиями, они натянуты, как натянутые резиновые ленты.
В результате появится сила, которая будет стремиться переместить проводник из более концентрированного магнитного поля в менее концентрированное магнитное поле, то есть из текущего положения вниз.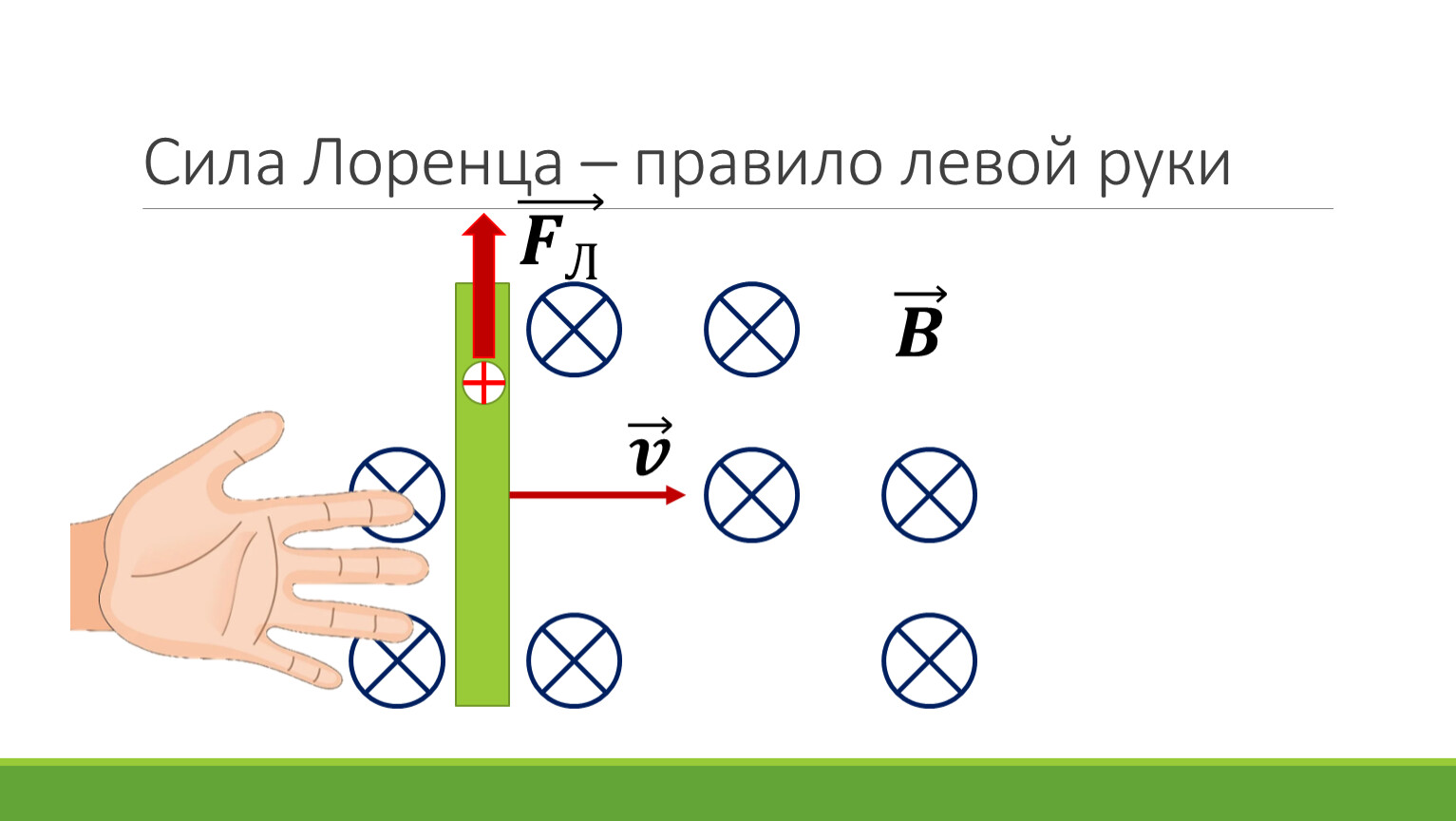
Теперь, если вы посмотрите на направление тока, силы и магнитного поля в приведенном выше объяснении, вы обнаружите, что направления соответствуют правилу левой руки Флеминга.
Что такое правило правой руки Флеминга?
Согласно закону электромагнитной индукции Фарадея, всякий раз, когда проводник движется внутри магнитного поля, в нем возникает индуцированный ток. Если этот проводник принудительно перемещается внутри магнитного поля, возникает связь между направлением приложенной силы, магнитным полем и током.
Это отношение между этими тремя направлениями определяется Правилом правой руки Флеминга .
Это правило гласит: «Вытяните правую руку так, чтобы указательный, указательный и большой пальцы находились под прямым углом друг к другу. Если указательный палец представляет направление силовой линии, большой палец указывает направление движения или приложенной силы, то второй палец указывает направление индуцированного тока».
Кто изобрел правило большого пальца левой и правой руки?
Правила большого пальца левой и правой руки были основаны Джоном Амброузом Флемингом в конце 19 -го -го века.
Джон открыл оба этих правила и назвал их своим именем. Эти правила теперь хорошо известны как правило левой и правой руки Флеминга .
Закон Ампера: определение и примеры – видео и расшифровка урока
Уравнение
Поле, создаваемое длинным прямым проводом с током, имеет форму концентрических окружностей. И по мере того, как вы удаляетесь от проволоки, эти круги становятся все дальше друг от друга — или, другими словами, поле становится слабее.Мы могли бы составить для этого уравнение, используя закон Ампера и проведя некоторые вычисления. Но на самом деле мы можем вывести это уравнение вообще без каких-либо вычислений.
Вместо интеграла будем использовать сумму. Сумма всех элементов магнитного поля, составляющих концентрическую окружность: магнитное поле B умножить на длину элемента дельта-L равно мю-ноль (проницаемость свободного пространства) умножить на ток в провод я . Это Закон Ампера.
Это Закон Ампера.
Затем осознайте, что суммируя все эти элементы, ваша дельта-L становится окружностью концентрического круга, 2pi r . Измените это, чтобы сделать магнитное поле объектом, и вы получите ЭТО окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в конкретной точке пространства, измеряемое в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от вас до провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии r от провода с током.
Благодаря уравнению можно рассчитать силу поля. Но как быть с направлением? Для этого мне нужно, чтобы вы показали мне большой палец вверх правой рукой. Нет, серьезно, сделай это прямо сейчас.
Используя эту схему токонесущего провода, укажите большим пальцем в направлении движения тока, в направлении стрелки, обозначенной I . Теперь представьте, что вы обхватываете провод пальцами, хватая его. Направление, на которое указывают ваши пальцы, представляет направление, на которое указывают линии поля — куда идут стрелки на концентрических кругах. Это называется правилом правой руки, и очень важно, чтобы вы случайно не использовали левую руку, потому что вы получите совершенно неверный ответ.
Примеры
Хорошо, давайте рассмотрим пример. Допустим, у вас есть провод с током, указывающий строго на север. Если по проводу течет ток 0,1 ампер, какова величина и направление магнитного поля на расстоянии 0,01 м над проводом?
Прежде всего, давайте запишем то, что мы знаем. Ток I равен 0,1, расстояние от провода r равно 0.-6 тесла. И в этом наша величина.
Чтобы определить направление, вы можете нарисовать ток на листе бумаги, указав вверх к верхней части страницы, которую вы можете отметить на север. Теперь поднимите большой палец вверх правой рукой, также направьте большой палец к верхней части страницы и представьте, что ваши пальцы скручиваются вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проволокой и направо над проволокой. Если вверху страницы север, то справа будет восток.-6 тесла на восток.
Теперь поднимите большой палец вверх правой рукой, также направьте большой палец к верхней части страницы и представьте, что ваши пальцы скручиваются вокруг проволоки. Если вы сделаете это правильно, вы увидите, что ваши пальцы будут указывать налево под проволокой и направо над проволокой. Если вверху страницы север, то справа будет восток.-6 тесла на восток.
Краткое содержание урока
Полная версия закона Ампера — одно из уравнений Максвелла, описывающих электромагнитное взаимодействие. Закон Ампера , в частности, говорит, что магнитное поле, создаваемое электрическим током, пропорционально величине этого электрического тока с константой пропорциональности, равной проницаемости свободного пространства. Стационарные заряды создают электрические поля, пропорциональные величине заряда. Но движущиеся заряды создают магнитные поля, пропорциональные току (заряд и движение).
Единственная проблема с законом Ампера заключается в том, что это дифференциальное уравнение, другими словами, чтобы его использовать, вам нужно выполнить некоторые вычисления. Но мы можем избежать этого, взглянув на результат всех этих расчетов для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Но мы можем избежать этого, взглянув на результат всех этих расчетов для конкретной ситуации. Если мы изучим магнитное поле, создаваемое длинным прямым проводом с током, мы получим это окончательное уравнение для поля, создаваемого проводом с током.
Здесь B — магнитное поле в конкретной точке пространства, измеряемое в теслах.-6. I — ток, протекающий по проводу, измеряется в амперах. А r — это радиальное расстояние от вас до провода, измеренное в метрах. Таким образом, вы можете использовать это уравнение, чтобы вычислить напряженность магнитного поля на расстоянии r от провода с током. Чтобы определить направление этого поля, мы должны использовать правило правой руки и указать большим пальцем направление тока.
Результаты обучения
После того, как вы закончите этот урок, вы должны быть в состоянии:
- Государственный закон Ампера
- Рассчитайте магнитное поле провода с током, используя закон Ампера
- Вызов правила правой руки при вычислении текущего направления
Правил правой руки
Правил правой рукиF магнитный – Сила магнитного поля, действующая на движущийся заряд 90 149
| Когда заряд помещается в магнитное поле, этот заряд испытывает
магнитная сила; при наличии двух условий: 1) заряд движется относительно магнитного поля, 2) скорость заряда имеет составляющую, перпендикулярную направление магнитного поля |
Правила правой руки применяются к положительным зарядам или положительный (обычный) ток
При использовании правил правой руки важно помнить
что правила предполагают, что заряды движутся в обычном токе (гипотетический
поток положительных зарядов). Чтобы применить либо правило правой руки
к движущемуся отрицательному заряду, скорость (v) этого заряда должна быть обращена на противоположную – к
представляют собой аналогичный условный ток. Чтобы применить либо правило правой руки
к движущемуся отрицательному заряду, скорость (v) этого заряда должна быть обращена на противоположную – к
представляют собой аналогичный условный ток. |
Создание иллюстраций магнитного поля и заряда взаимодействия в 3D
| Поскольку сила, действующая на движущийся заряд со стороны магнитного поле перпендикулярно как скорости заряда, так и направлению области, создание иллюстраций этих взаимодействий включает использование два символа слева обозначают движение в самолет или из него страницы. |
Правило правой руки №1 (RHR №1)
Правило правой руки №1 определяет
направления магнитной силы, обычного тока и магнитного поля.
При наличии любых двух тезисов можно найти третий.
| Правой рукой: ткните указательным пальцем в направлении скорости заряда, против , (вспомним обычный ток).  Укажите средним пальцем в направлении магнитного поля, B. Теперь ваш большой палец указывает в направлении магнитной силы, F магнитная . |
Правило правой руки №2 (RHR №2)
Правило правой руки №2 определяет направление магнитного поля.
поле вокруг провода с током и наоборот
| Правой рукой: Согните пальцы полукругом вокруг провода, они указывают внутрь. направление магнитного поля, B Укажите большим пальцем направление обычного тока. |
Применение правил правой руки:
Правила правой руки дают только направление магнитного поля.
Чтобы определить силу магнитного поля, некоторые полезные математические
можно применять уравнения.
| Для длинного прямого провода магнитное поле B равно:
В = м о I
/2пр;
где, м о = 4п х 10 -7 Т·м/А и ос называется проницаемость свободного пространства, r – радиальное расстояние от провода в метрах, I – ток в амперах.  |
| Для одного витка провода магнитное поле, B
через центр петли:
В = м о I
/ 2р;
где, м о – проницаемость свободного пространства, а R – радиус окружности петля провода, измеряемая в метрах. Оба поля для катушки проволоки и из этого уравнения можно построить соленоид. |
Вопросы для размышления:
1. Протон движется со скоростью 5,0 x 10 6 м. / с, когда он сталкивается с магнитным полем величиной 0,40 Тл, перпендикулярным к скорости протона. Составьте схему этой ситуации и укажите направления скорости протона, магнитного поля и магнитного сила. 2. Вот, длинный,
по прямому проводу течет ток I, равный 3.0 A. Частица, q
с зарядом +6,5 х 10 -6 C, движется параллельно проводу в указанном направлении на расстоянии
r = 0,050 м и скорость v = 280 м/с. Определить величину
и направление магнитного поля, испытываемого зарядом. Определить величину
и направление магнитного поля, испытываемого зарядом. |
Каталожные номера:
Катнелл, Дж. и Джонсон, К. (1998), Physics , Vol. 2, Уайли: Нью-Йорк, с. 631, 33, 46 и 49. Эта страница предоставлена Камило Тафуром и Дэном МакИсаком
[Вернуться к указателю экспериментов]
Правило левой руки Флеминга: объяснение теории электродвигателя
Твитнуть это:
Правило левой руки Флеминга может описать #движение в любом из множества различных типов #электродвигателей #моторный эффект
В теории #электродвигателя правило левой руки состоит из использования указательного, большого и среднего пальцев левая рука #motorcontrol
Когда проводник с током попадает в магнитное поле, естественно, на проводник действует сила.Правило левой руки Флеминга — это простой и точный способ найти направление силы/движения проводника в электродвигателе, когда известны направление магнитного поля и направление тока. Первоначально он был разработан английским инженером-электриком Джоном Амброузом Флемингом в конце 19 века.
Первоначально он был разработан английским инженером-электриком Джоном Амброузом Флемингом в конце 19 века.
По своей сути правило левой руки — это визуальная мнемоника, в которой используются большой, указательный и средний пальцы левой руки. Рука держится ладонью вверх, большой и средний пальцы выровнены, как если бы они были соединены встык, а указательный палец вытянут перпендикулярно.Рубрика для этого правила следующая:
- Большой палец : Большой палец представляет направление тяги на проводнике.
- Указательный палец: Также известный как указательный палец, представляет направление магнитного поля .
- Средний палец: Также известный как центральный палец, представляет направление текущего .

Какое отношение правило левой руки Флеминга имеет к работе электродвигателей?
Когда электрический ток проходит через проводник (в правиле Флеминга это средний палец), он создает цилиндрическое магнитное поле вокруг проводника.Если внешнее магнитное поле (указательный палец в правиле Флеминга) находится в непосредственной близости от проводника, находящегося под напряжением, магнитное поле и электромагнитное поле взаимодействуют. Это взаимодействие всегда создает физическую силу (большой палец в правиле Флеминга), которая перпендикулярна магнитному полю и электромагнитному полю.
В стандартном электродвигателе постоянного тока есть ротор и статор. Ротор вставлен в статор и может свободно вращаться внутри него. В простом двигателе статор представляет собой кольцо из постоянных магнитов, а ротор аккуратно обмотан токопроводящей медной проволокой.Ротор — единственный компонент, подключенный к внешнему источнику питания. Теперь давайте рассмотрим правило левой руки Флеминга. Электрический ток от внешнего источника питания проходит через витки медного провода на роторе. Создаваемое при этом электромагнитное поле взаимодействует с магнитным полем, создаваемым постоянными магнитами в статоре. Это взаимодействие вызывает генерацию физической силы, которая перпендикулярна полям. Из-за того, как устроен электродвигатель (ротор внутри статора), эта физическая сила проявляется как вращение ротора.
Теперь давайте рассмотрим правило левой руки Флеминга. Электрический ток от внешнего источника питания проходит через витки медного провода на роторе. Создаваемое при этом электромагнитное поле взаимодействует с магнитным полем, создаваемым постоянными магнитами в статоре. Это взаимодействие вызывает генерацию физической силы, которая перпендикулярна полям. Из-за того, как устроен электродвигатель (ротор внутри статора), эта физическая сила проявляется как вращение ротора.
В упрощенном виде правило левой руки Флеминга может описать движение любого из множества различных типов электродвигателей. Постоянный ток, переменный ток, щеточный, бесщеточный, индукционный — все они используют одни и те же концепции (1 электромагнитное поле, 1 поле, магнитное или электромагнитное, 1 генерируемая сила) для создания движения.
Чтобы получить экспертное руководство и решения для вашего приложения управления перемещением, свяжитесь с поставщиком управления движением, членом A3.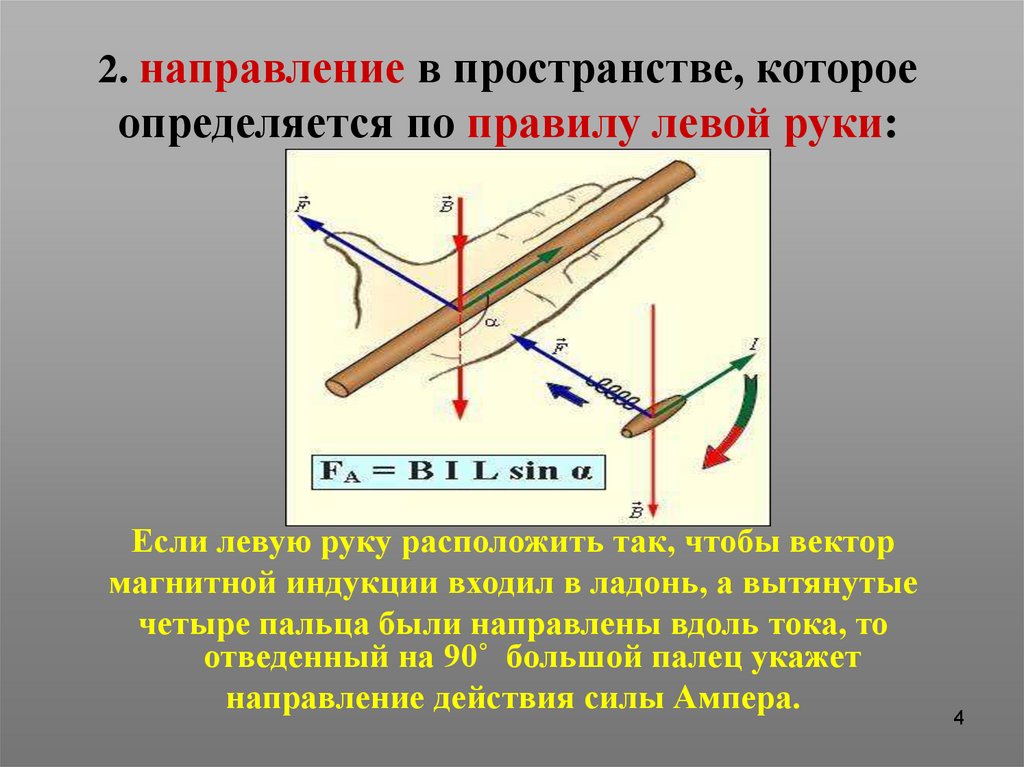
Ч32 Магнетизм | |||||||||||
По определению, магнитное поле линии выходят из северного полюса магнита и входят в южный полюс. Линии магнитного поля не могут пересекаться, точно так же, как линии электрического поля не могут. | |||||||||||
Магнитное поле | |||||||||||
Магнитное поле Земли по сути представляет собой полосу магнит.
Следует отметить, мы знаем, что северный полюс стрелки компаса указывают на Северный полюс. Это означает, что Северный полюс нашей Земли действительно Южный полюс. | |||||||||||
Магнитная сила на движущийся заряд | |||||||||||
F = q v X B Позволяет выполнить модульный анализ N = C (м/с) Тесла N = (Кл/с) м Тесла Н = А·м Тесла Т = Н/Ам |
| ||||||||||
Мне НЕ НРАВИТСЯ это правило правой рукиотличается от Закон Ампера
| Посмотрите направо, здесь большой палец все еще
ток, а пальцы еще магнитное поле. | ||||||||||
Пример Протон движется в магнитное поле с напряженностью 2,00 Тесла. поле. Протон перпендикулярен полю и движется со скоростью 62,5 м/с. Чему равно центростремительное ускорение протона? Откуда вы знаете, что это центростремительное? |
F C = q v X B м а = 1.6е-19(62,5)(2) 1,673е-27 а = 2е-17 а = 1,20 x 10 10 м/с 2 | ||||||||||
Движение Заряженные частицы в магнитном поле | |||||||||||
| |||||||||||
Пример Альфа-частица (ядро атома гелия)
состоит из двух протонов и двух нейтронов. |
F C = q v X B м v 2 /r = q v X B г = м v / кв Б г = 4(1,67e-27)(5e5)/ 1,6e-19(1) г = 20,9е-3 метра
| ||||||||||
Магнитный Сила, действующая на провод с током | |||||||||||
| |||||||||||
Пример А
Медный стержень длиной 20 см массой 0.02 кг несет ток 10 А в
положительное направление х. Пусть вверх будет положительным направлением y. Что
величина минимального магнитного поля, необходимого для левитации стержня? (Это
основе вашей текущей лаборатории баланса. | Ф = И Л Х В м (г) = I L X B .02(10) = 10(.2)(В) В = 0,010 Тесла | ||||||||||
Петли Ток и магнитный крутящий момент | |||||||||||
Электрический поля прикладывают тангенциальную силу и ускоряют электроны o Работайте!!! Магнитный Поля прикладывают центростремительную силу и заставляют электроны следовать по кругу. путь o не могу работать | В газовая хроматография масс-спектрометрия, ионы различной массы следуют по кругу пути разного радиуса, что позволяет разделить разные изотопы один и тот же элемент. | ||||||||||
Ф = И Л Х В г X F = I Lr х В τ = I A X B | Кому
увеличьте крутящий момент, оберните провод. τ = Н И А Х В
| ||||||||||
Пример Каждый из 10 витков провода по вертикали, прямоугольный контур несет ток 0,25 А. Высота контура равна 8.0 см и |
| Вертикальные стороны (левая и правая) перпендикулярны B F = N (I L X B) F = 10(0,25)(0,08)(0,049) F = 0,00898 Н (слева и справа) Верхняя и нижняя части не совсем параллельны так что это не отменяет sin25 = 0,423 F = N (I L X B)sin25 F = 10(0,25)(0,15)(0,049)(0,423) F = 0,007766 Н (сверху и снизу)
(b)Ток вокруг контура противоположный каталог слева, справа и снизу вверх, таким образом, НОЛЬ (в) τ = r X F τ = N I A B sin65 10(.25)(0,15)(0,08)(0,049)(0,906) τ =0,00133 Н·м | |||||||||
ширина
15 см. а. Находить величина магнитной силы с каждой стороны петли. б. Находить результирующая магнитная сила, действующая на петлю. в. Находить магнитный момент на петле.
| |||||||||||
Ампер Закон электрических токов, Магнитные поля | |||||||||||
B●dl = или I B●Δl = или I
Где o = 4π x 10 -7 Т м/А
Для длинного провода магнитное поле образует круговой путь по мере снижения интенсивности,
, поэтому dl равно 2πr; обычно становится В = o I / (2πr)
Справа ЕДИНСТВЕННОЕ право правило руки, которое мне нравится, и вариант, описанный выше, основан на этой правой руке правило |
| ||||||||||
Пример Рассмотрим
длинные, прямые, токонесущие провода. | |||||||||||
В точке A B = o I / 2πr В = o (I 1 + I 2 ) / 2πr В = 4π x 10 -7 (1 + 2) / 2π(.2) В = 30 х 10 -7 Тесла
| В точке B В = o (I 2 – I 1 ) / 2πr В = 4π x 10 -7 (2 – 1) / 2π(.2) В = 10 х 10 -7 Тесла | ||||||||||
Текущий Петли и соленоиды | |||||||||||
Закон Ампера упрощает внутри соленоида.
BL = o I N (N есть количество петель, если 1, отменяется) В = o I Н/Д В = или В
| |||||||||||
Пример Один из парней, перешедших на мой Программа бакалавриата по физике делала это с одной целью — делать большие соленоиды.Он сделал это, чтобы повысить напряжение для дугового разряда или ионизации пути между соленоидом и земля. (На нашем физическом факультете обычно отчетливо пахло озоном.) Какова длина этот провод с током 2 ампера обернут вокруг вашей трубы ПВХ длиной 1 метр 2 (диаметром 6 см) для создания магнитного поля в 1 Тесла? | Б●дл = или I Б = o I Н/Д Б = o В или (n = B/ o I)
Длина = N *2 πr = n L* π d = (B/ или I)L π d =1/(4πe-7*2)
1 π . = 75 000 метров | ||||||||||
Магнетизм в Материи | |||||||||||
Ферромагнитный
Парамагнитный |
| ||||||||||
Закон, связывающий напряженность магнитного поля H с его источник, плотность тока Дж , составляет
Обратите внимание, что в отличие от интегральной формулировки закона Гаусса,
(1.3.1) символы поверхностных интегралов справа не имеют кружков.
Это означает, что интегрирование ведется по открытым поверхностям, имеющим ребра
обозначен контуром C . Такая поверхность S , окруженная контуром C , является
показано на рис. 1.4.1. Другими словами, интегральный закон Ампера в виде (1)
требует, чтобы линия
интеграл (циркуляция) магнитного поля
интенсивность H вокруг замкнутого контура равна чистому току
прохождение через поверхность, охватывающую контур, плюс скорость времени
изменение чистой плотности потока смещения o E через
поверхность ( тока смещения ).
Направление плюса d a определяется по правилу правой руки, как также показано на рис. 1.4.1. Пальцами правой руки в направлении d s , большой палец имеет направление d a . В качестве альтернативы, большим пальцем правой руки в направлении d s , пальцы будут в положительном направлении d a .
В законе Ампера H появляется без или .Этот закон поэтому устанавливает базовые единицы H как кулон/(метр-секунда). В разд. 1.1, единицы плотности потока o H определяются силой Лоренца, поэтому второй эмпирический постоянная, проницаемость свободного пространства , равна o = 4 x 10 -7 генри/м (генри = вольт сек/ампер).
Постоянный ток в направлении z в круговом цилиндрическая область радиусом R , показанная на рис.1.4.2, расширяется от до бесконечности до + бесконечности по оси z и представлен плотность
где J o и R — заданные константы. Соответствующее магнитное поле
интенсивность имеет только азимутальную составляющую.
Соответствующее магнитное поле
интенсивность имеет только азимутальную составляющую.
Чтобы увидеть, что в этом поле не может быть компонентов r , заметим, что
вращение источника вокруг радиальной оси, как показано на рис. 1.4.2,
инвертирует источник (тогда ток идет в направлении -z ) и
следовательно, должно инвертировать поле. Но компонент r поля делает
не реверсируется при таком вращении и, следовательно, должен быть равен нулю. То
Компоненты H и H z не исключаются этим аргументом.
Однако, если они
существуют, они не должны зависеть от координат и z , т.к.
вращение источника вокруг оси z и перемещение источника
по оси z не меняет источник и, следовательно, не меняет
поле.
Ток не зависит от времени, поэтому мы предполагаем, что поля тоже. Следовательно, последнее слагаемое в (1) — смещение ток, равен нулю. Затем закон используется с S , поверхностью, имеющей свою охватывающий контур C произвольного радиуса r , как показано на рис. 1.4.2. Тогда элементы площади и линии равны
и правая часть (1) становится
Интегрирование в левой части сводится к умножению независимый H по длине C .
Эти последние два выражения используются для вычисления (1) и получения
Таким образом, азимутальная напряженность магнитного поля имеет радиальную распределение показано на рис. 1.4.2.
Компонент z H в лучшем случае однороден. Это можно увидеть по
применяя интегральный закон к контуру C ‘ , также показанному на
Рис. 1.4.2. Интеграция на верхней и нижней ногах дает ноль
потому что H r = 0 . Таким образом,
сделать взносы из-за H z на вертикальных опорах отменить, это
необходимо, чтобы H z не зависели от радиуса. Такое однородное поле должно
быть вызвано источниками на бесконечности и поэтому устанавливается равным нулю
если такие источники не постулируются в условии задачи.
Таким образом,
сделать взносы из-за H z на вертикальных опорах отменить, это
необходимо, чтобы H z не зависели от радиуса. Такое однородное поле должно
быть вызвано источниками на бесконечности и поэтому устанавливается равным нулю
если такие источники не постулируются в условии задачи.
Формула магнитной силы (ток-длина)
Когда провод, несущий электрический заряд, помещается в магнитное поле, на провод действует сила.Формула силы зависит от тока, длины провода и магнитного поля. «Вектор длины» провода определяет направление, в котором течет ток. Направление вектора силы можно найти путем вычисления векторного произведения вектора длины и магнитного поля, если направления векторов заданы, или с помощью «правила правой руки». Представьте свою правую руку с указательным пальцем, указывающим в направлении вектора длины. Затем согните пальцы в направлении вектора магнитного поля.Направление силы будет в направлении вашего большого пальца. Единицей силы является ньютон (Н), единицей силы тока является ампер (А), единицей длины является метр (м), а единицей магнитного поля является Тесла (Тл).
Единицей силы является ньютон (Н), единицей силы тока является ампер (А), единицей длины является метр (м), а единицей магнитного поля является Тесла (Тл).
= вектор магнитной силы (Ньютоны, Н)
I = величина тока (Ампер, А)
= вектор длины (м)
L = длина провода, амплитуда (м)
= вектор магнитного поля (Тесла, Тл)
B = величина магнитного поля (Тесла, Тл)
= угол между векторами длины и магнитного поля (радианы)
= вектор направления перекрестного произведения (безразмерный)
Формула магнитной силы (ток-длина) Вопросы:
1) По медному проводу течет ток 4.00 А через однородное магнитное поле магнитудой 2,20 Тл. Направление тока слева направо от страницы (экрана), а направление магнитного поля вверх-влево, под углом от направления тока. Какова величина и направление магнитной силы, действующей на отрезок провода длиной 0,100 м?
Ответ: Величину магнитной силы на сечении провода можно найти по формуле:
Сила на 0. Участок провода на 100 м имеет магнитуду 0,622Н.
Участок провода на 100 м имеет магнитуду 0,622Н.
Направление вектора силы можно найти с помощью «правила правой руки». Направление тока вправо, поэтому представьте, что ваш правый указательный палец указывает в этом направлении. Вектор магнитного поля направлен вверх-влево, так что согните пальцы. Теперь ваш большой палец будет направлен в сторону от страницы (или экрана). Это означает, что направление вектора силы выходит за пределы страницы (или экрана).
2) По проводу течет ток 20.0 А, при токе, протекающем в направлении. К проволоке приложено магнитное поле. Какова результирующая магнитная сила, действующая на отрезок провода длиной 1,00 м, выраженная в единичном векторе?
Ответ: Магнитная сила, действующая на провод, может быть найдена путем решения векторного произведения формулы силы:
Перекрестное произведение двух векторов и равно:
Вектор длины:
Вектор магнитного поля:
Итак, есть:
Магнитная сила, действующая на провод, теперь может быть рассчитана по формуле:
В представлении единичного вектора магнитная сила, действующая на провод, равна .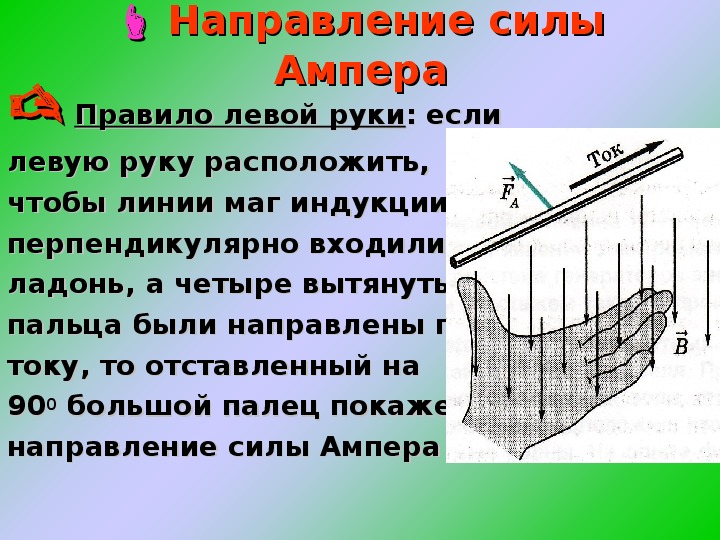

 сила ампера (формула, правило левой руки
сила ампера (формула, правило левой руки


 Ладонь руки
представляет направление силы. Примечание: скорость – это направление потока заряда
Ладонь руки
представляет направление силы. Примечание: скорость – это направление потока заряда Пучок альфа-частиц
разогнан до скорости 510 5 м/с.Этот пучок тяжелых частиц
попадает в вертикальное магнитное поле силой 1 Тесла. Сколько времени нужно для альфы
частица, чтобы совершить полный круг?
Пучок альфа-частиц
разогнан до скорости 510 5 м/с.Этот пучок тяжелых частиц
попадает в вертикальное магнитное поле силой 1 Тесла. Сколько времени нужно для альфы
частица, чтобы совершить полный круг? )
)  Оберните десять раз, затем десять раз
Крутящий момент.
Оберните десять раз, затем десять раз
Крутящий момент. Горизонтальное магнитное поле величиной 4,910 −2 T ориентирован под углом θ=65 относительно нормали к плоскости
петли.
Горизонтальное магнитное поле величиной 4,910 −2 T ориентирован под углом θ=65 относительно нормали к плоскости
петли.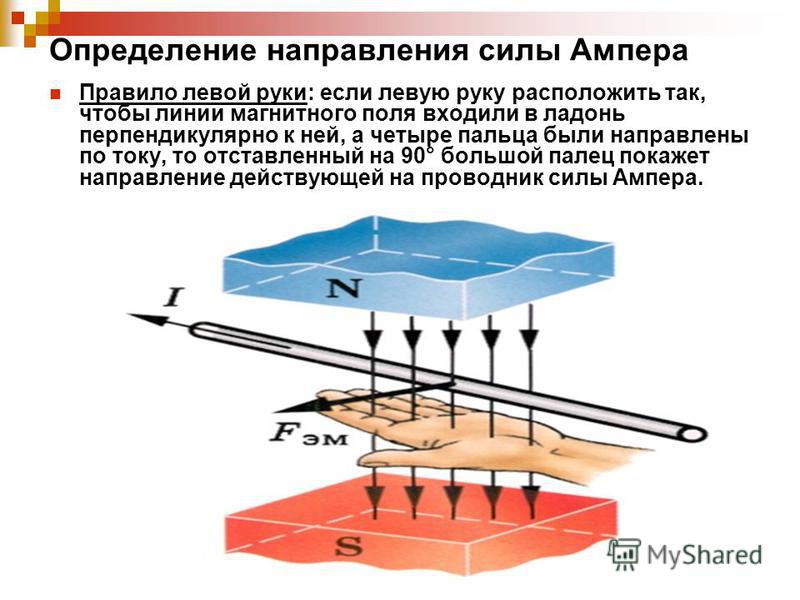 По одному проводу течет ток 1,0
A в положительном направлении y; по другому проводу течет ток 2,0 А в
положительное направление х. Рассчитать величину чистого магнитного поля
в точках А и В.
По одному проводу течет ток 1,0
A в положительном направлении y; по другому проводу течет ток 2,0 А в
положительное направление х. Рассчитать величину чистого магнитного поля
в точках А и В.
 06
06