Как определить спиновое число: 6. Спиновое квантовое число

6. Спиновое квантовое число

СПИНОВОЕ КВАНТОВОЕ ЧИСЛО – квантовое число, определяющее величину спина квантовой системы (атома, иона, атомного ядра, молекулы), т. е. её собств. (внутр.) момента кол-ва движения (момента импульса). Спиновый момент импульса s квантуется: его квадрат определяется выражением, где s – С. к. ч. (называемое часто просто спином). Проекция вектора s на произвольное направлениеz также квантуется: для частиц с ненулевой массой(гдеm_s – магнитное спиновое число), т. е. принимает 2s + 1 значений. Число s может принимать целые, нулевые или полуцелые значения.

7)Принцип Паули: в пределах одной квантовой системы в данном квантовом состоянии может находиться только одна частица, состояние другой должно отличаться хотя бы одним квантовым числом. Следствием принципа является наличие электронных оболочек в структуре атома. Количество электронов в отдельном атоме равно количеству протонов.

Так как электроны являются фермионами, принцип Паули запрещает им принимать одинаковые квантовые состояния.

8)Правило Гунда: определяет порядок заполнения орбиталей определённого подслоя и формулируется следующим образом: суммарное значение спинового квантового числа электронов данного подслоя должно быть максимальным. Сформулировано Фридрихом Хундом в 1925 году. Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон. При этом на одной орбитали находятся два электрона с полуцелыми спинами противоположного знака, которые спариваются (образуют двухэлектронное облако) и, в результате, суммарный спин орбитали становится равным нулю.

9. Квантовое число

Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He⁺, Li²⁺ и т. д.). В этом случае энергия электрона

где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.

В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.

10. Распределение электронов по энергетическим уровням

Ниже приведено распределение электронов по энергетическим уров­ням и подуровням у элементов, принадлежащих к группам (семействам) S, Р, D И F.

S-Элементы. S-элементами являются элементы главных подгрупп I и II групп, а также водород и гелий. Водород относят к VII главной подгруп­пе P-элементов, а гелий – к VIII подгруппе инертных P-элементов. В ато­мах S-элементов пополняется электронами подуровень S Внешнего уровня: во внешнем квантовом слое S-подуровня они имеют 1 или 2 (S1 или S2) электрона, удаленных на значительное расстояние от ядра. При химиче­ских реакциях элементы основных подгрупп I и II групп проявляют резко выраженные восстановительные свойства.

2.3 Квантовые числа — ЗФТШ, МФТИ

Для описания положения электрона в электронной оболочке используют четыре квантовых числа. Здесь мы не будем углубляться в квантово-механические подробности и опишем только утилитарный смысл данных чисел. Набор, состоящий из четырёх квантовых чисел – это «адрес» электрона в электронной оболочке.

Главное квантовое число `n` определяет полную энергию электрона на энергетическом уровне и показывает,

из скольких энергетических уровней состоит электронная оболочка атома. Принимает целочисленные положительные значения от `1` до `oo`. В периодической таблице Д. И. Менделеева `n` равно номеру периода.

При `n=1`, `l` принимает только одно значение `0` (этому числовому значению соответствует буквенное `s`), следовательно, на первом энергетическом уровне только один подуровень – `s`. Орбиталь  `s`-подуровня имеет сферическую форму (рис. 1).

При `n=2`, `l` принимает два значения: `0` `(s)` и `1` `(p)`. Значит, второй энергетический уровень состоит из двух подуровней – `s` и `p`. Форма `p`-орбитали похожа на объёмную восьмёрку.

При `n=3`, `l` принимает уже три значения: `0(s)`; `1(p)` и `2(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещенных объёмных восьмёрок либо объёмной восьмёрки с перемычкой (рис. 1).

При `n=4` значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.

Принимает значения от `-l` до `+l`, включая `0`.

Например, при `l=0` `m_l` принимает только одно значение – `0`. Следовательно, орбиталь, находящаяся на данном подуровне (`s`-подуровне), только одна. Мы уже знаем, что она имеет форму сферы с центром в начале координат.

При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу `(p_x,p_y,p_z)`. 2`.

Всё вышесказанное можно обобщить в Таблице 2.

Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n<=4`)

`n`	`l`	Обозначение орбитали	`ml`	Число орби-талей	Число электронов на подуровне
`1`	`0`	`1s`	`0`	`1`	`2`
`2`	`0` `1`	`2s` `2p`	`0` `−1`; `0`; `+1`	`1` `3`	`2` `6`
`3`	`0` `1` `2`	`3s` `3p` `3d`	`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2`	`1` `3` `5`	`2` `6` `10`
`4`	`0` `1` `2` `3`	`4s` `4p` `4d` `4f`	`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` `−3`; `−2`; `−1`; `0`; `+1`; `+2`; `+3`	`1` `3` `5` `7`	`2` `6` `10` `14`

Spin Quantum Number – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2581

Спиновое квантовое число (\(m_s\)) описывает угловой момент электрона.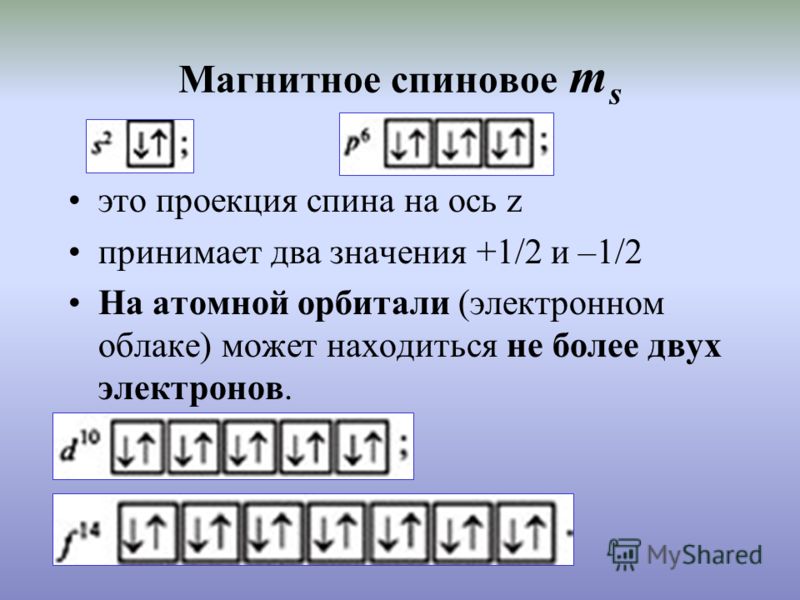 Электрон вращается вокруг оси и имеет как угловой момент, так и орбитальный угловой момент. Поскольку угловой момент является вектором, квантовое число спина (s) имеет как величину (1/2), так и направление (+ или -).

На каждой орбитали может находиться только два электрона. Один электрон будет иметь спин +1/2, а другой — -1/2. Электроны любят заполнять орбитали до того, как начнут образовываться пары. Поэтому первый электрон на орбитали будет иметь спин +1/2. После того, как все орбитали заполнены наполовину, электроны начинают спариваться. Этот второй электрон на орбите будет иметь спин -1/2. Если на одной орбитали находятся два электрона, то они будут вращаться в противоположных направлениях.

Комбинации квантовых чисел

• Три квантовых числа ( n , l и m ), описывающие орбиталь, являются целыми числами: 0, 1, 2, 3.
• Главное квантовое число ( n ) не может быть равно нулю. Следовательно, допустимые значения n : 1, 2, 3, 4. ..
• Угловое квантовое число ( l ) может быть любым целым числом от 0 до n – 1.
  • Если n = 3, l может быть 0, 1 или 2.
• Магнитное квантовое число ( m ) может быть любым целым числом от – l до + l .
  • Если l = 2, m может быть -2, -1, 0, +1 или +2.
• Орбитали с одинаковым значением главного квантового числа образуют Оболочку (n).
• Орбитали внутри оболочек делятся на подоболочки (л)
  • с: l = 0 p : l = 1 d : л = 2 ф : л = 3

Упражнение \(\PageIndex{1}\): Вольфрам

Какое спиновое квантовое число у вольфрама (символ W)?

Ответить

Вольфрам имеет 4 электрона на 5d-орбитали. Следовательно, на каждую орбиталь пойдет 1 электрон (без спаривания). Четвертый электрон будет иметь спин +1/2.

Упражнение \(\PageIndex{2}\): Золото

Какое спиновое квантовое число у золота (символ Au)?

Ответить

Золото имеет 9 электронов на 5d-орбитали. Следовательно, электроны начнут спариваться, а это означает, что 9-й электрон спарится, придав ему спин -1/2.

Упражнение \(\PageIndex{3}\): Сера

Какое спиновое квантовое число у серы (символ S)?

Ответить

Сера имеет 4 электрона на 3р-орбиталях. Четвертый электрон на этой орбитали будет первым, кто соединится с другим электроном, что даст ему спин -1/2.

Ссылки

1. Хаускрофт, Кэтрин Э. и Алан Г. Шарп. Неорганическая химия . 3-е изд. Харлоу: Pearson Education, 2008. Печать. (стр. 15).
2. Ностранд, Ван. Энциклопедия химии. 5-е изд. John Wiley and Sons, Inc., 2005. Печать. (стр. 1396).

---

Spin Quantum Number распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.

1. Вернуться к началу

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Показать страницу TOC

   № на стр.

2. Теги

   1. спин квантовое число

Спиновое квантовое число: определение, расчет и значение

В квантовой механике, когда вы пытаетесь провести аналогию между классическими величинами и их квантовыми аналогами, эти аналогии нередко терпят неудачу. Спин является прекрасным примером этого.

Электроны и структура атома

Чтобы понять вращение и последующее различие между орбитальным и собственным угловым моментом, важно понять структуру атома и то, как в нем расположены электроны.

В упрощенной модели атома Бора электроны рассматриваются как планеты, вращающиеся вокруг центральной массы, ядра. В действительности, однако, электроны действуют как диффузные облака, которые могут принимать различные орбитальные схемы. Поскольку энергетические состояния, которые они могут занимать, квантованы или дискретны, существуют разные орбитали или области, в которых существуют разные электронные облака при разных значениях энергии.

Обратите внимание на слово орбитальный вместо орбитальный ​. Эти электроны не вращаются по красивым круговым орбитам. Некоторые электроны могут занимать диффузную сферическую оболочку, но другие занимают состояния, которые создают узоры, отличные от штанги или тора. Эти разные уровни или орбитали также часто называют оболочками.

Орбитальный и собственный угловой момент

Поскольку электроны имеют спин, но также занимают состояние на орбитали атома, они имеют два различных угловых момента, связанных с ними. Орбитальный угловой момент является результатом формы облака, которое занимает электрон. Его можно рассматривать как аналог орбитального углового момента планеты вокруг Солнца, поскольку он относится к движению электронов относительно центральной массы.

Его собственный угловой момент равен его спину. Хотя это можно рассматривать как аналог углового момента вращения планеты на орбите (то есть угловой момент, возникающий в результате вращения планеты вокруг своей оси), это не идеальная аналогия, поскольку электроны считаются точечными массами. Хотя для массы, занимающей пространство, имеет смысл иметь ось вращения, для точки на самом деле не имеет смысла иметь ось. Несмотря на это, существует свойство, называемое вращением, которое действует таким образом. Спин также часто называют собственным угловым моментом.

Квантовые числа для электронов в атомах

Внутри атома каждый электрон описывается четырьмя квантовыми числами, которые сообщают вам, в каком состоянии находится этот электрон и что он делает. Этими квантовыми числами являются главное квантовое число n , азимутальное квантовое число l , магнитное квантовое число m и спиновое квантовое число s . Эти квантовые числа связаны друг с другом по-разному.

Главное квантовое число принимает целые значения 1, 2, 3 и так далее. Значение n указывает, какую электронную оболочку или орбиталь занимает конкретный электрон. Наибольшее значение n для конкретного атома — это число, связанное с самой внешней оболочкой.

Азимутальное квантовое число ​ l ​, которое иногда называют угловым квантовым числом или орбитальным квантовым числом, описывает соответствующую подоболочку. Может принимать целые значения от 0 до 9.2l(l+1)

Где ​ L ​ — орбитальный угловой момент электрона, а ℏ — приведенная постоянная Планка.

Магнитное квантовое число m , часто обозначаемое как m _l , чтобы было ясно, что оно связано с конкретным азимутальным квантовым числом, дает проекцию углового момента. Внутри подоболочки векторы углового момента могут иметь определенные разрешенные ориентации, и m _l обозначают, какой из них имеет конкретный электрон. m _l ​ может принимать целочисленные значения от -​ l ​ до +​ l ​.

Обычно квантовое число спина обозначается s . Однако для всех электронов с = ½. Ассоциированное число m _s дает возможные ориентации s ​ таким же образом, как m _l ​ дает возможные ориентации l ​. Возможные значения ​ м _с 92s(s+1)

, где S — собственный угловой момент. Следовательно, знание s может дать вам собственный угловой момент точно так же, как знание l может дать вам орбитальный угловой момент. Но опять же, внутри атомов все электроны имеют одно и то же значение s , что делает его менее захватывающим.

Стандартная модель физики элементарных частиц

Физика элементарных частиц стремится понять работу всех элементарных частиц. Стандартная модель классифицирует частицы на фермионы и бозоны , а затем далее классифицирует фермионы на кварки и лептоны , а бозоны на калибровочный и 3-бозонный скаляр.

Лептоны включают электрон , нейтрино и другие более экзотические частицы, такие как мюон , тау и связанные с ними античастицы . Кварки включают верхних и нижних кварков, которые в совокупности образуют нейтроны и протоны , а также кварки верхний , нижний , странный и очарованный и связанные с ними античастицы.

Бозоны включают ​ фотон ​, который опосредует электромагнитные взаимодействия; бозон глюон , бозон Z ⁰ , бозон W ⁺ и W ^– 3 0

Все фундаментальные фермионы имеют спин 1/2, хотя некоторые экзотические комбинации могут иметь спин 3/2 и теоретически выше, но всегда кратное 1/2. Большинство бозонов имеют спин 1, за исключением бозона Хиггса, который имеет спин 0. Предсказано, что гипотетический гравитон (еще не обнаруженный) будет иметь спин 2. Опять же, теоретически возможны более высокие спины.

Бозоны не подчиняются законам сохранения чисел, в отличие от фермионов. Существует также «закон сохранения лептонного» числа и «кваркового» числа, в дополнение к другим сохраняющимся величинам. Взаимодействие элементарных частиц опосредовано бозонами, переносящими энергию.

Принцип запрета Паули

Принцип запрета Паули гласит, что никакие два идентичных фермиона не могут одновременно находиться в одном и том же квантовом состоянии. В макроскопическом масштабе это все равно, что сказать, что два человека не могут занимать одно и то же место в одно и то же время (хотя известны случаи, когда ссорящиеся братья и сестры пытались это сделать).

Для электронов в атоме это означает, что на каждом энергетическом уровне имеется ограниченное количество «мест». Если в атоме много электронов, то многие из них должны оказаться в более высоких энергетических состояниях, как только все более низкие состояния будут заполнены. Квантовое состояние электрона полностью описывается его четырьмя квантовыми числами 9.0031 n ​, ​ l ​, ​ m _l ​ и ​ m _s ​. Никакие два электрона в одном атоме не могут иметь одинаковый набор значений этих чисел.

Например, рассмотрим разрешенные состояния электрона в атоме. Нижняя оболочка связана с квантовым числом n = 1. Тогда возможные значения l равны 0 и 1. Для l = 0 единственно возможное значение m _l ​ равно 0. Для ​ л ​ = 1, ​ м _л ​ может быть -1, 0 или 1. Тогда ​ м _с ​ = + 1/2 или -1/2. Это делает следующие комбинации возможными для N = 1 оболочка:

• L = 0, M _L = 0,

M _S 2223 M _S 229 M _S 2

M _S 9 = 1/2 * ​ л ​ = 0,

​ м _л ​ = 0,

​ м _с ​ = 1 0 0,0 3 ​ 3 90

M _L = -1,

M _S = 1/2 * L = 1,

M _L = -1 ,1 ,1,

M _L = -1, 1,

M _L = -1.

M _S = -1/2 * L = 1,

M _L = 0,

M _S 4 = 1/1/10023 M _S 4 = 1/10023 M _S

= 10023 M _S

M 2 * ​ л ​ = 1,

​ м _л ​ = 0,

​ м _с ​ = -1/2

90 ​0031 L = 1,

M _L = 1,

M _S = 1/2 * L = 1,

M 1 L = 1,

M

11 L = 1,

M

11 L = 1,

M

11 L = 1,

M 11 L = 1,

M 11 L = 1,

M 1 L l ​ = 1,

​ m _s ​ = -1/2

Следовательно, если атом имеет более восьми электронов, остальные должны занимать более высокие оболочки, такие как ​ n ​= 2 и так далее.

Бозонные частицы не подчиняются принципу запрета Паули.

Эксперимент Штерна-Герлаха

Самым известным экспериментом, демонстрирующим, что электроны должны иметь собственный угловой момент или спин, был эксперимент Штерна-Герлаха. Чтобы понять, как работал этот эксперимент, учтите, что заряженный объект с угловым моментом должен иметь связанный с ним магнитный момент. Это связано с тем, что магнитные поля создаются движущимся зарядом. Например, если вы посылаете ток через катушку с проводом, магнитное поле будет создано, как если бы внутри катушки находился стержневой магнит, выровненный с осью катушки.

Вне атома электрон не будет иметь орбитальный угловой момент. (То есть, если он не перемещается по круговой траектории каким-либо другим способом.) Если бы такой электрон двигался по прямой линии в положительном направлении x , он создал бы магнитное поле, огибающее ось его движения по окружности. Если бы такой электрон прошел через магнитное поле, направленное вдоль оси z , его траектория в результате должна немного отклониться в направлении y .

Однако при прохождении через это магнитное поле электронный пучок разделяется на две части в направлении z ​. Это могло бы произойти только в том случае, если бы электроны обладали собственным угловым моментом. Собственный угловой момент заставит электроны иметь магнитный момент, который может взаимодействовать с приложенным магнитным полем. Тот факт, что луч разделяется на две части, указывает на две возможные ориентации этого собственного углового момента.

Подобный эксперимент впервые был поставлен немецкими физиками Отто Штерном и Вальтером Герлахом в 1922. В своем эксперименте они пропустили пучок атомов серебра (которые не имеют чистого магнитного момента из-за орбитальных эффектов) через магнитное поле и увидели, как пучок разделился надвое.

Поскольку этот эксперимент показал, что существует ровно две возможные ориентации спина, одна отклонена вверх, а другая вниз, две возможные ориентации спина большинства фермионов часто называют «спин вверх» и «спин вниз». ».

Расщепление тонкой структуры атома водорода

Расщепление тонких структур энергетических уровней или спектральных линий в атоме водорода было еще одним свидетельством того, что электроны имеют спин, и этот спин имеет две возможные ориентации. Внутри электронных орбиталей атома каждая возможная комбинация n , l и m _l имеет два возможных значения m _s .

Вспомним, что внутри данного атома могут поглощаться или излучаться только очень определенные длины волн фотонов, в зависимости от разрешенных квантованных уровней энергии внутри этого атома. Спектры поглощения или испускания данного атома читаются как штрих-код, специфичный для этого атома.

Уровни энергии, связанные с различными значениями спина ​ m _s ​ для фиксированных ​ n ​, ​ l ​ и ​ ​ m _l ​, расположены очень близко друг к другу.