Как определяется мгновенная скорость при прямолинейном движении: Физический смысл производной — урок. Алгебра, 10 класс.

Скорость при равноускоренном прямолинейном движении

Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.

Что такое мгновенная скорость? Мгновенная скорость — скорость тела в данный момент времени. Обозначается v_мгн. Далее, когда мы будем говорить о скорости, мы будем понимать под ней мгновенную скорость тела и обозначать ее просто — v.

Определение

Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t₀ и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:

v = v₀ + at

v — скорость тела в данный момент времени, v₀ —скорость тела в начальный момент времени,

a — ускорение тела, t — время, в течение которого это тело двигалось

Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.

Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.

Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.

Скалярная формула скорости

В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:

v = v₀ ± at

Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.

Проекция скорости

Проекция скорости при равноускоренном прямолинейном движении имеет вид:

v_x = v_0x + a_xt

Знак проекции скорости

зависит от того, в какую сторону движется тело:

• Знак проекции скорости имеет знак «+», если тело движется в сторону направления оси ОХ.
• Знак проекции скорости имеет знак «–», если тело движется противоположно направлению оси ОХ.

Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.

График скорости

График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является

прямая.

Определение направления движения тела относительно оси ОХ по графику скорости

• Если график скорости лежит выше оси времени, то тело движется в направлении оси ОХ. На рисунке этому утверждению соответствует график 1.
• Если график скорости пересекает ось времени, то модуль скорости тела сначала уменьшался, и тело тормозило. Но с момента пересечения оси времени оно меняло направление движения в противоположную сторону и двигалось ускоренно. На рисунке этому соответствуют графики скорости 2 и 3.
• Если график скорости лежит ниже оси времени, тело движется в направлении, противоположном направлению оси ОХ. На рисунке тело 3 до пересечения с осью времени двигалось противоположно направлению ОХ. Но тело 2 двигалось противоположно оси только после пересечения с этой осью.

Сравнение модулей ускорения по графикам скоростей

Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.

Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.

На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.

Полезные факты

• Если тело начинало движение из состояния покоя, его начальная скорость равна 0, а его ускорение положительно: v₀ = 0, a > 0.
• Если тело заканчивает движение остановкой, то его мгновенная скорость в конечный момент времени равна 0, а его ускорение отрицательно: v = 0, a < 0.
• Если тело покоится, его скорость и ускорение равны 0: v₀ = 0, a = 0.

Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.

Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:

v = v₀ – at

Выразим начальную скорость:

v₀ = v + at

Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

v₀ = 0 + 2 ∙ 5 = 10 (м/с)

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

---

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22..

Теперь мы можем выделить кинематические характеристики движения тела:

• x₀ = 10 (м).

• v₀ = 5 (м/с).

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22..

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22..=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22..

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22..=0,22..(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

.

.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

---

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

• перемещение и путь;
• скорость;
• ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18202

Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков  совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

---

Алгоритм решения

1. Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
2. Вычислить ускорение движение тела на этом участке.
3. Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

• t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
• t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18027 На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

---

Алгоритм решения

1. Записать формулу ускорения.
2. Записать формулу для вычисления модуля ускорения.
3. Выбрать любые 2 точки графика.
4. Определить для этих точек значения времени и проекции скорости (получить исходные данные).
5. Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

• t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
• t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 6. 4k

Решение высшей математики онлайн

‹– Назад

Пусть материальная точка движется по координатной прямой , и её положение в момент времени имеет координату . Средняя скорость точки за произвольный промежуток времени , за который точка перемещается из положения в положение , определяется как . Если мы обозначим протекший промежуток времени через , то и , поэтому , при .

Мгновенная скорость точки в момент определяется как предел средней скорости за промежуток времени от до (), при условии . Таким образом, получаем формулу, служащую определением мгновенной скорости в момент :

(4.1)

Можно также рассматривать промежутки времени, протекшие до момента , то есть промежутки от до . Тогда средняя скорость точки за этот промежуток времени будет равна , при . Если положить , то, очевидно, , при . При этом придётся определять мгновенную скорость в момент формулой

(4.2)

        Определение 4.1   Число мы будем называть правой производной, или производной справа, функции в точке и обозначать или , а число  — левой производной, или производной слева, функции в точке и обозначать или . Иногда для уточнения говорят, что эти производные вычислены по переменной .     

Напомним ещё раз, что механический смысл как левой, так и правой производной координаты по времени  — это мгновенная скорость движения, вычисленная в момент , но либо по интервалам времени, предшествующим , либо по интервалам, последующим . Эти две мгновенных скорости не обязаны, вообще говоря, совпадать: если тело покоилось до момента , а затем двинулось с постоянной скоростью , то мгновенная скорость, вычисленная по предшествующим интервалам, очевидно, равна (так как до момента тело покоилось), а мгновенная скорость, вычисленная по последующим интервалам времени, равна ( — это изменение координаты точки, движущейся со скоростью , за промежуток времени продолжительности с момента до момента ). Эти две мгновенных скорости различны¹¹.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Скорость Средняя и мгновенная скорость — поступательное движение

Средняя скорость определяется как изменение положения (или смещения) за время движения, а мгновенная скорость — это скорость объекта в одной точке времени и пространства, рассчитанная наклон касательной.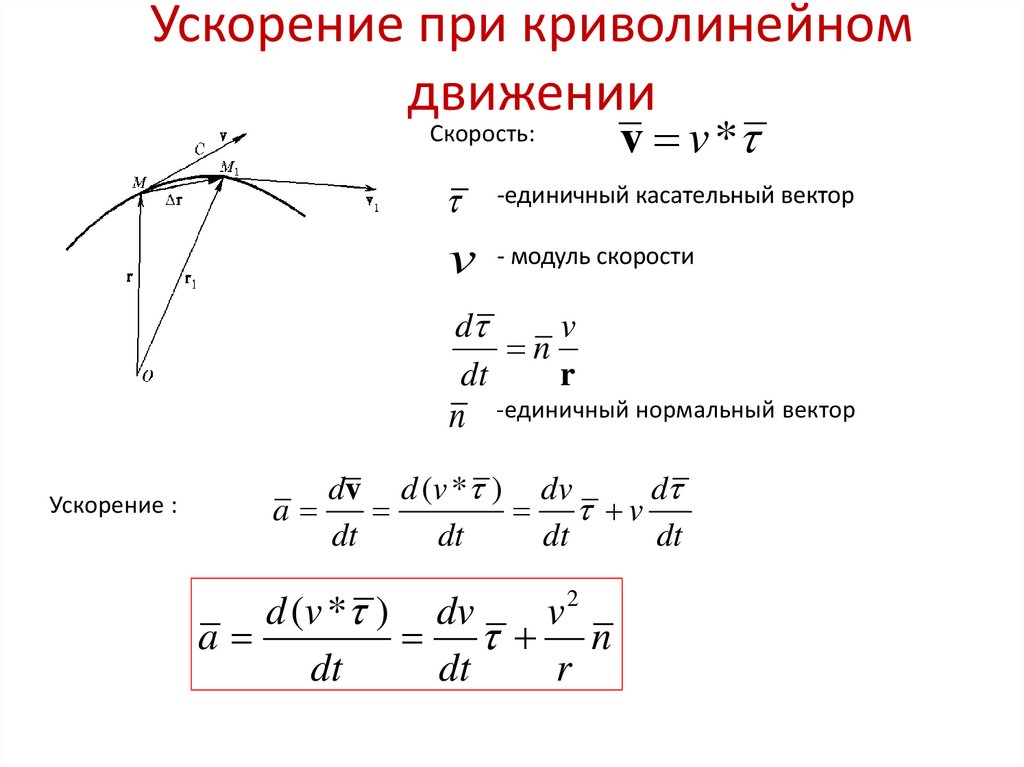

В повседневном использовании термины « скорость » и « скорость» взаимозаменяемы. Однако в физике это разные величины. Скорость является скалярной величиной и имеет только величину. Скорость, с другой стороны, является векторной величиной и поэтому имеет как величину, так и направление. Это различие становится более очевидным, когда мы вычисляем среднюю скорость и скорость. Средняя скорость рассчитывается как расстояние, пройденное за общее время в пути. Напротив, средняя скорость определяется как изменение положения (или смещения ) за общее время пути.

Как правило, движение происходит не с постоянной скоростью и скоростью. Например, когда мы едем в машине, мы постоянно ускоряемся и замедляемся. Таким образом, графическое представление нашего движения в терминах зависимости расстояния от времени будет более изменчивым или «извилистым», чем прямая линия, обозначающая движение с помощью постоянная скорость как показано ниже.

Чтобы вычислить скорость объекта по графику, представляющему постоянную скорость, все, что нужно, это найти наклон линии; это указывало бы на изменение расстояния по сравнению с изменением времени. Однако изменить скорость не так просто.

Поскольку наша скорость постоянно меняется, мы можем оценивать скорость по-разному. Один из способов состоит в том, чтобы посмотреть на нашу мгновенную скорость, представленную одной точкой на нашей изогнутой линии движения, на графике которой расстояние зависит от времени. Чтобы определить нашу скорость в любой данный момент, мы должны определить наклон в этой точке. Для этого мы находим линию, которая представляет нашу скорость в этот момент, показанную графически. Эта линия будет линией, касательной к кривой в этой точке. Если мы продолжим эту линию, мы сможем легко вычислить смещение расстояния во времени и определить нашу скорость в данной точке. Скорость объекта в любой данный момент представляет собой наклон касательной, проходящей через соответствующую точку на его графике x-t.

Вопросы практического экзамена

Тест выборочной Раздел P Вопрос 48

Ключевые моменты

• В повседневном использовании термины «скорость» и «скорость» взаимозаменяемы. Однако в физике это разные величины. Скорость является скалярной величиной и имеет только величину. Скорость, с другой стороны, является векторной величиной и поэтому имеет как величину, так и направление. Среднюю скорость можно рассчитать, определив общее перемещение, деленное на общее время в пути.

• Средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками.

• Средняя скорость отличается от средней скорости тем, что учитывает направление движения и общее изменение положения.

• Когда скорость постоянно меняется, мы можем оценить нашу скорость, взглянув на мгновенную скорость.

• Мгновенная скорость рассчитывается путем определения наклона линии, касательной к кривой в интересующей точке.

• Мгновенная скорость аналогична определению того, сколько метров объект пройдет за одну секунду в определенный момент.

Ключевые термины

Скорость: Векторная величина, обозначающая скорость изменения положения во времени или скорость с компонентом направления.

Скорость : Скалярная величина, имеющая только величину.

Средняя скорость : перемещение за определенный период времени.

Перемещение : изменение положения

Постоянная скорость : Объект, движущийся с постоянной скоростью в постоянном направлении происходит в течение незаметно короткого промежутка времени.

Чем мгновенная скорость отличается от средней скорости?

Скорость — важнейшая тема в физике. Многие свойства тела, такие как кинетическая энергия и вязкость, зависят от его скорости. Термин скорость описывает, насколько быстро или медленно движется объект. Скорость можно определить как скорость изменения положения объекта по отношению ко времени и системе отсчета. В таких разнообразных дисциплинах, как кинематика, кинетика, динамика, астрофизика и инженерия, обычно применяется понятие скорости. Чтобы преуспеть в таких дисциплинах, очень важно хорошо знать понятия мгновенной скорости и средней скорости. В этой статье мы подробно рассмотрим, чем мгновенная скорость отличается от средней скорости.

Мгновенная скорость

Скорость изменения положения за относительно короткий промежуток времени называется мгновенной скоростью или скоростью объекта в этот момент времени. Мгновенная скорость может быть рассчитана путем умножения мгновенной скорости объекта на направление, в котором он движется в данный момент времени. Скорость изменения смещения описывается как скорость в классической физике. Термин «скорость» относится к векторной величине. Они имеют числовое значение, а также направление. Объект с постоянной скоростью может иметь ту же немедленную скорость, что и его стандартная скорость. Международная система единиц (СИ) мгновенной скорости составляет метры в секунду (м/с).

Рассчитывается как средняя скорость, деленная на минимальный период. Отношение полного смещения к общему времени можно использовать для вычисления средней скорости. Смещение пропорционально интервалу времени. Предел этого отношения между временем и перемещением известен как мгновенная скорость.

Где

• V(t) мгновенная скорость в момент времени t
• x обозначает перемещение
• t обозначает время0115

Наклон касательной к функции в этом месте равен мгновенной скорости в любой заданной точке функции x(t). Наклон графика расстояние-время, часто известный как график x-t, также может быть использован для его иллюстрации. Формула мгновенной скорости:

 

Скорость между двумя положениями в пределе времени, когда время между ними постепенно становится равным 0, называется мгновенной скоростью. Расположение x по отношению к функции t обозначается X (t). Ниже приводится уравнение для средней скорости между двумя точками:

Пусть, t ₁ и t ₂ и

Δt должно быть равно 0, чтобы определить мгновенную скорость, V(t) = dx/dt

Средняя скорость

Средняя скорость рассчитывается путем деления изменения полного смещения на общее время. Средняя скорость объекта всегда меньше или равна его средней скорости. Это можно продемонстрировать, заметив, что в то время как расстояние всегда строго возрастает, смещение может менять направление, а также увеличиваться или уменьшаться по величине. Средняя скорость в Международной системе единиц (СИ) составляет метры в секунду (м/с)

, где,

• x ₁ является последним смещением
• x ₀ является начальным смещением
• T ₁ . время нахождения в начальном положении

Средняя скорость определяется как наклон секущей, соединяющей две точки с координатами t, соответствующие границам периода времени.

 

Средняя скорость равна скорости, усредненной по времени, или ее взвешенному по времени среднему значению, которое может быть определено как интеграл скорости по времени.

Where we can find out,

And,

△t = t ₁ − t ₀

Difference between Instantaneous Velocity and Average Velocity

Мгновенная скорость	Средняя скорость
Определение: Скорость изменения положения за относительно короткий промежуток времени называется мгновенной скоростью.	Definition: The average velocity is calculated by dividing the change in total displacement by the total time taken
Formula:	Formula:
Examples: speedometer, speed trap, etc.	Examples: Cable car’s average speed is actually average velocity stat, etc.

Sample Questions

Question 1: When the положение предоставленной частицы x(t) = 2,0t + 0,7 ³ м, рассчитайте мгновенную скорость при t = 3,0 с.

Решение:

Дано

x(t) = 2,0t + 0,7 ³ M

T = 3 Sec

V = 2T + 3 × 0,7 × T ²

V = 2T + 2,1T ²

AT = 3SEC

V = 2 × 3. + 3 × 0,7 × 3 ²

v = 6 + 2,1 × 9

v = 6 + 18 – 9

v = 24,9 м/с

t) = 4 с, используя функцию x = 3t ² – 5t + 2, чтобы получить положение движущегося автобуса.

Решение:

,

x = 3T ² – 5T + 2

T = 4SEC

V = 6t – 5

At T = 4 Sec

V = 6T = 6t – 5

AT = 4 Sec

V = 6T. – 5

V = 6 × 4 – 5

V = 19 м/с

Вопрос 3: За какое минимальное время хищник поймает добычу на расстоянии 200 м, если его средняя скорость равна 90 км/час?

Решение:

Дано,

V = 90 × 5/18 м/с

V = 25 м/с

A = 625/400

A = 1,56 м/с

T ^{2 999}

T ²

999

T ^{2 999}

T ^{2 99}

= 400/1,56

T ² = 256,4

T ² = 16 с

Вопрос 4: S (T) = 9t + 12T ² – уравнение для автомобиля в автомобиле в прямой путь в течение 15 секунд до аварии. Вычислите мгновенную скорость в точке 9.й-секундный интервал.

Решение:

Дано,

S (T) = 9T + 12T ²

V = 9 + 24T

Следовательно, V _Inst на = 9

V = V =

V =

V =

V = _{. + 24(9)}

V = 225 м/с

Вопрос 5: С функцией x = 7t ² + 3t + 3a данный снаряд движется по прямой за время (t) = 2с. Вычислите мгновенную скорость движущегося тела.

Solution:

Given,

x = 7t ² + 3t + 3

t = 2 sec

V _inst = 14t + 3

At t = 2 sec

V(2) = 14(2) + 3

V(2) = 31 м/с

Вопрос 6. За 4 минуты водитель автобуса проезжает 15 километров по дороге. Затем он сделал шаг назад и проехал 9 километров по дороге за 2 минуты. Какова его типичная скорость?

Решение:

 Average Velocity (v _avg ) =

 Average Velocity (v _avg ) = 6/6

 Average Velocity (v _avg ) =1 km/m

Question 7 : Рассчитайте среднюю скорость человека в определенное время, когда он проходит 5 метров за 3 секунды и 15 метров за 5 секунд по прямой линии вдоль оси x.