Ассемблер ARM64 | Умножение матриц
Последнее обновление: 17.01.2023
Рассмотрим расспространенную задачу – умножение матриц. Например, у нас есть следующие матрицы
матрица A
a11 | a12 | a13 |
a21 | a22 | a23 |
a31 | a32 | a33 |
матрица B
b11 | b12 | b13 |
b21 | b22 | b23 |
b31 | b32 | b33 |
То результат перемножения матриц будет равен
a11*b11 + a12*b21 + a13*b31 | a11*b12 + a12*b22 + a13*b32 | a11*b13 + a12*b23 + a13*b33 |
a21*b11 + a22*b21 + a23*b31 | a21*b12 + a22*b22 + a23*b32 | a21*b13 + a22*b23 + a23*b33 |
a31*b11 + a32*b21 + a33*b31 | a31*b12 + a32*b22 + a33*b32 | a31*b13 + a32*b23 + a33*b33 |
То есть для получения элемента результирующей матрицы, элементы строки первой матрицы последовательно перемножаются на элементы столбцов второй матрицы, и результаты умножений складываются.
С точки зрения псевдокода это выглядело бы так:
FOR row = 1 to 3 FOR col = 1 to 3 acum = 0 FOR i = 1 to 3 acum = acum + A[row, i]*B[i, col] NEXT I C[row, col] = acum NEXT col NEXT row
Напишем программу для перемножения двух матриц размером 3×3. Для упрощения вывода результатов на консоль воспользуемся функции printf языка С.
Итак, определим файл main.s со следующим кодом:
// Умножение двух матриц 3x3 // // Используемые регистры: // W1 - Индекс строки // W2 - Индекс столбца // X4 - Адрес строки // X5 - Адрес столбца // X7 - накопленная сумма для элемент результирующей матрицы // W9 - элемент матрицы A // W10 - элемент матрицы B // X19 - элемент матрицы C // X20 - счетчик цикла для печати // X12 - номер стороки в цикле dotloop // X6 - номер столбца в цикле dotloop .global main // точка входа в программу .equ N, 3 // Размер матрицы .equ WDSIZE, 4 // размер элемента в байтах main: STR LR, [SP, #-16]! // сохраняем значение регистра LR STP X19, X20, [SP, #-16]! // сохраняем значения регистров X19 и X20 MOV W1, #N // помещаем в W1 индекс строки LDR X4, =A // В X4 адрес текущей строки матрицы А LDR X19, =C // В X19 адрес материцы С rowloop: LDR X5, =B // первый столбец матрицы B MOV W2, #N // индекс столбца (считаем в обратном порядке до 0) colloop: MOV X7, #0 // регистр для накопления результата - по умолчанию равен 0 MOV W0, #N // счетчик цикла MOV X12, X4 // в X12 помещаем адрес строки для перемножения элементов MOV X6, X5 // в X6 помещаем адрес столбца для перемножения элементов dotloop: // Цикл для умножения элементов текущей строки матрицы A на элементы текущего столбца матрицы B LDR W9, [X12], #WDSIZE // загружаем A[row, i] и увеличиваем адрес в X12 на #WDSIZE байт LDR W10, [X6], #(N*WDSIZE) // загружаем в W10 данные из B[i, col] SMADDL X7, W9, W10, X7 // умножаем и сохраняем результат в X7 SUBS W0, W0, #1 // уменьшаем счетчик на 1 B. NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц STR W7, [X19], #4 // сохраняем результат из W7 в X19 - C[row, col] = W7, увеличиваем адрес в X19 на 4 байта ADD X5, X5, #WDSIZE // Переходим к следующему столбцу в матрице B - увеличиваем адрес в X5 на #WDSIZE байт SUBS W2, W2, #1 // увеличиваем счетчик столбцов B.NE colloop // если не все столбцы прошли, то переходим обратно к colloop ADD X4, X4, #(N*WDSIZE) // к адресу в X4 прибавляем #(N*WDSIZE) байт для перехода к адресу новой строки SUBS W1, W1, #1 // уменьшаем счетчик строк B.NE rowloop // если еще есть строки, переходим обратно к rowloop MOV W20, #3 // проходим по трем строкам LDR X19, =C // адрес результирующей матрицы C // выводим матрицу с помощью функции printf языка C printloop: LDR X0, =prtstr // загружаем строку форматирования для функции printf LDR W1, [X19], #WDSIZE // первый элемент текущей строки матрицы LDR W2, [X19], #WDSIZE // второй элемент текущей строки матрицы LDR W3, [X19], #WDSIZE // третий элемент текущей строки матрицы BL printf // Вызыв функции printf SUBS W20, W20, #1 // уменьшаем счетчик строк B. NE printloop // если есть еще строки, переходим обратно к printloop MOV X0, #0 // код возврата из функции LDP X19, X20, [SP], #16 // восстанавливаем значение регистров LDR LR, [SP], #16 // восстанавливаем регистр LR RET // выход из функции .data // первая матрица A: .word 1, 2, 3 .word 4, 5, 6 .word 7, 8, 9 // вторая матрица B: .word 9, 8, 7 .word 6, 5, 4 .word 3, 2, 1 // результирующая матрица C: .fill 9, 4, 0 prtstr: .asciz "%3d %3d %3d\n"
Вкратце рассмотрим данный код. Прежде всего в секции .data определены три матрицы. Матрицы A и B состоят из 9 элементов типа .fill, которая определяет набор из 9 элементов размеров 4 байта, каждый из которых по умолчанию равен 0.
Для упрощения работы определяем две дополнительные константы:
.equ N, 3 // Размер матрицы .equ WDSIZE, 4 // размер элемента в байтах
Вначале определяем значения для прохода по строкам:
MOV W1, #N // помещаем в W1 индекс строки LDR X4, =A // В X4 адрес текущей строки матрицы А LDR X19, =C // В X19 адрес материцы С
В W1 помещаем счетчик строк, то есть число 3 (надо пройти по трем строкам матрицы А). В регистр X4 загружается адрес матрицы A (адрес первого ее элемента) и в X19 помещается адрес матрицы С, в которую будем сохранять результат.
Дальше начинаем цикл для прохода по строкам и определяем значения для прохода по столбцам матрицы B:
rowloop:
LDR X5, =B // первый столбец матрицы B
MOV W2, #N // индекс столбца (считаем в обратном порядке до 0)
В регистр X5 помещается адрес матрицы В, а в W2 – счетчик столбцов (то есть надо пройтись по 3 столбцам матрицы В).
Затем начинаем цикл по столбцам
colloop:
MOV X7, #0 // регистр для накопления результата - по умолчанию равен 0
MOV W0, #N // счетчик цикла
MOV X12, X4 // в X12 помещаем адрес строки для перемножения элементов
MOV X6, X5 // в X6 помещаем адрес столбца для перемножения элементов
В регистр Х7 помещаем число 0 – этот регистр будет накапливать значения для одного элемента матрицы С. Кроме того, в W0 помещается счетчик цикла – надо перемножить 3 элемента из строки матрицы А и столбца марицы B. Регистр Х12 будет указывать на адрес текущего элемента строки матрицы А, а Х6 – на адрес текущего элемента столбца матрицы В.
Далее перемножаем все элементы текущей строки матрицы А и текущего столбца матрицы В:
dotloop: // Цикл для умножения элементов текущей строки матрицы A на элементы текущего столбца матрицы B
LDR W9, [X12], #WDSIZE // загружаем A[row, i] и увеличиваем адрес в X12 на #WDSIZE байт
LDR W10, [X6], #(N*WDSIZE) // загружаем в W10 данные из B[i, col]
SMADDL X7, W9, W10, X7 // умножаем и сохраняем результат в X7
SUBS W0, W0, #1 // уменьшаем счетчик на 1
B.
NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц
Для перемножения в W9 загружаем элемент по адресу X12, при этом увеличиваем данный адрес на #WDSIZE (4) байт, то есть адрес будет указываать на следующий элемент текущей строки матрицы А. Аналогично в W10 загружаем элемент по адресу X6, при этом увеличиваем данный адрес на #(N*WDSIZE) (12) байт, то есть адрес будет указываать на следующий элемент текущего столба матрицы В. Инструкция SMADDL перемножает значения W9 и W10 и прибавляет к содержимому в регистре X7. И пока не пройдем по всем 3 элементам текущих строки и столбца, продолжаем данные действия.
Таким образом, в цикле dotloop пройдем по 3 ячейкам текущих строки и столбца, получим результ и сохраним его в регистр X12.
Далее для вычисления элемента матрицы C в следующем столбце переходим к следующему столбцу матрицы B:
STR W7, [X19], #4 // сохраняем результат из W7 в X19 - C[row, col] = W7, увеличиваем адрес в X19 на 4 байта ADD X5, X5, #WDSIZE // Переходим к следующему столбцу в матрице B - увеличиваем адрес в X5 на #WDSIZE байт SUBS W2, W2, #1 // увеличиваем счетчик столбцов B.
NE colloop // если не все столбцы прошли, то переходим обратно к colloop
При этом полученный результат из X7 сохраняем в текущей элемент матрицы С, адрес которого хранится в Х19. При этом данный адрес увеличиваем на 4 байта, чтобы в следующий раз сохранить значение для следующего элемента матрицы С. Также увеличиваем адрес в X5 на #WDSIZE байт, то есть переходим к новому столбцу матрицы В и уменьшаем счетчик столбцов в регистре W2.
Если все столбцы матрицы В пройдены, то переходим к новой строке матрицы А:
ADD X4, X4, #(N*WDSIZE) // к адресу в X4 прибавляем #(N*WDSIZE) байт для перехода к адресу новой строки SUBS W1, W1, #1 // уменьшаем счетчик строк B.NE rowloop // если еще есть строки, переходим обратно к rowloop
Для этого изменяем адрес в Х4 на #(N*WDSIZE) байт (по сути на 12 байт – размер строки), уменьшаем счетчик строк в W1 и переходим к следующей строке.
Если все строки перебраны, то переходим к печати на консоль – проходим по трем строкам матрицы С и единосременно с помощью строки форматирования prtstr
выводим значения трех столбцов текущей строки матрицы C.
Поскольку в данном случае используется функция языка С, скомпилируем приложение с помощью следующей команды:
aarch64-none-linux-gnu-gcc main.s -o main -static
После запуска программа отобразит нам результирующую матрицу:
30 24 18 84 69 54 138 114 90
НазадСодержаниеВперед
Нейросеть превзошла математиков, найдя неизвестный алгоритм умножения
Исследователи из Google DeepMind показали, что ИИ может находить более быстрые алгоритмы для решения задачи умножения матриц, чем до сих пор нашли математики. Задача перемножения матриц — одна из самых трудоемких вычислительных проблем ИИ. Для поиска алгоритма умножения задача была переформулирована в игру и превзошла математиков.
Теги:
Нейросети
Нейронауки
Матрица
Нейросети учатся ускорять свою работу
Матрица — это прямоугольная таблица чисел.
Первые алгоритмы работы с матрицами были разработаны в древнем Китае 4 тысячи лет назад. Активное использование матриц для решения систем линейных уравнений началось в XVII — XVIII веках. Эта техника удобна, но для больших числовых таблиц очень трудоемка, и любое ускорение критически важно для вычислительной математики, в том числе для работы нейросетей.
Группа исследователей из Google DeepMind в Лондоне обнаружила, что ИИ может найти более быстрые алгоритмы для решения задачи умножения матриц. В своей статье, опубликованной в журнале Nature, группа описывает использование обучения с подкреплением для улучшения математических алгоритмов.
Матрицы
Математика постоянно используется в компьютерных вычислениях, как средство формального описания реального мира. Например, матрицы используются для представления пикселей на экране компьютера, погодных условий или узлов нейросети. Одним из основных алгоритмов в таких случаях является выполнение вычислений над матрицами.
Например, при программировании игр матрицы описывают возможные варианты движения. Для реализации таких движений матрицы часто перемножаются или складываются. Это требует большой вычислительной мощности, и чем больше матрицы — тем труднее с ними работать. Математики тратят много времени и энергии на разработку все более и более эффективных алгоритмов матричных вычислений.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
В 1969 году математик Фолькер Штрассен нашел способ перемножать две матрицы 2×2, используя всего семь операций умножения вместо восьми, которые были стандартом. Поскольку перемножение любых матриц можно свести к перемножению блоков 2×2, этот алгоритм на сегодня является основным вычислительным средством, которое используется в компьютерной математике.
ИИ ускоряет ИИ
В этой новой работе исследователи из DeepMind задались вопросом, можно ли использовать систему искусственного интеллекта, основанную на обучении с подкреплением, для создания новых алгоритмов с меньшим количеством шагов, чем те, которые используются сейчас.
Чтобы выяснить это, они обратились к игровым системам. Команда сосредоточилась на поиске по дереву, который обычно используется в программировании игр. Это средство, с помощью которого система может перебирать различные сценарии в поисках наилучшего. Такой подход дал отличный результат. Преобразование системы искусственного интеллекта в игру позволило отыскать более эффективный способ для перемножения матриц, чем до сих пор нашли математики. А ведь математики работают с матрицами очень давно и всегда хотели сделать работу с матрицами более быстрой.
Исследователи DeepMind позволили своей системе искать, просматривать и затем использовать существующие алгоритмы, используя вознаграждения за более короткие и быстрые способы перемножения. В результате система нашла факторы, влияющие на эффективность матричного умножения. Затем исследователи позволили системе создать собственный алгоритм. И она создала. Во многих случаях алгоритмы, выбранные системой, были лучше, чем те, которые были созданы математиками.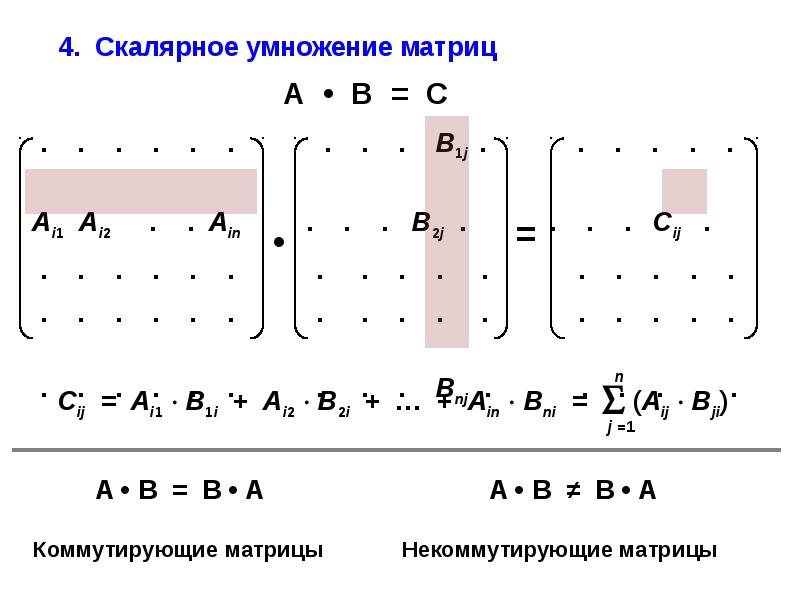
Теперь эту систему можно использовать для поиска самых разных быстрых алгоритмов во многих областях вычислительной математики.
Пушмит Кохли, соавтор работы сказал журналу Nature о работе нейросети: «У нее потрясающая интуиция, когда она играет в эти игры. Это не интуиция человека, и в некотором смысле ИИ должен создавать свои собственные знания о проблеме с нуля».
Начать работу за 5 минут
Главная/Блог/Программирование/Умножение матриц NumPy: Начать работу за 5 минут мощные математические функции. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение. Мы можем использовать NumPy для выполнения сложных математических вычислений, таких как умножение матриц.
Умножение матриц NumPy может помочь нам быстро приблизиться к очень сложным вычислениям. Это может помочь нам с теорией сетей, линейными системами уравнений, моделированием населения и многим другим. В этом руководстве мы рассмотрим некоторые базовые вычисления с умножением матриц NumPy и матричными операциями.
Начнем!
Мы рассмотрим :
- Что такое NumPy?
- Что такое матрица NumPy?
- Методы умножения матриц NumPy
- Подведение итогов и последующие шаги
Что такое NumPy?
NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и многим другим. Библиотека NumPy очень популярна в научных вычислениях, науке о данных и машинном обучении. NumPy совместим с различными типами данных и другими популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. это намного быстрее, чем Python перечисляет , потому что он интегрирует более быстрые коды, такие как C и C++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
Установка и импорт NumPy
Прежде чем мы начнем, убедитесь, что у нас установлен NumPy.
Если у вас уже есть Python, вы можете установить NumPy с помощью одной из следующих команд:
conda install numpy
pip install numpy
Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:
импортировать numpy как np
Если вы хотите изучить структуры данных Python, начните с этого полезного руководства по Python!
Что такое матрица NumPy?
Матрица представляет собой двумерный массив. Каждый элемент массива имеет два индекса. Давайте рассмотрим пример в NumPy:
импортировать numpy как np
A = [[6, 7],
[8, 9]]
print(np.array(A) [0,0])
В приведенном выше коде у нас есть матрица A [[6, 7], [8, 9]] . Мы запрашиваем элемент, заданный по адресу (0,0) , и наш вывод возвращает 6 . Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов.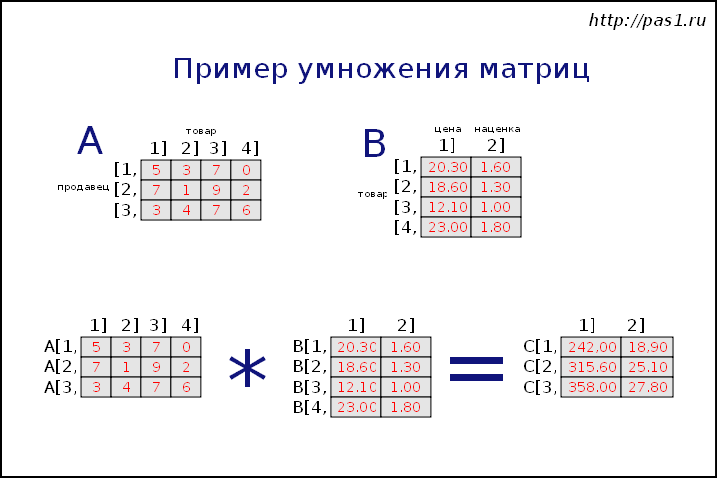
Это означает, что матрица A имеет форму 2×2.
Теперь давайте рассмотрим несколько различных методов умножения матриц NumPy.
Методы умножения матриц NumPy
Существует три основных способа выполнить умножение матриц NumPy:
-
np.dot(массив a, массив b): возвращает скалярное или точечное произведение двух массивов -
np.matmul(массив a, массив b): возвращает матричное произведение двух массивов -
np.multiply(массив a, массив b): возвращает поэлементное матричное умножение двух массивов
Давайте подробнее рассмотрим каждый из трех методов с учебным пособием NumPy по каждому из них:
Скалярное умножение или скалярное произведение с numpy.dot
Скалярное умножение — это простая форма матричного умножения. Скаляр — это просто число, например 1 , 2 или 3 . При скалярном умножении мы умножаем скаляр на матрицу .
Каждый элемент в матрице умножается на скаляр, в результате чего на выходе получается та же форма, что и у исходной матрицы.
При скалярном умножении порядок не имеет значения . Мы получим один и тот же результат, умножим ли мы скаляр на матрицу или матрицу на скаляр.
Давайте рассмотрим пример:
импортировать numpy как np
A = 5
B = [[6, 7],
[8, 9]]
print(np.dot (А ,B))
Теперь давайте умножим двумерную матрицу на другую двумерную матрицу. При умножении двух матриц порядок имеет значение . Это означает, что матрица A, умноженная на матрицу B, не совпадает с матрицей B, умноженной на матрицу A.
Прежде чем мы начнем, давайте посмотрим на визуализацию того, как выполняется умножение.
импортировать numpy как np
A = [[6, 7],
[8, 9]]
B = [[1, 3],
[5, 7]]
print(np .dot(A,B))
print("----------")
print(np.
dot(B,A)) Примечание : Важно отметить, что мы можем умножать две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.
Матричный продукт с numpy.matmul
Функция matmul() дает нам матричное произведение двух двумерных массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов является одномерным массивом, функция преобразует его в матрицу NumPy, добавляя 1 к его размерности. Это удаляется после выполнения умножения.
Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц по двум последним индексам. Метод matmul() отлично подходит для случаев, когда мы не уверены в том, какими будут размеры наших матриц.
Рассмотрим несколько примеров:
Умножение двумерного массива на другой двумерный массив
import numpy as np
A = [[2, 4],
[6, 8]]
B = [[1, 3],
[5, 7]]
print(np.
matmul(A,B)) Умножение двумерного массива на одномерный массив
импортировать numpy как np
A = [[5, 0],
[0, 5]]
B = [5, 2]
print(np.matmul(A,B))
Один массив с размерами больше 2-d
импортировать numpy как np
A = np.arange(8).reshape(2, 2, 2)
B = np.arange(4). reshape(2, 2)
print(np.matmul(A,B))
Поэлементное умножение матриц с numpy.multiply
Метод numpy.multiply() принимает две матрицы в качестве входных данных и выполняет элемент -мудрое умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы NumPy на эквивалентный элемент второй матрицы. При использовании этого метода обе матрицы должны иметь одинаковые размеры.
Давайте рассмотрим пример:
импортировать numpy как np
A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]])
B = np.
print(np.multiply(A,B))
array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]]) Мы может передавать определенные строки, столбцы или подматрицы методу numpy.multiply(). Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте рассмотрим пример:
импортировать numpy как np
A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(np.multiply(A[0,:], B[1,:]))
print("---- ------")
print(np.multiply(A[ 1,:], B[ 0,:]))
Завершение и следующие шаги
Поздравляем с первыми шагами с матрицей NumPy умножение! Это сложная, но важная часть линейной алгебры. Это помогает нам углубить наше понимание различных аспектов науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Нам еще многое предстоит узнать о NumPy и матрицах.
Ниже приведены некоторые рекомендуемые темы для обсуждения:
Транспонирование матрицы NumPy
массива NumPy (
ndarray)Векторизация NumPy
numpy.и ndarray ndarrayобъектыМногомерные массивы
ndarray Хотите начать работу с Python? Ознакомьтесь с планом обучения Educative от нуля до героя на Python . Этот практический путь обучения поможет вам овладеть навыками, необходимыми для извлечения информации из данных с использованием мощного ассортимента популярных библиотек Python.
Приятного обучения!
Продолжить изучение Python и NumPy
- 50 вопросов и ответов на собеседовании по Python
- Наука о данных стала проще: 5 основных приемов обучения Scikit
- Шпаргалка Pandas: 35 лучших команд и операций
WRITTEN BYErin Schaffer
Умножение матриц
До сих пор мы имели дело с достаточно простыми операциями: сложение и вычитание матриц ограничено матрицами одинакового размера, а скалярное умножение просто прогоняет одно число через всю матрицу .
Но поймите: настоящие матрицы также можно перемножать друг с другом.
Это немного сложнее, но в основном вам просто нужно помнить самое главное: размер имеет значение — по крайней мере, для перемножения матриц.
Размер задействованных матриц является наиболее важным фактором, поэтому будьте осторожны: для перемножения матриц количество столбцов в первой матрице должно совпадать с количеством строк во второй . И это сделает вашу жизнь намного, намного проще, если вы потратите секунду, чтобы освежить в памяти разницу между строкой и столбцом. Помните, строк — это по горизонтали (слева направо), а столбцов — это по вертикали (сверху вниз).
Пример задачи
Допустим, у нас есть матрица A и матрица B :
Как размер матриц, так и порядок, в котором мы их умножаем.
AB — это то, что мы не можем сделать, потому что в A есть два столбца и три строки в B . Игра окончена, чувак.
BA мы можем сделать, потому что B имеет два столбца, а A имеет две строки.
Идеальный. Следующее, что нужно помнить, это то, что матрица продукта будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица . Да, это так важно, что мы выделили всю чертову штуку курсивом.
Далее до BA . Вот как это выглядит:
Мы знаем, что в продукте будет три строки, например B 9.0302, а два столбца типа A :
Мы уже знаем, что первая матрица здесь — B , а вторая — A . Назовем наш продукт P . В этом случае записи в матрицах могут быть помечены следующим образом:
Вам нужно пройтись по ним и вниз, чтобы понять это:
P 11 = ( B 11 )( А 11 ) + ( Б 12 )( A 21 )
Умножаем и складываем элементы первой строки первой матрицы с элементами первого столбца второй матрицы. Поэтому размеры должны совпадать, чтобы ничего не осталось.
Затем для следующей записи в нашем продукте:
P 12 = ( B 11 )( A 12 ) + ( 9030 1 Б 12 )( А 22 )
Теперь переходим к следующей части. Вы умножаете и складываете элементы второй строки первой матрицы с элементами первого столбца второй матрицы. Пристегнитесь.
P 21 = ( B 21 )( A 11 ) + ( B 90 396 22 )( A 21 )
Затем вы разбиваете второй строку первой матрицы со вторым столбцом второй матрицы. Это дает вам второй ряд вашего продукта.
P 22 = ( B 21 )( A 12 ) + ( B 9 0396 22 )( А 22 )
Почти готово. Еще одна строка, и вы, вероятно, догадываетесь, как это выглядит:
P 31 = ( B 31 )( A 11 ) + ( Б 32 )( A 21 )
P 32 = ( B 31 )( A 12 ) + ( Б 32 )( А 22 )
Подключив весь этот хлам к общей картине, мы получим следующее:
Вот еще один способ взглянуть на это.
Из правил мы знаем, что P будет иметь три строки, например B , и два столбца, например A . Попробуйте визуализировать три из них вместе следующим образом:
Глядя на пересечения, мы можем видеть, какая строка B и какой столбец A сталкиваются, чтобы получить одно из P записи. Ниже мы видим, что X отмечает место, где первая строка из B и столбец один из A , авария:
Мы знаем, что эти четыре числа нужно объединить в одно. Как они это делают? Ну, читаем строки слева направо, как книгу. Читаем столбцы сверху вниз. Следовательно, умножаем первое число из B в первой строке на первое число из A в первом столбце:
(1)(2) = 2
Затем умножаем второе число из B первая строка со вторым номером от A первый столбец:
(3)(3) = 9
Складываем их вместе:
(1)(2) + (3)(3) = 2 + 9 = 11
Далее мы проверяем коллизию между первой строкой B и вторым столбцом A :
Да; X отмечает место, и мы делаем то же самое.
Читаем ряды слева направо, как книгу. И мы читаем столбцы сверху вниз. Умножаем первое число из B первого ряда на первое число из 9Второй столбец 0301 A : (1)(1) = 1. Затем мы умножаем второе число из первой строки B на второе число из второго столбца A : (3)(2) = 6. Сложите их вместе, чтобы получить нашу запись для X:
(1)(1) + (3)(2) = 1 + 6 = 7
Мы знаем, мы знаем. Мы как заезженная пластинка, но Х снова ставит точку, и мы делаем то же самое. Мы читаем строку слева направо и читаем столбец сверху вниз. На этот раз мы делаем вторую строку в произведении, поэтому мы умножаем первое число из B во второй строке с первым числом из A в первом столбце: (2)(2) = 4. Затем умножьте второе число из B во второй строке на второе число из A первый столбец: (1)(3) = 3. Теперь сложите их:
(2)(2) + (1)(3) = 4 + 3 = 7
Теперь мы действительно кое-что достигли.
Почти на месте.
Теперь это выглядит так, и мы можем видеть, что будет дальше:
X отмечает точку, друг, и мы делаем то же самое. Строка идет слева направо, столбец сверху вниз. На этот раз мы все еще делаем второй ряд в продукте, но мы переходим ко второму месту в нем. Умножаем первое число из B вторая строка с первым числом из A второй столбец: (2)(1) = 2. Затем мы умножаем второе число из B вторая строка со вторым числом из A Второй столбец : (1)(2) = 2. Добавьте этих парней:
(2)(1) + (1)(2) = 2 + 2 = 4
И мы это делаем снова, на этот раз с третьей строкой B , по одному разу для каждой записи в первом столбце A .
(4)(2) + (2)(3) = 8 + 6 = 14
И, наконец, соединяем третью строку B со вторым столбцом A 903 02 :
(4)(1) + (2)(2) = 4 + 4 = 8
У-у-у! Мы сделали это!
Мы не растерялись, и становится только легче, пока мы помним самые важные правила:
- Для перемножения матриц число столбцов в первой матрице должно быть таким же, как количество строк в второй.
- Матрица произведения будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.
Эй, помните, мы говорили, что даже когда у нас есть две матрицы одинакового размера, порядок имеет значение? Конечно, вы можете умножать в любом порядке, но ответ будет другим. Смотреть:
Образец задачи
Сначала мы можем сделать это в следующем порядке:
(2)(1) + (4)(4) = 2 + 16 = 18
(2)(0) + (4) )(2) = 0 + 8 = 8
(3)(1) + (3)(4) = 3 + 12 = 15
(3)(0) + (3)(2) = 0 + 6 = 6
Итак, это наш продукт:
А если мы поменяемся местами?
Расположим так, чтобы было легче увидеть:
(1)(2) + (0)(3) = 2 + 0 = 2 )( 3) = 4 + 0 = 4
(4)(2) + (2)(3) = 8 + 6 = 14
(4)(4) + (2)(3) = 16 + 6 = 22
Это наш продукт:
Совершенно другой. Странно, да?
Придержите прессы. Помните единичную матрицу и нулевую матрицу?
Мышление в двоичном виде
Единственный случай, когда число можно умножить и остаться прежним, это умножить его на число 1.
3 × 1 = 3
100 × 1 = 100
457 820 × 1 = 457 820
В Стране матриц единичная матрица представляет собой матричную версию 1. Все матрицы идентичности равны 0, за исключением диагональной линии из 1, проходящей от верхнего левого угла к нижнему правому. Они могут быть любых размеров, главное, чтобы они были квадратными:
Вот что важно: всякий раз, когда матрица умножается на единичную матрицу, произведение равно неединичной матрице. И мы можем это доказать.
Пример задачи
Действуем так же, как при умножении ранее. Мы назовем единичную матрицу I , произведение P , а другую матрицу назовем T для Теда. Нам просто нравится это имя, хорошо? Попробуйте визуализировать их троих вместе вот так:
Итак, мы объединяем первую строку T с первым столбцом I , чтобы найти X:
(2)(1) + (3) (0) + (2)(0) = 2 + 0 + 0 = 2
Мы продолжаем в том же духе и получаем произведение, точно такое же, как T , потому что умножение матрицы на I похоже на умножение числа на число 1.
Правило: Всякий раз, когда мы умножаем матрицу на единичную матрицу, ответ всегда такой же, как у неединичной матрицы. Да, мы вернули курсив для этого чрезвычайно важного правила.
А нулевая матрица? Ну, мы же помним, что любое число, умноженное на ноль, равно нулю. Точно так же нулевая матрица действует при умножении матриц. Это все нулевые матрицы:
Правило: Всякий раз, когда мы умножаем матрицу на нулевую матрицу, ответ всегда будет нулевой матрицей, которая имеет то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.
Пример задачи
Мы знаем, что их можно перемножить, потому что количество столбцов в первой матрице (3) совпадает с количеством строк во второй (тоже 3). Мы также знаем, что матрица произведения будет матрицей 3 × 3, потому что матрица произведения будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.