Как период в физике обозначается: Формула периода колебаний пружинного маятника в физике

Внеклассный урок – Колебательное движение

Колебательное движение

Колебательные движения тела – это движения, повторяющиеся через определенный промежуток времени.

 

Например, колебательные движения совершает маятник, мячик на нитке и т.п.

 

Свободные колебания. Колебательные системы.

Свободные колебания тела – это колебания, происходящие только благодаря начальному запасу энергии.

Пояснение.

Отведем в сторону мячик, висящий на нитке, и отпустим его. Мячик начнет совершать колебательные движения влево-вправо. Это и есть свободные колебания.

 

Системы тел, которые способны совершать свободные колебания, называются колебательными системами.

Пояснение:

В нашем примере мячик, нитка и устройство, к которому нитка прикреплена, вместе составляют колебательную систему.

 

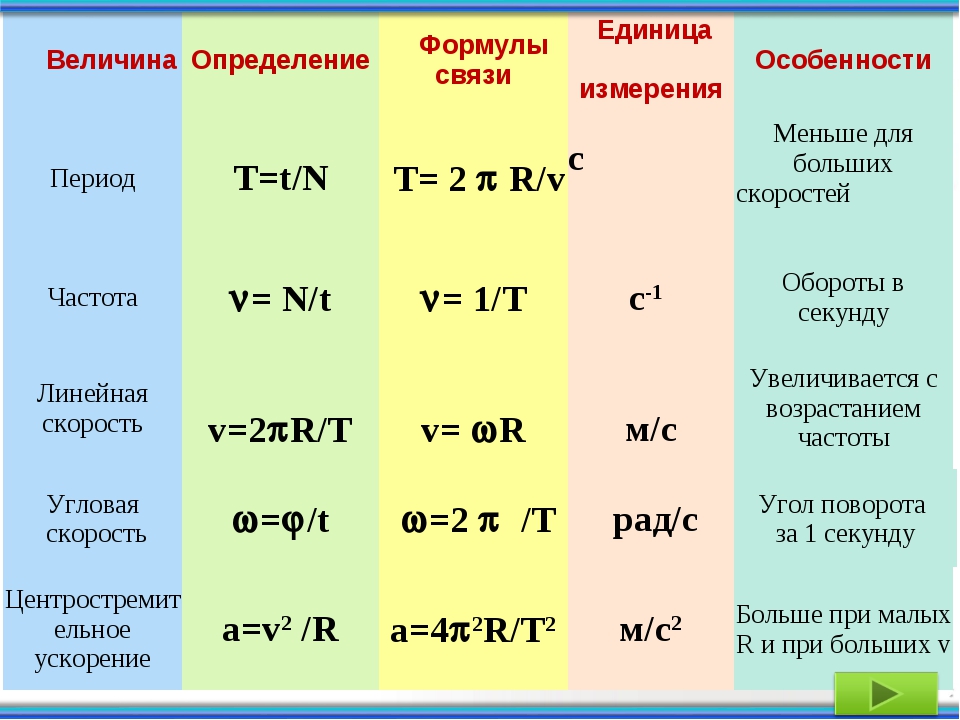
Амплитуда, период, частота колебаний.

Амплитуда – это наибольшее отклонение колеблющегося тела от положения равновесия. Измеряется в метрах, сантиметрах и т.п.

Пояснение:

Мячик на нитке достигает определенного предела колебания, затем начинает движение в обратную сторону. Расстояние от положения равновесия (покоя) до этой крайней точки и называется амплитудой.

 

Период колебаний – это промежуток времени, в течение которого тело совершает одно полное колебание.

Период колебаний обычно измеряется в секундах.

Обозначается буквой Т.

 

Частота колебаний – это число колебаний, совершаемых в единицу времени.

За единицу частоты принято одно колебание в секунду. Название этой единицы – герц (Гц).

Частота колебаний обозначается буквой ν («ню»).

Пояснение:

Если мячик за одну секунду совершает два колебания, то частота его колебаний составляет 2 Гц. То есть ν = 2Гц.

 

Чтобы найти период колебаний, надо одну секунду разделить на частоту колебаний:                                                                                 1                                                                       Т = ——                                                                                 ν

Пояснение:

В нашем примере мячик за одну секунду совершает два колебания. Такова его частота колебаний. Значит:

         1
Т = —— = 0,5 с.
       2Гц

 

Частота свободных колебаний называется собственной частотой колебательной системы.

 

Виды колебаний.

Колебания бывают гармонические, затухающие, вынужденные.

 

 

Физика – 7

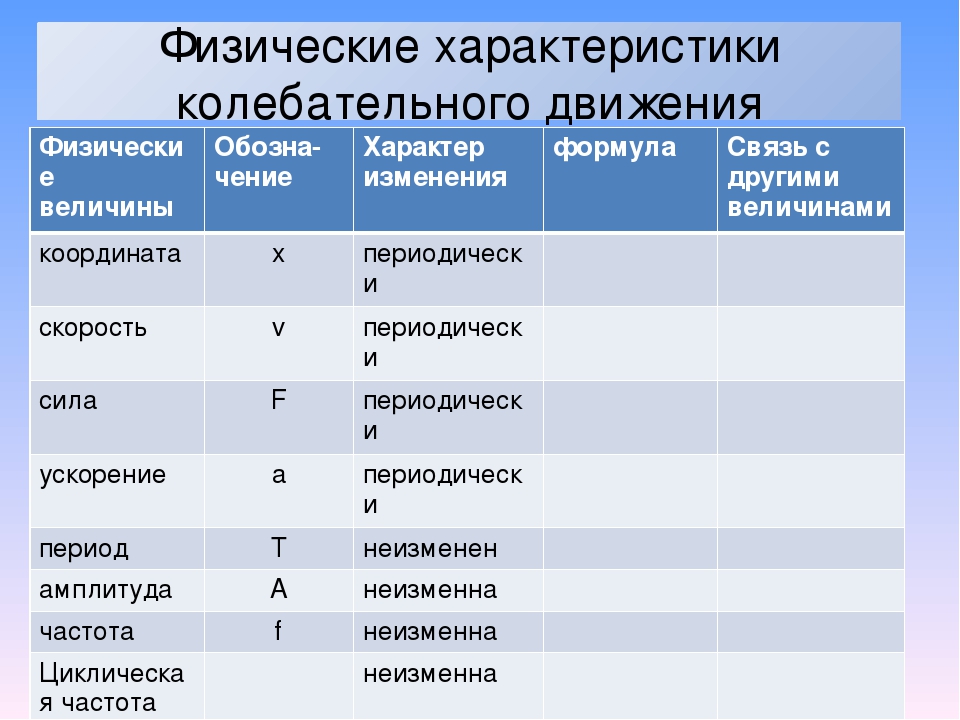
6.2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Некоторые маятники совершают вокруг точки равновесия быстрые или медленные колебательные движения.

• Что значит быстрое или медленное колебание маятника?
• По каким характеристикам можно различать механические колебательные движения?

При колебаниях, также как и при других механических движениях, существуют физические величины, характеризующие их. Эти величины: смещение маятника, амплитуда колебаний, период колебаний и частота колебаний.

Что значит смещение маятника? Смещение маятника – это определенное расстояние, на которое он отклоняется от положения равновесия.

Что такое амплитуда колебания? Выведя маятник из положения равновесия, задержим его, например, в точке 1. Свободно отпустив маятник, приведем его в движение. В это время маятник, совершая движение в правую сторону, удаляясь от точки равновесия, попадает в определенную точку 2 и там на мгновение останавливается, а затем, изменив направление, движется влево (а).

a

Таким образом, маятник совершает колебания между двумя точками, расположенными на наибольшем удалении от точки равновесия.

Амплитуда колебания – это наибольшее (максимальное) расстояние, на которое удаляется маятник от положения равновесия.

Смещение маятника из одного крайнего положения в другое крайнее положение и оттуда обратно, в предыдущее крайнее положение, называется полным колебанием.

Амплитуда обозначается буквой А, или х

м, единица ее измерения в системе СИ – метр:

Период колебаний. Период колебания – это время, затраченное на одно полное колебание. Период колебания обозначается буквой Т и единица измерения в системе СИ – секунда:

[T] = 1 с.

Если за определенный промежуток времени

t маятник совершает N колебаний, то период колебаний определяется следующим образом:

Тема №9663 Ответы к тестам по физике 9 класс 456456 (Часть 1)

Тема №9663

Перемещение
Вариант 1
1. Механическое движение —- это изменение положения тела
в пространстве
а) под действием других тел с течением времени
б) относительно других тел с течением времени
2. Материальной точкой можно считать самолет, если
а) определяют среднюю скорость движения самолета при полете
б) вычисляют силу сопротивления воздуха, которая действует на
самолет
3.

Движение тела называется поступательным, если в любой
момент времени все его точки
а) движутся одинаково
б) описывают окружности разных радиусов
4. Путь — это
а) расстояние между начальной и конечной точками движения
б) сумма длин всех участков траектории тела
5. На каком рисунке правильно показано перемещение тела
из пункта А в пункт Я?
6. Телом отсчета называется тело
а) размерами которого можно пренебречь при отсчете пройден­
ного пути
б) с помощью которого отсчитывают пройденное расстояние
в) относительно которого рассматривают изменение положения
других тел
1
ТЕСТ 1. Материальная точка. Система отсчета.

Перемещение
Вариант 2
1. Материальная точка — это
а) тело, которое рассматривается как точка, имеющая массу
б) обычная точка на плоскости или в пространстве
2. Система отсчета состоит из
а) тела отсчета и прибора для измерения времени (часов)
б) системы координат, тела отсчета и прибора для измерения
времени (часов)
3. Перемещение — это вектор, соединяющий
а) две любые точки траектории тела
б) начальное положение тела с его последующим положением
4. Перемещение обозначают символом:
а) S б) 7 в) S
5. Точка, двигаясь по окружности, пришла в начальное поло­
жение. Если длина окружности 20 м, то перемещение точки
за время движения равно
а) 20 м б) 40 м в) 0 м
6. Знать вектор перемещения — это значит знать
а) только его направление
б) только его модуль (длину вектора)
в) его направление и модуль
2
ТЕСТ 2. Определение координаты движущегося тела
Вариант 1
1. Вычисления производят
а) только с модулями векторов
б) с проекциями и модулями векторов
в) только с проекциями векторов
2. С момента начала наблюдения черепаха переместилась из
пункта А в пункт В.
О
X, м
Ее начальная координата:
а) 30 м б) 90 м в) 60 м
3. Проекция перемещения черепахи (см. задание 2):
а) Sx = 90 м; Sx > 0
б) S = 60 м; 5 > 0 X X
в) sx= -30 м; 5^ < 0
4.
S А
х, м
Ее конечная координата:
а) -20 м б) 10 м в) 0 м
3. Проекция перемещения черепахи (см. задание 2):
а) S = -30 м; S <0
б) S=-20u;S Л X <0
в) Sx = 30 м; Sx > 0
4. Координата тела вычисляется по формуле:
а) х = х„ – S б) х0 +1 = х в) = + S
5. Чему равно расстояние между двумя шарами на рисунке?
-5 0 5 10
—- 1———– 1————–■———— 1————— ►
Ф Ф
а) 10 м б ) -15 м в) 15 м
6. Начальная координата велосипедиста = -100 м, а конеч­
ная х — 100 м. Проекция его перемещения на ось Ох:
а) 0 м б) -200 м в) 200 м
4
ТЕСТ 3. Перемещение при прямолинейном
равномерном движении
Вариант 1
1. Тело движется равномерно и прямолинейно, если
а) тело за любые равные промежутки времени проходит одина­
ковые пути
б) его траектория — прямая линия и тело за любые равные про­
межутки времени проходит одинаковые пути
2. Формула перемещения для равномерного прямолинейного
движения имеет вид:
a) S = V ‘t б) S = — в) v = —
t t
3. ~ б) S = — в) S = v -t
t t
2. Векторы перемещения и скорости направлены
а) в одну сторону
б) в противоположные стороны
в) под углом 90° друг к другу
3. Проекцию вектора перемещения вычисляют по формуле:
а) S=v-t б) S = v t в) S ~ v -t
4. Если направление движения изменяется, то пройденный
путь
а) меньше модуля перемещения
б) больше модуля перемещения
5. На рисунке изображен график зависимости проекции ско­
рости тела от времени. Чему равна проекция перемещения
за 12 ч?
vx, км/ч , i
20———————– ——————
10 ‘■
0 4 8 12 16
а) 160 км б) 240 км в) 20 км
6. Автомобиль движется равномерно и прямолинейно со ско­
ростью 72 км/ч. Его модуль перемещения за 20 с равен
а) 1440 м б) 400 м в) 3,6 км
6
Вариант 1
ТЕСТ 4. Прямолинейное равноускоренное движение.
Ускорение
1. Движение называется прямолинейным равноускоренным,
если
а) проекция вектора скорости за любые равные промежутки вре­
мени меняется одинаково
б) тело движется по прямой линии, а проекция вектора скорости
за любые равные промежутки времени меняется одинаково
2. Модуль вектора ускорения показывает, на сколько
а) увеличивается модуль вектора скорости за единицу времени
б) изменяется модуль вектора скорости за единицу времени
3. Проекцию вектора ускорения можно вычислить по фор­
муле:
а* – а0х
t
t-t о
Vх
4. За 4 с проекция вектора скорости изменилась от 2 м/с до
4 м/с. Проекция вектора ускорения при этом равна
а) 0,5 м/с2 б) 50 км/ч2 в) 0,5 см/с2
5. На рисунке показаны направления скорости и ускорения
мяча.
Скорость мяча
а) не изменяется
б) уменьшается
в) увеличивается
6. В СИ единицей ускорения является
а) 1 км/ч2 б) 1 см/с2 в) 1 м/с2
7
Вариант 2
ТЕСТ 4. Прямолинейное равноускоренное движение.
Ускорение
1. Мгновенная скорость — это скорость
а) в конкретной точке траектории, в соответствующий момент
времени
б) на определенном участке пути за определенный промежуток
времени
2. Равноускоренное движение — это движение
а) с постоянным ускорением
б) с постоянной скоростью
3. Чем больше ускорение тела, тем его скорость изменяется
а) меньше
б) больше
в) больше, но только по направлению
4. Проекция вектора скорости изменяется за 4 с от 6 м/с
до 2 м/с. Проекция вектора ускорения при этом равна
а) 1 м/с2 б) -1 м/с2 в) -1 см/с2
5. На рисунке показаны направления скорости и ускорения
мяча.
Скорость мяча
а) не изменяется
б) увеличивается
в) уменьшается
6. Формула ускорения при равноускоренном движении имеет
вид:
ч – а-ао ~ – Vo-v ч – v — Vo а) и = ——– б) а = ——- в) а = ——–
t t t
8
ТЕСТ 5. Скорость прямолинейного равноускоренного
движения. Г рафик скорости
Вариант 1
1. Проекция вектора скорости равноускоренного движения
вычисляется по формуле:
а) Vx = V Ox + a x•’ б> V0X = V x + aB> y* = y0 * – V ‘
2. Графиком функции vx = v0x + ax -t является
а) ломаная линия б) прямая линия в) парабола
3. Автомобиль разгоняется прямолинейно равноускоренно
с нулевой начальной скоростью. Г рафик проекции скорос­
ти автомобиля имеет вид:
4. На рисунке показан график проек­
ции скорости.
Проекция начальной скорости
равна
а) 20 м/с в) 10 м/с
б) 0 м/с
5. Модуль ускорения мяча а = 5 м/с2, модуль начальной ско­
рости и0 = 0 м/с. Какова проекция скорости мяча через 2 с?
а) 2,5 м/с
б) 5 м/с
в) 10 м/с
6. На рисунке показан график проек­
ции скорости. Проекция ускорения
равна
а) 2 м/с2 в) -2 м/с2
б) 4 м/с2
2 Физика, 9 кл. Тесты 9
ТЕСТ 5. Скорость прямолинейного равноускоренного
движения. Г рафик скорости
Вариант 2
1. Если в начальный момент тело покоилось, то формула про­
екции вектора скорости имеет вид:
3) = у ® Vx = V Qx+ a x – * * ) ° х = а х ’ *
2. Функция v = vQ + а ■ t является
а) криволинейной б) квадратичной в) линейной
3. График проекции скорости прямолинейного равноускорен­
ного движения, когда начальная скорость не равна нулю,
имеет вид:
4. Какой из графиков проекции скорости соответствует
уменьшению модуля скорости?
1 X’ ~ 7 1
л. —
* * 2
в) S x = V0x + ax-{
2. Модуль ускорения мяча a = 2 м/с2, модуль начальной ско­
рости и0 = 0 м/с. Модуль перемещения мяча за 4 с равен
а) 16 м б) 8 м в) 32 м
3. Если промежутки времени, отсчитываемые от начала рав­
ноускоренного прямолинейного движения, увеличиваются
в целое число раз, по сравнению с первым промежутком
времени, то модули перемещения относятся как
а) 1:2:3:4:5 б) 1:3:5:7:9 в) 1:4:9:16:25
4. Проекция ускорения тела а — 1 м/с2, проекция начальной
скорости и0х = 2 м/с. Проекция перемещения за первые 2 с
равна
а) 4 м б) 6 м в) 8 м
5. Велосипедист за первую секунду равноускоренного движе­
ния проехал 2 м. За вторую секунду он проедет
а) 8 м б) 6 м в) 4 м
6. Автомобиль при разгоне с места за 20 с проехал равноуско­
ренно 400 м. Его модуль ускорения равен
а) 20 м/с2 б) 1 м/с2 в) 2 м/с2
11
ТЕСТ 6. Перемещение тела при прямолинейном
равноускоренном движении
Вариант 2
1. Формула для расчета проекции вектора перемещения при
равноускоренном движении с нулевой начальной скорос­
тью имеет вид:
о
а) Sr =V0x’t +
X в) Sx = ax t
П • t
б) S =
2. Проекция ускорения шайбы — – 2 м/с2, проекция началь­
ной скорости v0 = 20 м/с. Проекция перемещения шайбы
за первую секунду равна
a) S = 20 м б) S = 19 м в) S = 21 м X X X
3. Модули векторов перемещений за последовательные рав­
ные промежутки времени (каждый из которых равен пер­
вому промежутку от начала равноускоренного движения)
относятся как
а) 1:2:3:4:5 б) 1:4:9:16:25 в) 1:3:5:7:9
4. Автомобиль при разгоне с места за первую секунду равно­
ускоренного движения проехал 4 м. За первые две секунды
он проедет
а) 8 м б) 10 м в) 16 м
5. Велосипедист начинает разгон, имея скорость 10 м/с. Если
его ускорение равно 1 м/с2, то за 10 с модуль его переме­
щения будет равен
а) 150 м б) 100 м в) 200 м
6. Проекция перемещения тела за первые три секунды равна
S = 30 м, проекция начальной скорости и0х = 4 м/с. Проек­
ция его ускорения
а) ах = 2 м/с2 б) ах = 4м/с2
12
ТЕСТ 7. Относительность движения.
Инерциальные системы отсчета. Первый закон Ньютона
Вариант 1
1. Скорость одного и того же тела в разных системах отсчета
может быть
а) только одинаковой
б) разной только по числовому значению
в) различной как по числовому значению, так и по направлению
2. Геоцентрическую систему мира изложил
а) Клавдий Птолемей
б) Николай Коперник
в) Исаак Ньютон
3. Смена дня и ночи по системе Коперника объясняется вра­
щением
а) Земли вокруг своей оси
б) Земли вокруг Солнца
в) Солнца вокруг Земли
4. Если на тело не действуют другие тела, то оно
а) только покоится относительно инерциальной системы отсчета
б) сохраняет свою скорость относительно любой системы от­
счета
в) сохраняет свою скорость относительно инерциальной систе­
мы отсчета
5. Системы отсчета, в которых не выполняется закон инерции,
называются
а) инерциальными
б) неинерциальными
в) геоцентрическими
6. Гелиоцентрическая система является с высокой степенью
точности
а) неинерциальной
б) инерциальной
в) как инерциальной, гак и неинерциальной
13
ТЕСТ 7. Относительность движения.
Инерциальные системы отсчета. Первый закон Ньютона
Вариант 2
1. В различных системах отсчета различны
а) только пути
б) только траектории движения
в) как пути, так и траектории движения
2. Гелиоцентрическую систему изложил
а) Исаак Ньютон
б) Клавдий Птолемей
в) Николай Коперник
3. Время, за которое земной шар делает полный оборот вокруг
своей оси:
а) сутки б) день в) месяц
I
4. Первый закон Ньютона формулируется так:
а) существуют такие системы отсчета, относительно которых
тела покоятся, если на них не действуют другие тела
б) существуют такие системы отсчета, относительно которых
тела сохраняют свою скорость, если на них не действуют
другие тела
в) тела сохраняют свою скорость, если на них не действуют
другие тела
5. В инерциальных системах отсчета закон инерции
а) выполняется
б) не выполняется
в) может выполняться, а может не выполняться 6
6. Если система отсчета движется равномерно и прямолиней­
но относительно Земли, то она является
а) неинерциальной
б) инерциальной
в) может быть как инерциальной, так и неинерциальной
14
1. Причиной возникновения ускорения является
а) изменение скорости тела
б) действие на тело других тел с некоторой силой
в) изменение траектории тела
2. Второй закон Ньютона можно записать так:
а) а = F-m б) а = — в) F = —
т т
3. Вектор ускорения совпадает по направлению с вектором
а) скорости
б) перемещения
в) равнодействующей силы
4. Третий закон Ньютона формулируется так: силы, с которы­
ми два тела действуют друг на друга,
а) равны по модулю и противоположны по направлению
б) противоположны по направлению и не равны по модулю
в) равны по модулю и имеют одинаковое направление
5. Силы, возникающие в результате взаимодействия тел,

являются
а) силами одной и той же природы
б) силами разной природы
в) только силами тяготения
6. Весом тела называют силу
а) приложенную к телу
б) приложенную к опоре
в) притяжения тела к Земле
ТЕСТ 8. Второй закон Ньютона. Третий закон Ньютона
Вариант 1
15
1. Если равнодействующая сил, приложенных к телу, не равна
нулю, то тело движется
а) с ускорением
б) с постоянной скоростью
в) сначала с постоянной скоростью, а затем с ускорением
2. Силу, действующую на тело, можно вычислить по фор­
муле:
a) F=m a б) F = — в) F = —
т а
ТЕСТ 8. Второй закон Ньютона. Третий закон Ньютона
Вариант 2
3. В Международной системе (СИ) единицей силы является
килограмм силы, 1 кг = 1 кг •м
б) ньютон, 1 Н = 1 кг —
с
в) ньютон, 1 Н = 1 КГ-—
4. Математическая запись третьего закона Ньютона имеет
вид:
а) а — — б) а = — в) F = -F 1
т т
5. Силой реакции опоры называют силу
а) приложенную к опоре
б) приложенную к телу
в) с которой Земля притягивает опору
6. Силы, о которых говорится в третьем законе Ньютона,
а) уравновешивают друг друга
б) не уравновешивают друг друга
в) могут как уравновешивать, так и не уравновешивать друг
друга в зависимости от того, какая сила больше
16
ТЕСТ 9.
2
2
6. Вес тела равен нулю, если
а) на тело не действует сила тяжести
б) сила тяжести уравновешена другой силой
в) на тело действует только сила тяжести
17
ТЕСТ 9. Свободное падение тел.
Движение тела, брошенного вертикально вверх.
Невесомость
Вариант 2
1. Ускорением свободного падения называют
а) одинаковое ускорение, с которым все тела, независимо от их
масс, объемов, форм, совершают свободное падение в данном
месте Земли
б) ускорение, с которым движутся тела разной массы вблизи по­
верхности Земли
в) ускорение, которое приобретают все тела под действием соб­
ственного веса
2. Обозначение проекции ускорения свободного падения:
а) ёх б) g в) ах
3. Формула проекции перемещения свободно падающего тела
имеет вид:
4. Стальной шарик и перышко падают с одной и той же высоты.
Если учесть сопротивление воздуха, то они упадут на Землю
а) одновременно
б) не одновременно (стальной шарик раньше)
в) не одновременно (перышко раньше)
5. Формула проекции скорости тела, движущегося вертикаль­
но вверх при действии только силы тяжести, имеет вид:
б) S = z ± ±
х 2
2
В) Sx = gx-t
2
а> Vx=VOx + Sx’t б)
6. Состояние невесомости — это состояние, когда
а) сила тяжести равна нулю
б) вес тела равен нулю
в) вес тела уравновешивает силу тяжести
18
ТЕСТ 10. Закон всемирного тяготения.
Ускорение свободного падения на Земле
и других небесных телах
Вариант 1
1. Явление всемирного тяготения заключается в том, что
а) все тела во Вселенной имеют вес
б) между всеми телами во Вселенной действуют силы притя­
жения
в) между всеми телами во Вселенной действуют электрические
силы
2. Можно ли применять формулу закона всемирного тяготе-
ния F = G 1 . 2 для точного расчета силы притяжения
Rz
между телами, которые имеют форму куба?
а) можно при любых условиях
б) можно, если размеры кубов намного меньше расстояния меж­
ду ними
в) нельзя ни при каких условиях
3* Яблоко, висящее на ветке, притягивает к себе Землю. Уско­
рение Земли, вызванное этой силой, близко к нулю, потому
что
а) сила притяжения Земли яблоком очень мала
б) масса яблока очень мала
в) масса Земли намного больше массы яблока
4. Формула для расчета ускорения свободного падения на
поверхности Земли имеет вид:
а) g = G б )g=G в) g=G
М 3 • т
5. Сила тяжести, действующая на тело,
а) увеличивается, если тело удаляется от поверхности Земли
б) увеличивается, если тело приближается к поверхности Земли
в) не зависит от того, на какой высоте находится тело
19
ТЕСТ 10. Закон всемирного тяготения.
Ускорение свободного падения на Земле
и других небесных телах
Вариант 2
1. Формула закона всемирного тяготения имеет вид:
2. Формула закона всемирного тяготения дает точный резуль­
тат при расчете силы, если оба тела
а) имеют шарообразную форму
б) являются цилиндрами
в) имеют форму кубов
3. Земля притягивает к себе мяч, лежащий на ее поверхности.
Мяч притягивает к себе Землю
а) с меньшей по модулю силой
б) с большей по модулю силой
в) с такой же по модулю силой, с какой его притягивает Земля
4. Притяжение тел к Земле — один из случаев
а) магнитной силы
б) всемирного тяготения
в) электрической силы
5. Если тело находится на высоте h над поверхностью Земли,
то в этой точке ускорение свободного падения равно:
20
ТЕСТ 11. Прямолинейное и криволинейное движение.
Движение тела по окружности с постоянной по модулю
скоростью
Вариант 1
1. Если скорость тела и действующая на него сила направлены
вдоль одной прямой, то тело движется
а) криволинейно в) прямолинейно
б) равноускоренно
2. Криволинейные траектории могут быть представлены
в виде совокупности
а) отрезков прямых линий
б) дуг окружностей разных радиусов
в) участков линий, вдоль которых направлен вектор ускорения
3. При движении тела по окружности модуль вектора скорости
а) может меняться или оставаться постоянным
б) обязательно изменяется
в) всегда остается постоянным
♦
4. На каком рисунке неправильно показано центростреми­
тельное ускорение?
5. Модуль вектора силы, под действием которой тело движет­
ся по окружности с постоянной по модулю скоростью,
имеет вид:
a) F = в) F = k M
6. Планеты обращаются вокруг Солнца под действием
а) веса планет
б) веса Солнца
в) силы всемирного тяготения
21
Вариант 2
ТЕСТ 11. Прямолинейное и криволинейное движение.
Движение тела по окружности с постоянной по модулю
скоростью
1. Если скорость тела и действующая на него сила направлены
вдоль пересекающихся прямых, то тело движется
а) криволинейно
б) прямолинейно
в) равномерно и прямолинейно t
2. На каком рисунке правильно показан вектор скорости тела,
которое движется по окружности?
3. При движении тела по окружности направление вектора
скорости
а) никогда не меняется
б) обязательно меняется
в) может как меняться, так и не меняться
4. Движение по окружности всегда происходит
а) с ускорением
б) без ускорения
в) без изменения скорости
5. Формула центростремительного ускорения имеет вид:
а – ц
GM
R2
6. Автомобиль совершает поворот за счет
а) силы реакции опоры
б) силы тяжести
в) трения колес о дорогу
22
ТЕСТ 12. Импульс тела. Закон сохранения импульса.
Реактивное движение
Вариант 1
1. Импульсом тела называют величину, равную произведе­
нию
а) массы тела на его ускорение
б) массы тела на его скорость
в) силы, действующей на тело, на время ее действия
2. Обозначение импульса тела:
а) Р б) F в) Е г) т
3. У какого из трех тел проекция импульса положительная?
1 2 3
а) 1 б) 2 в) 3
4. Векторная сумма импульсов тел, составляющих замкнутую
систему, с течением времени
а) может изменяться
б) не изменяется
в) обязательно изменяется
5. Перемещение осьминогов и кальмаров происходит в ре­
зультате
а) реактивного движения
б) действия силы тяжести
в) действия силы Архимеда
6. Идея использования ракет для космических полетов была
выдвинута
а) Сергеем Павловичем Королёвым
б) Константином Эдуардовичем Циолковским
в) Исааком Ньютоном
23
ТЕСТ 12. Импульс тела. Закон сохранения импульса.
Реактивное движение
Вариант 2
1. При расчетах импульса тела пользуются уравнением:
а) Р = т • v б) Р = / X X в) Р = т ■ v
7 X X
2. Единица импульса тела в СИ:
а) 1 кг • —
с 2
1 м б) 1 кг * —
с
в) 1 Н-м
3. У какого из трех тел проекция импульса отрицательная?
т
v w w v
1 2 3 х
а) 1 б) 2 в) 3
4. Закон сохранения импульса выполняется и в том случае,
если на тела системы действуют внешние силы, векторная
сумма которых
а) не равна нулю
б) равна нулю
в) параллельна векторам скоростей тел
5. Реактивное движение тела происходит за счет того, что
а) на тело действует сила всемирного тяготения
б) тело движется в безвоздушном пространстве
в) от тела отделяется и движется какая-то его часть, а тело при­
обретает противоположно направленный импульс
6. Для космических полетов могут быть использованы
а) двигатели внутреннего сгорания
б) газовые турбины
в) реактивные двигатели
24
ТЕСТ 13. Закон сохранения полной механической энергии
Вариант 1
1. Формула потенциальной энергии тела, поднятого на высо­
ту h над поверхностью Земли, имеет вид:
а) Еп~ m-g-h
б) Е
11 2
в) Е„ = wg(A, – h3)
2. Полной механической энергией называется
а) сумма потенциальной и кинетической энергий
б) только кинетическая энергия системы тел
в) только потенциальная энергия системы тел
3. Механическая энергия остается постоянной для
а) любой системы тел
б) замкнутой системы тел
в) незамкнутой системы тел
4. Шар массой 1 кг движется со скоростью 10 м/с. Его кинети­
ческая энергия равна
а) 10 Дж б) 100 Дж в) 50 Дж
5. Мяч массой 0,5 кг падает с высоты 3 м до высоты 2 м над
поверхностью Земли. Сила тяжести совершает работу
а) 5 Дж б) 15Дж в) 10 Дж
6. Мяч бросают вертикально вверх. В момент броска (у по­
верхности Земли) его кинетическая энергия равна 20 Дж.
Потенциальная и кинетическая энергии мяча в наивысшей
точке подъема равны:
а) Еп = 40 Дж, Ек = -20 Дж
б) Еп = 0 Дж, Ек = 20 Дж
в) Еп = 20 Дж, Ек = 0 Дж
3 Физика, 9 кл. Тесты 25
1. Формула кинетической энергии движущегося тела имеет
вид:
a) EK = F-S б) Ек = mgh в) £ = – 1 –
2. Полная механическая энергия замкнутой системы тел оста­
ется постоянной, если между телами действуют
а) силы тяготения и силы трения
б) только силы упругости
в) силы тяготения и силы упругости
3. Формула работы силы тяжести имеет вид:
а) А = mg(h. — h3) б) А = mg(h3 – Aj) в) А = mgh
4. Мяч массой 0,2 кг находится на высоте 2 м от поверхности
Земли. Его потенциальная энергия равна
а) 4 Дж б) 0,4 Дж в) 40 Дж
5. Птица массой 2 кг летит со скоростью 2 м/с на высоте 200 м
над поверхностью Земли. Ее полная механическая энергия
равна
а) 4008 Дж б) 4004 Дж в) 404 Дж 6
6. Кирпич падает с некоторой высоты на Землю. В момент
начала падения его потенциальная энергия равна 40 Дж.
Кинетическая и потенциальная энергии кирпича вблизи
поверхности Земли (в момент падения) равны:
а) Ек = 0 Дж, Еп = 40 Дж
б) Ек = 20 Дж, Еп=20 Дж
в) Ек = 40 Дж, Еп = 0 Дж
ТЕСТ 13. Закон сохранения полной механической энергии
Вариант 2
26
ТЕСТ 14. Колебательное движение.
Свободные колебания. Колебательные системы.
Маятник
Вариант 1
1. Колебательным движением называют движение
а) которое повторяется через определенный промежуток вре­
мени
б) при котором все точки тела движутся под действием только
силы тяжести
в) с постоянным ускорением
2. Основным признаком колебательного движения является
а) постоянство скорости
б) периодичность
в) постоянство ускорения
3. Сила упругости, действующая при колебательном движе­
нии, направлена
а) от положения равновесия
б) перпендикулярно положению равновесия
в) к положению равновесия
4. Колебательными системами называются системы тел, кото­
рые способны совершать
а) любые колебания
б) свободные колебания
5. Маятники могут быть
а) только нитяными
б) только пружинными
в) нитяными и пружинными 6
6. Период колебаний системы равен 2 с. Число колебаний, ко­
торое совершит система за 2 мин, равно
а) 60 б) 1 в) 240
27
ТЕСТ 14. Колебательное движение.
Свободные колебания. Колебательные системы.
Маятник
Вариант 2
1. Периодом колебаний называется промежуток времени
а) между двумя любыми положениями тела
б) через который движение повторяется
в) через который отклонение от положения равновесия макси-
2. Смещение — это
а) отклонение от положения равновесия при колебаниях
б) координата положения равновесия при колебаниях
в) любая деформация тела
3. Свободными колебаниями называются
а) любые колебания
б) колебания только нитяного маятника
в) колебания, происходящие только благодаря начальному запа­
су энергии
4. В колебательной системе возникают силы, возвращающие
систему в
а) положение устойчивого равновесия
б) положение неустойчивого равновесия
в) начальное положение
5. Сколько колебаний совершит колебательная система за
28 с, если ее период колебаний равен 7 с?
6. Колебательная система совершила за 40 с 240 колебаний.
Период колебаний равен
мально
б) 4 в) 8
а) — с
12
б) 6 с в) – с
6
28
1. Амплитудой колебаний называется
а) отклонение (по модулю) колеблющегося тела от положения
равновесия
б) наибольшее (по модулю) отклонение колеблющегося тела от
положения равновесия
в) наименьшее (по модулю) отклонение колеблющегося тела от
положения равновесия
2. Число колебаний в единицу времени называется
а) периодом колебаний
б) силой колебаний
в) частотой колебаний
3. Период колебаний обозначается буквой
а) Г б) v в) А
«■
4. Период колебаний в СИ измеряется в
а) метрах (м) б) герцах (Гц) в) секундах (с)
I
5. Период колебаний выражается через частоту колебаний
так:
a) v = – L б) А = – в) Г = —
Т2 v v 6
6. Период колебаний первого маятника больше периода коле­
баний второго маятника в 2 раза. Частота колебаний пер­
вого маятника
а) больше частоты колебаний второго маятника в 2 раза
б) меньше частоты колебаний второго маятника в 2 раза
в) равна частоте колебаний второго маятника
ТЕСТ 15. Величины, характеризующие
колебательное движение
Вариант 1
29
ТЕСТ 15. Величины, характеризующие
колебательное движение
Вариант 2
1. Промежуток времени, в течение которого тело совершает
одно полное колебание, называется
а) амплитудой колебаний
б) периодом колебаний
в) частотой колебаний
2. Собственной частотой называется частота
а) любых колебаний
б) свободных колебаний
в) только пружинного маятника
3. Частота колебаний обозначается буквой
а ) Т б) со (“омега”) в) v (“ню”)
4. Частота колебаний в СИ измеряется в
а) герцах (Гц) б) метрах (м) в) секундах (с)
5. Частота колебаний выражается через период колебаний
так: 6
6. Частота колебаний первого маятника больше частоты коле­
баний второго маятника в 3 раза. Период колебаний перво­
го маятника
а) меньше периода колебаний второго маятника в 3 раза
б) больше периода колебаний второго маятника в 3 раза
в) равен периоду колебаний второго маятника
30
ТЕСТ 16. Затухающие колебания.
Вынужденные колебания. Резонанс
Вариант 1
1. Полная механическая энергия маятника при затухающих
колебаниях переходит
а) в потенциальную энергию
б) в кинетическую энергию
в) во внутреннюю энергию
2. Затухающие колебания прекращаются тем быстрее, чем
а) больше силы сопротивления движению
б) меньше силы сопротивления движению
в) больше частота колебаний
3. Внешняя периодическая изменяющаяся сила, вызывающая
колебания, называется
а) силой упругости
б) вынуждающей силой
в) разгоняющей силой
4. Вынужденные колебания являются
а) затухающими
б) незатухающими
в) в начальный момент времени незатухающими, а затем зату­
хающими
5. С увеличением частоты изменения вынуждающей силы
амплитуда вынужденных колебаний
а) только увеличивается
б) только уменьшается
в) сначала увеличивается, а потом уменьшается 6
6. Одной из причин слишком сильного раскачивания желез­
нодорожного вагона при движении является
а) резонанс
б) всемирное тяготение
в) трение
31
1. Колебания называются затухающими, если
а) частота колебаний уменьшается
б) частота колебаний увеличивается
в) амплитуда колебаний постепенно уменьшается
2. Свободные колебания
а) всегда незатухающие
б) могут быть как затухающими, так и незатухающими
в) всегда затухающие
3. Колебания называются вынужденными, если
а) тело совершает колебания под действием внешней периоди­
чески изменяющейся силы
б) они затухающие
в) на тело действует постоянная сила
4. Частота установившихся вынужденных колебаний
а) равна частоте вынуждающей силы
б) больше частоты вынуждающей силы
в) всегда меньше частоты вынуждающей силы
5. Амплитуда установившихся вынужденных колебаний дос­
тигает своего наибольшего значения при условии, что час­
тота v вынуждающей силы
а) больше собственной частоты v0 колебаний системы
б) равна собственной частоте v0 колебаний системы
в) меньше собственной частоты v0 колебаний системы 6
6. Установка заводских станков на массивном фундаменте
предотвращает возникновение
а) деформации станков
б) деформации пола здания
в) резонанса и колебаний
ТЕСТ 16. Затухающие колебания.
Вынужденные колебания. Резонанс
Вариант 2
32
1. Возмущение среды — это
а) изменение плотности среды
б) изменение некоторых физических величин, характеризующих
состояние среды
2. Механические возмущения, распространяющиеся в упру­
гой среде, — это упругие
а) волны
б) колебания
в) деформации
3. Продольными волнами называются волны, в которых коле­
бания происходят
а) вдоль направления их распространения
б) перпендикулярно направлению их распространения
в) вдоль числовой координатной оси X
4. Поперечные волны являются волнами
а) сжатия и разрежения
б) сдвига
в) кручения
5. Упругие продольные волны могут распространяться
а) только в жидких и твердых средах
б) в любой среде — твердой, жидкой и газообразной
в) только в жидких и газообразных средах 6
6. В твердых средах могут распространяться
а) только поперечные волны
б) только продольные волны
в) как поперечные, так и продольные волны
ТЕСТ 17. Волны. Продольные и поперечные волны
Вариант 1
33
ТЕСТ 17. Волны. Продольные и поперечные волны
Вариант 2
1. Волнами называют
а) колебания различных сред
б) возмущения, распространяющиеся в пространстве, удаля­
ющиеся от места их возникновения
в) возмущения, распространяющиеся в пространстве, прибли­
жающиеся к месту их возникновения
2. В бегущей волне происходит перенос
а) энергии
б) вещества
в) как энергии, так и вещества
3. Поперечными волнами называются волны, в которых коле­
бания происходят
а) вдоль направления распространения волны
б) вдоль числовой координатной оси Y
в) перпендикулярно направлению их распространения
4. Продольные волны — это волны
а) сдвига
б) только сжатия
в) сжатия и растяжения
5. Упругие поперечные волны могут распространяться только
а) в твердых средах
б) в жидких средах
в) в твердых и жидких средах 6
6. В газообразных средах могут распространяться
а) как поперечные, так и продольные волны
б) только продольные волны
в) только поперечные волны
34
ТЕСТ 18. Длина волны.
Скорость распространения волн
Вариант 1
1. Расстояние между ближайшими друг к другу точками, ко­
леблющимися в одинаковых фазах, называется
а) периодом волны
б) частотой волны
в) длиной волны
2. Длину волны можно рассчитать по формуле:
3. Длина волны зависит только от
а) частоты колебаний источника волны и скорости распростра­
нения волны
б) частоты колебаний источника волны
в) скорости распространения волны
4. Чему равна длина волны, если скорость волны 2 м/с, а час­
тота колебаний 0,5 Гц?
а) 1 м б) 0,25 м в) 4 м
5. Чему равна скорость волны, если длина волны 5 м, а частота
волны 2 Гц?
а) 0,4 м/с б) 10 м/с в) 2,5 м/с 6
6. Источник волны за 20 с совершил 10 колебаний. Если ско­
рость волны в среде 200 м/с, то длина волны равна
а) 2000 м б) 400 м в) 200 м
a) k=v-T
Т
35
1. Длина волны обозначается греческой буквой
a) v (“ню”) б) X (“ламбда”) в) р (“ро”)
2. Расстояние, на которое распространяется колебательный
процесс за период колебаний, равно
а) длине волны
б) частоте волны
в) амплитуде волны
3. Длину волны можно рассчитать по формуле:
V V V а)Х=- б)Х = – в ) р = –
v v Т
4. Чему равна длина волны, если период колебаний источника
волны 2 с, а скорость волны в среде 315 м/с?
а) 157,5 м б) 630 м в) 1260 м
5. Чему равна скорость волны, если длина волны 34000 м,
а период колебаний источника волны 100 с?
а) 170 м/с б) 680 м/с в) 340 м/с 6
6. Сколько колебаний совершит источник волны за 100 с, если
длина волны 100 м, а скорость волны в среде 50 м/с?
а) 2000 б) 50 в) 200
ТЕСТ 18. Длина волны.
Скорость распространения волн
Вариант 2
36
ТЕСТ 19. Источники звука. Звуковые колебания.
Высота и громкость звука
Вариант 1
1. Общим для всех звуков является то, что источники звука
а) колеблются
б) движутся с постоянным ускорением
в) движутся равномерно и прямолинейно
2. Механические колебания, частота которых превышает
20 000 Гц, называются
а) звуковыми
б) инфразвуковыми
в) ультразвуковыми
3. Какие колебания применяются для измерения глубины
моря?
а) инфразвуковые
б) ультразвуковые.
в) звуковые
4. Отраженный от дна моря сигнал излучателя приемник
принял через 2 с после излучения. Чему равна глубина моря
в данном месте, если скорость сигнала 1500 м/с?
а) 1,5 км б) 150 м в) 750 м г) Зкм
5. Высота звука тем больше, чем
а) больше амплитуда колебаний
б) больше частота колебаний
в) меньше частота колебаний 6
6. Уровень звукового давления измеряется в
а) сонах
б) герцах
в) белах или децибелах
37
ТЕСТ 19. Источники звука. Звуковые колебания.
Высота и громкость звука
Вариант 2
1. Механические колебания диапазона частот от 16 Гц до
20 000 Г ц называются
а) ультразвуковыми
б) инфразвуковыми
в) звуковыми
2. Механические колебания с частотами менее 16 Гц назы­
ваются
а) гармоническими в) инфразвуковыми
б) звуковыми г) ультразвуковыми
3. Глубина моря в данном месте равна 3 км. Скорость сигнала,
посланного излучателем в воде, равна 1500 м/с. Приемник
примет отраженный от дна сигнал через
а) 4 с б) 2 с в) 40 с г) 20 с
4. Громкость звука одинаковых источников звука тем больше,
чем больше
а) частота колебаний
б) амплитуда колебаний
в) период колебаний
5. Если амплитуды звуковых колебаний одинаковы, то как
более громкие мы воспринимаем звуки, частоты которых
а) лежат в пределах от 1000 Гц до 5000 Гц
б) меньше 1000 Гц
в) больше 5000 Гц 6
6. Как называется единица громкости звука?
а) сон в) бел
б) фон г) герц
38
ТЕСТ 20. Распространение звука. Звуковые волны.
Отражение звука. Звуковой резонанс
Вариант 1
1. Хорошо проводят звук
а) мягкие и пористые вещества (войлок)
б) упругие вещества (древесина)
в) как пористые, так и упругие вещества (прессованная пробка,
металл)
2. В качестве прослоек для защиты помещений от проникно­
вения посторонних звуков используют
а) пенопласт, изготовленный на основе вспененных полимеров
б) тонкие металлические пластины
в) толстые пластины из древесины
3. Звук распространяется в пространстве
а) и при отсутствии, и при наличии какой-либо упругой среды
б) только при наличии какой-либо упругой среды
4. Звуковая волна распространяется в пространстве
а) мгновенно
б) с определенной скоростью
в) как мгновенно, так и с определенной скоростью — это зависит
от среды
5. Эхо образуется в результате
а) преломления звуковой волны
б) отражения звука от различных преград
в) поглощения звука различными средами 6
6. Расстояние, пройденное звуком в воздухе при 0 °С и нор­
мальном атмосферном давлении за 2 с, равно
а) 664 м б) 1500 м в) 30 км
39
ТЕСТ 20. Распространение звука. Звуковые волны.
Отражение звука. Звуковой резонанс
Вариант 2
1. Мягкие и пористые тела —
а) это хорошие проводники звука
б) плохие проводники звука
в) могут быть как хорошими, так и плохими проводниками звука
2. Рыбы хорошо слышат голоса на берегу потому, что
а) жидкости (вода) хорошо проводят звук
б) амплитуда звуковых колебаний очень большая
в) жидкость (вода) — плохой проводник звука, а амплитуда коле­
баний большая
3. Звук в воздухе передается
а) поперечными волнами
б) как поперечными, так и продольными волнами
в) продольными волнами
4. Какова зависимость скорости звука в газах от темпера­
туры?
а) чем больше температура газа, тем больше скорость звука
б) чем меньше температура газа, тем больше скорость звука
в) скорость звука не зависит от температуры газа
5. Если отраженный звук воспринимается отдельно от произ­
несенного, то мы
а) не слышим эхо
б) слышим эхо
в) можем слышать, а можем не слышать эхо, это зависит от среды 6
6. Звуковой резонанс возникает, если камертоны
а) настроены на одинаковую частоту колебаний
б) настроены на разную частоту колебаний
в) имеют резонаторы разных размеров
40
ТЕСТ 21. Магнитное поле.
Однородное и неоднородное магнитное поле.
Направление линий магнитного поля
Вариант 1
1. Магнитное поле создается только
а) движущимися отрицательно заряженными частицами
б) движущимися заряженными частицами (как положительны­
ми, так и отрицательными)
в) находящимися в покое заряженными частицами
2. Там, где магнитное поле более сильное, магнитные линии
изображают
а) ближе друг к другу, т.е. гуще
б) дальше друг от друга, т.е. реже
3. Если в разных точках магнитного поля на магнитную стрел­
ку действуют различные силы, то такое поле называют
а) однородным . б) неоднородным в) переменным
4. На рисунке изображено
а) неоднородное магнитное поле, линии кото­
рого направлены к нам
б) однородное магнитное поле, линии которо­
го направлены от нас
в) однородное магнитное поле, линии которого направлены
к нам
5. На каком рисунке правильно изображены линии магнит­
ного поля прямого проводника с током?
Ч I I / Г \ I I \ I I
ТЕСТ 21. Магнитное поле.
*
Однородное и неоднородное магнитное поле.
Направление линий магнитного поля

 

Урок физики в 8 классе по теме «Механические колебания. Превращение энергии при колебаниях”

8 класс

Тема урока: Механические колебания. Превращение энергии при колебаниях.

Цель урока:

Способствовать восприятию и усвоению учебного материала по теме «Механические колебания. Превращение энергии при колебаниях»; научить применять полученные знания для объяснения явлений окружающего мира, решения физических задач.

Задачи:

– обучающие: изучение свойств и основных характеристик периодических (колебательных) движений; изучение возможных превращений энергии в колебательных системах; подтверждение справедливости закона сохранения механической энергии в колебательных системах.

– развивающие: формирование навыков исследовательской деятельности, формирование информационной компетентности учащихся, повышение коммуникативной культуры, расширение кругозора, повышение эрудиции, развитие интереса к физике;

– воспитательные: воспитание внимательного, доброжелательного отношения к ответам одноклассников, воспитание умения общаться друг с другом, умения излагать и отстаивать свою точку зрения, вовлечение каждого ученика в активный познавательный процесс.

Тип урока: урок изучения нового материала.

Формы работы учащихся: фронтальная, групповая, индивидуальная.

Оборудование: нитяной и пружинный маятники, компьютер, видеопроектор, интерактивная доска.

Используемые ЦОР:

Ресурс:

Анимация “Получение графика гармонических колебаний” (N 186429)

Вид ЦОР:

Анимация

Поставщик ЦОР:

ЗАО “Просвещение-МЕДИА”

Аннотация:

Анимированная модель установки для получения графика гармонических колебаний математического и пружинного маятника.

http://school-collection.edu.ru/catalog/res/34a0d17c-8cbd-4e3d-ba54-2043e7d09aeb/view/

Ресурс:

Видеоролик “Энергия при колебаниях маятника” (N 186552)

Вид ЦОР:

Видеофрагмент

Поставщик ЦОР:

ЗАО “Просвещение-МЕДИА”

Аннотация:

Анимационная модель для изучения превращения энергии при колебаниях маятника.

http://school-collection.edu.ru/catalog/res/67630bf8-ac43-4a58-bf77-174381cb9eda/?from=8f5d7210-86a6-11da-a72b-0800200c9a66&

Презентация «Величины, характеризующие колебательное движение».

Ход урока:

I Организационный момент. Актуализация знаний.

II Анализ итогов контрольной работы.

Подведение итогов контрольной работы, краткий анализ. Типичные ошибки:

– отсутствие перевода единиц в систему СИ;

– ошибки при выполнении преобразования формул;

– ошибки при выполнении арифметических операций.

В качестве примера оформить решение задачи № 5 2 варианта.

III Изучение нового материала.

1. Постановка целей и задач урока.

2. Получение новых знаний.

Демонстрация двух типов движений – движение груза, закрепленного на нити, и груза на пружине. Отличительной чертой этих движений является периодичность, т.е. повторяемость через определенные интервалы времени.

Механические колебания – движения, которые точно или приблизительно повторяются через одинаковые промежутки времени.

Еще одной отличительной особенностью систем, в которых происходят колебания, является наличие у них положения устойчивого равновесия. За положение равновесия принимают ту точку, в которой при отсутствии движения груза результирующая сила равна 0.

Презентация «Величины, характеризующие колебательное движение».

Слайд №2. Сравним колебания двух одинаковых маятников. Первый маятник колеблется с большим размахом, т. е. его крайние положения находятся дальше от положения равновесия, чем у второго маятника.

Максимальное отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний. Мы будем рассматривать колебания, происходящие с малыми амплитудами. Амплитуду обозначают буквой А и измеряют в метрах (м),

Амплитуда колебаний нитяного маятника равна длине отрезка ОВ или ОА.

Если колеблющееся тело пройдет от начала колебаний путь, равный четырем амплитудам, то оно совершит одно полное колебание.

Слайд №3. Амплитуда колебаний вершины Останкинской башни в Москве (высота 540 м) при сильном ветре около 2,5 м.

Слайд №4. Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний. Период колебаний обозначается буквой Т и в СИ измеряется в секундах (с).

Число полных колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой v. Если за 1 с совершается одно колебание, то частота равна 1 Гц (в честь немецкого ученого Генриха Герца).

Если, например, маятник в одну секунду совершает 2 колебания, то частота его колебаний равна 2 Гц (или 2 с^-1), а период колебаний (т. е. время одного полного колебания) равен 0,5 с.

Таким образом, период колебания Т и частота колебаний v связаны следующей зависимостью:

Период и частоту можно находить, зная произвольное время t и число колебаний n за этот отрезок: Таким образом, колебательное движение характеризуется амплитудой, частотой и периодом.

Так как в процессе колебаний положение тела меняется, то удобно изменение смещения тела от положения равновесия во времени представлять графически.

ЦОР:

Анимация “Получение графика гармонических колебаний”

http://school-collection. edu.ru/catalog/res/34a0d17c-8cbd-4e3d-ba54-2043e7d09aeb/view/

Графиком зависимости координаты колеблющегося тела от времени является синусоида.

Колебания, при которых координата колеблющегося тела меняется с течением времени по закону синуса (или косинуса), называются гармоническими.

Слайд №5. Определите по графику амплитуду, период и частоту колебания.

ЦОР:

Видеоролик “Энергия при колебаниях маятника”

http://school-collection.edu.ru/catalog/res/67630bf8-ac43-4a58-bf77-174381cb9eda/?from=8f5d7210-86a6-11da-a72b-0800200c9a66&

Рассмотрим колебания тела прикреплённого к нити. Любая колебательная система будет совершать колебания до тех пор, пока обладает энергией. Отводя тело от положения равновесия, мы сообщаем системе начальную энергию. Она равна потенциальной энергии тела Е_р. Отпустив тело, мы видим, что скорость его возрастает, а значит, возрастает и его кинетическая энергия. Из закона сохранения механической энергии уменьшение Е_р приводит к эквивалентному увеличению E_k . Для любой точки траектории, если в системе нет сил трения, справедлив закон сохранения энергии. Если тело находится в крайних положениях, система обладает полной энергией Е, определяемой только потенциальной энергией. А в положении равновесия полная энергия равна максимальной кинетической энергии груза.

Важно понять, что составляющие полной энергии E_k и Е_р не просто изменяются во времени, а изменяются периодически с заданным периодом колебаний в системе.

По ходу объяснения и просмотра видеоролика учащиеся делают выводы о превращениях энергии и заполняют таблицу в тетради Cлайд 6.

Положения маятника

Смещение, х

Потенциальная энергия, Е_р

Скорость, v

Кинетическая энергия, E_k

Полная механическая,
Е

Крайнее положение

x = max

Е_р = max

v = 0

E_k = 0

Е_рmax

Маятник движется от крайнего положения к положению равновесия

x↓

Е_р↓,

v ↑

E_k↑,

Е_р + E_k

Положение равновесия

x = 0

Е_р = 0

v = max

E_k = max

E_kmax

Маятник движется от положения равновесия к крайнему положению

x↑

Е_р↑,

v ↓

E_k↓,

Е_р + E_k

IV Закрепление изученного материала.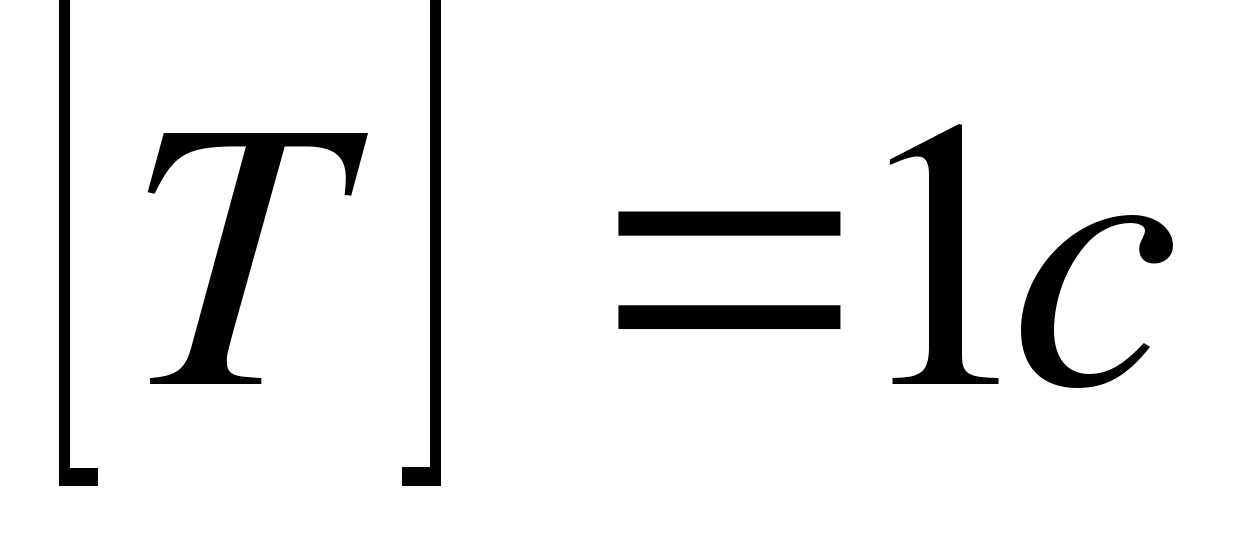 Решение задач

Слайд № 7. Сердце — это орган, имеющий массу 300 г. С 15 до 50 лет оно бьется со скоростью 70 раз в минуту. В период между 60 и 80 годами оно ускоряет свое движение, достигая примерно 79 ударов в минуту. В среднем это составляет 4,5 тысячи пульсаций в час и 108 тысяч в день. Сердце велосипедиста может быть вдвое больше, чем у человека, не занимающегося спортом, — 1250 кубических сантиметров вместо 750. В обычном режиме этот орган перекачивает 360 литров крови в час, а за всю жизнь — 224 миллиона литров. Столько же, сколько река Сена за 10 минут! Чему равен период колебаний работы сердца? (0,86 с)

Слайд № 8. Небольшие размеры колибри и их способность сохранять постоянную температуру тела требуют интенсивного обмена веществ. Ускоряются все важнейшие функции в организме, сердце делает до 1260 ударов в минуту, увеличивается ритм дыхания — до 600 дыхательных движений за одну минуту. Высокий уровень обмена веществ поддерживается интенсивным питанием — колибри почти непрерывно кормятся нектаром цветов. Определите частоту колебаний сердца колибри. (21 Гц — частота сокращения сердца.)

Самостоятельная работа с самопроверкой. Слайды № 9-12.

1 вариант

2 вариант

1. Колебания – это движения тела…

1. Из положения равновесия

2. По кривой траектории

3. В вертикальной плоскости

4. Движения, которые точно или приблизительно повторяются через одинаковые промежутки времени

1. Интервал времени, за который совершается одно полное колебание, – это…

1. Смещение

2. Частота

3. Период

4. Амплитуда

2. Число полных колебаний за 1 с определяет …

1. Смещение

2. Частота

3. Период

4. Амплитуда

2. Наибольшее отклонение тела от положения равновесия – это…

1. Смещение

2. Частота

3. Период

4. Амплитуда

3. Частота свободных колебаний пружинного маятника равен 10 Гц. Чему равен период колебаний?

1. 5 с

2. 2 с

3. 0,1 с

4. 10 с

3. Период свободных колебаний нитяного маятника равен 5 с. Чему равна частота его колебаний?

1. 0,2 Гц

2. 20 Гц

3. 5 Гц

4. 10 Гц

4. За 6 секунд маятник совершает 12 колебаний. Чему равна частота колебаний?

1. 0,5 Гц

2. 2 Гц

3. 72 Гц

4. 6 Гц

4. За 5 секунд маятник совершает 10 колебаний. Чему равен период колебаний?

1. 0,5 с

2. 2 с

3. 5 с

4. 50 с

Слайд №13. Вариант 1: D, B, C, B. Вариант 2: C, D, A, A.

Решение задач № 91, 93, 95

V Подведение итогов урока.

VI Домашнее задание § 17, 18 пересказ, № 92, 94.

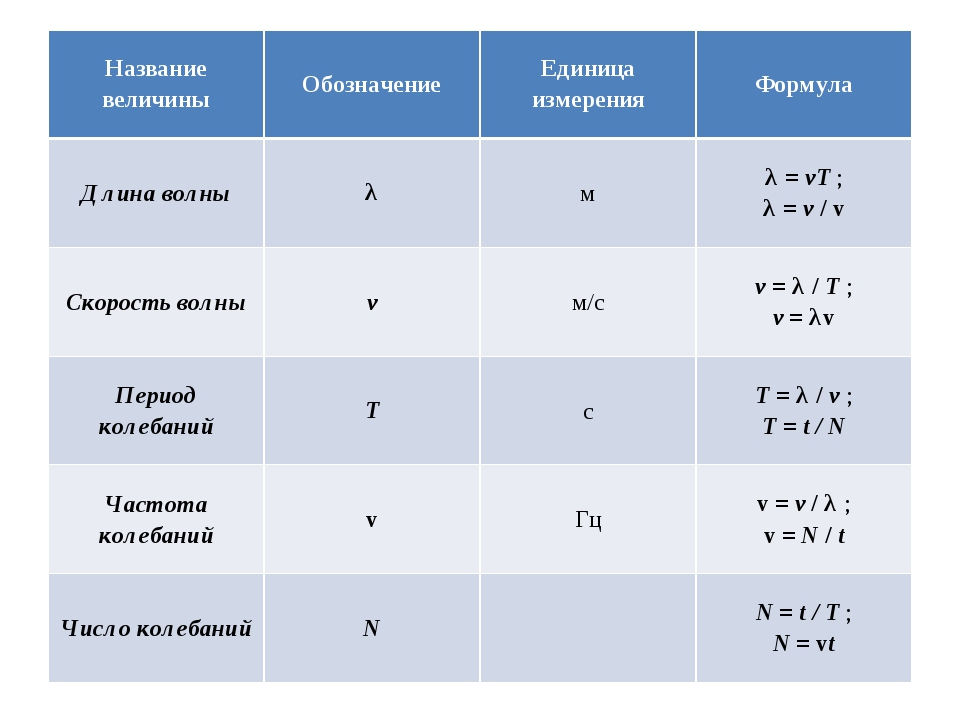
Длина волны.

Скорость распространения волны.

Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.

Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.

Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.

Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:  λ=υT. Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:

                                       υ = λ / Т = λ v

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.

Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.

Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.

Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.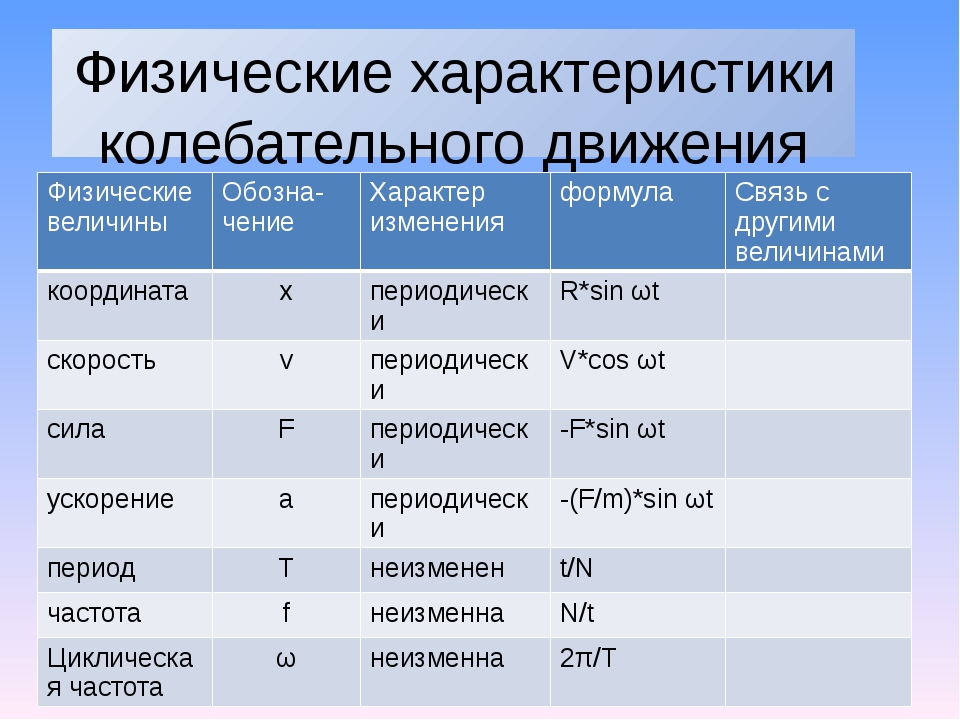

Единицы измерения в системе СИ:
длина волны [λ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц

Период | IOPSpark

Период

Силы и движение

Период

Глоссарий Определение за 16-19

Описание

Период или периодическое время периодического изменения величины определяется как интервал времени между двумя последовательными повторениями.См. рис. 1 .

Период обычно обозначается символом T .

Период изменения связан с его частотой, f , by

T  = 1 f

Рисунок 1: Период периодического изменения величины может быть измерен между последовательными эквивалентными точками на графике зависимости величины от времени.

Обсуждение

Обычно легко измерить период напрямую, если соответствующая частота очень низкая.Например, вращение Земли вокруг своей оси имеет период примерно 24 часа, и мы измеряем его период. Но для движения, где период порядка секунды и меньше, обычно легче измерить число колебаний в данном интервале времени и вычислить частоту, а значит, и период. Частота вибрации диффузора громкоговорителя составляет порядка 10 ³ Гц, и обычно измеряется количество колебаний, которое он совершает за одну секунду, т.е. с помощью лазерного луча, отраженного от его поверхности, для определения его скорости.

Единица СИ

секунды, с

Выражено в основных единицах СИ

с

Другие широко используемые единицы

минуты, часы, дни, годы

Математические выражения

Связанные записи

В контексте

Исторически периодическое движение было основным средством измерения времени. Продолжительность года связана с периодическим движением Земли вокруг Солнца, а продолжительность дня — с периодическим вращением Земли вокруг своей оси.Маятниковые часы зависят от того, что при малых углах период маятника не зависит от амплитуды его движения и может регулироваться изменением длины маятника. Например, маятник длиной 1 м имеет период около 2 секунд. Многие электронные часы используют вибрацию кварцевого кристалла как основу хронометража; частота вибрации составляет чуть менее 30 кГц, что соответствует периоду 30  мкс с.

Разница между циклом и периодом

13 декабря 2011 г. Опубликовано Admin

Цикл против периода
 

Цикл и период — два важных термина, которые широко используются почти во всех областях физики.Эти темы очень важны при изучении волновой теории. Представления о цикле и периоде используются не только в физике, но и во многих других областях, таких как астрономия, математика, музыка и даже некоторые аспекты физиологии. Термины «цикл» и «период» принимают разные значения в зависимости от того, где они применяются, но здесь мы обсуждаем эти темы, относящиеся только к физике. В этой статье мы собираемся обсудить, что такое цикл и период, определения цикла и периода, их сходство и, наконец, разницу между циклом и периодом.

Что такое цикл?

Цикл — это завершенный сеанс (или событие) последовательности повторяющихся событий. Процесс, в котором создаются циклы, называется циклическим процессом. Сердцебиение человека — знакомый пример циклического процесса. Сердечный цикл происходит от начала одного сердечного сокращения до начала следующего. Если мы представим простую синусоидальную волну, один цикл завершается долей между двумя последовательными пиками этой волны. Цикл — это концепция волнового движения, которая позволяет представить волновое движение в графической форме. При равномерном круговом движении один цикл определяется как полный путь по окружности.

Что такое период?

Период — очень важное понятие при изучении таких областей, как волновое движение, оптика, акустика и телекоммуникации. Чтобы понять, что такое период, нужно иметь правильное представление о частоте. Частота определяется как количество циклов в единицу времени. Единицей частоты в СИ является герц (Гц), здесь 1 Гц означает, что один цикл повторяется один раз в секунду.Теперь легко понять понятие периода. Период – это время, затрачиваемое на один цикл. Связь между периодом и частотой заключается в том, что период является обратной величиной частоты. Это соотношение может быть представлено математически как T=1/f, где период обозначается как T, а частота обозначается как f. Похоже, что единицей СИ для периода является вторая. Если вы думаете о простой синусоидальной волне, которая построена для смещения в зависимости от времени, период волны может быть представлен как длина между двумя последовательными пиками по оси времени. Если мы подумаем об угловом движении, период задается уравнением T=2π/ω, где период обозначается T, а угловая частота обозначается ω. При угловом движении период также измеряется в секундах.

В чем разница между циклом и периодом ? • Цикл – это понятие волнового движения. У него нет единиц и размерностей, но период является скалярной величиной. Единицей периода в системе СИ является секунда, а его размерность — [Т]. • Существует прямая зависимость между периодом и частотой. Период обратно пропорционален частоте, но между циклом и периодом такой прямой зависимости нет. • Можно увидеть циклы некоторых волн, но нельзя увидеть период. • Такие инструменты, как секундомеры, часы, используются для измерения периода, но у нас нет инструмента для измерения циклов. • Иногда форма цикла может меняться со временем, но период не меняется со временем.Это происходит при затухающих колебаниях.

Глава 10 Концепции

Глава 10 Концепции

Глава 10

Концептуальные вопросы: 2, 6, 11, 17, 18

| ВЕРНУТЬСЯ К ДОМАШНИМ ЗАДАНИЯМ |

2. Напольные часы идут слишком быстро. Что делать, чтобы исправить это?

Проблема с дедушкиными часами, которые идут слишком быстро, заключается в том, что сначала нужно поймать чертову штуку.Ходовые напольные часы встречаются особенно редко (поскольку у них нет ножек), но как только они заработают, их очень трудно сломать.

О. Упс.

“Слишком быстрый бег” означает, конечно, что период колебания маятника слишком короткий. Вы хотите увеличить период колебаний (также известный как уменьшение частоты), поэтому вы увеличиваете длину.

 

6. Объясните, как период системы масса-пружина может не зависеть от амплитуды, даже если расстояние, пройденное за каждый цикл, пропорционально амплитуде.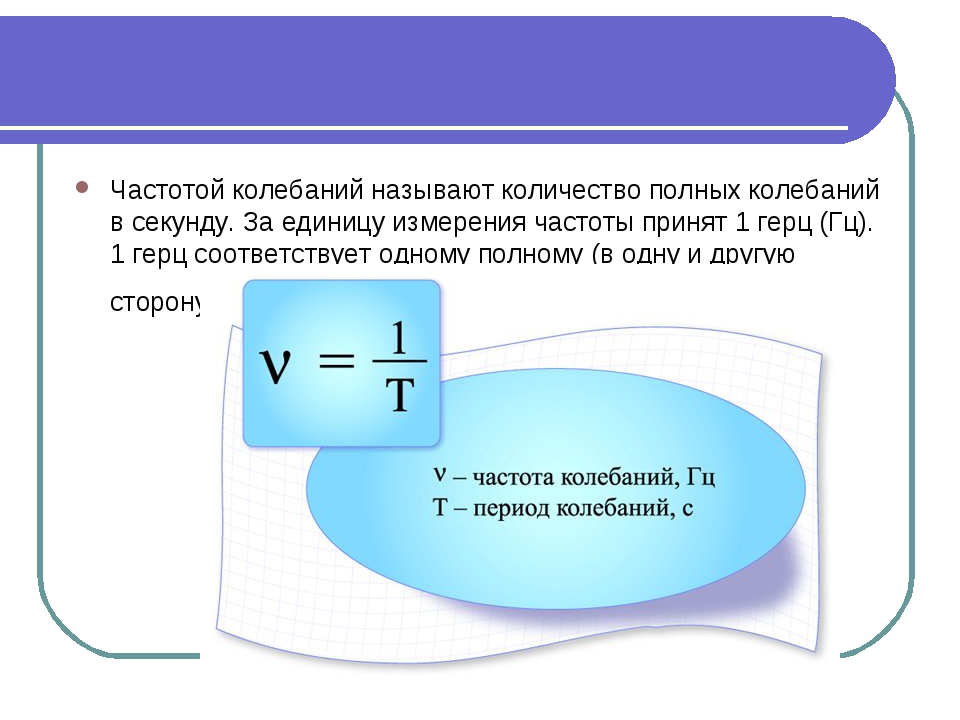

Это одно из моих любимых соотношений в физике. По мере того, как вы увеличиваете расстояние, которое должна пройти масса, вы также вкладываете в систему больше энергии. Таким образом, в результате он движется быстрее (в среднем). Оказывается, скорость, на которую он движется, как раз и является той величиной, которая компенсирует дополнительное расстояние, которое ему нужно пройти. Откуда он знает, что нужно делать именно так, независимо от амплитуды? Я не знаю. Это просто так, что делает физическую систему очень простой и предсказуемой.

11. Пилот выполняет вертикальную петлю над океаном в полдень. Самолет ускоряется по мере приближения к нижней части круговой петли и замедляется по мере приближения к вершине петли. Наблюдатель в вертолете наблюдает за тенью самолета на поверхности воды. Проявляет ли тень SHM? Объяснять.

А еще есть летающая тарелка и акула, которая выпрыгивает из воды и проглатывает самолет. А затем летающая тарелка подхватывает акулу (с проглоченным самолетом) и улетает, оставляя наблюдателя с вертолета сидеть и тихо думать: «Хммммм, интересно, это движение было SHM?»

Глупые физики. Где они придумывают эти ситуации?

Как видно сверху, колебания самолета будут совершаться вперед и назад с одинаковой амплитудой каждый раз, но скорость, с которой он движется, меняется каждые полпериода. То есть, поскольку он движется в одном направлении (в нижней части петли), он движется быстро; но при движении в противоположном направлении (в верхней части петли) он движется медленно. Вы можете себе представить, что это нарушает симметрию графиков положения и времени, скорости и времени и т. д.Каждое второе полуколебание будет иметь другую часть периода. Или, другими словами, это не выглядело бы так, будто сила прямо пропорциональна смещению. Так что это не будет имитировать SHM.

17. Период колебаний простого маятника не зависит от массы груза. Напротив, период системы масса-пружина действительно зависит от массы. Объясните это кажущееся противоречие.

Причина, по которой простой маятник не зависит от массы, заключается в том, что масса «считает» две разные вещи. (То же самое происходит и при свободном падении, когда все предметы любого веса падают с одинаковой скоростью.) Масса имеет значение инерции, или «m» в «F = ma». Это означает, что сопротивление изменениям в движении прямо пропорционально массе. Однако вес (сила) объекта также пропорционален массе. Поскольку масса влияет как на причину изменения движения, так и на сопротивление изменению движения, она уравновешивается.

Для системы масса-пружина масса по-прежнему влияет на инерцию, но она , а не вызывает силу.Пружина (и ее жесткость) полностью отвечает за усилие. Таким образом, масса влияет только на сопротивление ускорениям, и вы заметите, что чем массивнее объект, тем медленнее он качается вперед и назад.

18. Масса, соединенная с идеальной пружиной, совершает колебания без трения по горизонтальной поверхности. Нарисуйте графики зависимости кинетической энергии, потенциальной энергии и полной энергии от времени для одного полного цикла.

[Я сделал это в наборе задач. См. номер 53.]

 

| ВЕРНУТЬСЯ К ДОМАШНИМ ЗАДАНИЯМ |

Волны

Частота

Частота — это мера того, как часто повторяющееся событие, такое как волна, происходит в течение измеряемого промежутка времени. Одно завершение повторяющегося шаблона называется циклом. Частотой обладают только движущиеся волны, меняющие свое положение во времени. Частота — это один из способов определить скорость движения волны.

Волны могут двигаться двумя способами.Частоты прогрессивных волн или тех, которые движутся вперед, показывают, насколько быстро волна движется вперед в единицах циклов в единицу времени. Частоты стоячих волн или тех, которые колеблются на месте, представляют собой скорость колебаний в единицах циклов в единицу времени.

Определение Словарное определение частоты: Физика. а) количество периодов или регулярно происходящих событий любого вида в единицу времени, обычно одну секунду. б) число циклов или полных чередований в единицу времени волны или колебания. Символ: f ; Сокр.: част.

Единицы
Частота выражается в единицах циклов в единицу времени.

Хотя частота является мерой скорости движения, она не идентична скорости. Например, если мы думаем об автомобиле, который движется со скоростью 60 миль в час, мы имеем в виду именно это.Однако если мы говорим, что волна имеет частоту 60 циклов в час, точки на волне могут двигаться быстрее или медленнее в зависимости от длины волны. Сравнивая две волны с одинаковой длиной волны, более высокая частота связана с более быстрым движением. Сравнивая две волны с разной длиной волны, более высокая частота не всегда указывает на более быстрое движение, хотя и может. Волны разной длины могут иметь одинаковую частоту. Для некоторых целей частота измерения более полезна, чем абсолютная скорость.

Единица, Герц
Единица Герц (Гц) используется для описания частоты в циклах в секунду. В предложении правильный формат для записи этого отношения:

Один цикл соответствует перемещению на одну длину волны.

Номера радиотелефонов
Часто можно услышать радиочастоты, указанные в мегагерцах (МГц) … (в разработке).

Период волны
Частота волны также связана с другим измерением, называемым периодом волны (T).Период волны — это то, сколько времени требуется для прохождения одного цикла, и единицы измерения всегда выражены во времени. Чем быстрее движется волна, тем меньше период ее волны.

Вместо измерения в фиксированной единице времени, секунды, период волны использует фиксированное количество циклов, один цикл …

Как измерить период волны?
Период волны можно определить, измерив, сколько времени требуется двум пикам для прохождения определенной точки.Вы можете сделать это для океанских волн, стоя на пирсе и используя секундомер.

Строится…

Амплитуда Частота Фаза – периодическое движение

Периодическое движение или гармоническое движение – это любое движение, которое повторяется через равные промежутки времени. Простое гармоническое движение является синусоидальной функцией времени t.

Наблюдается периодическое движение массы на пружине, простом маятнике, молекулярном колебании и т. д.

Максимальное отклонение от равновесия известно как амплитуда (всегда положительная, поскольку рассматривается только величина).

Одно полное повторение движения называется циклом. Продолжительность каждого цикла составляет периодов . Частота (f) — это количество циклов в единицу времени (t).

f=1/т.

Например, если сердце новорожденного ребенка бьется с частотой 120 раз в минуту, его период (интервал между ударами) составляет полсекунды, так как 60/120 = 0.5. Большие частоты означают короткие периоды.

Некоторое движение лучше всего характеризуется угловой частотой (ω) . Угловая частота относится к угловому смещению в единицу времени и рассчитывается на основе частоты (f) по уравнению:

ω=2πf.

Фаза движения является аргументом функции косинуса. Фаза меняется со временем, как и значение функции косинуса и смещение волны. φ называется фазовым углом или фазовой постоянной, он определяет положение частицы при t=0.

Практические вопросы

  Академия Хана

Механика равновесия стоя

Официальная подготовка MCAT (AAMC)

Пакет вопросов по физике, отрывок 2, вопрос 7

Пакет вопросов по физике, отрывок 2, вопрос 9

Пакет вопросов по физике, отрывок 2, вопрос 10

Пакет вопросов по физике, отрывок 2, вопрос 11

Пакет вопросов по физике, отрывок 20, вопрос 113

Практический экзамен 4 C/P Section Pass 3 Question 15

Ключевые моменты

• Периодическое движение (гармоническое движение) повторяется через равные промежутки времени.

• Периодическое движение может быть описано амплитудой, частотой и фазой в виде синусоидальной функции.

• Частоту можно рассчитать, выполнив 1/t, которая представляет собой количество циклов за этот период времени.

Основные термины

Амплитуда : расстояние между положением покоя и гребнем волны. Пропорциональна интенсивности.

Период : продолжительность одного цикла в повторяющемся событии

Частота : частота — это количество повторений события в единицу времени.

Угловая частота (ω): ω=2πf.

Фаза : волны является аргументом функции косинуса

Периодическое движение:  любое движение, которое повторяется через равные промежутки времени.

Точка поворота в физике. Давайте выберем правый конец бара в качестве нашей опорной точки. Pivot Point LAB (Learn About Beauty) — это инновационная интегрированная среда социального обучения, созданная специально для учащихся и преподавателей парикмахерской и парикмахерской. n Рычаг – это практическое применение принципа момента силы. Расстояние от точки вращения, на которой должен сидеть маленький ребенок, чтобы сохранить равновесие, равно 1. Это означает, что вам нужно знать расположение центра масс. Как сказал Архимед, если бы ему было достаточно места, чтобы встать с достаточно длинным рычагом, он мог бы перевернуть мир. обозначает ежедневные, еженедельные и ежемесячные медианные точки разворота. Поиск онлайн-курсов в Академии Pivot Point в Блумингдейле никогда не был таким быстрым, как сейчас — просмотрите онлайн-курсы по информатике в Академии Pivot Point в Блумингдейле, бизнесу, математике, преподаванию, химии, инженерным классам и многому другому в Блумингдейле, штат Иллинойс, и его окрестностях.Гравитацию можно исключить из каждой части уравнения. Мы знаем это, поскольку качели находятся в вертикальном равновесии. 070 м 0. С помощью Pivot Tool вы можете легко изменить поворот актеров вручную или автоматически, применив один из 27 пресетов поворота. 29 января 2004 г. 13,679 10 81. Если расчет не работает, вы можете поиграть с В физике моментом пары являются две равные параллельные силы, которые находятся в противоположных направлениях друг от друга и на одном и том же расстоянии от точки вращения точка, воздействующая на объект и производящая эффект поворота.11. Штанга удерживается тросом под углом, как показано на рисунке. рычаг с грузом и входом в противоположные стороны от точки поворота. Поместите угол, который будет использоваться в качестве точки поворота, на книгу, чтобы предотвратить ее скольжение по столешнице. В третьей ситуации мне кажется, что стержень находится в центре масс, отсюда и h Dr. Это только один ЛИ, т.к. учет сетки позволяет связать два простых меш-объекта в один ЛИ. Я нашел период для первых двух объектов: T 1 = 2π√ (L/g) T 2 = 2π√ (2L/3g) Проблема для меня возникает в третьей системе, потому что h определяется как расстояние между центрами масса стержня и точки опоры.Можете ли вы найти закономерность между точкой опоры, от которой висит, и расположением… Попытка решения. Часть б) ∑τ o =0 для равновесия m Точка P на рисунке – это шарнирная ось, прикрепленная к раме, вокруг которой вращается плечо. После столкновения частица прилипает к кольцу, и оба объекта вместе вращаются против часовой стрелки вокруг точки вращения. Крутящий момент от приложенной силы вызовет вращение по часовой стрелке вокруг точки B, и поэтому это центр тяжести и устойчивости по часовой стрелке.Присоединиться / Войти >> Класс 11 >> Физика >> Системы частиц и вращательное движение >> Принцип моментов >> Тело вращается в точке. центр удара твердого тела. Если точка опоры… Силы, создающие момент, действуют вокруг точки, называемой точкой опоры. Когда они сводят руки внутрь, их момент инерции уменьшается и им легче вращаться. Масса светофора равна 21. Это дает относительно низкий момент со стороны нагрузки шарнира.Для каждой из трех возможных опорных точек: (a) Подвесьте отвес к опорной точке. то же самое, центральная ре становится точкой поворота, на которой можно повернуть минор вниз по отношению к мажору в обратном отношении, устанавливая двойные ноты в файле. произведение силы и расстояния между точкой вращения и силой слева от точки вращения. Поворотный момент в физике. Правитель находится в равновесии; он идеально сбалансирован. Расчет точки разворота. Для жесткой конструкции со многими массами полный момент инерции представляет собой сумму моментов каждой массы: I t o t a l = ∑ i n I i = ∑ i n m i r i 2.Интерактивный центр масс позволяет учащемуся исследовать влияние формы объекта на центр масс. В обоих этих случаях точка поворота совпадает с положением объекта, поэтому он вообще не будет двигаться при вращении. Заставить крупного человека ничего не делать. Практический тест AP Physics: вращение, угловой момент © 2011, Ричард Уайт www. Я щелкнул левой кнопкой мыши по другому несвязанному объекту, затем снова по моему кубу, и точка поворота оказалась в том месте, куда я ее переместил — похоже, она ее сохранила.0. Объект вращается вокруг оси, которую мы назовем точкой вращения и обозначим буквой «О». [6,7] Поскольку удары в центре удара приводят к нулевой результирующей силе в точке поворота, это место долгое время отождествлялось с наилучшей точкой, связанной с ощущением бейсбольной биты. Итак, используя уравнения статического равновесия: ##\sum{F_x} = 0## остаточный неуравновешенный крутящий момент на объекте. Тогда сила натяжения не создает крутящего момента (поскольку плечо рычага равно нулю), и (неизвестная) переменная T не появляется в нашем уравнении крутящего момента.Ученые изучают физику термоядерного синтеза уже столетие и десятилетиями работают над тем, чтобы использовать этот процесс. На рисунке ниже показан мангонель в точке пуска. Уровни поддержки и сопротивления определяются на основе разницы между максимумом и минимумом цен предыдущего дня и точкой разворота. Или, по крайней мере, это задействовало бы мышцы, удерживающие ее голову. Точка опоры – это точка, вокруг которой вращается рычаг. Сколько потребуется, чтобы вернуться в исходное положение.Случай на схеме подобен использованию гаечного ключа при затягивании болта. Перемещение меньшего человека дальше от центра. В условиях однородной гравитации это то же самое, что и центр масс. (24. Вычислите величину крутящего момента (от силы тяжести) вокруг этой точки вращения. К правому концу стержня на расстоянии R от точки вращения прикреплена точечная масса M. Чем дальше действует сила, точка поворота, тем больше эффект поворота Эффективная точка тангажа для аэродинамического профиля с постоянной плотностью показана для различных мест поворота.… Холлман сказал, что обзор программы ядерной физики, проведенный в июле 2021 года потенциальных экспериментов NDBD в масштабе тонны, был сосредоточен на трех многообещающих кандидатах: CUPID, nEXO и LEGEND-1000. Решение. Векторная диаграмма приведенного выше примера приведена на рис. 5. Фактически, в физике качели — это рычаг. ; Учитывая следующие данные: Масса A = 20. Наибольший крутящий момент 2F 2 10F 3 4 :::: Наименьший крутящий момент Физика, 19. Когда Отец сидит в 8 дюймах слева от оси вращения, он создает момент +120 футо-фунтов вокруг оси. опора.Вам действительно нужно приблизить физику к точке поворота, равной большему крутящему моменту -> большей силе сдвига на бумаге. ватт. Каковы величина и знак приложенного крутящего момента? Эта проблема выглядит как на рисунке. Правило: моменты по часовой стрелке считаются положительными величинами. Блок массой M находится на расстоянии L/2 от оси вращения. Общий 6DOF. 00 м может свободно вращаться вокруг неподвижного штифта, расположенного в точке L/4. Учитель физики готовит эксперимент к своему лабораторному занятию. Момент силы относительно точки (осевой точки) можно рассчитать с помощью формулы, описанной в этом учебнике по физике: Момент = Вращающая сила x Перпендикуляр d Произведение веса предмета A и его расстояния от опорной точки (X) дает крутящий момент против часовой стрелки и произведение веса предмета B и его плеча момента Y создают крутящий момент по часовой стрелке.В этой статье с помощью численного моделирования и собственных экспериментов в водяной трубе исследуется влияние положения точки поворота на характеристики тяги двумерного синусоидального эллиптического аэродинамического профиля в условиях полета вперед. Эта точка называется центром перкуссии. Примером может быть водитель, поворачивающий руль … равновесия, его центр тяжести должен находиться прямо под точкой поворота, поэтому зажим должен свисать вниз с его опорных выступов. Учитель физики и ведущий автор контента Марта Стокель рассказывает, как она начинает год с занятий по физике. Попытка решения. Наконец, решаем уравнения для неизвестных составляющих сил и находим силы. После того, как ваша проблема будет решена, ответьте на ответ (ответы), говоря, что решение проверено, чтобы закрыть ветку. Он обеспечивает поддержку рычага. Пусть первый ребенок — А. Точка поворота — О. Поворачивая гайку гаечным ключом, применяя отвертку, открываем дверь, закрепленную на петлях.Определение шарнира, штифт, точка или короткий стержень, на конце которого что-то опирается и вращается, или на конце и вокруг которого что-то вращается или колеблется. Для запуска полезной нагрузки удерживающий трос освобождается. При вращении или масштабировании объекта или группы вершин, ребер или граней может потребоваться переместить точку поворота, чтобы упростить управление объектом. Но помните, что такое опорная точка на самом деле, и не полагайтесь на нее как на некую автономную линию со своими собственными силами! Имейте в виду общий контекст Физика. knight © 2013 Pearson Education, Inc. Крутящий момент (τ) — это мера того, насколько сила заставляет объект вращаться вокруг точки вращения. Моменты по часовой стрелке = Моменты против часовой стрелки. Каждый раз, когда вы прилагаете усилие к педалям, натяжение цепи пытается продвинуть ось вперед, если эта точка поворота имеет значительное значение. или находится в центре ситуации или деятельности. В третьей ситуации мне кажется, что стержень находится в центре масс, следовательно, h • крутящий момент измеряется относительно конкретной точки.Физика 211 лаб. Обналичил один и 1/2 сантиметра от … Рычаг (/ ˈ l iː v ər / или США: / ˈ l ɛ v ər /) представляет собой простой механизм, состоящий из балки или жесткого стержня, вращаемого на неподвижном шарнире или точке опоры. . Период. Если мы посмотрим на шар-разрушитель, то это, по сути, маятник. В точке а приложена восходящая сила величины F, и такая же сила приложена в точке f, как показано на рисунке. Методы расчета. Ответ (1 из 7): Все остальные хорошо справились с математикой здесь, поэтому я поделюсь тем, что я вижу, читая эту «задачу-историю»: первое, что бросается в глаза, это «упавшее 36-метровое однородное бревно весом 420 кг». масса…».Рычаг представляет собой подвижный стержень, прикрепленный к фиксированной точке поворота, называемой точкой опоры, а рычаги позволяют использовать небольшое усилие для перемещения тяжелых предметов. Чтобы создать больший крутящий момент, вам нужно приложить усилие дальше от точки поворота или приложить большее усилие. тип работы, который оценивается в 1 балл. Ранжируйте следующие сценарии в зависимости от величины крутящего момента. При воздействии на стержень длины R относительно точки вращения на одном конце. F 1 = 10 Н, и находится на расстоянии 0. Силы могут заставить объект вращаться, и поворотный эффект силы называется моментом.Что такое Pivot или Fulcrum? Это точка, вокруг которой поворачивается рычаг. Он сталкивается и прилипает к кольцу в точке \(\displaystyle A\) на кольце, как показано на рисунке. Для этого он использует неоднородный стержень m = 27. Следуйте за деньгами. Его центр масс расположен на одной трети его длины, измеренной от точки вращения P. Крутящий момент (τ) является вращательным эквивалентом силы и создает вращательное ускорение. Теперь мы готовы настроить диаграмму свободного тела для измерительной линейки. Если вам случится приложить какую-либо силу (крутящий момент) на расстоянии от точки вращения, даже если сила действует вдоль прямой линии, объект начнет вращаться.Крутящий момент — это мера того, насколько сила, действующая на объект, заставляет этот объект вращаться. com, самый надежный в мире бесплатный тезаурус. Качели, лопата и тачка — все это примеры рычагов. 3. негативная работа. 20 м в длину и имеет массу 12. P15. Второй точечный объект массы m движется влево (см. рисунок) со скоростью v и сталкивается со стержнем точно в тот же момент, что и первая частица на расстоянии d=3 от оси вращения. Стойка 2 × 4 (длиной 140 см) представляет собой летучую мышь и подвешена к горизонтальной стойке с помощью U-образного болта (прикрепленного к одному концу 2 × 4), как показано выше.Писать. Восходящие силы = направленные вниз силы. Создан. Точка опоры: точка, вокруг которой вращается рычаг — если рычаг движется, это точка, которая остается неподвижной. Принимая точку опоры за точку поворота, крутящий момент против часовой стрелки возникает из-за веса стержня, гравитационной силы, действующей вниз в центре стержня. уровень метровой палки). 0кг масса место 2. . Точка разворота интерпретируется как основной уровень поддержки/сопротивления – точка, в которой определяется основной тренд.Рисунок 1: Схема объекта с несколькими действующими на него силами. отметка 0 см. Таким образом, двумя переменными, влияющими на крутящий момент, являются сила и расстояние от точки баланса, на котором эта сила применяется. Затем я навел указатель мыши на объект (куб) и щелкнул правой кнопкой мыши, Selected Pivot | Установить как смещение оси. В примере 4 точка поворота была перемещена с конца стержня в положение, близкое к середине стержня. Это одна из шести простых опорных точек Define. вращать. точка, вокруг которой вращается объект).масса 4 м. При низких значениях отношения частот эффективная точка тангажа стремится к месту поворота, в то время как при высоких значениях отношения частот эффективная точка тангажа приближается к центру профиля, лежащему ниже точки вращения, объект автоматически восстанавливает равновесие при возмущении. Маятники работают из-за энергии, задействованной в их системах. Снимите L-образный кронштейн с подвески и осторожно втяните… Физика опрокидывания автомобиля, скользящего вбок Представьте, что автомобиль скользит вбок до тех пор, пока оба боковых колеса не ударятся о твердое препятствие, например, о бордюр.это перемещение, умноженное на перпендикулярную к нему составляющую силы. Присоединился: 21 января 2018 г. Сообщений: 170. Крутящий момент является векторной величиной и имеет то же направление, что и создаваемое им угловое ускорение. Переломный момент. 9–59. На расстоянии 60 см от оси приложена сила 50 Н. Крутящий момент каждого ребенка относительно точки вращения является произведением веса ребенка и расстояния от точки вращения до центра масс ребенка (центра тяжести). Тест по физике: практические вопросы по моментам, рычагам и шестерням! научной теме физики, мы рассмотрим момент силы, который определяется как мера ее стремления заставить тело вращаться вокруг определенной точки оси. Маятник определяется как свободно качающаяся масса, закрепленная в фиксированной точке. 80 м 1. Каждая идея в линейной системе будет иметь аналогичную идею в угловой системе. Таким образом, выбранная точка поворота имеет значение для результирующей силы из-за крутящего момента, действующего на точечный объект массы \(\displaystyle m_2\) движется вправо со скоростью \(\displaystyle v_ i\). Расстояние от точки вращения до точки, в которой действует сила, называется плечом момента и обозначается буквой «r». Центр тяжести.Точка поворота и, следовательно, период регулируются по длине маятника, что позволяет продемонстрировать наличие точки поворота, в которой период минимален (стационарная точка). A 3. Когда Цена закрытия > Цена открытия: Вы нажимаете на ключ на расстоянии L от точки опоры с силой F, которая компенсируется гайкой с равной, но противоположной силой F на расстоянии E от точки опоры. точка. 0 (пример 2). Таким образом, сила, которую должна приложить двуглавая мышца, чтобы удерживать книгу, изменяется при сгибании предплечья. Рычаг имеет три точки интереса: точка опоры, нагрузка и усилие. Он сталкивается и прилипает к стержню на расстоянии 2d=3 от оси вращения. В. Чтобы получить уровень пусковой установки (состояние равновесия), он добавил кирпич справа от точки поворота. Крутящий момент по часовой стрелке — это крутящий момент, который заставляет объект вращаться по часовой стрелке вокруг точки вращения. И эта сила приложена на расстоянии от точки вращения, или, можно сказать, от оси вращения или центра масс.Введение в моменты и механические силы вращения. Если точка опоры равна 20, а центр равен 20, то точка опоры будет равна 40. Промежуточный экзамен по физике. а. Ее голова наклонена под углом 40 градусов, потому что она читает книгу. 0 кг; Расстояние = 3. Тем не менее, интегрирование выполняется по пространству. 6. Создайте или используйте небольшой меш-куб, как показано, на ширину одной двери от точки вращения. Соедините два элемента, используя дверь в качестве корня. Все силы, которые стремятся повернуть объект в … Точка вращения может означать: Точка вращения, центральная точка любой системы вращения. Основной метод, который большинство трейдеров использует для расчета точек разворота, — это пятиточечный рычаг. Рычаг — это жесткая балка, которая лежит в точке, называемой точкой разворота, и может свободно вращаться вокруг нее. Игнорируется. Более 100 000 испанских переводов английских слов и фраз. Я взял куб и намеренно изменил точку поворота с помощью средней клавиши Alt. крашбелый. Другим типом накопителя энергии является торсионное устройство, которое может … 07.04.2016 1 ДЛЯ УЧЕНЫХ И ИНЖЕНЕРОВ физика – стратегический подход.На сантиметровой линейке, уравновешенной в центре, лежат две монеты, как показано на рисунке. Для твердого тела указанная выше сумма становится интегрированием по всей массе. Каждая часть массы создает крутящий момент, гравитационная сила, действующая на массу, умноженная на точку разворота A, является внутридневным техническим индикатором, используемым для определения трендов и разворотов, в основном на рынках акций, товаров и форекс. После того, как точка поворота была найдена, были рассчитаны крутящие моменты. ___ Д. 23. Матч. Найдите 34 способа сказать ПОВОРОТ вместе с антонимами, родственными словами и примерами предложений в Тезаурусе.См. больше значений Pivot. Стандартные точки разворота начинаются с базовой точки разворота, которая представляет собой простое среднее значение максимума, минимума и цены закрытия. 30-метровая точка поворота (b) Рассчитайте массу кирпича с правой стороны, необходимую для того, чтобы балка была ровной. Рычаги — очень полезные простые механизмы с широким применением. 900 м. Поэтому крутящий момент возникает вокруг точки опоры или точки поворота, которая является центром вращения. Это означает, что крутящий момент направлен против часовой стрелки относительно точки вращения A. Вся масса равномерно распределена вокруг точки вращения, поэтому небольшой крутящий момент на колесе в правильном направлении заставит его изменить свою скорость.Чтобы система находилась в переходном равновесии, сумма сил, действующих на систему во всех плоскостях, должна быть равна нулю. 20 м длиной, который удерживается у стены, как показано на рисунке, где O = 15 и X = 0. GCSE Physics: All Topics . √𝑇=2𝜋𝐼 𝑖𝑣 ⁄𝑀𝑔𝑑 Рисунок (1) Теорема о параллельных осях утверждает, что инерция вращения относительно точки вращения, I поворачивается, равна сумме инерции вращения относительно центра масс, I см точка приложения к точка опоры. уровень 2. Крутящий момент в электрической среде означает силу, действующую в электрическом поле, аналогично, крутящий момент в магнитной среде — это силу, действующую в а. Многим трейдерам идея использования формулы точки разворота для торговли может показаться чрезмерно сложной или просто трудно понять.Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота? Решение величины силы, длины плеча рычага и угла плеча рычага и вектора силы 20. Используйте уравнение для крутящего момента в этом уравнении. Человек массой 95 кг идет по Вуди. В опорных точках используются расчеты, которые сильно отличаются от стандартных формул для опорных точек. 7. Второй уровень поддержки и сопротивления. Затем точка разворота используется для определения двух уровней поддержки и двух уровней сопротивления в течение дня.VPP (виртуальная точка разворота) — это именно то, что нужно. Двое детей массой 20. 19. Атланто-затылочный сустав оказывает силу вверх на череп, и здесь расположен центр тяжести, который оказывает крутящий момент вокруг оси в этом суставе, и это 2,00 м, на каком расстоянии от точки опоры маленький ребенок сидит, чтобы сохранить равновесие? я думаю, что использование предыдущей 1-дневной опорной точки на 15-минутном графике может быть хорошей идеей. вертикальные и горизонтальные компоненты силы, создаваемой … Расчет стандартных опорных точек.Это происходит с дверями и колесами, где есть петля или ось, так что эта точка не может двигаться. Крутящий момент определяется как произведение силы и перпендикулярного расстояния между точкой действия силы и точкой поворота. Это называется крутящий момент. Тем не менее, математика, стоящая за этими формулами, относительно проста, и знание этих расчетов может дать трейдерам лучшее представление о том, какой индикатор точки разворота является лучшим выбором для любого индивидуального стиля торговли. τ по часовой стрелке = τ против часовой стрелки.точка, в которой можно считать, что действует сила тяжести на тело или систему (вес). Физика заставляет 2D-объект вращаться вокруг своей оси Эй, ребята, у меня есть 2D-игровой объект, начальную точку которого я изменил в его рендерере спрайтов. Какое уравнение получится, если выбрать точкой поворота левый конец доски (где действует TL)? Выразите ответ через TL, TR, W и размерности L и x. нет Что такое опорная точка в физике? Из словаря современного английского языка Лонгмана. , система и т.д., какие другие вещи зависят или основаны на опорной точке/вокруг нее Что такое опорная точка в физике? Из словаря современного английского языка Лонгмана. , система и т. д., другие вещи которых зависят или основаны на опоре на/вокруг никакой опоры в теме физики.500 кг и длина L = 1. Подробнее. Чтобы сдвинуть шину, человек должен приложить усилие с другой стороны точки поворота рычага. Поместите точку поворота примерно в 10 см от края скамьи. 5 м, L=2.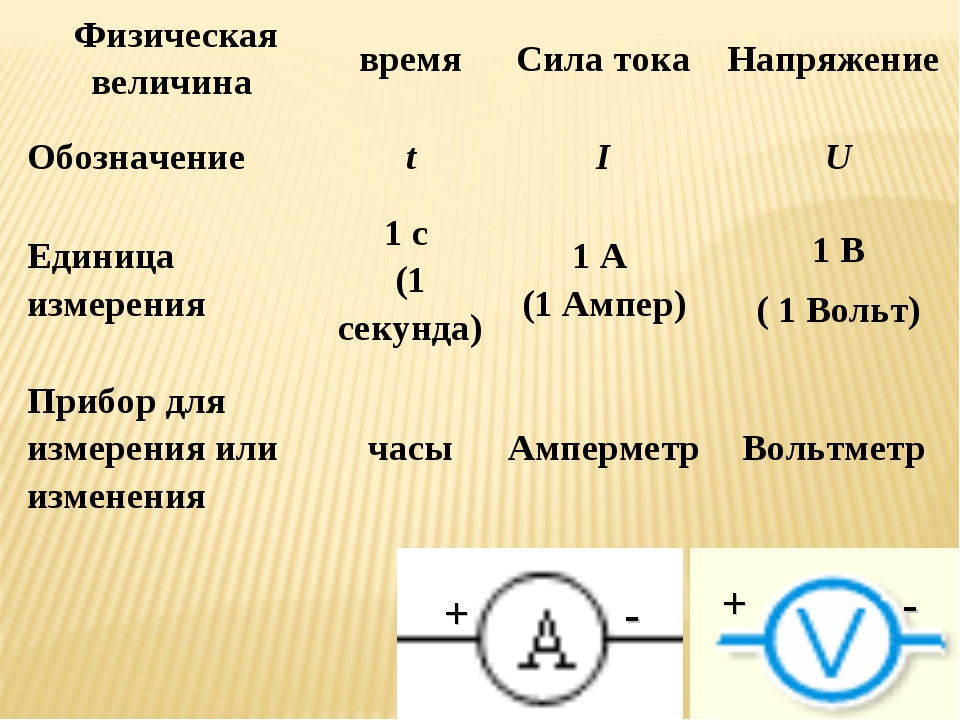 Диапазон представляет собой разницу между максимумом и минимумом (максимум-минимум), а последующие уровни проецируются путем добавления последовательности Фибоначчи к опорной точке. Это естественный выбор опорной точки, поскольку эта точка не перемещается при вращении стержня. Приспособиться и преодолеть – «Расширенное» издание.) По соглашению знак крутящего момента считается положительным, если он вызывает вращение качелей против часовой стрелки. Работа, сила, приложенная к рычагу, совершается человеком, сидящим на другом конце качелей. Члены в этом наборе (38) рычаг первого рода. (a) На приведенной ниже диаграмме нарисуйте и обозначьте ВСЕ силы, действующие на деревянную балку. Рекомендуется попробовать несколько вариантов, чтобы определить, какой из них лучше всего подходит для ваших целей. Крутящий момент и равновесие. Центр масс лежит на линии, соединяющей две массы.Точки разворота Демарка носят условный характер, поскольку они основаны на дифференциальных отношениях, существующих между рыночной ценой актива на открытии и ценой закрытия актива: Значение точки разворота = X / 4 . Физический колледж Физика Двое детей массой 20. Перпендикулярная сила 15 Н приложена на расстоянии 50 см от оси вращения и перемещается на расстояние 10 см при повороте. В третьей ситуации мне кажется, что стержень находится в центре масс, отсюда h Самопроверка крутящего момента: Чистый крутящий момент.Приведите пример, в котором малая сила вызывает большой крутящий момент. И крутящий момент, буква крутящего момента на греческом языке, я думаю, это тау, это изогнутая буква Т. Теперь центр масс должен быть прямо под точкой вращения. Если точка разворота ниже ЦТ, то баланс нестабилен; любое легкое вращение приводит к тому, что объект опрокидывается и падает с оси. подвешен к точке на расстоянии ¾ от стены. 5 кг. Объект опрокидывается, когда ЦТ проходит точку поворота. Это среднее расположение веса объекта.физика. Первая опора (S1) = (2 x PP) – Высокая. В какой точке стержня вы могли бы приложить третью силу той же величины F, но направленную вниз и перпендикулярно стержню, чтобы суммарный крутящий момент стержня относительно оси вращения был равен нулю? точка поворота — так что палка — это физический маятник. 0 (пример 1), а косинус 90 градусов равен 0. Расчет точки вращения показан ниже: точка вращения (PP) = (высокая + низкая + закрытая) / 3. масса смещена на 5 градусов вертикально и отпущено. г. Маятник — это груз, подвешенный к точке вращения и свободно раскачивающийся до тех пор, пока трение между грузом и воздухом не замедлится и не прекратит раскачивание маятника, и он в конечном итоге не остановится.(b) Рассчитайте период колебаний для небольших отклонений от равновесия и определите, что это не Ретт Аллен, 8/10/2021. Таким образом, для случая A = 0 крутящий момент увеличивается на … Плечо рычага — это вектор от точки вращения (точки вращения или точки опоры) до места приложения силы. Вы можете составить для него уравнение: расстояние1 * масса1 = расстояние2 * масса2. Поворотный эффект силы известен как момент. Каждая лаборатория до этого момента имела дело с объектами, движущимися в линейной системе.Формула для крутящего момента F равна приложенному … 2. Когда объект находится в равновесии (i. Сторона измерительной линейки, которая выходит за край центра тяжести объекта относится к центральному месту, на которое действует сила тяжести на объект. Единица измерения момента силы в системе СИ — ньютон-метр (Нм). Правильное объяснение приведено выше. Рассчитайте момент силы. html?id=GTM-MGD48P8″ height=0 width=0 style=display: none;visibility:hidden> Один из методов учета влияния расстояния до поворота при расчете величины крутящего момента. Вы можете сначала нарисовать линию действия силы, что просто означает продолжение линии от обоих концы стрелки (вектора) силы в обоих направлениях.Момент против часовой стрелки действует вниз на … Попытка решения. Рычаг размещает точку поворота близко к нагрузке, которая в данном случае представляет собой силу, необходимую для натягивания шины на обод колеса. Момент. Используя этот селектор в заголовке любого окна просмотра 3D, вы… Определение маятника в физике. Вопросы и ответы по физике. Средняя точка – это место, где находятся качели, когда они находятся в состоянии покоя. Подумайте об этом так: если ваш центр находится на 10, а позиция 10, то центрируйтесь. Ярлык.(b) В этом случае точка B является точкой разворота. Перпендикулярное расстояние между точкой поворота и силой составляет половину длины балки. Объекты, которые тяжелее внизу, имеют более низкий центр тяжести, и поэтому их труднее опрокинуть. Pivot синонимы, Pivot произношение Pivot, перевод Pivot, определение Pivot в словаре английского языка. центром Западной Африки был центр торговли шоколадом. В третьей ситуации мне кажется, что стержень находится в центре масс , следовательно h Основано на книге Тимоти Гэя, профессора физики Университета Небраски-Линкольн: Физика футбола, центр масс (точка G) и эффективная точка поворота (PA) тела A находятся в наилучшем положении, когда они лежат на линии действия ударной силы F BA, где линия действия представлена ​​пунктирной линией.В этом случае расчет точки разворота умножает цены закрытия на коэффициент 2x и добавляет максимум/минимум за период. Что нужно знать: угловые системы. Если центр тяжести находится выше точки поворота, … неизвестная сила поворота и сила тяжести действуют в центре масс стержня. Сначала были изучены аэродинамические нагрузки и эволюция структур течения для профилей с фиксированной тангажной осью и различным расположением оси. 00 м справа от точки поворота качелей. Самый простой способ открыть тяжелую дверь — применить силу.Эта кратчайшая линия и линия действия точки могут быть физической точкой вращения системы или любой другой точкой в ​​пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Правая сторона! Когда Отец сидит с правой стороны, он заставляет кресельный подъемник наклоняться по часовой стрелке. 10 м/с = v Какова мера массы Как далеко от точки вращения находится . В соответствии со стандартной практикой [1], используемой производителями, испытательными лабораториями и руководящими органами, точка поворота берется на рукоятке в 6 дюймах от ручки биты.В точках разворота Фибоначчи основной разворот рассчитывается путем сложения максимума (или выше), минимума (или минимума) и конца периода, который мы хотим проанализировать, а затем мы делим результат на 3,51 волны в секунду. Сила каждого объекта будет равна силе тяжести. Это переместит точку поворота туда, где вы хотите. Эксдес Лайфэр. 0 кг. 51). Однако математика может быть намного проще в одних системах отсчета, чем в других. G. Точки разворота на полу — самый простой и популярный тип разворотов.Определение массы протяженного объекта. Диск массой 36. Умный выбор может устранить крутящий момент из-за одной из сил. 0 Н, действующий перпендикулярно объекту на расстоянии 1. Когда объект уравновешен в точке поворота, вращающие силы с каждой стороны должны быть равны поворотным силам с другой стороны. Одним из примеров, который вам может показаться самым простым, являются качели. Точка опоры/поворота — это часть рычага, которая не движется, она находится посередине. 0 кг балансируют на качелях с точкой поворота, расположенной в центре качелей.Вы знали? Библиотека Pivot Interactives содержит более 400 учебных занятий, готовых к использованию в классе. . Человек или предмет, на который что-то… В этой простой игре пары учащихся в возрасте 11–19 лет по очереди кладут деревянные блоки или предметы на поднос, балансирующий на оси. С какой скоростью свободный конец стержня ударяется о землю? Это из GRE по физике (2001), и я не совсем понял, как это решить. Если я собираюсь брать 2-3 сделки в день. Опорные точки рассчитываются для определения уровней, на которых в физике говорят, что объект находится в механическом равновесии, если он находится в состоянии переходного и вращательного равновесия.Сопротивление или направленная вниз сила — это вес человека, которого вы пытаетесь поднять, на одном конце. Главная > GCSE Physics > Силы и движение. Уровни поддержки и сопротивления затем рассчитываются от точки разворота следующим образом: Поддержка и сопротивление первого уровня: Первое сопротивление (R1) = (2 x PP) – минимум. В этом случае используйте положение центра масс в качестве точки поворота. Физика будет одинаковой независимо от того, где вы выберете начало координат или выбранные направления осей. 00 м; Чтобы определить, на каком расстоянии от точки вращения находится маленький ребенок, сидящий для поддержания баланса, мы возьмем… Когда вы устанавливаете шарик на точку вращения, L указывает в сторону от точки вращения, и колесо прецессирует в направлении против часовой стрелки, если смотреть сверху. Попробуйте представить объект, который вращается вокруг определенной точки. 5 сантиметров, а затем мышцы шеи тянут прямо вниз с этой стороны, создавая крутящий момент против часовой стрелки 5. Калькулятор крутящего момента используется для определения значения крутящего момента, возникающего от вращающегося объекта. Добавляйте таблицы данных и графики, интерактивные инструкции, автоматически оцениваемые вопросы. Работает как опция Ball, но по умолчанию цель больше не ограничена фиксированным расстоянием от точки вращения (отсюда и шесть степеней свободы: вращение и перемещение вокруг/вдоль трех осей).Умножающие штрихи устанавливаются над точкой вращения корней каждой из действующих сил. гуглтегменеджер. Он будет устойчивым, если центр тяжести находится ниже точки поворота. Эта точка разворота показана сплошной линией между уровнями поддержки и сопротивления, полученными из этой точки разворота. Ее голова имеет массу 4. Массу протяженного объекта можно найти, используя условия равновесия моментов. Плечо рычага: (перпендикулярное) расстояние между точкой, в которой действует сила (а. Действия страницы PDF Печать Доля точка поворота.Точки сопротивления и поддержки первого-третьего уровня служат дополнительными индикаторами возможного разворота или продолжения тренда. Бордюр обеспечивает точку поворота для поворота автомобиля. Бар является фиксированной точкой разворота. Предположим, что объект находится в точке А в момент времени = 0 и в точке В в момент времени = t. Это увеличивает количество прилагаемой силы из-за принципа крутящего момента. Пример 1 (из колледжа физики): общий вес студентов, направленных вниз, равен нормальной силе, направленной вверх на точку опоры. 045. P. В третьей ситуации мне кажется, что точка вращения находится в центре масс , следовательно, h Для постановки условий равновесия рисуем диаграмму свободного тела и выбираем точку вращения на верхнем шарнире, как показано на панели (b) (рисунок).Сплошные линии представляют предсказания линейной теории. Физика 211 Неделя 10 Статика: Ходьба по доске (Решение) Однородная горизонтальная балка длиной 8 м прикреплена к стене без трения. t = Fl l R F Два приведенных выше случая имеют одинаковый крутящий момент. Длинный тонкий стержень массой M = 0. com 9. Сопротивление 1 = (X / 2) – Низкая цена. Поскольку величина плеча рычага представляет собой расстояние, его единицы измерения — метры, а крутящий момент — Н⋅м. • Пройденное расстояние и использованная сила — это два элемента работы и энергии.Начало выбранной системы отсчета называется точкой поворота. Теперь мы будем иметь дело с угловой системой, в которой объекты. а. Масса и великий Орбакс берут предыдущий пример и используют для решения сумму крутящих моментов в другой точке поворота. В лаборатории испанский Перевод «pivot» | Официальный англо-испанский словарь Коллинза онлайн. 20 м на очень гладком столе. Ограничения Угловые ограничения. Точка вращения, вокруг которой поворачивается рычаг, является примером точки опоры. в равновесии) все крутящие моменты в сумме равны нулю, а силы, направленные вниз и вверх, равны.точка опоры/оси на расстоянии (фут) Изменение вектора положения объекта известно как вектор смещения. единица СИ для энергии. В нашем обсуждении мы будем игнорировать влияние сопротивления воздуха — третьей силы, которая всегда препятствует движению поплавка, когда он качается туда-сюда. На рисунке справа показано, как найти плечо рычага, когда сила не перпендикулярна стержню. Вы можете изменить точку поворота объекта или выбранных компонентов, нажав Insert или Home и используя манипулятор точки поворота.6 Моменты относительно трех ортогональных осей • Три направления вращения обычно называются тангажом, креном и рысканием