Как по физике найти скорость: Скорость — урок. Физика, 7 класс.

Решение задач на скорость, путь и время движения | 7 класс

Содержание

Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:

• $\upsilon = \frac{S}{t}$
• $S = \upsilon t$
• $t = \frac{S}{\upsilon}$

Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $\upsilon_{ср} = \frac{S}{t}$.

Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.

Задача №1

Выразите в метрах в секунду ($\frac{м}{с}$) скорости: $60 \frac{км}{ч}$; $90 \frac{км}{ч}$; $300 \frac{км}{ч}$; $120 \frac{м}{мин}$.

Дано:
$\upsilon_1 = 60 \frac{км}{ч}$
$\upsilon_2 = 90 \frac{км}{ч}$
$\upsilon_3 = 300 \frac{км}{ч}$
$\upsilon_4 = 120 \frac{м}{мин}$

Показать решение и ответ

Скрыть

Решение:

Для перевода скорости в метры в секунду нам нужно:

• перевести километры в метры ($1 \space км = 1000 \space м$)
• выразить часы или минуты в секундах ($1 \space мин = 60 \space с$; $1 \space ч = 60 \space мин = 3600 \space с$)

Тогда,
$\upsilon_1 = 60 \frac{км}{ч} = 60 \frac{1000 \space м}{3600 \space c} = \frac{1000 \space м}{60 \space c} \approx 16.7 \frac{м}{с}$.

При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).

Если мы вычислим множитель $\frac{1000 \space м}{3600 \space c}$, то получим, что $1 \frac{км}{ч} = \frac{}{3.6} \frac{м}{с}$.

Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3. 6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.

Переведем следующие две скорости в единицы СИ:
$\upsilon_2 = 90 \frac{км}{ч} = 90 \frac{1000 \space м}{3600 \space c} = 1000 \cdot 0.025 \frac{м}{с} = 25 \frac{м}{с}$,
$\upsilon_3 = 300 \frac{км}{ч} = 300 \frac{1000 \space м}{3600 \space c} = \frac{1000 \space м}{12 \space c} \approx 83.3 \frac{м}{с}$.

Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$\upsilon_4 = 120 \frac{м}{мин} = 120 \frac{м}{60 \space c} = 2 \frac{м}{с}$.

Ответ: $\upsilon_1 \approx 16.7 \frac{м}{с}$; $\upsilon_2 = 25 \frac{м}{с}$; $\upsilon_1 \approx 83.3 \frac{м}{с}$; $\upsilon_4 = 2 \frac{м}{с}$.

Задача №2

Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 \space км$, за $2.5 \space с$. Найдите скорость пули.

Дано:
$S = 1 \space км$
$t = 2.5 \space с$

СИ:
$S = 1000 \space м$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

Формула для расчета скорости:
$\upsilon = \frac{S}{t}$.

Перед вычислениями не забывайте переводить единицы измерения величин в СИ!

Рассчитаем скорость:
$\upsilon = \frac{1000 \space м}{2.5 \space с} = 400 \frac{м}{с}$.

Ответ: $\upsilon = 400 \frac{м}{с}$.

Задача №3

Пароход, двигаясь против течения со скоростью $14 \frac{км}{ч}$, проходит расстояние между двумя пристанями за $4 \space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 \frac{м}{с}$?

Дано:
$\upsilon_1 = 14 \frac{км}{ч}$
$t_1 = 4 \space ч$
$\upsilon_2 = 5.6 \frac{м}{с}$

$t_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Найдем расстояние между двумя пристанями:
$S = \upsilon_1 t_1$,
$S = 14 \frac{км}{ч} \cdot 4 \space ч = 56 \space км = 56 \space 000 \space м$.

Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.

Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = \frac{S}{\upsilon_2}$,
$t_2 = \frac{56 \space 000 \space м}{5.6 \frac{м}{с}} = 10 \space 000 \space с$.

Ответ: $t_2 = 10 \space 000 \space с$.

Задача №4

Автомобиль проехал равномерно участок дороги длиной $3.5 \space км$ за $3 \space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 \frac{км}{ч}$”?

Дано:
$S = 3.5 \space км$
$t = 3 \space мин$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 \frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.

Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$\upsilon = \frac{S}{t}$.

Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 \space мин = \frac{3}{60} \cdot ч = 0.05 \space ч$.

Теперь мы можем рассчитать скорость движения автомобиля:
$\upsilon = \frac{3.5 \space км}{0.05 \space ч} = 70 \frac{км}{ч}$.

Получается, что водитель нарушил правила дорожного движения, ведь $70 \frac{км}{ч} > 50 \frac{км}{ч}$.

Ответ: нарушил.

Задача №5

Росток бамбука за сутки вырастает на $86.4 \space см$. На сколько он вырастает за $1 \space мин$?

Дано:
$S = 86.4 \space см$
$t = 1 \space сут$
$t_1 = 1 \space мин$

$S_1 — ?$

Показать решение и ответ

Скрыть

Решение:

Переведем сутки в минуты:
$t = 1 \space сут = 24 \space ч = 24 \cdot 60 \space мин = 1440 \space мин$.

Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$\upsilon = \frac{86.4 \space см}{1440 \space мин} = 0.06 \frac{см}{мин}$.

Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 \space см$, за $1 \space мин$.

Значит,
$S_1 =  0.06 \space см = 0.6 \space мм$.

Ответ: $S_1 =  0.6 \space мм$.

Задача №6

Самолет, летящий со скоростью $300 \frac{км}{ч}$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 \space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 \space ч$. Определите скорость ветра.

Дано:
$\upsilon_1 = 300 \frac{км}{ч}$
$t_1 = 2.2 \space ч$
$t_2 = 2.5 \space ч$

$\upsilon_в — ?$

Показать решение и ответ

Скрыть

Решение:

Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = \upsilon_1 t_1$,
$S = 300 \frac{км}{ч} \cdot 2. 2 \space ч = 660 \space км$.

Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$\upsilon_2 = \frac{S}{t_2}$,
$\upsilon_2 = \frac{660 \space км}{2.5 \space ч} = 264 \frac{км}{ч}$

Если бы ветра не было, то скорость самолета составила бы $300 \frac{км}{ч}$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$\upsilon_2 = \upsilon_1 — \upsilon_в$.

Рассчитаем скорость ветра:
$\upsilon_в = \upsilon_1 — \upsilon_2$,
$\upsilon_в = 300 \frac{км}{ч} — 264 \frac{км}{ч} = 36 \frac{км}{ч}$,
или в СИ $\upsilon_в = 36 \cdot \frac{1000 \space м}{3600 \space с} = 10 \frac{м}{с}$.

Ответ: $\upsilon_в = 10 \frac{м}{с}$.

Задача №7

Определите по графику равномерного движения, изображенному на рисунке 1:

• скорость движения
• путь, пройденный телом в течение $4. 5 \space с$
• время, в течение которого пройден путь, равный $15 \space м$
Рисунок 1. График равномерного движения

Показать решение и ответ

Скрыть

Решение:

Скорость равномерного движения рассчитывается по формуле:
$\upsilon = \frac{S}{t}$.

Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 \space с$, был пройден путь, равный $16 \space м$.

Используя эти данные, рассчитаем скорость:
$\upsilon = \frac{16 \space м}{4 \space с} = 4 \frac{м}{с}$.

Найдем путь, пройденный телом в течение $4.5 \space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 \space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = \upsilon t$,
$S = 4 \frac{м}{с} \cdot 4.5 \space с = 18 \space м$.

Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 \space м$. Поэтому вычислим его:
$t = \frac{S}{\upsilon}$,
$t = \frac{15 \space м}{4 \frac{м}{с}} = 3.75 \space с$.

Ответ: $4 \frac{м}{с}$, $18 \space м$, $3.75 \space с$.

Задача №8

Средняя скорость велосипедиста на всем пути равна $40 \frac{км}{ч}$. Первую половину пути он ехал со скоростью $60 \frac{км}{ч}$. С какой скоростью велосипедист проехал остаток пути?

Дано:
$\upsilon_{ср} = 40 \frac{км}{ч}$
$\upsilon_1 = 60 \frac{км}{ч}$
$S_1 = S_2 = \frac{1}{2}S$

$\upsilon_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Запишем формулу средней скорости при неравномерном движении:
$\upsilon_{ср} = \frac{S}{t}$.

Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$\upsilon_{ср} = \frac{S}{t_1 + t_2}$.

Время мы можем выразить через скорость на данном участке пути и пройденный за это время путь:
$t_1 = \frac{S_1}{\upsilon_1} = \frac{\frac{1}{2}S}{\upsilon_1} = \frac{S}{2 \upsilon_1}$,
$t_2 = \frac{S_2}{\upsilon_2} = \frac{\frac{1}{2}S}{\upsilon_2} = \frac{S}{2 \upsilon_2}$,
$\upsilon_{ср} = \frac{S}{\frac{S}{2 \upsilon_1} + \frac{S}{2 \upsilon_2}} = \frac{S}{\frac{S(\upsilon_1 + \upsilon_2)}{2 \upsilon_1 \upsilon_2}} = \frac{2 \upsilon_1 \upsilon_2}{\upsilon_1 + \upsilon_2}$.

Теперь выразим отсюда скорость $\upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 \upsilon_1 \upsilon_2 = \upsilon_{ср} \upsilon_1 + \upsilon_{ср} \upsilon_2$,
$2 \upsilon_1 \upsilon_2 — \upsilon_{ср} \upsilon_2 = \upsilon_{ср} \upsilon_1$,
$\upsilon_2 \cdot (2 \upsilon_1 —  \upsilon_{ср}) = \upsilon_{ср} \upsilon_1$,
$\upsilon_2 = \frac{\upsilon_{ср} \upsilon_1}{2 \upsilon_1 —  \upsilon_{ср}}$.

Рассчитаем эту скорость:
$\upsilon_2 = \frac{40 \frac{км}{ч} \cdot 60 \frac{км}{ч}}{2 \cdot 60 \frac{км}{ч} —  40 \frac{км}{ч}} = \frac{2400 \frac{км}{ч}}{80} = 30 \frac{км}{ч}$.

Ответ: $\upsilon_2 =  30 \frac{км}{ч}$.

Задача №9

На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 \space ч$ с начала его движения?

Рисунок 2. График движения поезда

Дано:
$t = 3 \space ч$

$\upsilon_1 — ?$, $\upsilon_2 — ?$, $\upsilon_3 — ?$
$S — ?$

Показать решение и ответ

Скрыть

Решение:

Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.

Определим скорость движения поезда на участке OA. В момент времени, равный $1 \space ч$, пройденный поездом путь составил $40 \space км$:
$\upsilon_1 = \frac{S_1}{t_1}$,
$\upsilon_1 = \frac{40 \space км}{1 \space ч} = 40 \frac{км}{ч}$.

Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $\upsilon_2 = 0 \frac{км}{ч}$.

Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 \space ч$ до $3 \space ч$, пройденный путь изменился с $60 \space км$ до $80 \space км$. Значит, за $1 \space ч$ поезд прошел путь, равный $20 \space км$:
$\upsilon_3 = \frac{S_3}{t_3}$,
$\upsilon_3 = \frac{20 \space км}{1 \space ч} = 20 \frac{км}{ч}$.

Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.

Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.

Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = \upsilon_1 t_1 + \upsilon_3 t_3$,

$S = 40 \frac{км}{ч} \cdot 1.5 \space ч + 20 \frac{км}{ч} \cdot 1 \space ч = 80 \space км$.

Ответ: $\upsilon_1 = 40 \frac{км}{ч}$, $\upsilon_2 = 0 \frac{км}{ч}$, $\upsilon_3 = 20 \frac{км}{ч}$, $S = 80 \space км$.

Задача №10

От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 \frac{км}{ч}$, второго $40 \frac{км}{ч}$. Второй поезд отправляется через $10 \space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.

Дано:
$\upsilon_1 = 30 \frac{км}{ч}$
$\upsilon_2 = 40 \frac{км}{ч}$
$t_{01} = 0 \space мин$
$t_{02} = 10 \space мин$
$t_1 = 40 \space мин$
$t_{1о} = 5 \space мин$

$t — ?$
$S — ?$

Показать решение и ответ

Скрыть

Решение:

Сначала займемся построением графика движения поездов.  

По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$. 

Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_{01} = 0 \space мин$.

Движется он со скоростью $30 \frac{км}{ч}$ в течение $t_1 = 40 \space мин$. Переведем эту скорость в $\frac{км}{мин}$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$\upsilon_1 = 30 \frac{км}{ч} = 30 \frac{км}{60 \space мин} = 0.5 \frac{км}{мин}$,
$S_1 = \upsilon_1 t_2$,
$S = 0.5 \frac{км}{мин} \cdot 40 \space мин = 20 \space км$.

Поставим эту точку на графике и соединим с началом координат.

Рисунок 3. График движения первого поезда

Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.

Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.

Теперь построим тут же график движения для второго поезда (рисунок 4).

Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_{02} = 10 \space мин$.

Он движется со скоростью $40 \frac{км}{ч}$. Это означает, что за $1 \space ч = 60 \space мин$ он проходит путь, равный $40 \space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.

Рисунок 4. Графики движения обоих поездов

Итак, графически мы получили, что

• Второй поезд догонит первый в момент времени $t = 40 \space мин$
• Поезда встретятся на расстоянии $S = 20 \space км$ от места отправления

Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = \upsilon_1 t$,
$S_2 = \upsilon_2 (t — t_{02})$.

Найдем это время:
$\upsilon_1 t = \upsilon_2 (t — t_{02})$,
$\upsilon_2 t — \upsilon_1 t = \upsilon_2 t_{02}$,
$t (\upsilon_2 — \upsilon_1) = \upsilon_2 t_{02}$,
$t = \frac{\upsilon_2 t_{02}}{\upsilon_2 — \upsilon_1}$.

Перед расчетом переведем $мин$ в $ч$: $t_{02} = 10 \space мин = \frac{10}{60} \space ч = \frac{1}{6} \space ч$.

Теперь рассчитаем время встречи двух поездов:
$t = \frac{40 \frac{км}{ч} \cdot \frac{1}{6} \space ч}{40 \frac{км}{ч} — 30 \frac{км}{ч}} = \frac{4}{6} \space ч = \frac{2}{3} \space ч = 40 \space мин$.

Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = \upsilon_1 t$,
$S = 30 \frac{км}{ч} \cdot \frac{2}{3} \space ч = 20 \space км$.

Ответ: $t = 40 \space мин$, $S = 20 \space км$.

Задача №11

Поезд прошел $25 \space км$ за $35 \space мин$, причем первые $10 \space км$ он прошел в течение $18 \space мин$, вторые $10 \space км$ в течение $12 \space мин$, а последние $5 \space км$ за $5 \space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.

Дано:
$S = 25 \space км$
$t = 35 \space мин$
$S_1 = 10 \space км$
$t_1 = 18 \space мин$
$S_2 = 10 \space км$
$t_2 = 12 \space мин$
$S_3 = 5 \space км$
$t_3 = 5 \space мин$

$\upsilon_{1ср} — ?$, $\upsilon_{2ср} — ?$, $\upsilon_{3ср} — ?$
$\upsilon_{ср} — ?$

Показать решение и ответ

Скрыть

Решение:

Переведем время из $мин$ в $ч$:

• $t = 35 \space мин = \frac{35}{60} \space ч = \frac{7}{12} \space ч$
• $t_1 = 18 \space мин = \frac{18}{60} \space ч = \frac{3}{10} \space ч = 0. 3 \space ч$
• $t_2 = 12 \space мин = \frac{12}{60} \space ч = \frac{1}{5} \space ч = 0.2 \space ч$
• $t_3 = 5 \space мин = \frac{5}{60} \space ч = \frac{1}{12} \space ч$

Теперь рассчитаем среднюю скорость на каждом участке пути:

• $\upsilon_{1ср} = \frac{S_1}{t_1}$,
  $\upsilon_{1ср} = \frac{10 \space км}{0.3 \space ч} \approx 33.3 \frac{км}{ч}$
• $\upsilon_{2ср} = \frac{S_2}{t_2}$,
  $\upsilon_{2ср} = \frac{10 \space км}{0.2 \space ч} = 50 \frac{км}{ч}$
• $\upsilon_{3ср} = \frac{S_3}{t_3}$,
  $\upsilon_{3ср} = \frac{5 \space км}{\frac{1}{12} \space ч} = 60 \frac{км}{ч}$

Рассчитаем среднюю скорость на на всем пути:
$\upsilon_{ср} = \frac{S}{t}$,
$\upsilon_{ср} = \frac{25 \space км}{\frac{7}{12} \space ч} \approx 42.9 \frac{км}{ч}$

Ответ: $\upsilon_{1ср}  \approx 33.3 \frac{км}{ч}$, $\upsilon_{2ср} = 50 \frac{км}{ч}$, $\upsilon_{3ср} = 60 \frac{км}{ч}$, $\upsilon_{ср} \approx 42.9 \frac{км}{ч}$.

расчёты и формулы / Справочник :: Бингоскул

Вычисление средней скорости движения в физике: расчёты и формулы

добавить в закладки удалить из закладок

Содержание:

Под средней скоростью движения какого-либо тела понимают отношение пройденного расстояния к временному промежутку, который был затрачен на его преодоление. Определение средней скорости может понадобиться в случае, когда в процессе перемещения тела на разных участках его скорость изменялась. Неважно в каком направлении совершалось движение и изменялось ли оно с течением времени. Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.

Как найти среднюю скорость тела?

Для случая, когда движение происходило с изменением скорости, но на протяжении равных отрезков времени наблюдалась разная скорость, применяют формулу среднего арифметического значения.

Пример. Автомобиль всего проехал 1 километр и 200 метров. После каждых 400 м он изменял скорость движения. Первые 400 метров он двигался со скоростью 20 км/ч, потом со скоростью 40 км/ч, 50 км/ч и последний участок проехал на скорости 35 км/ч. Определение средней скорости движения производим так:

   \frac {20+40+50+35} {4} = 36,25 км/ч

В любом другом случае вычисление средней скорости в физике производят более сложным путем по формуле:

• Si – отрезок пути, км;
• ti – время прохождения отрезка пути, ч.

Пример задачи на вычисление средней скорости в физике

Человек прошел 1 час со скоростью 7 км/ч, а затем на протяжении 2-х часов шел со скоростью 4 км/ч. Определить среднюю скорость движения.

Сначала найдем путь, который был пройден за каждый из промежутков времени:

S₁ =  1 х 7 = 7 км

S₂ =  2 х 4 = 8 км

Далее пишется вышеприведенная формула в более привычном виде, как обычно, подставляются необходимые данные и определяется средняя скорость:

vcp. = \frac { S_1 +  S_2 } { t_1 + t_2 } = \frac { 7 + 8 } { 1 + 2 } = 5 км/ч

Средняя скорость при равноускоренном движении 

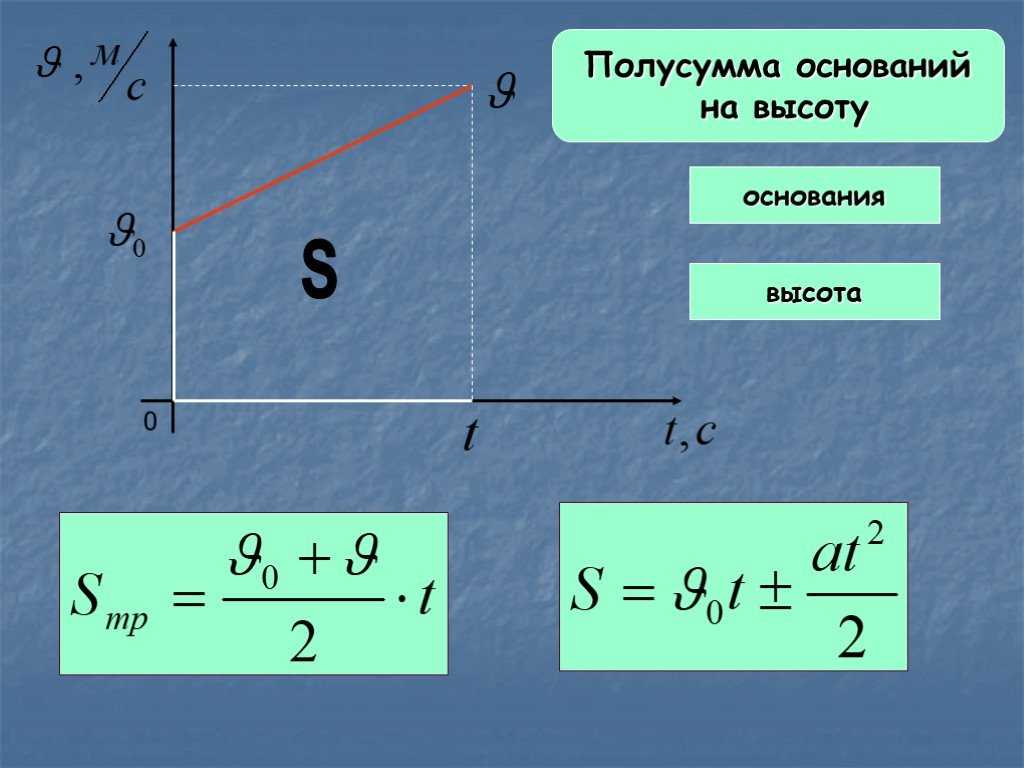
На практике очень часто встречаются задачи, когда вычисление средней скорости необходимо производить для случая, когда тело, двигаясь с какой-то начальной скоростью, с течением времени начало ускоряться и в конце пути достигло какой-то новой скорости. Тогда следует использовать формулу, которая выражает среднюю скорость через величину ускорения:

vcp. = v0 + \frac { at } { 2 } , где:

• v0 – начальная скорость,
• а – ускорение,
• t – время движения тела.

Пример. Двигаясь с начальной скоростью 160 м/с, самолет в течение двух минут ускорял свое движение на 1,5 м/с2. Какова его средняя скорость за этот промежуток времени?

vcp. = 160 + \frac { 1,5 * 120 } { 2 } = 250 м/с

Поделитесь в социальных сетях:

20 ноября 2021, 14:40

Геометрия

Could not load xLike class!





Физика скорости: определение, формула и единицы измерения

Скорость — это то, о чем мы все слышали и что мы осознаем, когда едем в машине. Двигаясь из точки А в точку Б, мы можем посмотреть в окно и посмотреть, какая у нас скорость. Если что-то движется, оно имеет скорость, независимо от того, маленькое оно или большое, легкое или тяжелое. Но что такое скорость, как она работает и какие есть примеры скорости в повседневной жизни? Давай выясним.

Определение скорости в физике

Прежде чем продолжить, нам будет полезно дать четкое определение скорости.

Скорость — это мера скорости изменения расстояния, пройденного движущимся объектом. скорость является скаляром, что означает, что это единица измерения, которая имеет величину, но не имеет направления.

• Скорость, с которой объект перемещается на определенное расстояние, называется скоростью.

• Быстро движущийся объект, который имеет высокую скорость, быстро перемещается и преодолевает значительное расстояние за короткий промежуток времени.

• Медленно движущийся объект с низкой скоростью, с другой стороны, проходит сравнительно небольшое расстояние за то же время.

• Объект с нулевой скоростью вообще не движется.

Скаляр против вектора. Скаляр имеет величину, тогда как вектор, подобный показанному выше, имеет величину и направление, адаптированное из изображения Ducksters.

Определение скорости в физике:

Физики используют основные понятия скорости и скорости для описания движения объектов в терминах:

1. Расстояние

2. Время

3. Направление.

Эти два слова имеют два уникальных значения: скорость и скорость. Тем не менее, мы часто слышим, как эти фразы используются взаимозаменяемо.

Другими словами, в то время как скорость является скалярной величиной, скорость является вектором, что означает, что это единица измерения, которая имеет как величину, так и направление.

Например, \(50\;\mathrm{км/ч}\) обозначает скорость автомобиля, движущегося по дороге, тогда как \(50\;\mathrm{км/ч}\) на запад обозначает скорость.

Формула скорости в физике:

Чтобы вычислить скорость движущегося объекта, мы делим пройденное расстояние на время, необходимое для прохождения такого расстояния. $$v=\frac{d}{t}$$

Где \(v\) – скорость, выраженная в милях в час (\(\mathrm{mph})\),

\(d\) это пройденное расстояние, выраженное в милях.

и \(t\) – время. выражается в часах \(\mathrm{h}\).

Маленький ребенок идет со скоростью \(4\;\mathrm{км/ч}\). Сколько времени ему потребуется, чтобы пройти \(20\;\mathrm{км}\)? $$t=\frac{d}{v}=\frac{20\;\mathrm{km}}{4\;\mathrm{kph}}=5\;\mathrm{h}. $$

За два часа велосипед может проехать \(16\;\mathrm{ми}\). Оцените его скорость. $$v=\frac{d}{t}=\frac{16\;\mathrm{mi}}{2\;\mathrm{h}}=8\;\mathrm{mph}.$$

Если автомобиль движется со скоростью \(20\;\mathrm{mph}\), ему требуется \(2\;\mathrm{h}\), чтобы пройти расстояние. С какой скоростью он должен двигаться, чтобы преодолеть такое же расстояние за \(0,5\;\mathrm{h}\)?$$d=20\;\mathrm{mph}\times2\;\mathrm{h}=40\ ;\mathrm{mi}$$

Скорость, необходимая для преодоления того же расстояния в \(0,5\;\mathrm{h}\): $$v=\frac{d}{t}=\frac{40\; \mathrm{mi}}{0,5\;\mathrm{h}}=80\;\mathrm{mph}.$$

Формула средней скорости в физике

В следующих таблицах отслеживается положение движущегося объекта во времени таким образом, что в каждый момент времени измеряется положение относительно начальной точки.

Первая таблица представляет движение объекта, движущегося с постоянной скоростью.

Time (s)	Position (m)
\(0\)	\(0\)
\(1\)	\(7\)
\(2\)	\(14\)
\(3\ )	\(21\)

Объект с изменяющейся скоростью будет иметь таблицу, подобную приведенной ниже.

Время (с)	Позиция (м)
\ (0 \)	\ (0 \)
\ (1 \)	\ (4 \)
\ (2 \)
\ (2 \) 2
\ (2 \)
\ (2 \)
\ (2 \)
\ (2 \)
\ (2 \)
\. \(12\)
\(3\)	\(20\)

Мы можем видеть, что разница между каждой парой последовательных измерений положения увеличивается со временем. Это указывает на то, что скорость менялась в процессе движения объекта. Это означает, что объект не имеет одной скорости на протяжении всего пути, а имеет постоянно меняющуюся скорость.

Итак, нам нужен параметр, который можно использовать для описания общей изменяющейся скорости объекта. Одним из таких показателей является средняя скорость. Поскольку скорость движущегося объекта часто меняется в процессе его движения, принято различать среднюю и мгновенную скорости.

Движущиеся объекты не всегда движутся с непредсказуемой скоростью. Предмет будет время от времени перемещаться с постоянной скоростью и с постоянной скоростью.

Поскольку скорость движущегося тела обычно непостоянна и колеблется во времени, требуется формула для средней скорости. Даже при изменении скорости можно использовать общее время и общее пройденное расстояние, и мы можем получить одно значение для описания полное движение по формуле средней скорости.

На примере движущегося автомобиля скорость автомобиля может быть:

1. ускорение с места

2. ускорение на время

3. затем 9 00103 3 3

   3 в конечном итоге остановка

• В каждый момент скорость автомобиля будет отражать его движение в соответствующий момент времени.

• Однако один параметр может учитывать все указанные выше изменения скорости.

• Этот параметр будет средней скоростью.

Чтобы вычислить среднюю скорость, мы делим общее пройденное расстояние на общее необходимое время.

Используйте формулу средней скорости, чтобы найти среднюю скорость Тома, который проезжает первые \(200\;\mathrm{км}\) за \(4\;\mathrm{ч}\) и оставшиеся \( 160\;\mathrm{km}\) в другом \(4\;\mathrm{h}\) по формуле средней скорости. Чтобы найти среднюю скорость, нам нужно вычислить общее расстояние и общее время.

Общее расстояние, пройденное Томом:

$$200\;\mathrm{км} + 160\;\mathrm{км}=360\;\mathrm{км}.$$

Общее время, пройденное Томом :

$$4\;\mathrm{h} + 4\;\mathrm{h}=8\;\mathrm{h}.$$

Среднюю скорость можно рассчитать: $$v_{\text{average }} = \ frac {d _ {\ text {total}}} {t _ {\ text {total}}} = \ frac {360 \; \ mathrm {km}} {8 \; \ mathrm {h}}. $ $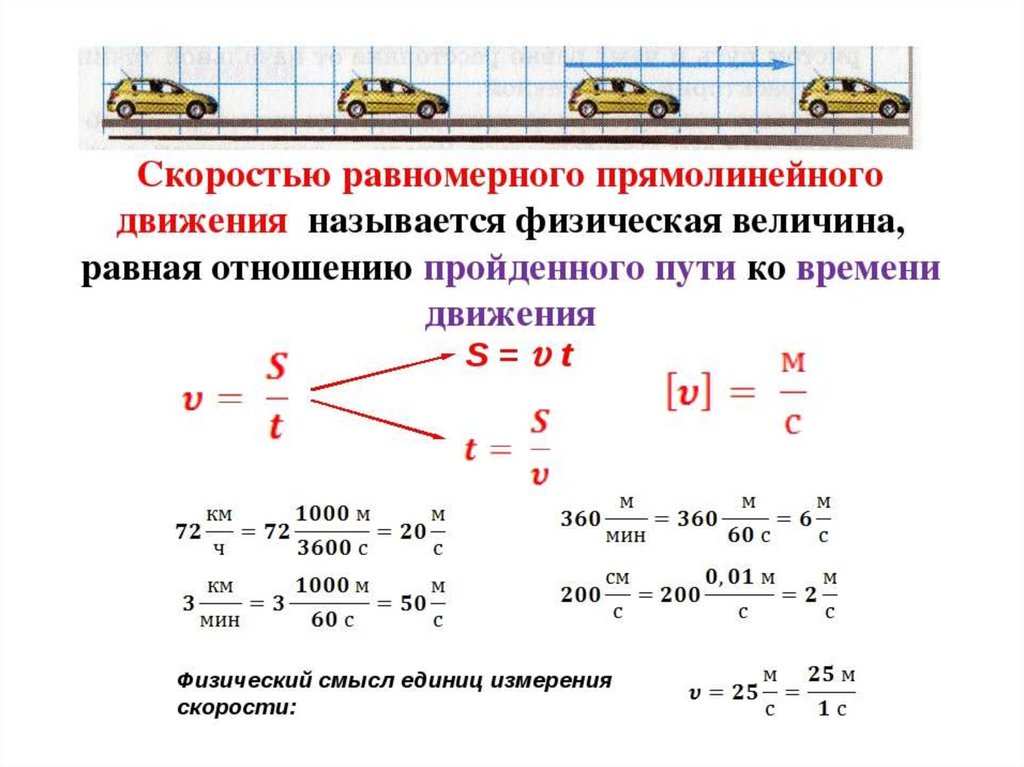

После \(3\;\mathrm{ч}\) движения со скоростью \(30\;\mathrm{км/ч}\) автомобиль решает снизить скорость до \(20\;\mathrm{км/ч}\ ) для следующих \(4\;\mathrm{h}\). Используя формулу средней скорости, рассчитайте среднюю скорость.

Расстояние, пройденное первым \(3\;\mathrm{h}\), можно рассчитать: $$d_{1}=vt=30\;\mathrm{kmph}\times3\;\mathrm{h}= 90\;\mathrm{mi}.$$ Расстояние, пройденное за секунду \(4\;\mathrm{h}\) часа: $$d_{2}=vt=20\;\mathrm{км/ч}\times4 \;\mathrm{h}=80\;\mathrm{mi}.$$ Общее пройденное расстояние: $$d_{\text{total}}=d_{1}+d_{2}=80\;\mathrm {mi}+90\;\mathrm{mi}=170\;\mathrm{mi}.$$

Используя формулу средней скорости: $$v_{\text{average}}=\frac{d_{\text {total}}}{t_{\text{total}}}=\frac{170\;\mathrm{mi}}{7\;\mathrm{h}}=24,3\;\mathrm{mph}.$$

Единицы скорости в физике

Как обсуждалось ранее, скорость относится к скорости, с которой объект меняет свое положение. Скорость может быть измерена или выражена в:

• Метров в секунду \((\mathrm{м/с})\), где расстояние будет выражено в метрах, а время в секундах.

• Километры в час \((\mathrm{км/ч})\), где расстояние измеряется в километрах, а время в часах.

• Мили в час \((\mathrm{mph})\), где расстояние выражается в милях, а время в часах.

Можно использовать больше единиц, чем указано выше, но они используются чаще всего.

Скорость — ключевые выводы

• Скорость — это скалярное число, описывающее «скорость, с которой движется объект».

• Верно, что скорость — это скорость, с которой объект движется по маршруту с точки зрения времени. Тогда как скорость – это скорость и направление движения.

• Скорость в любой момент времени называется мгновенной скоростью.

• Средняя скорость – сумма всех мгновенных скоростей; рассчитывается, когда скорость движущегося объекта меняется со временем.

• Термин “скорость” относится к скорости, с которой что-то движется. Метры в секунду \(\mathrm{(м/с)}\), километры в час \(\mathrm{(км/ч)}\) и мили в час \(\mathrm{(mph)}\) являются наиболее часто используемые единицы измерения скорости \(\mathrm{(mph)}\).

• Чтобы вычислить скорость, мы делим пройденное расстояние на необходимое время.

• Та же формула может быть применена для расчета средней скорости, где скорость будет меняться со временем.

• В случае средней скорости мы делим общее расстояние на общее время в пути

Формула скорости – Что такое формула скорости? Примеры

Формула скорости может быть определена как скорость, с которой объект проходит некоторое расстояние. Скорость можно измерить как расстояние, пройденное телом за определенный период времени. Единицей скорости в СИ является м/с. В этом разделе мы узнаем больше о формуле скорости и ее применении.

Что такое Формула скорости?

Давайте двигаться дальше и узнать больше о формуле скорости в этом разделе. Для выражения скорости могут использоваться различные единицы измерения, такие как м/с, км/ч, мили/ч и т. д. Размерная формула скорости [LT ^-1 ]. Скорость – это мера того, насколько быстро движется тело. Формула скорости данного тела может быть выражена следующим образом:

Формула скорости

Скорость = расстояние ÷ время

Как использовать формулу скорости?

Формулу скорости можно использовать для определения скорости объектов, учитывая расстояние и время, затраченное на преодоление этого расстояния. Мы также можем использовать формулу скорости для расчета расстояния или времени, подставляя известные значения в формулу скорости и далее вычисляя
. Расстояние = скорость × время или время = расстояние/скорость
Давайте кратко рассмотрим пример, показывающий, как использовать формулу для скорости.

Пример:  Какова скорость, если вы проедете 3600 м за 30 минут?

Решение:  Используя формулу для скорости,

Скорость = расстояние ÷ время
Скорость = 3600 ÷ (30 × 60) = 2

Ответ: Ваша скорость, если вы проедете 3600 м за 30 минут, составит 2 м/с.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Примеры на Speed ​​Formula

Давайте решим несколько интересных задач, используя формулу скорости.

Пример 1:  Поезд прошел расстояние 120 км за час. Определить скорость поезда в м/с по формуле скорости.

Решение: 

Чтобы найти: Скорость поезда.
Расстояние, пройденное поездом в метрах = 120×1000м = 120000м
Время движения поезда в секундах = 60×60 = 3600 секунд
Использование формулы скорости,


Скорость = Расстояние/Время = 120000/3600 = 33,3 м/с

Ответ: Скорость поезда 33,3 м/с.

Пример 2: Велосипедист проезжает 20 км за 50 минут. Используйте формулу скорости, чтобы вычислить скорость велосипедиста в м/с.

Решение:  Чтобы найти: Скорость велосипедиста.
Расстояние, пройденное велосипедистом в метрах = 20×1000 = 20000м
Время, затраченное велосипедистом в секундах = 50×60= 3000 секунд
Используя формулу скорости,
Скорость = Расстояние/Время = 20000/3000 = 6,67 м/с

Ответ: Скорость велосипедиста 6,67 м/с.

Пример 3: Используя формулу скорости, рассчитайте скорость человека в километрах в час, если расстояние, которое он проходит, составляет 40 километров за 2 часа?

Решение:

Формула скорости: [Скорость = Расстояние ÷ Время]
Расстояние = 40 километров
Время = 2 часа 
Скорость = (40 ÷ 2) км/ч
= 20 километров в час

Ответ: Скорость человека 20 километров в час.

Часто задаваемые вопросы о формуле скорости

Как рассчитать расстояние с помощью формулы скорости?

Формула скорости задается как [Скорость = Расстояние ÷ Время]. Чтобы рассчитать расстояние, формулу скорости можно представить в виде [Расстояние = Скорость × Время].

Как рассчитать время, используя формулу скорости?

Формула скорости задается как [Скорость = Расстояние ÷ Время]. Для расчета времени формула скорости будет иметь вид [Время = Пройденное расстояние ÷ Скорость].

Как использовать формулу скорости?

Формула скорости может использоваться в нашей повседневной жизни для определения скорости объектов. Чтобы понять, как использовать формулу скорости, рассмотрим пример.


Пример. Какова ваша скорость, если вы проедете 4000 м за 40 минут?
Решение: использование формулы скорости,
. Скорость = расстояние ÷ время
Скорость = 4000 ÷ (40 × 60) = 1,67 м/с.

Ответ: Ваша скорость, если вы проедете 4000 м за 40 минут, составит 1,67 м/с.