Как по графику найти производную: График производной функции

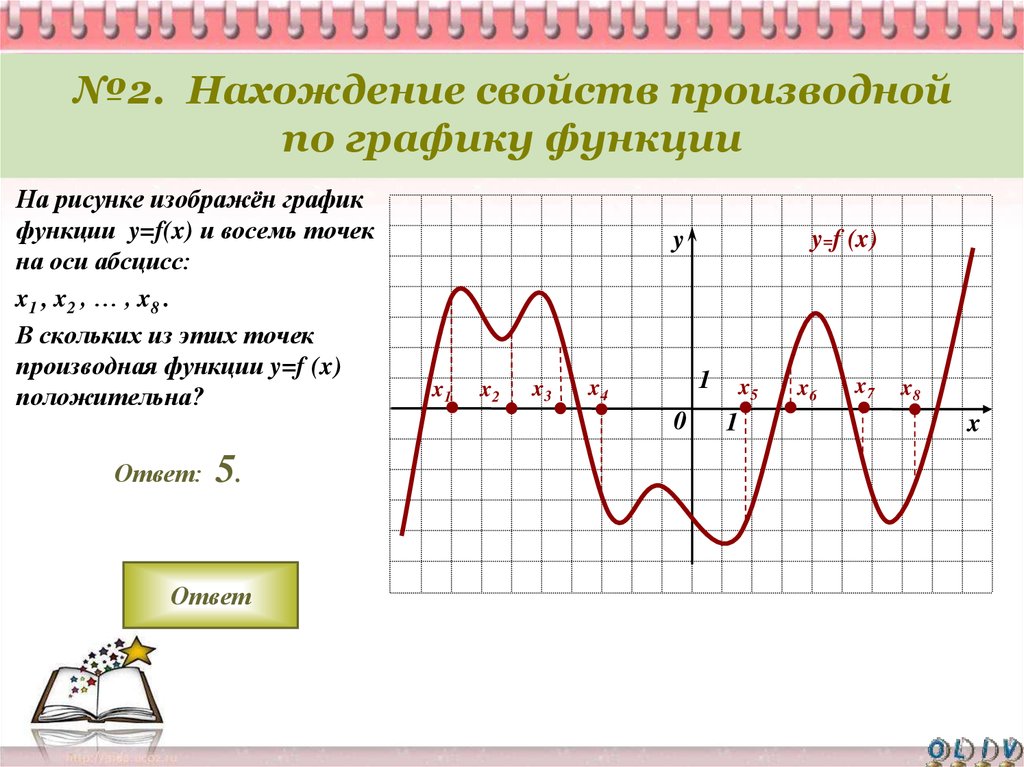
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

Определение 1

Угол наклона прямой y=kx+b называется  угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.

На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Определение 2

Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.

• Угол наклона прямой равняется 0 только при параллельности ох и  угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
• Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
• Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
• Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α – красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.

Определение 4

Получаем формулу для нахождения секущей вида:

k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) – это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).

Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Определение 5

Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0),  с наличием отрезка, который имеет множество значений х, близких к x0.

Пример 1

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке  с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y=2x сливается с прямой у=х+1.

Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.

Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.

Определение 6

Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.

Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.

То есть получаем, что f’(x) может существовать  в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной  в точке равняется производной  в точке x0. Тогда получаем, что kx=f'(x0).

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.

Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).

Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).

Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу – kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.

Пример 2

Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке  с координатами (1; 3) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.

Необходимо найти производную в точке со значением -1. Получаем, что

y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33

Значение f’(x) в точке касания является  угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда kx=tg αx=y'(x0)=33

Отсюда следует, что αx=arctg33=π6

Ответ: 

уравнение касательной приобретает вид

y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает  в увеличенном виде.

Пример 3

Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45

Если x0=1, тогда f’(x) не определена, но пределы записываются как  limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).

Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.

Для наглядности изобразим графически.

Пример 4

Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где

1. Касательная не существует;
2. Касательная располагается параллельно ох;
3. Касательная параллельна прямой y=85x+4.

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что

y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)

Необходимо продифференцировать функцию. Имеем, что

y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)

Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:

limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3

Вычисляем значение функции в точке х=-2, где получаем, что

1. y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
2. Касательная параллельна ох, когда угловой коэффициент равняется нулю. Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции  обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.

Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.

Решим:

-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2   15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞

Вычисляем соответствующие значения функции

y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43

Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

3. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 . 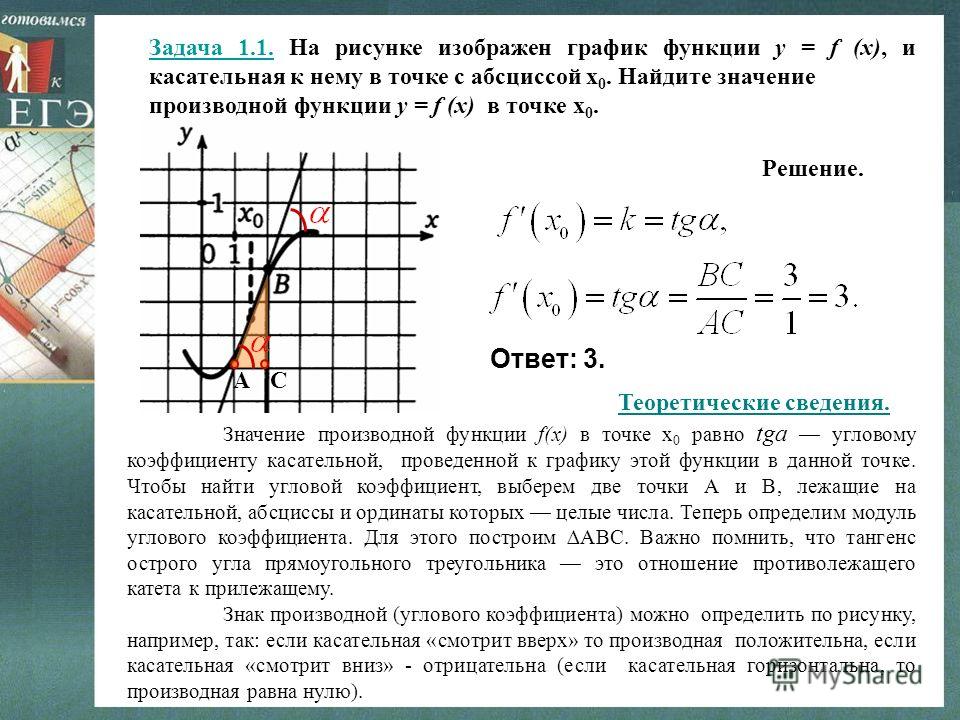Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0

Другое уравнение имеет два действительных корня, тогда

15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞

Перейдем к нахождению значений функции. Получаем, что

y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83

Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.

Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные  в точках -1; 415, 5; 83.

Возможно существование бесконечного количества касательных для заданных функций.

Пример 5

Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой  и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.

Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной  в точке
x0 получаем, что kx=y'(x0).  Из данного равенства найдем значения х для точек касания.

Получаем, что

y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk

32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk

x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z

Z- множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у:

y0=3cos32x0-π4-13

y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13

y0=3·1–192-13 или y0=3·-1–192-13

y0=45-13 или y0=-45+13

Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.

Ответ: необходимы уравнения запишутся как

y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности  с центром  в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.

Данное равенство может быть записано как объединение двух функций:

y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности  в точке x0; y0, которая располагается  в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.

Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а  в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.

Касательная к эллипсу

Когда эллипс имеет центр  в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter

Если  касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.

Пример 6

Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.

Решение

Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что

x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5

Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что

x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32

Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид

y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5

Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид

y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5

Графически касательные обозначаются  так:

Касательная к гиперболе

Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.

Гипербола может быть представлена в виде двух объединенных функций вида

y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter

В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.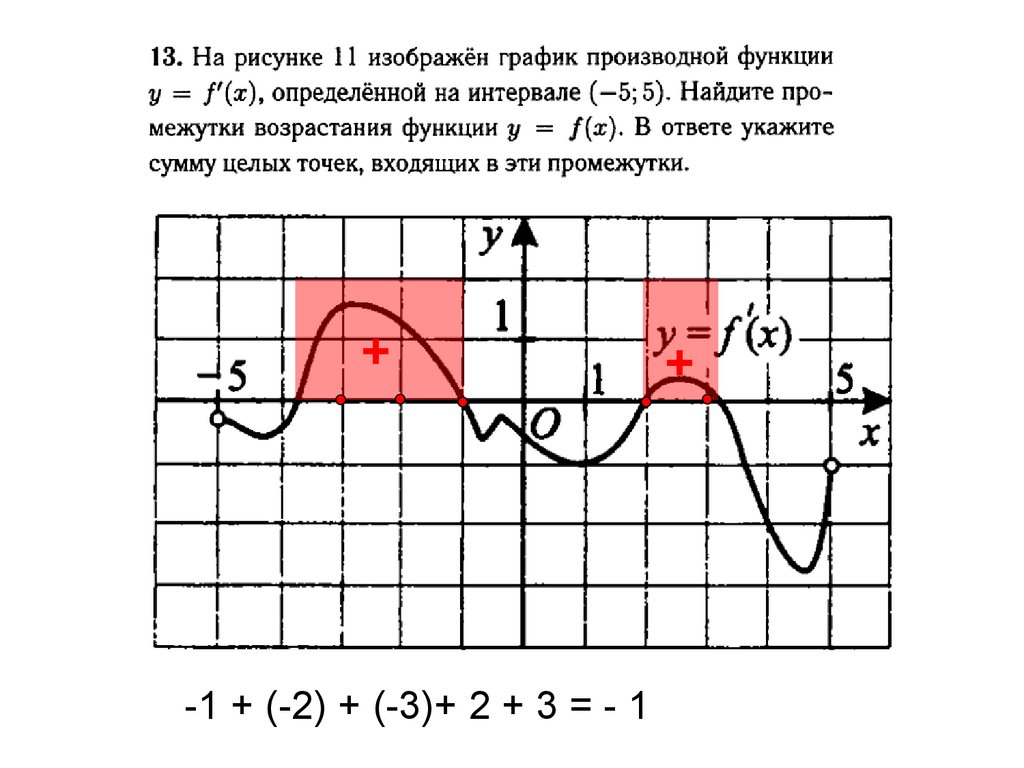

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Пример 7

Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.

Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

Получаем, что

y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3

Ответ: уравнение касательной можно представить как

y=-3·x-7-33-3=-3·x+43-3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0).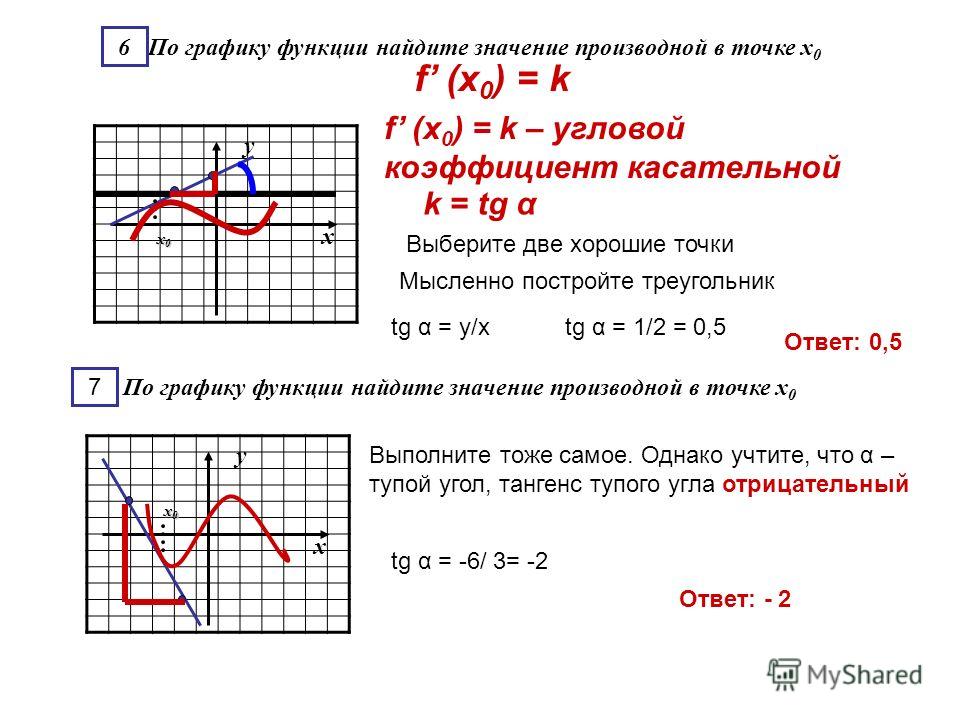 Такая касательная в вершине параллельна ох.

Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что

x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a

Графически изобразим как:

Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.

Пример 8

Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4

Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.

Получаем:

kx=y'(x0)=tg αx=tg 150°=-13

Отсюда определим значение х для точек касания.

Первая функция запишется как

y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.

Вторая функция запишется как

y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34

Имеем, что точки касания – 234; -5+34.

Ответ: уравнение касательной принимает вид

y=-13·x-234+-5+34

Графически изобразим это таким образом:

Методика восстановления графика производной по графику функции

Производная является функцией х; её вид можно приближенно восстановить по графику функции f(х). Проиллюстрируем это на конкретном примере. На рис.3, а изображен график функции f(х) Для того чтобы восстановить график , мысленно проследим, как ведет себя касательная к графику f(х) при «скольжении» точки касания слева направо.

На участке 1-2 крутизна касательной сначала возрастает, а затем убывает, в точке 2 касательная параллельна оси х. Следовательно, tgβ, оставаясь положительным, сначала возрастает, а затем убывает, доходя в точке 2 до нуля. Это поведение tgβ и отражено на участке 1-2 графика производной (рис.3,б). На участке 2-3 tgβ<0, а в точке 3 tgβ=0. Дальнейшие рассуждения предлагается провести читателю самостоятельно. В точках, где функция достигает максимума или минимума, производная обращается в нуль. Следовательно, чтобы найти, в каких точках функция достигает максимума или минимума, следует решить уравнение

=0. (4)

Техника отыскания производных

Найти производную функции (чаще говорят «продифференцировать функцию») можно, воспользовавшись определением (3). Однако если запомнить производные простейших функций, то отыскать производную любой элементарной функции можно с помощью нескольких несложных приемов. Производные простейших функций приведены в табл.1.

Таблица 1

№	f(х)			№	f(х)
1	хμ	μхμ-1		7	ctgx	-1/sin2x
2	ех	ех		8	arcsinx
3	lnx	1/x		9	arccosx
4	sinx	cosx		1	arctgx
5	cosx	-sinx		1	arcctgx
6	tgx	1/cos2x

Приведем основные правила дифференцирования более сложных выражений.

1. производная суммы функций равна сумме производных функций;

2) если функция f(х) является произведением функций f₁(х) и f₂(х), т.е. f(х)=f₁(х)· f₂(х), то

=(5)

В частности, если f₂(х)=А=сопst, то =А, поскольку производная от константы равна нулю;

3) производная «сложной» функции у(х)=f(φ(х)) вычисляется в два этапа. Сначала вычисляют производную f по φ, при этом временно рассматривают φ как независимую переменную (аргумент), а затем полученное выражение умножают на производную φ по х, т.е.

. (6)

Проиллюстрируем эти правила несколькими примерами дифференцирования функций.

П р и м е р 2: у=х²е^х, у является произведением функций =х², =е^х. Обратившись к табл.1, находим

и с помощью правила 2 формула (6)

.

П р и м е р 3: ; у является «сложной» функцией, которую можно представить в виде у=cosφ, φ=ax. Воспользовавшись формулой (7) и табл. 1, получим

.

П р и м е р 4: ; у представим в виде ,

, тогда .

П р и м е р 5: ; a,b,c=const. y(x) представляем в виде или, воспользовавшись свойством производной суммы, получим

.

Следует стремиться проводить дифференцирование в один прием, т.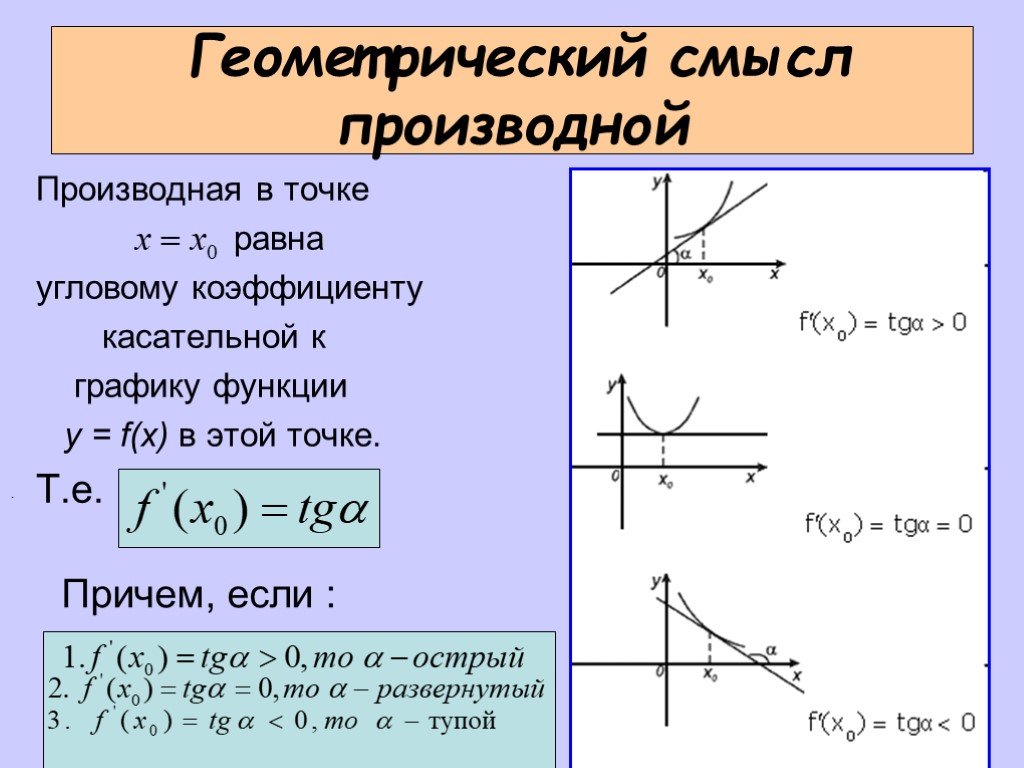 е. без промежуточных выкладок и без введения «промежуточных» функций φ(х), при этом все рассуждения, приводящие к ответу, должны делаться в уме.

Исчисление

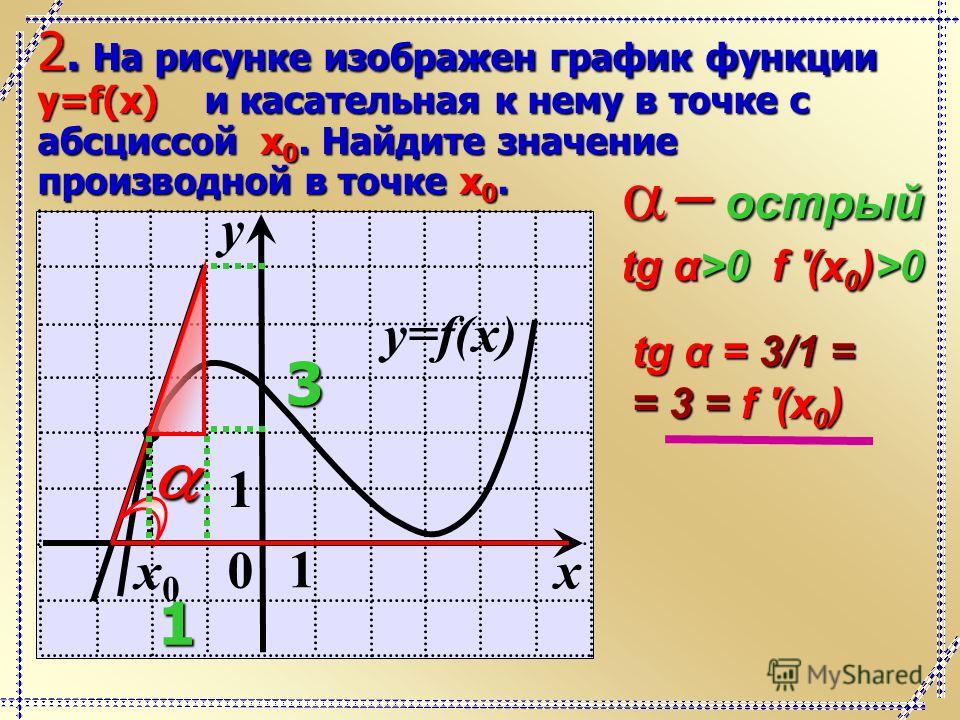
– Как я могу идентифицировать график функции и графики ее первой производной и второй производной?

спросил 6 лет, 3 месяца назад

Изменено 2 года, 3 месяца назад

Просмотрено 23 тысячи раз

$\begingroup$

Идентифицируйте графики $A$ (синий), $B$ (красный) и $C$ (зеленый) как графики функции и ее производных:

1. _____ является графиком функции
2. _____ — график первой производной функции
3. _____график второй производной функции

• исчисление
• производные

$\endgroup$

1

$\begingroup$

Вот список для подражания;

1. Проверить локальный минимум и максимум. Это будут нулевые значения в первой производной, поскольку их касательная параллельна оси x.
2. Проверить, увеличивается или уменьшается наклон графика в определенной точке. При увеличении производная будет находиться на положительной стороне оси y.
3. Посмотрите, как меняется знак первой производной, чтобы найти нули второй производной.

После списка ответ будет; е (х) = А е'(х)=В f”(х)=С 92}$.

$\endgroup$

$\begingroup$

функция имеет синий график.

первая производная равна нулю, когда функция достигает экстремума, ее график красный.

вторая производная дает информацию о кривизне. Она положительна, когда функция уменьшается, а сразу после этого возрастает. она отрицательна, когда функция возрастает, а затем убывает. его график зеленый.

$\endgroup$

$\begingroup$

Найдите, где одна всегда возрастает, а другая всегда соответствует положительной, и найдите, где функция убывает, чтобы найти соответствующую отрицательную функцию. График, который положительный и отрицательный, в то время как другой увеличивается и уменьшается, является производной функцией. График возрастания и убывания будет первообразной функцией.

$\endgroup$

Исчисление I. Форма графика, часть II

Онлайн-заметки Пола
Дом / Исчисление I / Применение производных / Форма графика, часть II

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4.6. Форма графика, часть II

В предыдущем разделе мы видели, как можно использовать первую производную функции, чтобы получить некоторую информацию о графике функции. В этом разделе мы рассмотрим информацию, которую вторая производная функции может дать нам о графике функции.

Прежде чем мы это сделаем, нам понадобится пара определений. Основная концепция, которую мы будем обсуждать в этом разделе, — вогнутость. Вогнутость легче всего увидеть на графике (чуть позже мы дадим математическое определение).

Итак, функция вогнута вверх , если она «открывается» вверх, и функция вогнута вниз , если она «открывается» вниз. Заметьте также, что вогнутость не имеет ничего общего с увеличением или уменьшением. Функция может быть вогнутой и либо возрастающей, либо убывающей. Точно так же функция может быть вогнутой вниз и либо возрастающей, либо убывающей.

Вероятно, это не лучший способ определить вогнутость, указав, каким образом она «открывается», поскольку это несколько расплывчатое определение. Вот математическое определение вогнутости.

Определение 1

Учитывая функцию \(f\left( x \right)\), тогда

1. \(f\left( x \right)\) равно вогнутой вверх на интервале \(I\) если все касательные к кривой на \(I\) находятся ниже графика \(f\left( x \right)\).
2. \(f\left( x \right)\) является вогнутым вниз на интервале \(I\), если все касательные к кривой на \(I\) находятся над графиком \(f\left ( х \справа)\).

Чтобы показать, что приведенные выше графики действительно имеют заявленную выше вогнутость, вот снова график (немного увеличенный, чтобы было понятнее).

Итак, как вы можете видеть, на двух верхних графиках все нарисованные касательные линии находятся под графиком функции и вогнуты вверх. На двух нижних графиках все касательные находятся над графиком функции и вогнуты вниз.

Опять же, обратите внимание, что вогнутость и аспект возрастания/убывания функции полностью разделены и не имеют ничего общего друг с другом. Это важно отметить, потому что учащиеся часто смешивают эти два понятия и используют информацию об одном для получения информации о другом.

Есть еще одно определение, от которого нам нужно избавиться.

Определение 2

Точка \(x = c\) называется точкой перегиба , если функция в этой точке непрерывна и вогнутость графика изменяется в этой точке.

Теперь, когда у нас есть все определения вогнутости, нам нужно добавить вторую производную. В конце концов, мы начали этот раздел с того, что собираемся использовать вторую производную для получения информации о графике. Следующий факт связывает вторую производную функции с ее вогнутостью. Доказательство этого факта находится в разделе «Доказательства производных приложений» главы «Дополнительно».

Факт

Учитывая функцию \(f\left( x \right)\), то

1. Если \(f”\left( x \right) > 0\) для всех \(x\) в некоторый интервал \(I\), тогда \(f\left( x \right)\) вогнут вверх на \(I\).
2. Если \(f”\left( x \right) < 0\) для всех \(x\) в некотором интервале \(I\), то \(f\left( x \right)\) вогнуто вниз на \(Я\).

Итак, этот факт говорит нам о том, что точками перегиба будут все точки, где вторая производная меняет знак. В предыдущей главе мы видели, что функция может менять знак, если она либо равна нулю, либо не существует. Обратите внимание, что мы работали с первой производной в предыдущем разделе, но тот факт, что функция может менять знак там, где она равна нулю или не существует, не имеет ничего общего с первой производной. Это просто факт, который применим ко всем функциям, независимо от того, являются ли они производными или нет.

Это, в свою очередь, говорит нам о том, что список возможных точек перегиба будет состоять из тех точек, где вторая производная равна нулю или не существует, поскольку это единственные точки, где вторая производная может изменить знак.

Будьте осторожны, однако не делайте предположения, что только потому, что вторая производная равна нулю или не существует, точка будет точкой перегиба. Мы узнаем, что это точка перегиба, только когда определим вогнутость с обеих сторон от нее. Это будет только точка перегиба, если вогнутость различна с обеих сторон точки.

Теперь, когда мы знаем о вогнутости, мы можем использовать эту информацию, а также информацию о возрастании/убывании из предыдущего раздела, чтобы получить довольно хорошее представление о том, как должен выглядеть график. Давайте посмотрим на пример этого.

Пример 1. Для следующей функции определите интервалы, на которых функция возрастает и убывает, и интервалы, на которых функция вогнута вверх и вогнута вниз. 3} + 3\] 92} – 1} \справа)\конец{выравнивание*}\]

Давайте начнем с увеличения/уменьшения информации, так как мы должны быть достаточно довольны этим после последнего раздела.

У этой функции есть три критические точки: \(x = – 1\), \(x = 0\) и \(x = 1\). Ниже находится числовая строка для увеличения/уменьшения информации.

Итак, похоже, мы получили следующие интервалы возрастания и убывания.

\[\begin{align*}{\mbox{По возрастанию: }} & – \infty < x < - 1{\mbox{и}}1 < x <\infty \\ {\mbox{По убыванию: }} & - 1 < х < 0, \, \, \, 0 < х < 1 \ конец {выравнивание *} \]

Обратите внимание, что из теста первой производной мы также можем сказать, что \(x = – 1\) является относительным максимумом, а \(x = 1\) – относительным минимумом. Также \(x = 0\) не является ни относительным минимумом, ни максимумом.

Теперь давайте получим интервалы, на которых функция вогнута вверх и вогнута вниз. Если подумать, этот процесс почти идентичен процессу, который мы используем для определения интервалов возрастания и убывания. Единственное отличие состоит в том, что мы будем использовать вторую производную вместо первой.

Первое, что нам нужно сделать, это определить возможные точки перегиба. Это будут случаи, когда вторая производная равна нулю или не существует. Вторая производная в этом случае является многочленом и поэтому будет существовать везде. В следующих точках он будет равен нулю.

\[x = 0,\,\,x = \pm \frac{1}{{\sqrt 2}} = \pm \,0,7071\]

Как и в случае с возрастающей и убывающей частями, мы можем нарисовать числовую линию вверх и использовать эти точки, чтобы разделить числовую линию на области. Мы знаем, что в этих областях вторая производная всегда будет иметь один и тот же знак, поскольку эти три точки являются единственными местами, где функция май сменить знак. Поэтому все, что нам нужно сделать, это выбрать точку из каждой области и подставить ее во вторую производную. Тогда вторая производная будет иметь этот знак во всей области, из которой исходит точка

Вот числовая прямая для этой второй производной.

Итак, похоже, что мы получили следующие интервалы вогнутости.

\[\begin{align*}{\mbox{Вогнутый вверх: }} & – \frac{1}{{\sqrt 2}} < x < 0{\mbox{and}}\frac{1}{{\ sqrt 2 }} < x < \infty \\ {\mbox{Вогнутый вниз: }} & - \infty < x < - \frac{1}{{\sqrt 2}}{\mbox{ и }}0 < x < \ frac {1} {{\ sqrt 2}} \ end {align *} \]

Это также означает, что

\[x = 0,\,\,x = \pm \frac{1}{{\sqrt 2}} = \pm 0,7071\]

— все точки перегиба.

Вся эта информация может быть немного ошеломляющей при построении графика. Первое, что мы должны сделать, это получить некоторые отправные точки.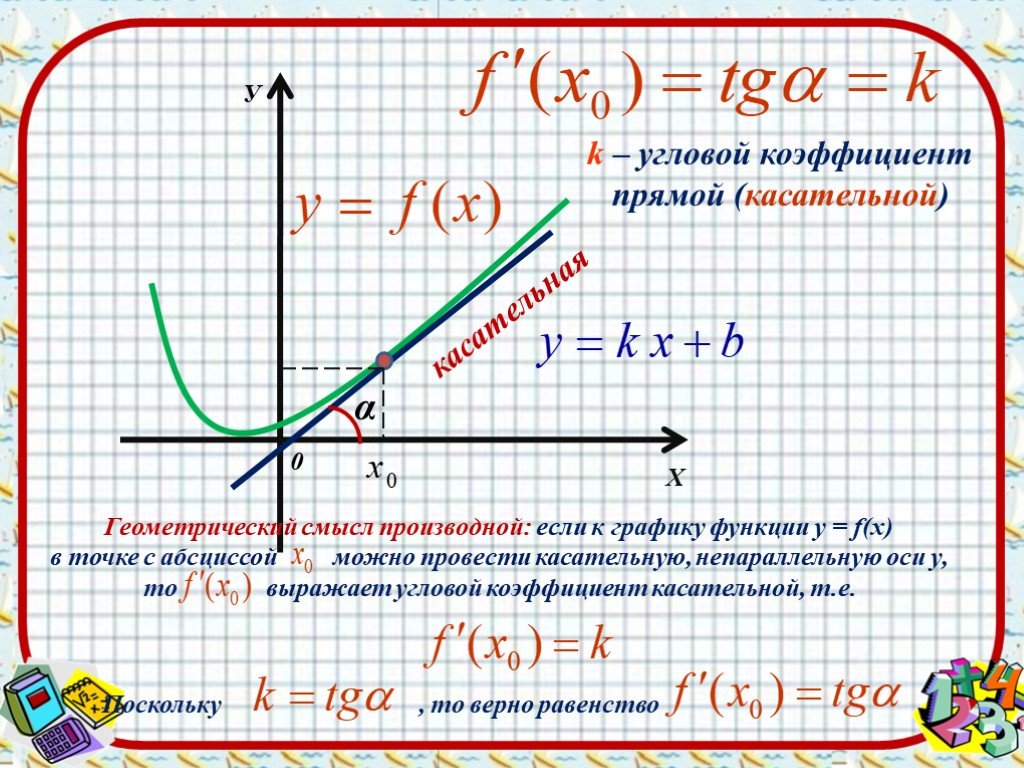 Критические точки и точки перегиба являются хорошими отправными точками. Итак, сначала нарисуйте эти точки.

С этого момента есть несколько способов приступить к рисованию графика. Способ, который мы считаем самым простым (хотя вы можете и не делать этого, и это совершенно нормально….), состоит в том, чтобы начать с увеличения/уменьшения информации и начать рисовать график только с этой информации, как мы делали в предыдущем разделе. Однако, в отличие от предыдущего раздела, на этот раз, когда мы рисуем возрастающую или убывающую часть кривой, мы также будем обращать внимание на вогнутость кривой.

Итак, если мы начнем с \(x < - 1\), мы знаем, что у нас есть возрастающая функция. В то же время мы знаем, что мы также должны быть вогнутыми в этом диапазоне. Итак, мы можем начать с рисования возрастающей кривой, которая также вогнута вниз, пока мы не достигнем \(x = - 1\).

В этот момент график начинает уменьшаться и будет продолжать уменьшаться, пока мы не достигнем \(x = 1\). Однако по мере того, как мы уменьшаем вогнутость, необходимо переключиться на вогнутость вверх при \(x \приблизительно – 0,707\), а затем снова переключиться на вогнутость вниз при \(x = 0\) с окончательным переключением на вогнутость вверх при \(x \ примерно 0,707\).

Как только мы достигаем \(x = 1\), график начинает увеличиваться и по-прежнему остается вогнутым, и оба эти поведения сохраняются для остальной части графика.

Объединив всю эту информацию, мы получим следующий график функции.

Мы можем использовать предыдущий пример, чтобы проиллюстрировать другой способ классификации некоторых критических точек функции как относительных максимумов или относительных минимумов.

Обратите внимание, что \(x = – 1\) является относительным максимумом и что в этой точке функция вогнута вниз. Это означает, что \(f”\left( { – 1} \right)\) должно быть отрицательным. Точно так же \(x = 1\) является относительным минимумом, и в этой точке функция вогнута вверх. Это означает, что \(f”\left( 1 \right)\) должно быть положительным.

Как мы вскоре увидим, нужно быть очень осторожным с \(x = 0\). В этом случае вторая производная равна нулю, но на самом деле это не будет означать, что \(x = 0\) не является относительным минимумом или максимумом. Чуть позже мы увидим некоторые примеры этого, но сначала нам нужно позаботиться о другой информации.

Здесь также важно отметить, что все критические точки в этом примере были критическими точками, в которых первая производная была равна нулю, и это необходимо для того, чтобы это работало. Мы не сможем использовать этот тест в критических точках, где производная не существует.

Вот тест, который можно использовать для классификации некоторых критических точек функции. Доказательство этого теста находится в разделе «Доказательства производных приложений» главы «Дополнительно».

Тест второй производной

Предположим, что \(x = c\) является критической точкой \(f\left( x \right)\) такой, что \(f’\left( c \right) = 0\) и что \(f”\left( x \right)\) непрерывно в области вокруг \(x = c\). Тогда

1. Если \(f”\left( c \right) < 0\), то \(x = c\) является относительным максимумом.
2. Если \(f”\left( c \right) > 0\), то \(x = c\) является относительным минимумом.
3. Если \(f”\left( c \right) = 0\), то \(x = c\) может быть относительным максимумом, относительным минимумом или ни тем, ни другим.

Важно отметить третью часть теста второй производной. Если вторая производная равна нулю, критическая точка может быть любой. Ниже приведены графики трех функций, каждая из которых имеет критическую точку при \(x = 0\), вторая производная всех функций равна нулю при \(x = 0\), и все же показаны все три возможности. 93}\), и этот график не имел ни относительного минимума, ни относительного максимума в точке \(x = 0\).

Итак, мы видим, что нужно быть осторожным, если попадем в третий случай. В тех случаях, когда мы попадаем в этот случай, нам придется прибегнуть к другим методам классификации критической точки.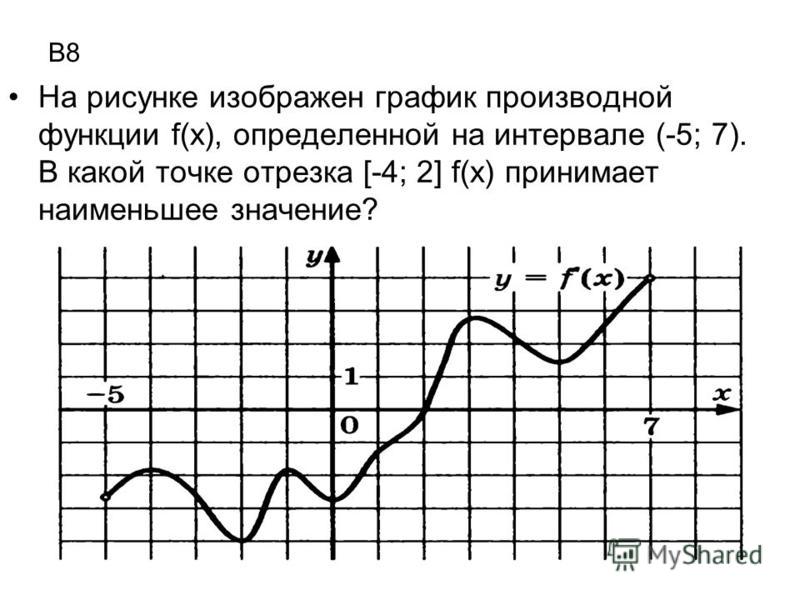 Обычно это делается с помощью теста первой производной.

Давайте вернемся назад и посмотрим на критические точки из первого примера и применим к ним тест второй производной, если это возможно.

93} – 30х\]

Три критические точки (\(x = – 1\), \(x = 0\) и \(x = 1\)) этой функции являются критическими точками, где первая производная равна нулю, поэтому мы знаем, что у нас, по крайней мере, есть шанс, что Второй Производный Тест сработает. Значение второй производной для каждого из них равно

. \[h”\left( { – 1} \right) = – 30\hspace{0.5in}h”\left( 0 \right) = 0\hspace{0.5in}h”\left( 1 \ справа) = 30\]

Вторая производная в точке \(x = – 1\) отрицательна, так что согласно тесту второй производной эта критическая точка является относительным максимумом, как мы видели в первом примере. Вторая производная в точке \(x = 1\) положительна, поэтому мы имеем здесь относительный минимум по тесту второй производной, как мы также видели в первом примере.

В случае \(x = 0\) вторая производная равна нулю, поэтому мы не можем использовать критерий второй производной для классификации этой критической точки. Обратите внимание, однако, что мы знаем из теста первой производной, который мы использовали в первом примере, что 9{\ гидроразрыва {4} {3}}}}} \]

Критические точки,

\[t = \frac{{18}}{5} = 3,6\hspace{0,5 дюйма}t = 6\]

Также обратите внимание, что мы не сможем использовать критерий второй производной для \(t = 6\) для классификации этой критической точки, поскольку в этой точке производная не существует. Чтобы классифицировать это, нам понадобится информация о возрастании/убывании, которую мы получим, чтобы набросать график.

Однако мы можем использовать тест второй производной, чтобы классифицировать другую критическую точку, так что давайте сделаем это, прежде чем мы приступим к работе над эскизом. Вот значение второй производной при \(t = 3,6\).

\[f”\влево( {3,6} \вправо) = – 1,245 < 0\]

Итак, согласно тесту второй производной \(t = 3,6\) является относительным максимумом.

Теперь давайте продолжим работу, чтобы получить набросок графика и заметить, что когда у нас будет информация о возрастании/убывании, мы сможем классифицировать \(t = 6\).

Вот числовой ряд для первой производной.

Таким образом, согласно тесту первой производной мы можем убедиться, что \(t = 3,6\) на самом деле является относительным максимумом. Мы также можем видеть, что \(t = 6\) является относительным минимумом.

Будьте внимательны и не думайте, что критическая точка, которую нельзя использовать в тесте второй производной, не будет относительным экстремумом. Теперь мы ясно видим, как на этом примере, так и в обсуждении после того, как у нас есть тест, что только потому, что мы не можем использовать тест второй производной или тест второй производной ничего не говорит нам о критической точке, не означает что критическая точка не будет относительным экстремумом.