Кроме того, существует оператор деления «в строку» [?], который по функции аналогичен обычному оператору деления. Все эти операторы находятся на вкладке Математика –> Операторы, но намного быстрее использовать для их ввода клавиатуру:
Использование бинарных операторов в Mathcadаналогично их использованию в обычном калькуляторе. Сначала щелкните мышью в пустой области, введите первое число, затем оператор, затем второе число. Для вывода результата следует нажать [=]. Например, ввод выражения [2/3=] приведет к следующему результату:
При использовании бинарных операторов Mathcad использует обычные правила старшинства операций. Попробуйте вычислить следующие выражения:
Правила старшинства операций и скобки
Используя скобки, можно изменить правила старшинства операций. В вычислениях скобки набираются сразу парой. В математической области введите открывающуюся скобку [(], и появится пара скобок:
В появившийся местозаполнитель вводите символы дальше, например, [3+7]:
Нажмите на стрелку вправо на клавиатуре, чтобы выделить закрывающую скобку, затем введите оператор деления: [?/]
Закончите вычисление, набрав [10=]:
Следующие выражения можно вычислить, набрав следующие комбинации клавиш [(2+3/5?*7=] и [2+3/5??*7=]:
При вводе бинарных операторов без чисел Вы получите оператор и два местозаполнителя:
При вводе сложных выражений часто бывает проще сначала ввести скобки и операторы, а затем вводить числа:
При вводе сложных выражений можно допустить ошибку.
Как их можно исправить, мы обсудим в уроке 6 «Редактирование выражений». А пока просто удаляйте неправильные выражения, выделяя их и нажимая [Delete].
Унарные операторы
Существует несколько «унарных» операторов, применение которых требует только одно число: квадратный корень [\], модуль [|], факториал [!]. Примеры:
Оператор корня может быть как унарным, так и бинарным. Если не заполнять местозаполнитель над знаком корня, используется квадратный корень:
Оператор [-] также может использоваться для двух случаев: как оператор вычитания и как оператор отрицания. При внимательном рассмотрении видно, что оператор отрицания находится ближе к числу, следующему за ним:
Константы
Стандартные константы Mathcad (доступны на вкладке Математика –> Операторы и символы –> Константы):
Странная, но полезная константа – NaN (Not a Number– Не число). Ее можно использовать, чтобы избегать пропущенные или ошибочные значения:
Многие другие константы также находятся на вкладке Математика –> Операторы и символы –> Константы.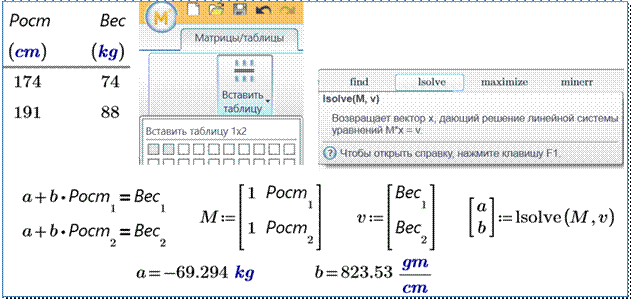
В следующем уроке мы научимся определять собственные константы.
Функции
Mathcad включает в себя большое число функций. Весь список можно увидеть, нажав Функции –> Все функции:
Вот пример некоторых использования некоторых из них (обратите внимание, что у некоторых из них не совсем привычные названия, например, функцию арккосинуса следует набирать acos, а не arccos):
Форматирование чисел
Чтобы изменить формат числа, следует щелкнуть по числу и выбрать нужный формат на вкладке Форматирование формул –> Результаты. Первое меню включает в себя пять форматов: Общий, Десятичный, Научный, Проектирование, Процент:
Второе меню позволяет настроить число знаков после запятой.
Продемонстрируем эти настройки на следующих числах (здесь используется оператор присваивания :=, о котором мы поговорим в следующем уроке):
Чаще всего используют общий формат – число от 0.001 до 1000 представляется в привычной записи, для остальных чисел используется стандартная запись (число от 1 до 10, умноженное на 10
Десятичный формат представляет все числа в привычной десятичной форме:
Научный формат представляет все числа в стандартной записи:
На него похож инженерный формат (формат Проектирование), но показатель степени кратен трем:
В процентном формате число умножается на 100 и отображается со знаком процента:
Резюме
- Щелкните мышью в пустой области, чтобы начать ввод математического выражения.
- Введите выражение с помощью операторов сложения [+], вычитания [-], умножения [*] и т.д.
- Используйте скобки для изменения правила старшинства операций. При вводе одной скобки на экране появляется сразу пара скобок. Чтобы войти или выйти из скобок, используйте стрелки или щелчок мышью.
- Чтобы составить сложное выражение, сначала наберите скобки и операторы.
- Три полезных унарных оператора: отрицание [-], модуль [|], факториал [!]. Оператор отрицания использует тот же символ, что и оператор вычитания.
- В Mathcad встроено большое число констант. Мы рассмотрели лишь ?, eи ?.
- В Mathcad есть множество функций. Большую часть из них можно ввести с клавиатуры, например, [sin(] для синуса, [exp(] для экспоненты и т.д.
- При необходимости, отформатируйте число с помощью вкладки Форматирование формул –> Результаты.
About Павел Демидов
Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.
View all posts by Павел Демидов →
Mathcad
15 новинок КОМПАС-3D V15
Урок 5. Переменные и функции в Mathcad
Лабораторная работа №2 Нахождение корней уравнения в MathCad
Цель работы: нахождение корней уравнения в программе MathCad с использованием встроенных функций
Указания к выполнению лабораторной работы:
I Нахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad .
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3.
Создать цикл из точек интервала, на
котором определяются корни, и вычислить
в этих точках функцию f(х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5.
Задать для независимой переменной х начальное приближение, которое выбирается
как значение точки пересечения кривых f(х) и х0.
Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой
переменной х,
для которой f(х) равняется 0)
и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х)
а) б)
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2.
Записать как вектор v все коэффициенты уравнения, расположить
их в порядке увеличения степеней.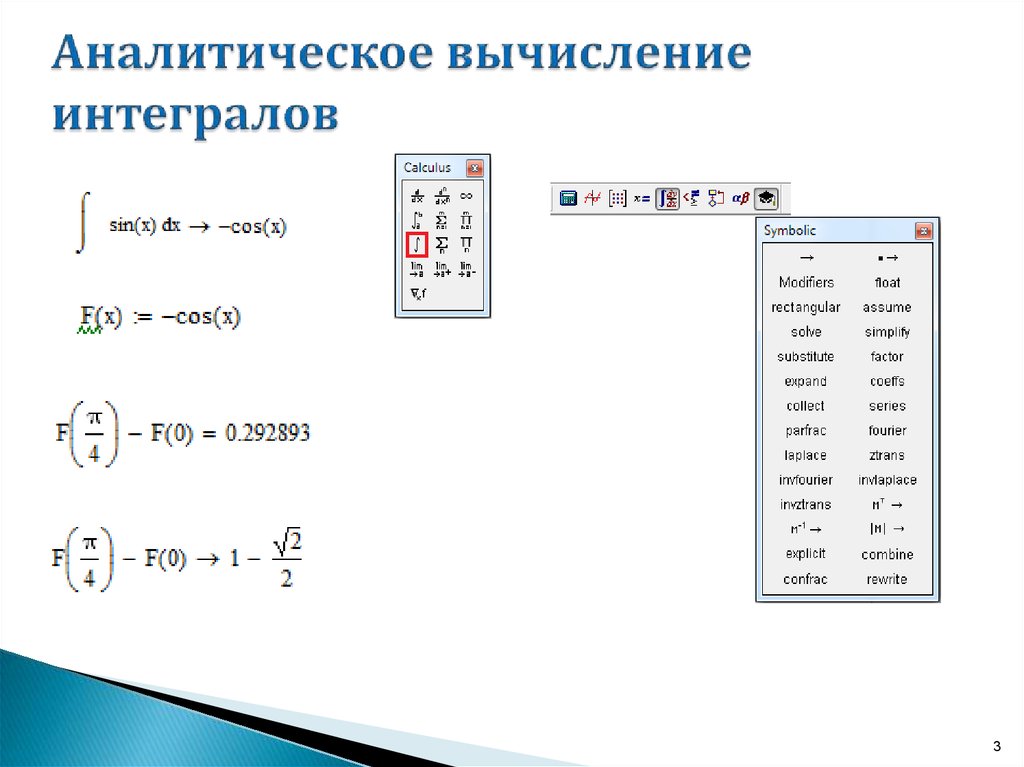
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора rT.
4. Для интервала нахождения корня и количества элементов вектора rT создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4.
Выделить переменную, относительно
которой решается уравнение.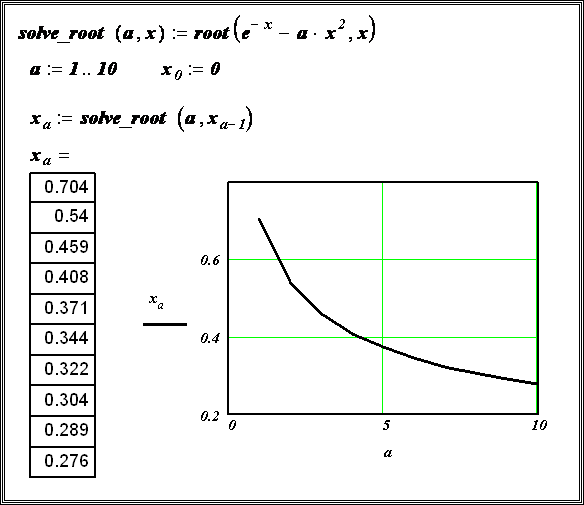
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr( x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
№ варианта | Интервал нахождения корней | Уравнение |
1 | 2 | 3 |
1 | [-1; 3] | x3-2,92x2+1,4355x+0,791=0 |
2 | [-2; 3] | x3-2,56x2-1,325x+4,395=0 |
3 | [-3,5; 2,5] | x3+2,84x2-5,606x-14,766=0 |
4 | [-2,5; 2,5] | x3+1,41x2-5,472x-7,38=0 |
Продолжение
табл.
1.1
1 | 2 | 3 | |
5 | [-1,6; 1,1] | x3+0,85x2-0,432x+0,044=0 | |
6 | [-1,6; 1,6] | x3-0,12x2-1,478x+0,192=0 | |
7 | [-1,6; 0,8] | x3+0,77x2-0,251x-0,017=0 | |
8 | [-1,4; 1] | x3+0,88x2-0,3999x-0,0376=0 | |
9 | [-1,4; 2,5] | x3+0,78x2-0,827x-0,1467=0 | |
10 | [-2,6; 1,4] | x3+2,28x2-1,9347x-3,90757=0 | |
11 | [-2,6; 3,2] | x3-0,805x2-7x+2,77=0 | |
12 | [-3; 3] | x3-0,345x2-5,569x+3,15=0 | |
13 | [-2; 3,4] | x3-3,335x2-1,679x+8,05=0 | |
14 | [-1; 2,8] | x3-2,5x2+0,0099x+0,517=0 | |
15 | [-1,2; 3] | x3-3x2+0,569x+1,599=0 | |
16 | [-2,5; 2,5] | x3-2,2x2+0,82x+0,23=0 | |
17 | [-1,2; 4,6] | x3-5x2+0,903x+6,77=0 | |
18 | [-1; 7,4] | x3-7,5x2+0,499x+4,12=0 | |
19 | [-1. | x3-7,8x2+0,899x+8,1=0 | |
20 | [-3,4; 2] | x3+2x2-4,9x-3,22=0 | |
21 | [-3,4; 1,2] | x3+3x2-0,939x-1,801=0 | |
22 | [-4,6; 3,0] | x3+5,3x2+0,6799x-13,17=0 | |
23 | [-2,4; 8,2] | x3-6,2x2-12,999x+11,1=0 | |
24 | [-3,2; 2,7] | x3-0,34x2-4,339x-0,09=0 | |
25 | [-1; 3] | x3-1,5x2+0,129x+0,07=0 | |
26 | [-1; 3] | x3-5,5x2+2,79x+0,11=0 | |
27 | [-1; 3] | x3-5,7x2-6,219x-2,03=0 | |
28 | [-1; 3] | x3-3,78x2-7,459x-4,13=0 | |
29 | [-1; 3] | x3-5x2-9,9119x+0,01=0 | |
30 | [-1; 3] | x3-7x2-1,339x-7,55=0 | |
6;
9]Пример
І Для уравнения найти корни на интервале [-1, 1], шаг
изменения переменной х равен 0.
1.
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции и х0=0.
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых и х0=0.
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).
Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения найти корни на интервале [-1.1, 7.1] , шаг изменения переменной х равен 0.1.
1.
Создать вектор из коэффициентов
уравнения, используя панель управления
Matrix (Матрица) (рис.19) и задав один столбец
и четыре строки для коэффициентов
уравнения.
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора rT, транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:
4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения
найти корни с использованием символьных
решений уравнений.
1. Записать левую часть уравнения
.
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:
IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr( x). Корень будет найдено.
5.
Аналогические действия выполнить для
двух других корней уравнения, поскольку
уравнения третьей степени имеет не
больше трех корней.
Например, 16 — это число в совершенной квадратной форме, и его квадратный корень может быть равен 4 или -4. Есть много методов, которые используются в математике, чтобы найти квадратный корень числа.
Работа и использование квадратного корня в Matlab с примерами
Matlab выполняет все математические функции, поэтому существуют также методы нахождения квадратного корня из числа. В Matlab мы используем функцию sqrt(), чтобы найти квадратный корень числа или каждого элемента, определенного в массиве. Входные аргументы, которые используются в функции, могут быть скалярными, векторными, массивными или многомерными массивами. Они также могут быть положительными, отрицательными или сложными по своей природе. Если ввод сложный или отрицательный по своей природе, то он приводит к комплексному числу. 9Пример №1
-3 -2 -1 0 1 2 3
A = SQRT (Y)
Выход:
(0,0000 + 1,7320i) (0,0000 + 1,4142i) (0,0000 + 1,0000 (0,0000 + 0,0000i) (1,0000 + 0,0000i) (1,4142 + 0,0000i) (1,7320+0,0000i)
Пример №2
Y = -5: -3
Таким образом, вход находится в форме 1*4
-5 -4 -3
A = SQRT (Y)
Выход:
(0,0000+2,2360I) (0,000014
(0,0000+2,2360I) (0,000014
(0,0000+2,2360i) +2.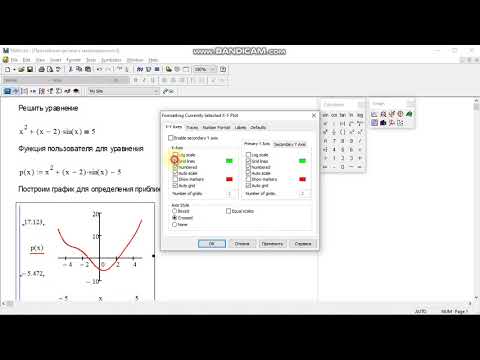
0000i) (0.0000+1.7320i)
Мы знаем, что если ввод массива отрицательный, то он приводит к комплексному числу. В приведенных выше двух примерах мы видим, что диапазон состоит из отрицательных и положительных чисел, поэтому его выход представляет собой комплексное число. Некоторые операции в Matlab отличаются от стандарта IEEE, например, квадратный корень из отрицательного нуля равен 0 в Matlab, тогда как в IEEE он равен -0, квадратный корень из значений меньше нуля приводит к комплексному числу в Matlab, в то время как то же самое недоступно в IEEE.
Если мы хотим найти квадратный корень только из положительных целых чисел в массиве, мы можем использовать функцию realsqrt() в Matlab. В отличие от функции sqrt(), она выдает сообщения об ошибках, когда мы передаем ввод как отрицательное или комплексное число. Итак, если мы хотим просмотреть результат отрицательного или комплексного числа, то предпочтительнее использовать функцию sqrt(). Размер вывода и размер ввода должны быть одинаковыми, если мы используем realsqrt().
Пример 3
Входные данные представляют собой матрицу 4*4 с именем A
Y=realsqrt(A)
Вывод:
В приведенном выше примере вычисляется квадратный корень каждого элемента матрицы. Входные аргументы могут быть матрицей, массивом, вектором, скаляром или многомерным массивом, и они должны быть положительными и действительными целыми числами. Существуют различные свойства квадратного корня в Matlab, которые следует отметить:
Квадратный корень из любого четного числа, являющегося полным квадратом, всегда должен быть четным.
Например: 16,36,64,100 и т.д.
Здесь 16, 36, 64 и 100 — четные числа, являющиеся полным квадратом, а квадратный корень из этих чисел — 4, 6, 8 и 10, которые также являются четными числами.
Умножение квадратных корней одного и того же числа приводит к положительному целому числу, в то время как квадратные корни числа также можно умножать и давать результат.
Например: √4 * √4 = 4
√3 * √2=√6
Квадратный корень любого нечетного числа, являющегося полным квадратом, всегда должен быть нечетным.
Например: 25,9,49,81
Здесь 25,9,47,81 — все квадраты нечетных чисел, а квадратный корень из этих чисел — 5,3,7,9, которые также являются нечетными числами. Единичная цифра элемента не может быть 3,2,8 или 7, чтобы быть полным квадратом.
Заключение
Квадратные корни широко используются в Matlab для различных бизнес-требований. Они широко используются при решении любых квадратных уравнений, таких темах машинного обучения, как вычисление стандартного отклонения и дисперсии. Таким образом, это важная функция во всех математических областях.
Рекомендуемые статьи
Это руководство по квадратному корню в Matlab. Здесь мы обсуждаем работу и использование квадратного корня в Matlab с примерами. Вы также можете просмотреть другие наши рекомендуемые статьи, чтобы узнать больше —
- Операции с матрицей
- Синтаксис встроенной функции
- Векторы в Matlab
- Математические свойства C#
- Изучите квадратный корень в Python
преобразование в и из формы с пересечением оси Y и стандартной формы | бесплатные электронные рабочие листы по математике для средней школы с пиццерией | упрощение радикальных уравнений | добавление рабочих листов с целыми числами |
простая алгебра факторинга | бесплатных печатных рабочих листа для старшеклассника | Калькулятор показателей степени | как писать математические уравнения в слайдах PowerPoint |
простых вопроса о способностях | упрощение рациональных алгебраических выражений | репетитор по математике | образцы задач по геометрии с решениями |
“Длинное деление” MathType | Рабочий лист сокращения дроби | клен решение двух уравнений | Рабочие листы полиномиальных функций для 5-го класса |
математическое исключение с делением | математические мелочи | бесплатных печатных рабочих листа ks3 | как найти домен функций на ti83 plus |
бесплатный калькулятор для решения уравнений с двумя переменными | радикальный калькулятор java | как использовать знак обратного логарифма на калькуляторе TI-83 | мгновенные решения по алгебре |
решить конические уравнения | прошлые документы pdf | калькулятор умножения рациональных выражений | “Том по математике для третьего класса” |
ПРОСТЫЕ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ И УРАВНЕНИЯ | алгебра поможет упростить калькулятор | весёлых рабочих листа по английскому языку ks3 | решатель сложных дробей |
освоение физики ответы | предварительные алгебраические перестановки и комбинации | бесплатная алгебра 2 | математические мелочи |
предварительная алгебра, упрощение положительных показателей | словесных задач на системы уравнений | заполнение квадратного учебного пособия | помощь по математике “сложные проценты” рабочий лист Excel |
практические тесты по логарифмическим уравнениям | градиент, листы наклона с ответами | Решение кубических уравнений на ТИ-83 | Рабочие листы с точками построения |
Калькулятор квадратных уравнений | вавилонская рекурсивная формула квадратного корня | математических стихотворения в радикалах | Тензорный анализ, бесплатная книга в формате pdf |
Рабочие листы по начальной математике | саксонская математика 87 второе издание тест 17, форма А | объединение сходных терминов | совета по решению задач перестановки и комбинации на уровне колледжа |
добавление вычитания целых чисел, рабочий лист | алгебра для колледжа БЕСПЛАТНОЕ РУКОВОДСТВО ПО ОБУЧЕНИЮ | два дифференциальных уравнения “второго порядка” Matlab | Помощник по алгебре и математике |
самая сложная задача по алгебре | mcdougal littell алгебра 2 стандартизированная тестовая рабочая тетрадь ответы | перевести дроби в децимели | бесплатных саттестов с ответами |
рабочих листа для четвероклассника выучить | стихотворения по тригонометрии | математические уравнения | Рабочий лист уклона с ключом |
рабочий лист уклона средней школы | решить и построить график рациональных функций | онлайн-решатель уравнений | бесплатная онлайн предварительная альгерба для начинающих |
БЕСПЛАТНЫЕ РАБОЧИЕ ТАБЛИЦЫ – ЧИСЛОВЫЕ ШАБЛОНЫ – 5 КЛАСС | листы задач по математике | ГДЕ МОЖНО ПРОЙТИ ОНЛАЙН-ТЕСТ ПО МАТЕМАТИКЕ ДЛЯ 9-ГО КЛАССА С ОТВЕТАМИ? | факторинг полинома 3-го порядка |
математический график скачать | решение нелинейного дифференциального уравнения | логарифмическое уравнение реального мира | Начальная статистика (2-е издание) Чит |
бесплатных элементарных вопросов и ответов по триве | Printable Year 11 Алгебра суммы | решить уравнения Matlab | бесплатных тестовых распечаток |
| Калькулятор равных десятичных дробей | факторинг функции с TI-83 плюс | бесплатных математических рабочих листа – нахождение наименьших общих кратных | бесплатных рабочих листа с показателями деления и умножения |
решение уравнений с несколькими переменными | системы уравнений реальной жизни | макдугал литтел американцы схема глава | Руководство по решателю уравнений ti 86 |
Экспоненциальная форма Free Algebra Solutions | предварительная алгебра для чайников | бесплатный онлайн калькулятор для деления и умножения десятичных дробей | год 9 практический тест по математике au |
реальных примера функции извлечения квадратного корня | магазин формул ти-84 плюс | ti-89 ввод уравнений с двумя переменными | скачать тест на пригодность |
т тест”+викторина+университет”+ | освоение физики ответы | Математика 3 класс | glencoe алгебра 1 ответы |
Калькулятор уравнения коэффициента | 11+ математических статей для печати | Excel формула преобразования дроби в десятичные дроби | игра сложных неравенств |
деление на факторинг в кубе | порядок действий casio fx-115ms | решать трехчлены | переменные: бесплатные рабочие листы по алгебре для старших классов |
Калькулятор упрощения квадратного корня | Решения простых задач “динамика конструкций” экзамен “скачать бесплатно” | Бесплатные рабочие листы по алгебре для печати | алгебраические стихотворения |
Glencoe Глава 9 ответы pdf | код Matlab для нахождения квадратного корня | онлайн калькулятор решить переменную | «Ответы на интегрированный курс математики II» |
алгебраизатор + скачать | наибольший общий делитель и наименьший общий кратный лист | Калькулятор рациональных уравнений | логарифмические шутки |
Бесплатный простой график с рабочим листом | триг скат холма | Читы калькулятор феникс | Рабочий лист начальных выражений алгебры |
игровые функции/ квадратичные формулы | как найти область определения радикальных полиномиальных уравнений | Matlab “нелинейная” система уравнений | самых сложных математических уравнения |
Шаги по нахождению десятичной дроби на калькуляторе TI-83 | aptitude Вопросительный лист | вводная и промежуточная помощь по алгебре | новые математические мелочи |
вычисление квадратного корня | радикальное упрощение онлайн | простых шага для решения и упрощения математических выражений | Решение уравнения в программе c |
План урока Метод исключения | как решить задачу статистики на TI-83 | последние документы об общих способностях | общая кратная диаграмма |
ТИ-83 Калькулятор кубического корня | быстрая помощь по элементарной алгебре | Тесты способностей + pdf | Математика для 7 класса |
математических рабочих листов, решающих уравнения с помощью вычитания | рабочих листа по алгебре для печати | вопросы экзамена “Учет затрат” | скачать бесплатно решение первой главы основ физики (шестое издание) |
математический десятичный | решатель рациональных выражений и приложений | Упражнения на дроби и рациональные числа и рациональные выражения | дроби в порядке от наименьшей к наибольшей |
правил экспоненты анимации | алгебра факторинга | как преобразовать десятичную дробь в дробь | алгебраизатор |
бесплатное сравнение порядковых дробей десятичных дробей рабочий лист | бесплатные онлайн тесты по математике для 8 класса | определитель наибольшего общего делителя три числа | калькулятор упрощения рациональных выражений |
год 10 карточек математические определения | Тригонометрический коэффициент масштабирования | освоить физику взломать | вопроса о квадратном корне + KS2 |
Рабочие листы с уравнениями для 5-го класса, которые можно распечатать бесплатно | метод десятичной точности Java | Алгебра 2 радикальные выражения шаг за шагом | простой способ определить общий знаменатель |
урок наибольший общий множитель gcf powerpoint 7th prime | алегра проблема | Бесплатные образцы бухгалтерских листов | дополнительные математические заметки |
ОНЛАЙН-ТЕСТ ПО АЛГЕБРЕ ДЛЯ 9 КЛАССА 2 | завершение квадратных правил | химические уравнения | Комбинация против элементарной перестановки |
ти-84 уроки | glencoe алгебра 2 оценки | мелочи по алгебре | бесплатный онлайн вступительный экзамен по математике 6 класса |
Правила идентификации TI-84 | nj. | нахождение квадратичной модели на TI 86 | онлайн-калькулятор алгебраических выражений |
ti 83 графический калькулятор онлайн | бесплатная викторина с множественным выбором, уменьшающая рабочий лист | упростить, разложив на множители | рабочих листа алгебра гленко я |
решение уравнения, содержащего калькулятор дробей | программы ти-84 фактор9 | www.take g.e.d.test онлайн | Математика 11 класс предыдущие работы |
Умножить десятичную дробь на | упрощение квадратного корня | калькулятор алгебра несколько переменных | БИНОМАЛЬНАЯ ТЕОРИЯ |
бесплатных рабочих листа kumon | дроби распределительного имущества | схемы, отношения и планы уроков по алгебраическому мышлению для второклассников | программная алгебра |
распечатать тесты по математике для 8 класса | саксонская предварительная алгебра помощь | алгебра нахождение наклона | Оценка рабочих листов выражения 5-й класс |
конвертер расширенной формы математического преобразования | домашняя парабола для 10 класса | факторизация стала проще | решенные листы теста способностей |
бесплатная печатная алгебра для начинающих | как ввести 4-й квадратный корень | упрощение выражений с использованием рабочих листов степени | простой показатель степени рабочий лист |
graphing. |
pre-alg.com