Устранение неопределённости «единица в степени бесконечность»
⇐ ПредыдущаяСтр 6 из 9Следующая ⇒
Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки.
Выделим существенные моменты формулы:
1) Речь идёт только об определённости и никакой другой.
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы, которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Готово.
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы, преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием.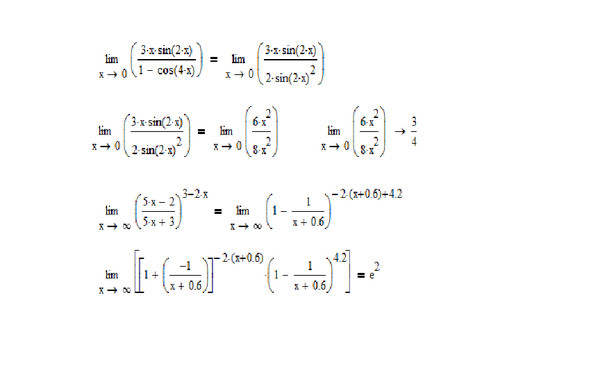
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим.
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты: .
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ.
! Примечание
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Решения и ответы:
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
Разделим числитель и знаменатель на :
Пример 4
Разделим числитель и знаменатель на
Примечание: самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание: слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя.
Пример 10
Пример 12
Умножим и разделим на сопряженное выражение:
Пример 13
Умножим и разделим на сопряженное выражение:
Разделим числитель и знаменатель на :
Пример 15
Проведём замену:
Если , то .
Пример 17
Проведём замену:
Если , то .
Далее используем формулу приведения , тригонометрическую формулу и первый замечательный предел:
Пример 20
Используем формулу
Пример 22
Примечание: бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Сложные пределы
Пример 1
Найти предел, не пользуясь правилом Лопиталя
При подстановке «единицы» в выражение под знаком предела, получается неопределённость , которая устраняется стандартным методом: числитель и знаменатель необходимо разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:
Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:
Рассмотрим многочлен положительной степени. Если число является корнем уравнения , то многочлен делится на многочлен без остатка. В результате деления получается многочлен , при этом: .
Да, многочлены, как и числа, можно делить друг на друга. Термины те же:
– делимое;
– делитель;
– частное.
Начнём оформлять решение и детально разберём техническую сторону вопроса:
Разложим числитель и знаменатель на множители.
Числитель: поскольку число является корнем уравнения , то многочлен делится на многочлен без остатка. Деление выполняется столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон:
Обратите внимание на очень важную вещь: в многочлене в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
Теперь в углу нужно разоблачить незнакомца :
Каким он должен быть? Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :
Очевидно, что данному критерию удовлетворяет . Действительно, . Записываем первый трофей:
Далее нашего героя необходимо умножить на делитель :
, а результат записать во второй строке слева:
Проводим отчёркивание и из первой строки почленно вычитаем вторую строку:
Если подробно, (ноль под чертой не пишем),
Сносим сверху следующее слагаемое:
Алгоритм идёт на следующий круг. Снова ищем одночлен , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :
В данном случае . Рисуем его справа под чертой:
и умножаем на делитель :
, результат записываем в 4-ую строку:
Ещё раз отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем), :
Сносим сверху последнее слагаемое:
Организуем завершающий цикл. Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :
Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :
Уравнению соответствует корень , который записываем справа под чертой:
Умножаем на делитель :
, результат записываем в 6-ую строку:
Выполняем завершающее отчёркивание и почленное вычитание:
В итоге получился ноль, и это значит, что все вычисления выполнены правильно. Иными словами, многочлен поделился на без остатка. Таким образом:
Желающие могут раскрыть скобки в правой части и убедиться, что получится исходный многочлен .
Рассмотренный алгоритм на самом деле не сложен, и рука набивается довольно быстро.
Знаменатель. Разборки аналогичны. Так как число является корнем уравнения , то соответствующий многочлен делится на без остатка:
В итоге
Открываем решение и записываем всё, что нажито непосильным трудом:
Приключения продолжаются – после сокращения неопределённость не устранена. Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление.
Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление.
Умножаем на делитель :
, результат записываем ниже, отчёркиваем и проводим почленное вычитание:
В остатке получился ноль, значит, деление выполнено верно. Таким образом:
Аналогично расправляемся со знаменателем:
То есть
Снова открываем решение и получаем окончательный ответ:
Выполним проверку. Дважды используем правило Лопиталя:
Сравните трудоёмкость двух способов решения. Думаю, теперь вам понятно, почему запрещают применять правило Лопиталя
ример 2
Найти предел, не пользуясь правилом Лопиталя
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Вернёмся к другому известному способу решения пределов, повысив их сложность:
Пример 3
Найти предел, не пользуясь правилом Лопиталя
Неопределённость ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:
1) для устранения разности домножаем числитель и знаменатель на сопряженное выражение ;
2) для устранения разности домножаем числитель и знаменатель на сопряженное выражение .
Далее дважды используется формула . Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.
Оформляем:
Оба вышеуказанных действия выгоднее выполнить «за один присест». Умножим числитель и знаменатель на сопряженные выражения:
Проверим решение по правилу Лопиталя:
Пример 4
Найти предел, не пользуясь правилом Лопиталя
Это более сложный пример для самостоятельного решения.
Иногда в пределах рассматриваемого типа приходится использовать не только формулу разности квадратов , но и формулу разности кубов:
Пример 5
Найти предел
Неопределённость устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах №№11-13 урокаМетоды решения пределов. Только здесь работает формула разности кубов:
В данном случае . И, согласно формуле, для разности сопряженным выражением будет вот этот вот страх:
Умножим и разделим на сопряженное выражение, чтобы использовать формулу :
Тоже знакомая картина….
Старшая степень числителя: 2
Старшая степень знаменателя: 2
Таким образом, числитель и знаменатель одного порядка роста, и сразу можно сказать, что предел равен конечному числу.
Разделим числитель и знаменатель на :
Готово.
Пример 6
Найти предел
Это пример для самостоятельного решения. После умножения/деления на сопряженное выражение и упрощений предел будет сведён к случаю Примеров №№1-3 статьи о бесконечно малых функциях. Полное решение и ответ в конце урока.
А сейчас обещанные на уроке Методы решения пределов плюшки на замену переменной. Повышенной сложности:
Пример 7
Найти предел, не пользуясь правилом Лопиталя
Аргумент стремится к не самому распространённому числу: , с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроемтригонометрическую таблицу, и выпишем следующие значения:
Проверим предел на наличие неопределённости:
Да, действительно, два бублика.
Проведём предварительный анализ. В пределе находятся тригонометрические функции, и решение, скорее всего, сведётся к первому замечательному пределу. В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.
Но перед заменой целесообразно провести некоторое упрощение выражения. В пределе есть тангенс, а работать с этой функцией неудобно (как и с котангенсом тоже). Таким образом, сначала лучше свести всё дело к синусам и косинусам. Пример свирепый, поэтому я закомментирую каждый шаг:
(1) Используем формулу .
(2) Дробь числителя приводим к общему знаменателю.
(3) Избавляемся от трёхэтажности дроби, а также от косинуса, указывая, что .
(4) Выносим константу за значок предела.
Неопределённость никуда не делась, но от тангенса мы избавились, что уже является небольшим достижением
Проведем замену переменной:
Если , то
Ну и ещё – из замены нужно выразить: .
(5) Выполняем подстановку в соответствии с выполненной заменой.
(6) Используем тригонометрические формулы:
(7) Используя значения , упрощаем выражение.
(8) Раскрываем скобки в числителе и знаменателе.
(9) Приводим подобные слагаемые в числителе.
(10) Константу –2 выносим за значок предела. В знаменателе переставляем слагаемые.
И снова два нуля, причём не видно как решать предел дальше…. Но если хорошенько пошуршать в тригонометрических формулах, то история закончится счастливым концом:
(11) Используем формулы половинного угла: . В числителе избавляемся от косинуса, указывая, что .
(12) В знаменателе выносим за скобки .
(13) Сокращаем числитель и знаменатель на .
Забавно, что всё обошлось даже без замечательного предела.
Не знаю, кто и на каком месте будет рвать себе волосы, но правило Лопиталя даёт ответ фантастически быстро:
Пример 8
Найти предел, не пользуясь правилом Лопиталя
Это пример для самостоятельного решения. В тригонометрической таблице нет информации об отрицательных значениях угла. Понятие ориентации угла дано в статьеПростейшие задачи с прямой на плоскости. Наглядная иллюстрация с конкретными примерами также фигурирует при нахождении аргумента комплексного числа. Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и – это один и тот же угол. Таким образом:
Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и – это один и тот же угол. Таким образом:
Полное решение и ответ в конце урока
Как-то незаслуженно оказались забыты степени:
Пример 9
Найти предел
На повестке дня неопределённость , и решение, очевидно, нужно свести к замечательной формуле . Но в нашем пределе нет единицы, только одинокий косинус. Что делать? Организуем!
(1) Приводим основание степени к виду , для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом:
(2) В целях применения 2-го замечательного предела возводим основание в степень , и, чтобы ничего не изменилось – в обратную степень .
(3) Используем замечательный предел .
(4) Теперь в показателе необходимо устранить неопределённость 0:0. Сначала меняем знак в числителе: , минус выносим из предела.
(5) В числителе используем формулу .
(6) Искусственно преобразуем знаменатель, чтобы получить два первых замечательных предела.
Очень кстати в одном примере подвернулись сразу оба замечательных предела, и после их повторения во второй части статьи рассмотрим:
Замечательные пределы с экспонентой и логарифмом
На практике чаще встречаются пределы и особенно их частные случаи . Предела лично ни разу не видел, а может быть, и видел, да не помню.
Иногда перечисленные пределы называют третьим, четвёртым и пятым замечательным пределом, но своё негативное отношение к избыточной нумерации я уже высказал на урокеПравила Лопиталя, поэтому пусть это будут «просто» замечательные пределы без номеров.
Сама техника решения мало чем отличатся от первого замечательного предела:
Пример 10
Найти предел, не пользуясь правилом Лопиталя
Чтобы использовать замечательный предел необходимо применить уже знакомый искусственный приём: в знаменателе умножаем и делим на 2:
Вот и всё. Напоминаю, что в качестве параметра «альфа» может выступать не только переменная «икс», но и сложная функция, лишь бы она стремилась к нулю. В рассмотренном примере .
В рассмотренном примере .
Короткий закусочный предел для самостоятельного решения:
Пример 11
Найти предел, не пользуясь правилом Лопиталя
Заметьте, что условие задачи не ограничивает нас в выборе действий, примеры можно было решить и через замечательные эквивалентности:
(эквивалентность ).
(эквивалентности )
Какой способ выбрать? Рекомендую всё-таки решать через замечательные пределы (конечно, если пример не дико сложный) – выглядит солиднее.
Существенная особенность пределов состоит в том, что при перестановке числителя и знаменателя результаты тоже «переворачиваются»:
Пример 12
Найти предел, не пользуясь правилом Лопиталя
Как говорится, мал пример да заковырист….
Решаем:
На первом шаге нужно перейти к новой переменной ТАК, чтобы она стремилась к нулю.
Проведём замену: , тогда:
Если , то
Для самостоятельного решения:
Пример 13
Найти предел, не пользуясь правилом Лопиталя
Если возникли затруднения на начальном этапе, пожалуйста, вернитесь к Примеру №9.
Разберём напоследок что-нибудь посложнее. Типовой и довольно распространённый предел:
Пример 14
Найти предел, не пользуясь правилом Лопиталя
Сначала полное решение, потом комментарии:
(1) На первых шагах избавляемся от синуса. Умножим числитель и знаменатель на .
(2) Используем первый замечательный предел , где . Константу выносим из предела.
(3) Проводим искусственное преобразование числителя. Возьмите его на заметку, разность экспонент раскручивается именно так.
(4) Почленно делим числитель на знаменатель.
(5) Числитель и знаменатель первой дроби умножаем на 2. Числитель и знаменатель второй дроби умножаем на –3.
(6) В обеих дробях используем замечательный предел , после чего остались от козлика рожки да ножки.
Используя правило Лопиталя, выполним проверку:
Заключительный пример посвящен раритету . Если его не встречал я, то это не значит, что его не встретите вы. Встретите. Причём, прямо сейчас =)
Встретите. Причём, прямо сейчас =)
Пример 15
Найти предел, не пользуясь правилом Лопиталя
Это пример для самостоятельного решения.
Всего примеров получилось таки 15-ть, а не 20-ть, и ваш покорный слуга постарался отобрать самые распространенные вещи. Желающие ознакомиться с другими пределами, могут закачать соответствующий архив решений в банке задач по высшей математике. Однако должен предупредить, будьте осторожнее – некоторые экземпляры не то, чтобы сильно сложные, но точно рождены воспалённым сознанием. Я постарался разобрать тему без навороченных нелепых примеров, поскольку убеждён, что студент должен мучиться с удовольствием =)
И приснится вам сегодня правило Лопиталя =)
Решения и ответы:
Пример 2
Разложим числитель и знаменатель на множители.
В числителе используем формулу суммы кубов :
Знаменатель:
Таким образом:
Пример 4
Умножим числитель и знаменатель на сопряженные выражения.
Разложим числитель и знаменатель на множители:
Пример 6
Умножим числитель и знаменатель на сопряженное выражение, используем формулу разности кубов :
Пример 8
Используем формулу :
Проведём замену переменной:
Если , то
Используем тригонометрическую формулу :
Используем формулы половинного аргумента :
Пример 11
Умножаем числитель и знаменатель на , используем замечательный предел , где . В конце используем 1-ый замечательный предел:
Пример 13
Пример 15
⇐ Предыдущая123456789Следующая ⇒
Поиск по сайту:
Тема 20 раскрытие неопределенности вида «ноль на ноль».
 Раскрытие неопределенности «бесконечность на бесконечность»
Раскрытие неопределенности «бесконечность на бесконечность»КОНСПЕКТ 20
20.1 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Пример 1
Решить предел Сначала попробуем подставить -1 в дробь:В данном случае получена так называемая неопределенность.
Общее правило:если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытиянужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Разложим числитель на множители.
Пример 2
Вычислить предел
Разложим числитель и знаменатель на множители.
Числитель: Знаменатель:,
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий
тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас
добавятся корни.
Единственное, помимо многочленов, у нас
добавятся корни.
Пример 3
Найти предел
Умножим числитель и знаменатель на сопряженное выражение.
20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример 4
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.
Теперь
смотрим на знаменатель и тоже находим
в
старшей степени:Старшая
степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: Для пометок лучше использовать простой карандаш.
Конечно,
можно ничего этого не делать, но тогда,
возможно, преподаватель отметит недочеты
в решении либо начнет задавать
дополнительные вопросы по заданию. А
оно Вам надо?
А
оно Вам надо?
Пример 5
Найти предел Снова в числителе и знаменателе находимв старшей степени:Максимальная степень в числителе: 3 Максимальная степень в знаменателе: 4 Выбираемнаибольшеезначение, в данном случае четверку. Согласно нашему алгоритму, для раскрытия неопределенностиделим числитель и знаменатель на. Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пример 6
Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 (можно записать как) Для раскрытия неопределенностинеобходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким
образом, при раскрытии неопределенности
вида
у
нас может получитьсяконечное число,
ноль или бесконечность.
ПРАКТИКУМ 20
ЗАДАНИЕ N 1Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение:Если вместо переменнойпоставить значение 7, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 2Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение:Если вместо переменнойпоставить значение 0, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 3Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение:Если вместо переменнойпоставить значение 6, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 4Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение:Так какито имеет место неопределенность видаДля ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на. Тогда, зная, чтополучим:
ЗАДАНИЕ N 5Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение:Так какито
имеет место неопределенность видаДля
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на. Тогда, зная, чтополучим:
Тогда, зная, чтополучим:
САМОСТОЯТЕЛЬНАЯ РАБОТА 20
ЗАДАНИЕ N 1Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 2Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 3Тема: Раскрытие неопределенности вида “ноль на ноль”
ЗАДАНИЕ N 4Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
ЗАДАНИЕ N 5Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”Предел функцииравен …
ЗАДАНИЕ N 6Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение пределов через раскрытие неопределённостей — Студопедия
Поделись
Неопределённость вида и вида – самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
Большая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Неопределённость вида
Пример 1. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или “супермалому числу”.
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Пример 2. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем “икс” под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо “икса”.
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Неопределённость вида
Пример 3.Раскрыть неопределённость и найти предел .
Решение. В числителе – разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе – квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Пример 4. Раскрыть неопределённость и найти предел
Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 5. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Пример 6. Вычислить
Решение: воспользуемся теоремами о пределах
Ответ: 11
Пример 7. Вычислить
Решение: в этом примере пределы числителя и знаменателя при равны 0:
; . Получили , следовательно, теорему о пределе частного применять нельзя.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3.
Квадратный трехчлен в числителе разложим по формуле , где x1 и х2 – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на (x-2), затем применим теорему 3.
Ответ:
Пример 8. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности, поэтому при непосредственном применении теоремы 3 получаем выражение , которое представляет собой неопределенность. Для избавления от неопределенности такого вида следует разделить числитель и знаменатель на старшую степень аргумента. В данном примере нужно разделить на х:
Ответ:
Пример 9. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т. е. х3:
е. х3:
Ответ: 2
Пример 10. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х5:
=
числитель дроби стремится к 1, знаменатель к 0, поэтому дробь стремится к бесконечности.
Ответ:
Пример 11. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х7:
Ответ: 0
Производная.
Производной функции y = f(x) по аргументу x называется предел отношения ее приращения y к приращению x аргумента x, когда приращение аргумента стремится к нулю: . Если этот предел конечен, то функция y = f(x)называется дифференцируемой в точке х. Если же этот предел есть , то говорят, что функция y = f(x) имеет в точке х бесконечную производную.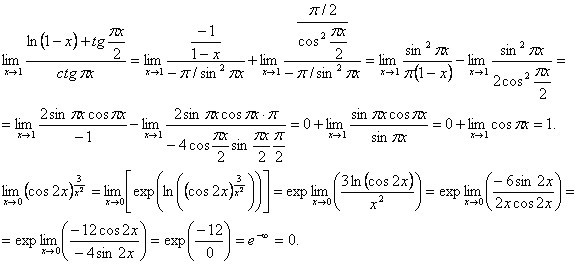
Производные основных элементарных функций:
1. (const)=0 9.
2. 10.
3. 11.
4. 12.
5. 13.
6. 14.
7.
8.
Правила дифференцирования:
a)
б)
в)
г) , где
Пример 1. Найти производную функции
Решение: Если производную от второго слагаемого находим по правилу дифференцирования дроби, то первое слагаемое представляет собой сложную функцию, производная которой находится по формуле:
, где , тогда
При решении были использованы формулы: 1,2,10,а,в,г.
Ответ:
Пример 21. Найти производную функции
Решение: оба слагаемых – сложные функции, где для первого , , а для второго , , тогда
Ответ:
Приложения производной.
1. Скорость и ускорение
Пусть функция s(t) описывает положение объекта в некоторой системе координат в момент времени t. Тогда первая производная функции s(t) является мгновенной скоростью объекта:
Тогда первая производная функции s(t) является мгновенной скоростью объекта:
v=s′=f′(t)
Вторая производная функции s(t) представляет собой мгновенное ускорение объекта:
w=v′=s′′=f′′(t)
2. Уравнение касательной
y−y0=f′(x0)(x−x0),
где (x0,y0) − координаты точки касания, f′(x0) − значение производной функции f(x) в точке касания.
3. Уравнение нормали
y−y0=−1f′(x0)(x−x0),
где (x0,y0) − координаты точки, в которой проведена нормаль, f′(x0) − значение производной функции f(x) в данной точке.
4. Возрастание и убывание функции
Если f′(x0)>0, то функция возрастает в точке x0. На рисунке ниже функция является возрастающей при xx2.
Если f′(x0)<0, то функция убывает в точке x0 (интервал x1<x<x2).
Если f′(x0)=0 или производная не существует, то данный признак не позволяет определить характер монотонности функции в точке x0.
5. Локальные экстремумы функции
Функция f(x) имеет локальный максимум в точке x1, если существует такая окрестность точки x1, что для всех x из этой окрестности выполняется неравенство f(x1)≥f(x).
Аналогично, функция f(x) имеет локальный минимум в точке x2, если существует такая окрестность точки x2, что для всех x из этой окрестности выполняется неравенство f(x2)≤f(x).
6. Критические точки
Точка x0 является критической точкой функции f(x), если производная f′(x0) в ней равна нулю или не существует.
7. Первый достаточный признак существования экстремума
Если функция f(x) возрастает (f′(x)>0) для всех x в некотором интервале (a,x1] и убывает (f′(x)<0) для всех x в интервале [x1,b), то функция f(x) имеет локальный максимум в точке x1.
Аналогично, если функция f(x) убывает (f′(x)<0) для всех x из интервала (a,x2] и возрастает (f′(x)>0) для всех x из интервала [x2,b), то функция f(x) имеет локальный минимум в точке x2.
8. Второй достаточный признак существования экстремума
Если f′(x1)=0 и f′′(x1)<0, то функция f(x) имеет локальный максимум в точке x1.
Если f′(x2)=0 и f′′(x2)>0, то функция f(x) имеет локальный минимум в точке x2.
9. Выпуклость функции
Функция f(x) является выпуклой вверх (или вогнутой) в точке x0, если производная f′(x) в этой точке убывает (промежуток x Аналогично, функция f(x) является выпуклой вниз (или просто выпуклой) в точке x0, если производная f′(x) в этой точке возрастает (промежуток x>x3).
10. Достаточные условия выпуклости функции вверх и вниз
Если f′′(x0)>0, то функция f(x) выпукла вниз в точке x0.
Если f′′(x0)<0, то функция f(x) выпукла вверх в точке x0.
Если f′′(x0)=0 или производная не существует в точке x0, то данный признак не позволяет определить характер выпуклости функции в этой точке.
11. Точка перегиба
Если первая производная f′(x3) существует в точке x3, а вторая производная f′′(x3) меняет знак при переходе через x=x3, то точка (x3,f(x3)) называется точкой перегиба графика функции f(x). Если вторая производная f′′(x3) существует в точке перегиба, то она равна нулю: f′′(x3)=0. 3 — возведение в степень x + 7 — сложение x — 6 — вычитание
3 — возведение в степень x + 7 — сложение x — 6 — вычитание
www.kontrolnaya-rabota.ru
Правило Лопиталя с примерами
Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет правило Лопиталя. В пределе отношение функций можно заменить отношением производных этих функций. Т.е. надо производную числителя разделить на производную знаменателя и от этой дроби взять предел.
1. Неопределенность 0/0. Первое п.Л.
Если = 0, то , если последний существует.
2. Неопределенность вида ∞/∞ Второе п. Л.
Нахождение пределов такого типа называется раскрытием неопределенностей.
Если = ∞, то , если последний существует.
3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.
Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.
Пример 1. В этом примере неопределенность 0/0
Пример 2. Здесь ∞/∞
В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.
Пример 3. Вид неопределенности 0⋅∞ .
Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.
Пример 4 Вычислить предел функции
Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел
Для получения ответа надо е возвести в степень -1, получим e -1 .
Пример 5. Вычислить предел от если x → 0
Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:
= = = =
= =
Пример 6 Решить
Решение. Вид неопределенности ∞/∞, раскрыв ее получим
= = = 0.
В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.
Пример 7. Вычислить предел
Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =
Тогда lnA = = = = 2.
Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .
Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.
Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.
Эта функция не имеет предела, т.к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.
www.mathelp.spb.ru
В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида $ 0/0 $ и $ \infty/\infty $ . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Содержание
Точная формулировка Править
Правило говорит, что если функции $ f(x) $ и $ g(x) $ обладают следующим набором условий:
тогда существует $ \lim_> = \lim_> $ . При этом теорема верна и для других баз (для указанной будет приведено доказательство).
История Править
Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализ бесконечно малых», изданном в 1696 году. В предисловии к этому сочинению Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованнного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704.
Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованнного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704.
Доказательство Править
1. Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида $ \left(\frac\right) $ ).
Поскольку мы рассматриваем функции $ f $ и $ g $ только в правой проколотой полуокрестности точки $ a $ , мы можем непрерывным образом их доопределить в этой точке: пусть $ f(a)=g(a)=0 $ . Возьмём некоторый $ x $ из рассматриваемой полуокрестности и применим к отрезку $ [a,\;x] $ теорему Коши. По этой теореме получим:
но $ f(a)=g(a)=0 $ , поэтому $ \forall x\, \exists c \in [a,\;x]\!:\frac=\frac$ .
Дальше, записав определение предела отношения производных и обозначив последний через $ A $ , из полученного равенства выводим:
$ \forall \varepsilon>0\, \exists \delta>0\, \forall x(x-a $ \forall M > 0\, \exists \delta>0\, \forall x(x-a M) $ для бесконечного,
что является определением предела отношения функций.
2. Докажем теорему для неопределённостей вида $ \left(\frac\right) $ .
Пусть, для начала, предел отношения производных конечен и равен $ A $ . Тогда, при стремлении $ x $ к $ a $ справа, это отношение можно записать как $ A+\alpha $ , где $ \alpha $ — O(1). Запишем это условие:
$ \forall\varepsilon_\, \exists \delta_\, \forall x(x-a
Зафиксируем $ t $ из отрезка $ [a,\;a+\delta_1] $ и применим теорему Коши ко всем $ x $ из отрезка $ [a,\;t] $ :
Для $ x $ , достаточно близких к $ a $ , выражение имеет смысл; предел первого множителя правой части равен единице (так как $ f(t) $ и $ g(t) $ — константы, а $ f(x) $ и $ g(x) $ стремятся к бесконечности). Значит, этот множитель равен $ 1+\beta $ , где $ \beta $ — бесконечно малая функция при стремлении $ x $ к $ a $ справа. Выпишем определение этого факта, используя то же значение $ \varepsilon $ , что и в определении для $ \alpha $ :
$ \forall \varepsilon_\, \exists \delta_\, \forall x(x-a
Получили, что отношение функций представимо в виде $ (1+\beta)(A+\alpha) $ , и $ \left|\frac-A\right| $ \forall M>0\, \exists \delta_>0\, \forall x(x-a 2M) $ .
В определении $ \beta $ будем брать $ \varepsilon_ \frac\cdot 2M=M\Rightarrow \lim_>=+\infty $ .
Для других баз доказательства аналогичны приведённым.
ru.math.wikia.com
Правило Лопиталя: теория и примеры решений
Правило Лопиталя и раскрытие неопределённостей
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
(),
то предел отношения этих функций равен пределу отношения их производных
Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(),
().
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 9. Вычислить
Вычислить
.
Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.
Пример 10. Вычислить
.
Подсказка. Здесь правило Лопиталя придётся применять трижды.
Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Пример 11. Вычислить
.
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
Вычисляем предел выражения в показателе степени
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
.
Раскрытие неопределённостей вида «бесконечность минус бесконечность»
Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т. д.
д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
function-x.ru
Ноль в бесконечной степени. Устранение неопределённости «единица в степени бесконечность. Понятие предела в математике
КОНСПЕКТ 20
20.1 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Пример 1
Решить предел Сначала попробуем подставить -1 в дробь:В данном случае получена так называемая неопределенность.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытиянужно разложить числитель и знаменатель на множители .
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Разложим числитель на множители.
Пример 2
Вычислить предел
Разложим
числитель и знаменатель на множители.
Числитель: Знаменатель:,
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 3
Найти предел
Умножим числитель и знаменатель на сопряженное выражение.
20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример 4
Вычислить предел
Согласно
нашему правилу попытаемся подставить
бесконечность в функцию. Что у нас
получается вверху? Бесконечность. А что
получается внизу? Тоже бесконечность.
Таким образом, у нас есть так называемая
неопределенность вида
.
Можно было бы подумать, что,
и ответ готов, но в общем случае это
вовсе не так, и нужно применить некоторый
прием решения, который мы сейчас и
рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим
числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих,
в пределе желательно помечать, что и
куда стремится. Когда работа оформляется
от руки, удобнее это сделать так:
Для
пометок лучше использовать простой
карандаш.
Когда работа оформляется
от руки, удобнее это сделать так:
Для
пометок лучше использовать простой
карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 5
Найти предел Снова в числителе и знаменателе находимв старшей степени:Максимальная степень в числителе: 3 Максимальная степень в знаменателе: 4 Выбираемнаибольшее значение, в данном случае четверку. Согласно нашему алгоритму, для раскрытия неопределенностиделим числитель и знаменатель на. Полное оформление задания может выглядеть так:
Пример 6
Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 (можно записать как) Для раскрытия неопределенностинеобходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под
записью
подразумевается
не деление на ноль (делить на ноль
нельзя), а деление на бесконечно малое
число.
Таким образом, при раскрытии неопределенности вида у нас может получитьсяконечное число , ноль или бесконечность.
ПРАКТИКУМ 20
ЗАДАНИЕ N 1
Решение: Если вместо переменнойпоставить значение 7, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 2 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 0, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 3 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 6, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 4
Решение: Так каки
ЗАДАНИЕ N 5 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение: Так какито
имеет место неопределенность видаДля
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на.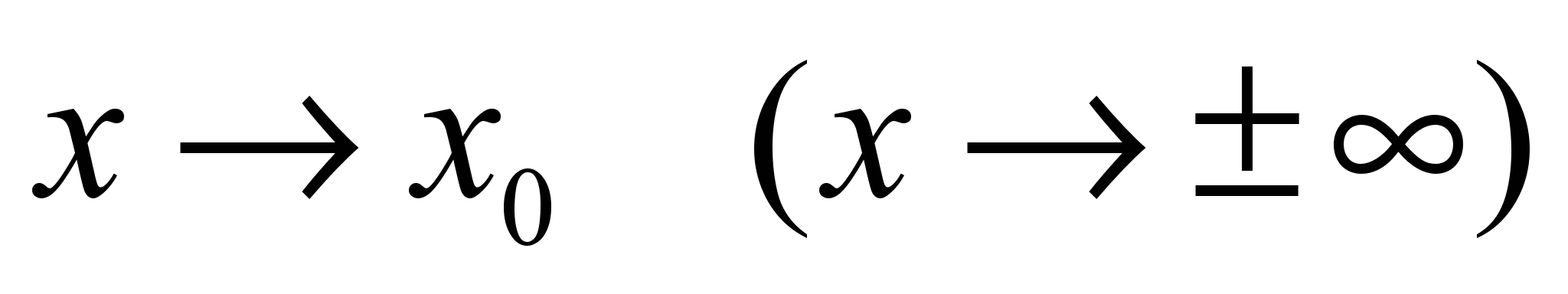 {3x} = 1 $$
{3x} = 1 $$
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.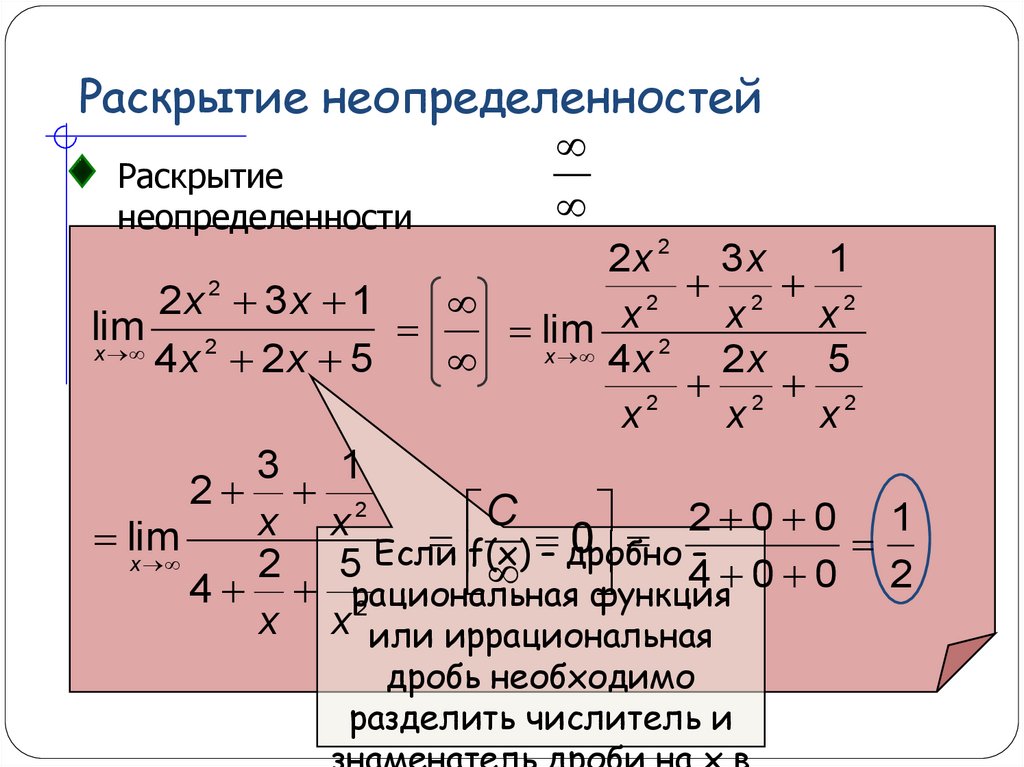
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):
Как показывает формула выше, при вычислении предела отношений двух бесконечно малых или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин . Пусть функции f (x ) и g (x a . А в самой точке a a производная функции g (x ) не равна нулю (g “(x a равны между собой и равны нулю:
.
Правило Лопиталя для случая предела двух бесконечно больших величин . Пусть функции f (x ) и g (x ) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a . А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g (x ) не равна нулю (g “(x )≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому числу, или бесконечный, то есть равный бесконечности).
Замечания .
1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x )
не определены при x = a .
2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
Пример 1.
x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе – производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x
Подстановка в заданную функцию значения x
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Раскрытие неопределённостей вида “ноль умножить на бесконечность”
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество
.
Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13.
Решение. Получаем
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
Решение. Получаем
Вычисляем предел выражения в показателе степени
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёттолько об определённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.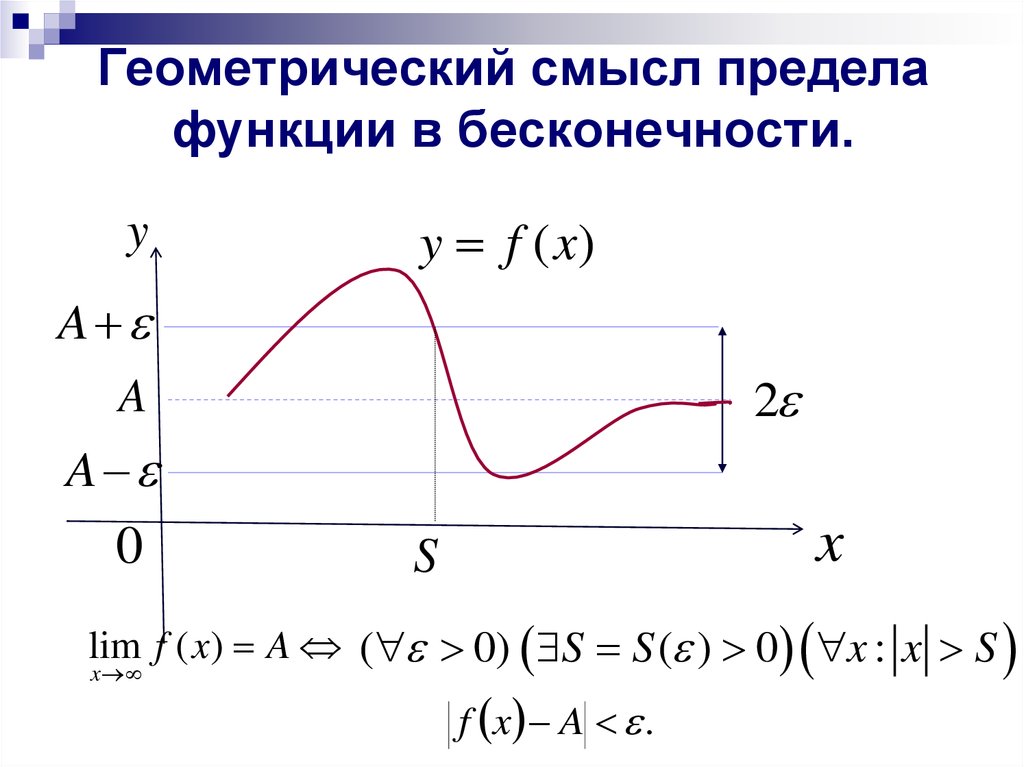
В результате:
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы , преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции . На пример: .
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица , значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны . На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим .
В других случаях при неопределённости 2-ой замечательный предел не применим .
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты : .
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ .
! Примечание : не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще :
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
:
Пример 4
Разделим числитель и знаменатель на :
Примечание : самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание : слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя. .
Пример 22
Примечание : бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Пределы функций.
 Примеры решений.
Примеры решений.Пределы функций. Примеры решений.
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Итак, что же такое предел?
Любой предел состоит из трех частей:
1) Всем
известного значка предела .
2) Записи под значком предела, в данном случае .
Запись читается «икс стремится к единице». Чаще всего – именно ,
хотя вместо «икса» на практике встречаются и другие переменные. В практических
заданиях на месте единицы может находиться совершенно любое число, а также
бесконечность ().
3) Функции под знаком предела, в данном случае .
Сама
запись читается
так: «предел функции при
икс стремящемся к единице».
Разберем
следующий важный вопрос – а что значит выражение «икс стремится к
единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое.
Построим последовательность: сначала ,
затем , ,
…, ,
….
То есть выражение «икс стремится к единице» следует понимать
так – «икс» последовательно принимает значения, которые бесконечно
близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся,
что такое ?
Это тот случай, когда неограниченно
возрастает, то есть: сначала ,
потом ,
потом ,
затем и
так далее до бесконечности.
А что
в это время происходит с функцией ?
, , , …
Итак: если , то функция стремится к минус бесконечности:
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять
начинаем увеличивать до
бесконечности, и смотрим на поведение функции:
Вывод:
при функция неограниченно
возрастает:
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
, , , , , , , , ,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного
потренироваться.
В том случае, если ,
попробуйте построить последовательность , , .
Если , то
, , .
Примечание:
строго говоря, такой подход с построением последовательностей из нескольких чисел
некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.
Пределы с неопределенностью вида и метод их решения
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел
Согласно
нашему правилу попытаемся подставить бесконечность в функцию. Что у нас
получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность.
Таким образом, у нас есть так называемая неопределенность вида .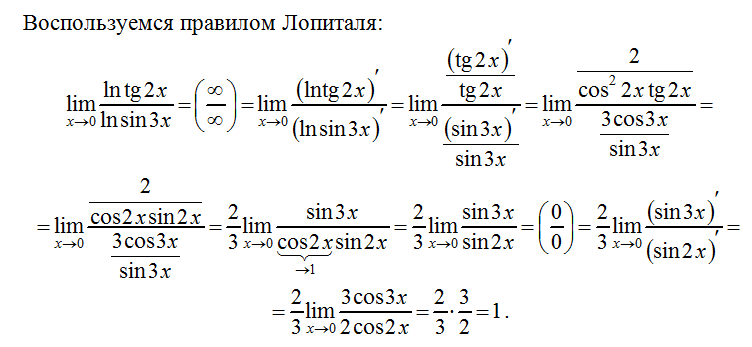 Можно было бы подумать, что , и
ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый
прием решения, который мы сейчас и рассмотрим.
Можно было бы подумать, что , и
ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый
прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала
мы смотрим на числитель и находим в
старшей степени:
Старшая степень в числителе равна двум.
Теперь
смотрим на знаменатель и тоже находим в
старшей степени:
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых,
желательно прервать решение для промежуточных объяснений. Я обычно использую
знак , он
не несет никакого математического смысла, а обозначает, что решение прервано
для промежуточного объяснения.
Я обычно использую
знак , он
не несет никакого математического смысла, а обозначает, что решение прервано
для промежуточного объяснения.
В-третьих,
в пределе желательно помечать, что и куда стремится. Когда работа оформляется
от руки, удобнее это сделать так:
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти
предел
Снова в числителе и знаменателе находим в
старшей степени:
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим
числитель и знаменатель на .
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пример 3
Найти
предел
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно
записать как )
Для раскрытия неопределенности необходимо
разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:
Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.
Пределы с неопределенностью вида и метод их решения
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить
предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность .
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для
этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы
сокращенного умножения.
Итак,
решаем наш предел
Разложим числитель и знаменатель на множители
Для
того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него: .
Далее
находим корни:
Таким
образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим
числитель на множители.
Пример 5
Вычислить предел
Сначала «чистовой» вариант решения
Разложим
числитель и знаменатель на множители.
Числитель:
Знаменатель:
,
Что
важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли
за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу
нужно знать и видеть.
Рекомендация: Если
в пределе (практически любого типа) можно вынести число за скобку, то всегда
это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем?
Да просто чтобы они не мешались под ногами. Главное, потом эти числа не
потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
!
Важно
В ходе решения фрагмент типа встречается
очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять
знак у числителя или у знаменателя (вынести -1 за скобки).
, то
есть появляется знак «минус», который при вычислении предела учитывается и
терять его совсем не нужно.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел
Начинаем решать.
Сначала
пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела.
Данное действие обычно проводится мысленно или на черновике.
Получена
неопределенность вида ,
которую нужно устранять.
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем
нашу нетленную формулу разности квадратов:
И смотрим на наш предел:
Что можно сказать? у
нас в числителе уже есть. Теперь для применения формулы осталось
организовать (которое
и называется сопряженным выражением).
Теперь для применения формулы осталось
организовать (которое
и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :
То
есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь
осталось разложить числитель и знаменатель на множители и сократить
«виновников» неопределённости, ну а предел константы – равен самой константе:
Готово.
Как
должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Пример 7
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим
числитель на множители:
Умножим числитель и знаменатель на сопряженное выражение
Простейшие виды пределов:
, , , , , , , , , , , ,
Правило 1: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Пример 1.
Разделим числитель и знаменатель на
Пример 2.
Разделим числитель и знаменатель на
Пример 3.
Разделим числитель и знаменатель на
Правило 2: если в числителе и
знаменателе находятся многочлены, и имеется неопределенности вида ,
то для ее раскрытия нужно разложить числитель и
знаменатель на множители.
Пример 1.
Разложим числитель на
множители.
Пример 2.
Разложим числитель и знаменатель на множители.
Числитель:
Знаменатель:
,
Правило 3: когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Пример 3.
Умножим числитель и знаменатель на сопряженное выражение.
Как считать до бесконечности
Нет самого большого, последнего числа… кроме бесконечности. Только бесконечность не число. Но некоторые бесконечности буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Эй, Всоус! Майкл здесь.
Какое самое большое число вы можете придумать? Гугол? Гуголплекс? Миллион-миллион-оплекс? Ну, на самом деле, самое большое число — 40.
Покрывая более 12 000 квадратных метров земли, эти 40, сделанные из стратегически посаженных деревьев в России, больше, чем маркеры батальонов на Сигнальном холме в Калгари, 6, найденные на значки Фованта в Англии — даже миля числа пи, которую Брейди развернул на Numberphile. 40 — это самое большое число на Земле с точки зрения площади поверхности.
Но с точки зрения количества вещей, которое мы обычно подразумеваем под «большим» числом, 40, вероятно, не самое большое число. Например, есть 41. О, а еще есть 42, и 43 … миллиард, триллион; знаете, какое бы большое число вы ни придумали, вы всегда можете подняться выше.
Значит, нет самого большого, последнего числа… кроме бесконечности? Нет. Бесконечность — это не число. Вместо этого это своего рода число. Вам нужны бесконечные числа, чтобы говорить о бесконечных количествах и сравнивать их, но некоторые бесконечные количества — некоторые бесконечности — буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Обо всем по порядку. Когда число указывает на количество вещей, оно называется «кардинальным числом». Например, 4 банана. 12 флагов. 20 точек. 20 — это «мощность» этого набора точек. Теперь два набора имеют одинаковую мощность, когда они содержат одинаковое количество вещей. Мы можем продемонстрировать это равенство, сопоставив каждый член одного набора один к одному с каждым членом другого. Та же кардинальность, довольно просто.
Мы используем натуральные числа — то есть 0, 1, 2, 3, 4, 5 и т. д. — в качестве количественных всякий раз, когда говорим о том, сколько существует вещей, но сколько существует натуральных чисел? Это не может быть какое-то число в натуральных числах, потому что после него всегда будет 1 плюс это число. Вместо этого у этой суммы есть уникальное название: «алеф-нуль» (ℵ 0 ). Алеф — первая буква еврейского алфавита, а алеф-нуль — первая наименьшая бесконечность. Это количество натуральных чисел. Это также сколько четных чисел, сколько нечетных чисел; это также то, сколько существует рациональных чисел, то есть дробей. Это может показаться удивительным, поскольку дроби на числовой прямой кажутся более многочисленными, но, как показал Кантор, существует способ упорядочить каждое возможное рациональное число так, чтобы натуральные числа можно было поставить в соответствие с ними один к одному. Они имеют одинаковую мощность.
Это может показаться удивительным, поскольку дроби на числовой прямой кажутся более многочисленными, но, как показал Кантор, существует способ упорядочить каждое возможное рациональное число так, чтобы натуральные числа можно было поставить в соответствие с ними один к одному. Они имеют одинаковую мощность.
Дело в том, что алеф-нуль — это большое количество; больше любой конечной суммы. Гугол, гуголплекс, гуголплекс факториал в степени гуголплекса в гуголплекс, умноженный на число Грэма в квадрате? Алеф-нуль больше. Но мы можем считать мимо него. Как? Что ж, давайте воспользуемся нашим старым другом — сверхзадачей. Если мы нарисуем кучу линий и сделаем каждую следующую линию частью размера и части расстояния от каждой последней линии, то мы сможем уместить бесконечное количество линий в конечное пространство. Количество строк здесь равно количеству имеющихся натуральных чисел. Эти два могут быть сопоставлены один к одному. Всегда есть следующий естественный, но всегда есть и следующая строка. Оба набора имеют кардинальность алеф-нуль.
Оба набора имеют кардинальность алеф-нуль.
Но что произойдет, если я это сделаю? Теперь, сколько линий есть? Алеф-нулевой плюс один? Нет. Бесконечные суммы не похожи на конечные суммы. Здесь по-прежнему только строки с нулевыми алефами, потому что я могу сопоставлять натуральные числа один к одному, как и раньше. Я просто начинаю здесь, а затем продолжаю с самого начала. Понятно, что количество строк не изменилось. Я даже могу добавить еще две строки, еще три, еще четыре — всегда получаю только нулевые алефы. Я могу даже добавить еще один бесконечный алеф-нуль строк и все равно не изменить количество. Каждое четное число может сочетаться с этими и каждое нечетное число с этими. На каждого натурала еще очередь.
Еще один классный способ увидеть, что эти линии не добавляются к общему количеству, — показать, что вы можете составить ту же самую последовательность, вообще не рисуя новые линии. Просто возьмите каждую вторую строку и переместите их все вместе в конец. Это то же самое.
Но подождите секунду. В этом и в этом может быть одинаковое количество вещей, но в них явно есть что-то другое, верно? Я имею в виду, если не из скольких вещей они сделаны, то из чего? Что ж, давайте вернемся к тому, чтобы иметь только одну строку после коллекции размером с нулевой алеф. Что, если вместо того, чтобы сопоставлять натуральные числа один к одному, мы настаиваем на нумерации каждой строки в соответствии с порядком, в котором она была нарисована? Итак, мы должны начать здесь и нумеровать слева направо. Теперь, какой номер получает эта строка? В царстве бесконечности маркировка вещей по порядку — это совсем другое, чем их подсчет. Видите ли, эта строка не участвует в сумме, но для того, чтобы пометить ее в соответствии с порядком, в котором она появилась, нам нужен набор меток чисел, выходящий за пределы натуральных чисел. Нам нужны порядковые номера.
Первый трансфинитный порядковый номер — это омега (ω), строчная греческая буква омега. Это не шутка и не уловка, это буквально просто следующая метка, которая вам понадобится после того, как вы сначала израсходуете бесконечную коллекцию каждого отдельного числа. Если бы вы заняли ω-е место в гонке, это означало бы, что гонку финишировало бесконечное количество людей, и тогда это сделали вы. После ω следует ω+1, которое на самом деле не похоже на число, но так оно и есть, точно так же, как 2, 12 или 800. Затем идут ω+2, ω+3… порядковые номера обозначают вещи по порядку. Порядковые числа — это не количество вещей, а то, как они устроены — тип их порядка.
Если бы вы заняли ω-е место в гонке, это означало бы, что гонку финишировало бесконечное количество людей, и тогда это сделали вы. После ω следует ω+1, которое на самом деле не похоже на число, но так оно и есть, точно так же, как 2, 12 или 800. Затем идут ω+2, ω+3… порядковые номера обозначают вещи по порядку. Порядковые числа — это не количество вещей, а то, как они устроены — тип их порядка.
Тип заказа набора — это просто первый порядковый номер, который не требуется для маркировки всего набора по порядку. Таким образом, для конечных чисел мощность и тип порядка одинаковы. Тип порядка всех натуральных чисел — ω. Тип порядка этой последовательности — ω+1, а теперь — ω+2. Какой бы длинной ни была аранжировка, пока она хорошо упорядочена, пока каждая ее часть содержит начальный элемент, все это описывает новый порядковый номер. Всегда. Это будет очень важно в дальнейшем.
Здесь следует отметить, что если вы когда-либо играли в игру, которая назовет наибольшее число, и вы думаете о том, чтобы сказать «омега плюс один», вам следует быть осторожным. Ваши оппоненты могут потребовать, чтобы число, которое вы называете, было кардиналом, обозначающим сумму. Эти числа относятся к одному и тому же количеству вещей, просто расположенных по-разному. ω+1 не больше, чем ω, оно просто идет после ω.
Ваши оппоненты могут потребовать, чтобы число, которое вы называете, было кардиналом, обозначающим сумму. Эти числа относятся к одному и тому же количеству вещей, просто расположенных по-разному. ω+1 не больше, чем ω, оно просто идет после ω.
Но алеф-нуль — это не конец. Почему? Ну, потому что можно показать, что существуют бесконечности больше алеф-нуль, которые буквально содержат больше вещей. Один из лучших способов сделать это — использовать диагональный аргумент Кантора. В моем эпизоде о парадоксе Банаха-Тарского я использовал его, чтобы показать, что количество действительных чисел больше, чем количество натуральных чисел. Но для целей этого видео давайте сосредоточимся на другом, более важном, чем алеф-нуль: наборе мощности алеф-нуль.
Силовой набор набора — это набор всех различных подмножеств, которые вы можете из него составить. Например, из набора 1 и 2 я могу составить набор из ничего, или 1, или 2, или 1 и 2. Степенной набор 1,2,3: пустой набор, 1 и 2, и 3, и 1 и 2, и 1 и 3, и 2 и 3, и 1,2,3. Как видите, набор мощности содержит гораздо больше элементов, чем исходный набор. Если быть точным, два в той степени, в какой сколько членов было в исходном наборе. Итак, какова мощность всего природного?
Как видите, набор мощности содержит гораздо больше элементов, чем исходный набор. Если быть точным, два в той степени, в какой сколько членов было в исходном наборе. Итак, какова мощность всего природного?
Что ж, посмотрим. Представьте себе список всех натуральных чисел. Прохладный. Теперь подмножество всех, скажем, четных чисел будет выглядеть так: да, нет, да, нет, да, нет и так далее. Подмножество всех нечетных чисел будет выглядеть так. Вот подмножество только 3, 7 и 12. А как насчет всех чисел, кроме 5. Или ни одного числа, кроме 5. Очевидно, что этот список подмножеств будет, ну, бесконечным. Но представьте, что все они сопоставляются один к одному с натуральным. Если даже в этом случае есть способ продолжать создавать новые подмножества, которые явно нигде здесь не перечислены, мы будем знать, что у нас есть множество, в котором членов больше, чем натуральных чисел — бесконечность больше, чем алеф-нуль.
Чтобы сделать это, нужно начать здесь, в первом подмножестве, и просто сделать противоположное тому, что мы видим. 0 является членом этого, поэтому наш новый набор не будет содержать 0. Затем двигайтесь по диагонали вниз к членству 1 во втором подмножестве. 1 является его членом, поэтому его не будет в нашем новом. 2 не находится в третьем подмножестве, поэтому оно будет в нашем, и так далее. Как видите, мы описываем подмножество, которое по определению будет отличаться по крайней мере одним способом от любого другого подмножества в этом нулевом списке. Даже если мы вернем это новое подмножество, диагонализация все еще может быть выполнена.
0 является членом этого, поэтому наш новый набор не будет содержать 0. Затем двигайтесь по диагонали вниз к членству 1 во втором подмножестве. 1 является его членом, поэтому его не будет в нашем новом. 2 не находится в третьем подмножестве, поэтому оно будет в нашем, и так далее. Как видите, мы описываем подмножество, которое по определению будет отличаться по крайней мере одним способом от любого другого подмножества в этом нулевом списке. Даже если мы вернем это новое подмножество, диагонализация все еще может быть выполнена.
Силовой набор натуралов всегда будет сопротивляться однозначному соответствию с натуралами. Это бесконечно больше, чем алеф-нуль. Многократное применение набора мощности приведет к созданию наборов, которые нельзя привести во взаимно-однозначное соответствие с последними, так что это отличный способ быстро создавать все большие и большие бесконечности. Дело в том, что кардиналов больше после нулевого алеф. Попробуем добраться до них.
Теперь вспомните, что после ω ординалы разделяются, и эти числа больше не являются количественными. Они не относятся к большему количеству, чем последний кардинал, которого мы достигли, но, возможно, они могут привести нас к одному из них. Подождите … что мы делаем? Алеф-нулевой? Омега? Да ладно, мы использовали эти числа, как будто в этом нет никакой проблемы, но если в какой-то момент здесь внизу вы всегда можете добавить один — всегда — можем ли мы действительно говорить об этом, об этом бесконечном процессе, как о целом, а затем проследить его с помощью что-нибудь?
Они не относятся к большему количеству, чем последний кардинал, которого мы достигли, но, возможно, они могут привести нас к одному из них. Подождите … что мы делаем? Алеф-нулевой? Омега? Да ладно, мы использовали эти числа, как будто в этом нет никакой проблемы, но если в какой-то момент здесь внизу вы всегда можете добавить один — всегда — можем ли мы действительно говорить об этом, об этом бесконечном процессе, как о целом, а затем проследить его с помощью что-нибудь?
Конечно можем. Это математика, а не наука! Вещи, которые мы считаем истинными в математике, называются аксиомами, и вероятность того, что аксиома, которую мы придумываем, верна, не выше, если она лучше объясняет или предсказывает то, что мы наблюдаем. Наоборот, это правда, потому что мы так говорим. Его последствия просто становятся тем, что мы наблюдаем. Мы не приспосабливаем наши теории к какой-то физической вселенной, чье поведение и основные законы были бы одинаковыми, были бы мы здесь или нет; мы сами создаем эту вселенную. Если аксиомы, которые мы провозглашаем истинными, приводят нас к противоречиям или парадоксам, мы можем вернуться и изменить их или просто отказаться от них, или мы можем просто отказаться позволять себе делать то, что вызывает парадоксы. Вот и все. Удивительно, однако, что, следя за тем, чтобы принимаемые нами аксиомы не приводили к проблемам, мы превратили математику в нечто, что, как говорится, «необоснованно эффективно в естественных науках». Так что в какой степени мы все это изобретаем или открываем — трудно сказать. Все, что нам нужно сделать, чтобы получить ω, это сказать «да будет омега», и все будет хорошо.
Если аксиомы, которые мы провозглашаем истинными, приводят нас к противоречиям или парадоксам, мы можем вернуться и изменить их или просто отказаться от них, или мы можем просто отказаться позволять себе делать то, что вызывает парадоксы. Вот и все. Удивительно, однако, что, следя за тем, чтобы принимаемые нами аксиомы не приводили к проблемам, мы превратили математику в нечто, что, как говорится, «необоснованно эффективно в естественных науках». Так что в какой степени мы все это изобретаем или открываем — трудно сказать. Все, что нам нужно сделать, чтобы получить ω, это сказать «да будет омега», и все будет хорошо.
Это то, что сделал Эрнест Цермело в 1908 году, когда он включил аксиому бесконечности в свой список аксиом для работы в математике. Аксиома бесконечности — это просто заявление о том, что существует одно бесконечное множество — множество всех натуральных чисел. Если вы отказываетесь принять это, ничего страшного — это делает вас финитистом, тем, кто верит, что существуют только конечные вещи. Но если вы примете это, как это делает большинство математиков, вы сможете продвинуться довольно далеко — мимо этого и через это… в конце концов мы придем к ω+ω, за исключением того, что мы достигли еще одного потолка. Пройти весь путь до ω + ω означало бы создать еще одно бесконечное множество, а аксиома бесконечности гарантирует только то, что это существует.
Но если вы примете это, как это делает большинство математиков, вы сможете продвинуться довольно далеко — мимо этого и через это… в конце концов мы придем к ω+ω, за исключением того, что мы достигли еще одного потолка. Пройти весь путь до ω + ω означало бы создать еще одно бесконечное множество, а аксиома бесконечности гарантирует только то, что это существует.
Придется ли нам добавлять новую аксиому каждый раз, когда мы описываем алеф-нуль-больше чисел? Нет. Здесь нам может помочь Аксиома Замещения. Это предположение гласит, что если вы возьмете набор — например, набор всех натуральных чисел — и замените каждый элемент чем-то другим — например, бананами, — то, что у вас останется, тоже будет набором. Звучит просто, но невероятно полезно. Попробуйте так: возьмите каждый порядковый номер до ω, а затем вместо бананов поставьте перед каждым «ω+». Теперь мы достигли ω+ω, или ω×2. Используя замену, мы можем делать прыжки любого размера, какого захотим, если мы используем только те числа, которые уже достигли. Мы можем заменить каждый порядковый номер вплоть до ω на омега-кратное число, чтобы получить ω×ω , ω 2 . Мы сейчас готовим! Аксиома замены позволяет бесконечно конструировать новые ординалы. В конце концов мы добираемся до ω до ω до ω до ω до ω… и у нас заканчиваются стандартные математические обозначения. Без проблем! Это просто называется «эпсилон-ноль» (ε 0 ), и мы продолжим отсюда.
Мы можем заменить каждый порядковый номер вплоть до ω на омега-кратное число, чтобы получить ω×ω , ω 2 . Мы сейчас готовим! Аксиома замены позволяет бесконечно конструировать новые ординалы. В конце концов мы добираемся до ω до ω до ω до ω до ω… и у нас заканчиваются стандартные математические обозначения. Без проблем! Это просто называется «эпсилон-ноль» (ε 0 ), и мы продолжим отсюда.
А теперь подумайте обо всех этих ординалах. Все разные способы упорядочить алеф-нулевые вещи. Ну, они хорошо упорядочены, поэтому у них есть тип порядка — некоторый порядковый номер, который идет после всех них. В данном случае этот порядковый номер называется «омега-один» (ω1). Теперь, поскольку по определению ω 1 следует после каждого отдельного типа заказа или вещей с нулевым алефом, он должен описывать расположение буквально большего количества вещей, чем последний алеф. Я имею в виду, что если бы это было не так, то оно было бы где-то здесь, но это не так. Кардинальное число, описывающее количество вещей, использованных для размещения с типом заказа ω 1 , равно «алеф-один» (ℵ 1 ).
Кардинальное число, описывающее количество вещей, использованных для размещения с типом заказа ω 1 , равно «алеф-один» (ℵ 1 ).
Неизвестно, где на этой прямой находится набор мощности натуралов. Этого не может быть между этими кардиналами, потому что между ними нет кардиналов. Оно может быть равно алеф-один — это убеждение называется гипотезой континуума. Но он также может быть больше; мы просто не знаем. Гипотеза континуума, между прочим, пожалуй, самый большой вопрос без ответа во всей этой теме, и сегодня, в этом видео, я не буду его решать, а буду подниматься все выше и выше, во все большие и большие бесконечности.
Теперь, используя аксиому замены, мы можем взять любой уже достигнутый порядковый номер, например, ω, и перейти от алеф к алеф до алеф-омега. Или, черт возьми, почему бы не использовать больший порядковый номер, например ω 2 , для построения алеф-омега-квадрат? Алеф-омега-омега-омега-омега-омега-омега-о… Наша система обозначений позволяет мне добавлять сюда только счетное число омег, но замена не заботится о том, есть ли у меня способ записать числа, которых она достигает. Где бы я ни приземлился, там будет еще больше чисел, что позволит мне совершать еще большие и многочисленные прыжки, чем раньше. Все это представляет собой дико ускоряющуюся петлю обратной связи эмбиггенинга. Мы можем продолжать в том же духе, достигая все больших и больших бесконечностей снизу.
Где бы я ни приземлился, там будет еще больше чисел, что позволит мне совершать еще большие и многочисленные прыжки, чем раньше. Все это представляет собой дико ускоряющуюся петлю обратной связи эмбиггенинга. Мы можем продолжать в том же духе, достигая все больших и больших бесконечностей снизу.
Замена и повторяющиеся наборы мощности, которые могут совпадать или не совпадать с алефами, могут продолжать наше восхождение вечно. Так что ясно, что за ними ничего нет, верно? Не так быстро. Это то, что мы говорили о переходе от конечного к омеге. Почему бы не принять как аксиому, что существует какое-то следующее число, настолько большое, что никакие замены или настройки чего-то меньшего никогда не смогут вас туда привести. Такое число называется «недоступным кардиналом», потому что до него невозможно добраться снизу.
Теперь интересно, что среди чисел, которых мы уже достигли, можно найти тень такого числа: алеф-нуль. Вы также не можете добраться до этого числа снизу. Все числа, меньшие этого, конечны, и конечное число конечных чисел нельзя складывать, умножать, возводить в степень, заменять конечными скачками конечное число раз или даже устанавливать мощность конечное число раз, чтобы получить что-либо, кроме другого конечного числа. количество. Несомненно, набор мощности от миллиона к гуголплексу, к гуголплексу к гуголплексу действительно велик, но он все же конечен. Даже близко не алеф-нуль, первая наименьшая бесконечность. По этой причине алеф-нуль часто считается недоступным числом. Однако некоторые авторы не делают этого, говоря, что недоступное также должно быть неисчисляемым, что, ладно, имеет смысл — я имею в виду, что мы уже получили доступ к алеф-нулю, но помните, что единственный способ, которым мы могли бы это сделать, — это прямо объявить его существование аксиоматически. Нам придется сделать то же самое для недоступных кардиналов.
количество. Несомненно, набор мощности от миллиона к гуголплексу, к гуголплексу к гуголплексу действительно велик, но он все же конечен. Даже близко не алеф-нуль, первая наименьшая бесконечность. По этой причине алеф-нуль часто считается недоступным числом. Однако некоторые авторы не делают этого, говоря, что недоступное также должно быть неисчисляемым, что, ладно, имеет смысл — я имею в виду, что мы уже получили доступ к алеф-нулю, но помните, что единственный способ, которым мы могли бы это сделать, — это прямо объявить его существование аксиоматически. Нам придется сделать то же самое для недоступных кардиналов.
Очень трудно понять, насколько непостижимы размеры недоступного кардинала. Я просто оставлю это на этом: концептуальный прыжок из ничего в первую бесконечность подобен прыжку из первой бесконечности в недоступное. Теоретики множеств описали числа больше, чем недоступные, каждое из которых требует новой аксиомы большого кардинального числа, утверждающей его существование, расширяющей высоту нашей вселенной чисел. Настанет ли когда-нибудь момент, когда мы придумаем аксиому, подразумевающую существование стольких вещей, что она подразумевает противоречащие друг другу вещи? Ответим ли мы когда-нибудь на гипотезу континуума? Может быть, и нет, но есть многообещающие направления, а до тех пор остается удивительным факт, что многие из этих бесконечностей — возможно, все они — настолько велики, что не совсем ясно, существуют ли они на самом деле или могут ли быть показаны в реальности. физическая вселенная. Если они есть, если однажды физика найдет им применение, это прекрасно, но если нет, то это тоже прекрасно. Это означало бы, что с этим мозгом, крошечной штукой, в септиллион раз меньшей, чем крошечная планета, на которой она живет, мы открыли что-то истинное за пределами физического мира. Что-то, что применимо к реальному миру, но в то же время достаточно сильное, чтобы идти дальше, за пределы того, что даже сама Вселенная может вместить, или показать нам, или чем быть.
Настанет ли когда-нибудь момент, когда мы придумаем аксиому, подразумевающую существование стольких вещей, что она подразумевает противоречащие друг другу вещи? Ответим ли мы когда-нибудь на гипотезу континуума? Может быть, и нет, но есть многообещающие направления, а до тех пор остается удивительным факт, что многие из этих бесконечностей — возможно, все они — настолько велики, что не совсем ясно, существуют ли они на самом деле или могут ли быть показаны в реальности. физическая вселенная. Если они есть, если однажды физика найдет им применение, это прекрасно, но если нет, то это тоже прекрасно. Это означало бы, что с этим мозгом, крошечной штукой, в септиллион раз меньшей, чем крошечная планета, на которой она живет, мы открыли что-то истинное за пределами физического мира. Что-то, что применимо к реальному миру, но в то же время достаточно сильное, чтобы идти дальше, за пределы того, что даже сама Вселенная может вместить, или показать нам, или чем быть.
Как всегда, спасибо за просмотр.
Еще один интересный факт о трансфинитных ординалах заключается в том, что арифметика с ними немного отличается. Обычно 2+1 совпадает с 1+2, но ω+1 не совпадает с 1+ω. Один плюс омега на самом деле просто омега. Думайте о них как о типах заказов: одна вещь, помещенная перед омегой, просто использует все натуральные числа и оставляет нас с типом заказа омега. Одна вещь, размещенная после омеги, требует каждого натурального числа, а затем омеги, оставляя нам омегу плюс один в качестве типа заказа.
Horizon SOC — Check Point Software
Выявляйте, расследуйте и пресекайте атаки быстрее с точностью 99,9 % в сети, облаке, конечных точках, мобильных устройствах и IoT. Эти же инструменты сбора данных и расследования используются Check Point Research и теперь доступны для вас.
ЗАПРОСИТЬ БЕСПЛАТНУЮ ПРОБНУЮ ДЕМОВЕРСИЮ
Веб-семинар: Знакомство с нашей платформой Prevention-First Security Operations Platform ЗАРЕГИСТРИРОВАТЬСЯ СЕЙЧАС
Смотреть обзор продукта
Посмотрите видео по запросу, чтобы узнать
из первых рук обо всех функциях и возможностях Horizon SOC.
ПОСМОТРИТЕ СЕЙЧАС
Horizon SOC
Потому что команды SOC заслуживают уверенности
Для многих групп SOC обнаружение вредоносной активности в сети похоже на поиск иголки в стоге сена. Им часто приходится собирать воедино информацию из нескольких решений для мониторинга и просматривать ежедневную перегрузку предупреждений практически без контекста. Результат: критические атаки пропускаются до тех пор, пока не становится слишком поздно.
Horizon SOC дает вашей команде уверенность, необходимую для более быстрого выявления и отражения атак, прежде чем ущерб распространится. Простота развертывания в виде единой облачной платформы повышает эффективность операций по обеспечению безопасности и рентабельность инвестиций.
Точность 99,9 %
Выявление и отключение только
реальных атак
Быстрое расследование
С самой мощной в отрасли 020102 Без развертывания, интеграции и Преодолевает ежедневную перегрузку оповещений о событиях, чтобы автоматически определять и блокировать реальные атаки Подробнее Анализ инцидентов на основе ИИ, дополненный глобальным обменом данными об угрозах и расширенным обзором угроз как внутри, так и за пределами вашего предприятия. Узнать больше Ускорение и углубление расследований с помощью тщательно обработанной аналитики и эксклюзивных исследовательских данных Узнать больше Horizon SOC использует возможности искусственного интеллекта для точного выявления реальных атак на основе миллионов ежедневных журналов и предупреждений. Это позволяет вам быстро реагировать на самые серьезные угрозы с помощью автоматической сортировки и одним щелчком мыши 9.0003 Respond Intelligently Based On Severity and Probability 1 Install lightweight client on infected host 2 Получить подробный отчет о судебной экспертизе с полезной информацией Посмотрите повтор веб-семинара, чтобы узнать о возможностях Horizon SOC и о том, как Terma, национальный поставщик безопасности, использует его для обнаружения и отражения реальных атак. Посмотрите видео с примерами из практики, чтобы узнать, как европейская энергетическая компания выявляет и блокирует атаки с помощью Horizon SOC «Поиск в Google» любой IoC с централизованного портала и быстрое получение тщательно обработанной информации об угрозах и уникальных данных исследований. Используйте эксклюзивные инструменты расследования, разработанные исследовательской группой Check Point и ежедневно используемые для выявления и расследования самых опасных и изощренных кибератак в мире. Компания Check Point признана лидером рейтинга лидерства KuppingerCole в отчете NDR ЗАГРУЗИТЕ СЕЙЧАС Информация об угрозах в режиме реального времени, полученная от сотен миллионов датчиков по всему миру, обогащенная механизмами на основе ИИ и эксклюзивными исследовательскими данными исследовательской группы Check Point.
аналитикой угроз 3
проблем с конфиденциальностью От миллионов журналов к реальным оповещениям
Раскрывает даже самые незаметные атаки Точность 99,9 %

«Поиск в Google» любой IOC с централизованного портала
Выявлять и отключать только РЕАЛЬНЫЕ АТАКИ
Через сеть, облако, конечные точки, мобильные устройства и Интернет вещей
From Millions of Logs to Only Real Alerts
Automated Triage
Minimize the Attack Impact With a Single-Click Remediation
Раскройте даже самые незаметные атаки с точностью 99,9%
Достижение уверенности в SOC
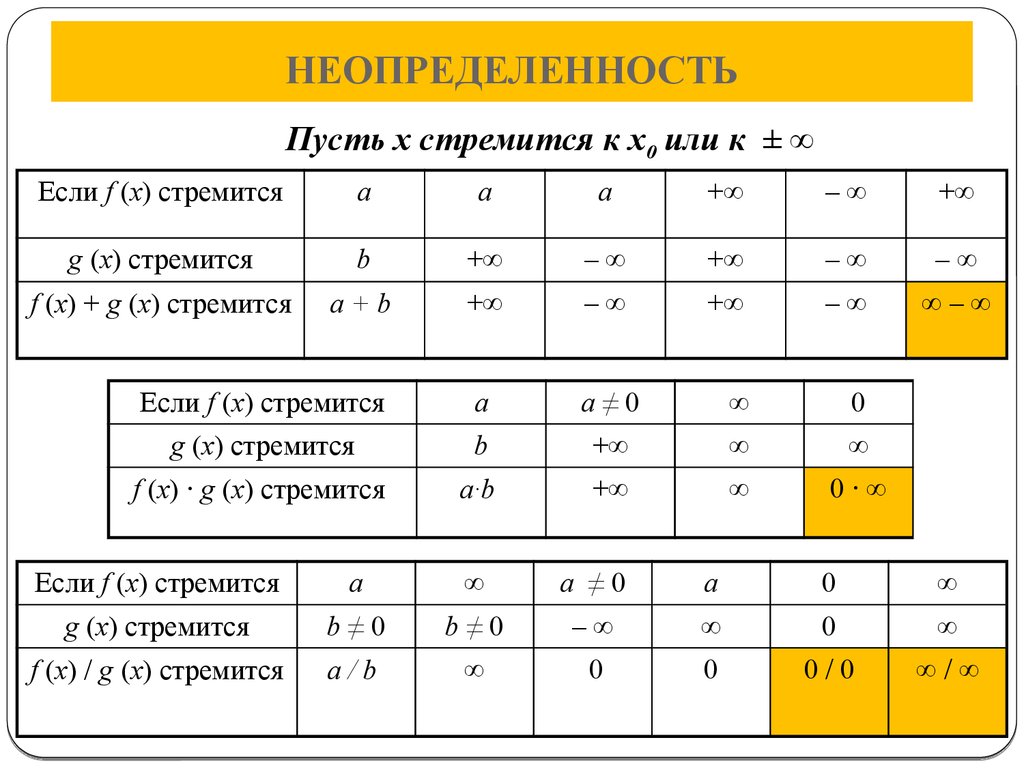
Eurowind Energy борется с внутренними угрозами с помощью Horizon SOC
Ускорение и углубление расследований
С помощью самой мощной в мире информации об угрозах Создано с помощью ThreatCloud

Сила ThreatCloud
2000
Файлы нулевого дня, обнаруженные ежедневно
150 000
Подключено
Сети
13 миллионов
Файлы, эмулируемые
Ежедневно
3 миллиарда
Веб-сайты и файлы, обрабатываемые ежедневно
«Поиск Google» Любой IOC с централизованного портала , ДНК вредоносных программ и многое другое.
Получение эксклюзивной разведывательной информации для углубления расследования
Быстрое определение того, является ли подозрительный файл вредоносным
Воспользуйтесь службой эмуляции угроз SandBlast, которая имеет лучшую в отрасли скорость обнаружения.
Информация об отчете об эмуляции угроз включает:
- Семейство вредоносных программ
- Геос нацелен на
- Методы MITRE ATT&CK
- Эмуляция видео
- Удаленные файлы
- URL-адреса C2
- И многое другое!
«Благодаря Horizon SOC мы смогли выявлять зараженные устройства в сети с точностью 99,9 % и устранять их до того, как будет нанесен какой-либо ущерб.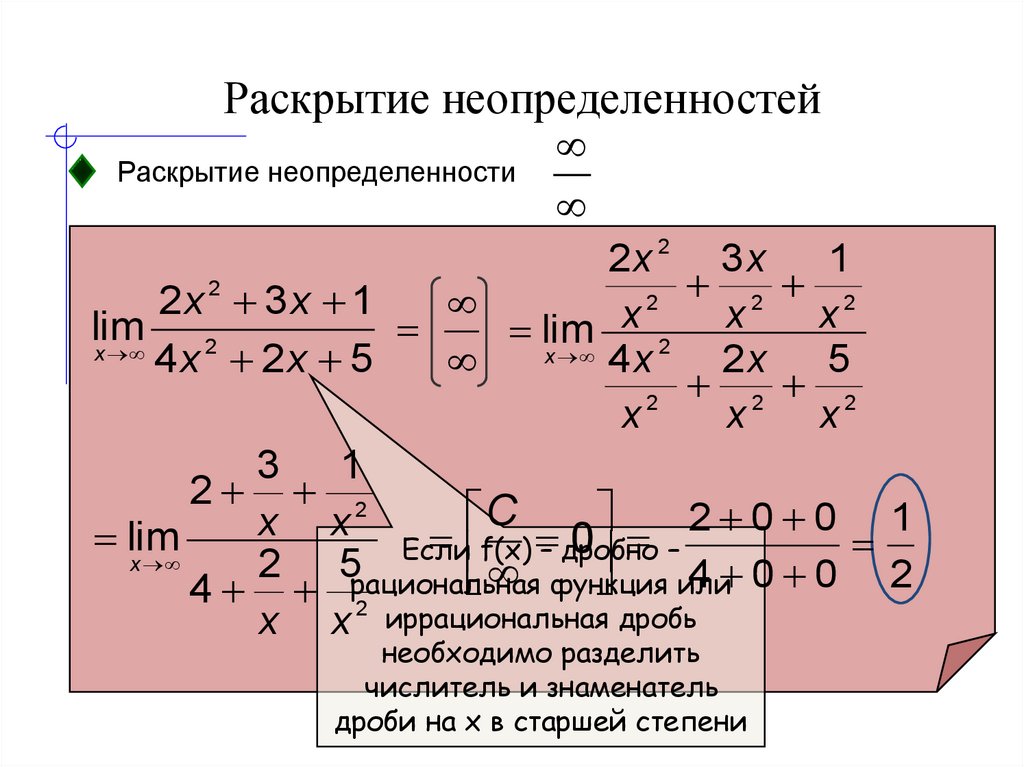 Кроме того, Horizon SOC было легко развернуть как единую унифицированную облачную платформу, что позволило нам повысить операционную эффективность и снизить совокупную стоимость владения».
Кроме того, Horizon SOC было легко развернуть как единую унифицированную облачную платформу, что позволило нам повысить операционную эффективность и снизить совокупную стоимость владения».
– Ким Моберг, ИТ-менеджер, Eurowind Energy
Zero Friction
Без проблем с развертыванием, интеграцией и конфиденциальностью
Используйте единую централизованно управляемую платформу SOC; Избегайте вводящих в заблуждение сведений из нескольких решений
Ненавязчивая реализация, занимающая менее трех минут. Нет необходимости развертывать дополнительные агенты конечных точек.
Избегайте дорогостоящего хранения журналов и проблем с конфиденциальностью с помощью революционного облачного анализа событий, который не экспортирует и не хранит ваши журналы.
Готовы попробовать Horizon SOC?
Получить цену
Контактные продажи
2022 Отчет о кибербезопасности
Глобальная кибер -пандемия. Вебинар SOC — Запись сеанса
Вебинар SOC — Запись сеанса
Horizon SOC SOCStock2021 Запись сеанса
СсылкиЧто такое центр управления безопасностью
SOC-as-a-Service
Роли и обязанности SOC
Важность SOC
Введение
В этом ответе мы рассмотрим
Как решить вопрос ОП, используя умную $D,N$-разложение.
Использование канонической формы Жордана для взятия бесконечных степеней матриц (а когда можно взять бесконечную степень?)
Бесконечные степени стохастических матриц.
Бесконечные степени матриц с использованием концепции обобщенных инверсий.
Введение в интервальные матрицы и краткая информация о том, почему изучение бесконечных степеней для таких матриц может помочь получить бесконечные степени для больших классов матриц.
Специальное наблюдение
Ваша матрица имеет вид $D+N$, где $D$ — диагональная матрица с элементами $[0,0,1,1,1]$ и $$ N = \begin{pmatrix} 0&0&0&0&0\\ \фракция 23 &0&0&0&0\\ \фракция 13&0&0&0&0\\ 0&\фракция 37&0&0&0\\ 0&\фракция 47&0&0&0 \end{pматрица} $$ 92+Н+И) $$
по желанию. Вычислите это количество для ваших $D$ и $N$, чтобы увидеть, что вы получите.
Вычислите это количество для ваших $D$ и $N$, чтобы увидеть, что вы получите.
Жордановая каноническая форма и условие N&S для сходимости мощности
Мы не использовали стандартный метод для решения этого вопроса. Действительно, то, что мы сделали, было относительно случайным: разбили матрицу на две части, которые легко возводятся в степень и чьи коммутативные свойства хороши.
Существует стандартный метод бесконечного возведения в степень: жордановая каноническая форма. 9k$ существует тогда и только тогда, когда для каждого собственного значения $\lambda$ оператора $A$
- Либо $|\lambda|<1$, либо
- $\lambda=1$, а $\lambda$ является регулярным (т.е. алгебраическая и геометрическая кратности $\lambda$ как собственного значения $A$ совпадают) и доминирующим (т.е. каждое второе собственное значение $\mu \neq \lambda$ удовлетворяет $|\mu|<1$).
Это будет отражено в матрице Джордана $D+N$ следующим образом: каждый диагональный элемент либо имеет модуль меньше, чем $1$, либо имеет $1$, где соответствующий элемент выше $1$ равен $0 $.
Стохастические матрицы и матрицы с положительными элементами
Большой класс матриц, для которых можно установить и найти предел при некоторых условиях, это класс матриц со строго положительными элементами (все элементы $>0$). Здесь нам поможет теорема Перрона и Фробениуса.
Теорема[7] : Пусть $A$ — матрица со строго положительными элементами. Тогда существует положительное действительное число $r>0$ со следующим свойством: $r$ является собственным значением $A$ кратности $1$, и каждое другое собственное значение меньше $r$ по модулю. Кроме того, собственный вектор, соответствующий $r$, имеет строго положительные элементы. 9l$ имеют строго положительные элементы (неприводимые апериодические).
Этот замечательный результат используется при анализе цепей Маркова с конечным временем, переходные матрицы которых часто обладают предложенным свойством.
Отношение с обобщенными обратными
Обобщенные обратные — довольно интересная концепция, поскольку они могут существовать, даже если матрица необратима. {\#}$ уникален, если они выполнены, и называется обобщенным обратным к $A$. 9*$) Здесь определяется главный минор матрицы.
{\#}$ уникален, если они выполнены, и называется обобщенным обратным к $A$. 9*$) Здесь определяется главный минор матрицы.
Подробнее о таких матрицах и их степенях см. в [3].
Интервальные матрицы
Очень интересная концепция – одна из интервальных матриц. Это матрицы, элементами которых являются не действительные числа, а на самом деле действительных интервала . Они используются для доказательства результатов для матриц, элементы которых лежат в пределах изображенных интервалов. Например, $$ \begin{pmatrix} 2 и 3\\ 4 и 5 \end{pматрица} \in\begin{pmatrix} [-1,3] & \{3\}\\ [2,5] & [1,5,7,65] \end{pматрица} $$ где $\in$ не означает «принадлежит», а скорее означает «покрыт в» , так что результат для этой конкретной матрицы интервалов будет справедлив и для реальной матрицы. Мы будем использовать $[\cdot]$ для обозначения интервальной матрицы. 9п]Х$.
Оказывается, есть результаты, которые могут доказать сходимость степеней и для этих интервальных матриц, тем самым доказав сходимость степеней для многих матриц сразу. Некоторые из них обсуждаются в [1].
Некоторые из них обсуждаются в [1].
Критерии назвать сложно, но они очень эффективны и находят применение в компьютеризированной проверке устойчивости решений линейных дифференциальных уравнений с периодическими коэффициентами (которые обычно лежат в некотором компактном интервале, отсюда необходимость интервального анализа) .
Ссылки
[1] Арндт, Ханс-Роберт; Майер, Гюнтер , Новые критерии полусходимости интервальных матриц , SIAM J. Matrix Anal. заявл. 27, № 3, 689-711 (2005). ЗБЛ1129.65029.
[2] Plemmons, R. J. , M-матрицы, ведущие к полусходящимся расщеплениям , Linear Algebra Appl. 15, 243-252 (1976). ЗБЛ0358.15016.
[3] Мейер, Карл Д. младший; Plemmons, R. J. , Сходящиеся степени матрицы с приложениями к итерационным методам для сингулярных линейных систем , SIAM J. Numer. Анальный. 14, 699-705 (1977). ЗБЛ0366.65017.
[4] Степень матрицы в жордановой форме
[5] Предельное распределение цепи Маркова
[6] Степени матриц
[7] Теорема Перрона-Фробениуса
Проблема с бесконечностью | plus.
 maths.org
maths.orgЭта статья является второй в серии из четырех статей по квантовой электродинамике. Предыдущую статью можно прочитать здесь, а следующую здесь.
Поль Дирак (1902-1984).
Были ли у вас в последнее время видения? Возможно, не в метафорическом смысле, но в физическом смысле он у вас есть все время. Это результат рассеяния света от объектов вокруг вас — компьютер экран, зеркало, чайник — и бьют по глазам. В школе мы узнайте, что свет, как и все электромагнитное излучение, состоит из волн и материи из маленьких частиц. Видение может быть объясняется взаимодействием этих волн и частиц.
Однако в начале двадцатого века физики
понял, что все гораздо сложнее: частицы и
электромагнитные волны были как волнообразными, так и корпускулярноподобными. Британский физик
Поль Дирак описал как электроны, так и частицы света, названные фотона с точки зрения квантовых полей : частицы
соответствуют единицам возбуждения, тщательно измеренным колчанам в тех полях (см. предыдущую статью). Его совершенно новый математический формализм описывал как поле электрона, так и фотонное поле — для описания взаимодействия материи и света все, что нужно было физикам, — это заставить этот формализм работать.
предыдущую статью). Его совершенно новый математический формализм описывал как поле электрона, так и фотонное поле — для описания взаимодействия материи и света все, что нужно было физикам, — это заставить этот формализм работать.
Живой пылесос
Но они быстро столкнулись с проблемой, которая оказалась довольно буквально, безграничной пропорции. Это было следствием центральный результат квантовой механики, новой физики, была разработана в 1920-х годов и послужило мотивом для нового трактовка электромагнетизма: неопределенность Гейзенберга принцип.
В своей обычной форме принцип гласит, что чем точнее
вы о положении частицы менее точны вы можете быть
о его импульсе (направлении, в котором он движется, и его скорости, умноженной на его массу)
наоборот. Если вы зафиксируете, скажем, импульс в хорошей степени
точность, ваша неуверенность в позиции возрастает. Дело не в том, что
частица где-то определена, но вы просто не знаете, где, скорее
в квантовой механике такие идеи, как местоположение и траектория частицы, просто не имеют смысла.
Дэвид Кайзер — историк науки в Массачусетском технологическом институте. Изображение: Донна Ковени.
Этот принцип можно также сформулировать в терминах энергии и время. Обычно энергия — это то, что сохраняется: как мы все знаем по опыту, его нельзя создать из ничего и точно так же он не может просто исчезнуть. Но неуверенность Гейзенберга Принцип означает, что есть компромисс. Энергия может стать доступна из ничего в течение очень коротких моментов времени. Как следствие, квантовое поле постоянно страдает от короткоживущих возбуждений. А поскольку возбуждения полей интерпретируются как частицы, они стали называться виртуальный частицы .
«Это похоже на непослушных школьников», — говорит Дэвид Кайзер, историк физики из Массачусетского технологического института, написавший увлекательную книгу, включающую введение в эту тему. «Если ты только
собирается высунуть язык, можно и дольше, но если
вы собираетесь запрыгнуть на стол, вам придется сделать это довольно быстро
если вы не хотите, чтобы учитель вас видел. Это то, что мы думаем
происходит все время, неудержимо, в квантово-механическом
уровень. Маленькие частицы постоянно крадут энергию у
вакуум. Они нарушают правила. В зависимости от того, сколько энергии они
брать взаймы, они должны соответственно быстро их возвращать» 9.0003
Это то, что мы думаем
происходит все время, неудержимо, в квантово-механическом
уровень. Маленькие частицы постоянно крадут энергию у
вакуум. Они нарушают правила. В зависимости от того, сколько энергии они
брать взаймы, они должны соответственно быстро их возвращать» 9.0003
Несмотря на свою загадочную природу, виртуальные частицы оказались полезными для объяснения действия электростатической силы. Нарушая закон на короткие моменты времени, электроны испускают виртуальные фотоны, которые будут поглощаться другим электроном, находящимся поблизости. Это взаимодействие раздвигает электроны, эффект, который мы наблюдаем как отталкивание между одноименными зарядами. В 1932 году Ганс Бете и Энрико Ферми объявили виртуальные фотоны силой, несущей частицы , которые опосредуют электростатическую силу.
Виртуальные спойлеры: проблема 1
Но виртуальные частицы также создали огромные проблемы. Согласно теории электрон постоянно испускает и поглощает
виртуальные фотоны, которые приходят со своей собственной энергией и импульсом. Более того, пары виртуальных
электроны и их античастицы, позитроны, постоянно появляются и исчезают, сгущаясь вокруг центрального электрона, создавая картину цветка, поскольку положительно заряженные виртуальные позитроны притягиваются к отрицательно заряженному центральному электрону.
Более того, пары виртуальных
электроны и их античастицы, позитроны, постоянно появляются и исчезают, сгущаясь вокруг центрального электрона, создавая картину цветка, поскольку положительно заряженные виртуальные позитроны притягиваются к отрицательно заряженному центральному электрону.
Виртуальные электрон-позитронные пары, обволакивающие центральный электрон с положительно заряженными позитронами, притянутыми к центру.
Этот виртуальный антураж воздействует на исходный электрон. Эффективный заряд электрона, заряд, который вы могли бы измерить в эксперименте, на самом деле является суммой двух частей: его «собственного» заряда, также называемого его голым зарядом , , и вклада, исходящего от виртуальных частиц, :
Точно так же эффективная масса электрона состоит из двух компонентов; голая масса и вклад виртуальных частиц:
Будучи созданными из вакуума, вы не ожидаете, что виртуальные частицы будут иметь большой эффект, поэтому вклады и должны быть небольшими. Но когда физики приступили к их вычислению, результат оказался просто возмутительным. Сроки исправления оказались бесконечными!
Но когда физики приступили к их вычислению, результат оказался просто возмутительным. Сроки исправления оказались бесконечными!
Это означало, что новый математический аппарат квантовой электродинамики был совершенно бесполезен, когда дело доходило до расчета даже простейших взаимодействий. «На самом базовом уровне приближения, игнорируя виртуальные частиц, я мог бы сказать, что вероятность рассеяния двух электронов друг от друга на 78%, — объясняет Кайзер. — Но я не могу отключить неопределенность принцип. Даже если я рассмотрю только одну виртуальную частицу, я все равно неожиданно получить 78% плюс бесконечность.”
Проблема заключалась в том, что нельзя было сказать, сколько энергии заимствовала виртуальная частица. «Эти виртуальные частицы могли украсть семь единиц энергии, или пятьдесят, или бесконечное количество, если они возвращали ее соответственно быстро», — объясняет Кайзер. При расчетах необходимо было учитывать все возможные уровни энергии даже одной виртуальной частицы, что давало бесконечную сумму с бесконечным ответом. С математической точки зрения они произвели расходящийся интеграл .
С математической точки зрения они произвели расходящийся интеграл .
Уважение к Эйнштейну
Альберт Эйнштейн (1879-1955) в 1921 году.
«Ну и что?», — можете сказать вы. Эффективная масса и заряд любого электрона конечны, в конце концов, мы можем их измерить, поэтому бесконечности должны быть артефактом теория. Один из способов справиться с ними — просто разрезать расходящийся интеграл off: рассматривать энергии только до определенного, очень высокого уровня. Используя этот трюк, интегралы действительно можно заставить сходиться , то есть становятся конечными. Но, к сожалению, такой подход нарушает теорию, с которой ни один уважающий себя физик не стал бы связываться: специальную теорию относительности Эйнштейна.
Согласно теории Эйнштейна, наблюдатели, пока они не ускоряются, а находятся в инерциальной системе отсчета , должны видеть законы
физики действуют одинаково независимо от того, насколько они быстры.
движение: это фундаментальная симметрия природы. Проблема в том, что количество энергии, которое вы
мера в движущейся частице зависит от скорости, с которой вы
сами двигаетесь. «Можно сказать, что, если я отключу энергию
уровень в расчете составляет десять газиллионов, — говорит Кайзер. — Этот маленький
приближение может показаться нам неважным, но кто-то
путешествие в 99,9% скорости света вопиюще увидели бы, что
разница, поэтому мы бы отдавали предпочтение нашему собственному состоянию движения. Если мы
серьезно относиться к принципу неопределенности и сочетать его с
специальной теории относительности, нет способа пресечь воровство
энергия в
конечное значение. Это нарушило бы симметрию особых
относительности.”
Проблема в том, что количество энергии, которое вы
мера в движущейся частице зависит от скорости, с которой вы
сами двигаетесь. «Можно сказать, что, если я отключу энергию
уровень в расчете составляет десять газиллионов, — говорит Кайзер. — Этот маленький
приближение может показаться нам неважным, но кто-то
путешествие в 99,9% скорости света вопиюще увидели бы, что
разница, поэтому мы бы отдавали предпочтение нашему собственному состоянию движения. Если мы
серьезно относиться к принципу неопределенности и сочетать его с
специальной теории относительности, нет способа пресечь воровство
энергия в
конечное значение. Это нарушило бы симметрию особых
относительности.”
Виртуальные спойлеры: проблема 2
Но потенциально бесконечные энергетические уровни были не единственными
проблема. Электроны взаимодействуют, обмениваясь виртуальными фотонами, и они действительно могут обмениваться любым количеством виртуальных фотонов. При расчетах необходимо было учитывать это неограниченное количество виртуальных фотонов, что приводило к сумме с бесконечным числом слагаемых: грубо говоря, это одно слагаемое
соответствующий обмену одной виртуальной частицей, другой термин соответствует обмену двумя частицами, другой – трем,
четыре, пять и так далее. В целом это дает двойную бесконечность, так как каждый отдельный член сам по себе был бы бесконечен,
из-за неограниченных уровней энергии, которые вам нужно было учитывать для каждой виртуальной частицы.
В целом это дает двойную бесконечность, так как каждый отдельный член сам по себе был бы бесконечен,
из-за неограниченных уровней энергии, которые вам нужно было учитывать для каждой виртуальной частицы.
Как и в случае с проблемой расходящихся интегралов, для решения проблемы с бесконечным числом членов существовало хитроумное решение. «В общем, каждый раз, когда электрон взаимодействует с фотоном, сила этого взаимодействия невелика», — объясняет Кайзер. «Электромагнетизм — не очень сильная сила. Она намного, намного слабее, например, ядерных сил, удерживающих частицы внутри атомного ядра». Действительно, взаимодействие электронов зависит от квадрата их измеряемого заряда, который можно определить в эксперименте и который очень мал: в соответствующих единицах. В бесконечных суммах, которые необходимо рассмотреть, последовательные члены (которые, грубо говоря, соответствуют все большему и большему числу обмениваемых виртуальных частиц) приходят с возрастающими степенями в качестве их коэффициентов: и так далее. Чем больше количество обмениваемых виртуальных частиц, тем выше мощность как коэффициента соответствующего члена.
Чем больше количество обмениваемых виртуальных частиц, тем выше мощность как коэффициента соответствующего члена.
Вернер Гейзенберг (1901-1976).
Когда вы возводите очень маленькое число в некоторую степень, результат становится еще меньше; в случае мы находим, что примерно в десять тысяч раз меньше, чем . Это означает, что в этих суммах можно просто игнорировать члены более высокого порядка, соответствующие большему числу виртуальных частиц: малость их коэффициента означала, что их вклады были пренебрежимо малы, по крайней мере, если предположить, что сами члены конечны (что, конечно, они не из-за проблемы 1).
Но при всей простоте в теории, на практике этот пертурбативный подход , как стало известно, мало чем помогал. Расчеты даже с несколькими виртуальными частицами по-прежнему были ужасно сложными: определение s и s было далеко не простым. В 1935 году Ганс Эйлер, ученик Вернера Гейзенберга, рассмотрел специфическое взаимодействие между фотонами, но ограничился терминами и. На его расчет ушло восемнадцать месяцев, в журнале он занимал пятьдесят страниц.0272 Annalen der Physik и был достаточно сложным, чтобы получить докторскую степень. И, конечно, вычисление Эйлера было приближением и в другом смысле: он не только отсек бесконечную сумму, но также должен был отсекать энергетические уровни, чтобы получить конечные интегралы в тех терминах, которые он рассматривал.
На его расчет ушло восемнадцать месяцев, в журнале он занимал пятьдесят страниц.0272 Annalen der Physik и был достаточно сложным, чтобы получить докторскую степень. И, конечно, вычисление Эйлера было приближением и в другом смысле: он не только отсек бесконечную сумму, но также должен был отсекать энергетические уровни, чтобы получить конечные интегралы в тех терминах, которые он рассматривал.
«Трудности расхождения, острые проблемы с бухгалтерским учетом — к середине 1930-х КЭД казался нечестивым беспорядком», — говорит Кайзер в Разделение теорий . «Настолько же трудновыполнимой с точки зрения расчетов, насколько и концептуально запутанной». Чтобы разобраться в этом беспорядке, понадобились два гиганта физики, Фриман Дайсон и Ричард Фейман. Их изобретательный подход — это то, что мы рассмотрим в следующей статье.
Дополнительная литература
Книга Дэвида Кайзера Разделение теорий исследует развитие диаграмм Фейнмана и содержит прекрасное введение в темы, обсуждаемые в этой статье.
Об этой статье
Марианна Фрейбергер и Рэйчел Томас являются редакторами Plus . Они взяли интервью у Дэвида Кайзера в Бостоне в феврале 2013 года. Они очень благодарны Джереми Баттерфилду, философу физики из Кембриджского университета, и Назиму Буатте, научному сотруднику по основам физики Кембриджского университета, за их многочисленные терпеливые объяснения. и помощь в написании этой статьи.
Да, вы можете манипулировать бесконечностью — в математике
Большинство из нас изучали основные системы счисления в средней школе — целые числа (целые положительные и отрицательные числа), дроби (отношения чисел), действительные числа (все эти бесконечно продолжающиеся десятичные дроби). ), а может быть, и комплексные числа (со злобной буквой «i», притаившейся и доставляющей неприятности). Для большинства повседневных математических вычислений эти числа работают очень хорошо.
Однако некоторые типы чисел плохо представлены действительными числами. Действительные числа не оперируют бесконечно большими числами или обратными им числами — числами, которые бесконечно малы. В лучшем случае реальные числа равны расширил символами положительной бесконечности (∞ или + ∞) или отрицательной бесконечности (- ∞) для обозначения чисел, которые слишком велики или слишком малы для обработки системой. Однако правила действительных чисел предотвращают любые реальные манипуляции с этими символами. Например, отношение ∞ – ∞ не равно нулю, а не определено.
Действительные числа не оперируют бесконечно большими числами или обратными им числами — числами, которые бесконечно малы. В лучшем случае реальные числа равны расширил символами положительной бесконечности (∞ или + ∞) или отрицательной бесконечности (- ∞) для обозначения чисел, которые слишком велики или слишком малы для обработки системой. Однако правила действительных чисел предотвращают любые реальные манипуляции с этими символами. Например, отношение ∞ – ∞ не равно нулю, а не определено.
Гиперреальная система счисления расширяет действительные числа, чтобы точно обрабатывать бесконечность. Обратите внимание, что на самом деле существует несколько способов обработки бесконечно больших чисел. Но я обнаружил, что одна конкретная система имеет более практическое применение, чем другие системы, поэтому я думаю, что ее стоит обсудить. Думать о бесконечностях несколько уму непостижимо, но оказывается, что на самом деле Манипулирование бесконечностями с помощью гиперреальной системы невероятно просто, если вы знакомы с основами алгебры.
Для гиперреалов введено новое число, обозначающее бесконечность. Поскольку гиперреальные числа являются новыми, не существует универсального стандарта для обозначения бесконечности, поэтому я обычно использую строчную греческую омегу (ω). Так что же такое ω? Вы должны думать о ω как о своего рода единице, но вместо того, чтобы представлять физическую величину (например, фут, милю или килограмм), он представляет числовую величину, которая является бесконечностью.
Как мы увидим, существует множество различных бесконечностей. Итак, если мы не можем считать до бесконечности (у кого есть время?) и существует несколько бесконечностей, то какая из них является ω? Как оказалось, конкретная бесконечность, к которой он относится, на самом деле не имеет значения, при условии, что мы последовательны в этом отношении. То есть мы можем сказать, что ω представляет некоторую конкретную бесконечность. Нам не нужно знать, какой именно, мы просто должны согласиться, что он не изменится.
Если вам нужно представить конкретное число, представьте себе единицу с бесконечным числом нулей, следующих за ней. Если у вас есть такая бесконечная единица, как ω, вы можете многое с ней сделать. Мы можем умножить бесконечность на два и получить 2 ω. Мы можем добавить к нему единицу и получить ω + 1. Это все гипердействительные числа. Можем даже квадрат бесконечность и ω 2 . Что такое ω 2 ? Подумайте об этом так: если у меня есть число 100 (два нуля в конце) и я умножу его на 100 (два нуля в конце), я получу число 10 000 (четыре нуля в конце). Итак, если я возьму число ω и умножу его на ω, я получу ω 2 , что вы можете представить как наличие двух бесконечных наборов нулей в конце.
Итак, как и обычные математические символы, гиперреальные числа можно складывать, вычитать, умножать и делить. ω + ω равно 2ω. ω х ω равно ω 2 . ω 7 /ω 3 есть ω 4 . По сути, вы можете обращаться с ω так, как если бы оно было x , за исключением того, что оно имеет несколько особых свойств, поскольку оно бесконечно.
Действительные числа — это, в основном, числа, у которых нет компоненты ω. В качестве альтернативы вы можете представить их как умноженные на ω 0 (поскольку все, что возведено в нулевую степень, равно 1).
Что, если мы разделим на ω? Что такое 1/ω или ω -1 ? Это известно как бесконечно малая, бесконечно малая величина. Поскольку бесконечно малые числа используются так часто, полезно иметь для них специальный символ — строчную букву греческого эпсилон (ε). Если у меня есть, скажем, 5 + ε, я имею в виду число, бесконечно близкое к 5. То есть не существует действительного числа между 5 и 5 + ε.
Точно так же, как мы изобразили ω как 1 с бесконечным числом нулей после нее, вы можете изобразить ε как десятичное число, похожее на 0,0000001, за исключением того, что есть бесконечное число 9.0273 количество нулей между десятичным знаком и 1. Точно так же, если у вас есть ε 2 , вы можете думать об этом как о числе, которое имеет два бесконечных набора нулей между десятичным знаком и 1.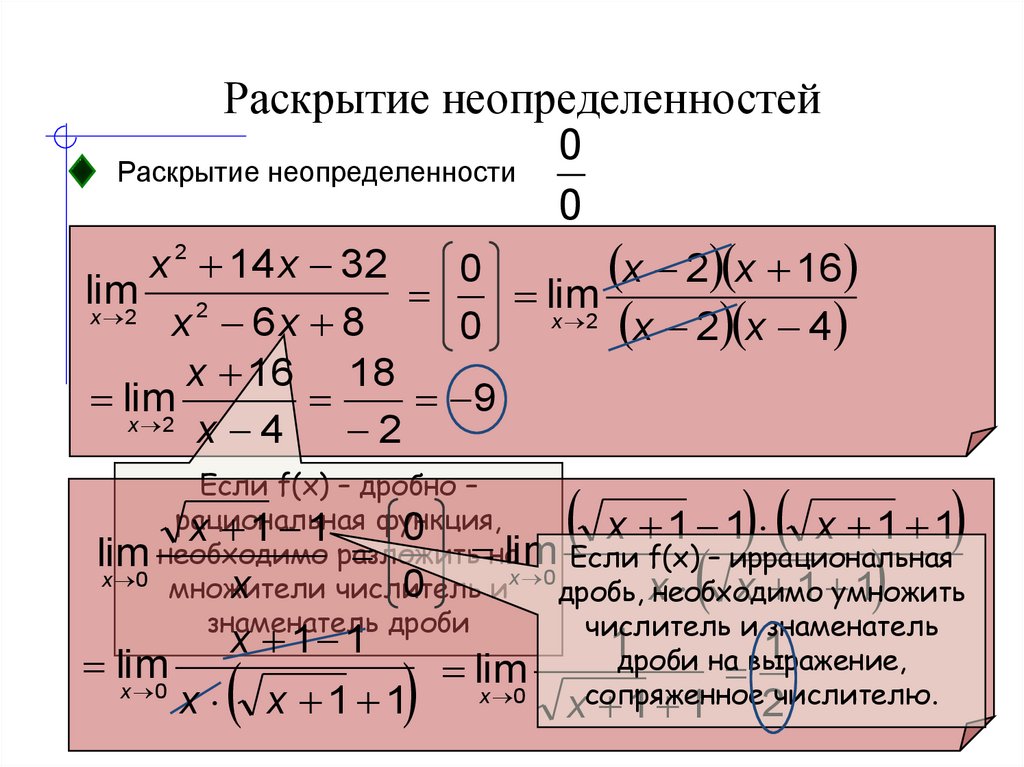
Итак, например , 5 + ε + 7 ε 2 — это гипердействительное число, которое бесконечно близко к 5, но немного дальше на числовой прямой, чем 5 + ε (но ненамного!).
Как это помогает нам заниматься математикой и решать задачи? Оказывается, гипердействительная система счисления значительно упрощает некоторые аспекты математики. В качестве простого примера предположим, что у нас есть следующее уравнение:
Допустим, мы хотели узнать, каково значение этого уравнения при x = 5. Что мы получим? У нас получится:
Ноль, деленный на ноль, является неизвестным значением. Итак, если мы не можем понять, что это такое при x = 5, что, если мы немного подтолкнем x ? Что, если мы посмотрим на x = 5,01? Оказывается, это выражение имеет проблему только при x = 5; любой другой номер работает отлично. Однако с реальными числами нам пришлось бы изменить x небольшое конечное количество, чтобы получить ответ. Однако это будет неточно, потому что мы всегда можем выбрать значение немного ближе к 5. Например, мы могли бы посмотреть на 5,0001 или 5,0000001. Но с гиперреальными мы можем вместо этого увеличить x на бесконечно малую величину. Если мы посчитаем значение при 5 + ε, расчет получится:
Например, мы могли бы посмотреть на 5,0001 или 5,0000001. Но с гиперреальными мы можем вместо этого увеличить x на бесконечно малую величину. Если мы посчитаем значение при 5 + ε, расчет получится:
Итак, результатом этого является 10 + ε, что бесконечно близко к числу 10. Чтобы быть явным, вы можете использовать функцию «стандартной части» std, чтобы «округлить» значение до ближайшего действительного числа. Другими словами, std(10 + ε) = 10. Следовательно, для данной дроби мы можем сказать, что для всех практических целей, когда x = 5, результат равен 10. Это невозможно сделать с действительными числами. Концепция «лимита» в реальных числах очень похожа на этот процесс. Однако ограничения опираются на множество доказательств и дополнительных правил, которые по сути не нужны при использовании гиперреальных чисел. С гиперреальными числами вы можете просто рассчитать значения напрямую.
Короче говоря, гиперреальные числа — это новый тип чисел, который был разработан, чтобы упростить и переосмыслить то, как мы имеем дело с очень большими и очень маленькими числами. Это снижает сложность задачи и позволяет нам использовать наши отточенные школьные навыки алгебры для легкого решения сложных задач.
Это снижает сложность задачи и позволяет нам использовать наши отточенные школьные навыки алгебры для легкого решения сложных задач.
Если вам понравилось это обсуждение гиперреальных чисел, вам также может понравиться:
Не выходите из дома без этих трех кривых: три математические кривые объясняют многое из того, что происходит — и не происходит — в повседневной жизни. (Джонатан Бартлетт)
и
Существуют непостижимые вещи. Учебник по номеру Чайтина (Роберт Дж. Маркс)
Вот короткая серия из пяти статей Роберта Дж. Маркса об уникальной, бросающей вызов реальности природе математических бесконечностей:
Часть 1: Почему бесконечности не существует в реальности. Несколько примеров покажут, к каким абсурдным результатам приводит предположение, что в окружающем нас мире существует бесконечность, как в математике. В серии из пяти постов я объясняю разницу между тем, что означает — и не означает — бесконечность как понятие.
Несколько примеров покажут, к каким абсурдным результатам приводит предположение, что в окружающем нас мире существует бесконечность, как в математике. В серии из пяти постов я объясняю разницу между тем, что означает — и не означает — бесконечность как понятие.
Часть 2. Бесконечность показывает, что у Вселенной есть начало. Логические последствия буквально бесконечного прошлого абсурдны, как покажет простой пример. Абсурдность, которую создало бы бесконечное прошедшее время, хотя и не является окончательным математическим доказательством, является веским доказательством того, что наша Вселенная имела начало.
Часть 3. В бесконечности линии и квадраты имеют одинаковое количество точек Роберт Дж. Маркс: Мы можем продемонстрировать этот факт с помощью простой диаграммы. Этот контринтуитивный результат, основанный на теории бесконечностей Кантора, кажется странным. Тем не менее, это верное свойство бесконечности.
Часть 4. Как практически любые числа можно закодировать Библиотека Конгресса. Роберт Дж. Маркс: Это странное, парадоксальное, но вполне реальное следствие концепции бесконечности в математике. Математика: Почти каждое число между нулем и единицей, случайно выбранное при подбрасывании монеты, в какой-то момент будет содержать двоичную кодировку Библиотеки Конгресса.
Роберт Дж. Маркс: Это странное, парадоксальное, но вполне реальное следствие концепции бесконечности в математике. Математика: Почти каждое число между нулем и единицей, случайно выбранное при подбрасывании монеты, в какой-то момент будет содержать двоичную кодировку Библиотеки Конгресса.
и
Часть 5. Некоторые бесконечности больше других, но самой большой из них не существует Георг Кантор придумал гениальное доказательство того, что бесконечности могут различаться по размеру, даже если обе остаются бесконечными. В этой короткой серии из пяти частей мы показываем, что бесконечность — это красивая и доказуемая математическая теория, которая не может существовать в реальности без нелепых последствий.
Вы также можете прочитать: Да, вы можете манипулировать бесконечностью в математике. Гиперреалы больше (и меньше), чем ваше среднее число — и лучше! (Джонатан Бартлетт)
Начало бесконечности, часть 2
Часть 2 моего интервью с Бреттом Холлом о начале бесконечности. См. также часть 1.
См. также часть 1.
С хорошей теорией познания вы можете решить, что еще верно
Теория Дэвида Дойча основана на хороших объяснениях
Военно-морской флот: У Дэвида Дойча прекрасное видение мира, согласно которому он считает, что все важное понятно одному человеку. Под важным он подразумевает базовые теории, лежащие в основе большей части реальности.
Дойч зацикливается на четырех теориях. Я мог бы возразить, что, может быть, есть еще несколько, особенно если вы начнете углубляться в Адама Смита и Богатство наций и несколько других более социологических. Но он, очевидно, физик, которого больше интересует реальность и поиск истины, а не человеческие системы.
Он выбрал четыре теории эпистемологии; теория эволюции путем естественного отбора; квантовая теория, в которую он включает теорию относительности и другую физику; и теория вычислений, которая включает его теорию квантовых вычислений.
Эти четверо очаровательны. Наверное, стоит изучить, что интересного в каждом из них. В чем здесь прорыв, который может быть неочевидным?
Наверное, стоит изучить, что интересного в каждом из них. В чем здесь прорыв, который может быть неочевидным?
Начнем с эпистемологии.
Причина, по которой я люблю Начало бесконечности в том, что Дойч делает очень тщательный обзор того, что является правильным в эпистемологии, что мы знаем как лучшие ответы. Когда у вас есть хорошая теория познания, вы можете решить, что еще верно.
Если вы начинаете с плохой основы для теории познания, то вы будете принимать решение о множестве вещей, которые ложны, когда вы думаете, что они могут быть правдой.
И его эпистемология сосредоточена вокруг хороших объяснений. Он принимает точку зрения Поппера на науку и поиск истины как на механизмы исправления ошибок и расширяет ее. Я хотел бы услышать ваше краткое изложение теории познания или эпистемологии, как ее излагает Дойч.
Никакая истина не может быть оправдана
«Знание» — это всего лишь наше лучшее предположение в то время
Бретт: Первоначальные предположения о том, что такое «знание», сводились к тому, что известно как «обоснованное истинное убеждение».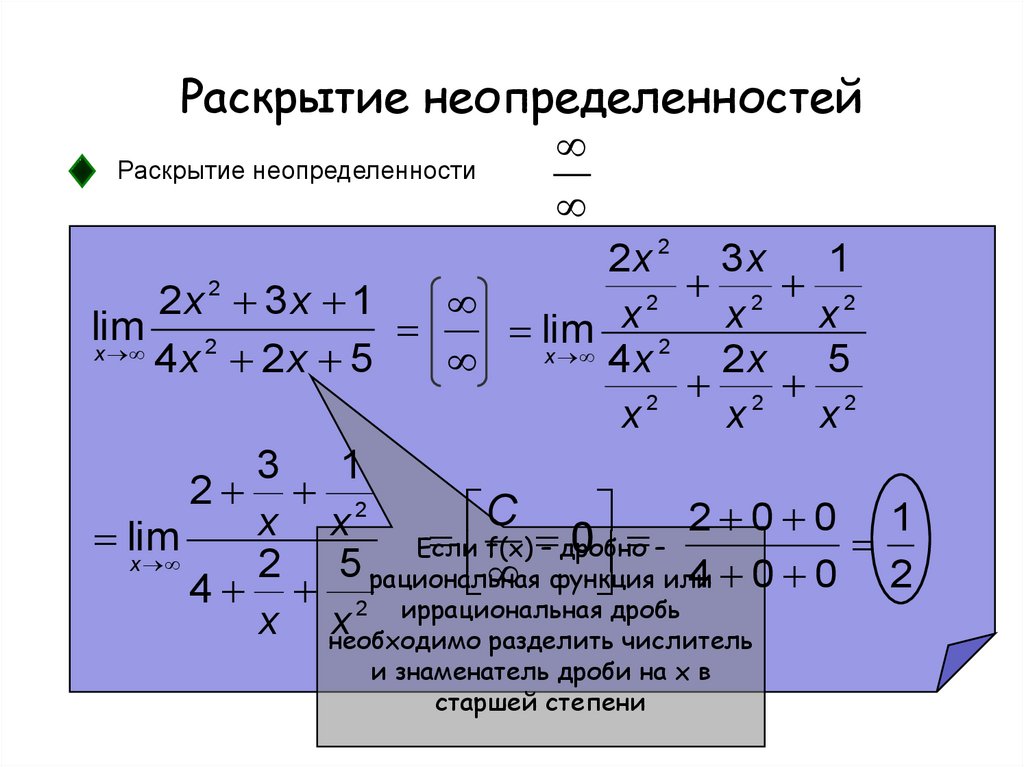 видение знания, и это все еще самая распространенная идея сегодня. Любой, кто называет себя байесианцем, является оправданным истинным верующим.
видение знания, и это все еще самая распространенная идея сегодня. Любой, кто называет себя байесианцем, является оправданным истинным верующим.
Это заблуждение, что знание — это попытка оправдать ваши убеждения как истинные. И если вы это сделали, то можете сказать: «Я знаю эту штуку». Если я могу обосновать свою теорию тяготения как истинную, то я должен поверить в эту теорию тяготения и только тогда я могу сказать, что она известна.
Проблема в том, что нет никакого способа показать, что какое-либо знание истинно. Улучшение, которое Дойч продвигает в своих книгах, — это видение, которое дал нам Поппер, что все, что у нас есть, — это догадки о реальности. Это предположения.
Люди думают: «О, это звучит немного расплывчато. Это просто предположение». Ну, это не случайное предположение. Это догадка, которая устояла против испытаний, против попыток показать, что она ложна. Дело не в том, что все, кто решает угадать, находятся в равных условиях.
Когда люди не могут доказать, что что-то ложно — с помощью этого метода опровержения — тогда мы принимаем это как часть знания. Это позволяет нам принять тот факт, что мы сможем добиться прогресса в будущем, потому что все наши знания носят предположительный характер. Все это наши лучшие предположения на данный момент.
Это позволяет нам принять тот факт, что мы сможем добиться прогресса в будущем, потому что все наши знания носят предположительный характер. Все это наши лучшие предположения на данный момент.
В знании есть эластичность, которая позволяет нам сказать: «Будут ошибки. Мы их исправим и, таким образом, сможем продвинуться в бесконечное будущее».
Это не похоже на предыдущую концепцию знания, которая гласит: «Если вы признали что-то истинным, значит, это правда». Если это правда, то это означает, что в этом нет ничего ложного, и, следовательно, оно не может быть опровергнуто. Это очень религиозное понятие.
Современным заклинанием этого является байесианство, которое гласит: «У вас есть теория, вы собираете больше доказательств и со временем становитесь все более и более уверенным в том, что ваша теория верна».
Дальше становится немного хуже, потому что потом говорится: «Это байесовское рассуждение позволяет генерировать новые теории». Что не может. Лучшее, на что он может надеяться, — это показать вам, что вы более уверены в этой теории, чем в ней.
Попперовский взгляд гласит: «Если вы можете показать, что в конкретной теории есть изъян, вы можете отказаться от этой теории».
Не может быть окончательной теории гравитации
Все, что у нас есть, — это все более и более совершенные приближения к реальности
Бретт: Почти во всех случаях у вас есть только одна теория.
В случае с гравитацией на данный момент предлагается буквально только одна теория. Есть общая теория относительности. Раньше у нас было две теории. У нас была ньютоновская гравитация и общая теория относительности, но мы провели решающий эксперимент.
Эта идея важного эксперимента — вишенка на вершине науки. У вас есть две конкурирующие теории. Если эксперимент пойдет в одну сторону, одна теория будет исключена, а другая — нет. В этом случае вы придерживаетесь этой теории до тех пор, пока не возникнет никаких проблем.
Такое видение знания позволяет нам двигаться вперед без ограничений.
Это совершенно не похоже на любое другое представление о знаниях. Подавляющее большинство физиков по-прежнему байесовцы. И причина, по которой они все еще байесовцы, заключается в том, что этому обычно учат в университетах, и именно это считается интеллектуально строгим способом понимания мира.
Но все это то, что я бы назвал разновидностью сциентизма. Это потому, что за ними стоит формула, теорема Байеса, которая является вполне приемлемой статистической формулой. Люди постоянно используют его совершенно законными способами. Просто это не эпистемология. Это не способ гарантировать или даже быть уверенным в том, что ваша теория действительно верна.
Мой любимый пример этого: до 1919 года каждый эксперимент, который проводился с гравитацией, показывал, что он согласуется с теорией гравитации Ньютона. Что говорят байесовцы в такой ситуации? Говорят, вы все больше и больше доверяете теории Ньютона.
Как это понимать? Как вы увязываете это с тем, что за день до того, как было доказано, что это ложь, был день, когда вы были в этом больше всего уверены?
Теперь у попперианца нет этой проблемы. Попперианец говорит: «Никогда теория Ньютона не была на самом деле верна. В нем была доля правды, но эту правду мы не можем измерить».
Попперианец говорит: «Никогда теория Ньютона не была на самом деле верна. В нем была доля правды, но эту правду мы не можем измерить».
Я говорю, что в нем есть доля правды, потому что оно определенно имеет более прямую связь с реальностью, чем догадки какого-то другого случайного человека о природе гравитации. Гравитация действительно приблизительно изменяется по закону обратных квадратов, но не точно. Нам нужна была общая теория относительности, чтобы исправить ошибки в ньютоновской теории гравитации.
И хотя общая теория относительности является нашим лучшим предположением прямо сейчас, она не может в конечном счете быть окончательной теорией гравитации. Не может быть окончательной теории гравитации. Все, что у нас есть, — это все лучшее и лучшее приближение к реальности.
Флот: Я думаю, что причина, по которой мы так легко впадаем в байесианство, вероятно, связана с тем, почему мы так легко впадаем в пессимизм. Мы эволюционно запрограммированы на байесианство.
Любое другое животное на планете, которое может дать хорошее объяснение, является байесовцем. Они просто смотрят на повторяющиеся события и говорят: «Вчера взошло солнце. Завтра взойдет солнце». Или: «То, к чему я прикоснулся, горячее. Вероятно, в будущем будет жарко». Так работало большинство наших биологических систем и большая часть нашего эволюционного наследия.
Просто сейчас у нас есть неокортекс, который может давать хорошие объяснения видимого с точки зрения невидимого. Это дает нам более высокий уровень рассуждений, но этот более высокий уровень рассуждений не является для нас инстинктивным. Это требует усилий. Это требует глубокого мышления.
Мы по умолчанию придерживаемся байесовского подхода, потому что именно так устроена большая часть окружающего нас природного мира, по крайней мере, на чисто биологическом уровне.
Генетическая эволюция была прелюдией к меметической эволюции
Идеи проходят тот же эволюционный процесс, что и гены
Бретт: У Поппера есть книга под названием « Объективное знание » с подзаголовком «Эволюционный подход». И это тоже не случайно. Существует симметрия между теорией эпистемологии и теорией эволюции, как мы ее понимаем.
И это тоже не случайно. Существует симметрия между теорией эпистемологии и теорией эволюции, как мы ее понимаем.
До того, как мы поняли, что известно как дарвиновская теория эволюции, единственная идея, которая была у людей, заключалась в том, что эти существа должны быть созданы. Все растения и животные, которых вы видите вокруг себя, должны были быть созданы творцом. Другого объяснительного механизма не было.
Некоторым людям пришла в голову идея постепенных изменений с течением времени. Ламарк был одним из них. Его идея заключалась в том, что причина, по которой у жирафов длинная шея, заключается в том, что у их предков шеи были немного короче, поэтому они пытались вытянуть шею, чтобы дотянуться до листьев, до которых они не могли дотянуться.
Но опять же, для этого не было никакого механизма, кроме того факта, что человек ходит в спортзал и работает над своими бицепсами, и их бицепсы со временем становятся немного больше. Хотя вы можете тренироваться в спортзале и увеличить размер своих бицепсов, это не означает, что ваши дети унаследуют эти характеристики.
То, что придумал Дарвин, похоже на то, что придумал Поппер. Это было исправлением ошибки. Идея состоит в том, что организм испытывает себя в определенной среде, и если он, как мы говорим, не подходит для этой среды, то он вымирает. Но если бы он был приспособлен к этой среде, то он бы выжил.
Итак, вы столкнулись с реальностью между живыми организмами и окружающей средой. И именно окружающая среда дает вам обратную связь с реальностью и уничтожает те организмы, которые недостаточно приспособлены для выживания.
Неодарвинистская точка зрения должна дать нам то, что является единицей отбора. Это не группа или стадо; это даже не личность. Это ген. Это идея эгоистичного гена, пришедшая к нам от Ричарда Докинза, который говорит, что если какой-либо из этих генов окажется неподходящим для конкретной среды, это может привести к гибели этого организма. Вид может выжить, но вся его ДНК будет очень тонко меняться с течением времени по мере изменения окружающей среды.
Теперь мы подняли этот уровень. Мы, человеческие существа, являемся следующим шагом в этом эволюционном процессе, когда мы можем создавать объяснительные знания, которые делают то же самое. Дойч любит говорить: «Генетическая эволюция была лишь прелюдией. Что будет дальше, так это меметическая эволюция».
Мы, человеческие существа, являемся следующим шагом в этом эволюционном процессе, когда мы можем создавать объяснительные знания, которые делают то же самое. Дойч любит говорить: «Генетическая эволюция была лишь прелюдией. Что будет дальше, так это меметическая эволюция».
С этого момента история Вселенной будет историей идей, проходящих тот же эволюционный процесс, что и гены.
Люди исключительны
Люди — это не просто форма бактерий, заполонивших планету
Военно-морской флот: Три из этих четырех теорий имеют интересную закономерность. С хорошими объяснениями в эпистемологии мы говорим, что предположения, их опровержения и исправление ошибок — это то, как мы улучшаем знания. Генетическая эволюция, генетические мутации, изменчивость и естественный отбор отсеивают те, которые не сработали. Кроме того, существует меметическая эволюция, когда у нас появляются идеи, а затем критика отсеивает идеи, которые не работают.
В связи с этим в изобретательстве есть метод проб и ошибок. При капитализме стартапы создаются, а те, у кого плохие идеи, терпят неудачу. Мы видим, что эта закономерность повторяется снова и снова.
При капитализме стартапы создаются, а те, у кого плохие идеи, терпят неудачу. Мы видим, что эта закономерность повторяется снова и снова.
Что интересно, здесь есть еще один метапаттерн, что люди исключительны. В эпистемологии люди — единственные небайесовские мыслители. В эволюции люди — единственные известные нам меметические существа. В теории вычислений люди являются единственными известными нам универсальными объяснителями, кроме, конечно, изобретенных нами компьютеров.
Наука привела нас от представления о том, что люди находятся в центре Вселенной, к следующему: «На самом деле в людях нет ничего особенного. Вы всего лишь одна маленькая планета из почти бесконечного числа планет Кеплера , на которых может быть жизнь». Но три из этих четырех теорий, о которых мы говорим, указывают нам на то, что люди являются исключительными. Человек способен к максимальному знанию.
Одно интересное осознание для меня заключалось в том, что даже если бы вы были Богом, даже если бы вы обладали бесконечными знаниями и силой, даже если бы вы контролировали всю вселенную, вы все равно не знали бы, что находитесь не в симуляции. Вы все равно никогда не сможете доказать, что вы не в симуляции. И даже как Бог, нет понятия, которое вы могли бы удержать в своей голове, чего не мог бы удержать человек.
Вы все равно никогда не сможете доказать, что вы не в симуляции. И даже как Бог, нет понятия, которое вы могли бы удержать в своей голове, чего не мог бы удержать человек.
Если, конечно, законы физики другие. Если законы физики другие, то все ставки сняты, и кто знает? Но работая в рамках действующих законов физики, люди способны к максимальному знанию и максимальному осознанию. Это указывает на мир, в котором люди исключительны, а не просто еще одна форма бактерий, которые вышли из-под контроля и заполонили эту планету.
Многие из этих фундаментальных теорий ведут к точке зрения, что люди особенные, знания безграничны, и пока мы не уничтожаем средства исправления ошибок и постоянно создаем новые знания, есть все основания оптимистичный.
Мы качественно отличаемся от других видов
Нет континуума между людьми и шимпанзе
Бретт: Вы указываете на мнение меньшинства. Я думаю, что культура все еще застряла во второй части того, о чем вы говорили.
Изначально мы думали, что находимся в центре вселенной. Это была религиозная концепция места человека в космосе. Земля была окружена небесными сферами, и все вращалось вокруг нее. Так что мы были наследниками всей вселенной, и Бог наградил нас этим.
Затем наука показала нам, что на самом деле мы не находимся в особом месте во Вселенной. Это космологический принцип, эта идея о том, что Вселенная примерно одинакова в каждом отдельном месте, а мы являемся лишь одним из этих особенно необычных мест.
Мы не только не особенные в космологическом смысле, но и биологически мы не являемся чем-то особенным. Мы просто находимся на континууме между бактериями, тараканами, собаками и шимпанзе.
Нил Деграсс Тайсон, астрофизик, которого я очень люблю почти по всем остальным темам, говорил о том, что шимпанзе намного умнее, чем мы думаем, и что мы, возможно, не намного лучше. Так думают почти все.
Третья точка зрения, которую сейчас пытаются продвигать многие из нас, состоит в том, что между шимпанзе и нами нет незначительной количественной разницы. Существует континуум между бактериями, тараканами, собаками и шимпанзе, но мы отклоняемся от оси.
Существует континуум между бактериями, тараканами, собаками и шимпанзе, но мы отклоняемся от оси.
Мы качественно разные. Все, что нам нужно сделать, это открыть глаза. Вы смотрите в окно на этот прекрасный город, который оказался там, и его нельзя объяснить постепенным увеличением биологической сложности.
Больше вычислительной мощности не создает AGI
Даже самые мощные компьютеры не могут ответить на вопрос “почему?” сила, и вы получите интеллект», когда мы не знаем, что находится внутри, что делает нас творческими и позволяет нам придумывать хорошие объяснения.
Люди много говорят о GPT-3, механизме сопоставления текстов, разработанном OpenAI , который является очень впечатляющим программным обеспечением. Они говорят: «Эй, я могу использовать GPT-3 для создания отличных твитов». Это потому, что, во-первых, как человек, вы выбираете хорошие твиты из всего мусора, который он генерирует. Во-вторых, он использует некоторую комбинацию плагиата и сопоставления синонимов и так далее, чтобы придумать правдоподобно звучащий материал.
Самый простой способ понять, что то, что он генерирует, на самом деле не имеет никакого смысла, — это задать ему дополнительный вопрос. Возьмите вывод, сгенерированный GPT-3, и спросите его: «Почему это так?» Или сделайте прогноз, основанный на этом, и наблюдайте, как он полностью разваливается, потому что нет никакого основного объяснения.
Это попугай. Это блестящее байесовское рассуждение. Он экстраполирует то, что он уже видит, созданное людьми в Интернете, но у него нет базовой модели реальности, которая могла бы объяснить видимое с точки зрения невидимого. И я думаю, что это критично.
Это то, что люди делают уникально, чего не делает ни одно другое существо, никакой другой компьютер, никакой другой разум — биологический или искусственный — с которым мы когда-либо сталкивались.
И мы не только делаем это уникально, но если бы мы встретили инопланетный вид, который также обладал способностью генерировать эти хорошие объяснения, не было бы объяснения, которое они могли бы генерировать, которое мы не могли бы понять.
Мы максимально способны понимать. Не существует концепции, возможной в этой физической реальности, которую человек, обладающий достаточным временем, ресурсами и образованием, не смог бы понять.
Удивительно, что наши умы не могут быть взорваны
Люди могут понять каждую идею, если у них достаточно времени и усилий
Бретт: совокупность законов физики. Возможно, мы не сможем понять инопланетян». Это не что иное, как обращение к сверхъестественному. Это логически эквивалентно «Бог где-то рядом, и вы никак не можете понять, что такое Бог. Бог — это бесконечное, всеведущее существо, которое находится за пределами нас».
Можешь в это поверить, если хочешь. Вы можете поверить в гипотезу симуляции. Вы можете верить любой из этих вещей. Все это метафизические заявления о реальности, к которой у нас нет доступа. Независимо от того, хотите ли вы представить инопланетян, у которых будут идеи, которые мы не можем понять, все это стоит на одной ноге.
Флот: По крайней мере, в метафизике Бога вы могли бы сказать: «Хорошо, это в другой вселенной. Это выходит за рамки наших законов физики». Но инопланетяне, предположительно, будут подчиняться тем же законам физики, так что я даже не понимаю, на чем это основано.
Любой вид, достаточно умный, чтобы покинуть свою родную планету, знает, что ограничивающим фактором являются идеи. Так что больше всего они должны хотеть от любого другого вида, с которым они сталкиваются, — это новых идей. И торговля, которой они должны заниматься, — это торговля идеями.
В научной фантастике есть мальтузианская философия – теперь она называется гипотезой темного леса – что каждый вид человека похож на бактерию, и нам скоро не хватит места. Нет, вселенная бесконечна в размерах; он расширяется. Мультивселенная еще более бесконечна в размерах.
Мы в начале бесконечности. У нас не заканчиваются ресурсы. Все создают идеи. Умные инопланетные цивилизации обмениваются идеями, а успешные человеческие цивилизации обмениваются идеями. Потому что эти идеи берут вещи, которые раньше были бесполезны, и превращают их в ресурсы.
Потому что эти идеи берут вещи, которые раньше были бесполезны, и превращают их в ресурсы.
Каждая инопланетная цивилизация может обмениваться идеями с любой другой цивилизацией, потому что все они являются универсальными объяснителями. Они способны к максимальному пониманию.
На самом деле, сногсшибательная вещь здесь заключается в том, что ваш мозг нельзя взорвать. Нет такой идеи, которую ваш разум не смог бы воспринять, учитывая время и усилия.
Так что, если мы столкнемся с инопланетянами, нам, наверное, следует радоваться. Им не нужно ничего от нашей планеты, кроме наших идей. И лучший способ обмениваться идеями — иметь динамичную, изобильную, процветающую цивилизацию.
Поскольку я вырос на механической фантастике, я пессимистично относился к встречам с инопланетянами. «О да, если мы столкнемся с инопланетянами, они просто уничтожат нас». Например, в «Путеводителе автостопом по Галактике» вогоны бездумно разрушили Землю, чтобы освободить место для обхода гиперпространства.
Реальность такова, что любой вид, который найдет нас, немедленно передаст нам все свои знания. И они будут жаждать новых знаний, которые есть у нас, потому что они поймут, что это позволит им осветить темную материю, темную энергию, неиспользованные ресурсы во Вселенной, чтобы позволить им также процветать.
Где инопланетяне?
Вселенная должна быть кишит инопланетянами
Военно-морской флот: Давайте кратко поговорим о парадоксе Ферми , поскольку мы говорим об инопланетянах. Для тех, кто не знает, Энрико Ферми был известным физиком, участвовавшим в Манхэттенском проекте. Он сказал: «Где инопланетяне?»
Вселенная так велика, и в ней, вероятно, так много планет, которые способны поддерживать ту или иную жизнь. Разве мы не должны были увидеть их сейчас?
Бретт: Почти у каждой звезды есть группа планет, очень похожих на нашу Солнечную систему. Количество звезд, которые существуют в типичной галактике, такой как Млечный Путь, составляет около 200 миллиардов, хотя оценки доходят до 400 миллиардов. Количество галактик, которые мы можем видеть, составляет от 200 до 300 миллиардов.
Количество галактик, которые мы можем видеть, составляет от 200 до 300 миллиардов.
Наблюдаемая Вселенная – это лишь малая часть всей Вселенной, а это значит, что количество планет абсолютно астрономическое.
Несомненно, учитывая эти цифры, должно быть так, что есть не только планеты, пригодные для жизни, но и что Вселенная должна изобиловать цивилизациями, намного более развитыми, чем наша, менее развитыми, чем наша, и некоторыми, которые по развитию аналогичны нашим.
Так где же они?
Разумные виды возродились только один раз на планете Земля
Творческий интеллект не был неизбежен
Бретт: Итак, это один аргумент, и мы должны быть скромными перед лицом неопределенности, потому что никто не знает. Но я хочу привести аргумент, который редко получает эфирное время.
Аргумент в том, что мы одни.
Аргумент не имеет ничего общего с астрономией; это имеет прямое отношение к биологии. Аргумент звучит так: посмотрите на планету Земля и посмотрите на количество видов, которые существуют не только сейчас — их миллионы, — но и на количество видов, которые когда-либо существовали на планете Земля, а это сотни миллионов.
Жизнь возникла примерно три с половиной миллиарда лет назад, и около двух с половиной миллиардов лет не существовало ничего, кроме бактерий. Таким образом, жизнь, по-видимому, не имеет особого стимула для быстрого развития помимо бактерий; он просто остается настолько простым, насколько это возможно.
У многих людей есть неверное представление, от которого Дарвин действительно отказался, — представление о том, что эволюция имеет определенное направление. Вы видите эти картины эволюции, которые появляются в школьных учебниках с изображением обезьяны, которая ковыляет на четвереньках; затем он сгорбился; а затем, в конце концов, он встает и держит портфель, как будто это то, что имела в виду эволюция. Это только кажется, что эволюция имела в виду в ретроспективе, оглядываясь назад.
Есть американский ученый Чарли Лайнуивер, который называет это гипотезой «Планеты обезьян» — например, если вы уберете людей с планеты, обезьяны естественным образом эволюционируют, чтобы заполнить нишу интеллекта.
Он сказал, что вы можете представить себе другую ситуацию, когда вы слон, способный думать о себе. Они размышляют о длине своего хобота, оглядываются на биологическую эволюцию и видят, что хоботы становятся все короче. Итак, они заключают: «Ах, эволюция была направлена на создание все более длинных стволов. Вот что такое эволюция».
Конечно, мы видим, что это смешно. Просто так случилось, что это существо, называемое слоном, эволюционировало, и у него такой длинный хобот, но длина хобота, похоже, не является конвергентной характеристикой эволюции.
Конвергентная особенность эволюции — это особенность, существующая в биологических объектах, которая возникает снова и снова независимо. Крылья – мой любимый пример. У рыб есть крылья определенного вида. Есть летучие рыбы. У бабочек есть крылья, поэтому они есть у насекомых. Они возникли и у млекопитающих, у летучих лисиц и некоторых видов опоссумов. И, конечно, у птиц и динозавров тоже были крылья.
Крылья у всех этих видов продолжают расти независимо друг от друга. Так же как и глаза, и органы для звука.
Так же как и глаза, и органы для звука.
Теперь давайте подумаем о способности заниматься математикой или строить радиотелескопы — другими словами, быть разумным, творческим видом. Сколько раз это возникало в геологической истории Земли? У одного вида и только у одного вида.
Можем ли мы на этом основании заключить, что возникновение разумных видов неизбежно? Если бы вы повторили эксперимент, разбросав несколько бактерий вокруг всех экологически чистых планет, существующих во Вселенной, вы бы гарантированно получили существо, подобное нам?
Вероятность существования человека бесконечно мала
С точки зрения эволюции это практически невозможно
Бретт: Вот еще один способ подумать об этом, математически пугающий для людей, которые думают, что инопланетяне где-то там и они собираются посетить нас когда-нибудь в будущем.
Ранее мы говорили о триллионах планет, существующих по всей известной вселенной, которые могут даже быть благоприятными для возникновения жизни. Представьте, что между нами, разумными людьми, и самой простой формой бактерий, которую мы можем себе представить, всего 100 независимых эволюционных ступеней. Это неправда — вероятно, должен был произойти миллион или более различных мутаций, чтобы позволить организмам выжить так, как мы существуем сегодня, — но давайте сделаем только 100.
Представьте, что между нами, разумными людьми, и самой простой формой бактерий, которую мы можем себе представить, всего 100 независимых эволюционных ступеней. Это неправда — вероятно, должен был произойти миллион или более различных мутаций, чтобы позволить организмам выжить так, как мы существуем сегодня, — но давайте сделаем только 100.
Представьте, что каждый из этих независимых шагов имеет вероятность только один из 10. Теперь, на самом деле, это, вероятно, больше похоже на один на миллион, но мы будем великодушны и скажем один на 10. 10…100 раз. Это единица на 10, все в степени 100, то есть единица на единицу, за которой следуют 100 нулей. Это число затмевает астрономическое число планет, о котором я говорил ранее.
Другими словами, вероятность того, что мы поднимемся в этом споре, ничтожно мала. Тот факт, что это произошло однажды, должен поразить нас.
Если вы не можете это запрограммировать, значит, вы этого не поняли
Эволюционные алгоритмы не производят живых существ
Бретт: так много об эволюции посредством естественного отбора, чего мы не знаем.
У Дэвида Дойча есть небольшая шутка: «Если вы не можете это запрограммировать, значит, вы этого не поняли».
В случае с ОИИ это означает, что мы не можем его запрограммировать, потому что не понимаем идею общего интеллекта.
То же самое происходит и с эволюцией путем естественного отбора. Есть вещи, называемые эволюционными алгоритмами, но это не программирование эволюции путем естественного отбора. Это не возможность создавать искусственные объекты внутри компьютера, которые, подвергаясь реальному давлению окружающей среды, способны развиваться в направлении этой возрастающей сложности.
Инопланетяне могут быть слишком далеко
Возможно, мы не одни во Вселенной, мы просто слишком далеко друг от друга
Бретт: У нас все еще есть проблема, связанная с тем, что делала ДНК в течение примерно двух с половиной миллиардов лет — подавляющей части истории жизни на Земле. Почему он вообще не развивался в то время? В чем дело?
Есть книга Rare Earth Питера Уорда и Дональда Браунли, и эти ребята рассказывают обо всех причудливых вещах, которые произошли в эволюционной истории Земли. Я просто обратил внимание на тот факт, что мы, универсальные объяснители, развились, по-видимому, случайно, по-видимому, когда-то; но вы можете вернуться назад и понять, что эволюция от одноклеточных бактерий к многоклеточному организму была странной и необычной и не могла быть повторена в лабораторных условиях.
Я просто обратил внимание на тот факт, что мы, универсальные объяснители, развились, по-видимому, случайно, по-видимому, когда-то; но вы можете вернуться назад и понять, что эволюция от одноклеточных бактерий к многоклеточному организму была странной и необычной и не могла быть повторена в лабораторных условиях.
Затем переход от многоклеточного организма к чему-то, похожему на растение, а затем к чему-то, похожему на животное — все это, кажется, произошло по причинам, которые мы не понимаем.
Военно-морской флот: Возможно сочетание нескольких вещей. Ваш аргумент может быть статистическим, а не абсолютным. Мы можем быть не одиноки во Вселенной, но стать универсальными объяснителями может быть настолько редко, что, если вы начнете умножать это на межзвездные расстояния, которые довольно велики, мы можем оказаться слишком далеко друг от друга.
Я думаю, что у Ферми также было необоснованное предположение, что межзвездные инопланетяне поймут, как превысить скорость света, когда у нас нет никакой гипотезы относительно того, как это возможно. У нас нет ничего даже смутного в категории того, как превысить скорость света.
У нас нет ничего даже смутного в категории того, как превысить скорость света.
Так что, если вы ограничены скоростью света и если переход к универсальным объяснителям редок, тогда мы можем быть слишком далеки друг от друга. И это может занять намного больше времени.
Вселенная очень большая, но она также почти полностью пуста, по крайней мере, в том, что касается планет и звезд. Учитывая это, вполне разумно будет сказать, что люди и человекоподобные объяснители довольно редки; они все еще находятся на ранней стадии своего формирования по всей вселенной; и они просто разбросаны на такие невероятно огромные расстояния, что мы не встречались друг с другом.
Если бы мы встретились, я думаю, мы бы знали.
Например, к тому времени, когда сюда прилетит инопланетный космический корабль, их радиоволны придут задолго до этого. В истории цивилизации есть довольно долгий период, когда она изобретает радио и начинает транслировать радиоволны, прежде чем она изобретет межзвездные путешествия и отправит ракеты и цивилизации по всей Вселенной.
Инопланетяне придут за знаниями, а не за ресурсами
Единственное, чего им будет не хватать, так это знаний, которых у них нет
Бретт: Я думаю, Стивен Хокинг сказал, что транслировать радиоволны во Вселенную было ошибкой, потому что инопланетяне будут там, и они будут похожи на конкистадоров. Они захотят захватить нашу планету из-за своих ресурсов и других вещей.
У вас может быть несколько ответов на мысль о том, что нас преследуют злые инопланетяне.
Во-первых, единственный способ продвинуться в бесконечное будущее и получить технологии, которые позволят вам путешествовать по галактике, — это иметь такое видение знаний, которое было у Поппера, а именно то, что вы можете свободно исследовать пространство идей, способное фальсифицировать предположения, и не иметь централизованной власти и применения силы к людям, что подавляет творчество.
Чтобы создать максимально созидательное общество, у вас должна быть свобода, у вас должна быть свобода, и поэтому у вас будет ненасильственное общество. У вас будет общество, которое ценит творчество как самоцель.
У вас будет общество, которое ценит творчество как самоцель.
Когда мы сталкиваемся с инопланетянами, мы не должны ожидать, что они будут безнравственными ублюдками, которые захотят завладеть нашими ресурсами, а наоборот: они будут смотреть на нас и думать, какие примитивные дикари что мы есть. Они подумают, что мы моральные карлики, и захотят нас учить. Они не захотят посадить нас в тюрьму или что-то в этом роде.
Знание — это единое целое. Если их физика настолько лучше нашей, что позволяет им приближаться к скорости света или использовать какую-то странную гравитационную штуку общей теории относительности, которая создает червоточину, чтобы они могли перемещаться в космосе быстрее, чем скорость света, то все их ученые будут намного дальше вперед. Все их знания уйдут далеко вперед: их математика, их мораль, их политические институты.
Так что нам не нужно беспокоиться об инопланетянах.
И, кстати, нам не нужно беспокоиться о том, что они украдут наши ресурсы. Не то чтобы они собирались сказать: «А, есть планета, полная угля и воды. Мы возьмем это».
Не то чтобы они собирались сказать: «А, есть планета, полная угля и воды. Мы возьмем это».
Нет, у них будут знания, позволяющие извлекать водород из межгалактического пространства, превращать его в термоядерный реактор и использовать 3D-печать для создания любой технологии, которую они захотят.
На самом деле это может быть еще одним ответом на парадокс Ферми. Им не нужно покидать свой район, потому что у них уже есть технология, которая идеально их поддерживает.
Флот: У них есть сферы Дайсона, и они могут собрать всю необходимую им энергию. Они могут собрать всю материю, они могут создать все, что захотят, и они могут иметь любую реальность в VR-пространстве, какую захотят.
Единственное, чего им будет не хватать, так это новых знаний, которых у них нет.
Идеи — новая нефть
Все новые состояния создаются идеями
Военно-морской флот: У людей есть история завоеваний, потому что мы боремся за одни и те же ресурсы, но даже в истории человечества первые исследователи были торговцами . Они шли туда, чтобы найти специи, золото, шелк, новые растения для приручения, новых животных.
Они шли туда, чтобы найти специи, золото, шелк, новые растения для приручения, новых животных.
Они не обязательно собирались завоевывать земли. В конце концов они это сделали из-за дилеммы ограниченных ресурсов, когда вы застряли на Земле. Но в тот момент, когда у вас есть технология, позволяющая оторваться от земли, конечные ресурсы исчезают.
Если вам нужен ресурс, найдите нейтронную звезду или звездную систему. Ты не гонишься за маленькой планетой. Есть бесконечное количество кеплеровых планет, которые будут намного ближе к ним.
Людям нужны идеи и торговля.
Если вы посмотрите на современное общество — хотя я знаю, что это не общепринятое мнение — мы становимся менее воинственными по мере того, как становимся более цивилизованными. Причина в том, что вы больше не завоюете Россию ее природными ресурсами. Сейчас самые богатые места в мире — это те, где рождаются лучшие идеи. Силиконовая долина какое-то время была на вершине как двигатель создания богатства, потому что у нее были лучшие идеи.
Новая нефть – это идеи. Это все цифровое. Все новые состояния создаются в пространстве идей.
На самом деле, если вы начинаете сегодня молодым амбициозным человеком, вы не изучаете недвижимость; вы не учитесь добывать уголь и нефть; вы не занимаетесь добычей физических ресурсов для создания богатства. Вы входите в пространство идей. Вы занимаетесь программированием, книгами, фильмами, блогами и подкастами, а также созданием роботов, которые в основном являются интеллектуальной собственностью.
Даже как человеческая цивилизация, мы отходим от завоевания физических ресурсов и больше занимаемся торговлей идеями.
Обратный сценарий для человеческого вида заключается в том, что слишком многие из наших больших стран и национальных государств считают, что они достигли максимальных идей и теперь пришло время экономить ресурсы. В конечном итоге они уничтожают средства совершенствования, исправления ошибок и творчества и в конечном итоге стагнируют.
Тогда у вас есть идея поколения, выходящего из гораздо меньшего набора городов-государств, которые затем должны защищать себя от этих массивных, более хищных, окостеневших государств.
Люди говорят о том, что Китай такой впечатляющий — «посмотрите на их ракету», или «посмотрите на их ВВП», или «посмотрите на город, который они построили». Позвони мне, когда они изобретут что-то новое. Звоните мне, когда у них появится какая-то невероятная идея, которой у нас не было, и они создадут технологию, которой у нас не было. Потому что пока все подражательно. Это они используют технологии, которые они переняли у нас, и теперь они их догоняют. Они просто применяют масштабирование, потому что у них больше людей.
Позвоните мне, когда их ВВП на душу населения пересечет наш. Звоните мне, когда они придумают лекарства, или вакцины, или космические корабли, или генераторы энергии, или термоядерные реакторы, которые мы не знаем, как построить. Позвоните мне, когда авторитарное общество сверху вниз решит, как создать что-то совершенно новое, когда оно станет более творческим, когда их искусство станет лучше, когда их наука станет лучше, когда их технологии станут лучше.
Позвоните мне, когда это произойдет в демократическом, свободном, капиталистическом обществе, потому что я никогда не видел такого случая, никогда.
Один Эйнштейн стоит легиона докторских дронов
Креативность возрастает от 0 до 1, и тела не решат проблему еще в мире. Китайские университеты выпускают больше выпускников естественных наук, чем мы, но они не выпускают больше новаторов.
Не похоже, чтобы студенты, которые выходят из этих университетов в Китае с их научными степенями, уезжали и занимались инновационными вещами. Наоборот, потому что они были обучены особым образом. Их учат запоминать этот учебник, отвечать на этот экзамен. Они не могут мыслить нестандартно.
Их учили: «Это правда. Это бесспорно правильный способ мышления о науке». Это может быть хорошо для возможности подражания, как мы видим, но это не будет тем, что позволит вам продвинуться вперед в технологии, не говоря уже о фундаментальной физике или где-либо еще.
Меня не волнует статистика о том, сколько у них выпускников естественных наук. Это не имеет значения. Дайте мне 10 новаторских, творческих, молодых выпускников-физиков из более чем 50 000 выпускников-физиков, способных сдать экзамен со 100% эффективностью в любой день.
Это не имеет значения. Дайте мне 10 новаторских, творческих, молодых выпускников-физиков из более чем 50 000 выпускников-физиков, способных сдать экзамен со 100% эффективностью в любой день.
Флот: Итак, один Эйнштейн стоит легиона дронов с докторской степенью по физике. Это не имеет значения. Творчество идет от нуля к единице. И никакое количество бросающихся тел в проблему не приведет вас к ней. Такова природа меметической эволюции; это просто природа творчества.
Не полагайтесь на штампы авторитета
Переход от институтов к личностям на протяжении поколений будет беспорядочным
Военно-морской флот: Сегодня в нашем обществе существует множество институтов, которые полагаются на штампы авторитета.
Раньше они помогали завоевать авторитет в обществе. Если вы были журналистом, пишущим для The New York Times или The Washington Post , то у вас был заголовок The Times и The Post . Если вы профессор Гарварда, вам доверяют, потому что вы профессор Гарварда.
Если вы профессор Гарварда, вам доверяют, потому что вы профессор Гарварда.
Конечно, эти системы были взломаны. Многие социологи, которые не имеют никакого права указывать миру, что делать, сейчас находятся там с бессмысленными политическими моделями, маскирующимися под экономистов или ученых-естествоиспытателей. У вас есть люди, которые являются активистами, пишущими под мачтами этих некогда великих газет и сжигающими капитал доверия, который эти газеты накопили с течением времени.
Интернет раскрывает их медленно, но неуклонно, и мы переживаем переходный этап, когда массы все еще верят в институты.
Мы застряли в этой точке Шеллинга, в этой точке координации для учреждений: как мне узнать, следует ли мне нанять вас? У тебя будет диплом Гарварда? Я знаю, что это не так хорошо, как раньше. Я знаю, что диплом Гарварда по гуманитарным наукам на данный момент, вероятно, ерунда, но у меня нет другого показателя доверия, чтобы отфильтровать вас, и мне нужно сделать это эффективным способом.
То, что мы наблюдаем, — это переход власти от институтов к отдельным лицам, но это будет беспорядочно и займет как минимум одно поколение.
Тем временем учреждения сопротивляются. Мы находимся в фазе Империя наносит ответный удар , когда они пытаются захватить новые платформы, такие как Twitter, Facebook, Patreon, которые расширяют возможности людей.
Бретт: Университет и все академические круги имеют очень большие возможности для подготовки собственного следующего поколения учителей, которые затем продолжают обучать следующее поколение учеников начальной и средней школы.
Флот: Это священство. Вам разрешено говорить только то, что одобрено священниками, и вы можете говорить это только в том случае, если вы священник, а священники решают, кто является священником.
Инновации требуют децентрализации и расширения границ
В последнее десятилетие технологии повернули нас к централизации
Военно-морской флот: Для инноваций требуется несколько вещей. Одна из вещей, которая, по-видимому, требуется, — это децентрализация.
Одна из вещей, которая, по-видимому, требуется, — это децентрализация.
Я не думаю, что это совпадение, что афинские города-государства, или итальянские города-государства, или даже Соединенные Штаты — когда они были более свободными и менее контролируемыми федеральным правительством — были очагами инноваций, потому что у вас было много-много конкуренции. Люди могли переключаться из одного состояния в другое, если их идеи не приветствовались, и существовала жесткая конкуренция идей.
Реальное разнообразие, которое имеет значение, — это разнообразие идей, а не разнообразие цвета кожи.
Вам тоже нужна граница. Вам нужно что-то новое для исследования — либо интеллектуальные, либо физические границы. Мы оккупировали Калифорнию. Если уж на то пошло, теперь Калифорния — это институт, истэблишмент. Это больше не фронт Дикого Запада. Может быть, он нам нужен в космосе. Может быть, нам нужны интеллектуальные, как в криптовалютах.
Природа Дикого Запада такова, что он всегда полон мошенников; они всегда полны преступлений; они всегда наполнены очень странными и странными вещами, потому что они, как правило, привлекают странную толпу. Но в то же время именно здесь происходит много инноваций.
Но в то же время именно здесь происходит много инноваций.
Я вижу много жалоб от ученых и предпринимателей старой школы. «Где ждут новых предпринимателей?» Кажется, Пол Грэм, основатель Y Combinator, гениальный парень, написал в Твиттере что-то вроде: «Стив Джобс… и такие люди, как он, не продержатся и дня в компаниях, которые они создали». Его отменит собственная команда.
Но Стив Джобс сегодня был бы в криптовалюте. Он был бы в криптографии со всеми мошенниками, всеми преступниками и всеми чудаками, но, по крайней мере, там у него было бы место, чтобы быть чудаком. У него было бы место, чтобы быть другим. У него было бы место, где он мог бы попробовать что-то новое, без необходимости постоянно кому-то отчитываться.
Существует маятник между централизацией и децентрализацией.
Например, если вы посмотрите на криптомир, централизованные финансы в конечном итоге очень окостенеют. У вас есть правительство и регулирующие органы, которые точно говорят вам, что вы можете и не можете делать. Вы получаете регулятивный захват, и следующее, что вы знаете, Уолл-стрит высасывает 20% прибыли из экономики, и криптовалюта может заменить это.
Вы получаете регулятивный захват, и следующее, что вы знаете, Уолл-стрит высасывает 20% прибыли из экономики, и криптовалюта может заменить это.
Таким образом, вы получаете давление децентрализации, когда люди могут делать это в произвольной форме, программно. Но тогда вы получите гораздо больше мошенничества, мошенничества и убытков.
Аналогией может быть то, что в старые времена вы беспокоились о разбойниках и разбойниках в лесу, поэтому вы обратились к королю. Король строит хороший замок, король чеканит деньги. Но следующее, что вы знаете, король обесценивает валюту, и король бросает людей в тюрьму. Потом некоторые люди убегают в лес и снова становятся разбойниками, потому что хотят свободы. Но теперь, конечно, они подвергаются нападкам и преследованиям со стороны своих сверстников.
Итак, в истории происходит естественное маятниковое колебание между централизацией и децентрализацией, и я думаю, что дуга технологии фактически качнула нас в сторону централизации в последнее десятилетие.
Я большой поклонник Amazon, но это очень централизованная организация. Я думаю, что даже в этой отрасли происходит дуга децентрализации. Появляются такие вещи, как Shopify, которые позволяют небольшим магазинам конкурировать. Местные службы доставки, такие как DoorDash, являются централизованными службами, но они позволяют децентрализованной армии ресторанов и местных магазинов конкурировать с централизованными службами.
Мы увидим, как эта дуга движется вперед и назад.
Нищета компромиссов
Компромиссы Тестовые идеи, которые никто никогда не считал правильными с самого начала
Бретт: Эта идея подвергать сомнению вещи, которые до сих пор считались неопровержимыми в определенной области, действительно интересна.
На протяжении тысячелетий люди задавались вопросом, как лучше всего понять, что такое демократия.
Платон спросил: «Что такое демократия?» и у него был вопрос о том, кто должен править. Вот и вся идея демократии, предположительно. Нам нужно выяснить, кто будет править. Должны ли править цари-философы? Должно ли это быть население граждан?
Нам нужно выяснить, кто будет править. Должны ли править цари-философы? Должно ли это быть население граждан?
Платон решил, что толпа с готовностью проголосует против прав меньшинства, и это то, что он считал демократией.
Но Поппер поставил под сомнение всю эту идею рассмотрения того, что такое демократия. Он пошел еще глубже и грубо сказал: «Демократия не имеет ничего общего с тем, кто должен править. Демократия — это система, которая позволяет вам устранять политику и правителей наиболее эффективно, без насилия. И именно так вы судите о различных демократических системах».
Таким образом, вы можете судить о Франции, Англии, США, Австралии, Канаде. Есть ли в этих местах лучшие или худшие виды демократии в той мере, в какой мы действительно можем избавиться от людей, которые нам не нравятся, из демократической системы быстро, эффективно, легко, без насилия?
Это мера хорошей демократической системы, а не попытка выяснить, какая из них даст нам лучших правителей. Это такая же ошибка, как сказать: «Какой научный метод даст нам истинную теорию?» Никакой научный метод не даст нам истинной теории.
Это такая же ошибка, как сказать: «Какой научный метод даст нам истинную теорию?» Никакой научный метод не даст нам истинной теории.
Наука — это механизм исправления ошибок. Все, на что мы можем надеяться, это избавиться от плохих идей. Сделав это, мы исправили некоторые из наших ошибок, а затем мы можем двигаться вперед, чтобы найти что-то, что является лучшей теорией, чем та, что была у нас раньше.
Это поднимает идею о том, как принимать правильные решения, когда вы в ссоре с кем-то другим.
Существует идея, что компромисс должен быть своего рода добродетелью, но это не так. Предпочтительнее иметь насильственную конфронтацию, если у вас есть два человека, которые иначе не могут прийти к соглашению, и они собираются вступить в какую-то битву.
Если вы находитесь в ситуации, когда у человека А есть идея X, а у человека Б есть идея Y, обычное понимание компромисса состоит в том, что он находится где-то между X и Y: человек А не получит всего, что хочет, а человек Б не получат всего, что хотят. Они приходят к компромиссу — теории Z.
Они приходят к компромиссу — теории Z.
Нас не должно удивлять, что теория Z не работает, потому что никто никогда не думал, что это лучшая идея. Человек А возвращается к словам: «Я всегда говорил вам, что X — правильная идея», а человек Б возвращается к словам: «Я всегда говорил вам, что идея Y — лучшая идея».
Они не добились никакого прогресса. Они показали, что Z ошибается, но никто никогда не думал, что Z был прав с самого начала.
Это нищета компромиссов, и это то, что вы получаете в науке в определенные времена. В политике это тоже везде.
Свободные рынки обеспечивают лучшую обратную связь
Альтернативой является обратная связь от того, у кого больше всего оружия
Военно-морской флот: Марк Андриссен красиво резюмирует это как «твердое мнение, которого не придерживаются».
Как общество, если вы ищете истину, вы хотите иметь твердое мнение, но очень слабое. Вы хотите попробовать их, посмотреть, работают ли они, а затем исправить ошибки, если они не работают.
Но вместо этого мы получаем либо твердое мнение, которого придерживаются нетерпимое меньшинство, либо слабое мнение, которое свободно придерживается, что представляет собой скомпрометированную модель, в которой никто на самом деле не берет на себя вину, никто не получает кредита, никто не может пробуйте так, как они хотят, и тогда все могут вернуться к «настоящему коммунизму еще не пробовали». Хотя в этом случае был испытан настоящий коммунизм; это просто не сработало.
В качестве отступления, один из распространенных критических замечаний, которые я слышу от людей, звучит так: «Нам нужно двигаться в посткапиталистический мир. Капитализм не работает». Хорошо, какая у тебя альтернатива? Обычно именно здесь люди начинают возиться, потому что вариантов не так много.
Когда вы пытаетесь понять, как разделить кредит, ресурсы и вознаградить людей за их работу, у вас есть два варианта: обратная связь от свободного рынка и реальности — и лучшая модель для этого — деньги — или обратная связь от люди, на чем заканчивается коммунизм, это группа людей, которые решают, что вы сделали лучшую работу.
Итак, кто решает, что вы лучше всех поработали? Кто-то должен взять на себя ответственность за это, и это неизменно заканчивается самым большим головорезом.
Я не думаю, что это случайность, что каждая коммунистическая страна вырождается в диктатуру. Коммунизм, кажется, никогда не управляется распределенным большинством людей. Это всегда заканчивается тем, что им управляет группа людей, которые берут на себя ответственность.
Такова человеческая природа, что если я решу, кому достанется золото, оно достанется моим друзьям, семье и людям, которые мне нравятся. И это неизменно заканчивается тем, что происходит.
Либо вам нужна целевая функция, чтобы разделить ее — а деньги — известная целевая функция, — либо все становится субъективным. А если субъективно, то кто сказал, что вы делите его вместо меня? Мы просто решим, у кого больше физической силы, у кого больше оружия.
Бретт: Что мы говорим о свободных рынках, так это то, что мы извлекли принуждение из этого процесса принятия решений. Никто не принуждается к покупке услуги или заключению договора.
Никто не принуждается к покупке услуги или заключению договора.
Сила применяется только тогда, когда вмешивается правительство. Тогда люди наверху говорят: «Это лучшее решение, и вам придется с ним согласиться; в противном случае у вашей двери появится человек со значком и пистолетом».
Все, что мы говорим о свободном рынке, это то, что человек может принимать решения без принуждения. Я могу ошибаться, но почему бы им не попробовать и не ошибиться? Это единственный способ добиться прогресса.
Единственный способ исправить ошибку — попробовать что-то еще.
Создание чего-то социального разрушает правду об этом
Крупнейшие прорывы науки были сделаны непопулярными людьми ладить — и консенсус заключается в компромиссе, а не в поиске истины.
Наука — по крайней мере, естественные науки — была той уникальной дисциплиной, в которой вы могли искать истину индивидуально от имени остального общества. Другие люди подтверждают, что у них действительно есть наилучшая современная модель того, как работает реальность, а затем она может быть распространена с помощью изобретений на остальную часть общества.
Но социальные науки — это вирус, проникший в академические круги и захвативший их. Социальные науки полностью коррумпированы.
Во-первых, им нужно обратиться к обществу за финансированием, поэтому они политически мотивированы. Затем они сами находятся под влиянием общества, потому что исследования и модели используются для управления политикой. Так что, конечно, это тоже портится. Теперь даже естественные науки подвергаются нападкам со стороны социальных наук, и они становятся все более и более социализированными.
Чем больше группового мышления вы видите вовлеченным, тем дальше вы от истины. Вы можете иметь гармоничное общество, в то же время позволяя искателям истины внутри общества находить истину и находить средства для изменения и улучшения реальности для всей группы.
Исторически сложилось так, что большинство научных прорывов исходило не от научных учреждений. Большие исходили от отдельных натурфилософов, которые были очень независимыми мыслителями, которых в свое время поносили, часто преследовали, которые боролись против остального общества на основе своих истин. И потребовались десятилетия или столетия — часто после их смерти — прежде чем эти истины были приняты.
И потребовались десятилетия или столетия — часто после их смерти — прежде чем эти истины были приняты.
Многие из этих академических теорий на самом деле не выдерживают ни повторения — если вы посмотрите на то, что происходит в психологии, — ни даже реальности.
У Рори Сазерленда есть замечательная цитата, в которой он сказал что-то вроде: «Маркетинг — это наука о том, в чем ошибаются экономисты». Экономисты исходят из совершенно рационального поведения, но люди, очевидно, являются биологическими существами с программным обеспечением, так что вы можете обойти это с помощью маркетинга.
Нассим Талеб пошел бы еще дальше и сказал бы, что они предполагают ложную рациональность. Люди оценивают риск разорения, риск обращения к нулю, а ученые ошибаются в эргодических рассуждениях. Они предполагают, что то, что хорошо для ансамбля, хорошо и для человека, а это не так.
Индивидуум не хочет стремиться к нулю — не хочет умирать — поэтому он не пойдет на риск разорения и не пойдет на риск банкротства; в то время как группа должна быть готова пойти на риск банкротства, потому что это распределено среди очень многих разных людей.
Группы никогда не признают неудачу
Вместо этого вы получаете раскол
Военно-морской флот: Группы никогда не признают неудачи. Группа скорее продолжит жить в мифологии «нас репрессировали», чем когда-либо признает неудачу. Люди — единственные, кто признает неудачу. Даже люди не любят признавать неудачи, но в конце концов их можно заставить.
Группа никогда не признает свою неправоту. Группа никогда не признает: «Мы совершили ошибку», потому что группа, пытающаяся изменить свое мнение, распадается. Мне трудно найти примеры в истории больших групп, которые говорили бы: «Мы думали А, но ответ на самом деле Б».
Обычно в этом случае происходит раскол, когда вы переходите из католической церкви в протестантскую и так далее. Есть расхождения и, как правило, много распрей. Это происходит и в криптосфере, где монеты разветвляются. Биткойн не говорит внезапно: «У нас должны быть смарт-контракты». ETH не говорит внезапно: «Мы должны были быть неизменными».
Я был членом правления фонда, которому было поручено раздавать деньги на благотворительность, и это меня очень разочаровало, потому что я узнал, что независимо от того, что делает фонд, они объявят о своей победе. Каждый проект был победным. Каждый проект был успешным. Было много хлопков по спине. Было много громких заявлений о миссии и видении, много поздравлений, много приятных обедов, но ничего не было сделано.
Я понял, что это из-за отсутствия объективной обратной связи. Поскольку потерь нет — все это социальная выгода, — они не могли потерпеть неудачу. И поскольку они не могли потерпеть неудачу, они весь день неправильно направляли ресурсы. И в конце концов, конечно, у таких групп заканчиваются деньги.
Если вы хотите изменить мир к лучшему, лучший способ сделать это — это коммерческая деятельность, потому что коммерческая деятельность должна опираться на реальность. По иронии судьбы, коммерческие организации более устойчивы, чем некоммерческие. Они самодостаточны. Вы же не все время ходите с чашей для подаяния.
Вы же не все время ходите с чашей для подаяния.
Конечно, вы теряете красивый некоммерческий статус; вы должны платить налоги; а также вы можете быть коррумпированы, работая исключительно ради прибыли. Но я бы сказал, что лучшие предприятия — это те, которые являются коммерческими, устойчивыми и этичными, чтобы вы могли привлечь лучших людей. Вы можете поддерживать его, потому что это миссия, и дело не только в деньгах — потому что отдача от зарабатывания денег уменьшается.
Предельная полезность денег в вашей жизни уменьшается.
Знание делает существование ресурсов бесконечным
Мы будем продолжать создавать новые знания и новые ресурсы
Бретт: Знание — это то, что делает существование ресурсов бесконечным. Создание знаний безгранично. Мы собираемся продолжать создавать больше знаний и, таким образом, узнавать о большем количестве различных ресурсов.
Есть замечательная притча о европии в Начало бесконечности где Дэвид рассказывает о том, когда около 60 лет назад начали производить первый цветной телевизор. Был тип электронно-лучевой трубки, в котором поток электронов направлялся на фосфоресцирующий экран. Фосфоресцентный экран имел бы эти пиксели трех разных цветов, один из которых был красным, а эти красные люминофоры на экране были бы заполнены элементом европием.
Был тип электронно-лучевой трубки, в котором поток электронов направлялся на фосфоресцирующий экран. Фосфоресцентный экран имел бы эти пиксели трех разных цветов, один из которых был красным, а эти красные люминофоры на экране были бы заполнены элементом европием.
Интересная особенность европия заключается в том, что когда вы пропускаете через него электричество, когда вы возбуждаете его, он светится красным цветом. Особенно интересным в европии является то, что это единственный такой элемент в периодической таблице; это единственный химикат, который может это сделать. Если вы выстрелите в него электронами, он будет светиться красным цветом, который необходим для цветного телевидения.
Было подсчитано, что на Земле есть только определенное количество европия, и это количество европия быстро расходуется производителями электронно-лучевых трубок. Таким образом, у ученых была совершенно надежная математическая теория о том, что количество электронно-лучевых трубок конечно; поэтому у нас закончатся электронно-лучевые трубки.
Это правда, в очень узком смысле, что для любого данного ресурса у вас будет конечное количество на планете Земля. Конечно, в космосе будет европий, и вы, вероятно, могли бы добывать его там, но суть в том, что ни у кого больше нет электронно-лучевых трубок. Вся идея цветного телевидения в наши дни не имеет ничего общего с добычей европия.
У всех нас есть ЖК-экраны, у нас есть плазменные экраны, и, вероятно, в будущем появится что-то еще, что не будет иметь абсолютно ничего общего с технологиями, которые у нас есть сегодня. Но у нас по-прежнему будут цветные телевизоры или цветные экраны.
Это справедливо для абсолютно любого ресурса, о котором мы только можем подумать.
Вы вполне можете сделать очень хороший мальтузианский расчет, что мы не можем продолжать сжигать дрова, если вы живете в африканской саванне, потому что в конечном итоге все леса будут сожжены. Очевидно, у нас кончатся дрова. Существует конечное количество древесины. Даже если вы сможете вырастить больше древесины, в конечном итоге потребление древесины превысит ее количество. И это аргумент в пользу угля, нефти и всего остального, что мы потребляем.
И это аргумент в пользу угля, нефти и всего остального, что мы потребляем.
Флот: Даже в так называемом пустом пространстве есть много материи и множество вещей, которые можно преобразовать в энергию. Количество доступных ресурсов не ограничено. Есть просто предел знаниям.
К сожалению, здесь присутствует пессимистическое предположение о том, что люди исходят из того, что человеческое творчество ограничено, и я думаю, что люди, которые ничего не строили, которые не создавали новые вещи с нуля, кажется, чувствуют это больше всего.
Для пещерного человека очень немногие вещи являются ресурсами
Было время, когда уголь не был ресурсом
Бретт: На ITV в Великобритании рассказывалось о том, сколько предполагаемых отходов производит Amazon, что Amazon регулярно уничтожает целую кучу продуктов.
Я подумал: «Почему эти люди вкладывают свое мнение в дело, в котором они абсолютно ничего не смыслят?» Предпочли бы они, чтобы Amazon точно знала, сколько продуктов нужно произвести? Другими словами, это эпистемологически невозможная ситуация. Или они предпочли бы, чтобы Amazon производил недостаточно продуктов, чтобы люди, которые хотели их купить, не могли их получить?
Или они предпочли бы, чтобы Amazon производил недостаточно продуктов, чтобы люди, которые хотели их купить, не могли их получить?
Amazon, конечно же, производит немного больше, чем им нужно. Так бывает в любом бизнесе. Они делают чуть больше, чем им нужно время от времени.
Военно-морской флот: Однажды один венчурный капиталист поспорил со мной, что существует слишком много видов обуви, и это был пример того, как капитализм потерпел неудачу, потому что никому не нужно столько видов кроссовок.
Я спросил его: «Когда ты узнал, что обуви слишком много?» В какой момент в истории мы решили, что обуви слишком много? Прежде чем нам понадобилось больше обуви, потому что нам нужна была более эластичная обувь, нам нужна была более прочная обувь, нам нужна была обувь с более толстой подошвой, нам нужна была более легкая обувь, нам нужны были всевозможные удивительные инновации в области обуви.
А потом в какой-то момент кто-то решает: «На самом деле у нас достаточно обуви. Теперь нам нужно уничтожить все остальные линии обуви». Откуда вы взяли эту мысль, что вы просто родились в нужное время и в нужном месте, чтобы определить, что да, у нас достаточно обуви?
Теперь нам нужно уничтожить все остальные линии обуви». Откуда вы взяли эту мысль, что вы просто родились в нужное время и в нужном месте, чтобы определить, что да, у нас достаточно обуви?
Это некий местничество, в которое впадают все.
Есть более макроверсия, которая заключается в философии «у нас заканчиваются ресурсы». Все начинается с идеи о том, что Земля конечна, что существует конечный набор ресурсов, и мы потребляем их все. И поэтому мы все умрем, если не снизим потребление.
Во-первых, как вы решили, что это Земля? Как вы решили, что в вашем городе не заканчиваются ресурсы? Почему город не был той областью, которую вы хотели спасти, а все за его пределами было чуждым и недоступным?
Зачем проводить границу вокруг Земли? Мы могли бы отправиться в солнечную систему. Мы могли бы отправиться в галактику, мы могли бы отправиться во вселенную. Мы могли бы отправиться в мультивселенную. Есть много ресурсов, если вы знаете, как их использовать.
Тогда как определить, что такое ресурс? Ресурс — это всего лишь то, что благодаря знаниям вы можете преобразовать из одного в другое.
