Собраны формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью первого замечательного предела. Даны подробные решения примеров с использованием первого замечательного предела его следствий.
СодержаниеСм. также: Доказательство первого замечательного предела и его следствий
Применяемые формулы, свойства и теоремы
Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется первый замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.
- Первый замечательный предел и его следствия:
. - Тригонометрические формулы для синуса, косинуса , тангенса и котангенса :
;
;
;
при , ;
;
;
;
;
;
.
Примеры решений
Пример 1
Для этого.
1. Вычисляем предел .
Поскольку функция непрерывна для всех x
,
и в том числе в точке ,
то
.
2. Поскольку функция не определена (и, следовательно, не является непрерывной) при , то нам нужно убедиться, что существует такая проколотая окрестность точки , на которой . В нашем случае при . Поэтому это условие выполнено.
3. Вычисляем предел . В нашем случае он равен первому замечательному пределу:
.
Таким образом,
.
Аналогичным образом, находим предел функции в знаменателе:
;
при ;
.
И наконец, применяем арифметические свойства предела функции :
.
Применим .
При .
Из таблицы эквивалентных функций находим:
при ;
при .
Тогда .
Пример 2
Найдите предел:
.
Решение с помощью первого замечательного предела
При , , . Это неопределенность вида 0/0 .
Преобразуем функцию за знаком предела:
.
Сделаем замену переменной .
Поскольку и при ,
то
.
Аналогичным образом имеем:
.
Поскольку функция косинус непрерывна на всей числовой оси, то
.
Применяем арифметические свойства пределов:
.
Решение с помощью эквивалентных функций
Применим теорему о замене функций эквивалентными в пределе частного .
При .
Из таблицы эквивалентных функций находим:
при ;
при .
Тогда .
Пример 3
.
Подставим в числитель и знаменатель дроби:
;
.
Это неопределенность вида 0/0 .
Попробуем решить этот пример с помощью первого замечательного предела. Поскольку в нем значение переменной стремится к нулю, то сделаем подстановку, чтобы новая переменная стремилась не к , а к нулю. Для этого от x перейдем к новой переменной t , сделав подстановку , . Тогда при , .
Предварительно преобразуем функцию за знаком предела, умножив числитель и знаменатель дроби на :
.
Подставим и воспользуемся приведенными выше тригонометрическими формулами.
;
;
.
Функция непрерывна при .
Находим ее предел:
Преобразуем вторую дробь и применим первый замечательный предел:
.
В числителе дроби мы сделали подстановку .
Применяем свойство предела произведения функций:
.
.Пример 4
Найти предел:
.
При , , . У нас неопределенность вида 0/0 .
Преобразуем функцию под знаком предела. Применим формулу:
.
Подставим :
.
Преобразуем знаменатель:
.
Тогда
.
Поскольку и при ,
то сделаем подстановку ,
и применим теорему о пределе сложной функции и первый замечательный предел:
Применяем арифметические свойства предела функции:
.
Пример 5
Найдите предел функции:
.
Нетрудно убедиться, что в этом примере мы имеем неопределенность вида 0/0 .
Для ее раскрытия, применим результат предыдущей задачи, согласно которому
.
Введем обозначение:
(П5.1) .
Тогда
(П5.2) .
Из (П5.1) имеем:
.
Подставим в исходную функцию:
,
где ,
,
;
;
;
.
Используем (П5. 2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
,
здесь m
– отличное от нуля число, ;
;
;
.
Пример 6
Найти предел:
.
При ,
числитель и знаменатель дроби стремятся к 0 .
Это неопределенность вида 0/0 .
Для ее раскрытия, преобразуем числитель дроби:
.
Применим формулу:
.
Подставим :
;
,
где .
Применим формулу:
.
Подставим :
;
,
где .
Числитель дроби:
.
Функция за знаком предела примет вид:
.
Найдем предел последнего множителя, учитывая его непрерывность при :
.
Применим тригонометрическую формулу:
.
Подставим ,
.
Тогда
.
Разделим числитель и знаменатель на , применим первый замечательный предел и одно из его следствий:
.
Окончательно имеем:
Примечание 1.
Также можно было применить формулу
.
Тогда .
Данная статья: «Второй замечательный предел» посвящена раскрытию в пределах неопределенностей вида:
$ \bigg[\frac{\infty}{\infty}\bigg]^\infty $ и $ ^\infty $. {3x} = 1 $$
{3x} = 1 $$
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Первый замечательный предел выглядит следующим образом: lim x → 0 sin x x = 1 .
В практических примерах часто встречаются модификации первого замечательного предела: lim x → 0 sin k · x k · x = 1 , где k – некоторый коэффициент.
Поясним: lim x → 0 sin (k · x) k · x = п у с т ь t = k · x и з x → 0 с л е д у е т t → 0 = lim t → 0 sin (t) t = 1 .
Следствия первого замечательного предела:
- lim x → 0 x sin x = lim x → 0 = 1 sin x x = 1 1 = 1
- lim x → 0 k · x sin k · x = lim x → 0 1 sin (k · x) k · x = 1 1 = 1
Указанные следствия достаточно легко доказать, применив правило Лопиталя или замену бесконечно малых функций.
Рассмотрим некоторые задачи на нахождение предела по первому замечательному пределу; дадим подробное описание решения.
Пример 1
Необходимо определить предел, не используя правило Лопиталя: lim x → 0 sin (3 x) 2 x .
Решение
Подставим значение:
lim x → 0 sin (3 x) 2 x = 0 0
Мы видим, что возникла неопределенность нуль делить на нуль. Обратимся к таблице неопределенностей, чтобы задать метод решения. Сочетание синуса и его аргумента дает нам подсказку об использовании первого замечательного предела, однако для начала преобразуем выражение. Произведем умножение числителя и знаменателя дроби на 3 x и получим:
lim x → 0 sin (3 x) 2 x = 0 0 = lim x → 0 3 x · sin (3 x) 3 x · (2 x) = lim x → 0 sin (3 x) 3 x · 3 x 2 x = = lim x → 0 3 2 · sin (3 x) 3 x
Опираясь на следствие из первого замечательного предела, имеем: lim x → 0 sin (3 x) 3 x = 1 .
Тогда приходим к результату:
lim x → 0 3 2 · sin (3 x) 3 x = 3 2 · 1 = 3 2
Ответ: lim x → 0 sin (3 x) 3 x = 3 2 .
Пример 2
Необходимо найти предел lim x → 0 1 – cos (2 x) 3 x 2 .
Решение
Подставим значения и получим:
lim x → 0 1 – cos (2 x) 3 x 2 = 1 – cos (2 · 0) 3 · 0 2 = 1 – 1 0 = 0 0
Мы видим неопределенность нуль делить на нуль. Произведем преобразование числителя с использованием формул тригонометрии:
lim x → 0 1 – cos (2 x) 3 x 2 = 0 0 = lim x → 0 2 sin 2 (x) 3 x 2
Видим, что теперь здесь возможно применение первого замечательного предела:
lim x → 0 2 sin 2 (x) 3 x 2 = lim x → 0 2 3 · sin x x · sin x x = 2 3 · 1 · 1 = 2 3
Ответ: lim x → 0 1 – cos (2 x) 3 x 2 = 2 3 .
Пример 3
Необходимо произвести вычисление предела lim x → 0 a r c sin (4 x) 3 x .
Решение
Подставим значение:
lim x → 0 a r c sin (4 x) 3 x = a r c sin (4 · 0) 3 · 0 = 0 0
Мы видим неопределенность делить нуль на нуль. Произведем замену:
a r c sin (4 x) = t ⇒ sin (a r c sin (4 x)) = sin (t) 4 x = sin (t) ⇒ x = 1 4 sin (t) lim x → 0 (a r c sin (4 x)) = a r c sin (4 · 0) = 0 , значит t → 0 при x → 0 .
В таком случае, после замены переменной, предел принимает вид:
lim x → 0 a r c sin (4 x) 3 x = 0 0 = lim t → 0 t 3 · 1 4 sin (t) = = lim t → 0 4 3 · t sin t = 4 3 · 1 = 4 3
Ответ: lim x → 0 a r c sin (4 x) 3 x = 4 3 .
Для более полного понимания материала статьи следует повторить материал темы «Пределы, основные определения, примеры нахождения, задачи и решения».
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формула второго замечательного предела имеет вид lim x → ∞ 1 + 1 x x = e . Другая форма записи выглядит так: lim x → 0 (1 + x) 1 x = e .
Когда мы говорим о втором замечательном пределе, то нам приходится иметь дело с неопределенностью вида 1 ∞ , т.е. единицей в бесконечной степени.
Рассмотрим задачи, в которых нам пригодится умение вычислять второй замечательный предел.
Пример 1
Найдите предел lim x → ∞ 1 – 2 x 2 + 1 x 2 + 1 4 .
Решение
Подставим нужную формулу и выполним вычисления.
lim x → ∞ 1 – 2 x 2 + 1 x 2 + 1 4 = 1 – 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 – 0 ∞ = 1 ∞
У нас в ответе получилась единица в степени бесконечность. Чтобы определиться с методом решения, используем таблицу неопределенностей. Выберем второй замечательный предел и произведем замену переменных.
t = – x 2 + 1 2 ⇔ x 2 + 1 4 = – t 2
Если x → ∞ , тогда t → – ∞ .
Посмотрим, что у нас получилось после замены:
lim x → ∞ 1 – 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t – 1 2 t = lim t → ∞ 1 + 1 t t – 1 2 = e – 1 2
Ответ: lim x → ∞ 1 – 2 x 2 + 1 x 2 + 1 4 = e – 1 2 .
Пример 2
Вычислите предел lim x → ∞ x – 1 x + 1 x .
Решение
Подставим бесконечность и получим следующее.
lim x → ∞ x – 1 x + 1 x = lim x → ∞ 1 – 1 x 1 + 1 x x = 1 – 0 1 + 0 ∞ = 1 ∞
В ответе у нас опять получилось то же самое, что и в предыдущей задаче, следовательно, мы можем опять воспользоваться вторым замечательным пределом. Далее нам нужно выделить в основании степенной функции целую часть:
x – 1 x + 1 = x + 1 – 2 x + 1 = x + 1 x + 1 – 2 x + 1 = 1 – 2 x + 1
После этого предел приобретает следующий вид:
lim x → ∞ x – 1 x + 1 x = 1 ∞ = lim x → ∞ 1 – 2 x + 1 x
Заменяем переменные. Допустим, что t = – x + 1 2 ⇒ 2 t = – x – 1 ⇒ x = – 2 t – 1 ; если x → ∞ , то t → ∞ .
Допустим, что t = – x + 1 2 ⇒ 2 t = – x – 1 ⇒ x = – 2 t – 1 ; если x → ∞ , то t → ∞ .
После этого записываем, что у нас получилось в исходном пределе:
lim x → ∞ x – 1 x + 1 x = 1 ∞ = lim x → ∞ 1 – 2 x + 1 x = lim x → ∞ 1 + 1 t – 2 t – 1 = = lim x → ∞ 1 + 1 t – 2 t · 1 + 1 t – 1 = lim x → ∞ 1 + 1 t – 2 t · lim x → ∞ 1 + 1 t – 1 = = lim x → ∞ 1 + 1 t t – 2 · 1 + 1 ∞ = e – 2 · (1 + 0) – 1 = e – 2
Чтобы выполнить данное преобразование, мы использовали основные свойства пределов и степеней.
Ответ: lim x → ∞ x – 1 x + 1 x = e – 2 .
Пример 3
Вычислите предел lim x → ∞ x 3 + 1 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 .
Решение
lim x → ∞ x 3 + 1 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x – 1 x 3 3 2 x – 5 x 4 = = 1 + 0 1 + 0 – 0 3 0 – 0 = 1 ∞
После этого нам нужно выполнить преобразование функции для применения второго замечательного предела. У нас получилось следующее:
lim x → ∞ x 3 + 1 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = 1 ∞ = lim x → ∞ x 3 – 2 x 2 – 1 – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = = lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5
lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = = lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5
Поскольку сейчас у нас есть одинаковые показатели степени в числителе и знаменателе дроби (равные шести), то предел дроби на бесконечности будет равен отношению данных коэффициентов при старших степенях.
lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 2 x 2 + 2 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = = lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 6 2 = lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 3
При замене t = x 2 + 2 x 2 – 1 – 2 x 2 + 2 у нас получится второй замечательный предел. Значит, что:
lim x → ∞ 1 + – 2 x 2 + 2 x 3 + 2 x 2 – 1 x 3 + 2 x 2 – 1 – 2 x 2 + 2 – 3 = lim x → ∞ 1 + 1 t t – 3 = e – 3
Ответ: lim x → ∞ x 3 + 1 x 3 + 2 x 2 – 1 3 x 4 2 x 3 – 5 = e – 3 .
Выводы
Неопределенность 1 ∞ , т.е. единица в бесконечной степени, является степенной неопределенностью, следовательно, ее можно раскрыть, используя правила нахождения пределов показательно степенных функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Ноль в бесконечной степени. Устранение неопределённости «единица в степени бесконечность. Понятие предела в математике
КОНСПЕКТ 20
20. 1
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
1
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Пример 1
Решить предел Сначала попробуем подставить -1 в дробь:В данном случае получена так называемая неопределенность.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытиянужно разложить числитель и знаменатель на множители .
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Разложим числитель на множители.
Пример 2
Вычислить предел
Разложим числитель и знаменатель на множители.
Числитель: Знаменатель:,
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 3
Найти предел
Умножим
числитель и знаменатель на сопряженное
выражение.
20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример 4
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:Старшая степень знаменателя равна двум.
Затем
мы выбираем самую старшую степень
числителя и знаменателя: в данном примере
они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим
числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 5
Найти
предел
Снова
в числителе и знаменателе находимв
старшей степени:Максимальная
степень в числителе: 3
Максимальная
степень в знаменателе: 4
Выбираемнаибольшее значение, в данном
случае четверку. Согласно нашему
алгоритму, для раскрытия неопределенностиделим
числитель и знаменатель на.
Полное
оформление задания может выглядеть
так:
Согласно нашему
алгоритму, для раскрытия неопределенностиделим
числитель и знаменатель на.
Полное
оформление задания может выглядеть
так:
Пример 6
Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 (можно записать как) Для раскрытия неопределенностинеобходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получитьсяконечное число , ноль или бесконечность.
ПРАКТИКУМ 20
ЗАДАНИЕ N 1
Решение: Если вместо переменнойпоставить значение 7, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 2 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 0, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 3 Тема: Раскрытие неопределенности вида “ноль на ноль”
Решение: Если вместо переменнойпоставить значение 6, к которому она стремится, то получим неопределенность видатогда
ЗАДАНИЕ N 4
Решение: Так каки
ЗАДАНИЕ N 5 Тема: Раскрытие неопределенности вида “бесконечность на бесконечность”
Решение: Так какито
имеет место неопределенность видаДля
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на. {3x} = 1 $$
{3x} = 1 $$
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):
Как показывает формула выше, при вычислении предела отношений двух бесконечно малых
или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким
образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин . Пусть функции f (x ) и g (x a . А в самой точке a a производная функции g (x ) не равна нулю (g “(x a равны между собой и равны нулю:
.
Правило Лопиталя для случая предела двух бесконечно больших величин . Пусть функции f (x ) и g (x ) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a . А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g (x ) не равна нулю (g “(x )≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:
.
Тогда предел отношения этих функций равен пределу отношения их производных:
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций
равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому
числу, или бесконечный, то есть равный бесконечности).
Замечания .
1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .
2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
Пример 1.
x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе – производную сложной
логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо
икса двойку.
Перед последним знаком равенства вычисляли обычный предел , подставляя вместо
икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять
дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Раскрытие неопределённостей вида “ноль умножить на бесконечность”
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13.
Решение. Получаем
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
Решение. Получаем
Получаем
Вычисляем предел выражения в показателе степени
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёттолько об определённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы , преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-ым замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции . На пример: .
Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции . На пример: .
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица , значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны . На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-ой замечательный предел не применим .
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты : .
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ .
! Примечание : не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще :
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
:
Пример 4
Разделим числитель и знаменатель на :
Примечание : самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание : слагаемое стремиться к нулю медленнее, чем , поэтому является «главным» нулём знаменателя. .
Пример 22
Примечание : бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Пределы. Примеры решений – matematika
Теория пределов – это один из разделов математического анализа.
Вопрос решения пределов является достаточно обширным, поскольку
существуют десятки приемов решений пределов различных видов. Существуют
десятки нюансов и хитростей, позволяющих решить тот или иной предел.
Тем не менее, мы все-таки попробуем разобраться в основных типах
пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
Любой предел состоит из трех частей:
1) Всем известного значка предела .
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно ,
хотя вместо «икса» на практике встречаются и другие переменные. В
практических заданиях на месте единицы может находиться совершенно
любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .
Сама запись читается так: «предел функции при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , ….
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое ? Это тот случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.
А что в это время происходит с функцией ?
, , , …
Итак: если , то функция стремится к минус бесконечности:
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять начинаем увеличивать до бесконечности, и смотрим на поведение функции:
Вывод: при функция неограниченно возрастает:
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
, , , , , , , , ,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то , , .
Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.
Пределы с неопределенностью вида и метод их решенияСейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в
функцию. Что у нас получается вверху? Бесконечность. А что получается
внизу? Тоже бесконечность. Таким образом, у нас есть так называемая
неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Что у нас получается вверху? Бесконечность. А что получается
внизу? Тоже бесконечность. Таким образом, у нас есть так называемая
неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти предел
Снова в числителе и знаменателе находим в старшей степени:
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пример 3
Найти предел
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:
Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.
Пределы с неопределенностью вида и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность .
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него: .
В случае если дискриминант большой, например 361, используем
калькулятор, функция извлечения квадратного корня есть на самом простом
калькуляторе.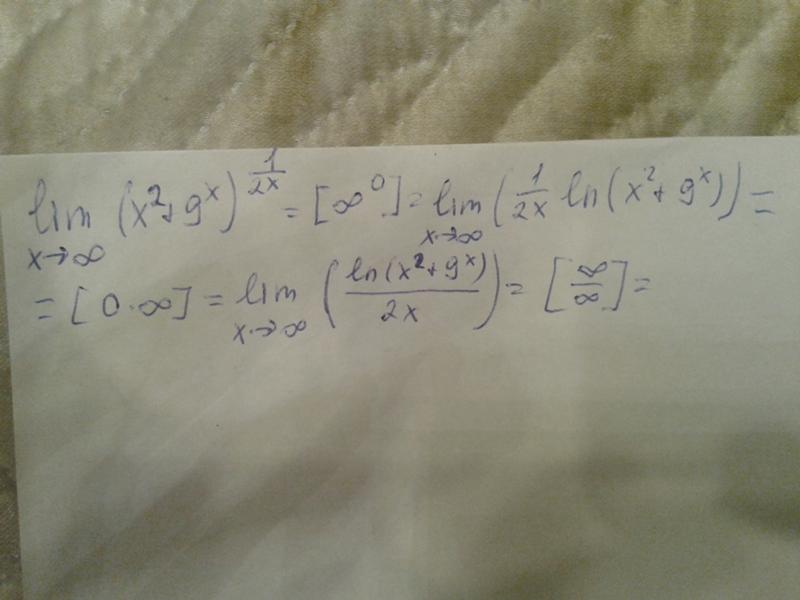
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители.
Пример 5
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель:
Знаменатель:
,
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель,
сначала мы вынесли за скобку 2, а затем использовали формулу разности
квадратов. Уж эту-то формулу нужно знать и видеть.
Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
Вообще, я заметил, что чаще всего в нахождении пределов данного
типа приходится решать два квадратных уравнения, то есть и в числителе и
в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида , которую нужно устранять.
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или
корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов:
И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
Как это сделать? Да просто подставить тройку под корни:
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Пример 7
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители:
Умножим числитель и знаменатель на сопряженное выражение
Как считать до бесконечности
Нет самого большого, последнего числа… кроме бесконечности. Только бесконечность не число. Но некоторые бесконечности буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Эй, Всоус! Майкл здесь.
Какое самое большое число вы можете придумать? Гугол? Гуголплекс? Миллион-миллион-оплекс? Ну на самом деле самое большое число 40.
Покрывая более 12 000 квадратных метров земли, эти 40, сделанные из стратегически посаженных деревьев в России, больше, чем маркеры батальона на Сигнальном холме в Калгари, 6, найденные на значках Фована в Англии, — даже миля числа пи. Брэди развернулся на Numberphile.40 — это самое большое число … на Земле с точки зрения площади поверхности.
Но с точки зрения количества вещей, которое мы обычно подразумеваем под «большим» числом, 40, вероятно, не самое большое число. Например, есть 41. О, а еще есть 42, и 43 … миллиард, триллион; знаете, какое бы большое число вы ни придумали, вы всегда можете подняться выше.
Значит, нет самого большого, последнего числа… кроме бесконечности? Нет. Бесконечность — это не число. Вместо этого это своего рода число. Вам нужны бесконечные числа, чтобы говорить о бесконечных количествах и сравнивать их, но некоторые бесконечные количества — некоторые бесконечности — буквально больше других. Давайте посетим некоторые из них и посчитаем мимо них.
Давайте посетим некоторые из них и посчитаем мимо них.
Обо всем по порядку. Когда число указывает на количество вещей, оно называется «кардинальным числом». Например, 4 банана. 12 флагов. 20 точек. 20 — это «мощность» этого набора точек. Теперь два набора имеют одинаковую мощность, когда они содержат одинаковое количество вещей. Мы можем продемонстрировать это равенство, сопоставив каждый член одного набора один к одному с каждым членом другого. Та же кардинальность, довольно просто.
Мы используем натуральные числа — то есть 0, 1, 2, 3, 4, 5 и т. д. — в качестве количественных всякий раз, когда говорим о том, сколько существует вещей, но сколько существует натуральных чисел? Это не может быть какое-то число в натуральных числах, потому что после него всегда будет 1 плюс это число.Вместо этого у этой суммы есть уникальное название: «алеф-нуль» (ℵ 0 ). Алеф — первая буква еврейского алфавита, а алеф-нуль — первая наименьшая бесконечность. Это количество натуральных чисел. Это также сколько четных чисел, сколько нечетных чисел; это также то, сколько существует рациональных чисел, то есть дробей. Это может показаться удивительным, поскольку дроби кажутся более многочисленными на числовой прямой, но, как показал Кантор, существует способ упорядочить каждое возможное рациональное число так, чтобы натуральные числа могли быть поставлены во взаимно однозначное соответствие с ними.Они имеют одинаковую мощность.
Это также сколько четных чисел, сколько нечетных чисел; это также то, сколько существует рациональных чисел, то есть дробей. Это может показаться удивительным, поскольку дроби кажутся более многочисленными на числовой прямой, но, как показал Кантор, существует способ упорядочить каждое возможное рациональное число так, чтобы натуральные числа могли быть поставлены во взаимно однозначное соответствие с ними.Они имеют одинаковую мощность.
Дело в том, что алеф-нуль — это большое количество; больше любой конечной суммы. Гугол, гуголплекс, гуголплекс факториал в степени гуголплекса в гуголплекс, умноженный на число Грэма в квадрате? Алеф-нуль больше. Но мы можем считать мимо него. Как? Что ж, давайте воспользуемся нашим старым другом — сверхзадачей. Если мы нарисуем кучу линий и сделаем каждую следующую линию частью размера и части расстояния от каждой последней строки, мы можем уместить бесконечное количество линий в конечное пространство.Количество строк здесь равно количеству имеющихся натуральных чисел. Эти два могут быть сопоставлены один к одному. Всегда есть следующий естественный, но всегда есть и следующая строка. Оба набора имеют кардинальность алеф-нуль.
Эти два могут быть сопоставлены один к одному. Всегда есть следующий естественный, но всегда есть и следующая строка. Оба набора имеют кардинальность алеф-нуль.
Но что произойдет, если я это сделаю? Теперь, сколько линий есть? Алеф-нулевой плюс один? Нет. Бесконечные суммы не похожи на конечные суммы. Здесь по-прежнему только строки с нулевыми алефами, потому что я могу сопоставлять натуральные числа один к одному, как и раньше. Я просто начинаю здесь, а затем продолжаю с самого начала.Понятно, что количество строк не изменилось. Я даже могу добавить еще две строки, еще три, еще четыре — всегда получаю только нулевые алефы. Я могу даже добавить еще один бесконечный алеф-нуль строк и все равно не изменить количество. Каждое четное число может сочетаться с этими и каждое нечетное число с этими. На каждого натурала еще очередь.
Еще один интересный способ увидеть, что эти линии не добавляются к сумме, — показать, что вы можете составить ту же последовательность, вообще не рисуя новые линии. Просто возьмите каждую вторую строку и переместите их все вместе в конец.Это то же самое.
Просто возьмите каждую вторую строку и переместите их все вместе в конец.Это то же самое.
Но подождите секунду. В этом и в этом может быть одинаковое количество вещей, но в них явно есть что-то другое, верно? Я имею в виду, если не из скольких вещей они сделаны, то из чего? Что ж, давайте вернемся к тому, чтобы иметь только одну строку после коллекции размером с нулевой алеф. Что, если вместо того, чтобы сопоставлять натуральные числа один к одному, мы настаиваем на нумерации каждой строки в соответствии с порядком, в котором она была нарисована? Итак, мы должны начать здесь и нумеровать слева направо. Теперь, какой номер получает эта строка? В царстве бесконечности маркировка вещей по порядку — это совсем другое, чем их подсчет.Видите ли, эта строка не участвует в сумме, но для того, чтобы пометить ее в соответствии с порядком, в котором она появилась, нам нужен набор меток чисел, выходящий за пределы натуральных чисел. Нам нужны порядковые номера.
Первый трансфинитный порядковый номер — это омега (ω), строчная греческая буква омега. Это не шутка и не уловка, это буквально просто следующая метка, которая вам понадобится после того, как вы сначала израсходуете бесконечную коллекцию каждого отдельного числа. Если бы вы заняли ω-е место в гонке, это означало бы, что гонку финишировало бесконечное количество людей, и тогда это сделали вы.После ω следует ω+1, которое на самом деле не похоже на число, но так оно и есть, точно так же, как 2, 12 или 800. Затем идут ω+2, ω+3… порядковые номера обозначают вещи по порядку. Порядковые числа — это не количество вещей, а то, как они устроены — тип их порядка.
Это не шутка и не уловка, это буквально просто следующая метка, которая вам понадобится после того, как вы сначала израсходуете бесконечную коллекцию каждого отдельного числа. Если бы вы заняли ω-е место в гонке, это означало бы, что гонку финишировало бесконечное количество людей, и тогда это сделали вы.После ω следует ω+1, которое на самом деле не похоже на число, но так оно и есть, точно так же, как 2, 12 или 800. Затем идут ω+2, ω+3… порядковые номера обозначают вещи по порядку. Порядковые числа — это не количество вещей, а то, как они устроены — тип их порядка.
Тип заказа набора – это просто первый порядковый номер, который не нужен для маркировки всего в наборе по порядку. Таким образом, для конечных чисел мощность и тип порядка одинаковы. Тип порядка всех натуральных чисел — ω.Тип порядка этой последовательности — ω+1, а теперь — ω+2. Какой бы длинной ни была аранжировка, пока она хорошо упорядочена, пока каждая ее часть содержит начальный элемент, все это описывает новый порядковый номер. Всегда. Это будет очень важно в дальнейшем.
Всегда. Это будет очень важно в дальнейшем.
Здесь следует отметить, что если вы когда-либо играли в игру, которая назовет наибольшее число, и вы думаете сказать «омега плюс один», вам следует быть осторожным. Ваши оппоненты могут потребовать, чтобы число, которое вы называете, было кардиналом, обозначающим сумму.Эти числа относятся к одному и тому же количеству вещей, просто расположенных по-разному. ω+1 не больше, чем ω, оно просто идет после ω.
Но алеф-нуль — это не конец. Почему? Ну, потому что можно показать, что существуют бесконечности больше алеф-нуль, которые буквально содержат больше вещей. Один из лучших способов сделать это — использовать диагональный аргумент Кантора. В моем эпизоде о парадоксе Банаха-Тарского я использовал его, чтобы показать, что количество действительных чисел больше, чем количество натуральных чисел. Но для целей этого видео давайте сосредоточимся на другом, более важном, чем алеф-нуль: наборе мощности алеф-нуль.
Силовой набор набора — это набор всех различных подмножеств, которые вы можете сделать из него. Например, из набора 1 и 2 я могу составить набор из ничего, или 1, или 2, или 1 и 2. Степенной набор 1,2,3: пустой набор, 1 и 2, и 3, и 1 и 2, и 1 и 3, и 2 и 3, и 1,2,3. Как видите, набор мощности содержит гораздо больше элементов, чем исходный набор. Если быть точным, два в той степени, в какой сколько членов было в исходном наборе. Итак, какова мощность всего природного?
Например, из набора 1 и 2 я могу составить набор из ничего, или 1, или 2, или 1 и 2. Степенной набор 1,2,3: пустой набор, 1 и 2, и 3, и 1 и 2, и 1 и 3, и 2 и 3, и 1,2,3. Как видите, набор мощности содержит гораздо больше элементов, чем исходный набор. Если быть точным, два в той степени, в какой сколько членов было в исходном наборе. Итак, какова мощность всего природного?
Что ж, посмотрим.Представьте себе список всех натуральных чисел. Прохладный. Теперь подмножество всех, скажем, четных чисел будет выглядеть так: да, нет, да, нет, да, нет и так далее. Подмножество всех нечетных чисел будет выглядеть так. Вот подмножество только 3, 7 и 12. А как насчет всех чисел, кроме 5. Или ни одного числа, кроме 5. Очевидно, что этот список подмножеств будет, ну, бесконечным. Но представьте, что все они сопоставляются один к одному с натуральным. Если даже в этом случае есть способ продолжать создавать новые подмножества, которые явно нигде здесь не перечислены, мы будем знать, что у нас есть множество, в котором членов больше, чем натуральных чисел — бесконечность больше, чем алеф-нуль.
Чтобы сделать это, нужно начать здесь, в первом подмножестве, и просто сделать противоположное тому, что мы видим. 0 является членом этого, поэтому наш новый набор не будет содержать 0. Затем двигайтесь по диагонали вниз к членству 1 во втором подмножестве. 1 является его членом, поэтому его не будет в нашем новом. 2 не находится в третьем подмножестве, поэтому оно будет в нашем, и так далее. Как видите, мы описываем подмножество, которое по определению будет отличаться по крайней мере одним способом от любого другого подмножества в этом нулевом списке.Даже если мы вернем это новое подмножество, диагонализация все еще может быть выполнена.
Силовой набор натуралов всегда будет сопротивляться однозначному соответствию с натуралами. Это бесконечно больше, чем алеф-нуль. Многократное применение набора мощности приведет к созданию наборов, которые нельзя привести во взаимно-однозначное соответствие с последними, так что это отличный способ быстро создавать все большие и большие бесконечности. Дело в том, что кардиналов больше после нулевого алеф. Попробуем добраться до них.
Дело в том, что кардиналов больше после нулевого алеф. Попробуем добраться до них.
Теперь вспомните, что после ω ординалы расщепляются, и эти числа больше не являются количественными.Они не относятся к большему количеству, чем последний кардинал, которого мы достигли, но, возможно, они могут привести нас к одному из них. Подождите … что мы делаем? Алеф-нулевой? Омега? Да ладно, мы использовали эти числа, как будто в этом нет никакой проблемы, но если в какой-то момент здесь внизу вы всегда можете добавить один — всегда — можем ли мы действительно говорить об этом, об этом бесконечном процессе, как о целом, а затем проследить его с помощью что-то?
Конечно можем. Это математика, а не наука! Вещи, которые мы считаем истинными в математике, называются аксиомами, и вероятность того, что аксиома, которую мы придумываем, верна, не выше, если она лучше объясняет или предсказывает то, что мы наблюдаем.Наоборот, это правда, потому что мы так говорим. Его последствия просто становятся тем, что мы наблюдаем. Мы не приспосабливаем наши теории к какой-то физической вселенной, чье поведение и основные законы были бы одинаковыми, были бы мы здесь или нет; мы сами создаем эту вселенную. Если аксиомы, которые мы провозглашаем истинными, приводят нас к противоречиям или парадоксам, мы можем вернуться и изменить их или просто отказаться от них, или мы можем просто отказаться позволять себе делать то, что вызывает парадоксы. Вот и все.Удивительно, однако, что, следя за тем, чтобы принимаемые нами аксиомы не приводили к проблемам, мы превратили математику в нечто, что, как говорится, «необоснованно эффективно в естественных науках». Так что в какой степени мы все это изобретаем или открываем — трудно сказать. Все, что нам нужно сделать, чтобы получить ω, это сказать «да будет омега», и все будет хорошо.
Мы не приспосабливаем наши теории к какой-то физической вселенной, чье поведение и основные законы были бы одинаковыми, были бы мы здесь или нет; мы сами создаем эту вселенную. Если аксиомы, которые мы провозглашаем истинными, приводят нас к противоречиям или парадоксам, мы можем вернуться и изменить их или просто отказаться от них, или мы можем просто отказаться позволять себе делать то, что вызывает парадоксы. Вот и все.Удивительно, однако, что, следя за тем, чтобы принимаемые нами аксиомы не приводили к проблемам, мы превратили математику в нечто, что, как говорится, «необоснованно эффективно в естественных науках». Так что в какой степени мы все это изобретаем или открываем — трудно сказать. Все, что нам нужно сделать, чтобы получить ω, это сказать «да будет омега», и все будет хорошо.
Это то, что сделал Эрнест Цермело в 1908 году, когда он включил аксиому бесконечности в свой список аксиом для работы в математике.Аксиома бесконечности — это просто заявление о том, что существует одно бесконечное множество — множество всех натуральных чисел. Если вы отказываетесь принять это, ничего страшного — это делает вас финитистом, тем, кто верит, что существуют только конечные вещи. Но если вы примете это, как это делает большинство математиков, вы сможете продвинуться довольно далеко — мимо этого и через это… в конце концов мы придем к ω+ω, за исключением того, что мы достигли еще одного потолка. Пройти весь путь до ω + ω означало бы создать еще одно бесконечное множество, а аксиома бесконечности гарантирует только то, что это существует.
Если вы отказываетесь принять это, ничего страшного — это делает вас финитистом, тем, кто верит, что существуют только конечные вещи. Но если вы примете это, как это делает большинство математиков, вы сможете продвинуться довольно далеко — мимо этого и через это… в конце концов мы придем к ω+ω, за исключением того, что мы достигли еще одного потолка. Пройти весь путь до ω + ω означало бы создать еще одно бесконечное множество, а аксиома бесконечности гарантирует только то, что это существует.
Придется ли нам добавлять новую аксиому каждый раз, когда мы описываем алеф-нуль-больше чисел? Нет. Здесь нам может помочь Аксиома Замещения. Это предположение гласит, что если вы возьмете набор — например, набор всех натуральных чисел — и замените каждый элемент чем-то другим — например, бананами, — то, что у вас останется, тоже будет набором. Звучит просто, но невероятно полезно. Попробуйте так: возьмите каждый порядковый номер до ω, а затем вместо бананов поставьте перед каждым «ω+». Теперь мы достигли ω+ω, или ω×2. Используя замену, мы можем делать прыжки любого размера, какого захотим, если мы используем только те числа, которые уже достигли. Мы можем заменить каждый порядковый номер до ω на омега, умноженную на него, чтобы получить ω×ω , ω 2 . Мы сейчас готовим! Аксиома замены позволяет бесконечно конструировать новые ординалы. В конце концов мы добираемся до ω до ω до ω до ω до ω… и у нас заканчиваются стандартные математические обозначения. Без проблем! Это просто называется «эпсилон-ноль» (ε 0 ), и мы продолжим отсюда.
Используя замену, мы можем делать прыжки любого размера, какого захотим, если мы используем только те числа, которые уже достигли. Мы можем заменить каждый порядковый номер до ω на омега, умноженную на него, чтобы получить ω×ω , ω 2 . Мы сейчас готовим! Аксиома замены позволяет бесконечно конструировать новые ординалы. В конце концов мы добираемся до ω до ω до ω до ω до ω… и у нас заканчиваются стандартные математические обозначения. Без проблем! Это просто называется «эпсилон-ноль» (ε 0 ), и мы продолжим отсюда.
А теперь подумайте обо всех этих ординалах. Все разные способы упорядочить алеф-нулевые вещи. Ну, они хорошо упорядочены, поэтому у них есть тип порядка — некоторый порядковый номер, который идет после всех них. В данном случае этот порядковый номер называется «омега-один» (ω1). Теперь, поскольку по определению ω 1 идет после каждого отдельного типа порядка или вещей с нулевым алефом, оно должно описывать расположение буквально большего количества вещей, чем последний алеф. Я имею в виду, что если бы это было не так, то оно было бы где-то здесь, но это не так.Кардинальное число, описывающее количество вещей, использованных для размещения с типом заказа ω 1 , равно «алеф-один» (ℵ 1 ).
Я имею в виду, что если бы это было не так, то оно было бы где-то здесь, но это не так.Кардинальное число, описывающее количество вещей, использованных для размещения с типом заказа ω 1 , равно «алеф-один» (ℵ 1 ).
Неизвестно, где на этой линии находится набор мощности натуралов. Этого не может быть между этими кардиналами, потому что между ними нет кардиналов. Оно может быть равно алеф-один — это убеждение называется гипотезой континуума. Но он также может быть больше; мы просто не знаем. Гипотеза континуума, между прочим, пожалуй, самый большой вопрос без ответа во всей этой теме, и сегодня в этом видео я не буду его решать, а буду подниматься все выше и выше, во все большие и большие бесконечности.
Теперь, используя аксиому замены, мы можем взять любой порядковый номер, которого мы уже достигли, например, ω, и перейти от алеф к алеф до алеф-омега. Или, черт возьми, почему бы не использовать больший порядковый номер, например ω 2 , для построения алеф-омега-квадрат? Алеф-омега-омега-омега-омега-омега-омега-о… Наша система обозначений позволяет мне добавлять сюда только счетное число омег, но замена не заботится о том, есть ли у меня способ записать числа, которых она достигает.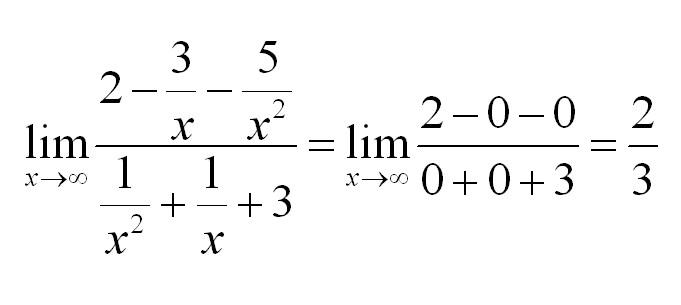 Где бы я ни приземлился, там будет еще больше чисел, что позволит мне совершать еще большие и многочисленные прыжки, чем раньше.Все это представляет собой дико ускоряющуюся петлю обратной связи эмбиггенинга. Мы можем продолжать в том же духе, достигая все больших и больших бесконечностей снизу.
Где бы я ни приземлился, там будет еще больше чисел, что позволит мне совершать еще большие и многочисленные прыжки, чем раньше.Все это представляет собой дико ускоряющуюся петлю обратной связи эмбиггенинга. Мы можем продолжать в том же духе, достигая все больших и больших бесконечностей снизу.
Замена и повторяющиеся наборы мощности, которые могут совпадать или не совпадать с алефами, могут поддерживать наше восхождение навсегда. Так что ясно, что за ними ничего нет, верно? Не так быстро. Это то, что мы говорили о переходе от конечного к омеге. Почему бы не принять как аксиому, что существует какое-то следующее число, настолько большое, что никакие замены или настройки чего-то меньшего никогда не смогут вас туда привести.Такое число называется «недоступным кардиналом», потому что до него невозможно добраться снизу.
Теперь интересно, что среди чисел, которых мы уже достигли, можно найти тень такого числа: алеф-нуль. Вы также не можете добраться до этого числа снизу. Все числа, меньшие этого, конечны, и конечное число конечных чисел нельзя складывать, умножать, возводить в степень, заменять конечными скачками конечное число раз или даже устанавливать мощность конечное число раз, чтобы получить что-либо, кроме другого конечного числа. количество.Несомненно, набор мощности от миллиона к гуголплексу, к гуголплексу к гуголплексу действительно велик, но он все же конечен. Даже близко не алеф-нуль, первая наименьшая бесконечность. По этой причине алеф-нуль часто считается недоступным числом. Однако некоторые авторы этого не делают, говоря, что недоступное также должно быть неисчисляемым, что, ладно, имеет смысл — я имею в виду, что мы уже получили доступ к алеф-нулю, но помните, что единственный способ, которым мы могли бы это сделать, — это прямо объявить его существование аксиоматически.Нам придется сделать то же самое для недоступных кардиналов.
Все числа, меньшие этого, конечны, и конечное число конечных чисел нельзя складывать, умножать, возводить в степень, заменять конечными скачками конечное число раз или даже устанавливать мощность конечное число раз, чтобы получить что-либо, кроме другого конечного числа. количество.Несомненно, набор мощности от миллиона к гуголплексу, к гуголплексу к гуголплексу действительно велик, но он все же конечен. Даже близко не алеф-нуль, первая наименьшая бесконечность. По этой причине алеф-нуль часто считается недоступным числом. Однако некоторые авторы этого не делают, говоря, что недоступное также должно быть неисчисляемым, что, ладно, имеет смысл — я имею в виду, что мы уже получили доступ к алеф-нулю, но помните, что единственный способ, которым мы могли бы это сделать, — это прямо объявить его существование аксиоматически.Нам придется сделать то же самое для недоступных кардиналов.
Очень трудно передать, насколько непостижимы размеры недоступного кардинала. Я просто оставлю это на этом: концептуальный прыжок из ничего в первую бесконечность подобен прыжку из первой бесконечности в недоступное. Теоретики множеств описали числа большие, чем недоступные, каждое из которых требует новой аксиомы большого кардинального числа, утверждающей его существование, расширяющей высоту нашей вселенной чисел. Настанет ли когда-нибудь момент, когда мы придумаем аксиому, подразумевающую существование стольких вещей, что она подразумевает противоречащие друг другу вещи? Ответим ли мы когда-нибудь на гипотезу континуума? Может быть, и нет, но есть многообещающие направления, а до тех пор остается удивительным факт, что многие из этих бесконечностей — возможно, все они — настолько велики, что не совсем ясно, существуют ли они на самом деле или могут ли быть показаны в реальности. физическая вселенная.Если они есть, если однажды физика найдет им применение, это прекрасно, но если нет, то это тоже прекрасно. Это означало бы, что с этим мозгом, крошечной штукой, в септиллион раз меньшей, чем крошечная планета, на которой она живет, мы открыли что-то истинное за пределами физического мира. Что-то, что применимо к реальному миру, но в то же время достаточно сильное, чтобы идти дальше, за пределы того, что даже сама Вселенная может вместить, или показать нам, или чем быть.
Теоретики множеств описали числа большие, чем недоступные, каждое из которых требует новой аксиомы большого кардинального числа, утверждающей его существование, расширяющей высоту нашей вселенной чисел. Настанет ли когда-нибудь момент, когда мы придумаем аксиому, подразумевающую существование стольких вещей, что она подразумевает противоречащие друг другу вещи? Ответим ли мы когда-нибудь на гипотезу континуума? Может быть, и нет, но есть многообещающие направления, а до тех пор остается удивительным факт, что многие из этих бесконечностей — возможно, все они — настолько велики, что не совсем ясно, существуют ли они на самом деле или могут ли быть показаны в реальности. физическая вселенная.Если они есть, если однажды физика найдет им применение, это прекрасно, но если нет, то это тоже прекрасно. Это означало бы, что с этим мозгом, крошечной штукой, в септиллион раз меньшей, чем крошечная планета, на которой она живет, мы открыли что-то истинное за пределами физического мира. Что-то, что применимо к реальному миру, но в то же время достаточно сильное, чтобы идти дальше, за пределы того, что даже сама Вселенная может вместить, или показать нам, или чем быть.
И как всегда спасибо за просмотр.
Еще один интересный факт о трансфинитных ординалах заключается в том, что арифметика с ними немного отличается.Обычно 2+1 совпадает с 1+2, но ω+1 не совпадает с 1+ω. Один плюс омега на самом деле просто омега. Думайте о них как о типах заказов: одна вещь, помещенная перед омегой, просто использует все натуральные числа и оставляет нас с типом заказа омега. Одна вещь, размещенная после омеги, требует каждого натурального числа, а затем омеги, оставляя нам омегу плюс один в качестве типа заказа.
«объяснений, которые преобразовывают мир» Дэвида Дойча
Расширение философии Карла Поппера, «Начало бесконечности» Дэвида Дойча является определяющим трудом по философии двадцать первого века. Я подозреваю, что при первом знакомстве может быть не совсем ясно, что лежит в основе сообщения и философии. Структура книги, заголовки глав и частые отступления заставят некоторых читателей либо отказаться от книги, либо упустить главное. Но для тех, кто придерживается этого и действительно усваивает уроки, эта философия сильна. Хотя ни один обзор не может передать содержание этой книги, как бы оно ни стоило, вот основные моменты, которые я вынес из книги.
Но для тех, кто придерживается этого и действительно усваивает уроки, эта философия сильна. Хотя ни один обзор не может передать содержание этой книги, как бы оно ни стоило, вот основные моменты, которые я вынес из книги.
В целом, Дойч утверждает, что знания и биологическая адаптация имеют схожую историю развития (хотя они сильно различаются в других важных аспектах).С точки зрения биологической адаптации, изменчивость генов приводит к различным биологическим формам, которые затем отбираются в процессе естественного отбора. Информация, необходимая для создания биологических форм, содержится в генах.
Точно так же знание развивается путем вариаций в форме предположений или объяснений о каком-либо явлении, которые затем отбираются с помощью традиций критики и экспериментов.
Таким образом, процесс изменчивости и отбора приводит к эволюции как биологических форм, так и знаний.Однако, в отличие от биологической эволюции, знание выражается в форме объяснений, имеющих потенциально бесконечный охват. Например, теория гравитации — это объяснение, которое может предоставить информацию о самых дальних уголках Вселенной, несмотря на то, что мы никогда туда не путешествовали.
Например, теория гравитации — это объяснение, которое может предоставить информацию о самых дальних уголках Вселенной, несмотря на то, что мы никогда туда не путешествовали.
Вариация в виде догадок порождает различные объяснения, которые затем можно подвергнуть критике и проверке. Но только благодаря традиции критики и проверки знание может эволюционировать и стать более совершенным.И этот факт объясняет взрыв знаний, который мы наблюдаем за последние 400 или около того лет, начиная с научной революции и эпохи Просвещения.
Просвещение, которое включало в себя научную революцию, характеризовалось отказом от авторитетов, догм и любой системы верований, которые изолировали себя от критики и изменений. Эта изоляция от критики и перемен характерна для всех неудавшихся обществ и систем мышления.
Новая научная чувствительность, напротив, ничего не принимала как должное и даже рассматривала свои собственные теории как предварительные или подлежащие изменению перед лицом новых данных или лучших объяснительных теорий.
Таким образом, все знания рассматриваются как догадки, подвергающиеся отбору, критике и проверке, что позволяет знаниям бесконечно расти и расширяться.
В процессе мы обнаружили критерии хороших объяснений. Природа нашего разума такова, что мы никогда ничего не можем знать с полной уверенностью; наше знание, в результате, должно быть вероятностным. Но в рамках этого ограничения мы можем разрабатывать объяснения, которые становятся все более точными и точными.
Точность и точность являются важными стандартами в нашей оценке объяснений; стандарты, которые отсутствуют в плохих объяснениях.Например, использование креационизма для объяснения биологической адаптации — плохое объяснение, потому что утверждение, что «жизнь создал Бог», на самом деле ничего не объясняет. В нем ничего не говорится о природе Бога, о том, как появился сам Бог и почему были разработаны определенные приспособления, исключающие другие.
Что еще более важно, в плохих объяснениях детали легко изменить. Креационист, столкнувшись с любым конкретным примером плохого замысла в нашей собственной биологии, может просто придумать объяснение его существования или заявить, что Бог бесконечно мудрее нас, так что должна быть причина.
Креационист, столкнувшись с любым конкретным примером плохого замысла в нашей собственной биологии, может просто придумать объяснение его существования или заявить, что Бог бесконечно мудрее нас, так что должна быть причина.
Это признак плохого объяснения: такого, которое никогда не может быть неверным, независимо от любых новых мыслей, критики, открытий, доказательств или процедур проверки. Эволюция, напротив, представляет собой хорошее объяснение, потому что она не только соответствует фактам, но и детали трудно изменить. Это означает, что эволюцию можно было бы опровергнуть, обнаружив окаменелость не на своем месте или проявив биологическую адаптацию, которая возникла спонтанно без предковых предшественников.
Во всей этой эпистемологии есть понятие фаллибилизма, важность теории и важность системы критики.
Фаллибилизм — это принцип, согласно которому все наши теории, как научные, так и основанные на здравом смысле, в той или иной степени подвержены сомнению и поэтому никогда не могут быть окончательно доказаны. Даже формальные системы, такие как математика и логика, не могут доказывать свои собственные аксиомы из своих собственных систем и должны полагаться на внешние источники, до бесконечности.
Даже формальные системы, такие как математика и логика, не могут доказывать свои собственные аксиомы из своих собственных систем и должны полагаться на внешние источники, до бесконечности.
Каждый аргумент включает в себя посылки в поддержку вывода, но сами посылки остаются неаргументированными. Если эти посылки затем поддерживаются дальнейшим аргументом, то посылки для этого аргумента остаются без поддержки.
Это приводит к бесконечному регрессу и постоянному состоянию сомнений, и чем глубже наши объяснения, тем больше возникает вопросов. Вот почему проблемы неизбежны. Но проблемы также разрешимы, даже если наше знание только вероятностно. Мы можем решать проблемы по мере их возникновения, но — и вот еще один ключевой момент — мы не можем знать, какие проблемы разрешимы, до того, как решим их.
Вот почему преждевременное когнитивное закрытие противоречит теории Дойча; отказ от проблем как от неразрешимых или от существующей веры как достоверной препятствует возможности роста знания.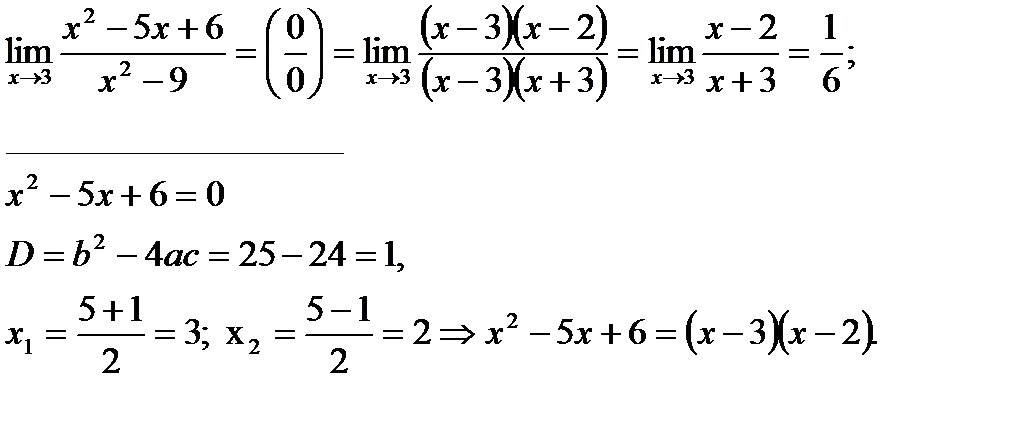 Возможно, некоторые проблемы неразрешимы, но поскольку мы заранее не знаем, какие из них будут решены, мы должны с практической необходимостью предположить, что они решаемы.
Возможно, некоторые проблемы неразрешимы, но поскольку мы заранее не знаем, какие из них будут решены, мы должны с практической необходимостью предположить, что они решаемы.
Это приведет к развитию объяснительных теорий (вариации), которые затем могут быть подвергнуты критике и проверке (отбор). Теории, которые выдерживают проверку, становятся лучшими объяснениями на данный момент. Итак, в уме происходит своего рода эволюционный процесс.
Теория и абстрактные объяснения всегда предшествуют проверке, поскольку генная изменчивость всегда предшествует естественному отбору.Это потому, что экспериментальные данные всегда нужно фильтровать и оценивать в соответствии с какой-то теорией. Идея эмпиризма, согласно которой данные наблюдений спонтанно превращаются в теорию и знание, заведомо ложна. Законы универсального движения Ньютона, например, нельзя вывести просто из наблюдения движущихся объектов. Это объяснительная теория, которую можно проверить, но прежде всего она должна быть теорией.
Это, по сути, то, что я считаю основной философией книги.Это философия, которая заменяет поиск определенности поиском лучших объяснений и безграничным ростом знаний, которая может помочь человечеству раз и навсегда выйти из темных веков.
Спор о бесконечности делит математиков
From Quanta (оригинальную историю можно найти здесь).
В ходе исследования своей вселенной математики время от времени натыкались на дыры: утверждения, которые нельзя ни доказать, ни опровергнуть с помощью девяти аксиом, которые в совокупности называются «ZFC» и служат фундаментальными законами математики.Большинство математиков просто игнорируют дыры, которые находятся в абстрактных сферах и не имеют практических или научных разветвлений. Но для хранителей логических основ математики их присутствие вызывает беспокойство по поводу основ всего предприятия.
«Как я могу оставаться в какой-либо области и продолжать доказывать теоремы, если фундаментальные понятия, которые я использую, проблематичны?» — спрашивает Питер Келлнер, профессор философии Гарвардского университета, специализирующийся на математической логике.
Главной из дыр является гипотеза континуума, утверждение 140-летней давности о возможных размерах бесконечности.Каким бы непостижимым это ни казалось, бесконечность выражается во многих измерениях: например, на числовой прямой, называемой «континуумом», больше точек, чем счетных чисел. За континуумом лежат еще большие бесконечности — бесконечная прогрессия все более огромных, но все же бесконечных сущностей. Гипотеза континуума утверждает, что нет бесконечности между наименьшим видом — набором счетных чисел — и тем, что, как она утверждает, является вторым по величине — континуумом.Она «должна быть либо истинной, либо ложной, — писал логик-математик Курт Гёдель в 1947 году, — и ее неразрешимость исходя из аксиом, известных сегодня, может означать только то, что эти аксиомы не содержат полного описания реальности».
Десятилетние поиски более полной аксиоматической системы, которая могла бы решить вопрос о бесконечности и в то же время закрыть многие другие пробелы в математике, подошли к перепутью. Во время недавней встречи в Гарварде, организованной Келлнером, ученые в основном согласились с двумя основными претендентами на дополнения к ZFC: аксиомы форсирования и аксиома внутренней модели «V = окончательный L.
Во время недавней встречи в Гарварде, организованной Келлнером, ученые в основном согласились с двумя основными претендентами на дополнения к ZFC: аксиомы форсирования и аксиома внутренней модели «V = окончательный L.
«Если аксиомы принуждения верны, то континуум-гипотеза ложна», — сказал Кельнер. «И если аксиома внутренней модели верна, то континуум-гипотеза верна. Вы проходите через целый список проблем в других областях, и аксиомы принуждения ответят на эти вопросы одним способом, а конечная L ответит на них другим способом».
По мнению исследователей, выбор между кандидатами сводится к вопросу о назначении логических аксиом и природе самой математики.Должны ли аксиомы быть крупицами истины, из которых состоит самая нетронутая математическая вселенная? В этом случае V=предельное L может оказаться наиболее многообещающим. Или цель найти самые плодотворные семена математических открытий — критерий, который, кажется, благоприятствует принудительным аксиомам? «У обеих сторон несколько разные взгляды на цель», — сказал Джастин Мур, профессор математики Корнельского университета.
Аксиоматические системы, такие как ZFC, предоставляют правила, управляющие коллекциями объектов, называемыми «множествами», которые служат строительными блоками математической вселенной.Точно так же, как ZFC теперь проверяет математическую истину, добавление дополнительной аксиомы в книгу правил помогло бы сформировать будущее области — особенно ее взгляд на бесконечность. Но в отличие от большинства аксиом ZFC, новые аксиомы «не являются самоочевидными или, по крайней мере, не самоочевидными на данном этапе наших знаний, поэтому перед нами стоит гораздо более сложная задача», — сказал Стево Тодорчевич, математик из Университет Торонто и Французский национальный центр научных исследований в Париже.
Сторонники V=предельное L говорят, что установление отсутствия бесконечности между целыми числами и континуумом обещает внести порядок в хаос бесконечных множеств, разнообразие которых непостижимо бесконечно.Но эта аксиома может иметь минимальные последствия для традиционных разделов математики.
«Теория множеств заключается в понимании бесконечности», — сказал Хью Вудин, математик из Калифорнийского университета в Беркли; архитектор V=предельное L; и один из самых выдающихся теоретиков живых множеств. Знакомые числа, имеющие отношение к большей части математики, утверждает Вудин, «представляют собой незначительную часть вселенной множеств».
Между тем, форсирование аксиом, которые считают континуум-гипотезу ложной, путем добавления нового размера бесконечности, расширило бы границы математики и в других направлениях.Это рабочие лошадки, которые обычные математики «могут, так сказать, выйти и использовать в полевых условиях», — сказал Мур. «Для меня это, в конечном счете, то, что должны делать основы [математики]».
Новые достижения в изучении V = предельное L и новые способы использования форсирующих аксиом, особенно та, которая названа «максимумом Мартина» в честь математика Дональда Мартина, активизировали дебаты о том, какую аксиому принять. И есть третья точка зрения, которая не согласуется с самой предпосылкой дебатов. По мнению некоторых теоретиков, существует множество математических вселенных, в одних из которых континуум-гипотеза верна, а в других — нет, но все они в равной степени заслуживают изучения. Между тем, «есть некоторые скептики, — сказал Кёлльнер, — люди, которые по философским причинам считают, что теория множеств и высшая бесконечность вообще не имеют никакого смысла».
По мнению некоторых теоретиков, существует множество математических вселенных, в одних из которых континуум-гипотеза верна, а в других — нет, но все они в равной степени заслуживают изучения. Между тем, «есть некоторые скептики, — сказал Кёлльнер, — люди, которые по философским причинам считают, что теория множеств и высшая бесконечность вообще не имеют никакого смысла».
Бесконечные парадоксы
Бесконечность всколыхнула перья в математике почти с самого начала ее существования. Противоречие возникает не из-за понятия потенциальной бесконечности — числовая линия обещает продолжаться вечно, — а из-за представления о бесконечности как о реальном, законченном объекте, которым можно манипулировать.
«Какие действительно бесконечные объекты существуют в реальном мире?» — спрашивает Стивен Симпсон, математик и логик из Пенсильванского государственного университета. Принимая точку зрения, первоначально поддержанную Аристотелем, Симпсон утверждает, что фактическая бесконечность на самом деле не существует, и поэтому не следует с такой легкостью предполагать, что она существует в математической вселенной. Он возглавляет попытку отучить математику от фактической бесконечности, показывая, что подавляющее большинство теорем можно доказать, используя только понятие потенциальной бесконечности.«Но потенциальная бесконечность сейчас почти забыта», — сказал Симпсон. «В мышлении теории множеств ZFC люди, как правило, даже не помнят этого различия. Они просто думают, что бесконечность означает настоящую бесконечность, вот и все».
Он возглавляет попытку отучить математику от фактической бесконечности, показывая, что подавляющее большинство теорем можно доказать, используя только понятие потенциальной бесконечности.«Но потенциальная бесконечность сейчас почти забыта», — сказал Симпсон. «В мышлении теории множеств ZFC люди, как правило, даже не помнят этого различия. Они просто думают, что бесконечность означает настоящую бесконечность, вот и все».
Бесконечность была упакована и продана математическому сообществу в конце 19 века немецким математиком Георгом Кантором. Кантор изобрел раздел математики, связанный с множествами — наборами элементов, которые варьируются от пустых (эквивалент числа ноль) до бесконечных.Его «теория множеств» была настолько удобным языком для описания математических объектов, что за несколько десятилетий она стала лингва-франка в этой области. Список правил из девяти пунктов, называемый теорией множеств Цермело-Френкеля с аксиомой выбора, или ZFC, был установлен и широко принят к 1920-м годам. В переводе на простой язык одна из аксиом гласит, что два множества равны, если они содержат одни и те же элементы. Другой просто утверждает, что существуют бесконечные множества.
В переводе на простой язык одна из аксиом гласит, что два множества равны, если они содержат одни и те же элементы. Другой просто утверждает, что существуют бесконечные множества.
Допущение фактической бесконечности приводит к тревожным последствиям.Кантор доказал, например, что бесконечное множество четных чисел {2,4,6,…} может быть поставлено во “однозначное соответствие” со всеми счетными числами {1,2,3,…}, что указывает на что четных ровно столько, сколько нечетных.
Еще более шокирующим было его доказательство в 1873 году, что континуум действительных чисел (таких как 0,00001, 2,568023489, пи и т. д.) является «неисчислимым»: действительные числа не соответствуют однозначным образом счетным числам, потому что для любой их нумерованный список, всегда можно найти реальный номер, которого нет в списке.Бесконечные наборы действительных и счетных чисел имеют разные размеры, или, говоря языком Кантора, разные «количественные числа». На самом деле он обнаружил, что существует не два, а бесконечная последовательность постоянно увеличивающихся кардиналов, причем каждая новая бесконечность состоит из множества степеней или множества всех подмножеств бесконечного множества, предшествующего ей.
Некоторые математики презирали этот беспорядок бесконечностей. Один из коллег Кантора назвал их «серьезной болезнью»; другой назвал его «развратителем молодежи». Но по логике теории множеств это было правдой.
Кантор задумался о двух самых маленьких кардиналах. «В каком-то смысле это самый фундаментальный вопрос, который вы можете задать, — сказал Вудин. «Существует ли бесконечность между ними, или бесконечность действительных чисел есть первая бесконечность после бесконечности счетных чисел?»
Все очевидные кандидаты на бесконечность среднего размера терпят неудачу. Рациональные числа (соотношения целых чисел, такие как ½) счетны и, таким образом, имеют ту же мощность, что и счетные числа. И в любом сегменте континуума столько же действительных чисел (например, от 0 до 1), сколько и во всем множестве.Кантор догадался, что между счетными множествами и континуумом нет бесконечности. Но он не смог доказать эту «гипотезу континуума», используя аксиомы теории множеств. И никто другой не мог.
И никто другой не мог.
Затем, в 1931 году, Гёдель, недавно защитивший докторскую диссертацию в Венском университете, сделал поразительное открытие. С помощью пары доказательств 25-летний Гёдель показал, что поддающаяся спецификации, но достаточно сложная аксиоматическая система, такая как ZFC, никогда не может быть одновременно непротиворечивой и полной. Доказательство того, что его аксиомы непротиворечивы (то есть, что они не приводят к противоречиям), требует дополнительной аксиомы, которой нет в списке.И чтобы доказать, что ZFC-плюс-эта-аксиома непротиворечива, нужна еще одна аксиома. «Теоремы Гёделя о неполноте говорят нам, что мы никогда не сможем поймать собственный хвост», — сказал Мур.
Неполнота ZFC означает, что математическая вселенная, которую порождают ее аксиомы, неизбежно будет иметь дыры. «Будут [утверждения], которые не могут быть решены этими принципами», — сказал Вудин. Вскоре стало ясно, что континуум-гипотеза, «самый фундаментальный вопрос, который вы можете задать» о бесконечности, была такой дырой. Сам Гёдель доказал, что истинность гипотезы континуума согласуется с ZFC, а Пол Коэн, американский математик, доказал обратное, что отрицание гипотезы также согласуется с ZFC. Их объединенные результаты показали, что континуум-гипотеза на самом деле не зависит от аксиом. Чтобы доказать или опровергнуть это, необходимо что-то помимо ZFC.
Сам Гёдель доказал, что истинность гипотезы континуума согласуется с ZFC, а Пол Коэн, американский математик, доказал обратное, что отрицание гипотезы также согласуется с ZFC. Их объединенные результаты показали, что континуум-гипотеза на самом деле не зависит от аксиом. Чтобы доказать или опровергнуть это, необходимо что-то помимо ZFC.
Поскольку гипотеза не решена, многие другие свойства количественных чисел и бесконечности также остаются неопределенными. Для таких скептиков теории, как Соломон Феферман, почетный профессор математики и философии Стэнфордского университета, это не имеет значения.«Они просто не имеют отношения к повседневной математике», — сказал Феферман.
Но для тех, кто целыми днями блуждает во вселенной множеств, известной как «V», где почти все бесконечно, вопросы кажутся большими. «У нас нет четкого представления о вселенной наборов, — сказал Вудин. «Почти любой вопрос, который вы пишете о множествах, неразрешим. Это неудовлетворительная ситуация».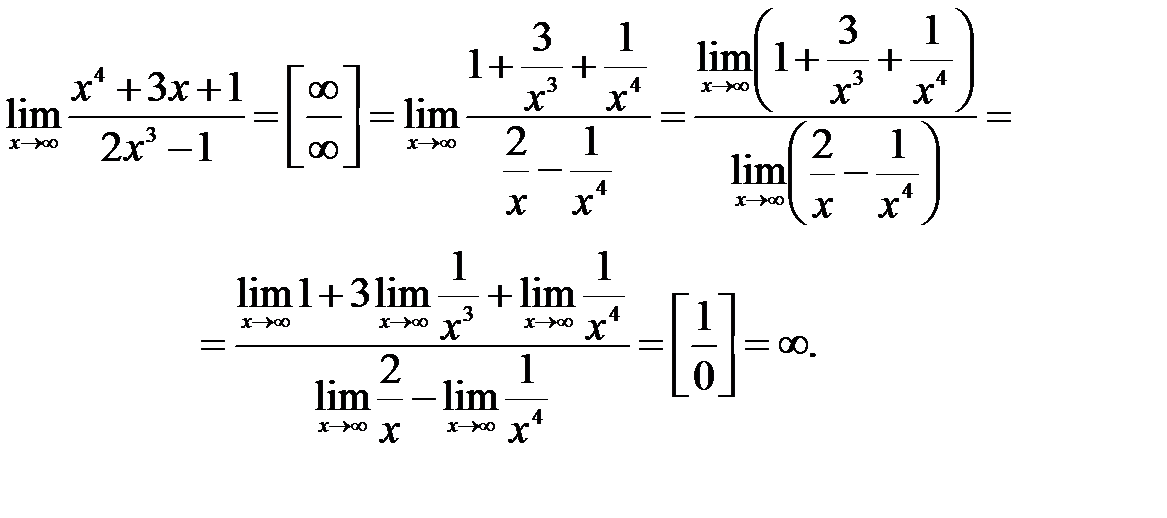
Набор наборов
Гёдель и Коэн, чья совместная работа привела к нынешнему перекрестку в теории множеств, оказались основателями двух школ мысли о том, куда двигаться дальше.
Гёдель задумал маленькую и конструируемую модельную вселенную под названием «L», населенную, начиная с пустого множества и итерируя его для построения все больших и больших множеств. Во вселенной множеств, которая получается, гипотеза континуума верна: между множеством целых чисел и континуумом нет бесконечного множества. «В отличие от хаоса вселенной множеств, вы действительно можете анализировать L», — сказал Вудин. Это делает аксиому «V = L» или утверждение, что вселенная множеств V равна «внутренней модели» L, привлекательной.По словам Вудина, есть только одна проблема: «Это сильно ограничивает природу бесконечности».
L слишком мал, чтобы охватить «большие кардиналы», бесконечные множества, которые восходят в бесконечной иерархии с уровнями, названными «недоступный», «измеримый», «Вудин», «сверхкомпактный», «огромный» и так далее, вместе взятые. составляя какофоническую симфонию бесконечностей. Периодически обнаруживаемые в течение 20-го века, эти большие кардиналы не могут быть доказаны с помощью ZFC и вместо этого должны быть постулированы с помощью дополнительных «больших кардинальных аксиом».Но на протяжении десятилетий было показано, что они генерируют богатую и интересную математику. «По мере того, как вы поднимаетесь вверх по большой кардинальной иерархии, вы получаете все более и более важные последствия», — сказал Келлнер.
составляя какофоническую симфонию бесконечностей. Периодически обнаруживаемые в течение 20-го века, эти большие кардиналы не могут быть доказаны с помощью ZFC и вместо этого должны быть постулированы с помощью дополнительных «больших кардинальных аксиом».Но на протяжении десятилетий было показано, что они генерируют богатую и интересную математику. «По мере того, как вы поднимаетесь вверх по большой кардинальной иерархии, вы получаете все более и более важные последствия», — сказал Келлнер.
Чтобы сохранить эту симфонию бесконечностей, теоретики множеств десятилетиями стремились найти внутреннюю модель, столь же чистую и поддающуюся анализу, как L, но включающую большие кардиналы. Однако для создания вселенной наборов, включающих каждый тип большого кардинала, требовался уникальный набор инструментов. Для каждой более крупной и всеобъемлющей внутренней модели «нужно было делать что-то совершенно другое», — сказал Келлнер.«Поскольку большая кардинальная иерархия просто продолжается и продолжается вечно, казалось, что нам тоже нужно продолжать и продолжать вечно, создавая столько новых внутренних моделей, сколько точек перехода в большой кардинальной иерархии. И это выглядит безнадежно, потому что, знаете ли, жизнь коротка».
И это выглядит безнадежно, потому что, знаете ли, жизнь коротка».
Поскольку не существовало наибольшего большого кардинала, казалось, что не может быть конечной L, внутренней модели, которая их всех охватывала. «Затем произошло нечто очень удивительное, — сказал Вудин. В работе, опубликованной в 2010 году, он обнаружил точку разрыва в иерархии.
«Вудин показал, что если вы можете просто достичь уровня суперкомпактных, тогда происходит переполнение, и ваша внутренняя модель также улавливает все более крупные кардиналы», — объяснил Келлнер. «Это был своего рода ландшафтный сдвиг. Это дало новую надежду на то, что этот подход может работать. Все, что вам нужно сделать, это поразить один суперкомпакт, и тогда у вас есть все».
Хотя это еще не построено, окончательная L — это название гипотетической внутренней модели, которая включает сверхкомпактные и, следовательно, все большие кардиналы.Аксиома V=предельное L утверждает, что эта внутренняя модель есть вселенная множеств.
Вудин, который в январе переезжает из Беркли в Гарвард, недавно завершил первую часть четырехэтапного доказательства окончательной L-гипотезы и сейчас проверяет его с небольшой группой коллег. Он говорит, что «очень оптимистичен в отношении второго этапа» доказательства и надеется закончить его к следующему лету. «Все сводится к этой гипотезе, и если ее можно доказать, то доказывается существование предельного L и подтверждается, что она совместима со всеми понятиями бесконечности, не только о которых мы думали сегодня, но и о которых когда-либо могли подумать, ” он сказал.«Если конечная гипотеза L верна, то есть абсолютно убедительный случай, что V — это конечная L».
Расширение вселенной
Даже если предельная L существует, может быть построена и настолько великолепна, как надеется Вудин, это не идеальная вселенная для всех. «Существует противоположный импульс, пронизывающий большую часть теоретико-множественной истории, который говорит нам, что Вселенная должна быть как можно более богатой, а не как можно меньше», — сказала Пенелопа Мэдди, философ математики из Калифорнийского университета в Ирвине и автор. «Защита аксиом», опубликованной в 2011 году.«И именно это мотивирует форсирующие аксиомы».
«Защита аксиом», опубликованной в 2011 году.«И именно это мотивирует форсирующие аксиомы».
Чтобы расширить ZFC, обратиться к гипотезе континуума и лучше понять бесконечность, сторонники форсирования аксиом используют метод, называемый форсированием, первоначально разработанный Коэном. Если внутренние модели строят вселенную множеств с нуля, форсирование расширяет ее наружу во всех направлениях.
Тодорчевич, один из ведущих специалистов по методу, сравнивает форсирование с изобретением комплексных чисел, которые являются действительными числами с дополнительным измерением.Но вместо того, чтобы начинать с действительных чисел, «вы начинаете со вселенной множеств, а затем расширяете ее, чтобы сформировать новую, большую вселенную», — сказал он. В расширенной вселенной, созданной форсированием, существует более широкий класс действительных чисел, чем в исходной вселенной, определенной ZFC. Это означает, что действительные числа ZFC составляют меньший бесконечный набор, чем полный континуум. «Таким образом вы опровергаете континуум-гипотезу», — сказал Тодорчевич.
«Таким образом вы опровергаете континуум-гипотезу», — сказал Тодорчевич.
Аксиома принуждения, называемая «максимум Мартина», открытая в 1980-х годах, расширяет Вселенную настолько далеко, насколько это возможно.Это самый сильный соперник для V=ultimate L, хотя и гораздо менее красивый. «С философской точки зрения обосновать эту аксиому гораздо сложнее, — сказал Тодорчевич. «Это может быть оправдано только с точки зрения влияния, которое оно оказывает на остальную часть математики».
Вот где сияют аксиомы форсирования. В то время как V=ultimate L строит замок из невообразимых бесконечностей, принудительные аксиомы заполняют некоторые проблемные выбоины в повседневной математике. Работа Тодорчевича, Мура, Карлоса Мартинеса-Ранеро и других за последние несколько лет показывает, что они наделяют многие математические структуры прекрасными свойствами, которые упрощают их использование и понимание.
Для Мура такого рода результаты дают принудительным аксиомам преимущество перед внутренними моделями. «В конечном счете, решение должно основываться на следующем: «Что это дает для математики?», — сказал он. «Помимо собственного внутреннего интереса, какую хорошую математику он производит?»
«В конечном счете, решение должно основываться на следующем: «Что это дает для математики?», — сказал он. «Помимо собственного внутреннего интереса, какую хорошую математику он производит?»
«Я бы ответил, что это правда, что максимум Мартина отлично подходит для понимания структур в классической математике», — сказал Вудин. «Для меня теория множеств не в этом. Непонятно, как максимум Мартина приведет к лучшему пониманию бесконечности.
На недавней встрече в Гарварде исследователи из обоих лагерей представили новые работы по внутренним моделям и форсирующим аксиомам и обсудили их относительные достоинства. По их словам, споры, скорее всего, будут продолжаться до тех пор, пока тот или иной кандидат не уйдет на второй план. Например, Ultimate L может не существовать. Или, возможно, максимум Мартина не так полезен, как надеются его сторонники.
Как указывали многие математики, сами дебаты свидетельствуют об отсутствии у человека интуиции относительно понятия бесконечности.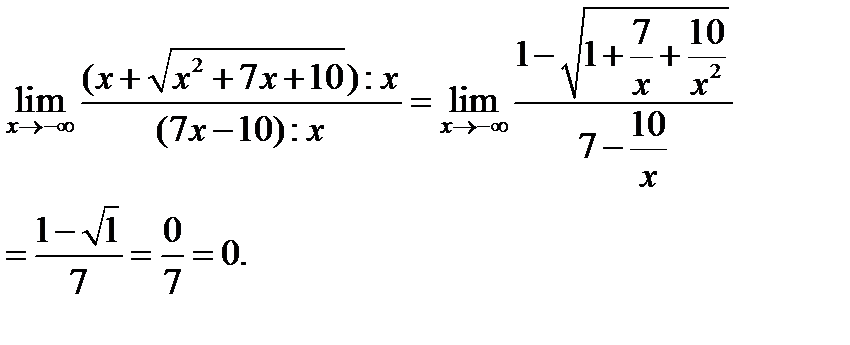 «Пока вы не исследуете последствия континуум-гипотезы, у вас не будет реальной интуиции относительно того, истинна она или ложна», — сказал Мур.
«Пока вы не исследуете последствия континуум-гипотезы, у вас не будет реальной интуиции относительно того, истинна она или ложна», — сказал Мур.
Математика имеет репутацию объективной. Но без бесконечных объектов реального мира, на которых можно основывать абстракции, математическая истина становится в какой-то степени вопросом мнения — что является аргументом Симпсона в пользу полного исключения фактической бесконечности из математики. Выбор между V=предельное L и максимумом Мартина, возможно, является не столько проблемой «верно-ложно», сколько вопросом, что красивее, английский сад или лес?
— Это личное дело, — сказал Мур.
Тем не менее, область математики известна своим единством и сплоченностью. Подобно тому, как ZFC стал доминировать в альтернативных фундаментальных схемах в начале 20-го века, прочно внедрив фактическую бесконечность в математическое мышление и практику, вполне вероятно, что выживет только одна новая аксиома, определяющая более полную природу бесконечности.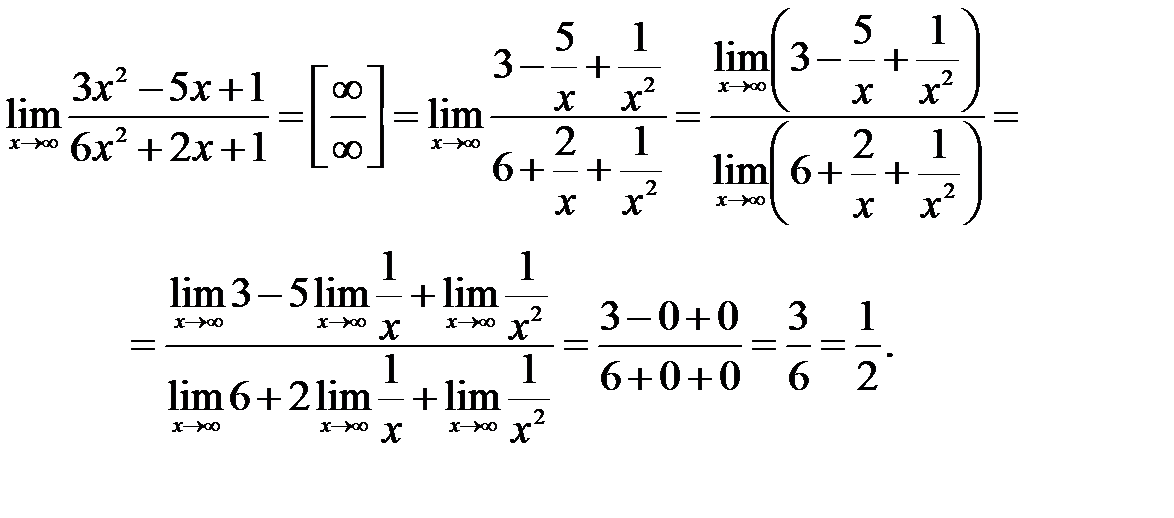 По словам Келлнера, «одна сторона должна быть неправа».
По словам Келлнера, «одна сторона должна быть неправа».
Перепечатано с разрешения Quanta Magazine , редакционно независимого подразделения SimonsFoundation.org, чья миссия состоит в том, чтобы улучшить общественное понимание науки, освещая исследовательские разработки и тенденции в математике, физических науках и науках о жизни.
Исследование математических отношений нуля и бесконечности в JSTOR
Перейти к основному содержанию Есть доступ к библиотеке? Войдите через свою библиотекуВесь контент Картинки
Поиск JSTOR Регистрация Вход- Поиск
- Расширенный поиск
- Изображения
- Просматривать
- По тематике
Журналы и книги - По названию
Журналы и книги - Издатели
- Коллекции
- Изображения
- По тематике
- Инструменты
- Рабочее пространство
- Анализатор текста
- Серия JSTOR Understanding
- Данные для исследований
фракталов – способ увидеть бесконечность
1 апреля 2021 г.
Категория: Исследования
Поделиться этой публикацией:
Вы когда-нибудь задумывались, почему река, похожая на дерево, похожа на лист? IBMer Бенуа Мандельброт сделал.Его причудливый взгляд на мир привел к открытию фрактальной геометрии. Фракталы позволили математически исследовать виды грубых неровностей, существующих в природе. Облака — не идеальные сферы, горы — несимметричные конусы, а молния не движется по прямой. «Во всей науке, во всей математике гладкость была всем. Что я сделал, так это открыл шероховатости для расследования», — сказал Мандельброт.
Так что же такое фрактал? Фрактал — это бесконечный паттерн.Они создаются путем многократного повторения простого процесса. Вместо того чтобы сосредоточиться на жесткой геометрии, Мандельброт создал новые уравнения в формах, которые были грубыми и зазубренными. «Я задумал и разработал новую геометрию природы и реализовал ее использование в ряде разнообразных областей. Он описывает множество неправильных и фрагментированных паттернов вокруг нас и ведет к полноценным теориям, определяя семейство форм, которые я называю фракталами».
«Я задумал и разработал новую геометрию природы и реализовал ее использование в ряде разнообразных областей. Он описывает множество неправильных и фрагментированных паттернов вокруг нас и ведет к полноценным теориям, определяя семейство форм, которые я называю фракталами».
Вы можете увидеть, как работают фракталы, в видео ниже.
В этом заключительном интервью, снятом режиссером Эролом Моррисом, Мандельброт рассказывает о своей любви к математике и о том, как она привела его к чудесному открытию фракталов. Его работа живет сегодня во многих инновациях в науке, дизайне, телекоммуникациях, медицине, возобновляемых источниках энергии, кино (спецэффекты), играх (компьютерная графика) и многом другом.
Фракталы в кино и графическом дизайне
После того, как Лорен Карпентер, соучредитель Pixar Animation Studios, прочитал книгу Бенуа Мандельброта « Фракталы: форма, шанс и размерность », он начал экспериментировать с фракталами, чтобы его компьютерная графика выглядела более реалистично.Эта техника привела к появлению программ, которые теперь широко используются в индустрии компьютерной графики для создания специальных эффектов, включая вымышленные пейзажи и воображаемые миры, такие как последовательность планет Бытия в Star Trek II: The Wrath of Khan и поврежденная Звезда Смерти в Возвращение джедая .
Фрактальное сжатие изображений
Фрактальное сжатие преобразует изображения, состоящие из случайной информации, в фрактальный код, сохраняя лишь небольшой репрезентативный объем информации, который впоследствии используется для воссоздания исходного изображения. Поскольку фрактальное изображение теперь представляет собой код, а не пиксели, размер файла резко уменьшен, и изображение можно масштабировать до любого размера без потери резкости.
Поскольку фрактальное изображение теперь представляет собой код, а не пиксели, размер файла резко уменьшен, и изображение можно масштабировать до любого размера без потери резкости.
Фракталы в биологии
Фрактальная геометрия используется в биологических науках для точного моделирования человеческих легких, сердцебиения и кровеносных сосудов, неврологических систем и множества других физиологических процессов. Врачи и исследователи теперь используют математику, лежащую в основе фрактальной геометрии, для построения моделей, которые, как они надеются, будут идентифицировать микроскопические закономерности заболеваний и аномалий раньше, чем когда-либо прежде.
Фракталы на фондовом рынке
В свете финансового кризиса, начавшегося в 2007 году, многие теоретики рынка обращаются к учению Бенуа Мандельброта, чей фрактальный подход к колебаниям цен показал, что крах не так уж невероятен, как предсказывает общепринятое мнение. Мандельброт отверг теорию эффективных рынков как упрощенную и чрезмерно обобщенную, отметив, что мир не является упорядоченным или бесконечно стабильным — турбулентность — это естественная неизбежная сила. Эти взгляды более подробно обсуждаются в книге Мандельброта 2004 года (Неправильное) поведение рынков: фрактальный взгляд на риск, крах и вознаграждение , написанной в соавторстве с Ричардом Л.Хадсон.
Эти взгляды более подробно обсуждаются в книге Мандельброта 2004 года (Неправильное) поведение рынков: фрактальный взгляд на риск, крах и вознаграждение , написанной в соавторстве с Ричардом Л.Хадсон.
Фракталы в климатологии
Ученые недавно показали, что распределение крупных ветвей по более мелким в одном дереве точно повторяет распределение крупных деревьев по более мелким деревьям во всем лесу. В настоящее время проводятся исследования по использованию этой информации для измерения того, сколько углекислого газа способен переработать один лес. Оттуда ученые смогут применить свои открытия к каждому лесу на земле, определяя количество углекислого газа, которое весь мир может безопасно поглотить.
Сегодня мы только поверхностно коснулись того, чему нас может научить фрактальная геометрия. Погодные паттерны, колебания цен на фондовом рынке и скопления галактик оказались фрактальными по своей природе, но что мы будем делать с этим открытием? Куда приведет нас кроличья нора? Возможности, как и множество Мандельброта, безграничны.
Бенуа Мандельброт был интеллектуальным мастером на все руки. Хотя он всегда будет известен своим открытием фрактальной геометрии, Мандельброт также заслуживает признания за преодоление разрыва между искусством и математикой и демонстрацию того, что эти два мира не исключают друг друга.Его творческий подход к решению сложных проблем вдохновил сверстников, коллег и студентов и вселил в IBM твердую веру в силу перспективы.
Куратор команды Hive
Надежный путеводитель по бесконечности в Python
Числа — неотъемлемая часть программирования. Следовательно, языки программирования поддерживают различные типы данных для представления различных типов чисел и предоставляют различные методы для работы с ними.
Каждый из этих типов данных имеет определенные ограничения на диапазон чисел, которые они могут представлять; в то время как некоторые могут представлять небольшой диапазон чисел, другие поддерживают очень большой диапазон чисел. В зависимости от нашего варианта использования, мы можем выбрать один из них.
В зависимости от нашего варианта использования, мы можем выбрать один из них.
Но ни один из них не может представить бесконечность.
Мы часто сталкиваемся и вынуждены иметь дело с бесконечностью во многих реальных сценариях, поэтому нам нужен способ представить ее в языках программирования.
В этом руководстве мы научимся представлять бесконечность и работать с ней в Python.
Что такое бесконечность?
Прежде чем погрузиться в ноу-хау программирования работы с бесконечностью, давайте сначала поймем, что такое бесконечность, дав формальное определение
Существуют десятки определений бесконечности в зависимости от ее использования в различных контекстах и областях. Мы сосредоточимся на тех, которые используются в математике и вычислительной технике.
Бесконечность определяется как большое «неопределенное» число, которое больше любого действительного числа.
Он существует на обоих концах числовой прямой, и, следовательно, у нас есть как положительные, так и отрицательные бесконечности.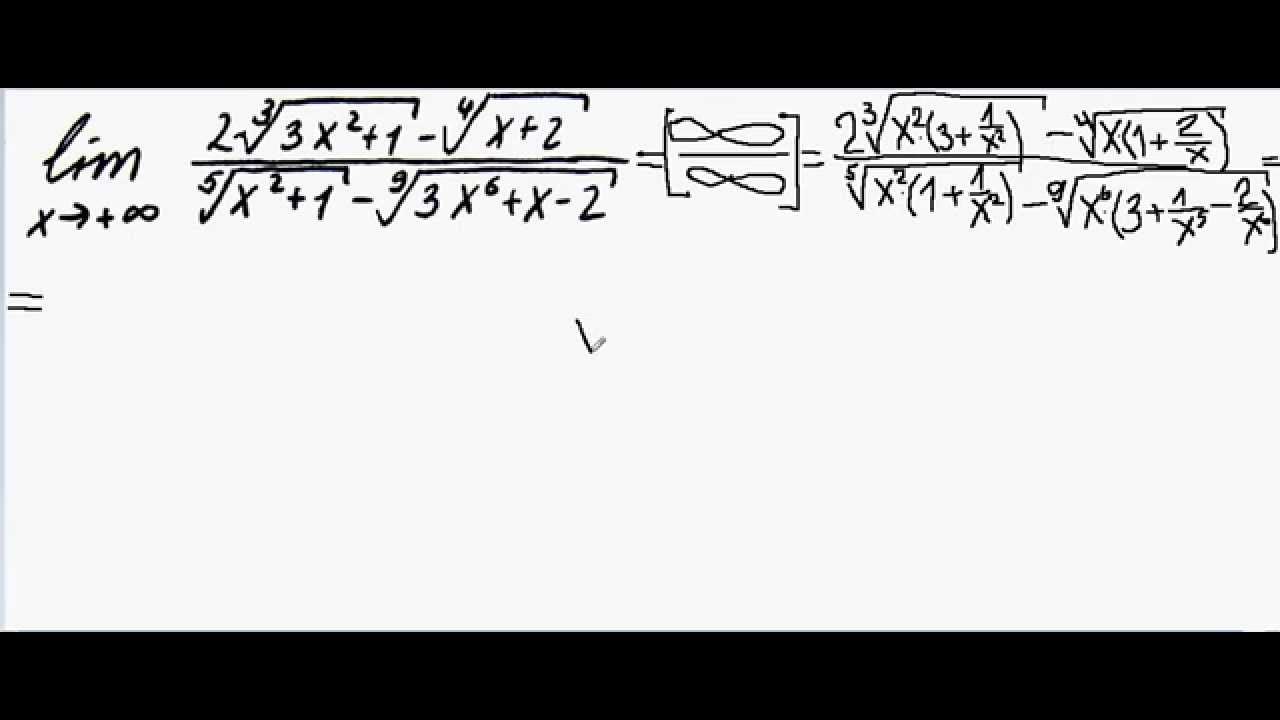
Бесконечность обозначается символом ∞.
В информатике это также определяется как результат «неопределенной операции», такой как деление на ноль. В программировании бесконечность используется для определения абсолютного максимального/минимального значения в алгоритмах, определенных для оптимизации.
Например. в алгоритмах поиска кратчайшего пути между двумя узлами графа начальное значение для shortest_path_distance может быть установлено равным бесконечности.
Объявление бесконечности
В Python существует несколько различных способов представления бесконечности.Давайте посмотрим на некоторые из них.
Мы можем объявить бесконечность как число с плавающей запятой, передав строковое значение ‘inf’ или ‘infinity’ методу float .
а = число с плавающей запятой ("инф")
print(f"значение a = {a}")
print(f"тип a = {тип(a)}")
Вывод:
Как мы уже говорили, существует и «отрицательная бесконечность».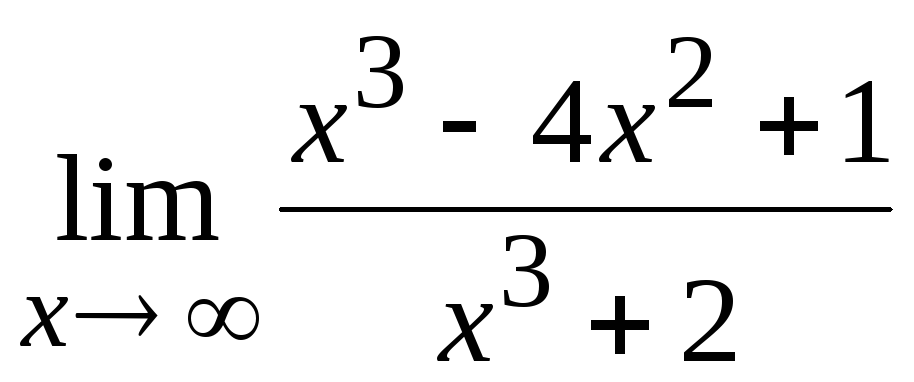 Мы можем объявить то же самое, передав «-inf» или создав положительную бесконечность и поставив перед ней знак «-».
Мы можем объявить то же самое, передав «-inf» или создав положительную бесконечность и поставив перед ней знак «-».
б = число с плавающей запятой ("-inf")
print(f"значение b = {b}")
print(f"значение -float('inf') = {-float('inf')}")
Выходные данные:
Обратите внимание , что строка, которую мы передаем методу float , не зависит от регистра .Таким образом, передача «INF» или «inFINIty» также будет правильно оценена как inf .
Мы также можем использовать модуль math Python для представления бесконечности.
Модуль имеет предопределенное значение math.inf , которое может быть присвоено переменным для представления бесконечности.
импорт математики
с = math.inf
d = -math.inf #отрицательная информация
print(f"значение c равно {c}")
print(f"значение d равно {d}")
print(f"тип c = {тип(c)}")
Вывод:
Оказывается, математический модуль также определяет бесконечность как число с плавающей запятой, и, очевидно, бесконечности, объявленные двумя методами, эквивалентны.
Давайте проверим.
float_inf = число с плавающей запятой ("inf")
math_inf = math.inf
print(f"float_inf == math.inf есть {float_inf == math.inf}")
Вывод:
Таким образом, это были просто два разных способа представления одного и того же значения, т. е. inf .
Почему бесконечность является плавающей?
Вам должно быть интересно, почему бесконечность не имеет тип int , и если это неопределенное число, какое значение имеет его тип данных?
Ответ заключается в способе представления чисел в Python.
Целое число представляется с использованием его двоичного представления, например. 5 представляется как 0101.
Числа с плавающей запятой, с другой стороны, представлены с использованием 3 компонентов — знака, мантиссы и экспоненты. Это соответствует стандарту IEEE 754 для хранения чисел с плавающей запятой.
Стандарт IEEE 754 резервирует некоторые значения для представления специальных чисел. Одним из таких специальных чисел является бесконечность.
Одним из таких специальных чисел является бесконечность.
В соответствии с этим стандартом число с плавающей запятой представляет бесконечность, когда все биты экспоненты равны 1, а все биты мантиссы равны 0.
Кроме того, если бит знака равен 0, это положительная бесконечность, а 1 в бите знака означает отрицательную бесконечность.
Итак, поскольку бесконечность — это особое значение, которое не может быть представлено с помощью простого двоичного представления, следовательно, его тип данных — float в Python.
Арифметические операции над бесконечностью
Поскольку бесконечность — это число с плавающей запятой, мы можем выполнять над ним различные арифметические операции, и результаты таких операций также определяются стандартом IEEE.
Сложение
Если мы прибавим любое конечное действительное число к бесконечности, результатом будет бесконечность.
Если мы добавим бесконечность к бесконечности, результатом снова будет бесконечность.
Однако, если мы добавим отрицательную бесконечность к положительной бесконечности, результат будет неопределенным или NaN (не число). NaN — это еще одно специальное число, похожее на бесконечность, которое представлено в Python с использованием типа данных float в соответствии со стандартом IEEE 754.
инф = число с плавающей запятой ("бесконечность")
печать (f "inf + 100 = {inf + 100}")
распечатать(f"inf + 0.52 = {инф + 0,52}")
печать (f"инф + инф = {инф + инф}")
print(f"-inf + inf = {-inf + inf}")
Вывод:
Вычитание
Вычитание положительного действительного числа из бесконечности дает бесконечность.
Вычитание бесконечности из любого положительного действительного числа возвращает отрицательную бесконечность.
Вычитание бесконечности из бесконечности дает неопределенный результат, т. е. NaN (как было замечено в предыдущем разделе).
Вычитание бесконечности из отрицательной бесконечности дает отрицательную бесконечность.
print(f"inf - 50 = {inf - 50}")
печать (f"299,9 - инф = {299,9 - инф}")
печать (f"инф - инф = {инф - инф}")
print(f"-inf - inf = {-inf - inf}")
Вывод:
Умножение
Умножение любого положительного числа на бесконечность дает в результате бесконечность.
Умножение бесконечности на другую бесконечность также дает бесконечность.
Умножение бесконечности на ноль не определено, возвращается NaN .
Умножение бесконечности на отрицательную бесконечность или любое отрицательное число дает отрицательную бесконечность.
печать (f"inf * 1000 = {inf * 1000}")
печать (f"инф * инф = {инф * инф}")
print(f"inf * (-inf) = {inf * (-inf)}")
печать (f"inf * 0 = {inf * 0}")
печать (f"inf * 0,5 = {inf * 0,5}")
Вывод:
Деление
Деление бесконечности на любое положительное или отрицательное число возвращает положительную или отрицательную бесконечность соответственно.
Деление бесконечности на саму себя или на отрицательную бесконечность возвращает NaN .
Деление любого конечного числа на бесконечность дает 0 или -0.
Наконец, деление бесконечности на 0 приводит к «ZeroDivisonError»
print(f"inf / 20 = {inf / 20}")
печать (f"-inf / 34 = {-inf / 34}")
печать (f"inf/inf = {inf/inf}")
печать (f"inf / -inf = {inf / -inf}")
печать(f"99/-inf = {99/-inf}")
печать (f"0/inf = {0/inf}")
Вывод:
Обратите внимание, что при десятичном делении бесконечности на любое число получается бесконечность; однако при делении этажей получается NaN .
print(f"inf // 20 = {inf // 20}")
Вывод:
Операция по модулю
Операция по модулю над двумя числами возвращает остаток, когда между ними выполняется целочисленное деление.
Поведение операции по модулю на бесконечности немного странное.
В то время как модуль бесконечности (как положительного, так и отрицательного) с любым числом (положительным, отрицательным, бесконечностью) дает NaN , модуль действительного числа с +бесконечностью, тем не менее, возвращает это число.
Модуль действительного числа с -бесконечностью, с другой стороны, дает в результате -бесконечность.
print(f" 67 % 5 = {67 % 5}")
печать (f"inf% 20 = {inf% 20}")
print(f"-inf% 34 = {-inf% 34}")
print(f"inf % inf = {inf % inf}")
печать (f"inf % -inf = {inf % -inf}")
print(f"99% данных = {99% данных}")
print(f"99%-inf = {99%-inf}")
print(f"0 % инф = {0 % инф}")
Выход:
Numpy Infinity
В дополнение к модулю Math и методом поплавок метода бесконечность также может быть назначена с использованием NUMPY NP.inf константа.
NumPy также соответствует стандарту IEEE 754 для хранения чисел с плавающей запятой, поэтому значение np.inf равно float("inf") и math.inf . Тип данных np.inf также является плавающим.
Доступ к константе бесконечности NumPy также можно получить с помощью нескольких псевдонимов, таких как np. ,  Infinity
Infinity np.Inf и np.infty .
NumPy также определяет отдельные константы для положительной и отрицательной бесконечности.Доступ к положительной бесконечности можно получить с помощью np.PINF (псевдоним для np.inf), а к отрицательной бесконечности можно получить доступ с помощью константы np.NINF .
импортировать numpy как np
импортировать математику
а = np.inf
print(f"значение a = {a}")
print(f"np.inf == float('Infinity') оценивается как {np.inf == float('Infinity')}")
print(f"np.inf == math.inf оценивается как {np.inf == math.inf}")
print(f"тип данных np.inf {тип(np.inf)}")
print(f"np.PINF оценивается как {np.PINF}")
print(f"np.NINF оценивается как {np.НИНФ}")
print(f"np.PINF is np.inf оценивается как {np.PINF is np.inf}") #проверка псевдонима
Вывод:
В NumPy также есть методы, позволяющие определить, является ли значение бесконечностью или нет. Он также имеет отдельные методы для проверки того, является ли значение положительной или отрицательной бесконечностью.
б = np.inf
печать (f"b = {b}")
печать (f "np.isinf (б): {np.isinf (б)}")
print(f"np.isposinf(b): {np.isposinf(b)}")
print(f"np.isneginf(b): {np.isneginf(b)}")
c = np.NINF
печать (f"\nc = {c}")
печать (f"np.isneginf(c): {np.isneginf(c)}")
Вывод:
Обратите внимание, что мы также можем передавать массивы NumPy этим методам; он вернет массив логических значений, обозначающих позиции в массиве, где значение равно бесконечности.
x = np.array([1,8, float("inf"), 10, 99, -math.inf]).reshape((2,3))
печать (f"x:\n {x}\n")
печать (f"np.isinf(x):\n{np.isinf(x)}\n")
print(f"np.isneginf(x):\n{np.isneginf(x)}\n")
print(f"np.isposinf(x):\n{np.isposinf(x)}\n")
Вывод:
Модуль math также имеет метод isinf , хотя в нем нет методов проверки положительной или отрицательной бесконечности, таких как np.isposinf и np.isneginf .
И наоборот, NumPy также имеет метод с именем np.isfinite , чтобы проверить, является ли значение конечным или нет.
Максимальное значение для бесконечности
Мы обсуждали, что бесконечность — это «большое неопределенное число», которое больше любого конечного числа.
Но в компьютере есть ограничение на максимальное значение, которое может хранить переменная. Мы не можем объявить какое-то большое значение и сравнить его с бесконечностью.
В Python существует значение от 1e+308 до 1e+309, которое является максимальным значением, которое может хранить переменная с плавающей запятой.Точное значение можно узнать с помощью атрибута sys.float_info .
Отображает различные свойства типа данных с плавающей запятой на этом компьютере, включая максимальное значение, которое переменная с плавающей запятой может хранить в Python.
Любое значение, превышающее это значение, интерпретируется как бесконечность.
Аналогично, на отрицательном конце любое значение ниже определенного минимального значения интерпретируется как отрицательная бесконечность.
print(f"значение 1e+308 равно {1e+308}")
print(f"значение 1e+309 равно {1e+309}")
импорт системы
print(f"\nfloat информация: {sys.float_info}\n")
print(f"значение 1,7976931348623157e+308 = {1,7976931348623157e+308}")
print(f"значение 1,79769313486231585e+308 = {1,79769313486231585e+308}")
Вывод:
Пока мы этим занимаемся, давайте также обсудим поведение оператора возведения в степень (степени) на бесконечности.
Если мы попытаемся найти любую степень (кроме 0) бесконечности, или если мы вычислим значение любого числа (кроме 1), возведенного в степень бесконечности, результатом будет бесконечность.
Однако, если мы выполняем операцию возведения в степень, используя два конечных числа, и если результат превышает максимально допустимое значение, вместо того, чтобы возвращать в качестве результата бесконечность, мы получаем «OverflowError» с сообщением «Числовой результат вне диапазона».309 = {10,0**309}”)
Вывод:
Сравнение бесконечности
В этом разделе мы обсудим различные операции сравнения в Python, использующие бесконечность.
Любое число меньше +inf . Любое число больше -inf .
inf не меньше и не больше inf >. Оно равно inf и не равно -inf .
инф = число с плавающей запятой ("Инф")
print(f"1000 inf равно {1000 > inf}")
print(f"1000 > -inf равно {1000 > -inf}")
print(f"-1000 > -inf равно {-1000 > -inf}")
print(f"inf > inf равно {inf > inf}")
print(f"inf = inf is {inf >= inf}")
print(f"inf == inf is {inf == inf}")
print(f"inf == -inf есть {inf == -inf}")
print(f"1e+309 Выходные данные:
Передать бесконечность в качестве аргумента командной строки
Когда мы запускаем файл Python из командной строки, мы можем дополнительно передать любое количество аргументов, которые захотим.
Доступ к этим аргументам можно получить, используя sys. argv
argv .
sys.argv содержит список аргументов командной строки, передаваемых программе Python. Первый элемент в списке — это имя файла Python, а остальные элементы — это дополнительные значения, переданные (разделенные пробелом) после имени файла.
Все значения в этом списке хранятся в виде строк Python.
#cmd_args.py
импорт системы
print(f"аргументы, полученные из командной строки: {sys.argv}\n")
типы данных = [тип (x) для x в sys.argv]
print(f"тип каждого аргумента командной строки: {типы данных}")
Вывод:
Поскольку все аргументы командной строки по умолчанию принимаются в виде строк, если мы хотим, чтобы аргументы имели определенный тип данных (например, float, int и т. д.), нам нужно преобразовать строковые аргументы в желаемый тип данных.
Таким образом, если пользователю нужно передать «бесконечность» в качестве одного из аргументов, мы можем преобразовать его с помощью метода float и сохранить в переменной.
Возьмем пример, в котором мы ожидаем 3 числовых аргумента командной строки, первый из которых является целым числом, а остальные — с плавающей запятой.
#cmd_arg_inf.py
импорт системы
аргументы = sys.argv[1:]
x1 = целое (аргументы [0])
x2 = число с плавающей запятой (аргументы [1])
max_val = число с плавающей запятой (аргументы [2])
print(f"полученные аргументы: x1={x1}, x2={x2}, max_val={max_val}")
Вывод:
Заключение
В этом руководстве мы поняли, что такое бесконечность, как она представлена в памяти с использованием стандарта IEEE и как представлять ее и работать с ней в Python.
Мы начали с определения бесконечности с точки зрения математики и вычислений.
Затем мы обсудили различные способы объявления бесконечности (и их эквивалентность) в Python.
Мы обосновали необходимость определения бесконечности с помощью типа данных float, обсудив стандарт IEEE 754 для чисел с плавающей запятой.
Мы рассмотрели различные арифметические операции, которые мы можем выполнять над бесконечностью. При этом мы обнаружили еще одно специальное значение, называемое NaN , которое также хранится в Python как значение с плавающей запятой.
Мы рассмотрели способ объявления бесконечности в NumPy и работали с различными методами в NumPy, чтобы проверить, является ли значение (или несколько значений в массиве NumPy) бесконечным, -бесконечным, +бесконечным и т. д.
Мы обсудили максимальное значение для переменная с плавающей запятой, которую мы можем хранить в Python, за пределами которой все считается бесконечностью.
Затем мы обсудили поведение различных операторов сравнения на бесконечности.
Наконец, мы узнали, как передать бесконечность в качестве аргумента командной строки в Python.
Инженер по машинному обучению и разработчик программного обеспечения, работающий над сложными проблемами компьютерного зрения в Центре исследований и разработок IITK.
Не менее 3 лет опыта программирования на Python, не менее 1 года опыта в науке о данных и машинном обучении.
Навыки: C++, OpenCV, Pytorch, Darknet, Pandas, ReactJS, Django.
Восстание Японии как космической державы – дипломат
Реклама За последние несколько десятилетий Япония стала ведущей космической державой. Будучи известным мировым лидером в области высоких технологий, страна использовала свой опыт в ключевых областях, таких как робототехника, чтобы занять место среди элитных космических держав.Примечательно, что в отличие от других крупных игроков, таких как США, Китай и Россия, Япония добилась своего статуса, оставаясь в рамках того, что представляет собой «использование космического пространства в мирных целях» в соответствии с Договором о космосе (ДКП) 1967 года. было три учреждения, занимающихся аэрокосмической деятельностью: Институт космических и астронавтических наук (ISAS), Национальное агентство по развитию космического пространства (NASDA) и Национальная аэрокосмическая лаборатория Японии (NAL). Однако объединение трех организаций в Японское агентство аэрокосмических исследований (ДЖАКСА) в 2003 году стало знаменательным моментом в превращении страны в крупную космическую державу.
Однако объединение трех организаций в Японское агентство аэрокосмических исследований (ДЖАКСА) в 2003 году стало знаменательным моментом в превращении страны в крупную космическую державу.
Космические исследования в Японии проводились в условиях строгих ограничений в первые годы после ее поражения во Второй мировой войне. По условиям американо-японского Договора о взаимном сотрудничестве и безопасности стране запрещалось разрабатывать авиационные и аэрокосмические технологии. Такие ограничения помешали Японии добиться прогресса в развитии собственных космических технологий, хотя она была четвертой страной, которая успешно запустила спутник на орбиту после Соединенных Штатов, Советского Союза и Франции.В 1969 году эти ограничения были ослаблены, хотя и не полностью, после подписания США и Японией соглашения о передаче незасекреченных технологий ракет-носителей. Японии по-прежнему не разрешалось передавать технологию третьей стороне, что ограничивало перспективы коммерциализации. Зависимость от технологий, лицензированных американскими фирмами, продолжалась до 1994 года, когда совместными усилиями NASDA и Mitsubishi Heavy Industries Limited (MHI) была разработана ракета H-2.Серия пусковых установок H-2, H-2A, а затем H-2B, постоянно совершенствовалась с точки зрения простоты изготовления, надежности и экономической эффективности. Инженеры JAXA и MHI в настоящее время разрабатывают более мощную ракету H-3, которая, как ожидается, скоро будет введена в эксплуатацию.
Зависимость от технологий, лицензированных американскими фирмами, продолжалась до 1994 года, когда совместными усилиями NASDA и Mitsubishi Heavy Industries Limited (MHI) была разработана ракета H-2.Серия пусковых установок H-2, H-2A, а затем H-2B, постоянно совершенствовалась с точки зрения простоты изготовления, надежности и экономической эффективности. Инженеры JAXA и MHI в настоящее время разрабатывают более мощную ракету H-3, которая, как ожидается, скоро будет введена в эксплуатацию.
Япония в значительной степени полагалась на свою нишу в области робототехники, чтобы стать ключевой космической державой. В 2013 году Япония стала первой страной, запустившей робота-космонавта Киробо на Международную космическую станцию (МКС).Киробо успешно продемонстрировал свою способность выполнять задачи, получив устные инструкции от астронавта Коити Ваката. Использование робототехники в космических миссиях распространилось и на область исследования дальнего космоса, а также благодаря широко известным миссиям Hayabusa. Космический корабль «Хаябуса», запущенный в 2003 году, вошел в историю как первая миссия по возвращению астероидной пыли на Землю. Его преемник, Hayabusa-2, уже провозглашен большим успехом. Космический аппарат, запущенный в декабре 2014 года, в течение полутора лет проводил подробный анализ углеродистого астероида Рюгу, изучая такие параметры, как минеральный состав и тепловая инерция.Что наиболее важно, он стал первым космическим кораблем, который собрал образцы поверхности и недр астероида. Научный мир с нетерпением ждет возвращения «Хаябусы-2» в 2020 году.
Космический корабль «Хаябуса», запущенный в 2003 году, вошел в историю как первая миссия по возвращению астероидной пыли на Землю. Его преемник, Hayabusa-2, уже провозглашен большим успехом. Космический аппарат, запущенный в декабре 2014 года, в течение полутора лет проводил подробный анализ углеродистого астероида Рюгу, изучая такие параметры, как минеральный состав и тепловая инерция.Что наиболее важно, он стал первым космическим кораблем, который собрал образцы поверхности и недр астероида. Научный мир с нетерпением ждет возвращения «Хаябусы-2» в 2020 году.
Еще одна область, в которой Япония надеялась применить свои достижения в области робототехники, — это поиск инновационных решений для борьбы с угрозой космического мусора. JAXA, а также различные частные игроки были в авангарде разработки технологий, которые потенциально могут решить эту проблему, которая угрожает всему глобальному космическому сообществу.JAXA проверило концепцию электродинамического троса, который будет улавливать космический мусор и спускать его на низкую околоземную орбиту (НОО), откуда эти мусорные частицы в конечном итоге сгорают при входе в атмосферу. Первое испытание этой концепции с использованием механизма, похожего на рыболовную сеть, состоящего из проволоки из алюминия и нержавеющей стали, не увенчалось успехом. Однако от этой идеи не отказались, и возможность реализации такого механизма все еще изучается. Между тем, сингапурская компания по удалению орбитального мусора Astroscale, которой руководит предприниматель японского происхождения Нобу Окада, также предложила несколько нестандартных решений.На 2020 год у компании запланирована серия технологических демонстраций, включая демонстрацию End-of-Life Service от Astroscale (ELSA-d). Космический аппарат ELSA-d попытается схватить обломки космического мусора и опустить их в атмосферу.
Первое испытание этой концепции с использованием механизма, похожего на рыболовную сеть, состоящего из проволоки из алюминия и нержавеющей стали, не увенчалось успехом. Однако от этой идеи не отказались, и возможность реализации такого механизма все еще изучается. Между тем, сингапурская компания по удалению орбитального мусора Astroscale, которой руководит предприниматель японского происхождения Нобу Окада, также предложила несколько нестандартных решений.На 2020 год у компании запланирована серия технологических демонстраций, включая демонстрацию End-of-Life Service от Astroscale (ELSA-d). Космический аппарат ELSA-d попытается схватить обломки космического мусора и опустить их в атмосферу.
Diplomat Brief
Еженедельный информационный бюллетень
N Получайте информацию о событиях недели и развивайте сюжеты для просмотра в Азиатско-Тихоокеанском регионе.
Получить информационный бюллетень Япония также использовала космическую дипломатию в качестве основной части своей стратегии стать космической державой. Япония предложила свой технологический опыт для реализации крупных инициатив в области международного сотрудничества, таких как МКС. Например, некоторые из более ранних исследовательских попыток Японии были направлены на получение исследовательского опыта, подходящего для МКС. В рамках программы Национального управления по аэронавтике и исследованию космического пространства США (НАСА) Endeavor Space Shuttle Япония в 1992 году запустила Spacelab-J, модуль, в котором проводится несколько научных экспериментов. Уроки, полученные в ходе таких миссий, привели к разработке японского экспериментального модуля (более известного как Кибо), который является ключевым компонентом МКС и ее крупнейшим таким модулем для проведения научных экспериментов.Между тем, JAXA совместно с НАСДА также разработала грузовые суда для доставки грузов на МКС. Агентство находится в процессе разработки более мощной пусковой установки H-3 для грузового транспортера HTV-X, который будет доставлять на МКС более тяжелые грузы.
Япония предложила свой технологический опыт для реализации крупных инициатив в области международного сотрудничества, таких как МКС. Например, некоторые из более ранних исследовательских попыток Японии были направлены на получение исследовательского опыта, подходящего для МКС. В рамках программы Национального управления по аэронавтике и исследованию космического пространства США (НАСА) Endeavor Space Shuttle Япония в 1992 году запустила Spacelab-J, модуль, в котором проводится несколько научных экспериментов. Уроки, полученные в ходе таких миссий, привели к разработке японского экспериментального модуля (более известного как Кибо), который является ключевым компонентом МКС и ее крупнейшим таким модулем для проведения научных экспериментов.Между тем, JAXA совместно с НАСДА также разработала грузовые суда для доставки грузов на МКС. Агентство находится в процессе разработки более мощной пусковой установки H-3 для грузового транспортера HTV-X, который будет доставлять на МКС более тяжелые грузы.
Нравится эта статья? Щелкните здесь, чтобы подписаться на полный доступ. Всего 5 долларов в месяц.
В ближайшие годы Япония также сыграет важную роль в миссиях по исследованию Луны, инициированных Соединенными Штатами.Продолжая сотрудничество с НАСА и другими членами МКС, JAXA позиционируется как важный партнер в проекте создания лунной орбитальной платформы Gateway. В рамках этой межведомственной миссии JAXA предложило отправить своих астронавтов, а также разработать жилой модуль, аналогичный Кибо, для проведения научных экспериментов. Агентство в сотрудничестве с MHI также заявило о своем намерении модифицировать ракету H-3 для полета на большее расстояние, чем требуется для МКС.Между тем, JAXA, как полагают, также работает с Индийской организацией космических исследований (ISRO) над лунной миссией в ближайшие годы.
Участие Японии в космическом сотрудничестве не ограничивается крупными державами. Проект «ПТИЦЫ» (Совместный глобальный спутниковый проект многонациональных птиц), поддерживаемый Технологическим институтом Кюсю, продемонстрировал успешную модель технической помощи в облегчении космических запусков для некосмических стран. Помощь Японии в рамках этой программы позволила четырем странам — Нигерии, Монголии, Бангладеш и Гане — запустить свои собственные кубические спутники на борту ракеты SpaceX Falcon-9 в июне 2017 года.В 2018 году JAXA также запустила кубсаты от имени Бутана, Малайзии, Филиппин, Коста-Рики и Кении. Спутники, разработанные этими странами, разрабатываются и запускаются из модуля Кибо на МКС.
Помощь Японии в рамках этой программы позволила четырем странам — Нигерии, Монголии, Бангладеш и Гане — запустить свои собственные кубические спутники на борту ракеты SpaceX Falcon-9 в июне 2017 года.В 2018 году JAXA также запустила кубсаты от имени Бутана, Малайзии, Филиппин, Коста-Рики и Кении. Спутники, разработанные этими странами, разрабатываются и запускаются из модуля Кибо на МКС.
Позиция Японии на космической арене в основном была мирной. Однако зарождающаяся геополитика в Восточной Азии побудила Японию пересмотреть эту позицию. Страна начала уделять больше внимания развертыванию и использованию космических средств для укрепления своей национальной безопасности.Японский парламент в 2008 году внес поправки в Основной космический закон страны, чтобы привести его в соответствие с ДКП. Поправка позволила Японии развернуть оборонительные силы в космосе, проложив путь к более активному использованию космического пространства в военных целях.
Реклама Это стратегическое переосмысление было вызвано тремя основными факторами. Предполагаемые сомнения относительно надежности гарантий безопасности со стороны Соединенных Штатов были серьезной проблемой для Японии. Еще одним смягчающим фактором является растущая угроза со стороны все более враждебного соседа, Северной Кореи.В-третьих, Япония, кажется, осознает тот факт, что размещение стратегических активов в космосе имеет решающее значение для ее собственного возрождения, поскольку демонстрация технологического мастерства в высокотехнологичных секторах все чаще рассматривается как отличительная черта великой державы. С этой целью JAXA целенаправленно работает над развитием своих собственных возможностей определения местоположения, навигации и синхронизации (PNT) с помощью квазизенитной спутниковой системы (QZSS). Система была разработана на фоне опасений по поводу внешнего вмешательства в работу США.S. Глобальная система позиционирования (GPS). В отличие от китайской Beidou, российской ГЛОНАСС (Глобальная навигационная спутниковая система) и индийской IRNSS (Индийская региональная навигационная спутниковая система), QZSS дополняет GPS и работает как спутниковая система дополнений.
Предполагаемые сомнения относительно надежности гарантий безопасности со стороны Соединенных Штатов были серьезной проблемой для Японии. Еще одним смягчающим фактором является растущая угроза со стороны все более враждебного соседа, Северной Кореи.В-третьих, Япония, кажется, осознает тот факт, что размещение стратегических активов в космосе имеет решающее значение для ее собственного возрождения, поскольку демонстрация технологического мастерства в высокотехнологичных секторах все чаще рассматривается как отличительная черта великой державы. С этой целью JAXA целенаправленно работает над развитием своих собственных возможностей определения местоположения, навигации и синхронизации (PNT) с помощью квазизенитной спутниковой системы (QZSS). Система была разработана на фоне опасений по поводу внешнего вмешательства в работу США.S. Глобальная система позиционирования (GPS). В отличие от китайской Beidou, российской ГЛОНАСС (Глобальная навигационная спутниковая система) и индийской IRNSS (Индийская региональная навигационная спутниковая система), QZSS дополняет GPS и работает как спутниковая система дополнений. Созвездие из четырех спутников ориентировано на регион Азии и Океании с особым акцентом на Японию. Система может похвастаться точностью до 10 сантиметров по сравнению с GPS, погрешность которого составляет около 10 метров.
Созвездие из четырех спутников ориентировано на регион Азии и Океании с особым акцентом на Японию. Система может похвастаться точностью до 10 сантиметров по сравнению с GPS, погрешность которого составляет около 10 метров.
Работая в условиях жестких ограничений и невзирая на многочисленные неудачи, Япония неуклонно продвигалась к созданию надежных собственных возможностей в космосе.Усилия JAXA по использованию технологического опыта страны на благо мирового космического сообщества, безусловно, повысили статус Японии как крупной державы. Он проложил свой курс в довольно доброжелательной и мирной манере и занял достойное место в пантеоне космических путешественников. Во многих случаях Япония играла ключевую роль в демонстрации эффективных международных моделей технологического сотрудничества, даже несмотря на то, что повествование о геополитической конкуренции продолжало усиливаться.Успех таких миссий, как Hayabusa-2, также позволил Японии стать центром знаний, поскольку данные, собранные в ходе таких проектов, могут стать ключом к разгадке нескольких тайн Вселенной.

 argv
argv 


 Однако объединение трех организаций в Японское агентство аэрокосмических исследований (ДЖАКСА) в 2003 году стало знаменательным моментом в превращении страны в крупную космическую державу.
Однако объединение трех организаций в Японское агентство аэрокосмических исследований (ДЖАКСА) в 2003 году стало знаменательным моментом в превращении страны в крупную космическую державу. Зависимость от технологий, лицензированных американскими фирмами, продолжалась до 1994 года, когда совместными усилиями NASDA и Mitsubishi Heavy Industries Limited (MHI) была разработана ракета H-2.Серия пусковых установок H-2, H-2A, а затем H-2B, постоянно совершенствовалась с точки зрения простоты изготовления, надежности и экономической эффективности. Инженеры JAXA и MHI в настоящее время разрабатывают более мощную ракету H-3, которая, как ожидается, скоро будет введена в эксплуатацию.
Зависимость от технологий, лицензированных американскими фирмами, продолжалась до 1994 года, когда совместными усилиями NASDA и Mitsubishi Heavy Industries Limited (MHI) была разработана ракета H-2.Серия пусковых установок H-2, H-2A, а затем H-2B, постоянно совершенствовалась с точки зрения простоты изготовления, надежности и экономической эффективности. Инженеры JAXA и MHI в настоящее время разрабатывают более мощную ракету H-3, которая, как ожидается, скоро будет введена в эксплуатацию. Космический корабль «Хаябуса», запущенный в 2003 году, вошел в историю как первая миссия по возвращению астероидной пыли на Землю. Его преемник, Hayabusa-2, уже провозглашен большим успехом. Космический аппарат, запущенный в декабре 2014 года, в течение полутора лет проводил подробный анализ углеродистого астероида Рюгу, изучая такие параметры, как минеральный состав и тепловая инерция.Что наиболее важно, он стал первым космическим кораблем, который собрал образцы поверхности и недр астероида. Научный мир с нетерпением ждет возвращения «Хаябусы-2» в 2020 году.
Космический корабль «Хаябуса», запущенный в 2003 году, вошел в историю как первая миссия по возвращению астероидной пыли на Землю. Его преемник, Hayabusa-2, уже провозглашен большим успехом. Космический аппарат, запущенный в декабре 2014 года, в течение полутора лет проводил подробный анализ углеродистого астероида Рюгу, изучая такие параметры, как минеральный состав и тепловая инерция.Что наиболее важно, он стал первым космическим кораблем, который собрал образцы поверхности и недр астероида. Научный мир с нетерпением ждет возвращения «Хаябусы-2» в 2020 году.  Первое испытание этой концепции с использованием механизма, похожего на рыболовную сеть, состоящего из проволоки из алюминия и нержавеющей стали, не увенчалось успехом. Однако от этой идеи не отказались, и возможность реализации такого механизма все еще изучается. Между тем, сингапурская компания по удалению орбитального мусора Astroscale, которой руководит предприниматель японского происхождения Нобу Окада, также предложила несколько нестандартных решений.На 2020 год у компании запланирована серия технологических демонстраций, включая демонстрацию End-of-Life Service от Astroscale (ELSA-d). Космический аппарат ELSA-d попытается схватить обломки космического мусора и опустить их в атмосферу.
Первое испытание этой концепции с использованием механизма, похожего на рыболовную сеть, состоящего из проволоки из алюминия и нержавеющей стали, не увенчалось успехом. Однако от этой идеи не отказались, и возможность реализации такого механизма все еще изучается. Между тем, сингапурская компания по удалению орбитального мусора Astroscale, которой руководит предприниматель японского происхождения Нобу Окада, также предложила несколько нестандартных решений.На 2020 год у компании запланирована серия технологических демонстраций, включая демонстрацию End-of-Life Service от Astroscale (ELSA-d). Космический аппарат ELSA-d попытается схватить обломки космического мусора и опустить их в атмосферу. Япония предложила свой технологический опыт для реализации крупных инициатив в области международного сотрудничества, таких как МКС. Например, некоторые из более ранних исследовательских попыток Японии были направлены на получение исследовательского опыта, подходящего для МКС. В рамках программы Национального управления по аэронавтике и исследованию космического пространства США (НАСА) Endeavor Space Shuttle Япония в 1992 году запустила Spacelab-J, модуль, в котором проводится несколько научных экспериментов. Уроки, полученные в ходе таких миссий, привели к разработке японского экспериментального модуля (более известного как Кибо), который является ключевым компонентом МКС и ее крупнейшим таким модулем для проведения научных экспериментов.Между тем, JAXA совместно с НАСДА также разработала грузовые суда для доставки грузов на МКС. Агентство находится в процессе разработки более мощной пусковой установки H-3 для грузового транспортера HTV-X, который будет доставлять на МКС более тяжелые грузы.
Япония предложила свой технологический опыт для реализации крупных инициатив в области международного сотрудничества, таких как МКС. Например, некоторые из более ранних исследовательских попыток Японии были направлены на получение исследовательского опыта, подходящего для МКС. В рамках программы Национального управления по аэронавтике и исследованию космического пространства США (НАСА) Endeavor Space Shuttle Япония в 1992 году запустила Spacelab-J, модуль, в котором проводится несколько научных экспериментов. Уроки, полученные в ходе таких миссий, привели к разработке японского экспериментального модуля (более известного как Кибо), который является ключевым компонентом МКС и ее крупнейшим таким модулем для проведения научных экспериментов.Между тем, JAXA совместно с НАСДА также разработала грузовые суда для доставки грузов на МКС. Агентство находится в процессе разработки более мощной пусковой установки H-3 для грузового транспортера HTV-X, который будет доставлять на МКС более тяжелые грузы.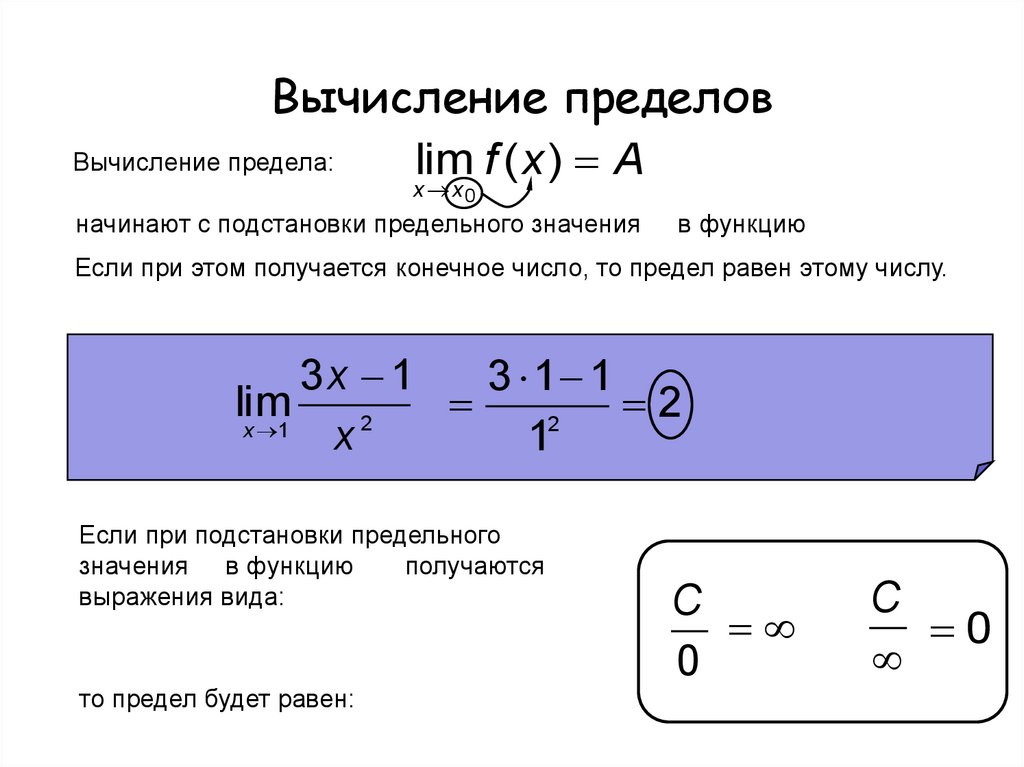
 Помощь Японии в рамках этой программы позволила четырем странам — Нигерии, Монголии, Бангладеш и Гане — запустить свои собственные кубические спутники на борту ракеты SpaceX Falcon-9 в июне 2017 года.В 2018 году JAXA также запустила кубсаты от имени Бутана, Малайзии, Филиппин, Коста-Рики и Кении. Спутники, разработанные этими странами, разрабатываются и запускаются из модуля Кибо на МКС.
Помощь Японии в рамках этой программы позволила четырем странам — Нигерии, Монголии, Бангладеш и Гане — запустить свои собственные кубические спутники на борту ракеты SpaceX Falcon-9 в июне 2017 года.В 2018 году JAXA также запустила кубсаты от имени Бутана, Малайзии, Филиппин, Коста-Рики и Кении. Спутники, разработанные этими странами, разрабатываются и запускаются из модуля Кибо на МКС. Предполагаемые сомнения относительно надежности гарантий безопасности со стороны Соединенных Штатов были серьезной проблемой для Японии. Еще одним смягчающим фактором является растущая угроза со стороны все более враждебного соседа, Северной Кореи.В-третьих, Япония, кажется, осознает тот факт, что размещение стратегических активов в космосе имеет решающее значение для ее собственного возрождения, поскольку демонстрация технологического мастерства в высокотехнологичных секторах все чаще рассматривается как отличительная черта великой державы. С этой целью JAXA целенаправленно работает над развитием своих собственных возможностей определения местоположения, навигации и синхронизации (PNT) с помощью квазизенитной спутниковой системы (QZSS). Система была разработана на фоне опасений по поводу внешнего вмешательства в работу США.S. Глобальная система позиционирования (GPS). В отличие от китайской Beidou, российской ГЛОНАСС (Глобальная навигационная спутниковая система) и индийской IRNSS (Индийская региональная навигационная спутниковая система), QZSS дополняет GPS и работает как спутниковая система дополнений.
Предполагаемые сомнения относительно надежности гарантий безопасности со стороны Соединенных Штатов были серьезной проблемой для Японии. Еще одним смягчающим фактором является растущая угроза со стороны все более враждебного соседа, Северной Кореи.В-третьих, Япония, кажется, осознает тот факт, что размещение стратегических активов в космосе имеет решающее значение для ее собственного возрождения, поскольку демонстрация технологического мастерства в высокотехнологичных секторах все чаще рассматривается как отличительная черта великой державы. С этой целью JAXA целенаправленно работает над развитием своих собственных возможностей определения местоположения, навигации и синхронизации (PNT) с помощью квазизенитной спутниковой системы (QZSS). Система была разработана на фоне опасений по поводу внешнего вмешательства в работу США.S. Глобальная система позиционирования (GPS). В отличие от китайской Beidou, российской ГЛОНАСС (Глобальная навигационная спутниковая система) и индийской IRNSS (Индийская региональная навигационная спутниковая система), QZSS дополняет GPS и работает как спутниковая система дополнений. Созвездие из четырех спутников ориентировано на регион Азии и Океании с особым акцентом на Японию. Система может похвастаться точностью до 10 сантиметров по сравнению с GPS, погрешность которого составляет около 10 метров.
Созвездие из четырех спутников ориентировано на регион Азии и Океании с особым акцентом на Японию. Система может похвастаться точностью до 10 сантиметров по сравнению с GPS, погрешность которого составляет около 10 метров.