Как решать матрицы методом гаусса для чайников: Как решить методом Гаусса СЛАУ (систему линейных уравнений). Правила, примеры

вычисление ранга матрицы

вычисление ранга матрицы

Вы искали вычисление ранга матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление ранга матрицы с помощью элементарных преобразований, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вычисление ранга матрицы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление ранга матрицы,вычисление ранга матрицы с помощью элементарных преобразований,вычислить ранг матрицы,вычислить ранг матрицы методом элементарных преобразований,вычислить ранг матрицы с помощью элементарных преобразований онлайн,задачи на ранг матрицы,как вычислить ранг матрицы,как вычислить ранг матрицы для чайников,как искать ранг матрицы,как найти ранг,как найти ранг матрицы,как найти ранг матрицы 3 на 3,как найти ранг матрицы 4х4,как найти ранг матрицы для чайников,как найти ранг матрицы методом окаймляющих миноров,как найти ранг матрицы методом элементарных преобразований,как найти ранг матрицы онлайн с решением,как найти ранг матрицы расширенной,как найти ранг расширенной матрицы,как находить ранг матрицы,как находить ранг матрицы для чайников,как находить ранг матрицы примеры,как определить ранг матрицы,как определить ранг матрицы для чайников,как определять ранг матрицы,как посчитать ранг матрицы,как рассчитать ранг матрицы,как решать ранг матрицы,как считать ранг матрицы,как узнать ранг матрицы,матпрофи ранг матрицы,матрица ранг,матрица ранги,матриці ранг,матрицы как найти ранг матрицы,матрицы ранг примеры,матрицы ранги,метод гаусса ранг матрицы,метод окаймляющих миноров нахождения ранга матрицы,методом окаймляющих миноров найти ранг матрицы,методом элементарных преобразований найти ранг матрицы,минор второго порядка,минор первого порядка,найдите ранг матрицы,найти онлайн ранг матрицы методом окаймляющих миноров,найти ранг,найти ранг матрицы,найти ранг матрицы как найти,найти ранг матрицы методом гаусса,найти ранг матрицы методом окаймляющих миноров,найти ранг матрицы методом окаймляющих миноров онлайн,найти ранг матрицы методом элементарных преобразований,найти ранг матрицы методом элементарных преобразований онлайн,найти ранг матрицы онлайн методом окаймляющих методом,найти ранг матрицы онлайн методом окаймляющих миноров,найти ранг матрицы с помощью элементарных преобразований,нахождение ранга матрицы,нахождение ранга матрицы методом окаймляющих миноров,нахождение ранга матрицы методом элементарных преобразований,нахождение ранга матрицы с помощью элементарных преобразований,онлайн найти ранг матрицы методом окаймляющих миноров,онлайн определение ранга матрицы,определение ранг матрицы,определение ранга матрицы,определитель матрицы ранг матрицы,определить ранг матрицы,посчитать ранг матрицы,примеры ранг матрицы,ранг как найти,ранг матрица,ранг матриці,ранг матрицы,ранг матрицы вычислить,ранг матрицы для чайников,ранг матрицы и ранг расширенной матрицы,ранг матрицы как вычислить,ранг матрицы как искать,ранг матрицы как найти,ранг матрицы как находить,ранг матрицы как определить,ранг матрицы как посчитать,ранг матрицы как решать,ранг матрицы как считать,ранг матрицы матпрофи,ранг матрицы метод гаусса,ранг матрицы методом гаусса,ранг матрицы методом окаймляющих миноров,ранг матрицы методом окаймляющих миноров онлайн,ранг матрицы методом элементарных преобразований,ранг матрицы найти,ранг матрицы онлайн как найти,ранг матрицы онлайн методом окаймляющих миноров,ранг матрицы определение,ранг матрицы определить,ранг матрицы посчитать,ранг матрицы примеры,ранг матрицы примеры с решением,ранг матрицы равен,ранг матрицы ранг расширенной матрицы,ранг матрицы расширенной,ранг матрицы решение,ранг матрицы с помощью элементарных преобразований,ранг матрицы это,ранг матрицы это для чайников,ранг методом гаусса матрицы,ранг расширенной матрицы,ранг расширенной матрицы как найти,ранги матриц,ранги матрица,ранги матрицы,ранги матрицы для чайников,рангом матрицы называется,расширенной матрицы ранг,решение матрицы ранг,решение матрицы ранг матрицы,решение матрицы ранг онлайн,решение ранг матрицы,с помощью элементарных преобразований найти ранг матрицы,чему равен ранг матрицы,чему равен ранг матрицы равен,что такое ранг матрицы,что такое ранг матрицы и как его найти.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление ранга матрицы. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить ранг матрицы).

Решить задачу вычисление ранга матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Решение матриц ℹ️ методы решений и примеров для чайников, формулы

Понятие выражения

Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.

От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.

Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:

• a — действительная часть числа;
• b — мнимая часть;
• i — мнимая единица (квадратный корень из -1).

На приведенном примере показаны варианты.

Простейшие действия с матрицами могут быть разными. К их числу относятся:

• умножение;
• вычитание;
• умножение на число;
• перемножение между собой;
• транспортирование матриц.

Сложение и вычитание

Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.

Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.

Умножение на число

Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:

​

Операция перемножения

Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.

Возведение в степень

Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:

Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:

Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.

2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.

3 этап: в итоге получаем:

Расчёт определителя

В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле.

Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.

Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.

Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу.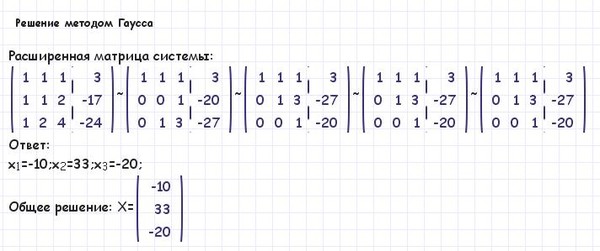 Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.

При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

3 этап: находят алгебраические дополнения.

4 этап: определяют транспонированную матрицу.

Итогом будет:

Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.

В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.

Нахождение собственных векторов

Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:

Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:

Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.

Метод Гаусса

Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:

• действия, когда в системе переставляются местами два уравнения;
• произведение одного из уравнений в системе на действительное ненулевое число;
• сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.

Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.

Следует переписать эту систему в матричный вид:

А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.

В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.

Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:

Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:

На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:

Обращают внимание на последние строки.

В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).

Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.

Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».

Способ Крамера

Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

Её необходимо заменить равноценным матричным уравнением.

Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:

1. Высчитывают определитель дельта базовой матрицы.
2. В матричной таблице А замещают первый столбец на вектор свободных элементов b.
3. Выполняют расчёт определителя дельта1 выявленной матрицы А1.
4. Определяют переменную Х1 = дельта1/дельта.
5. Повторяют шаги со 2 по 4 пункт в матрице А для столбов 2,3…n.

Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.

Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.

Метод исключения Гаусса с учебным пособием по матричному представлению

В предыдущих разделах мы говорили о методе исключения Гаусса и рассмотрели несколько примеров. Сегодня нам нужно решить еще одну систему линейных уравнений, но на этот раз мы применим матричное представление для систем линейных уравнений:

\left\{\begin{align}2x_1+4x_2-3x_3+2x_4=0\\x_1 -2x_2+5x_3+2x_4=2\\2x_2-4x_3+5x_4=-1\\-2x_3+x_4=-3 \end{выровнено}\вправо.

A=\begin {pmatrix} 2&4&-3 &2 \\1& -2&5 &2 \\0& 2&-4 &5 \\0&0&-2 &1 \end {pmatrix}, \vec{b}=\begin{pmatrix }0\\2\\-1\\3\end{pmatrix},\vec{x}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix},  \tilde{A} =\begin{pmatrix}2&4&-3 &2&|&0 \\1& -2&5 &2&|&2 \\0& 2&-4 &5&|&-1 \\0&0&-2 &1&|&-3 \end{pmatrix}

Тогда наша система представляется следующим образом:

A \vec{x}=\vec{b}

Идея решения та же, мы намерены получить нашу систему в треугольной (или ступенчатой) форме. Для удобства преобразуем матрицу системы, что в точности то же самое, только предполагает более компактную форму представления. Обратите внимание, что мы можем менять местами строки матрицы, складывать или вычитать их, умножать или делить на действительное ненулевое число.

Так как у нас ненулевая правая часть системы, т.е. наша система неоднородна, мы должны преобразовать матрицу \tilde{A}, содержащую ненулевые правые части вместо A. Эта новая матрица называется дополненной (или расширенная) матрица данной системы.

Хорошо, начнем. Теперь мы работаем с этой матрицей:

\tilde{A}=\begin{pmatrix}2&4&-3 &2&|&0 \\1& -2&5 &2&|&2 \\0& 2&-4 &5&|&-1 \\ 0&0&-2 &1&|&-3 \end{pmatrix}

Сначала поменяем местами первую и вторую строки нашей матрицы, чтобы получить x_1 с коэффициентом 1 в первой строке. Таким образом, мы получаем:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2 \\2&4&-3 &2&|&0 \\0& 2&-4 &5&|&-1 \\0&0&-2 &1&| &-3 \end{pmatrix}

Второй шаг — исключить x_1 из всех уравнений нашей системы, кроме первого. В терминах матрицы \tilde{A} это означает, что нам нужно получить нули в первом столбце, кроме первого элемента. Затем проделайте то же самое для других переменных, чтобы в конце получить матрицу в виде эшелона. Итак, сначала мы вычитаем первую строку, умноженную на 2, из второй. Измененная матрица выглядит следующим образом:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2 \\0&8 &-13&-2&|&-4 \\0& 2&-4 &5&|&-1 \\ 0&0&-2 &1&|&-3 \end{pmatrix}

Затем вычтите третью строку, умноженную на 4, из второй:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2 \\0&0 &3&-22&|&0 \\0& 2&-4 &5&|& -1 \\0&0&-2 &1&|&-3 \end{pmatrix}

Теперь поменяем местами третью и вторую строки:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2  \\ 0& 2&-4 &5&|&-1\\0&0 &3&-22&|&0 \\0&0&-2 &1&|&-3 \end{pmatrix}

Разделить вторую строку на 2:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2  \\0& 1&-2 &\frac{5}{2}&|&-\frac{ 1}{2}\\0&0 &3&-22&|&0 \\0&0&-2 &1&|&-3 \end{pmatrix}

Добавить последнюю строку к третьей:

\tilde{A}=\begin{pmatrix }1& -2&5 &2&|&2  \\0& 1&-2 &\frac{5}{2}&|&-\frac{1}{2}\\0&0 &1&-21&|&-3 \\0&0&-2 &1& |&-3 \end{pmatrix}

Добавьте третью строку, умноженную на 2, к четвертой:

\tilde{A}=\begin{pmatrix}1& -2&5 &2&|&2  \\0& 1&-2 &\frac{5}{2}&|& -\frac{1}{2}\\0&0 &1&-21&|&-3 \\0&0&0 &-41&|&-9 \end{pmatrix}

Теперь наша расширенная матрица (и, следовательно, система) представлена ​​в виде треугольника. форма. Таким образом, мы можем найти все неизвестные обратным ходом метода Гаусса.

Для удобства запишем нашу систему в обычном виде:

\left\{ \begin{align}x_1-2x_2+5x_3+2x_4=2\\x_2-2x_3+\frac{5}{2}x_4=-\frac{1}{2}\\x_3-21x_4= -3\\-41x_4=-9 \end{выровнено}\вправо.

В последнем уравнении есть только x_4 и свободный член. Начиная снизу, постепенно вычисляем все неизвестные и в итоге получаем ответ:

\left\{ \begin{aligned}x_1=-\frac{88}{41}\\x_2=\frac{89}{41 }\\x_3=\frac{66}{41}\\x_4=\frac{9}{41} \end{выровнено}\right.

Проверить подстановкой в ​​исходную систему. Кстати, вы можете сделать проверку, применив умножение матриц. Наша система может быть представлена ​​следующим образом:

A \vec{x}=\vec{b}

или

\begin{pmatrix} 2&4&-3 &2 \\1& -2&5 &2 \\0& 2&-4 &5 \\0&0&-2 &1 \end{ pmatrix} \cdot \begin{pmatrix} -88/41\\ 89/41\\ 66/41\\ 9/41\end{pmatrix}=\begin{pmatrix}0\\2\\-1\\3 \end{pmatrix}

Упрощение дает:

\frac{1}{41} \begin{pmatrix} 2&4&-3 &2 \\1& -2&5 &2 \\0& 2&-4 &5 \\0&0&-2 &1 \end {pmatrix} \cdot \begin{pmatrix} -88\\ 89\\ 66\\ 9\end{pmatrix}=\begin{pmatrix}0\\2\\-1\\3 \end{pmatrix}

Все, что вам нужно сделать, это перемножить две матрицы в левой части и проверить, выполняется ли это равенство. Если у вас возникли проблемы с умножением матриц, прочитайте наш учебник по основным операциям с матрицами. Онлайн математические калькуляторы также очень полезны. Внимательно выполняйте матричные операции при выполнении домашних заданий и всегда проверяйте, чтобы все получилось правильно.

0 Акции

• Фейсбук
• Твиттер
• Копировать ссылку

Решающие системы с исключением Гаусса · Предварительное исчисление

Решающие системы с исключением Гаусса · Предварительное исчисление

В этом разделе вы:

• Напишите расширенную матрицу системы уравнений.
• Напишите систему уравнений из расширенной матрицы.
• Выполнение операций со строками над матрицей.
• Решите систему линейных уравнений с помощью матриц.

Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика, среди прочих. Его открытия, касающиеся теории матриц, изменили то, как математики работали последние два столетия.

Впервые мы столкнулись с методом исключения Гаусса в книге «Системы линейных уравнений: две переменные». В этом разделе мы вернемся к этой технике решения систем, на этот раз с использованием матриц.

Написание расширенной матрицы системы уравнений

Матрица может служить устройством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства. Когда система записывается в такой форме, мы называем ее дополненная матрица .

Например, рассмотрим следующее 2 × 2 

система уравнений.

3x+4y=74x−2y=5

Мы можем записать эту систему в виде расширенной матрицы:

[344−2  \| 75]

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

[344−2]

Три на три система уравнений , такая как

3x−y−z=0        x+y=5     2x−3z=2

имеет матрицу коэффициентов

[3−1−111020−3]

и представлен расширенной матрицей

[3−1−111020−3  \| 052]

Обратите внимание, что матрица написана таким образом, что переменные располагаются в своих собственных столбцах: x -термы идут в первом столбце, y -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было записано в стандартной форме ax+by+cz=d 

, чтобы переменные совпали. Когда в уравнении отсутствует переменный член, коэффициент равен 0,9. 0003

Учитывая систему уравнений, напишите расширенную матрицу.

1. Запишите коэффициенты x -членов в виде чисел в первом столбце.
2. Запишите коэффициенты y -членов в виде чисел во втором столбце.
3. Если имеется z -членов, запишите коэффициенты в виде чисел в третьем столбце.
4. Нарисуйте вертикальную линию и запишите константы справа от линии.

Запись расширенной матрицы для системы уравнений

Запись расширенной матрицы для заданной системы уравнений.

   x+2y-z=3 2x-y+2z=6 x-3y+3z=4

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

[12−12−121−33  \| 364]

Запишите расширенную матрицу данной системы уравнений.

4x−3y=113x+2y=4

[4−33  2\|11  4]

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не перегружены переменными. Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы написать систему уравнений в стандартной форме.

Написание системы уравнений из формы расширенной матрицы

Найдите систему уравнений из расширенной матрицы.

[1-3-52-5-4-354  \| −256]

Когда столбцы представляют переменные x, 

y, 

и z,

[1−3−52−5−4−354 \| −256]→       x−3y−5z=−2    2x−5y−4z=5−3x+5y+4z=6

Напишите систему уравнений из расширенной матрицы.

[1−1  12−1  30   1  1   \| 5  1−9]

x    −   y    +    z=52x   −  y   +  3z=1            y   +    z=−9

Выполнение операций со строками над матрицей

Теперь, когда мы можем записывать системы уравнений в расширенной матричной форме, мы рассмотрим различные операции со строками, которые можно выполнять над матрицей, такие как сложение, умножение на константу и перестановка строк.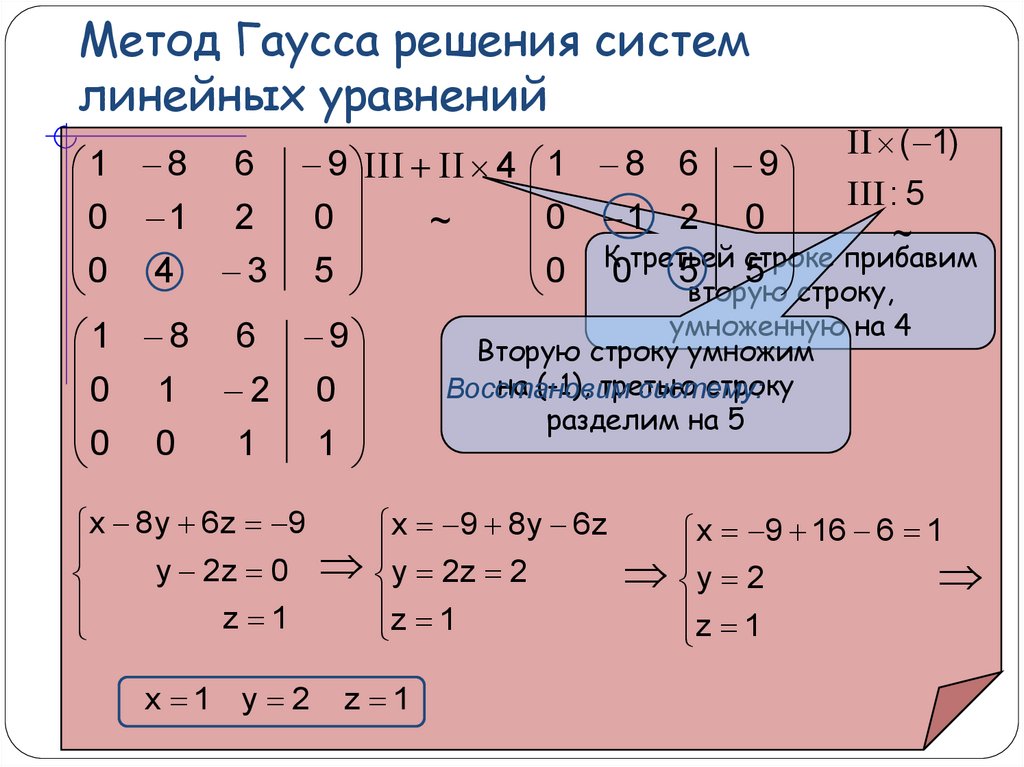

Выполнение операций со строками над матрицей — это метод, который мы используем для решения системы уравнений. Для того, чтобы решить систему уравнений, мы хотим преобразовать матрицу в строк-ступенчатую форму , в котором есть единицы по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали, как показано.

Строко-эшелонная форма[1ab01d001]

Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, которая эквивалентна по строкам в более простой форме. Вот рекомендации по получению формы ряд-эшелон.

1. В любой ненулевой строке первое ненулевое число равно 1. Оно называется ведущий 1.
2. Любые строки со всеми нулями помещаются внизу матрицы.
3. Любой интерлиньяж 1 находится ниже и правее предыдущего интерлиньяжа 1.
4. Любой столбец, содержащий ведущую единицу, имеет нули во всех остальных позициях в столбце.

Чтобы решить систему уравнений, мы можем выполнить следующие операции над строками, чтобы преобразовать матрицу коэффициентов в форму ступенчатой ​​строки и выполнить обратную подстановку, чтобы найти решение.

1. Поменять местами ряды. (Обозначение: Ри ↔  Rj

   )

2. Умножить строку на константу. (Обозначение: CRi

   )

3. Добавить произведение строки, умноженной на константу, к другой строке. (Обозначение: Ri+cRj)

Каждая из операций строки соответствует операциям, которые мы уже изучили для решения систем уравнений с тремя переменными. С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.

Исключение по Гауссу

Метод исключения по Гауссу относится к стратегии, используемой для получения ступенчато-строковой формы матрицы. Цель состоит в том, чтобы записать матрицу  A 

с числом 1 в качестве записи вниз по главной диагонали и со всеми нулями ниже.

A=[a11a12a13a21a22a23a31a32a33]→После исключения Гаусса A=[1  b12  b130  1  b230  0  1]

строка 1 может использоваться для изменения строк ниже.

Для расширенной матрицы выполните операции над строками, чтобы получить эшелонированную форму.

1. В первом уравнении старший коэффициент должен быть равен 1. При необходимости поменяйте местами строки или умножьте на константу.
2. Используйте операции со строками, чтобы получить нули в первом столбце после первой записи 1.
3. Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
4. Используйте операции со строками, чтобы получить нули вниз по столбцу 2, ниже записи 1.
5. Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
6. Продолжайте этот процесс для всех строк, пока не будет 1 в каждом элементе вниз по главной диагонали, а ниже не будут только нули.
7. Если какие-либо строки содержат все нули, поместите их внизу.

Решение 2×2 Система методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

2x+3y=6    x−y=12

Сначала запишем это как расширенную матрицу.

[231−1  \| 612]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

R1↔R2→[1−123\|126]

первая запись в строке 1, столбце 1. Теперь давайте получим 0 в строке 2, столбце 1. Этого можно добиться, умножив строку 1 на  −2,

, а затем прибавив результат к строке 2.

−2R1+R2 =R2→[1−105\|125]

Остался только один шаг, чтобы умножить строку 2 на 15.

15R2=R2→[1−101\|121]

Использовать обратную замену. Вторая строка матрицы представляет  y=1.

Подставьте обратно y=1 

в первое уравнение.

x−(1)=12         x=32

Решением является точка (32,1).

Решите данную систему методом исключения Гаусса.

4x+3y=11 x−3y=−1

(2, 1)

Использование исключения Гаусса для решения системы уравнений

Использование исключения Гаусса для решения заданного 2 × 2 

система уравнений .

  2x+y=14x+2y=6

Запишите систему в виде расширенной матрицы .

[2142  \| 16]

Получите 1 в строке 1, столбце 1. Этого можно добиться, умножив первую строку на 12.

12R1=R1→[11242  \| 126] ​​

Затем нам нужен 0 в строке 2 столбца 1. Умножьте строку 1 на  −4 

и добавьте строку 1 к строке 2.

−4R1+R2=R2→[11200  \| 124]

Вторая строка представляет уравнение 0=4.

Следовательно, система несовместна и не имеет решения.

Решение зависимой системы

Решение системы уравнений.

3x+4y=126x+8y=24

Выполните операций со строками над расширенной матрицей, чтобы попытаться получить эшелонированную форму строк .

A=[3468\|1224]

−12R2+R1=R1→[0068\| 024]R1↔R2→[6800\|24   0]

В последней строке матрицы заканчиваются все нули: 0y=0.

Таким образом, существует бесконечное число решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и найдите  y.

3x+4y=12         4y=12−3x           y=3−34x

Таким образом, решение этой системы  (x,3−34x).

Выполнение операций над строками над расширенной матрицей 3×3 для получения формы строк-эшелонов

Выполнение операций над строками данной матрицы для получения формы строк-эшелонов.

[1−342−56−334  \| 366]

В первой строке уже есть 1 в строке 1, столбце 1. Следующим шагом является умножение строки 1 на  −2 

и прибавление к строке 2. Затем замените строку 2 результатом.

−2R1+R2=R2→[1−3401−2−334\|306]

Далее получаем ноль в строке 3 столбца 1.

3R1+R3=R3→[1−3401−20− 616\|3015]

Далее получаем ноль в строке 3, столбце 2.

6R2+R3=R3→[1−3401−2004\|3015]

Последний шаг – получение единицы в строке 3 , столбец 3.

14R3=R3→[1−3401−2001  \| 3−6154]

Запишите систему уравнений в строчно-кулисной форме.

  x−2y+3z=9     −x+3y=−42x−5y+5z=172]

Решение системы линейных уравнений с использованием матриц

Мы увидели, как написать систему уравнений с расширенной матрицей , а затем, как использовать операции со строками и обратную подстановку для получения ступенчато-строковой формы . Теперь мы сделаем еще один шаг вперед, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.

Решение системы линейных уравнений с использованием матриц

Решение системы линейных уравнений с использованием матриц.

х    −    y   +    z=    82x  +   3y   −   z=            −9z=    9

Сначала запишем расширенную матрицу.

[1−1123−13−2−9   \| 8−29]

Далее выполняем операции над строками, чтобы получить строчно-эшелонную форму.

−2R1+R2=R2→[1−1105−33−2−9\|8−189]−3R1+R3=R3→[1−1105−301−12\|8−18−15]

Самый простой способ получить 1 в строке 2 столбца 1 — поменять местами  R2 

и  R3.

Развязка R2 и R3→[1−11801−12−1505−3−18]

Затем

−5R2+R3=R3→[1−1101−120057\|8−1557]−157R3=R3→[ 1−1101−12001\|8−151]

Последняя матрица представляет эквивалентную систему.

 x−y+z=8   y−12z=−15             z=1

Используя обратную подстановку, мы получаем решение как (4,−3,1).

Решение зависимой системы линейных уравнений с помощью матриц

Решите следующую систему линейных уравнений с помощью матриц.

−x−2y+z=−1 2x+3y=2    y−2z=0    

Запишите расширенную матрицу.

[−1−2123001−2  \| −120]

Сначала умножьте строку 1 на  −1 

, чтобы получить 1 в строке 1 столбца 1. Затем выполните 90 107 операций со строками 90 108, чтобы получить форму строки-эшелона.

−R1→[12−123001−2  \| 120]

R2↔R3→[12−101−2230  \|102]

−2R1+R3=R3→[12−101−20−12\|100]

R2+R3=R3→[12− 101−2000\|210]

Последняя матрица представляет следующую систему.

 x+2y−z=1        y−2z=0               0=0

Из тождества  0=0 

мы видим, что это зависимая система с бесконечным числом решений. Затем находим универсальное решение. Решая второе уравнение для  y 

и подставляя его в первое уравнение, мы можем решить для  z 

через x.

     x+2y−z=1                            y=2zx+2(2z)−z=1            x+3z=1                                          z=1−x3

0003

во второе уравнение, чтобы найти  y 

через x.

              y−2z=0                          z=1−x3 y−2(1−x3)=0                              

Общее решение  (x,2−2×3,1−x3).

Решите систему с помощью матриц.

x+4y−z=42x+5y+8z=15x+3y−3z=1

(1,  1,  1)

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Дана система уравнений. Решите ее с помощью матриц с помощью калькулятора.

1. Сохранить расширенную матрицу как матричную переменную [А], [Б], [С], ….
2. Используйте функцию ref( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

 5x+3y+9z=−1−2x+3y−z=−2−x−4y+5z=1    

Запишите расширенную матрицу для системы уравнений.

[539-23-1-1-45  \| −1−2−1]

На странице матрицы калькулятора введите указанную выше расширенную матрицу в качестве переменной матрицы [A].

[A]=[539−1−23−1−2−1−451]

Используйте функцию ref( в калькуляторе, вызывающую матричную переменную [A].

ref([A] )

Оценить. =−24187

Используя обратную замену, решение  ( 61187,−92187,−24187).

Применение матриц 2 × 2 к финансам

Кэролин инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых приносит 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?

У нас есть система двух уравнений с двумя переменными. Пусть x= 

сумма, инвестированная под 10,5% годовых, и  y= 

сумма, инвестированная под 12% годовых.

               x+y=12 0000,105x+0,12y=1 335

В качестве матрицы имеем

[110. 1050.12  \| 12 0001 335]

Умножьте строку 1 на  −0,105 

и прибавьте результат к строке 2.

[1100,015  \| 12,00075]

Тогда

0,015y=75         y=5,000

Итак 12,000−5,000=7,000.

Таким образом, 5000 долларов были вложены под 12% годовых, а 7000 долларов — под 10,5%.

Применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 долларов США в три счета, один из которых приносит 5% годовых, другой — 8% годовых, а третий — 9% интерес. Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, вдвое превышала сумму, вложенную под 5%. Сколько было вложено по каждой ставке?

У нас есть система из трех уравнений с тремя переменными. Пусть x 

будет суммой, инвестированной под 5% годовых, пусть y 

будет суммой, инвестированной под 8% годовых, и пусть z 

будет суммой, инвестированной под 9% годовых. Таким образом,

                     x+y+z=10 0000,05x+0,08y+0,09z=770                       2x−z=0

В качестве матрицы мы имеем

[1110. 050.080.0920−1  \| 10,0007700]

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелона.

−0,05R1+R2=R2→[11100,030,0420−1\|10,0002700]      −2R1+R3=R3→[11100,030,040−2−3\|10 000270               10,03R2=R2→ [01101430−2−3\|10,0009,000−20,000]              2R2+R3=R3→[111014300−13\|10,0009,000−2,000]

Третья строка сообщает−2,0−3 us ;

таким образом z=6000.

Вторая строка говорит нам y+43z=9000.

Подставляя  z=6000,

, получаем

y+43(6000)=9000y+8000=9000y=1000

Первая строка говорит нам x+y+z=10000.

Подставляя y=1,000 

и z=6,000,

получаем

x+1,000+6,000=10,000                      0         

Ответ: 3000 долларов инвестировано под 5% годовых, 1000 долларов инвестировано под 8% и 6000 долларов инвестировано под 9% годовых.

Небольшая обувная компания взяла кредит в размере 1 500 000 долларов США, чтобы расширить свой ассортимент. Часть денег была взята в долг под 7%, часть – под 8%, а часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовой процент по всем трем кредитам составлял 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.

150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем линейных уравнений с использованием исключения Гаусса.

• Решение системы двух уравнений с помощью расширенной матрицы
• Решение системы трех уравнений с использованием расширенной матрицы
• Расширенные матрицы на калькуляторе

Ключевые понятия

• Расширенная матрица — это матрица, содержащая коэффициенты и константы системы уравнений. См. [ссылка].
• Матрица, дополненная постоянным столбцом, может быть представлена ​​в виде исходной системы уравнений. См. [ссылка].
• Операции со строками включают умножение строки на константу, добавление одной строки к другой строке и перестановку строк.
• Мы можем использовать исключение Гаусса для решения системы уравнений. См. [ссылка], [ссылка] и [ссылка].
• Операции со строками выполняются над матрицами для получения ступенчатой ​​формы строк. См. [ссылка].
• Чтобы решить систему уравнений, запишите ее в расширенной матричной форме. Выполните операции со строками, чтобы получить форму строки-эшелона. Обратно заменить, чтобы найти решения. См. [ссылка] и [ссылка].
• Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. [ссылка].
• Многие реальные проблемы можно решить с помощью расширенных матриц. См. [ссылка] и [ссылка].

Раздельные упражнения

Устный

Можно ли любую систему линейных уравнений записать в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как записать эту расширенную матрицу.

Да. Для каждой строки коэффициенты при переменных записываются поперек соответствующей строки и ставится вертикальная черта; то константы располагаются справа от вертикальной черты.

Можно ли любую матрицу представить в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как записать эту систему уравнений.

Существует ли только один правильный метод использования строковых операций над матрицей? Попробуйте объяснить две разные операции со строками, которые можно использовать для решения расширенной матрицы[931−2  \| 06].

Нет, существует множество правильных методов использования строковых операций над матрицей. Возможны следующие два пути: (1) Поменять местами строки 1 и 2. Тогда R2=R2−9R1.

(2) R2=R1-9R2.

Затем разделите строку 1 на 9.

Можно ли решить матрицу, запись которой равна 0 по диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?

Может ли матрица, состоящая из 0 элементов для всей строки, иметь одно решение? Объясните, почему да или почему нет.

Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.

Алгебраический

Для следующих упражнений напишите расширенную матрицу для линейной системы.

8x−37y=82x+12y=3

    16y=49x−y=2

[0169−1\|42]

 3x+2y+10z=3−6x+2y+5z=13             4x+z=18

  x+5y+8z=19     12x+3y=43x+4y+9z=−7

[1581230349\|164−7]

6x+12y+16z=4  19x−5y+3z=−9             x+2y=−8

Для следующих упражнений напишите линейную систему из расширенной матрицы.

[−256−18  \| 526]

−2x+5y=56x−18y=26

[341017  \| 10439]

[320−1−94857  \| 3−18]

3x+2y=13−x−9y+4z=538x+5y+7z=80

[8291−175003  \| 433810]

[45−2015887−3  \| 122−5]

4x+5y−2z=12        y+58z=28x+7y−3z=−5

Для следующих упражнений решите систему методом исключения Гаусса.

[1000  \| 30]

[1010  \| 12]

Нет решений

[1245  \| 36]

[−124−5  \| −36]

(−1,−2)

[−2002  \| 1−1]

  2x−3y=−95x+4y=58

(6,7)

6x+2y=-43x+4y=-17

2x+3y=12 4x+y=14

(3,2)

−4x−3y=−2   3x−5y=−13

−5x+8y=3 10x+6y=5

(15,12)

   3x+4y=12−6x−8y=−24

−60x+45y=12  20x−15y=−4

(x,415(5x+1))

11x+10y=4315x+20y=65

 2x−y=23x+2y=17

(3,4)

−1,06x−2,25y=5,51−5,03x−1,08y=5,40

34x−35y=414x+23y=1

(19639,−513)

14x−23y=−112x+13y=3

[100011001  \| 314587]

(31,−42,87)

[101110011  \| 5020−90]

[123056008  \| 479]

(2140,120,98)

[−0. 10.3−0.1−0.40.20.10.60.10.7  \| 0,20,8−0,8]

 −2x+3y−2z=3      4x+2y−z=9     4x−8y+2z=−6

(1813,1513,−1513)

      x+y-4z=-4  5x-3y-2z=0  2x+6y+7z=30

      2x+3y+2z=1  −4x−6y−4z=−2 10x+15y+10z=5

(x,y,12(1−2x−3y))

    x+2y−z=1−x−2y+2z=−23x+6y−3z=5

     x+2y−z=1−x−2y+2z=−2 3x+6y−3z=3

(x,−x2,−1)

​   x+y=2   x+z=1−y−z=−3

x+y+z=100    x+2z=125−y+2z=25

(125,−25,0)

14x−23z=−1215x+13y=4715y−13z=29

−12x+12y+17z=−5314   12x−12y+14z=3    14x+15y+13z=2315

(8,1,−2)

−12x−13y+14z=−296   15x+16y−17z=431210−18x+19y+110z=−4945

Расширения

В следующих упражнениях используйте метод исключения Гаусса для решения системы.

x-17+y-28+z-34=0                    x+y+z=6     x+23+2y+z-33=5

(1,2,3)

x−14−y+14+3z=−1  x+52+y+74−z=4         x+y-z−22=1

      x−34−y−13+2z=−1x+52+y+52+z+52=8                     x+y+z=1

(x,3128−3×4,128(−7x−3))

x−310+y+32−2z=3 x+54−y−18+z=32x−14+y+42+3z=32

     x−34−y−13+2z=−1x+52+y+52+z+52=7                             x+y+z=1

Решений не существует.

Реальные приложения

Для следующих упражнений создайте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.

Каждый день в магазине кексов продается 5000 кексов с шоколадным и ванильным вкусом. Если шоколадный вкус в 3 раза популярнее ванильного, сколько каждого кекса продается в день?

В конкурирующем магазине кексов ежедневно продаются кексы на 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы «Красный бархат» — 1,75 доллара. Если общее количество кексов, продаваемых в день, равно 2200, сколько каждого вкуса продается каждый день?

860 красный бархат, 1340 шоколадный

Вы вложили 10 000 долларов США в два счета: один с простой процентной ставкой 3%, другой с процентной ставкой 2,5%. Если ваш общий процентный платеж через год составил 283,50 доллара, сколько было на каждом счете по прошествии года?

Вы вложили 2300 долларов США на счет 1 и 2700 долларов США на счет 2. Если общая сумма процентов через год составляет 254 доллара США, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим, простые процентные ставки.

4% на счет 1, 6% на счет 2

Bikes’R’Us производит велосипеды, которые продаются по цене 250 долларов. Это обходится производителю в 180 долларов за велосипед плюс первоначальный взнос в размере 3500 долларов. Через какое количество проданных велосипедов производитель станет безубыточным?

Крупный магазин бытовой техники рассматривает возможность покупки пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по цене 86 долларов каждый, а стоимость доставки составит 9200 долларов, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько он должен брать за пылесосы?

$126

Три самых популярных вкуса мороженого — шоколадное, клубничное и ванильное — составляют 83 % вкусов, продаваемых в магазине мороженого. Если ванильное мороженое продается на 1% больше, чем клубничное, более чем в два раза, а шоколадное — на 11% больше, чем ванильное, то какую долю от общего потребления мороженого составляют ароматы ванили, шоколада и клубники?

В магазине мороженого растет спрос на три вкуса. В прошлом году банановое, тыквенное и каменистое мороженое составили 12% от общего объема продаж мороженого. В этом году те же три мороженого составили 16,9% от продаж мороженого. Продажи каменистой дороги увеличились вдвое, продажи бананов выросли на 50%, а продажи тыквы выросли на 20%. Если мороженое «Каменная дорога» имеет на один процент меньше продаж, чем банановое мороженое, выясните процент продаж каждого отдельного мороженого в прошлом году.

Банан 3%, тыква 7%, каменистая дорога 2%

Пакет ореховой смеси содержит кешью, фисташки и миндаль. Всего в пакете 1000 орехов, а миндаля на 100 меньше, чем фисташек. Орехи кешью весят 3 г, фисташки — 4 г, а миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида находится в мешке.

Пакет ореховой смеси содержит кешью, фисташки и миндаль. Изначально в мешке было 900 орехов. 30 % миндаля, 20 % кешью и 10 % фисташек были съедены, и теперь в мешке осталось 770 орехов. Изначально орехов кешью было на 100 штук больше, чем миндаля. Для начала подсчитайте, сколько орехов каждого типа было в пакете.

100 миндаля, 200 кешью, 600 фисташек

Глоссарий

расширенная матрица

матрица коэффициентов, присоединенная к столбцу констант, разделенному вертикальной чертой в скобках матрицы

матрица коэффициентов

матрица, содержащая только коэффициенты из системы уравнений

Исключение Гаусса

использование элементарных операций со строками для получения матрицы в виде эшелона строк

главная диагональ

элементов из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы

рядно-эшелонная форма

после выполнения операций со строками, форма матрицы, которая содержит единицы вниз по главной диагонали и нули на каждом месте ниже диагонали

эквивалент строки

две матрицы А 

и

B 

эквивалентны по строкам, если одно может быть получено из другого путем выполнения основных операций со строками

рядные операции

добавление одной строки к другой строке, умножение строки на константу, перестановка строк и т.