Решение методом Крамера системы линейных уравнений 3-4-го порядка
Решать системы линейных алгебраических уравнений второго, третьего, изредка четвертого порядка методом Крамера достаточно часто придется студентам младших курсов учебы при изучении основ линейной алгебры. Для большинства студентов стационарной формы учебы такие задания не являются сложными, однако кто выбрал заочную учебу или дистанционную, или пропустил по определенным причинам практические занятия, вычисления выглядят непонятными и тяжелыми. Чтобы исправить такую ситуацию в данной статье будут приведены наиболее распространены примеры данной темы и схема их решения. Если Вы хорошо поймете принцип их решения, то на практике у Вас не будет трудностей с подобными заданиями.
Для начала выберем задание из сборника задач Дубовика В.П., Юрика І.І. “Высшая математика”.
———————————–
Примеры
Решить систему линейных алгебраических уравнений.
1) (1. 153)
2) (4. 165)
165)
3) (4. 174)
Решение.
1) В случае двух уравнений решение можно получить более простым способом. Выражаемый из второго уравнения
и подставим в первое
Раскрыв скобки, сгруппируем подобные слагаемые
Отсюда получим решение
Переменнуюнайдем подстановкой в любое из уравнений
Таким образом решением системы двух уравнений будут следующие значения
Поскольку цель статьи научить студентов решать по методике Крамера то решим данный пример и етим методом.
Для этого выпишем систему линейных уравнений в виде
Найдем детерминант основной части
Для вычисления вспомогательных определителей ставим столбец свободных членов на место первой строки для и на место второй для . В результате получим
Подставим найденные значения в формулы Крамера
и найдем неизвестные
Из рассмотренного примера видим что вычисление при двух уравнениях с двумя неизвестными достаточно простые.
2) Запишем систему трех алгебраических уравнений в удобном для решения виде
Найдем детерминант системы по правилу треугольников
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим
Вычисляем неизвестные за формулами Крамера
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.
3) Записываем систему уравнений четвертого порядка в виде
Находим главный определитель системы. При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой
и найдем соответствующие детермиінанты третьего порядка
Подставим найденные значения в определитель
По такой же схеме вычисляем вспомогательные определители, напомню лишь, что они образуются заменой столбца в главном определителе на столбец свободных членов (обозначен черным цветом). Я не буду приводить детальных излаганий, однако Вы можете проверить, что детерминанты примут значение
Я не буду приводить детальных излаганий, однако Вы можете проверить, что детерминанты примут значение
Подставив в формулы Крамера, после вычислений будем иметь
На этом пример решено.
Системы четырех линейных уравнений наиболее трудоемкие в вычислениях, для вычисления их решения нужно решать 5*4 определители третьего порядка, в то время как системы трех уравнений лиш 4. Будьте внимательные при вычислениях ведь самая малая ошибка может иметь следствием неверный результат.
———————————————-
Посмотреть материалы:
Как решать методом крамера примеры. Примеры решения систем линейных алгебраических уравнений методом Крамера
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений,
сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение.
Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
–
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите
ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю.
По формулам Крамера находим:
Итак, решение системы – (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6.
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть
не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.
Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений.

- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель.

- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т. е. имеет вид
е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1.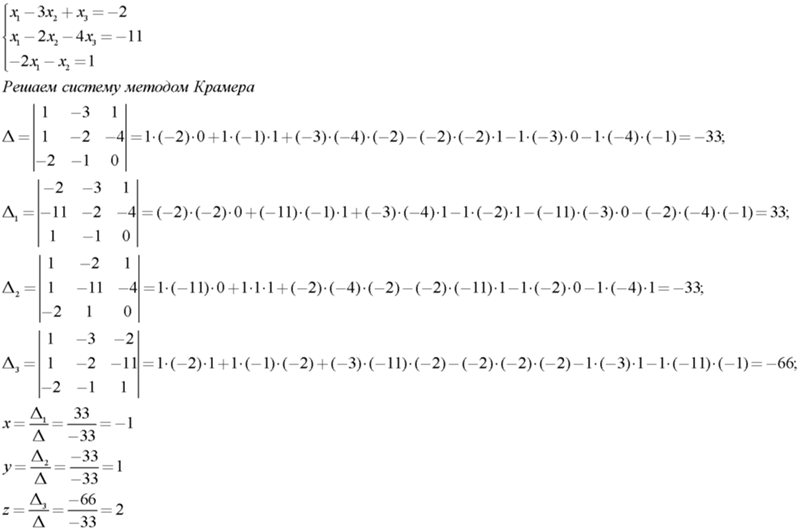 Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A – 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A – 1 , мы получим решение системы:
14) слева на A – 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
| ………………………………………………………………….. | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
| …………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = – 3 + 2t
x 2 = – 1 – 3t
x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где – определитель основной матрицы , i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.5. Основные свойства определителей
Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Методическая разработка урока по математики на тему «Решение системы линейных уравнений методом Крамера»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная методическая разработка предназначена для проведения учебного занятия по дисциплине «Математика» на тему «Решение систем линейных уравнений методом Крамера» для студентов первого курса по программе учебной дисциплины, разработанной на основе Федерального государственного образовательного стандарта для специальностей среднего профессионального образования.
В результате изучения темы студент должен:
знать:
- решение систем линейных уравнений методом Крамера;
- применение знаний при решении систем линейных уравнений.
уметь:
- решать системы двух линейных уравнений с двумя неизвестными методом Крамера
- решать системы трех линейных уравнений с тремя неизвестными методом Крамера
При разработке данного урока в зависимости от специфики подготовки студентов можно внести дополнения и изменения в содержание, последовательность изучения материала урока и распределение времени.
Наблюдается связь истории с математикой, при изучении материала использована задача прикладного характера для будущей практической деятельности, что прививает интерес к предмету. Данная методическая разработка содержит: учебно-методическую карту, ход, где сформулированы цели занятия и последовательность проведения урока, указан список литературы.
При проведении занятия, использованы учебные пособия, технические и наглядные средства обучения
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА
Дисциплина: Математика
Тема занятия: Решение систем линейных уравнений методом Крамера
Вид занятия (тип урока): Комбинированный
Цели урока:
Дидактическая:
- повторить пройденный материал;
- углубить знания студентов по теме «Решение систем линейных уравнений»;
3) изучить решение систем линейных уравнений c помощью метода Крамера;
4) научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.
Развивающая:
способствовать развитию:
- логического мышления;
- памяти;
- умению сравнивать, обобщать, анализировать;
- интереса к избранной специальности.
Воспитательная:
стремиться воспитывать:
- чувства ответственности, исполнительности, аккуратности;
- чувство гордости за избранную профессию;
- положительное отношение к знаниям, учениям;
- интерес к математике
Межпредметные связи:
Обеспечивающие: история, русский язык, информатика
Обеспечиваемые: специальные предметы
Обеспечение занятия:
- Наглядные пособия: Приложение (Презентация к уроку), меловые иллюстрации
- Раздаточный материал: карточки.
- Технические средства обучения: калькуляторы, компьютеры, интерактивная доска
ПЛАН УРОКА
1. Организационный момент
Здравствуйте, студенты. Тема урока: «Решение систем линейных уравнений методом Крамера». Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.
2. Постановка целей занятия
Цели урока: повторить пройденный материал; углубить знания по теме «Решение систем линейных уравнений»; изучить решение систем линейных уравнений с помощью метода Крамера; научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.
3. Проверка домашнего задания
4. Проверка знаний
Экспресс – опрос
- Какое уравнение называется линейным?
- Напишите систему m линейных уравнений с n переменными.
- Назовите коэффициенты при переменных.
- Какие числа называются свободными членами?
- Что является решением системы?
- Какие методы решения систем линейных уравнений знаете?
Ответы: Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
5. Изучение нового материала
В школьном курсе рассматриваются способ подстановки и способ сложения. В курсе высшей математике решают методом Крамера, методом Гаусса и с помощью обратной матрицы. Рассмотрим решение систем линейных уравнений методом Крамера
5.1 Знакомство с биографией Крамера
При изучении новой темы «Решение систем линейных уравнений методом Крамера» важное место занимает связь истории с математикой, что прививает интерес к предмету. Познакомимся с биографией Габриэля Крамера.
Сведения из истории
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.
Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача.
Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне и других. Со многими из них он продолжал переписываться всю жизнь.
В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.
В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.
Габриэль Крамер скончался 4 января 1752 года во Франции
5.2 Решение системы линейных уравнений методом Крамера
Теорема Крамера.
Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Заменяя столбец с коэффициентами соответствующей переменной свободными членами:
6. Закрепление.
6.1 Решение системы двух линейных уравнений с двумя неизвестными методом Крамера
2) Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?
Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году.
Тогда условие задачи можно записать в виде системы:
Решив систему, получим x = 4, y = 8.
Ответ: а) прибыль в минувшем году первого отделения – 4 млн усл. ед., второго – 8 усл.ед.:
б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед.,
второго 1,4. 8 = 11,2 млн усл. ед.
При решении системы уравнений могут встретиться три случая:
1) система линейных уравнений имеет единственное решение
(система совместна и определённа)
Условия:
2) система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
Условия:
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
3) система линейных уравнений решений не имеет
(система несовместна)
Условия:
Система называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
6.2 Решение системы трех линейных уравнений с тремя двумя неизвестными методом Крамера
Ответ: (1; 0; -1) .
Решение. Находим определители системы:
Ответ: (1; 0; -1) .
7. Домашнее задание (слайд № 23)
Решите системы:
8. Подведение итогов
Подведем итоги урока. По результатам работы на уроке выставляются оценки, с последующей демонстрацией успеваемости в виде диаграммы на интерактивной доске.
Урок окончен. Спасибо за внимание. До свидания.
Литература:
Основная
- Григорьев В.П.Дубинский Ю.А Элементы высшей математики. Москва, 2014
- Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика. Москва, 2008
Дополнительная
- Богомолов Н.В. Практические занятия по математики. Москва, 2013
Интернет-ресурсы: www.en.edu.ru
ХОД УРОКА
№п/п | Элементы урока, содержание и последовательность изучаемых вопросов | Формы и методы обучения, контроля | Наглядные пособия, ТСО, дидактический материал | Преподаватель | Студенты | Время 45 мин. |
1. | Организационный момент. Взаимное приветствие. | Проверка отсутствующих, рабочих мест | Интерактивная доска слайд №1 | Приветствует, отмечает в журнале отсутствующих. | Приветствуют | 1 мин |
2. | Постановка целей занятия. | Организация внимания | Интерактивная доска | Ставит цели урока | Слушают | 1 мин |
3. | Проверка домашнего задания | Групповая работа | Интерактивная доска | Контролирует | Дежурный проверяет | 5 мин |
4. | Проверка знаний | Экспресс-опрос | Слайды № 2,3,4 | Задает вопрос, поправляет ответ | Думают, отвечают | 5 мин |
5. | Изучение нового материала | Организация внимания | Интерактивная доска | Объясняет | Слушают, рассуждают, отвечают на вопросы. |
|
5.1 | Знакомство с биографией Крамера | Рассказ материала | Слайды № 5-10 | Рассказывает | Смотрят | 5 мин |
5.2 | Решение системы линейных уравнений методом Крамера | Изучение темы | Слайды № 11-15 | Объясняет | Смотрят, слушают | 10 мин |
6. | Закрепление | Самостоятельная работа | Интерактивная доска | Выдает задания | Думают, решают |
|
6.1 | Решение системы двух линейных уравнений с двумя неизвестными методом Крамера | Групповая работа | Слайды № 16-19 | Выдает задания, проверяет | Решают | 5 мин |
6.2 | Решение системы трех линейных уравнений с тремя неизвестными методом Крамера | Самостоятельная работа | Слайды № 20-22 | Контролирует, проверяет | Думают, решают | 10 мин |
7. | Домашнее задание |
| Слайды № 23 | Выдает задания | Пишут | 1 мин |
8. | Подведение итогов. | Анализ работы | Интерактивная доска | Подводит итоги, обобщает | Получают оценки | 2 мин |
Презентация «Решение системы линейных уравнений методом Крамера»
Теорема Крамера
Системы линейных алгебраических уравнений При решении систем линейных уравнений обсуждаются 3 вопроса: а) существует ли решение системы уравнений, б) сколько разных решений имеет система уравнений, в) алгоритм решения. Ниже излагаются основные результаты в этой области математики, позволяющие исчерпывающим образом ответить на эти вопросы.Теорема Крамера
Система двух уравнений, два неизвестных
Рассмотрим систему линейных алгебраических уравнений \[ a_{11}x_1+a_{12}x_2=b_1, \quad \quad(17) \] \[ a_{21}x_1+a_{22}x_2=b_2, \quad \quad(18) \]числа \(a_{ik}, b_i\), \(i,k=1,2\) считаются заданными, требуется найти неизвестные \(x_1,x_2\) . Эту систему можно решить исключением неизвестных. Например, умножим первое уравнение на \(a_{22}\) и вычтем второе, умноженное на \(a_{12}\), получим:
\[ (a_{11}a_{22}-a_{21}a_{12})x_1=b_1a_{22}-b_2a_{12}, \]так что если \(a_{11}a_{22}-a_{21}a_{12} \neq 0, \) \[ x_1=\frac{b_1a_{22}-b_2a_{12}}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(19) \]
Если второе уравнение умножить на \(a_{11}\) и вычесть из него первое уравнение, умноженное на \(a_{21}\), получим: \[ x_2=\frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(20) \]
Введем следующие обозначения. Матрицей коэффициентов системы уравнений (17)-(18) назовем матрицу \[ A=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right), \] столбец правых частей системы \[ B=\left (\begin{array}{c} b_1 \\b_2 \end{array} \right). \]
Тогда формулы (19), (20) можно переписать следующим образом: \[ x_1=\frac{detC_1}{detA}, x_2=\frac{detC_2}{detA}, \quad \quad(21) \] где матрица \(C_k\), \(k=1,2\), получается из матрицы \(A\) заменой ее \(k\)-того столбца на столбец \(B\). Формулы (21) называются формулами Крамера для системы из 2 уравнений с двумя неизвестными. Они описывают единственное решение системы уравнений в данном случае.
Система \(n\) уравнений, \(n\) неизвестных
Рассмотрим систему \(n\) линейных алгебраических уравнений с \(n\) неизвестными, \[ a_{11}x_1+a_{12}x_2+ .{-1}B. \]
В целом решение систем методом Крамера и методом обратной матрицы требует выполнения 2 условий: матрица коэффициентов системы должна быть квадратной ( т.е. число уравнений должно совпадать с числом неизвестных) и эта матрица должна быть невырожденной. К тому же практическая реализация этих методов связана с весьма громоздкими вычислениями, так что они имеют лишь теоретическое значение. На практике используют существенно более простой в реализации метод Гаусса, который к тому же позволяет решать и более общие системы уравнений. Этот метод описан ниже.
Решить системы методом Крамера и методом обратной матрицы.
а) \[ x_1+x_2+2x_3=-1, \] \[ 2x_1-x_2+2x_3=-4, \] \[ 4x_1+x_2+4x_3=-2. \]
б) \[ 3x_1+2x_2+x_3=5, \] \[ 2x_1+3x_2+x_3=1, \] \[ 2x_1+x_2+3x_3=11. \]
в) \[ 2x_1+x_2-x_3=2, \] \[ 3x_1+x_2-2x_3=3, \] \[ x_1+x_3=3. \]
Как решить уравнение методом крамера. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера. Продолжаем решать системы методом Крамера вместе
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Пусть дана система трех линейных уравнений:
Для
решения системы линейных уравнений
методом Крамера из коэффициентов при
неизвестных составляется главный
определитель
системы .
Для системы (1) главный определитель
имеет вид
.
Далее
составляются определители по переменным
,,.
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
,
,
.
Тогда решение системы находится по формулам Крамера
,
,
Следует
отметить, что система имеет единственное
решение
,
если главный определитель
. Если же
и
=
0,=
0,=
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же
и
0,
или0,или0,
то система уравнений несовместна, то
есть решений не имеет.
Пример
Решение:
1) Составим и вычислим главный определитель системы, состоящий из коэффициентов при неизвестных.
.
Следовательно, система имеет единственное решение.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов.
По формулам Крамера находим неизвестные:
,
,
.
Сделаем проверку, чтобы убедиться в правильности решения
Т.е.
.
,
т.е.
,
т.е.
Ответ: .
Пример
Решить систему уравнений методом Крамера:
Решение:
1) Составим и вычислим главный определитель системы из коэффициентов при неизвестных:
.
Следовательно, система не имеет единственного решения.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов:
,
,
следовательно, система несовместна.
Ответ: система несовместна .
Метод Гаусса
Метод Гаусса состоит из двух этапов. Первый этап заключается в последовательном исключении переменных из уравнений системы при помощи действий, не нарушающих равносильности системы. Например, рассмотрим два первых уравнения системы (1).
(1)
Необходимо
путем сложения этих двух уравнений
получить уравнение, в котором отсутствует
переменная
.
Умножим первое уравнение на,
а второе на (
)
и сложим полученные уравнения
Заменим коэффициент перед y , z и свободный член на ,исоответственно, получим новую пару уравнений
Заметим, что во втором уравнении отсутствует переменная x .
Проведя аналогичные действия над первым и третьим уравнениями системы (1), а затем над полученными в результате сложения вторым и третьим уравнениями, преобразуем систему (1) к виду
(2)
Такой результат возможен, если система имеет единственное решение. В этом случае решение находится при помощи обратного хода метода Гаусса (второй этап). Из последнего уравнения системы (2) находим неизвестную переменную z , затем из второго уравнения находим y , а x соответственно из первого, подставляя в них уже найденные неизвестные.
Иногда в результате сложения двух уравнений суммарное уравнение может принять один из видов:
А)
,
где
.
Это означает, что решаемая система
несовместна.
Б)
,
то есть
.
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
Пример
Решение:
Рассмотрим следующий способ осуществления первого этапа решения методом Гаусса. Запишем три строки коэффициентов при неизвестных и свободных членов, соответствующих трем уравнениям системы. Свободные члены отделим от коэффициентов вертикальной линией, а под третьей строкой проведем горизонтальную прямую.
Первую строку, которая соответствует первому уравнению системы, обведем – коэффициенты в этом уравнении останутся неизменными. Вместо второй строки (уравнения) надо получить строку (уравнение), где коэффициент при равен нулю. Для этого все числа первой строки умножим на (–2) и сложим с соответствующими числами второй строки. Полученные суммы запишем под горизонтальной чертой (четвертая строка). Для того чтобы вместо третьей строки (уравнения) также получить строку (уравнение), в которой коэффициент приравен нулю, умножим все числа первой строки на (–5) и сложим с соответствующими числами третьей строки. Полученные суммы запишем пятой строкой и проведем под ней новую горизонтальную черту. Четвертую строку (или пятую – по выбору) обведем. Выбирается строка с меньшими коэффициентами. В этой строке коэффициенты останутся неизменными. Вместо пятой строки надо получить строку, где уже два коэффициента равны нулю. Умножим четвертую строку на 3 и сложим с пятой. Сумму запишем под горизонтальной чертой (шестая строка) и обведем ее.
Все описанные действия изображены в таблице 1 при помощи арифметических знаков и стрелок. Обведенные в таблице строки запишем снова в виде уравнений (3) и, применив обратный ход метода Гаусса, найдем значения переменных x , y и z .
Таблица 1
Восстанавливаем систему уравнений, полученную в результате наших преобразований:
(3)
Обратный ход метода Гаусса
Из
третьего уравнения
находим
.
Во
второе уравнение системы
подставим найденное значение
,
получим
или
.
Из
первого уравнения
,
подставляя уже найденные значения
переменных, получаем
,
то есть
.
Чтобы убедиться в правильности решения, проверку необходимо сделать во всех трех уравнениях системы.
Проверка:
,
получим
Получим
Получим
значит, система решена верно.
Ответ:
,
,
.
Пример
Решить
систему методом Гаусса:
Решение:
Порядок действий в этом примере аналогичен порядку в предыдущем примере, а конкретные действия указаны в таблице 2.
В результате преобразований получим уравнение вида , следовательно, заданная система несовместна.
Ответ: система несовместна .
Пример
Решить
систему методом Гаусса:
Решение:
Таблица 3
В результате преобразований получим уравнение вида , которое исключается из рассмотрения. Таким образом, имеем систему уравнений, в которой число неизвестных 3, а число уравнений 2.
Система имеет бесчисленное множество решений. Чтобы отыскать эти решения, введем одну свободную переменную. (Число свободных переменных всегда равно разности между числом неизвестных и числом уравнений, оставшихся после преобразования системы. В нашем случае 3 – 2 = 1).
Пусть
– свободная переменная.
Тогда
из второго уравнения найдем
,
откуда
,
а затем найдемx из первого уравнения
или
.
Таким
образом,
;
;
.
Сделаем проверку в уравнениях, которые не участвовали в нахождении и, то есть во втором и в третьем уравнениях первоначальной системы.
Проверка:
или
,
получаем
.
или
,
получаем
.
Система решена верно. Давая произвольной постоянной различные значения, будем получать различные значенияx , y и z .
Ответ:
;
;
.
В нашем калькуляторе вы бесплатно найдете решение системы линейных уравнений методом Крамера онлайн с подробным решением и даже с комплексными числами . Каждый определитель, использованный в расчетах, можно просмотреть отдельно, а также проверить точный вид системы уравнений, если вдруг определитель основной матрицы оказался равен нулю.
Подробнее о том, как пользоваться нашим онлайн калькулятором, вы можете прочитать в инструкции .
О методе
При решении системы линейных уравнений методом Крамера выполняются следующие шаги.
- Записываем расширенную матрицу.
- Находим определитель основной (квадратной) матрицы.
- Для нахождения i-ого корня подставляем столбец свободных членов в основную матрицу на i-ое место и находим ее определитель. Далее находим отношение полученного определителя к основному, это и есть очередное решение. Проделываем данную операцию для каждой переменной.
- В случае, если основной определитель матрицы равен нулю, то система уравнений либо несовместна, либо имеет бесконечное множество решений. К сожалению метод Крамера не позволяет более точно ответить на этот вопрос. Тут вам поможет
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
Проект на тему “Метод Крамера, как способ решения практических задач”
Пятая лицейская научно-практическая конференция «Познание и творчество»
Физика-математика
Тема: «Метод Крамера, как способ решения практических задач»
Исследовательский проект
Автор: Кротова Анна
Ученица 10 «Б» класса МАОУ
« Лицей №21»
Руководитель:
Балашова Елена Ивановна,
учитель математики
Кротова Ирина Леонидовна,
учитель математики
Тема моего исследовательского проекта – «Метод Крамера, как способ решения практических задач».
В школьном курсе алгебры изучают методы решения систем линейных уравнений, такие как: метод подстановки, метод сложения, графический метод. Каждый из методов имеет свои достоинства и недостатки. Общее для них то, что большинство учащихся не могут их усвоить на необходимом уровне.
Я считаю, что тема моего проекта достаточно актуальна в первую очередь для меня, поскольку в математике есть такие задачи, которые нужно решать с помощью систем уравнений. Однако в школьном курсе изучаются системы уравнений, содержащие только две переменные. Мне бы хотелось познакомиться самой, а потом и научить других решать системы, содержащие большее количество неизвестных, что может помочь в решении более сложных задач не только в математике, но и в экономике. Но для того, чтобы познакомиться с самим методом, нужно знать что такое определитель второго порядка и научиться их вычислять.
Гипотеза: эффективность решения систем уравнений повышается, если использовать метод Крамера.
Задачи:
Рассмотреть метод Крамера.
Научить учащихся 8-10 класса пользоваться данным методом.
Предложить учащимся 8-10 класса, на выбор, решить несколько систем уравнений понравившимся способом.
Проанализировать полученный данные в ходе проведения самостоятельной работы, которую выполнят учащиеся.
Сделать выводы, на основе которых определить достоверность моей гипотезы.
Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария). Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы.
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Понятие определителя вводится только для квадратной матрицы.
Определитель– это число, которое считается по определенным правилам. Порядок определителя– это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.
Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:
Определителем второго порядка называется число, вычисляемое по правилу:
.
Пример . .
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.Решения систем методом Крамера
Метод Крамера – это метод решения систем линейных уравнений. Он применяется только к системам линейных уравнений, у которых число уравнений совпадает с числом неизвестных и определитель отличен от нуля.
Любая крамеровская система уравнений имеет единственное решение , которое определяется формулами , где – определитель матрицы, полученной из основной матрицы заменой -го столбца на столбец свободных членов системы, а – определитель основной матрицы. Эта формула называется формулой Крамера.
Пример 1:Задание: Решить систему методом Крамера.
Решение: Запишем основную матрицу системы
Найдем её определитель
Определитель , следовательно, заданная система может быть решена методом Крамера.
Вычислим определитель , для этого заменим первый столбец в основной матрице на столбец свободных членов , получим
Аналогично, заменяя второй столбец основной матрицы на , найдем :
Далее по формуле Крамера находим неизвестные переменные:
Ответ:
Пример 2:Задание: Решить систему методом Крамера.
Решение: В уравнениях системы перенесем свободный член вправо:
Тогда основная матрица , а столбец свободных членов .
Найдем определитель матрицы системы:
Определитель , следовательно, система имеет единственное решение и может быть решена методом Крамера. Заменяя первый столбец на столбец свободных членов, найдем, что
Заменяя второй столбец основной матрицы на столбец , получаем:
Тогда, по формуле Крамера, решением системы будет
Ответ:
Пример 3:Задание: Решить систему методом Крамера.
Решение: Найдем определитель основной матрицы системы:
Найдем определитель , для этого подставим в последний определитель вместо первого столбца столбец свободных членов :
Подставляя вместо второго столбца столбец свободных членов, найдем :
Аналогично найдем :
Далее по формуле Камера находим решение заданной системы
Ответ:
Пример 4:Задание: Решить систему методом Крамера.
Решение: Запишем основную матрицу системы:
и найдем её определитель по правилу треугольника:
Определитель основной матрицы равен нулю, следовательно, к данной системе нельзя применить метод Крамера.
Ответ: Данная система не может быть решена методом Крамера.
Конструкт урока для 7 классаКонструкт урока по теме «Метод Крамера как способ решения систем уравнений»
Учитель: Кротова Анна
Учебный предмет: математика
Класс: 7
Цель урока: показать применение метода Крамера, и закрепить умения и навыки при решении систем уравнений методом подстановки и методом алгебраического сложения. Продолжить отрабатывать вычислительные навыки при решении систем уравнений. Продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать.
Задачи:
– составлять системы уравнений и решать системы, используя алгоритмы;
– применять метод Крамера для решения систем уравнений, как один из рациональных методов решений.
Ход урока
Актуализация знанийУчитель предлагает учащимся задачу с двумя переменными: «на чашечных весах взвесили четырех кошек и трех котят, их вес оказался 15 кг. Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, если считать вес всех кошек одинаковым и вес всех котят также одинаковым.»
Ученики составляют систему и решают задачу вместе с учителем методом алгебраического сложения и подстановки.
Регулятивные: самостоятельно анализировать условия задачи.
Учитель предлагает решить задачу вторым способом, воспользовавшись методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Регулятивные: самостоятельно анализировать условия задачи.
Познавательные: ученики осваивают новый, ранее не изученный ими метод.
.
Постановка проблемы
Учитель предлагает решить самостоятельно систему методом алгебраического сложения и подстановки.
Сформулировать алгоритм решения данной системы.
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Учитель предлагает самостоятельно решить произвольную систему уравнений методом Крамера
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Рефлексия
Учитель предлагает задание для самостоятельного решения, проверяет самостоятельную работу и анализирует результаты.
Применение алгоритма при решении многошаговых уравнений.
Работают с заданием на анализ предъявляемой информации, формулируют свои оценочные суждения, аргументируют их примерами
Личностные: формулирование оценочных суждений, их аргументация;
Регулятивные: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.
Коммуникативные: умение вступать в диалог с учителем и со сверстниками.
Познавательные: оценка результатов деятельности.
Конструкт урока для 9 классаКонструкт урока по теме «Метод Крамера как способ решения систем уравнений»
Учитель: Кротова Анна
Учебный предмет: математика
Класс: 7
Цель урока: показать применение метода Крамера, и закрепить умения и навыки при решении систем уравнений методом подстановки и методом алгебраического сложения. Продолжить отрабатывать вычислительные навыки при решении систем уравнений. Продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать.
Задачи:
– составлять системы уравнений и решать системы, используя алгоритмы;
– применять метод Крамера для решения систем уравнений, как один из рациональных методов решений.
Ход урока
Актуализация знанийУчитель предлагает учащимся задачу с двумя переменными: «на чашечных весах взвесили четырех кошек и трех котят, их вес оказался 15 кг. Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, если считать вес всех кошек одинаковым и вес всех котят также одинаковым.»
Ученики составляют систему и решают задачу вместе с учителем методом алгебраического сложения и подстановки.
Регулятивные: самостоятельно анализировать условия задачи.
Учитель предлагает решить задачу вторым способом, воспользовавшись методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Регулятивные: самостоятельно анализировать условия задачи.
Познавательные: ученики осваивают новый, ранее не изученный ими метод.
.
Постановка проблемы
Учитель предлагает решить самостоятельно систему методом алгебраического сложения и подстановки.
Сформулировать алгоритм решения данной системы.
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Учитель предлагает решить систему из трех уравнений методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Учитель предлагает самостоятельно решить произвольную систему уравнений методом Крамера
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Рефлексия
Учитель предлагает задание для самостоятельного решения, проверяет самостоятельную работу и анализирует результаты.
Применение алгоритма при решении многошаговых уравнений.
Работают с заданием на анализ предъявляемой информации, формулируют свои оценочные суждения, аргументируют их примерами
Личностные: формулирование оценочных суждений, их аргументация;
Регулятивные: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.
Коммуникативные: умение вступать в диалог с учителем и со сверстниками.
Познавательные: оценка результатов деятельности.
В итоге работы над данным проектом я выполнила все поставленные перед собой задачи. С помощью дополнительной литературы я изучила метод Крамера, узнала, что такое определитель, как он находится и научилась применять данный метод на практике. Я провела уроки в 7 и в 9 классе. На уроке я предложила учащимся решить системы уравнений новым методом. Большинство учащихся, воспользовавшись методом Крамера, решили системы уравнений правильно.
Перед тем, как начать писать проект, я определила для себя такие риски и сложности как: исследуемая информация может быть сложна, в связи с тем, что изучаемый мною материал выходит за рамки школьной программы. Кроме того, может возникнуть трудность при передаче информации другим учащимся в связи с моей методической неграмотностью, т.е. незнание методов изложения материала. Но риск оказался не оправдан, т.к. тема не вызвала затруднений, и я смогла преподнести информацию так, что учащиеся смогли ее реализовать.
В ходе работы над моим проектом я доказала справедливость моей гипотезы, что эффективность решения систем уравнения повышается, если использовать метод Крамера.
Результаты самостоятельной работы в 7 классе Результаты самостоятельной работы в 9 классеЛекция 3 СЛУ Метод Крамера
6
Лекция 3. Системы линейных уравнений.
метод Крамера
Содержание
Основные определения.
Метод Крамера (определителей) решения систем линейных уравнений.
1. Основные определения
Системой линейных уравнений с неизвестными называется совокупность уравнений, в каждом из которых неизвестные присутствуют в первой степени:
где числа – коэффициенты при неизвестных, – номер уравнения, – номер неизвестной, – свободные члены.
,
который при подстановке в каждое уравнение системы вместо неизвестных соответственно обращает их в верные равенства.
Решить СЛУ – это значит указать все решения системы, то есть такие наборы значений неизвестных, которые обращают уравнения системы в тождества.
Система линейных уравнений называется:
а) совместной, если она имеет хотя бы одно решение;
б) несовместной, если она не имеет решений;
в) определенной, если она имеет единственное решение;
г) неопределенной, если она имеет бесконечное множество решений;
д) однородной, если все свободные члены равны нулю ;
е) неоднородной, если есть .
2. Метод Крамера (определителей) решения систем линейных уравнений
Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители.
2.1. Число уравнений и неизвестных равно 2
Рассмотрим систему линейных уравнений
Вычисляются определители:
, , .
Здесь
– определитель системы, составленный из коэффициентов при неизвестных;
– это определитель, полученный из определителя заменой столбца коэффициентов при на столбец свободных членов;
– это определитель, полученный из определителя заменой столбца коэффициентов при на столбец свободных членов.
1. Если , то система совместная и определенная, то есть имеет единственное решение, которое находится по формулам Крамера:
.
2. Если , а хотя бы один из определителей , отличен от нуля, то система не имеет решений (несовместная).
3. Если , то система имеет бесконечно много решений (совместная и неопределенная).
Пример 1. Решить с помощью метода Крамера систему уравнений
Решение
, поэтому СЛУ имеет единственное решение.
, .
Тогда ; .
Ответ: система уравнений совместна и определенна, ее единственное решение .
Пример 2. Решить с помощью метода Крамера систему уравнений
.
Решение
Определитель системы равен нулю: , однако один из вспомогательных определителей не равен нулю: , значит, СЛУ не имеет решений, то есть СЛУ несовместная.
Пример 3. Решить с помощью метода Крамера систему уравнений
Решение
, , .
Поэтому система имеет бесконечно много решений.
Разделив коэффициенты 2-го уравнения на 3, получим: Оставим только одно из этих уравнений: .
Выразим через : , значение – любое действительное число. Это и есть выражение для общего решения СЛУ. Ответ можно записать так: , где .
Придавая различные значения, будем получать бесконечное множество частных решений. Например, при получим и первое частное решение . При получим и второе частное решение , и так далее.
2.2. Число уравнений и неизвестных равно 3
Рассмотрим СЛУ
Вычисляются определители:
, ,
, .
1. Если , то система имеет единственное решение, которое находится по формулам Крамера:
, .
2. Если , а хотя бы один из определителей , , отличен от нуля, то система не имеет решений.
3.Если , то система имеет бесконечно много решений.
Пример 4. Решить систему линейных уравнений .
Составим определитель из коэффициентов при неизвестных и вычислим его: ,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители и значения неизвестных.
Ответ: Система совместная и определенная, единственное решение .
Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера.
Пример 5. Решить СЛУ
Решение
Вычислим определитель системы:
Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений.
Отбросив третье уравнение, получим равносильную систему двух уравнений с тремя неизвестными:
Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю.
Например, коэффициенты при и образуют определитель . Поэтому оставим в левой части уравнений слагаемые с и , а слагаемые с перенесем в правую часть с противоположным знаком.
Неизвестное назовем свободным, а неизвестные и – базисными неизвестными.
Запишем систему в виде и применим к ней правило Крамера:
;
Выражение
–
общее решение неопределенной СЛУ, где – любое действительное число.
Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение.
Например, пусть , тогда ; тогда частное решение . И так далее.
Контрольные вопросы
Запишите общий вид системы 2 линейных уравнений с тремя неизвестными.
Что называется решением СЛУ?
Что значит «решить систему линейных уравнений»?
Какие системы линейных уравнений называются совместными и несовместными?
При каком условии система линейных уравнений с неизвестными имеет единственное решение?
Напишите формулы Крамера для решения системы линейных уравнений. В каком случае они применимы?
Как, зная общее решение, записать частное решение неопределенной системы?
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее. Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведение записей на по каждой из трех диагоналей (нижний левый верхний правый).Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]
- Дополните [латекс] A [/ латекс] первыми двумя столбиками.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ конец {массив} | \ begin {массив} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \ begin {array} {c } {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {array} | [/ latex]
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали.Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Рисунок 2
Алгебра выглядит следующим образом:
[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} – {a} _ {3} {b} _ {2} {c} _ {1} – {b} _ {3} {c} _ {2} {a} _ {1} – {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]
Пример 3: Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 из
[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} | \ begin {array} {c} 0 \\ 3 \\ 4 \ end {array} \ begin {array} {c} 2 \\ -1 \\ 0 \ end {array} | \ hfill \\ = 0 \ left (-1 \ right ) \ влево (1 \ вправо) +2 \ влево (1 \ вправо) \ влево (4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ left (1 \ right) -0 \ left (1 \ right) \ left (0 \ right) -1 \ left (3 \ right) \ left (2 \ right) \ hfill \\ = 0 + 8 + 0 + 4 – 0-6 \ hfill \\ = 6 \ hfill \ end {array} [/ latex]
Попробуй 2
Найдите определитель матрицы 3 × 3.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]
Вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] \ text {3} \ text {} \ times \ text {} 3 [/ латексные] матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными .Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что детерминант равен нулю, правило Крамера не дает указания на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
Рисунок 3
[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]
где
Рисунок 4
Если мы записываем определитель [latex] {D} _ {x} [/ latex], мы заменяем столбец [latex] x [/ latex] на столбец констант.Если мы пишем определитель [latex] {D} _ {y} [/ latex], мы заменяем столбец [latex] y [/ latex] постоянным столбцом. Если мы пишем определитель [latex] {D} _ {z} [/ latex], мы заменяем столбец [latex] z [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Пример 4: Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x – 2y + z = -5 \\ x + 3y – 2z = 14 \ end {array} [/ latex]
Решение
Используйте правило Крамера.
[латекс] D = | \ begin {array} {ccc} 1 & 1 & -1 \\ 3 & -2 & 1 \\ 1 & 3 & -2 \ end {array} |, {D} _ {x} = | \ begin { array} {ccc} 6 & 1 & -1 \\ -5 & -2 & 1 \\ 14 & 3 & -2 \ end {array} |, {D} _ {y} = | \ begin {array} {ccc} 1 & 6 & -1 \\ 3 & -5 & 1 \\ 1 & 14 & -2 \ end {array} |, {D} _ {z} = | \ begin {array} {ccc} 1 & 1 & 6 \\ 3 & -2 & -5 \\ 1 & 3 & 14 \ end {array} | [/ latex]
Затем,
[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = – 2 \ hfill \ end {array} [/ latex]
Решение [латекс] \ left (1,3, -2 \ right) [/ latex].
Попробовать 3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс] \ begin {array} {r} \ hfill x – 3y + 7z = 13 \\ \ hfill x + y + z = 1 \\ \ hfill x – 2y + 3z = 4 \ end {array} [/ латекс]
Пример 5: Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 3x – 2y = 4 \ text {} \ left (1 \ right) \\ 6x – 4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ latex]
Решение
Начнем с нахождения определителей [латекс] D, {D} _ {x}, \ text {и} {D} _ {y} [/ latex].
[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс].
- Добавьте результат к уравнению [латекс] \ left (2 \ right) [/ latex].
[латекс] \ begin {array} \ text {} \ hfill − 6x + 4y = −8 \\ \ hfill6x − 4y = 0 \\ \ hfill \ text {_____________} \\ \ hfill 0 = 8 \ end { array} [/ latex]
Получаем уравнение [латекс] 0 = -8 [/ латекс], которое неверно.Следовательно, у системы нет решения. График системы показывает две параллельные линии.
Рисунок 5
Пример 6. Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
[латекс] \ begin {array} {rr} \ hfill x – 2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y – 2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x – 4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]
Решение
Давайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.
[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]
Затем,
[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) – \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ left (3 \ right) \ left (-2 \ right) = 0 [/ латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс] и добавьте результат к уравнению (3):
[латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y – 6x = 0 \\ \ hfill 2x – 4y + 6z = 0 \ end {array}} {0 = 0} [/ latex ]
- Получение ответа [latex] 0 = 0 [/ latex], утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Рисунок 6
Правило Крамера: метод определителей
Содержание | Дом
Урок 35
.Одновременные уравнения: Раздел 2
Вернуться в раздел 1
Правило Крамера: метод определителей
Пример 4. Решите эту систему одновременных уравнений:
| 1) | 3 x | + | 4 y | = | 19 |
| 2) | 2 x | – | y | = | 9 |
Решение .Если мы сложим уравнения как есть, ни одно из неизвестных не сократится. Теперь, если бы коэффициент при y в уравнении 2) был равен −4, тогда y были бы сокращены. Поэтому мы расширим нашу стратегию следующим образом:
Сделайте одну пару коэффициентов отрицательными друг друга – умножив
обеих сторон уравнения на одно и то же число, . После добавления уравнений это неизвестное будет удалено.
Чтобы получить коэффициенты 4 и −4 при y , умножим обе части уравнения 2) на 4:
.| 1) | 3 x | + | 4 y | = | 19 | 3 x | + | 4 y | = | 19 | |
| 2) | 2 x | – | y | = | 9 | 8 x | – | 4 y | = | 36 | |
| 11 x | = | 55 | |||||||||
| x | = | 55 11 | |||||||||
| x | = | 5 | |||||||||
Число 4 над стрелкой в уравнении 2) означает, что обе части этого уравнения были умножены на 4.Уравнение 1) не изменилось.
Чтобы найти y , подставьте x = 5 в любое из исходных уравнений. В уравнении 1):
| 3 · 5 + 4 y | = | 19 |
| 4 y | = | 19–15 |
| 4 y | = | 4 |
| y | = | 1 |
Решение (5, 1).
Студент всегда должен проверять решение, заменяя x и y на (5, 1) в исходных уравнениях.
Пример 5. Решить одновременно:
| 1) | 3 x | + | 2 y | = | −2 |
| 2) | 2 x | + | 5 y | = | −5 |
Решение .Мы должны сделать одну пару коэффициентов отрицательной по отношению друг к другу. В этом примере мы должны решить, какие из неизвестных нужно исключить: x или y . В любом случае мы сделаем новые коэффициенты наименьшим общим кратным (НОК) исходных коэффициентов, но с противоположными знаками.
Таким образом, если мы исключим x , мы получим новые коэффициенты 6 и −6. (НОК 3 и 2 равно 6.) Хотя, если мы исключим y , мы сделаем их новые коэффициенты 10 и -10.(НОК 2 и 5 равно 10.)
Давайте выберем исключение x :
| 1) | 3 x | + | 2 y | = | −2 | 6 x | + | 4 y | = | −4 | |
| 2) | 2 x | + | 5 y | = | −5 | −6 х | – | 15 y | = | 15 | |
| ________________________________________________________________________ | |||||||||||
| – | 11 y | = | 11 | ||||||||
| y | = | -1. | |||||||||
Уравнение 1) было умножено на 2. Уравнение 2) было умножено на −3 – потому что мы хотим сделать эти коэффициенты 6 и −6, так что при сложении y отменяется.
Чтобы найти x , мы подставим y = −1 в исходное уравнение 1):
| 3 х + 2 (-1) | = | −2 |
| 3 x -2 | = | −2 |
| 3 x | = | 0 |
| x | = | 0 |
Решение: (0, −1).
Проблема 3. Решайте одновременно.
| 1) | 2 х | + | 3 y | = | 13 |
| 2) | 5 х | – | y | = | 7 |
Чтобы отменить y , умножьте уравнение 2) на 3:
| 1) | 2 x | + | 3 y | = | 13 | 2 x | + | 3 y | = | 13 | |
| 2) | 5 x | – | y | = | 7 | 15 x | – | 3 y | = | 21 | |
| ________________________________________________________________________ | |||||||||||
| 17 x | = | 34 | |||||||||
| x | = | 2 | |||||||||
Решить для y :
Подставьте x = 2 в одно из исходных уравнений.
В уравнении 1:
| 2 · 2 + 3 y | = | 13 |
| 4 + 3 y | = | 13 |
| 3 y | = | 9 |
| y | = | 3 |
Решение (2, 3).
Проблема 4. Решайте одновременно.
| 1) | х | + | 2 y | = | -1 |
| 2) | 2 х | – | 3 y | = | 5 |
Чтобы уменьшить x , умножьте уравнение 1) на −2:
| 1) | x | + | 2 y | = | -1 | −2 x | – | 4 y | = | 2 | |
| 2) | 2 x | – | 3 y | = | 5 | 2 x | – | 3 y | = | 5 | |
| ________________________________________________________________________ | |||||||||||
| – | 7 y | = | 7 | ||||||||
| y | = | -1 | |||||||||
Чтобы найти x :
Подставим y = −1 в одно из исходных уравнений.
В уравнении 1:
| х + 2 (-1) | = | -1 |
| x -2 | = | -1 |
| x | = | -1 + 2 |
| x | = | 1 |
Решение: (1, −1).
Мы могли бы исключить y , умножив уравнение 1) на 3 и уравнение 2) на 2.
Задача 5. Решить одновременно:
| 1) | 3 x | – | 4 y | = | 1 |
| 2) | 2 х | + | 3 y | = | 12 |
Чтобы отменить y :
Умножьте уравнение 1) на 3 и уравнение 2) на 4:
.| 1) | 3 x | – | 4 y | = | 1 | 9 x | – | 12 y | = | 3 | |
| 2) | 2 x | + | 3 y | = | 12 | 8 x | + | 12 y | = | 48 | |
| ________________________________________________________________________ | |||||||||||
| 17 x | = | 51 | |||||||||
| x | = | 51 17 | |||||||||
| x | = | 3 | |||||||||
Решить для y :
Подставьте x = 3 в одно из исходных уравнений.
В уравнении 2 (поскольку знак y уже положительный):
| 2 · 3 + 3 y | = | 12 |
| 6 + 3 y | = | 12 |
| 3 y | = | 6 |
| y | = | 2 |
Решение (3, 2).
Задача 6. Решить одновременно:
| 1) | 3 x | + | 2 y | = | −4 |
| 2) | 2 х | + | 5 y | = | 1 |
Чтобы отменить x :
Умножьте уравнение 1) на 2 и уравнение 2) на −3:
.| 1) | 3 x | + | 2 y | = | −4 | 6 x | + | 4 y | = | −8 | |
| 2) | 2 x | + | 5 y | = | 1 | −6 x | – | 15 y | = | −3 | |
| ________________________________________________________________________ | |||||||||||
| – | 11 y | = | −11 | ||||||||
| y | = | 1 | |||||||||
Чтобы найти x :
Подставляем y = 1 в одно из исходных уравнений.
В уравнении 1:
| 3 x + 2 · 1 | = | −4 |
| 3 x + 2 | = | −4 |
| 3 x | = | −4-2 |
| 3 x | = | −6 |
| x | = | −2 |
Решение (−2, 1).
Мы могли бы исключить y , умножив уравнение 1) на 5 и уравнение 2) на −2.
Задача 7. Решить одновременно:
| 1) | 5 х | + | 3 y | = | −11 |
| 2) | 2 х | + | 4 y | = | −10 |
Чтобы отменить x :
Умножьте уравнение 1) на 2 и уравнение 2) на −5:
.| 1) | 5 x | + | 3 y | = | −11 | 10 x | + | 6 y | = | −22 | |
| 2) | 2 x | + | 4 y | = | −10 | −10 x | – | 20 y | = | 50 | |
| ________________________________________________________________________ | |||||||||||
| – | 14 y | = | 28 | ||||||||
| y | = | −2 | |||||||||
Чтобы найти x :
Подставляем y = −2 в одно из исходных уравнений.
В уравнении 1:
| 5 х + 3 (-2) | = | −11 |
| 5 x -6 | = | −11 |
| 5 x | = | −11 + 6 |
| 5 x | = | −5 |
| x | = | -1 |
Решение: (−1, −2).
Мы могли бы исключить y , умножив уравнение 1) на 4 и уравнение 2) на −3.
Правило Крамера: метод определителей
Система двух уравнений с двумя неизвестными имеет следующий вид:
и – это коэффициенты x . b являются коэффициентами y . Ниже приводится матрица этих коэффициентов.
Число a 1 b 2 – b 1 a 2 называется определителем этой матрицы.
| дет | = | a 1 b 2 – b 1 a 2 |
Обозначим этот определитель через D.
Теперь рассмотрим эту матрицу, в которой c заменяют коэффициенты x :
Тогда определитель этой матрицы, которую мы назовем D x , равен
c 1 b 2 – b 1 c 2
И рассмотрим эту матрицу, в которой c заменяют коэффициенты y :
Определитель этой матрицы – D y – равен
a 1 c 2 – c 1 a 2
Правило Крамера гласит следующее:
В каждой системе двух уравнений с двумя неизвестными
, в которой определитель D не равен 0,
| x | = | D x D |
| y | = | D y D |
Пример.Используйте правило Крамера для решения этой системы уравнений (Задача 7):
| 5 x | + | 3 y | = | −11 |
| 2 x | + | 4 y | = | −10 |
Решение .
| Д | = | дет | = | 5 · 4 – 3 · 2 | |
| = | 20–6 | ||||
| = | 14. | ||||
| D x | = | дет | = | −11 · 4 – 3 · −10 | |
| = | −44 + 30 | ||||
| = | −14. | ||||
| D y | = | дет | = | 5 · −10 – (−11) · 2 | |
| = | −50 + 22 | ||||
| = | −28. | ||||
Следовательно,
| x | = | D x D | = | −14 14 | = | -1. |
| y | = | D y D | = | −28 14 | = | −2. |
Проблема. Используйте правило Крамера для решения этих одновременных уравнений.
| 3 x | – | 5 y | = | −31 |
| 2 x | + | y | = | 1 |
| Д | = | дет | = | 3 · 1 – (−5) · 2 | |
| = | 3 + 10 | ||||
| = | 13. | ||||
| D x | = | дет | = | −31 · 1 – (−5) · 1 | |
| = | −31 + 5 | ||||
| = | −26. | ||||
| D y | = | дет | = | 3 · 1 – (−31) · 2 | |
| = | 3 + 62 | ||||
| = | 65. | ||||
Следовательно,
| x | = | D x D | = | −26 13 | = | −2. |
| y | = | D y D | = | 65 13 | = | 5. |
Если определитель D не равен 0, мы говорим, что уравнения линейно независимы . В любой системе линейно независимых уравнений есть одно и только одно решение.
Если определитель D равен 0, то либо 1) нет единственного решения, можно назвать много; или 2) решения нет вообще. В случае 1) уравнения линейно зависимы . Один из них просто кратен другому.Например,
x + y = 3
2 x + 2 y = 6.
В случае 2) уравнения противоречивы .
x + y = 3
x + y = 4.
Раздел 3: Три уравнения с тремя неизвестными
Вернуться в раздел 1
Следующий урок: задачи со словами, которые приводят к одновременным уравнениям
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Правило Крамера
Правило Крамера10. Решить используя правило Крамера
2х + 3у + г = 10 х – у + г = 4 4x – y – 5z = -8Каждое неизвестное будет частным от определителя, полученного подставляя ответы в правые части уравнений для коэффициенты неизвестного, деленные на определитель, образованный принимая коэффициенты в левых частях уравнений.
и
Чтобы оценить детерминанты 3×3, мы сокращаем задачу до нахождение определителей 2×2. Начнем с определителя, которым является во всех низах.
Сначала составьте шахматную доску 3×3 из знаков + и -.
Начало в верхнем левом углу со знаком + и альтернативными знаками в обоих направления.
Затем выберите любую строку или любой столбец.В нашем примере выберем третий ряд. Поскольку не имеет значения, какая строка или столбец, который мы выбираем, в третьей строке больше отрицательных записей, и поэтому будет более поучительным в качестве примера. Умножьте каждую запись в строка или столбец по определителю 2×2, который вы получаете, выбрасывая строку и столбец, в котором мы находим запись.
Если вход происходит с положительной позиции на шахматной доске массив, добавьте товар. Если это происходит с отрицательной позиции, вычесть произведение.
Это дает нам
4 (3 – (-1)) + (2-1) – 5 (-2-3) = 4 (4) + (1) – 5 (-5) = 16 + 1 + 25 = 42Давайте проверим наш результат, расширив средний столбец.
= -3 (-5-4) – (-10-4) + (2-1) = -3 (-9) – (-14) + (1) = 27 + 14 + 1 = 42Вы можете показать это независимо от того, какую строку или столбец вы используете в расширение, вы получите тот же ответ. Важно найти определитель внизу внизу, потому что, если он равен нулю, этот метод не будет работать.Будет какой-то параллелизм с плоскости на графике, и единственного решения не будет. Теперь что у нас есть основания в вычислениях для всех трех неизвестных, расширим верхние детерминанты в каждом случае на верхнюю строку.
= 10 (5 – (-1)) – 3 (-20 – (-8)) + (-4-8)42 = 10 (6) – 3 (-12) + (-12)
42 = 60 + 36-12
42 = 84
42 = 2 = 2 (-20 – (- 8)) – 10 (-5-4) + (-8-16)
42 = 2 (-12) – 10 (-9) + (-24)
42 = -24 + 90-24
42 = 42
42 = 1 = 2 (8 – (- 4)) – 3 (-8-16) + 10 (-1 – (-4))
42 = 2 (12) – 3 (-24) + 10 (3)
42 = 24 + 72 + 30
42 = 126
42 = 3
, и мы получаем тот же ответ, что и с метод замещения, метод сложения, строковые операции, а обратный метод, и этот ответ будет проверить.
верх
TTU Сеть CAE
Приносим извинения за неудобства, но страница, к которой вы пытались получить доступ, находится не по этому адресу. Вы можете использовать приведенные ниже ссылки, чтобы найти то, что вы ищете.
Если вы уверены, что имеете правильный веб-адрес, но столкнулись с ошибкой, пожалуйста, связаться с Администрацией сайта.
Спасибо.
Возможно, вы искали…
- Сеть TTU CAE
- Доступ к файлам вне кампуса
- Безопасный доступ к своим исследованиям или академическим файлам из дома или из любой точки мира.
- Отправка ссылки на личный файл по электронной почте
- Отправьте ссылку на файл в личном веб-пространстве, чтобы избежать превышения квоты электронной почты получателей и других технических проблем.
- Справка и поддержка пользователей
- Файловый сервер CAE Lab
- Введение и документация по файловому серверу CAE Lab.
- Файловый сервер CAE Lab
- В следующем наборе документов подробно описаны возможности файлового сервера CAE Lab и доступ к файлам, хранящимся в университетском городке и за его пределами.
- Подключение к файловому серверу CAE Lab (пользователи Windows в кампусе)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из других мест в университетском городке, если на нем установлена Windows 7…
- Подключение к файловому серверу CAE Lab (пользователи Mac OS X в кампусе)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из других мест в кампусе, если на нем установлена Mac OS X…
- Подключение к файловому серверу CAE Lab (пользователи Windows за пределами кампуса)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из мест за пределами кампуса, если у вас установлена последняя версия…
- Подключение к файловому серверу CAE Lab (пользователи Mac OS X за пределами кампуса)
- Следующие инструкции помогут вам подключиться к центральному файловому серверу CAE Lab из мест за пределами кампуса, если на нем установлена Mac OS X…
- Подключение к файловому серверу CAE Lab (пользователи Unix в кампусе)
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из других мест на территории кампуса, при условии некоторого относительного типа…
(PDF) Сравнение правила Крамера и предлагаемого метода исключения Крамера 2 на 2 для решения систем из трех или более линейных уравнений
Сравнение правила Крамера и предлагаемого метода исключения Крамера 2 × 2
для решения системы трех или более линейных уравнений
DKR Babajee
†
Совет по научным и академическим исследованиям, Союзная сеть по политике, исследованиям и действиям в интересах устойчивого развития (ANPRAS), Маврикий
электронная почта: dkrbabajee @ gmail.com
Abstract
Правило Крамера – это 262-летний подход к решению систем из n линейных уравнений от n переменных. Для системы
из 3 линейных уравнений правило Крамера требует вычисления определителей четырех матриц 3 × 3 (9
определителей матриц 2 × 2 или 9 сомножителей). Метод также не работает, когда определитель матрицы коэффициентов
равен нулю.
В этой работе мы предлагаем метод исключения Крамера 2 × 2, который состоит из решения первых 2 линейных уравнений
с использованием правила Крамера и получения выражений первой и второй переменных через третью переменную
.Подставляя эти выражения в третье уравнение, мы получаем значение третьей переменной, а затем непосредственно получаются
решений других переменных. Таким образом, мы уменьшаем количество определителей
вычислений до 5.
Мы показываем, что предлагаемый нами метод эквивалентен классическому правилу Крамера для решения общих систем линейных уравнений 3
, и его можно использовать для решения систем из 3 линейные уравнения, когда определитель матрицы коэффициентов
3 × 3 равен нулю.Мы показываем на примере, как применить метод исключения Крамера 2 × 2 для системы из n линейных
уравнений, и показываем его преимущество перед классическим правилом Крамера.
Ключевые слова
Правило Крамера, системы линейных уравнений, Детерминанты, метод исключения Крамера 2 × 2.
1 Правило Крамера для решения систем из n линейных уравнений
Правило Крамера [2] обычно преподается на курсах бакалавриата как ценный инструмент для решения систем линейных уравнений.
Правило Крамерса дает явное выражение для решения системы и поэтому является теоретически важным
.Кляйн [6] описал педагогический подход, основанный на правиле Крамера.
Система n линейных уравнений задается формулой
a
1,1
x
1
+ a
1,2
x
2
+ a
1,3
x
3
+ a
1,4
x
4
+ … + a
1, n
x
n
= b
1
, ( 1)
a
2,1
x
1
+ a
2,2
x
2
+ a
2,3
x
3
+ a
2,4
x
4
+… + a
2, n
x
n
= b
2
, (2)
a
3,1
x
1
+ a
3, 2
x
2
+ a
3,3
x
3
+ a
3,4
x
4
+ … + a
3, n
x
n
= b
3
, (3)
a
4,1
x
1
+ a
4,2
x
+ a
4,3
x
3
+ a
4,4
x
4
+… + a
4, n
x
n
= b
4
, (4)
.
.
.
a
n, 1
x
1
+ a
n, 2
x
2
+ a
n, 3
x
3
n, 4x
4
+ … + a
n, n
x
n
= b
n
.(5)
Систему можно записать в матричной форме
Ax = b, (6)
, где
A =
a
1,1
a
1,2
a
1,3
a
1,4
. . . a
1, n
a
2,1
a
2,2
a
2,3
a
2,4
.. . a
2, n
a
3,1
a
3,2
a
3,3
a
3,4
. . . a
3, n
a
4,1
a
4,2
a
4,3
a
4,4
. . . а
4, н
.
.
.
.
.
.
.
.
.
.
.
. . . .
.
.
.
a
n, 1
a
n, 2
a
n, 3
a
n, 4
. . . а
n, n
, x =
000 9000 9000 9000 9000 9000 9000 9000
x
1
x
2
x
3
x
4.
.
.
x
n
000 9000 9000 9000 9000 9000 9000 9000
b
1
b
2
b
3
b
4.
.
.
b
n
Система уравнений 4-го порядка для системы уравнений Крамера 4-го порядка. Правило Крамера
Для того, чтобы освоить этот абзац, вы должны уметь открывать квалификаторы «два на два» и «три на три». Если классификаторы плохие, изучите урок Как вычислить определитель?
Сначала мы более подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными.Зачем? – Ведь простейшую систему можно решить школьным методом, методом сложения семестров!
Дело в том, что даже иногда, но встречается такая задача – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет вам понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом этапе вычисляем определитель, он называется главным определителем системы .
Метод Гаусса.
Если, то у системы есть только решение, и чтобы найти корни, нам нужно вычислить еще два детерминанта:
и
На практике вышеуказанные классификаторы также можно обозначать латинскими буквами.
Находим корни уравнения по формулам:
,
Пример 7
Решаем систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, на справа – десятичные числа с запятой.Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Вы можете попробовать выразить одну переменную через другую, но в этом случае вы, вероятно, получите ужасные причудливые дроби, с которыми крайне неудобно работать, и дизайн решения будет выглядеть просто ужасно. Вы можете умножить второе уравнение на 6 и выполнить почленное вычитание, но здесь будут отображаться те же дроби.
Что делать? В таких случаях на помощь приходят формулы Крамера.
;
;
Ответ :,
Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже часто) для эконометрических задач.
Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательно фрагментом присвоения является следующий фрагмент: «Что означает, что в системе есть только одно решение» … В противном случае рецензент может наказать вас за неуважение к теореме Крамера.
Не лишним будет проверить, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В результате с небольшой ошибкой вы должны получить числа, которые находятся в нужных частях.
Пример 8
Ответ представлен обычными неправильными дробями. Сделайте чек.
Пример для самостоятельного решения (пример окончания и ответ в конце урока).
Теперь перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Найдите главный определитель системы:
Если, то система имеет бесконечно много решений или противоречива (не имеет решения). В этом случае правило Крамера не поможет; вам нужно использовать метод Гаусса.
Если, то система имеет уникальное решение, и чтобы найти корни, мы должны вычислить еще три определителя:
“
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «ходит» слева направо по столбцам главного определителя.
Пример 9
Решите систему, используя формулы Крамера.
Решение : Решим систему, используя формулы Крамера.
, а значит, в системе есть уникальное решение.
Ответ :.
Собственно, и здесь комментировать особо нечего, в виду того, что решение принимается по готовым формулам.Но следует отметить несколько моментов.
Бывает, что в результате вычислений получаются “плохие” несократимые дроби, например :.
Рекомендую следующий алгоритм “лечения”. Если под рукой нет компьютера, делаем так:
1) Возможна ошибка расчета. Как только вы столкнулись с “плохой” дробью, вы должны немедленно проверить , правильно ли переписано условие … Если условие переписано без ошибок, то необходимо пересчитать определители, используя расширение по другой строке ( столбец).
2) Если в результате проверки ошибок не обнаружено, то, скорее всего, в условии задачи была опечатка. В этом случае спокойно и ВНИМАТЕЛЬНО решаем задачу до конца, а потом обязательно проверяем и оформляем на чистую копию после решения. Конечно, проверка дробного ответа – урок неприятный, но это будет обезоруживающий аргумент для учителя, который, ну, любит ставить минус любому подобному бяке. Как работать с дробями, подробно описано в ответе к примеру 8.
Если под рукой есть компьютер, то для его проверки воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до запуска решения), вы сразу увидите промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение матричного метода системы.
Второе замечание. Время от времени встречаются системы, в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении нет переменной, во втором нет переменной.В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– вместо пропущенных переменных ставятся нули.
Кстати, открывать определители с нулями рационально по той строке (столбцу), в которой стоит ноль, так как вычислений гораздо меньше.
Пример 10
Решите систему, используя формулы Крамера.
Это пример самостоятельного решения (образец отделки и ответ в конце урока).
Для случая системы из 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно найти в уроке «Определяющие свойства». Уменьшение порядка определителя – пять определителей 4-го порядка вполне разрешимы. Хотя задание уже довольно напоминает сапог профессора на груди удачливого ученика.
Решение системы с использованием обратной матрицы
Метод обратной матрицы По сути, это частный случай матричного уравнения (см. Пример № 3 указанного урока).
Чтобы изучить этот раздел, вам необходимо уметь расширять определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут предоставлены по пути.
Пример 11
Решите систему с помощью матричного метода
Решение : Давайте запишем систему в матричной форме:
, где
Обратите внимание на систему уравнений и матрицы. По какому принципу мы записываем элементы в матрицы, думаю, все понимают.Единственное замечание: если бы в уравнениях отсутствовали какие-то переменные, то в соответствующие места в матрице пришлось бы ставить нули.
Найдите обратную матрицу по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы.
Сначала мы имеем дело с определителем:
Здесь квалификатор раскрывается в первой строке.
Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно.В этом случае система решается методом исключения неизвестных (метод Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Артикул: Полезно знать значение двойных нижних индексов в линейной алгебре. Первая цифра – это номер строки, в которой расположен этот элемент. Вторая цифра – это номер столбца, в котором расположен этот элемент:
То есть двойной нижний индекс указывает, что элемент находится в первой строке, третьем столбце, и, например, элемент находится в строке 3, столбце 2
По ходу решения подсчета несовершеннолетних лучше расписывать подробно, хотя при определенном опыте их можно приучить считать с ошибками устно.
2. Решение систем уравнений матричным методом (с использованием обратной матрицы).
3. Метод Гаусса для решения систем уравнений.
Метод Крамера.
Метод Крамера используется для решения систем линейных алгебраических уравнений ( SLAU ).
Формулы для примера системы двух уравнений с двумя переменными.
Дано: Решите систему методом Крамера
Переменные NS и на .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы Вычисление определителей.:
Применяем формулы Крамера и находим значения переменных:
и.
Пример 1:
Решите систему уравнений:
относительно переменных NS и на .
Решение:
Замените первый столбец в этом определителе на столбец коэффициентов из правой части системы и найдите его значение:
Проделаем аналогичное действие, заменив второй столбец в первом определителе:
Применимые формулы Крамера и найдем значения переменных:
и.
Ответ:
Комментарий: Этот метод можно использовать для решения систем более высоких измерений.
Комментарий: Если оказывается, что и на ноль делить нельзя, то говорят, что в системе нет единого решения. В этом случае у системы либо бесконечно много решений, либо их нет вовсе.
Пример 2 (бесконечное количество решений):
Решите систему уравнений:
относительно переменных NS и на .
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы – равенство, которое верно для любых значений переменных (потому что 4 всегда равно 4). Итак, осталось только одно уравнение. Это уравнение взаимосвязи между переменными.
Получается, что решением системы является любая пара значений переменных, связанных равенством.
Общее решение будет записано так:
Частные решения могут быть определены путем выбора произвольного значения y и вычисления x с использованием этого равенства связи.
и т. Д.
Таких решений бесконечно много.
Ответ: общее решение
Частное решение:
Пример 3 (решений нет, система несовместима):
Решите систему уравнений:
Решение:
Найдем определитель матрицы, составленной из коэффициентов системы:
Формулы Крамера неприменимы.Решим эту систему методом подстановки
Второе уравнение системы – равенство, что неверно для любых значений переменных (конечно, поскольку -15 не равно 2). Если одно из уравнений системы не выполняется ни при каких значениях переменных, то вся система не имеет решений.
Ответ: решений нет
При количестве уравнений, равном количеству неизвестных с главным определителем матрицы, который не равен нулю, коэффициенты системы (для таких уравнений есть решение и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы отличен от нуля, это означает, что система непротиворечива и имеет одно решение, и его можно найти по формулам Крамера :
где Δ – определитель матрицы системы ,
Δ i – определитель матрицы системы, в которой вместо i -го столбца стоит столбец правых частей.
Когда детерминант системы равен нулю, это означает, что система может стать совместной или несовместимой.
Этот метод обычно используется для небольших систем с большими вычислениями и когда необходимо определить одно из неизвестных. Сложность метода заключается в том, что необходимо вычислить множество детерминант.
Описание метода Крамера.
Имеется система уравнений:
Систему трех уравнений можно решить методом Крамера, который был рассмотрен выше для системы из двух уравнений.
Составим определитель из коэффициентов неизвестных:
Это будет с системным идентификатором … Когда D ≠ 0 , значит система совместима. Теперь составим 3 дополнительных определителя:
,,
Решаем систему формул Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Учитывая систему:
Решим его методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Поскольку Δ ≠ 0, следовательно, по теореме Крамера система непротиворечива и имеет одно решение.Вычисляем дополнительные детерминанты. Определитель Δ 1 получается из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же образом получим определитель Δ 2 из определителя матрицы системы, заменив второй столбец столбцом свободных коэффициентов:
Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера можно использовать для решения системы из такого количества линейных уравнений, в каждом из которых есть неизвестные. Если определитель системы не равен нулю, то в решении можно использовать метод Крамера, если он равен нулю, то нельзя. Кроме того, метод Крамера можно использовать для решения систем линейных уравнений, имеющих единственное решение.
Определение … Определитель, составленный из коэффициентов неизвестных, называется определителем системы и обозначается (дельта).
Детерминанты
получаются заменой коэффициентов соответствующими неизвестными свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, а неизвестное равно отношению определителей. Знаменатель содержит определитель системы, а числитель содержит определитель, полученный из определителя системы заменой коэффициентов в этой неизвестной на свободные члены.Эта теорема верна для системы линейных уравнений любого порядка.
Пример 1. Решите систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятор, решающий метод Крамера.
Три случая решения систем линейных уравнений
Как видно из теоремы Крамера , при решении системы линейных уравнений могут иметь место три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система последовательная и определенная)
Второй случай: система линейных уравнений имеет бесконечное число решений
(система непротиворечивая и неопределенная)
**,
тех.коэффициенты при неизвестных и свободных членах пропорциональны.
Третий случай: система линейных уравнений не имеет решений
(система несовместима)
Итак, система m линейных уравнений с n переменными называется несовместимой, , если у нее нет решений, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определенным , а более одного – неопределенным .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основе теоремы Крамера
………….
,
где
–
системный определитель. Остальные определители получаем заменой столбца с коэффициентами соответствующей переменной (неизвестной) свободными членами:
Пример 2.
.
Следовательно, система определенная. Чтобы найти ее решение, вычислим определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие элементы равны нулю! Это следующий пример.
Пример 3. Решите систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Внимательно посмотрите на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решение, вычислим определители для неизвестных
По формулам Крамера находим:
Итак, решение системы (2; -1; 1).
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
Вернуться к началу страницы
Продолжаем решать системы по методу Крамера вместе
Как уже упоминалось, если определитель системы равен нулю, а определители для неизвестных не равны нулю, система несовместима, то есть не имеет решений. Проиллюстрируем это следующим примером.
Пример 6. Решите систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определена, либо несовместна, то есть не имеет решений. Для большей точности вычислим определители неизвестных
Определители для неизвестных не равны нулю, следовательно, система непоследовательна, то есть не имеет решений.
Чтобы проверить решения систем уравнений 3 X 3 и 4 X 4, вы можете использовать онлайн-калькулятор, который решает метод Крамера.
В задачах о системах линейных уравнений встречаются и такие, в которых помимо букв, обозначающих переменные, есть еще и другие буквы. Эти буквы представляют собой определенное число, чаще всего действительное число. На практике поисковые задачи приводят к таким уравнениям и системам уравнений общих свойств любых явлений и объектов.То есть изобрели ли вы какой-либо новый материал или устройство, и для описания его свойств, которые являются общими независимо от размера или количества экземпляров, необходимо решить систему линейных уравнений, где вместо некоторых коэффициентов переменных есть буквы. За примерами далеко ходить не надо.
Следующий пример предназначен для аналогичной задачи, только количество уравнений, переменных и букв, обозначающих какое-то действительное число, увеличивается.
Пример 8. Решите систему линейных уравнений методом Крамера:
Решение.Находим определитель системы:
Найдите определители неизвестных
Пусть система линейных уравнений содержит столько уравнений, сколько независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратичными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Обозначим его греческой буквой D. Таким образом,
.(1,6)
Если главным определителем является произвольный ( j -й) столбец, заменим его столбцом свободных членов системы (1.5), то мы можем получить еще n вспомогательных определителей:
( j = 1, 2,…, n ). (1,7)
Правило Крамера Решение квадратных систем линейных уравнений выглядит следующим образом. Если главный определитель D системы (1.5) отличен от нуля, то система имеет единственное решение, которое находится по формулам:
(1.8)
Пример 1.5. Использование метода Крамера для решения системы уравнений
.
Вычислим главный определитель системы:
Поскольку D¹0, система имеет единственное решение, которое находится по формулам (1.8):
Таким образом,
Матричные операции
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2.Чтобы умножить матрицу на число, нужно умножить все ее элементы на это число. То есть
. (1,9)
Пример 1.6. .
Добавление матриц.Эта операция вводится только для матриц одного порядка.
Чтобы сложить две матрицы, необходимо добавить соответствующие элементы другой матрицы к элементам одной матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если количество столбцов в матрице A совпадает с количеством строк в матрице V , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы A габаритами м ´ n на матрицу V габаритами n ´ k получаем матрицу С габаритами м ´ k … Причем элементы матрицы СО вычисляются по формулам:
Задача 1.8. Найдите, если возможно, произведение матриц AB и BA :
Решение. 1) Чтобы найти работу AB , нужно строки матрицы A умножить на столбцы матрицы B :
2) Графическое изображение BA не существует, так как количество столбцов в матрице B не совпадает с количеством строк в матрице A .
Обратная матрица. Матричное решение систем линейных уравнений
Матрица A – 1 называется обратной квадратной матрицы A , если выполняется равенство:
, где через I обозначает единичную матрицу того же порядка, что и матрица A :
.
Чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы ее определитель был ненулевым. Обратная матрица находится по формуле:
, (1.13)
, где A ij – алгебраические дополнения к элементам a ij матриц A (обратите внимание, что алгебраические дополнения к строкам матрицы A расположены в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A – 1 к матрице
.
Находим обратную матрицу по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдите дет. A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Поскольку определитель исходной матрицы отличен от нуля, обратная матрица существует.
1) Найдите алгебраические дополнения A ij :
Для удобства поиска обратной матрицы мы поместили алгебраические добавления к строкам исходной матрицы в соответствующие столбцы.
Из полученных алгебраических дополнений составляем новую матрицу и делим ее на определитель det A … Таким образом, получаем обратную матрицу:
Квадратичные системы линейных уравнений с ненулевым главным определителем могут быть решены с помощью обратной матрицы. Для этого система (1.5) записывается в матричном виде:
где
Умножая обе части равенства (1.14) слева на A – 1, получаем решение системы:
, где
Таким образом, чтобы найти решение квадратной системы, нужно найти матрицу, обратную основной матрице системы, и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решите систему линейных уравнений
с использованием обратной матрицы.
Решение. Запишем систему в матричном виде :,
где – основная матрица системы, – столбец неизвестных и – столбец свободных элементов. Поскольку основной определитель системы, то основная матрица системы A имеет обратную матрицу A -1. Чтобы найти обратную матрицу A -1, вычислим алгебраические дополнения ко всем элементам матрицы A :
Из полученных чисел составляем матрицу (причем алгебраические дополнения к строкам матрицы A записываем в соответствующие столбцы) и делим ее на определитель D.Таким образом, мы нашли обратную матрицу:
Находим решение системы по формуле (1.15):
Таким образом,
Решение систем линейных уравнений методом обычных жордановых исключений
Пусть дана произвольная (не обязательно квадратичная) система линейных уравнений:
(1,16)
Требуется найти решение системы, т.е. набор переменных, удовлетворяющий всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесконечное количество решений. У нее также может вообще не быть решений.
При решении таких задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называют методом обычных исключений Джордана. Суть этого метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы.В результате получается система, которая содержит на одно уравнение и на одну переменную меньше, чем исходная система. Запоминается уравнение, из которого была выражена переменная.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. Например, в процессе исключения неизвестных некоторые уравнения могут превратиться в истинные тождества. Такие уравнения исключаются из системы, так как они выполняются при любых значениях переменных и, следовательно, не влияют на решение системы.Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может быть выполнено ни при каких значениях переменных (например), то мы заключаем, что система не имеет решения.
Если в процессе решения не возникло противоречивых уравнений, то одна из оставшихся в нем переменных находится из последнего уравнения. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются другие переменные, то они считаются параметрами, и переменная, выраженная через них, будет функцией этих параметров.Потом так называемый «реверс». Найденная переменная подставляется в последнее запомненное уравнение и находится вторая переменная. Затем две найденные переменные подставляются в предпоследнее запомненное уравнение, и находится третья переменная, и так далее до первого запомненного уравнения.
В результате получаем решение системы. Это решение будет уникальным, если найденные переменные являются числами. Если первая найденная переменная, а затем все остальные зависят от параметров, то система будет иметь бесконечное количество решений (каждому набору параметров соответствует новое решение).Формулы, позволяющие найти решение системы в зависимости от определенного набора параметров, называются общим решением системы.
Пример 1.11.
х
Запомнив первое уравнение и сократив аналогичные члены во втором и третьем уравнениях, мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Давайте вспомним второе уравнение, и из первого находим z :
Делая обратный ход, последовательно находим y и z … Для этого сначала подставляем в последнее запомненное уравнение, откуда находим y :
.
Затем подставляем в первое запомненное уравнение, откуда находим x :
Задача 1.12. Решите систему линейных уравнений, исключив неизвестные:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Давайте вспомним первое уравнение
В этой системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получаем, что 14 = 17. Это равенство не выполняется ни при каких значениях переменных x , y и z … Следовательно, система (1.17) несовместима. , то есть не имеет решения.
Предлагаем читателям самостоятельно проверить, что основной детерминант исходной системы (1.17) равен нулю.
Рассмотрим систему, которая отличается от системы (1.17) только одним свободным членом.
Задача 1.13. Решите систему линейных уравнений, исключив неизвестные:
. (1.18)
Решение. Как и раньше, мы выражаем из первого уравнения переменную x и подставляем ее во второе и третье уравнения:
.
Давайте вспомним первое уравнение и дадим аналогичные члены во втором и третьем уравнениях.Заходим в систему:
Выражая y из первого уравнения и подставляя его во второе уравнение, получаем тождество 14 = 14, которое не влияет на решение системы, а значит, может быть исключено из системы.
В последнем запомненном равенстве переменная z будет считаться параметром. Мы верим. Тогда
Подставьте y и z в первое запомненное равенство и найдите x :
.
Таким образом, система (1.18) имеет бесконечное множество решений, и любое решение можно найти по формулам (1.19), выбрав произвольное значение параметра t :
(1.19)
Итак, решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. Д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
В случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обычных жордановых исключений кажется громоздким.Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы за один шаг в общем виде и сформулировать решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где xj – независимые (искомые) переменные, a ij – постоянные коэффициенты
( i = 1, 2,…, m ; j = 1, 2,…, № ).Правая часть системы y i ( i = 1, 2,…, m ) может быть как переменными (зависимыми), так и константами. Требуется найти решения этой системы, исключив неизвестные.
Рассмотрим следующую операцию, в дальнейшем называемую «один шаг обычных исключений Джордана». Из произвольного ( r -го) равенства выразим произвольную переменную ( x s ) и подставим все остальные равенства. Конечно, это возможно только при и ¹ 0.Коэффициент и RS называют разрешающим (иногда направляющим или основным) элементом.
Получаем следующую систему:
. (1,21)
Далее из s -го равенства системы (1.21) находим переменную x s (после того, как найдены остальные переменные). S -я строка запоминается и в дальнейшем исключается из системы. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты получившейся системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть так:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1,23)
Теперь вычислим новые коэффициенты b ij ( i ¹ r ) произвольного уравнения.Для этого подставим переменную, выраженную в (1.22) x s v i -ое уравнение системы (1.20):
Приведя аналогичные термины, получаем:
(1.24)
Из равенства (1.24) получаем формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обычных жордановых исключений формализуется в виде таблиц (матриц).Эти таблицы называются «жордановы».
Таким образом, задача (1.20) связана со следующей таблицей Иордании:
Таблица 1.1
| x 1 | x 2 | … | х | … | х | … | х | |
| y 1 = | a 11 | a 12 | a 1 j | a 1 s | a 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | a i 1 | a i 2 | a ij | а это | а в | |||
| ………………………………………………………………… .. | ||||||||
| г = | и 1 | и 2 | RJ | а RS | а рн | |||
| …………………………………………………………………. | ||||||||
| да нет = | а м 1 | а м 2 | а mj | а мс | а мин |
Jordan Таблица 1.1 содержит левый столбец заголовка, в котором записаны правые части системы (1.20), и верхний ряд заголовка, в котором записаны независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу A на матрицу, состоящую из элементов верхней строки заголовка, то получится матрица, состоящая из элементов левого столбца заголовка. То есть, по сути, жорданова таблица – это матричная запись системы линейных уравнений:. В этом случае системе (1.21) соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | х | … | г | … | х | |
| y 1 = | б 11 | б 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | б это | б в | |||
| ………………………………………………………………… .. | ||||||||
| x s = | b r 1 | b r 2 | B RJ | b rs | млрд р-н | |||
| …………………………………………………………………. | ||||||||
| да n = | мм 1 | мм 2 | b mj | b мс | млрд мин |
Разрешающий элемент a RS выделим жирным шрифтом. Напомним, что для того, чтобы имел место один шаг жордановых исключений, разрешающий элемент должен быть ненулевым. Строка в таблице, содержащая разрешающий элемент, называется разрешающей строкой.Столбец, содержащий разрешающий элемент, называется разрешающим столбцом. При переходе от этой таблицы к следующей таблице одна переменная ( xs ) из верхней строки заголовка таблицы перемещается в левый столбец заголовка и, наоборот, один из свободных членов системы ( г. г.) из левый верхний столбец таблицы перемещается в верхний верхний ряд.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), что следует из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным:
2. Остальные элементы разрешительной линии разделяются разрешающим элементом и меняют знак на противоположный:
3. Остальные элементы разрешающей колонки делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последнюю формулу легко запомнить, если вы заметите, что элементы, составляющие дробь, находятся на пересечении i -й и r -ой строк и j -го и s -го столбцов (разрешающая строка, разрешающий столбец, а также строка и столбец, на пересечении которых находится пересчитываемый элемент).Точнее, при запоминании формулы может использоваться следующая диаграмма:
Принимая первый шаг исключения Jordan, любой элемент таблицы 1.3, расположенный в столбцах x 1,…, x 5 (все указанные элементы не равны нулю). Вы должны не только выбрать разрешающий элемент в последнем столбце, потому что вам нужно найти независимые переменные x 1,…, x 5.Выберем, например, коэффициент 1 с переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент выделен жирным шрифтом). В таблице 1.4 переменная x 3 из верхней строки заголовка заменяется константой 0 левого столбца (третья строка). В этом случае переменная x 3 выражается через остальные переменные.
Строка x 3 (Таблица 1.4) после запоминания может быть исключена из Таблицы 1.4.Третий столбец с нулем в верхней строке заголовка также исключен из таблицы 1.4. Дело в том, что независимо от коэффициентов этого столбца b i 3 все соответствующие члены каждого уравнения 0 b i 3 системы будут равны нулю. Поэтому эти коэффициенты можно не указывать. Исключив одну переменную x 3 и запомнив одно из уравнений, приходим к системе, соответствующей таблице 1.4 (с перечеркнутой линией x 3). Выбор по таблице 1.4 как разрешающий элемент b 14 = -5, перейдите к таблице 1.5. В таблице 1.5 мы запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем вверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = – 3 + 2 x 5.
Последовательно подставляя уже найденные переменные в сохраненные строки, находим оставшиеся переменные:
Таким образом, в системе есть бесчисленное множество решений. Переменная x 5, можно присвоить произвольные значения.Эта переменная действует как параметр x 5 = t. Мы доказали совместимость системы и нашли ее общее решение:
x 1 = – 3 + 2 т
x 2 = – 1-3 т
x 3 = – 2 + 4 т . (1,27)
x 4 = 4 + 5 т
x 5 = т
Придавая параметру t разные значения, мы получаем бесчисленное множество решений исходной системы.Так, например, решение системы – это следующий набор переменных (- 3; – 1; – 2; 4; 0).
Правило Крамера
Правило Крамера использует детерминанты для
решать системы линейных уравнений
. Рассмотрим систему двух линейных уравнений от двух переменных:
а
Икс
+
б
у
знак равно
c
d
Икс
+
е
у
знак равно
ж
Используя метод линейной комбинации, вы можете убедиться, что
Икс знак равно c е – б ж а е – б d а также у знак равно а ж – c d а е – б d если а е – б d ≠ 0
Обратите внимание, что знаменатели равны детерминант коэффициентов.
D знак равно | а б d е |
Числители равны определителям D Икс а также D у куда
D Икс знак равно | c б ж е | а также D у знак равно | а c d ж |
D Икс формируется заменой столбца коэффициентов Икс в D со столбцом констант и D у формируется заменой столбца коэффициентов у в D со столбцом констант.
Путем подстановки
Икс знак равно | c б ж е | | а б d е | знак равно D Икс D а также у знак равно | а c d ж | | а б d е | знак равно D у D .
Пример:
Используйте определители для решения системы уравнений: { Икс – 5 у знак равно 2 2 Икс + у знак равно 4
Икс знак равно D Икс D знак равно | 2 – 5 4 1 | | 1 – 5 2 1 | знак равно 2 + 20 1 + 10 знак равно 22 11 знак равно 2 у знак равно D у D знак равно | 1 2 2 4 | | 1 – 5 2 1 | знак равно 4 – 4 1 + 10 знак равно 0 11 знак равно 0
Следовательно, решение ( 2 , 0 ) .
Определители также можно использовать для решения системы линейных уравнений с тремя переменными:
а 1 Икс + б 1 у + c 1 z знак равно d 1 а 2 Икс + б 2 у + c 2 z знак равно d 2 а 3 Икс + б 3 у + c 3 z знак равно d 3
Потом,
D знак равно | а 1 б 1 c 1 а 2 б 2 c 2 а 3 б 3 c 3 | ≠ 0 D Икс знак равно | d 1 б 1 c 1 d 2 б 2 c 2 d 3 б 3 c 3 | D у знак равно | а 1 d 1 c 1 а 2 d 2 c 2 а 3 d 3 c 3 | D z знак равно | а 1 б 1 d 1 а 2 б 2 d 2 а 3 б 3 d 3 |
А также,
Икс знак равно D Икс D , у знак равно D у D , z знак равно D z D .
