Главная
Как решать пределы функций: Как решать пределы для чайников, примеры решений

Как решать пределы функций: Как решать пределы для чайников, примеры решений

Содержание

Как решать пределы с корнями с примерами решения

Содержание:

  1. Примеры с решением
  2. Раскрытие неопределенностей вида

При вычислении предела вначале проверяют принадлежит ли точка области определения. Если то предел равен значению функции в точке

(это объясняется непрерывностью элементарной функции на своей области определения)

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Примеры с решением

Пример 1:

Вычислить:

a)

б)

в)

Решение:

а)

б)

в)

Правило сохраняет силу, если Запись например, означает, что когда абсолютное значение

неограниченно возрастает, функция стремится к нулю (это ясно из графика функции).

Возможно вам будут полезны данные страницы:

Как решать пределы: пример решения

Пределы для чайников

Уравнение прямой в пространстве

Метод вариации произвольных постоянных

Пример 2:

Найти:

а)

б)

в)

Решение:

а)

б)

в)

Пример 3:

Найти

Решение:

При подстановке в значение функции вместосимвола бесконечности, результат может оказаться не конечным числом. Например:

Что считать ответом в этом случае?

При вычислении подобных пределов пользуются одним из следующих правил (в приводимых ниже формулах с означает число):

Приведенные формулы следуют из соображений здравого смысла. Например, первая из приведенных формул по существу утверждает, что если одна из функций становится очень большой и положительной, а другая ограничена, то сумма их становится очень большой и положительной.

Те же соображения приводят и к формальному доказательству: надо только вместо «очень больших» значений говорить о «больших любого заданного числа».

Применим эти правила для вычисления пределов, которые были оставлены без вычисления:

Соображениями здравого смысла руководствуются и при вычислении пределов от функций при Надо проследить ио графику функции куда стремится значение функции, если аргумент стремится к

Пример 4:

Вычислить:

а)

б)

в)

Решение:

а) При знаменатель неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина бесконечно малой. Произведение бесконечно малой на ограниченную величину (постоянная — частный случай ограниченной еличины) есть величина бесконечно малая, и предел ее при равен нулю. Следовательно,

Этот же ответ получается при применении последнего из приведенных выше правил

б)

в)

Приведенные рассуждения не являются строгими. Однако они вполне достаточны для приложений и интуитивно понятны . Как уже было отмечено ранее, выражение при можно считать равным

Выражение взято в скобки, чтобы подчеркнуть условность записи.

Пример 5:

Найти:

а)

б)

в)

Решение:

а)

б)

в)

Имеются случаи, не охватываемые правилами из предыдущего параграфа. Не существует «общей формулы» для выражения . В самом деле, пусть где —целое число. Частное этих функций. при является частным бесконечно малых. Оно может стремиться к нулю (при), или (при ), или (при ). Поэтому выражение и подобные ему называются неопределенностями. К неопределенностям относятся следующие выражения:

Как для случая неопределенности вида встретившейся при сравнении бесконечно малых, здесь для раскрытия неопределенности уже недостаточно знать лишь пределы функций и а нужно учесть и закон их изменения. Примеры раскрытия неопределенностей приведены ниже.

Пример 6:

Найти

Решение:

Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, поскольку получается неопределенность вида

Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент стремится к своему предельному значению, никогда не принимая этого значения (вспомним, что в определении предела по Коши оэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:

Пример 7:

Найти

Решение:

Пределы числителя и знаменателя при равны нулю

Разложим квадратный трехчлен в числителе на линейные множители по формуле где и – корни трехчлена. Разложив на множители и знаменатель, сократим на получим

Пример 8:

Найти

Решение:

и

Пример 9:

Найти

Решение:

Пределы числителя и знаменателя при равны нулю. Умножим числитель и знаменатель на сопряженный знаменателю множитель и затем, сократив дробь на получим:

Пример 10:

Найти

Решение:

Когда числитель и знаменатель дроби стремятся к нулю, получается неопределенность вида Желая избавится от иррациональности в знаменателе, преобразуем данное выражение:

Перейдя к пределу, получим

В предыдущих примерах неопределенность вида раскрывалась путем выделения в числителе и знаменателе общего множителя. Однако этот прием «срабатывает» не во всех случаях. Например, в случае предела неясно, как выделить общий множитель. Этот предел можно вычислить с помощью принципа замены эквивалентных. Вычислим этот предел другим способом — сведением к пределу

называемому 300 лет назад первым замечательным пределом. Доказательство равенства нетрудно и опирается оно не приводится.

Заметим, что выражение взято в скобки, поскольку писать нельзя! Скобки в записи подчеркивают ее условность. Равенство означает, что в данном конкретном случае неопределенность раскрыта и значение соответствующего предела равно единице.

Пример 11:

Найти

Решение:

Пример 12:

Найти

Решение:

Пример 13:

Найти

Решение:

При числитель и знаменатель — величины бесконечно большие. Поэтому при непосредственной подстановке символа вместо получаем выражение которое представляет собой неопределенность. Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):

Пример 14:

Найти

Решение:

При непосредственной подстановке символа вместо получаем неопределенность вида Для вычисления предела этой функции нужно и числитель и знаменатель разделить на (наивысшую степень аргумента в знаменателе):

(при слагаемые — величины бесконечно малые и, следовательно, их пределы равны нулю).

Пример 14:

Наити

Решение:

Вообще, предел отношения полиномов при равен отношению коэффициентов при старших членах, если степени числителя и знаменателя одинаковы, и равен нулю или бесконечности, если степень числителя соответственно меньше или больше знаменателя.

Пример 15:

Найти

Решение:

Пример 16:

Найти

Решение:

В подобных примерах полезно иметь в виду, что функция где — многочлен степени стремится к бесконечности так же, как и функция Это позволяет выделить высшую степень входящую в данное выражение, и разделить числитель и знаменатель на эту степень В данном примере надо делить на

Неопределенности вида и путем преобразования можно привести к неопределенности вида или которая раскрывается уже известными способами.

Покажем на примерах, как находятся такие пределы.

Пример 17:

Найти

Решение:

Произведем вычитание дробей, получим

Пример 18:

Найти

Решение:

Пример 19:

Найти

Решение:

(сделали замену ).

Пример 20:

Найти

Ответ:

Раскрытие неопределенностей вида

Рассмотрим последовательность где

Может показаться, что неограниченное возрастание показателя степени должно повлечь неограниченное возрастание целочисленной функции Но рост показателя компенсируется тем, что основание стремится к В результате последовательность оказывается возрастающей и ограниченной. А всякая ограниченная и возрастающая последовательность имеет конечный предел. Предел, к торому стремится при обозначается

Обозначением числа и его широким применением во многих вопросах математики мы обязаны Эйлеру. Это число иррационально и с точностью до шестой значащей цифры равно

Функция имеет пределом число не только при целочисленных значениях но и тогда, когда стремится к бесконечности, пробегая числовую прямую непрерывно. Более того, аргументможет принимать как положительные, так и отрицательные значения, лишь бы неограниченно росло по абсолютному значению. Чтобы отмстить это обстоятельство, заменим букву буквой и напишем:

или короче

Этот предел часто используется в математике для раскрытия неопределенности и именуется вторым замечательным пределом

Пример 21:

Найти пределы:

а)

б)

Решение:

а)

б)

Пример 22:

Найти пределы

а)

б)

Решение:

а) При основание степени стремится к единице, а показатель стремится к бесконечности. Следовательно, имеем неопределенность вида Представим основание в виде суммы единицы и некоторой бесконечно малой величины:

тогда

б)

Число во многих случаях выгодно брать за основание логарифмов. Логарифм от с основанием носит название натурального логарифма и обозначается Показательная функция широко используется в науке и называется экспоненциальной.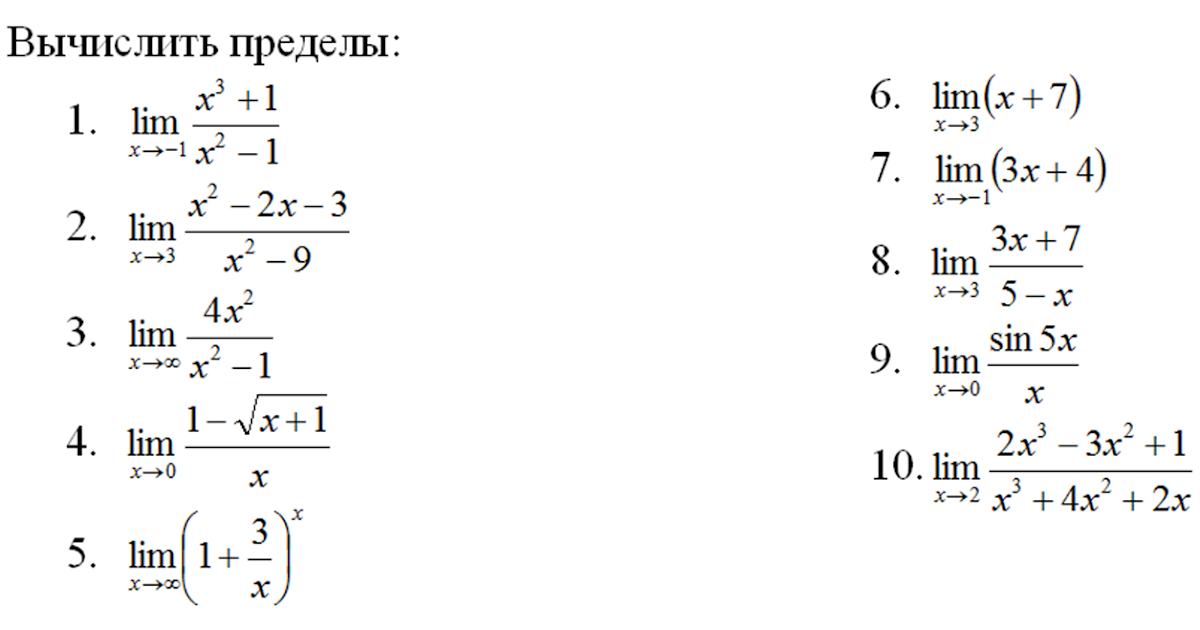 Другое обозначение этой функции –

Неопределенности вида и можно свести к неопределенности вида следующим образом:

включение значения x и факторинг, рационализация числителя, самый низкий общий знаменатель

Чтобы вычислить пределы функции алгебраически, вы можете выбрать один из четырех методов: включение значения x, факторинг, рационализация числителя и поиск самого низкого общего знаменателя. Лучшим выбором является первый метод. Вы можете использовать эту технику только в том случае, если f непрерывна по значению x, в котором вы принимаете ограничение. Если f при этом не определена в значении х, вы должны перейти к другим методам, чтобы упростить вашу функцию и найти приблизительное значение для х.

Содержание:

  • Включение значения x
  • Факторинг
  • Рационализация числителя
  • Самый низкий общий знаменатель
  • Видео

Включение значения x

Первым методом алгебраического решения для нахождения f (x) является включение числа, в котором х приближается к функции. Если вы получаете неопределенное значение (0 в знаменателе или бесконечность), вы должны стремиться перейти к другому методу. Но если ваша f при этом непрерывна в значении х, вы получите значение, и все готово — вы нашли решение! Например, с помощью этого метода вы можете найти:

Пределом будет 3, так как f (5) = 3, и эта f непрерывна при х

Факторинг

Факторинг — это метод, который следует попробовать при сбое в подключении — особенно когда любая часть данной функции является полиномиальным выражением.

Если нужно выполнить это задание:

то сначала попробуйте подключить 4 к функции, и вы получите 0 в числителе и знаменателе, который говорит вам перейти к следующему методу. Квадратичное выражение в числителе говорит, чтобы вы попытались разложить его. Заметим, что числитель предыдущей функции имеет значение (х— 4) ( x — 2). Х — 4 отменяет на верхней и нижней части фракции. Этот шаг оставляет вас с f (х) = х— 2. Вы можете подключить 4 к этой непрерывной функции, чтобы получить 2.

Если вы нарисуете эту функцию, она выглядит как прямая f ( x ) = x — 2, но она имеет отверстие при x = 4, потому что исходная f все еще не определена (потому что она создает 0 в знаменателе). Эта цифра иллюстрирует это.

Если после того как вы учли верхнюю и нижнюю части дроби, термин в знаменателе не сократилось и значение, которое вы ищете не определен, f при этом значении x не существует (который вы можете написать как DNE ).

Например, эта f действует как показано:

(Х — 7) сверху и снизу сократятся. Поэтому, если вас попросят найти функцию, когда x подходит 7, вы можете подключить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти

лимит DNE, потому что вы получите 0 в знаменателе. Следовательно, эта f имеет предельность где угодно, кроме как x приближается к -1.

Рационализация числителя

Третий метод требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, скажем, вас попросят вычислить предел этой функции по мере приближения x к 13:

Забивание номеров не получается, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет полиномиального фактора. В этой ситуации, если вы умножаете числитель и знаменатель на сопряжение числителя, термин в знаменателе, который был проблемой, отменяется, и вы сможете вычислить пределы:

  1. Умножьте верхнюю и нижнюю части дроби конъюгатом.

    Конъюгатом числителя является

    Умножая, вы получаете эту настройку:

    ИЗОБРАЖИТЕ числитель, чтобы получить

    который упрощается до x — 13 (средние два члена отменяют, и вы объединяете как условия из FOIL).

  2. Отменить факторы.

    Отмена дает вам следующее выражение:

    Условия ( x — 13) отменяются, оставляя вас с таким результатом:

  3. Вычислите пределы.

    Когда вы вставляете 13 в функцию, вы получаете 1/6, что является пределом.

Самый низкий общий знаменатель

Когда вам дается сложная рациональная f, вы используете четвертую и окончательную алгебраическую методику определения пределов. Техника подключения не работает, потому что вы получаете 0 в одном из знаменателей. Функция не факторизуема, и у вас нет квадратных корней для рационализации. Поэтому вы можете перейти к последней технике. С помощью этого метода вы комбинируете функции, найдя наименьший общий знаменатель (LCD). Термины отменяются, и в этот момент вы можете найти предельность.

Например, выполните следующие действия, чтобы найти ограничение:

  • Найдите ЖК-дисплей фракций сверху.

  • Распределите числители сверху.

  • Добавьте или вычтите числители, а затем отмените условия.

    Вычитание числителей дает вам

    который затем упрощает

    1. Используйте правила для фракций для дальнейшего упрощения

      .

    2. Замените предельное значение на эту функцию и упростите.

      Для нахождения предела необходимо, когда x приближается к 0, поэтому здесь будет равен -1/36.

    ​Вот и все методы с подробным описанием — надеюсь, теперь вы поняли, как решать пределы.

    Видео

    Этот видеоурок поможет вам лучше разобраться в материале, изложенном в статье и запомнить его.

    Вычисление простейших пределов, 11 класс (теория+практика).

    Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
    Записывается предел следующим образом   .

    Вычислим предел: 
    Подставляем вместо х – 3.
    Заметим, что предел числа равен самому числу.

    Примеры: вычислите пределы 

    Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

    Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.

    Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.

    Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

    Основные виды неопределенностей:  

    Раскрытие неопределенностей

    Для раскрытия неопределенностей используют следующее:

    • упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т. д., и т.п.;

    • если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

    Пример: вычислим предел.
    Разложим числитель на множители 

    3. Вычисление пределов функции

     Пример 1. Вычислите предел функции: 

    При прямой подстановке, получается неопределенность:

    Разложим на множители числитель и знаменатель и вычислим предел.

    Пример 2. Вычислите предел функции: 

    При прямой подстановке, получается неопределенность.

    Помножим и числитель,  и знаменатель на  .

    Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел  Аналогично   

    Пример 3. Вычислите предел функции: 

    При прямой подстановке, получается неопределенность.

    Помножим и числитель,  и знаменатель на  .

    Мы учли, что 

    4.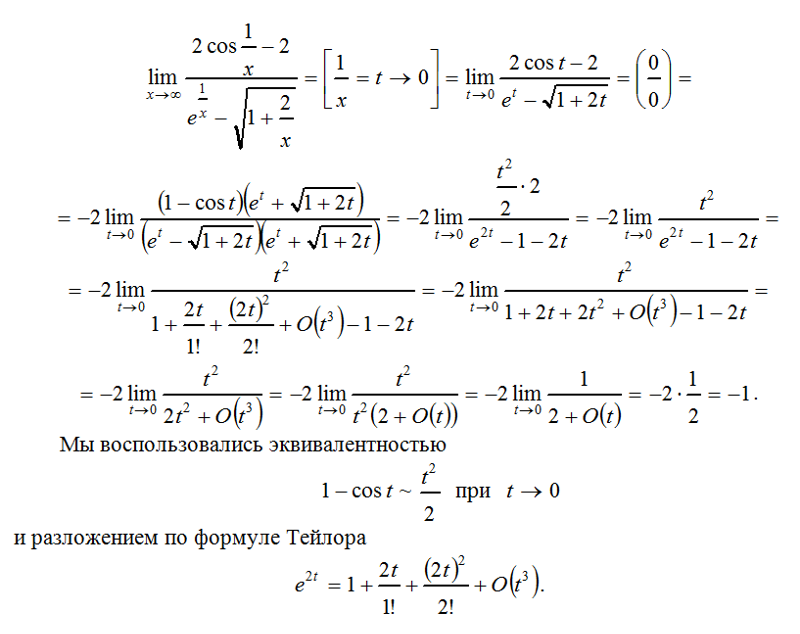 Самостоятельные упражнения

    Вычислите пределы:

    6. Домашнее задание

    Домашнее задание раздается на карточках каждому ученику.

    Свойства пределов функции

    1. Предел постоянной величины равен самой постоянной величине:

    2. Предел суммы двух функций равен сумме пределов этих функций: Аналогично предел разности двух функций равен разности пределов этих функций.

    3. Постоянный коэффициент можно выносить за знак предела:

    4. Предел произведения двух функций равен произведению пределов этих функций:

    5. Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

    Замечание.Принято считать, что  Следующие пределы считают неопределенностью:  . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:

    1) если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида   или  , то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения и имеется неопределенности вида   или  , то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения и имеется неопределенности вида   или  , то для решения используют формулу замечательного предела 

    Вычисление пределов функции

    Пример 1. Найти предел функции:

    Пример 2.Найти предел функции:

    Пример 3.Найти предел функции:

    Пример 4.Найти предел функции:

    Пример 5.Найти предел функции:

    Пример 6.Найти предел функции:

    Пример 7.Найти предел функции:

    Пример 8.Найти предел функции:

    Пример 9.Найти предел функции:

    Пример 10.Найти предел функции: Непрерывность функции Мы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной, если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции в целом, сначала надо разобраться, что такое непрерывность функции в точке.Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке: Т. е. должны выполняться одновременно три условия:

    1) функция определена и в самой точке х = с и в некоторой окрестности этой точки, причем U(с) ϵ D(f);2) существует  ;3) A = f(c).

    Заметим, что в случае непрерывной функции в точке x = c, на графике данная точка выколотой быть не может.Для иллюстрации, как работает данное определение, рассмотрим три функции (см. табл.). Все три условия определения выполняются только у первой функции у = х + 1. У второй — не выполняется третье условие, а у третьей функции — первое.

    Непрерывная функция

    Разрывная в т. х = 1

    Разрывная в т. х = 1

    Пример 11. Найти точку разрыва функции 

    Решение

    Найдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.

    Пример 12.Найти сумму значений точек разрыва функции 

    РешениеНайдем область определения функции: х2 + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х1 ≠ 1, x2 ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.

    Пример 13.Указать точку разрыва функции:

    РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.

    Пределы функции одной переменной

    Лекция 4.2

    Тема 4 . Пределы и непрерывность функции одной переменной.

    Время: 2 часа

    Цель лекции: Познакомить с понятиями числовой последовательности, предела числовой последовательности; пределом функции в точке.

    План лекции:

    1.       Числовая последовательность.

    2.       Предел числовой последовательности.

    3.       Предельный переход в неравенствах.

    4.       Предел функции в точке.

    5.       Односторонние пределы.

    6.       Предел функции при .

    7.       Бесконечно большая функция.

    8.       Бесконечно малые функции.

    9.       Связь между функцией, её пределом и бесконечно малой функцией

    10.   Основные теоремы о пределах.

    11.   Признаки существования пределов.

     

    1.     Числовая последовательность.

    Под числовой последовательностью х1, х2,…,хп… понимается функция  заданная на множестве N натуральных чисел. Кратко последовательность обозначается  Число х1 называется первым членом (элементом) последовательности,…, хп ‒ общим или п-ым членом последовательности.

    Чаще всего последовательность задаётся формулой её общего члена, которая позволяет вычислить любой член последовательности по его номеру

    п. Например,   ;

      ;

       ;

       .

    Последовательность  называется ограниченной, если существует такое число М > 0, что выполняется неравенство  В противном случае последовательность называется неограниченной. В нашем примере последовательности  и  ограничены, а  и  ‒ неограничены.

    Последовательность  называется возрастающей (неубывающей), если  выполняется неравенство . Аналогично определяется убывающая (невозрастающая) последовательность.

    Все эти последовательности называются монотонными. В нашем примере только  не монотонная последовательность.

    Если все элементы последовательности  равны одному и тому же числу

    с, то её называют постоянной.

    2.     Предел числовой последовательности.

    Можно заметить, что все члены последовательности  неограниченно приближаются к числу 1.

    Число а называется пределом последовательности , если для любого положительного числа  найдётся такое натуральное число N, что при всех выполняется неравенство:  В этом случае пишут или . Говорят также, что последовательность  сходится к а.

    Коротко определение предела можно записать так:

    Пример 1: Доказать, что .

    Решение: По определению число 1 будет пределом последовательности  если для любого положительного числа  найдётся такое натуральное число

    N, что при всех  выполняется неравенство:  т.е. . Оно справедливо для всех т.е. для всех . Если  то в качестве N можно взять , где целая часть числа  (целая часть числа х, обозначаемая , есть наибольшее целое число, не превосходящее х, так ). Итак,  указано соответствующее значение N. Это и доказывает, что .

    Выясним геометрический смысл определения предела последовательности. Неравенство  равносильно неравенствам  или , которые показывают, что элемент хп находится в -окрестности точки а.

                                             хп

                 О                        а                                       х

    Поэтому определение предела последовательности геометрически можно сформулировать так: число а называется пределом последовательности , если для любой -окрестности точки а найдётся натуральное число N, что все значения хп, для которых , попадут в -окрестность точки а.

    Ясно, что чем меньше , тем больше число N, но в любом случае внутри -окрестности точки а находится бесконечное число членов последовательности, а вне её может быть лишь конечное число.

    Отсюда следует, что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся. Постоянная последовательность =с имеет предел, равный с.

    3.     Предельный переход в неравенствах.

    Рассмотрим последовательности , и .

    Теорема 1: Если ,  и, начиная с некоторого номера, выполняется неравенство , то .

    r Допустим, что . Из равенств  и  следует, что  и , т.е.

       и    .

    Возьмём . Тогда , т.е.

       , т.е. . Отсюда следует, что . Это противоречит условию (). Следовательно .

    Теорема 2: Если ,  и справедливо неравенство (начиная с некоторого номера), то .

    4.     Предел функции в точке.

    Пусть функция  определена в некоторой окрестности точки х0, кроме, быть может, самой точки х0.

    Определение 1 (на «языке» последовательностей, или по Гейне). Число А называется пределом функции  в точке х0 (или при ), если для любой последовательности допустимых значений аргумента хп, ( ), сходящейся к х0, (т.е. ), последовательность соответствующих значений функции  сходится к числу А (т.е. ).

    В этом случае пишут  или  при . Геометрически смысл предела функции означает, что для всех точек х, достаточно близких к точке х0, соответствующие значения функции как угодно мало отличаются от числа А.

    Определение 2 (на «языке », или по Коши). Число А называется пределом функции  в точке х0, если для любого положительного  найдётся такое положительное число , что для всех , удовлетворяющих неравенству выполняется неравенство . Или короче:

    ,

    Геометрический смысл предела функции: , если для любой -окрестности точки А найдётся такая -окрестность точки х0, что для всех  из этой -окрестности соответствующие значения функции  лежат в -окрестности точки А.

    Пример 2: Доказать, что

    Решение: Возьмём произвольное , найдём такое, что для всех х, удовлетворяющих неравенству  выполняется неравенство  т.е.  Взяв  видим, что для всех х, удовлетворяющих неравенству  выполняется неравенство  Следовательно

    5.      Односторонние пределы.

    В определении предела функции считается, что х стремится к х0 любым способом: оставаясь меньшим, чем х0 (слева от х0), большим, чем х0 (справа от х0), или колеблясь около точки х0. Бывают случаи, когда способ приближения аргумента х к х0 существенно влияет на значение предела функции.

    Число А1 называется пределом функции  в точке х0 слева, если

    .

    Аналогично определяется предел функции справа:

    .

    Пределы функции справа и слева называются односторонними пределами. Очевидно, что если существует , то существуют и оба односторонних предела. Справедливо и обратное: если существую оба односторонних предела и они равны, то существует

    .

    Если же , то  не существует.

    6.     Предел функции при .

    Пусть функция  определена на промежутке . Число А называется пределом функции  при , если для любого положительного числа  существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству выполняется неравенство .

    .

    Геометрически смысл этого определения таков: , что при  или  соответствующие значения функции попадают в -окрестность точки А.

                                         у

     

     

     

     


                    ‒М                           О                                     М                            х

     

    7.     Бесконечно большая функция (ББФ).

    Функция  называется бесконечно большой при , если для любого числа , существует число , что для всех х, удовлетворяющих неравенству , выполняется неравенство . Записывают  или  при . Коротко:

    .

    Функция , заданная на всей числовой прямой называется бесконечно большой при  если для любого числа  найдётся такое число , что при всех х, удовлетворяющих неравенству , выполняется неравенство . Коротко:

    .

    Очевидно, всякая ББФ в окрестности точки х0является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть ББФ (например, ).

    Однако, если , где А ‒ конечное число, то функция  ограничена в окрестности точки х0.

     

    8.     Бесконечно малые функции (БМФ).

    Функция у= называется бесконечно малой при , если

    По определению предела функции, это означает: найдётся число такое, что для всех х, удовлетворяющих неравенству , выполняется неравенство .

    Аналогично определяются бесконечно малые функции при : во всех этих случаях .

    Примерами б.м.ф. служат функции  при ;  при ;  при

    Теорема 3: Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

    Теорема 4: Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

    Следствие 1: Так как всякая б.м.ф. ограничена, то из теоремы 4 вытекает: произведение двух б.м.ф. есть функция бесконечно малая.

    Следствие 2: Произведение б.м.ф. на число есть функция бесконечно малая.

    Следствие 3: Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

    Теорема 5: Если функция ‒ бесконечно малая , то функция  есть бесконечно большая функция и наоборот: если  ‒ бесконечно большая, то  ‒ бесконечно малая.

    9.     Связь между функцией, её пределом и бесконечно малой функцией

    Теорема 6: Если функция  имеет предел, равный А, то её можно представить как сумму числа А и б. м.ф. ,

    т.е., если , то =А+.

    Теорема 7 (обратная): Если функцию  можно представить в виде суммы числа А и б.м.ф. , то число А является пределом функции ,

    т.е., если =А+, то .

    10. Основные теоремы о пределах.

    Теорема 8: предел суммы (разности) двух функций равен сумме (разности) их пределов:          

    Теорема 9: Функция может иметь только один предел при .

    Теорема 10: Предел произведения двух функций равен произведению их пределов:           

    Следствие 1: Постоянный множитель можно выносить за знак предела:

    .

    Следствие 2: Предел степени с натуральным показателем равен той же степени предела:  . В частности .

    Теорема 11: Предел дроби равен пределу числителя, делённому на предел знаменателя, если последний не равен нулю:

     ,  .

    Пример 3: Вычислить .

    Решение: .

    Пример 4: Вычислить .

    Решение: Здесь применить теорему о пределе дроби нельзя, т.к. предел знаменателя, при , равен 0. Кроме того, предел числителя равен 0. В таких случаях говорят, что имеем неопределённость вида . Для её раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на ( т.к. , но ).

    Пример 5: Вычислить .

    Решение: Здесь мы имеем дело  с неопределённостью вида . Для нахождения предела дроби разделим числитель и знаменатель на х2:

    .

    Функция  есть сумма числа 2 и б.м.ф., поэтому . Аналогично, .

    11. Признаки существования пределов.

    Теорема 12 (о пределе промежуточной функции): Если функция  заключена между двумя функциями  и , стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т.е., если

    , , , то .

    Теорема 13 (о пределе монотонной функции): Если функция  монотонна и ограничена при  или при , то существует соответственно её левый предел  или её правый предел.

    Теорема 14: Ограниченная монотонная последовательность хп, , имеет предел.

     

    Техника вычисления пределов. | Методическая разработка по алгебре (10 класс):

    Теория пределов. Основные понятия и формулы.

    Определение: Число А называется пределом функции y=f(х) при х, стремящемся к а, если для любого сколь угодно малого положительного числа ε существует такое положительное число δ, что для всех x, удовлетворяющих условиюδ , выполняется неравенство ε . 
    Предел функции в точке а обозначается .

    Основные теоремы о пределах:

    1.  ;
    2.  ; 
    3.  ;
    4.  ;
    5.  ;
    6.  


    Примечание: Все правила имеют смысл, если пределы функций f(x) и g(x) существуют.

    Замечательные пределы

    Первый замечательный предел

    Следствия из первого замечательного предела

    1.   

    2.   

    3.     

    4.     

    Пример1.

    Найти предел  

    Разложим tgx на sinx и cosx и воспользуемся свойствами пределов.

    = ====

    ===

    Ответ: = 

    Второй замечательный предел   


    Следствия из второго замечательного предела

    1.   

    2.    

    3.    

    4.    

    5.   

    6.    

    Пример2.

    Найти предел

    Подставим , получим неопределённость и для решения предела воспользуемся вторым замечательным пределом.

    =

    Ответ:.

    Техника вычисления пределов

    а) Чтобы раскрыть неопределенность типа ,  необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной. 
    б) Чтобы раскрыть неопределенность типа , где под знаком предела стоит рациональная дробь, достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности. 
    в) Чтобы раскрыть неопределенность типа, если под знаком предела стоит иррациональная дробь, необходимо умножить числитель и знаменатель дроби на сопряженный множитель и сократить множитель, приводящий к неопределенности. 
    г) Необходимо помнить, что 

    1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

    2) Вы должны понимать и сразу решать простейшие пределы, такие как

    , ,   и т.д.

    Пределы с неопределенностью вида      и метод их решения

    Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

    Пример3.

            Вычислить предел

     Согласно нашему правилу попытаемся подставить бесконечность в функцию. Таким образом, у нас есть так называемая неопределенность вида .

    Для того, чтобы раскрыть неопределенность   необходимо разделить числитель и знаменатель на x в старшей степени.

    ==(*)


    Разделим числитель и знаменатель на x

    (*)====

    Ответ: 

    Пример 4.

    Найти предел   
    В числителе и знаменателе находим x в старшей степени:

      


    Максимальная степень в числителе: 3
    Максимальная степень в знаменателе: 4
    Выбираем наибольшее значение, в данном случае 4
    Согласно нашему алгоритму, для раскрытия неопределенности   делим числитель и знаменатель на  .

    Полное оформление задания может выглядеть так:

    ==(*)

    Разделим числитель и знаменатель на  

    =====0

    Ответ: 0

    Пример 5.

    Найти предел 
    Максимальная степень «икса» в числителе: 2
    Максимальная степень «икса» в знаменателе: 1 (x можно записать как )
    Для раскрытия неопределенности необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

    ==(*)

    Разделим числитель и знаменатель на 

    (*)====

    Ответ: 

    Под записью   подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число (.

    Таким образом, при раскрытии неопределенности вида  у нас может получиться конечное число, ноль или бесконечность.

    Пределы с неопределенностью вида    и метод их решения

    Пример 6. 

    Решить предел
    Сначала попробуем подставить -1 в дробь: = 
    В данном случае получена так называемая неопределенность
     

    Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

    Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. 

    ==(*)

    Разложим числитель и знаменатель на множители

    Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

    (*)===

    Ответ:

    Пример 7.

    Вычислить предел 

    Сначала «чистовой» вариант решения

    (*)

    Разложим числитель и знаменатель на множители.

    Числитель: 
    Знаменатель:

     

    (*)22

    Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
    Более того, такие числа целесообразно выносить за значок предела. 

     встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).

    , то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

    Метод умножения числителя и знаменателя на сопряженное выражение

    Пример 8.

    Найти предел 

     

    Сначала пробуем подставить 3 в выражение под знаком предела 

    Получена неопределенность вида , которую нужно устранять.

    (*)

    Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности  используют метод умножения числителя и знаменателя на сопряженное выражение.


    Умножаем числитель на сопряженное выражение:

    (*)

    =

    Ответ:

    Пример 9.

    Найти предел 

    Окончательное решение примера может выглядеть так:

    =(*)

    Разложим числитель на множители:


    Умножим числитель и знаменатель на сопряженное выражение

    (*)=

    Ответ: 

    Правило (теорема) Лопиталя.

    Пусть функция и удовлетворяют следующим условиям:

    1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

    2)  и в этой окрестности;

    3)

    4) существует, конечный или бесконечный.

    Тогда существует и , причем

    Таким образом, вычисление предела отношения двух функций может быть заменено, при выполнении условий теоремы вычислением предела отношения производных этих функций.

    Замечание: Правило Лопиталя распространяется на случай неопределенности типа  при

    Применение правила Лопиталя на практике.

    Пример 10.

    Найти предел

    Получаем неопределенность:

    (*)

    Воспользуемся правилом Лопиталя:

    (*)

    Ответ: 0

    Замечание:

    Правило Лопиталя распространяется и на случай . Чтобы убедиться в этом, достаточно сделать замену  и воспользоваться результатом выше приведенной теоремы.

    Замечание: Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми.

    Замечание: Хотя правило Лопиталя работает только с неопределенностями  и, неопределенности других типов могут быть раскрыты с его помощью, если путем преобразований удастся привести изучаемую неопределенность к указанному типу. 2

    пределов — Криста Кинг Математика | Онлайн-помощь по математике

    Сообщения с тегами ограничений Как решать тригонометрические предельные задачи

    Тригонометрические предельные задачи вращаются вокруг трех формул, поэтому очень важно, чтобы мы знали эти формулы тригонометрического предела. Когда мы решаем тригонометрические предельные задачи, наша цель всегда состоит в том, чтобы свести функцию к комбинации только этих трех формул и простых констант.

    Читать далее

    Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление, исчисление i, исчисление 1, исчисление с одной переменной, вычисление с одной переменной, пределы, пределы и непрерывность, пределы триггеров, тригонометрические пределы, пределы тригонометрических функций, пределы тригонометрических функций

    Решение пределов сопряженным методом

    Метод сопряжения можно использовать только в том случае, если либо числитель, либо знаменатель содержат ровно два члена. Чтобы использовать его, мы должны умножить на сопряженную часть той части дроби, которая содержит радикал. Сопряжение двух терминов — это те же самые два термина с противоположным знаком между ними. Обратите внимание, что мы умножаем и числитель, и знаменатель на сопряженную, потому что это похоже на умножение на 1, которое не меняет значение исходной функции.

    Читать далее

    Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление, исчисление 1, исчисление i, исчисление с одной переменной, вычисление с одной переменной, пределы, пределы и непрерывность, метод сопряжения, пределы решения, решение пределы сопряженным методом, сопряженный метод пределов, сопряженный

    Как решать лимиты с подстановкой

    Как мы видели в предыдущих уроках, самый простой способ оценить предел — подставить значение, к которому мы приближаемся, в функцию. Поскольку это самый простой и быстрый метод, мы всегда должны сначала пробовать замену. Но замена не всегда работает.

    Читать далее

    Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, исчисление одной переменной, вычисление одной переменной, пределы, пределы решения, решение с заменой, замена

    Нахождение бесконечных пределов на вертикальных асимптотах

    Есть разница между «ограничениями в бесконечности» и «бесконечными пределами». Когда мы видим пределов на бесконечности , это означает, что мы говорим о пределе функции по мере приближения к бесконечности или отрицательной бесконечности. Сравните это с бесконечными пределами , что означает, что значение предела равно бесконечности или отрицательной бесконечности, когда мы приближаемся к определенной точке.

    Читать далее

    Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, исчисление одной переменной, вычисление одной переменной, пределы, бесконечные пределы, вертикальные асимптоты, пределы на вертикальных асимптотах

    Теорема о промежуточном значении

    Теорема о промежуточном значении — это теорема, которую мы используем для доказательства того, что функция имеет корень внутри определенного интервала. корень функции графически представляет собой точку, в которой график функции пересекает ось x. Алгебраически корень функции — это точка, в которой значение функции равно 0.

    Читать далее

    Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, теорема о промежуточном значении, замкнутый интервал, корень функции, вычисление одной переменной, одиночное исчисление переменных, пределы, пределы и непрерывность

    Непрерывность и типы разрывов

    Вы должны иметь некоторое представление о том, что означает непрерывность графа. В принципе, функция непрерывна, если на ее графике нет дыр, разрывов, скачков, переломов, сломанных костей и т.п. Вы также можете думать об этом так: функция непрерывна, если вы можете нарисовать ее целиком, не поднимая карандаша. Потратим некоторое время на классификацию наиболее распространенных типов разрывов.

    Читать далее

    Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, пределы и непрерывность, непрерывность, пределы, разрыв, разрывы, точечный разрыв, разрывы в конечной точке , бесконечные разрывы, существенные разрывы, скачкообразные разрывы

    Как и когда использовать правило Лопиталя

    Правило Лопиталя используется, чтобы вывести вас из затруднительных ситуаций с неопределенными формами ограничения. Если вы подставите число, к которому приближаетесь, в функцию, для которой пытаетесь найти предел, и ваш результат будет одной из неопределенных форм, приведенных выше, вам следует попробовать применить правило Лопиталя.

    Читать далее

    Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, исчисление 1, исчисление i, пределы, неопределенные формы, пределы неопределенных форм, правило больницы, l’ правило Хопиталя, производные, пределы решения

    Решение лимитов с факторингом

    Если вы попытались решить ограничение с помощью подстановки, и это не сработало, следующей попыткой будет факторинг. Цель будет состоять в том, чтобы разложить функцию на множители, а затем отменить любые устранимые разрывы, чтобы упростить функцию, чтобы ее можно было вычислить.

    Читать далее

    Изучайте математикуКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, исчисление 1, исчисление i, пределы, пределы и непрерывность, решение ограничений, факторинг, решение лимитов с факторингом, факторинг лимитов, факторинг для решения лимитов, отмена, съемный разрыв

    Односторонние ограничения

    Когда вы слышите, как ваш профессор говорит о пределах, он или она обычно говорит об общем пределе.

    Читать далее

    92 в функцию sin(x). Думайте о любой функции как о «внешней части» и «внутренней части» как о составных функциях.

    Читать далее

    Learn mathKrista King пределы, пределы составных функций

    Что это такое и как они решаются. Боковые ограничения.

    В этом посте я объясню ограничения функций. Мы рассмотрим самые основные вещи, которые вам нужно знать, чтобы понять ограничения: что такое ограничения функций и как они разрешаются (в общем).

    Я начну с того, что дам вам определение предела, чтобы вы поняли концепцию, а затем мы продолжим определение простых пределов, чтобы вы все прекрасно поняли. Это основа, на которой вы можете научиться решать более сложные пределы с неопределенностями.

    Я объясню вам, что такое боковые ограничения.

    Índice de Contenidos

    Каков предел функции?

    Предел функции в точке состоит в том, чтобы получить значение, к которому эта функция приближается, когда x стремится к определенной точке, но не достигая этой точки

    .

    Представляется следующим образом:

    Это означает, как я только что сказал вам, что при стремлении X к точке Xo значение функции приближается к L, следовательно, предел этой функции при стремлении X к Xo есть L. Графически это будет выглядеть так:

    Если вы заметили, по мере приближения к значению Xo по оси x, по оси y значение функции будет приближаться к значению L.

    x может стремиться к любому значению, от менее бесконечного к более бесконечному (включая оба значения), и предел функции также может быть от менее бесконечного к бесконечному (включая оба значения).

    Не путайте предел функции со значением функции в точке, которое является значением функции прямо в этой точке. Будьте очень осторожны, потому что они могут не совпадать (см. ниже).

    Давайте рассмотрим это на примере.

    Каков предел следующей функции:

    , когда x стремится к -1?

    Предел функции при стремлении x к -1 записывается:

    Чтобы вы понимали, как значение функции будет приближаться к определенному значению, при этом x будет стремиться к -1, посмотрим, какое значение функции для точек, близких к -1, и каждый раз мы будем приближаться к -1.

    Сначала мы будем приближаться к -1 слева, чтобы посмотреть, что произойдет.

    При x=-1,3 значение функции равно:

    При x=-1,2 значение функции равно:

    При x=-1,1 значение функции равно :

    Если вы заметили, по мере того, как мы приближаемся к -1, значение функции приближается к 0.

    Сейчас мы собираемся сделать то же самое, но приближаясь к 1 справа.

    При x=-0,7 значение функции:

    При x=-0,8 значение функции равно:

    При x=-0,9 значение функции равно:

    Как видите, получаем ближе к x=-1 справа, функция становится все ближе и ближе к 0.

    Если мы посмотрим на это графически, мы увидим, как график функции приближается к точке 0 на оси y, когда значения x приближаются к точке -1 по оси x:

    Следовательно, предел функции при стремлении x к -1 равен 0:

    Для определения предела нет необходимости выполнять эту процедуру, которую мы только что сделали. Я сделал это только для того, чтобы вы могли видеть, как мало-помалу значение функции приближается к точке.

    Нахождение предела этой функции намного проще, и это то, что я объясню в следующем разделе.

    Как найти предел функции

    В случаях, когда областью определения функции является все R (функция непрерывна во всех R), например многочлены, предел функции в точке будет вычисляться так же как значение функции в этой точке, т.е. заменив значение на x.

    Давайте решим предел предыдущей функции, когда x стремится к -1:

    Чтобы решить это, мы должны заменить x на -1 и выполнить:

    И мы получим результат предела, который равен 0

    Обратите внимание, когда мы заменяем значение, к которому стремится x, на x, предел исчезает.

    В этом случае предел функции при x стремится к -1, и значение функции при -1 совпадают, но это не обязательно так.

    В функциях, которые не являются непрерывными (область определения не вся R), есть точки, где предел имеет значение, но функция в этой точке не существует или значение функции имеет другое значение.

    Например, в следующей функции:

    Предел при стремлении x к -1 равен 0, но однако значение функции при x=-1 равно 2:

    Или случай этой другой функции:

    Давайте посмотрим, что произойдет, если мы вычислим предел функции, когда x стремится к 1:

    Мы заменим x на 1:

    И мы не можем придумать решение, потому что число между нулем является неопределенностью. В курсе «Пределы» я подробно объясню типы неопределенности и способы их разрешения.

    Латеральные пределы

    Мы уже видели, что пределом функции является значение, к которому эта функция приближается, когда x стремится к некоторой точке как слева, так и справа.

    Однако можно вычислить предел функции при подходе только слева или при подходе только справа. Их называют боковыми границами.

    Значение боковых пределов функции может совпадать или не совпадать.

    Чтобы предел функции существовал в точке, значение боковых пределов должно совпадать, и это будет предельное значение в этой точке.

    Если боковые границы не совпадают, то граница не существует.

    Давайте рассмотрим это на примере, чтобы вам было понятнее.

    У нас есть следующая функция:

    Подсчитаем, сколько стоит предел функции, когда x стремится к 4.

    Если подойти к x=4 слева, предел равен 3:

    Когда боковой предел находится слева, знак минус добавляется в качестве показателя степени к значению x, до которого простирается предел.

    Если мы приближаемся к x=4 справа, предел равен 5:

    Когда боковой предел находится справа, знак плюс добавляется как показатель степени к значению x, до которого простирается предел.

    Боковые пределы в данном случае не совпадают, поэтому предела функции при стремлении x к 4 ​​(в обе стороны) не существует:

    Знак «не существует» — это заглавная Е в обратном порядке.

    Нахождение пределов: определение, правила и функции

    Подобно бусам на нитке, ведущей к подвеске, точки на графике могут привести вас к пределу функции. Как мы можем использовать точки на графике для оценки пределов? Хороший вопрос! Здесь мы рассмотрим некоторые из различных способов нахождения пределов функций!

    Нахождение пределов в исчислении

    Существует множество способов найти предел функции!

    • Вы можете использовать определение предела и написать доказательство. См. Пределы функции для примеров этого метода.

    • Вы можете посмотреть на график или таблицу значений, чтобы увидеть, каким может быть предел. См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.

    • Вы можете посмотреть на ограничение слева и справа функции и посмотреть, совпадают ли они. См. Односторонние ограничения для определений и примеров использования этого метода.

    • Вы можете использовать законы пределов, которые являются уже доказанными теоремами для нахождения предела. Если ваша функция хороша, люди часто находят предел именно так. Для получения дополнительной информации о свойствах лимитов см. Законы лимитов 9.0003

    • Вам может понадобиться использовать специальную теорему, чтобы найти предел, например, теорему сжатия или теорему о промежуточном значении. Оба они очень полезны, и теорема о промежуточном значении появится позже в таких темах, как нахождение максимального значения функции. См. «Теорему о сжатии» или см. «Теорему о промежуточном значении», чтобы узнать, как их использовать.

    Здесь вы увидите пример способов нахождения предела функции.

    Использование определения предела

    Для просмотра определения предела функции см. Пределы функции.

    Где и – постоянные действительные числа. Правда ли, что

    ?

    Ответ:

    Да. Используя определение, для любого вам дано

    независимо от того, что вы используете. Таким образом, константные функции имеют предел, которого вы от них ожидаете.

    Возьмем и пусть будет постоянным действительным числом. Откуда вы знаете, что

    ?

    Ответ:

    Возможно, у вас возникнет соблазн сказать: «Конечно, ограничение есть — функция — это просто строка». На самом деле этого почти достаточно. Вы не можете использовать какие-либо свойства пределов, но вы можете использовать определение и взятие, чтобы показать, что предел равен .

    Использование правил нахождения пределов

    Для обзора различных свойств пределов и способов их использования см. Законы пределов.

    Возьмем функцию , и будем постоянным вещественным числом. Найдите

    .

    Ответ:

    Обратите внимание, что функция представляет собой просто сумму и произведение степеней вместе с константой . Вы уже знаете, что

    и

    из двух приведенных выше примеров, что означает выполнение условий для применения правила суммы, правила произведения и правила константы. Затем их применение дает

    Нахождение пределов графически

    Ниже приведен пример использования графика для нахождения предела функции. Дополнительные сведения о подобных проблемах см. в разделе Поиск пределов с помощью графика или таблицы.

    Рассмотрим функцию

    ,

    Найдите предел функции как .

    Ответ:

    Сначала начертите график функции и составьте таблицу значений рядом с . Хотя у функции больше корней, чем показано на графике, поскольку вас интересует только предел как , имеет смысл увеличить масштаб функции там.

    Использование графика и таблицы для нахождения предела функции | StudySmarter Original

    Точки на графике соответствуют точкам в таблице. Как на графике, так и в таблице видно, что по мере приближения к , значения функции становятся все ближе и ближе к Это означает, что

    .

    Обратите внимание, что при поиске предела значение функции в действительности не интересует, потому что в определении говорится, что нужно смотреть близко к, но не к .

    Алгебраическое нахождение пределов

    Другие примеры алгебраического нахождения пределов приведены в отдельной статье. См. раздел «Нахождение пределов определенных функций».

    На самом деле ограничения и непрерывность тоже идут рука об руку.

    Если функция непрерывна в точке, то предел функции существует и равен значению функции в этой точке.

    Из предыдущего примера у нас было

    ,

    и мы нашли предел как . Поскольку вы знаете, что все многочлены везде непрерывны (см. Непрерывность и см. Теоремы непрерывности для более подробной информации), вы знаете, что предел функции существует и равен значению функции. Так как это означает

    .

    Посмотрите на функцию

    и найдите предел как .

    Ответ:

    Функция не определена в , поэтому вы не можете просто подставить значение функции, чтобы найти предел. Но вы можете разложить числитель, чтобы получить

    до тех пор, пока . Это означает, что график функции на самом деле представляет собой прямую линию с отверстием в точке . Итак,

    Нахождение производной с использованием определения предела

    Использование определения производной требует ограничений. Это большая тема, и ей посвящена целая статья! См. нашу статью о производных, чтобы узнать больше о том, как найти производную с использованием предела.

    В поисках пределов — основные выводы

    • Для любого многочлена , .
    • Таблицу или график можно использовать для нахождения предела функции.
    • Алгебраическое нахождение пределов может включать факторизацию числителя и знаменателя и проверку того, не уравняется ли что-либо. Это особенно полезно в тех случаях, когда в графике есть дыра.
    • Свойства пределов также можно использовать для ограничения функций.

    Часто задаваемые вопросы о нахождении пределов

    Существует множество способов нахождения пределов, в том числе с использованием определения, с помощью графика или таблицы, с использованием свойств и теорем о пределах или алгебраически.

    Посмотрите на значения функции рядом с точками, в которых вы берете предел. Если все значения функции приближаются к одному и тому же числу, то это предел.

    Существует множество методов нахождения пределов, в том числе с помощью определения, с помощью графика или таблицы, с использованием свойств и теорем пределов или алгебраически.

    Существует множество алгебраических методов нахождения предела, включая разложение на множители и использование непрерывности.

    Посмотрите на значения последовательности, поскольку n становится очень большим. Если все значения последовательности приближаются к одному числу, то это число является пределом последовательности.

    Окончательное определение пределов викторины

    Вопрос

    Какой из способов не является способом нахождения предела функции

    Показать ответ

    Ответ

    Позволить собаке выбрать ответ.

    Показать вопрос

    Вопрос

    Какой из способов не является способом нахождения предела функции.

    Показать ответ

    Ответить

    Спросить совета у кошки.

    Показать вопрос

    Вопрос

    Если функция непрерывна в точке, имеет ли она там предел?

    Показать ответ

    Ответить

    Да и на самом деле предел там равен значению функции.

    Показать вопрос

    Вопрос

    Верно или неверно: при нахождении предела функции в точке имеет значение значение функции в этой точке.

    Показать ответ

    Ответить

    Неверно. Вы заботитесь о значениях функции рядом с точкой, но не в точке.

    Показать вопрос

    Вопрос

    Всегда ли существуют пределы функций?

    Показать ответ

    Ответить

    Нет. Вы говорите, что он существует только в том случае, если пределом функции является число. Есть много функций, которые имеют вертикальные асимптоты, и в этих местах функция не имеет предела.

    Показать вопрос

    Вопрос

    Верно или неверно: всегда можно использовать определение, чтобы найти предел функции.

    Показать ответ

    Ответ

    Технически это верно, но часто это может быть довольно сложно. Вот почему у нас есть такие вещи, как предельные законы и теорема сжатия.

    Показать вопрос

    Вопрос

    Верно ли, что полиномиальные функции везде имеют пределы?

    Показать ответ

    Ответить

    Да. Так как полиномы везде непрерывны, то они везде имеют предел и он равен значению функции.

    Показать вопрос

    Вопрос

    Всегда ли можно использовать правило частного, чтобы найти предел рациональной функции?

    Показать ответ

    Ответить

    Нет, можно использовать только в том случае, когда предел знаменателя не равен нулю.

    Показать вопрос

    Вопрос

    Что можно сделать, чтобы попытаться найти предел рациональной функции?

    Показать ответ

    Ответить

    Вы можете попробовать разложить на множители и отменить, или заняться алгеброй, чтобы упростить задачу, или использовать свойства пределов.

    Показать вопрос

    Вопрос

    Если вы пытаетесь найти предел функции, в которой есть корень, какой метод вы можете использовать?

    Показать ответ

    Ответить

    Можно попробовать умножить и числитель, и знаменатель на сопряженную часть с корнем.

    Показать вопрос

    Вопрос

    Если вы хотите найти предел кусочно определенной функции в точке изменения определения функции, что вам нужно сделать?

    Показать ответ

    Ответить

    Найдите предел слева и предел справа и проверьте, совпадают ли они. Если они не совпадают, то предела не существует.

    Показать вопрос

    Вопрос

    Как найти предел показательной функции?

    Показать ответ

    Ответ

    Вы можете думать об этом как о композиции двух функций, а затем использовать тот факт, что экспоненциальная функция непрерывна, чтобы найти предел.

    Показать вопрос

    14.2 Пределы и непрерывность

    Чтобы разработать исчисление для функций одной переменной, нам нужно было сделать смысл понятия предела, который нам нужно было понять непрерывные функции и определить производную. Ограничения, связанные функции двух переменных могут быть значительно сложнее иметь дело с; к счастью, большинство функций, с которыми мы сталкиваемся, довольно просты чтобы понять.

    Потенциальные трудности во многом связаны с тем, что есть много способов «приблизиться» к точке на плоскости $x$-$y$. Если мы хотим скажем, что $\ds\lim_{(x,y)\to(a,b)}f(x,y)=L$, нам нужно захватить идея о том, что когда $(x,y)$ приближается к $(a,b)$, тогда $f(x,y)$ приближается к $L$. Для функций одной переменной $f(x)$ есть только два способа что $x$ может приближаться к $a$: слева или справа. Но есть бесконечное количество способов приблизиться к $(a,b)$: по любому из бесконечное число линий, или бесконечное число парабол, или бесконечное количество синусоид и так далее. Мы могли бы надеяться, что это на самом деле не так уж плохо — предположим, например, что вдоль всех возможных через $(a,b)$ значение $f(x,y)$ приближается к $L$; конечно это означает, что “$f(x,y)$ приближается к $L$, когда $(x,y)$ приближается к $(а,б)$”. К сожалению нет. 92$. Приближаясь к начало пути по прямой, переходим через гребень и спускаемся вниз к 0, но приближаясь по гребню высота постоянна $1/2$. Таким образом, в $(0,0)$ нет предела. $\квадрат$

    К счастью, мы можем определить понятие предела без необходимости указать, как приближаться к конкретной точке — действительно, в определение 2.3.2, нам не нужно было понятие “подход”. Грубо говоря, это определение говорит, что когда $x$ близко к $a$, то $f(x)$ близко к $L$; нет упоминания о “как” мы приближаемся к $a$. Мы можем адаптировать это определение к двум переменные довольно легко: 92}$

    Обратите внимание, что в отличие от этого примера мы не можем исправить пример 14.2.1 в $(0,0)$, потому что предел не существует. Независимо от того, какое значение мы пытаемся присвоить $f$ в $(0,0)$, поверхность будет иметь «прыжок».

    К счастью, функции, которые мы будем исследовать, обычно непрерывно практически везде. Обычно это легко следует из тот факт, что тесно связанные функции одной переменной непрерывны. Как и в случае с функциями с одной переменной, существуют два класса общих функций. особенно полезно и легко описать. n$, где $a$ — действительное число, а $m$ и $n$ — целые неотрицательные числа. Рациональное функция является частным многочленов. 92+2x+1)

    x-> 1

    2.) Постройте таблицу значений для числа 1 (примечание: не округляйте значения. Запишите все десятичные разряды каждого значения в соответствии с проекцией в калькулятор)

    (пожалуйста, представьте эти два в виде таблиц, потому что здесь нет возможности добавить одну. Добавьте пошаговое решение и ответьте на пробел в «f(x)» )

    x л 0 л 0,3 л 0,7 л 0,9l 0.99 l 0.999 l

    f(x) l l l l l l l

    x l 2 l 1.5 l 1.3 l 1.1 l 1.01 l 1.001 l

    f(x) l l l l l l l

    3.) Lim g( x)

    x-> -4

    4. ) Lim g(x)

    x-> -2

    3.) Lim g(x) 90 904×2+2)

    7.) Какие предельные теоремы вы применили для решения числа 6?

    (множественный выбор)

    A.) Предел постоянного

    B.) Предел идентичности

    C.) Предел постоянного множественного

    D.) Предел из -за предела постоянного множественного

    D.) Сумма или разность

    E.) Предел произведения

    F.) Предел частного

    G.) Предел степени 95x+3 – 5

    x-> 2/5

    13.) lim log2 (2x+1)

    x-> 3/2

    14.) lim (3/4 csc x)

    x- > 5π/4

    Подписаться І 1

    Подробнее

    Отчет

    2 ответа от опытных наставников

    Лучший Новейшие Самый старый

    Автор: Лучшие новыеСамые старые

    Пол М. ответил 11.05.21

    Репетитор

    5 (22)

    Узнайте, “как” делать математику и почему “как” работает!

    Об этом репетиторе ›

    Об этом репетиторе ›

    Вы пытались решить любую из этих задач.

    Ты должен!

    Тогда задавайте конкретные вопросы, когда вы застряли.

    Если вы не можете начать ни с одной из этих задач, вам нужен урок с репетитором, а не ответы на этот вопрос.

    Помните, что полиномы везде непрерывны.

    Рациональные функции непрерывны, за исключением нулей знаменателя.

    Sin и cos непрерывны везде, но тангенс разрывается там, где cos=0.

    В #10 нужно разделить числитель и знаменатель на x 3 .

    Голосовать за 2 Понизить голос

    Подробнее

    Отчет

    Майкл М. ответил 12.05.21

    Репетитор

    4.9 (216)

    Математика, химия, физика, репетиторство с Майклом (“800” SAT математика)

    Смотрите таких репетиторов

    Смотрите таких репетиторов

    Я расскажу о некоторых из них.

    Для числа 1 вы начинаете ограничивать, подставляя значение, к которому x приближается, в функцию. В этом случае мы подставляем 1. Получаем (1) 2 + 2(1) + 1 = 4. Таким образом, предел равен 4

    . Для числа 8 вы подставляете 1 вместо x и получаете 0/0 . Итак, здесь вы должны использовать некоторую алгебру

    Фактор числителя:

    lim (2x-3)(x-1)

    x→1 x -1

    x-1 в числителе и знаменателе отменить, оставив нам

    lim 2x-3

    x→1

    Повторная подстановка 1 дает нам, что предел равен -1

    Для числа 9 вы подставляете 3 вместо x и получаете -1/0. Ненулевое число, деленное на ноль, может дать вам либо бесконечность, либо отрицательную бесконечность, либо DNE (это произойдет, если оно уйдет в бесконечность с одной стороны и к отрицательной бесконечности с другой). Мы подходим с положительной стороны, что означает, что x немного больше 3. Это означает, что x – 3 (знаменатель) положителен. Числитель дает нам -1, поэтому у нас есть отрицательное, деленное на положительное, что дает нам отрицательное значение. Таким образом, предел равен -∞.

    Голосовать за 1 Понизить

    Подробнее

    Отчет

    Все еще ищете помощь? Получите правильный ответ, быстро.

    Задайте вопрос бесплатно

    Получите бесплатный ответ на быстрый вопрос.
    Ответы на большинство вопросов в течение 4 часов.

    ИЛИ

    Найдите онлайн-репетитора сейчас

    Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

    Ограничения

    Ограничения

    Пример

    Рассмотрим функцию

    х 2 – 1
    f(x) =                               
    х 2 +2х – 3

    Если мы подставим 1, мы получим 0/0 который не определен. Как выглядит эта функция около х = 1?

    Мы можем построить следующую таблицу:

    х .9 .99 1,1 1,01 1.001
    ф(х) . 487 .499 .512 .501 .5001

    Мы можем видеть, что эта функция приближается к 0,5, когда x приближается к 1. Ниже приведен график этой функции.

    Этот пример приводит нас к следующему определению

    Определение предела

    Если f(x) становится сколь угодно близким к одному числу L по мере приближения x c с обеих сторон, затем

    Мы можем думать об определении предела как x -> c как о двух туристах, один идущий справа, а другой идущий слева. Если они будут идти к одному и тому же месту, тогда это место называется пределом.

    Свойства пределов

    Предположим, что

    и что а является константой. затем

    А)

    Б)

    С)

    Д)

    Е)

    Пример

    Предположим, что

    затем

    Алгебра и пределы

    При нахождении предела всегда сначала подставляйте число. Если вы получите определенное значение, то это и есть ответ. В противном случае вам, возможно, придется сделать алгебра, чтобы найти предел.

    Пример:

    lim как х -> 1 (х 2 – 1)/(х 2 +2x – 3)

    = lim as x -> 1  (x – 1)(x + 1)/(x + 3)(x – 1)

    = lim как х -> 1 (х + 1)/(х + 3) = 2/4 = 0,5

    Найдите предел

    Решение

    Во-первых, обратите внимание: если мы подставим 1 вместо x, мы получим 0/0. Алгебра, которая будет работа факторинговая.

    Теперь подключите 1, чтобы получить

    2/4 =  1/2

    Пример

    Найдите предел

    Решение

    Опять же, если мы подключаемся, мы получаем 0/0. Какая алгебра подойдет для этого проблема? Вспомните из основ алгебры, как рационализировать знаменатель. Наша стратегия будет заключаться в рационализации числителя. Мы умножаем числитель и знаменатель на сопряженный корень.

    Теперь мы можем подставить 9 вместо х получить

    1 1
    =          
    4 + 4            8

    Односторонние ограничители

    Определим левый предел

    как координата y кривой при движении точки слева.

    Аналогично определим правый предел

    как координата y кривой, когда точка движется слева.

    Пример

    Находить

    Решение

    График функции изображен ниже.

    Прогуливаясь с левой стороны, значение y приближается к -1. Следовательно предел -1. Обратите внимание, что без знака “-” предел не существовало бы.

    Оставить комментарий