Бином Ньютона, биноминальное разложение с использованием треугольника Паскаля, подмножества
Биноминальное разложение с использованием треугольника Паскаля
Рассмотрим следующие выражения со степенями (a + b)n, где a + b есть любой бином, а n – целое число.
Каждое выражение – это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до “половины пути”, а потом уменьшаются на те же значения обратно к 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b)6. Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a6 + c1
Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:
Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b)
Мы видим, что в последней строке
первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.
Таким образом, выражение (a + b)6 будет равно
(a + b)6 = 1a6 + 6a5b +
Для того, чтобы возвести в степень (a + b)8, мы дополняем две строки к треугольнику Паскаля:
Тогда
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Мы можем обобщить наши результаты следующим образом.
Бином Ньютона с использованием треугольника ПаскаляДля любого бинома a+ b и любого натурального числа n,
(a + b)n
 … + cn-1a1bn-1 + cna0bn,
… + cn-1a1bn-1 + cna0bn,где числа c0, c1, c2,…., cn-1, cn взяты с (n + 1) ряда треугольника Паскаля.
Пример 1 Возведите в степень: (u – v)5.
Решение У нас есть (a + b)n, где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:
1 5 10 10 5 1
(u – v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.
Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.

Пример 2 Возведите в степень: (2t + 3/t)4
Решение У нас есть (a + b)n, где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
1 4 6 4 1
Тогда мы имеем
Разложение бинома используя значения факториала
Предположим, что мы хотим найти значение (a + b)11. Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку – скажем, 8-ю строку – без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента .
Мы можем сформулировать бином Ньютона следующим образом.
Для любого бинома (a + b) и любого натурального числа n,
.
Бином Ньютона может быть доказан методом математической индукции. Она показывает почему называется биноминальным коэффициентом.
Пример 3 Возведите в степень: (x2 – 2y)5.
Решение У нас есть (a + b)n, где a = x2, b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем
Наконец, (x2 – 2y)5 = x10 – 10x8y + 40x6y2 – 80x
Пример 4 Возведите в степень: (2/x + 3√x)4.
Решение У нас есть (a + b)n, где a = 2/x, b = 3√x, и n = 4. Тогда, используя бином Ньютона, мы получим
Finally (2/x + 3√x)4 = 16/x4 + 96/x5/2 + 216/x + 216x1/2 + 81x2.
Нахождение определенного члена
Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.
Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.
Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.
Нахождение (k + 1) члена(k + 1) член выражения (a + b)n есть .
Пример 5 Найдите 5-й член в выражении (2x – 5y)6.
Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет
Пример 6 Найдите 8-й член в выражении (3x – 2)10.
Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет
Общее число подмножеств
Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть . Общее число подмножеств множества есть число подмножеств с 0 элементами, а также число подмножеств с 1 элементом, а также число подмножеств с 2-мя элементами и так далее. Общее число подмножеств множества с n элементами есть
Общее число подмножеств множества с n элементами есть
.
Теперь давайте рассмотрим возведение в степень (1 + 1)n:
.
Так. общее количество подмножеств (1 + 1)n, или 2n. Мы доказали следующее.
Полное число подмножеств множества с n элементами равно 2n.
Пример 7
Решение Множество имеет 5 элементов, тогда число подмножеств равно 25, или 32.
Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
{кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр}.
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?
Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно
.
Модули math и numpy – Основы Python
Давайте рассмотрим библиотеки math и numpy для решения математических задач.
Важное уточнение: количество функций и внутренних модулей во многих библиотеках не позволяет рассмотреть их полностью в одной главе. Поэтому при изучении библиотек мы будем рассматривать лишь некоторые их возможности, а более подробную информацию вы сможете найти в документации. Ссылка на документацию будет в конце главы.
Библиотека math
Библиотека math является стандартной в Python и содержит много полезных математических функций и констант. Официальная документация Python выделяет следующие виды функций этого модуля:
Функции теории чисел и функции представления. Рассмотрим некоторые из них:
math.comb(n, k)— возвращает количество сочетаний изnэлементов поkэлементам без повторений и без учёта порядка. Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):
Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):import math print(math.comb(12, 3)) # 220
math.factorial(x)— возвращает факториал целого неотрицательного числаx:print(math.factorial(5)) # 120
math.gcd(*integers)— возвращает наибольший общий делитель (НОД) для чисел-аргументов. Возможность определения НОДа для более чем двух чисел появилась в Python версии 3.9:print(math.gcd(120, 210, 360)) # 30
math.lcm(*integers)— возвращает наименьшее общее кратное (НОК) для чисел-аргументов. Функция появилась в Python версии 3.9:print(math.lcm(10, 20, 30, 40)) # 120
math.perm(n, k=None)— возвращает количество размещений изnэлементов поkэлементам без повторений и с учётом порядка. Если значение аргументаkне задано, то возвращается количество перестановок множества изnэлементов:print(math.
 perm(4, 2)) # 12
print(math.perm(4)) # 24
perm(4, 2)) # 12
print(math.perm(4)) # 24
math.prod(iterable, start=1)— возвращает произведение элементов итерируемого объектаiterable. Еслиiterableпустой, то возвращается значение именованного аргументаstart:print(math.prod(range(10, 21))) # 6704425728000
Степенные и логарифмические функции. Некоторые из функций:
math.exp(x)— возвращает значение экспоненциальной функции ex:print(math.exp(3.5)) # 33.11545195869231
math.log(x, base)— возвращает значение логарифма отxпо основаниюbase. Если значение аргументаbaseне задано, то вычисляется натуральный логарифм. Вычисление производится по формулеlog(x) / log(base):print(math.log(10)) # 2.302585092994046 print(math.log(10, 2)) # 3.3219280948873626
math.pow(x, y)— возвращает значениеxв степениy. В отличие от операции
В отличие от операции **, происходит преобразование обоих аргументов в вещественные числа:print(math.pow(2, 10)) # 1024.0 print(math.pow(4.5, 3.7)) # 261.1477575641718
Тригонометрические функции. Доступны функции синус (
sin(x)), косинус (cos(x)), тангенс (tan(x)), арксинус (asin(x)), арккосинус (acos(x)), арктангенс (atan(x)). Обратите внимание: угол задаётся и возвращается в радианах. Имеются особенные функции:math.dist(p, q)— возвращает Евклидово расстояние между точкамиpиq, заданными как итерируемые объекты одной длины:print(math.dist((0, 0, 0), (1, 1, 1))) # 1.7320508075688772
math.hypot(*coordinates)— возвращает длину многомерного вектора с координатами, заданными в позиционных аргументахcoordinates, и началом в центре системы координат. Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:print(math.
 hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
Функции преобразования угла. Доступны функции:
math.degrees(x)— преобразует угол из радианов в градусы:print(round(math.sin(math.radians(30)), 1)) # 0.5
math.radians(x)— преобразует угол из градусов в радианы.print(round(math.degrees(math.asin(0.5)), 1)) # 30.0
Гиперболические функции. Доступны функции
acosh(x),asinh(x),atanh(x),cosh(x),sinh(x),tanh(x).Специальные функции. Среди специальных функций интерес представляет Гамма-функция. Она описывает гладкую непрерывную функцию f(x) = (x – 1)!, график которой проходит через точки, соответствующие значениям функции факториала для целых чисел. Другими словами, гамма-функция интерполирует значения факториала для вещественных чисел:
print(math.
 gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
В библиотеке math можно воспользоваться значениями числа пи (math.pi) и экспоненты (math.e).
Библиотека numpy
Язык программирования Python удобен для быстрого создания программ с целью проверки какой-либо идеи. Однако зачастую его используют и в решении научных задач, а также при анализе больших данных и машинном обучении.
Возникает вопрос: каким образом может быстро обрабатывать много данных интерпретируемая, а не скомпилированная программа?
Оказывается, что в решении некоторых математических задач программы на Python могут быть такими же быстрыми, как и программы, созданные на компилируемых языках.
Существенную прибавку в скорости обеспечивает библиотека numpy (Numerical Python, читается как «нампАй»). Библиотека numpy частично написана на языках С и «Фортран», благодаря чему и работает быстро. Таким образом,
Таким образом, numpy сочетает в себе вычислительную мощность языков С и «Фортран» и простоту синтаксиса Python.
Библиотека numpy является нестандартной библиотекой.
Нестандартные модули можно установить в Python несколькими способами. Мы рассмотрим самый простой — установку из репозитория PyPI (Python Package Index). Репозиторий — коллекция дополнительных библиотек для Python, хранящаяся на сервере. В настоящий момент количество библиотек в репозитории составляет более 400 тысяч.
Для установки библиотек из репозитория необходимо подключение к сети Интернет, а далее нужно выполнить команду в консоли (терминале):
pip install название>
Установим библиотеку numpy командой:
pip install numpy
После ввода команды начнётся загрузка установочного пакета и дополнительных библиотек, от которых зависит numpy. Затем начнётся процесс установки. Если установка пройдёт успешно, то вы увидите вывод в командной строке:
Successfully installed numpy
Для импорта numpy обычно используют следующий код:
import numpy as np
В программе мы сможем обращаться к numpy по новому имени — np. Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Библиотека numpy работает с объектами-массивами, которые способны хранить много значений и быть многомерными. При этом, в отличие от списков, массивы могут хранить только значения одного типа. За счёт этого массивы в numpy занимают меньше памяти и работают быстрее, чем списки.
Создать массив можно разными способами. Один из них — использовать функцию array() для преобразования списка в массив. Для доступа к элементам массива необходимо указать индекс элемента в квадратных скобках. Индексация начинается с нуля:
import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a[0] = {a[0]}")
print(f"b[0] = {b[0]}")
Вывод программы:
a[0] = 1 b[0] = [1 2]
В нашем примере массив a имеет размерность, равную 1. Размерность массива
Размерность массива b равна 2. В терминологии numpy массив a имеет одну ось (термин «axis» из документации) длиной четыре элемента, а массив b имеет две оси: первая имеет длину 4, а длина второй оси равна 2.
Массивы numpy являются объектами класса ndarray. Наиболее важными атрибутами класса ndarray являются:
ndarray.ndim— размерность (количество осей) массива;ndarray.shape— кортеж, значения которого содержат количество элементов по каждой из осей массива;ndarray.size— общее количество элементов массива;ndarray.dtype— объект, описывающий тип данных элементов массива;ndarray.itemsize— размер памяти в байтах, занимаемый одним элементом массива.
import numpy as np
a = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a.ndim = {a.ndim}, a.shape = {a.shape}, a.size = {a. size}, a.dtype = {a.dtype}")
size}, a.dtype = {a.dtype}")
Вывод программы:
a.ndim = 2, a.shape = (4, 2), a.size = 8, a.dtype = int32
Встроенные в numpy типы данных аналогичны типам данных в языке программирования С. Например, в предыдущем примере мы создали массив со значениями типа int32, то есть целые числа со знаком (отрицательные и положительные) и размером занимаемой памяти 32 бита. Из ограничения в размере памяти для типов данных в numpy следует то, что массивы каждого типа данных могут хранить значения из определённого диапазона. Например, для int32 этот числовой диапазон составляет от -2 147 483 648 до 2 147 483 647.
Покажем на примере, что произойдёт, если попытаться записать значение не из диапазона для типа данных. Для этого создадим массив типа uint8 — целые числа без знака размером 8 бит. Диапазон значений для этого типа от 0 до 255. Тип данных можно указать через именованный аргумент dtype при создании массива:
import numpy as np a = np.array([1, 2, 3], dtype="uint8") a[0] = 256 print(a)
Вывод программы:
[0 2 3]
Значение элемента не вышло за пределы диапазона, а было взято с его начала.
В numpy существуют и другие встроенные типы данных. С ними можно ознакомиться в документации.
При создании массива без указания его типа в аргументе dtype библиотека numpy попытается привести его к тому типу данных, который сможет хранить все значения исходной коллекции.
Рассмотрим пример:
import numpy as np a = np.array([1, 2.5, 3]) print(a) print(a.dtype) b = np.array(['text', 1, 2.5]) print(b) print(b.dtype)
Вывод программы:
[1. 2.5 3. ] float64 ['text' '1' '2.5'] <U32
В примере для массива a был выбран тип данных float64, так как исходный список содержит вещественное число. Для массива b был выбран тип данных <U32, который может хранить строки в кодировке Unicode длиной 32 символа. Такой тип данных был выбран, поскольку в исходной коллекции есть элемент-строка.
Такой тип данных был выбран, поскольку в исходной коллекции есть элемент-строка.
Для создания массива из нулей используется функция np.zeros(), которая принимает кортеж с количеством чисел, соответствующим количеству осей массива, а значения в кортеже — количество элементов по каждой из осей.
import numpy as np a = np.zeros((4, 3)) print(a) print() a = np.zeros((4, 3), dtype="int32") print(a)
Вывод программы:
[[0. 0. 0.] [0. 0. 0.] [0. 0. 0.] [0. 0. 0.]] [[0 0 0] [0 0 0] [0 0 0] [0 0 0]]
Функция np.ones() создаёт массив аналогично функции np.zeros(), только из элементов-единиц.
import numpy as np a = np.ones((4, 3)) print(a)
Вывод программы:
[[1. 1. 1.] [1. 1. 1.] [1. 1. 1.] [1. 1. 1.]]
Функция np.eye() создаёт единичную матрицу, то есть массив с единицами на главной диагонали и нулевыми остальными элементами:
import numpy as np a = np.eye(5, 5, dtype="int8") print(a)
Вывод программы:
[[1 0 0 0 0] [0 1 0 0 0] [0 0 1 0 0] [0 0 0 1 0] [0 0 0 0 1]]
Для создания массива, заполненного значениями из диапазона, используется функция np.. Эта функция похожа на стандартную функцию  arange()
arange()range(), но возвращает массив и может создавать диапазон значений из вещественных чисел.
import numpy as np a = np.arange(1, 10) print(a) print() a = np.arange(1, 5, 0.4) print(a)
Вывод программы:
[1 2 3 4 5 6 7 8 9] [1. 1.4 1.8 2.2 2.6 3. 3.4 3.8 4.2 4.6]
Функция np.linspace() создаёт массив из заданного количества вещественных равномерно распределённых значений из указанного диапазона.
import numpy as np a = np.linspace(1, 5, 10) # задаётся начало, конец диапазона и количество значений print(a)
Вывод программы:
[1. 1.44444444 1.88888889 2.33333333 2.77777778 3.22222222 3.66666667 4.11111111 4.55555556 5. ]
Для изменения размерности массива используется функция reshape(). Она принимает кортеж, значения которого задают новые размеры массива по осям. Функция reshape() возвращает новый массив. Обратите внимание: при изменении размерности количество элементов в массиве не должно измениться.
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 6)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[0 0 0 0 0 0] [0 0 0 0 0 0]]
Метод resize() меняет размерность исходного массива:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a.resize((2, 2, 3)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0 0] [0 0 0]] [[0 0 0] [0 0 0]]]
Если при изменении размерности в функции reshape() указать значение -1 по одной или нескольким осям, то значения размерности рассчитаются автоматически:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 3, -1)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0] [0 0] [0 0]] [[0 0] [0 0] [0 0]]]
Для работы с массивами доступны все стандартные арифметические операции, а также тригонометрические, экспоненциальная и другие функции. Выполнение математических операций над массивами происходит поэлементно. Размерность массивов должна совпадать при выполнении этих операций. Применение некоторых из операций приведено в примере:
Выполнение математических операций над массивами происходит поэлементно. Размерность массивов должна совпадать при выполнении этих операций. Применение некоторых из операций приведено в примере:
import numpy as np a = np.array([9, 8, 7]) b = np.array([1, 2, 3]) print(a + b) print(a - b) print(a * b) print(a / b)
Вывод программы:
[10 10 10] [8 6 4] [ 9 16 21] [9. 4. 2.33333333]
Для умножения матриц используется операция @ или функция dot:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = np.array([[0, 0, 1],
[0, 1, 0],
[1, 0, 0]])
print(a @ b)
Вывод программы:
[[3 2 1] [6 5 4] [9 8 7]]
Матрицы можно транспонировать функцией transpose() и поворачивать функцией rot90(). При повороте можно указать направление поворота вторым аргументом:
import numpy as np a = np.arange(1, 13).reshape(4, 3) print(a) print("Транспонирование") print(a.transpose()) print("Поворот вправо") print(np.rot90(a)) print("Поворот влево") print(np.rot90(a, -1))
Вывод программы:
[[ 1 2 3] [ 4 5 6] [ 7 8 9] [10 11 12]] Транспонирование [[ 1 4 7 10] [ 2 5 8 11] [ 3 6 9 12]] Поворот вправо [[ 3 6 9 12] [ 2 5 8 11] [ 1 4 7 10]] Поворот влево [[10 7 4 1] [11 8 5 2] [12 9 6 3]]
Функции вычисления суммы элементов массива, поиска минимального и максимального элементов и многие другие по умолчанию работают для всех элементов массива, не учитывая размерность:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a.sum())
print(a.min())
print(a.max())
Вывод программы:
45 1 9
Дополнительно в указанных функциях можно указать номер оси (индексация с 0), на которой будет работать функция:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a. sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
Вывод программы:
[12 15 18] [ 6 15 24] [1 2 3] [3 6 9]
В массивах можно брать срез. Для одномерных массивов эта операция аналогична стандартному срезу в Python. Для многомерного массива можно задавать диапазон среза отдельно для каждой оси. Таким образом, можно взять срез отдельной части матрицы, указав, какие строки и столбцы должны попасть в срез:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) print() print(a[:2, 2:]) print() print(a[:, ::2])
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[3 4] [7 8]] [[ 1 3] [ 5 7] [ 9 11]]
В цикле for можно пройти по элементам первой оси массива:
import numpy as np
a = np.arange(1, 13).reshape(3, 4)
print(a)
for row in a:
print(row)
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [1 2 3 4] [5 6 7 8] [ 9 10 11 12]
Для линеаризации многомерного массива можно использовать атрибут flat, который является итератором, возвращающим последовательно значения массива:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) print() print("; ".join(str(el) for el in a.flat))
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12
Покажем на примере различие в скорости работы массивов и списков. Посчитаем сумму квадратных корней первых 107 чисел.
import numpy as np
from time import time
t = time()
print(f"Результат итератора: {sum(x ** 0.5 for x in range(10 ** 7))}.")
print(f"{time() - t} с.")
t = time()
print(f"Результат numpy: {np.sqrt(np.arange(10 ** 7)).sum()}.")
print(f"{time() - t} с.")
Вывод программы:
Результат итератора: 21081849486.439312. 1.7823209762573242 с. Результат numpy: 21081849486.442448. 0.05197310447692871 с.
Библиотека numpy решила задачу в 30 раз быстрее, чем итератор.
За счёт скорости работы и удобной обработки массивов библиотека numpy используется для расчётов во многих других библиотеках. С одной из них мы поработаем в следующей главе. 2} $$ 92}=\frac{3(n+1)}{n}\sim_\infty 3.$$
2} $$ 92}=\frac{3(n+1)}{n}\sim_\infty 3.$$
$\endgroup$
Репетитор по математике – Последовательности – Решенные задачи
Репетитор по математике – Последовательности – Решенные задачи – ПределыПроблема: Оценить следующий предел (если он существует)
Решение: Мы видим, что у нас есть соотношение мощностей, поэтому мы хотели бы использовать интуитивная оценка; однако, есть небольшая проблема в числителе. Если бы числитель был просто суммой п 2 − ln( n ), мы бы знали, что делать; к сожалению, это выражение переводится в экспоненциальное, что означает, что интуитивное рассуждение больше не применимо. Что мы можем сделать?
В знаменателе мы знаем, что когда n действительно огромно, то n 3 ничтожно мало по сравнению с факториалом n ! и мы
может игнорировать это. Мы также знаем, что ln( n ) ничтожно мало по сравнению с n 2 , но так как это происходит в экспоненте, это
какой-то хитрый. Мы знаем, что если игнорировать ln( n ) мы бы сделали просто
небольшая ошибка для больших n , но тогда мы делаем “2 в степени, равной
эта маленькая ошибка», и мы не знаем, что тогда происходит.
Мы знаем, что если игнорировать ln( n ) мы бы сделали просто
небольшая ошибка для больших n , но тогда мы делаем “2 в степени, равной
эта маленькая ошибка», и мы не знаем, что тогда происходит.
Если мы не знаем, что делать, обычно лучше начать с более простую задачу, а затем посмотрим, сможем ли мы использовать полученное понимание в более сложная ситуация. Итак, начнем с расследования
шкала полномочий говорит «факториалы побеждают экспоненты», но это относится только к таким вещам, как 2 n . Мы знаем, что кратные в показателе степени не имеют значения, например, мы могли бы поспорить 2 3 n = (2 3 ) n = 8 n и факториал украл бы его, но квадрат – это вообще другое животное. Мы не можем измениться алгебраически 2 n 2 во что-то вроде а п .
Итак, мы, к сожалению, делаем вывод, что шкала полномочий не даст нам никакого
ответь здесь.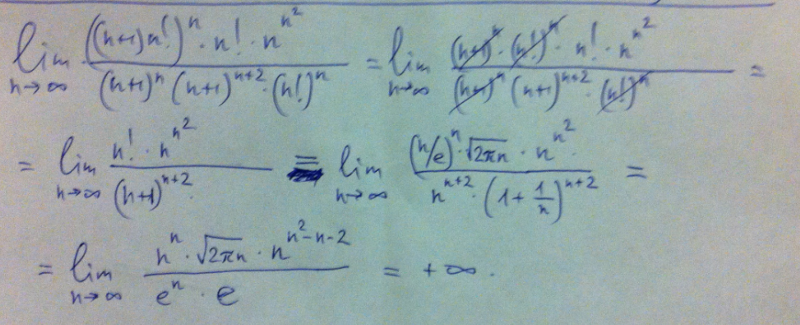 Тем не менее, это немного помогает. Когда шкала была установлена,
в
доказательства использовали спаривание и
сравнение. Здесь у нас есть две вещи. Факториал n !, который является
произведение n элементов (номера 1, 2,…, n ), и
2 n 2 , который является произведением n 2 элементы (цифры 2). Можем ли мы как-то грамотно сгруппировать этих двоих? Мы можем попробовать
этот:
Тем не менее, это немного помогает. Когда шкала была установлена,
в
доказательства использовали спаривание и
сравнение. Здесь у нас есть две вещи. Факториал n !, который является
произведение n элементов (номера 1, 2,…, n ), и
2 n 2 , который является произведением n 2 элементы (цифры 2). Можем ли мы как-то грамотно сгруппировать этих двоих? Мы можем попробовать
этот:
Насколько велико это число? Обратите внимание, что все маленькие дроби не меньше один, начиная с 2 n > n . Если мы применим его к все, кроме последнего члена, мы получаем
Последний факт следует из шкалы степеней и может быть доказан с помощью l’Больничное правило. Мы только что доказали с использованием сравнение с упрощенным последовательность, которую мы пробовали, уходит в бесконечность:
Теперь мы проникаем в часть n 3 и утверждаем, что, поскольку факториал преобладает над ним и, следовательно, пренебрежимо мал, у нас все еще есть
Как бы мы это обосновали? Есть две возможности. Традиционный способ
из коробочных полиномов и отношений
с степенями – это факторизовать доминирующие термины. Мы получаем
Традиционный способ
из коробочных полиномов и отношений
с степенями – это факторизовать доминирующие термины. Мы получаем
Ноль в оценке знаменателя следует из шкалы силы, «факториалы бьют силы». Как бы мы это доказали, если бы нам это было нужно? Это делается путем сравнения (факториал нельзя дифференцировать, поэтому Лопиталь определенно нет, и другого выбора не так много).
Это завершает доказательство того, что действительно
Другой способ проникнуть в n 3 состоит в том, чтобы использовать подход из Обратите внимание на интуитивные расчеты. Идея такова: две последовательности имеют одинаковый предел, если их отношение сходится к 1. Итак, мы просто сравниваем две приведенные выше последовательности, с и без н 3 .
Обратите внимание, что он был очень похож на предыдущий расчет и использовал тот же
дополнительный факт о соотношении н 3 / н !.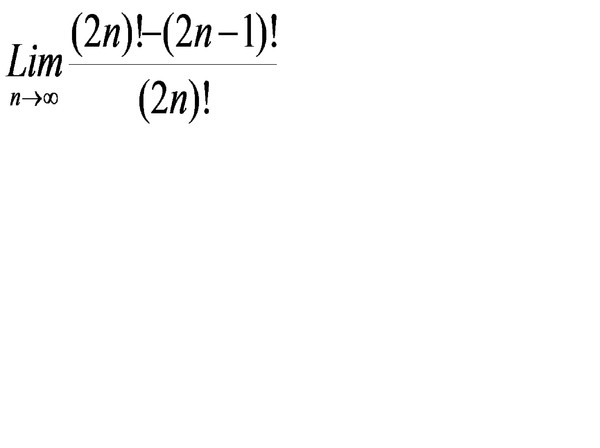
На самом деле есть гораздо более простой способ. Поскольку мы хотим показать, что эта последовательность стремится к бесконечности, достаточно найти подходящую оценку снизу, используя известный результат. Но это легко, от н ! − n 3 < n ! мы получаем
2 N 2 / ( N ! – N 3 )> 2 N 2 / N !
Обратите внимание, что если бы в знаменателе был «+», это сравнение не было бы работать больше:
2 N 2 / ( N !+ N 3 ) <2 N 2 / N !
Это говорит о том, что последовательность слева имеет предел, не превосходящий бесконечности (если она
существует), но это оставляет слишком много свободы — все, что меньше или равно
бесконечность, последовательность слева может, например, колебаться (и, таким образом, иметь
без ограничений), а может и уйти в бесконечность, только медленнее, чем тот, что справа,
что на самом деле и происходит! Как бы мы это доказали? Легко, первые два доказательства
который мы использовали, также будет работать со знаком «+» в знаменателе.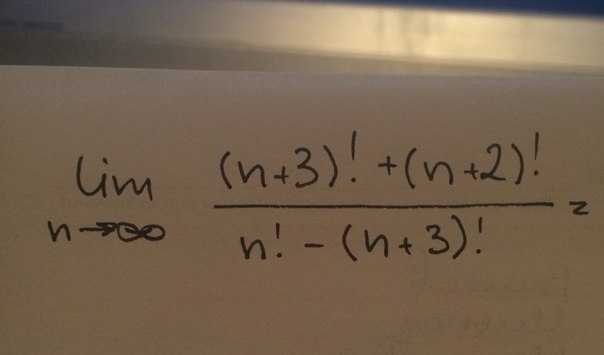
Но хватит об этом среднем шаге. Теперь мы хотели бы проникнуть внутрь пер( н ) как-то. К сожалению, наше подозрение выше, что все не так просто оказывается быть правильным, когда мы попробуем это. А именно, может ли быть правдой, что 2 п 2 и 2 n 2 − ln( n ) примерно одинаковы около бесконечности? Смотрим на предел их отношения и находим, что он не правда:
Это показывает, что 2 n 2 несравненно больше около бесконечности, чем 2 n 2 − ln( n ) . Как мы тогда перейти от последнего доказанного результата к пределу, который мы действительно ищем? Мы не можем использовать то, что мы сделали до сих пор, в качестве строительного блока:
Мы получили неопределенное соотношение и мы не можем применить правило Лопиталя, так как
мы не можем взять производную от факториала. Таким образом, алгебраически мы не можем пройти
от известного к данному.
Таким образом, алгебраически мы не можем пройти
от известного к данному.
Как насчет сравнения? У нас есть n 2 − ln( n ) < n 2 , поэтому мы можем попробовать следующее:
К сожалению, из такого сравнения мы не можем сделать никаких выводов. Если данная последовательность имеет предел, он должен быть меньше или равен бесконечности (приходится переходить к “меньше или равно”, сравнение не работает для резких неравенства), а значит, речь может идти о чем угодно, в том числе и о вероятность того, что она вообще не имеет предела.
Итак, мы видим, что мы не можем перейти от известного результата к заданной последовательности напрямую, мы должны сделать это независимо от последнего известного результата. Все еще, поскольку проблемы очень похожи, возможно, мы можем получить некоторое вдохновение от работу, которую мы уже сделали.
Одна из возможностей состоит в том, чтобы использовать тот факт, что n в конечном итоге намного больше. чем ln( n ). Заметим, что в предпоследнем расчете мы имели
2 n 2 сверху и
2 л( н ) дюймов
знаменатель, и мы знаем из шкалы полномочий, что прежний
преобладает над последним. К сожалению, мы уже израсходовали
2 n 2 , чтобы «перебить» факториал в знаменателе.
Однако, если вы посмотрите на соответствующее сравнение выше, вы увидите, что
неравенство там было очень щедрым, мы довольно много потеряли в этом
оценивать. Возможно, нам не нужно все
2 п 2 до
убить факториал. Можно было бы “одолжить” кусок
2 n 2 чтобы тоже побить логарифмическую часть? Пробуем:
чем ln( n ). Заметим, что в предпоследнем расчете мы имели
2 n 2 сверху и
2 л( н ) дюймов
знаменатель, и мы знаем из шкалы полномочий, что прежний
преобладает над последним. К сожалению, мы уже израсходовали
2 n 2 , чтобы «перебить» факториал в знаменателе.
Однако, если вы посмотрите на соответствующее сравнение выше, вы увидите, что
неравенство там было очень щедрым, мы довольно много потеряли в этом
оценивать. Возможно, нам не нужно все
2 п 2 до
убить факториал. Можно было бы “одолжить” кусок
2 n 2 чтобы тоже побить логарифмическую часть? Пробуем:
В последнем неравенстве мы использовали тот факт, что
2 n /2 > 1,2 n /3 > 1,…,2 n / n > 1. Вывод о пределе
то следовало из того, что n 2 − ln( n ) стремится к бесконечности (см.

 Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):
Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен): perm(4, 2)) # 12
print(math.perm(4)) # 24
perm(4, 2)) # 12
print(math.perm(4)) # 24
 В отличие от операции
В отличие от операции  hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
 gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
 size}, a.dtype = {a.dtype}")
size}, a.dtype = {a.dtype}")
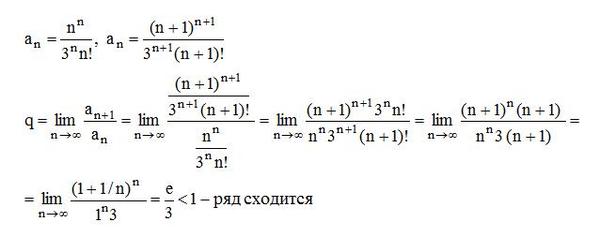 array([1, 2, 3], dtype="uint8")
a[0] = 256
print(a)
array([1, 2, 3], dtype="uint8")
a[0] = 256
print(a)
 reshape(4, 3)
print(a)
print("Транспонирование")
print(a.transpose())
print("Поворот вправо")
print(np.rot90(a))
print("Поворот влево")
print(np.rot90(a, -1))
reshape(4, 3)
print(a)
print("Транспонирование")
print(a.transpose())
print("Поворот вправо")
print(np.rot90(a))
print("Поворот влево")
print(np.rot90(a, -1))
 sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
sum(axis=0)) # сумма чисел в каждом столбце
print(a.sum(axis=1)) # сумма чисел в каждой строке
print(a.min(axis=0)) # минимум по столбцам
print(a.max(axis=1)) # максимум по строкам
 arange(1, 13).reshape(3, 4)
print(a)
print()
print("; ".join(str(el) for el in a.flat))
arange(1, 13).reshape(3, 4)
print(a)
print()
print("; ".join(str(el) for el in a.flat))