Как решать пределы с логарифмами: Пределы с логарифмами, примеры решений

Что такое логарифмы и зачем они нужны — Журнал «Код»

Для многих логарифм — это самая странная часть в математике: непонятно, как их считать, где применять и как они могут пригодиться в жизни. Сегодня ответим на все эти вопросы.

Если интересно, как в математике работают остальные функции и символы, вот что у нас уже есть:

Что такое логарифм

Задача логарифма — ответить на такой вопрос:

В какую степень нужно возвести одно число, чтобы получилось другое?

На языке математики это будет выглядеть вот так:

Теперь сделаем то же самое, но уже с числами. Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.

Десятичный, натуральный и другие логарифмы

Число A, которое возводят в какую-то степень, называется основанием логарифма. Самые популярные у математиков логарифмы — десятичный и натуральный.

Десятичный логарифм — это когда в основании логарифма стоит число 10. Наша задача в этом случае — найти, в какую степень нужно возвести 10, чтобы получить желаемое число. Обозначается так — lg: 

Натуральный логарифм устроен похоже, только вместо десятки в основании логарифма стоит число e, которое примерно равно 2,71828 и называется числом Эйлера. В математике число e играет такую же важную роль, как в геометрии — число пи, поэтому логарифм по основанию e часто встречается во многих математических выкладках и доказательствах.

Обозначается натуральный логарифм так — ln:

Логарифмическая шкала

Если мы возьмём линию и отметим на ней точки через каждый сантиметр, то мы получим арифметическую шкалу. Арифметическую — потому что каждая новая отметка считается арифметическим действием — сложением шага и предыдущего значения:

Но если мы вместо сложения возьмём логарифм, например, по основанию 10, то каждая новая отметка будет зависеть от значения десятичного логарифма:

Это выглядит странно, но логарифмическая шкала постоянно применяется в экономике и маркетинге, когда нужно оценить рост или падение стоимости товара. Если взять обычную арифметическую шкалу, то разница между парами (1, 2) и (9, 10) будет одной и той же — 1 пункт. 

Но при этом в первом случае цена выросла в 2 раза, с 1 до 2, а во втором случае — всего лишь на 10%. С логарифмической шкалой рост цены будет выглядеть логичнее:

Зачем нужны логарифмы в жизни

Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется. Вот несколько примеров.

Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.

В химии активность водородных ионов тоже считается по логарифмической шкале.

Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.

В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.

Логарифмы в природе

Больше всего логарифмов можно встретить в природе в виде логарифмической спирали. Математическая формула спирали выглядит так:

Если мы захотим построить график этого уравнения, то он будет выглядеть так:

Логарифмическая спираль в математике.

А вот логарифмическая спираль в природе — в ракушках, подсолнечнике и капусте. С капустой ещё связана другая интересная тема — фракталы, но про них поговорим в другой раз.

Даже рога у горных козлов закручиваются по логарифмической спирали:

Что дальше

Теперь мы знаем про логарифмы достаточно, чтобы понять, как они работают. В следующей статье напишем простую программу из двух циклов, которая посчитает нам практически любой логарифм по любому основанию.

Текст:

Михаил Полянин

Редактор:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Кирилл Климентьев

Соцсети:

Алина Грызлова

Логарифмические ряды, Логарифмы, log, ln, lg

Ряды Маклорена не могут быть использованы для нахождения ряда для logx, поэтому должен быть найден еще один метод. 5}{5}….$

Когда упрощаются коэффициенты путем деления на множители факториала, они являются своего рода гармоническим рядом, который не сходится очень быстро. Числители – это последовательные степени х, а знаменатели простые числа, не факториалы.

Вы захотите логарифмы чисел больших, чем 2. Здесь скорость сходимости показана в нахождении логарифма 2 этим методом. На сходимость влияет: единственный уменьшающийся фактор гармонического ряда интегральных обратных чисел. Он колеблется между наивысшим значением, а значит, должен сходиться гораздо дальше, чтобы достичь своего наивысшего значения.

Логарифмические ряды: изменение

Вот трюк, для чего введены логарифмы. Если вы изменяете переменную снова, используя (1 + x)/(1 – x), по принципу логарифмов, логарифм этой переменной будет логарифмом (1 + x) минус логарифм (1 – x).

Во-первых, ряд логарифмов (l – x) был последовательностью степеней x разделенных на гармоническую последовательность интегральных чисел, меняющих свой знак. Ряды для log(l – x) используют те же численные члены, но все их знаки – отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.

Этот метод делает две вещи: удаляет четные степени x и и объединяет их. Эти ряды заключены в большие скобки, умноженные на 2.

Чтобы показать, насколько быстрее эти ряды сходятся, используйте это для вычисления log 2, что при применении первого метода заняло бы вечность. Решите (x + 1)/(x – 1) = 2. Здесь еще одна переменная изменится. Решая этого уравнения, переменная в ряде не 1, а 1/3. Так как каждый другой член выпал, последовательные члены уменьшаются на х (или 1/9). Это соотношение приводит к гораздо быстрому схождению. Он сходится так быстро, что только 4 члена необходимы для получения log2 c четырьмя цифрами после запятой.

Расчет логарифмов

Здесь вы рассчитываете два логарифма, чтобы найти сравнения в скорости сходимости. Для расчета log1,1 сделайте х = 1 / 21.

Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.

Как вы уже видели, для вычисления log2, х = 1/3, где сходимость около одной десятой за каждый дополнительный член. Для точности до шести цифр, требуется семь членов.

Теперь попробуйте найти значение log 3; x = 1/2. Этот ряд сходится более медленно, но попробуйте по-другому. Вы уже посчитали log 2. Log 3 = log 2 + log 1.5, потому что 3 = 2.1,5. Поэтому, найдите log1.5 и сложите его значение с log2. Log 1.5 использует x = 1/5 и его ряд сходится быстрее чем в случае с log 2. Теперь у вас есть значение с 6-ю цифрами для log 3.

В примере выше вы пробовали найти значение логарифмов до 10. Обратите внимание, что есть способы для упрощения вычислений. Log 4 есть удвоенный log 2. Вы можете получить его либо из 4 = 2.2 или из 4 = 2². Log 5 есть log 4 + log 1.25. Log 6 есть log 2 + log 3. Log 7 есть log 4 + log 1.75. Log 8 есть log 2 взятый 3 раза, потому что 8 есть 2³. Log 9 есть удвоенной log 3 потому что 9 = 3². Наконец, log 10 есть log 2+ log 5.

Общие логарифмы

Хотя все алгоритмы должны быть вычислены в их основной форме с основанием e, иногда называемыми

гиперболическими или логарифмами Непера (от имени изобретателя логарифмов). Но более распространенное названия натуральные логарифмы или логарифмы с основанием e.
Log₁₀x = y       x = 10^y       Log_ε10 = t       ε^t = 10
      So x = (ε^t)^y = ε^ty       Log_εx = ty

Если у логарифма основание 10, тогда логарифм 10 по основанию 10 равен 1. Вы можете изменить основание, разделив натуральный логарифм на логарифм 10.

Использование логарифмов: умножение и деление

Конечно, нахождение логарифмов с помощью карманных калькуляторов намного проще, чем использование таблиц. Калькулятор вычисляет логарифмы обоих видов, натуральные и общие.

Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.

Примеры, которые мы здесь приводим, взяты из таблиц с логарифмами с четырьмя цифрами. Ваш калькулятор, возможно, показывает больше цифр, чем таблица. На своем калькуляторе я ввел логарифм 32 и получил 1.505149978; значение логарифма 256 равно 2.408239965. Суммируя их, получим 3.9133889944. Используя сдвиг, ответ равен точно 8192!

Последний пример показывает еще одну разницу с таблицами. Таблица дала только мантиссу – дробную часть. Вам необходимо вставить характеристику – целое число слева от запятой. 0.0969 есть мантиссой (в четырехзначных таблицах) для чисел 125. Риска над 1 указывает, что характеристика отрицательная. Поэтому, log есть -1 + 0.0969. Мой калькулятор пишет -0.903089987. Однако, если я ввожу 1.25 вместо 0.125, калькулятор пишет 0.096910013. Если число больше 1, мантисса не меняется, только характеристика изменяется и смещается десятичная точка.

Использование логарифмов: индексы

Здесь снова примеры, которые были приготовлены с помощью четырехзначных логарифмических таблиц. Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, x

y. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.

Логарифм 12 считается калькулятором как 1.079181246. Умножая на 3, получаем 3.23764 3738. Используя смещение и логарифм дает точно 1728. Вводим 12 снова. Нажимаем x^y, затем 3, и =. Калькулятор снова высвечивает 1728.

В следующем примере log 2 равен 0.301029995, правильный ответ снова. Однако, если ввести log 1024, высвечивается предыдущее значение 3.010299957 с одной дополнительной цифрой.

Выше использованы логарифмы или x^y клавиши, где индексы были очевидны. Иногда ответ не такой простой. Возьмем следующее: 35

4/5. С использованием калькулятора: Log 35 = 1.544068044. Используя клавиши x^y, получаем тот же ответ.

Кроме того, можно вычислить это значение используя биномиальное разложение, если калькулятор оснащен достаточной памятью. Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.

Биноминальным разложением

Биноминальным разложением

В этот раз, 4-х значные логарифмы довольно ограниченны. Используя тот же калькулятор с клавишами логарифмов или с x

y, результат равен 353.5533906. Биноминальное разложение дает тот же результат за исключением последних двух цифр.

Конечно, ваш калькулятор не сделает биномиальный ряд для вас. Для того-то и упражнения, чтобы показать, что биномиальный ряд работает. Как калькулятор это делает? Он имеет встроенные программы, которые вычисляют логарифмические ряды очень быстро – за доли секунды. Помните, что калькулятор работает в двоичной системе, даже если он высвечивает десятичные цифры.

Использование логарифмов с формулами

Формула здесь связывает давление и объем в физическом расширение и сжатии газа.

Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.

В таблице приведены значения v от 10 до 30 (предполагается, что этот диапазон охватывает необходимые значения в нашей конкретной задаче) и используются логарифмы для расчета соответствующего значения р (в последнем столбце). В 3-й колонке приведены значения 0,4logv в качестве помощи нахождения log1,4v. Табулирование с помощью этого метода облегчало процесс до появления калькуляторов.

Четвертая колонка есть вычитание из 3, что есть log1000. Чтобы сделать это на калькуляторе, у вас есть выбор: использовать клавишу logs или x^y

. В любом случае, вы должны вставить k в это. Если k было другим, чем степень 10, это немного усложнит вычисление. Метод: использовать клавишу 1/x (обратное значение) а потом умножить на 1000 (или на соответсвующее значение к).

Поиск закона логарифмов

Вы знаете, что v и p относится друг к другу по закону типа: pvⁿ = k. Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши x^y является не таким легким; использование клавиши log есть более легким.

Возьмем логарифмы значения p: 1.361727836 и 1.176091259. После вычитания получим 0.185636579. Возьмем логарифмы значения v: 1.176091259 и 1.301029996. После вычитания получим: 0.124938736. Разделим первое значение на второе: 0.185636579/0.124938736= 1.485820827 – значение n. Такое вычисление требовало использование ячейки памяти вашего калькулятора. И все эти цифры после запятой точные, но необязательные. Числа, с которыми вам необходимо работать, скорее всего, имеют две значащие цифры.

Вопросы и задачи

1. Рассмотрим следующий рисунок. Эти функции нарисованы на логарифмической шкале. Перерисуйте приближения этих функций в полулогарифмическом масштабе (ось х – линейные, ось у – логарифмическая). Выберите масштаб, который является обоснованными для угла значения в каждом конкретном случае.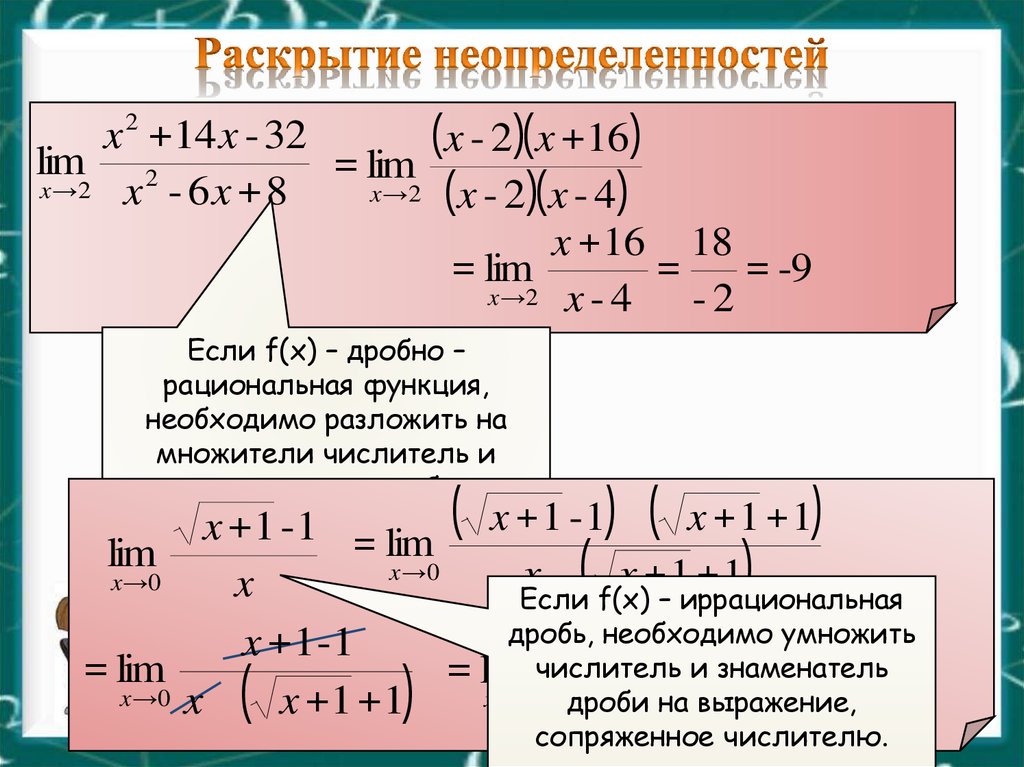

2. Нарисуйте приблизительные значения функции в прямоугольных координатах поверх приведенного графика. Выберите масштаб, который является наиболее подходящим для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными.

3. Рассмотрите следующий рисунок. Эти функции нарисованы в прямоугольных координатах. Нарисуйте приблизительные значения функции в полулогарифмическом масштабе (ось х – линейная и ось у – логарифмическая). Выберите подходящий масштаб для диапазона значений в каждом случае.

4. Нарисуйте приблизительные значения функции в логарифмическом масштабе . Выберите подходящий масштаб для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными.

5. Используя формулу log₁₀xy = log₁₀x + log₁₀y, найдите значения следующих множителей путем сложений чисел. Вы можете использовать калькулятор. Запишите ответы с тремя цифрами после запятой.
(a) 5.44 • 3.67       (b) 10.5 • 0.567
(c) 36.7 • 2.56       (d) 0.987 • 0.822

6. Используя формулу log₁₀x^y = ylog₁₀x, найдите значения (стремя цифрами после запятой). Вы можете использовать калькулятор.
(a) 5.44^3,67       (b) 10.5^3,67
(c) 36.7^2,56       (d) 0.987^0,822

7. Если бы в решении задачи №6 натуральные логарифмы (с основанием e) были бы использованы вместо логарифмов с основанием 10 был бы результат верным?

8. Если бы в решении задачи №6 логарифмы по основанию 7 были бы использованы вместо десятичных логарифмов, был бы результат верным?

Пределы логарифмических функций

Главная Алгебра II Логарифмы и экспоненциальные функции Темы Логарифмические функции Пределы логарифмических функций

Темы

• Введение
• Темы
• Связывание экспонент и логарифмов
• Обратные функции
• Правила для обратных функций
• Основание
• The Natural Log
• Экспоненциальные функции
• Линейный и экспоненциальный рост
• Экспоненциальные и распах
• Повторение обратных операций
• Изменение основания
• Пределы логарифмических функций
• Свойства экспонент и логарифмов
• В реальном мире
• Примеры
• Упражнения
• Задачи Math Shack
• Условия
• Лучшее из Интернета
• Викторины
• Раздаточный материал
• Содержание

• НАЗАД
• СЛЕДУЮЩИЙ

Так же, как экспоненциальные функции, логарифмические функции имеют свои пределы. Помните, чего не могут экспоненциальные функции: они не могут выводить отрицательное число вместо 9.0084 ф ( х ). Функция, на которую мы обратили внимание, когда думали об экспоненциальных функциях, была f ( x ) = 4 ^x .

Поднимем зеркало, взяв логарифм по основанию 4, чтобы получить обратную функцию: f ( x ) = log ₄ x .

Если бы мы попытались сделать x отрицательными или равными нулю в этой логарифмической функции, в известной вселенной нет y -значения, которое позволило бы нам это сделать, поэтому логарифмическая функция не определена в x – значения нуля или меньше. Другими словами, его домен равен x > 0.

Вот как выглядит график f ( x ) = log ₄ x :

3 экспоненциальная функция никогда не может быть нулевой или отрицательной, обратная (логарифмическая) функция никогда не может иметь отрицательное входное значение нуля.

Пример задачи

Когда будет f ( x ) = log ₅ x быть больше г ( x ) = log ₂₀ x ? Игнорировать отрицательные значения x .

Результатом этих журналов является показатель степени , необходимый выше 5 или 20, чтобы равняться x.

Когда x больше 1, log ₅ x будет больше, потому что для 5 требуется экспонента на больше, чем для 20, чтобы равняться любому x в этой области. Пятерка — это маленькая креветка, которой, по сути, нужна поддержка. Например:

Для х = 2 получаем 5 ^0,43 или 20 ^0,23 .
За х = 5 получаем 5 ¹ или 20 ^0,54 .

Однако, когда x меньше 1, log ₂₀ x будет больше, чем log ₅ x , поскольку для уменьшения этого 20 до размера по сравнению с 5 необходим отрицательный показатель степени, близкий к нулю. , У этого 20 много мускулов, и ему нужен большой толчок со стороны экспоненты, чтобы уменьшить размер.

Для  получаем 5 ^-0,43 или 20 ^-0,23 .

Для  получаем 5 ^-0,86 или 20 ^-0,46 .

• НАЗАД
• СЛЕДУЮЩИЙ

Процитировать эту страницу

---

ПРЕДЕЛЫ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ

Логарифмическая функция является обратной экспоненциальной функцией. Логарифмическая функция определяется следующим образом:

y=logax тогда и только тогда, когда x=ay ; для всех x>0, a>0 и a≠1

Обозначим логарифмическую функцию как

f(x)=logax   , где a — основание логарифма.

Есть две наиболее часто используемые базы. Они имеют основание 10 и основание e.

Когда мы используем основание 10, функция известна как функция десятичного логарифма и представляется как f(x)=log10x

Когда мы используем основание e, функция известна как функция натурального логарифма и представлена ​​как f(x)=logex

График логарифмической функции выглядит следующим образом:

Методы нахождения предела логарифмической функции обсуждаются ниже.

ПРЕДЕЛЫ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ-

При вычислении предела логарифмической функции используются два основных свойства. Результаты этих двух свойств можно напрямую использовать в качестве формул для нахождения предела. Два свойства:

1. x→0loge(1+x)x=1

2. x→0logb(1+x)x=1logeb

Мы также можем вычислить предел логарифмической функции, используя Правило госпиталя. Обсудим это правило подробнее.

Правило Ло Хоспиталя :

В соответствии с этим правилом для дифференцируемых функций f и g на открытом интервале I за исключением, возможно, точки c, содержащейся в I, если

x→cf(x)=x→cg(x )=0 или ∞ или -∞ и g'(x)≠0 для всех x в I с x≠c и x→cf'(x)g'(x) существует, то

x→cf(x)g (x)=x→cf'(x)g'(x)

Дифференцирование числителя и знаменателя обычно упрощает и преобразует его в форму, которую можно оценить непосредственно.

ВАЖНЫЕ ПРИМЕРЫ

1. Вычислить x→elogex-2 / x-2e

Чтобы оценить этот предел, нам нужно применить правило L’Hospital.

Используя правило Л’Госпиталя, мы получаем

НЕКОТОРЫЕ ВАЖНЫЕ ПРЕДЕЛЫ ЛОГАРИТМИЧЕСКИХ ФУНКЦИЙ:

При работе над нахождением пределов логарифмических функций рекомендуется помнить некоторые важные пределы. Это ускорит и упростит расчеты. Ниже приведены некоторые важные ограничения.

АЛГЕБРА ПРЕДЕЛОВ-

При решении сложных задач на нахождение пределов очень важно понимать алгебру пределов. Таким образом, проблема разбивается на более простые пределы, что облегчает ее решение. Обсудим несколько теорем о пределах и функциях, которые помогают решить проблемы пределов.

  Частный случай — если g — постоянная функция такая, что g(x)=λ, для некоторого действительного числа λ, то

 x→a[λ f(x)]= λ x→af(x)   

ЗАКЛЮЧЕНИЕ 

Обратные экспоненциальные функции также известны как логарифмические функции.