Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.
Так, сумма a3 и b2 есть a3 + b2.
Сумма a3 – bn и h5 -d4 есть a3 – bn + h5 – d4.
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a2 и 3a2 равна 5a2.Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.
Так, сумма a2 и a3 есть сумма a2 + a3.
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a3bn и 3a5b6 есть a3bn + 3a5b6.
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
| Из | 2a4 | 3h2b6 | 5(a – h)6 |
| Вычитаем | -6a4 | 4h2b6 | 2(a – h)6 |
| Результат | 8a4 | -h2b6 | 3(a – h)6 |
Или:
2a4 – (-6a4) = 8a4
3h2b6 – 4h2b6 = -h2b6
5(a – h)6 – 2(a – h)6 = 3(a – h)6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a3 на b2 равен a3b2 или aaabb.
| Первый множитель | x-3 | 3a6 | a2b3y2 |
| Второй множитель | am | -2x | a3b2y |
| Результат | amx-3 | -6a6xy2 | a2b3y2a3b2y |
Или:
x-3 ⋅ am = amx-3
3a6y2 ⋅ (-2x) = -6a6xy2
a2b3y2 ⋅ a3b2y = a2b3y2a3b2y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат – это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a2.a3 = aa.aaa = aaaaa = a5.
Здесь 5 – это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, an.am = am+n
Для an, a берётся как множитель столько раз, сколько равна степень n;
И am, берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a2.a6 = a2+6 = a8. И x3.x2.x = x3+2+1 = x6.
| Первый множитель | 4an | b2y3 | (b + h – y)n |
| Второй множитель | 2an | b4y | (b + h – y) |
| Результат | 8a2n | b6y4 | (b + h – y)n+1 |
Или:
4an ⋅ 2an = 8a2n
b2y3 ⋅ b4y = b6y4
(b + h – y)n ⋅ (b + h – y) = (b + h – y)n+1
Умножьте (x3 + x2y + xy2 + y3) ⋅ (x – y).
Ответ: x4 – y4.
Умножьте (x3 + x – 5) ⋅ (2x3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых – отрицательные.
1. Так, a-2.a-3
2. y-n.y-m = y-n-m.
3. a-n.am = am-n.
Если a + b умножаются на a – b, результат будет равен a2 – b2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a – y).(a + y) = a2 – y2.
(a2 – y2)⋅(a2 + y2) = a4 – y
(a4 – y4)⋅(a4 + y4) = a8 – y8. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a2/a3 и a-3/a-4 и приведите к общему знаменателю.
a2.a-4 есть a-2 первый числитель.
a3.a-3 есть a0 = 1, второй числитель.
a3.a-4 есть a-1, общий числитель.
После упрощения: a-2/a-1 и 1/a-1.
4. Уменьшите показатели степеней 2a
Ответ: 2a3/5a7 и 5a5/5a7 или 2a3/5a2 и 5/5a2.
5. Умножьте (a3 + b)/b4 на (a – b)/3.
6. Умножьте (a5 + 1)/x2 на (b2 – 1)/(x + a).
7. Умножьте b4/a-2 на h-3/x и an/y-3.
8. Разделите a4/y3 на a3/y2.
9. Разделите (h3 – 1)/d4 на (dn + 1)/h.
§ 8. Примеры вычисления пределов
Пример 1. Вычислить предел функции целочисленного
аргумента при
; .
Решение примера 1:
о
.
о
При вычислении предела в числителе и знаменателе пренебрегли постоянными слагаемыми по сравнению с бесконечно большой величиной ~ .
.
Здесь было использовано свойства бесконечности (бесконечно больших величин):
.
о о
.
о о
Здесь
сначала пренебрегли постоянными в
числителе и знаменателе по сравнению
с бесконечно большими слагаемыми. Затем
в числителе пренебрегли величиной по сравнению с бесконечно большой
величиной высшего порядка .
В знаменателе также, величина ,
которой пренебрегаем, может рассматриваться
как бесконечно малая по сравнению с
величиной .
Затем
в числителе пренебрегли величиной по сравнению с бесконечно большой
величиной высшего порядка .
В знаменателе также, величина ,
которой пренебрегаем, может рассматриваться
как бесконечно малая по сравнению с
величиной .
о о
.
о
Здесь опять постоянной величиной пренебрегали по сравнению с бесконечно большой величиной , которая сама является бесконечно малой по сравнению с , поскольку для степеней имеет место неравенство < 2/3.
В знаменателе по тем же причинам пренебрегли величиной по сравнению с ее квадратом . Последняя является бескончно большой величиной высшего порядка по сравнению с величиной .
Замечание: При сравнении порядков бесконечно больших степенных функций можно пользоваться шкалой бесконечно больших функций (см. §7 ).

Здесь учтено, что бесконечно большие величины в отрицательной степени становятся бесконечно малыми. Действительно, например,
.
о
.
о
Здесь пренебрегли постоянными величинами по сравнению с бесконечно большими, а также учтено, что бесконечно большая величина в отрицательной степени является бесконечно малой величиной.
Пример 2. Вычислить предел функции целочисленного аргумента при .
.
Решение примера 2.
.
При раскрытии неопределенности была использована формула разности кубов:
.
Ее использование
приводит к уничтожению кубических
корней. Формула срабатывает после
умножения и деления заданного выражения
на неполный квадрат суммы.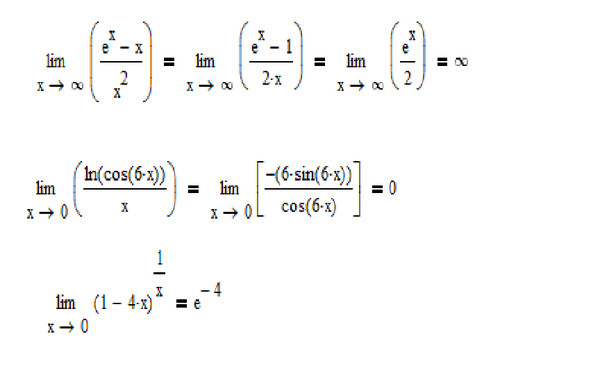
Приведем другой способ решения, с помощью различного представления функций, эквивалентных в нуле, см § 4.
.
.
В первом слагаемом под корнем единицей можно пренебречь по сравнению с бесконечно большой величиной . При сравнении двух бесконечно больших функций и первой из них можно пренебречь как бесконечно большой, низшего порядка, поскольку 1 / 7 < 1 / 2.
.
Здесь постоянными числами в числителе и знаменателе пренебрегаем по сравнению с бесконечно большой величиной .
.
Как и в предыдущем примере, постоянными числами пренебрегаем по сравнению с бесконечно большой величиной .
.
Для раскрытия неопределенности вида применяется стандартное преобразование с использованием основного логарифмического тождества в соответствии с формулой .
Для
преобразования логарифмической функции
использована формула эквивалентных в
нуле функций (см. § 4):
,
§ 4):
,
причем в качестве бесконечно малой величины здесь берется выражение
.
Пример 3. Вычислить предел функции целочисленного аргумента
при
.
Замечание. При вычислении пределов с использованием понятия факториала помимо определения факториала:
или
(например, 5 ! = )
необходимо использовать свойства факториала, следующие из его определения:
1°
2°
3°
……………………………………………………………………….
!
Решение примера 3.
о
.
При
решении было использовано второе
свойство факториала, записанное в форме . Под знаком предела пренебрегли единицей
по сравнению с бесконечно большой
величиной .
Под знаком предела пренебрегли единицей
по сравнению с бесконечно большой
величиной .
.
Здесь было использовано первое свойство факториала, записанное в форме .
o
.
о
Здесь было использовано второе свойство факториала, записанное в форме . Кроме того, под знаком предела пренебрегли единицей по сравнению с бесконечно большой величиной ~ .
о
.
о
Здесь в числителе и знаменателе пренебрегли постоянными величинами (не зависящими от ), затем было использовано первое свойство факториала, записанное в форме .
.
Здесь
было использовано третье свойство
факториала, записанное в форме ,
а также первое свойство факториала,
записанное в форме .
.
Здесь было дважды использовано первое свойство факториала, записанное в формах и .
Пример 4. Вычислить пределы функций, если они существуют, при и при
.
Решение примера 4.
.
Ввиду того, что пределы слева и справа в точке х = 0 не совпадают, искомый предел не существует.
о
.
Последний предел вычисляется аналогично предыдущему. В числителе дроби пренебрегли постоянным числом по сравнению с бесконечно большим слагаемым ~ .
.
Ввиду совпадения пределов слева и справа в нуле, искомый предел также равен бесконечности: .
В
числителе пренебрегли единицей по
сравнению с бесконечно большим слагаемым
~
.
о о
.
о
В числителе пренебрегли бесконечно малыми величинами по сравнению с конечным числом два. В знаменателе пренебрегли вторым слагаемым как величиной бесконечно малой по сравнению с первым слагаемым ( известно, что при возведении числа , меньшего единицы в положительную степень, число становится тем меньше, чем больше степень).
Заметим здесь, что в этом конкретном примере пренебрегать вторым слагаемым в знаменателе было не обязательно, однако такое действие в некоторых случаях играет существенную роль.
Ввиду того, что оба вычисленных предела совпадают, искомый предел существует и равен тому же значению предела: .
о о о о
.
о о
Здесь в соответствии
со шкалой бесконечно больших функций
два первых слагаемых числителя и первое
слагаемое знаменателя являются по
сравнению с оставленными слагаемыми
бесконечно малыми величинами, которыми
можно пренебречь. Последнее можно
объяснить и тем, что при возведении
чисел, больших единицы в положительную
степень, результат будет тем больше,
чем больше величина степени, а в нашем
случае в степень возводится сколь угодно
большая величина.
Последнее можно
объяснить и тем, что при возведении
чисел, больших единицы в положительную
степень, результат будет тем больше,
чем больше величина степени, а в нашем
случае в степень возводится сколь угодно
большая величина.
.
.
Ввиду равенства обоих пределов искомый предел существует и равен вычисленному значению предела: .
о
.
о
Здесь второе и третье слагаемые числителя взаимно уничтожаются (при любых положительных значениях ).
В знаменателе в соответствии со шкалой бесконечно больших функций слагаемым с меньшей степенью можно пренебречь. Единицей в числителе пренебрегаем по сравнению с бесконечно большим значением .
о о
.
о
Здесь
второе и третье слагаемые числителя
складываются (при любых отрицательных
значениях
),
образуя положительную величину .
Вторым слагаемое знаменателя пренебрегаем как величиной бесконечно большой низшего порядка, по сравнению с первым слагаемым (т.е. бесконечно малой по сравнению с первым слагаемым).
.
.
Ввиду того, что вычисленные пределы не совпадают, искомый предел – не существует.
о о о
.
о о
.
Оба последних предела вычисляются одинаково. Постоянными числами 1 и 4 пренебрегаем по сравнению с бесконечно большим значением .
Величиной также пренебрегаем, т. к. она является бесконечно малой: при .
Пример 5. Вычислить пределы функций, если они существуют, при и при
.
Решение
примера 5.
.
– не существует.
Последний предел не существует, т. к. под корнем в знаменателе стоит отрицательная величина. Это можно было сразу заметить, если бы мы рассмотрели область определения функции, стоящей под знаком предела.
Таким образом искомого предела функции при также не существует. Существует лишь предел слева в единице, который и был найден выше.
– предел не существует.
Последний предел не существует т. к. опять под корнем в знаменателе стоит отрицательная величина. Предела слева в точке x = 2 также не существует по тем же причинам.
.
Ввиду совпадения обоих пределов, в точке х =1, искомый предел существует и равен значению вычисленного предела:
.
.
Здесь
мы не стали вычислять отдельно левый и
правый пределы в точке х=2, ввиду того,
что скобка возводится в квадрат, и вычисления как
левого, так и правого пределов не
отличались бы друг от друга.
– не существует.
Здесь не существование предела связано с тем, окрестность точки х =1 не входит в область определения рассматриваемой функции, ввиду того, что аргумент логарифма должен быть только положительным: .
.
Предел слева в точке х = 2 не существует поскольку область определения рассматриваемой функции: . Таким образом, в точке х = 2 предел также не существует. (Существует лишь предел справа, который и был вычислен).
.
.
Поскольку в точке х = 1 пределы слева и справа не совпадают, искомый предел – не существует.
.
.
Ввиду того, что в точке х = 2 пределы справа и слева не совпадают, искомый не существует.
При вычислении значения арксинуса в нуле можно использовать график функции
y=arcsin x
-1 0 1 x
Пример
6. Вычислить пределы функций при
Вычислить пределы функций при
Решение примера 6.
.
Здесь мы воспользовались формулами для функций, эквивалентных в нуле (см. § 4), причем для синуса и арктангенса ограничились лишь первым членом разложения в ряд Тейлора этих функций.
.
Здесь опять использованы различные формы функций, эквивалентных в нуле (см. § 4). Для синуса ограничились лишь первым членом разложения, а для показательной функции использованы ее два первых члена разложения в ряд Тейлора.
Необходимость учета именно двух членов разложения диктуется требованием, что в результате подстановки разложения под знак предела, после взаимного уничтожения слагаемых, какие то слагаемые должны оставаться. Здесь в знаменателе дроби осталось слагаемое ( ).
.
Здесь при
использовании различных форм функций,
эквивалентных в нуле (см. § 4), для
логарифмической функции оставлен первый
ее член разложения, а для косинуса
оставлены два его первых члена разложения
в ряд Тейлора.
§ 4), для
логарифмической функции оставлен первый
ее член разложения, а для косинуса
оставлены два его первых члена разложения
в ряд Тейлора.
Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали.
= .
Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали. Выражение, стоящее в знаменателе, преобразовывалось следующим образом:
.
Пример 7. Вычислить пределы функций, если они существуют, при
Решение примера 7.
.
Здесь
были использованы различные формы
функций, эквивалентных в нуле (см. § 4),
причем в качестве «нуля» выступала
величина .
.
Здесь были опять использованы различные формы эквивалентных в нуле функций (см. § 4), где в качестве «нуля» выступала величина .
.
Здесь были опять использованы различные формы функций, эквивалентных в нуле, а в качестве «нуля» выступала величина .
.
Здесь было использовано свойство логарифма: , где последнее равенство справедливо лишь при .
Рассмотрим теперь предел справа при :
–предел не существует,
поскольку в знаменателе дроби имеется логарифм от отрицательной величины, в то время как действительная функция логарифм определена лишь для положительных значений аргумента. Таким образом, и искомый предел не существует.
Пример 8. Вычислить пределы функций, если они существуют, при и при
Решение
примера 8.
о
.
о
Здесь пренебрегали бесконечно малой величиной в числителе по сравнению с единицей, а в знаменателе по сравнению с тройкой. Учтено также, что при возведении в бесконечно большую степень положительного числа, меньшего единицы, получается ноль.
о
.
о
Здесь в числителе и в знаменателе пренебрегли постоянными конечными числами по сравнению с бесконечно большим слагаемым ~ .
о
о
о о
о
Здесь в числителе и знаменателе, а также в показателе степени пренебрегли конечными величинами по сравнению с бесконечно большой величиной, ~ .
.
Для
раскрытия неопределенности вида воспользовались основным логарифмическим
тождеством: ,
а для освобождения от логарифма
воспользовались различными формами
функций, эквивалентных в нуле (см. § 4).
§ 4).
о
.
Для раскрытия неопределенности вида , опять воспользовались представлением
При раскрытии неопределенности вида использовали правило Лопиталя, при этом для упрощения под знаком логарифма пренебрегли единицей по сравнению с бесконечно большой величиной.
Аналогичного предела при не существует, ввиду того, что при больших отрицательных значениях основание действительной степенно-показательной функции становится отрицательным , при этом мы выходим за рамки ее области определения.
.
Здесь пренебрегалось бесконечно малыми величинами по сравнению с конечными – единицей, четверкой и двойкой.
о о
о о
.
Для
раскрытия неопределенности вида воспользовались представлением: . Затем бесконечно малыми величинами
(двойкой по сравнению с
,
четверкой по сравнению с , единицей по сравнению с
и по
сравнению с ) пренебрегли.
Затем бесконечно малыми величинами
(двойкой по сравнению с
,
четверкой по сравнению с , единицей по сравнению с
и по
сравнению с ) пренебрегли.
Аналогичный предел при не существует, поскольку основание действительной степенно-показательной функции при больших отрицательных значениях
становится отрицательным: , что не соответствует ее области определения: .
о
.
Здесь для раскрытия неопределенности вида воспользовались представлением . Далее пренебрегли единицей по сравнению с бесконечно большой величиной . При раскрытии неопределенности вида использовали правило Лопиталя.
.
Здесь
при раскрытии неопределенности вида воспользовались представлением
.
Для разложении логарифма использовали
формы функций, эквивалентных в нуле,
см. § 4.
.
При раскрытии неопределенности вида воспользовались представлением .
Для раскрытия неопределенности вида использовали правило Лопиталя.
Искомый предел при не существует, ввиду отрицательности основания степени рассматриваемой функции .
Пример 9. Вычислить пределы функций при и при
Решение примера 9
о
.
Здесь
для удобства введена новая переменная .
Затем с помощью основного логарифмического
тождества степенная функция выражена
через показательную. Далее с учетом
шкалы бесконечно больших функций
пренебрегаем по сравнению с бесконечно большой
величиной ~
.
После раскрытия неопределенности вида по правилу Лопиталя, и представления
предела как произведения пределов,
вновь учитываем, что является величиной бесконечно малой
по сравнению с
.
.
Здесь после раскрытия неопределенности вида по правилу Лопиталя, в соответствии со шкалой бесконечно больших функций учтено, что является бесконечно малой величиной, по сравнению с .
о
.
о
Здесь неопределенности вида раскрывается по правилу Лопиталя.
о
.
о
Здесь в соответствии со шкалой бесконечно больших функций величиной пренебрегли как величиной бесконечно малой по сравнению с .
.
Здесь конечная величина обозначена как .
.
Здесь использовали различные формы функций, эквивалентных в нуле (см. § 4), в частности, при .
о
.
о
Здесь вводим новую переменную . Затем степенную функцию выражаем через показательную. Далее в соответствии со шкалой бесконечно больших функций, пренебрегаем бесконечно малой величиной по сравнению с величиной ~ . И наконец учитываем, что является бесконечно малой по сравнению и с показательной функцией .
о
.
Здесь в соответствии со шкалой бесконечно больших функций, пренебрегаем логарифмической функцией по сравнению со степенной .
о
.
Здесь бесконечно малой величиной пренебрегли по сравнению с бесконечно большой величиной .
о
.
Здесь
неопределенность вида
с помощью основного логарифмического
тождества преобразовали в неопределенность
вида
,
которую раскрывали с помощью правила
Лопиталя. Далее в соответствии со шкалой
бесконечно больших функций учтено, что является бесконечно малой величиной
по сравнению со степенной функций
,
в результате чего, оказалось возможным
пренебречь бесконечно малой величиной
~
по сравнению с единицей.
Далее в соответствии со шкалой
бесконечно больших функций учтено, что является бесконечно малой величиной
по сравнению со степенной функций
,
в результате чего, оказалось возможным
пренебречь бесконечно малой величиной
~
по сравнению с единицей.
.
.
о
Здесь пренебрегли степенной функцией по сравнению с показательной , поскольку их отношение . (Соотношение легко проверяется, если к нему применить правило Лопиталя). Затем, неопределенность вида раскрывали с использованием правила Лопиталя.
Пример 10. Вычислить указанные пределы
.
Решение примера 10.
.
Ввиду того, что пределы слева и справа в точке не совпадают, искомого предела не существует.
.
Здесь учтено, что .
о
.
Здесь после освобождения от модуля для раскрытия неопределенности вида использовано правило Лопиталя. Затем, пренебрегая единицей по сравнению с бесконечно большой величиной, и желая применить шкалу бесконечно больших функций, вводим новую переменную .
В соответствии со шкалой бесконечно больших функций, учитываем, что является бесконечно малой по сравнению с функцией.
о
Здесь после выяснения вида неопределенности мы не стали применять правило Лопиталя, т. к. оно привело бы к усложнению функции, стоящей по знаком предела.
Вместо этого, используя основное логарифмическое тождество, прологарифмировали первоначально заданную функцию. Затем, пренебрегая конечной величиной по сравнению с бесконечно большой величиной , получаем конечный результат.
Пример 11. Найти поведение функции при
Решение
примера 11.
.
.
Здесь после освобождения от модуля использована формула для эквивалентных в нуле функций: .
Поведение заданной функции определяется найденными пределами. Добавки (-0) означают, что график функции располагается ниже соответствующих значений пределов (см. Рис 1). Стрелки на графике означают исключение из области допустимых значений аргумента точки с абсциссой .
y y
1
o x
0 1 x
-1
Рис. 1 Рис. 2
.
.
Здесь
неопределенность вида раскрывалась по правилу Лопиталя.
Поведение заданной функции определяется найденными значениями пределов. Схематический рисунок графика функции в окрестности точки см. на Рис. 2. Стрелка на графике означает, что точка с абсциссой исключена из области допустимых значений аргумента.
.
Здесь для раскрытия неопределенности вида было использовано правило Лопиталя.
Предела слева в точке рассматривать нет необходимости, т. к. заданная функция определена только для положительных значений аргумента .
Поведение функции справа от нуля изобразим на Рис. 3
y y
1
o x x
Рис. 3 Рис. 4
.
Здесь
для раскрытия неопределенности вида использовали основное логарифмическое
тождество. Затем использовали различные
формы представления функций, эквивалентных
в нуле. В частности, для логарифма
использовали формулу ,
справедливую при
.
Далее, по шкале бесконечно больших
функций определили, что логарифм
является бесконечно малой величиной
по сравнению со степенной функцией
.
Затем использовали различные
формы представления функций, эквивалентных
в нуле. В частности, для логарифма
использовали формулу ,
справедливую при
.
Далее, по шкале бесконечно больших
функций определили, что логарифм
является бесконечно малой величиной
по сравнению со степенной функцией
.
Поведение заданной функции при изображено на Рис. 4.
Исчисление. Есть ли способ запомнить определение предела для $e$?
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 471 раз
$\begingroup$
Время от времени я вижу пруфы, в которых всплывает определение предела для $e$, но каждый раз я его почему-то не узнаю! 9х\cdot C_a,
$$
где $C_a$ — некоторая константа, зависящая от $a$, но не зависящая от $x$. x\ln a$. И таким образом мы 9{n+1}$ убывает, что означает (поскольку $b_n=\left(1+\frac{1}{n}\right)a_n>a_n$ для каждого $n$), обе последовательности ограничены $a_1 =2$ снизу и $b_1=4$ сверху, а значит, обе последовательности сходятся, причем к одному и тому же пределу. Можно показать (см. один из других ответов здесь), что этим пределом является то же число $e$, которое нам, естественно, понадобилось для дифференцирования экспоненциальных функций.
x\ln a$. И таким образом мы 9{n+1}$ убывает, что означает (поскольку $b_n=\left(1+\frac{1}{n}\right)a_n>a_n$ для каждого $n$), обе последовательности ограничены $a_1 =2$ снизу и $b_1=4$ сверху, а значит, обе последовательности сходятся, причем к одному и тому же пределу. Можно показать (см. один из других ответов здесь), что этим пределом является то же число $e$, которое нам, естественно, понадобилось для дифференцирования экспоненциальных функций.
Итак, “почему это определено именно так?” Потому что он нужен нам во многих местах, а не для каких-то жестоких или необычных целей. И $e$, и $\pi$ — сложные числа, но это компромисс за все их замечательные свойства.
$\endgroup$
4
Предел экспоненциальной функции
В этой статье мы обсудим, как решать экспоненциальные функции с ограничениями. Но прежде чем обсуждать это, сначала давайте посмотрим, что такое экспоненциальная функция.
Что такое экспоненциальная функция?
Показательная функция — это функция, в которой независимая переменная, т. е. x, является показателем степени или степенью основания. Он имеет форму:
Здесь:
- a — положительное действительное число, не равное единице
- Область определения экспоненциальной функции — все действительные числа
- Диапазон экспоненциальной функции — все положительные действительные числа
- Точка пересечения по оси y равна (0, 1), а горизонтальная асимптота равна y и равна нулю которые обсуждаются ниже. Эти стандартные результаты можно использовать в качестве формул при оценке пределов экспоненциальных функций.
Стандарт 1
Стандарт 2
Стандарт 3
Стандарт 4
Стандарт 5
В следующем разделе мы решим пару примеров, в которых будем оценивать пределы экспоненциальных функций
Пример 1
Оцените следующую экспоненциальную функцию:
Решение
Дано, что предел функции должен оцениваться по мере того, как x приближается к 0.
 Таким образом, когда мы прямо ставим 0 в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.
Таким образом, когда мы прямо ставим 0 в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.Итак, сначала продифференцируем числитель . Производная от первого члена равна . Аналогично, производная второго члена равна .
Теперь продифференцируем знаменатель. Производная x равна 1. Подставьте эти производные в вышеприведенную функцию следующим образом:
Теперь примените ограничение к приведенному выше выражению, как показано ниже: 05
Пример 2
Вычислите следующее выражение:
Решение
Дано, что предел функции должен оцениваться, когда x приближается к 0. Таким образом, когда мы подставляем 0 непосредственно в приведенное выше выражение, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.
 9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна .
9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна .Теперь продифференцируем знаменатель. Производная от первого члена равна . Аналогично, производная второго члена равна .
Подставьте эти производные в приведенное выше выражение следующим образом:
Теперь примените ограничение к приведенному выше выражению, как показано ниже:
900 05
Пример 3
Оцените предел следующей экспоненциальной функции:
Решение
Дано, что предел функции должен оцениваться, когда x приближается к 0. Итак, когда мы подставляем 0 непосредственно в приведенное выше выражение, мы получаем неопределенная форма. Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.
Сначала найдем производную от числителя, которая равна .
 Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже:
Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже:Теперь возьмем предел выражения:
Пример 4
Решение
Легче оценить вышеуказанное потому что после подстановки мы не получим неопределенную форму или . Таким образом, в этом примере нет необходимости применять правило Лопиталя.
Пример 5
Оцените следующее выражение:
Решение
В этом примере, если мы подставим x = 2 непосредственно в вышеприведенное выражение, мы не получим неопределенный вид, поэтому правило Лопиталя неприменимо. здесь. Все, что нам нужно сделать, это заменить x = 2 в приведенном выше выражении:
Пример 6
Вычислить следующее выражение:
Решение
Основное понятие, которое будет использоваться при решении этой задачи, будет таким же, как и в случае с рациональными выражениями.



 Таким образом, когда мы прямо ставим 0 в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.
Таким образом, когда мы прямо ставим 0 в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.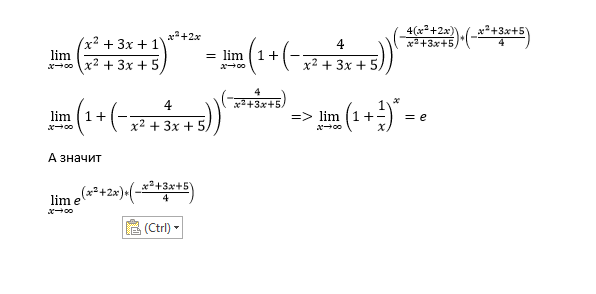 9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна .
9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна . Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже:
Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже: