О методах решения большеразмерных задач строительной механики на многоядерных компьютерах
%PDF-1.6 % 149 0 obj >/OCGs[151 0 R 272 0 R 329 0 R 399 0 R]>>/Type/Catalog>> endobj 146 0 obj >stream 2013-09-04T16:45:36+04:002013-08-26T13:59:29+04:002013-09-04T16:45:36+04:00PScript5.dll Version 5.2application/pdf
Векторное Произведение Векторов.
Свойства, определениеОпределение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи.
Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.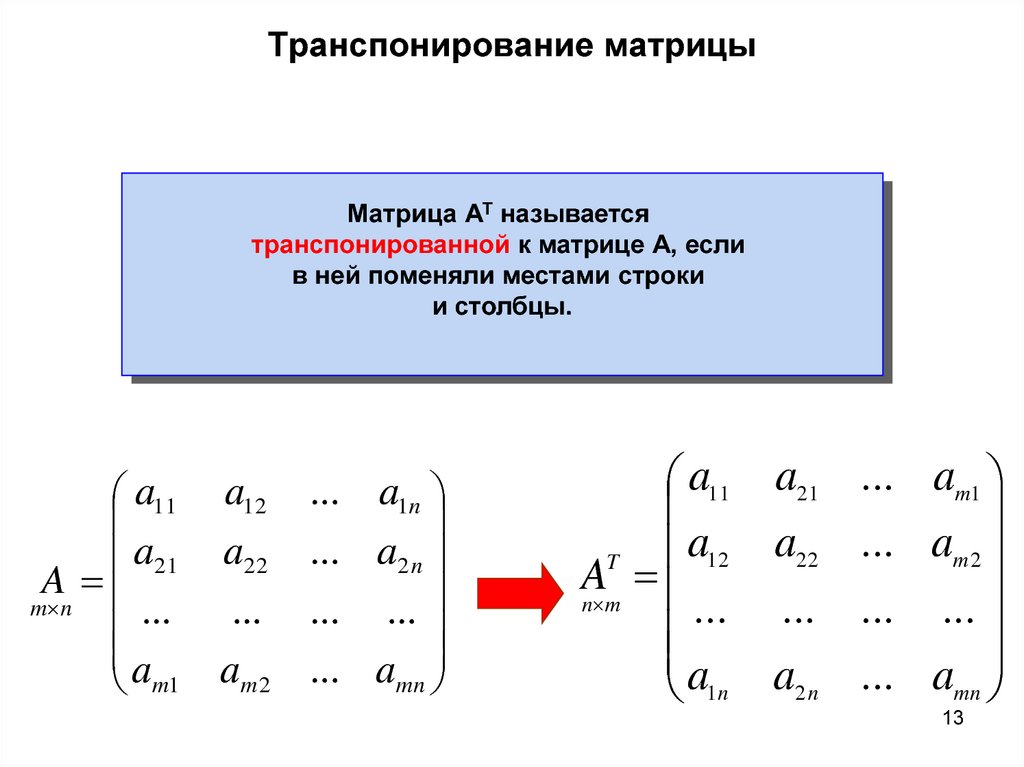
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Линейная алгебра 5: Решение Ax = b в необратимых, неквадратных матрицах | by adam dhalla
Это продолжение моей серии по линейной алгебре, которую следует рассматривать как дополнительный ресурс при изучении класса 18.
06 Гилберта Стрэнга на OCW. Это можно близко сопоставить с Лекция 8 в его серии.
Здесь мы продолжаем обсуждение решения линейных систем с исключением. В моей серии «Исключение по Гауссу» мы исследовали, как можно решать квадратные обратимые матрицы методом исключения и замены строк, но никогда не углублялись в решение прямоугольных необратимых систем.
На прошлом уроке мы рассмотрели, как можно решать неквадратные системы с помощью исключения Гаусса. В частности, мы решили системы в формате Ax = 0 и обнаружили нуль-пространственные векторы x , которые дают x = 0. мою серию «Линейная алгебра», которую следует рассматривать как дополнительный ресурс при изучении…
adamdhalla.medium.com
Самая большая разница между Ax = b и Ax = 0 заключается в том, что теперь наша правая часть отлична от нуля, и мы должны выполнить операции над обеими сторонами. Это подводит нас к нашей первой теме — -условию разрешимости.
Условия разрешимости
Все эти примеры будут иметь дело с прямоугольными необратимыми матрицами. Если у вас есть квадратная и обратимая матрица (что часто бывает), используйте более простое исключение Гаусса .
Условия разрешимости — это то, как мы узнаем, является ли некое b в Ax = b решением, которое на самом деле возможно. Это станет совершенно ясно на примере. Помните, что теперь, при выполнении исключения с матрицами, которые, как мы ожидаем, будут зависимыми, мы не остановимся на опорных точках в нулевом месте. Мы просто продолжим переход к следующему столбцу.
Наша цель — узнать, как должен выглядеть ответ b, чтобы задача была решаемой.
Итак, первый пример.
Строки 1 и 3 кратны друг другу и после исключения будут заменены строкой нулей. После использования первой строки для исключения первой и второй строк мы получаем:
Но теперь, когда у нас есть ненулевые числа в правой части, мы должны выполнить те же шаги исключения в правой части.
Что мы сделали? Чтобы исключить вторую строку, мы умножили первую строку на минус и вычли из нижней строки (или, можно подумать, мы добавили первую строку). Затем мы умножаем первую строку на 2 и вычитаем из последней строки. Итак, теперь с нашими переменными b, как это выглядит?
Из-за равенства мы должны выполнять те же операции над строками b. Таким образом, после этого мы можем получить представление о том, как выглядит нашего b.
Условия разрешимости появляются, когда левая часть равна 0. Если бы мы записали это в виде системы уравнений, мы получили бы:
Первые два уравнения не дают нам много информации или ограничений на b, , так как они зависят от того, какие значения мы в итоге присвоим нашим переменным х, у, z и т.
Последнее уравнение, с другой стороны, дает нам определенное ограничение на б. Чтобы Ax = b было истинным, b3 – 2b1 должно быть = 0. Переставляя это, мы получаем ограничение на b , что:
Теперь мы ограничены в различных b3, которые мы можем поместить в нашу матрицу.
Вот несколько примеров векторов b , удовлетворяющих этому ограничению:
Это может дать нам быстрое представление о том, возможно ли Ax = b или нет, или, при составлении уравнения, может дать нам представление о возможных ответах, которые мы можем получить.
Это дает нам два разных способа понимания этого конкретного Ax = b.
- Используя наши знания о пространстве столбцов, мы знаем, что b должно быть частью пространства столбца A. Другими словами, b ∈ C(A)
- Наше новое понимание — b должно удовлетворить все ограничения на него.
Теперь, когда мы это знаем, давайте решим задачу.
Нахождение полного решения задачи Ax = b
Я беру этот пример непосредственно со страницы 91 учебника Гилберта Стрэнга «Линейная алгебра и ее приложения», 4-е издание.
Возьмем эту систему:
Чтобы решить это, нам сначала нужно найти ответ b , который удовлетворяет любым ограничениям, которые у нас могут быть.
Чтобы найти эти ограничения (и одновременно перевести A в U), используйте исключение Гаусса, чтобы исключить левую и правую части.
Мы умножили первую строку на 2 и вычли из второй строки. Затем мы умножили первую строку на -1 и вычли из третьей строки (прибавили). Мы отразили эти же изменения на правой стороне.
Теперь мы должны исключить последнюю строку из нашей второй строки.
Это b5 должно быть b3, но мне лень его менятьЗдесь мы вычтем два раза вторую строку из третьей строки. Нам нужно не забыть сделать это с правой стороны. Здесь все становится немного запутанным, так как мы опираемся на прошлые шаги исключения, но мы все еще можем это сделать.
Опять же, наше условие разрешимости находится в третьей строке. Если мы упростим это, мы получим наше условие разрешимости.
Теперь, когда у нас есть условие разрешимости, мы можем выбрать ответ b , который с ним работает. Почему бы нам не выбрать (1, 5, 5)? Вы можете проверить сами, что это работает.
Просто напомню, что как только мы найдем наш b , чтобы заменить его в исходном уравнении Ax = b, где A находится слева, а не U.
Теперь мы проходим тот же процесс исключения, просто на этот раз с конкретными цифрами, и, как и предсказывалось, он удовлетворяет ограничениям, которые мы на него накладываем.
Заметка о комплексном решении
Теперь, глядя на это, есть множество решений. Но важно отметить, что наш окончательный ответ будет также должны включать все ответы с нулевым пробелом.
Поясню. Поскольку эта матрица A не является независимой, в нулевом пространстве обязательно будет хотя бы один вектор x. Это x решает для Ax = 0.
Таким образом, если мы находим конкретное решение этого, некоторого x, которое решает Ax = b, мы должны также добавить все наши нулевые пространственные векторы для полного ответа. Поскольку все векторы нулевого пространства делают Ax = 0, наш полный ответ должен включать A(x_null + x_particular) = b, поскольку добавление нулевого пространства ничего не делает с b, поскольку Ax_null = 0,
Если это не имеет смысла, продолжим.
Давайте сначала найдем частное решение этого уравнения. Это x , которое непосредственно решает для Ax = b.
Поиск частного решения
Мы стремимся найти конкретное решение, некоторое значение x, y, z и t, которое соответствует нашему ответу (1, 3, 0). Поскольку у нас есть только двух полных уравнений, мы можем найти только две из этих переменных. Два других мы должны будем установить в константы.
Опять же, аналогично решению для нулевого пространства, переменные, которые мы установим в качестве констант, будут свободными переменными. Это переменные, связанные со свободными столбцами, то есть столбцами, не содержащими сводных данных.
Выделены свободные столбцы и переменные. У нас снова двойная бесконечность ответов, так как у нас есть две переменные, которые мы можем установить как любых констант. Таким образом, у нас есть бесконечное количество частных ответов, которые решают (1, 3, 0). Итак, если мы можем выбрать любую константу для y или t, мы можем выбрать самую простую, то есть 0, для обоих.
После этого наша линейная комбинация и система уравнений выглядят так:
Таким образом, одно из (наших многих возможных) частных решений было принято. Как я уже сказал, это не полный ответ. Мы можем добавить любой вектор из нулевого пространства (и любой из их кратных) к этому конкретному ответу и все равно получить Ax = b, поскольку все эти векторы нулевого пространства составляют Ax = 0.
Таким образом, мы также должны найти нулевое значение космические векторы. Я уже рассказал, как вычислять нулевые пространственные векторы в очень похожей матрице, поэтому на этот раз я не буду подробно рассказывать об этом, а просто дам вам ответы на нулевые пространственные векторы.
Итак, теперь мы можем добавить эту комбинацию к нашему единственному конкретному ответу. Важно отметить, что, хотя векторы нулевого пространства представляют собой комбинацию, мы не можем поставить кратное перед нашим конкретным ответом — поскольку наша правая часть не равна нулю, мы не можем просто умножить каждые x, y, z, t и получите эквивалентный ответ.
Итак, наш окончательный ответ:
Как выглядит этот ответ графически? Ну, это , а не подпространство. Вы можете думать об этом как о почти расширенном нулевом пространстве — нулевом пространстве, но с каждой точкой, сдвинутой на вектор хп. Таким образом бежим уже не через ориджин, а хп.
И это наше полное решение Ax = b.
Есть еще кое-что. Как и в нашей статье с нулевым пространством, мы можем использовать сокращенную форму -строки-эшелона , чтобы сделать ответ еще проще.
Немедленное нахождение конкретного решения с помощью RREF
Вернемся к тому моменту, когда у нас была система Ux = c. Мы можем дополнительно сократить это U до R и довести наше c до 9.0003 д. Как бы мы это сделали?
Ну, как и в предыдущей статье, мы будем использовать исключение Gauss-Jordan для устранения вверх после объединения всех разворотов в один. Единственная дополнительная трудность заключается в том, что мы должны проделать те же операции и с правой частью, поскольку правая часть теперь не равна нулю.
Единственный стержень, который нам нужно превратить в ноль, находится во второй строке. Разделите каждый элемент в строке и соответствующий элемент в b, , чтобы сделать это.
Затем мы можем умножить эту вторую строку на три, чтобы исключить три над точкой опоры в первой строке. Затем то же самое делаем с правой стороны.
Теперь наша матричная система находится в Rx = b. Теперь мы можем напрямую извлечь наше конкретное решение xp. Ответ скрыт у всех на виду.
Так как мы превращаем наши свободные переменные y и t в 0. В форме линейной комбинации эти нули исключают два свободных столбца 2 и 4.
Тогда у нас остается тождество, умноженное на х = д.
Итак, чтобы решить это, наше конкретное решение ЕСТЬ d. Таким образом, при поиске частного решения мы можем просто преобразовать нашу матрицу A в R и взять правую часть d в качестве нашего частного решения.
Обо мне Я профессор физики в Университете Олд Доминион (ODU)
и старший сотрудник теоретического отдела в
Национальный ускорительный комплекс лаборатории Томаса Джефферсона (JLab). M y основная сфера интересов Квантовая хромодинамика (КХД). У меня около 100 статей, опубликованных в ведущих журналов по физике с общим числом цитирований более 10000. Два моих любимых результата — это померон БФКЛ в КХД и Уравнение БК для эволюции цветовых диполей. Профессиональные интересы T Вот две причины, по которым Теория рассеяния высоких энергий в квантовой хромодинамике (КХД)
по-прежнему интересен спустя тридцать лет после его создания. Во-первых, сведения об основных
Структура материи исходит из экспериментов, проводимых на ускорителях высоких энергий, таких как
Новый Большой адронный коллайдер (БАК). Для поиска Новая физика на БАК нужно отделить
сигнал (рождение новой частицы) от фона (излучение нескольких сотен “старых”
частиц), которые должны быть описаны КХД с достаточной точностью. M y Основным интересом в настоящее время является изучение поведения высоких энергий в КХД высокой плотности.
Наиболее изученным случаем является глубоконеупругое рассеяние (ГНР) при малых значениях переменной Бьоркена x .
Поведение структурных функций ДИС при малых x описывается эволюцией цветовых диполей.
В ведущем порядке оно дается уравнением Балицкого-Ковчегова (БК), которое в настоящее время является исходным.
точка обсуждения эволюции малых x в режиме насыщения.
Уравнение БК является асимптотическим, и чтобы выяснить, актуально ли оно в настоящее время
энергий нужно знать поправки следующего за ведущим порядка (NLO).
Это была давняя проблема в физике насыщения, и после года вычислений мой
мы со студентом Г. A Другим процессом, который несколько менее изучен теоретически, является рассеяние тяжелых ионов.
учился в RHIC и LHC. В отличие от DIS, который можно интерпретировать (в лабораторной рамке)
как создание диполей виртуальным фотоном с последующим рассеянием
этих диполей от ядра, рассеяние двух тяжелых ядер должно
включают эволюцию, идущую в обоих направлениях к любому из ядер. Кажется, что
единственная надежда на аналитический расчет в КХД состоит в том, чтобы построить эффективный 2+1
действие (со временем = быстрота), которое включает в себя два
эволюции. Такое эффективное действие будет включать как создание, так и уничтожение
диполей и, следовательно, допускают померонные петли, которые
возможно, являются источником унитаризации высокоэнергетических амплитуд. |
Я получил докторскую степень. Кандидат физических наук Петербургского института ядерной физики (Санкт-Петербург, Россия) в 1984 г.
После этого я работал в ПИЯФ, Университете штата Пенсильвания, Массачусетском технологическом институте, а с 1996 года работаю в ODU/JLab.
Во-вторых, есть ускорители.
которые исследуют структуру вещества КХД как в нормальных условиях (лаборатория Джефферсона),
и в экстремальных условиях, которые могли существовать в начале Вселенной
(исследования кварк-глюонной плазмы на ускорителе RHIC в Брукхейвенской национальной лаборатории).
Чирлилли смогли ее решить.
Тщательный анализ поправок NLO очень важен как с теоретической, так и с экспериментальной точек зрения.
точек зрения, поскольку определяет, может ли описание DIS в терминах цветовых диполей
быть полезным для будущего электронно-ионного коллайдера.