Как решать задачи на растворы по математике егэ: Задачи ЕГЭ на сплавы, смеси, растворы. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Задачи ЕГЭ на сплавы, смеси, растворы.

Задачи на сплавы, смеси, растворы встречаются и в математике, и в химии. У химиков сложнее – там вещества еще и взаимодействуют, превращаясь во что-то новое. А в задачах по математике мы просто смешиваем растворы различной концентрации. Покажем правила решения на примере задач на растворы. Для сплавов и смесей – действуем аналогично.

. В сосуд, содержащий литров -процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?

В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично — так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим .

Первый сосуд содержал литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством -процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Пусть масса первого раствора равна . Масса второго — тоже . В результате получили раствор массой . Рисуем картинку.

Получаем:

Ответ: .

. Виноград содержит влаги, а изюм — . Сколько килограммов винограда требуется для получения килограммов изюма?

Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным.

В винограде содержалось воды, значит, «сухого вещества» было . В изюме воды и «сухого вещества». Пусть из кг винограда получилось кг изюма. Тогда

от от

Составим уравнение:

и найдем .

Ответ: .

. Имеется два сплава. Первый сплав содержит никеля, второй — никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий никеля. На сколько килограммов масса первого сплава меньше массы второго?

Пусть масса первого сплава равна x, а масса второго равна y. В результате получили сплав массой .

Запишем простую систему уравнений:

Первое уравнение — масса получившегося сплава, второе — масса никеля.

Решая, получим, что .

Ответ: .

. Смешав -процентный и -процентный растворы кислоты и добавив кг чистой воды, получили -процентный раствор кислоты. Если бы вместо кг воды добавили кг -процентного раствора той же кислоты, то получили бы -процентный раствор кислоты. Сколько килограммов -процентного раствора использовали для получения смеси?

Пусть масса первого раствора , масса второго равна . Масса получившегося раствора равна . Запишем два уравнения, для количества кислоты.

Решаем получившуюся систему. Сразу умножим обе части уравнений на , поскольку с целыми коэффициентами удобнее работать, чем с дробными. Раскроем скобки.

Ответ: .

Решение задач на смеси, сплавы и растворы для ЕГЭ по математике

Хочу продолжить тему, начатую одним из моих коллег –

решение задач на смеси, сплавы и растворы.

Подобные задачи довольно часто встречаются в реальных и демонстрационных вариантах ОГЭ и ЕГЭ. В обычных школах таким задачам не уделяется должного внимания и даже у учеников 11 классов возникают сложности при их решении.

Рассмотрим решение на примере не сложной задачи.

Имеется два сплава. Первый содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 105 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.

Обозначим: m1 – масса первого сплава. Если третий сплав, получившийся из двух, равен 105 кг, то масса второго сплава (105-m1)кг.

Главная идея решения – равенство масс чистого вещества в начале и после соединения сплавов.

Найдём количество чистого никеля в первом сплаве – 0,1 m1

Количество чистого никеля во втором сплаве – 0,25(105-m1).

Тогда общая масса чистого никеля в обоих сплавах – (0,1 m1+0,25(105-m1))кг. (1)

После соединения сплавов общая масса 105кг, а содержание никеля 20%, тогда в новом славе чистого никеля будет – 0,20*105кг. (2).

Чистый никель никуда не исчез и нового чистого никеля не добавлено, значит величины (1) и (2) равны.

Запишем уравнение ( 0,1 m1+0,25(105-m1))= 0,20*105, решая его находим m1=35,

масса второго сплава 105 -35 = 70кг. И в итоге 70 – 35=35кг – масса первого сплава больше массы второго на 35кг. Ответ: 35

Решим ещё задачу.

Имеется два сосуда. Первый содержит 100кг. , а второй -20кг. раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 72% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 78% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Решение.

Пусть к – концентрация первого раствора, р – концентрация второго раствора. Чистой кислоты в первом растворе – 100к кг., во втором – 20р кг. и всего в двух растворах – (100к +20р) кг.

Если смешать растворы, то вес нового раствора -120кг. и концентрация 72%., при том же количестве, что и в начале, чистой кислоты, т.е (100к +20р) = 0,72*120 (1).

Возьмём теперь равные массы растворов, для простоты возьмём по 10кг.

Определим начальное количество чистой кислоты в обоих растворах. В первом растворе 10к чистой кислоты, во втором 10р чистой кислоты. Тогда всего вначале чистой кислоты было (10к +10р) кг. Масса нового раствора 10+10 =20 кг и по условию его концентрация 0,78.

Чистой кислоты в новом растворе – 0,78*20. По условию равенства чистого вещества (10к +10р)= 0,78*20 (2).

Решая совместно (1) и (2) получаем к = 0,69, тогда чистой кислоты в первом растворе – 69кг. Отв.: 69

Теперь посмотрим как легко решается известная задача про изюм и виноград.

Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 14 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение.

Если в винограде 90% воды, значит 10% чистого изюма (название образное).

В изюме (магазинном) должно быть 95% чистого изюма. В 14кг. магазинного изюма чистого изюма будет чуть меньше – 14*0,95= 13,3кг. Это количество необходимо набрать из винограда, где только 10% чистого изюма. Значит 13,3 кг в винограде, должны составлять десятую часть, тогда необходимо взять 133 кг. винограда. В 133кг. винограда будет 13,3 чистого изюма, что позволит иметь 14 кг магазинного изюма.

Ответ: 133

При решении всех простых задачах на сплавы, смеси, и растворы применяют условие равенства чистых масс вещества в начале и после соединения. В более сложных, это условие помогает найти ходы решения.

В завершении приведу решение сложной задачи, решение которой опирается на понятие «концентрация». Такая задача может быть в задании 11 профильного ЕГЭ. Обычно такого рода задачи прорешивают заранее, чтобы на экзамене не возникла тревога при виде сложного и на первый взгляд, запутанного условия.

В сосуде было 20 литров соляной кислоты. Часть кислоты отлили, и сосуд дополнили водой. Затем отлили в два раза большую (чем в первый раз) часть полученной смеси и снова дополнили сосуд водой. В результате получился 28% раствор кислоты. Сколько литров кислоты отлили в первый раз?

Редакция не несет ответственности за наполнение блогов, они есть персональным мнением автора

Задачи на смеси и сплавы (ЕГЭ — 2021)

Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора

.

То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.

Обычно концентрация измеряется в процентах.

Что такое процент?

Напомню, что это сотая доля числа. То есть, если массу или объем разделить на \( \displaystyle 100\), получим \( \displaystyle 1\%\) этой массы или объема.

Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на \( \displaystyle 100\%\).

Почему?

Сейчас покажу: пусть масса всего раствора равна \( \displaystyle M\), а масса растворенного вещества (например, соли или кислоты) – \( \displaystyle m\). Тогда один процент от массы раствора равен \( \displaystyle \frac{M}{100}\).

Как узнать, сколько таких процентов содержится в числе \( \displaystyle m\)?

Просто: поделить число \( \displaystyle m\) на этот один процент: \( \displaystyle \frac{m}{\frac{M}{100}}=\frac{m}{M}\cdot 100\), но ведь \( \displaystyle \frac{m}{M}\) – это концентрация.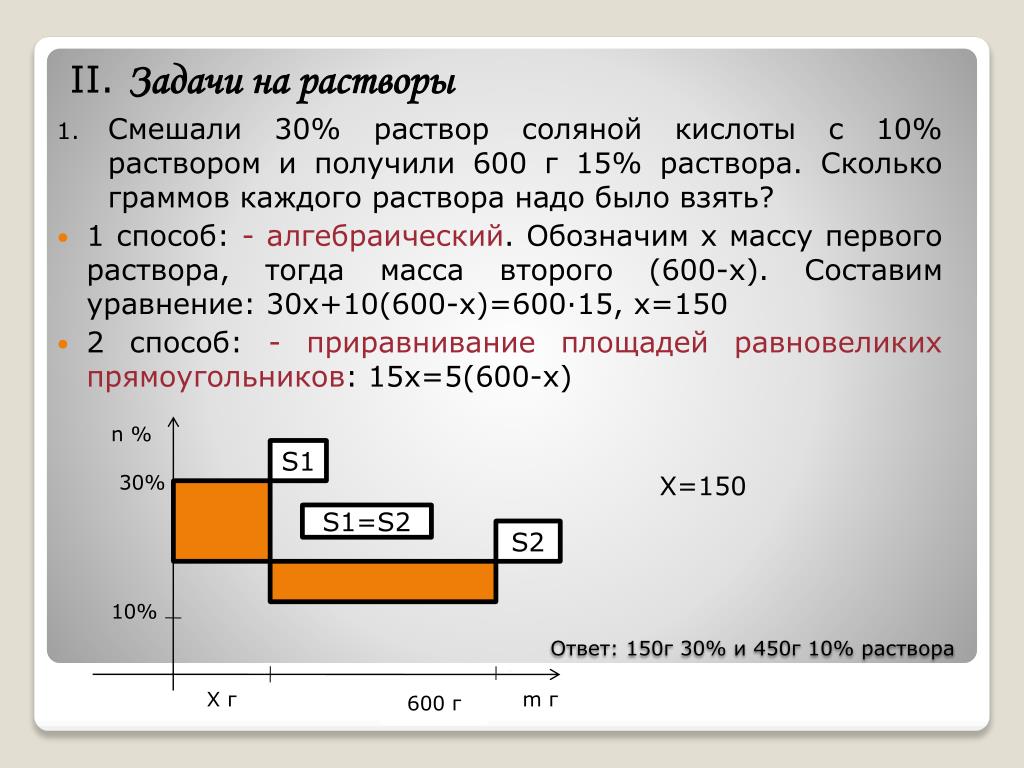

Вот и получается, что ее надо умножить на \( \displaystyle 100\), чтобы узнать, сколько процентов вещества содержится в растворе.

Более подробно о процентах – в темах “Дроби, рациональные числа”, “Проценты”.

Поехали дальше.

Масса раствора, смеси или сплава равна сумма масс всех составляющих.

Логично, правда?

Например, если в растворе массой \( \displaystyle 10\) кг содержится \( \displaystyle 3\) кг соли, то сколько в нем воды? Правильно, \( \displaystyle 7\)кг.

И еще одна очевидность:

При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.

А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.

Например: в первом растворе массой \( \displaystyle 10\) кг содержится \( \displaystyle 3\) кг кислоты, а во втором растворе массой \( \displaystyle 14\) кг – \( \displaystyle 5\) кг кислоты.

Когда мы их смешаем, чему будет равна масса нового раствора?

\( \displaystyle 10+14=24\) кг.

А сколько в новом растворе будет кислоты? \( \displaystyle 3+5=8\) кг.

Теперь соединим полученные знания и решим несколько примеров.

Разбор примеров

Решение примера №10

В \( \displaystyle 10\%\) раствор кислоты массой \( \displaystyle 3\) кг добавили \( \displaystyle 1,8\) кг чистой воды. Чему стала равна концентрация раствора (в процентах)?

Решил? Смотри:

1
Вычисляем массу кислоты. Для этого запишем, что такое концентрация:
\( \displaystyle \frac{m}{M}\cdot 100\%=10\%\text{ }\Rightarrow \text{ }\frac{m}{M}=0,1\text{ }\Rightarrow \text{ }m=0,1\cdot M=0,1\cdot 3=0,3\) кг.
Впредь проценты всегда будем сразу записывать в виде десятичной дроби:
\( \displaystyle 1\%=0,01\).
2
Вычисляем массу нового раствора: \( \displaystyle 3+1,8=4,8\) кг.
3
Новая концентрация: \( \displaystyle \frac{0,3}{4,8}=0,0625=6,25\%\).

Решение примера №11

Смешали два раствора: \( \displaystyle 2\) кг \( \displaystyle 10\%\)-ного и \( \displaystyle 3\) кг \( \displaystyle 20\%\)-ного. Какова концентрация полученного раствора?

Решение:

Визуализируем ситуацию: схематично изобразим емкости с растворами, около них подпишем массу раствора, а внутри – содержание кислоты:

Решение примера №12

Изюм содержит \( \displaystyle 5\%\) влаги. Его получают из винограда, содержащего \( \displaystyle 90\%\) влаги. Сколько потребуется винограда, чтобы получить \( \displaystyle 3\) кг изюма?

Решение:

Готовимся к ЕГЭ задачи на растворы и сплавы | Методическая разработка по математике (10, 11 класс):

Интегрированный урок по математике и химии

Готовимся к ЕГЭ

«Задачи на растворы и сплавы»

Яппарова Светлана Васильевна, учитель математики МОУ «ТШИСОО» п. Толька

Дорджиева Деляш Борисовна, учитель химии и биологии МОУ «ТШИСОО» п.Толька

«Всё впереди!

Как мало за плечами!

Пусть химия нам будет вместо рук,

Пусть станет математика очами.

Не разлучайте этих двух подруг».

М. Алигер

Данный урок посвящен решению задач типа №11 ЕГЭ по математике профильный уровень и №27, №33 ЕГЭ по химии. Неважно, как задача решена – химическим или математическим способом, главное получить правильный ответ. При решении математических задач на составление уравнений и систем уравнений мы стараемся регулярно использовать таблицы. На этом уроке мы показываем, как составить опорную таблицу при решении задач на растворы и сплавы. Многим ученикам это помогает разобраться в условии. Такие уроки можно проводить в 10х и 11х классах при подготовке к ЕГЭ. Подобные уроки дают возможность раскрывать взаимосвязи между предметами, сопоставлять различные варианты к решению задач, позволяют ученику выявлять свои сильные стороны. Мы использовали различные формы работы: коллективную, индивидуальную, в парах.

Цели и задачи урока:

Рассмотреть различные типы задач на растворы, сплавы и приемы их решения.
Сформировать целостную картину о взаимосвязи предметов в школе.
Совершенствовать интеллектуальные умения (анализ, прогнозирование, умения устанавливать причинно-следственные связи).

Оборудование:

Химические препараты и посуда.
Мультимедиа проектор.
Раздаточный материал.

Ход урока

Организационный момент

Сегодня у нас необычный урок, это интегрированный урок математики и химии и вести его будут два учителя. Данный урок посвящен решению задач на растворы и сплавы. А именно это задачи №11 ЕГЭ по математике профильный уровень и №27 , № 33 ЕГЭ по химии. На этом уроке мы посмотрим с вами на задачи с двух точек зрения – с химической и математической, и выясним: как математика помогает в решении химических задач и как химия решает некоторые математические задачи.

Устная работа

Математическая разминка (проводит учитель математики).

Перевести проценты в десятичную дробь:

10% = 30%= 5%=

72%= 25%= 50%=

Найти:

0,3 от 200кг 72% от х

10% от 50 кг 35% от у

Решить систему уравнений:

х+у=10

3х+2у=20

Химическая разминка (проводит учитель химии).

В химии много задач на проценты. Решим несколько из них.

В бронзе – сплаве меди с оловом, на долю олова приходится 20%. Сколько весит олово, пошедшее на создание Медного всадника, если масса памятника 5 тонн? (1 тонна)
Определите массу золота и серебра, которое содержится в обручальном кольце массой 2 г и пробой 585°. (m(Au)= 2,19 г m(Ag)=1,56г)

(Проба 585°, например, означает, что в сплаве массовая доля золота составляет 0,585, или 58,5%)

Процентное содержание компонента в смеси или растворенного вещества в растворе называют массовой долей и обозначают греческой буквой ω.

ω= m раств.вещества ω%= m раствор.вещества 100%

m раствора m раствора

3) Найти массу 10% раствора, в котором растворено 90 г вещества. (900 г)

4) Рассчитать массовую долю раствора, полученного растворением 25 кг кислоты в 75 кг воды. (25%)

Демонстрация химического опыта:

В стакан с концентрированным раствором хлорида меди (II) зеленого цвета добавляется вода. Раствор становится голубым. Почему?

Объяснение: раствор изменил окраску из-за изменения массовой доли.

3.Решение задач

Прекрасно, разминку мы закончили, а теперь решим задачи.

Задача 1.

Определите массу воды, которую добавили к 300 г 50% раствора хлорида

меди(II), чтобы получить 20% раствор.

Решение:

0,2= 300• 0,5/ 300+х

60+0,2х=150

х= 450

В задачах на смеси, растворы и сплавы важно уметь определять концентрацию вещества. Что же такое концентрация? Концентрация вещества в растворе (смеси, сплаве) – это отношение массы или объема вещества к массе или объему всего раствора (смеси, сплава). Концентрацию обозначаем буквой С.

Задача 2.

В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Концентрация раствора равна

Объём вещества в исходном растворе равен V(в-ва) = 0,12∙ 5= 0,6л. При добавлении 7 литров воды общий объём раствора увеличится, а объём растворенного вещества останется прежним. Таким образом, концентрация полученного раствора равна:

С= 0,6/5+7 ∙100%= 5%

Задача 3 (учащиеся решают самостоятельно)

Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение:

Концентрация раствора равна . Таким образом, концентрация получившегося раствора равна:

Решение задач на сплавы (объясняет учить математики)

Задача 4

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух

сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение

	Общая масса сплава (кг)	% содержание никеля	Масса никеля (кг)
Первый сплав	х	10	0,1х
Второй сплав	у	30	0,3у
Третий сплав	200	25	0,25*200

х+у=200 х=50

0,1х+0,3у=0,25*200 у=150

Ответ. Первый сплав легче второго на 100 кг.

Задача 5 (учащиеся вместе с учителем заполняют таблицу и составляют уравнение)

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго

сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение

	Общая масса сплава (кг)	% содержание меди	Масса меди (кг)
Первый сплав	х	10	0,1х
Второй сплав	х+3	40	0,4(х+3)
Третий сплав	х+ х+3	30	(2х+3)*0,3

0,1х+0,4(х+3)=(2х+3)*0,3

Ответ. 9 кг

Задача 6 (учащиеся работают в группах)

Имеется два сплава. Первый содержит 5% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение

	Общая масса сплава (кг)	% содержание никеля	Масса никеля (кг)
Первый сплав	х	5	0,05х
Второй сплав	у	35	0,35у
Третий сплав	225	25	0,25*225

х=75

х+у=225

0,05х+0,35у=0,25*225 у=150

Ответ. Масса первого сплава на 75кг меньше массы второго сплава.

Задача7

Смешав 11-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 51- процентный раствор кислоты. Сколько килограммов 11- процентного раствора использовали для получения смеси?

Решение

	Общая масса сплава (кг)	%содержание никеля	Масса никеля (кг)
Первый раствор	х	11	0,11х
Второй раствор	у	72	0,72у
Первый + второй раствор	х+у+10	31	0,31(х+у+10)
Первый раствор	х	11	0,11х
Второй раствор	у	72	0,72у
Третий раствор	10	50	0,1*50
Первый+второй+третий растворы	х+у+10	51	0,51(х+у+10)

0,11х+0,72у=0,31(х+у+10) х=5

0,11х+0,72у+5=0,51(х+у+10) у=10

Ответ: 5 кг

4. Домашнее задание (Учащиеся получают перечень задач из открытого банка ЕГЭ по математике и химии)

1.Имеется два сплава. Первый содержит 10% никеля, второй —35% никеля. Из этих двух сплавов получили третий сплав массой 125 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

2. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

3.Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды,

получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-

процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты.

Сколько килограммов 30-процентного раствора использовали для получения смеси?

(Ответ: 60).

4. К 30 г раствора с массовой долей бромида кальция 6% добавили 50 мл воды и 20г соли. Определите массовую долю соли в полученном растворе ( Ответ: 10,3)

5. При растворении в воде 50г медного купороса (CuSO4 ∙ 5Н2О) получен 20% -ный раствор сульфата меди. К этому раствору добавили 39г цинка, а после завершения реакции добавили 292 г 12%-ного раствора соляной кислоты. Определите массовую долю соляной кислоты в полученном растворе. (Ответ: 0,012 или 1,2%)

6. При растворении в серной кислоте сплава цинка с магнием массой 10г выделилось 5,75 л водорода (н.у.). Вычислите массовую долю (%) каждого металла в сплаве. (Ответ: 60% Zn; 40% Mg)

5.Итог урока

Рефлексия

Учащиеся заполняют таблицу

Цель урока

(все понятно)

–

(ничего не понял)

(интересно, хочу узнать подробнее)

Уметь решать задачи на растворы, сплавы химическими и математическими способами

Список литературы:

В. К. Егерев и др. Сборник задач по математике для поступающих в вузы / Под ред. М.И. Сканави. Канон, Киев, 1997г.
Образовательный портал «РЕШУ ЕГЭ» (https://math-ege.sdamgia.ru)
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи. Пособие.
Ю.Н. Медведев. Химия ЕГЭ 2018. Типовые тестовые задания. Издательство «Экзамен» Москва, 2018.
Образовательный портал «РЕШУ ЕГЭ» (https://chem -ege.sdamgia.ru)
И.И. Новошинский., Н.С. Новошинская. Типы химических задач и способы их решения. 8-11 классы. Учебное пособие для общеобразовательных учреждений. Москва «Оникс 21 век» «Мир и Образование» 2004.

Задачи на сплавы и смеси: подробный разбор

Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.

Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!

Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.

Как решить задачу на смеси и сплавы: 3 действия
Примеры решения задач на смеси: от простого к сложному
Примеры решения задач на сплавы: от простого к сложному

Как решить задачу на смеси и сплавы: 3 действия

Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:

Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.

Примеры решения задач на смеси: от простого к сложному

А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.

Задача 1

Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.

Решение:

Для решения задачи выполняем три действия, о которых мы говорили выше:

1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.

Из условий задачи имеем три раствора:

Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6

Раствор 2: 5 литров с 40% кислотой, т. е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2

Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:Первое действие выполнено, переходим ко второму.

2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:

3 + 5 = х

0,6 + 2 = у

Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.

Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.

3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.

Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.

Таким образом, концентрация кислоты в растворе 3 равна:

2,6 / 8 = 0,325

Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:

0,325 * 100 = 32,5%

Ответ: 32,5%

Задача 2

Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.

Решение:

1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:2. Составляем уравнение. Известно, что третий газ имеет содержание кислорода 14,6%, соответственно мы можем приравнять массу чистого вещества газа 3 к 0,146 * (х + (х +300)). Получим уравнение:

(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))

0,21х + 63 + 0,05х = 0,292х + 43,8

0,26х + 63 = 0,292х + 43,8

0,032х = 19,2

х = 600

3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:

600 + 600 + 300 = 1500 г

Ответ: масса третьего газа равна 1500 г.

Задача 3

Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?

Решение:

1. Составляем таблицу. По условиям задачи мы имеем пять растворов:

Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х

Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х

Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0

Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4

Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0

Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.

Сводим полученные результаты в таблицу:2. Составляем уравнение.

По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:

(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4

Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:

(х + у + 3) * 0,2 = 0,4х + 0,15у

Объединяем полученные уравнения в систему:Решаем систему и получаем х = 3,4, у = 1,6

3. Возвращаемся к условиям задачи.

По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Примеры решения задач на сплавы: от простого к сложному

Задача 1

Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг

Решение:

1. Составим таблицу. Обозначим массу второго куска – х.2. Составим уравнение. По условию задачи сплав 3 содержит 1/11 часть олова, тогда масса чистого вещества равна 1/11 * (84 + х). Таким образом, можно составить следующее уравнение:

1/12 * 84 + 1/10 * х = 1/11 * (84 + х)

7 + х/10 = 84/11 + х/11

х/10 – х/11 = 7/11

х/110 = 7/11

х/10 = 7

х = 70

3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.

Ответ: 70 кг.

Задача 2

Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Решение.

1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:2. По условиям задачи масса третьего сплава равна 200 г, значит:

х + у = 200

Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:

0,15х + 0,65у = 0,3(х + у)

Получившиеся уравнения сводим в систему и решаем ее:х = 200 – у

0,15(200 – у) + 0,65у = 0,3 * 200

30 – 0,15у + 0,65у = 60

0,5у = 30

у = 60

х = 140

3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.

Ответ: 140 г и 60 г.

Задача 3

В первом сплаве содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?

Решение:

1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:2. По условиям задачи содержание меди в третьем сплаве равно 50%. Таким образом, масса чистого вещества равна 0,5 (х + у). Приравняем полученное уравнение к массе чистого вещества в составе третьего сплава из таблицы, получим:

0,7х + 0,4у = 0,5 (х + у)

0,7х + 0,4у = 0,5х + 0,5у

0,2х = 0,1у

х/у = ½

3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.

Ответ: ½

Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте.

Как решать 34 задание ЕГЭ по химии, примеры и алгоритмы решения заданий 34 по химии (Ростов-на-Дону)

Решение расчётных задач по химии подчиняется логике и проводится по определенным алгоритмам. Прежде всего, нужно внимательно прочитать и проанализировать условие задачи, написать необходимые уравнения химических реакций. Важно осознать ключевой (главный) вопрос в задаче и понять, количество какого вещества следует найти и по количеству какого вещества будет производиться расчёт. На основе анализа условия определить причинно-следственные связи и составить план последовательности решения задачи. Почему мы главным вопросом задачи считаем нахождение количества вещества? По количеству вещества всегда можно найти его массу, объём и массу раствора (массу и объём газа) и ответить на возможные дополнительные вопросы, содержащиеся в задаче.

В рассматриваемых примерах мы не будем пояснять выполнение формальных расчётов, предполагая, что вы проводите их без затруднений.

Пример 1. Электролиз 470 г 5%-ного раствора нитрата меди(II) прекратили после того, как масса раствора уменьшилась на 8 г. Из полученного раствора отобрали порцию массой 92,4 г. Вычислите массу 11,2 %-ного раствора едкого кали, необходимого для полного осаждения меди из отобранной порции раствора.

Дано:	Анализ и решение:

А) Проводим анализ условия

(составляем уравнения химических реакций, о которых упоминается в условии задачи).

1-й фрагмент.

«Электролиз 470 г 5%-ного раствора нитрата меди(II) прекратили… ».

При проведении этого этапа стараемся не обращать внимания на численные значения, а выделяем только химическую часть условия – она выделена в тексте фрагмента полужирным шрифтом.

2-й фрагмент.

«…Из полученного раствора отобрали порцию массой 92,4 г. Вычислите массу 11,2 %-ного раствора едкого кали, необходимого для полного осаждения меди из отобранной порции раствора».

Необходимо понять: в смеси после реакции находятся продукты реакции (Cu, O2, HNO3) и исходные вещества, которые не прореагировали, были «в избытке» (Cu(NO3)2, h3O), и следует рассматривать возможность взаимодействия каждого из этих веществ с добавляемым реагентом.

Б) Устанавливаем логические связи (формулируем главный вопрос задачи, т.е. находим вещество, количество которого необходимо рассчитать, и логическую цепочку, связывающую количество этого вещества с веществами, количество которых мы знаем или можем вычислить).

Главный вопрос – найти количество KOH (прореагировавшего с HNO3 и Cu(NO3)2, находящимися в отобранной части раствора).

Выводы (логическая цепочка):

При проведении расчётов будем использовать уменьшение массы раствора на 8 г (единственная количественная величина, относящаяся к протеканию реакции), которое происходит за счёт осаждения меди и выделения кислорода.

1) Количество KOH связано с количеством Cu(NO3)2 и HNO3 в порции раствора (уравнения (2) и (3)).

2) Количество HNO3 связано с количеством Cu и O2, которые образовались в процессе электролиза (уравнение (1)).

3) Количество Cu(NO3)2 в растворе после электролиза (избыток Cu(NO3)2) связано с количеством выделившихся Cu и O2.

В) План решения задачи.

1) Найти количество Cu(NO3)2 до электролиза.

2) Найти количество образовавшейся HNO3 по количеству выделившихся Cu и O2 (уравнение 1).

3) По уменьшению массы (т.е. по количеству выделившихся Cu и O2) найти количество прореагировавшего Cu(NO3)2 по уравнению (1).

4) Найти количество непрореагировавшего Cu(NO3)2.

5) Найти количество Cu(NO3)2 и HNO3в отобранной порции раствора.

6) По количеству Cu(NO3)2 и HNO3 в порции найти количество прореагировавшего KOH.

7) Вычислить массу раствора KOH.

Г) Решение.

1) Находим количество вещества Cu(NO3)2 до электролиза.

2) По уравнению (1) находим количество прореагировавшего Cu(NO3)2:

Пусть прореагировало x моль Cu(NO3)2, тогда

г)

3) По уравнению (1) находим количество прореагировавшего HNO3:

г)

4) Находим количество вещества Cu(NO3)2 и HNO3 в отобранной порции раствора.

а)

б) находим количество вещества Cu(NO3)2 с помощью пропорции – концентрация вещества одинакова как во всём растворе, так и в любой его части

а)

в) находим количество вещества HNO3 в отобранной порции:

а)

5) Находим количество KOH и массу добавленного раствора KOH.

а) По уравнению (2).

б) По уравнению (3).

в)

Пример 2. Насыщенный раствор нитрата алюминия получили, растворив кристаллогидрат Al(NO3)3·12h3O (растворимость 241 г в 100 г воды при 25 ºС) в 250 г воды. Полученный раствор разделили на две части. В первую добавили раствор Na2CO3 (избыток), во вторую 400 г раствора аммиака (избыток). Во второй колбе осадок в 4 раза тяжелее, чем в первой. Найдите концентрацию соли во второй колбе.

В ответе приведите уравнения реакций, которые указаны в условии задачи, и все необходимые вычисления (указывайте единицы измерения искомых физических величин).

Дано:	Анализ и решение:

А) Проводим анализ условия

Разбиваем условие на смысловые фрагменты, выделяем ключевые слова и понятия и составляем уравнения реакций (химическая часть задачи).

1-й фрагмент:

«Насыщенный раствор нитрата алюминия получили, растворив кристаллогидрат Al(NO3)3·12h3O (растворимость 241 г в 100 г воды при 25 ºС) в 250 г воды. Полученный раствор разделили на две части».

2-й фрагмент:

« В первую добавили раствор Na2CO3 (избыток), …»

3-й фрагмент:

«во вторую 200 г раствора аммиака (избыток)»

4-й фрагмент:

«Во второй колбе осадок в 4 раза тяжелее, чем в первой. Найдите концентрацию соли во второй колбе».

Химических превращений нет.

Главный вопрос – найти количество Nh5NO3.

Выводы (логическая цепочка):

Единственная цифра, которую можно использовать при проведении расчётов, это «4» – отношение масс Al(OH)3, образовавшихся во 2-й и 1-й колбах.

В) План решения задачи.

1) Найти количество Al(NO3)3(общее).

2) Найти количество Al(NO3)3 в 1-й части (уравнение (1) по Al(OH)3.

3) Найти количество Al(NO3)3 во 2-й части (уравнение 2) по Al(OH)3.

4) Найти количество Nh5NO3 (по уравнению (3)) по количеству AlCl3 (2-я часть)).

5) Найти ω(Nh5NO3) по уравнению (3).

Г) Решение

1) Находим количество Al(NO3)3 в исходном растворе.

а) находим количество Al(NO3)3·12h3O, которое растворилось в 250 г воды:

Используя данные по растворимости (растворимость 241 г в 100 г воды при 25 ºС), составляем пропорцию,

б)

2) Находим количество Al(NO3)3, прореагировавшего по уравнениям (2) и (3):

Пусть по уравнению (1) прореагировало x моль Al(NO3)3, по уравнению (2) – y моль Al(NO3)3, тогда

а) x + y = 1,4

б) по уравнению (2):

в) по уравнению (3):

г)

3) По уравнению (3) находим количество Nh5NO3:

а)

4) По уравнению (3) находим количество образовавшегося Al(OH)3:

5) Находим массу 2-й части раствора Al(NO3)3.

Концентрация вещества в растворе и в любой его части одинакова, следовательно

6) Находим массовую долю Nh5NO3 в растворе:

а)

б)

Решение задач на сплавы, смеси и растворы

Текстовые задачи входят в ОГЭ и ЕГЭ. Поэтому, данная тема имеет важнейшее значение в обучении математике. Хорошее преподавание текстовых задач играет неоценимую роль в этот период, для того, чтобы при встрече текстовых задач в заданиях ОГЭ и ЕГЭ они не вызывали затруднений.

Хочу поделиться уже опробованным и получившим положительный отзыв от учителей, работающих в 9-11-х классах, и самих учащихся, приемом для решения задач на «смеси и сплавы».

По моему опыту, научить решать большинство текстовых задач, содержащихся в открытом банке, можно практически любого выпускника. Конечно, при этом определяющими факторами являются желание и стремление ученика, и владение простыми вычислительными навыками. В данной статье хотела бы показать простое решение задач на растворы, смеси и сплавы. Мне кажется, что именно такой тип задач вызывают основные трудности.

В качестве практического материала мною были использованы задачи «от составителей» из «открытого банка заданий».

Существует много способов решения задач на растворы, смеси и сплавы. Но я бы хотела остановится на одном из них, который, по моему мнению, самый простой для усвоения решения таких задач.

При решении этих задач полезно применить очень удобную модель и научить школьников пользоваться ею. Изображаем каждую смесь (сплав) в виде римских цифр (I – первый сплав, II – второй сплав и т.п.), количество которых соответствует количеству составляющих эту смесь (этот сплав) элементов. Данная модель позволяет компактно и наглядно представить процессы сплавления, смешивания, и упрощает составление уравнения.

Вначале решения данных задач необходимо напомнить, что процентом называется его сотая часть и три основные задачи на проценты:

1. Найти 15% от числа 40.

Решение: 40•0,15=6.

2. Найти число, 15% которого равны 30.

Решение: 30:0,15=200.

3. Сколько процентов составляет число 180 от 600?

Решение: 180:600•100%=30%.

Рассмотрим задачу.

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Изобразим каждый из сплавов в виде римских цифр I, II и получившийся сплав после сплавления III (то есть по числу составляющих элементов). Кроме того, на модели отобразим характер операции – сплавление, поставим знак «+» между первым и вторым числом. Поставив знак «=» между вторым и третьим числом, мы тем самым показываем, что третий сплав получен в результате сплавления первых двух.

Полученная схема имеет следующий вид:

I + II = III

Теперь заполняем в соответствии с условием задачи:

Сверху над числом будем отмечать массу соответствующего сплава, а снизу процентное содержание чистого вещества.

Решение. Пусть х кг – масса первого сплава. Тогда, (х+3) кг – масса второго сплава. Дополним последнюю схему этими выражениями.

Получим следующую схему:

Необходимо учащимся объяснить, основное правило смешивания смесей или сплавления сплавов:

Масса раствора (смеси, сплава) равна сумме масс всех составляющих.
При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Масса растворенного вещества при смешивании двух растворов суммируется.

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=3. При этом значении х выражение 2х+3=9. Таким образом, масса третьего сплава равна 9 кг.

Ответ: 9 кг.

Рассмотрим сложнее задачу. Для данной задачи провожу аналогичные рассуждения только ведем записи совместно для двух случаем, которые описываются в этой задачи.

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Пусть масса 30-процентного раствора кислоты – х кг, а масса 60-процентного – у кг.

Упрощая каждое по отдельности уравнение, затем эти уравнение запишем в систему уравнений и решим

Получим х=60, у=30. Таким образом масса 30-процентного раствора кислоты 60 кг.

Ответ: 60 кг.

Такую визуализацию удобно использовать в задачах на растворы, смеси и сплавы. Такая модель помогает зрительно воспринимать задачу.
Таким способом можно решать задачи на проценты на «сушку». Только необходимо учащимся объяснить, что при высыхании из абрикоса испаряется вода, количество сухого вещества не меняется. Для начала найти процентное содержание сухого вещества в свежих фруктах, а потом в сушенных. Потом составить аналогичную схема для решения такой задачи.

Из моего опыта очень много ребят после этого объяснения стали решать такие задачи.

Наборы решений – SAT Math

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Задач, вопросов и онлайн-тестов по математике

Бесплатные онлайн-задачи по математике, вопросы и самопроверки по предвычислительным темам. Предоставляются ответы и подробные решения.

Практика тестов по математике

Бесплатные практические вопросы по тесту ACT по математике с ответами. 60 вопросов по математике с ответами, аналогичными вопросам в тесте ACT по математике. Ответы внизу страницы.
Free SAT Maths Test Practice Вопросы с ответами – образец 1. Набор из 25 вопросов по математике с ответами, аналогичными вопросам в тесте SAT по математике. Ответы внизу страницы.

Задачи и вопросы по математике

Решите задачи по математике (1) и предоставьте решения.
Решение задач численной, графической и аналитической математики (1). Проблема увеличения площади прямоугольного сада рассматривается с использованием трех подходов: численного, графического и аналитического. Также представлено обсуждение для сравнения трех методов.
Линейные функции Задачи с решениями Представлен набор задач, связанных с линейными функциями, а также подробные решения. Задачи разработаны с упором на значение наклона и точки пересечения оси y.
Математические задачи и решения для целых чисел.Проблемы, связанные с целыми числами, представлены вместе с их решениями.
Смесь проблем с растворами. Проблемы смеси и их решения представлены вместе с их решениями. Проценты также используются для решения подобных проблем.
Полиномиальные задачи с решениями. Полиномиальные задачи с подробными решениями.
Написание рациональных функций – проблемы с решениями. Напишите рациональные функции с учетом их характеристик, таких как вертикальные асимптоты, горизонтальные асимптоты, точки пересечения по оси x, отверстие.
Скорость, время, дистанция. Задачи с решениями. Соотношение между расстоянием, скоростью (скоростью) и временем Расстояние = время * скорость используется для решения задач равномерного движения. Предоставляются подробные решения проблем.
Work Rate Проблемы с решениями. Представлен комплекс проблем, связанных с работой и темпами работы, с подробными решениями.
Проблемы с снарядами и их решения. Учебник по решению проблем со снарядами. Предоставляются подробные решения проблем.
Вопросы с ответами по математике (1), а также подробные объяснения и решения этих вопросов.
Математические вопросы с ответами (2), решениями и пояснениями. Представлен набор вопросов по математике с несколькими вариантами ответов и ответы на них. Эти вопросы были разработаны для проверки глубокого понимания математических концепций.
Математические вопросы с ответами (3). Математические вопросы по логарифмическим и экспоненциальным выражениям и уравнениям с ответами.
Математические вопросы с ответами (4).Математические вопросы по решению уравнений и неравенств с абсолютной величиной. Также включены уравнения со сложными решениями.
Математические вопросы с ответами (5). Математические вопросы о кругах и расстоянии между двумя точками.
Математические вопросы с ответами (6). Математические вопросы об уклонах и уравнения прямых.
Математические вопросы с ответами (7). Математические вопросы о том, как найти область определения функции.
Математические вопросы с ответами (8). Математические вопросы по упрощению многочленов.
Математические вопросы с ответами (9). Математические вопросы по синтетическому делению многочленов.
Математические вопросы с ответами (10). Математические вопросы о степени и кратности нулей многочленов.
Математические вопросы с ответами (11). Математические вопросы по факторизации многочленов.
Математические вопросы с ответами (12). Математические вопросы о разложении на дроби.
Математические вопросы с ответами (13): Квадратичные функции. Математика Вопросы с ответами на поиск максимальных и минимальных значений, вершины, оси симметрии, интервала увеличения и уменьшения и диапазона квадратичных функций.
Процент математических задач Представлено несколько словесных задач в процентах с подробными решениями.
Процентные вопросы по математике Представлены несколько вопросов о процентах с подробными решениями.
Решение проблем с уклоном и решения.
Уравнения линий: задачи с решениями
Решайте экспоненциальные и логарифмические задачи и решения.
Решение проблем с расстоянием с включенными подробными решениями.
Вопросы о функциях с решениями.
Математическая индукция – Задачи с решениями. Представлено несколько задач математической индукции с подробными решениями.

Векторы

Сложение векторов и скалярное умножение. Учебник о том, как найти компоненты вектора, сложить два вектора, умножить вектор на скаляр. Включены примеры, решения, упражнения и ответы.
Точечное произведение двух векторов и приложений. Учебное пособие по скалярному произведению двух векторов и его применению для определения угла между двумя векторами.Найдите величину и направление векторов.

Последовательности

Геометрические последовательности Задачи с решениями. Представлены задачи и упражнения, включающие геометрические последовательности, а также подробные решения и ответы.
Арифметические последовательности Задачи с решениями. Задачи и упражнения, включающие арифметические последовательности, а также подробные решения и ответы.

Алгебра, уравнения и неравенства.

Алгебра Задачи и их подробные решения. У вас есть выбор между набором вопросов с ответами на них или набором из 50 вопросов в апплете для самопроверки знаний по алгебре.
Решите квадратные уравнения с рациональными выражениями – проблемы и подробные решения предоставлены. Решите комплекс задач, связанных с квадратными и рациональными уравнениями. У вас есть выбор между набором из 10 задач и 50 вопросов из апплета.
Решение линейных уравнений – Вопросы. Вопросы с множественным выбором решения линейных уравнений. Ответы включены.
Абсолютные уравнения значений и вопросы неравенства с подробными решениями и объяснениями.
Полиномиальные и рациональные неравенства, вопросы и ответы на них: представлены вопросы по решению полиномиальных и рациональных неравенств.Их можно использовать в качестве самопроверки.

Функции, область, композиция и обратные

Найдите область определения функции – Проблемы с подробными решениями: представлен набор из 10 задач по поиску области определения функции с их решениями.
Состав функций Вопросы с решениями.
Найти обратные функции – Вопросы и их подробные решения. Представлены вопросы о том, как найти обратное линейное, квадратичное с ограниченной областью, логарифмическое, экспоненциальное и рациональное, а также подробные решения.
Вопросы по индивидуальным функциям. Несколько вопросов с подробными решениями, а также упражнения с ответами на то, как доказать, что данная функция является функцией один к одному.

Логарифмы

Решите экспоненциальные и логарифмические уравнения, примеры с подробными решениями и пояснениями.

Графики функций

Графики функций – Вопросы и ответы на них: Для данного уравнения функции определите возможный график (из 4), соответствующий данной функции.Включены алгебраические функции, включая линейные функции, функции квадратного корня, квадратичные и абсолютные значения.
Графики полиномиальных функций – Вопросы с ответами: Вопросы и ответы на них представлены на графиках полиномиальных функций. Эти вопросы можно использовать в качестве самопроверки.
Графики рациональных функций – Вопросы с ответами: представлены вопросы и ответы на них по идентификации графиков рациональных функций.
Графики логарифмических и экспоненциальных функций – Вопросы с ответами: Вопросы и ответы на них представлены на графиках логарифмических и экспоненциальных функций.Их можно использовать в качестве самопроверки.

Тригонометрия

Решите тригонометрические уравнения – Задачи с ответами: 10 задач с ответами на решение тригонометрических уравнений представлены здесь и другие в апплете ниже.
Графики Тригонометрические функции – Вопросы с ответами: Набор вопросов с ответами на них по идентификации графиков тригонометрических функций sin (x), cos (x), tan (x), sec (x), csc (x), cot (x) представлены. Их можно использовать как самопроверку на графиках тригонометрических функций.
Найти значения тригонометрических функций – Вопросы с ответами. Представлен набор вопросов с ответами на них по нахождению точных значений тригонометрических функций sin (x), cos (x), tan (x), sec (x), csc (x), cot (x).

Преобразование единиц измерения

Преобразование единиц длины. Набор вопросов о том, как преобразовать одну единицу длины в другую: метры, километры, миллиметры, сантиметры, дециметры, футы, дюймы, ярды, мили, нанометры и микрометры. Используются как метрические, так и британские единицы.
Преобразование единиц скорости. Вопросы с ответами о том, как переводить из одной единицы скорости (скорости) в другую. Для длины используются как метрические, так и британские единицы измерения.

Комплексные числа

Вопросы о комплексных числах с ответами. Вопросы касаются сложения, умножения и деления комплекса, а также поиска комплексного сопряжения.
Комплексные числа в экспоненциальной форме. Примеры и вопросы с подробными решениями.
Комплексные числа в полярной форме.Примеры и вопросы с подробными решениями.
Теорема Де Муавра Степень и корень. Примеры и вопросы с подробными решениями по использованию теоремы Де Муавра для нахождения степеней и корней комплексных чисел. .
Бесплатная практика для тестов SAT, ACT по математике
Бесплатная практика для тестов GAMT Maths
Бесплатная практика GRE Quantitative for Practice

Как изучать математику: 7 советов по решению проблем

Как изучать математику

Математика – предмет, от которого нельзя отказаться.Некоторым это нравится, но, честно говоря, большинство людей ненавидят изучение математики. Важность математики для студентов как никогда. Предметы STEM – основа технологий завтрашнего дня. Большинство университетских курсов включают определенный уровень математики, в то время как почти каждая профессия использует математику в той или иной форме ежедневно. Проблема многих студентов заключается в том, что они не знают, как изучать математику, чтобы добиться хороших результатов.

Математика – один из тех предметов, на изучение которых вы можете легко потратить часы, но в конечном итоге не окажетесь мудрее.Сколько бы вы ни изучали, если вы не можете решить задачу в день теста, вы потеряны. К счастью, есть техник изучения математики , которые вы можете использовать независимо от вашего уровня. К концу сообщения в блоге вы можете даже полюбить математику!

7 советов по решению математических задач

1. Практика, практика и дополнительная практика

Невозможно правильно изучать математику, просто читая и слушая.Чтобы изучать математику, вам нужно засучить рукава и решить некоторые задачи. Чем больше вы тренируетесь решать математические задачи, тем лучше . У каждой проблемы есть свои особенности, и важно решить ее множеством способов, прежде чем приступить к экзамену. От этой реальности никуда не деться, чтобы хорошо сдать экзамен по математике, вам нужно заранее решить МНОГО математических задач.

2. Просмотрите ошибки

Когда вы практикуетесь с этими проблемами, важно проработать процесс для каждого решения .Если вы допустили какие-либо ошибки, вы должны просмотреть их и понять, где ваши навыки решения проблем подвели вас. Понимание того, как вы подошли к проблеме и где вы ошиблись, – отличный способ стать сильнее и избежать тех же ошибок в будущем.

Присоединяйтесь к тысячам студентов в нашей математической группе и ощутите всю мощь совместного обучения. Это бесплатно!

3. Овладейте ключевыми понятиями

Не пытайтесь запоминать процессы. Это контрпродуктивно. В долгосрочной перспективе гораздо лучше и полезно сосредоточиться на понимании процесса и логики, которые задействованы. Это поможет вам понять, как вам следует подходить к таким проблемам в будущем.

Помните, что математика – это последовательный предмет , поэтому важно иметь твердое понимание ключевых понятий, лежащих в основе математической темы, прежде чем переходить к другим, более сложным решениям, основанным на понимании основ.

4. Разберитесь в своих сомнениях

Иногда вы можете застрять, пытаясь решить часть математической задачи, и вам трудно перейти к следующему этапу. Многие студенты часто пропускают этот вопрос и переходят к следующему. Вам следует избегать этого и вместо этого тратить время на попытки понять процесс решения проблемы. Как только вы поймете исходную проблему, вы можете использовать ее как ступеньку для перехода к оставшейся части вопроса.

Помните: освоение математики требует времени и терпения.

Хорошая идея – учиться с другом, с которым вы можете посоветоваться и поделиться идеями при решении сложных проблем.

5. Создайте среду обучения, свободную от отвлекающих факторов

Математика – предмет, требующий более концентрации , чем любой другой. Правильная учебная среда и свободное пространство могут быть определяющим фактором при решении сложных уравнений или задач по геометрии, алгебре или тригонометрии!

Обучение под музыку может помочь создать расслабляющую атмосферу и стимулировать поток информации.Наличие подходящей фоновой музыки может способствовать достижению максимальной концентрации. Конечно, стоит держаться подальше от Pitbull и Eminem , инструментальная музыка – лучшее в наше время.

В нашем сообщении в блоге «Музыка для учебы: 10 советов по выбору лучшей музыки для учебы» дается больше советов по выбору лучшей музыки для учебы.

6. Создайте математический словарь

Математика имеет специфическую терминологию с большим количеством словаря .Мы предлагаем вам создать заметки или карточки со всеми понятиями, терминологией и определениями, которые вам нужно знать. Вы должны указать их значение, некоторые ключевые моменты и даже несколько примеров ответов, чтобы вы могли в любое время проконсультироваться с ними и подвести итоги.

7. Применение математики к реальным задачам

При приближении к математике старайтесь, насколько это возможно, применять реальные задачи. Математика может быть очень абстрактной, поэтому поиск практического применения может помочь изменить вашу точку зрения и по-другому усвоить идеи.

Вероятность, например, может использоваться в повседневной жизни, чтобы предсказать исход происходящего и определить, хотите ли вы пойти на риск, например, если вы должны купить лотерейный билет или сыграть в азартные игры.

О, и не забывайте, что также важно быть уверенным в себе и сдать экзамен, зная, что вы подготовились правильно!

О блоге GoConqr

Наш блог является частью GoConqr, бесплатной обучающей платформы для создания, обмена и поиска учебных ресурсов, которые помогают учащимся и учителям в достижении их учебных целей.Щелкните здесь, чтобы начать создавать интеллектуальные карты, карточки, заметки, викторины, блок-схемы слайдов и курсы прямо сейчас!

Как решать сложные математические задачи

17 ноября 2017 Ричард Рушик

Родитель одного из наших студентов написал сегодня о том, что его дочь время от времени разочаровывалась в сложности некоторых проблем на наших курсах. Она отлично работает на наших курсах и легко входила в число самых лучших учеников в классе, который она брала со мной, и все же она до сих пор иногда сталкивается с проблемами, которые не может решить.Более того, у нее есть доступ к отличному учителю математики в ее школе, который иногда также не может помочь ей решить эти проблемы. (Это немаловажно для него – у меня есть ученики, которые приносят мне проблемы, которые я тоже не могу решить!) Ее вопрос: «Почему это должно быть так сложно?»

Мы задаем сложные вопросы, потому что многие проблемы, которые стоит решать в жизни, являются сложными. Если бы они были легкими, кто-то другой решил бы их, прежде чем вы добрались до них. Вот почему в колледжах ведущих университетов есть тесты, по которым почти никто не сдает 70%, не говоря уже о наивысшем балле.Они обучают будущих исследователей, и весь смысл исследований состоит в том, чтобы найти и ответить на вопросы, которые никогда не были решены. Вы не можете научиться это делать, не борясь с проблемами, которые не можете решить. Если вы постоянно решаете каждую задачу в классе, вы не должны быть слишком счастливы – это означает, что вы учитесь недостаточно эффективно. Вам нужно найти класс посложнее.

Проблема отсутствия достаточного количества вызовов выходит далеко за рамки того, что вы не выучили математику (или что-то еще) так быстро, как вы можете.Я думаю, что многое из того, что мы делаем в AoPS, готовит студентов к решению задач, выходящих далеко за рамки математики. Стратегии того же типа, которые используются при решении очень сложных математических задач, могут использоваться для решения очень многих задач. Я считаю, что мы учим студентов думать, как решать сложные задачи, и что математика оказывается для многих лучшим способом сделать это.

Первый шаг в решении сложных проблем – это принять и понять их важность. Не уклоняйся от них.Они научат вас гораздо большему, чем просто рабочий лист с простыми задачами. Блестящий «Ага!» момента почти всегда возникают из умов, культивируемых долгими периодами разочарования. Но без этого разочарования никогда не появятся эти блестящие идеи.

Вот несколько стратегий решения сложных проблем и связанных с ними разочарований:

Сделай что-нибудь . Да, проблема сложная. Да, вы не представляете, что делать, чтобы решить эту проблему. В какой-то момент вам нужно перестать пялиться и начать пробовать что-то.По большей части это не сработает. Примите тот факт, что большая часть ваших усилий будет потрачена впустую. Но есть шанс, что один из ваших ударов поразит что-то, и даже если этого не произойдет, усилия могут подготовить ваш разум к победной идее, когда придет время. Мы начали разрабатывать программу начальной школы за несколько месяцев до того, как у нас появилась идея, которая стала Академией зверей. Наш ведущий разработчик учебной программы написал 100–200 страниц содержания, придумав множество различных стилей и подходов, которые мы могли бы использовать.Ни одной из этих страниц не будет в финальной версии, но они породили множество идей для контента, который мы будем использовать. Возможно, что более важно, это подготовило нас к тому, что, когда мы, наконец, натолкнулись на идею Академии Зверей, мы были достаточно уверены в ее реализации.

Упростите задачу . Попробуйте меньшие числа и особые случаи. Снимите ограничения. Или добавьте ограничения. Установите прицел немного ниже, а затем поднимите его, когда решите более простую задачу.

Размышляйте об успехах .Вы решили много проблем. Некоторые из них были даже тяжелыми! Как ты сделал это? Начните с проблем, похожих на ту, с которой вы столкнулись, но даже подумайте о других, которые не имеют ничего общего с вашей текущей проблемой. Подумайте о стратегиях, которые вы использовали для решения этих проблем, и вы можете наткнуться на решение. Несколько месяцев назад я играл с некоторыми проблемами Project Euler и натолкнулся на проблему, которая (в конечном итоге) сводилась к генерации целочисленных решений для c ² = a ² + b ² + ab эффективно.Теория чисел не моя сила, но мой путь к решению заключался в том, чтобы сначала вспомнить метод генерации пифагоровых троек. Затем я подумал о том, как создать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших более опытных в математике читателей настолько усвоили процесс решения для этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!)

Сосредоточьтесь на том, что вы еще не использовали . Многие проблемы (особенно геометрические) имеют много движущихся частей.Оглянитесь на проблему и на свои открытия и спросите себя: «Что я еще не использовал конструктивным образом?» Ответ на этот вопрос часто является ключом к вашему следующему шагу.

Назад . Это особенно полезно при поиске доказательств. Вместо того, чтобы начинать с того, что вы знаете, и работать над тем, что вы хотите, начните с того, что вы хотите, и спросите себя, что вам нужно для этого.

Обратиться за помощью . Многим выдающимся ученикам это нелегко.Вы так привыкли все делать правильно, быть тем, кого все просят, что трудно признать, что вам нужна помощь. Когда я впервые попал в MOP на втором курсе, я был не в себе. Я очень мало понимал, что происходило в классе. Однажды я попросил помощи у профессора – очень трудно было набраться смелости. Я не понимал ничего из того, что он мне рассказывал, за те 15 минут, что работал со мной наедине. Я просто не мог признаться в этом и попросить помощи, поэтому перестал спрашивать.Я мог бы узнать гораздо больше, если бы просто был более готов признаться людям, которых просто не понимал. (Это одна из причин, почему в наших классах теперь есть функция, позволяющая студентам задавать вопросы анонимно.) Преодолейте это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь большего, чем если бы вы этого не сделали.

Начало раннего . Это не очень помогает с тестами по расписанию, но с более долгими заданиями, которые являются частью учебы в колледже и в жизни, это очень важно.Не ждите до последней минуты – сложные задачи достаточно сложны, и вам не нужно иметь дело с нехваткой времени. Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся безумно умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, – это часто люди, которые просто думали о проблемах намного дольше, чем вы. Я использовал эту стратегию на протяжении всего колледжа с большим успехом – в первые несколько недель каждого семестра я работал далеко вперед во всех моих классах.Поэтому к концу семестра я размышлял над ключевыми идеями намного дольше, чем большинство моих одноклассников, что значительно упростило экзамены и тому подобное в конце курса.

Сделайте перерыв . Отойдите ненадолго от проблемы. Когда вы вернетесь к этому, вы можете обнаружить, что совсем не ушли от проблемы полностью – фоновые процессы в вашем мозгу продолжали отключаться, и вы окажетесь намного ближе к решению. Конечно, намного легче сделать перерыв, если вы начнете раньше.

Начать более . Отложите всю свою предыдущую работу, возьмите новый лист бумаги и попробуйте начать с нуля. Другая ваша работа все еще будет там, если вы захотите извлечь из нее позже, и она, возможно, подготовила вас к тому, чтобы воспользоваться идеями, которые вы сделаете во время второго раунда.

Сдаться . Вы не решите их всех. В какой-то момент пришло время сократить свои потери и двигаться дальше. Это особенно верно, когда вы тренируетесь и пытаетесь научиться чему-то новому.Одна сложная задача обычно научит вас большему в первые час или два, чем за следующие шесть, и есть гораздо больше проблем, на которых можно учиться. Итак, установите себе ограничение по времени, и если вы все еще безнадежно застряли в его конце, прочтите решения и двигайтесь дальше.

Будьте самоанализом . Если вы сдадитесь и прочтете решение, то читайте его активно, а не пассивно. Читая его, подумайте, какие ключи к разгадке проблемы могли привести вас к этому решению.Подумайте, что вы сделали неправильно в своем расследовании. Если в решении есть математические факты, которых вы не понимаете, приступайте к исследованию. Я был совершенно сбит с толку, когда впервые увидел кучу материалов о «модах» в решении олимпиады – тогда у нас не было Интернета, поэтому я не мог легко понять, насколько проста модульная арифметика! Теперь у вас есть Интернет, так что вам нет оправдания. Если вы все-таки решили проблему, не похлопывайте себя по плечу. Подумайте о ключевых шагах, которые вы сделали, и о знаках, по которым можно их попробовать.Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли бы их избежать. Эти уроки пригодятся вам позже.

Вернись . Если вы сдались и посмотрели на решения, вернитесь и попробуйте снова решить проблему через несколько недель. Если у вас нет никаких решений, оставьте проблему в живых. Храните это на бумаге или в уме. Ричард Фейнман однажды написал, что в глубине души он будет держать четыре или пять проблем активными. Всякий раз, когда он слышал новую стратегию или технику, он быстро перебирал свои проблемы и смотрел, сможет ли он использовать их для решения одной из своих проблем.Он считает, что эта практика стала причиной некоторых анекдотов, которые дали Фейнману такую репутацию гения. Это еще одно свидетельство того, что быть гением – значит очень много усилий, подготовки и уверенности в себе.

Советы и стратегии по подготовке к количественному / математическому тесту

Следующие ниже стратегии помогут вам эффективно подготовиться к количественным и математическим тестам. Хотя часто кажется невозможным набрать высокие баллы на тестах по математике, советы и стратегии, которые мы представим вам ниже, помогут вам достичь высоких результатов на следующем экзамене.

повтор

Лучший способ изучить и усвоить математические понятия – это практика и повторение. Повторение – ключ к успеху. Сначала освоите основные математические концепции и формулы, а затем выполните как можно больше практических задач. Старайтесь не повторять одни и те же практические задачи снова и снова. Выберите практические задачи, которые бросают вызов вашему пониманию проверяемых фундаментальных математических концепций и которые подготовят вас к решению любого типа математических вопросов, которые могут быть представлены на экзамене.Преподаватели и преподаватели часто вводят новые или слегка незнакомые форматы задач на экзаменах по математике, чтобы действительно проверить понимание и усвоение учащимися фундаментальных понятий, которые изучаются.

Испытайте себя

Опять же, цель вашего инструктора, проведя сложный тест по математике, заключается не в том, чтобы сделать вашу жизнь несчастной, а в том, чтобы убедиться, что вы понимаете и усваиваете изучаемую математическую концепцию. При подготовке к тестам по математике выполняйте практические задания, относящиеся к каждой концепции, по которой вы, возможно, будете тестироваться, и найдите время, чтобы отработать сложные задачи.Если возможно, просмотрите проблемы из прошлых тестов, проведенных вашим инструктором. Выберите для выполнения множество практических задач и убедитесь, что вы охватываете все концепции, которые могут появиться в тесте.

Сначала решайте проблемы самостоятельно

Самостоятельная работа над математическими задачами до обращения за помощью является ключом к развитию хороших математических навыков и глубокому пониманию основных математических концепций. Слишком часто, когда учащиеся борются со сложными математическими концепциями, их первым инстинктом является поиск помощи, прежде чем вернуться к своему учебнику, классным заметкам или другому справочному материалу, чтобы самостоятельно разобраться в проблеме или концепции – но борьба – это хорошо.Когда человеческий мозг изо всех сил пытается понять, он приобретает большую способность понимать. Прежде чем обращаться за помощью, потратьте пять-десять минут, пытаясь самостоятельно понять сложные математические концепции. Однако, если вы по-прежнему не можете решить проблему, проконсультируйтесь с другим учеником, репетитором или вашим учителем.

Сосредоточьтесь на понимании принципов

Можно пройти урок истории, запомнив даты, события и имена. В математике все иначе. В то время как математика требует запоминания наборов формул и процессов, гораздо более важно понимание того, как использовать и применять математические формулы и процессы, а также соответствующую логику.Совершенно необходимо понять ключевые концепции и принципы, лежащие в основе каждой математической темы, чтобы продвигаться по математике, поскольку математика является накопительной.

Например, запоминание некоторых математических формул, таких как формула исчисления для интегрирования по частям для интегралов, бесполезно, если вы не понимаете, как использовать формулу и идентифицировать соответствующие части интеграла. Другие формулы имеют особые ограничения. Например, квадратная формула требует, чтобы вы сначала привели квадратичную формулу в стандартную форму.Чтобы использовать множество математических формул, вы должны сначала понять, как части формулы соответствуют задаче.

Всегда сосредотачивайтесь на понимании математических принципов. Понимание математических принципов не только улучшит вашу способность изучать математику, но и повысит вашу успеваемость на математических тестах.

Математика является накопительной. Так что продолжай!

Зубчик для теста по математике неэффективен. Это особенно верно для более продвинутых математических курсов, таких как алгебра и исчисление в колледже.Математика, как дисциплина, носит накопительный характер. Почти каждая новая математическая концепция основана на понимании более базовой математической концепции. Например, вы не сможете изучить математику, пока не освоите алгебру и тригонометрию. К концу определенного курса математики вам может потребоваться изучить четыре или пять новых математических тем, которые вместе позволят вам понять и применить только одну математическую концепцию. Если вы прибудете в конце семестра, не изучив и не усвоив необходимые строительные блоки, вам будет практически невозможно выучить все в одночасье.Ключом к изучению математики и хорошей успеваемости по математическим тестам является своевременное выполнение домашнего задания и уверенность в том, что вы понимаете все концепции по мере прохождения курса.

Мы даже можем пойти дальше и предложить приходить на каждый математический класс, предварительно прочитав главы и концепции, которые будут рассмотрены в классе. Базовое понимание или даже знакомство с концепциями, которые будет описывать ваш инструктор, улучшит вашу способность понимать концепции и подготовит вас к вопросам, которые вы, вероятно, не ожидали бы, пока не будет завершена лекция.

Составьте список важных формул / концепций

Запишите все формулы, которые вы должны знать для своего теста по математике, на одном листе бумаги и запомните эти формулы. Многие студенты записывают формулы, которые им придется использовать в тесте, на полях или на противоположной стороне теста сразу после его получения. Часто люди забывают важные математические концепции и формулы во время теста. Полезно записать их в легкодоступном месте, когда тест становится трудным и возникает стресс.

Использовать учебные группы

Если вы прочитаете нашу статью об учебных группах, вы сможете узнать обо всех преимуществах использования учебных групп и о том, как создать эффективную учебную группу. Учебные группы могут быть особенно полезны для изучения математики и повышения успеваемости на экзаменах по математике по следующим причинам. Во-первых, групповая подготовка к тестам по математике может помочь убедиться, что вы охватили весь материал, который может появиться в тесте. Если вы что-то пропустили, есть вероятность, что кто-то из вашей группы это раскроет.Во-вторых, вы получите пользу от знаний и понимания других членов вашей группы. Если вы боретесь с определенной математической концепцией, вы можете опереться на других членов группы, чтобы получить ясность и понимание. Наконец, совместные усилия группы могут позволить каждому члену группы более быстро и тщательно подготовиться к экзамену по математике.

Исправить домашнее задание

Соберите набор домашних заданий, которые вы выполнили на протяжении всего курса, и доработайте их.Не просто просматривайте домашние задания, а исправляйте их. Запишите шаги, необходимые для решения каждой проблемы, а затем переработайте проблему, не глядя на решение. Используйте свои ранее выполненные домашние задания, чтобы проверить свои ответы, когда они будут выполнены.

Практикуйте задачи разными способами

Ваш профессор или преподаватель заинтересован в проверке ваших знаний и понимания основных математических принципов и концепций. Следовательно, они, вероятно, поставят на тест проблемы, которые будут представлены в несколько ином виде или формате, чем то, к которому вы привыкли.Практические задачи ставятся по-разному, поскольку вопросы часто задаются непонятным образом, чтобы проверить ваши знания. Это также поможет вам узнать, как использовать и применять многочисленные типы формул.

Внимательно прочтите инструкции

Поскольку вопросы могут состоять из нескольких частей, внимательно прочтите инструкции в каждом разделе. Также нередко вопрос запрашивает только частичный ответ или запрос, который завершает только один процесс. Внимательное и внимательное чтение инструкций гарантирует, что вы ответите только на заданный вопрос.

Оцените правильный ответ

Если возможно, оцените правильный ответ, прежде чем решать проблему. Если ваш ответ не соответствует вашим ожиданиям, может быть полезно перепроверить свою работу, чтобы убедиться, что ваши цифры верны и что вы использовали правильный процесс или формулы.

Покажи свою работу

Вы должны показать шаги, которые вы предприняли, чтобы получить окончательный ответ на тестах по математике. Вы всегда можете вернуться и просмотреть предпринятые вами шаги, если вы не уверены в ответе, а учителя часто дают частичную оценку неправильным ответам, когда вы показываете свою работу.Во многих случаях ваш профессор будет больше заинтересован в том, чтобы узнать, как вы пришли к своему ответу, чем в самом вашем ответе. В некоторых тестах не засчитывается правильный ответ, если он не подкреплен работой.

Не игнорируйте сбивающие с толку проблемы

Никогда не игнорируйте запутанные проблемы. Если вы не знаете, с чего начать, все же попытайтесь решить проблему. Не стирайте свою работу, так как ваш учитель может наградить вас частичной оценкой. Не пытайтесь разобраться во всей проблеме сразу.Столкнувшись со сложными проблемами, начните с записи всего, что вам известно о проблеме, включая тип проблемы, информацию, содержащуюся в вопросе / проблеме, и формулы, которые вы, возможно, можете использовать для решения проблемы. Также попробуйте определить, в какой форме должен быть ответ.

Просмотрите свои ответы

Если позволяет время, просмотрите свои окончательные ответы. Вы даже можете повторно решить проблемы, чтобы перепроверить свою работу на отдельном листе бумаги. Если после повторной обработки проблем вы получите новые ответы, еще раз изучите инструкции или поищите ошибки в расчетах.

4 шага для решения даже самой сложной математической задачи

Есть несколько способов решения математических задач; однако упрощенный метод, который может помочь каждому решить даже самую сложную проблему, представляет собой трехэтапный процесс.

Процесс:

1. Визуализируйте проблему
2. Подход, которого следует придерживаться для этой проблемы
3. Наконец, решите задачу

Этот трехэтапный процесс, вероятно, поможет вам улучшить свои математические навыки в целом. .

Вот четыре шага, которые помогут легко решить любые математические задачи:

1. Внимательно прочтите, поймите и определите тип задачи

Определите категорию, к которой относится ваша математическая задача, прежде чем двигаться дальше, как это поможет найти лучшее решение для ее решения.

Когда вы впервые начинаете изучать математику, проверьте тип задачи – проблема со словами, о дробях, квадратные уравнения или любой другой тип.

Определите категорию, к которой относится ваша математическая задача, прежде чем двигаться дальше, поскольку это поможет найти лучшее решение для ее решения.

Внимательное прочтение проблемы и обеспечение правильного понимания проблемы чрезвычайно важны для выполнения следующих шагов.

2. Нарисуйте и проанализируйте свою задачу

Возможно, вы также можете поискать шаблоны или использовать графики для решения математической задачи.

После того, как вы поняли проблему, следующим шагом может быть ее обозначение, поскольку это поможет вам в дальнейшем. Рисунок может быть простым в виде фигур или фигур с числами.

Здесь вы также, вероятно, могли бы поискать закономерности или использовать графики. После того, как весь этот процесс понимания, чтения и рисования будет завершен, вам необходимо пересмотреть анализ, который вы сделали на его основе.

Это поможет вам определиться с типом проблемы и методом ее решения.

3. Разработайте план решения

Сначала нужно выяснить формулу, которая понадобится вам для решения математической задачи.

Есть четыре простых шага, которые нужно пройти, чтобы разработать план решения этой проблемы.Шаги, указанные ниже:

Во-первых, нужно выяснить формулу, которая понадобится вам для решения проблемы. Здесь вам нужно потратить некоторое время на изучение концепций в ваших учебниках, которые помогут вам решить проблему.

Чтобы получить ответ на проблему, вам нужно записать свои потребности. Для этого вам нужно составить пошаговый список того, что вам нужно для решения проблемы, а также помочь вам оставаться организованным

Если есть более простая проблема, которая доступна, вы, вероятно, могли бы работать на то, чтобы сначала ее решить.Иногда формулы повторяются для решения обеих задач. Это даст вам больше времени для решения сложной задачи.

Вы можете сделать обоснованное предположение об ответе, чтобы вы могли попытаться оценить ответ, прежде чем приступить к его решению. Здесь вы можете определить количество и другие факторы, которые будут способствовать тому же. Наконец, просмотрите оценку, а затем проверьте, не упустили ли вы что-нибудь

4. Решите проблему

Убедитесь, что все шаги, которые вы перечислили для решения математической задачи, выполнены. и метод решения проблемы готовы, вы можете приступить к ее решению.Шаги следующие:

Убедитесь, что все шаги, которые вы указали для решения проблемы, выполнены. Перекрестно проверьте каждый из ответов, чтобы убедиться, что точность идеальная.

Сравните ответ с оценками, которые вы указали после завершения каждого шага. Это поможет вам сэкономить время в случае, если конечный результат окажется не тем, что вы искали. Также проверьте, тщательно ли вы выполнили все шаги.

Если в середине вы понимаете, что ваш план не работает, вы всегда можете вернуться к этапу планирования и составить новый план.Иногда это происходит из-за типичных ошибок, но вам следует научиться принимать это и быть готовым с Планом Б для ее решения

После того, как вы правильно решили проблему, вам следует вернуться и посмотреть на процесс. Найдите минутку, чтобы поразмыслить над проблемой и методом, с помощью которого вы ее решили. Это поможет определить концепции, которые вам нужно изучить во время практики.

– Статья Судханшу Синхала, управляющего директора, Sinhal Classes Pvt. ООО

Прочтите: CBSE Class 12 Mathematics: Экзаменатор указывает 8 распространенных ошибок, мешающих студентам получить полный 100

Прочтите: CBSE Class 10 Mathematics Board Exam 2018: Решите образец работы здесь !

Прочтите: Математика, основанная на развлечениях и занятиях! Этот новый метод может сделать изучение математики интересным

Онлайн-решение математических задач

Абсолютно бесплатный универсальный инструмент для решения математических задач:

Программа решения математических задач онлайн

Решайте свои математические задачи в Интернете.Бесплатная версия дает вам только ответы. Если вы хотите, чтобы решения, вам необходимо подписаться на бесплатную пробную учетную запись.

Базовый математический план

Basic Math Solver предлагает вам решение онлайн-задач с дробями, метрических преобразований, степенных и радикальных задач.
Можно найти площадь и объем прямоугольников, кругов, треугольники, трапеции, коробки, цилиндры, конусы, пирамиды, сферы.
Вы можете упрощать и оценивать выражения, множить / множить многочлены, комбинировать выражения.

Онлайн-решатель предварительной алгебры (геометрии)

Вы можете решать все задачи из основного математического раздела, а также решать простые уравнения, неравенства и задачи с координатной плоскостью.
Вы также можете оценивать выражения, факторные полиномы, выражения объединения / умножения / деления.

Онлайн-решатель алгебры

Я советую вам подписаться на этот решатель алгебры.
Вы можете шаг за шагом решать свои задачи по алгебре онлайн – уравнения, неравенства, радикалы, строить графики, решать полиномиальные задачи.
Если ваша домашняя работа по математике включает уравнения, неравенства, функции, многочлены, матрицы, это правильный пробный счет.

Онлайн-программа для определения тригонометрии

Решите все типы тригонометрических (sin, cos, tan, sec, scs, cot) выражений, уравнений, неравенств.
График тригонометрических функций.
Тригонометрия прямоугольного треугольника.

Онлайн-программа для предварительного вычисления

Включите все вышеперечисленное плюс нахождение пределов (lim), сумм, матриц.

Онлайн-поисковая программа

Решайте интегральные задачи – определенные, неопределенные интегралы.

Решатель онлайн-статистики

Решите свои проблемы вероятности, комбинации, перестановки. Статистика – найти медиану, среднее (арифметическое, геометрическое, квадратичное), моду, дисперсию, нормальные распределения, t-распределение.
Решатель успешно выполняет статистическую проверку гипотез

Онлайн-программа для определения химии

Вы можете решать уравнения химии онлайн.

Задачи ЕГЭ на сплавы, смеси, растворы.

Решение задач на смеси, сплавы и растворы для ЕГЭ по математике

Задачи на смеси и сплавы (ЕГЭ — 2021)

Разбор примеров

Решение примера №10

Решение примера №11

Решение примера №12

Готовимся к ЕГЭ задачи на растворы и сплавы | Методическая разработка по математике (10, 11 класс):

Задачи на сплавы и смеси: подробный разбор

Как решать 34 задание ЕГЭ по химии, примеры и алгоритмы решения заданий 34 по химии (Ростов-на-Дону)

РЕКОМЕНДУЕМЫЕ ТОВАРЫ

Решение задач на сплавы, смеси и растворы

Наборы решений – SAT Math

Задач, вопросов и онлайн-тестов по математике

Практика тестов по математике

Задачи и вопросы по математике

Векторы

Последовательности

Алгебра, уравнения и неравенства.

Функции, область, композиция и обратные

Логарифмы

Графики функций

Тригонометрия

Преобразование единиц измерения

Комплексные числа

Как изучать математику: 7 советов по решению проблем

Как изучать математику

7 советов по решению математических задач

О блоге GoConqr

Как решать сложные математические задачи

Как решать сложные математические задачи

17 ноября 2017 Ричард Рушик

Советы и стратегии по подготовке к количественному / математическому тесту

повтор

Испытайте себя

Сначала решайте проблемы самостоятельно

Сосредоточьтесь на понимании принципов

Математика является накопительной. Так что продолжай!

Составьте список важных формул / концепций

Использовать учебные группы

Исправить домашнее задание

Практикуйте задачи разными способами

Внимательно прочтите инструкции

Оцените правильный ответ

Покажи свою работу

Не игнорируйте сбивающие с толку проблемы

Просмотрите свои ответы

4 шага для решения даже самой сложной математической задачи

Онлайн-решение математических задач

Программа решения математических задач онлайн

Базовый математический план

Онлайн-решатель предварительной алгебры (геометрии)

Онлайн-решатель алгебры

Онлайн-программа для определения тригонометрии

Онлайн-программа для предварительного вычисления

Онлайн-поисковая программа

Решатель онлайн-статистики

Онлайн-программа для определения химии

Другие калькуляторы:

Оставить комментарий Отменить ответ