Как решаются матрицы: определение, свойства и примеры решения задач

Решение матричных уравнений онлайн

Назначение сервиса. Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word
• Также решают

Инструкция. Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.

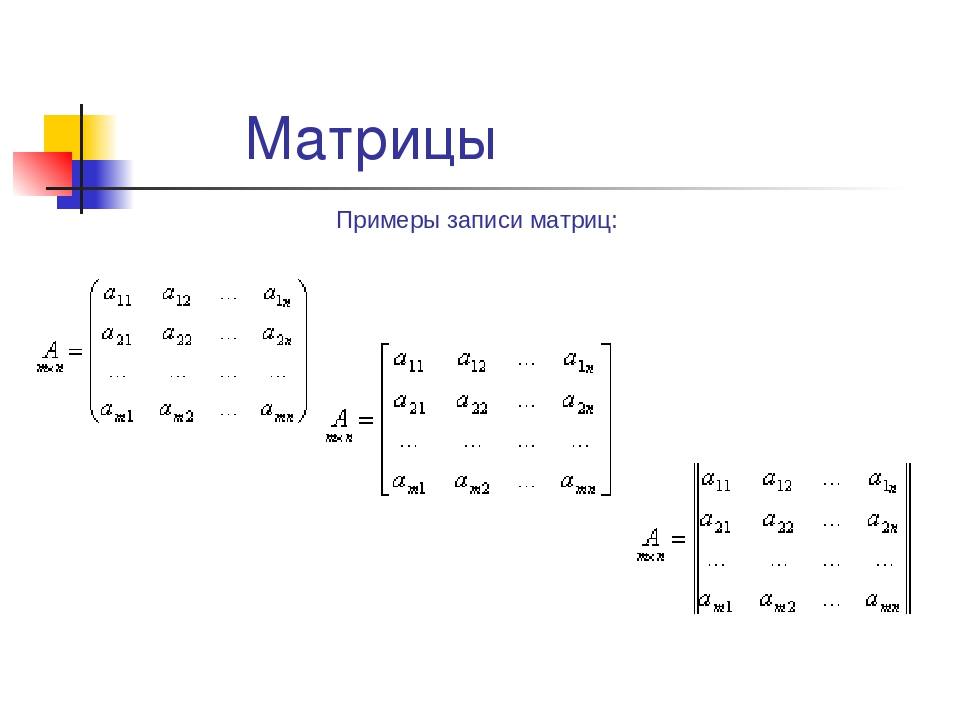
Вид уравнения:

• A·X = B

• X·A = B

• A·X·B = C

Размерность матрицы А 12345678910 x 12345678910
Размерность матрицы B 12345678910 x 12345678910

Размерность матрицы C 12345678910 x 12345678910

где А,В,С — задаваемые матрицы, Х – искомая матрица.

Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A^-1. Если задано выражение A·X - B = C, то необходимо, сначала сложить матрицы C + B, и находить решение для выражения A·X = D, где D = C + B. Если задано выражение A*X = B2, то предварительно матрицу B надо возвести в квадрат.

Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы

Координаты вектора в базисе

По координатам вершин пирамиды найти

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

Вычисление интегралов

Рекомендуется также ознакомиться с основными действиями над матрицами.

Пример №1. Задание. Найти решение матричного уравнения
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1

Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим слева обе части уравнения на A^-1:Умножаем обе части этого равенства слева на A^-1 и справа на B^-1: A^-1·A·X·B·B^-1 = A^-1·C·B^-1. Так как A·A^-1 = B·B^-1 = E и E·X = X·E = X, то X = A^-1·C·B^-1
Найдем обратную матрицу A^-1.
Транспонированная матрица A^T:
Обратная матрица A^-1:
Найдем обратную матрицу B^-1.
Транспонированная матрица B^T:
Обратная матрица

B-1 = -½

8 -6 -7 5

Матрицу X ищем по формуле: X = A^-1·C·B^-1

X = –

-2 1 -5 3

*

14 16 9 10

-½

8 -6 -7 5

=

Ответ:

Пример №2. Задание. Решить матричное уравнение
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.

Пример №3. Задание. Найти решение матричного уравнения
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60

Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим справа обе части уравнения на A^-1: X·A·A^-1 = B·A^-1, откуда находим, что X = B·A^-1
Найдем обратную матрицу A^-1.
Транспонированная матрица A^T:
Обратная матрица A^-1:
Матрицу X ищем по формуле: X = B·A^-1

Ответ:

Пример №4. Задание. Решить матричное уравнение
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.

Определитель матрицы А равен detA=1
Так как A невырожденная матрица, то существует обратная матрица A^-1. Умножим слева обе части уравнения на A^-1: A^-1·A·X = A^-1·B, тогда получим E·X = A^-1·B, или X = A^-1·B.
Найдем обратную матрицу A^-1.
Транспонированная матрица A^T:
Обратная матрица A^-1:
Матрицу Х ищем по формуле: X = A^-1·B

Ответ:

Матрицы 2.

В прошлый раз мы рассмотрели матрицы, их виды, увидели определитель и способ его нахождения, и простейшие действия с матрицами. Сегодня мы добавим инфы по определителю, узнаем про ранг матрицы, научимся находить обратную матрицу и увидим провождение матрицы к ступенчатому виду.

Свойства определителя.
1. У транспонированной матрицы не меняется определитель. То есть если мы поменяем строки и столбы местами, то нихуя не поменяется.
2. Если мы поменяем местами 2 строки или 2 столбца, то определитель меняет знак.
3. Умножение строк или столбцов матрицы на какое-то число, также умножит определитель на это число. Отсюда можно нахуй выносить общие множители за детерминант.
4. Если в матрице есть ряд нулей, то определитель 0.

5. Если есть 2 одинаковых строки или столбца, либо они пропорциональны, то детерминант равен 0.
6. Определитель треугольной матрицы равен произведению элементов главной диагонали.
7. Если строка или столбец матрицы – это сумма 2-х каких-то чисел (a_(kn)+b_(kn)), то определитель можно расписать суммой 2-х определителей, где в первом мы пишем строку с a_(kn), а во втором b_(kn).
8. Определитель не изменится, если плюсануть какую-то строчку (столбец), помноженную на какое-нибудь число, на какую-нибудь другую строчку (столбец).
9. Если у 2-х матриц определитель одинакового порядка, то определитель произведения матриц равен произведению определителей. (i+j) и получаем алгебраическое дополнение. После этого нам нудно будет поделить алгебраические дополнения ТРАНСПОНИРОВАННОЙ матрицы на определитель матрицы А. Это я сделал на 2 пикче.

И наконец, ранг матрицы. Ранг – это хуйнина, на которой многие делают ошибки; показывает ранг наибольшее число линейно независимых строк (строк, которые нельзя получить из других строк в этой матрице (преобразования матрицы)). Мы находим детерминант, если он не 0, то порядок этого определителя и есть ранг матрицы, если 0, то мы ищем наименьшее алгебраическое дополнение и его определитель и действуем по отработанной схеме. 0 ранг имеет только нулевая матрица, поэтому, если у вас в матрице 2х2 детерминант будет 0, то вы тупо пишите, что её ранг равен 1.

В 3 и последнем посте про матрицы мы рассмотрим всякую оставшуюся хуйню, про которую я сча ещё не знаю.

1 часть: https://vk.com/wall-147914213_6494

Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite

Использование матриц для решения систем уравнений | безграничная алгебра |

Матричные уравнения

Матрицы можно использовать для компактного написания и работы с системами нескольких линейных уравнений.

Цели обучения

Определите, как матрицы могут представлять систему уравнений.0016 n×1n \times 1n×1

 матрица) из

nnn

 переменные

x1,x2,…,xnx_1, x_2,…, x_nx1​,x2​,…,xn​

и

bbb

— это вектор-столбец размером

м × 1 м × 1 м × 1

 , тогда матричное уравнение имеет вид:

Ax=bAx=bAx=b

.

Ключевые термины

• матрица : Прямоугольное расположение чисел или термов, имеющее различные применения, такие как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.

Матрицы можно использовать для компактной записи и работы с системами уравнений. Как мы узнали из предыдущих разделов, матрицами можно манипулировать так же, как и обычным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений. Полезно понять, как организовать матрицы для решения этих систем.

Написание системы уравнений с матрицами

Эту систему можно решить методом исключения или замены, но можно и с помощью матричной операции. Прежде чем мы приступим к настройке матриц, важно сделать следующее:

• Убедитесь, что все уравнения написаны одинаково, то есть все переменные должны быть в одном порядке.
• Убедитесь, что одна часть уравнения состоит только из переменных и их коэффициентов, а другая часть – только из констант.

Решение системы линейных уравнений с помощью обратной матрицы требует определения двух новых матриц: 

XXX

 матрица, представляющая переменные системы, и 

BBB

— матрица, представляющая константы. Используя умножение матриц, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:

A⋅X=B\displaystyle A\cdot X=BA⋅X=B

Чтобы решить систему линейных уравнений с помощью обратной матрицы, пусть

AAA

 будет матрицей коэффициентов, пусть

XXX

 будет матрицей переменных, а 9001  006  BBB

  — постоянная матрица.

Учитывая систему:

x+8y=72x−8y=−3\displaystyle \начать{выравнивать} х+8у&=7 \\ 2x-8y&=-3 \end{align}x+8y2x−8y​=7=−3​

Матрица коэффициентов:

A=[182−8]A=\begin{bmatrix} 1 и 8\\ 2 и -8 \end{bmatrix}A=[12​8−8​]

Переменная матрица:

X=[xy]\displaystyle X=\begin{bmatrix} х\\у \end{bmatrix}X=[xy​]

Постоянная матрица:

B=[7−3]\displaystyle B=\begin{bmatrix} 7\\-3 \end{bmatrix}B=[7−3​]

9{-1} \right)(A−1)

 существует, эта формула решит систему.

Если матрица коэффициентов необратима, система может быть несовместной и не иметь решения или быть зависимой и иметь бесконечно много решений.

Матрицы и операции со строками

Две матрицы эквивалентны по строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.

Цели обучения

Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы

Key Takeaways

Key Points

• Элементарная операция со строками — это любое из следующих действий: переключение строк (перестановка двух строк матрицы), умножение строк (умножение строки матрицы на ненулевую константу) , или сложение строк (добавление к одной строке матрицы некоторого числа, кратного другой строке).
• Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы.

Ключевые термины

• пространство строк : Набор всех возможных линейных комбинаций его векторов-строк.
• эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой с помощью последовательности элементарных операций над строками.

Элементарные операции с рядами (ERO)

В линейной алгебре две матрицы эквивалентны по строкам, если одну можно заменить на другую с помощью последовательности элементарных операций со строками. Или два

m×nm \times nm×n

матрицы эквивалентны по строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство 90 159 строк 90 160 матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы. Две матрицы одинакового размера эквивалентны по строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство. Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).

Элементарной операцией со строками является любой из следующих трех ходов:

1. Переключение строк (своп): поменять местами две строки матрицы.
2. Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
3. Добавление строки (поворот): добавление к одной строке матрицы числа, кратного другой строке.

Создание эквивалентных матриц с использованием элементарных операций со строками

Поскольку матрица по существу представляет собой коэффициенты и константы линейной системы, операции с тремя строками сохраняют матрицу. Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных инверсий, чтобы переменная сокращалась. Наконец, добавление строк также совпадает с методом исключения, когда для получения переменной выбирают добавление или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод решения системы уравнений.

Пример 1. Покажите, что эти две матрицы эквивалентны по строкам:

A=(1−10211)B=(301031)\displaystyle A=\begin{pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \end{pmatrix}\quad B=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix }A=(12​−11​01​)B=(30​03​11​)

Начните с

AAA

, добавьте вторую строку к первой:

A=(301211)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \end{pmatrix}A=(32​01​11​)

Затем умножьте вторую строку на 3, а затем вычтите первую строку из второй:

A=(301332)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \end{pmatrix}A=(33​03​12​)

Наконец, вычтите первую строку из второй:

A= (301031)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix}A=(30​03​11​)

Вы можете видеть, что

A=BA=BA=B

, чего мы достигли с помощью серии элементарных операций над строками.

Сокращение строк: решение системы линейных уравнений

При сокращении строк линейная система:

x+3y−2z=53x+5y+6z=72x+4y+3z=8\displaystyle х+3у-2г=5 \\ 3х+5у+6з=7\\ 2x+4y+3z=8x+3y−2z=53x+5y+6z=72x+4y+3z=8

Представляется расширенной матрицей:

A=(13−2535672438)\displaystyle A=\begin{pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \end{pmatrix}A=⎝

⎛​132​354​−263​578​⎠

⎞​

Эта матрица затем модифицируется с помощью элементарных операций со строками до тех пор, пока она не примет форму сокращенного эшелона строк.

Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.

Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление может быть выполнено вручную (с использованием трех типов ERO) или на калькуляторе с помощью матричной функции ‘rref’ (форма с уменьшенной ступенчатой ​​строкой).

Окончательная матрица имеет сокращенную ступенчатую форму и представляет собой систему

.

A=(100−1501080012)\displaystyle A=\begin{pmatrix} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{pmatrix}A=⎝

⎛​100​010​001 ​−1582​⎠

⎞​

Упрощение матриц с помощью операций со строками

Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелонирования строк.

Цели обучения

Используйте элементарные операции со строками, чтобы представить матрицу в упрощенной форме

Ключевые выводы

Ключевые точки

• Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк эшелонированной формы строк такое же, как и исходное матрица.
• Существует три типа операций с элементарными строками: поменять местами две строки, умножить строку на ненулевой скаляр и добавить к одной строке скаляр, кратный другому.
• На практике системы обычно не рассматриваются в терминах уравнений, а вместо этого используется расширенная матрица (которая также подходит для компьютерных манипуляций).

Ключевые термины

• расширенная матрица : Матрица, полученная путем сложения столбцов двух данных матриц, обычно с целью выполнения одних и тех же элементарных операций над строками для каждой из данных матриц.

С помощью конечной последовательности элементарных операций над строками, называемой методом исключения Гаусса, любая матрица может быть преобразована в ступенчатую форму строк. Это преобразование необходимо для решения системы линейных уравнений.

Прежде чем перейти к более подробному рассмотрению, необходимо упомянуть несколько ключевых терминов:

• Расширенная матрица : расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одни и те же элементарные операции над строками на каждой из заданных матриц.
• Форма верхнего треугольника : Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это либо нижняя треугольная, либо верхняя треугольная. Матрица, имеющая как верхнюю, так и нижнюю треугольную форму, является диагональной матрицей.
• Элементарные операции со строками : Перестановка строк, добавление строк или умножение строк.

Исключение Гаусса

1. Напишите расширенную матрицу для линейных уравнений.
2. Используйте элементарные операции со строками над расширенной матрицей

   [A∣b][A|b][A∣b]

   , чтобы преобразовать

   AAA

   в форму верхнего треугольника. Если на диагонали стоит ноль, меняйте местами строки, пока на его месте не окажется ненулевое значение.
3. Используйте обратную замену, чтобы найти решение.

Пример 1. Решите систему методом исключения Гаусса:

2x+y−z=8−3x−y+2z=−11−2x+y+2z=−3\displaystyle 2x+y-z=8\\ -3x-y+2z=-11\\ -2x+y+2z=-32x+y-z=8-3x-y+2z=-11-2x+y+2z=-3

Запишите расширенную матрицу:

[21-18-3-12 −11−212−3]\left[\begin{array}{rrr|r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & – 3 \end{array} \right] ⎣

⎡​2−3−2​1−11​−122​8−11−3​⎦

⎤​

Используйте элементарные операции над строками, чтобы уменьшить матрицу до уменьшенной форма эшелона ряда:

[10020103001−1]\left[\begin{array}{rrr|r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{массив } \right] ⎣

⎡​100​010​001​23−1​⎦

⎤​

Используя элементарные операции со строками для получения сокращенной эшелонированной формы строки (‘rref’ в калькуляторе), решение системы в последнем столбце:

x=2,y=3,z=-1x=2, y=3, z=-1x=2,y=3,z=-1

.

Лицензии и атрибуты

Контент под лицензией CC, совместно используемый ранее

• Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

• Решающие системы с инверсиями. Предоставлено : Openstax. Расположен по адресу : https://openstax.org/books/college-алгебра/pages/7-7-solving-systems-with-inverses. Лицензия : CC BY-SA: Attribution-ShareAlike
• Матричное уравнение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
• Эквивалентность строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Матрица (математика). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• система линейных уравнений. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/System_of_linear_equations. Лицензия : CC BY-SA: Attribution-ShareAlike
• эквивалент строки. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Исключение Гаусса. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Форма эшелона строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Треугольная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Дуг Дэниелс и Стивен Кокс, Сокращенная форма строки. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
• Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Элементарные операции со строками. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Дополненная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• дополненная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike

Решение одновременных уравнений с использованием матриц

Матрицы используются во многих сферах жизни, от шифрования данных до проектирования трехмерных игр, но они также чрезвычайно полезны в других математических областях. контекстах, таких как решение одновременных уравнений. Набор одновременных уравнений (также известный как система уравнений) может быть решен с помощью различных приложений матричной алгебры с использованием обратных матриц и таких методов, как сокращение строк.

В этой статье мы рассмотрим решение одновременных уравнений с использованием матриц, сначала записав их в матричной форме, а затем изучив различные методы их решения, такие как использование обратных матриц и сокращение строк.

Система уравнений в матричной форме

Чтобы решить систему уравнений с помощью матриц, вы должны иметь возможность переписать эти уравнения в виде матриц.

Следующий пример подробно объясняет процесс.

Перепишите следующий набор уравнений в матричной форме (также известной как \(Ax = b\)):

\begin{equation}\begin{split}-4x + 4y + z & = 3 \\11y – 7x + z & = 4 \\-5x + 3y + 2z & = 5 \\\end{split}\ qquad\begin{matrix}(1) \\ (2) \\ (3)\end{matrix}\end{equation}

Решение

ШАГ 1 : Убедитесь, что переменные в том же порядке для каждого уравнения (т. е. если порядок, который вы выбрали для первого уравнения, равен \(x, y, z\), то переменные в каждом последующем уравнении также должны быть в порядке \(x, y, z \)).

В этом примере мы выберем порядок \(x, y, z\).

Переменные во втором уравнении не в правильном порядке. Мы исправим это, просто перестроив уравнение так, чтобы порядок переменных был таким же, как и в двух других уравнениях.

Таким образом, второе уравнение будет выглядеть следующим образом:

\[-7x + 11y + z = 4\]

ШАГ 2 : Перепишите уравнения в матричной форме .

Первая матрица, которая нам нужна, это матрица коэффициентов. Это квадратная матрица, содержащая коэффициенты каждой переменной, и ее размер зависит от количества переменных в данных уравнениях.

Каждый столбец в матрице коэффициентов содержит коэффициенты для определенной переменной. Например, столбец 1 содержит коэффициенты \(x\). Столбцы 2 и 3 содержат коэффициенты для \(y\) и \(z\) соответственно. Вот почему так важен порядок переменных в данных уравнениях; если они в неправильном порядке, то коэффициенты будут в неправильных столбцах.

Каждая строка в матрице коэффициентов соответствует одному из заданных уравнений. Все коэффициенты в строке 1 взяты из уравнения 1, в строке 2 содержатся коэффициенты из уравнения 2 и т. д.

Когда мы соединим все вышеперечисленное вместе, мы получим матрицу, которая выглядит так:

\[\begin{bmatrix}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{bmatrix}\]

Как видите, столбцы 1, 2 и 3 содержат коэффициенты для \(x, y\) и \(z\) соответственно, а строки 1, 2 и 3 удерживать коэффициенты для уравнений 1, 2 и 3 соответственно.

Вторая матрица, которая нам нужна, представляет собой матрицу 3 x 1, содержащую переменные, и она известна как матрица переменных. Он всегда должен располагаться справа от матрицы коэффициентов.

Переменные в матрице перечислены сверху вниз в том порядке, который вы выбрали для них, и это должно выглядеть следующим образом:

\[\begin{bmatrix}x \\ y \\ z\end{bmatrix} \]

Последняя необходимая матрица — это матрица 3 x 1, расположенная справа от знака равенства. Она называется постоянной матрицей, и, как и в матрице коэффициентов, каждая строка содержит постоянное значение, принадлежащее соответствующему уравнению.

Это будет выглядеть так:

\[\begin{bmatrix}3 \\ 4 \\ 5\end{bmatrix}\]

Наш окончательный ответ состоит из всех трех матриц и будет выглядеть следующим образом:

\[\begin{bmatrix}-4 & 4 & 1 \\11 & -7 & 1 \\-5 & 3 & 2 \ \\end{bmatrix}\begin{bmatrix}x \\ y \\ z\end{bmatrix}=\begin{bmatrix}3 \\ 4 \\ 5 \\\end{bmatrix}\]

Что произойдет если бы вы умножили матрицы?

\[\begin{align}\begin{bmatrix}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}& = \begin{bmatrix}3 \\ 4 \\ 5\end{bmatrix} \\\hspace{1cm} \\\begin{bmatrix}-4x & 4y & z \\ 11x & -7y & z \\ -5x & 3y & 2z\end{bmatrix} & = \begin{bmatrix}3 \\ 4 \\ 5 \end{bmatrix} \\\end{align}\]

Результат дает нам исходные уравнения. Именно по этой причине эти конкретные матрицы изложены таким особым образом.

Расширенные матрицы

Наиболее распространенный метод решения одновременных уравнений с матрицами включает использование сокращения строк. Чтобы выполнить сокращение строк, нужно уметь записывать данные уравнения в расширенной матрице.

Используя те же уравнения, что и в предыдущем примере, перепишите их в расширенной матрице.

\begin{equation}\begin{split}-4x + 4y + z & = 3 \\-7x +11y + z & = 4 \\-5x + 3y + 2z & = 5 \\\end{split} \end{уравнение}

Решение

ШАГ 1 : Сначала убедитесь, что все ваши уравнения имеют одинаковый порядок. В этом случае нет никакого уравнения, которое нужно переставлять.

ШАГ 2 : Запишите коэффициенты переменных, чтобы начать матрицу.

\[\left[\begin{array}{rrr}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{array}\right.\]

ШАГ 3 : Проведите вертикальную линию справа от коэффициентов.

\[\left[\begin{array}{rrr|}-4 & 4 & 1 \\ 11 & -7 & 1 \\ -5 & 3 & 2\end{array}\right.\]

ШАГ 4 : Запишите константы в правой части строки и закройте скобки

Ваш ответ должен выглядеть следующим образом:

\[\left[\begin{array}{rrr|r}-4 & 4 & 1 & 3 \\11 & -7 & 1 & 4 \\-5 & 3 & 2 & 5 \end{массив}\right]\]

Решение одновременных линейных уравнений с использованием матриц

Интерпретация систем уравнений

Система уравнений может не иметь единственного решения. Можно использовать расширенные матрицы для определения количества решений, если таковые имеются, в системе уравнений.

Если дана система уравнений с тремя уравнениями с тремя неизвестными, мы можем смоделировать эти три уравнения как плоскости. Одним из уникальных решений было бы пересечение всех плоскостей. Если система имеет бесконечное число решений, то это означает, что все три плоскости пересекаются на линии пересечения. Система без решений не будет иметь точки пересечения всех трех плоскостей.

Бесконечное множество решений

Некоторые системы уравнений могут иметь бесконечное число решений. Это происходит в результате того, что свободная переменная является частью уравнений.

Свободная переменная — это переменная, значение которой может свободно изменяться.

В следующем примере показано, как определить бесконечное количество решений, которые может иметь система уравнений.

Рассчитайте решение следующей системы уравнений:

\[\begin{align}x + 5y – z & = 1 \\2x + 7y – 4z & = 0 \\4x + 11y -10z & = -2\end{align}\]

Решение

ШАГ 1 : Запишите расширенную матрицу.

\[\left[\begin{array}{rrr|r}1 & 5 & -1 & 1 \\ 2 & 7 & -4 & 0 \\ 4 & 11 & -10 & -2\end{массив }\right]\]

ШАГ 2 : Выполнение вычислений строк.

Выполняем следующие операции со строками:

\[\begin{align}R_{3} – 2R_{2} & \to R_{3} \\R_{2} – 2R_{1} & \to R_{ 2} \\R_{3} – R_{2} & \to R_{3} \end{align}\]

для получения расширенной матрицы:

\[\left[\begin{array}{rrr|r}1 & 5 & -1 & 1 \\ 0 & -3 & -2 & -2 \\ 0 & 0 & 0 & 0\end{array}\right]\]

В форме \(Ax = B\) это будет выглядеть следующим образом:

\[\begin{bmatrix}1 & 5 & -1 \\ 0 & -3 & -2 \\ 0 & 0 & 0\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}=\begin{bmatrix}1 \\ -2 \\ 0\ end{bmatrix}\]

Отсюда мы знаем, что \(x + 5y – z = 1\) и \(-3y – 2z = -2\).

Теперь упростим уравнения, чтобы получить следующее:

\[\begin{align}y & = \frac{2}{3} -\frac{2}{3}z \\\hspace{1cm} \ \x & = -5y + 1 + z \qquad \text{Подстановка} \; у \; \текст{в} \; x \\\hspace{1cm} \\\поэтому x & = -\frac{7}{3} + \frac{7}{3}z\end{align}\]

Пусть \(\frac{z {3}\) — свободная переменная \(t\).

Таким образом, уравнения будут выглядеть следующим образом:

\[\begin{align}x & = -\frac{7}{3} + 7t \\y & = \frac{2}{3} – 2t\end {выравнивание}\]

и когда в матричной форме даст нам:

\[\begin{bmatrix}x \\ y \\ z \end{bmatrix} =\begin{bmatrix}-\frac{7}{3} \\ \ frac{2}{3} \\ 0\end{bmatrix} +\begin{bmatrix}7 \\ -2 \\ 3\end{bmatrix} t\]

Оба \(x\) и \(y\ ) зависят от \(z\), поэтому мы можем ввести их в систему. \(z\) — свободная переменная, то есть она может свободно изменять свое значение, а поскольку \(x\) и \(y\) зависят от \(z\), это означает, что существует бесконечное число решений к этой системе уравнений.

Помните, что мы обозначили \(\frac{z}{3} = t\), поэтому \(z = 3t\).

Пример того, как может выглядеть система уравнений с бесконечным числом решений, показан ниже:

Система уравнений с бесконечным числом решений, смоделированных как плоскости. Плоскости пересекаются на линии пересечения — StudySmarter Originals

Нет решений

В следующем примере показано, как определить, не имеет ли система уравнений решений.

Покажите, что следующая система уравнений не имеет решений:

\[\begin{align}x + 2y – z = -8 \\ 2x – y + z = 4 \\ 8x + y + z = 2\end{align}\]

Решение

ШАГ 1 : Запишите расширенную матрицу.

\[\begin{array}{rrr|r}1 & 2 & -1 & -8 \\ 2 & -1 & 1 & 4 \\ 8 & 1 & 1 & 2\end{array}\]

ШАГ 2 : Выполняйте вычисления строк, пока не будут получены необходимые нули.

\(R_{3} – R_{2} \к R_{3}, \; R_{2} + R_{1} \к ​​R_{2}, \; R_{3} – 2R_{2} \ до R_{3}\) выполняются для получения:

\[\left[\begin{array}{rrr|r}1 & 2 & -1 & -8 \\ 3 & 1 & 0 & 4 \\ 0 & 0 & 0 & -6\end {массив} \right]\]

Когда вы посмотрите на последнюю строку, вы увидите, что в ней указано, что \(0 = -6\). Это заведомо неверно, и поэтому система не имеет решений.

При моделировании с использованием плоскостей система без решений может выглядеть следующим образом:

Система трех одновременных уравнений без решений, смоделированных как плоскости – StudySmarter Originals 9{-1}\), должен быть на левой стороне других матриц; в противном случае вы не сможете их умножить.

В следующем примере показано, как решать одновременные уравнения с использованием обратных матриц.

Решите одновременно следующие уравнения с помощью матричной алгебры:

\[\begin{align}4x + y & = -7 \\3x-2y & = 3 \\\end{align}\]

Решение

ШАГ 1 : Перепишите два уравнения в виде матричного уравнения. Ваш ответ должен выглядеть так:

\[\begin{bmatrix}4 & 1 \\3 & -2 \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix}-7 \\ 3\end {bmatrix}\]

ШАГ 2 : Вычислить обратную матрицу коэффициентов.

Мы хотим найти \(x\) и \(y\), поэтому мы должны изолировать эти две переменные на одной стороне уравнения. Для этого мы должны задействовать единичную матрицу. Мы делаем это, умножая обе части уравнения на обратную матрицу коэффициентов.

9{-1}\) слева, чтобы получить это.

Ваш результат будет выглядеть следующим образом:

\[\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} =-\frac{ 1}{11}\begin{bmatrix}-2 & -1 \\ -3 & 4\end{bmatrix}\begin{bmatrix}-7 \\ 3 \end{bmatrix} \]

ШАГ 4 : Упростите, чтобы получить решения для \(x\) и \(y\).

\[\begin{align}\begin{bmatrix}x \\ y\end{bmatrix}& =-\frac{1}{11} \times\begin{bmatrix}11 \\ 33\end{bmatrix} \\\hspace{1cm}\\\begin{bmatrix}x \\ y \end{bmatrix}& = \begin{bmatrix} -1 \\ -3 \end{bmatrix}\end{align}\]

\(\следовательно, \quad x = -1\) и \(y = -3\)

В следующем примере показано, как использовать обратные матрицы для решения одновременных уравнений, содержащих три переменные.

Используйте обратные матрицы для решения следующей системы одновременных уравнений:

\[\begin{align}x – y – z & = 4 \\2x + 3y – z & = 2 \\- x – 2y + 3z & = -3\end{align}\]

Решение

ШАГ 1 : Перепишите уравнения в матричной форме.

9{-1}\) слева от обеих частей уравнения.

\[\frac{1}{13} \begin{bmatrix}7 & 5 & 4 \\-5 & 2 & -1 \\-1 & 3 & 5\end{bmatrix}\begin{bmatrix}1 & -1 & -1 \\ 2 & 3 & -1 \\-1 & -2 & 3 \\\end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix} =\frac {1}{13} \begin{bmatrix}7 & 5 & 4 \\-5 & 2 & -1 \\-1 & 3 & 5\end{bmatrix} \begin{bmatrix}4 \\ 2 \\ – 3\end{bmatrix}\]

ШАГ 4 : Упрощение.

\[\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}x \\ y \\ z \end{bmatrix}= \frac{1}{13} \begin{bmatrix}26 \\ -13 \\ -12 \end{bmatrix}\]

\[\begin{bmatrix}x \\ y\\z \end{bmatrix} = \begin{bmatrix} 2 \\ -1 \\ -1 \end{bmatrix}\]

\(\следовательно, \quad x = 2,\quad y = -1\quad\) и \(\quad z = -1\).

Хотя можно решить для трех неизвестных, используя обратные матрицы (как показано выше), этот метод не рекомендуется, так как он быстро становится утомительным и чрезмерно сложным. Вместо этого следует использовать сокращение строк, которое будет подробно рассмотрено в следующем разделе.

Решение одновременных уравнений с использованием сокращения строк

Сокращение строк — это еще один метод решения одновременных уравнений с использованием матриц. Также известное как исключение Гаусса , редукция строк использует вычисления строк в расширенной матрице для решения неизвестных в наборе одновременных уравнений.

Вы хотите получить строку с двумя нулями, чтобы можно было вычислить значение одной из переменных, а затем вам нужна строка с одним нулем, чтобы можно было вычислить значение второй переменной.

При выполнении этих вычислений строк следует помнить несколько важных моментов:

В приведенном ниже примере показано, как это сделать.

Используйте сокращение строк для решения следующей системы уравнений:

\[\begin{align}2x + y – 3z = -11 \\x – 2y + z = -3 \\-3x + 4y – 2z = 9 \end{align}\qquad \quad \quad \begin{matrix}(1) \\ (2) \\ (3) \end{matrix}\]

Решение

ШАГ 1 : Запишите расширенная матрица для этих уравнений. Это должно выглядеть следующим образом:

\[\left[\begin{array}{rrr|r}2 & 1 & -3 & -11 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {array}\right]\qquad \quad \quad \begin{array}{r}(1) \\ (2) \\ (3)\end{array}\]

ШАГ 2 : Выполнение вычислений строк .

Сначала запишите расширенную матрицу.

\[\left[\begin{array}{rrr|r}2 & 1 & -3 & -11 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {массив}\right]\]

Какие вычисления мы можем сделать, чтобы получить наш первый ноль?

\[\left[\begin{array}{rrr|r}5 & 0 & -5 & -25 \\ 1 & -2 & 1 & -3 \\ -3 & 4 & -2 & 9\end {array}\right]\quad \begin{array}{r}2 \times R_{1} + R_{2} \to R_{1} \\ \hspace{1cm} \\ \hspace{1cm}\end {массив}\]

Мы всегда записываем вычисления строк, которые мы делаем, рядом с матрицей.

Второй ноль должен находиться в том же столбце, что и первый.

\[\left[\begin{array}{rrr|r}5 & 0 & -5 & -25 \\ -1 & 0 & 0 & 3 \\ -3 & 4 & -2 & 9\end{массив}\right]\quad \begin{array}{r}\hspace{1cm} \\ 2 \times R_{2} + R_{3} \to R_{2} \\ \hspace{1cm} \end{array}\]

Так уж получилось, что и второй, и третий нуль были получены с помощью этого вычисления второй строки. Это не всегда так, и вам часто придется выполнять вычисление третьей строки, чтобы получить третий ноль.

ШАГ 3 : Рассчитать значения неизвестных.

Из строки 2: \[\begin{align}-x & = 3 \\\поэтому \qquad x & = -3 \end{align}\]

Из строки 1 (замените \(x\) в): \[\begin{align}5x – 5z & = -25 \\5(-3) – 5z & = -25 \\-5z & = -10 \\\поэтому \qquad z & = 2\end{align}\]

Из строки 3 (замените \(x\) и \(z\) в):

\[\begin{align}-3x + 4y – 2z & = 9 \\-3(-3) + 4y – 2(2) & = 9 \\4y & = 4 \\\поэтому \qquad y & = 1 \end{align}\]

\ (\поэтому \qquad x = -3; \; y = 1\) и \(z = 2\)

Существует множество различных способов решения одновременных уравнений с использованием редукции строк, и расчеты строк, которые вы выберете, могут быть отличаются от используемых здесь.

Примеры решения одновременных уравнений с использованием матриц 2×2

Следующие примеры сосредоточены на решении одновременных уравнений 2-го порядка, то есть вам придется использовать матрицы 2 x 2.

Найдите \(x\) и \(y\), используя обратные матрицы.

\[\begin{align}6x – 5y & = 7 \\12x + 20y & = -4 \end{align}\]

Решение

Сначала мы должны переписать уравнения в матричной форме.

\[\begin{bmatrix}6 и -5 \\ 12 и 20 \end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix}7 \\ -4\end {bматрица}\] 9{-1}=\frac{1}{180}\begin{bmatrix}20 & 5 \\ -12 & 6\end{bmatrix}\end{align}\]

Умножить на обратную матрицу слева от обе части уравнения, чтобы получить:

\[\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \end{bmatrix}= \frac{1} {180} \begin{bmatrix}20 и 5 \\ -12 и 6\end{bmatrix}\begin{bmatrix}7 \\ -4\end{bmatrix}\]

Упростите дальше, чтобы получить окончательный результат:

\[\begin{bmatrix}x \\ y\end{bmatrix}=\frac{1}{180}\begin{bmatrix}120 \\ -108\end{bmatrix}\]

\(\следовательно \qquad x = \frac{2}{3} \; \text{and} \; y = -\frac{3}{5}\)

Можно также решить множество одновременного только с 2 неизвестными с использованием сокращения строк. Следующий пример показывает, как это делается.

Найдите \(x\) и \(y\), используя сокращение строк.

\[\begin{align}8x – 3y & = 6 \\-16x + y & = -\frac{31}{3}\end{align}\]

Решение

Запишите дополненную матрица для системы.

\[\left[\begin{array}{rr|r}8 & -3 & 6 \\ -16 & 1 & -\frac{31}{3}\end{array}\right]\]

Далее выполнять операции со строками до тех пор, пока в одной из строк не будет получен ноль. Поскольку есть только две переменные для решения, нам нужен только один ноль, так как это позволит нам вычислить значение одной из переменных. Затем мы можем использовать вычисленную переменную, чтобы найти значение другой неизвестной, подставив ее обратно в уравнение.

\[\left[\begin{array}{rr|r}8 & -3 & 6 \\ 0 & -5 & \frac{5}{3}\end{array}\right]\qquad\begin {matrix}\hspace{1cm} \\ R_{2} + 2R_{1} \to R_{2}\end{matrix}\]

Найдите \(x\) и \(y\).

\[\begin{align}-5y & = \frac{5}{3} \\y & = -\frac{1}{3} \\\hspace{1cm} \\\поэтому \qquad8x – 3y & = 6 \\8x – 3(-\frac{1}{3}) & = 6 \\x & = \frac{5}{8}\end{align}\]

Решение одновременных уравнений с использованием матриц 3×3 примеры

В некоторых случаях невозможно избежать вычислений, которые приводят к большим числам.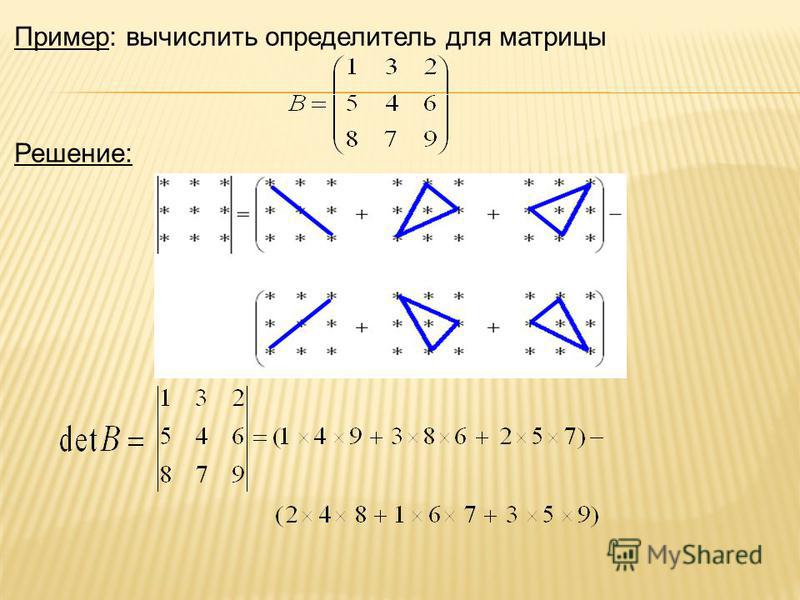 Следующий пример иллюстрирует это.

Решите следующую систему уравнений, используя сокращение строк:

\[\begin{align}-4x – 5y +3z & = 7\\-2x + 3y – z & = -25 \\3x – 2y – 4z & = -6\end{align}\]

Решение

ШАГ 1 : Запишите расширенную матрицу.

\[\left[\begin{array}{rrr|r}-4 & – 5 & 3 & 7 \\ -2 & 3 & -1 & -25 \\ 3 & -2 & -4 & -6 \end{массив}\right]\]

ШАГ 2 : Выполнение вычислений строк.

\[\left[\begin{array}{rrr|r}-10 & 4 & 0 & -68 \\ -2 & 3 & -1 & -25 \\ 3 & -2 & -4 & -6 \end{массив}\right]\quad\begin{array}{r}R_{1} + 3R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{ массив}\]\[\left[\begin{array}{rrr|r}-10 и 4 и 0 и -68 \\ -11 и 14 & 0 и -94 \\ 3 & -2 & -4 & -6\end{массив}\right]\quad\begin{массив}{r}4R_{2} – R_{3} \to R_{2}\end{массив }\]\[\left[\begin{array}{rrr|r}-48 & 0 & 0 & -288 \\ -11 & 14 & 0 & -94 \\ 3 & -2 & -4 & -6 \end{массив}\right]\quad\begin{массив}{r}7R_{1} – 2R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{ array}\]

ШАГ 3 : Вычислите значения переменных.

\[\begin{align}-48x & = – 288 \\x & = 6\end{align}\]

\[\begin{align}-11x + 14y & = -94 \\\qquad -11(6) + 14y & = -94 \\14y & = -28 \\y & = -2\end{align}\]

\[\begin{align}3x – 2y – 4z & = -6 \\3(6) – 2(-2) – 4z & = -6 \\-4z & = -28 \\z &= 7\end{align}\]

\(\поэтому \qquad x = 6, \; y = -2\) и \(z = 7\)

Некоторые уравнения могут содержать только две переменные. В этих случаях вы просто используете ноль в качестве коэффициента для отсутствующей переменной.

Решите следующие одновременные уравнения, используя сокращение строк:

\[\begin{align}2b + c & = – 8 \\a – 2b – 3c & = 0 \\-a + b + 2c & = 3\end{align}\]

Решение

ШАГ 1 : Запишите расширенную матрицу.

\(2b + c= – 8\) – это то же самое, что сказать \(0a + 2b + c\), поэтому мы говорим, что коэффициент \(a\) равен 0 для уравнения 1.

\[\ left[\begin{array}{rrr|r}0 & 2 & 1 & -8 \\ 1 & -2 & -3 & 0 \\ -1 & 1 & 2 & 3\end{массив}\right]\ ]

ШАГ 2 : Выполните вычисления строк.

Ноль на самом деле облегчает решение системы уравнений, так как требуется меньше шагов для получения трех необходимых нулей.

\[\left[\begin{array}{rrr|r}0 & 2 & 1 & -8 \\ 0 & -1 & -1 & 3 \\ -1 & 1 & 2 & 3 \end{array }\right]\quad\begin{array}{r}\hspace{1cm} \\R_{2} + R_{3} \to R_{2} \\\hspace{1cm}\end{array}\] \[\left[\begin{array}{rrr|r}0 & 1 & 0 & -5 \\ 0 & -1 & -1 & 3 \\ -1 & 1 & 2 & 3\end{array}\ right]\quad\begin{array}{r}R_{1} + R_{2} \to R_{1} \\\hspace{1cm} \\\hspace{1cm}\end{array}\]

ШАГ 3 : Рассчитать значения переменных.

\[\begin{align}b & = -5 \end{align}\]

\[\begin{align}-b – c & = 3 \\-(-5) – c & = 3 \ \c & = 2 \end{align}\]

\[\begin{align}-a + b + 2c & = 3 \\-a + (-5) + 2(2) & = 3 \\a & = -4 \end{align}\]

\( \следовательно \qquad a = -4, \; b = -5\) и \(c = 2\)

Решение одновременных уравнений с использованием матриц – основные выводы

• Чтобы записать одновременные уравнения в матричной форме, вы должны сначала написать квадратную матрицу, содержащую коэффициенты, затем переменную матрицу, а справа от знака равенства вы должны написать постоянную матрицу.