Как решаются пределы: Примеры решения пределов с корнями с ответами - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

3-8}=\frac{5}{384}$.

Пример №6

Найти $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}$.

Решение

Так как $\lim_{x\to 2}(\sqrt[5]{3x-5}-1)=0$ и $\lim_{x\to 2}(\sqrt[3]{3x-5}-1)=0$, то мы имеем дело с неопределенностью $\frac{0}{0}$. В таких ситуациях, когда выражения под корнями одинаковы, можно использовать способ замены. Требуется заменить выражение под корнем (т.е. $3x-5$), введя некоторую новую переменную. Однако простое использование новой буквы ничего не даст. Представьте, что мы просто заменили выражение $3x-5$ буквой $t$. Тогда дробь, стоящая под пределом, станет такой: $\frac{\sqrt[5]{t}-1}{\sqrt[3]{t}-1}$. Иррациональность никуда не исчезла, – лишь несколько видоизменилась, что нисколько не облегчило задачу.

Здесь уместно вспомнить, что корень может убрать лишь степень. Но какую именно степень использовать? Вопрос не тривиален, ведь у нас два корня. Один корень пятого, а другой – третьего порядка. Степень должна быть такой, чтобы одновременно убрать оба корня! Нам нужно натуральное число, которое одновременно делилось бы на $3$ и на $5$.

2+1+1}=\frac{3}{5}. $$

Ответ: $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\frac{3}{5}$.

Содержание

УК РФ Статья 12. Действие уголовного закона в отношении лиц, совершивших преступление вне пределов Российской Федерации / КонсультантПлюс

УК РФ Статья 12. Действие уголовного закона в отношении лиц, совершивших преступление вне пределов Российской Федерации

1. Граждане Российской Федерации и постоянно проживающие в Российской Федерации лица без гражданства, совершившие вне пределов Российской Федерации преступление против интересов, охраняемых настоящим Кодексом, подлежат уголовной ответственности в соответствии с настоящим Кодексом, если в отношении этих лиц по данному преступлению не имеется решения суда иностранного государства.

(часть первая в ред. Федерального закона от 27.07.2006 N 153-ФЗ)

2. Военнослужащие воинских частей Российской Федерации, дислоцирующихся за пределами Российской Федерации, за преступления, совершенные на территории иностранного государства, несут уголовную ответственность по настоящему Кодексу, если иное не предусмотрено международным договором Российской Федерации.

3. Иностранные граждане и лица без гражданства, не проживающие постоянно в Российской Федерации, совершившие преступление вне пределов Российской Федерации, подлежат уголовной ответственности по настоящему Кодексу в случаях, если преступление направлено против интересов Российской Федерации либо гражданина Российской Федерации или постоянно проживающего в Российской Федерации лица без гражданства, а также в случаях, предусмотренных международным договором Российской Федерации или иным документом международного характера, содержащим обязательства, признаваемые Российской Федерацией, в сфере отношений, регулируемых настоящим Кодексом, если иностранные граждане и лица без гражданства, не проживающие постоянно в Российской Федерации, не были осуждены в иностранном государстве и привлекаются к уголовной ответственности на территории Российской Федерации.

(в ред. Федеральных законов от 27.07.2006 N 153-ФЗ, от 06.07.2016 N 375-ФЗ)

Открыть полный текст документа

Вопросы профилактики нарушений в сфере организации детского отдыха решаются в рамках межведомственного взаимодействия · Новости Архангельска и Архангельской области.

Сетевое издание DVINANEWS

Вопросы профилактики нарушений в сфере организации детского отдыха рассмотрели в рамках итогового совместного заседания комиссии по организации отдыха, оздоровления и занятости детей и межведомственной комиссии по профилактике правонарушений и предупреждению чрезвычайных ситуаций в местах отдыха детей в Архангельской области, обеспечению безопасности организованных групп детей по маршрутам их следования всеми видами транспорта 28 ноября 2019 года.

Данная работа ведется в рамках межведомственного взаимодействия со всеми заинтересованными в качественном детском отдыхе структурами, в том числе по вопросам обеспечения комплексной безопасности. Участие в заседании приняли представители администраций всех муниципальных образований Архангельской области, а также руководители детских оздоровительных лагерей.

В текущем году организованными формами отдыха охвачено более 53 тысяч детей Архангельской области. В 2019 году выехали на отдых за пределы региона 8056 детей, в 2018 году – 7482 ребенка.

Одним из важнейших направлений при осуществлении регионального государственного контроля в сфере организации отдыха и оздоровления детей является соблюдение требований трудового законодательства.

По данному вопросу перед организаторами детского отдыха выступил руководитель Государственной трудовой инспекции по Архангельской области и Ненецкому автономному округу Анна Гиеш. Она акцентировала внимание на неукоснительном соблюдении статьи 351.1 Трудового кодекса Российской Федерации по предоставлению справок об отсутствии судимости всеми работниками организации отдыха детей и их оздоровления и полном медицинском обследовании сотрудников, работающих с детьми.

Вопросы обеспечения безопасности на объектах детского отдыха прокомментировал заместитель начальника полиции (по охране общественного порядка) УМВД России по Архангельской области Александр Якушев.

Также на заседании комиссий при участии специалистов Управления федеральной службы по надзору в сфере защиты прав потребителей и благополучия человека по Архангельской области были рассмотрены вопросы профилактики нарушений санитарно-эпидемиологического законодательства.

Министерство труда, занятости и социального развития Архангельской области

Теорема косинусов и синусов треугольника. Формулы и примеры

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

a²> + b²> = c²>, где a, b — катеты, с — гипотенуза.

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).

Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC² = a² = (b cos α – c)² + b²sin²α = b²cos²α + b²sin²α – 2bc cos α + c² = b²(cos²α + sin²α) – 2bc cos α + c²

cos²α + sin²α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

С помощью теоремы косинусов можно найти косинус угла треугольника:

Когда b² + c² – a² > 0, угол α будет острым.
Когда b² + c² – a² = 0, угол α будет прямым.
Когда b² + c² – a² < 0, угол α будет тупым.

Запоминаем

Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

AD = b × cos α,
DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

h² = b² – (b × cos α)²
h² = a² – (c – b × cos α)²

Приравниваем правые части уравнений:

b² – (b × cos α)² = a² – (c – b × cos α)²

либо

a² = b² + c² – 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

b² = a² + c² – 2ac × cos β;
c² = a² + b² – 2ab × cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² – 2bc cos α

b² = c² + a² – 2ca cos β

c² = a² + b² – 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Аналогично:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

Если cos α > 0, то α ∈ (0°;90°)
Если cos α < 0, то α ∈ (90°;180°)
Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Ответ: СМ = .

Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:

Для доказательства нужно вспомнить теорему косинусов для угла ∠C:

Так как a² + b² < c², то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

Если c² = a² + b², то ∠C = 90°.

Если c² < a² + b², то ∠C — острый.

ЕГЭ по математике — это несерьёзно / Newtonew: новости сетевого образования

Подготавливая материалы для нашего спецпроекта по ЕГЭ по информатике, я не удержался и скачал с сайта ФИПИ демо-версии по математике. Как многие из вас уже, наверное, слышали, школьники теперь могут сдавать два варианта ЕГЭ по математике: базовый и профильный. В общем-то, идея хорошая, ибо зачем, к примеру, гуманитарию знать интегралы и производные в совершенстве, или, скажем, высшую математику. Однако то, что я увидел, меня убило. И я бы хотел обратиться с восклицанием в сторону составителей:

вы офигели. Я, конечно, понимаю, что уровень знаний наших школьников оставляет желать лучшего, но не настолько же.

Я хотел бы сразу договориться о следующем:

Я не хочу обсуждать в данной статье, плохо ЕГЭ или хорошо. Это тема отдельного разговора.
Статья имеет несколько разделов: вначале — комментарии к задачам по базовому и профильному уровням, а уже затем — выводы. Пожалуйста, дочитайте до конца.
Отдельно хотелось бы попросить не обижаться учителей математики. Я уверен, что среди них есть много хороших, но к остальным у меня много «плохих» вопросов. Слишком много.

Давайте взглянем внимательнее на те задачи, которые предлагают решить после одиннадцати лет изучения математики в школе.

Базовый уровень

Для решения предлагается 20 задач. В прошлом году для получения удовлетворительной оценки было необходимо решить 7 задач. 7 задач, Карл! Но, может, эти задачи действительно хорошие и неочевидные? Давайте взглянем на них.

Начнём с задачи 1. Вычислить: $\cfrac{2}{5}+\cfrac{1}{4}+2$

Дроби, Карл, в ЕГЭ пришли дроби! Ну ладно, может, первая задача действительно проходная, совсем простенькая, для затравочки. Давайте возьмём что-нибудь из середины. Например, 6-ую задачу:

ФИПИ
Федеральный институт педагогических измерений
Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?

Высшая математика, Карл! Серьёзно, неужели для того, чтобы научиться складывать числа (что лично я умел делать в 3-4 года), нужно 11 лет изучать математику по 3 или больше часа в день? А я скажу так: если ребёнок доучился до 11-го класса и не может решить эту задачу, то у меня один простой вопрос к учителю, завучам и директору школы: ребята, вы что, совсем? Эту задачу обязан уметь решать каждый первоклассник. Ну, максимум, во втором классе. Тут нечему учить — тут просто нужно понимать, что такое рубли, что такое копейки и как складывать два числа.

Может, мы опять попали на «проходную» задачу? Давайте возьмём что-нибудь ещё. Например, задачу 11.

Беру свои слова назад. По сравнению с этой задачей прошлая — вершина математической мысли. Неужели нам нужно обучать детей одиннадцать лет математике, чтобы они могли ткнуть на графике в самую высокую точку в промежутке? Неужели недостаточно, блин, одного урока, чтобы объяснить это раз и навсегда всем детям? Как это можно не объяснить? Учителя, ответьте!

Вдумчивый читатель, наверное, скажет: там же есть задачи на проверку знания формул. 2-x-6=0\).

Вот тут надо воскликнуть: так вот же где она, математика, в формулах. Спешу огорчить: дружелюбные составители все необходимые формулы вставили в инструкции:

Инструкция к демо-версии ЕГЭ 2016 по математике, базовый уровень. Формулы с логарифмами

Источник: Официальный сайт ФИПИ

То есть, вы поняли весь цимес задания? Мне не надо помнить формулы, мне не надо знать их, мне не надо помнить условия, мне не надо помнить и понимать определения. Мне просто надо уметь подставлять циферки вместо буковок. То, чему учится ребёнок за два часа с помощью приложения Dragonbox Algebra. Я бы предложил составителям добавить в самом начале ещё и таблицу с ответами, чтоб уж наверняка не было неуспевающих учеников!

В завершение я хочу, чтобы вы испытали настоящую гордость за наш уровень образования. Внимание, встречайте самую сложную задачу № 20:

Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10м. Через сколько дней улитка впервые окажется на вершине дерева?
— ФИПИДемо-версия ЕГЭ-2016 по математике, базовый уровень

Где-то я это уже видел… Ах да, в книге Перельмана (или чём-то подобном) для детей 10-11 лет, в качестве простой тренировки мозга. Значит, вот так оценивает государство уровень современных непрофильных выпускников.

Ну что же, может, в профильном экзамене дела обстоят по-другому.

Профильный уровень

Первое отличие — тут уже нет формул в Инструкции. И на том спасибо. Начнём с первой проходной задачи:

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
— ФИПИДемо-версия ЕГЭ-2016 по математике, профильный уровень

Что нужно знать и уметь для решения этой задачи? Логическое мышление? Умение мыслить аналитически? Знание методов решения задач? Или помнить сложные формулы? Нет, Карл, нет. {x-5}=81\)

Вы думаете, что для решения этой задачи нужно помнить формулы или логарифмы? Нет, достаточно просто вспомнить, в какой же это степени тройка даёт 81: в первой — 3, во второй — 9, в третьей — 27, в четвёртой — 81. Вот оно, четвёртая степень. Значит, x=9. Всё. И это — профильный уровень ЕГЭ 11 класса?

Или другой пример: в задаче 9 нужно найти значение синуса, если дано значение косинуса. Серьёзно, эти задачки должны щёлкать как орешки в церковно-приходской школе, а не решать на ЕГЭ.

Рассмотрим одну из последних задач повышенной сложности.

31 декабря 2013 г. Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
— ФИПИДемо-вариант ЕГЭ-2016 по математике, профильный уровень

До чего мы с вами дожили? Одна из сложнейших задач ЕГЭ — на решение линейного уравнения. Предлагаю читателю самостоятельно решить за пару минут эту задачу и восхититься её непревзойдённой сложностью. Решая её в первый раз, я даже перепроверил себя по ответу — не слишком ли всё просто, не ошибся ли я. Нет, не ошибся. И это печально.

Даже две последние задачи (18 и 19), которые должны быть самыми сложными, решаются за 10 и 5 минут соответственно (графически и путём обычных логических размышлений). Но эти задачи уже требуют простейшего навыка абстрактного мышления (действительно простейшего, никак сложных рассуждений от противного, цепочек силлогизмов, мега-замен и/или хитрых ходов).

Вопросы

В результате у меня возникло два глобальных вопроса:

Вопрос 1. Почему государство создаёт столь простые варианты ЕГЭ, следуя в угоду тренду хороших показателей? Какая ценность в том, что все сдадут ЕГЭ на уровне 2-3 класса церковно-приходской школы? Что они хотят проверить таким экзаменом?

Математика — это прежде всего обучение абстрактному мышлению, построению логических цепочек и рассуждений, умению формализовать различные процессы, навыку моделирования реальных физических, экономических и других задач. Это то, что мы хотим видеть на выходе. Чтобы, давая задачу программисту о вычислении расстояния маршрута, руководитель не добавлял в задачу ссылку на теорему Пифагора. Чтобы студент-химик мог сам сделать N%-ный раствор, без гугления и помощи старших друзей-товарищей. Чтобы потребитель мог оценить навскидку переплату по кредиту. Чтобы «прикидки в уме» были с точностью хотя бы до порядка. Чтобы экономист/студент финансового вуза мог посчитать с первого раза НДФЛ. Я готов мириться с тем, что в Инструкции добавляют формулы, ведь, в конце концов, в реальной жизни есть Интернет, где это можно подсмотреть. Но я не готов мириться с тем, чтобы государственная итоговая аттестация за 11 классов математики сводилась к подстановке чисел вместо букв.

Почему нельзя сказать: «Да, у нас системный кризис в образовании. Мы собираем через месяц 50 лучших педагогов страны, 50 лучших учителей в мире, 50 родителей, 50 детей, 50 работодателей, 50 преподавателей вузов, 50 чиновников и пр. Садимся и за две недели работы создаём план, устраивающий все стороны. С постепенным внедрением «от и до». И с чёткими, конкретными результатами. А затем будет максимальная политическая и экономическая воля для внедрения решений. Никаких отклонений, никаких отговорок, никаких задержек». Под таким подходом, как мне кажется, подпишутся практически все стороны, готовые к конструктивному диалогу.

Вопрос 2. Уважаемые учителя математики! Как так получилось, что ваши дети не сдают столь простой экзамен? Я всё понимаю, сам нахожусь по эту же сторону баррикад и готов понять, почему они не умеют вычислять пределы, считать сложные производные и интегралы, не умеют решать задачи на формулы условной вероятности и теорему Байеса. Но, уважаемые учителя:

Как так случилось, что дети просто-напросто не умеют складывать дроби?
Как так получилось, что существуют дети, не решающие квадратное уравнение с формулой-записанной-в-инструкции-сверху?
Как так получилось, что умение посмотреть на график считается чем-то, к чему надо готовиться?
Как так получилось, что вы жалуетесь на то, что детей требуется теперь готовить к ЕГЭ, при наличии задач, к которым не то, что готовиться не надо, а которые можно давать в качестве примеров отстающим детям, которые не могут решить задачи.
Как так получилось, что теорема Пифагора стала задачей повышенной сложности?

Есть ещё много «как так получилось». И, знаете, сравнивая вклад государства и ваш в падение уровня математики, я бы сказал, что именно вы стали тем звеном, из-за которого государству приходится понижать уровень. Не было бы 25% не набравших минимальный балл, не было бы ЕГЭ церковно-приходского (базового) уровня. Скажите просто — КАК? Я, как учитель информатики, действительно не понимаю. Я учу детей информатике, и, вы не поверите, средняя задача по информатике в ЕГЭ на порядки сложнее задачи по математике. И, вы опять не поверите, они их решают. Все. Все те, кому я ставлю хотя бы 3.

Почему вам стало всё равно? Почему вы не хотите заставлять их понять хотя бы базу? Я всё понимаю: да, зарплаты низкие, да, нагрузка большая, да, много бумажек. Да, мир меняется, меняются поколения, меняется формат и форма. Меняются технологии, за которыми всё время приходится поспевать. Но проявите хоть какую-никакую ответственность. Хороший учитель сможет объяснить даже с мелом и доской. Начните учить. Или уходите.

23 ноября 2015, 15:15
Мнение автора может не совпадать с позицией редакции.
Данная статья распространяется по лицензии Creative Commons.

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Решение высшей математики онлайн

‹– Назад В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись: которая расшифровывается так

(14.1)

где — функция целочисленного аргумента.

Здесь символ (большая греческая буква “сигма”) означает суммирование. Запись внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой и что начальное значение этой переменной равно . Запись вверху обозначает последнее значение, которое принимает переменная .

В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому

С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:

(14.2)

где для трехмерного пространства , для плоскости .

Для единообразия будем считать, что

и говорить, что это сумма, содержащая одно слагаемое.

Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например, Или в правой части никакой буквы нет, значит, и результат от не зависит.

Доказательство этого предложения предоставляется читателю.

Предложение 14.2

(14.3)

Это предложение является частным случаем следующего утверждения. Доказательство. Пусть Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования.

Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).
Замечание 14.2 Двойные суммы из равенства (14.4) можно записывать и без использования скобок

Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.

Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида

Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись

означает, что в сумму не включаются величины , ,…, , то есть с равными индексами.

Иногда в записи суммы не указываются границы изменения индексов, например,

Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Конфликтное поведение сотрудников или как решать конфликты на работе

Все, что нужно знать о конфликтных ситуациях на работе. Полезная статья про решение конфликтных ситуаций с вашими сотрудниками.

Все сталкиваются с конфликтными ситуациями на работе. Иногда здоровый конфликт идет на пользу, приводит к дискуссиям и открывает новые способы решения проблем. Но есть ситуации, когда конфликты негативно влияют на производительность и вовлеченность, что в целом плохо отражается на работе команды и эффективности всей компании.

В этой статье мы разберемся с темой конфликтного поведения и расскажем, как правильно себя вести в конфликтной ситуации.

Что такое конфликтное поведение

Конфликт – это столкновение между людьми из-за различий во взглядах, интересах, целях, восприятии, возникающее в процессе социального взаимодействия. Проще говоря, ситуация когда несколько людей или групп имеют разные взгляды и не могут прийти к соглашению.

Конфликтное поведение – это проявление в эмоциях, разговоре и действиях негативной реакции на конфликтную ситуацию. Такое поведение является следствием конфликта.

Конфликты не возникают на ровном месте, от первопричин до разрешения они проходят целых 5 фаз:

Прелюдия к конфликту включает в себя все факторы, из-за которых конфликт может возникнуть. Отсутствие взаимопонимания, различия в интересах, культуре, религии, образовании – все это способствует возникновению конфликта.
Инициирующее событие. Сам по себе конфликт не возникает. Должно быть событие, которое его провоцирует.
Фаза инициации фактически является периодом, когда конфликт уже начался. Непреклонность во мнении, словесные разногласия – все это предупреждающие сигналы, указывающие на то, что конфликт уже начался.
Фаза дифференциации начинается, когда люди высказывают друг другу свои претензии и показывают недовольство. На этом этапе поднимаются причины конфликта.
Фаза разрешения. Люди должны попытаться пойти на компромисс и разрешить конфликт. На этом этапе рассматриваются различные варианты разрешения конфликта.

Причины конфликтного поведения

Разница во мнениях. Это конфликт между способностью сузить число возможных решений проблемы путем применения логики и знаний и мышлением вовне.

Положение. Это ситуация, когда не тот человек повышен в должности.

Несогласованность. Сотрудник обязан заниматься деятельностью, которая не соответствует его потребностям или интересам.

Несовместимость. Кто-то придерживается целей и взглядов, которые не отвечают мировоззрению другого и исключают удовлетворение его профессиональных потребностей и желаний.

Экономика. Недостаточное вознаграждение работникам.

Стресс. Конфликты от стресса из внешних источников.

Плохая или неадекватная организационная структура и недостаток командной работы.

Власть. Часто конфликт за власть бывает, когда несколько человек претендуют на руководящую должность.

Слабое лидерство. Конфликт неизбежен, если кто-то руководит более квалифицированным и опытным работником.

Произвольное толкование и применение правил и политик. Недостаток прозрачности и открытости вызывает недовольство среди сотрудников.

Почему важно уметь разрешать конфликты на рабочем месте

Конфликты на рабочем месте негативно влияют на отношения в коллективе, продуктивность, отнимают время и силы, которые можно потратить на более важные дела.

Если сотрудники вовлечены в конфликт, они, как правило, теряют концентрацию и плохо сосредоточены на работе. Они вкладывают всю свою энергию в борьбу друг с другом, и в результате цели организации остаются вне приоритетов.

Конфликты также приводят к неуважению и ненужной напряженности в коллективе. Когда сотрудники плохо говорят друг о друге – это нарушает положительную атмосферу внутри организации и мешает всем работать.

Независимо от типов конфликтов на рабочем месте, игнорирование и надежда на то, что они исчезнут, могут дорого обойтись компании.

Последствия рабочих конфликтов для лидеров:

Потраченное время на слушание жалоб людей
Потеря производительности, так как люди тратят больше времени на беспокойство о конфликте, чем на цели организации,
Прогулы
Текучесть кадров

Если вы вовлечены в конфликт, то, скорее всего, будете чувствовать недовольство, разочарование и обиду. К сожалению, как правило, большинство людей не способны оставить эти чувства на работе, поэтому от конфликтных ситуаций страдают еще и близкие.

В любом бизнесе будут сотрудники, которые время от времени не ладят. Из-за различий в их личностях, образе жизни, мнениях или каких-то других факторах, иногда сотрудники просто не могут работать в команде. А когда на рабочем месте разногласия, это затрагивает всех.

Конструктивное урегулирование конфликта между сотрудниками может привести к здоровой конкуренции, улучшению процессов, инновациям и повышению креативности.

Типы конфликтов

Конфликты взаимозависимости

Эти типы конфликтов случаются, когда работа одного сотрудника зависит от работы другого. Например, если продавец всегда опаздывает с вводом месячных данных о продажах, бухгалтер опаздывает с отчетами.

Конфликты взаимозависимости можно легко преодолеть, если:

Сотрудники хорошо разбираются в навыках делегирования
Умеют вести сложные переговоры и договариваться
Срывы дедлайнов сопровождаются последствиями

Конфликты, основанные на взаимозависимости, возникают из-за рабочих причин. Проще говоря, сотрудники ругаются не потому, что не разделяют какие-то идеи друг друга, а потому что один подводит другого.

Разные подходы

Такие конфликты часто случаются, потому что сотрудники по-разному видят способы достижения цели. Например, один сотрудник хочет выполнить работу быстро (ориентируется на задачу) и как можно быстрее перейти к следующему делу. В то время как другой больше заботится о том, чтобы подогнать продукт под клиента и учитывать его мнение в процессе (ориентируется на людей).

Разные подходы к выполнению задач могут быть полезны для работы команды, поэтому очень важно находить компромиссы и использовать разногласия для пользы, а не во вред.

Разные стили управления

Лидеры по-разному руководят своими командами. Члены команды, которым приходится иметь дело с разными лидерами в течение дня, могут запутаться и раздражаться из-за разных способов руководства. Например, один лидер может быть более открытым, в то время как другой строгий и требует жесткой субординации.

Чтобы избежать такого рода конфликтов, убедитесь, что у лидеров компании одинаковые ценности и взгляды на основные вопросы управления. Лидеры должны быть последовательны в решениях, уважать подчиненных и оставаться человечными. Из-за деспотичного лидера может снизиться вовлеченность и удовлетворенность сотрудников.

Личностные конфликты

Личные столкновения – это основная причина конфликтов на рабочем месте. Эти типы конфликтов возникают из-за эмоций и представлений о чьих-либо мотивах и характере. Например, руководитель команды критикует кого-то за опоздание, потому что считает члена команды ленивым и неуважительным. Член команды видит лидера команды, как несправедливого и предвзятого человека.

Справляться с личностными конфликтами можно только взглянув на ситуацию под другим углом, со стороны другого участника конфликта. Большинство людей в таких ситуациях перекладывают ответственность на других, но не видят, что отчасти и сами виноваты. В личностных конфликтах, чаще всего, обе стороны несправедливы друг к другу.

Тест на проработку личностного конфликта

Подумайте о конфликте, который у вас сейчас есть. Возьмите лист бумаги и нарисуйте линию посередине.
В одной колонке запишите все, что вас не устраивает. Все чувства, мысли, суждения, ярлыки, выводы, которые приходят в голову.
В другой колонке запишите все реальные факты. Факты наблюдаемые, объективные, конкретные действия и информация.
Затем запишите, как ваши реакции или действия могли повлиять на ситуацию.

Чтобы различать факты и личные суждения, используйте простой пример: небо голубое – это факт, небо красивого цвета – это личное суждение.

Просматривая список, вы можете обнаружить, что ваши претензии не подтверждаются фактами. Что вы сделали много предположений и толкований о том, что может значить поведение другого человека, но не факт, что значит. Это упражнение предназначено для того, чтобы стать более объективным в сложившейся ситуации.

Стили конфликта

Для того чтобы понять, как решать тот или иной конфликт нужно иметь представление о стилях конфликтов.

Конкуренция – это стиль, в котором собственные потребности ставятся над потребностями других. Он опирается на агрессивный стиль общения. Те, кто использует конкурентный стиль, стремятся контролировать дискуссию. Они опасаются, что утрата контроля приведет к принятию решений, которые не будут отвечать их потребностям. Конкуренция, как правило, приводит к ответным мерам, усугублению ситуации и нарастанию напряжения в коллективе.

Приспособление, также известное как сглаживание, противоположно конкуренции. Люди, использующие этот стиль, уступают другим, стараясь быть дипломатичными. Они, как правило, позволяют желаниям группы подавлять свои собственные, которые вообще редко выносятся на обсуждение, поскольку сохранение отношений является приоритетным.

Избегание – это обычная реакция на негативное отношение к конфликтам в принципе. Люди, избегающие конфликтов, думают, что если они не будут поднимать эту тему, все уляжется само собой. Но, как правило, чувства сдерживаются, мнение остается невыраженным, и конфликт разрастается до тех пор, пока его уже невозможно будет игнорировать. Из-за того, что претензии остаются невыраженными, а отношения неизбежно портятся, вторая сторона часто даже не понимает, что произошло.

Компромисс – это подход к конфликту, в котором люди обсуждают свои желания и договариваются. Хотя компромисс и является оптимальным решением, он, как правило, не приносит удовлетворения. Каждая сторона по-прежнему верна своим взглядам и не всегда достаточно хорошо понимает другую сторону.

Сотрудничество – это объединение индивидуальных потребностей и целей для достижения общей цели. Часто называемое беспроигрышным решением проблем, сотрудничество требует общения, чтобы достичь оптимального решения. Сотрудничество дает возможность достичь консенсуса, интегрировать потребности и потенциально превысить бюджет возможностей, который ранее ограничивал конфликт.

Понимая каждый стиль и его последствия, больше шансов урегулировать конфликт наиболее подходящим путем:

Если используется конкурирующий стиль, можно заставить других принять “удобное” решение, но это принятие может сопровождаться недовольством.
Если мы приспосабливаемся, отношения могут быть хорошими, но остается разочарование, что наше мнение не учитывается.
Если мы идем на компромисс, то хорошие отношения сохранятся, но обиды могут остаться надолго.
Если мы сотрудничаем, то, скорее всего, будем более уверены в шансах продуктивно работать вместе и сохранять нормальные отношения.
И если конфликт вообще не обсуждается, обе стороны могут остаться в неведении относительно реальных вопросов и проблем, что является наихудшим вариантом, потому что рано или поздно конфликт обострится.

7 шагов к разрешению конфликта

Понять природу конфликта

Не стоит строить теории и догадки по поводу причины конфликта. Стоит просто поговорить об этом и выяснить истинные причины разногласий.

Небольшой список вопросов, которые помогут лучше разобраться в ситуации:

Есть ли другие обстоятельства, которые могут усугубить конфликт?
Не являются ли стили работы сторон конфликтными?
Атмосфера в коллективе способствует повышению уровня стресса?
Насколько сильная рабочая загрузка у обеих сторон?
Как насчет трудного клиента?
Распространяет ли кто-то слухи, чем провоцирует развитие конфликта?

Выяснение причин, которые лежат в основе разногласий, необходимо для успешного решения проблемы и предотвращения конфликтов в будущем.

Поощрять сотрудников самим разбираться

Вы наверняка хотите, чтобы ваши сотрудники были максимально самостоятельными. В конце концов, вы их руководитель, а не личный психолог. Имейте в виду, что реагирование на каждую жалобу работника может усугубить ситуацию. Это может даже заставить некоторых сотрудников думать, что вы предвзяты и выделяете кого-то среди остальных.

Поощрение команды к самостоятельному решению проблем не означает, что от руководства не потребуется содействие. При необходимости предоставьте рекомендации или темы для разговора, чтобы помочь каждому сотруднику преодолеть ситуацию с минимальными эмоциональными затратами. Не стоит решать проблему за сотрудников, просто помогите начать обсуждение.

Как подтолкнуть сотрудников к конструктивному разговору о своих разногласиях:

Определите, является ли ситуация эмоционально напряженной и насколько она серьезна.
После того как вы оценили проблему, при необходимости поговорите с каждым сотрудником по отдельности, чтобы сообщить им, что вы осведомлены о ситуации.
Поощряйте открытое общение среди вовлеченных в ситуацию сотрудников. Спросите их, чувствуют ли они себя комфортно, обращаясь к другому сотруднику и общаясь с ним один на один.

Разрешение конфликтов не обязательно должно заканчиваться соглашением. Иногда лучше согласиться не соглашаться, но с уважением. Когда это происходит, сотрудники должны признать, что у них разные взгляды или подходы, и совместно найти решение, как двигаться дальше.

Быстро реагировать

К сожалению, некоторые ситуации не выходит решить без участия менеджера или руководителя. Если их игнорировать, споры между сотрудниками могут негативно повлиять на весь коллектив и даже испортить репутацию компании. Другие сотрудники могут оказаться непреднамеренно втянутыми в конфликт. Это может привести к снижению производительности.

Следует четко дать понять, что конфликтное поведение неприемлемо и разногласия не должны мешать работе.

Выслушать обе стороны

Если пришлось вмешаться, не следует воспринимать ситуацию так, как вам рассказали. В первую очередь необходимо лично выслушать мнение обеих сторон и на основе этого принимать решение о том, как могут развиваться события.

Большинство сотрудников хотят, чтобы их выслушали, поэтому попросите каждое причастное лицо объяснить свою сторону истории. Прежде чем решить, встречаться ли с несогласными сторонами вместе или по отдельности, попытайтесь оценить степень враждебности между ними. Помните, что вы здесь, чтобы обсуждать факты, а не эмоции.

Что бы вы ни делали, не принимайте ничью сторону. Это только ухудшает положение. Вы должны быть максимально объективными.

Для успешного разрешения конфликта важно, чтобы ваша компания обучала руководителей и менеджеров методам работы с конфликтным поведением. Плохо подготовленные менеджеры могут ухудшить ситуацию, что приведет к увольнению сотрудников и даже увеличению текучести кадров.

Определить реальную проблему

Часто истинная причина спора спрятана за эмоциями. К тому времени, когда проблема доводится до сведения менеджера, ссорящиеся сотрудники уже могли перейти к конфликтному поведению.

Чтобы выйти за пределы этой эмоциональной стены, попросите каждого сотрудника сформулировать проблему спокойно. Разберитесь в сути дела, чтобы найти эффективное решение, которое поможет избежать подобных инцидентов.

Найти решение

Сотрудники не должны быть лучшими друзьями, им просто нужно выполнять свою работу. Иногда, единственный способ эффективно сгладить ситуацию – это реорганизация команд и минимизация рабочих контактов конфликтующих сотрудников. Также может быть полезно дать сотрудникам, вовлеченным в ситуацию, время остыть, прежде, чем они снова будут работать вместе.

Помните, что цели компании стоят на первом месте и если конфликт продолжится, это может серьезно повлиять на производительность. Один токсичный работник может нанести ущерб всей компании, поэтому не стоит держаться за него, если он мешает работать коллективу.

Подать пример

Формирование культуры, где уважают друг друга и хорошо работают вместе, является лучшей профилактикой конфликтов. Говоря со своими сотрудниками честно и уважительно, вы создаете среду, которая способствует честности и общению. Когда вы открыты и честны, сотрудники, скорее всего, последуют примеру.

Большая часть культуры вашей компании основана на том, как все взаимодействуют друг с другом. И если менеджеры и руководители будут уважительно относиться друг к другу, и к подчиненным – конфликтное поведение будет возникать все реже.

Конфликт – это не всегда плохо

Не все конфликтные ситуации имеют негативные последствия. Здоровые конфликты, наоборот, иногда открывают новые пути решения задач и помогают посмотреть на вещи с другой стороны. Здоровая конкуренция отлично помогает быть более продуктивными и развиться.

Лучший способ минимизировать негативные конфликты – создавать правильную атмосферу в компании, регулярно работать с командами и сотрудниками по отдельности, проводить встречи 1:1, чтобы лучше понимать сотрудников и вовремя замечать, если что-то идет не так. Если каждый сотрудник будет знать, что отдел кадров и руководство готово его поддержать в сложной рабочей ситуации, он будет более вовлечен и случаи конфликтного поведения будут происходить реже.

Пределы разрешения – 1-е издание – Жоффри де Вилье

Описание книги

«Эту красивую книгу можно читать как роман, в котором подробно описывается наш поиск все большего и большего количества информации из наших наблюдений и измерений. Ее авторы особенно хорошо умеют рассказывать об этом». – Пьер К. Сабатье

«Это уникальный текст – труд любви, впервые объединивший воедино удивительно большой набор математических и статистических методов, используемых для анализа разрешения во многих важных сегодня системах – оптических, акустических, радар и т. д.Я верю, что она найдет широкое применение и ценность “. – Доктор Роберт Г. В. Браун, главный исполнительный директор, Американский институт физики

” Сочетание физики и математики – уникальная особенность этой книги, которая может быть базовой не только для Аспиранты, но также и исследователи в области компьютерной визуализации », – Марио Бертеро, профессор, Женевский университет

« Тур де сил, охватывающий аспекты истории, математической теории и практических приложений. Авторы глубоко проникают в часто сбиваемую с толку тему разрешения проблем и тем самым предлагают объединяющий подход к этой теме, применимый не только к традиционным оптическим системам, но и к современным компьютерным системам, таким как радары и радиосвязь.”- Профессор Ян Праудлер, Университет Лафборо

” “должно быть” для всех, кто интересуется визуализацией и пространственным разрешением изображений. В этой книге содержится подробный и легко читаемый отчет о разрешении при построении изображений и превосходно систематизируется новейшая история этого предмета … Я настоятельно рекомендую это », – Майкл А. Фидди, профессор Университета Северной Каролины в Шарлотте

Эта книга объединяет концепцию разрешения, которая ограничивает то, что мы можем определить о нашем физическом мире, с теорией линейных обратных задач, уделяя особое внимание практическим приложениям.В книге основное внимание уделяется методам решения некорректных задач, не имеющих однозначных устойчивых решений. После введения основных понятий мы

Содержание

Ранние концепции разрешения. Современные концепции разрешения. Элементарный функциональный анализ. Решительность и некорректность.
Оптимизация. Детерминированные методы решения линейных обратных задач. Уравнения свертки и детерминированный спектральный анализ. Статистические методы
и разрешение. Статистический спектральный анализ.Разрешение в оптической микроскопии. Некоторые другие оптические приложения. Приложения.
Происхождение очков. Теория множеств и отображения. Методы нахождения собственных значений и сингулярных разложений. Топологические пространства
. Основная теория вероятностей

Автор (ы)

Биография

Джеффри Де Вильерс (M Inst P. C.Phys., FIMA, C.Math) в настоящее время является почетным старшим научным сотрудником Школы электроники, электротехники и системотехники Университета Бирмингема.Он прикладной математик с более чем 30-летним опытом работы в области обработки сигналов. Его специальность – линейные обратные задачи с особым упором на методы сингулярных функций и улучшение разрешения. Он работал над широким кругом практических обратных задач в области фотонной корреляционной спектроскопии, радара, гидролокатора, связи, сейсмологии, проектирования антенных решеток, обработки широкополосных решеток, компьютерных изображений и, в настоящее время, гравитационных изображений.

Э. Рой Пайк FRS был профессором теоретической физики в Королевском колледже Лондона и руководителем его Школы физических наук и инженерии, а в настоящее время является почетным профессором физики.

Обзоры

“Это уникальный текст – я подозреваю, труд любви – впервые объединивший воедино удивительно большой набор математических и статистических методов, используемых для анализа разрешения во многих важных сегодня системах – оптических, акустических, радиолокационных и т. Д. . Последние две главы представляют собой перспективу практических проблем разрешения во множестве ситуаций, от рассеяния света и определения размеров частиц до микроскопии и томографии. Эти главы будут иметь большое значение для тех, кто обеспокоен фундаментальными ограничениями в этих областях….Я верю, что он найдет широкое применение и ценность ».
– Д-р Роберт Г.В. Браун, главный исполнительный директор, Американский институт физики
« Тур де сил, охватывающий аспекты истории, математической теории и практических приложений. Авторы глубоко проникают в часто запутанную тему разрешения проблем и при этом предлагают объединяющий подход к этому вопросу, применимый не только к традиционным оптическим системам, но и к современным компьютерным системам, таким как радары и радиосвязь.«
– Проф. Ян Праудлер, Университет Лафборо,
» Это книга о предельных пределах разрешения изображений, когда рассматривается цифровая обработка изображений. Таким образом, это также книга по линейным обратным задачам, основному инструменту построения компьютерных изображений. Он подробно описывает эту тему, показывая, что решение обратной задачи – это математическая игра, которая требует глубокого понимания ее физических основ. Сочетание физики и математики – уникальная особенность этой книги, которая может быть базовой не только для аспирантов, но и для исследователей в области компьютерной визуализации.«
– Марио Бертеро, профессор Женевского университета
» Эту красивую книгу можно рассматривать как роман, в котором подробно описываются наши поиски получения все большей и большей информации на основе наших наблюдений и измерений. Его авторы особенно хорошо рассказывают об этом. “
– Pierre C. Sabatier
” необходимо

Критерий Рэлея – Физика Дугласского колледжа 1207

Цели обучения

Обсудите критерий Рэлея.
Расчет пределов разрешающей способности микроскопов и телескопов

Свет рассеивается при движении в пространстве, огибая препятствия, конструктивно и разрушительно вмешиваясь.Хотя это можно использовать как спектроскопический инструмент – например, дифракционная решетка рассеивает свет в соответствии с длиной волны и используется для получения спектров – дифракция также ограничивает детализацию, которую мы можем получить на изображениях. На рисунке ниже показан эффект прохождения света через маленькое круглое отверстие. Вместо яркого пятна с острыми краями получается пятно с нечетким краем, окруженное кругами света. Эта картина вызвана дифракцией, аналогичной той, что создается одной щелью. Свет из разных частей круглой апертуры мешает конструктивно и деструктивно.Эффект наиболее заметен при маленькой диафрагме, но эффект присутствует и для больших диафрагм.

Рис. 1. (a) Монохроматический свет, прошедший через маленькую круглую апертуру, дает эту дифракционную картину. (b) Два точечных источника света, которые расположены близко друг к другу, создают перекрывающиеся изображения из-за дифракции. (c) Если они расположены ближе друг к другу, их нельзя разрешить или различить.

Как дифракция влияет на детали, которые можно наблюдать, когда свет проходит через апертуру? На рис. 1 (b) показана дифракционная картина, создаваемая двумя точечными источниками света, расположенными близко друг к другу.Картина похожа на картину для одиночного точечного источника, и едва ли можно сказать, что есть два источника света, а не один. Если бы они были ближе друг к другу, как на рисунке 1 (c), мы не смогли бы их различить, что ограничило бы детализацию или разрешение, которое мы можем получить. Этот предел – неизбежное следствие волновой природы света.

Во многих случаях дифракция ограничивает разрешение. Острота зрения ограничена, потому что свет проходит через зрачок, круглое отверстие нашего глаза.Имейте в виду, что дифракционное распространение света происходит из-за ограниченного диаметра светового луча, а не из-за взаимодействия с отверстием. Таким образом, свет, проходящий через линзу диаметром D , демонстрирует этот эффект и распространяется, размывая изображение, точно так же, как свет, проходящий через апертуру диаметром D . Таким образом, дифракция ограничивает разрешение любой системы, имеющей линзу или зеркало. Телескопы также ограничены дифракцией из-за конечного диаметра их главного зеркала D .

Эксперимент на вынос: разрешение глаза

Нарисуйте две линии на белом листе бумаги (на расстоянии нескольких мм друг от друга). Как далеко вы можете быть и все еще различать две линии? Что это говорит вам о размере зрачка глаза? Можете ли вы быть количественным? (Размер зрачка взрослого обсуждается в другой главе.)

Каков же предел? Чтобы ответить на этот вопрос, рассмотрим дифракционную картину для круглой апертуры, центральный максимум которой шире и ярче, чем окружающие максимумы (аналогично щели) [см. Рисунок 2 (а)].Можно показать, что для круглой апертуры диаметром D первый минимум в дифракционной картине происходит при θ = 1,22 λ / D (при условии, что апертура большая по сравнению с длиной волны света, что имеет место для большинства оптических инструментов). Принятый критерий определения дифракционного предела разрешения на основе этого угла был разработан лордом Рэлеем в 19 веке. Критерий Рэлея для дифракционного предела разрешающей способности утверждает, что два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого . См. Рисунок 2 (б). Первый минимум находится под углом θ = 1,22λ / D, так что два точечных объекта можно разрешить, только если они разделены углом

θ = 1,22λ / D

, где – длина волны света (или другого электромагнитного излучения), а D – диаметр апертуры, линзы, зеркала и т. Д., С помощью которых наблюдаются два объекта. В этом выражении θ имеет единицы радиан.

Рис. 2. (a) График интенсивности дифракционной картины для круглой апертуры.Обратите внимание, что, как и в случае одиночной щели, центральный максимум шире и ярче, чем боковые. (b) Два точечных объекта создают перекрывающиеся дифракционные картины. Здесь показан критерий Рэлея просто разрешимости. Центральный максимум одного паттерна лежит на первом минимуме другого.

Подключения: границы знаний

Все попытки наблюдать размер и форму объектов ограничиваются длиной волны зонда. Даже малая длина волны света не позволяет добиться точной точности. Когда используются зонды с очень малой длиной волны, как в электронном микроскопе, система нарушается, что по-прежнему ограничивает наши знания, подобно тому, как электрическое измерение изменяет цепь. Принцип неопределенности Гейзенберга утверждает, что этот предел является фундаментальным и неизбежным, как мы увидим в квантовой механике.

Пример 1: Расчет дифракционных пределов космического телескопа Хаббла

Главное зеркало орбитального космического телескопа Хаббл имеет диаметр 2.40 мес. Находясь на орбите, этот телескоп избегает негативного воздействия атмосферных искажений на его разрешающую способность. а) Каков угол между двумя точно разрешимыми точечными источниками света (возможно, двумя звездами)? Предположим, что средняя длина волны света 550 нм. (b) Если эти две звезды находятся на расстоянии 2 миллионов световых лет от галактики Андромеды, насколько близко они могут быть друг к другу и все еще оставаться разрешенными? (Световой год – это расстояние, которое свет проходит за 1 год. )

Стратегия

Критерий Рэлея в уравнении θ = 1.22 λ / D дает наименьший возможный угол θ между точечными источниками или наилучшее достижимое разрешение. Как только этот угол найден, можно рассчитать расстояние между звездами, поскольку нам известно, как далеко они находятся.

Решение для (а)

Критерий Рэлея для минимально разрешимого угла

θ = 1,22 λ / D

Ввод известных значений дает

Решение для (b)

Расстояние s между двумя объектами на расстоянии r и разделенных углом θ составляет s = r θ, по определению угла в радианах.

Подстановка известных значений дает

Обсуждение

Угол, найденный в части (а), чрезвычайно мал (менее 1/50 000 градуса), потому что главное зеркало настолько велико по сравнению с длиной волны света. Как было замечено, эффекты дифракции наиболее заметны, когда свет взаимодействует с объектами, имеющими размер порядка длины волны света. Однако эффект все еще присутствует, и есть дифракционный предел тому, что можно наблюдать. Фактическое разрешение телескопа Хаббла не так хорошо, как здесь.Как и в случае со всеми приборами, есть и другие эффекты, такие как неоднородность зеркал или аберрации в линзах, которые еще больше ограничивают разрешение. Однако рисунок 3 показывает степень детализации, которую можно наблюдать с помощью телескопа Хаббл, из-за его размера и качества, и особенно потому, что он находится над атмосферой Земли.

Рис. 3. Эти две фотографии галактики M82 дают представление о деталях, наблюдаемых с помощью космического телескопа Хаббла, по сравнению с фотографиями с помощью наземного телескопа.(а) Слева – наземное изображение. (кредит: Ricnun, Wikimedia Commons) (б) Фотография справа была сделана Хабблом. (кредит: НАСА, ЕКА и группа «Наследие Хаббла» (STScI / AURA))

Ответ в части (b) показывает, что две звезды, разделенные примерно половиной светового года, могут быть разрешены. Среднее расстояние между звездами в галактике составляет порядка 5 световых лет во внешних частях и около 1 светового года рядом с центром галактики. Следовательно, Хаббл может разрешить большинство отдельных звезд в галактике Андромеды, даже если он находится на таком огромном расстоянии, что его свету требуется 2 миллиона лет, чтобы его свет достиг нас.На рисунке 4 показано другое зеркало, используемое для наблюдения радиоволн из космоса.

Рис. 4. Естественная чаша диаметром 305 м в Аресибо в Пуэрто-Рико облицована отражающим материалом, что превращает ее в радиотелескоп. Это самая большая в мире изогнутая фокусирующая тарелка. Хотя D для Аресибо намного больше, чем для телескопа Хаббла, он обнаруживает гораздо более длинноволновое излучение, а его дифракционный предел значительно хуже, чем у телескопа Хаббла. Аресибо по-прежнему очень полезен, потому что важная информация передается с помощью радиоволн, а не видимого света.(Источник: Татьяна Темирбулатова, Flickr)

Дифракция – это проблема не только оптических приборов, но и самого электромагнитного излучения. Любой луч света, имеющий конечный диаметр D и длину волны λ , демонстрирует дифракционное распространение. Луч распространяется под углом θ , определяемым уравнением θ = 1,22 λ / D . Возьмем, например, лазерный луч, состоящий из лучей, как можно более параллельных (углы между лучами как можно ближе к θ = 0 ^o ), вместо этого распространяется под углом θ = 1.22 λ / D , где D – диаметр луча, а λ – его длина волны. Это распространение невозможно наблюдать для фонаря, потому что его луч изначально не очень параллелен. Однако при передаче на большие расстояния лазерных лучей или микроволновых сигналов дифракционное распространение может быть значительным (см. Рисунок 5). Чтобы этого избежать, мы можем увеличить D . Это делается для лазерного луча, посылаемого на Луну, чтобы измерить ее расстояние от Земли. Лазерный луч расширяется через телескоп, чтобы сделать D намного больше и θ меньше.

Рис. 5. Луч, создаваемый этой передающей микроволновой антенной, будет расширяться под минимальным углом θ = 1,22 λ / D из-за дифракции. Невозможно получить почти параллельный луч, потому что луч имеет ограниченный диаметр.

В большинстве биологических лабораторий разрешение отображается при использовании микроскопа. Способность линзы создавать четкие изображения двух близко расположенных точечных объектов называется разрешением.Чем меньше расстояние x, на котором два объекта могут быть разделены и по-прежнему видны как отдельные, тем выше разрешение. Разрешающая способность объектива определяется как это расстояние x . Выражение для разрешающей способности получается из критерия Рэлея. На рисунке 6 (а) у нас есть два точечных объекта, разделенных расстоянием x. По критерию Рэлея разрешение возможно при минимальном угловом расстоянии

θ = 1,22 λ / D = x / d

, где d – расстояние между образцом и линзой объектива, и мы использовали приближение малых углов (т. е.е., мы предположили, что x намного меньше, чем d ), так что tan θ ≈ sinθ ≈ θ, когда выражается в радианах.

Следовательно, разрешающая способность

x = 1,22 λ d / D

Забавный интерактив, показывающий размеры ячеек, можно найти по адресу https://www.cellsalive.com/howbig.htm

Сравнение размеров ячеек.

Когда я пишу это в марте 2020 года, серьезную озабоченность вызывает Covid-19, поскольку у нас еще нет вакцины. Коронавирусы имеют диаметр около 82-94 нм, не считая шипов.

Другой способ взглянуть на это – пересмотреть концепцию числовой апертуры ( NA ), обсуждавшуюся в предыдущей главе, которая касается линз в микроскопе, но не говорит о волновой природе света. Глава Микроскопы. Здесь NA – это мера максимального угла приема, при котором волокно будет принимать свет и по-прежнему удерживать его внутри волокна. На рисунке 6 (b) показаны линза и объект в точке P. Модель NA – это мера способности линзы собирать свет и разрешать мелкие детали.Угол, образуемый линзой в ее фокусе, определен как θ = 2 α . Из рисунка и снова используя приближение малых углов, мы можем написать

θ = x / d = D / d, но sin θ = θ = D / d для малых углов.

, но по определению α = θ / 2 или θ = 2α, поэтому

sinθ / 2 = θ / 2 = x / 2d = D / 2d дает

sin α = D / 2d или 2 sin α = D / d

NA для линзы составляет NA = n sinα , где n – показатель преломления среды между линзой объектива и объектом в точке P.

Из этого определения для NA мы можем увидеть, подставив приведенное выше уравнение, что

x = 1,22 λ d / D = (1,22 λ) / (2 sin α) = 0,61 λ (n / NA)

В микроскопе значение NA важно, поскольку оно связано с разрешающей способностью линзы. Объектив с большим NA сможет разрешить более мелкие детали. Объективы с более крупными линзами NA также смогут собирать больше света и, таким образом, давать более яркое изображение.Другой способ описать эту ситуацию: чем больше NA , тем больше световой конус, который может попасть в линзу, и, таким образом, будет собрано больше дифракционных мод. Таким образом, микроскоп имеет больше информации для формирования четкого изображения и, следовательно, его разрешающая способность будет выше.

Рис. 6. (a) Две точки, разделенные расстоянием x и расположенным на расстоянии d от объектива. (Источник: Infopro, Wikimedia Commons) (b) Термины и символы, используемые при обсуждении разрешающей способности линзы и объекта в точке P.(кредит: Infopro, Wikimedia Commons)

Одним из следствий дифракции является то, что фокус луча имеет конечную ширину и распределение интенсивности. Рассмотрите возможность фокусировки только при рассмотрении геометрической оптики, показанной на рисунке 7 (а). Точка фокусировки бесконечно малая с огромной интенсивностью и способностью сжигать большинство образцов независимо от NA линзы объектива. Для волновой оптики из-за дифракции точка фокусировки расширяется и становится фокусным пятном (см. Рисунок 7 (b)), причем размер пятна уменьшается с увеличением NA .Следовательно, интенсивность в фокусном пятне увеличивается с увеличением NA . Чем выше NA , тем больше шансов фотодеградации образца. Однако пятно никогда не становится истинной точкой.

Рис. 7. (a) В геометрической оптике фокус – это точка, но физически невозможно создать такую точку, потому что это подразумевает бесконечную интенсивность. (б) В волновой оптике фокус – это протяженная область.

Если вы хотите узнать больше об этой и других темах, посетите веб-сайт The Microscope Organization по адресу https: // microscope-microscope. org / microscope-info / numeric-aperture /

Разрешение дифракционных пределов.
Для круглой апертуры, линзы или зеркала критерий Рэлея утверждает, что два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого.
Это происходит для двух точечных объектов, разделенных углом θ = 1,22 λ / D , где λ – длина волны света (или другого электромагнитного излучения), а D – диаметр апертуры, линзы, зеркала, и Т. Д.Это уравнение также дает угловое распространение источника света диаметром D .

Концептуальные вопросы

1: Луч света всегда распространяется. Почему нельзя создать луч с параллельными лучами, чтобы предотвратить распространение? Почему нельзя использовать линзы, зеркала или диафрагмы для исправления разброса?

Задачи и упражнения

1: Радиотелескоп Аресибо диаметром 300 м, изображенный на рисунке 4, обнаруживает радиоволны с помощью 4. Средняя длина волны 00 см.

(а) Каков угол между двумя точно разрешимыми точечными источниками для этого телескопа?

(b) Насколько близко друг к другу могут быть эти точечные источники на расстоянии 2 миллионов световых лет от галактики Андромеды?

2: Какую наименьшую деталь можно было наблюдать на Луне, когда она находится на расстоянии 384 000 км от телескопа Хаббла? Предположим, что угловое разрешение, найденное для телескопа Хаббла, такое же, как объяснено в примере 1 – у телескопа Хаббла диаметр зеркала равен 2.40 метров, длина волны света 550.0 нм.

3: Дифракционное распространение фонарика незначительно по сравнению с другими ограничениями его оптики, такими как сферические аберрации в его зеркале. Чтобы показать это, вычислите минимальное угловое распространение луча фонарика, который изначально имеет диаметр 5,00 см при средней длине волны 600 нм.

4: (a) Каков минимальный угловой разброс луча гелий-неонового лазера с длиной волны 633 нм, который изначально равен 1. 00 мм в диаметре?

(b) Если этот лазер направлен на горный обрыв на расстоянии 15 км, насколько большим будет освещенное пятно?

(c) Насколько большое пятно будет освещено на Луне, если не учитывать атмосферные эффекты? (Это может быть сделано для удара об угловой отражатель для измерения времени прохождения туда и обратно и, следовательно, расстояния.) Явно покажите, как вы выполняете шаги, описанные в главе «Стратегии решения проблем для волновой оптики».

5: Телескоп можно использовать для увеличения диаметра лазерного луча и ограничения дифракционного распространения.Луч лазера проходит через телескоп в направлении, противоположном нормали, и затем его можно проецировать на спутник или Луну.

(a) Если это делается с помощью телескопа Mount Wilson, производящего луч диаметром 633 нм диаметром 2,54 м, каков минимальный угловой разброс луча?

(b) Если пренебречь атмосферными эффектами, каков размер пятна, которое этот луч оставил бы на Луне, если предположить, что расстояние до Луны составляет 3,84 x 10 ⁸ м?

6: Предел остроты зрения фактически связан с дифракцией на зрачке.

(a) Каков угол между двумя точно разрешимыми световыми точками для зрачка диаметром 3,00 мм при средней длине волны 550 нм?

(b) Считайте свой результат практическим пределом для глаза. На каком максимально возможном расстоянии может находиться автомобиль от вас, если вы можете разрешить две его фары, учитывая, что они находятся на расстоянии 1,30 м друг от друга?

(c) Каково расстояние между двумя точно разрешимыми точками, находящимися на расстоянии вытянутой руки (0,800 м) от вашего глаза?

(d) Как ваш ответ на (c) соотносится с деталями, которые вы обычно наблюдаете в повседневных обстоятельствах?

7: a) Зеркало какого минимального диаметра на телескопе позволит вам видеть детали размером до 5?00 км на Луне на расстоянии 384 000 км? Предположим, что средняя длина волны принимаемого света составляет 550 нм. Сначала найдите нужный угол в радианах.

b) Зеркало какого минимального диаметра на телескопе позволит вам видеть детали размером до 5 метров? Это то, что вам нужно, чтобы увидеть свидетельство приземления на Луну.

8: Вам говорят не стрелять, пока вы не увидите белки их глаз. Если расстояние между глазами составляет 6,5 см, а диаметр зрачка равен 5.0 мм, на каком расстоянии вы можете разрешить два глаза, используя свет с длиной волны 555 нм?

9: (a) Планета Плутон и ее Луна Харон разделены 19 600 км. Если не учитывать атмосферные эффекты, сможет ли телескоп на горе Паломар диаметром 5,08 м разрешить эти тела, когда они находятся на расстоянии 4,50 x 10 ⁹ км от Земли? Предположим, что средняя длина волны 550 нм.

(b) На самом деле, с помощью земного телескопа едва ли можно различить, что Плутон и Харон – отдельные тела.В чем причины этого?

10: Когда точки размещаются на странице с помощью лазерного принтера, они должны располагаться достаточно близко, чтобы вы не видели отдельные чернильные точки. Для этого расстояние между точками должно быть меньше критерия Рэли. Зрачок глаза принять равным 3,0 мм, а расстояние от бумаги до глаза 35 см; найти минимальное расстояние между двумя точками, при котором они не могут быть разрешены. Какому количеству точек на дюйм (dpi) это соответствует?

11: Необоснованные результаты

Астроном-любитель хочет построить телескоп с дифракционным пределом, который позволит ему увидеть, есть ли люди на лунах Юпитера.

(a) Зеркало какого диаметра необходимо, чтобы можно было видеть детали 1,00 м на Луне Юпитера на расстоянии 7,50 x 10 ⁸ км от Земли? Длина волны света составляет в среднем 600 нм.

(b) Что необоснованного в этом результате?

12: Создайте свою проблему

Учитывать дифракционные пределы для электромагнитной волны, взаимодействующей с круглым объектом. Постройте задачу, в которой вы вычисляете предел углового разрешения с помощью устройства, используя этот круглый объект (например, линзу, зеркало или антенну) для проведения наблюдений.Также рассчитайте предел пространственного разрешения (например, размер объектов, наблюдаемых на Луне) для наблюдений на определенном расстоянии от устройства. Среди прочего следует учитывать длину волны используемого электромагнитного излучения, размер круглого объекта и расстояние до наблюдаемой системы или явления.

Микроскопы

13: Базовый простой микроскоп с увеличением используется при освещении с длиной волны 555 нм.Он имеет линзу объектива диаметром 5,00 см. Это апертура. Образец находится на расстоянии 15,0 см от линзы объектива. Какое разрешение в метрах? В микрометрах, которые еще называют микронами? Ширина человеческого волоса составляет 20 микрон. Сможет ли этот микроскоп разрешить человеческие волосы?

14 : вирус Covid-19 имеет размер 88 нм. Оптический составной микроскоп, который можно найти в большинстве лабораторий первокурсников колледжа, имеет линзу объектива с диаметром 2 дюйма.0 см, и вирус находится на слайде, просматриваемом с расстояния 0,50 см. Если на него смотреть при свете с длиной волны 555 нм. а) какое разрешение в а) метрах б) нанометрах у этого микроскопа? Вы можете увидеть вирус с помощью этого микроскопа? Да или нет?

15: На какой длине волны электромагнитного излучения вам нужно увидеть частицу вируса Covid-19 размером 82 нанометра? Предположим, что диаметр линзы объектива составляет 2,0 мм, и на нее смотрят с высоты 3. На расстоянии 0 см.

Глоссарий

Критерий Рэлея: два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого

Решения

Задачи и упражнения

1: (а) 1,63 x 10 ^-4 рад (б) 326 св. Лет

2: угол = 2,80 x 10 ^-7 радиан, расстояние = 3,84 x 10 ⁸ м, поэтому s = x = 107 метров

3: 1.46 x 10 ^-5 рад

5: (а) 3,04 x 10 ^-7 рад (б) Диаметр 235 м

6: угол = 2,24 x 10 ^-4 радиан = x / расстояние, поэтому расстояние = 5,81 x 10 ³ м = 5,81 км c) s = 1,79 x 10 ^-4 м = 0,179 мм. Возьмите линейку и держите ее подальше от себя. Большинство из вас могут легко увидеть расстояние в 1 мм, поэтому 0,2 мм имеет смысл.

7: a) угол = 1,30 x 10 ^-5 радиан D = 5,15 см или около 2 дюймов.Это примерно размер телескопа Галилея.

б) угол = 1,30 х 10 ^-8 радиан D = 51,3 м. Люди часто спрашивают меня, почему они не могут увидеть Лунную посадку в свой телескоп, который обычно имеет диаметр около 2 дюймов. Вот почему.

8: 480 м

9: (а) Да. Должен легко различаться. (б) Тот факт, что едва ли можно различить, что это отдельные тела, указывает на серьезность атмосферных аберраций.У нас нет идеального неба.

10 : расстояние = 7,9 x 10 ^-5 м Теперь отношение 1 дюйм = 2,54 см. 2,54 x 10 ^-2 м / 7,9 x 10 ^-5 м = 321 точка на дюйм. Общий. https://computer.howstuffworks.com/printer-ink3.htm заявляет, что стандартные разрешения составляют 300-600 dpi.

13: Микроскопы: x = 1,22 λ (d / D) = 2,01 × 10 ^-6 m = 2,03 мкм, что намного меньше, чем размер 20-микронного волоса, поэтому он сможет его разрешить.

14: 1,7 x10 ^-7 m = 170 нм Нет, вирус не виден, так как его разрешение меньше разрешения этого микроскопа.

15 : 4,5 x 10 ^-9 m = 4,5 нм намного меньше, чем видимый свет. Это ультрафиолетовое электромагнитное излучение.

Пределы разрешения

в электронном микроскопе Пределы разрешения

в электронном микроскопе БОТ / МИКРО / ЗООЛ 5364
Пределы разрешения в просвечивающем электронном микроскопе
Желательно понять несколько фундаментальных принципов световой оптики, чтобы понять ограничения электронной микроскопии.
Дифракция. Во-первых, невозможно достичь абсолютного фокуса с помощью какой-либо оптической системы, в которой используются частицы с волнообразными свойствами, из-за дифракции и интерференции. Дифракция возникает, когда волновому фронту препятствует какой-либо объект, и, конечно же, край области линзы образует объект, как и любая наложенная апертура. Ниже приведен пример того, как дифракция изменяет волновой фронт при наличии небольшой апертуры. Обратите внимание, что это заставляет параллельный волновой фронт выходить из апертуры в виде сферического волнового фронта.
Воздушный диск. Во-вторых, даже с использованием «идеальной» оптической системы световая точка не может быть сфокусирована как идеальная точка. Вместо этого изображение, если смотреть критически, представляет собой диск, состоящий из концентрических кругов с уменьшающейся интенсивностью. Он известен как диск Эйри и представлен ниже. Разрешение. Обратите внимание на первичный, вторичный и третичный волновые фронты, генерируемые диском Эйри. (Конечно, они продолжают излучаться на более высоких порядках, но их влияние на оптические явления ослабевает с каждым более высоким порядком.) Разрешение обычно описывается как расстояние между пиком первого порядка и впадиной первого порядка (обозначено выше “r”). Разрешение эмпирически описывается как способность различать две точки. Если объект находится чуть ниже уровня разрешения, пики, генерируемые двумя точками, заставят объект казаться одной точкой.
Уравнение Аббе. Разрешение в идеальной оптической системе можно математически описать уравнением Аббе. В этом уравнении:
d = _0.612 * л_
n sin a
где:
d = разрешение
l = длина волны визуализирующего излучения
n = показатель преломления среды между точечным источником и линзой относительно свободного пространства
a = половина угла светового конуса от плоскости образца, принимаемого объективом (половина угла апертуры в радианах)
n sin a часто выражается как NA (числовая апертура)
Это ограниченное дифракцией разрешение оптической системы.Если в оптической системе исключить все аберрации и искажения, это будет пределом разрешения. Если аберрации и искажения присутствуют, они определяют практический предел разрешения.
Уравнение Де Бройля. Объединив некоторые принципы классической физики с квантовой теорией, де Бройль предположил, что движущиеся частицы обладают волнообразными свойствами и что их длину волны можно вычислить на основе их массы и уровней энергии. Общий вид уравнения де Бройля следующий:
л = __ ч __
м * в
где:
l = длина волны
ч = постоянная Планка (6.6 х 10 ^-27)
м = масса частицы (9,1 X 10 ^-28)
v = скорость частицы
Когда электрон проходит через разность потенциалов (поле ускоряющего напряжения) V, его кинетическая энергия равна энергии поля, т.е. эВ (энергия в электрон-вольтах) = V ( ускоряющее напряжение). Как вы помните, e = mc ². Повторяя это для скоростей ниже скорости света и частиц с истинной массой, энергия электрона может быть выражена следующим образом:
эВ = 1/2 мВ ²
, где:
эВ = энергия в электрон-вольтах ( e = 4. 8 х 10 ^-10)
m = масса частицы
v = скорость частицы
Используя некоторые предположения о скорости частицы и ее массе, можно выразить либо длину волны (l), либо скорость ( v ) через ускоряющее напряжение (V ). При дальнейшей подстановке значений h и m выше уравнение для l сводится к следующему:
л
= _1,23 нм_
В ^1/2
Одно предостережение заключается в том, что по мере приближения скорости электрона к скорости света необходимо использовать специальные уравнения относительности Эйнштейна для большей точности, поскольку масса и импульс электронов возрастают с увеличением скорости.
Уравнение для разрешения в ПЭМ: Это значение для l можно затем подставить в уравнение Аббе. Поскольку угол a обычно очень мал, например 10 ^-2 радиан (вероятное значение для TEM), значение a приближается к значению sin a, поэтому мы его заменяем. Поскольку n (показатель преломления) по существу равен 1, мы исключаем его и умножаем 0,612 на 12,3, чтобы получить 0,753. Следовательно, уравнение сводится к следующему:
д = __0.753__
a V ^1/2
где:
d = разрешение в нм
a = половина угла апертуры
V = ускоряющая скорость
Теперь, решая для 100000 вольт, результат равен 0.24 нм или 2,4 Å. Это улучшается при более высоком ускоряющем напряжении и ухудшается при более низком напряжении. (Согласно расчетам Эйнштейна, разрешение составляет: 0,22 нм или 2,2 Å.) Каждая линза и диафрагма имеют свой собственный набор аберраций и искажений. Если аберрации и искажения присутствуют, они определяют практический предел разрешения.
Критерий Рэлея – Физика колледжа, главы 1-17
Пределы разрешения: критерий Рэлея
Обсудите критерий Рэлея.
Свет рассеивается при движении в пространстве, огибая препятствия, конструктивно и разрушительно вмешиваясь. Хотя это можно использовать как спектроскопический инструмент – например, дифракционная решетка рассеивает свет в соответствии с длиной волны и используется для получения спектров – дифракция также ограничивает детализацию, которую мы можем получить на изображениях. [ссылка] (а) показывает эффект прохождения света через маленькую круглую апертуру. Вместо яркого пятна с острыми краями получается пятно с нечетким краем, окруженное кругами света.Эта картина вызвана дифракцией, аналогичной той, что создается одной щелью. Свет из разных частей круглой апертуры мешает конструктивно и деструктивно. Эффект наиболее заметен при маленькой диафрагме, но эффект присутствует и для больших диафрагм.
(а) Монохроматический свет, прошедший через маленькую круглую апертуру, дает эту дифракционную картину. (b) Два точечных источника света, которые расположены близко друг к другу, создают перекрывающиеся изображения из-за дифракции.(c) Если они расположены ближе друг к другу, их нельзя разрешить или различить.
Как дифракция влияет на детали, которые можно наблюдать, когда свет проходит через апертуру? [ссылка] (b) показывает дифракционную картину, создаваемую двумя точечными источниками света, расположенными близко друг к другу. Картина похожа на картину для одиночного точечного источника, и едва ли можно сказать, что есть два источника света, а не один. Если бы они были ближе друг к другу, как в [ссылка] (c), мы не смогли бы их различить, что ограничило бы детализацию или разрешение, которое мы можем получить.Этот предел – неизбежное следствие волновой природы света.
Во многих случаях дифракция ограничивает разрешение. Острота зрения ограничена, потому что свет проходит через зрачок, круглое отверстие нашего глаза. Имейте в виду, что дифракционное распространение света происходит из-за ограниченного диаметра светового луча, а не из-за взаимодействия с отверстием. Таким образом, свет, проходящий через линзу диаметром DD размером 12 {D} {}, демонстрирует этот эффект и распространяется, размывая изображение, точно так же, как свет, проходящий через апертуру диаметром DD размером 12 {D} {}.Таким образом, дифракция ограничивает разрешение любой системы, имеющей линзу или зеркало. Телескопы также ограничены дифракцией из-за конечного диаметра DD размером 12 {D} {} их главного зеркала.
Эксперимент на вынос: разрешение глаза
Нарисуйте две линии на белом листе бумаги (на расстоянии нескольких мм друг от друга). Как далеко вы можете быть и все еще различать две линии? Что это говорит вам о размере зрачка глаза? Можете ли вы быть количественным? (Размер зрачка взрослого обсуждается в Физике глаза.)
Каков же предел? Чтобы ответить на этот вопрос, рассмотрим дифракционную картину для круглой апертуры, центральный максимум которой шире и ярче, чем окружающие максимумы (аналогично щели) [см. [Ссылка] (а)]. Можно показать, что для круглой апертуры диаметром DD размером 12 {D} {} первый минимум в дифракционной картине возникает при θ = 1,22λ / Dθ = 1,22λ / D размер 12 {θ = 1 “». «22» λ / D} {} (при условии, что апертура больше по сравнению с длиной волны света, что характерно для большинства оптических инструментов).Принятый критерий определения дифракционного предела разрешения на основе этого угла был разработан лордом Рэлеем в 19 веке. Критерий Рэлея для дифракционного предела разрешающей способности утверждает, что два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого . См. [Ссылка] (б). Первый минимум находится под углом θ = 1,22λ / Dθ = 1,22λ / D размером 12 {θ = 1 “.” «22» λ / D} {}, так что два точечных объекта разрешимы, если они разделены углом
θ = 1.22λD, θ = 1,22λD, размер 12 {θ = 1 “.” «22» {{λ} больше {D}}} {}
где λλ размер 12 {λ} {} – длина волны света (или другого электромагнитного излучения), а размер DD 12 {D} {} – диаметр апертуры, линзы, зеркала и т. Д., С помощью которых два объекта наблюдаемый. В этом выражении θθ size 12 {θ} {} имеет единицы радиан.
(а) График интенсивности дифракционной картины для круглой апертуры. Обратите внимание, что, как и в случае одиночной щели, центральный максимум шире и ярче, чем боковые.(b) Два точечных объекта создают перекрывающиеся дифракционные картины. Здесь показан критерий Рэлея просто разрешимости. Центральный максимум одного паттерна лежит на первом минимуме другого.
Связи: границы знаний
Все попытки наблюдать размер и форму объектов ограничиваются длиной волны зонда. Даже малая длина волны света не позволяет добиться точной точности. Когда используются зонды с очень малой длиной волны, как в электронном микроскопе, система нарушается, что по-прежнему ограничивает наши знания, подобно тому, как электрическое измерение изменяет цепь.Принцип неопределенности Гейзенберга утверждает, что этот предел является фундаментальным и неизбежным, как мы увидим в квантовой механике.
Расчет дифракционных пределов космического телескопа Хаббл
Главное зеркало орбитального космического телескопа Хаббл имеет диаметр 2,40 м. Находясь на орбите, этот телескоп избегает негативного воздействия атмосферных искажений на его разрешающую способность. а) Каков угол между двумя точно разрешимыми точечными источниками света (возможно, двумя звездами)? Предположим, что средняя длина волны света 550 нм.(b) Если эти две звезды находятся на расстоянии 2 миллионов световых лет от галактики Андромеды, насколько близко они могут быть друг к другу и все еще оставаться разрешенными? (Световой год – это расстояние, которое свет проходит за 1 год. )
Стратегия
Критерий Рэлея, сформулированный в уравнении θ = 1,22λDθ = 1,22λD размер 12 {θ = 1 “.” «22» {{λ} над {D}}} {} дает наименьший возможный угол θθ размером 12 {θ} {} между точечными источниками или наилучшее доступное разрешение. Как только этот угол найден, можно рассчитать расстояние между звездами, поскольку нам известно, как далеко они находятся.
Решение для (а)
Критерий Рэлея для минимально разрешимого угла
θ = 1,22λD. Θ = 1,22λD. размер 12 {θ = 1 “.” «22» {{λ} больше {D}}} {}
Ввод известных значений дает
θ = 1,22550 × 10−9м2,40 м = 2,80 × 10−7рад. Θ = 1,22550 × 10−9м2,40 м = 2,80 × 10−7рад.
Решение для (b)
Расстояние ss размером 12 {s} {} между двумя объектами на расстоянии rr размером 12 {r} {} и разделенных углом θθ размером 12 {θ} {} составляет s = rθs = rθ размер 12 {s = rθ } {}.
Подстановка известных значений дает
с = (2,0 × 106 световых лет) (2,80 × 10–7рад) = 0,56 световых лет. С = (2,0 × 106 световых лет) (2,80 × 10–7рад) = 0,56 световых лет.
Обсуждение
Угол, найденный в части (а), чрезвычайно мал (менее 1/50 000 градуса), потому что главное зеркало настолько велико по сравнению с длиной волны света. Как было замечено, эффекты дифракции наиболее заметны, когда свет взаимодействует с объектами, имеющими размер порядка длины волны света. Однако эффект все еще присутствует, и есть дифракционный предел тому, что можно наблюдать.Фактическое разрешение телескопа Хаббла не так хорошо, как здесь. Как и в случае со всеми приборами, есть и другие эффекты, такие как неоднородность зеркал или аберрации в линзах, которые еще больше ограничивают разрешение. Однако [ссылка] дает представление о степени детализации, которую можно наблюдать с помощью Хаббла, из-за его размера и качества, и особенно потому, что он находится над атмосферой Земли.
Эти две фотографии галактики M82 дают представление о деталях, наблюдаемых с помощью космического телескопа Хаббла, по сравнению с фотографиями с использованием наземного телескопа. (а) Слева – наземное изображение. (кредит: Ricnun, Wikimedia Commons) (б) Фотография справа была сделана Хабблом. (Источник: НАСА, ЕКА и группа «Наследие Хаббла» (STScI / AURA))
Ответ в части (b) показывает, что две звезды, разделенные примерно половиной светового года, могут быть разрешены. Среднее расстояние между звездами в галактике составляет порядка 5 световых лет во внешних частях и около 1 светового года рядом с центром галактики. Следовательно, Хаббл может разрешить большинство отдельных звезд в галактике Андромеды, даже если он находится на таком огромном расстоянии, что его свету требуется 2 миллиона лет, чтобы его свет достиг нас.[ссылка] показывает другое зеркало, используемое для наблюдения радиоволн из космоса.
Естественная чаша диаметром 305 м в Аресибо в Пуэрто-Рико облицована отражающим материалом, что превращает ее в радиотелескоп. Это самая большая в мире изогнутая фокусирующая тарелка. Хотя размер DD 12 {D} {} для Аресибо намного больше, чем для телескопа Хаббла, он обнаруживает гораздо более длинноволновое излучение, а его дифракционный предел значительно хуже, чем у телескопа Хаббла.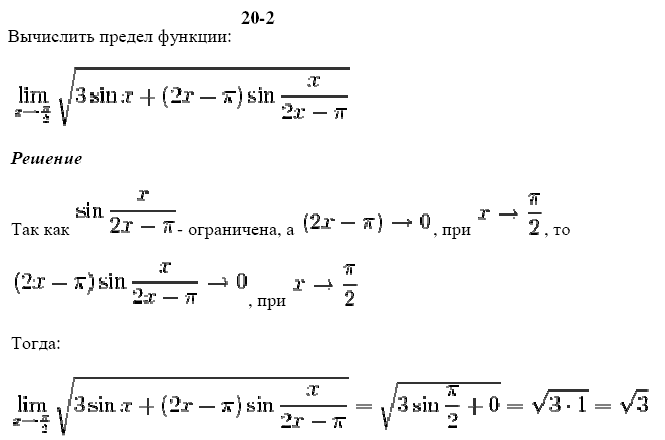 Аресибо по-прежнему очень полезен, потому что важная информация передается с помощью радиоволн, а не видимого света.(Источник: Татьяна Темирбулатова, Flickr)
Дифракция – это проблема не только оптических приборов, но и самого электромагнитного излучения. Любой луч света с конечным диаметром DD размером 12 {D} {} и длиной волны λλ размером 12 {λ} {} демонстрирует дифракционное распространение. Луч распространяется под углом θθ размер 12 {θ} {}, задаваемым уравнением θ = 1,22λDθ = 1,22λD размер 12 {θ = 1 “.” «22» {{λ} больше {D}}} {}. Возьмем, к примеру, лазерный луч, состоящий из лучей, как можно более параллельных (углы между лучами как можно ближе к θ = 0ºθ = 0º размер 12 {θ = 0 °} {}), вместо этого распространяется под углом θ = 1.22λ / Dθ = 1,22λ / D размер 12 {θ = 1 “.” «22» λ / D} {}, где размер DD 12 {D} {} – это диаметр луча, а размер λλ 12 {λ} {} – его длина волны. Это распространение невозможно наблюдать для фонаря, потому что его луч изначально не очень параллелен. Однако при передаче на большие расстояния лазерных лучей или микроволновых сигналов дифракционное распространение может быть значительным (см. [Ссылка]). Чтобы этого избежать, мы можем увеличить размер DD на 12 {D} {}. Это делается для лазерного луча, посылаемого на Луну, чтобы измерить ее расстояние от Земли.Лазерный луч расширяется через телескоп, чтобы сделать размер DD 12 {D} {} намного больше, а размер θθ 12 {θ} {} меньше.
Луч, создаваемый этой передающей микроволновой антенной, будет распространяться под минимальным углом θ = 1,22λ / Dθ = 1,22λ / D размер 12 {θ = 1 “». «22» λ / D} {} из-за дифракции. Невозможно получить почти параллельный луч, потому что луч имеет ограниченный диаметр.
В большинстве биологических лабораторий разрешение отображается при использовании микроскопа. Способность линзы создавать четкие изображения двух близко расположенных точечных объектов называется разрешением.Чем меньше расстояние xx size 12 {x} {}, на котором два объекта могут быть разделены и по-прежнему видны как отдельные, тем выше разрешение. Разрешающая способность линзы определяется как расстояние xx размером 12 {x} {}. Выражение для разрешающей способности получается из критерия Рэлея. В [link] (a) у нас есть два точечных объекта, разделенных расстоянием xx размером 12 {x} {}. По критерию Рэлея разрешение возможно при минимальном угловом расстоянии
θ = 1,22 λD = xd, θ = 1.22λD = xd, размер 12 {θ = 1 “.” «22» {{λ} больше {D}} = {{x} больше {d}}} {}
, где размер dd 12 {d} {} – это расстояние между образцом и линзой объектива, и мы использовали приближение малого угла (т. Е. Предположили, что размер xx 12 {x} {} намного меньше размера dd 12 {d} {}), так что tanθ≈sinθ≈θtanθ≈sinθ≈θ размер 12 {«tan» θ примерно «sin» θ примерно θ} {}.
Следовательно, разрешающая способность
x = 1,22λdD.x = 1,22λdD. размер 12 {x = 1 “.” «22» {{λd} больше {D}}} {}
Другой способ взглянуть на это – пересмотреть концепцию числовой апертуры (размер NANA 12 {ital «NA»} {}), обсуждаемую в статье «Микроскопы». Здесь размер NANA 12 {ital «NA»} {} – это мера максимального угла приема, при котором волокно будет принимать свет и по-прежнему удерживать его внутри волокна. [ссылка] (b) показывает линзу и объект в точке P. Размер 12 NANA {ital «NA»} {} – это мера способности линзы собирать свет и разрешать мелкие детали. Угол, образуемый линзой в ее фокусе, определяется как θ = 2αθ = 2α размер 12 {θ = 2α} {}. Из рисунка и снова используя приближение малых углов, мы можем написать
sinα = D / 2d = D2d.sinα = D / 2d = D2d. размер 12 {“sin” α = {{{D} косая черта {2}} над {d}} = {{D} над {2d}}} {}
NANA для объектива: NA = nsinαNA = nsinα size 12 {ital «NA» = n` ”sin» α} {}, где nn size 12 {n} {} – показатель преломления среды между объективом. линза и объект в точке P.
Из этого определения для NANA размера 12 {ital «NA»} {} мы видим, что
x = 1,22λdD = 1,22λ2sinα = 0,61λnNA. X = 1,22λdD = 1,22λ2sinα = 0,61λnNA. размер 12 {x = 1 “.” «22» {{λd} over {D}} = 1 «.» «22» {{λ} больше {2 ″ sin »α}} = 0«. »« 61 »{{λn} больше {ital« NA »}}} {}
В микроскопе размер NANA 12 {ital «NA»} {} важен, поскольку он связан с разрешающей способностью линзы. Объектив с большим размером 12 NANA {ital «NA»} {} сможет отображать более мелкие детали. Линзы большего размера NANA 12 {ital «NA»} {} также смогут собирать больше света и, таким образом, давать более яркое изображение. Другой способ описать эту ситуацию: чем больше размер NANA 12 {ital «NA»} {}, тем больше световой конус, который может попасть в линзу, и, таким образом, будет собрано больше дифракционных мод.Таким образом, микроскоп имеет больше информации для формирования четкого изображения и, следовательно, его разрешающая способность будет выше.
(a) Две точки, разделенные расстоянием xx размером 12 {x} {}, и a, расположенные на расстоянии dd размером 12 {d} {} от объектива. (кредит: Infopro, Wikimedia Commons) (b) Термины и символы, используемые при обсуждении разрешающей способности линзы и объекта в точке P. (кредит: Infopro, Wikimedia Commons)
Одним из следствий дифракции является то, что фокус луча имеет конечную ширину и распределение интенсивности. Рассмотрите возможность фокусировки только при рассмотрении геометрической оптики, показанной в [ссылка] (а). Точка фокусировки бесконечно мала, с огромной интенсивностью и способностью сжигать большинство образцов, независимо от размера линзы объектива NANA 12 {ital «NA»} {}. Для волновой оптики из-за дифракции точка фокусировки расширяется и становится фокусным пятном (см. [Ссылка] (b)), при этом размер пятна уменьшается с увеличением размера NANA 12 {курсив «NA»} {}. Следовательно, интенсивность в фокусном пятне увеличивается с увеличением размера NANA 12 {ital «NA»} {}.Чем выше размер NANA 12 {ital «NA»} {}, тем выше шансы фотодеградации образца. Однако пятно никогда не становится истинной точкой.
(а) В геометрической оптике фокус – это точка, но физически невозможно создать такую точку, потому что это подразумевает бесконечную интенсивность. (б) В волновой оптике фокус – это протяженная область.
Разрешение дифракционных пределов.
Для круглой апертуры, линзы или зеркала критерий Рэлея утверждает, что два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого.
Это происходит для двух точечных объектов, разделенных углом θ = 1,22λDθ = 1,22λD размером 12 {θ = 1 “.” «22» {{λ} над {D}}} {}, где λλ размером 12 {λ} {} – длина волны света (или другого электромагнитного излучения), а размер DD 12 {D} {} – диаметр диафрагма, линза, зеркало и т. д. Это уравнение также дает угловое расширение источника света диаметром DD размером 12 {D} {}.
Луч света всегда распространяется. Почему нельзя создать луч с параллельными лучами, чтобы предотвратить распространение? Почему нельзя использовать линзы, зеркала или диафрагмы для исправления разброса?
Радиотелескоп Аресибо диаметром 300 м, изображенный на [ссылка], обнаруживает радиоволны с помощью 4.Средняя длина волны 00 см.
(а) Каков угол между двумя точно разрешимыми точечными источниками для этого телескопа?
(b) Насколько близко друг к другу могут быть эти точечные источники на расстоянии 2 миллионов световых лет от галактики Андромеды?
(a) 1,63 × 10–4рад1,63 × 10–4рад размер 12 {1 “.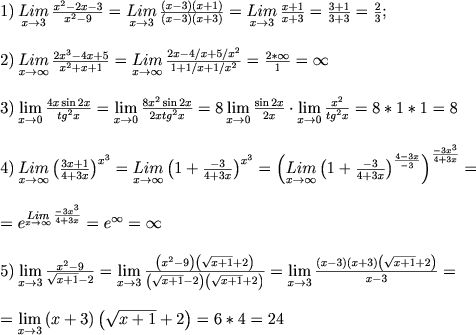 ” «63» умножить на «10» rSup {размер 8 {- 4}} «» рад »} {}
(б) 326 св. Лет
Если предположить угловое разрешение телескопа Хаббла из [ссылка], то какую наименьшую деталь можно было бы наблюдать на Луне?
Дифракционное распространение фонарика незначительно по сравнению с другими ограничениями его оптики, такими как сферические аберрации в его зеркале.Чтобы показать это, вычислите минимальное угловое распространение луча фонарика, который изначально имеет диаметр 5,00 см при средней длине волны 600 нм.
1,46 × 10–5рад1,46 × 10–5рад размер 12 {1 “.” «46» умножить на «10» rSup {размер 8 {- 5}} «» рад »} {}
(a) Каков минимальный угловой разброс луча гелий-неонового лазера с длиной волны 633 нм и первоначальным диаметром 1,00 мм?
(b) Если этот лазер направлен на горный обрыв на расстоянии 15 км, насколько большим будет освещенное пятно?
(c) Насколько большое пятно будет освещено на Луне, если не учитывать атмосферные эффекты? (Это может быть сделано, чтобы ударить по угловому отражателю, чтобы измерить время прохождения туда и обратно и, следовательно, расстояние. ) Ясно покажите, как вы выполняете шаги, указанные в Стратегии решения проблем для волновой оптики.
Телескоп можно использовать для увеличения диаметра лазерного луча и ограничения дифракционного распространения. Луч лазера проходит через телескоп в направлении, противоположном нормали, и затем его можно проецировать на спутник или Луну.
(a) Если это делается с помощью телескопа Mount Wilson, производящего луч диаметром 633 нм диаметром 2,54 м, каков минимальный угловой разброс луча?
(b) Без учета атмосферных эффектов, каков размер пятна, которое этот луч оставил бы на Луне, если предположить, что расстояние до Луны равно 3.84 × 108 м 3. 84 × 108 м?
(a) 3,04 × 10–7рад 3,04 × 10–7рад размер 12 {3 “.” «04» умножить на «10» rSup {размер 8 {- 7}} «» рад »} {}
(б) Диаметр 235 м235 м
Предел остроты зрения на самом деле связан с дифракцией на зрачке.
(a) Каков угол между двумя точно разрешимыми световыми точками для зрачка диаметром 3,00 мм при средней длине волны 550 нм?
(b) Считайте свой результат практическим пределом для глаза. На каком максимально возможном расстоянии может быть машина от вас, если вы можете разрешить две его фары, учитывая, что они равны 1.30 м друг от друга?
(c) Каково расстояние между двумя точно разрешимыми точками, находящимися на расстоянии вытянутой руки (0,800 м) от вашего глаза?
(d) Как ваш ответ на (c) соотносится с деталями, которые вы обычно наблюдаете в повседневных обстоятельствах?
Зеркало какого минимального диаметра на телескопе позволит вам видеть детали размером до 5 км на Луне на расстоянии 384 000 км? Предположим, что средняя длина волны принимаемого света составляет 550 нм.
Вам говорят не стрелять, пока вы не увидите белки их глаз.Если глаза разделены на 6,5 см, а диаметр зрачка составляет 5,0 мм, на каком расстоянии вы можете разрешить два глаза, используя свет с длиной волны 555 нм?
(a) Планета Плутон и ее спутник Харон разделены 19 600 км. Если пренебречь атмосферными эффектами, если телескоп Mount Palomar диаметром 5,08 м сможет разрешить эти тела, когда они имеют размер 4,50 × 109 км4,50 × 109 км, размер 12 {4 “. ” «50» умножить на «10» rSup {размер 8 {9}} «» км »} {} от Земли? Предположим, что средняя длина волны 550 нм.
(b) На самом деле, с помощью земного телескопа едва ли можно различить, что Плутон и Харон – отдельные тела. В чем причины этого?
(а) Да. Должен легко различаться.
(b) Тот факт, что едва ли можно различить, что это отдельные тела, указывает на серьезность атмосферных аберраций.
Расстояние между фарами автомобиля составляет 1,3 м. На каком максимальном расстоянии глаз может различить эти две фары? Принять диаметр зрачка равным 0.40 см.
Когда точки размещаются на странице с помощью лазерного принтера, они должны располагаться достаточно близко, чтобы вы не видели отдельные чернильные точки. Для этого расстояние между точками должно быть меньше критерия Рэли. Зрачок глаза принять равным 3,0 мм, а расстояние от бумаги до глаза 35 см; найти минимальное расстояние между двумя точками, при котором они не могут быть разрешены. Какому количеству точек на дюйм (dpi) это соответствует?
Необоснованные результаты
Астроном-любитель хочет построить телескоп с дифракционным пределом, который позволит ему увидеть, есть ли люди на лунах Юпитера.
(a) Зеркало какого диаметра необходимо для того, чтобы можно было видеть детали 1,00 м на Луне Юпитера на расстоянии 7,50 × 108 км 7,50 × 108 км размером 12 {7 “.” «50» умножить на «10» rSup {размер 8 {8}} «» км »} {} от Земли? Длина волны света составляет в среднем 600 нм.
(b) Что необоснованного в этом результате?
(c) Какие предположения необоснованны или непоследовательны?
Создайте свою проблему
Учитывать дифракционные пределы для электромагнитной волны, взаимодействующей с круглым объектом.Постройте задачу, в которой вы вычисляете предел углового разрешения с помощью устройства, используя этот круглый объект (например, линзу, зеркало или антенну) для проведения наблюдений. Также рассчитайте предел пространственного разрешения (например, размер объектов, наблюдаемых на Луне) для наблюдений на определенном расстоянии от устройства. Среди прочего следует учитывать длину волны используемого электромагнитного излучения, размер круглого объекта и расстояние до наблюдаемой системы или явления.
Глоссарий
Критерий Рэлея
два изображения разрешимы, когда центр дифракционной картины одного находится непосредственно над первым минимумом дифракционной картины другого
Пределы разрешения | Джеффри де Вильерс, Э. Рой Пайк
«Эту красивую книгу можно рассматривать как роман, в котором подробно описывается наш поиск получения все большей и большей информации из наших наблюдений и измерений. Ее авторы особенно хорошо умеют рассказывать об этом.”- Пьер К. Сабатье
“Это уникальный текст – труд любви, впервые объединивший воедино удивительно большой набор математических и статистических методов, используемых для анализа разрешения во многих важных сегодня системах – оптических, акустических, радиолокационных и т. Д. Я считаю он найдет широкое применение и ценность “. – Д-р. Роберт Г.В. Браун, генеральный директор, Американский институт физики
«Сочетание физики и математики – уникальная особенность этой книги, которая может быть базовой не только для аспирантов, но и для исследователей в области компьютерной визуализации. “- Марио Бертеро, профессор Женевского университета
“путеводитель, охватывающий аспекты истории, математической теории и практических приложений. Авторы дают глубокое понимание часто запутанной темы разрешения и тем самым предлагают объединяющий подход к предмету, который применим не только к традиционной оптике. системы, но также и современные компьютерные системы, такие как радары и радиосвязь ». – Проф. Ян Праудлер, Университет Лафборо,
“must have” для всех, кто интересуется визуализацией и пространственным разрешением изображений.В этой книге содержится подробный и очень понятный отчет о разрешении при построении изображений и прекрасная организация новейшей истории предмета… Я настоятельно рекомендую это », – Майкл А. Фидди, профессор Университета Северной Каролины в Шарлотте
Эта книга объединяет концепцию разрешения, которая ограничивает то, что мы можем определить о нашем физическом мире, с теорией линейных обратных задач, уделяя особое внимание практическим приложениям. В книге основное внимание уделяется методам решения некорректных задач, не имеющих однозначных устойчивых решений.После введения основных понятий в содержании подробно рассматриваются проблемы с «непрерывными» данными, прежде чем переходить к случаям дискретных наборов данных. В качестве одного из объединяющих принципов текста авторы объясняют, что неоднозначность – это особенность проблем измерения в науке, где точность и разрешение по существу всегда ограничиваются каким-то шумом.
Исправить ограничения экранного времени, не работающие
Если вы настроили экранное время, но оно не работает должным образом, вот несколько вещей, которые вы можете попробовать:
Установите одно расписание: С последним обновлением Windows вы можете настроить одно расписание, которое будет применяться ко всем устройствам вашего ребенка.Это означает, что если вы дадите им пять часов в день, у них будет пять часов между их устройствами Xbox и Windows 10. В противном случае время отслеживается отдельно, поэтому один час экранного времени означает один час на одно устройство.
Обновление Windows: Выберите Пуск > Настройки > Обновление и безопасность > Центр обновления Windows > Проверьте наличие обновлений и установите все доступные обновления.Проверьте устройство вашего ребенка на наличие обновления
Перезагрузите устройство Windows: Выберите Пуск > Питание> Перезагрузить .
Войти: Убедитесь, что ваш ребенок вошел в систему со своей учетной записью Microsoft на своем устройстве. Если это так, вы можете проверить, правильно ли синхронизируется их учетная запись.Выберите Пуск > Настройки > Учетные записи и следуйте инструкциям, чтобы подтвердить свою учетную запись.
Оставьте его в семейной группе : На аккаунты, не входящие в вашу семейную группу, не распространяется установленное вами ограничение по времени использования. Чтобы дети не могли создавать новые учетные записи, нажмите на Xbox кнопку Xbox , затем выберите Система > Настройки > Система > Ограничения для выхода из системы .Создайте гостевой ключ и выключите Разрешите людям загружать и создавать новые учетные записи . С этого момента вам понадобится гостевой ключ для добавления новых учетных записей.
Пределы разрешения литографии: зазоры на концах линий
В предыдущей статье [1] критерий Рэлея упоминался как предел разрешения для расстояния между двумя объектами. С другой стороны, в следующей статье [2] минимальный шаг был упомянут для предела разрешения для объектов с массивом.В этой статье мы согласовываем эти два аспекта, рассматривая промежутки между элементами массива, например, между концом линии с минимальным шагом и краем перпендикулярной линии.
Подсчет пространственных гармоник (порядки дифракции)
Количество элементов, которые могут поместиться в шаг, равно количеству пространственных гармонических интервалов (= длина волны / шаг), которые проходят числовой апертурой (NA) оптической системы. Если пройдены 5 пространственных гармоник или порядков дифракции за пределами нуля, появляются пять пиков интенсивности, что указывает на минимальный размер элемента в одну пятую шага (рис. 1).
Рис. 1. Основная гармоника (1-я гармоника) генерирует только одну характеристику на высоту звука, а пятая гармоника генерирует пять.
При минимальном шаге длины волны / NA в горизонтальном направлении и более широком шаге в вертикальном направлении количество элементов, разнесенных по вертикали в пределах шага по вертикали, будет не более чем количеством порядков дифракции в вертикальном направлении (помимо нулевого ), и это будет зависеть от освещенности. Минимальный шаг диктует оптимальное освещение (например,g. , диполь или квадруполь), который ограничивает количество порядков дифракции двумя в горизонтальном направлении и заданным числом в вертикальном направлении. Разделив вертикальный шаг на количество интервалов порядка дифракции, можно оценить минимальный зазор в вертикально бегущей линии (рисунок 2).
Рис. 2. Слева: Оптимальное освещение для данного шага между вертикальными линиями будет организовано таким образом, чтобы порядки дифракции находились на равных расстояниях по горизонтали от центра, в то же время позволяя некоторым числам распространяться по вертикали.Круг представляет числовую апертуру, которая отсекает дифракционные порядки, выходящие за пределы. В центре: вид сверху прямоугольника между горизонтальными линиями, полученного с воздуха. Аэрофотоснимок линии разреза (справа) от центральной линии разреза показывает промежуток, в котором падение интенсивности составляет примерно 1/5 вертикального шага, как и ожидалось из числа включенных интервалов порядка дифракции.
Это рассчитано для диапазона минимальных шагов и поперечных шагов и показано на Рисунке 3.
Рисунок 3.Слева: межосевой промежуток для шага линии длины волны / NA, как функции поперечного шага, нормированного на длину волны / NA. Справа: зазор между концом для поперечного шага, равного 4-кратному шагу линии, в зависимости от шага линии, нормированный на длину волны / NA. Освещение оптимизировано для шага линии.
Фактически, нижний предел размера зазора может быть точно рассчитан, если минимальный шаг линии не превышает длины волны / NA. Это sqrt (3) / 3 * длина волны / NA. Доказательство приведено в Приложении.
Проверка работоспособности: соответствие критерию Рэлея
Как критерий Рэлея, так и результаты массивов функций получены из преобразований Фурье, усеченных числовой апертурой.Диск Эйри, лежащий в основе критерия Рэлея, является результатом преобразования Фурье круглой апертуры, в то время как преобразование Фурье массива дает ряд Фурье, свернутый с апертурами в пределах шага. Следовательно, не должно быть противоречий между приведенными выше и предыдущими [2] результатами массивов функций и критерием Рэлея.
Уменьшение зазора ниже k1 = 0,6
Интересный эффект предсказывается, когда зазор меньше 0,6 длины волны / числовая апертура. Похоже, что меньше света поглощается или передается (отражается для случая EUV) функцией сжатия.Это может привести, например, к образованию накипи [4]. Это можно понять, рассматривая амплитуды гармоник (рисунок 4).
Рис. 4. Амплитуды пространственных гармоник (порядков дифракции), которые не отсекаются числовой апертурой, все уменьшаются, когда размер зазора падает ниже 0,6 длины волны / NA (k1 = 0,6), но чем выше этот размер, тем выше гармоники уменьшаются, а нижние – увеличиваются.
Для элементов с длиной волны менее 0,5–0,6 / числовая апертура амплитуды всех гармоник уменьшаются с уменьшением размера.Однако для элементов размером 0,6 длины волны / числовая апертура и выше амплитуды высших гармоник уменьшаются по мере увеличения размера, в то время как более низкие гармоники имеют противоположную тенденцию, что указывает на тенденцию к более резким краям [5]. Ниже 0,6 длины волны / числовая апертура пропуски в линиях лучше структурировать с помощью отдельной экспозиции срезанной маски [6]. Это позволяет компенсировать меньшие зазоры на концах линии более высокой дозой.
Зазор между концом линии и перпендикулярным краем линии также может быть уменьшен ниже ~ 0,6 длины волны / числовая апертура путем создания спейсерного рисунка в первоначально более широком начальном зазоре (Рисунок 5).Этот подход также известен как самовыравнивающееся двойное структурирование «спейсер-диэлектрик» (SID SADP) [7].
Рис. 5. Подход SID SADP к уменьшению ширины зазора.
Сводка пределов разрешения литографии
Пределы разрешения литографии теперь резюмируются следующим образом:
Зазор между изолированными парами: длина волны 0,61 / нет данных
Минимальный шаг массивов элементов: 0,5 длины волны / нет данных / (допуск на 1 угол)
Промежутки между концами линий для шага <= длина волны / NA: 0. 58 длина волны / NA
Приложение: Определение нижнего предела размера упорядоченного зазора для минимального шага линии длины волны / NA или менее
Отправной точкой здесь является то, что для минимального шага p <= длина волны / NA (плотная линия k1 <= 0,5) освещение сначала создаст распределение порядка дифракции, показанное слева на рисунке 2. С точки зрения пространственно-частотных координат, это означает, что координаты x равны +/- 0,5 длины волны / p. Здесь мы выражаем шаг по оси y как кратное минимальному шагу, т.е.2-1]. (2)
Поскольку p лежит в диапазоне 0,5–1 длины волны / NA, минимальный размер зазора возникает для p = длина волны / NA, что дает размер зазора 1 / sqrt (3) длина волны / NA = sqrt (3) / 3 длины волны / NA ~ 0,58 длины волны / числовая апертура (рисунок 6). Обратите внимание, что это больше, чем номинальный межстрочный интервал (k1 <= 0,5). Итак, для соединений со следующим слоем, которое не должно превышать k1 = 0,5, зазор необходимо напечатать с помощью маски среза.
Рис. 6. Размер зазора в зависимости от шага линии, где оба значения нормированы на длину волны / NA (k1 = размер / (длина волны / NA)).
Список литературы
[1] https://www.linkedin.com/pulse/lithography-resolution-limits-paired-features-frederick-chen/
[2] https://www.linkedin.com/pulse/lithography-resolution-limits-arrayed-features-frederick-chen/
[3] https://en.wikipedia.org/wiki/Fourier_optics
[4] Д. Чоу, К. Макаллистер, «Оптимизация конца линии с помощью коррекции оптической близости (OPC): пример из практики», Proc. SPIE 6154, 61543A (2006).
[5] https: // пользователь.eng.umd.edu/~tretter/enee322/FourierSeries.pdf
[6] З. Ли и др., «Исследование интегрированного процесса формирования поли-двойного паттерна в 28-нанометровом узле», CSTIC 2015.
[7] Y. Du et al., «Улучшенный процесс разложения спейсер-диэлектрик (sid) с проверкой на основе модели», Proc.