Как решить lim: Как найти lim примеры. Как решать пределы для чайников - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Как решать пределы?

В данной статье вы узнаете о том, как решать пределы?

Решение пределов является одним из важных разделов математического и вычислительного анализа. Многие ученики и учащиеся вузов справляются с данной проблемой свободно, когда другие постоянно задают один и тот же вопрос: «Как решать пределы?». Нахождение пределов тема актуальная. Существует множество способов решения пределов. Идентичные пределы можно найти согласно закону Лопиталя и без его помощи. Однако сначала нам следует разобраться, что же такое предел?

Предел имеет три части

Первая — это всем известный значок lim, вторая, это то, что написано под ним.

Например: x -> 1. Данная запись будет читаться так (икс стремиться к 1).

Третья часть это сама функция, которая стоит после знака lim.

Хотелось бы уточнить, значение икс стремится к 1, это то значение x, при котором х принимает определенные значения, которые близки к единице или почти с ней совпадают.

Решать пределы, дело легкое, если в них разобраться.

Первое правило решения пределов

В случае если предоставлена нам функция, попросту подставьте число в функцию. Это элементарные пределы, которые действительно встречаются в примерах и очень часто.

Есть пределы, где х->? Тогда бесконечность это та функция, где икс бесконечно возрастает. Значение такой функции является (1-х). Чтобы решить данный предел, нам необходимо следуя нашему первому правилу подставить значение (1-х) в функцию и получить ответ.

Из вышесказанного, для того чтобы обучиться решать наиболее непростые пределы, вы обязаны помнить правила решение элементарных пределов.

Правило первое: Дана функция, подставляем число в функцию.
Правило второе: Дана бесконечность, подставляем (1-х) в функцию.

Как только вы это поймете, то сразу начнете замечать элементарные пределы и сможете их решить. ?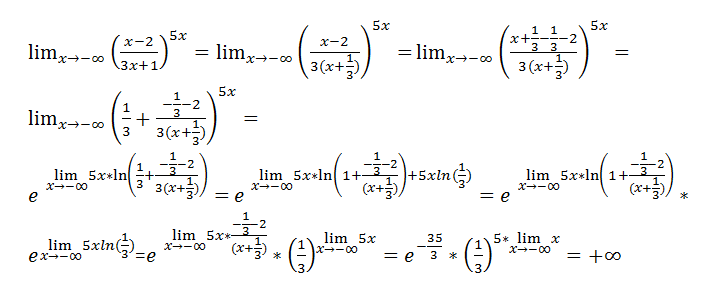

Мы видим, что старшая степень в числителе это 2

Теперь, нам необходимо сделать тоже самое только со знаменателем. В знаменателе старшая степень тоже 2.

Принцип: Для того чтобы разрешить эту функцию, нам следует и делимое и делитель разделить на х в самой старшей степени в пределе. В случае если бы она равнялась 2. Если бы степень числителя равна была 4, а знаменателя 2, то мы бы выбирали 4. Потому, что это самая старшая степень в данной нам функции. Смотрите, как быстро мы обучились решать пределы вида ?/?

Теперь рассмотрим, решение самых сложных пределов. Это вид 0/0.

Подобные пределы очень напоминают нам решение пределов вида бесконечность на бесконечность. Но есть отличие, которое важно помнить при решении.

Когда икс стремится к бесконечности, то он бесконечно увеличивается, а тут он равен 0, т.е. конечному числу.

Чтобы разрешить подобную функцию, нам следует, и числители и знаменатель разложить на множители.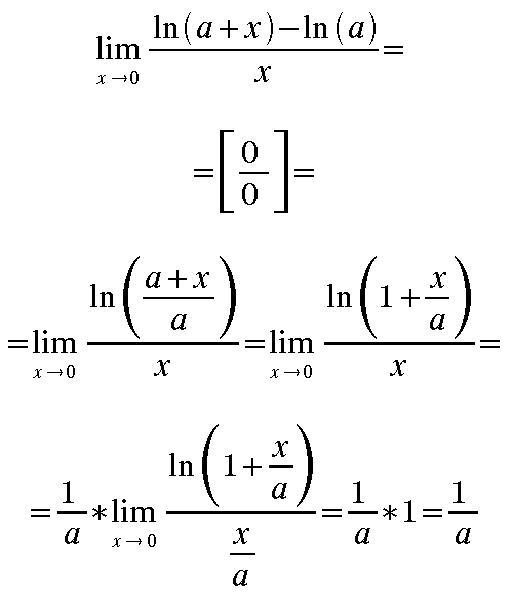 (2х+3) ?

Теперь нам необходимо почленно разделить числитель на знаменатель. Тогда же наше основание будет похоже на нашу неопределенность, но там знак минус, который нам мешает. Делаем дробь с тремя этажами и видим нашу неопределённость ?/?. А такую функцию мы уже умеем вычислять. Делим обе части дроби на х, и готово. У нас получился ответ.

Хочу поздравить вас, дорогие читатели, вы научились решать пределы. Надеюсь, моя статья была познавательной, увлекательной и интересной!

объяснение, теория, примеры решений. Понятие предела в математике

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству

Записывают это следующим образом: или x n → a.

Неравенство (6.1) равносильно двойному неравенству

a – ε x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .

Последовательность, имеющая предел, называется сходящейся , в противном случае – расходящейся .

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .

Пусть дана функция f(x) и пусть a – предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от

a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.

Определение 2 . Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех

x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0

Это определение называют определением предел функции по Коши, или “на языке ε – δ “

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде

В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел,

и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1 . Если существует каждый предел

(6.4)

(6.5)

(6.6)

Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.

Теорема 2.

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,

Теорема 3.

(6.11)

где e » 2.7 – основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно

предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x o , если предел

и непрерывной слева в точке x o, если предел

Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке

x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .

2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .

Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода – в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3. 1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.

Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1|

Возьмем любое ε > 0. Так как x n -1 =(n+1)/n – 1= 1/n, то для отыскания N достаточно решить неравенство 1/n1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .

Пример 3.2. Найти предел последовательности, заданной общим членом .

Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:

Пример 3. 3 . . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4 . Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.

Пример 3.6 . Доказать, что предел не существует.

Решение. Пусть x 1 , x 2 ,…, x n ,… – последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞

Если x n = p n, то sin x n = sin (p n) = 0 при всех n и предел Если же
x n =2 p n+ p /2, то sin x n = sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a .

Или другими словами, число A является пределом функции y = f (x) в точке x 0 , если для всякой последовательности точек из области определения функции , не равных x 0 , и которая сходится к точке x 0 (lim x n = x0) , последовательность соответствующих значений функции сходится к числу A .

График функции, предел которой при аргументе, который стремится к бесконечности, равен L :

Значение А является пределом (предельным значением) функции f (x) в точке x 0 в случае, если для всякой последовательности точек , которая сходится к x 0 , но которая не содержит x 0 как один из своих элементов (т. е. в проколотой окрестности x 0 ), последовательность значений функции сходится к A .

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке x 0 в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x , удовлетворяющего условию 0 , будет выполнено неравенство | f (x) A | .

Будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A , записывается таким образом:

Причем значение, к которому стремится переменная x , может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.

Чтоб понять, как находить пределы функции , лучше всего посмотреть примеры решения.

Необходимо найти пределы функции f (x) = 1/ x при:

x → 2, x → 0, x → ∞.

Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:

Найдем второй предел функции . Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции f (x) будет увеличиваться: 100; 1000; 10000; 100000 и так далее. Т.о., можно понять, что при x → 0 значение функции, которая стоит под знаком предела, будет неограниченно возрастать, т.е. стремиться к бесконечности. А значит:

Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x .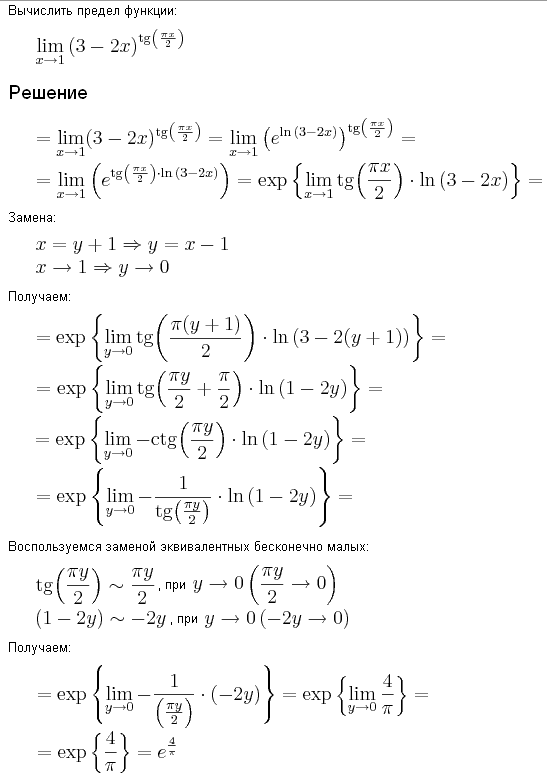 Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/ x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:

Необходимо вычислить предел функции

Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя – это x 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

Ответ

Первым шагом в нахождении этого предела , подставим значение 1 вместо x , в результате чего имеем неопределенность . Для её решения разложим числитель на множители , сделаем это методом нахождения корней квадратного уравнения x 2 + 2 x – 3 :

D = 2 2 – 4*1*(-3) = 4 +12 = 16 → √ D = √16 = 4

x 1,2 = (-2 ± 4) / 2 → x 1 = -3; x 2 = 1.

Таким образом, числитель будет таким:

Ответ

Это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом. 2 стремится к нулю.

Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1

В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность – ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f”(x)/l”(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. (n-1)

Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim – от английского limit – предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача – найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Вычисление пределов. Пределы с неопределенностью

Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью “Пределы. Понятие пределов. Вычисление пределов”.
Теперь перейдем к рассмотрению пределов с неопределенностью.

Существует группа пределов, когда x , а функция представляет собой дробь, подставив в которую значение х = получим неопределенность вида .

Пример.

Необходимо вычислить предел

Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность .

В числителе находим х в старшей степени, которая в нашем случае = 2:

То же самое проделаем со знаменателем:

Здесь также старшая степень = 2.

Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.

Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x²:

Ответ: 2/3.

Существуют также пределы с другой неопределенностью – вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к , а к конечному числу.

Пример.

Необходимо вычислить предел .

Снова воспользуемся правилом №1 и подставим в место х число -1:

Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.

В нашем случае решаем уравнение:

Находим дискриминант:

Если корень не извлекается целый вероятней всего D вычислен неправильно.

Теперь находим корни уравнения:

Подставляем:

Числитель разложили.

В знаменателе у нас х + 1, что итак является простейшим множителем.

Тогда наш предел примет вид:

х + 1 красиво сокращается:

Теперь подставим вместо х значение -1 в функцию и получаем:

2*(-1) – 5 = -2 – 5 = -7

Ответ: -7.

Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:

На этом с вычислением пределов с неопределенностью всё. Еще в статье “Замечательные пределы: Первый и второй замечательный предел” мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.

Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

X стремится к 1 0.

Методы решения пределов. Неопределённости.Порядок роста функции. Метод замены. Предел функции по Коши

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim – от английского limit – предел.

Приведем конкретный пример. Задача – найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

Сократим и получим:

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Наглядно правило Лопиталя выглядит так:

А теперь – реальный пример:

Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что “скучная теория” должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.

Примеры решений

Пример 1

Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $

Решение

а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$

б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$

Нам часто присылают эти пределы с просьбой помочь решить.2-1}{x+1} = \infty $$

Алгоритм вычисления лимитов

Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:

Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: “ноль делить на ноль” или “бесконечность делить на бесконечность” и переходим к следующим пунктам инструкции.
Чтобы устранить неопределенность “ноль делить на ноль” нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
Если неопределенность “бесконечность делить на бесконечность”, тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.

В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.

Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

Записывают это следующим образом: или x n → a.

Неравенство (6.1) равносильно двойному неравенству

Последовательность, имеющая предел, называется сходящейся , в противном случае – расходящейся .

Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.

Это определение называют определением предел функции по Коши, или “на языке ε – δ “

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1 . Если существует каждый предел

(6.4)

(6.5)

(6.6)

Теорема 2.

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,

Теорема 3.

(6.11)

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x o , если предел

и непрерывной слева в точке x o, если предел

Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

Пример 3.1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.

Пример 3.2. Найти предел последовательности, заданной общим членом .

Пример 3.3 . . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4 . Найти ().

Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Пример 3.6 . Доказать, что предел не существует.

Пример 4

Найти предел

Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).

Если «икс» стремится к «минус бесконечности»

Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.

Рассмотрим 4 фишки, которые потребуются для решения практических заданий:

1) Вычислим предел

Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:

2) Вычислим предел

Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:

3) Вычислим предел

Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:

4) Вычислим предел

Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.

Пример 5

Найти предел

Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:

Решение тривиально:

Пример 6

Найти предел

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

А сейчас, пожалуй, самый тонкий из случаев:

Пример 7

Найти предел

Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:

Решаем:

Разделим числитель и знаменатель на

Пример 15

Найти предел

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

Ещё пара занятных примеров на тему замены переменной:

Пример 16

Найти предел

При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?

Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.

Проведем замену:

Если , то

Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .

Завершаем решение:

(1) Проводим подстановку

(2) Раскрываем скобки под косинусом.

(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .

Задание для самостоятельного решения:

Пример 17

Найти предел

Полное решение и ответ в конце урока.

Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)

В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:

Устранение неопределённости «единица в степени бесконечность»

Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.

Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?

На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):

Неопределённость можно устранить по формуле:

Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.

Выделим существенные моменты формулы:

1) Речь идёт только о неопределённости и никакой другой .

2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.

С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :

В данном случае , и по формуле :

Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.

Понятия пределов последовательностей и функций. Когда требуется найти предел последовательности, это записывают следующим образом: lim xn=a.2 стремится к нулю.

Решение пределов с дробями из многочленов

Здесь мы рассмотрим примеры и методы решения пределов функций, составленных из отношений многочленов. Это дроби из многочленов и разности дробей. Обзор и обоснование методов решения пределов изложены на странице «Методы вычисления пределов функций и раскрытия неопределенностей».

Методы решения пределов дробей из многочленов

1. Рассмотрим предел функции, которая является отношением многочленов:
, где
(1) ,
и – многочлены степеней m и n, соответственно:
;
.

1.1. Пусть есть бесконечность:
.
Тогда возникает неопределенность вида . Для ее раскрытия, нужно числитель и знаменатель дроби разделить на x^s, где s – наибольшее из чисел m и n. Примеры ⇓

1.2. Пусть есть конечное число. Найдем значение знаменателя дроби, подставив :
.
1.2.1. Если , то неопределенности нет. Функция определена и непрерывна при . Значение предела равно значению функции в точке :
. Пример ⇓

1.2.2. Если знаменатель равен нулю, а числитель нет: ,
то неопределенность также отсутствует. Предел равен бесконечности:
. Пример ⇓

1.2.3. Пусть теперь и числитель, и знаменатель равны нулю:
.
В этом случае у нас возникает неопределенность вида 0/0. Для ее раскрытия, делим числитель и знаменатель на . Деление можно выполнять либо уголком, либо в уме, приравнивая коэффициенты при одинаковых степенях переменной x. Примеры ⇓

2. Теперь рассмотрим пределы от суммы или разности отношений многочленов. В этом случае, может возникнуть неопределенность вида бесконечность плюс-минус бесконечность: . Для ее раскрытия, нужно привести дроби к общему знаменателю. В результате получим предел от функции вида (1), методы решения которого мы уже рассмотрели. Пример ⇓

Примеры решений

Все примеры Далее мы приводим подробные решения пределов дробей из многочленов.
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓

Пределы при x стремящемся к бесконечности

Пример 1

Все примеры ⇑ Найти предел отношения многочленов при x стремящемся к бесконечности:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
На основании свойств степенной функции, при . Применяя арифметические свойства предела функции, находим:
.

Ответ

Пример 2

Все примеры ⇑ Найти предел функции, которая является отношением многочленов:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применяя арифметические свойства предела функции, находим:
.

Ответ

Пример 3

Все примеры ⇑ Найти предел:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применим арифметические свойства предела функции к числителю и знаменателю:
;
.
Применим свойства бесконечно малых и бесконечно больших функций:
.

Мы получили правильную величину предела: . Но бесконечно удаленная точка может включать в себя два частных случая: и . Как , так и являются . Если и, для достаточно больших |x|, , то . Если, для достаточно больших |x|, то .

Выясним, имеет ли наш предел определенный знак? Для этого преобразуем знаменатель и переведем бесконечно большую часть в числитель:
;
.
Поскольку , то . Тогда

.

Ответ

Пределы в конечной точке

Пример 4. Непрерывные функции

Все примеры ⇑ Найти пределы функции

a) при ; б) при .

Решение

а) Найдем значение знаменателя в точке :
.
Поскольку знаменатель не обращается в нуль, то функция непрерывна в точке . Поэтому предел функции равен ее значению при :
.

б) Найдем значение знаменателя в точке :
.
Здесь также знаменатель не обращается в нуль. Функция непрерывна. Ее предел при равен значению при :
.

Ответ

а) ; б) .

Пример 5. Бесконечно большие функции

Все примеры ⇑ Задана функция в виде отношения многочленов:
.
Найти односторонние пределы:
а) ; б) .

Решение

Найдем значение знаменателя дроби в точке :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной при . Выясним, есть ли неопределенность вида 0/0? Для этого найдем значение числителя в этой точке:
.
Числитель не равен нулю. Поэтому неопределенности вида 0/0 нет. Предел при равен бесконечности:
.

Но нам нужно найти односторонние пределы. Для этого выделим из многочлена в знаменателе множитель . То есть представим знаменатель в следующем виде:
.
Раскрываем скобки:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
;
.

Функция непрерывна в точке , поскольку знаменатель дроби не обращается в нуль. При , имеем:
.
Тогда
;
при .
а) Подставим :
.
б) Подставим :
.

Ответ

а) , б) .

Если бы знаменатель дроби не равнялся нулю при , то функция была бы непрерывной в точке . В этом случае, пределы слева и справа были бы равны:
.

Неопределенность вида 0/0

Пример 6

Все примеры ⇑ Найти предел
.

Решение

Найдем значение знаменателя дроби при :

.
Знаменатель дроби равен нулю. Поэтому функция не определена и, следовательно, не является непрерывной в точке .

Найдем значение числителя при :
.
Числитель дроби также равен нулю. Мы имеем неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Ищем разложение знаменателя в виде:
.
Раскрываем скобки и группируем члены с одинаковыми степенями x:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
.

На практике, нет необходимости выписывать неопределенные коэффициенты разложения, а затем решать систему уравнений. Подобные вычисления легко проводить в уме. Для числителя имеем:
.

Находим предел:

.

Ответ

Пример 7

Все примеры ⇑ Найти предел отношения многочленов:
.

Решение

Найдем значение знаменателя при :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной в точке .

Найдем значение числителя дроби при :
.
Числитель дроби также равен нулю. У нас неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Вычисления делаем в уме:
,
.
Делим числитель и знаменатель на . Тогда при имеем:
.

Снова находим значения числителя и знаменателя при : ;
.
Опять неопределенность 0/0. Снова выделяем множитель :
;
.

При имеем:
.
Функция непрерывна в точке , поскольку знаменатель дроби не равен нулю при . Поскольку функции и отличаются только в одной точке ( определена и непрерывна при , а не определена), то их пределы в любой точке равны (см. «Влияние значений функции в конечном числе точек на величину предела»). Находим искомый предел:
.

Ответ

Пример 8. Неопределенность вида ∞

&pm;∞

Все примеры ⇑ Найти предел разности дробей из многочленов:
.

Решение

При имеем:
;
;
;
.
Поскольку знаменатель каждой из дробей равен нулю, а числители отличны от нуля, то при , каждая из дробей стремится к бесконечности:
при .
То есть мы имеем неопределенность вида “бесконечность минус бесконечность”.

Для раскрытия неопределенности, приводим дроби к общему знаменателю. Чтобы упростить выкладки, предварительно выделим в знаменателях дробей множитель .
;
;

;
.

Таким образом, задача свелась к вычислению предела от дроби многочленов:
.
Применяем описанные выше методы.

Находим значения числителя и знаменателя при :
;
.
Поскольку числитель и знаменатель равны нулю, то это неопределенность вида 0/0. В знаменателе множитель уже выделен. Выделим этот множитель в числителе:
.
Находим предел:

.

Ответ

Автор: Олег Одинцов. Опубликовано: 23-01-2019

Пределы (формальное определение)

Приближается …

Иногда мы не можем что-то придумать напрямую … но мы можем видеть, что это должно быть, когда мы приближаемся все ближе и ближе!

Пример:

(x ² – 1) (x – 1)

Давайте разберемся с x = 1:

(1 ² – 1) (1 – 1) = (1 – 1) (1 – 1) = 0 0

Теперь 0/0 – это сложность! Мы действительно не знаем значение 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.

Итак, вместо того, чтобы пытаться вычислить это для x = 1, давайте попробуем приближаться к все ближе и ближе:

Продолжение примера:

х		(x ² – 1) (x – 1)
0,5		1.50000
0.9		1,
0,99		1,99000
0,999		1.99900
0,9999		1.99990
0,99999		1.99999
…		…

Теперь мы видим, что когда x приближается к 1, тогда (x ² −1) (x − 1) получает , близкое к 2

Мы столкнулись с интересной ситуацией:

Когда x = 1, мы не знаем ответа (это неопределенно )
Но мы видим, что будет 2

Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»

Предел из (x ² −1) (x − 1) , когда x приближается к 1, составляет 2

И записывается символами как:

lim x → 1 x ² −1 x − 1 = 2

Таким образом, это особый способ сказать, “игнорируя то, что происходит, когда мы приближаемся к цели, но по мере того, как мы приближаемся все ближе и ближе, ответ становится все ближе и ближе к 2”

В виде графика это выглядит так:

Итак, по правде говоря, мы не можем сказать, каково значение при x = 1.

Но мы можем сказать, что по мере приближения к 1, предел равен 2.

Более формальный

Но вместо того, чтобы говорить, что предел равен некоторому значению, потому что выглядело так, как будто оно приближалось к , мы можем иметь более формальное определение.

Итак, начнем с общей идеи.

От английского языка к математике

Сначала скажем по-английски:

“f (x) приближается к некоторому пределу , поскольку x приближается к некоторому значению”

Когда мы называем предел «L» и значение, при котором x приближается к «a», мы можем сказать

“f (x) приближается к L, когда x приближается к”

Расчет «закрытия»

Теперь, что является математическим способом сказать “близко”… можем ли мы вычесть одно значение из другого?

Пример 1: 4,01 – 4 = 0,01 (выглядит хорошо)
Пример 2: 3,8 – 4 = -0,2 ( отрицательно, близко?)

Так что же делать с негативом? Нас не интересует положительное или отрицательное, мы просто хотим знать, как далеко … это абсолютное значение.

“Как близко” = | a − b |

Пример 1: | 4.01−4 | = 0,01
Пример 2: | 3.8−4 | = 0.2

А когда | a − b | маленький мы знаем, что близки, поэтому пишем:

“| f (x) −L | мало, когда | x − a | мало”

И эта анимация показывает, что происходит с функцией

f (x) = (x ² −1) (x − 1)

изображения / limit-lines.js

f (x) приближается к L = 2, когда x приближается к a = 1,
, поэтому | f (x) −2 | мала, когда | x − 1 | маленький.

Дельта и Эпсилон

Но «small» по-прежнему английский, а не «математический».

Давайте выберем два значения меньше :

δ		, что \| x − a \| должно быть меньше
ε		, что \| f (x) −L \| должно быть меньше

Примечание: эти две греческие буквы (δ – «дельта» и ε – «эпсилон») – это
, поэтому часто используется фраза « дельта-эпсилон »

А у нас:

| f (x) −L | <ε при | x − a | <δ

Вот и все! Итак, если вы понимаете, что вы понимаете пределы…

… но чтобы быть абсолютно точным , нам нужно добавить эти условия:

верно для любого ε> 0
δ существует и> 0
x равно , не равно a, что означает 0 <| x − a |

И вот что получаем:

Для любого ε> 0 существует δ> 0, так что | f (x) −L | <ε при 0 <| x − a | <δ

Это формальное определение. На самом деле это выглядит довольно устрашающе, не правда ли?

Но по сути он говорит о чем-то простом:

f (x) приближается к L , когда x приближается к

Как использовать это в доказательстве

Чтобы использовать это определение в доказательстве, мы хотим пойти

Из:		Кому:
0 <\| x − a \| <δ		\| f (x) −L \| <ε

Обычно это означает поиск формулы для δ (в единицах ε), которая работает.

Как найти такую формулу?

Угадай и попробуй!

Верно, мы можем:

Поиграйте, пока не найдете формулу, по которой может работать
Проверьте , чтобы убедиться, что эта формула работает

Пример: попробуем показать, что

lim x → 3 2x + 4 = 10

Используя буквы, о которых мы говорили выше:

Значение, к которому приближается x, “a”, составляет 3
Предел «L» равен 10

Итак, мы хотим знать, как мы перейдем от:

0 <| x − 3 | <δ от
до
| (2x + 4) −10 | <ε

Шаг 1. Поэкспериментируйте, пока не найдете формулу, по которой

может работать

Начнем с: | (2x + 4) −10 | <ε

Упрощать: | 2x − 6 | <ε

Переместите 2 наружу ||: 2 | x − 3 | <ε

Разделите обе стороны на 2: | x − 3 | <ε / 2

Итак, теперь мы можем предположить, что δ = ε / 2 может работать

Шаг 2:

Протестируйте , чтобы убедиться, что эта формула работает.

Итак, можем ли мы получить от 0 <| x − 3 | <δ до | (2x + 4) −10 | <ε …?

Посмотрим …

Начнем с: 0 <| x − 3 | <δ

Заменим δ на ε / 2: 0 <| x − 3 | <ε / 2

Умножьте все на 2: 0 <2 | x − 3 | <ε

Переместите 2 внутрь ||: 0 <| 2x − 6 | <ε

Заменить «−6» на «+ 4−10»: 0 <| (2x + 4) −10 | <ε

Да! Мы можем перейти от 0 <| x − 3 | <δ к | (2x + 4) −10 | <ε , выбрав δ = ε / 2

СДЕЛАНО!

Итак, мы увидели, что при заданном ε можно найти δ, поэтому верно, что:

Для любого ε существует такое δ, что | f (x) −L | <ε при 0 <| x − a | <δ

И мы доказали, что

lim x → 3 2x + 4 = 10

Заключение

Это было довольно простое доказательство, но, надеюсь, оно объясняет странное «существует… “формулировка, и это действительно показывает хороший подход к такого рода доказательств.

MathScene – Пределы – Урок 1

2008 Rasmus ehf og Jhann sak

Урок 1.

Пределы и функции, определяемые интервалом

Что происходит со значением функции как x становится бесконечно большим? Неужели функция тоже становится бесконечно большой? Делает он достигает максимума или минимума? Что на самом деле происходит? Это то, что мы собираемся для размышления в следующем тексте.

Мы знаем, что не можем делим на ноль, но что произойдет, если мы разделим на число, очень близкое к нулю? Мы увидим, что иногда график функция идет вверх или вниз почти перпендикулярно около этой точки, а иногда график не может пройти через точку, оставив бесконечно малую дыру.

Математика использует концепция пределов для рассмотрения проблем такого рода.

Посмотрите на функцию

Калькулятор Casio, кажется, рисует прямую линии, когда вас попросят построить график этой функции (см. диаграмму).Если вы выберете большой масштаб, например INIT в V-Window, вы можете заметить крошечный разрыв на графике, когда x = 1. Это потому, что, когда x = 1, мы делим на ноль, и функция не определено в этом пункте. Область определения функции – D _f = R \ {1}.

Сейчас попробуем отработать что происходит как x приближается к 1. Математически это записывается следующим образом:

Лим – это аббревиатура от латинского слова “лаймы”. что означает предел.Приведенное выше обозначение означает значение, до которого функция стремится по мере приближения x к 1.

Мы можем использовать алгебру, чтобы упростить функцию но не следует упускать из виду исходную функцию и проблему деления на нуль.

Теперь у нас больше нет проблема деления на ноль, поэтому мы можем поместить значение x = 1 в выражение ( вычислитьf (1)).

= 1 + 1 = 2

Это показывает нам, что функция стремится к значению 2, когда x стремится к 1.

На графике f (x) действительно есть дыра, где x = 1 (см. График)

Мы можем заполнить эту дыру, если определим непрерывная функция с тем же алгебраическим выражением, но с добавлением значения что функция может принимать при x = 1. Эта новая функция g (x) определена следующим образом:

Таким образом получаем показан непрерывный график .

Функции, которые определены таким образом, с дополнительными чем одно выражение, в зависимости от значений, которые принимает x, называются интервальные определенные функции.

Пример 1

Найдите значение

В этом случае нет проблема деления на ноль, поэтому мы можем поместить число 2 в выражение вместо x.

2 ³ 2 ² = 8 4 = 4

Функция f (x) = x ³ x ² становится все ближе и ближе к 4 по мере приближения x к 2.

Пример 2

Найти предел

В этом случае мы не можем дать x значение 3, так как это будет означать деление на ноль. Однако мы можем факторизовать выражение в числителе и исключить множитель x 3

Положите значение 3 дюйма для x.

Пример 3

Найдите предел

Теперь мы не можем упростить выражение, поэтому мы пытаемся найти решение, подставляя значения x, близкие к 1.Мы выбираем значения как немного больше, так и немного меньше 1.

См. Следующую таблицу значений.

График состоит из двух частей. с вертикальной асимптотой по x = 1.

Давайте посмотрим, что происходит когда x приближается к значению 1. Из графика видно, что мы должны рассматривать отдельно значения выше и ниже x = 1.2 / (D11). Обе формулы скопировал.

Мы видим, что когда x равно меньше 1, то есть когда x приближается к значению 1 слева (слева от число 1 на оси x) значения f (x) (столбец B) все ближе и ближе к ∞. Когда x больше чем 1, который приближается к 1 справа, функция f (x) стремится к + ∞. Конечно, бесконечности не существует, как бы большое число вы ни вообразили. всегда существует еще больший.

Рисуем следующие вывод:

Предел не существует.

Снидми 4

Учтите предел.

Мы не можем ввести значения x которые меньше нуля, потому что квадратный корень отрицательного числа не существовать.
В этих условиях мы можем говорить только о пределе справа, то есть когда x больше 0.

Следующие обозначения используемый:

The + Знак показывает, что x приближается к 0 справа (x> 0).

Калькулятор CASIO показывает следующий график:

График спускается с ось y, а затем идет вправо по оси x. Ни x, ни f (x) не принимают отрицательные значения. Для малых значений x значения y большие
и для больших значений x значения y малы.Очевидно, что f (x) стремится к бесконечность, когда x стремится к нулю, поэтому не существует.

Пример 5

Найти если он существует.

Не очевидно, как мы можем отменить это выражение, но тот факт, что значение x = 1 делает как числитель и нулевой знаменатель говорят нам, что факторизация возможна. Используя правило (a b) (a + b) = a ² b ² дает следующий.

Найти предел функции f (x), когда x стремится к a, существует три различные ситуации, которые могут возникнуть:

1. Вычисляем f (a) (a подставляется в выражение вместо x).

2. Если числитель и знаменатель f (x) равен нулю, когда x = a, тогда f (x) может быть факторизован и упрощается за счет отмены.Затем, если возможно, вычисляется f (a).

3. Если, когда x = a, знаменатель равен нулю, а числитель не равен ноль, то предел не существует.

Пример 6

Рассмотрим следующий интервал определенная функция:

График показан здесь. Прямая
y = x + 3 заканчивается точкой (1, 4) (не доходя до точки).Линия
y = x + 1 начинается в точке (1, 2)
(включая эту точку, которая показана на графике сплошной точкой)

В этом примере предел f (x) поскольку x стремится к 1, не существует, поскольку это зависит от того, больше ли x или менее 1.

Говорят, что функция f (x) быть непрерывным в точке (a, f (a)), если оно существует в интервале около x = a и

Если это верно для всех значений x в области определения f (x), то мы говорим, что функция непрерывный.

Наоборот, если функция непрерывна, то она непрерывна в каждом точка своего домена.

Теперь посмотрим на пределы когда x стремится к + или бесконечность.

Это не проблема при рассмотрении полиномиальных функций. Поскольку x стремится к бесконечности (+ или), функция также стремится к бесконечности. Будет ли это + или бесконечность, зависит на срок с наибольшей мощностью. Ни логарифма функции, экспоненциальные функции или функции квадратного корня представляют любые проблема.

Это другое дело однако с рациональными функциями (функции в виде f (x) / g (x)).

При рассмотрении нам нужно посмотреть, числитель или знаменатель увеличивает быстрее.

Если числитель, f (x), увеличивается быстрее, чем x стремится к бесконечности, тогда предел не существует, но стремится к + или бесконечности.

Однако, если знаменатель g (x) увеличится больше быстро, то ограничение, вероятно, будет стремиться к определенному значению.

Пример 7

А теперь давайте посмотрим на некоторые примеры, где x стремится к бесконечности.

а)
Здесь знаменатель стремится к бесконечности, а числитель не меняется. Когда мы делим на число, которое становится все больше и больше, результат становится меньше и
меньшее стремится к нулю. Так что предел равен нулю.

б)

Здесь знаменатель увеличивается быстрее, чем числитель, поэтому дробь становится меньше и меньшее стремится к нулю.

в)

Это противоположно пункту b). Числитель увеличивается быстрее, а результат становится все больше и больше. стремится к бесконечности. Мы говорим, что предела не существует.
(NB. В некоторых текстах предел называется бесконечностью).

г)

В этом примере знаменатель имеет более высокую степень, чем числитель, и поэтому увеличивает больше быстро.Дробь стремится к нулю, поэтому

0, если g (x) увеличивается быстрее, чем f (x)

. Это произойдет, если для Например, степень знаменателя g (x) больше, чем степень числителя f (x).

Пример 8

Найти .

Что происходит, когда числитель и знаменатель – многочлены одной степени? Оба увеличивают одинаково быстро. Если мы разделим все на наивысшую степень x (в этот чехол x ²) мы можем найти решение.

Поскольку x стремится к бесконечности, два члены в числителе x / x ² и 2 / x ² стремятся к нулю, оставляя us с 1 в числителе и 2 в знаменателе.Таким образом, результат:

Проблемы с пределами рациональных функций, где числитель и знаменатель – многочлены одинаковой степени, могут быть решается делением всего на наивысшую степень x.

Попрактикуйтесь в этих методах, затем возьмите тест 1 по пределам.

шт. не забудьте заполнить свой контрольный список.

Ограничение

при замене | Brilliant Math & Science Wiki

Предел определяется как значение, к которому функция приближается, когда переменная в этой функции становится все ближе и ближе к определенному значению. Предположим, у нас есть предел, описанный как lim⁡x → af (x) {\ lim_ {x \ rightarrow a} f (x)} limx → a f (x).Это указывает значение f (x) f (x) f (x), когда xxx бесконечно близко к a, a, a, но не точно равно aaa. Правило замещения – это метод нахождения пределов путем простой замены xxx на aaa. Математическое проявление этого правила будет

lim⁡x → af (x) = f (a). \ Displaystyle {\ lim_ {x \ rightarrow a} f (x) = f (a)}. X → alim f (x) = f (a) . 2} x → −1lim x2.2 = 1. \ _ \ squarex → −1lim x2 = x2∣∣ x = −1 = (- 1) 2 = 1. □

Однако правило замены выполняется не всегда. Чтобы использовать правило подстановки, функция f (x) f (x) f (x) должна удовлетворять следующему условию:

“Функция f (x) должна быть непрерывной.” \ Text {“Функция} f (x) \ text {должна быть непрерывной.”} “Функция f (x) должна быть непрерывной.”

Это означает, что график f (x) f (x) f (x) нигде не распадается в пределах своего домена. Пример прерывистой функции: f (x) = 1xf (x) = \ frac {1} {x} f (x) = x1.Попробуйте нарисовать это. Вы заметите, что график распадается при x = 0x = 0x = 0, и, следовательно, он прерывается при x = 0x = 0x = 0, поэтому мы не можем использовать правило подстановки при нахождении lim⁡x → 01x \ displaystyle {\ lim_ {x \ rightarrow0} \ frac {1} {x}} x → 0lim x1. На самом деле этого ограничения вообще не существует, но мы обсудим это позже.

Найдите значение lim⁡x → 0x∣x∣. \ Displaystyle {\ lim_ {x \ rightarrow0} \ frac {x} {\ lvert x \ rvert}}. X → 0lim ∣x∣x.
прерывистый
На рисунке изображен график функции f (x) = x∣x∣.2 + 6x-5 \ вправо) = – \ infty. \ _ \ squarex → −∞lim (−x2 + 6x − 5) = – ∞. □

Найдите lim⁡x → ∞1x + 7. \ Displaystyle {\ lim_ {x \ rightarrow \ infty} \ frac {1} {x + 7}}. X → ∞lim x + 71.
Поскольку знаменатель стремится к бесконечности, то есть x + 7 → ∞x + 7 \ rightarrow \ inftyx + 7 → ∞ при x → ∞, x \ rightarrow \ infty, x → ∞, ответ будет
.
lim⁡x → ∞1x + 7 = 1lim⁡x → ∞ (x + 7) = 0. □ \ lim_ {x \ rightarrow \ infty} \ frac {1} {x + 7} = \ frac {1} {\ displaystyle {\ lim_ {x \ rightarrow \ infty} (x + 7)}} = 0. \ _ \ squarex → ∞lim x + 71 = x → ∞lim (x + 7) 1 = 0.□

Как решить односторонние ограничения. Примеры, изображения и практические задачи

Ошибка: Нажмите «Не робот» и повторите попытку. + $$ означает, что $$ x $$ приближается справа.- $$ означает, что $$ x $$ приближается слева.

Примеры

Пример 1

Используйте график, чтобы аппроксимировать значение обоих односторонних пределов, поскольку $$ x $$ приближается к 3.

Шаг 1

Посмотрите, что происходит, когда $$ x $$ приближается слева.

Поскольку $$ x $$ приближается к 3 слева, функция кажется приближается к 2.

Шаг 2

Посмотрите, что происходит, когда x приближается справа

Поскольку $$ x $$ приближается к 3 справа, функция кажется приближается к 3.

Отвечать Предел слева: $$ \ displaystyle \ lim_ {x \ to3 ^ -} f (x) \ приблизительно 2 $$
Правый предел: $$ \ displaystyle \ lim_ {x \ to3 ^ +} f (x) \ приблизительно 3 $$

Пример 2: Использование таблиц

Используя приведенные ниже таблицы, что можно сказать об односторонних пределах, когда $$ x $$ приближается к 6?

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline 5 и 8.32571 \ hline 5.5 и 8.95692 \ hline 5.9 и 8.99084 \ hline 5,99 и 8,99987 \ hline 5.999 и 8.99992 \ hline 5.9999 и 8.99999 \\\ hline \ end {массив} $$

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline 7 и 1 \ hline 6.5 и 95 \ hline 6.1 и 1230 \ hline 6.01 и 9658 \ hline 6.001 и 54231 \ hline 6.0001 и 834366 \ end {массив} $$

Шаг 1

Посмотрите, что происходит, когда $$ x $$ приближается к 6 слева.

Поскольку $$ x $$ приближается к 6 слева…

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline 5 и 8.32571 \ hline 5.5 и 8.95692 \ hline 5.9 и 8.99084 \ hline 5.99 и 8.99987 \ hline 5.999 и 8.99992 \ hline 5.9999 и 8.99999 \ end {массив} $$

… функция приближается к 9.

Шаг 2

Посмотрите, что происходит, когда $$ x $$ приближается к 6 справа.

Когда $$ x $$ приближается к 6 слева …

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline 7 и 1 \ hline 6.5 и 95 \ hline 6.1 и 1230 \ hline 6.01 и 9658 \ hline 6. -} f (x) $$ не существует.+} f (x) \ приблизительно 1 $$

Проблема 5

Используйте приведенные ниже таблицы, чтобы оценить оба односторонних предела, поскольку $$ x $$ приближается к -4.

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline -5 и -4.5 \ hline -4,5 и -44,5 \ hline -4,1 и -444,5 \ hline -4.01 и -4444.5 \ hline -4,001 и -44444,5 \ hline -4,0001 и -444444,5 \ end {массив} $$

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline -3 и 2.13671 \ hline -3,5 и 2,52240 \ hline -3,9 и 2,59684 \ hline -3,99 и 2,59987 \ hline -3.999 и 2.59990 \ hline -3,9999 и 2,59999 \ end {массив} $$

Покажи ответ Шаг 1

Посмотрите, что происходит, когда $$ x $$ приближается к -4 слева.

Шаг 1 Ответ

Когда $$ x $$ приближается к -4 слева …

…. функция становится все больше.

Шаг 2

Посмотрите, что происходит, когда $$ x $$ приближается к -4 справа.

Шаг 2 Ответ

Поскольку $$ x $$ приближается к -4 справа…

$$ \ begin {array} {l | c} x & f (x) \\\ hline \ hline -3 & 2.13671 \ hline -3,5 и 2,52240 \ hline -3.9 и 2.59684 \ hline -3,99 и 2,59987 \ hline -3.999 и 2.59990 \ hline -3,9999 и 2,59999 \ end {массив} $$

… функция приближается к 2.6.

Шаг 4 Покажи ответ

Левый предел: $$ \ displaystyle \ lim \ limits_ {x \ to -4} f (x) $$ не существует.Правый предел: $$ \ displaystyle \ lim \ limits_ {x \ to-4} f (x) \ приблизительно $$ 2.6.

Ошибка: Нажмите «Не робот» и повторите попытку. 2 – 16} {x-4} = \ dfrac {16 – 16} {4-4} = \ dfrac {«0»} {0}
$$

Откройте, чтобы прочитать, почему мы заключили этот результат в кавычки.2 – 16} {x-4} & = \ lim_ {x \ to 4} \ dfrac {(x + 4) (x-4)} {x-4} \\ \\
& = \ lim_ {x \ в 4} \ dfrac {(x + 4) \ cancel {(x-4)}} {\ cancel {x-4}} \\ \\
& = \ lim_ {x \ to 4} [x + 4] \\ \\
& = 8 \ quad \ cmark
\ end {align *}

Мы, , гарантируем , что если вы можете множить числитель или знаменатель, проблемный член «0» в знаменателе будет отменен, как это было. здесь. На этом этапе вы можете просто подключить x и готово.

Откройте, чтобы увидеть еще два примера задач, использующих факторинг.2 – 4x – 5} {x – 5} & = \ text {?} \\ \\
& = \ lim_ {x \ to 5} \ dfrac {(x-5) (x + 1)} {x – 5} \\ \\
& = \ lim_ {x \ to 5} \ dfrac {\ cancel {(x-5)} (x + 1)} {\ cancel {x – 5}} \\ \\
& = \ lim_ {x \ to 5} [x + 1] \\ \\
& = 6 \ quad \ cmark \ end {align *}

[свернуть]

Результат: Фактор по возможности.

II. Разверните многочлен

У вас, вероятно, есть проблемы, которые выглядят как
$$ \ lim_ {h \ to 0} \ dfrac {\ text {stuff в числителе}} {h} =? $$
Опять же, если вы просто подключите $ h = 0 $, вы получите этот проблемный «0» в знаменателе.2 – 10h} {h} \\ \\
& = \ lim_ {h \ to 0} \ dfrac {h (h – 10)} {h} \\ \\
& = \ lim_ {h \ to 0} \ dfrac {\ cancel {h} (h-10)} {\ cancel {h}} \\ \\
& = \ lim_ {h \ to 0} [h – 10] \\ \\
& = -10 \ quad \ cmark
\ end {align *}

[свернуть]

Результат: Разверните многочлен.
(На данный момент. Позже в курсе мы увидим, как эти проблемы $ \ lim_ {h \ to 0} $ напрямую связаны с определением производной, и в этот момент вы можете использовать ярлык, но пока нет.Вы, , должны, , знать, как решить эти проблемы, используя описанный здесь подход. . . и действительно, это просто алгебра.)

III. Рационализируйте

Есть ли в вашей проблеме какие-то квадратные корни, как эта?
$$ \ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} =? $$
Затем рационализируйте выражение так же, как вы практиковались в алгебре: умножьте оба числитель и знаменатель на сопряженные $ \ sqrt {x + 5} + \ sqrt {5} $.
\ begin {align *}
\ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} & = \ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} \ cdot \ dfrac {\ sqrt {x + 5} + \ sqrt {5}} {\ sqrt {x + 5} + \ sqrt {5}} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} \ sqrt {x + 5} + \ sqrt {x + 5} \ sqrt {5} – \ sqrt {5 } \ sqrt {x + 5} – \ sqrt {5} \ sqrt {5}} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ в 0} \ dfrac {(x + 5) – 5} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac { x} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {\ cancel {x}} {\ cancel {x} [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {1} {\ sqrt {x + 5} + \ sqrt {5} } \\ \\
& = \ dfrac {1} {2 \ sqrt {5}} \ quad \ cmark
\ end {align *}
Мы, , гарантируем , что если вы рационализируете выражение, проблемный термин «0» в знаменателе отменит, как здесь.На этом этапе вы можете просто подключить x и готово.

Кстати, обратите внимание, что при переходе от первой строки выше ко второй мы умножили члены в числителях, чтобы избавиться от корней. Но мы не умножали члены в знаменателе, потому что исходное значение x в знаменателе было отменено через несколько шагов.

Итог: Если есть радикалы, рационализируйте.

Конечно вам нужно попрактиковаться.

Конечно, прочитать наши решения недостаточно. Вместо этого вам нужно попрактиковаться – и сделать несколько ошибок для себя, – чтобы все это стало для вас рутиной, когда вы будете сдавать экзамен. У нас есть множество проблем, которые вы можете попробовать, все с комплексными решениями на расстоянии одного клика, поэтому вы можете быстро проверить свою работу (или выйти из строя) без каких-либо проблем.

А пока мы приглашаем вас оставить комментарий ниже:

Какие у вас есть вопросы?
Какими советами вы можете поделиться по решению проблем с ограничениями?
Как мы можем сделать такие сообщения, как этот, более полезными для вас?

Прокомментируйте, пожалуйста, ниже!

1.Пределы и дифференциация

М. Борна

Чтобы понять, что на самом деле происходит в дифференциальном исчислении, нам сначала нужно понять пределы .

Лимиты

При изучении исчисления нас интересует, что происходит со значением функции поскольку независимая переменная очень близка к определенному значению. Мы столкнулись с этой концепцией во введении, где увеличили масштаб кривой, чтобы получить приблизительное значение наклона этой кривой.

Иногда определение предельного значения выражения означает просто подставив число.

Пример 1

Найдите предел, когда t приближается к `10` выражения `P = 3t + 7`.

Ответ

Мы запишем это с использованием обозначения предела как: `lim_ (trarr10) (3t + 7)`

В этом примере нет никаких сложностей – мы просто подставить и написать

`lim_ (trarr10) (3t + 7) = 37`

Нет никаких сложностей, потому что f (t) = 3t + 7 – непрерывная функция.2-2х-3) / (х-3) `

Каково значение функции, когда x приближается к `3`?

Ответ

Мы видим, что функция приближается к определенному значение x приближается к `3` слева:

x	2,5	2,6	2,7	2,8	2,9
f ( x )	3.5	3,6	3,7	3,8	3,9

Продолжая, мы приближаемся к `x = 3`:

x	2,9	2,92	2,94	2,96	2,97	2,98	2,99
f ( x )	3,9	3.92	3,94	3,96	3,97	3,98	3,99

Аналогично, приближение к `x = 3` справа дает то же предельное значение:

3,5

3,1

3,01

3.00001

f ( x )

4,5

4,1

4.2-2х-3) / (х-3) `

`= lim_ (xrarr3) ((x + 1) (x-3)) / (x-3)`

`= lim_ (xrarr3) (x + 1)`

`= 4`

ВНИМАНИЕ: Процесс факторизации возможен только в этом примере, потому что мы имеем: x ≠ 3.

Это типичная проблема при изучении вводных ограничений. Это кажется немного глупым, поскольку мы могли бы его разложить на множители, отменить и заменить x = 3, как мы только что видели. Но пример важен для концепции, что нет фактического значения функции, когда `x = 3`, но если мы действительно очень, очень близко к` 3`, значение функции действительно близко к некоторому значению (`4` , в таком случае).

Пределы как

x Подходы 0

Мы должны помнить, что мы не можем делить на ноль – это неопределенный.

Но есть некоторые интересные и важные ограничения, в которых существует предельное значение, так как x приближается к «0», и где может показаться, что у нас есть знаменатель «0».

Пример 3

Найдите предел, когда x приближается к `0` из` (sin \ x) / x`

Ответ

Обратите внимание, что мы не можем просто подставить 0, потому что `(sin \ 0) / 0` не определено.

Нет никакого алгебраического процесса, чтобы найти этот предел. Мы можем подставить значения x , которые все ближе и ближе к `0` (как с левой, так и с правой стороны), и заключить, что

`lim_ (xrarr0) (sin \ x) / x = 1.`

Способ проверить это – построить график и увидеть, что предел приближения x к «0» действительно равен «1»:

Мы указали, что есть “дыра” в точке x = 0 на нашем графике, используя открытый кружок.

Пределы при приближении

x к бесконечности

Пример 4

Рассмотрим дробь «5 / x».Что происходит как `x -> oo`?

Ответ

Очевидно, что если мы возьмем все большие и большие значения x , значение дроби становится все меньше и меньше, пока не станет очень близко к `0`. 2)) = 0`

Мы используем эти пределы при оценке пределов функций и особенно полезен при построении кривых.

Пример 5

Найдите предел `lim_ (x-> oo) ((5-3x) / (6x + 1)).`

Ответ

На этот раз не так очевидно, каково предельное значение. Мы можно было бы заменить все большие и большие значения x , пока мы мог видеть, что происходит (попробуйте `100`, затем` 1 \ 000`, затем `1 \ 000 \ 000` и так далее).

Или мы могли бы изменить выражение и использовать тот факт, что

`lim_ (x-> oo) (1 / x) = 0`

, чтобы найти предельное значение.

Делим на x , чтобы получить выражение в форме, в которой мы можете оценить это.

`lim_ (x-> oo) ((5-3x) / (6x + 1))`
`= lim_ (x-> oo) ((5 / x-3) / (6 + 1 / x))`
`= (0-3) / (6 + 0)`
`= -1 / 2`

Обратите внимание, что мы не можем подставить ∞ в дробь `((5 / x-3) / (6 + 1))`, потому что это не делает математический смысл.

Пожалуйста, не пишите `((5-3 (oo)) / (6 (oo) +1))`. Это очень расстраивает математиков.2)) `

`= -1 / 8`

Шутка

Объяснив студенту ограничения, я привел ему следующий пример:

Я попытался проверить, действительно ли он это понял, поэтому привел ему другой пример.

Его ответ был:

Непрерывность и дифференциация

В этой главе мы будем дифференцировать многочлены. Но позже мы столкнемся с более сложными функциями, и порой мы не сможем их различить.2-x) ` не определено для` x = 0` и `x = 1`.

В этих точках он прерывается. Следовательно, мы не можем дифференцировать функцию для этих значений.

Функции разделения и дифференциация

Мы встречали функции разделения раньше в главе «Функции и графики».

Функция разделения дифференцируема для всех x , если она непрерывна для всех x .

Пример 7

Мы встречали этот пример в предыдущей главе.2 + 2, текст (для) \ x> = 1):} `

Эта функция имеет разрыв при x = 1, но на самом деле она определена для `x = 1` (и имеет значение` 1`). Он дифференцируемый для всех значений x , кроме «x = 1», поскольку он не является непрерывным при «x = 1».

Непрерывные функции

Все наши функции, описанные в предыдущих главах, посвященных дифференциации и интеграции, будут непрерывно . В следующих главах мы увидим прерывистые функции, особенно функции разделения.(см. Ряд Фурье и преобразования Лапласа)

Далее …

Теперь мы переходим к рассмотрению того, как ограничения применяются к проблеме нахождения скорости изменения функции из первых принципов. Это то же самое, что найти наклон касательной.

Неопределенные формы

Неопределенные формы \ (\ large \ frac {0} {0} \ normalsize \)

Пусть \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) две функции такие, что

\ [{\ lim \ limits_ {x \ to a} f \ left (x \ right) = 0 \; \; \;} \ kern-0.3pt
{\ text {and} \; \; \ lim \ limits_ {x \ to a} g \ left (x \ right) = 0.}
\]

Тогда функция \ (\ large \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \ normalsize \) имеет неопределенный вид \ (\ large \ frac {0 } {0} \ normalsize \) at \ (x = a. \) Чтобы найти предел в \ (x = a \), когда функция \ (\ large \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \ normalsize \) имеет неопределенную форму \ (\ large \ frac {0} {0} \ normalsize \) в этой точке, мы должны разложить числитель и знаменатель на множители, а затем уменьшить условия, приближающиеся к нулю.

Примечание. В этой главе мы не применяем правило L’Hopital.

Неопределенные формы \ (\ large \ frac {\ infty} {\ infty} \ normalsize \)

Пусть \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) две функции такие, что

\ [{\ lim \ limits_ {x \ to a} f \ left (x \ right) = \ pm \ infty \; \; \;} \ kern-0.3pt
{\ text {and} \; \; \ lim \ limits_ {x \ to a} g \ left (x \ right) = \ pm \ infty.}
\]

, где \ (a \), где a – действительное число, или \ (+ \ infty \), или \ (- \ infty. \)

Говорят, что функция \ (\ large \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \ normalsize \) имеет неопределенный вид \ (\ large \ frac {\ infty} {\ infty} \ normalsize \) в этой точке.2} – y – 6}} = \ left [{\ frac {0} {0}} \ right]}
= {\ lim \ limits_ {y \ to – 2} \ frac {{y \ left ({y + 1} \ right) \ cancel {\ left ({y + 2} \ right)}}} {{\ left ({y – 3} \ right) \ cancel {\ left ({y + 2} \ right) }}}}
= {\ lim \ limits_ {y \ to – 2} \ frac {{y \ left ({y + 1} \ right)}} {{y – 3}} = \ frac {{\ lim \ limits_ {y \ to – 2} y \ cdot \ lim \ limits_ {y \ to – 2} \ left ({y + 1} \ right)}} {{\ lim \ limits_ {y \ to – 2} \ left ({y – 3} \ right)}}}
= {\ frac {{- 2 \ cdot \ left ({- 1} \ right)}} {{- 5}} = – \ frac {2} { 5}.}
\]

(по правилам частного и произведения для лимитов).

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.