Как решить по химии задачи: Как решать задачи по химии, готовые решения

“Методика решения расчетных задач с использованием основных физических величин”

Расчётные задачи по химии учащиеся решают с начала VIII класса и до конца обучения в школе. Решение задач позволяет:

• расширять кругозор учащихся;
• развивать умение логически мыслить;
• воспитывать самостоятельность, внимательность, умение анализировать, делать правильные выводы;
• устанавливать связь химии с другими науками: физикой, математикой, биологией, экологией и др.;
• способствует политехнической подготовке учащихся, готовиться к успешной аттестации по предмету (в том числе и в форме ЕГЭ).

Решая задачи, учащиеся более глубоко усваивают учебный материал, учатся применять приобретённые теоретические знания на практике.

Традиционная методика обучения решения химических задач (чаще всего – это решение задач методом составления пропорций) имеет ряд недостатков. В результате лишь немногие учащиеся сознательно и творчески овладевают общим подходом к решению, умеют оценивать свои действия в процессе решения, самостоятельно составлять условия задач, умеют выбирать рациональные способы решения и др.

Представленная методика обучения решения задач от общих приёмов к частным позволяет решить недостатки традиционных способов обучения. В данной работе показываются приёмы решения задач с использованием основных физических величин. Среди них величина n (или ν) – количество вещества – позволяет связать все основные физические величины друг с другом. Это даёт возможность составлять логические схемы решения задач с использованием этих физических величин.

Задача учителя состоит в том, чтобы научить учащихся понимать смысл этих физических величин и применять физические формулы при решении расчётных задач различных типов, научить анализировать условия задач, через составление логической схемы решения конкретной задачи на основе знания общего подхода к решению. Составление логической схемы задачи предотвращает многие ошибки, которые допускают учащиеся.

Ниже приведены основные формулы физических величин и их взаимосвязи, которые учащиеся должны знать в обязательном порядке и использовать их при решении.

В данной работе показываются примеры решения некоторых основных типов задач, по которым можно понять методический подход при обучении учащихся.

Исходные формулы, отображающие взаимосвязь физических величин.

1. Относительная атомная масса (Ar):

, где x – любой химический элемент.

2. Относительная молекулярная масса (Mr): ;

.

3. Плотность вещества (ρ) позволяет связать собой массу (m) и объем (V) вещества: .

4. Масса, объем, число частиц (N), количество теплоты (Q) связаны между собой универсальной физической величиной – количеством вещества – n(или ν):

5. Относительная плотность (D):

6. Массовая доля ω:

элемента в веществе: ; ;

примеси в веществе: ;

растворенного вещества в растворе: ; mр-ра = mр.в.+ mр-ля

mр-ра=Vр-ра· ρр-ра.

7. Объемная доля вещества в смеси (φ) (для газов): .

8. Молярная концентрация (Сm или С): .

9. Уравнение Клапейрона – Менделеева: . 

Методика решения задач различных типов.
Расчеты по химическим формулам.

Решение данного типа задач начинается с осмысления понятия записи химической формулы, с осмыслением того, что учащиеся могут узнать по записи химической формулы. Рассмотрим примеры решения задач с использованием веществ только молекулярного строения. Молекулярная (истинная) формула показывает действительное число атомов каждого элемента в молекуле. В таблице №1 показано, какие сведения о веществе можно узнать по записи формулы вещества.

Таблица № 1.

Алгоритм решения базовой задачи.

1. Заданный по условиям параметр переводим в количество вещества (n или ν).
2. По индексам определяем количество вещества искомого химического элемента (n(х) или ν(х)).
3. По формулам, отображающим взаимосвязь величин, рассчитываем неизвестный параметр.  

Графическая схема решения базовой задачи.

 

Примеры задач

Задача 1. Рассчитайте число атомов углерода и кислорода в 11,2 л. (н.у.) углекислого газа.

Задача 2. В каком объеме углекислого газа содержится 9,03·1023 атомов кислорода?

Какова его масса?

Задача 3. Газ, плотность которого равна 1,96 г/л (н.у.), состоит из углерода и кислорода, причем ω(C) = 0,27. Определите формулу данного вещества.

Логическая схема решения задачи:

Расчёты по химическим уравнениям.

Химическими уравнениями называют условную запись химической реакции посредством химических знаков, формул и коэффициентов.

Уравнение химической реакции показывает, какие вещества вступают в реакцию и какие образуются, а также соотношение количеств этих веществ. Иными словами, химическое уравнение – это способ выражения (передачи) качественной и количественной информации о химическом явлении.

Запишем уравнение реакции в общем виде: aA + bB ® cC +dD, где А и В – исходные вещества, С и D – продукты реакции, a, b, c, d – стехиометрические коэффициенты.

Стехиометрические коэффициенты подбирают на основе того, что число атомов каждого элемента до и после реакции остается неизменным. Это можно рассматривать как следствие закона сохранения массы.

Рассмотрим информацию, содержащуюся в стехиометрических коэффициентах.

Отношение стехиометрических коэффициентов равно:

отношению числа частиц, вступивших в реакцию и образовавшихся в результате реакции

a : b : c : d = N(A) : N(B) : N(C) : N(D)

отношению молярных количеств веществ, вступивших в реакцию и образовавшихся в результате реакции a : b : c : d = n(A) : n(B) : n(C) : n(D)

отношению объемов, вступивших в реакцию и образовавшихся в результате реакции газообразных веществ a : b : c : d = V(A) : V(B) : V(C) : V(D).

Последнее отношение выполняется, если:

1. это газообразные вещества, близкие по свойствам к идеальному газу,
2. объемы этих газов измерены при одинаковом давлении и температуре.

Несмотря на большое разнообразие задач данного типа, принцип решения их одинаков: по известному параметру (N, m, V) одного вещества рассчитывается неизвестный параметр X (Nx, mx, Vx) другого вещества. Такая задача является простейшей (базовой).

Алгоритм решения базовой задачи (последовательность действий).

1. Составляем уравнение химической реакции и выписываем мольные соотношения прореагировавших и получившихся веществ.
2. По формулам, отображающим взаимосвязь физических величин, переводим заданную по условию величину в количество (n или ν) исходного вещества.
3. По мольным отношениям рассчитываем n определяемого вещества (Х).
4. По формулам, отображающим взаимосвязь физических величин, рассчитываем неизвестный параметр X.

Графическая схема решения базовой задачи.

В качестве базовых рассмотрим решение следующих задач:

Задача 1. Вычислите n, m, V углекислого газа, полученного при действии на 50 г карбоната кальция избытком раствора соляной кислоты.

Задача 2. При взаимодействии цинка с избытком раствора соляной кислоты выделилось 1,12 л водорода (н.у.). Вычислите массы растворившегося цинка и образовавшейся соли.

Задача 3. При взаимодействии с избытком соляной кислоты металла (валентность, которого во всех соединениях равна II) массой 12 г образовался водород объемом 6,72 л (н.у.).

Определите, какой это металл.

Усложнение базовой задачи.

Расчет массы реагирующих или образующихся химических соединений на практике осложнен. Это обусловлено несколькими причинами:

1. Исходные вещества или продукты реакции задаются в условиях отличных от нормальных.
2. Исходные вещества вводятся в виде растворов.
3. Во многих случаях реагенты содержат примеси, которые в данной конкретной реакции либо не участвуют вообще, либо образуют отличные от целевого продукта вещества.
4. Выход продуктов не соответствует теоретическому, т.к. очистка целевого вещества приводит не только к освобождению от многочисленных примесей, но и к частичной потери основного вещества.

Таким образом, перед использованием исходных данных для решения задачи и подстановки их в основную цепь расчетов необходимо провести те или иные дополнительные преобразования. Для перевода условий, отличных от нормальных (для газообразных веществ) используется исходная формула 9 – расчеты физико-химических величин по управлению Клапейрона – Менделеева.

1. Исходные вещества вводятся в виде раствора.

Задача. Сколько граммов 10%-ного раствора гидроксида натрия требуется для нейтрализации

20 г 4,9%-нго раствора серной кислоты?

2. Расчет количественных параметров продуктов реакции, если исходные вещества содержат примеси, расчет массовой доли примеси.

Абсолютно чистого вещества в природе не бывает, поэтому в химических производствах вынуждены использовать исходные вещества, содержащие примеси. Эти примеси обычно имеют отличные от основного вещества свойства и, поэтому не образуют в процессе производства нужные продукты.

В связи с этим, чтобы определить количественные параметры получаемого продукта, необходимо вначале рассчитать количественные параметры вступающего в реакцию чистого вещества, которое содержится в исходном объекте. После этого решается базовая задача.

Обратные задачи заключаются в оценке чистоты исходных веществ по количеству продуктов реакции.

Содержание примеси обычно выражают в частях от единицы (или выражают в %). Эта величина показывает массовую долю чистого вещества (примеси) в исходном образе (формула 1).

Для вычисления массы чистого вещества (или примесей), содержащегося в смеси, используют формулу 2.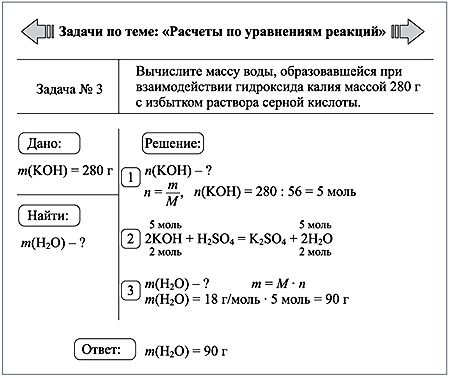

(1)

m(смеси) = m(осн.в.) + m(прим.) (2)

Задача. При взаимодействии 10,8 г кальцинированной соды (безводный карбонат натрия)

с избытком раствора соляной кислоты получили 2,24 л (н.у.) оксида углерода (IV).

Вычислите содержание примеси в соде.

3. Расчеты по химическим уравнениям, если одно из реагирующих веществ дано в избытке.

Как быть, если одновременно заданы параметры нескольких реагирующих веществ? По какому из них вести расчет? Это определяют, сравнения отношения стехиометрических коэффициентов и отношение количеств вещества, взятых для данной реакции.

Если один из реагентов присутствует в количестве больше, чем стехиометрическое, то часть его остается неиспользованной после окончания реакции (избыток вещества). Очевидно, что расчеты нужно вести по веществу, которое в данной реакции расходуется полностью (т.е. находится в недостатке).

Задача. В реакционном сосуде смешали 6,72 л оксида углерода (II) и 2,24 л кислорода и смесь подожгли. Определите объемный состав полученной смеси.

Используемая литература:

1. Кузнецова Н.Е., Лёвкин А.Н. Задачники по химии для учащихся 8 и 9 классов общеобразовательных учреждений. М.: Вентана-Граф, 2008.
2. Лидин Р.А., Аликберова Л.Ю. Химия: Справочник для старшеклассников и поступающих в вузы – М.: АСТ-ПРЕСС ШКОЛА, 2002.
3. Лидин Р.А., Аликберова Л.Ю. Задачи, вопросы и упражнения по химии: 8-11 кл.: Пособие для учащихся общеобразовательных учреждений. – М.: Просвещение, 2002.

Решение задач по химии, 8-11 классы: Решения, методики, советы (Иван Хомченко)

335 ₽

230 ₽

+ до 50 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии больше 30 шт.

В наличии в 330 магазинах. Смотреть на карте

51

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Настоящее издание является дополнением к книге И. Г. Хомченко “Сборник задач и упражнений для средней школы” (М., 1996-2007). В нем даны решения типовых задач из указанного выше сборника, а также задач, вызывающих наибольшие трудности у преподавателей и учащихся. Издание предназначено для преподавателей химии, а также может быть рекомендовано для самостоятельной работы при подготовке к поступлению в вуз. .

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Решение задач по химии, 8-11 классы: Решения, методики, советы» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Иван Хомченко «Решение задач по химии, 8-11 классы: Решения, методики, советы» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Насколько хорош ChatGPT в химии? | Иван Резников

Недавно я использовал ChatGPT для проверки его возможностей на задачах, которые теоретически могут быть решены с помощью языковой модели. Ранее я публиковал сообщение LinkedIn об использовании ChatGPT для решения проблем с викторинами в пабах, но мне удалось решить только 0 из 5 из них.

Я также написал статью об использовании ChatGPT для объяснения дебюта в шахматах.

Я видел успешные эксперименты, в которых ChatGPT смог пройти кодирование и другие тесты, связанные с ИТ. Мне любопытно посмотреть, насколько хорошо модель языка шумихи справляется с решением простого химического уравнения. В частности, я попрошу ChatGPT предсказать результат химической реакции, классифицировать ее и сбалансировать коэффициенты.

Будет протестирована простая реакция горения натрия. Как можно заметить, ChatGPT правильно отвечает «в результате реакции натрия и кислорода образуется оксид натрия (Na2O)». Система может быть не такой точной, когда ее запрашивают о конкретной информации, но, похоже, она адекватна своим общим ответам.

ОК. Хотя инструкция по балансировке правильная, сама балансировка плохая. С другой стороны, если модель полагает, что с обеих сторон есть атомы 2Na, она правильно рассчитала баланс. Мы попытаемся переубедить ChatGPT, указав количество атомов натрия и перебалансировав уравнение.

Если 2 атома натрия слева и 4 атома натрия справа, произойдут ли какие-либо изменения?

Нет. Текстовая модель ChatGPT уверена, что баланс правильный. К сожалению нет.

С точки зрения машинного обучения малая вероятность появления неверного уравнения в данном случае может рассматриваться как признак отсутствия переобучения. Это означает, что коэффициенты действительно генерируются, что интересно.

К нашему удивлению, модель чата, казалось, не знала о реакции, которую мы обсуждали ранее. Напомним ему.

Несмотря на первоначальные сомнения, реакция была правильно классифицирована и объяснение правильное. Удивительно, что модель смогла набрать 2 правильных ответа из 3. Это может навести на мысль, что у модели есть какие-то познания в химии, но так ли это на самом деле?

Химик не заботится о балансировке уравнения. Мы создадим несколько вымышленных элементов, чтобы отбросить модель. Не может быть, чтобы он видел нашу реакцию раньше.

Промах.

Еще один промах. Он также не может ни классифицировать, ни уравновесить неверную реакцию. Хотя ответ вполне очевиден для любого химика.

В моей предыдущей статье « Насколько хорошо ChatGPT играет в шахматы? » Я обсуждал концепцию зловещей долины применительно к моделям машинного обучения.

ChatGPT, например, предназначен для того, чтобы отвечать на вопросы по-человечески, но он не всегда точен. Крайне важно тщательно проверять и проверять результаты языковых моделей, чтобы не попасть в пропасть и не использовать такие модели для целей, выходящих за рамки их предполагаемой функции.

Напоминаем, что на снимке экрана ниже показан пример впечатляющего, но полностью фальшивого вывода ChatGPT.

До следующего раза!

#chatgpt #chatgpt3 #openai #machinelearning #datascience #ml #ds #nlp #language #chemistry #lifesciences #lifescience

Об авторе: кандидат наук, ведущий специалист по данным.
Дополнительный контент: https://www.linkedin.com/in/reznikovivan/

[PDF] Решение стехиометрических задач по химии в средней школе

• Schmidt1994СтехиометрическийPS, title={Решение стехиометрических задач по химии в средней школе}, автор = {Х. Дж. Шмидт}, journal={Международный журнал научного образования}, год = {1994}, объем = {16}, страницы = {191-200} }
  • H. Schmidt
  • Опубликовано 1 марта 1994 г.
  • Образование
  • International Journal of Science Education

  стратегии решения проблем учащихся. Настоящее исследование было частью более комплексного исследования, в ходе которого 7441 немецкому старшекласснику было предложено выполнить 154 задания теста по 10 различным темам. Случайная выборка из 7441 учащегося, состоящая из 4181 человека, выполнила бумажно-карандашные тесты по стехиометрии. Дополнительно…

  Посмотреть через издатель

  files.erc.ed.gov

  Стратегии студентов в решении алгоритмических проблем стехиометрии

  • H. Schmidt, Cecilia Jignéus

  • . заключалась в том, чтобы выяснить, будут ли шведские студенты вести себя аналогично тому, что описано в литературе, и как они меняют стратегии при переходе от простой для расчета задачи к более сложному вопросу.

    Стратегии решения проблем студентов в стехиометрии и их связь с концептуальным пониманием и подходами к обучению

    • Саума Бужауд, Хала Баракат

    • Образование

    • 2003
    определенные типы стратегий решения проблем и что подавляющее число используемых стратегий были алгоритмическими с очень небольшим количеством эффективных.

    Дилеммы студентов в реакции стехиометрия Решение проблем: вывести ограниченный реагент в химических реакциях

    • A. L. Chandrasegaran, D. Treagust, B. Waldrip, Antonia Chandrasegaran

    • . ограниченная уверенность во время решения проблем для определения ограничивающего реагента и выполнения связанных вычислений по сравнению с несколькими результатами, опубликованными в исследовательской литературе.

      Результаты опроса как основа для разработки ступенчатых вспомогательных инструментов для решения стехиометрических задач

      • М. Фах, Т. Д. Бур, И. Парчманн

      • Образование

      • 2007

      , был разработан набор ступенчатых вспомогательных инструментов (SST), основанный на результатах опроса, исследующего фазы процессов решения немецких школьников по этим проблемам.

      Тайский 10 и 11 класс, понимание стехиометрии и связанных с ними концепций

      • Чаньях Дахса, Р. Кол –

      • Образование

      • 2008

      . Исследование в этом случае. Исследование. Изучение Стихоме. тайских учащихся 10-х и 11-х классов после масштабной реформы национальной учебной программы.…

      Альтернативный путь к решению стехиометрических задач

      • Х. Шмидт

      • Образование

      • 1997

      В этой статье будет обсуждаться альтернативный путь обучения вводной стехиометрии, основанный на результатах исследований, и дана рекомендация использовать такие задачи, которые легко решить. решается быстрым умственным расчетом.

      Изучение стратегий решения проблем учителей химии: на пути к разработке основы преподавания стехиометрии

      • Аллен А. Эспиноса, Р. К. Н. Эспанья, А. Марасиган

      • Образование

      • 2016

      Результаты показывают, что эти учителя химии до начала работы имеют тенденцию преподавать стехиометрию, используя только метод кротов, и что они могут придерживаться альтернативной концепции числа Авогадро, когда начинают свою преподавательскую карьеру. .

      Взаимосвязь между структурой знаний учащихся и стратегией решения задач в стехиометрических задачах на основе химического уравнения

      • Z. Tóth, A. Sebestyén

      • Образование. 11 Осмысление стехиометрической химии учащимися

        • Анита Джон Филип, Гави дю Туа, Кобус Ван Бреда

        • Образование, материаловедение

          European Journal of STEM Education

        • 2023

        Это исследование под названием «Влияние компьютерного моделирования на концептуализацию стехиометрической химии учащимися 11 класса» было проведено в школе округа Фрэнсис Баард Северного…

        Влияние использования явного общего подхода к обучению решению проблем на способность учителей начальной школы решать проблемы теплопередачи.

        • Ллойд М. Матака, В. В. Коберн, Меган Л. Грунерт, Хасинта М. Мутамбуки, Джордж Аком

        • Образование

        • 2014

        В этом исследовании изучается эффективность добавления «явной общей стратегии обучения решению проблем» (EGPS) к управляемому опросу (GI) о способности учителей начальной школы решать…

        ПОКАЗАНО 1-6 ИЗ 6 ССЫЛОК

        Стратегии учащихся средней школы в стехиометрии

        • Х. Шмидт

        • Образование

        • 1990

        – вопросы на выбор по стехиометрическим задачам и моделям рассуждений учащихся и (2) изучить…

        Навыки решения задач у школьников-химиков

        • D. Gabel, R. Sherwood, L. Enochs

        • Образование

        • 1984

        Какие стратегии используют школьники при решении задач по химии? Целью проведения данного исследования было определить общие навыки решения задач, которые учащиеся используют при решении…

        Решение задач и химическое равновесие: успешное и неудачное выполнение

        • Moises Camacho, R. Good

        • Образование

        • 1989

        Целью данного исследования было описание поведения экспертов и новичков при решении семи проблем химического равновесия. Тринадцать новичков (пять старшеклассников,…

        Когнитивное развитие и решение проблем афроамериканских учащихся по химии

        • Мэри М.